Interday Stability of Taxi Travel Flow in Urban Areas
Abstract
1. Introduction
2. Related Studies
3. Methodology
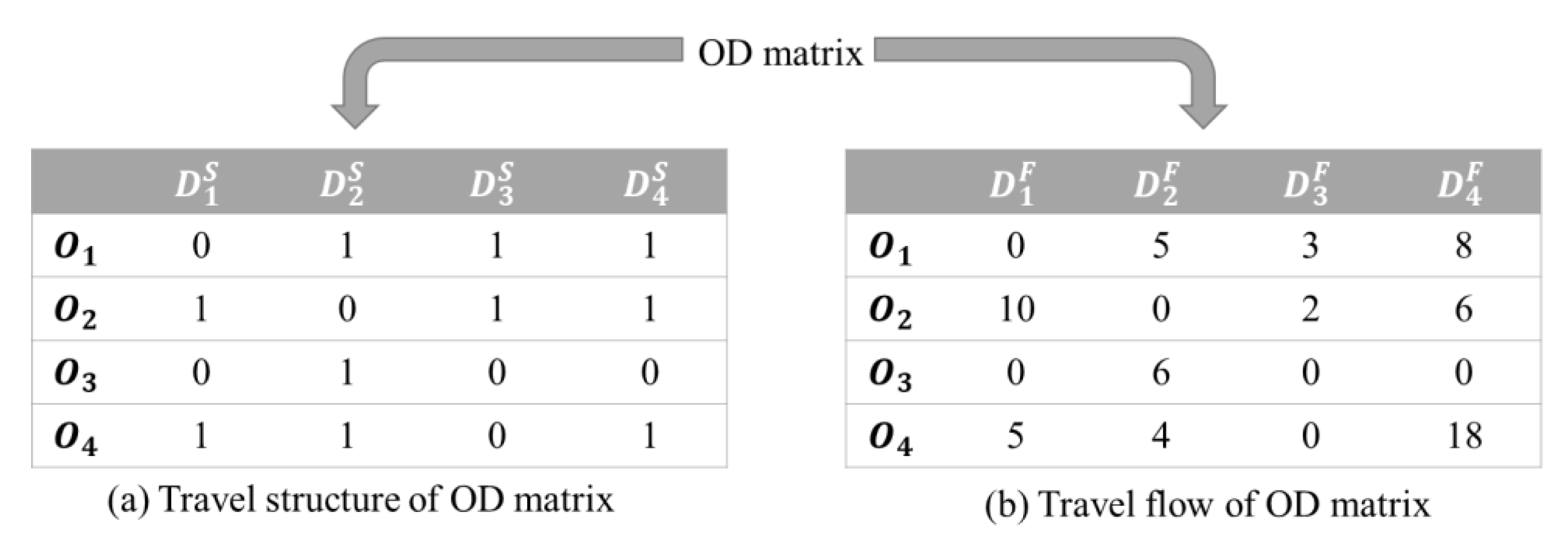
3.1. OD Matrix Construction
3.2. Stability Measurement of the Travel Spatial Structure and Flow
- (1)
- Structural similarity
- (2)
- Flow similarity
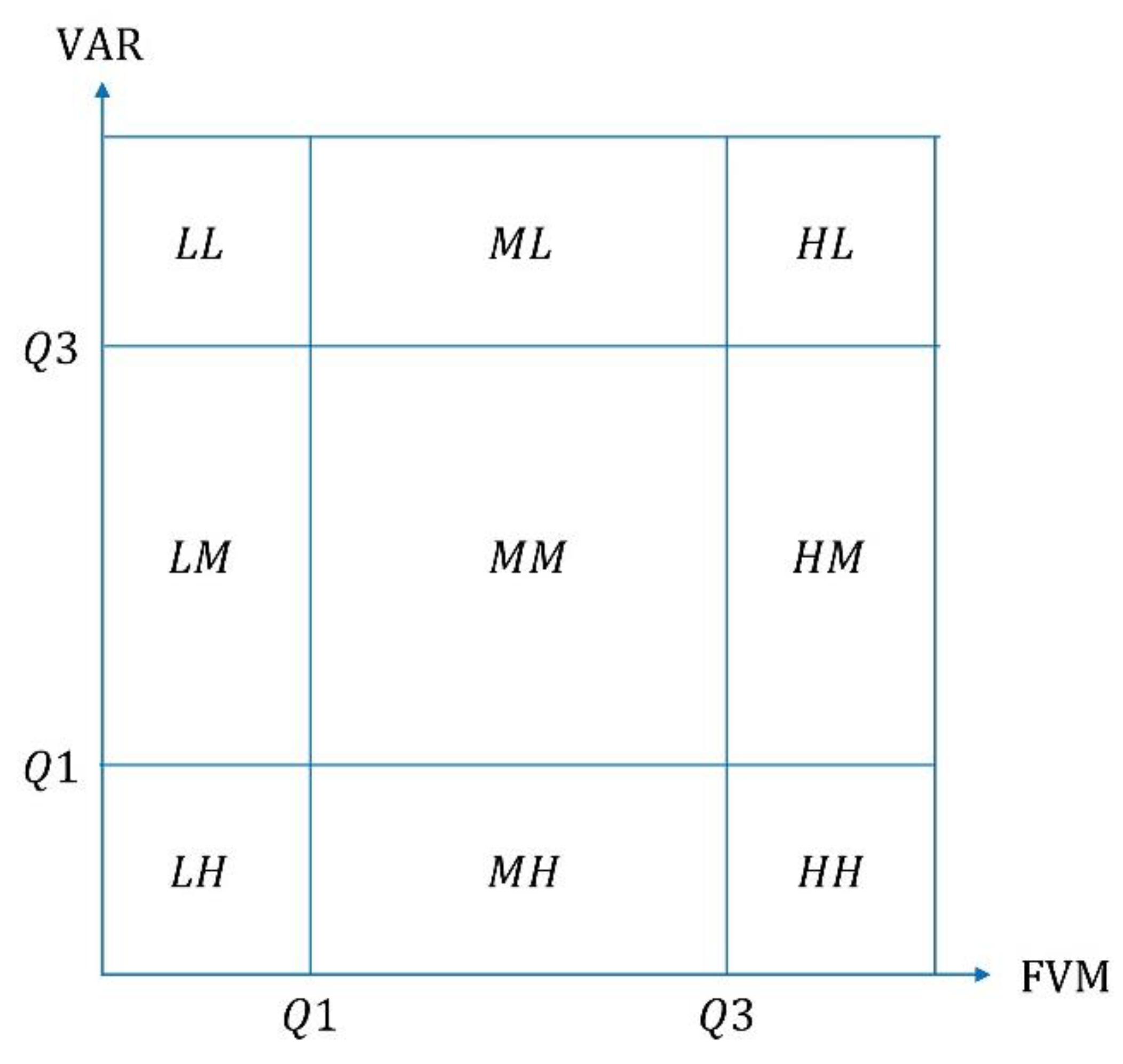
3.3. Stability Measurement of Each OD Flow
4. Data
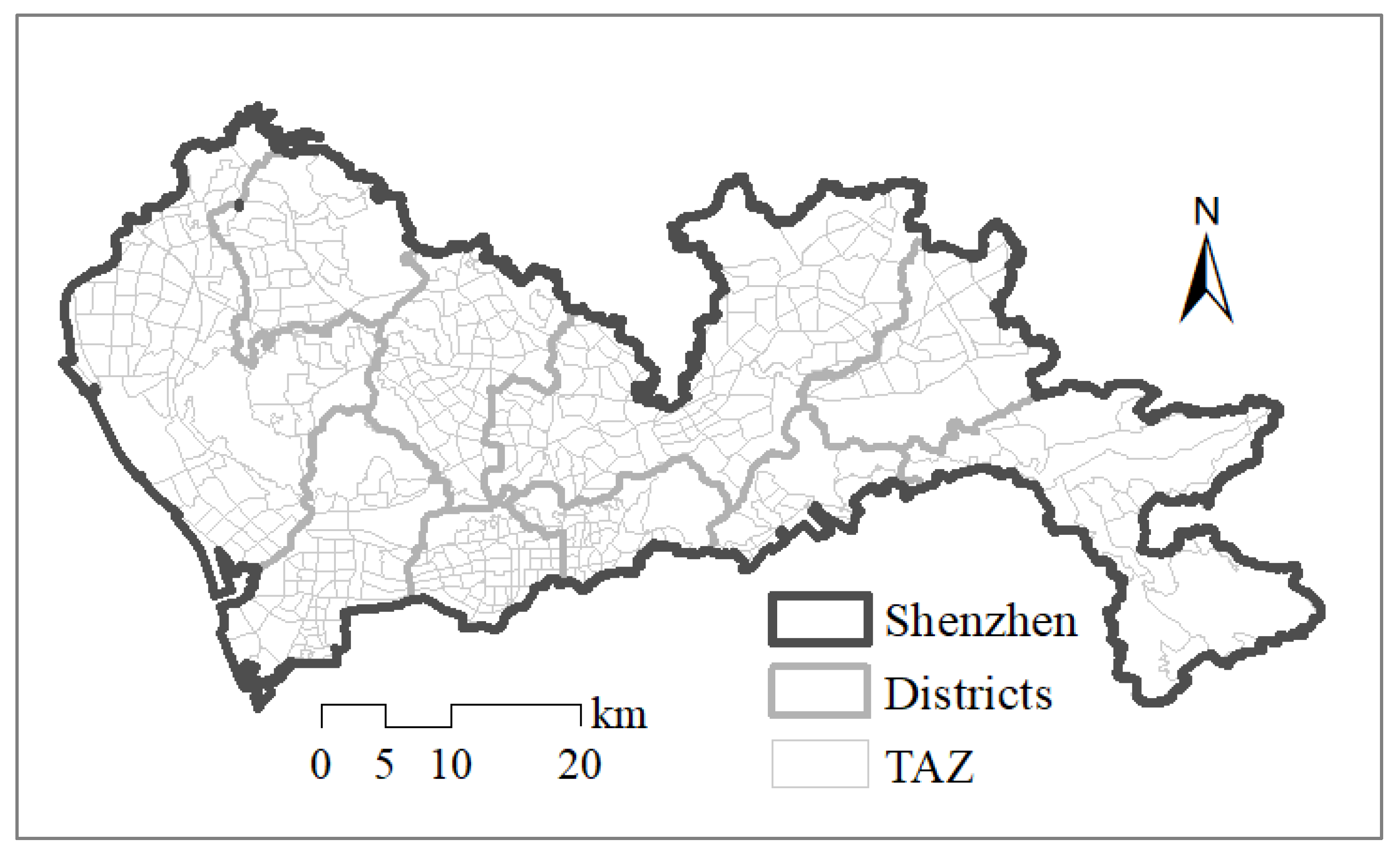
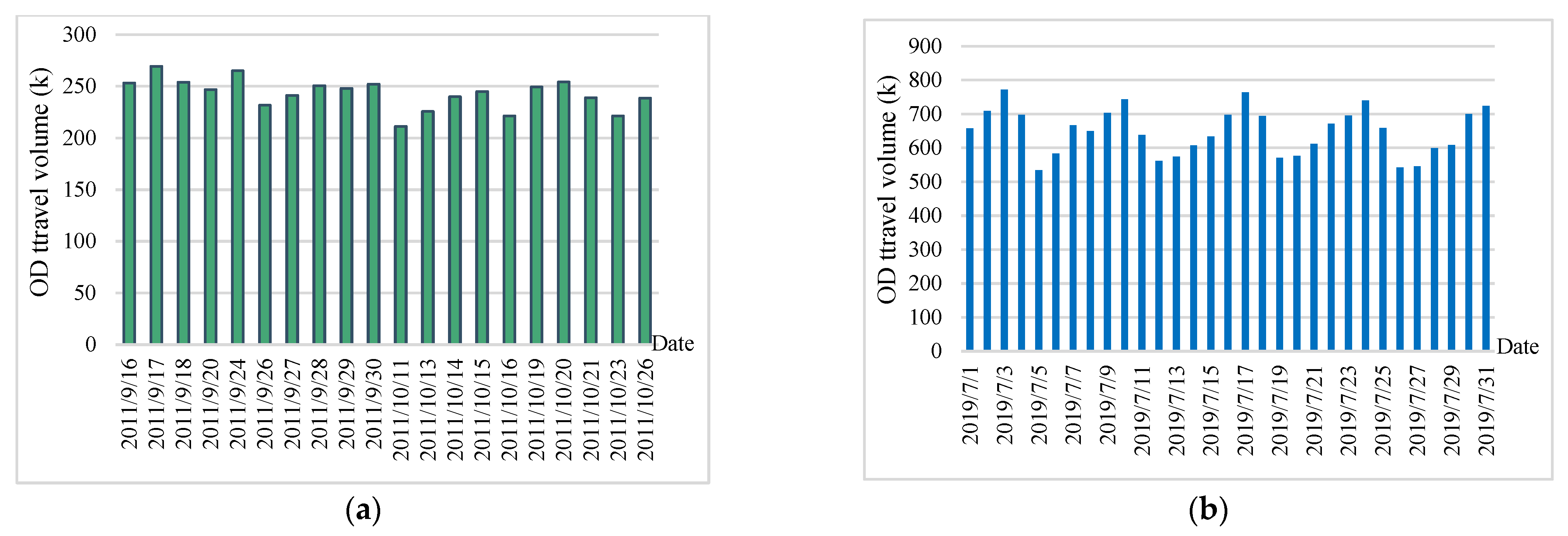
4.1. Dataset of Shenzhen
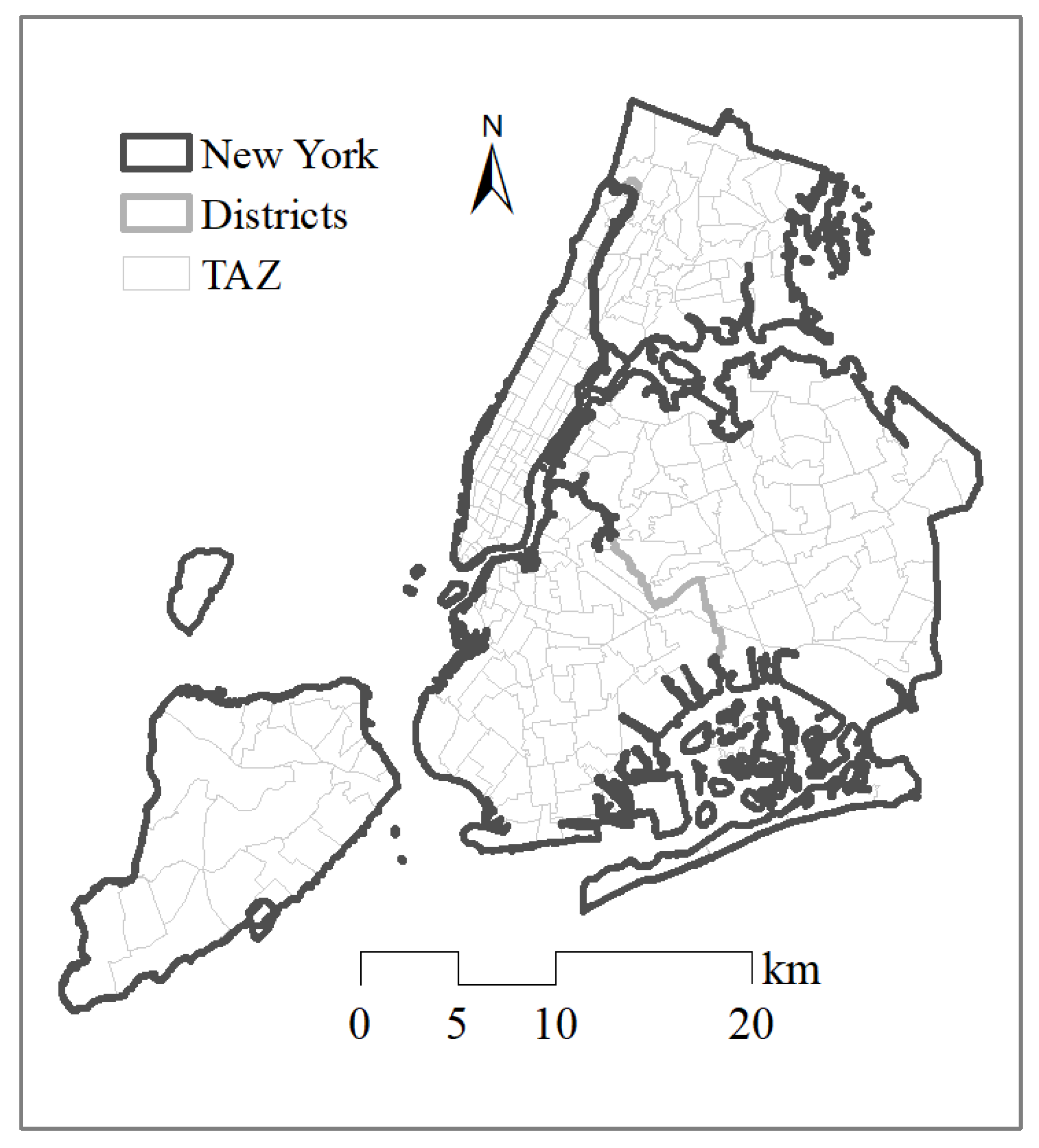
4.2. Dataset of New York
5. Results
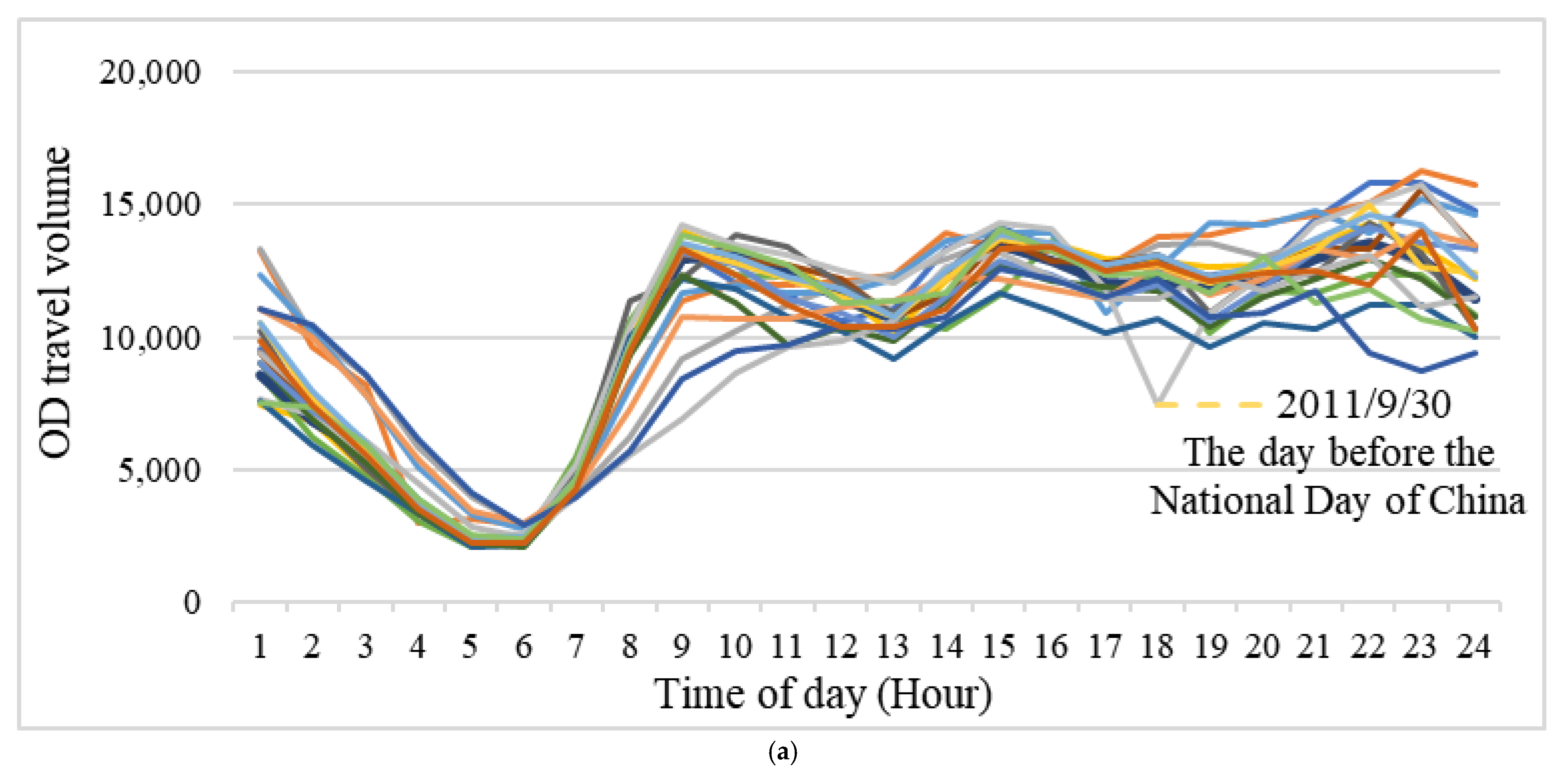
5.1. Volume and Distance Characteristics of Interday Taxi Travel
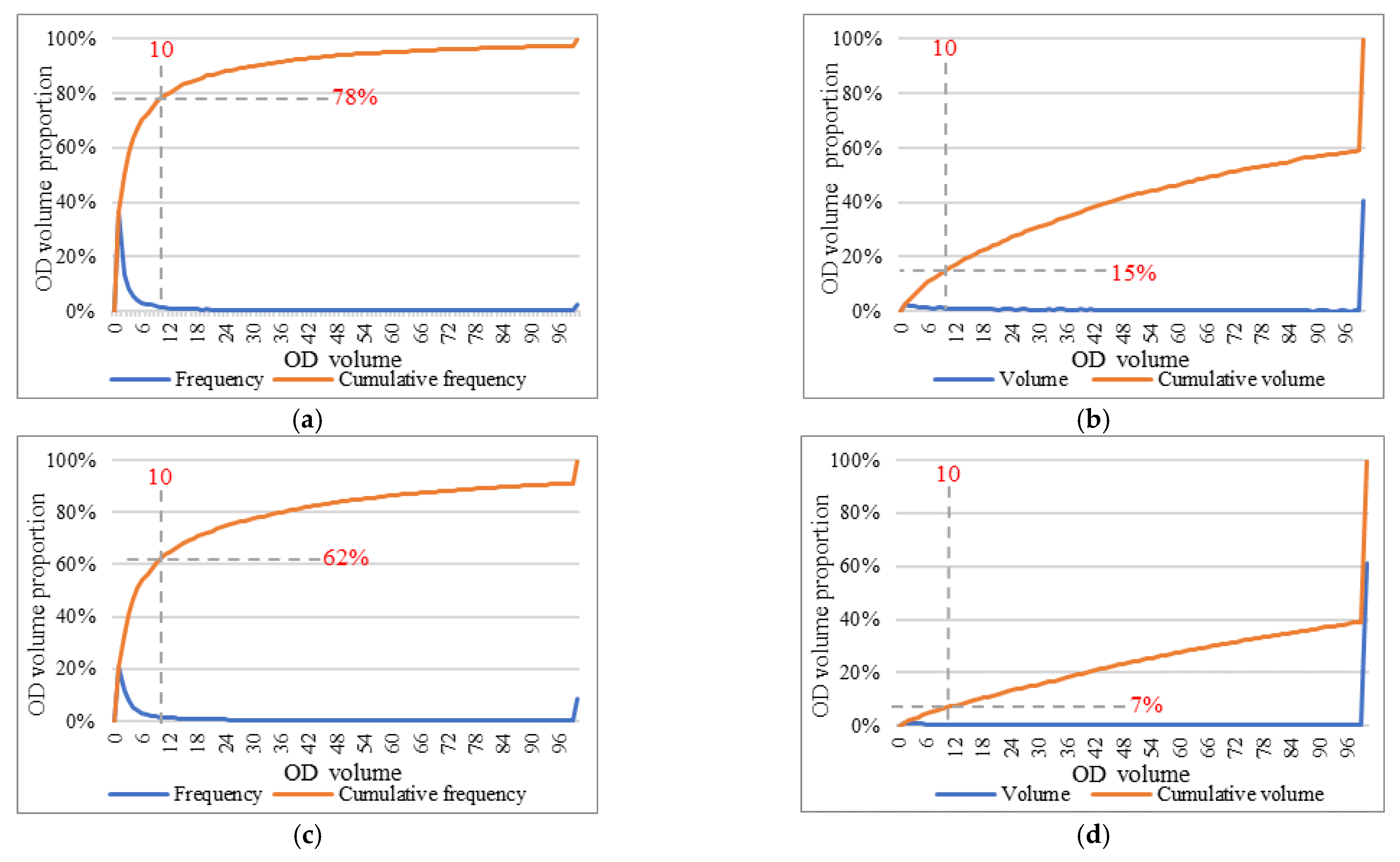
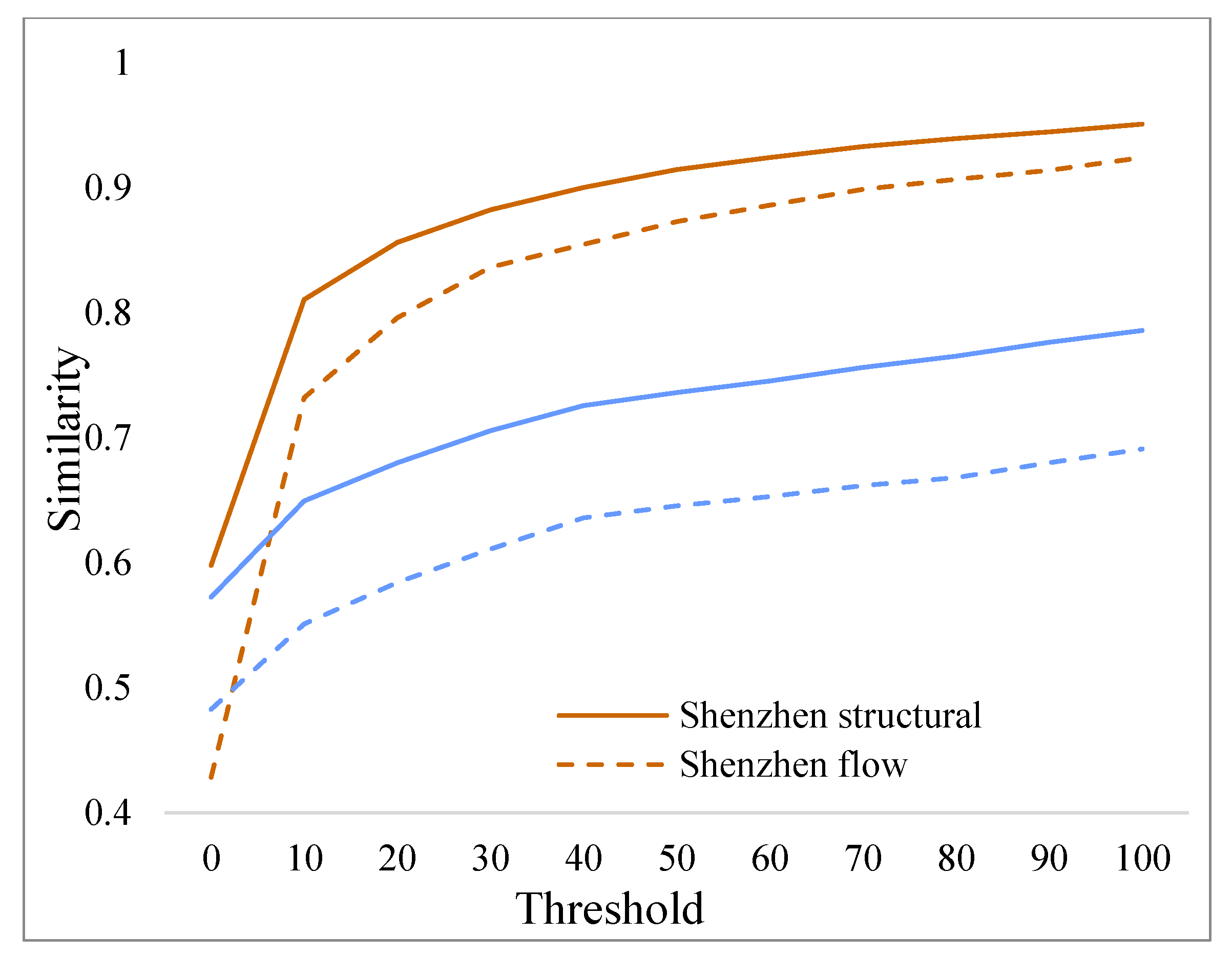
5.2. Influence of the Flow Threshold on the Similarity in the Travel OD Flow Matrix
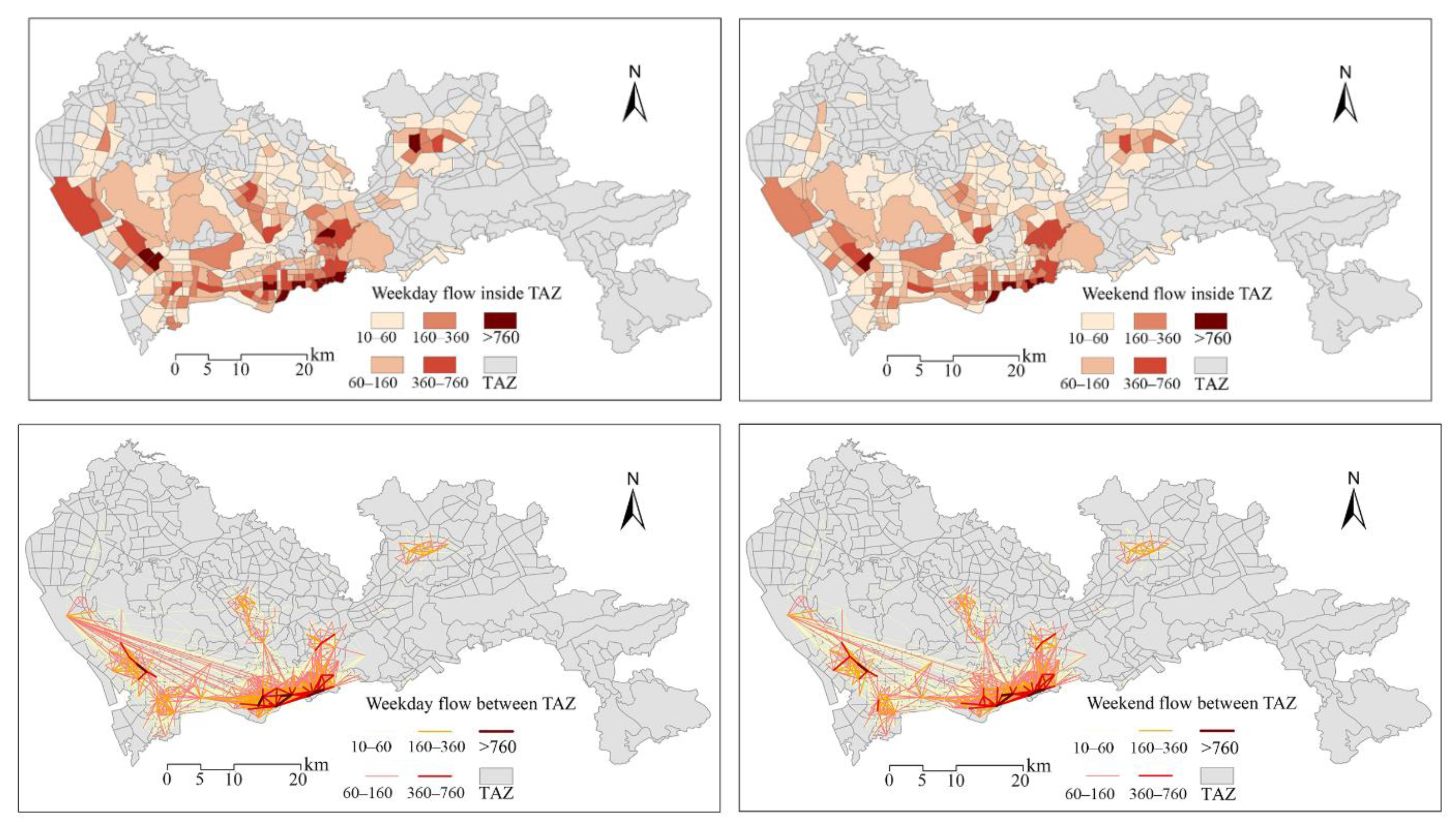
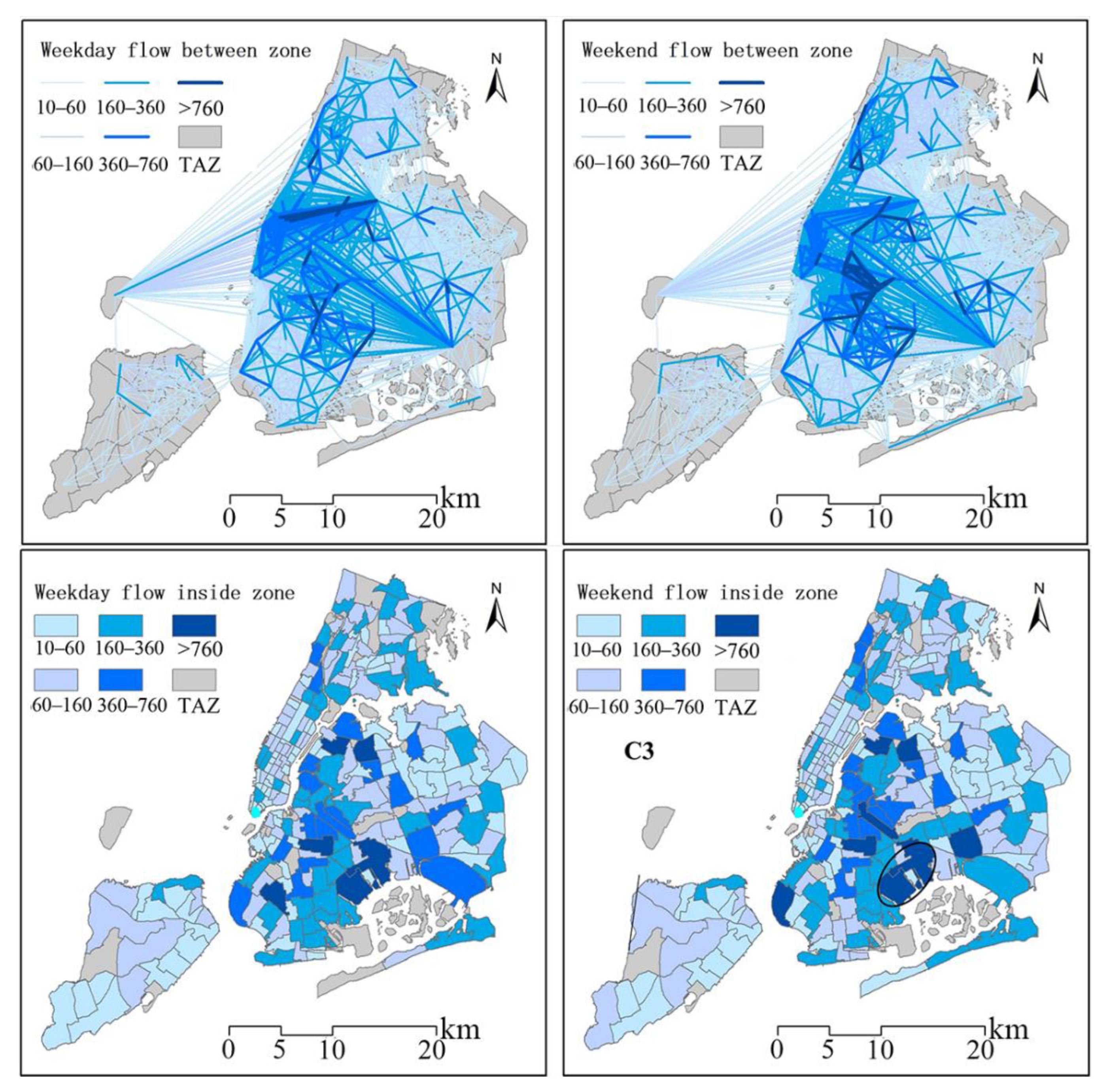
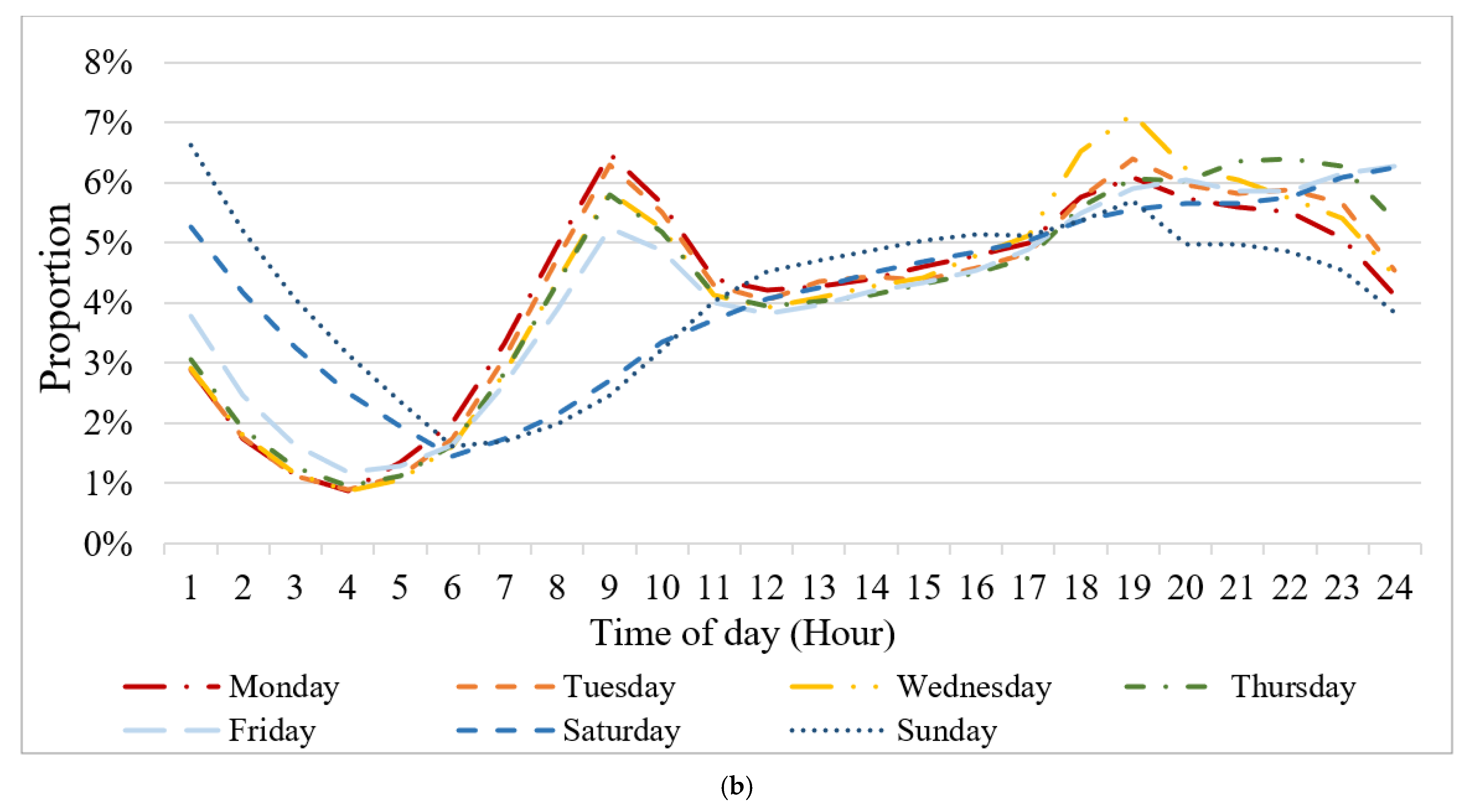
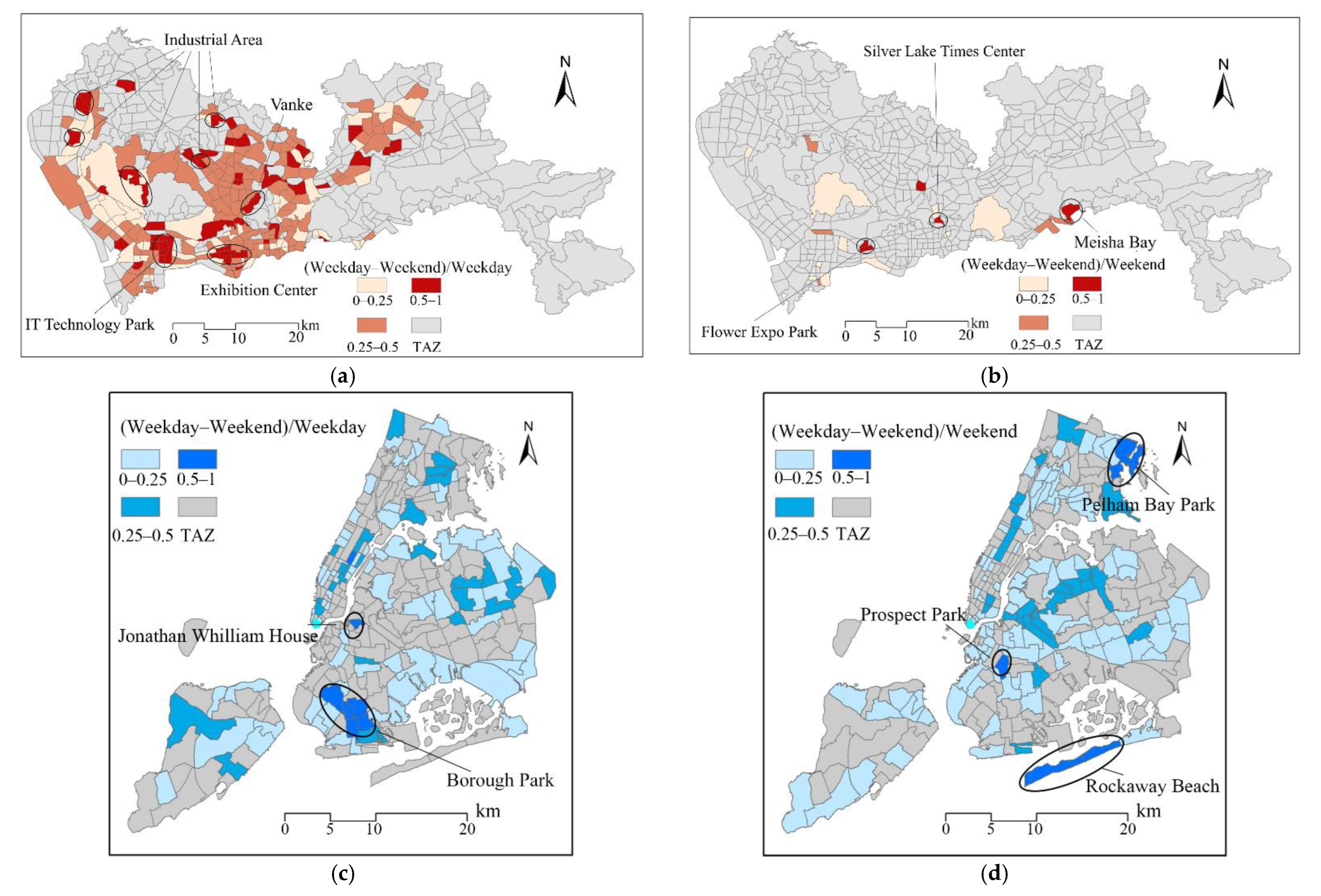
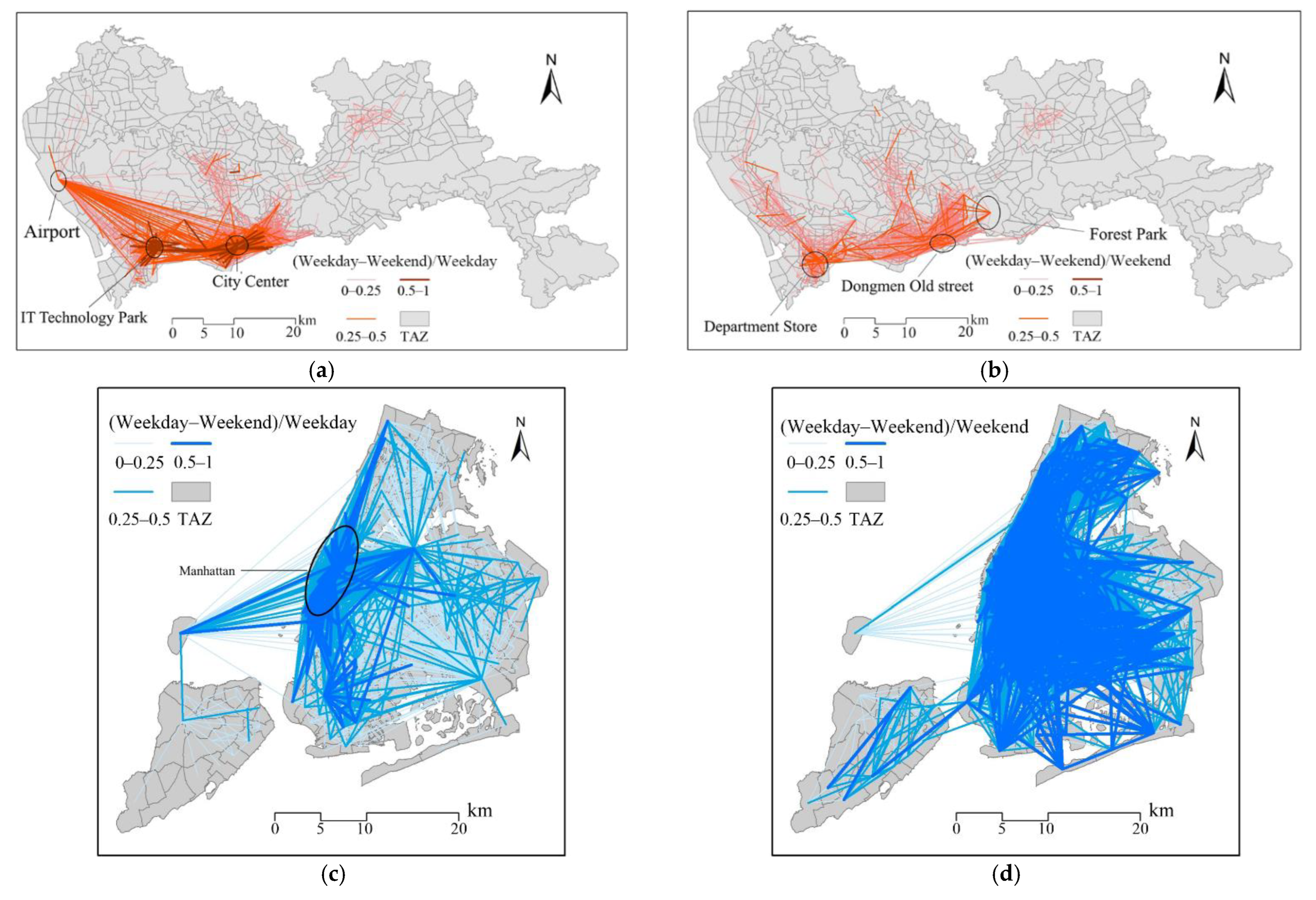
5.3. Stability of Travel Spatial Structure and Flow between Weekdays and Weekends
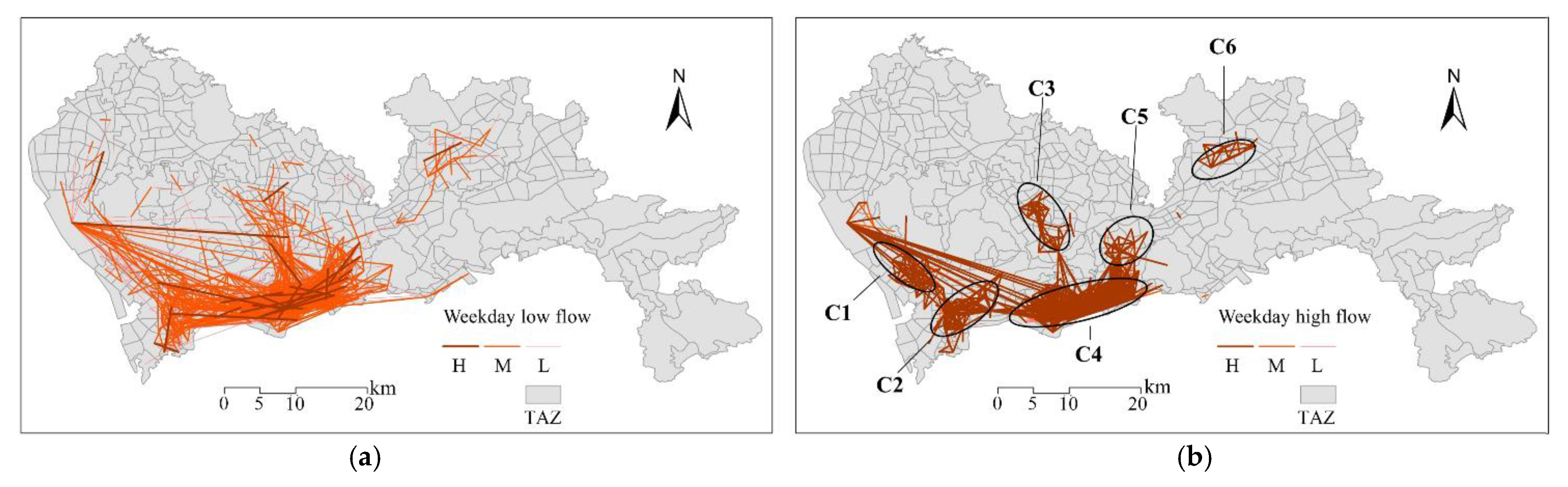
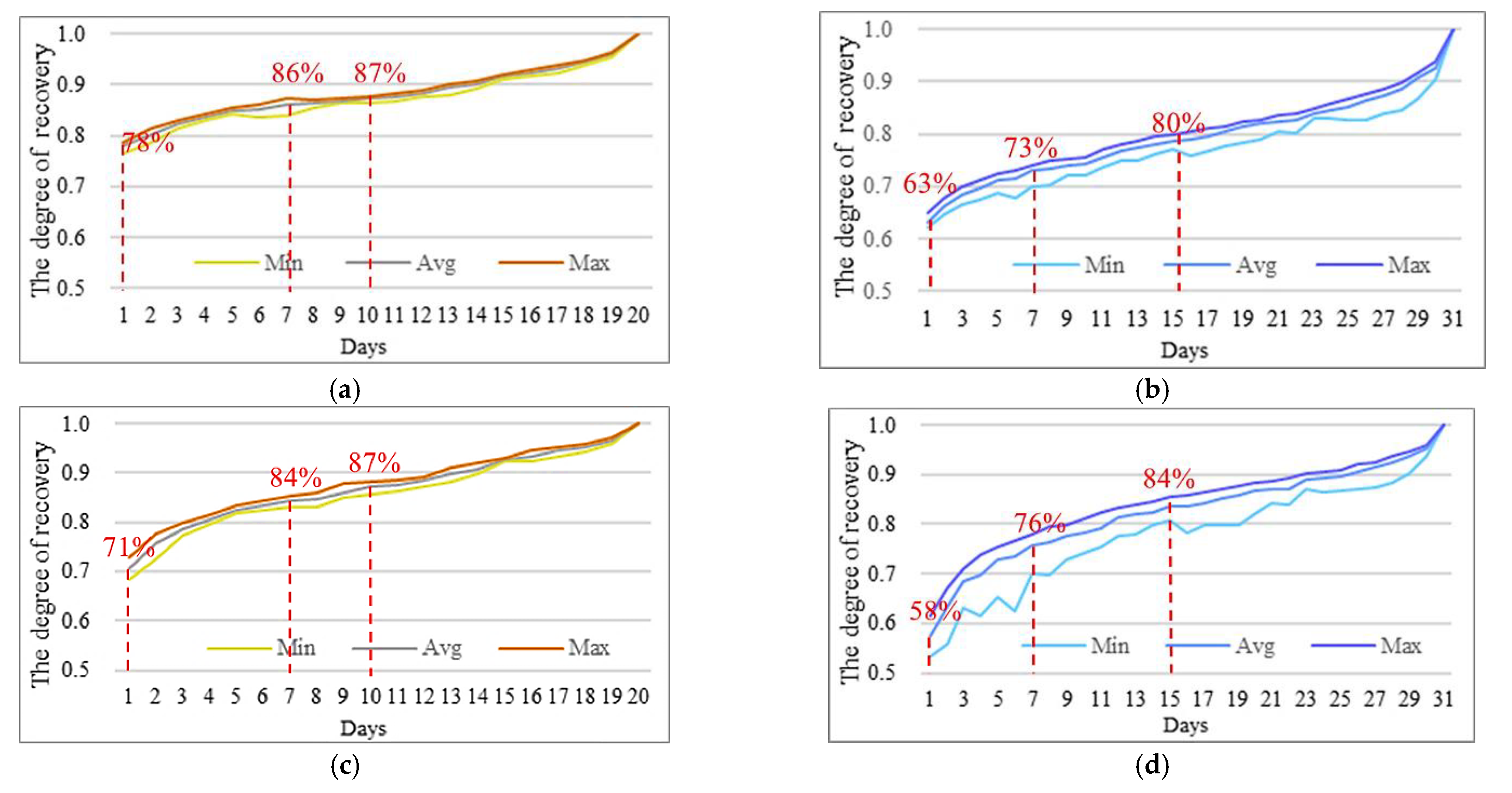
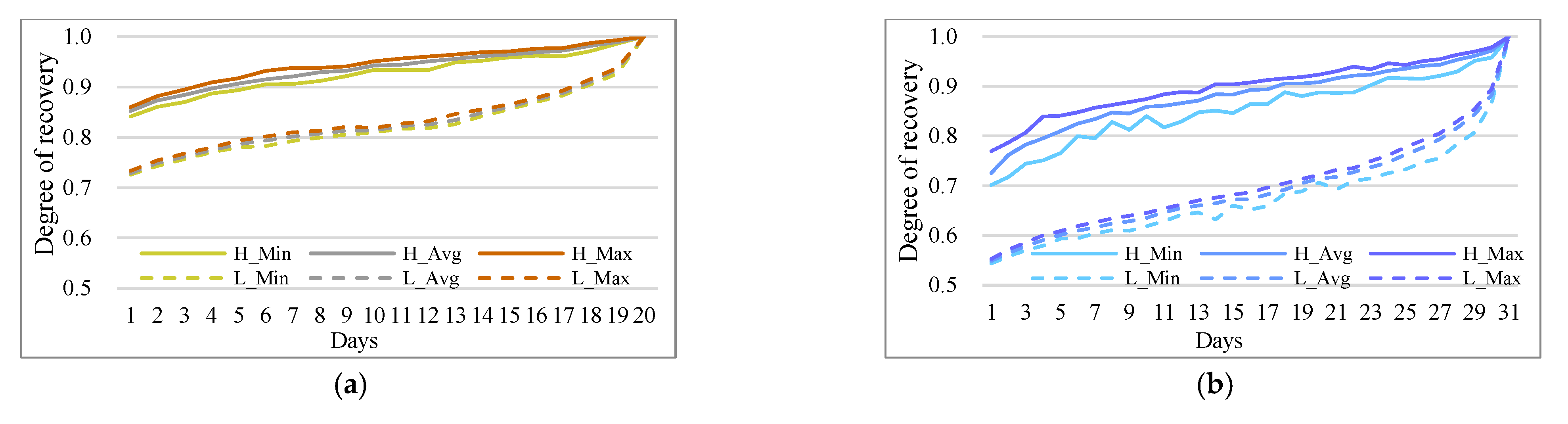
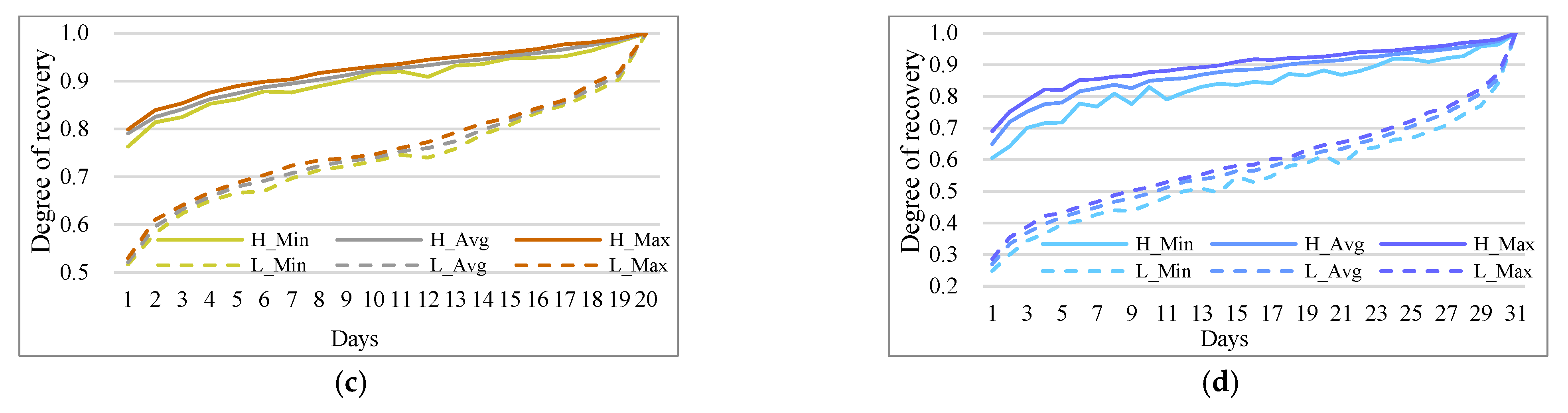
5.4. Stability of OD Flows between Days
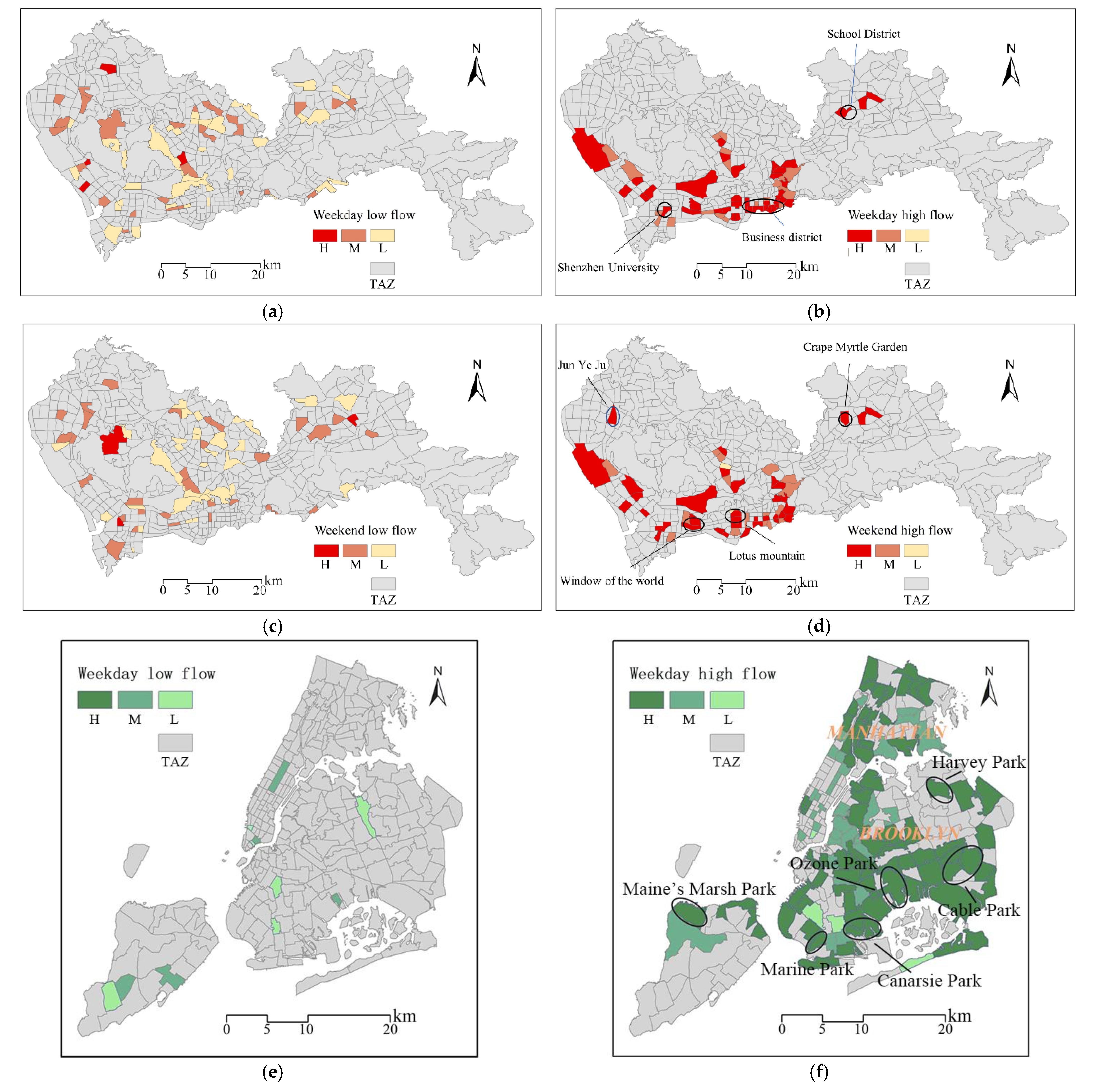
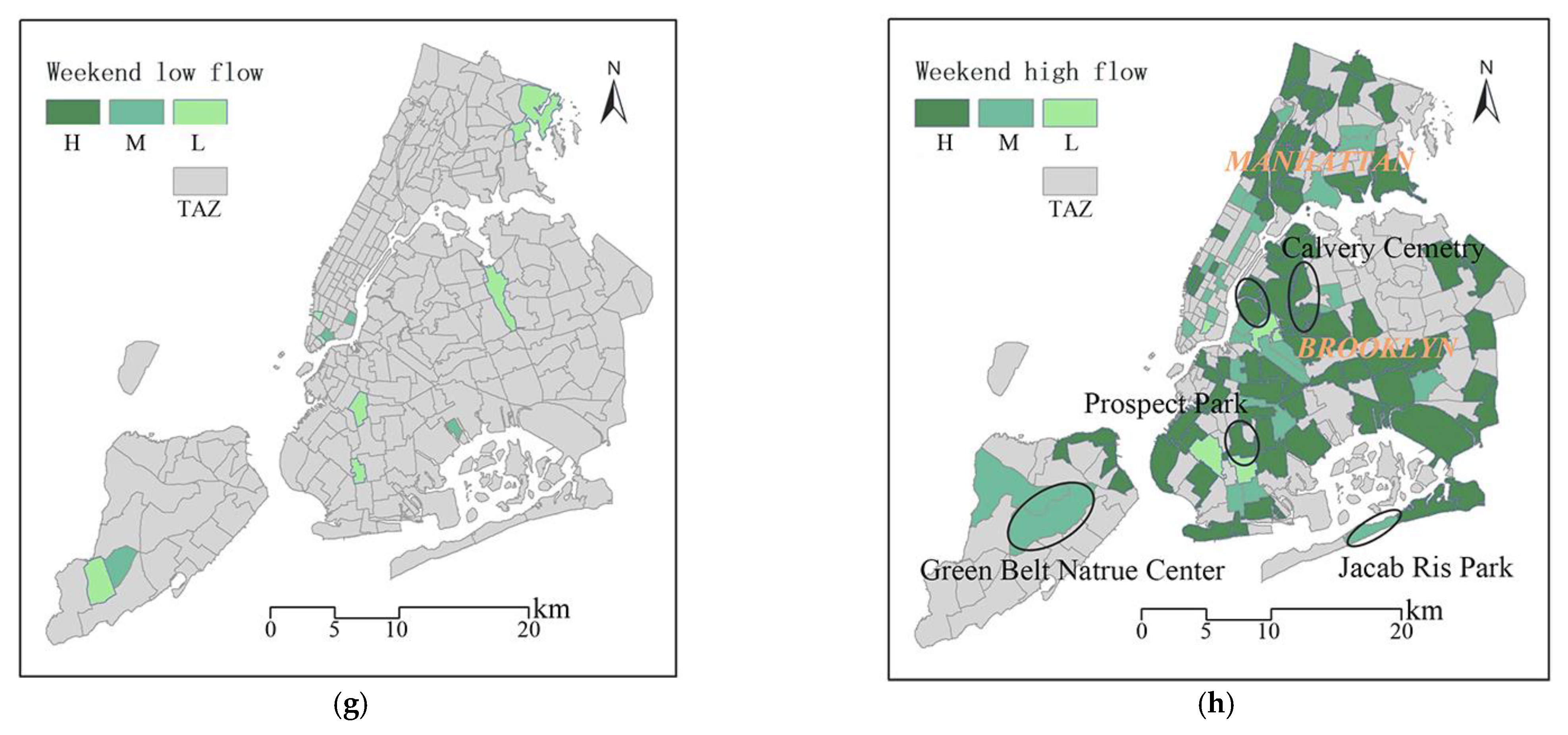
5.5. Representative Data Analysis
6. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Original Data Feature Analysis and Screening
- (1)
- Interday period characteristics of positioning points
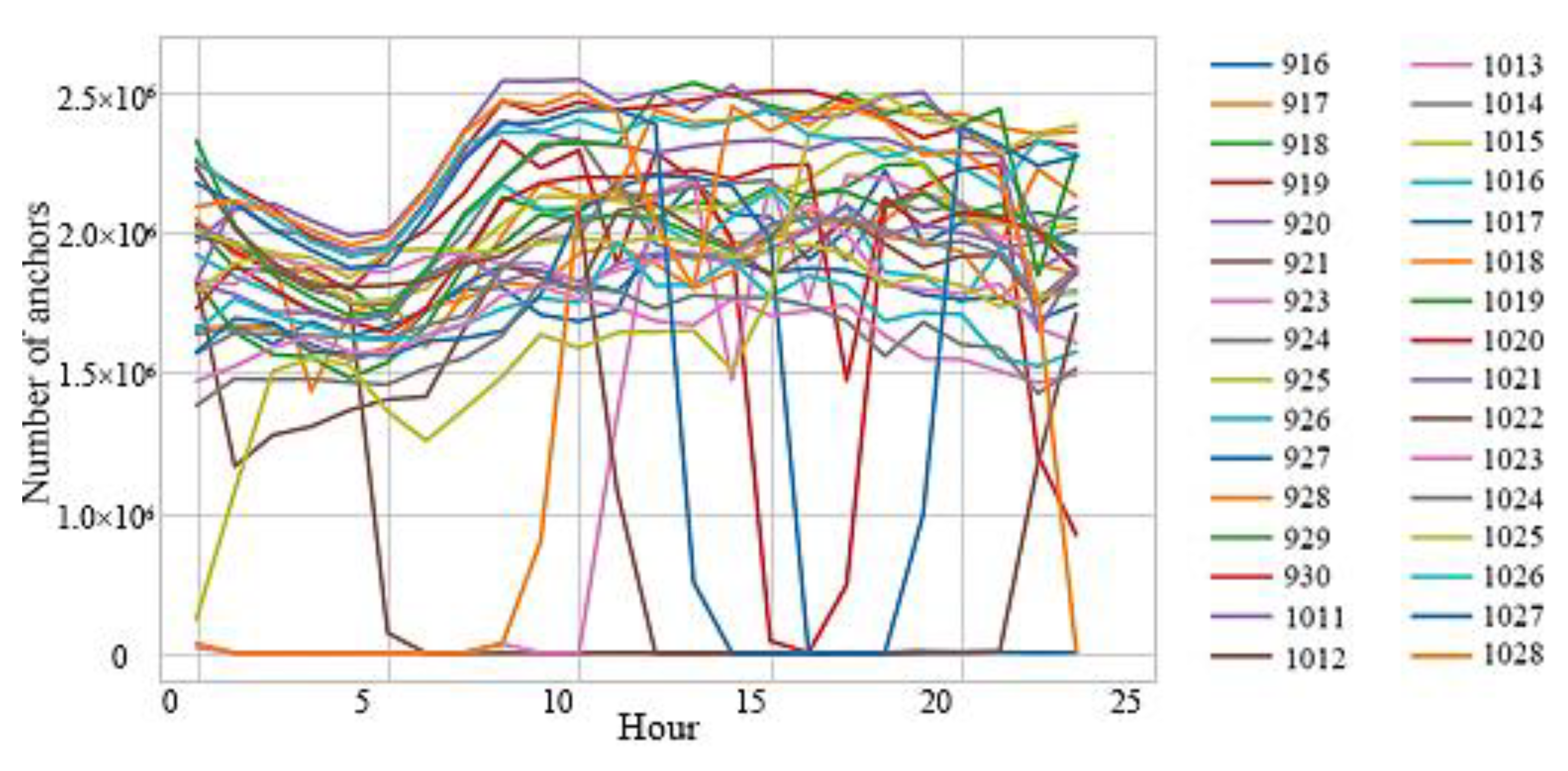
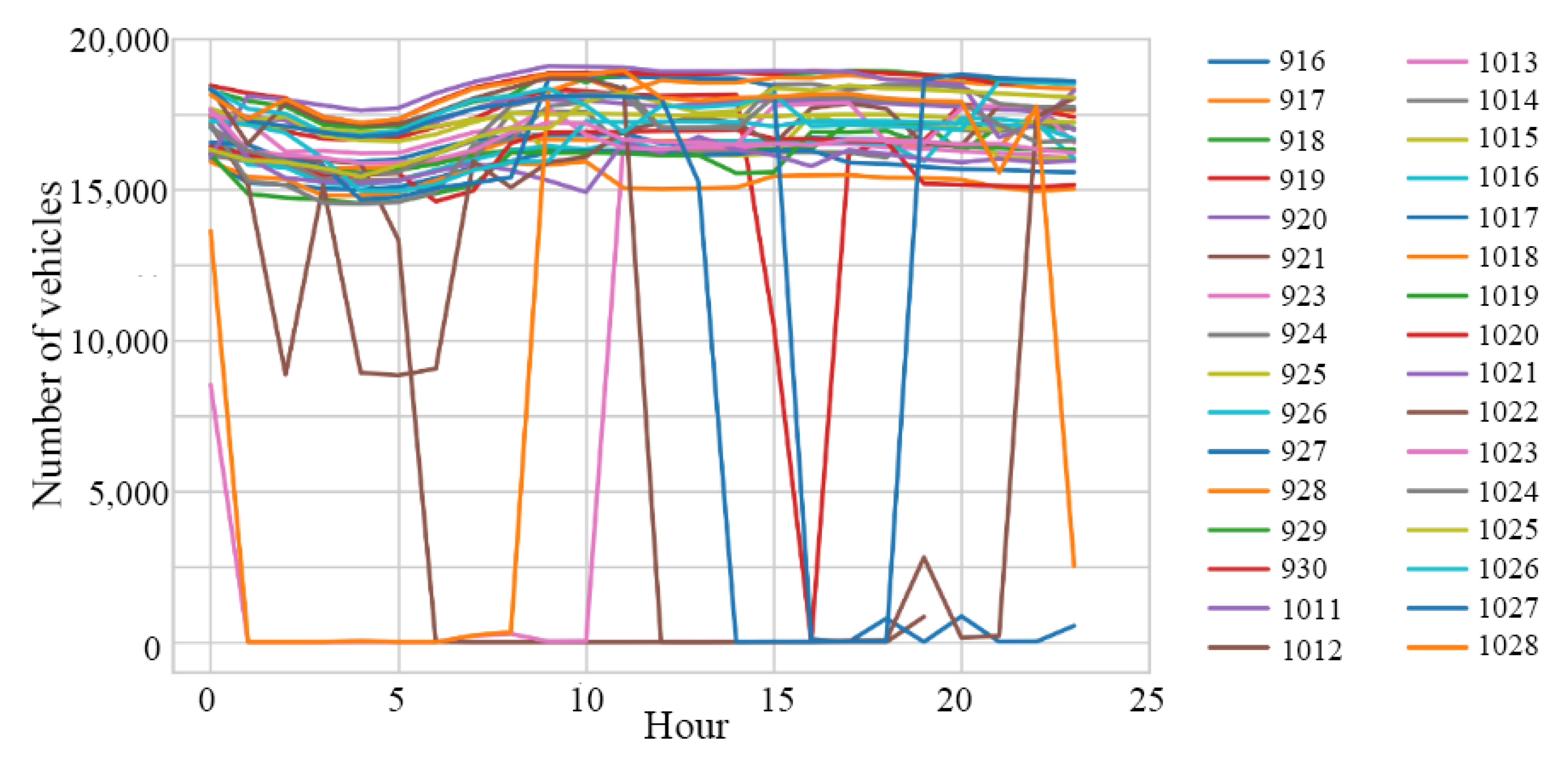
- (2)
- Interday period characteristics of the number of vehicles
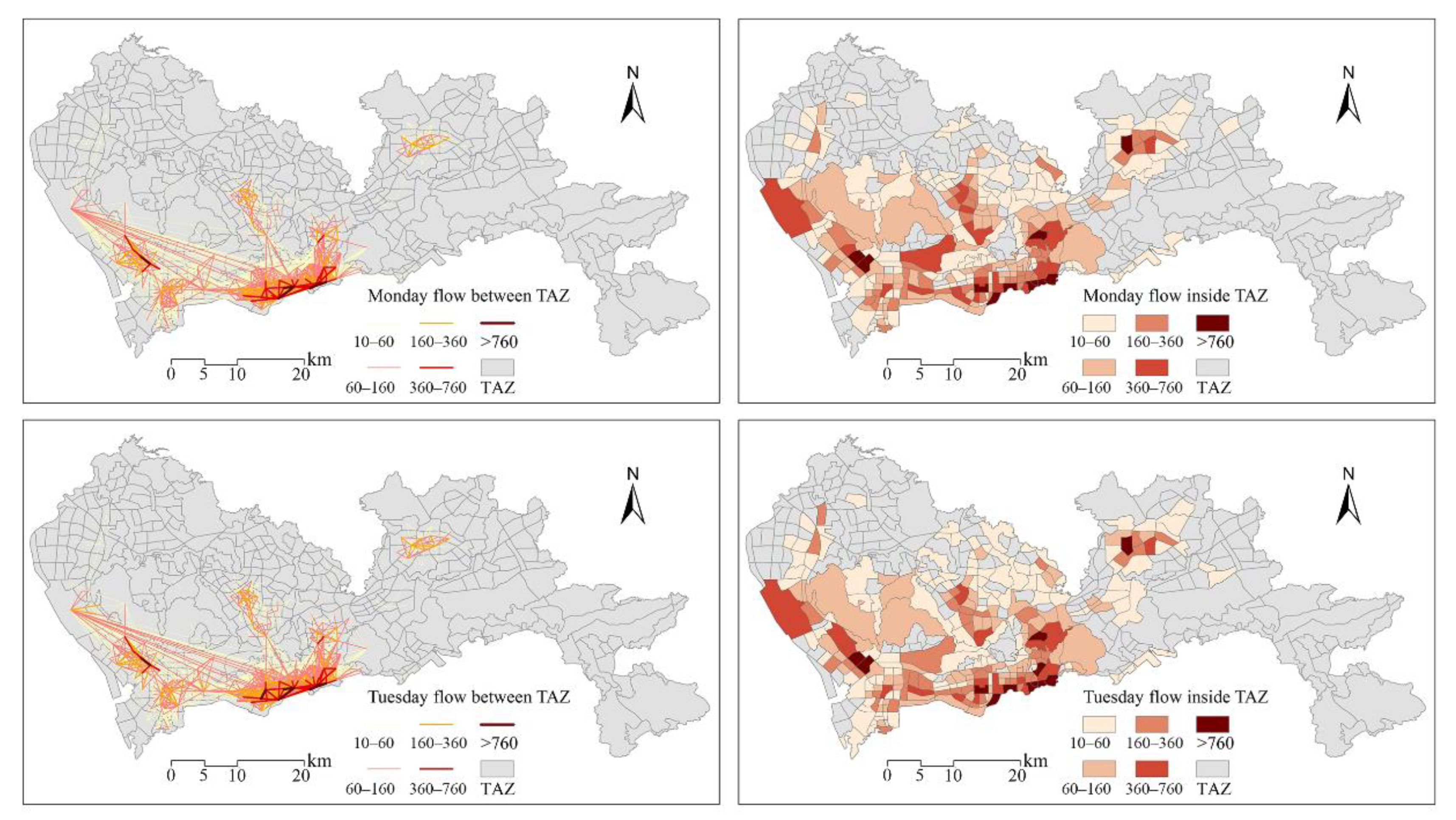
Appendix B. Daily OD Distribution
References
- Angrist, J.D.; Caldwell, S.; Hall, J.V. Uber versus taxi: A driver’s eye view. Am. Econ. J. Appl. Econ. 2021, 13, 272–308. [Google Scholar] [CrossRef]
- Bao, J.; Yang, Z.; Zeng, W.; Shi, X. Exploring the spatial impacts of human activities on urban traffic crashes using multi-source big data. J. Transp. Geogr. 2021, 94, 103118. [Google Scholar] [CrossRef]
- Behara, K.N.; Bhaskar, A.; Chung, E. A DBSCAN-based framework to mine travel patterns from origin-destination matrices: Proof-of-concept on proxy static OD from Brisbane. Transp. Res. Part C Emerg. Technol. 2021, 131, 103370. [Google Scholar] [CrossRef]
- Behara, K.; Bhaskar, A.; Chung, E. A novel approach for the structural comparison of origin-destination matrices: Levenshtein distance. Transp. Res. Part C Emerg. Technol. 2020, 111, 513–530. [Google Scholar] [CrossRef]
- Cai, H.; Zhan, X.; Zhu, J.; Jia, X.; Chiu, A.S.; Xu, M. Understanding taxi travel patterns. Phys. A Stat. Mech. its Appl. 2016, 457, 590–597. [Google Scholar] [CrossRef]
- Chen, F.; Yin, Z.; Ye, Y.; Sun, D. Taxi hailing choice behavior and economic benefit analysis of emission reduction based on multi-mode travel big data. Transp. Policy 2020, 97, 73–84. [Google Scholar] [CrossRef]
- Chen, X.; Xie, J.; Xiao, C.; Lu, B.; Shan, J. Recurrent origin–destination network for exploration of human periodic collective dynamics. Trans. GIS 2022, 26, 317–340. [Google Scholar] [CrossRef]
- Cheng, T.; Adepeju, M. Modifiable Temporal Unit Problem (MTUP) and Its Effect on Space-Time Cluster Detection. PLoS ONE 2014, 9, e100465. [Google Scholar] [CrossRef]
- Correa, D.; Xie, K.; Ozbay, K. Exploring the Taxi and Uber Demand in New York City: An Empirical Analysis and Spatial Modeling. In Proceedings of the 96th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
- Fang, Z.; Su, R.; Huang, L. Understanding the Effect of an E-Hailing App Subsidy War on Taxicab Operation Zones. J. Adv. Transp. 2018, 2018, 7687852. [Google Scholar] [CrossRef]
- Gong, S.; Cartlidge, J.; Bai, R.; Yue, Y.; Li, Q.; Qiu, G. Geographical and temporal huff model calibration using taxi trajectory data. GeoInformatica 2021, 25, 485–512. [Google Scholar] [CrossRef]
- Guo, D.; Zhu, X.; Jin, H.; Gao, P.; Andris, C. Discovering Spatial Patterns in Origin-Destination Mobility Data. Trans. GIS 2012, 16, 411–429. [Google Scholar] [CrossRef]
- Guo, X.; Xu, Z.; Zhang, J.; Lu, J.; Zhang, H. An OD Flow Clustering Method Based on Vector Constraints: A Case Study for Beijing Taxi Origin-Destination Data. ISPRS Int. J. Geo-Inf. 2020, 9, 128. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Deng, M.; He, Z. Mining crowdsourced trajectory and geo-tagged data for spatial-semantic road map construction. Trans. GIS 2022, 26, 735–754. [Google Scholar] [CrossRef]
- Kou, Z.; Cai, H. Understanding bike sharing travel patterns: An analysis of trip data from eight cities. Phys. A Stat. Mech. Appl. 2019, 515, 785–797. [Google Scholar] [CrossRef]
- Lei, Y.; Ozbay, K. A robust analysis of the impacts of the stay-at-home policy on taxi and Citi Bike usage: A case study of Manhattan. Transp. Policy 2021, 110, 487–498. [Google Scholar] [CrossRef]
- Li, S.; Zhuang, C.; Tan, Z.; Gao, F.; Lai, Z.; Wu, Z. Inferring the trip purposes and uncovering spatio-temporal activity patterns from dockless shared bike dataset in Shenzhen, China. J. Transp. Geogr. 2021, 91, 102974. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Wilson, B. Beyond absolute space: An exploration of relative and relational space in Shanghai using taxi trajectory data. J. Transp. Geogr. 2021, 93, 103076. [Google Scholar] [CrossRef]
- Li, X.; Pan, G.; Wu, Z.; Qi, G.; Li, S.; Zhang, D.; Zhang, W.; Wang, Z. Prediction of urban human mobility using large-scale taxi traces and its applications. Front. Comput. Sci. 2012, 6, 111–121. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]
- Liu, Y.; Singleton, A.; Arribas-Bel, D.; Chen, M. Identifying and understanding road-constrained areas of interest (AOIs) through spatiotemporal taxi GPS data: A case study in New York City. Comput. Environ. Urban Syst. 2021, 86, 101592. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Xiao, Y.; Gao, S. Urban land uses and traffic ‘source-sink areas’: Evidence from GPS-enabled taxi data in Shanghai. Landsc. Urban Plan. 2012, 106, 73–87. [Google Scholar] [CrossRef]
- Lyu, T.; Wang, P.; Gao, Y.; Wang, Y. Research on the big data of traditional taxi and online car-hailing: A systematic review. J. Traffic Transp. Eng. 2021, 8, 1–34. [Google Scholar] [CrossRef]
- Monahan, T.; Lamb, C.G. Transit’s downward spiral: Assessing the social-justice implications of ride-hailing platforms and COVID-19 for public transportation in the US. Cities 2022, 120, 103438. [Google Scholar] [CrossRef]
- Navarro, G. A guided tour to approximate string matching. ACM Comput. Surv. 2001, 33, 31–88. [Google Scholar] [CrossRef]
- Poongodi, M.; Malviya, M.; Kumar, C.; Hamdi, M.; Vijayakumar, V.; Nebhen, J.; Alyamani, H. New York City taxi trip duration prediction using MLP and XGBoost. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 16–27. [Google Scholar] [CrossRef]
- Shehzad, K.; Bilgili, F.; Koçak, E.; Xiaoxing, L.; Ahmad, M. COVID-19 outbreak, lockdown, and air quality: Fresh insights from New York City. Environ. Sci. Pollut. Res. 2021, 28, 41149–41161. [Google Scholar] [CrossRef]
- Shenzhen Transportation Bureau. Passenger Flow Volume of Public Transport; Shenzhen Transportation Bureau: Shenzhen, China, 2021.
- Shu, H.; Pei, T.; Song, C.; Chen, X.; Guo, S.; Liu, Y.; Chen, J.; Wang, X.; Zhou, C. L-function of geographical flows. Int. J. Geogr. Inf. Sci. 2021, 35, 689–716. [Google Scholar] [CrossRef]
- Tu, W.; Cao, R.; Yue, Y.; Zhou, B.; Li, Q.; Li, Q. Spatial variations in urban public ridership derived from GPS trajectories and smart card data. J. Transp. Geogr. 2018, 69, 45–57. [Google Scholar] [CrossRef]
- Kumar, T.M.V. International Collaborative Research: “Smart Global Mega Cities” and Conclusions of Cities Case Studies Tokyo, New York, Mumbai, Hong Kong-Shenzhen, and Kolkata. In Smart Global Megacities; Springer: Singapore, 2022; pp. 411–460. [Google Scholar] [CrossRef]
- Wang, F.; Ross, C.L. New potential for multimodal connection: Exploring the relationship between taxi and transit in New York City (NYC). Transportation 2019, 46, 1051–1072. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, K.; Chen, J.; Wang, Z.; Li, G.; Yang, Y. System dynamics model of taxi management in metropolises: Economic and environmental implications for Beijing. J. Environ. Manag. 2018, 213, 555–565. [Google Scholar] [CrossRef]
- Wang, J.; Rui, X.; Song, X.; Tan, X.; Wang, C.; Raghavan, V. A novel approach for generating routable road maps from vehicle GPS traces. Int. J. Geogr. Inf. Sci. 2015, 29, 69–91. [Google Scholar] [CrossRef]
- Li, Y.; Xiang, L.; Zhang, C.; Jiao, F.; Wu, C. A Guided Deep Learning Approach for Joint Road Extraction and Intersection Detection from RS Images and Taxi Trajectories. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8008–8018. [Google Scholar] [CrossRef]
- Yang, X.; Hou, L.; Guo, M.; Cao, Y.; Yang, M.; Tang, L. Road intersection identification from crowdsourced big trace data using Mask-RCNN. Trans. GIS 2022, 26, 278–296. [Google Scholar] [CrossRef]
- Zhang, D.; Wan, J.; He, Z.; Zhao, S.; Fan, K.; Park, S.O.; Jiang, Z. Identifying Region-Wide Functions Using Urban Taxicab Trajectories. ACM Trans. Embed. Comput. Syst. 2016, 15, 1–19. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Senousi, A.M. A multilayer mobility network approach to inferring urban structures using shared mobility and taxi data. Trans. GIS 2021, 25, 2840–2865. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, J.; Wang, H.; Wang, Y.; An, S. Revealing intra-urban travel patterns and service ranges from taxi trajectories. J. Transp. Geogr. 2017, 61, 72–86. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Qian, X.; Qiu, A.; Zhang, F. An Automatic Road Network Construction Method Using Massive GPS Trajectory Data. ISPRS Int. J. Geo-Inf. 2017, 6, 400. [Google Scholar] [CrossRef]
- Zhou, Y.; Fang, Z.; Thill, J.-C.; Li, Q.; Li, Y. Functionally critical locations in an urban transportation network: Identification and space–time analysis using taxi trajectories. Comput. Environ. Urban Syst. 2015, 52, 34–47. [Google Scholar] [CrossRef]


| Device Number | Longitude | Latitude | Positioning Time | Working Status |
|---|---|---|---|---|
| 104***3 | 113.****05 | 22.****18 | 26 September 2011 11:18:55 | 0 |
| 104***3 | 113.****49 | 22.****07 | 26 September 2011 11:19:32 | 1 |
| 104***3 | 113.****32 | 22.****56 | 26 September 2011 11:20:02 | 1 |
| 104***3 | 113.****07 | 22.****95 | 26 September 2011 11:21:00 | 1 |
| PickUp_Datetime | DropOff_Datetime | PULocationID | DPLocationID |
|---|---|---|---|
| 1 July 2019 00:12:33 | 1 July 2019 00:25:00 | 228 | 89 |
| 1 July 2019 00:41:26 | 1 July 2019 00:51:21 | 97 | 188 |
| 1 July 2019 00:18:50 | 1 July 2019 00:32:48 | 81 | 220 |
| 1 July 2019 00:29:01 | 1 July 2019 00:45:50 | 69 | 239 |
| Structural Similarity | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| Monday | 1.000 | 0.810 | 0.808 | 0.811 | 0.804 | 0.796 | 0.793 |
| Tuesday | 0.810 | 1.000 | 0.808 | 0.809 | 0.806 | 0.802 | 0.801 |
| Wednesday | 0.808 | 0.808 | 1.000 | 0.810 | 0.812 | 0.802 | 0.798 |
| Thursday | 0.811 | 0.809 | 0.810 | 1.000 | 0.813 | 0.801 | 0.801 |
| Friday | 0.804 | 0.806 | 0.812 | 0.813 | 1.000 | 0.806 | 0.802 |
| Saturday | 0.796 | 0.802 | 0.802 | 0.801 | 0.806 | 1.000 | 0.806 |
| Sunday | 0.793 | 0.801 | 0.798 | 0.801 | 0.802 | 0.806 | 1.000 |
| Structural Similarity | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| Monday | 1.000 | 0.740 | 0.732 | 0.735 | 0.724 | 0.712 | 0.709 |
| Tuesday | 0.740 | 1.000 | 0.735 | 0.733 | 0.730 | 0.723 | 0.719 |
| Wednesday | 0.732 | 0.735 | 1.000 | 0.743 | 0.743 | 0.721 | 0.716 |
| Thursday | 0.735 | 0.733 | 0.743 | 1.000 | 0.741 | 0.721 | 0.717 |
| Friday | 0.724 | 0.730 | 0.743 | 0.741 | 1.000 | 0.729 | 0.721 |
| Saturday | 0.712 | 0.723 | 0.721 | 0.721 | 0.729 | 1.000 | 0.734 |
| Sunday | 0.709 | 0.719 | 0.716 | 0.717 | 0.721 | 0.734 | 1.000 |
| Structural Similarity | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| Monday | 1.000 | 0.567 | 0.567 | 0.567 | 0.564 | 0.565 | 0.562 |
| Tuesday | 0.567 | 1.000 | 0.568 | 0.567 | 0.565 | 0.566 | 0.563 |
| Wednesday | 0.567 | 0.568 | 1.000 | 0.569 | 0.567 | 0.566 | 0.563 |
| Thursday | 0.567 | 0.567 | 0.569 | 1.000 | 0.565 | 0.563 | 0.561 |
| Friday | 0.564 | 0.565 | 0.567 | 0.565 | 1.000 | 0.559 | 0.559 |
| Saturday | 0.565 | 0.566 | 0.566 | 0.563 | 0.559 | 1.000 | 0.558 |
| Sunday | 0.562 | 0.563 | 0.563 | 0.561 | 0.559 | 0.558 | 1.000 |
| Structural Similarity | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| Monday | 1.000 | 0.590 | 0.576 | 0.576 | 0.538 | 0.462 | 0.489 |
| Tuesday | 0.590 | 1.000 | 0.599 | 0.587 | 0.543 | 0.459 | 0.481 |
| Wednesday | 0.576 | 0.599 | 1.000 | 0.595 | 0.557 | 0.470 | 0.487 |
| Thursday | 0.576 | 0.587 | 0.595 | 1.000 | 0.573 | 0.484 | 0.498 |
| Friday | 0.538 | 0.543 | 0.557 | 0.573 | 1.000 | 0.517 | 0.513 |
| Saturday | 0.462 | 0.459 | 0.470 | 0.484 | 0.517 | 1.000 | 0.530 |
| Sunday | 0.489 | 0.481 | 0.487 | 0.498 | 0.513 | 0.530 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, P.; Yao, W.; Zhao, Z.; Wang, P.; Wu, S.; Fang, Z. Interday Stability of Taxi Travel Flow in Urban Areas. ISPRS Int. J. Geo-Inf. 2022, 11, 590. https://doi.org/10.3390/ijgi11120590
Tu P, Yao W, Zhao Z, Wang P, Wu S, Fang Z. Interday Stability of Taxi Travel Flow in Urban Areas. ISPRS International Journal of Geo-Information. 2022; 11(12):590. https://doi.org/10.3390/ijgi11120590
Chicago/Turabian StyleTu, Ping, Wei Yao, Zhiyuan Zhao, Pengzhou Wang, Sheng Wu, and Zhixiang Fang. 2022. "Interday Stability of Taxi Travel Flow in Urban Areas" ISPRS International Journal of Geo-Information 11, no. 12: 590. https://doi.org/10.3390/ijgi11120590
APA StyleTu, P., Yao, W., Zhao, Z., Wang, P., Wu, S., & Fang, Z. (2022). Interday Stability of Taxi Travel Flow in Urban Areas. ISPRS International Journal of Geo-Information, 11(12), 590. https://doi.org/10.3390/ijgi11120590







