A Novel Deep Learning Approach Using Contextual Embeddings for Toponym Resolution
Abstract
1. Introduction
- Geo/geo ambiguity happens when the same place name is shared by different locations. For instance, the name Kent can be related to either Kent County, Delaware, United States, or New Kent Count, Virginia, United States;
- Geo/non-geo ambiguity happens when common language words are used to identify places names, i.e., when the same name is shared by a location and also by a non-location. For instance, the word Charlotte can refer to the specific location of Charlotte County, Virginia, United States or to a person name. The word Manhattan can also refer to a cocktail beverage, or to the specific location of Manhattan, New York, United States;
- Reference ambiguity, which arises when the same place can be referred by multiple names. For instance, Motor City is a commonly used name to refer to Detroit, Michigan, United States.
2. Related Work
2.1. Heuristic Methods for Toponym Resolution
2.2. Combining Heuristics through Supervised Learning
2.3. Methods Combining Geodesic Grids and Language Models
2.4. Deep Learning Techniques for Toponym Resolution
2.5. Corpora from Previous Studies Employed in Our Work
3. The Proposed Toponym Resolution Method
3.1. Recurrent Neural Networks
3.2. Representing Text through Contextual Word Embeddings
3.3. The Neural Architecture for Toponym Resolution
4. Experimental Evaluation
4.1. Experimental Evaluation Methodology
- ELMo models—This corresponds to our base approach, leveraging recurrent neural networks as described on Section 3.2, and using the ELMo method for generating contextual embeddings when representing the textual inputs.
- BERT models—To observe the impact of using different text representation methods, we replaced ELMo by BERT contextual word embeddings. This particular approach, based on the Transformer neural architecture and also described on Section 3.2, has been previously shown to provide superior results across a range of NLP tasks.
- Wikipedia models—To understand the impact of the size of the training dataset, we built a new corpus containing random articles collected from the English Wikipedia. We identified existing hyperlinks towards pages associated with geographic coordinates, and collected the source article text, the hyperlink text (i.e., the automatically generated place reference), and the target geographic coordinates. These data were used to create additional training instances, which were then filtered to match with the HEALPix regions present in the original corpora. Thus, Wikipedia was used to augment the available training instances, without modifying the region classification space of each corpus. Experiments were performed with either ELMo or BERT embeddings, in the setting that involved Wikipedia data. A total of 15,000 new instances were added to each of the three training datasets.
- Models integrating geophysical properties—We also experimented with the use of additional information corresponding to geophysical terrain properties associated with each of the HEALPix regions, namely terrain development (i.e., a quantification on the amount of impervious/developed versus natural terrain, inferred from historical land coverage datasets in the case of experiments with the WOTR corpus, and from modern sources in the remaining cases), percentage of vegetation, terrain elevation, and minimum distance from water zones. We collected this information from public raster datasets, incorporating it into the model using a similar technique to that associated with the interpolation of geographic coordinates. Specifically, we encoded each of the four geophysical properties as real values, and then created column vectors with values corresponding to the measurements associated with the centroid coordinates of each HEALPix class. We then computed a dot product between each of the column vectors and the adjusted HEALPix class probability vector, resulting in estimates for the geophysical properties. Additional loss functions were incorporated into the model, corresponding to the absolute difference between the predicted and the ground-truth values. The main intuition behind this set of experiments relates to seeing if the geophysical properties of the terrain, which are perhaps described in the text surrounding the place references, can guide the task of predicting the geographic coordinates. As in the previous case, experiments under this setting were performed with either ELMo or BERT contextual word embeddings.
4.2. The Obtained Results
4.3. Discussion on the Overall Results
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amitay, E.; Har’El, N.; Sivan, R.; Soffer, A. Web-a-where: Geotagging web content. In Proceedings of the ACM SIGIR Conference on Research and Development in Information Retrieval, Sheffield, UK, 25–29 July 2004; pp. 273–280. [Google Scholar]
- Monteiro, B.; Davis, C.; Fonseca, F. A survey on the geographic scope of textual documents. Comput. Geosci. 2016, 96, 23–34. [Google Scholar] [CrossRef]
- Cardoso, N.; Martins, B.; Chaves, M.; Andrade, L.; Silva, M.J. The XLDB group at GeoCLEF 2005. In Workshop of the Cross-Language Evaluation Forum for European Languages, Proceedings of the 6th Workshop of the Cross-Language Evalution Forum, CLEF 2005, Vienna, Austria, 21–23 September 2005; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Martins, B.; Calado, P. Learning to rank for geographic information retrieval. In Proceedings of the ACM SIGSPATIAL Workshop on Geographic Information Retrieval, Zurich, Switzerland, 18–19 February 2010. [Google Scholar]
- Coelho, J.A.; Magalhães, J.A.; Martins, B. Improving Neural Models for the Retrieval of Relevant Passages to Geographical Queries. In Proceedings of the ACM SIGSPATIAL Conference on Advances in Geographic Information Systems, Beijing, China, 2–5 November 2021. [Google Scholar]
- Purves, R.S.; Clough, P.; Jones, C.B.; Hall, M.H.; Murdock, V. Geographic Information Retrieval: Progress and Challenges in Spatial Search of Text. Found. Trends Inf. Retr. 2018, 12, 164–318. [Google Scholar] [CrossRef]
- Wing, B. Text-Based Document Geolocation and Its Application to the Digital Humanities. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Melo, F.; Martins, B. Automated geocoding of textual documents: A survey of current approaches. Trans. GIS 2017, 21, 3–38. [Google Scholar] [CrossRef]
- Berman, M.; Mostern, R.; Southall, H. Placing Names: Enriching and Integrating Gazetteers; Indiana University Press: Bloomington, IN, USA, 2016. [Google Scholar]
- Manguinhas, H.; Martins, B.; Borbinha, J.; Siabato, W. The DIGMAP geo-temporal web gazetteer service. E-Perimetron 2009, 4, 9–24. [Google Scholar]
- Ardanuy, M.; Sporleder, C. Toponym disambiguation in historical documents using semantic and geographic features. In Proceedings of the Conference on Digital Access to Textual Cultural Heritage, Göttingen, Germany, 1–2 June 2017; pp. 175–180. [Google Scholar]
- Leidner, J. Toponym Resolution in Text. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2007. [Google Scholar]
- Freire, N.; Borbinha, J.; Calado, P.; Martins, B. A metadata geoparsing system for place name recognition and resolution in metadata records. In Proceedings of the Annual International ACM/IEEE Joint Conference on Digital Libraries, Ottawa, ON, USA, 13–17 June 2011; pp. 339–348. [Google Scholar]
- Karimzadeh, M.; Pezanowski, S.; MacEachren, A.; Wallgrün, J. GeoTxt: A scalable geoparsing system for unstructured text geolocation. Trans. GIS 2019, 23, 118–136. [Google Scholar] [CrossRef]
- Lieberman, M.; Samet, H. Adaptive context features for toponym resolution in streaming news. In Proceedings of the ACM SIGIR Conference on Research and Development in Information Retrieval, Portland, OR, USA, 12–16 August 2012; pp. 731–740. [Google Scholar]
- Santos, J.; Anastácio, I.; Martins, B. Using machine learning methods for disambiguating place references in textual documents. GeoJournal 2015, 80, 375–392. [Google Scholar] [CrossRef]
- DeLozier, G.; Baldridge, J.; London, L. Gazetteer-independent toponym resolution using geographic word profiles. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2382–2388. [Google Scholar]
- Speriosu, M.; Baldridge, J. Text-driven toponym resolution using indirect supervision. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Sofia, Bulgaria, 4–9 August 2013; Volume 1, pp. 1466–1476. [Google Scholar]
- Adams, B.; McKenzie, G. Crowdsourcing the character of a place: Character-level convolutional networks for multilingual geographic text classification. Trans. GIS 2018, 22, 394–408. [Google Scholar] [CrossRef]
- Gritta, M.; Pilehvar, M.; Collier, N. Which Melbourne? Augmenting geocoding with maps. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, 15–20 July 2018; Volume 1, pp. 1285–1296. [Google Scholar]
- Weissenbacher, D.; Magge, A.; O’Connor, K.; Scotch, M.; Gonzalez-Hernandez, G. SemEval-2019 task 12: Toponym resolution in scientific papers. In Proceedings of the Workshop on Semantic Evaluation, Minneapolis, MN, USA, 6–7 June 2019; pp. 907–916. [Google Scholar]
- Yan, Z.; Yang, C.; Hu, L.; Zhao, J.; Jiang, L.; Gong, J. The Integration of Linguistic and Geospatial Features Using Global Context Embedding for Automated Text Geocoding. ISPRS Int. J. Geo-Inf. 2021, 10, 572. [Google Scholar] [CrossRef]
- Peters, M.; Neumann, M.; Iyyer, M.; Gardner, M.; Clark, C.; Lee, K.; Zettlemoyer, L. Deep contextualized word representations. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 1–6 June 2018; Volume 1, pp. 2227–2237. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 6–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Górski, K.; Hivon, E.; Banday, A.; Wandelt, B.; Hansen, F.; Reinecke, M.; Bartelman, M. HEALPix: A framework for high-resolution discretization and fast analysis of data distributed on the sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- Bensalem, I.; Kholladi, M.K. Toponym disambiguation by arborescent relationships. J. Comput. Sci. 2010, 6, 653. [Google Scholar] [CrossRef][Green Version]
- Moncla, L. Automatic Reconstruction of Itineraries from Descriptive Texts. Ph.D. Thesis, University of Pau and Pays de l’Adour, Pau, France, 2015. [Google Scholar]
- Xu, C.; Li, J.; Luo, X.; Pei, J.; Li, C.; Ji, D. DLocRL: A deep learning pipeline for fine-grained location recognition and linking in tweets. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019. [Google Scholar]
- Wing, B.; Baldridge, J. Simple supervised document geolocation with geodesic grids. In Proceedings of the Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, Portland, OR, USA, 19–24 June 2011; pp. 955–964. [Google Scholar]
- DeLozier, G.; Wing, B.; Baldridge, J.; Nesbit, S. Creating a novel geolocation corpus from historical texts. In Proceedings of the ACL Linguistic Annotation Workshop, Berlin, Germany, 11 August 2016; pp. 188–198. [Google Scholar]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Lieberman, M.; Samet, H.; Sankaranarayanan, J. Geotagging with local lexicons to build indexes for textually-specified spatial data. In Proceedings of the IEEE Conference on Data Engineering, Long Beach, CA, USA, 1–6 March 2010; pp. 201–212. [Google Scholar]
- Mani, I.; Doran, C.; Harris, D.; Hitzeman, J.; Quimby, R.; Richer, J.; Wellner, B.; Mardis, S.; Clancy, S. SpatialML: Annotation scheme, resources, and evaluation. Lang. Resour. Eval. 2010, 44, 263–280. [Google Scholar] [CrossRef]
- Gritta, M.; Pilehvar, M.; Limsopatham, N.; Collier, N. What’s missing in geographical parsing? Lang. Resour. Eval. 2018, 52, 603–623. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Hu, Y. Enhancing spatial and textual analysis with EUPEG: An extensible and unified platform for evaluating geoparsers. Trans. GIS 2019, 23, 1393–1419. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Y. Are we there yet? Evaluating state-of-the-art neural networkbased geoparsers using EUPEG as a benchmarking platform. In Proceedings of the ACM SIGSPATIAL Workshop on Geospatial Humanities, Chicago, IL, USA, 5 November 2019; pp. 1–6. [Google Scholar]
- Goldberg, Y. Neural Network Methods in Natural Language Processing; Morgan & Claypool: San Rafael, CA, USA, 2017. [Google Scholar]
- Schmidhuber, J.; Hochreiter, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Smith, N.A. Contextual word representations: A contextual introduction. arXiv 2019, arXiv:1902.06006. [Google Scholar]
- Liu, Q.; Kusner, M.J.; Blunsom, P. A Survey on Contextual Embeddings. arXiv 2020, arXiv:2003.07278. [Google Scholar]
- Qiu, X.; Sun, T.; Xu, Y.; Shao, Y.; Dai, N.; Huang, X. Pre-trained Models for Natural Language Processing: A Survey. arXiv 2020, arXiv:2003.08271. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. In Proceedings of the International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Melo, F.; Martins, B. Geocoding textual documents through the usage of hierarchical classifiers. In Proceedings of the Workshop on Geographic Information Retrieval, Paris, France, 26–27 November 2015; pp. 1–9. [Google Scholar]
- Eger, S.; Youssef, P.; Gurevych, I. Is it time to swish? Comparing deep learning activation functions across NLP tasks. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 4415–4424. [Google Scholar]
- Smith, L. Cyclical learning rates for training neural networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Vincenty, T. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Surv. Rev. 1975, 23, 88–93. [Google Scholar] [CrossRef]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Online, 16–20 November 2020. [Google Scholar]
- Rogers, A.; Kovaleva, O.; Rumshisky, A. A Primer in BERTology: What we know about how BERT works. Trans. Assoc. Comput. Linguist. 2020, 8, 842–866. [Google Scholar] [CrossRef]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. RoBERTa: A robustly optimized BERT pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Yamada, I.; Asai, A.; Shindo, H.; Takeda, H.; Matsumoto, Y. Luke: Deep contextualized entity representations with entity-aware self-attention. arXiv 2020, arXiv:2010.01057. [Google Scholar]
- Qin, Y.; Lin, Y.; Takanobu, R.; Liu, Z.; Li, P.; Ji, H.; Huang, M.; Sun, M.; Zhou, J. ERICA: Improving entity and relation understanding for pre-trained language models via contrastive learning. arXiv 2020, arXiv:2012.15022. [Google Scholar]
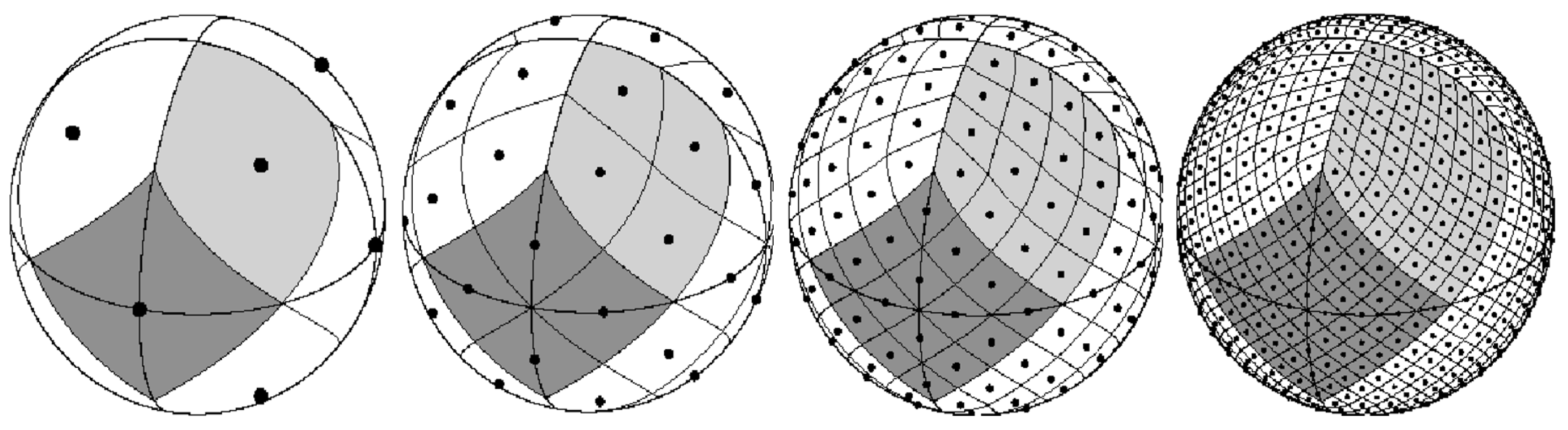

| Statistic | WOTR | LGL | SpatialML |
|---|---|---|---|
| Number of documents | 1644 | 588 | 428 |
| Number of toponyms | 10,377 | 4462 | 4606 |
| Average number of toponyms per document | 6.3 | 7.6 | 10.8 |
| Average number of word tokens per document | 246 | 325 | 497 |
| Average number of sentences per document | 12.7 | 16.1 | 30.7 |
| Vocabulary size | 13,386 | 16,518 | 14,489 |
| Number of HEALPix classes/regions | 999 | 761 | 461 |
| Dataset | Mean Dist. (km) | Median Dist. (km) | Accuracy@161 km (%) |
|---|---|---|---|
| WOTR corpus | |||
| TopoCluster [30] | 604 | 57.0 | |
| TopoClusterGaz [30] | 468 | - | 72.0 |
| GeoSem [11] | 445 | - | 68.0 |
| Our Neural Model | 164 | 11.48 | 81.5 |
| LGL corpus | |||
| GeoTxt [20] | 1400 | - | 68.0 |
| CamCoder [20] | 700 | - | 76.0 |
| TopoCluster [17] | 1029 | 28.00 | 69.0 |
| TopoClusterGaz [30] | 1228 | 0.00 | 71.4 |
| Learning to Rank [16] | 742 | 2.79 | - |
| Our Neural Model | 237 | 12.24 | 86.1 |
| SpatialML corpus | |||
| Learning to Rank [16] | 140 | 28.71 | - |
| Our Neural Model | 395 | 9.08 | 87.4 |
| Model and Dataset | Mean Distance (km) | Median Distance (km) | Accuracy@161 km (%) |
|---|---|---|---|
| WOTR corpus | |||
| ELMo | 164 | 11.48 | 81.5 |
| ELMo + Wikipedia | 158 | 11.28 | 82.4 |
| ELMo + Geophysical | 166 | 11.35 | 81.9 |
| BERT | 117 | 10.99 | 87.3 |
| BERT + Wikipedia | 122 | 11.04 | 86.4 |
| BERT + Geophysical | 114 | 10.99 | 87.3 |
| LGL corpus | |||
| ELMo | 237 | 12.24 | 86.1 |
| ELMo + Wikipedia | 304 | 12.16 | 87.4 |
| ELMo + Geophysical | 282 | 12.24 | 87.7 |
| BERT | 193 | 11.81 | 90.1 |
| BERT + Wikipedia | 226 | 11.51 | 90.6 |
| BERT + Geophysical | 216 | 12.24 | 87.9 |
| SpatialML corpus | |||
| ELMo | 395 | 9.08 | 87.4 |
| ELMo + Wikipedia | 364 | 9.08 | 88.5 |
| ELMo + Geophysical | 387 | 9.08 | 87.4 |
| BERT | 363 | 9.08 | 89.2 |
| BERT + Wikipedia | 205 | 9.08 | 92.4 |
| BERT + Geophysical | 339 | 9.08 | 89.4 |
| Corpus | Lowest Distance Errors (km) | Highest Distance Errors (km) |
|---|---|---|
| (0.63) Mexico | (3104.59) Fort Welles | |
| WOTR | (1.00) Resaca | (3141.29) Washington |
| (1.09) Owen’s Big Lake | (3682.01) Astoria | |
| (1.21) W.Va. | (8854.04) Ohioans | |
| LGL | (1.36) Butler County | (9225.86) North America |
| (1.51) Manchester | (9596.54) Nigeria | |
| (0.45) Tokyo | (9687.43) Capital | |
| SpatialML | (2.38) Lusaka | (10,818.50) Omaha |
| (2.44) English | (13,140.64) Atlantic City |
| Predicted vs. Ground-Truth Coordinates | Textual Contents |
|---|---|
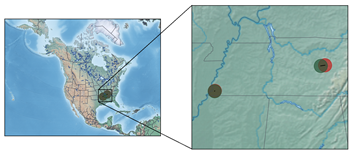 | [Indorsement.] HDQRS. DETACHMENT SIXTEENTH ARMY CORPS, Memphis, Tenn., 12 June 1864. Respectfully referred to Colonel David Moore, commanding THIRD DIVISION, SIXTEENTH Army Corps, who will send the THIRD Brigade of his command, substituting some regiment for the Forty-ninth Illinois that is not entitled to veteran furlough, making the number as near as possible to 2000 men. They will be equipped as within directed, and will move to the railroad depot as soon as ready. You will notify these headquarters as soon as the troops are at the depot. By order of Brigadier General A. J. Smith: J. HOUGH, Assistant Adjutant-General. |
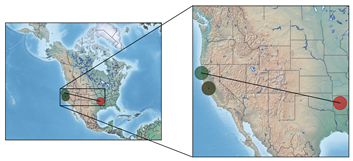 | HYDESVILLE, 21 October 1862 SIR: I started from this place this morning, 7.30 o’clock, en route for Fort Baker. The express having started an hour before, I had no escort. About two miles from Simmons’ ranch I was attacked by a party of Indians. As soon as they fired they tried to surround me. I returned their fire and retreated down the hill. A portion of them cut me off and fired again. I returned their fire and killed one of them. They did not follow any farther. I will start this evening for my post as I think it will be safer to pass this portin of the country in the night. Those Indians were lurking about of rthe purpose of robbing Cooper’s Mills. They could have no othe robject, and I think it would be well to have eight or ten men stationed at that place, as it will serve as an outpost for the settlement, as well as a guard for the mills. The expressmen disobeyed my orders by starting without me this morning. I have the honor to be, very respectfully, your obedient servant, H. FLYNN, Captain, Second Infantry California Volunteers. First Lieutenant JOHN HANNA, Jr., Acting Assistant Adjutant-General, Humboldt Military District. |
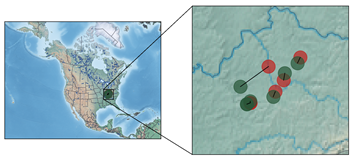 | LEXINGTON, KY., 11 June 1864–11 p.m. Colonel J. W. WEATHERFORD, Lebanon, Ky. Have just received dispatch from General Burbridge at Paris. He says direct Colonel Weatherford to closely watch in the direction of Bardstown and Danville, and if any part of the enemy’s force appears in that region to attack and destroy it. J. BATES DICKSON, Captain and Assistant Adjutant-General. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardoso, A.B.; Martins, B.; Estima, J. A Novel Deep Learning Approach Using Contextual Embeddings for Toponym Resolution. ISPRS Int. J. Geo-Inf. 2022, 11, 28. https://doi.org/10.3390/ijgi11010028
Cardoso AB, Martins B, Estima J. A Novel Deep Learning Approach Using Contextual Embeddings for Toponym Resolution. ISPRS International Journal of Geo-Information. 2022; 11(1):28. https://doi.org/10.3390/ijgi11010028
Chicago/Turabian StyleCardoso, Ana Bárbara, Bruno Martins, and Jacinto Estima. 2022. "A Novel Deep Learning Approach Using Contextual Embeddings for Toponym Resolution" ISPRS International Journal of Geo-Information 11, no. 1: 28. https://doi.org/10.3390/ijgi11010028
APA StyleCardoso, A. B., Martins, B., & Estima, J. (2022). A Novel Deep Learning Approach Using Contextual Embeddings for Toponym Resolution. ISPRS International Journal of Geo-Information, 11(1), 28. https://doi.org/10.3390/ijgi11010028







