Machine Learning of Spatial Data
Abstract
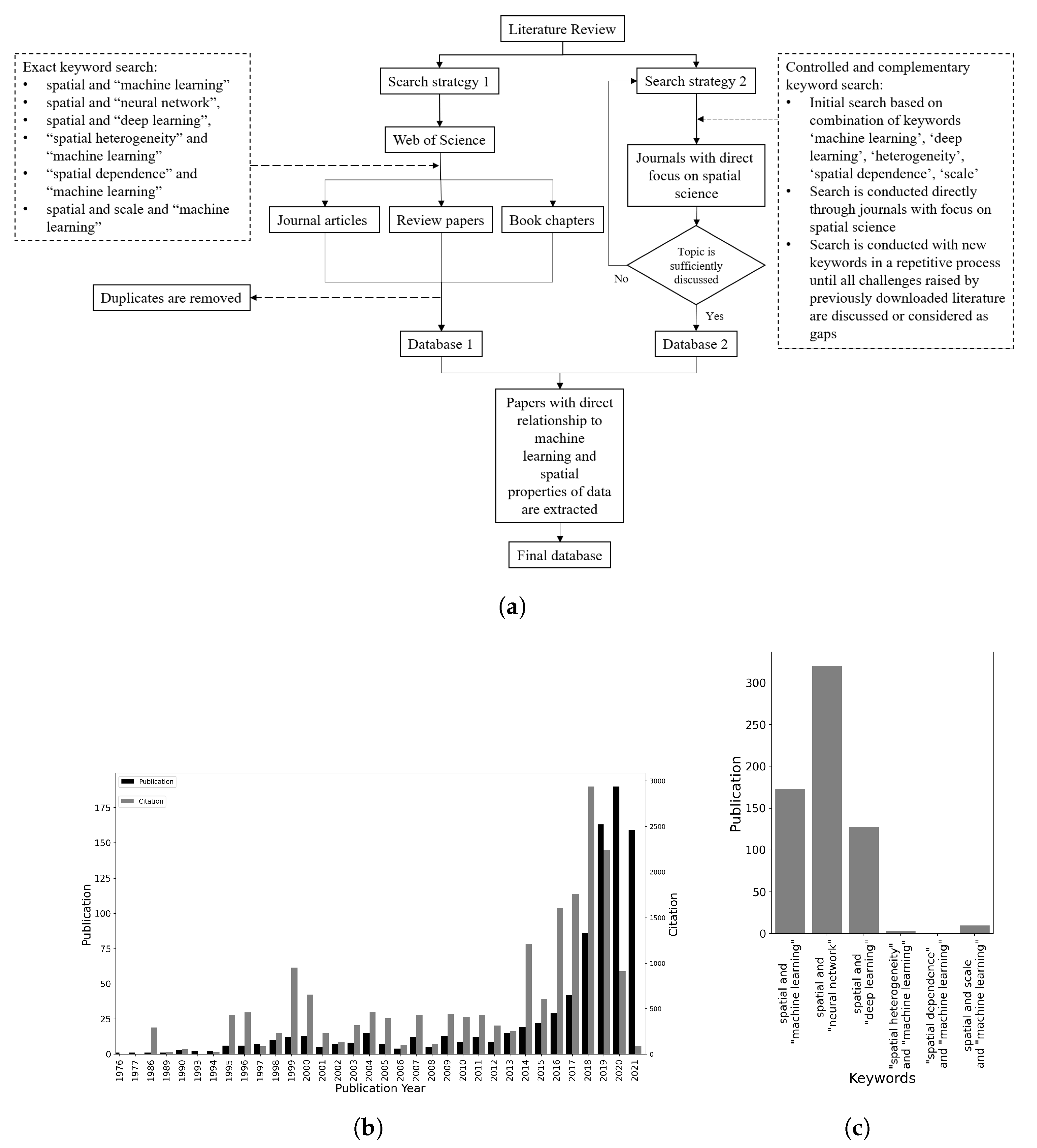
:1. Introduction
- How much progress in handling spatial properties of data in ML has been accomplished?
- What are some of the best practices in this respect?
- What are the gaps that may remain in this literature, and where do opportunities exist for future research with, and on, spatially explicit ML?
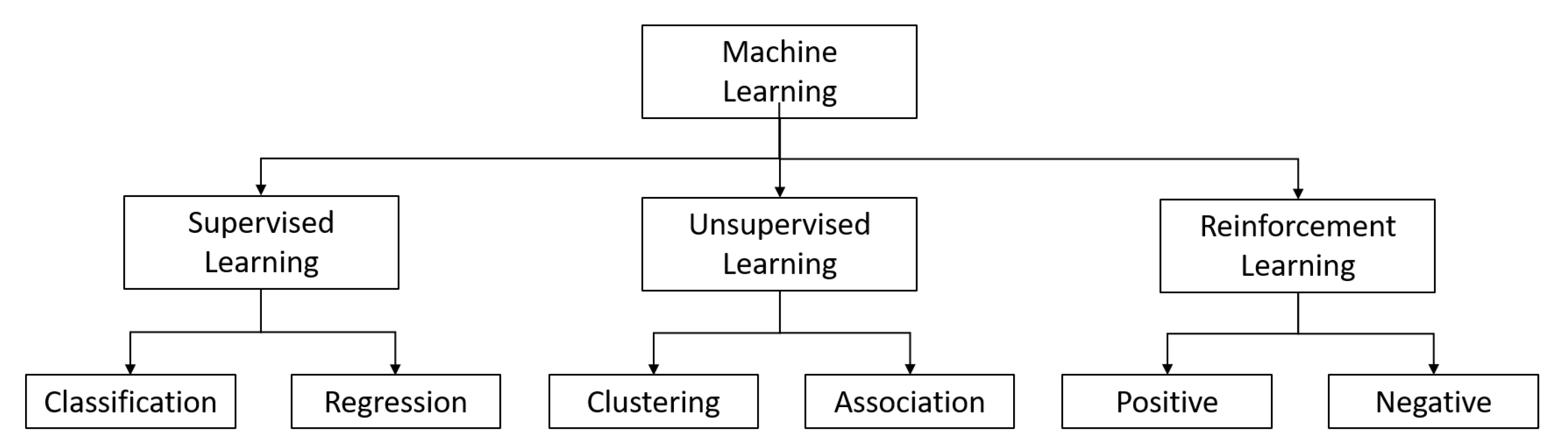
2. Machine Learning
3. Spatial Data Properties
3.1. Spatial Dependence
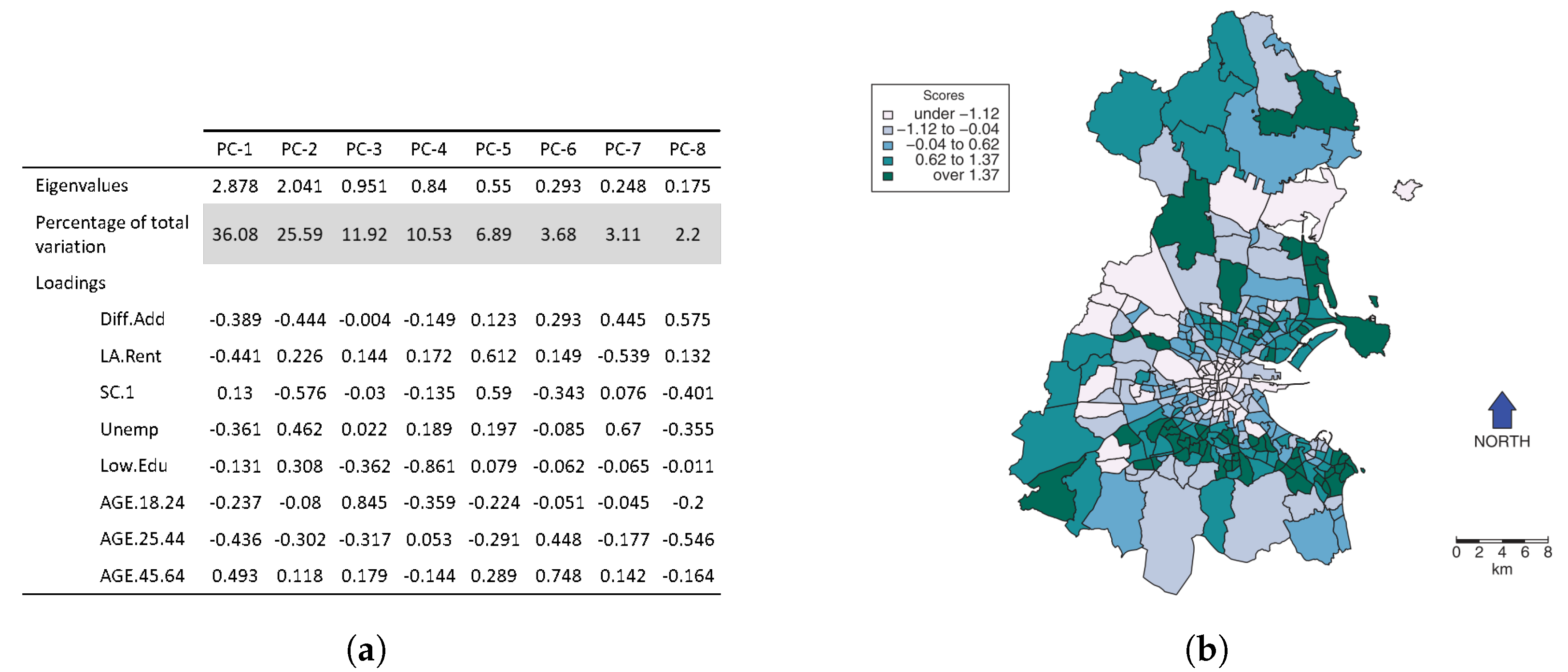
3.2. Spatial Heterogeneity
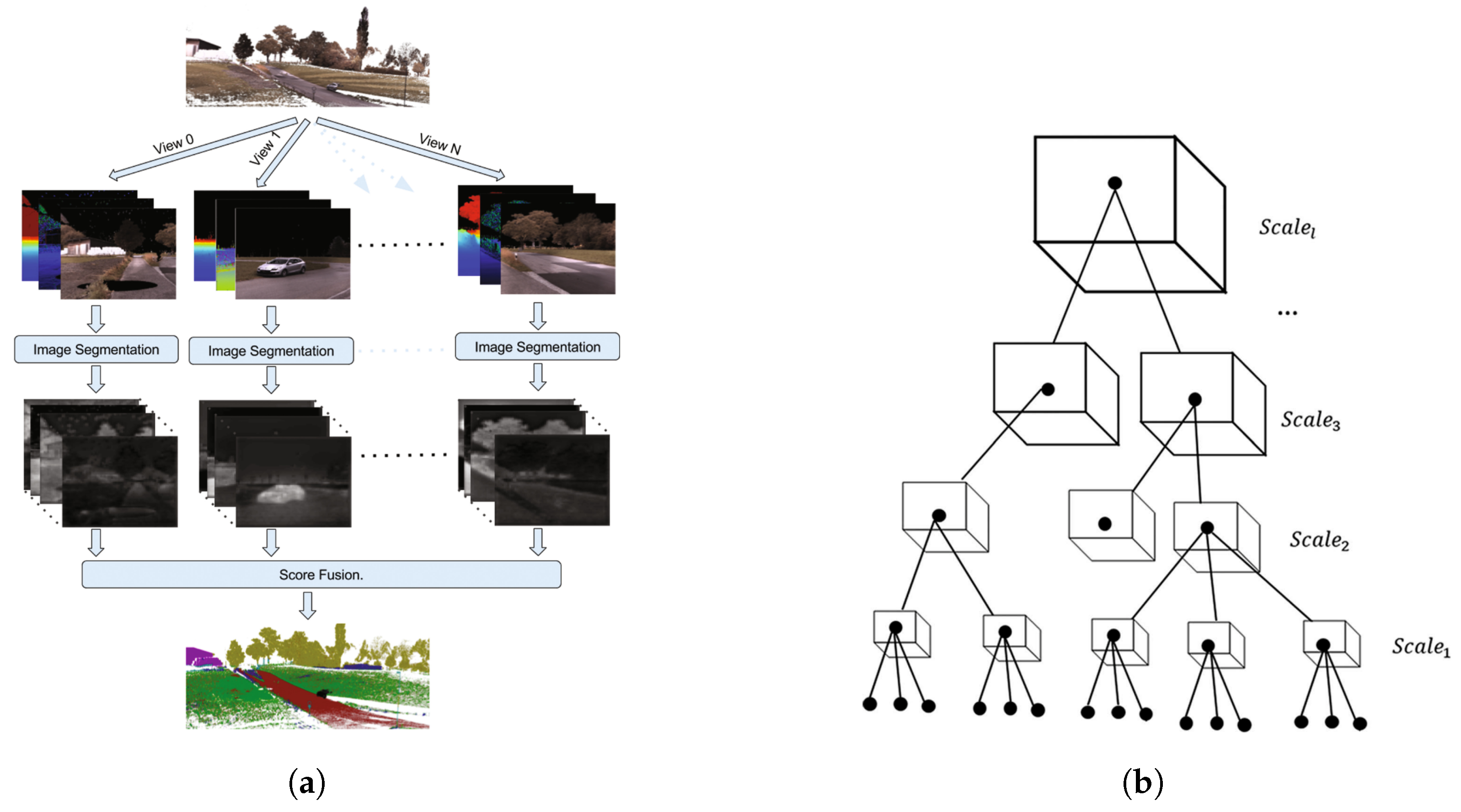
3.3. Scale
3.4. Other Properties
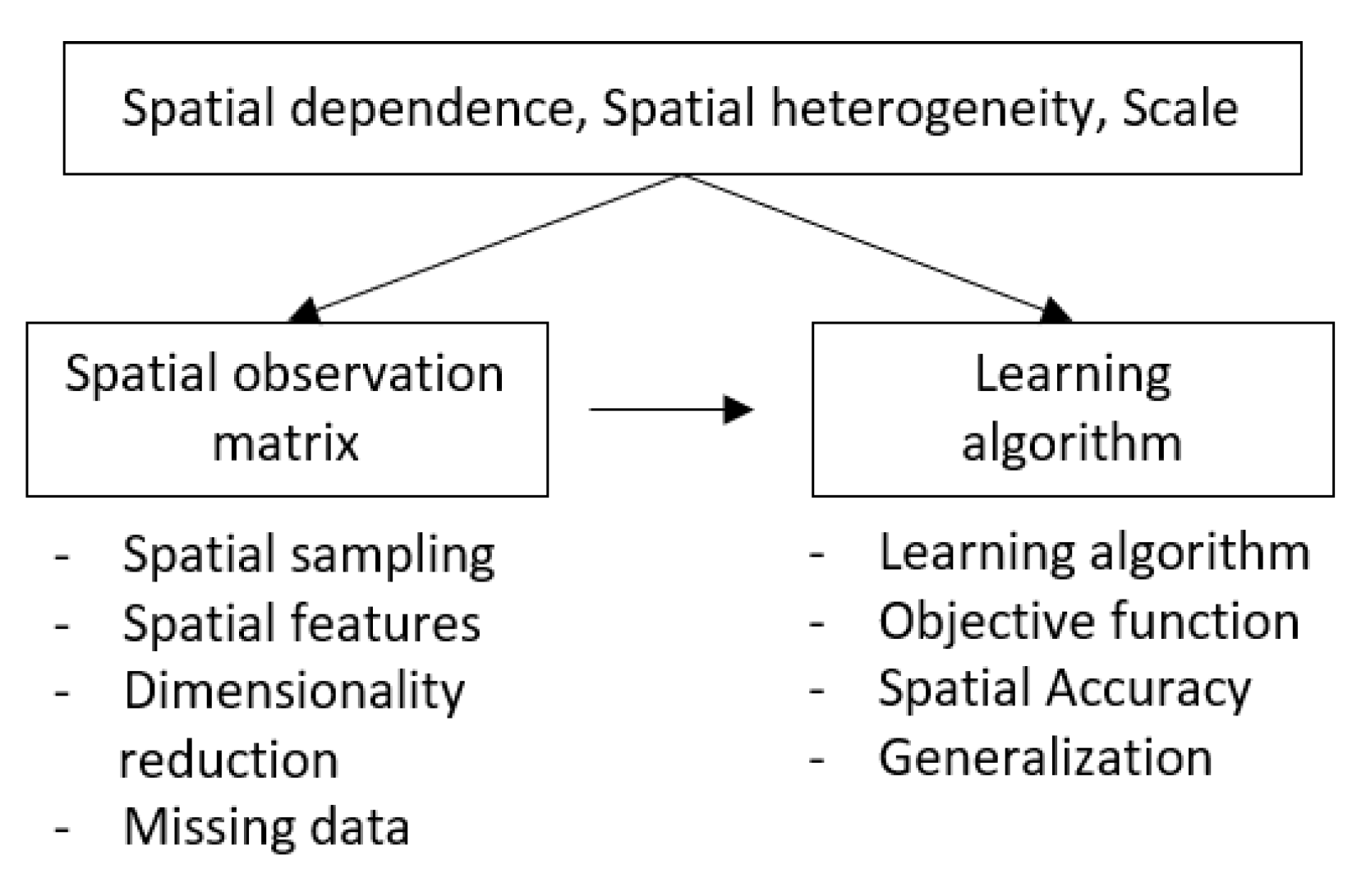
4. Machine Learning of Spatial Data
4.1. Spatial Observation Matrix
4.1.1. Spatial Sampling
4.1.2. Spatial Features
4.1.3. Dimensionality Reduction
4.1.4. Missing Data
4.2. Learning Algorithm
4.2.1. Decision Trees
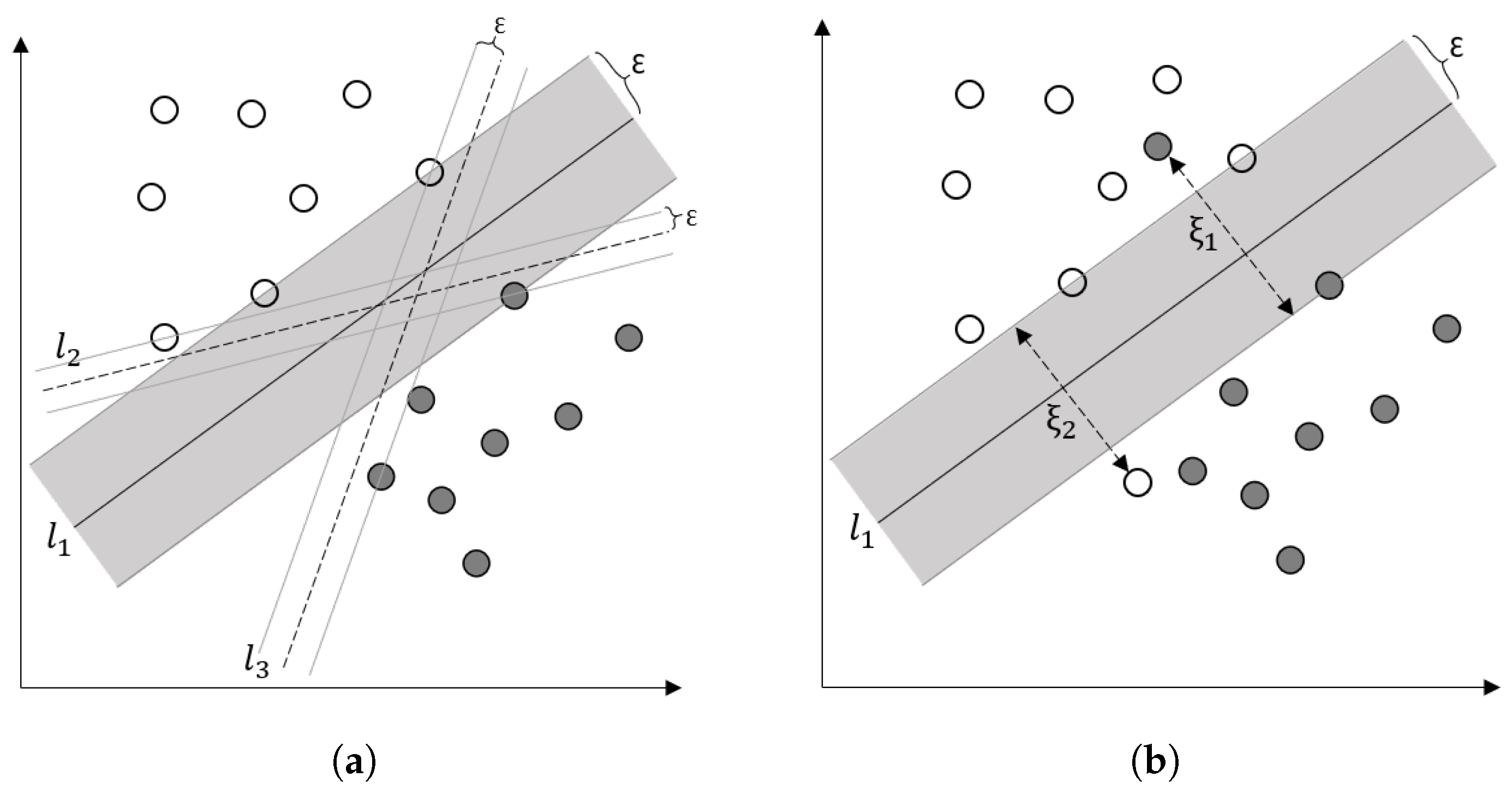
4.2.2. Support Vector Machines
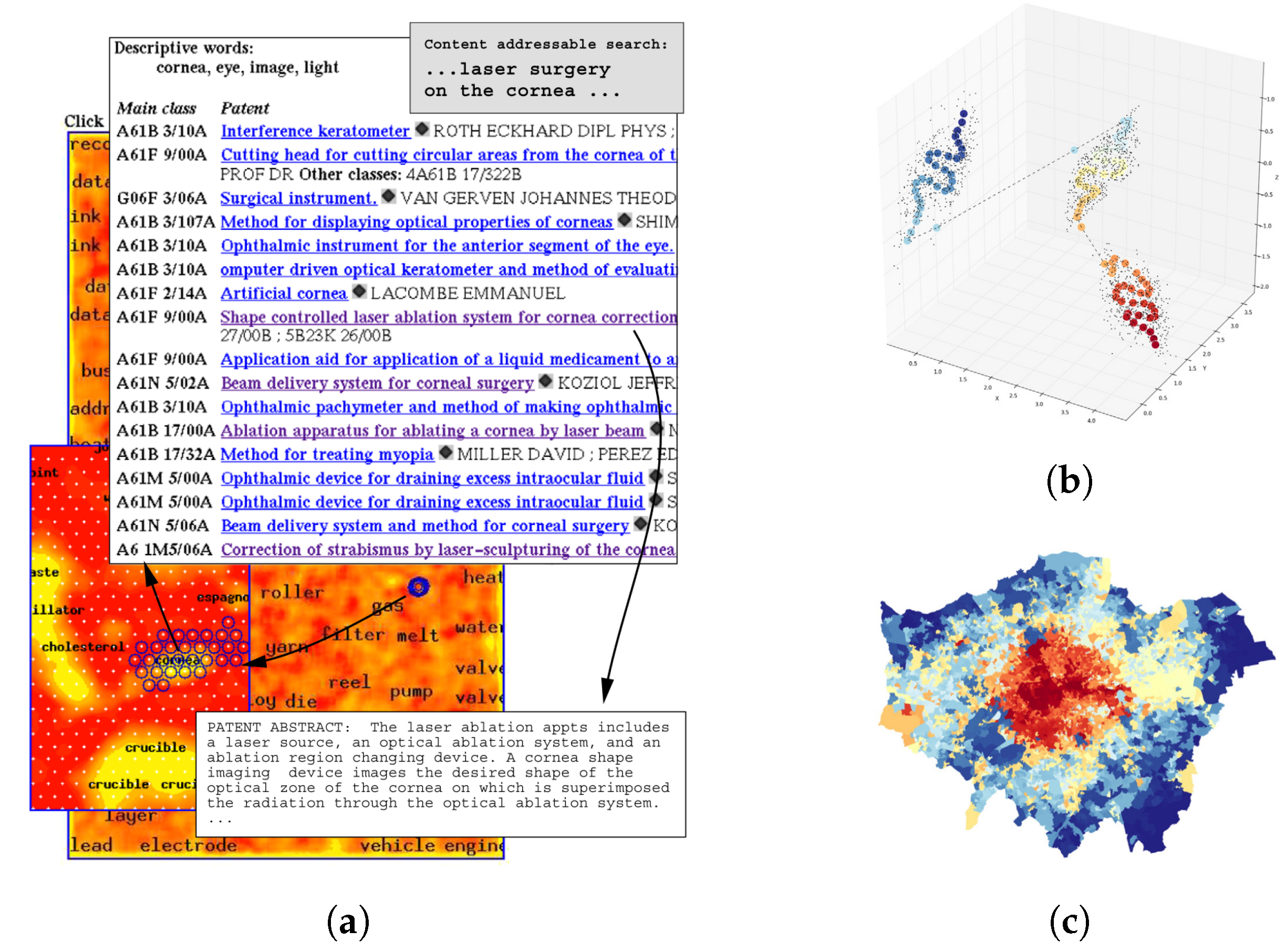
4.2.3. Self-Organizing Maps
4.2.4. Radial Basis Function Networks
4.2.5. Adaptive Resonance Theory Networks
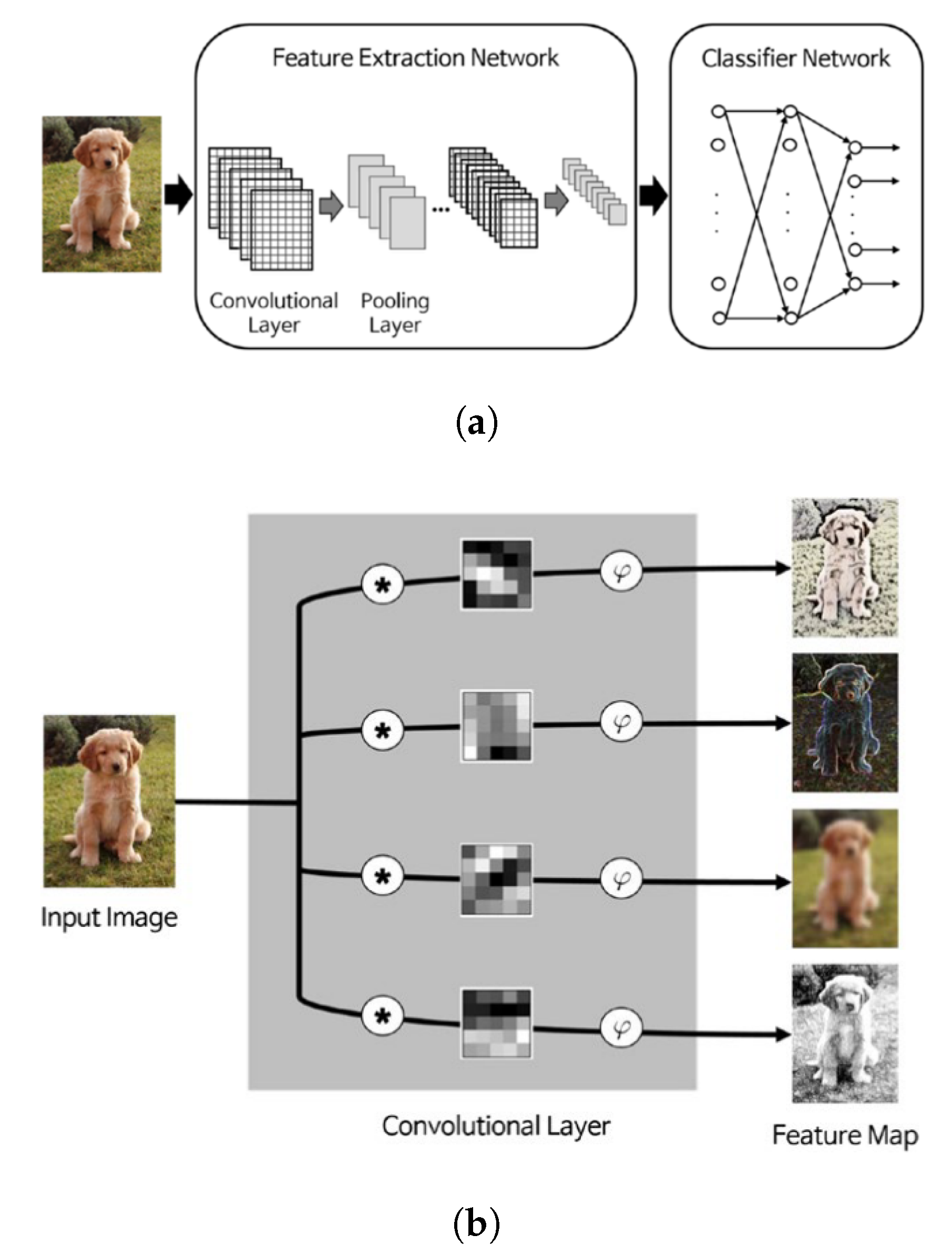
4.2.6. Deep Convolutional Neural Networks
4.2.7. Deep Graph Neural Networks
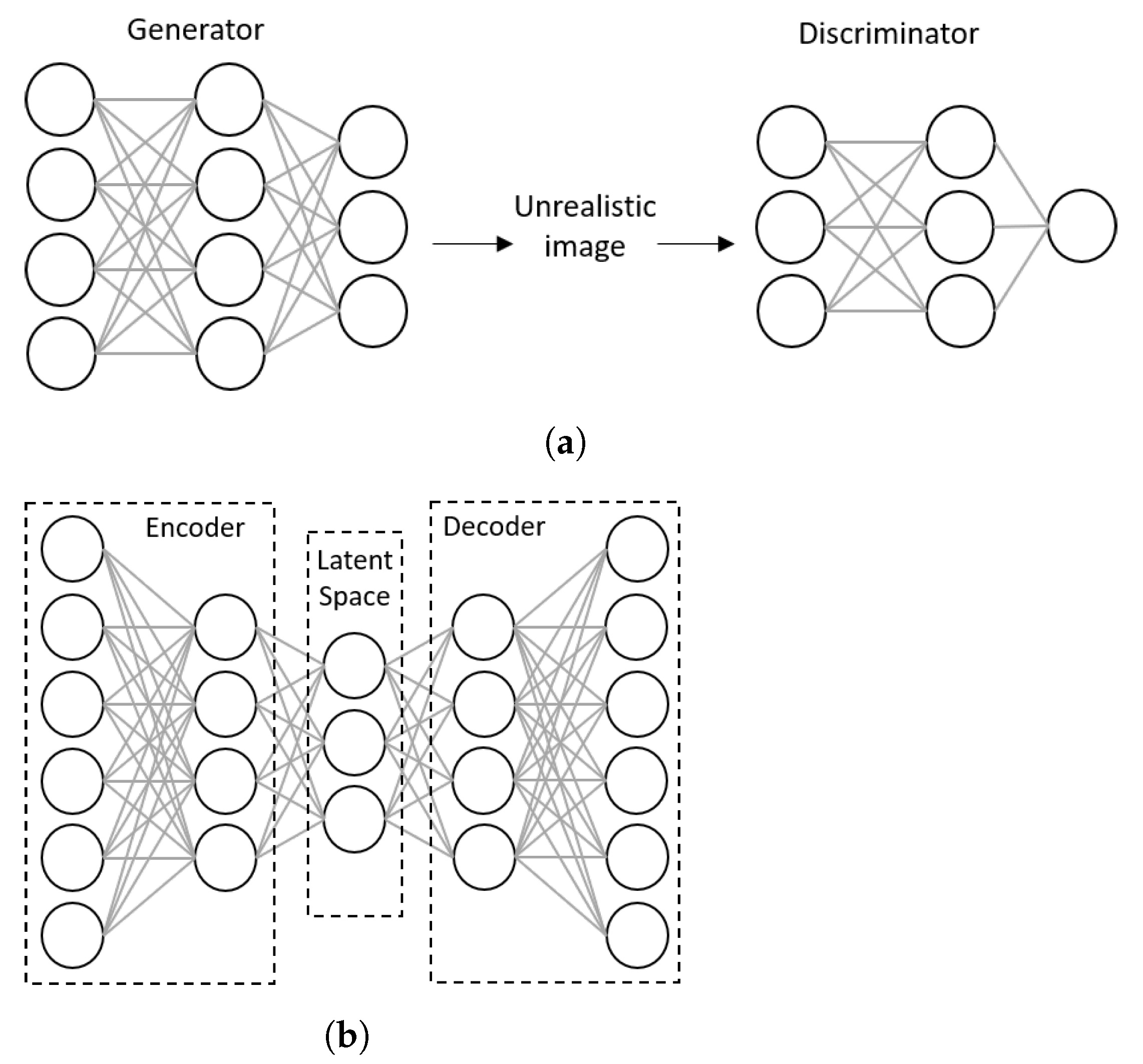
4.2.8. Deep Generative Neural Networks
4.2.9. Learning with DNNs
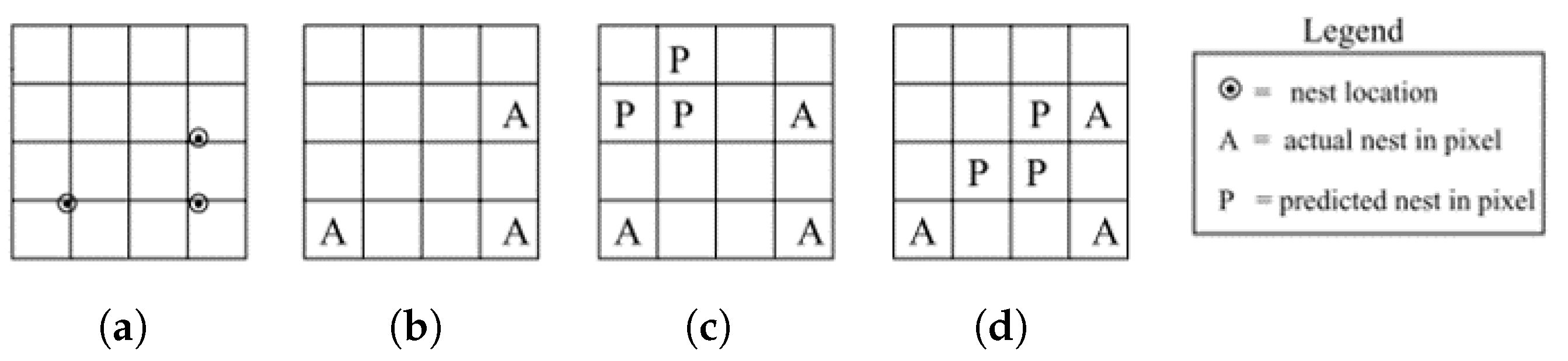
4.2.10. Spatial Accuracy
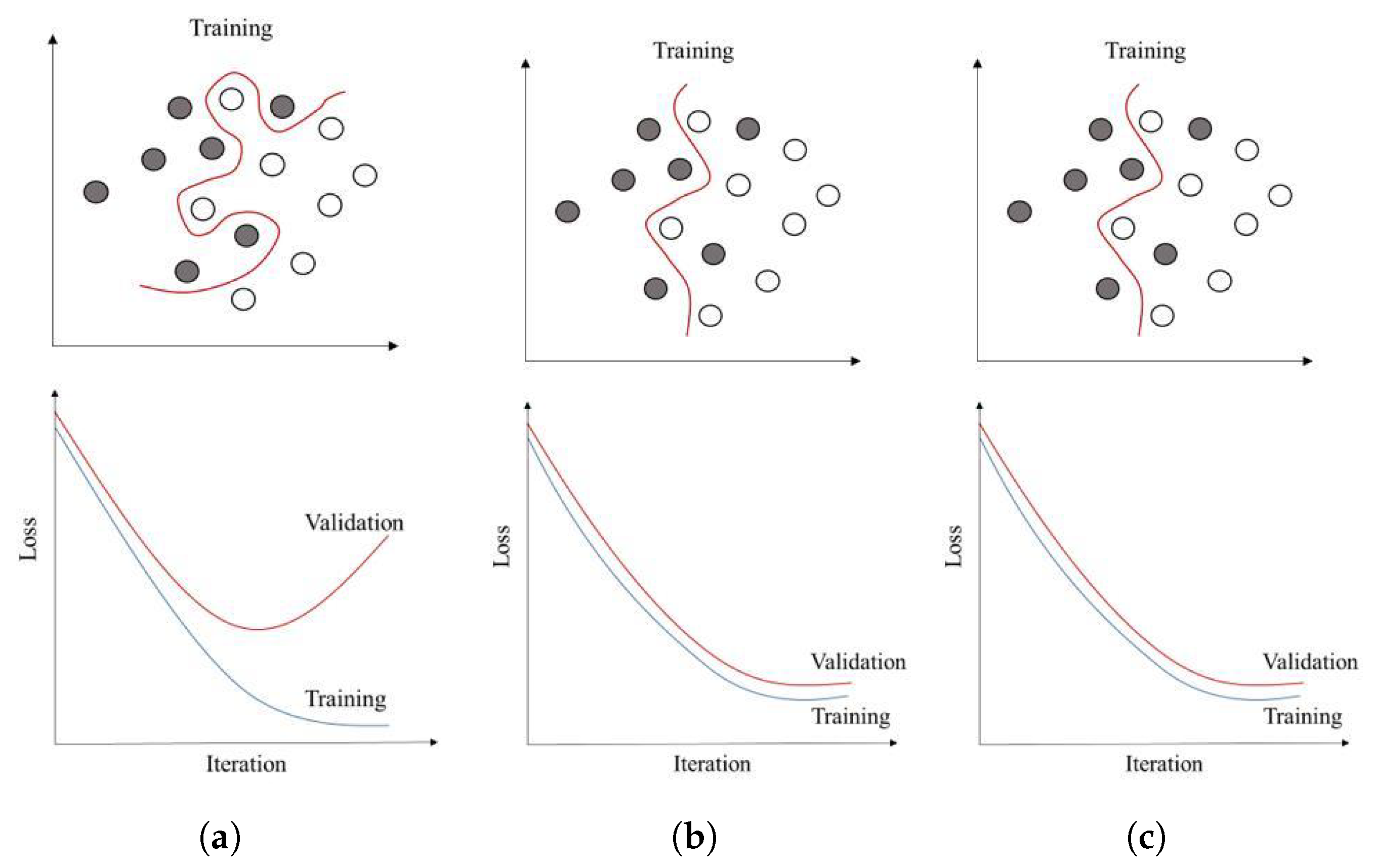
4.2.11. Generalization
5. Spatiotemporal Learning
6. Discussion and Concluding Remarks
- CNNs can be used to automatically estimate the spatial weight matrix, which is usually unknown and needs to be defined by the user to reflect spatial data properties in many spatial problems. Advances may be anticipated in several areas;
- Deep neural networks with convolutional layers have been shown to automatically extract patterns from multiple scales and hierarchies. However, they have so far mainly been used to recognize patterns in raster data sets. Therefore, use cases in a broader range of domains of applications are called for;
- Graph-based deep learning methods provide a new opportunity to apply CNN-based deep learning to problems with graph structure (e.g., social networks) or when the geographic units are irregularly shaped (e.g., census data);
- Further studies for learning in spatio-temporal domains will need to be undertaken as well. Deep neural networks based on a combination of LSTM and CNNs introduce simultaneous learning across space, time, scales, and hierarchies. When augmented with reinforcement learning to add feedback within systems, which is the case in many spatial, social and environmental applications, they can realize the dream of a single universal ML method [139].
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 2018, 216, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. Joint Deep Learning for land cover and land use classification. Remote Sens. Environ. 2019, 221, 173–187. [Google Scholar] [CrossRef] [Green Version]
- Law, S.; Seresinhe, C.I.; Shen, Y.; Gutierrez-Roig, M. Street-Frontage-Net: Urban image classification using deep convolutional neural networks. Int. J. Geogr. Inf. Sci. 2020, 34, 681–707. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, S.; Vargas Munoz, J.E.; Lobry, S.; Tuia, D. Fine-grained landuse characterization using ground-based pictures: A deep learning solution based on globally available data. Int. J. Geogr. Inf. Sci. 2020, 34, 1117–1136. [Google Scholar] [CrossRef]
- Hagenauer, J.; Omrani, H.; Helbich, M. Assessing the performance of 38 machine learning models: The case of land consumption rates in Bavaria, Germany. Int. J. Geogr. Inf. Sci. 2019, 33, 1399–1419. [Google Scholar] [CrossRef] [Green Version]
- Guan, Q.; Wang, L.; Clarke, K.C. An artificial-neural-network-based, constrained CA model for simulating urban growth. Cartogr. Geogr. Inf. Sci. 2005, 32, 369–380. [Google Scholar] [CrossRef] [Green Version]
- Reades, J.; De Souza, J.; Hubbard, P. Understanding urban gentrification through machine learning. Urban Stud. 2019, 56, 922–942. [Google Scholar] [CrossRef] [Green Version]
- Resch, B.; Usländer, F.; Havas, C. Combining machine-learning topic models and spatiotemporal analysis of social media data for disaster footprint and damage assessment. Cartogr. Geogr. Inf. Sci. 2018, 45, 362–376. [Google Scholar] [CrossRef] [Green Version]
- Masjedi, A.; Crawford, M.M. Prediction of Sorghum Biomass Using Time Series Uav-Based Hyperspectral and Lidar data. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3912–3915. [Google Scholar]
- Adhikari, B.; Xu, X.; Ramakrishnan, N.; Prakash, B.A. Epideep: Exploiting embeddings for epidemic forecasting. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 577–586. [Google Scholar]
- Effati, M.; Thill, J.C.; Shabani, S. Geospatial and machine learning techniques for wicked social science problems: Analysis of crash severity on a regional highway corridor. J. Geogr. Syst. 2015, 17, 107–135. [Google Scholar] [CrossRef]
- Skupin, A.; Hagelman, R. Visualizing demographic trajectories with self-organizing maps. GeoInformatica 2005, 9, 159–179. [Google Scholar] [CrossRef]
- Steiniger, S.; Taillandier, P.; Weibel, R. Utilising urban context recognition and machine learning to improve the generalisation of buildings. Int. J. Geogr. Inf. Sci. 2010, 24, 253–282. [Google Scholar] [CrossRef]
- Cunha, E.; Martins, B. Using one-class classifiers and multiple kernel learning for defining imprecise geographic regions. Int. J. Geogr. Inf. Sci. 2014, 28, 2220–2241. [Google Scholar] [CrossRef]
- Chegoonian, A.; Mokhtarzade, M.; Valadan Zoej, M. A comprehensive evaluation of classification algorithms for coral reef habitat mapping: Challenges related to quantity, quality, and impurity of training samples. Int. J. Remote Sens. 2017, 38, 4224–4243. [Google Scholar] [CrossRef]
- Lin, Y.; Kang, M.; Wu, Y.; Du, Q.; Liu, T. A deep learning architecture for semantic address matching. Int. J. Geogr. Inf. Sci. 2020, 34, 559–576. [Google Scholar] [CrossRef]
- Shi, W.; Liu, Z.; An, Z.; Chen, P. RegNet: A neural network model for predicting regional desirability with VGI data. Int. J. Geogr. Inf. Sci. 2021, 35, 175–192. [Google Scholar] [CrossRef]
- Yang, C.; Gidófalvi, G. Detecting regional dominant movement patterns in trajectory data with a convolutional neural network. Int. J. Geogr. Inf. Sci. 2020, 34, 996–1021. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Pang, M.; Wang, J. Classifying airborne LiDAR point clouds via deep features learned by a multi-scale convolutional neural network. Int. J. Geogr. Inf. Sci. 2018, 32, 960–979. [Google Scholar] [CrossRef]
- Yan, J.; Thill, J.C. Visual data mining in spatial interaction analysis with self-organizing maps. Environ. Plan. B Plan. Des. 2009, 36, 466–486. [Google Scholar] [CrossRef]
- Rigol, J.P.; Jarvis, C.H.; Stuart, N. Artificial neural networks as a tool for spatial interpolation. Int. J. Geogr. Inf. Sci. 2001, 15, 323–343. [Google Scholar] [CrossRef]
- Deng, M.; Yang, W.; Liu, Q. Geographically weighted extreme learning machine: A method for space–time prediction. Geogr. Anal. 2017, 49, 433–450. [Google Scholar] [CrossRef]
- Deng, M.; Yang, W.; Liu, Q.; Jin, R.; Xu, F.; Zhang, Y. Heterogeneous space–time artificial neural networks for space–time series prediction. Trans. GIS 2018, 22, 183–201. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Z.; Du, Z.; Huang, B.; Zhang, F.; Liu, R. Geographically and temporally neural network weighted regression for modeling spatiotemporal non-stationary relationships. Int. J. Geogr. Inf. Sci. 2021, 35, 582–608. [Google Scholar] [CrossRef]
- Kanevski, M. Machine Learning for Spatial Environmental Data: Theory, Applications, and Software; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Quiñones, S.; Goyal, A.; Ahmed, Z.U. Geographically weighted machine learning model for untangling spatial heterogeneity of type 2 diabetes mellitus (T2D) prevalence in the USA. Sci. Rep. 2021, 11, 1–13. [Google Scholar]
- Koperski, K.; Adhikary, J.; Han, J. Spatial data mining: Progress and challenges survey paper. In Proceedings of the ACM SIGMOD Workshop on Research Issues on Data Mining and Knowledge Discovery, Montreal, QC, Canada, 4–6 June 1996; Citeseer: University Park, PA, USA, 1996; pp. 1–10. [Google Scholar]
- Mennis, J.; Guo, D. Spatial data mining and geographic knowledge discovery—An introduction. Comput. Environ. Urban Syst. 2009, 33, 403–408. [Google Scholar] [CrossRef]
- Miller, H.J.; Han, J. Geographic Data Mining and Knowledge Discovery; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Jiang, Z. A survey on spatial prediction methods. IEEE Trans. Knowl. Data Eng. 2018, 31, 1645–1664. [Google Scholar] [CrossRef]
- Gopal, S. Artificial neural networks in geospatial analysis. In International Encyclopedia of Geography: People, the Earth, Environment and Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2016; pp. 1–7. [Google Scholar]
- Yang, L.; MacEachren, A.M.; Mitra, P.; Onorati, T. Visually-enabled active deep learning for (geo) text and image classification: A review. ISPRS Int. J. Geo-Inf. 2018, 7, 65. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, T.M. Machine Learning; McGraw-Hill Science: New York, NY, USA, 1997; Volume 1. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Ghahramani, Z. Unsupervised learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 72–112. [Google Scholar]
- Zhu, X.; Goldberg, A.B. Introduction to semi-supervised learning. Synth. Lect. Artif. Intell. Mach. Learn. 2009, 3, 1–130. [Google Scholar] [CrossRef] [Green Version]
- Settles, B. Active Learning Literature Survey; Department of Computer Sciences, University of Wisconsin-Madison: Madison, WI, USA, 2009. [Google Scholar]
- Wulfmeier, M.; Rao, D.; Wang, D.Z.; Ondruska, P.; Posner, I. Large-scale cost function learning for path planning using deep inverse reinforcement learning. Int. J. Robot. Res. 2017, 36, 1073–1087. [Google Scholar] [CrossRef]
- Ma, X.; Li, J.; Kochenderfer, M.J.; Isele, D.; Fujimura, K. Reinforcement learning for autonomous driving with latent state inference and spatial-temporal relationships. arXiv 2020, arXiv:2011.04251. [Google Scholar]
- Ganapathi Subramanian, S.; Crowley, M. Using spatial reinforcement learning to build forest wildfire dynamics models from satellite images. Front. ICT 2018, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Zhang, M.; Ren, F.; Tan, G. Emotional multiagent reinforcement learning in spatial social dilemmas. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3083–3096. [Google Scholar] [CrossRef]
- Haining, R. The special nature of spatial data. In The SAGE Handbook of Spatial Analysis; SAGE Publications: Los Angeles, CA, USA, 2009; pp. 5–23. [Google Scholar]
- Anselin, L. What Is Special about Spatial Data? Alternative Perspectives on Spatial Data Analysis (89-4); eScholarship University of California Santa Barbara: Santa Barbara, CA, USA, 1989. [Google Scholar]
- Getis, A. Spatial dependence and heterogeneity and proximal databases. In Spatial Analysis and GIS; Taylor & Francis: London, UK, 1994; pp. 105–120. [Google Scholar]
- Thill, J.C. Is spatial really that special? A tale of spaces. In Information Fusion and Geographic Information Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–12. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Getis, A. Spatial autocorrelation. In Handbook of Applied Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 255–278. [Google Scholar]
- Griffith, D.A. Spatial autocorrelation. In A Primer; Association of American Geographers: Washington, DC, USA, 1987. [Google Scholar]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Geary, R.C. The contiguity ratio and statistical mapping. Inc. Stat. 1954, 5, 115–146. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Delmelle, E. Spatial sampling. In The SAGE Handbook of Spatial Analysis; Sage: Thousand Oaks, CA, USA, 2009; Volume 183, p. 206. [Google Scholar]
- Dao, T.H.D.; Thill, J.C. The SpatialARMED framework: Handling complex spatial components in spatial association rule mining. Geogr. Anal. 2016, 48, 248–274. [Google Scholar] [CrossRef]
- Dao, T.H.D.; Thill, J.C. CrimeScape: Analysis of socio-spatial associations of urban residential motor vehicle theft. Soc. Sci. Res. 2021, 102618. [Google Scholar] [CrossRef]
- Dale, M.R.; Fortin, M.J. Spatial Analysis: A Guide for Ecologists; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Thill, J.C. Research on urban and regional systems: Contributions from gis&t, spatial analysis, and location modeling. In Innovations in Urban and Regional Systems; Springer International Publishing: London, UK, 2020; pp. 3–20. [Google Scholar]
- Murwira, A.; Skidmore, A.K. The response of elephants to the spatial heterogeneity of vegetation in a Southern African agricultural landscape. Landsc. Ecol. 2005, 20, 217–234. [Google Scholar] [CrossRef]
- Webster, R. Is soil variation random? Geoderma 2000, 97, 149–163. [Google Scholar] [CrossRef]
- McLaughlin, G.A.; Langdon, E.M.; Crutchley, J.M.; Holt, L.J.; Forest, M.G.; Newby, J.M.; Gladfelter, A.S. Spatial heterogeneity of the cytosol revealed by machine learning-based 3D particle tracking. Mol. Biol. Cell 2020, 31, 1498–1511. [Google Scholar] [CrossRef]
- Mohsenzadeh, Y.; Mullin, C.; Lahner, B.; Oliva, A. Emergence of Visual center-periphery Spatial organization in Deep convolutional neural networks. Sci. Rep. 2020, 10, 4638. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Li, W.; Wright, D.; Aydin, O.; Wilson, D.; Maher, O.; Raad, M. Artificial intelligence approaches. arXiv 2019, arXiv:1908.10345. [Google Scholar] [CrossRef] [Green Version]
- Lam, N. FC-21-Resolution; University Consortium for Geographic Information Science GIS and T Body of Knowledge: Ann Arbor, MI, USA, 2019. [Google Scholar]
- Shekhar, S.; Gandhi, V.; Zhang, P.; Vatsavai, R.R.; Fotheringham, A.; Rogerson, P. Availability of spatial data mining techniques. In The SAGE Handbook of Spatial Analysis; Sage: Thousand Oaks, CA, USA, 2009; pp. 159–181. [Google Scholar]
- Fotheringham, A.S.; Wong, D.W. The modifiable areal unit problem in multivariate statistical analysis. Environ. Plan. A 1991, 23, 1025–1044. [Google Scholar] [CrossRef]
- Openshaw, S. A million or so correlation coefficients, three experiments on the modifiable areal unit problem. In Statistical Applications in the Spatial Sciences; Pion: London, UK, 1979; pp. 127–144. [Google Scholar]
- Arbia, G. Spatial Data Configuration in Statistical Analysis of Regional Economic and Related Problems; Springer Science & Business Media: New York, NY, USA, 2012; Volume 14. [Google Scholar]
- Batty, M.; Sikdar, P. Spatial aggregation in gravity models. 1. An information-theoretic framework. Environ. Plan. A 1982, 14, 377–405. [Google Scholar] [CrossRef]
- Xiao, J. Spatial Aggregation Entropy: A Heterogeneity and Uncertainty Metric of Spatial Aggregation. Ann. Am. Assoc. Geogr. 2021, 111, 1236–1252. [Google Scholar] [CrossRef]
- Kwan, M.P. The uncertain geographic context problem. Ann. Assoc. Am. Geogr. 2012, 102, 958–968. [Google Scholar] [CrossRef]
- Robinson, W.S. Ecological correlations and the behavior of individuals. Int. J. Epidemiol. 2009, 38, 337–341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, W.; Lin, C.; Lin, J.; Jiang, J.; Xia, J.; Turkay, C.; Chen, W. Revisiting the modifiable areal unit problem in deep traffic prediction with visual analytics. IEEE Trans. Vis. Comput. Graph. 2020, 27, 839–848. [Google Scholar] [CrossRef] [PubMed]
- Chawla, S.; Shekhar, S.; Wu, W.; Özesmi, U. Predicting Locations Using Map Similarity (PLUMS): A Framework for Spatial Data Mining. In Proceedings of the International Workshop on Multimedia Data Mining (MDM/KDD’2000), in Conjunction with ACM SIGKDD Conference, Boston, MA, USA, 20 August 2000; pp. 14–24. [Google Scholar]
- Chen, J.; Lu, F.; Peng, G. A quantitative approach for delineating principal fairways of ship passages through a strait. Ocean. Eng. 2015, 103, 188–197. [Google Scholar] [CrossRef]
- Acheson, E.; Volpi, M.; Purves, R.S. Machine learning for cross-gazetteer matching of natural features. Int. J. Geogr. Inf. Sci. 2020, 34, 708–734. [Google Scholar] [CrossRef]
- Santos, R.; Murrieta-Flores, P.; Calado, P.; Martins, B. Toponym matching through deep neural networks. Int. J. Geogr. Inf. Sci. 2018, 32, 324–348. [Google Scholar] [CrossRef] [Green Version]
- Purves, R.; Jones, C. Geographic information retrieval. SIGSPATIAL Spec. 2011, 3, 2–4. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Thill, J.C. Spatial queries with qualitative locations in spatial information systems. Comput. Environ. Urban Syst. 2006, 30, 485–502. [Google Scholar] [CrossRef]
- Guo, Z.; Feng, C.C. Using multi-scale and hierarchical deep convolutional features for 3D semantic classification of TLS point clouds. Int. J. Geogr. Inf. Sci. 2020, 34, 661–680. [Google Scholar] [CrossRef]
- Li, X.; Ma, R.; Zhang, Q.; Li, D.; Liu, S.; He, T.; Zhao, L. Anisotropic characteristic of artificial light at night–Systematic investigation with VIIRS DNB multi-temporal observations. Remote Sens. Environ. 2019, 233, 111357. [Google Scholar] [CrossRef]
- Özyeşil, O.; Voroninski, V.; Basri, R.; Singer, A. A survey of structure from motion. Acta Numer. 2017, 26, 305–364. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendón-Mancha, J.M. Visual simultaneous localization and mapping: A survey. Artif. Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Jain, S.; Smit, A.; Truong, S.Q.; Nguyen, C.D.; Huynh, M.T.; Jain, M.; Young, V.A.; Ng, A.Y.; Lungren, M.P.; Rajpurkar, P. VisualCheXbert: Addressing the discrepancy between radiology report labels and image labels. In Proceedings of the Conference on Health, Inference, and Learning, Virtual Event, Toronto, ON, Canada, 8–10 April 2021; pp. 105–115. [Google Scholar]
- Zhang, J.; Liu, J.; Pan, B.; Shi, Z. Domain adaptation based on correlation subspace dynamic distribution alignment for remote sensing image scene classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7920–7930. [Google Scholar] [CrossRef]
- Gahegan, M. Is inductive machine learning just another wild goose (or might it lay the golden egg)? Int. J. Geogr. Inf. Sci. 2003, 17, 69–92. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Pontius Jr, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hase, N.; Ito, S.; Kaneko, N.; Sumi, K. Data augmentation for intra-class imbalance with generative adversarial network. In Proceedings of the Fourteenth International Conference on Quality Control by Artificial Vision, Mulhouse, France, 15–17 May 2019; Volume 11172. [Google Scholar]
- Uzkent, B.; Yeh, C.; Ermon, S. Efficient object detection in large images using deep reinforcement learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 1824–1833. [Google Scholar]
- Mathe, S.; Pirinen, A.; Sminchisescu, C. Reinforcement learning for visual object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2894–2902. [Google Scholar]
- Martin, R.; Aler, R.; Valls, J.M.; Galván, I.M. Machine learning techniques for daily solar energy prediction and interpolation using numerical weather models. Concurr. Comput. Pract. Exp. 2016, 28, 1261–1274. [Google Scholar] [CrossRef]
- Zanella, L.; Folkard, A.M.; Blackburn, G.A.; Carvalho, L.M. How well does random forest analysis model deforestation and forest fragmentation in the Brazilian Atlantic forest? Environ. Ecol. Stat. 2017, 24, 529–549. [Google Scholar] [CrossRef] [Green Version]
- Cui, W.; Shen, K.; Yu, W. Spatial deep learning for wireless scheduling. IEEE J. Sel. Areas Commun. 2019, 37, 1248–1261. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of spatial predictor variable selection in machine learning applications–Moving from data reproduction to spatial prediction. Ecol. Model. 2019, 411, 108815. [Google Scholar] [CrossRef] [Green Version]
- Anselin, L.; Arribas-Bel, D. Spatial fixed effects and spatial dependence in a single cross-section. Pap. Reg. Sci. 2013, 92, 3–17. [Google Scholar] [CrossRef]
- Sommervoll, Å.; Sommervoll, D.E. Learning from man or machine: Spatial fixed effects in urban econometrics. Reg. Sci. Urban Econ. 2019, 77, 239–252. [Google Scholar] [CrossRef]
- Wu, S.S.; Qiu, X.; Usery, E.L.; Wang, L. Using geometrical, textural, and contextual information of land parcels for classification of detailed urban land use. Ann. Assoc. Am. Geogr. 2009, 99, 76–98. [Google Scholar] [CrossRef]
- Cristóbal, G.; Bescós, J.; Santamaría, J. Image analysis through the Wigner distribution function. Appl. Opt. 1989, 28, 262–271. [Google Scholar] [CrossRef]
- Myint, S.W. A robust texture analysis and classification approach for urban land-use and land-cover feature discrimination. Geocarto Int. 2001, 16, 29–40. [Google Scholar] [CrossRef]
- Turner, M. Texture transformation by Gabor function. Biol. Cybernation 1986, 55, 71–82. [Google Scholar]
- Zhu, C.; Yang, X. Study of remote sensing image texture analysis and classification using wavelet. Int. J. Remote Sens. 1998, 19, 3197–3203. [Google Scholar] [CrossRef]
- Platt, R.V.; Rapoza, L. An evaluation of an object-oriented paradigm for land use/land cover classification. Prof. Geogr. 2008, 60, 87–100. [Google Scholar] [CrossRef]
- Zhan, Q.; Molenaar, M.; Gorte, B. Urban land use classes with fuzzy membership and classification based on integration of remote sensing and GIS. Int. Arch. Photogramm. Remote Sens. 2000, 33, 1751–1759. [Google Scholar]
- Herold, M.; Liu, X.; Clarke, K.C. Spatial metrics and image texture for mapping urban land use. Photogramm. Eng. Remote Sens. 2003, 69, 991–1001. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4490–4499. [Google Scholar]
- Lawin, F.J.; Danelljan, M.; Tosteberg, P.; Bhat, G.; Khan, F.S.; Felsberg, M. Deep projective 3D semantic segmentation. In International Conference on Computer Analysis of Images and Patterns; Springer: Berlin/Heidelberg, Germany, 2017; pp. 95–107. [Google Scholar]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Hagenauer, J.; Helbich, M. Mining urban land-use patterns from volunteered geographic information by means of genetic algorithms and artificial neural networks. Int. J. Geogr. Inf. Sci. 2012, 26, 963–982. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal components in regression analysis. In Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 1986; pp. 129–155. [Google Scholar]
- Kohonen, T. Self-Organization and Associative Memory; Springer Science & Business Media: New York, NY, USA, 2012; Volume 8. [Google Scholar]
- Harris, P.; Brunsdon, C.; Charlton, M. Geographically weighted principal components analysis. Int. J. Geogr. Inf. Sci. 2011, 25, 1717–1736. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Qu, L.; Li, L.; Zhang, Y.; Hu, J. PPCA-based missing data imputation for traffic flow volume: A systematical approach. IEEE Trans. Intell. Transp. Syst. 2009, 10, 512–522. [Google Scholar]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Harris, P.; Fotheringham, A.; Crespo, R.; Charlton, M. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Math. Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Chen, H. Principal Component Analysis with Missing Data and Outliers; Electrical and Computer Engineering Department, Rutgers University: Piscataway, NJ, USA, 2002. [Google Scholar]
- Li, Y.; Li, Z.; Li, L.; Zhang, Y.; Jin, M. Comparison on PPCA, KPPCA and MPPCA based missing data imputing for traffic flow. In ICTIS 2013: Improving Multimodal Transportation Systems-Information, Safety, and Integration; American Society of Civil Engineers: New York, NY, USA, 2013; pp. 1151–1156. [Google Scholar]
- Li, L.; Li, Y.; Li, Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence. Transp. Res. Part C Emerg. Technol. 2013, 34, 108–120. [Google Scholar] [CrossRef]
- Stojanova, D.; Ceci, M.; Appice, A.; Malerba, D.; Džeroski, S. Global and local spatial autocorrelation in predictive clustering trees. In International Conference on Discovery Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 307–322. [Google Scholar]
- Jiang, Z.; Shekhar, S.; Zhou, X.; Knight, J.; Corcoran, J. Focal-test-based spatial decision tree learning: A summary of results. In Proceedings of the 2013 IEEE 13th International Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; pp. 320–329. [Google Scholar]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Lee, C.H.; Greiner, R.; Schmidt, M. Support vector random fields for spatial classification. In European Conference on Principles of Data Mining and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2005; pp. 121–132. [Google Scholar]
- Agarwal, P.; Skupin, A. Self-Organising Maps: Applications in Geographic Information Science; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef]
- Bação, F.; Lobo, V.; Painho, M. The self-organizing map, the Geo-SOM, and relevant variants for geosciences. Comput. Geosci. 2005, 31, 155–163. [Google Scholar] [CrossRef]
- Moosavi, V. Contextual mapping: Visualization of high-dimensional spatial patterns in a single geo-map. Comput. Environ. Urban Syst. 2017, 61, 1–12. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Hagenauer, J.; Farajzadeh, M.; Helbich, M. Performance analysis of radial basis function networks and multi-layer perceptron networks in modeling urban change: A case study. Int. J. Geogr. Inf. Sci. 2015, 29, 606–623. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. A spatial interpolation method based on radial basis function networks incorporating a semivariogram model. J. Hydrol. 2004, 288, 288–298. [Google Scholar] [CrossRef]
- Yeh, I.C.; Huang, K.C.; Kuo, Y.H. Spatial interpolation using MLP–RBFN hybrid networks. Int. J. Geogr. Inf. Sci. 2013, 27, 1884–1901. [Google Scholar] [CrossRef]
- Gong, Z.; Thill, J.C.; Liu, W. ART-P-MAP neural networks modeling of land-use change: Accounting for spatial heterogeneity and uncertainty. Geogr. Anal. 2015, 47, 376–409. [Google Scholar] [CrossRef]
- Malamiri, H.R.G.; Aliabad, F.A.; Shojaei, S.; Morad, M.; Band, S.S. A study on the use of UAV images to improve the separation accuracy of agricultural land areas. Comput. Electron. Agric. 2021, 184, 106079. [Google Scholar] [CrossRef]
- Yariyan, P.; Ali Abbaspour, R.; Chehreghan, A.; Karami, M.; Cerdà, A. GIS-based seismic vulnerability mapping: A comparison of artificial neural networks hybrid models. Geocarto Int. 2021. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S.; Reynolds, J.H. ARTMAP: Supervised real-time learning and classification of nonstationary data by a self-organizing neural network. Neural Netw. 1991, 4, 565–588. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, G.A.; Grossberg, S.; Markuzon, N.; Reynolds, J.H.; Rosen, D.B. Fuzzy ARTMAP: A neural network architecture for incremental supervised learning of analog multidimensional maps. IEEE Trans. Neural Netw. 1992, 3, 698–713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Kim, P. Matlab Deep Learning. With Machine Learning, Neural Networks and Artificial Intelligence; Apress: New York, NY, USA, 2017; Volume 130. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef] [Green Version]
- Min, S.; Gao, Z.; Peng, J.; Wang, L.; Qin, K.; Fang, B. STGSN—A Spatial–Temporal Graph Neural Network framework for time-evolving social networks. Knowl.-Based Syst. 2021, 214, 106746. [Google Scholar] [CrossRef]
- Zeng, Y.; Tang, J. RLC-GNN: An Improved Deep Architecture for Spatial-Based Graph Neural Network with Application to Fraud Detection. Appl. Sci. 2021, 11, 5656. [Google Scholar] [CrossRef]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 2, pp. 729–734. [Google Scholar]
- Bui, K.H.N.; Cho, J.; Yi, H. Spatial-temporal graph neural network for traffic forecasting: An overview and open research issues. Appl. Intell. 2021. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Estrach, J.B.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. In Proceedings of the 2nd International Conference on Learning Representations, ICLR, Banff, AB, Canada, 14–16 April 2014; Volume 2014. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Wu, D.; Gao, L.; Xiong, X.; Chinazzi, M.; Vespignani, A.; Ma, Y.A.; Yu, R. DeepGLEAM: A hybrid mechanistic and deep learning model for COVID-19 forecasting. arXiv 2021, arXiv:2102.06684. [Google Scholar]
- Ye, J.; Zhao, J.; Ye, K.; Xu, C. How to build a graph-based deep learning architecture in traffic domain: A survey. IEEE Trans. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Ahmedt-Aristizabal, D.; Armin, M.A.; Denman, S.; Fookes, C.; Petersson, L. Graph-Based Deep Learning for Medical Diagnosis and Analysis: Past, Present and Future. arXiv 2021, arXiv:2105.13137. [Google Scholar]
- Vashishth, S.; Yadati, N.; Talukdar, P. Graph-based deep learning in natural language processing. In Proceedings of the 7th ACM IKDD CoDS and 25th COMAD, Hyderabad, India, 5–7 January 2020; ACM: New York, NY, USA, 2020; pp. 371–372. [Google Scholar]
- Zhang, C.; James, J.; Liu, Y. Spatial-temporal graph attention networks: A deep learning approach for traffic forecasting. IEEE Access 2019, 7, 166246–166256. [Google Scholar] [CrossRef]
- Shang, R.; Meng, Y.; Zhang, W.; Shang, F.; Jiao, L.; Yang, S. Graph Convolutional Neural Networks with Geometric and Discrimination information. Eng. Appl. Artif. Intell. 2021, 104, 104364. [Google Scholar] [CrossRef]
- Iddianozie, C.; McArdle, G. Towards Robust Representations of Spatial Networks Using Graph Neural Networks. Appl. Sci. 2021, 11, 6918. [Google Scholar] [CrossRef]
- Jilani, M.; Corcoran, P.; Bertolotto, M. Multi-granular street network representation towards quality assessment of OpenStreetMap data. In Proceedings of the Sixth ACM SIGSPATIAL International Workshop on Computational Transportation Science, Orlando, FL, USA, 5 November 2013; pp. 19–24. [Google Scholar]
- Ahmadzai, F.; Rao, K.L.; Ulfat, S. Assessment and modelling of urban road networks using Integrated Graph of Natural Road Network (a GIS-based approach). J. Urban Manag. 2019, 8, 109–125. [Google Scholar] [CrossRef]
- Anderson, T.; Dragićević, S. Representing complex evolving spatial networks: Geographic network automata. ISPRS Int. J. Geo-Inf. 2020, 9, 270. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Cui, P.; Zhu, W. Deep learning on graphs: A survey. IEEE Trans. Knowl. Data Eng. 2020. [Google Scholar] [CrossRef] [Green Version]
- Lafferty, J.; McCallum, A.; Pereira, F.C. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the 18th International Conference on Machine Learning, San Francisco, CA, USA, 28 June–1 July 2001; ACM: New York, NY, USA, 2001; pp. 282–289. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. arXiv 2019, arXiv:1906.02691. [Google Scholar] [CrossRef]
- Zhu, D.; Cheng, X.; Zhang, F.; Yao, X.; Gao, Y.; Liu, Y. Spatial interpolation using conditional generative adversarial neural networks. Int. J. Geogr. Inf. Sci. 2020, 34, 735–758. [Google Scholar] [CrossRef]
- Li, L.; Franklin, M.; Girguis, M.; Lurmann, F.; Wu, J.; Pavlovic, N.; Breton, C.; Gilliland, F.; Habre, R. Spatiotemporal imputation of MAIAC AOD using deep learning with downscaling. Remote Sens. Environ. 2020, 237, 111584. [Google Scholar] [CrossRef]
- Mikołajczyk, A.; Grochowski, M. Data augmentation for improving deep learning in image classification problem. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Swinoujscie, Poland, 9–12 May 2018; pp. 117–122. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Penatti, O.A.; Nogueira, K.; Dos Santos, J.A. Do deep features generalize from everyday objects to remote sensing and aerial scenes domains? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 44–51. [Google Scholar]
- Zhang, S.; Zhang, X.; Zhang, A.; Fu, H.; Cheng, J.; Huang, H.; Sun, G.; Zhang, L.; Yao, Y. Fusion Of Low-And High-Level Features For Uav Hyperspectral Image Classification. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–4. [Google Scholar]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land use classification in remote sensing images by convolutional neural networks. arXiv 2015, arXiv:1508.00092. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Zou, Q.; Ni, L.; Zhang, T.; Wang, Q. Deep learning based feature selection for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2321–2325. [Google Scholar] [CrossRef]
- Chawla, S.; Shekhar, S.; Wu, W.L.; Ozesmi, U. Modeling Spatial Dependencies for Mining Geospatial Data: An Introduction; Citeseer: University Park, PA, USA, 2000. [Google Scholar]
- Schaffer, C. Selecting a classification method by cross-validation. Mach. Learn. 1993, 13, 135–143. [Google Scholar] [CrossRef]
- Zheng, M.; Tang, W.; Zhao, X. Hyperparameter optimization of neural network-driven spatial models accelerated using cyber-enabled high-performance computing. Int. J. Geogr. Inf. Sci. 2019, 33, 314–345. [Google Scholar] [CrossRef]
- Heremans, S.; Van Orshoven, J. Machine learning methods for sub-pixel land-cover classification in the spatially heterogeneous region of Flanders (Belgium): A multi-criteria comparison. Int. J. Remote Sens. 2015, 36, 2934–2962. [Google Scholar] [CrossRef] [Green Version]
- Du, Z.; Wu, S.; Zhang, F.; Liu, R.; Zhou, Y. Extending geographically and temporally weighted regression to account for both spatiotemporal heterogeneity and seasonal variations in coastal seas. Ecol. Inform. 2018, 43, 185–199. [Google Scholar] [CrossRef]
- Shi, X.; Yeung, D.Y. Machine learning for spatiotemporal sequence forecasting: A survey. arXiv 2018, arXiv:1808.06865. [Google Scholar]
- Mazzia, V.; Khaliq, A.; Chiaberge, M. Improvement in land cover and crop classification based on temporal features learning from Sentinel-2 data using recurrent-convolutional neural network (R-CNN). Appl. Sci. 2020, 10, 238. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Peng, H.; Wang, H.; Du, B.; Bhuiyan, M.Z.A.; Ma, H.; Liu, J.; Wang, L.; Yang, Z.; Du, L.; Wang, S.; et al. Spatial temporal incidence dynamic graph neural networks for traffic flow forecasting. Inf. Sci. 2020, 521, 277–290. [Google Scholar] [CrossRef]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Zhang, W.; Thill, J.C. Mesoscale structures in world city networks. Ann. Am. Assoc. Geogr. 2019, 109, 887–908. [Google Scholar] [CrossRef]
- Lee, C.; Wilkinson, D.J. A review of stochastic block models and extensions for graph clustering. Appl. Netw. Sci. 2019, 4, 1–50. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikparvar, B.; Thill, J.-C. Machine Learning of Spatial Data. ISPRS Int. J. Geo-Inf. 2021, 10, 600. https://doi.org/10.3390/ijgi10090600
Nikparvar B, Thill J-C. Machine Learning of Spatial Data. ISPRS International Journal of Geo-Information. 2021; 10(9):600. https://doi.org/10.3390/ijgi10090600
Chicago/Turabian StyleNikparvar, Behnam, and Jean-Claude Thill. 2021. "Machine Learning of Spatial Data" ISPRS International Journal of Geo-Information 10, no. 9: 600. https://doi.org/10.3390/ijgi10090600
APA StyleNikparvar, B., & Thill, J.-C. (2021). Machine Learning of Spatial Data. ISPRS International Journal of Geo-Information, 10(9), 600. https://doi.org/10.3390/ijgi10090600






