A Trajectory Scoring Tool for Local Anomaly Detection in Maritime Traffic Using Visual Analytics

Abstract

With the recent increase in the use of sea transportation, the importance of maritime surveillance for detecting unusual vessel behavior related to several illegal activities has also risen. Unfortunately, the data collected by surveillance systems are often incomplete, creating a need for the data gaps to be filled using techniques such as interpolation methods. However, such approaches do not decrease the uncertainty of ship activities. Depending on the frequency of the data generated, they may even confuse operators, inducing errors when evaluating ship activities and tagging them as unusual. Using domain knowledge to classify activities as anomalous is essential in the maritime navigation environment since there is a well-known lack of labeled data in this domain. In an area where identifying anomalous trips is a challenging task using solely automatic approaches, we use visual analytics to bridge this gap by utilizing users’ reasoning and perception abilities. In this work, we propose a visual analytics tool that uses spatial segmentation to divide trips into subtrajectories and score them. These scores are displayed in a tabular visualization where users can rank trips by segment to find local anomalies. The amount of interpolation in subtrajectories is displayed together with scores so that users can use both their insight and the trip displayed on the map to determine if the score is reliable.

1. Introduction

Currently, maritime transportation is essential; approximately 90 percent of everything traded in the world is transported by sea vessels [1,2,3,4], and it grows approximately 8.5% per year [5]. Since 2004, vessels of 300 gross tonnages or more that travel internationally and cargo ships of 500 gross tonnages or more are required by the International Maritime Organization (IMO) to have an automatic identification system (AIS) onboard (http://www.imo.org/en/OurWork/Safety/Navigation/Pages/AIS.aspx). The AIS produces a constant high volume of data [6,7]. This technology transmits the vessel destination, speed, position, and many other items of static information [4], such as ship name and Maritime Mobile Service Identity (MMSI), which is used to identify a ship uniquely [1].

Defence Research and Development Canada (DRDC) and surveillance authorities, such as coastal Marine Security Operation Centres (MSOC), which are responsible for guaranteeing coastal safety, have an interest in using this data to uncover several potential issues [8,9,10], such as illegal transport of drugs, human trafficking, fishing in illegal areas, illegal immigration, sea pollution, piracy, and even terrorism [11]. These activities have a significant impact on society, the environment, and the economy, and for such, it is essential to identify these types of events as soon as possible [12,13].

Vessels involved in these illegal activities usually follow specific patterns such as unexpected stops, speeding, and deviations from standard routes [1,11,14]. Ships that are operating legally commonly travel through the same route due to regulations [15] and because it is usually the shortest path between ports, minimizing fuel consumption. For this reason, ships that navigate nonstandard routes or show signals of route deviation can be potentially labeled as presenting anomalous behavior [11].

However, identifying anomalous trips is not an easy task for maritime operators due to the large volume of data that AIS produces [4]; the large volume of data creates an overload of instances to be analyzed manually. Currently, operators usually use systems that display vessels on a world map that they can use to track their movements [16]. Although this can help operators reach some awareness of what is going on in the sea, trying to identify anomalous vessels among a large number of normal vessel can prove to be a difficult task [10].

Many works focus on finding anomalies in an automated manner by creating alerts or events when a possible anomaly is discovered. However, the problem of automatically identifying anomalies is complex and not well-defined [17]; additionally, it requires dynamic adaptation since humans will always try to change their modus operandi to not get caught, which in turn, makes automatic systems less reliable [18]. Thus, systems that automatically detect anomalies are rarely used in the real world [17,18]. Visualizations make use of humans’ inherent ability to perceive patterns and filter information in combination with their creativity and background knowledge [17,19,20], which enables them to analyze and understand complex, massive, and dynamic data [21].

Second, the vast majority of algorithms proposed to identify anomalies automatically may not work for local anomalies [22], or they require labeled data to train a model [23,24]. This means that deviations from normality that happen just in a small portion of a vessel trajectory may be left out when considering the trajectory as a whole, especially when analyzing works in the maritime domain. According to the literature review conducted in this paper, most work involving visual analytics also does not focus on segmenting trajectories to find local anomalies; those who tried to address this issue are limited.

Last, when analyzing vessel trajectories from raw AIS data, the data can be faulty and incomplete, and it happens for multiple reasons. First, one of the frequencies used by AIS transceivers is very high frequency (VHF), which makes the AIS data-link unreliable [25]. Second, Vessel Traffic Service (VTS) stations may miss several AIS messages from vessels traveling close to the coast due to information overloading [26]. Third, even though satellite AIS has become more common since it can capture longer ranges than shore-based AIS, it is common for the data received by it to have gaps since its field of view and footprint limits the satellite, and the number of messages it can lose increases in regions with a high number of vessels [27]. Finally, there are also cases where vessel crews interfere with AIS signals or turn the transponder off to cover illegal activities [28]. For this reason, vessel trajectories often need to be interpolated, which can increase an algorithm’s accuracy [29]. However, anomalies found in the interpolated data may be incorrect when data gaps are large. Therefore, it is essential to present information about the degree of uncertainty when an anomaly is detected in an interpolated region of a trajectory. A system could consider, for example, the quality of the data in that region, or it could show the interpolated data itself, so that one can assess whether an event is indeed an anomaly. The user could also further investigate what may have happened when there was no signal. However, to our knowledge, there is no work in this field that allows users to explore the potential impact of interpolation on anomalies.

In this paper, a tool that aims to tackle the problems mentioned above is proposed. Few assumptions are made about who the users of this tool could be in this work, and, therefore, the desire is that such a system should be easy to use and learn. Based on the problems previously mentioned, we try to answer the following research questions in the current work:

• Is it possible to identify local anomalies using one or a combination of features given a port of origin and a port of destination?
• Is it possible to make sense of the interpolation and the uncertainty it may cause when determining anomalies?

The contribution of this work is the proposal and development of a visual analytics tool called Trajectory Outlier Scoring Tool (TOST). TOST finds local anomalies in trajectory trips while also taking into account the trip’s interpolation. Finally, our tool is evaluated with use cases and tests with users.

This work is structured as follows. In Section 2, we provide a background with common terms used in this work. In Section 3, we give an overview regarding works that propose to detect anomalies either in an automated process or using visualization tools. In Section 4, we describe the proposed tool and discusses some of the decisions made. In Section 5, a use case of our tool is shown. In Section 6, we show some early tests with users. Finally, in Section 7, we present a summary of this work, along with a discussion of some of the tool’s limitations, and we propose ideas for future work.

2. Background

The background and definitions of essential concepts used in this work are discussed in this section. Section 2.1 details the automatic identification system (AIS), which is the primary source of the data used in this work, including how it is collected, features, and problems related to it. After that, we discuss and list the types of anomalies found in the maritime domain (Section 2.2). Section 2.3 provides the definitions of a spatial region, trajectory, and subtrajectory, which are essential to understand how this work handles the ship data used in the experiments. Next, we present an essential concept used in this work: the difference between global and local anomalies (Section 2.4). Finally, we define and characterize the term visual analytics used to design our tool (Section 2.5).

2.1. Automatic Identification System (AIS)

AIS is a self-reporting device capable of transmitting information about a vessel to other vessels and to coastal authorities. It was initially created to help avoid collisions between vessels at sea, but currently, maritime authorities use it heavily to find potential threats at sea. AIS works by integrating very high frequency (VHF) transceivers with Global Positioning Systems (GPS) and ship sensors, such as gyrocompass and rate of turn indicators, to broadcast information every 2 to 10 s, depending on the vessel speed, and every 3 min if it is anchored. The messages consist of dynamic kinematic data, such as vessel speed, position, rate of turn, and a Maritime Mobile Service Identity (MMSI) number, which uniquely identifies each device. It also sends dynamic nonkinematic information, which is voyage-related information such as destination, time of arrival, together with static information about the vessel, such as the type of ship, the vessel name, and the International Maritime Organization (IMO) number.

Other vessels can receive the broadcast information and use it to avoid collisions, especially when navigating under conditions of restricted visibility. It is also collected by coastal receivers, which can receive signals from vessels up to 40 nm (nautical miles) away [30]. Due to this coverage limitation, satellite-based AIS (S-AIS) has also been used to receive messages that are out of range of coastal stations. However, S-AIS is less consistent and has a lower update rate when compared to terrestrial AIS [27]. The AIS position accuracy, using its standard operation, can be quantified from the GPS or Global Navigation Satellite System (GLONASS) system used onboard the vessel. When these systems have an unobstructed view of four satellites, the positional error is on the order of 15 m for GPS and 5–10 m for GLONASS. The AIS message protocol itself may add a small amount of error by reducing the accuracy of the stored coordinate to a precision of 1/10,000 of a minute (1/600,000 of a degree) for most messages.

2.2. Anomaly Detection

2.2.1. Types of Anomalies

The term anomaly can have different interpretations depending on the context used. In this work, we use a similar definition to that given by [9] where something is considered anomalous if it deviates from what is usual, normal, or expected. This work aggregate all vessel data from the same type of vessel, given that distinct classes of vessels can have different behaviors [31], to decide what is a normal behavior. We consider that values that deviate from this aggregation will be viewed as an anomaly. Examples of abnormal behaviors are vessels of high tonnage traveling at high speed near the coast or vessels that do not travel in sea lanes.

Anomalies were divided by Roy [9] into two categories: static and dynamic anomalies. Static anomalies are related to vessel information that should not change, such as its name or its ID given by IMO. Dynamic anomalies were divided into two subcategories: kinematic and nonkinematic. Some anomalies categorized as nonkinematic are associated with missing or wrong information about the vessel crew, cargo, or passengers. In contrast, kinematic anomalies are related to vessel location, speed, course, and maneuvers.

2.2.2. Anomaly Detection by Vessel Type

There are many types of vessel, such as cargo, passenger, tanker, and others (https://www.marineinsight.com/guidelines/a-guide-to-types-of-ships/). When looking for normal behavior, we need to compare vessels that belong to the same type since vessels that belong to the same class travel at similar speed [9] and have similar maneuvering behavior [31]. Large vessels are also obligated to travel in specific routes (http://www.imo.org/en/OurWork/Safety/Navigation/Pages/ShipsRouteing.aspx/) [15] created by IMO.

However, anomalies are not always a threat, such as piracy, illegal fishing, and many others [16]. It is of interest to operators to receive recommendations of vessels with some abnormal behavior, triggering a further investigation from the operator to decide whether it is a threat or not [16]. In this work, we handle only kinematic anomalies; more specifically, we look into anomalies related to speed, course, zone, and navigability between vessels of the same type.

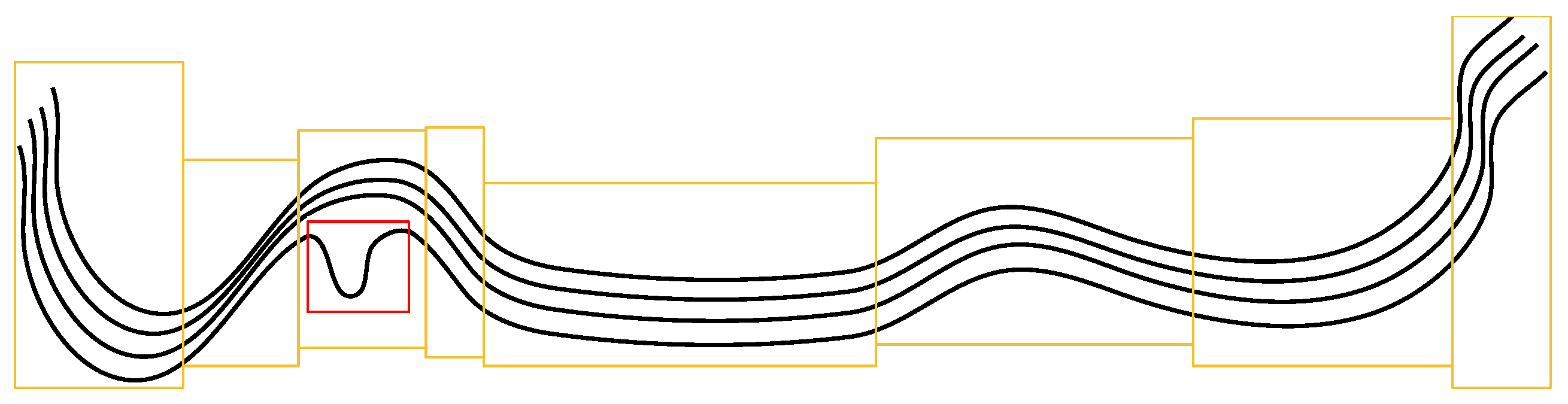
2.3. Spatial Region, Trajectory, and Subtrajectory

We define a spatial region since our user needs to identify anomalies that may happen more frequently in potential areas of interest. Then, ships that travel through these spatial regions will have their trajectories checked against the normal behavior.

Definition 1

(Spatial Region). A spatial region is a two-dimensional polygon with straight sides $S=\left(\right(x_1, y_1), (x_2, y_2), \dots , (x_n, y_n\left)\right)$ where $x_n$ and $y_n$ are geographical coordinates.

Definition 2

(Trajectory). A ship’s trajectory is a finite sequence $T=\left(\right(x_1, y_1, t_1, f_1),$$(x_2, y_2, t_2, f_2), \dots , (x_m, y_m, t_m, f_m))$, where $x_m$ and $y_m$ are geographical coordinates, $f_m$ ∈ distance_traveled, time_traveled, speed, heading are point features (i.e., attributes calculated between two consecutive trajectory points following its temporal ordering), and $t_i$ is the timestamp such that $t_m<t_{i+1} for i = 1, \dots , m$.

Definition 3

(Subtrajectory). A subtrajectory is defined as $ST=((x_p,y_p,t_p,f_p),\dots (x_q,y_q,t_q,f_q))$, and it is a subsequence of the trajectory T ($ST\subset T$) starting in index p and ending at index q ($1\le p\le q\le m$). It only contains positions that are inside the boundaries of a spatial region.

2.4. Global and Local Anomaly Detection

Different works have diverse definitions of what they consider to be a local anomaly [22,32]. In this work, we consider global detection algorithms as being the ones that use the whole trajectory to find anomalies. In contrast, local detection algorithms are the ones that divide trajectories into subparts and find anomalies in those subtrajectories. Figure 1 exemplifies some trajectory data where most paths are similar. Still, one of them has a slight deviation, which could be detected as normal if a model uses the whole trajectory.

2.5. Visual Analytics

Visual analytics uses interactive visual interfaces to help the user make decisions more efficiently and effectively [33] by combining interactivity with automated visual analysis [34]. It is a comprehensive solution for problems that cannot be solved by an automated tool nor solvable by humans without the cost of a substantial cognitive overload. The problems solved using visual analytics are generally not well-defined; therefore, users are not sure they can trust the system output. However, visual analytics uses input from users and allows some degree of exploration, which increases the user’s reliability on the system [34].

Since finding anomalies is not a well-defined problem and since maritime operators lack trust in fully automated systems [17,18], using visual analytics seems to be a suitable decision for solving the problem of finding local anomalies in maritime traffic.

3. Related Work

3.1. Automated Anomaly Detection of Vessel Trajectories

Since AIS data has been made publicly available, many researchers have started working on tools to analyze and detect anomalous vessel behavior. The vast majority of work conducted in this field is related to automated detection. One of the works in automated anomaly detection of vessel trajectories was conducted by Pallotta et al. [1]. They proposed a methodology called TREAD that reads AIS data streams and uses density-based spatial clustering of applications with noise (DBSCAN) to extract routes. Traffic anomalies are detected by comparing a new route with a group of routes with the same start and end locations. After that, kernel density estimation (KDE) is used to remove outliers from the group of trajectories of a given route.

Mascaro et al. [8] also use AIS data to detect anomalous behaviors in vessel trajectories. Their work is different from [1], as their solution works with historical data that is cleaned and merged with other data sources, such as weather data. First, it clusters trajectories similarly to [1]; then, their strategy uses causal discovery via MML(CaMML) to learn a Bayesian network (BN).

Trajectory clustering and Bayesian methods are used to classify anomalous behavior by Zhen et al. [3], which is similar to what [8] does. However, differently to [1,8], Zhen et al. use k-medoids to cluster vessel trajectories [3]. Finally, they use a naive Bayes classifier to label the routes.

Laxhammer and Falkman focus on decreasing the error rate when identifying anomalies in vessel trajectories using nonconformal prediction on streaming AIS data [35]. They use kinematic features, such as position and velocity, to classify vessels into a vessel type, such as cargo ship, tanker, or passenger ship. In case any class does not seem plausible, a vessel is considered anomalous.

The framework proposed by Yang et al. [22] is based on trajectory segmentation and multi-instance learning to identify local outliers. It tests a combination of different segmentation algorithms, representation models, and multi-instance learning. There are four possible segmentation methods: minimum description length (MDL), maximum acceleration (MA), log-likelihood of regression function (LRF), and heterogeneous curvature distribution (HCD); the segmentation produced by each of these methods is evaluated based on measuring how different the subtrajectories are to each other and the number of segments created to avoid oversegmentation. The subtrajectories can be represented as either hidden Markov model (HMM) or hierarchical Dirichlet process hidden Markov model (HDP-HMM). Either diverse density (DD) or k-nearest neighbors (KNN) [36] can be used to detect the anomalies. If a subtrajectory is classified as anomalous, the whole trajectory is classified as such.

Unlike previous approaches, Kazemi et al. [37] propose a system that uses expert knowledge through rules to detect dynamic nonkinematic anomalies displayed for the user in a map with the vessel trajectory. Similarly, Idiri et al. [38] also use a rule-based approach to identify anomalies. However, it differs from the previous work by automatically extracting the expert knowledge from historical data using a rule learning technique on a database with maritime accidents, the Marine Accident Investigation Branch (MAIB) database.

3.2. Visual Anomaly Detection of Trajectories in Maritime Traffic

One of the main works in visual anomaly detection of trajectories in maritime trajectories is the visualization of vessel movements proposed by Willems et al. [15]. They use kernel density estimation (KDE) to show ships’ area usage, such as sea highways and anchoring zones, and it can be used to identify the most common paths used by vessels. However, their visualization is not interactive and is more focused on area usage rather than finding outliers. Their work was extended by Scheepens et al. [39] to allow users to select multiple attributes when creating the density maps. One of the possible user interactions with this system is subtracting a density field from a considered normal density field to find potential outliers.

The Maritime Visual Analytics Prototype (MVAP) [10] is a prototype created by Defence R&D Canada to allow maritime operators to find anomalies and to analyze vessels of interest (VOI). Their prototype contains different widgets that will enable user exploration of kinematic and nonkinematic data through interactive visualizations such as magnet grid for exploration of several vessels properties at once. Another widget provided by this tool allows users to compare a trip trajectory against an expected path; however, the predicted path is a straight line from the origin to destination, which might not be correct since vessels have to follow specific trajectories such as sea lanes.

Traseer is another tool to find anomalous trajectories [40]. It works by grouping trajectories based on their pairwise distance. Then, for each of these clusters, it chooses N equally spatially distributed sample points. Afterward, it classifies as anomalous routes containing positions with low probabilistic density and displays them on a map. However, this work may miss some local anomalies depending on the number of samples chosen, and it only uses vessel position to identify which trips are outliers.

In [17], a framework that uses a hybrid approach between data-driven, signature-based, and visual analytics called VISAD is proposed. It uses self-organizing maps with Gaussian mixture models to find anomalies in kinematic data and uses nonkinematic anomalies rules. It then highlights anomalous vessels on a map and allows the user to interact and adjust the model by interacting with the mixing proportions of self-organizing maps visually in the case of detecting an incorrect anomaly. However, the operators from maritime traffic control centers would not be allowed to update the normal models since changes could decrease the model efficiency. In our solution, we do not use any traditional artificial intelligence model to classify anomalies because we want the operator to interact with the system and change the way the anomaly trajectories are detected.

Although they do not focus on anomaly detection in the maritime domain, other papers are significant in the visualization field. For example, Lu, Wang, and Yuan [41] proposed a tool that aims to understand how travel duration varies in different road sections at specific times of the day and on weekends. It works by allowing the user to split a road into several segments, and for each of them, the trajectories are clustered based on travel duration. Afterward, an overall rank is calculated for each trajectory. It also displays the distribution of travel time for each segment in a box plot view.

Our work is focused on the maritime domain, and it uses several AIS-derived attributes, such as position, speed, bearing, and duration, to find anomalies. Using multiple attributes can help the user to get a better insight into how trajectories may have deviated from normality. However, our work is differentiated from other works by its focus not only on analyzing the trajectory as a whole but also on different regions of a trajectory where local anomalies may stand out. This is somewhat similar to what is proposed by Wang et al. in [40]. Still, instead of comparing a single point of a trip against other trips, this work aggregates all points inside a spatial region to calculate attribute values, such as average speed. Then, a score, based on how this attribute deviates from the mean, is calculated. This work also takes ship type into account when comparing trajectories, while [40] only used the AIS position to find anomalies. Using all relevant points of all trajectories that belong to the same vessel type, we calculate a mean trajectory for comparison against the other trajectories to show the correct path that vessels should have used. This is similar to the method of Lavigne [10]; however, the path is displayed as a simple straight line from the origin to destination, while we compute it based on all other trajectories of the same group.

To the best of our knowledge, ours is the only work in the maritime domain that prioritizes the trajectories based on how anomalous they are compared to others. This strategy is similar to [41], but their work is for land trajectories. However, we use multiple attributes to calculate the score, whereas [41] uses only the travel duration. This work also allows users to select which features they want to use for calculating scores. Furthermore, this work is the only one that aims to help users make sense of the interpolated data in the maritime domain to decide if an anomaly can be trusted.

4. Methods

In this section, we list the requirements that our solution should support and details of how we developed a tool that meets these requirements.

4.1. Requirements

In this work, we aim to develop a tool for identifying local anomalies in trajectory trips and for providing some information (e.g., where and how it happened and how many interpolations were used) about the interpolation to the user. Some high-level requirements are used as guidance for the development of this tool:

• The tool should support the identification of trips that may have anomalous behavior.
• The tool should support the identification of local anomalies.
• The tool should improve the user’s understanding of where interpolation has happened in a trajectory and its impact, if any, on anomalies.
• The tool should support some explanation of the cause of the anomaly.

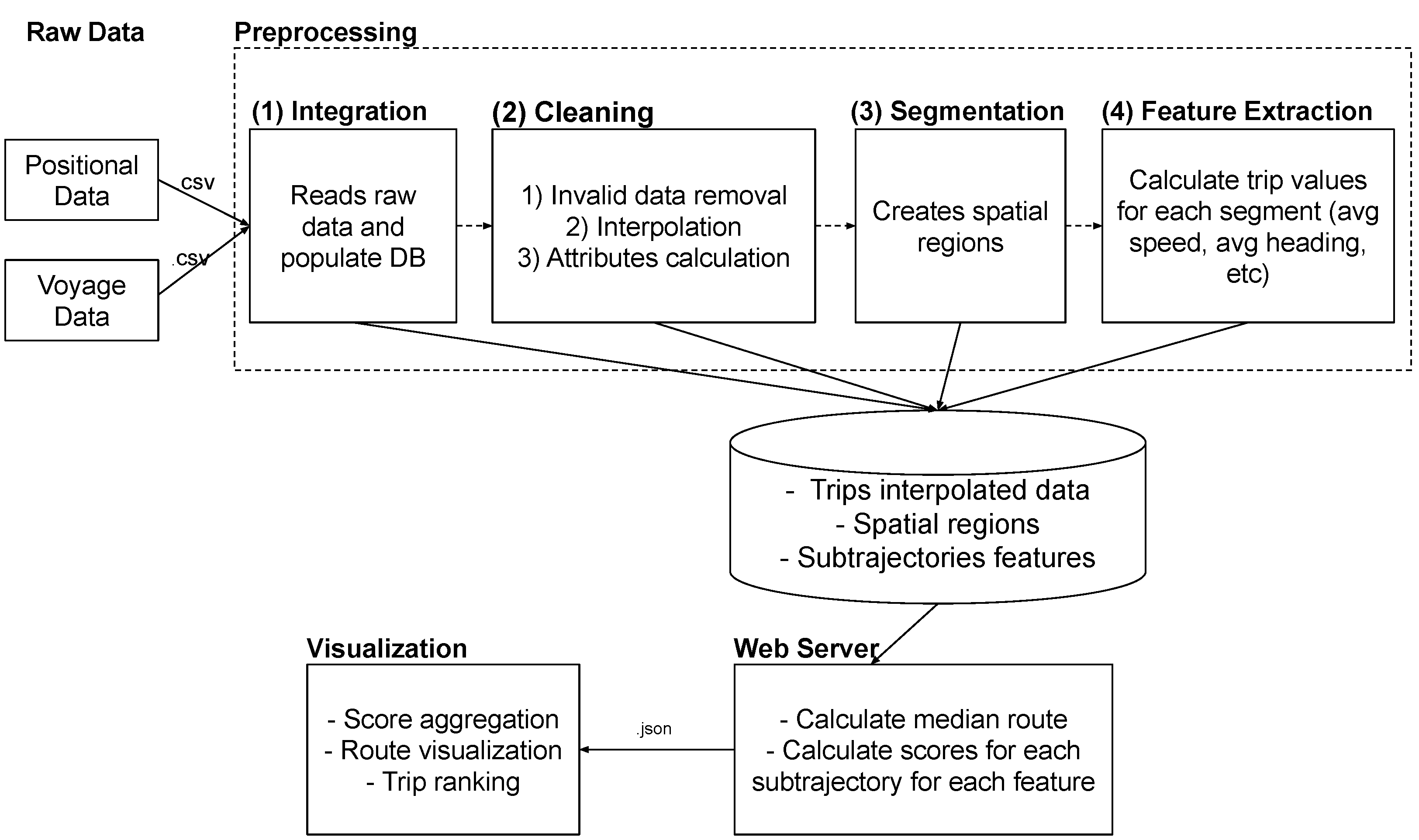
4.2. Framework Overview

An overview of the framework used for our tool can be seen in Figure 2. It illustrates a preprocessing step that combines two sources of AIS data to get ship voyage information. Invalid trips are removed at this step, and the remaining trips go through a cleaning process where invalid data are removed, and gaps in the data are interpolated. Rows with duplicated timestamps are removed in the cleaning process. A Hampel filter [42] is also used to identify positional jumps to be removed from the data set. The Hampel filter works using a moving window that computes the median of this window and the standard deviation; if the observation deviates from the window median by more than a predefined number of standard deviations, the data point is considered an outlier and can be removed from the data. The filter’s parameters were defined empirically, and the geographic coordinates of each ship’s trajectory were used as the data points. A window of 10 trajectory points and 5 standard deviations (i.e., large jumps in the data) were used as the Hampel filter input parameters. It was observed that these parameters removed the large positional jumps in the data since no trip showed in the map was out of the bounding box of the studied area. Afterward, spatial regions were created and their objective is to partition each trip (i.e., trajectory) into subtrajectories. The subtrajectories’ attributes (e.g., average speed, acceleration, etc.) are scored based on how much they deviate from the mean over all other trips attribute values. The combined final score for each subtrajectory is then displayed in a tabular visualization. Each trip is represented as a line in the table where the first column may show the maximum or average score for a trip, depending on which option the user has selected. The other columns show the subtrajectory scores, which are represented by a bar length, while the bar’s color indicates the amount of interpolation in the subtrajectory.

Following the visual information seeking mantra [43], first, an overview of the overall maritime situation is displayed in the table. The users can then use filters to remove data that seem to be anomalous, showing only trips of interest. They can hover or select an individual row to see the score and interpolation values. By clicking on a row, the trajectory will be displayed on the map. The user can then compare the trip trajectory against the mean trajectory to see any deviations and whether the interpolation seems reasonable. The user can also choose which attributes and spatial regions should be used during the score computation, which updates the subtrajectory score.

4.3. Tool Rationale

4.3.1. Why Use Spatial Regions?

This work uses spatial regions to detect local anomalies in trajectory data since it makes the location where the anomalies took place visible for the user. There is also the potential for the user to define regions that could be areas of specific interest for the operator [44]. Automatically finding the spatial regions could be achieved using strategies that try to divide a trajectory into multiple meaningful subtrajectories in unsupervised [45,46] or semisupervised [47] ways by applying minimum description length (MDL) or sliding window segmentation (SWS) techniques. In this work, we created several spatial regions between the two ports being analyzed. The procedure is described as follows. Given all trajectory points, the minimum and maximum geographic coordinates (latitude, longitude) are extracted to define a 2D bounding box. After that, this bounding box is divided into 10 regions of the same size (63 × 448 km). It is essential to point out that TOST can accommodate any spatial region in an area analyzed either created by the user or created by other methods such as the ones mentioned above. The decisions concerning the size and orientation of these spatial regions could influence the scores assigned to the subtrajectories, so they should be carefully considered when studying an area.

4.3.2. Why Use Mean and Scores?

Since we analyze trajectories of the same type of vessel going in the same direction, the trajectories and attribute values are not likely to be very different. The z-score is used in this work, giving the number of standard deviations of a value away from the mean. Considering the mean represents the normal behavior, this score shows the trajectory attributes as a distributional measure concerning the other trips to see how much it deviates from normality. Furthermore, using such scores makes it fast to calculate and update elements based on weights compared to working with machine learning models. Machine learning models cannot be updated on an everyday basis by an operator, reducing their ability to manipulate the output of a tool. Moreover, by using and combining scores, the operator can prioritize the anomalies based on what they believe is essential. This approach is different to automated approaches that use data mining techniques to output a label based on the previous data and different to the rule-based approaches, which have a particular threshold to trigger an alert. In our approach, the user can look at just a subset of the vessels and then see whether that one specific group looks anomalous or not.

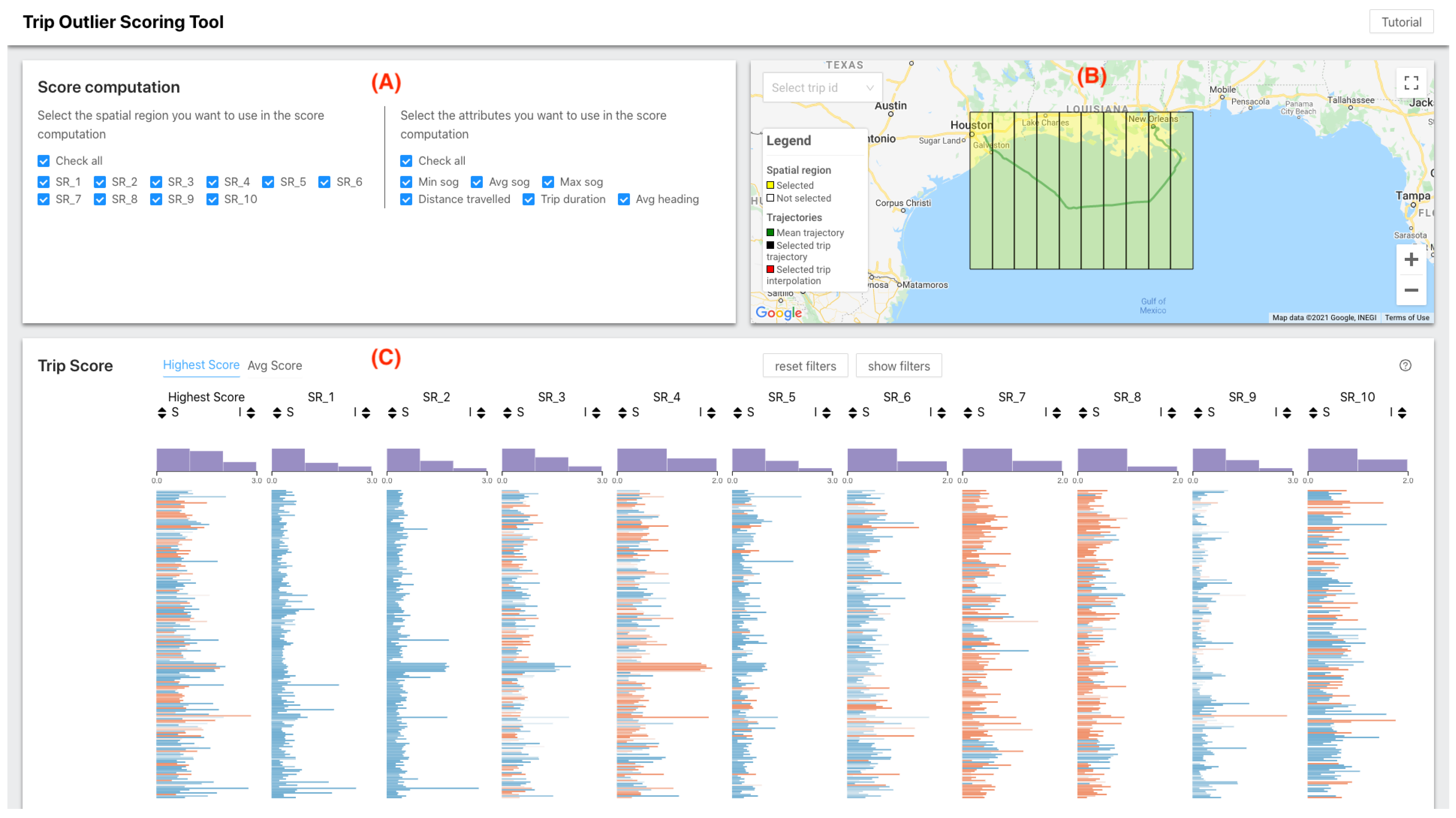
4.3.3. Why Show a Map?

A map is a crucial component for maritime operators to visualize how a trajectory occurred spatially and temporally. This work uses a map to display a selected trajectory in which original and interpolated points are plotted and differentiated by color. In this way, the operator can have an idea if the interpolation looks correct, and if so, it may indicate that the score in that subtrajectory is more reliable. The map also shows a mean trajectory, so the user can estimate if a trip trajectory is anomalous. The map also allows the user to visualize where the regions are located.

4.3.4. Why Show Scores in a Table-Like Visualization?

This work uses a tabular visualization based on a table lens [48] because it allows us to visualize two attributes for each “cell” easily. In our work, we want the user to overview each trip’s scores and how reliable they are in terms of the amount of interpolation in a subtrajectory. Thus, we can easily display these two attributes in our table, using the length of a bar as the score of a subtrajectory and the color as the amount of interpolation. Then, if the user wants to see information about a single trip, they can hover or click in the trip row to have the values score and interpolation values highlighted displayed.

4.4. Trip Outlier Scoring Tool (TOST)

Our tool has three main components: the score computation (A), a map (B), and the trip score table (C), as shown in Figure 3. The score computation (A) panel allows users to choose which spatial regions and attributes they want to use to compute the scores for each subtrajectory. For example, the user may want to analyze only ships with abnormally high speeds in a given spatial region, or they may want to pick a combination of average speed and heading in spatial regions 1 and 10 where certain ports are. The map control (B) allows the user to filter and visualize an entire trip performed by a ship. The map component (B) was created to display the previously created regions and the trajectories. It is displayed with a zoom on the area containing the two ports used in our experiments. Since we want the user to differentiate the original points from the ones that were interpolated, we distinguish them by color, and an example can be seen in Figure 4. The black portion of the trajectory was created from the original data points, while the red portion was interpolated. The tool also displays in the map a mean trajectory, which should represent a mean path that a trip is likely to make. In this work, we used the Teatool [49] mean trajectory function, which averages a number of equidistant points. It is worth mentioning that although averaging points is a simple solution, the points generated may not represent reality. Extracting a mean trajectory from a set of trajectories is a recognized problem in the literature, and this topic is out of the scope of this work. The mean trajectory shown by TOST has the purpose of only providing a spatial reference for the user to understand how abnormal the track of an analyzed trip may be. Finally, the score table component (C) shows the trip scores and provides functions for sorting and selecting trajectory trips. The user can click on the bar chart at the top to filter trips above or below a z-score threshold, and finally, the trip and its details are displayed in the map by clicking a line in the horizontal bar chart. We discuss details regarding the data interpolation techniques, subtrajectory attributes, and scores in the next subsections.

4.4.1. Data Interpolation

The technique used to interpolate the trajectory data was kinematic interpolation [50], which is suitable for data on moving objects. Kinematic interpolation works by taking the speed (i.e., latitudinal and longitudinal velocities) at the last point before the gap and the first point after the gap. It then calculates the acceleration between those two points to create the interpolations, which are modeled as a linear function of time. Vessels’ positions were interpolated in this work every 3 min only if ships stopped transmitting their AIS signal for those 3 min. This decision was based on the maximal time that the AIS devices may refrain from transmitting a message, which is 3 min when ships are anchored, moored, or have low speeds (0–2 knots). The threshold of 3 min guarantees that positions are only created through kinematic interpolation if something happened with the AIS message collection (i.e., information overloading, satellite field of view and footprint limits, etc.). If the sampling rates are lower than 3 min, we keep the original AIS messages, reinforcing the idea that more trustworthy information about the ship in a spatial region is available. This threshold also avoids oversampling a spatial region where enough information about a ship is available and could potentially mislead the user not to trust a score produced in an area. Finally, such a strategy also guarantees that the subtrajectories for each ship in a spatial region would contain a minimal number of trajectory points (interpolated or not), and the score values, which are based on the trajectory points attributes, would likely reflect the ship’s behavior in an area.

4.4.2. Subtrajectory Attributes

Our tool uses the spatial regions provided by the user for a given domain. Each trajectory is segmented based on the spatial regions, creating one subtrajectory for each spatial region. Afterward, TOST computes the features that are used to make comparisons against normal behavior. For each subtrajectory inside a spatial region, we extract the point features $(f_p,\dots ,f_q)$ and calculate: (i) the minimum, (ii) average and (iii) maximum speed in knots, (iv) average heading in degrees, (v) distance traveled in nautical miles, and (vi) time traveled in seconds.

The reason why these attributes were chosen is that kinematic anomalies, such as ship speed, are of interest to maritime operators [9]. TOST uses average speed to generalize how fast a vessel traveled in an ocean section. The maximum and minimum speed are also used to highlight possible deviations that the average speed could not show. The average heading is used to understand maneuverability deviations [9] and deviations from normal routes without the need to plot all trajectories in the map, which could be cluttered. Distance and time traveled are two pieces of information that are easy to compare between trajectories and may raise questions as to why a ship voyage was longer than others. Finally, the interpolation percentage of a subtrajectory indicates how many points of that trajectory are interpolated and can be used as a degree of trust in the data available for that particular situation.

4.4.3. Subtrajectory Score

After the features are computed for each subtrajectory, the system calculates the z-score for each subtrajectory attribute based on the user’s request. Then, for each subtrajectory, TOST averages the absolute values of the z-scores, which only use the attributes the user has selected in the panel (A). As an aggregate final score for each trip, we can show the highest score, which is the highest value amongst all subtrajectories, or it can show the average score of the subtrajectories. This process is formally defined as follows. Given a set of subtrajectories $ST=\{{st}_1,{st}_2,\dots ,{st}_n\}$ defined at a spatial region and the set of the subtrajectory attributes A = {a₁, a₂, …, a_m} ($A\in$ {minimum speed, average speed, maximum speed, average heading, distance traveled, time traveled}), the score of a subtrajectory $s{t}_i$ is described as:

$$score\left(s{t}_i\right)=\frac{1}{m}\sum _{j=1}^m\mid \frac{a_j-{\mu }_j}{{\sigma }_j}\mid$$

where ${\mu }_j$ is the average and ${\sigma }_j$ is the standard deviation of the subtrajectory attribute $a_j$ in a spatial region. Since the idea of TOST is to give the user the task of subselecting features to be evaluated, the set A with m attributes is chosen by the user and the final score changes if the set A is modified. Finally, since using the z-score produces positive and negative values (i.e., how below or above the mean a value is), we need to get the absolute value for the z-score of each feature to avoid a negative sum. Negative values for the z-score would decrease the total score of a subtrajectory and could rank it as a normal behavior.

In the score table component (C), each line in this table represents a trip. For each column, there is a bar in which its length represents the subtrajectory aggregated score, and the color represents the percentage of interpolated points. The color hue varies from dark blue (i.e., no interpolation) to dark orange (i.e., full interpolation), indicating the level of confidence in the information regarding a spatial region. This means that the more AIS messages were captured for a given ship in a spatial region, the color will go toward dark blue. Suppose most AIS messages in a spatial region are interpolated. In that case, the color will tend to be dark orange, and not much information about the ship is available in that spatial region. This reflects the idea that the more real AIS messages are available, the more confidence the user should have to point out that a situation is abnormal. The bar’s height is dynamic; it changes based on how many trips are being displayed at a given time. A more extended bar may indicate a higher deviation from normality since our score is derived from the z-score. Longer bars also stand out in comparison to smaller bars, and the interpolation is displayed as a gradient from blue to red. The exact scores and interpolation values for a trip, as well as the trip ID, can be seen at the bottom of a table when a user hovers over a row with the mouse. At the top of the table, we show the distribution of the scores for each region as purple bars. This visualization has two purposes: first, the user can brush the region to filter out uninteresting vessels, decreasing the number of ships displayed at the table, improving the table visibility. Second, showing the distribution may reveal a spatial region with a higher number of outliers than others or an area where the outliers have a much higher score. One of the objectives of our tool is to evaluate how the user would perceive untrustworthy outliers due to the lack of information about a ship in a particular spatial region. This is the main reason why we did not consider any threshold to discard trajectories that had a low sampling rate on a spatial region.

5. A Use Case

In this use case, we exemplify the use of TOST (https://gitlab.com/Fernando-Abreu/thesis_project) for finding speed anomalies far from shore. The data set used in our work includes trips of cargo ships that traveled from Houston to New Orleans from 2009 to 2018. We first used the score computation (see Figure 3A) to select only regions 5, 6, and 7, and we selected only the average speed attribute that is the main target of this analysis. Other options for regions could have also been used by clicking on the yellow areas on the map (see Figure 3B). If the user clicks on those controls, these interactions would recompute the scores and update the visualization only to display the regions of interest.

Next, we selected the first column to display by highest score or average score. Since we want to highlight trips that may have an outlier behavior, we picked the one with the highest score in a single region. Given that many trips were displayed, we filtered out trips with a score above 2.5 by brushing the score distribution in the highest score column at the top of Figure 5. This could also have been accomplished by inputting this value manually after clicking “show filters”, which is useful when high precision is necessary. The updated trip score table can be seen in Figure 5. By looking at the filtered trips, we can see that most subtrajectories have some degree of interpolation, especially in region 7, indicating that it is a region where the tower or the satellite could not capture the AIS messages.

After that, we ranked the trajectories by the highest score and hovered the mouse on top of the row to see the trip’s scores, which has the subtrajectory with the highest score. This score belongs to the trip with id equal to 2187, as can be seen in Figure 6. Trip 2187 has a high score, especially in regions 6 and 7. We can also see that in region 7, all points are interpolated, which indicates that this score is not reliable since the region has a considerable size. If we click on the row to plot this trip trajectory in the map, we can see that this interpolation does not seem reliable; thus, the score for this subtrajectory cannot be trusted. After plotting, the expert should consider whether this gap size makes sense or whether this trip needs further investigation.

Another example is trip 339, which is found at rank 10 of our selection. When we look at the table, we can see that although the tool added some interpolated points on subtrajectories in regions 6 and 7, region 5 had an outlier behavior. When we hover on this row, we see a 0 percent interpolation and a score of 3.28. Therefore, this score is reliable, and the user may frame this as an outlier behavior. If the user decides to have a closer look at the data, they could see that this trip had an average speed of 5.93 knots in region 5, while the average speed in that particular region is generally 15.69 knots with a 3.24 standard deviation. Now it is the expert’s job to understand why the vessel navigated so slowly in that region compared to other vessels. The conclusion of the investigation could point to engine issues or unregulated or illegal activity associated with the vessel.

6. Tests with Users

We conducted a user study to evaluate software usability and possible improvements. The study was conducted individually and online due to in-person restrictions. During the study, the participants received a short tutorial on how to use the tool. Then, they had to interact with the TOST to answer a few scenario-based questions. Finally, they had to complete a small demographic questionnaire and answer a few closed and open-ended questions about the tool. A session with a user took between 45 and 60 min.

In this experiment, we first invited computer science students from Dalhousie University to simulate a junior maritime operator responsible for finding such anomalies in this environment. The decision to invite only computer science students was that students in this field usually have some knowledge working with computers and some familiarity with statistics, which can help them better understand what the subtrajectory score represents. We sent an open invitation by email to two mailing lists that all Computer Science students are subscribed to by default. Then, we picked the first 10 potential participants that replied to our email. Most of them were undergraduate students, one student was a master’s student, and another was completing a Ph.D. Half of the users had no familiarity with AIS data, and only three felt that they were somewhat familiar. Finally, we interviewed two senior information specialists in the maritime domain that use AIS data in their daily activities. The objective was to compare to some extent the perspective of junior and senior operators using our tool.

6.1. Experimental Setup

For this experiment, a picker component was added to the tool to allow users to select specific scenarios as requested during the study. We also added an option to sort trips by the amount of interpolation. Meetings with participants were conducted online through Microsoft Teams, and participants had access to the web tool through a link that was shared with them. Training was given to each participant on the day of the study to teach them essential concepts about the tool and how it works. No previous knowledge about the maritime domain or AIS was required. During the training, the screen was shared, and we used a previously created tutorial to highlight the explained component. Afterward, a use case of the tool, based on different data from what they would be using during the study, was introduced. In the use case, we showed the users how to use the filtering to display only potential outlier trips. We also showed how to sort based on the score, to visualize trip scores and interpolation information, to find out on which spatial region a trip had an outlier behavior, to see which spatial regions had more outliers than others, and how to display trip trajectory on the map. The whole tutorial took around five minutes.

6.2. Scenarios

Before the experiment, the tool had been slightly modified to display a dropdown component containing different scenario options (e.g., eight scenarios in total) for the participant to choose from. When a scenario was selected, the data displayed to the user changed; this was done so that we could make the same question for different data to evaluate whether the user was able to use the tool in various settings. An example of scenarios is shown in Figure 7. The participants then received an online questionnaire that was divided into sections. At the beginning of each section, the participants were instructed to select a specific scenario and then answer a few questions that require the operator to use the tool.

The scenarios were all presented in the same order to the participants. For the whole exercise, we defined that any trip with a subtrajectory score above 3 should be considered an outlier, except for questions 19, 20, and 21, where the users needed to take the interpolation into account. It is worth mentioning that throughout the whole study, we used the term outlier instead of an anomaly since it is a common term in statistics.

6.3. User Test Questions

In this subsection, we detail the overall rationale of what we would expect the users to understand from the scenarios while using TOST and if they could use the filters to find a targeted trajectory or a group of them.

• How many trips are outliers?
  Our idea with this question was to validate whether the participants could identify which trips were outliers. They would have to filter the data either by brushing or typing directly into the filter component. Since asking for several IDs can be time-consuming and prone to errors, we asked for the number of trips that were outliers.
• What is the identifier of the trip with the highest score?
  In this question, we tried to see if the participants understood both how to sort trips and the ranking concept to find the trajectory that was the most anomalous in a given scenario.
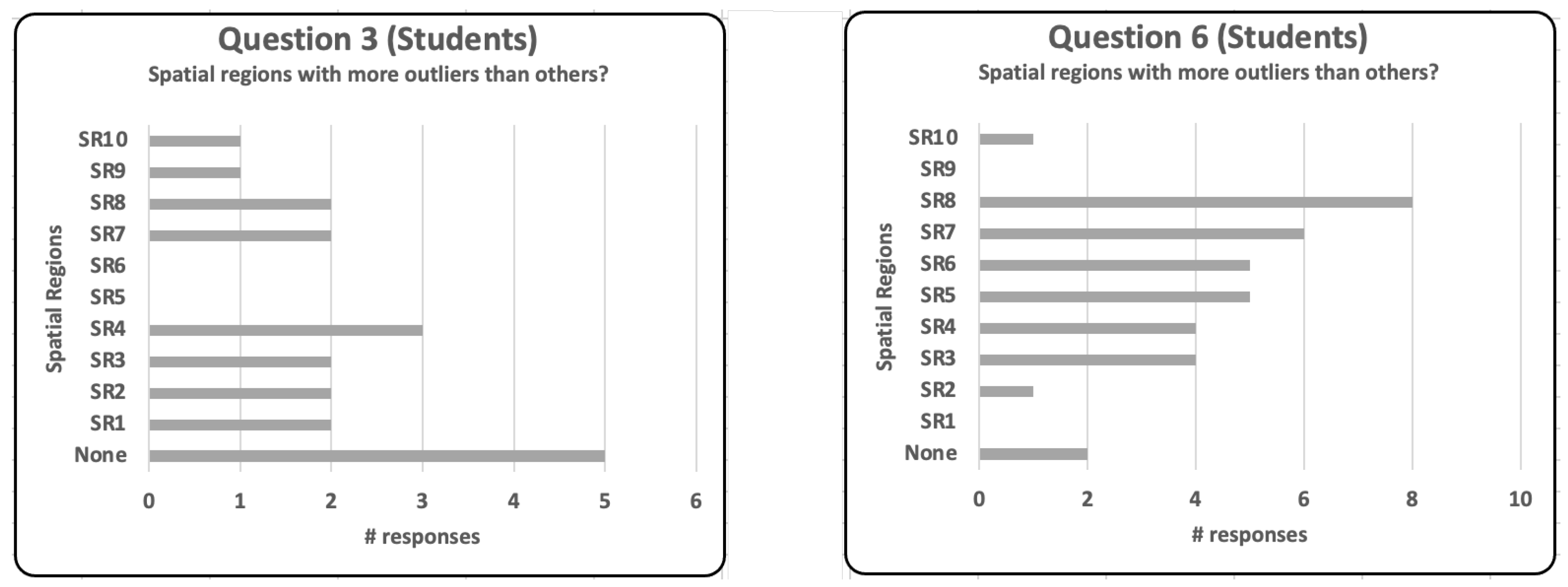
• Which spatial regions have more outliers than others?
  The purpose of this question was to check whether the participants could use the score distribution plots to identify and visualize spatial regions with a higher number of anomalies.
• In which spatial regions did trip X have an outlier behavior?
  In this question, we wanted to see if the participants understood the score concept and how to visualize it, either by hovering over a row and seeing the score at the bottom of the table or by looking at the axis at the top of the table.
• How much interpolation do you think there is in this scenario?
  Ideally, we would like to see the data set with few interpolations. Based on this information, and without using any type of sorting, how much interpolation do you think there is in this data set? This question tries to assess if using color to interpret the interpolation gives an overall idea of the amount of interpolation used in the data set.
• How many trips have, on average, above 50% interpolation?
  This question tries to verify if the participant understood how the interpolation concept is displayed and if they are able to find the number of trajectories for which there is not enough information to label it as anomalous.
• For a given trip in a scenario, choose the most appropriate option.
  In this question, we put together the concepts of score, interpolation, and trajectory together. The user then had to choose one of the following options:

  -

  It is not an outlier; it has a good score and good interpolation.

  -

  It is an outlier; it has a bad score and bad interpolation.

  -

  I can’t say, there is too much interpolation, or the interpolation seems incorrect.

6.4. Results

We show a summary of how many participants got each question correct in

Table 1. User responses (students and specialists) for all questions asked in the interview.

Scenario	Question	Correct Answer	Students	Specialists
1	(1) How many trips are outliers?	0	100%	100%
	(2) What is the Id of the trip with the highest score?	542	80%	100%
	(3) Which spatial regions have more outliers than others?	None	50%	50%
2	(4) How many trips are outliers?	10	70%	100%
	(5) What is the Id of the trip with the highest score?	270	90%	100%
	(6) Which spatial regions have more outliers than others?	3;4;5;6;7;8	30%	50%
3	(7) How many trips are outliers?	25	60%	100%
	(8) What is the Id of the trip with the highest score?	2276	90%	100%
4	(10) In which spatial regions the trip 1006 had an outlier behaviour?	4	70%	100%
	(11) In which spatial regions the trip 1059 had an outlier behaviour?	6	80%	100%
	(12) In which spatial regions the trip 1079 had an outlier behaviour?	9	80%	100%
5	(13) How much interpolation do you think there is in this dataset	-	-	-
	(14) How many trips have, on average, above 50% interpolation?	14	80%	100%
6	(15) How much interpolation do you think there is in this dataset	-	-	-
	(16) How many trips have, on average, above 50% interpolation?	21	70%	100%
7	(17) How much interpolation do you think there is in this dataset	-	-	-
	(18) How many trips have, on average, above 50% interpolation?	32	70%	100%
8	(19) Given the trip 2276 choose the most appropriate option	It is an outlier	20%	100%
	(20) Given the trip 1963 choose the most appropriate option	It is not an outlier	100%	100%
	(21) Given the trip 3062 choose the most appropriate option	I can’t say	80%	100%

. The students in Table 1 are the 10 Dalhousie students and the specialists are the senior information specialists in the maritime domain. We can see that the participants had no issues identifying when there were no outliers in the data set; however, as the number of the outliers increased, the number of correct answers decreased, and the answers were more diverse. A possible reason may be that the users did not understand how to use the filter properly or which columns they should apply the filter to; it is hard to explain why some users chose 0 or 1 as the number of outliers in question 7.

We can see that most users were able to properly sort by score and select the trips with the highest outlier score when we see the results of questions 2, 7, and 8. However, for questions 3 and 6, few students were able to give all correct answers. Only 50 percent and 30 percent of the participants, respectively, chose all the correct options in the students group. One of the specialists also made similar mistakes as the students for questions 3 and 6, but the other answered all questions right. All answers for questions 3 and 6 are detailed in Figure 8 since they had several options.

Even though all participants correctly answered question 1, a possible reason for them to have selected some spatial regions as having more outliers than others in question 3 is that the score was higher in some spatial regions than others. Some participants had chosen spatial regions 4, 7, and 8 as having more outliers, even though there was no subtrajectory with a score above 2 in those regions. This result might have happened because the question was not well-formulated or the participants did not understand this functionality. In question 6, we can see that although the number of total correct responses was low, most of the spatial regions selected were right, except for two participants who marked that no spatial region was more anomalous than others.

Most of the users were also able to correctly answer questions 10, 11, and 12, which shows that they could identify which subtrajectories contributed to the trip being considered an outlier. This means that they correctly understood how a more significant score or larger bar correlates more to being an outlier trip. They were also able to use the bar width to get this information correctly, or they were able to hover over a row and check for the score at the bottom of the table.

Questions 13, 15, and 17 do not necessarily have a correct answer. We wanted to understand how the users feel when they see the bar colors representing the interpolation. We also expected that none of them would choose the option “There seems to be almost no interpolation,” but one participant selected it. Most of the time, participants felt that the interpolation amount was reasonable, which is understandable, although there were too many gaps in this data set. However, when asked about the number of trips that had interpolation above 50 percent in questions 14, 16, and 18, most participants got it correct.

For this study, the most important questions were 19, 20, and 21, since they put together all essential concepts used in this tool. Most of the users correctly identified that trip 1963, in question 20, was not an outlier, and most of them understood that the interpolation affected the lousy score of trip 3062 in question 21. The results with the specialist was even better since the correct answers to questions 19, 20, and 21 were given.

The results in Table 1 show that in general, the two groups (e.g., students and specialists) were able to answer most of the questions correctly. The users had difficulty answering questions 3 and 6, but we believe that the question might have been misleading since both groups made mistakes. We believe that since a threshold was not defined for this question, the definition of having more or the same level of outliers was perceived by the users differently. For question 19, the students were not able to correctly answer that the trip is indeed an outlier. However, the specialist was able to tag that the trip was indeed an outlier. We believe that the students’ and the specialists’ high number of correct answers are a strong indication that, even with a quick training (i.e., a 5 min tutorial prior to the task), TOST helped them to find, reason, and decide whether there was a local anomaly in a given region and whether there was enough confidence to confirm such an anomaly.

7. Conclusions and Limitations

In this work, we identified local anomalies using a combination of features and used an interpolation strategy to give the user a certain degree of reliability concerning the anomaly. We achieved this goal by proposing and developing a web tool that partitions and scores each subtrajectory regarding its attributes. Users can interact with this tool through filtering and sorting to find trips with local anomalies. They can also plot trajectories of trips in the map and identify which portions of that trajectory were interpolated. Afterward, TOST was evaluated with junior and expert users. Overall, the users were able to find trips with outlier behavior and identify in which spatial segment the anomaly took place. They were also able to use interpolation to increase or decrease their confidence in a score. The experiments conducted indicate that the tool’s main goals were achieved to a great extent. Since there is a known lack of labeled data in this domain for validating models, we envision that TOST is a tool that may be a first step toward collecting labeled data for unusual situations in maritime traffic. The labeled data could be used in a second step to learn models for identifying anomalous situations in maritime traffic, and thresholds for discarding unreliable abnormal situations could also be learned from such tagged data and a broader use of this system. The unusual situations that TOST could potentially tag include deliberate AIS turn-off, signal spoofing, and illegal, unreported, or unregulated (IUU) fishing activities.

One of the main limitations in this work is the way in which we calculate the score. We assume that the subtrajectory values follow a single normal distribution, with most data being represented by nonanomalous trips. We believe that the second assumption should be valid in most cases; however, even when comparing the same class of vessels, some abnormal conditions, such as windy weather, may affect vessel speed and trajectory, causing them to be perceived as anomalous in our system. To solve this limitation, we plan to use a clustering algorithm, such as k-means or DBSCAN, to group trips with similar trajectories. Then, we could extract the normal behavior and give a score for each of these groups.

Another limitation is that our local anomaly detection only works with well-partitioned subtrajectories. The system may miss some anomalies in cases where the spatial region is too large. We plan to address some of these issues by adding a page that allows the users to choose between creating the spatial regions automatically or manually. If the user chooses to create manually, the user should draw spatial regions on a map using drawing tools. Otherwise, we will create regions based on trajectory patterns, such as straight lines, loops, etc. For each trip, we only create one subtrajectory per spatial region; this means that it will not work well for trajectories that pass through the same spatial region more than once, which would be the case for fishing vessels or trips that start and end at the same port.

We believe it is essential for maritime operators to identify anomalies and understand what causes them—for example, understanding whether the deviation is related to low speed or to deviation from the path. We plan to address this in the future by showing each attribute’s value. We also intend to implement other interpolation strategies (i.e., linear, cubic, quadratic, etc.) to study how they may affect how the user would interpret the anomalies in a spatial region. Finally, the impact of the number of different ship tracks in one spatial region is worth studying to define a minimum number of subtrajectories needed to extract meaningful statistics from that data set.