1. Introduction
When using geolocated social media data as a source for academic studies, researchers have to be aware of the caveats of using such data. Uncertainties and biases may cause a range of limitations when using geolocated Twitter data [
1], both technically and for geospatial analysis in a broader context, such as privacy, semantics, handling and processing of large data volumes, as well as the issue of trust, or lack thereof in geo-social media [
2]. Despite these shortcomings, Twitter has been proven to be a valuable data source in a variety of contexts, such as epidemiology [
3,
4,
5], stock market predictions [
6], predictions of political affiliation [
7], the assessment of refugee movement [
8], disaster management [
9,
10], the analysis of mobility patterns [
11], or the assessment of emotional responses in urban research [
12,
13]. The reasons for using user-generated data as a surrogate variable rather than measuring a phenomenon of interest directly include resource and time constraints and ethical concerns. For example, in cases of geo-social media aided emergency management [
14,
15], some traditional data acquisition methods lack the required timeliness or would require dangerous in-situ measurements. In other cases, effects cannot be directly measured in the first place, but are embedded in user-generated text as latent information such as emotions [
16] or crime risk [
17].
There is a fundamental premise that unites these studies that is, in some instances, silently taken for granted: The collected geo-social media data represent the modeled population adequately enough to allow for inferring information about it. In this context, the concept of representativeness stands for a measure that expresses how well data from a given area are suited to stand in for the underlying population. Auxiliary data about the population can be incorporated to increase the robustness of the measure.
The number of studies that were successful in validating their obtained results show that Twitter as a data source is certainly useful. However, given its highly heterogeneous usage patterns in terms of demography, socioeconomic status and geography, the degree of representativeness for a given set of tweets changes with its particular co-located covariates [
18,
19]. This problem becomes relevant when the population under investigation is only a subset like a certain demographic or age group of the total population. The severity of this bias can be assessed by interpreting Twitter users’ text data and deriving information about their occupation and other socioeconomic characteristics [
20,
21]. The geographic context of where the Twitter data were produced is also of importance, as urban areas are represented disproportionally stronger than rural areas [
22].
In this paper, we provide insights into how to evaluate the representativeness of geographic Twitter data on the raster level and, leaning on the principles of the geon paradigm [
23], extend the explanatory value of our results by providing spatially contiguous regions of similar representation errors. The value of our results lies in the knowledge about whether using Twitter data as a proxy for the population living in a given study area has the potential to yield adequate results. We delineate spatially contiguous regions of high spatial autocorrelation of errors that are achieved with spatially consistent predictor variables. The result are areas of equal representativeness. We show that the resulting regions vary across space in their quantitative and qualitative characteristics, representing not only differences in prediction quality, but also in suitable predictor variables. Studying their characteristics and distributions, we gain insights into the processes that lead to an area being representative of a population. By doing so, we show that it can be misleading to have fixed assumptions about the population modeled by the Twitter data. In the research presented in this paper, we address the following research questions:
How can we measure the representativeness of Twitter data?
Are geo-social media data representative for different socio-demographic subgroups and over time?
How do spatial relationships impact the representativeness of spatially homogeneous regions?
2. Related Work
The concept of representativeness heuristics was originally defined as the apparent probability of an object A belonging to a class B, or an event A being generated by a process B [
24]. If A is reasonably representative of B, it must therefore be possible to derive information about B from observations of A. We borrow this definition and translate it from the field of psychology to our context in the way that by using Twitter data (A), or some derivative thereof, as proxy for a process under investigation (B), we are able to draw information about B from observations of A. In the case of this study, we investigate the representativeness of Twitter data (A) of different socioeconomic groups within a population (B).
Methods and limitations of previous efforts to assess the quality of the representativeness of user-generated data have been discussed recently [
25,
26,
27]. The prediction error of the number Twitter users on the United States (US) county level can be explained using geographically weighted regression models and socioeconomic variables [
28].
In public opinion mining, the problem of inadequate representativeness of results obtained from geo-social media can also be addressed by integrating results of a smaller opinion poll with known participant demographics and adjusting the results [
29]. A similar approach suggests mitigating representativeness problems by measures such as qualitative analysis of a subset of the data in question or the integration of knowledge from the platform providers in the analysis process where possible [
30]. Gender differences between the users of a geo-social media and the local demographics can be explored and accounted for using spatial autocorrelation methods, although this requires information about the geo-social media user’s gender [
31]. Gender differences can also be used to partly explain political affiliations and therefore be used as a correction factor when deriving public political opinions from Twitter data [
32].
One way to integrate a larger number of covariates is via logistic regression modeling. This approach can also give insights into the preferred geo-social media of different user groups [
33] From previous work, there are three general approaches emerging for assessing the problem geo-social media representativeness: (1) evaluating representativeness of contributors; (2) evaluating the completeness of the data; and (3) comparing geo-social media data to reference data [
34]. The requirement for method (3) is the need for suitable reference data. In our study design we can use available geographic and socio-demographic data as reference. This makes the approach a good fit for our study.
We see the main research gap in the work listed above in the gap between the quantitative and qualitative interpretation of prediction results. Evaluating prediction results in spatially contiguous groups of high similarity allows us to evaluate the impact of covariates in a useful context. It therefore ultimately aids the interpretability of results. We address this gap by providing methods to explore how different covariates impact predictions over time. Under the assumption that the Twitter data somewhat robustly represent the same portion of a population over time, we would expect little variation in yearly prediction models. We show that this is not always the case and therefore argue in favor of new investigations of the idiosyncrasies of different prediction models. Additionally, we provide insights into the spatial characteristics of the prediction results, thereby highlighting the importance of geographic context of the data. We aim to do so by providing geons, that is, spatially contiguous coherent units that allow quantitative interpretation and of the underlying covariates and their spatial idiosyncrasies. Further, we show how to perform the analyses using data of fine spatial granularity, while presenting the results in aggregated, easily interpretable regions.
3. Data and Preprocessing
The Twitter data used in our study comprise eight years of data collected in the conterminous US via the Twitter REST and streaming application programming interfaces (API) [
35]. The bounding box of the collected data covers 24.50° N–49.38° N and 66.75° W–124.73° W. We considered only tweets with a point coordinate as their geographic reference. We aggregated into a regular rectangular raster with a cell size of 1 km
2 by summing up the number of tweets within each cell, grouped by year.
Table 1 gives an overview of the number of individual cells containing tweets, the number of tweets and some summary statistics aggregated on the raster level. All data include a timestamp and a geographic point location defined by a pair of coordinates. The point location of a tweet is provided by the user, usually as a GPS position. The number of tweets varies strongly over time. Potential causes for this effect are changes in Twitter’s data distribution model, such as the removal of precise geotagging in 2019 [
36], restrictions in the number of available tweets via the API or shifts in user behavior. The strong changes in standard deviation are also worth noting, since they appear to have a significant effect on the global prediction quality.
For the covariates under examination, we combined data from different sources. We obtained the census data from the Integrated Public Use Microdata Series National Historical Geographic Information System [
37] from the 2011 and 2017 American Community Survey. The data include 90 variables about the population’s age, sex, socioeconomic status, race, and educational attainment on the county level, with the individual demographic variables listed in
Table 2. We also included the Euclidean distance to the nearest city. The population raster on a 30 arc second scale are taken from the Gridded Population of the World (GPW), v4 dataset [
38]. Point data of city locations with ≥100,000 inhabitants are taken from the United States Census Bureau (
https://www.census.gov/programs-surveys/geography.html accessed on 7 May 2021). These points act as reference points when calculating the euclidean distance to the closest city of a raster cell.
In this study, we use socio-demographic data on the county level. The county’s shapes are highly heterogeneous and their surface areas vary by a factor of almost 1000. They also contain no information about the large spatial variation of population density. This contributes to the modifiable areal unit problem (MAUP), which can strongly affect multivariate analysis, because simply by changing unit area’s sizes and shapes, spatial models can produce significantly varying results [
39]. Because of the heterogeneity of the county areas, the MAUP is likely to have an influence on our results. To lessen the influence of arbitrarily shaped administrative units on the results, we disaggregated the data to regular grids based on GPW population raster data.
Figure 1 illustrates the process of zonal disaggregation we performed on county level data to break it down to the raster level. Given an input feature (a) and a population raster (b), we divide the population raster based on the features of (a). We then normalize the raster values such that each zone has a raster sum of 1 (d). Multiplying the normalized raster values with the feature values of (a) results in a disaggregated version of the original features (e). A side effect of this approach is that the resulting rasters share the population raster’s spatial variability, which may lead a to misrepresentation of some variables.
We also needed to aggregate the Twitter data to the raster level. Starting with raw point data from Twitter we identified automatically generated tweets from chat bots and removed them. We did so in an iterative manual process in which we selected random samples of the whole data set and sorted them by the post frequency of their users. If we identified a user who generated large amounts of tweets with obvious traits of automatically generated content, such as highly repetitive text, advertisements or random strings of text, we removed all tweets of that user from the data. We repeated the process until we were not able to identify any more automatically generated content. This process eliminated approximately ten percent of tweets. We then overlaid a raster grid with the same extent and cell size of the other data sets and summed up the number of tweets per cell.
To model the distance to the closest larger city for each cell, we calculated the Euclidean distance of the cell to the next city of the United States Census Bureau point data of cities with ≥100,000 inhabitants.
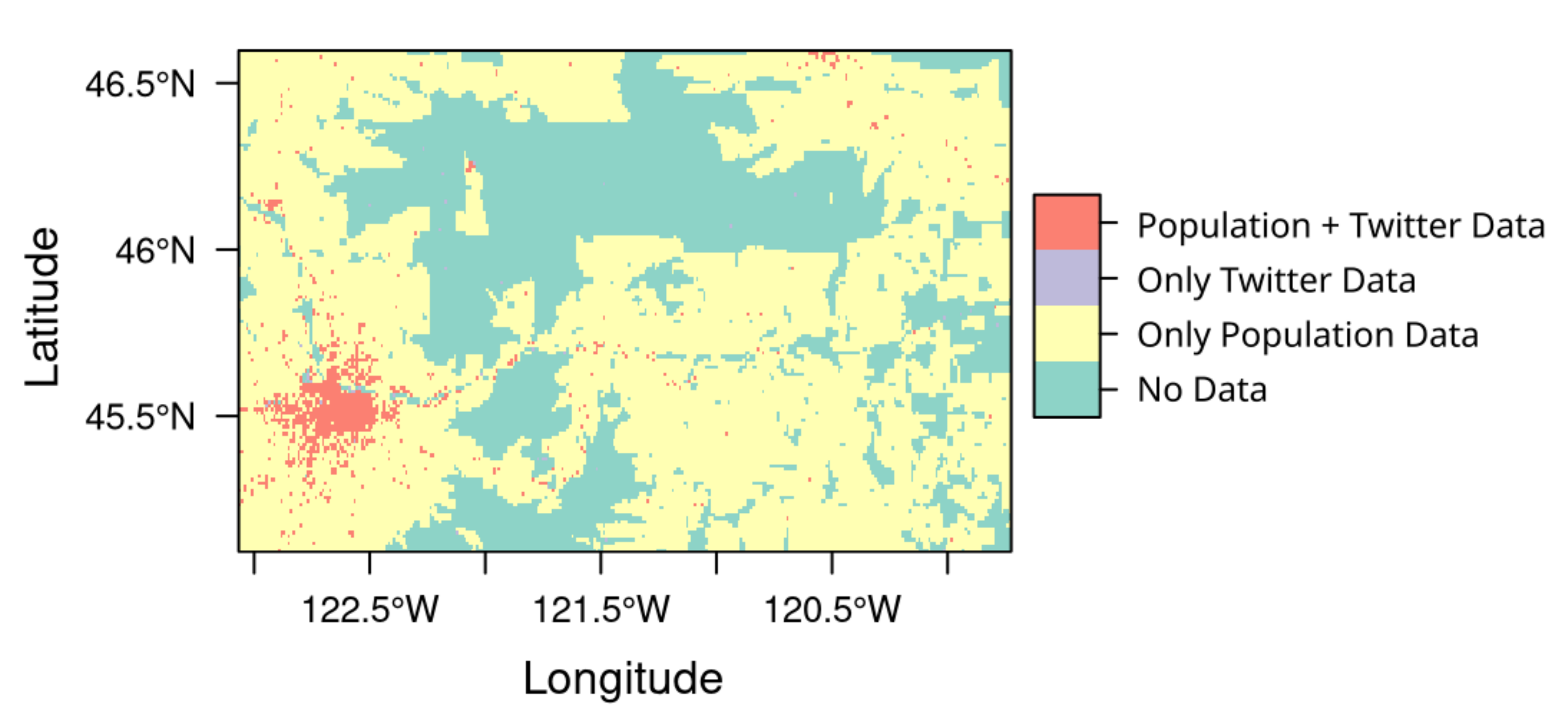
The preprocessed population and Twitter data are both represented as sparse rasters which are not identical in their spatial structure. We mitigated this problem in our experiments by imputation. Each cell stack represents one observation. When merging the population and Twitter data, the presence and absence of a value in a given cell results in four combinations for each cell stack. Within the boundaries of the conterminous US, the overlap of cells with values present in both layers is about 3.8%, cells with only population data are 68.0%, cells with only Twitter data are 0.2% and cells with no data at all are 28.0%. If none or both of the layers contain a value, the data can be used as is. If only one value exists, the counterpart is set to the value 0. We use this strategy to account for Twitter usage in unpopulated areas.
Figure 2 shows an example of how the cell combinations can be distributed. The clustered pixels containing population and Twitter data are a typical footprint of an urban area. The vast majority of the remaining area is almost entirely divided into populated and unpopulated area, both without any Twitter data. There are only marginal areas scattered throughout the study area that contain Twitter data but no population. In the map, they only appear as individual pixels.
4. Methods
We operate on the premise that if we are able to predict the number of tweets in a given area based on data about the local population, the number of tweets in conclusion can be employed as a proxy of that population and is therefore representative of it. The acceptable error, and therefore the boundary of representativeness, for such predictions is highly dependent on the use case, however. An example for an application with high error tolerance would be the mere detection of human presence in a study area, in which the number of people are not of primary interest. Applications with the aim of providing quantitative information about a population in the study area, however, would typically operate with a lower error tolerance.
The implication of successful tests in this study is that Twitter as a data source provides data with which it is reasonable to project observations made in the data onto the real world. We use generalized linear regression models (GLM) with the number of tweets as the dependent variable and data describing demographics, population numbers, and income as independent variables. Thereby, we predict the number of tweets based on co-located variables describing the local population. We compare the attained results from the models with the validation data and calculate the resulting local and global prediction errors.
4.1. Generalized Linear Models
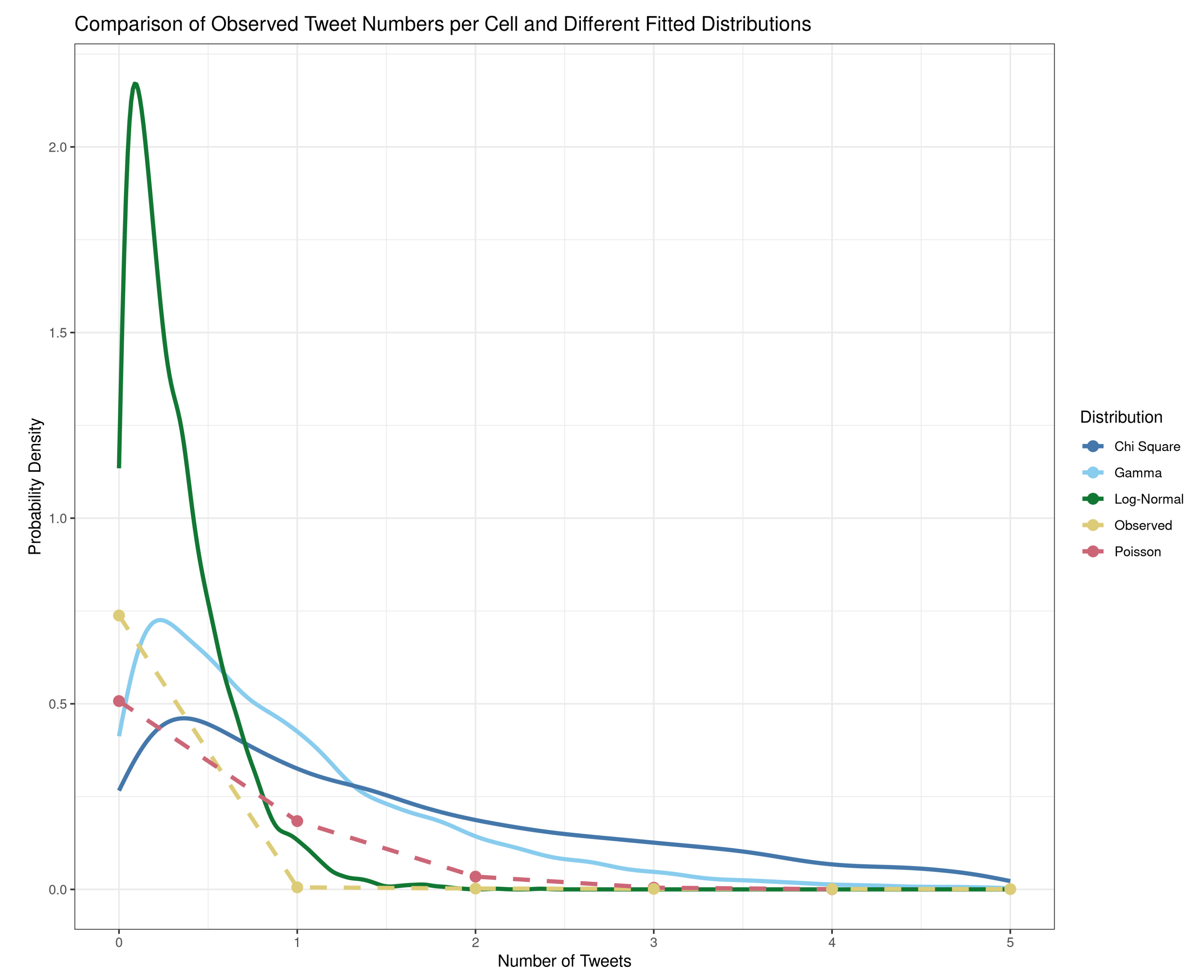
We fit the data to a generalized linear regression model with the number of tweets as dependent variable and the geographic and demographic data as independent variables. The model assumes a Poisson distribution for the number of tweets, which reflects our assumption of the data being produced in a constant and independent process. We justify this design decision based on different distribution shapes to which we fitted the Twitter count data using maximum likelihood estimation. Visual interpretation of the resulting curves in
Figure 3 show the good fit of the Poisson distribution versus the rest. Because of the high number of predictor variables modeling the population, we were expecting strong multicollinearity among some of them. To substantiate this presumption, we calculated the Kendall rank correlation coefficient
τ and the variance inflation factor (VIF) [
40]. We found consistently high values for both
τ and VIF, confirming our expectations. The main negative effects of this characteristic are the danger of overfitting the model and misjudgement when interpreting the explanatory value of individual variables.
We mitigated these effects by employing the least absolute shrinkage and selection operator (lasso) regularization [
41,
42] to penalize and remove regression coefficients based on the residual sum of squared errors (RSS) of the model. As discussed in [
43], this introduces bias to the regression model with the benefit of reducing its variance, therefore resulting in a model less prone to overfitting. This method requires defining a tuning parameter
for dimensioning the shrinkage penalty. The optimal value for
can be approximated by minimizing the RSS using
k-fold cross-validation [
44]. The precision with which we can approximate
increases with
k; as does computation time with
, so linearly. We chose
as a reasonable trade-off between optimizing
and computational effort.
The lasso method requires a training and testing dataset to fit a model and determine its error. With n observations per year, we chose the number of training data to be and the number of testing data to be . The training data are a uniformly distributed, randomly drawn sample without replacements of n.
4.2. Identification of Representativeness Groups
The resulting regression models can be used to predict the number of tweets for individual cells. The data used in this study are not necessarily spatially contiguous, meaning that there are numerous cells that are in close proximity, but not direct neighbours. Also, by splitting the data into testing and training cells through random sampling, some contiguous patches of cells are broken up into sparse groups of individual cells that are not spatially contiguous anymore. If the input data for the model are not spatially contiguous, the results are neither. This is problematic, because we use a cell’s direct spatial neighbourhood to determine their self-similarity. To mitigate this problem, we interpolate the introduced gaps in the data. Specifically, we interpolate the prediction error, based on which we quantify the self-similarity. To achieve this, we apply a buffer around the sparse data regions and interpolate the prediction error within the buffered regions using inverse distance weighting (IDW) [
45]. The resulting regions are restricted in space by the buffer threshold, but do not adhere to any administrative regions. We use the Getis-Ord
[
46] statistic of the prediction error within the individual regions to identify subregions of similar prediction errors. Because the
statistic results in a z-score, we can categorize the bottom and top five percent values as subregions of significant under- and overprediction, respectively. We refer to these spatially coherent regions of similar prediction error as representativeness groups (RG). To aid the qualitative interpretation of prediction errors, we calculate the correlation coefficients between the total number of tweets and the values of the different covariates separated by year and RG. An analysis of variance (ANOVA) between the RG confirms that the inter-group differences are significant.
4.3. Spatial Models
The next step is to explore whether there are spatial effects governing the distribution of prediction errors in the RG. For each region in an RG, we have the number of tweets and the originally identified covariates in a given year. Fitting the data in to spatial lag, spatial error [
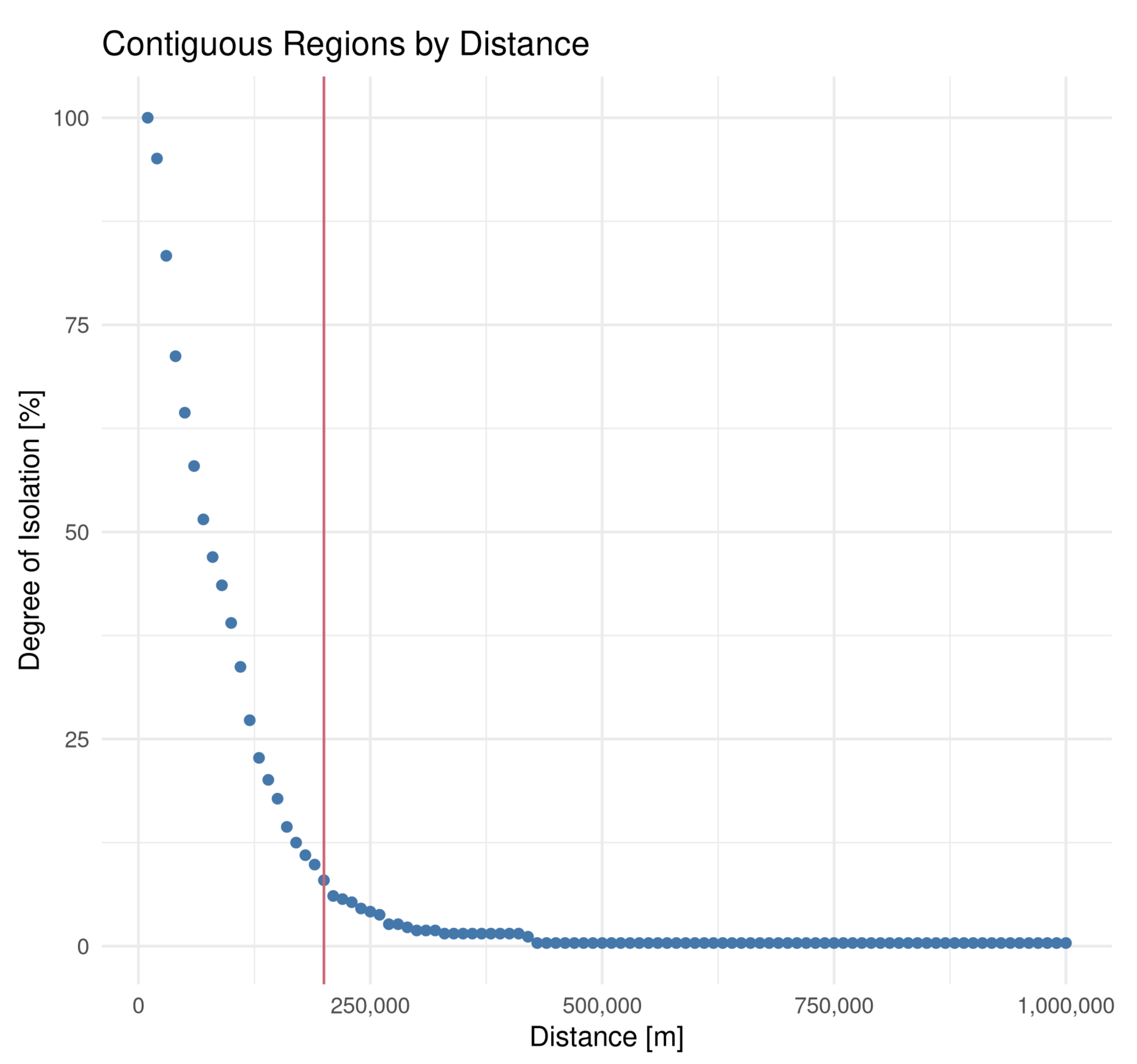
47] and linear regression models allows us to determine if and how spatial effects play a role in their representativeness. Given that we have three RG, eight years of data and three models, we end up computing and evaluating 72 models for this use case. The spatial models require a definition of neighbourhood. As most of the regions are disjoint, we chose a fixed distance as neighbourhood criterion. We chose the distance parameter by plotting the relative number of isolated regions as a function of distance and determining a visible “elbow” in the plot, similar to the method of determining a suitable neighbourhood for clustering [
48].
Figure 4 shows the number of contiguous regions calculated for different distances. The vertical line indicates the 200,000 m mark that we chose based on the plot.
The spatial lag model is defined as
, where
y is the dependent variable,
denotes the factor weighing the spatial neighbourhood
W,
are the dependent variables and
is the error term. A higher, significant value of
indicates a spatial lag. The spatial error model on the other hand fits the data to
. Here,
denotes the factor determining the spatial effect, but it scales the errors of a region’s neighbourhood instead of the predicted value.
is the remaining error in the model not associated with the neighbouring errors. Note that despite representing different concepts, both the regularization parameter of the lasso method introduced above and the spatial error model parameter are typically denoted with
. Further methodological and implementation details can be found in [
49,
50], respectively. We use the coefficient of determination
and the Akaike information criterion (AIC) [
51] to compare the different models and determine the most appropriate ones. The
can take values
. With increasing predictive power of the model,
converges towards 1. Similarly, the AIC can be used to compare multiple models fitted to the same data. It penalizes both the information loss and the number of parameters of statistical models, which in turn result in a higher AIC. Depending on which models show the best fit, we can make statements about the relationship of covariates, tweets and spatial relations of regions.
5. Results
5.1. Generalized Linear Models
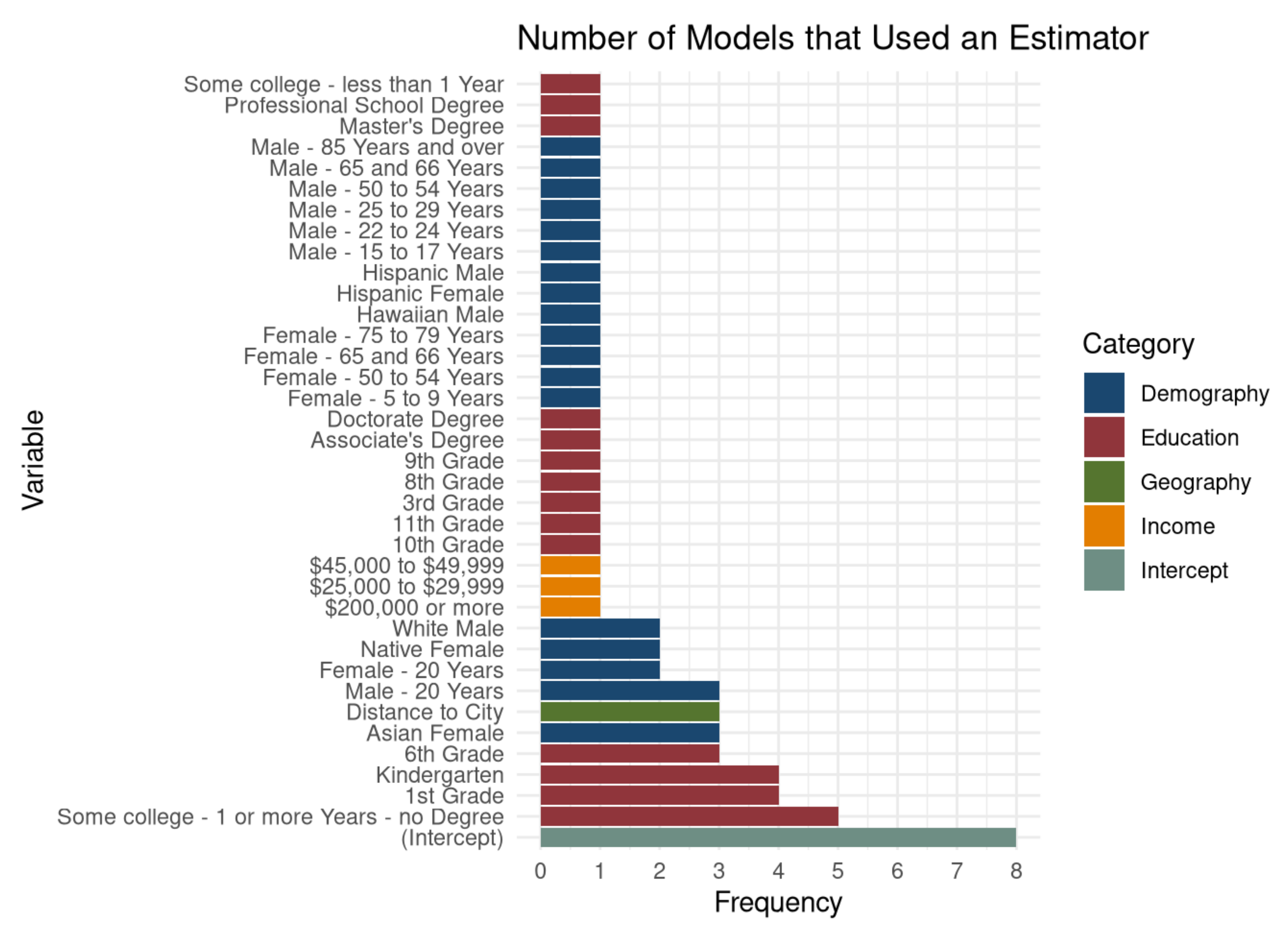
Each model contains a number of variables that were used as predictors.
Figure 5 shows how frequently the different predictor variables were used in the generalized regression models. The low number of predictor variables indicates that most models were simplified significantly by the lasso process. The strong decimation of predictor variables is expected because of the high values for
and the VIF calculated above. For ease of interpretation, we placed the individual parameters into demographic, educational, geographical and income categories. Apart from the model intercept, that each model has by definition, the most frequent predictor category are education and demography. Only two variables of the income category are used. On the one hand, this is surprising given that income is typically seen as a strong predictor of tweet numbers, on the other hand, the strong multicollinearity in the data may lead to the exclusion of expected predictors in the regularization process. The Euclidean distance to the closest city appears in three models as the only geographical variable in the otherwise non-spatial models.
After training and validating the models, we assessed their predictive power by running them against testing data and calculating
and the root-mean-square error (RMSE) of the results.
Table 3 shows some information about the GLM, their prediction errors and the number of independent variables used in the regression model after regularization. The individual variables are shown in Figure 7. Note that cases with only one predictor, it is not possible to calculate for
because the prediction model can only produce a single response value which is the intercept of the model. The same is true for cases with very low values for
, as is the case in years 2015 and 2017. The models perform very well for predicting the overall number of tweets, as indicated by the small relative differences between expected total and predicted total number of tweets. The RMSE confirms the small divergence in the prediction of tweet counts. However, the
values are extremely small, which indicates that the GLM do not appropriately model the data distribution. Because the distribution is largely governed by spatial effects, such as the population density, we need to address the GLM’s shortcomings using spatial models.
5.2. Identification of Representativeness Groups
To explore the spatial effects in the data, we determined subregions of similar representativeness. The initial delineation using a spatial buffer resulted in a set of 92 regions. By calculating the
statistic of the individual cells, we determined clusters of spatially coherent similar prediction error values within the regions. We selected the cells containing the bottom and top five percent of
values as the ares of low and high representativeness, respectively.
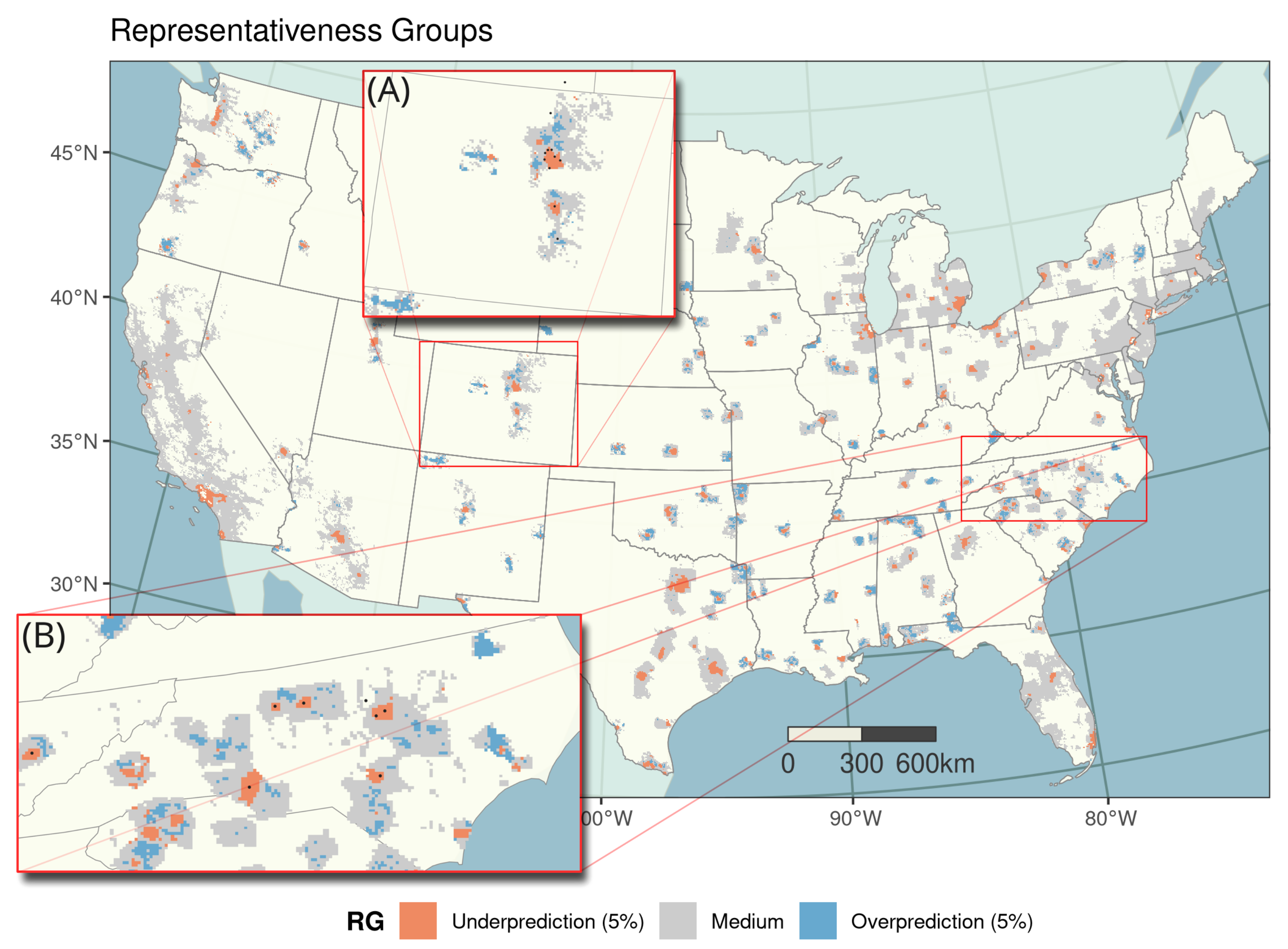
Figure 6 shows an overview of these subregions and more detailed zoom of the States Colorado (A) and North Carolina (B) to showcase the results in more detail. To represent the results of the entire study period, the map shows which RG appeared most frequently in each cell. For better interpretation, state capitals and cities above 100,000 inhabitants are added as dark grey dots. Areas drawn in red represent regions where the actual number of tweets was higher than predicted. This effect is pertinent in areas with high population numbers such as the densely populated coastal areas, but also large cities inland. Areas of overrepresentation are often situated in the proximity of large metropolitan areas, but also as individual regions. North Carolina exhibits a typical pattern of underrepresentation in highly populated areas, indicating that the number of modeled tweets is smaller than observed.
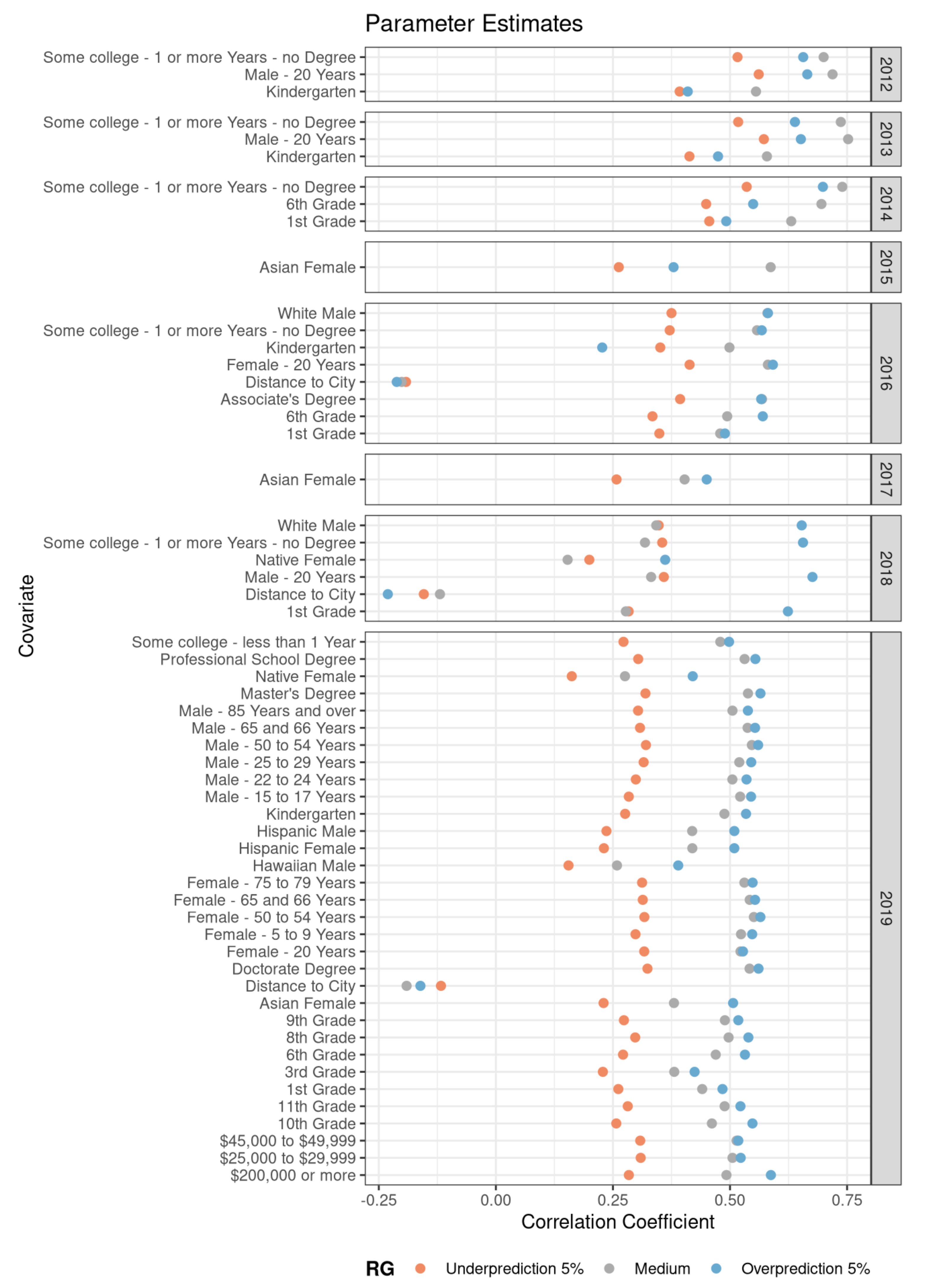
Calculating the grouped regional correlation coefficients between the covariates and the number of tweets results in the metrics shown in
Figure 7. From top to bottom, the figure shows, for every year, the correlation coefficient between the number of tweets and covariates that were integrated in the respective model. For each year and covariate, there are three color coded results, representing the RG. The RG appear to be consistently grouped. This is an indicator that the RG are an appropriate tool to split the data into groups that differ in representativeness, but are also consistent in their covariates. Using ANOVA to confirm this visual impression, under the null hypothesis that there is no significant difference in the group means, yields an F-value of 20.3 (the critical value for
is 7.2).
5.3. Spatial Models
To explore the relations between the RG, we compare effect sizes predicted by different spatial and non-spatial models. For each year and RG, we fitted a spatial lag, a spatial error and a linear regression model to predict the number of tweets from the covariates identified by the respective year’s GLM.
Table 4 shows the different spatial and linear model parameter estimations. For reasons of space, the RG are encoded numerically. We can see that, for the 24 possible combinations of year and RG, the spatial error model is the most appropriate one 12 times, the linear regression model ten times and the spatial lag model only two times. We can also see that especially RG 1 and 3, so the underrepresentative and overrepresentative ones are most consistently linked with the spatial error model (ten out of 16 times), whereas the linear regression model is the best fit for five out of eight data sets in the medium RG. It is worth noting, however, that the differences in AIC and
are relatively small overall.
We can extract the individual parameter estimates from the 24 best models above and compare them to address the question of which covariates play a stronger role in the different RG.
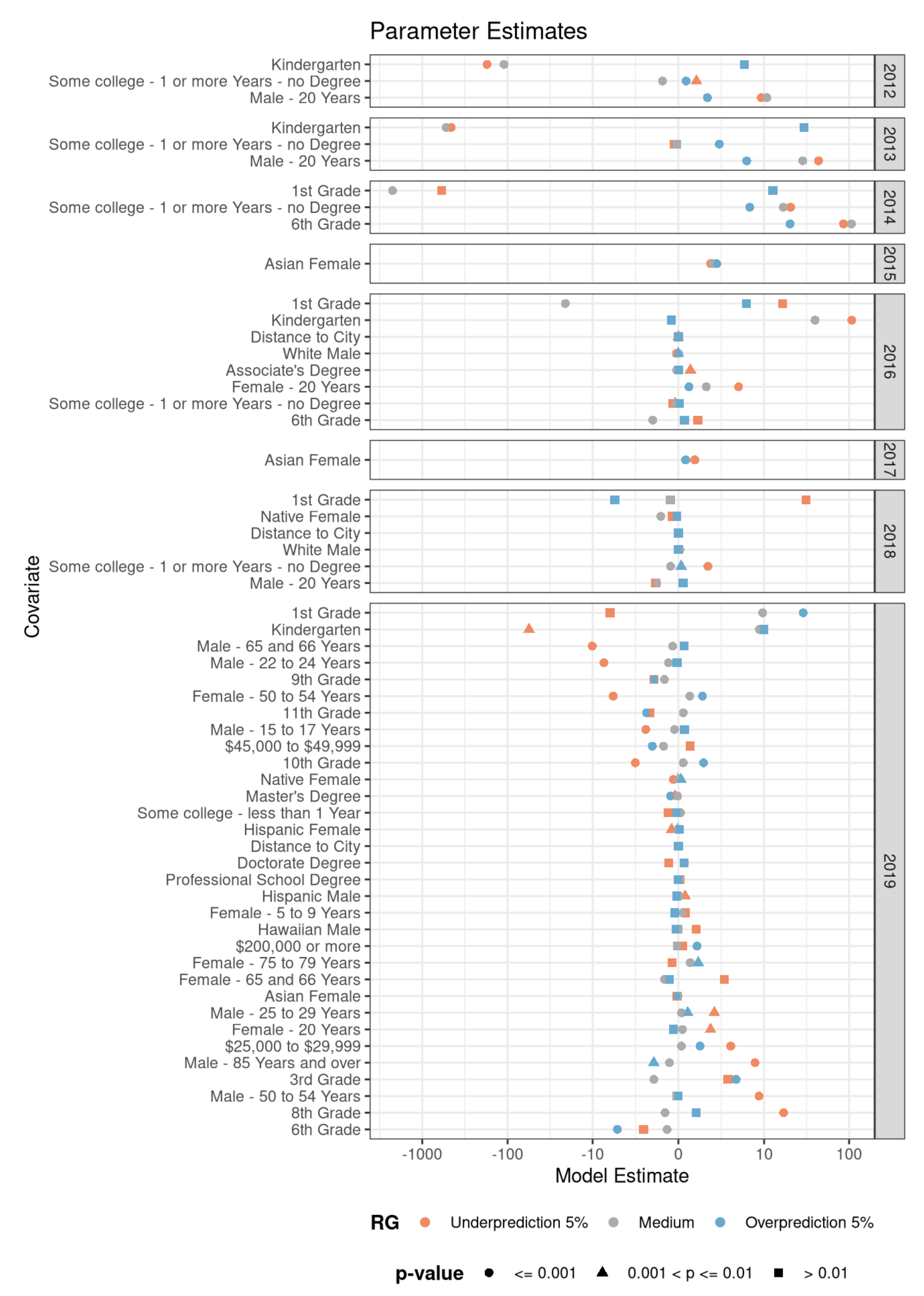
Figure 8 shows the different covariates’ parameter estimations on the x axis and the covariate names, grouped by year, on the y axis. The figure is therefore a more granular representation of all models shown in bold in
Table 4.
Each individual datum in the figure represents the parameter estimate for a single covariate of the most appropriate model for a given RG and year. The significant absolute value of a covariate indicates the effect size on the dependent variable, the number of tweets. Its sign indicates whether high or low values of the covariate lead to higher or lower values for the dependent variable. The figure can therefore be used to interpret the role of individual covariates in the prediction models. A negative value indicates that the respective covariate within its RG and year is lower than expected, a positive one indicates the opposite.
The figure shows a number of noteworthy effects. There is a large discrepancy to
Figure 7, which appears much more grouped. As above, we can quantify this observation using ANOVA. We can confirm the visual impression, under the null hypothesis that the group means do not differ significantly, with an F-value of 1.0 (critical value for
p = 0.001 is 7.2) and show that for the parameters the clear separation by RG is not evident anymore on this level. On the contrary, especially for 2019, the under- and overrepresentative RG appear to be almost divergent. We conclude from this that the different RG alone are not granular enough to adequately explain the number of predicted tweets and therefore warrants closer examination of individual covariates. Looking at individual parameters and their values, the very lowest parameters are consistently the ones associated with a young age, such as Kindergarten and first grade education levels, especially in the years 2012 through 2014. Assuming that Twitter users abide by the company’s terms of service (
https://twitter.com/en/tos accessed on 7 May 2021), they would be at least 13 years old by definition, which would be one way to explain the strong effect. However, the effect seems to change in later years and seems to be stronger divided by RG. Another effect that was to be expected is that the distance to the nearest city is close to cancelled out based on the maps shown above. There are also covariates with a consistently high association with prediction quality, such as college attendance and age groups in their twenties. Aside from the parameters themselves, an important observation is the fact that many parameters are unstable throughout the years. This makes it evident that the overall question of whether a set of data is representative of a population is more than a mere yes/no one.
6. Discussion
The GLM results show that the non-spatial models alone are not suitable for adequate predictions beyond the total number of tweets. Even though for the total number of tweets, the predictions produce errors in an overall acceptable magnitude, the consistently low values indicate that the real and predicted data differ strongly in their distribution. However, composing RG and fitting spatial lag and error models allows us to explore the spatial characteristics of prediction results in a more accessible form. The results confirm the significant spatial relationships among the RG, in most cases in spatial error models. The predominance of spatial error models in the results suggest the presence of spatially clustered unknown covariates that would benefit the model. In case of linear models explaining the RG, the data within the specific RG are not strongly dependent on their spatial neighbourhood. In the remaining results, where the spatial lag model is most appropriate, the covariates of an RG in the model are significantly linked to the covariates in neighbouring RG.
We show that Twitter data can be grouped by their representativeness, which helps in interpreting prediction results and in reducing erroneous interpretations. Given a set of Twitter data and covariates, we show how to calculate and interpret RG. The methods are not limited to Twitter data, but can be applied to any dataset for which a reasonable amount of data points and adequate covariates are available. The choice of five percent as cutoff values for the confidence intervals of different RG is largely arbitrary. The method itself is not limited to any number of RG, but three groups make for interpretable results while still being able to convey a lot the complexity of the underlying data. The large number of spatial error models among the best performing ones may indicate inadequacies in the underlying data. This could be explained by the relatively high multicollinearity in the covariates. Despite being having a large number of covariates, their high similarity limits their explanatory power.
Our preprocessing routine for zonal disaggregation of the county-level variables assumes an equal distribution of each variable within the county, which may lead to misrepresentations of different groups within the county. The process biases the covariates’ distributions within a county towards the distribution of the population number and therefore increases the multicollinearity. This in turn leads to stronger penalties in the lasso regularization, thereby impacting the explanatory power of our results. On one hand, this approach adds an error term to our models, but on the other hand, we see this as an acceptable trade off in order to make use of the high resolution of the input data and to counteract the MAUP imposed by county boundaries.
The input data for the prediction models are in parts interpolated using IDW to fill gaps between cells introduced by the random sampling process for model training. A risk of this process is the possibility of obscuring outliers in the data, if the interpolation occurs in an outlier cell.
The exclusive usage of georeferenced tweets in this study eliminates the majority of tweets from the population. This leads to a selection bias of unknown magnitude. However, this selection is necessary, because the spatial nature of the tweet representativeness is at the focus of this study. As a consequence, the models presented in the study only apply to georeferenced tweets.
Another important aspect of using geotagged data is that the study adheres to adequate privacy by design guidelines [
52,
53] to protect the users who contributed the data.
The data from 2014 contains by far the highest number of tweets and also its distribution and descriptive metrics differ strongly from the other years. We speculate that this is the reason for the models to perform particularly poorly for this year. Possible causes for this outlier are changes in Twitter’s API, great overall user activity on the platform or changes in Twitter user groups. The latter would also explain the larger number of identified geographic and socio-demographic parameters in the GLM in the years after 2015. Another aspect of the data that could influence on the results is the input data’s internal structure. For example, the male and female age groups are binned with highly variable age intervals. Small, equal interval bins could allow for more detailed insights within the RG.
As Twitter discontinued their precise geotagging functionality that this work is built on in favour of a point-of-interest location scheme, future studies of a similar study design need to account for the difference in location precision. This could either be achieved by procuring data from a different, more precise source or by developing methods to account for the difference in data quality.
This should also be a reminder to practitioners who rely on the availability of a single data source, especially in the case of a private company which gives no data availability and quality guarantees, should be carefully considered.
7. Conclusions and Outlook
We addressed the first research question by introducing the RG as a concept to make prediction errors and the differences in covariates interpretable for users. Utilizing this concept in our use case, we showed that covariates predicting the number of tweets are qualitatively and quantitatively highly variable over time.
The model estimates resulting from the 24 most appropriate spatial models show how differently socioeconomic groups are represented within their RG and over time. One effect in these results pertaining to the second research question is the fact that some individual socio-demographic subgroups are represented differently over time. For example the Kindergarten or 1st Grade covariates, which vary strongly depending on the year, whereas the Distance to City is very stable in comparison. This effect also becomes clear when considering that some of the socio-demographic variables are temporally dependent. For example, if the 1st Grade variable was identified as significant in 2014, it would be reasonable to expect the 2nd Grade variable to be significant in 2015, the 3rd Grade in 2016 and so on. These observations lead to the conclusion, that the representativeness of many covariates can vary quite significantly. Therefore, practitioners should carefully evaluate existing models and assumptions from older models when applying them to new data.
The results of the different spatial models pertain to the third research question. We showed that, depending on RG and year, most RG can be most appropriately explained using spatial error models. However, some RG can also be explained using linear or spatial lag models. This knowledge can inform the decision process of whether it is appropriate to use the present data for predictions or there is need to identify additional covariates. It can also strengthen the decision of whether using a spatial model for predictions is appropriate.
Other strains of research in a similar direction could include comparative studies with other communication platforms than Twitter, for example cell phone connection, credit card usage or other platforms of geo-social media data. One shortcoming in our work is its limited geographic extent. Using only part of the US as a study region limits its significance to mostly that area. Twitter-based studies are conducted all over the world, however, which warrants similarly designed studies in other regions of the world as well. It will, however, hardly be possible to reproduce this exact study design, because it relies on demographic data which varies in availability, thematic composition, and reliability across the world. A suitable candidate for a similar study across several countries could be the European Union. Because of the largely homogenized geodata infrastructure [
54], setting up a large comparative study across the entire area would be feasible.
Author Contributions
Conceptualization, Andreas Petutschnig, Bernd Resch and Stefan Lang; Data curation, Andreas Petutschnig; Formal analysis, Andreas Petutschnig; Investigation, Andreas Petutschnig; Methodology, Andreas Petutschnig, Bernd Resch and Stefan Lang; Software, Andreas Petutschnig; Supervision, Bernd Resch and Stefan Lang; Validation, Andreas Petutschnig, Bernd Resch and Clemens Havas; Visualization, Andreas Petutschnig; Writing—original draft, Andreas Petutschnig, Bernd Resch, Stefan Lang and Clemens Havas. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Austrian Science Fund (FWF) through the projects “Geographic Information Science. Integrating interdisciplinary concepts and methods” (reference number W 1237) and “The Scales and Structures of Intra-Urban Spaces” (reference number P 29135-N29). This study has been carried out in the GeoSHARING project, which has been funded by the Austrian research programme BRIDGE of the Federal Ministry for Climate Action, Environment, Energy, Mobility, Innovation and Technology (BMK), project number 878652.
Data Availability Statement
Data available in a publicly accessible repository The data presented in this study are openly available in Harvard Center for Geographic Analysis Geotweet Archive at
https://doi.org/10.7910/DVN/3NCMB6 accessed on 7 May 2021.
Acknowledgments
We would like to thank Harvard University’s Center for Geographic Analysis for their support in providing us with the Twitter data for our study. Open Access Funding by the Austrian Science Fund (FWF).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Steiger, E.; Westerholt, R.; Resch, B.; Zipf, A. Twitter as an indicator for whereabouts of people? Correlating Twitter with UK census data. Comput. Environ. Urban Syst. 2015, 54, 255–265. [Google Scholar] [CrossRef]
- Sui, D.; Goodchild, M. The convergence of GIS and social media: Challenges for GIScience. Int. J. Geogr. Inf. Sci. 2011, 25, 1737–1748. [Google Scholar] [CrossRef]
- Lee, K.; Agrawal, A.; Choudhary, A. Real-Time disease surveillance using twitter data: Demonstration on flu and cancer. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; Part F1288. Association for Computing Machinery: New York, NY, USA, 2013; pp. 1474–1477. [Google Scholar] [CrossRef]
- Santillana, M.; Nguyen, A.T.; Dredze, M.; Paul, M.J.; Nsoesie, E.O.; Brownstein, J.S. Combining Search, Social Media, and Traditional Data Sources to Improve Influenza Surveillance. PLoS Comput. Biol. 2015, 11, e1004513. [Google Scholar] [CrossRef]
- Kogan, N.E.; Clemente, L.; Liautaud, P.; Kaashoek, J.; Link, N.B.; Nguyen, A.T.; Lu, F.S.; Huybers, P.; Resch, B.; Havas, C.; et al. An early warning approach to monitor COVID-19 activity with multiple digital traces in near real time. Sci. Adv. 2021, 7, eabd6989. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Wei, W.; Wang, B.; Liu, B. Correlating S&P 500 stocks with Twitter data. In Proceedings of the 1st ACM International Workshop on Hot Topics on Interdisciplinary Social Networks Research (HotSocial 2012), Beijing, China, 12 August 2012; pp. 69–72. [Google Scholar] [CrossRef]
- Conover, M.D.; Gonçalves, B.; Ratkiewicz, J.; Flammini, A.; Menczer, F. Predicting the political alignment of twitter users. In Proceedings of the 2011 IEEE International Conference on Privacy, Security, Risk and Trust and IEEE International Conference on Social Computing, PASSAT/SocialCom 2011, Boston, MA, USA, 9–11 October 2011; pp. 192–199. [Google Scholar] [CrossRef]
- Petutschnig, A.; Havas, C.R.; Resch, B.; Krieger, V.; Ferner, C. Exploratory Spatiotemporal Language Analysis of Geo-Social Network Data for Identifying Movements of Refugees. GI_Forum 2020, 1, 137–152. [Google Scholar] [CrossRef]
- Sakaki, T.; Okazaki, M.; Matsuo, Y. Earthquake Shakes Twitter Users: Real-Time Event Detection by Social Sensors; Association for Computing Machinery: New York, NY, USA, 2010; p. 851. [Google Scholar] [CrossRef]
- Resch, B.; Usländer, F.; Havas, C. Combining machine-learning topic models and spatiotemporal analysis of social media data for disaster footprint and damage assessment. Cartogr. Geogr. Inf. Sci. 2018, 45, 362–376. [Google Scholar] [CrossRef]
- Hawelka, B.; Sitko, I.; Beinat, E.; Sobolevsky, S.; Kazakopoulos, P.; Ratti, C. Geo-located Twitter as proxy for global mobility patterns. Cartogr. Geogr. Inf. Sci. 2014. [Google Scholar] [CrossRef]
- Resch, B.; Summa, A.; Zeile, P.; Strube, M. Citizen-centric urban planning through extracting emotion information from twitter in an interdisciplinary space-time-linguistics algorithm. Urban Plan. 2016, 1, 114–127. [Google Scholar] [CrossRef]
- Roberts, H.; Resch, B.; Sadler, J.; Chapman, L.; Petutschnig, A.; Zimmer, S. Investigating the Emotional Responses of Individuals to Urban Green Space Using Twitter Data: A Critical Comparison of Three Different Methods of Sentiment Analysis. Urban Plan. 2018, 3, 21–33. [Google Scholar] [CrossRef]
- Havas, C.; Resch, B.; Francalanci, C.; Pernici, B.; Scalia, G.; Fernandez-Marquez, J.L.; Van Achte, T.; Zeug, G.; Mondardini, M.R.R.; Grandoni, D.; et al. E2mC: Improving emergency management service practice through social media and crowdsourcing analysis in near real time. Sensors 2017, 17, 2766. [Google Scholar] [CrossRef]
- De Albuquerque, J.P.; Herfort, B.; Brenning, A.; Zipf, A. A geographic approach for combining social media and authoritative data towards identifying useful information for disaster management. Int. J. Geogr. Inf. Sci. 2015, 29, 667–689. [Google Scholar] [CrossRef]
- Resch, B.; Summa, A.; Sagl, G.; Zeile, P.; Exner, J.P. Urban Emotions—Geo-Semantic Emotion Extraction from Technical Sensors, Human Sensors and Crowdsourced Data. In Progress in Location-Based Services; Springer: Cham, Switzerland, 2015; pp. 199–212. [Google Scholar] [CrossRef]
- Kounadi, O.; Ristea, A.; Leitner, M.; Langford, C. Population at risk: Using areal interpolation and Twitter messages to create population models for burglaries and robberies. Cartogr. Geogr. Inf. Sci. 2018, 45, 205–220. [Google Scholar] [CrossRef]
- Mislove, A.; Lehmann, S.; Ahn, Y.Y.; Onnela, J.P.; Rosenquist, J.N. Understanding the Demographics of Twitter Users. In Proceedings of the International AAAI Conference on Weblogs and Social Media (ICWSM), Barcelona, Spain, 17–21 July 2011; pp. 554–557. [Google Scholar]
- Li, L.; Goodchild, M.F.; Xu, B. Spatial, temporal, and socioeconomic patterns in the use of twitter and flickr. Cartogr. Geogr. Inf. Sci. 2013, 40, 61–77. [Google Scholar] [CrossRef]
- Sloan, L.; Morgan, J.; Housley, W.; Williams, M.; Edwards, A.; Burnap, P.; Rana, O. Knowing the Tweeters: Deriving Sociologically Relevant Demographics from Twitter. Sociol. Res. Online 2013, 18, 74–84. [Google Scholar] [CrossRef]
- Sloan, L.; Morgan, J.; Burnap, P.; Williams, M. Who tweets? deriving the demographic characteristics of age, occupation and social class from twitter user meta-data. PLoS ONE 2015, 10, e0115545. [Google Scholar] [CrossRef]
- Hecht, B.; Stephens, M. A tale of cities: Urban biases in volunteered geographic information. In Proceedings of the 8th International Conference on Weblogs and Social Media (ICWSM 2014), Ann Arbor, MI, USA, 1–4 June 2014; pp. 197–205. [Google Scholar]
- Lang, S.; Kienberger, S.; Tiede, D.; Hagenlocher, M.; Pernkopf, L. Geons-domain-specific regionalization of space. Cartogr. Geogr. Inf. Sci. 2014, 41, 214–226. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Judgment under uncertainty: Heuristics and biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhu, A.X. A representativeness-directed approach to mitigate spatial bias in VGI for the predictive mapping of geographic phenomena. Int. J. Geogr. Inf. Sci. 2019, 33, 1873–1893. [Google Scholar] [CrossRef]
- Zhu, A.X.; Zhang, G.; Wang, W.; Xiao, W.; Huang, Z.P.; Dunzhu, G.S.; Ren, G.; Qin, C.Z.; Yang, L.; Pei, T.; et al. A citizen data-based approach to predictive mapping of spatial variation of natural phenomena. Int. J. Geogr. Inf. Sci. 2015, 29, 1864–1886. [Google Scholar] [CrossRef]
- Fink, D.; Hochachka, W.M.; Zuckerberg, B.; Winkler, D.W.; Shaby, B.; Munson, M.A.; Hooker, G.; Riedewald, M.; Sheldon, D.; Kelling, S. Spatiotemporal exploratory models for broad-scale survey data. Ecol. Appl. 2010, 20, 2131–2147. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Z.; Ye, X. Understanding demographic and socioeconomic biases of geotagged Twitter users at the county level. Cartogr. Geogr. Inf. Sci. 2019, 46, 228–242. [Google Scholar] [CrossRef]
- Kaschesky, M.; Sobkowicz, P.; Lobato, J.M.H.; Bouchard, G.; Archambeau, C.; Scharioth, N.; Manchin, R.; Gschwend, A.; Riedl, R. Bringing representativeness into social media monitoring and analysis. In Proceedings of the Annual Hawaii International Conference on System Sciences, Wailea, HI, USA, 7–10 January 2013; pp. 2003–2012. [Google Scholar] [CrossRef]
- Tufekci, Z. Big questions for social media big data: Representativeness, validity and other methodological pitfalls. In Proceedings of the Eighth International AAAI Conference on Weblogs and Social Media, Ann Arbor, MI, USA, 1–4 June 2014. [Google Scholar]
- Yuan, Y.; Wei, G.; Lu, Y. Evaluating gender representativeness of location-based social media: A case study of Weibo. Ann. GIS 2018, 24, 163–176. [Google Scholar] [CrossRef]
- Barberá, P.; Rivero, G. Understanding the Political Representativeness of Twitter Users. Soc. Sci. Comput. Rev. 2015, 33, 712–729. [Google Scholar] [CrossRef]
- Blank, G.; Lutz, C. Representativeness of Social Media in Great Britain: Investigating Facebook, LinkedIn, Twitter, Pinterest, Google+, and Instagram. Am. Behav. Sci. 2017, 61, 741–756. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, A.X. The representativeness and spatial bias of volunteered geographic information: A review. Ann. GIS 2018, 24, 151–162. [Google Scholar] [CrossRef]
- Lewis, B. Harvard CGA Geotweet Archive v2.0. 2016. Available online: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/3NCMB6 (accessed on 7 May 2020). [CrossRef]
- Hu, Y.; Wang, R.Q. Understanding the removal of precise geotagging in tweets. Nat. Hum. Behav. 2020, 4, 1219–1221. [Google Scholar] [CrossRef] [PubMed]
- Manson, S.; Schroeder, J.; Van Riper, D.; Ruggles, S. IPUMS National Historical Geographic Information System: Version 12.0 [Database]. 2018. Available online: https://ipums.org/projects/ipums-nhgis/d050.v12.0 (accessed on 7 May 2020).
- Center for International Earth Science Information Network (CIESIN), Columbia University. Gridded Population of the World, Version 4 (GPWv4): Data Quality Indicators; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2016.
- Fotheringham, A.S.; Wong, D.W.S. The Modifiable Areal Unit Problem in Multivariate Statistical Analysis. Environ. Plan. A Econ. Space 1991, 23, 1025–1044. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S. An {R} Companion to Applied Regression, 2nd ed.; Number September 2012; Sage Publications: Newbury Park, CA, USA, 2011; p. 2016. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularized paths for generalized linear models via coordinate descent (Technical Report). Citeseer 2008, 33, 1. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Shao, J. Linear model selection by cross-validation. J. Am. Stat. Assoc. 1993, 88, 486–494. [Google Scholar] [CrossRef]
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with {R}; Chapman and Hall/CRC Press: London, UK, 2015. [Google Scholar]
- Ord, J.K.; Getis, A. The Analysis of Spatial Association. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models. In Studies in Operational Regional Science; Springer: Dordrecht, The Netherlands, 1988; Volume 4. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 2017. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with {R}, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bivand, R.; Piras, G. Comparing Implementations of Estimation Methods for Spatial Econometrics. J. Stat. Softw. 2015, 63, 1–36. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar] [CrossRef]
- Kounadi, O.; Resch, B.; Petutschnig, A. Privacy Threats and Protection Recommendations for the Use of Geosocial Network Data in Research. Soc. Sci. 2018, 7, 191. [Google Scholar] [CrossRef]
- Kounadi, O.; Resch, B. A Geoprivacy by Design Guideline for Research Campaigns That Use Participatory Sensing Data. J. Empir. Res. Hum. Res. Ethics 2018, 13, 203–222. [Google Scholar] [CrossRef]
- INSPIRE Directive. Directive 2007/2/EC of the European Parliament and of the Council of 14 March 2007 Establishing an Infrastructure for Spatial Information in the European Community (INSPIRE). Off. J. 2007. Available online: https://inspire.ec.europa.eu/inspire-directive/2 (accessed on 7 May 2020).
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).