Non-Stationary Modeling of Microlevel Road-Curve Crash Frequency with Geographically Weighted Regression
Abstract
1. Introduction
2. Related Works
3. Methodologies
3.1. Non-Spatial Models
3.2. Spatial Models
3.3. Measures of Goodness of Fit
4. Data Description
5. Results and Discussion
5.1. Model Comparison
5.2. Statistics of Estimated Parameters
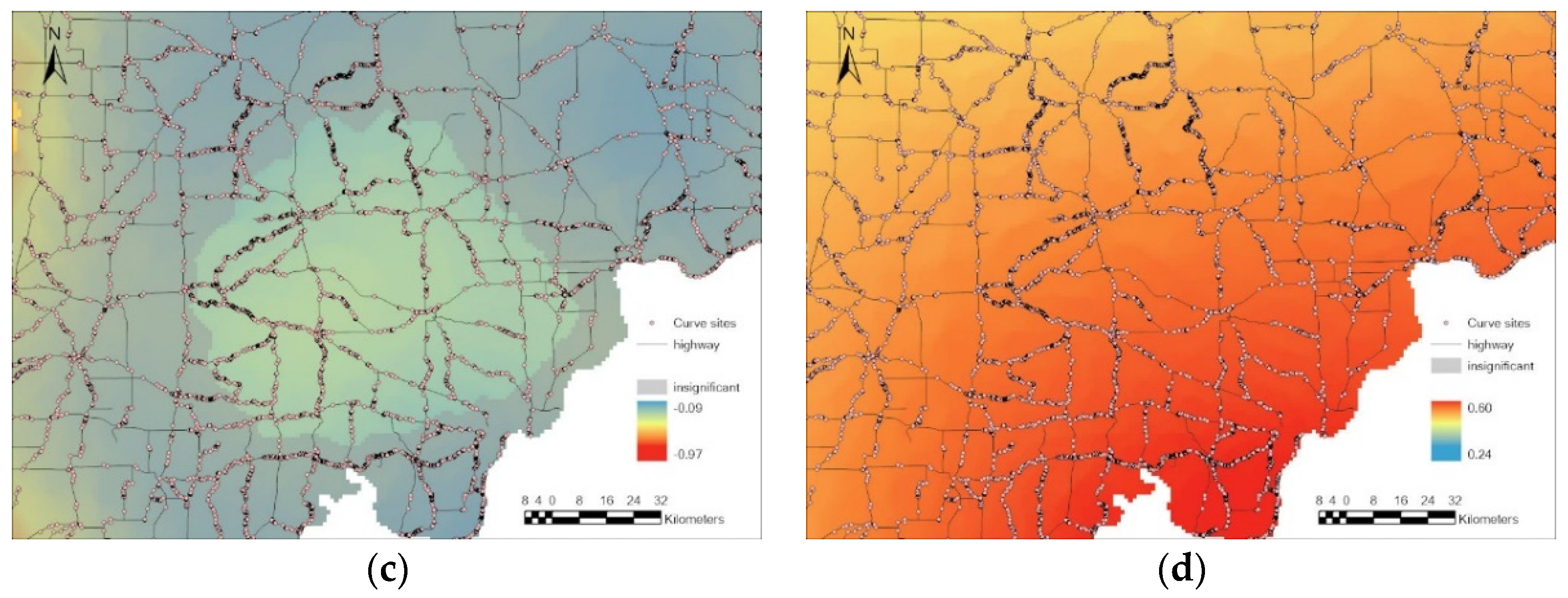
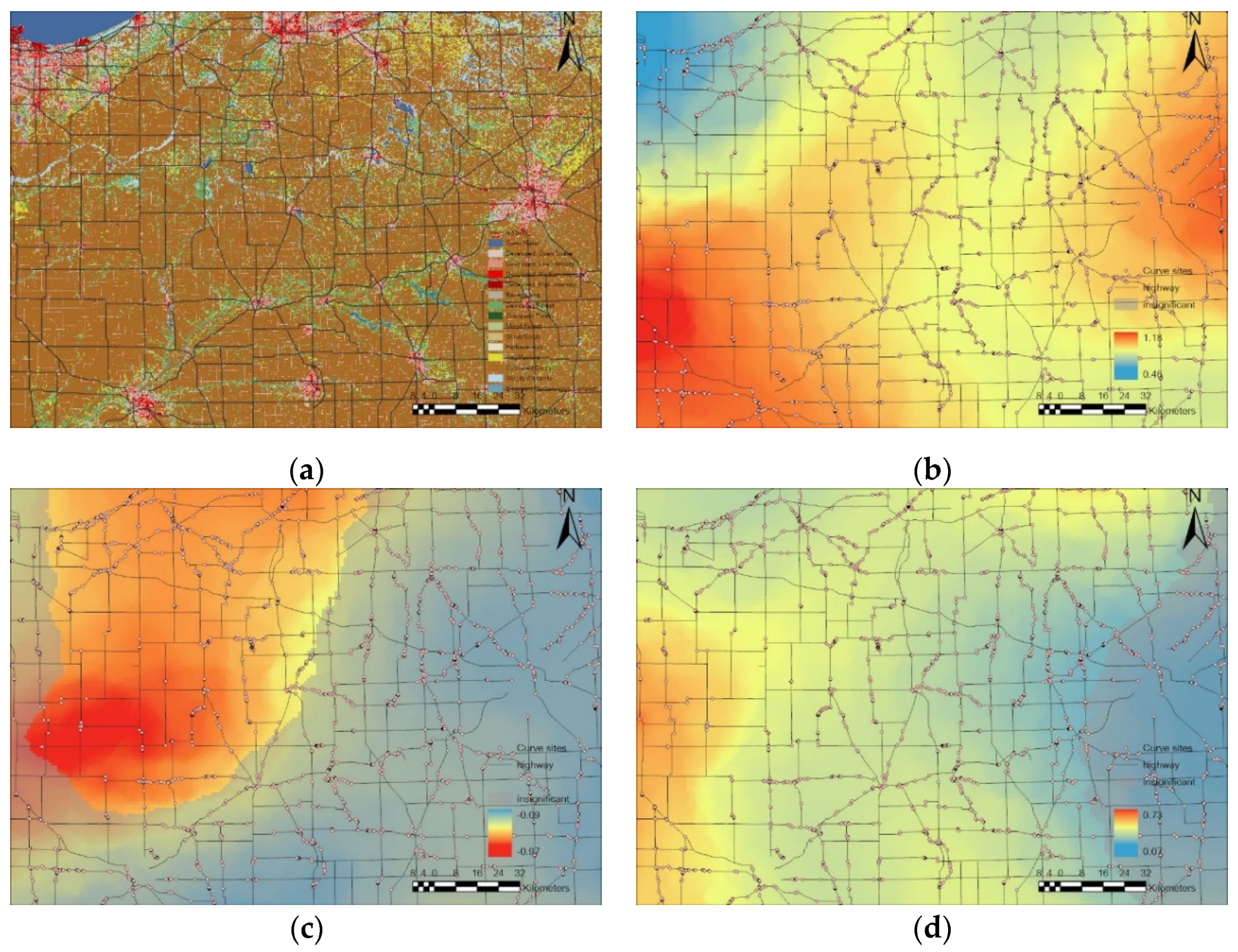
5.3. Spatial Heterogeneity of Estimated Parameters
5.4. Local Analysis of GWR Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Low-Cost Treatments for Horizontal Curve Safety 2016–Safety|Federal Highway Administration. Available online: https://safety.fhwa.dot.gov/roadway_dept/countermeasures/horicurves/fhwasa15084/#toc (accessed on 11 March 2021).
- Buddhavarapu, P.; Banerjee, A.; Prozzi, J.A. Influence of Pavement Condition on Horizontal Curve Safety. Accid. Anal. Prev. 2013, 52, 9–18. [Google Scholar] [CrossRef]
- Schneider, W.H.; Savolainen, P.T.; Moore, D.N. Effects of Horizontal Curvature on Single-Vehicle Motorcycle Crashes along Rural Two-Lane Highways. Transp. Res. Rec. 2010, 2194, 91–98. [Google Scholar] [CrossRef]
- Musey, K.; Park, S. Pavement Skid Number and Horizontal Curve Safety. Procedia Eng. 2016, 145, 828–835. [Google Scholar] [CrossRef]
- Gooch, J.P.; Gayah, V.V.; Donnell, E.T. Quantifying the Safety Effects of Horizontal Curves on Two-Way, Two-Lane Rural Roads. Accid. Anal. Prev. 2016, 92, 71–81. [Google Scholar] [CrossRef] [PubMed]
- Venkataraman, N.; Shankar, V.; Ulfarsson, G.F.; Deptuch, D. A Heterogeneity-in-Means Count Model for Evaluating the Effects of Interchange Type on Heterogeneous Influences of Interstate Geometrics on Crash Frequencies. Anal. Methods Accid. Res. 2014, 2, 12–20. [Google Scholar] [CrossRef]
- Mannering, F.L.; Shankar, V.; Bhat, C.R. Unobserved Heterogeneity and the Statistical Analysis of Highway Accident Data. Anal. Methods Accid. Res. 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Cai, Q.; Abdel-Aty, M.; Lee, J.; Huang, H. Integrating Macro- and Micro-Level Safety Analyses: A Bayesian Approach Incorporating Spatial Interaction. Transp. Transp. Sci. 2019, 15, 285–306. [Google Scholar] [CrossRef]
- Wan, D. The Spatial Analysis of Crash Frequency and Injury Severities in New York City: Applications of Geographically Weighted Regression Method. Ph.D. Thesis, The City College of New York, New York, NY, USA, 2018. [Google Scholar]
- Duddu, V.R.; Pulugurtha, S.S. Neural Networks to Estimate Crashes at Zonal Level for Transportation Planning. In Proceedings of the European Transport Conference 2012, Glasgow, Scotland, 8–10 October 2012. [Google Scholar]
- Lee, J.; Abdel-Aty, M.; Jiang, X. Development of Zone System for Macro-Level Traffic Safety Analysis. J. Transp. Geogr. 2014, 38, 13–21. [Google Scholar] [CrossRef]
- Gomes, M.J.T.L.; Cunto, F.; da Silva, A.R. Geographically Weighted Negative Binomial Regression Applied to Zonal Level Safety Performance Models. Accid. Anal. Prev. 2017, 106, 254–261. [Google Scholar] [CrossRef] [PubMed]
- Soroori, E.; Moghaddam, A.M.; Salehi, M. Modeling Spatial Nonstationary and Overdispersed Crash Data: Development and Comparative Analysis of Global and Geographically Weighted Regression Models Applied to Macrolevel Injury Crash Data. J. Transp. Saf. Secur. 2020, 1–25. [Google Scholar] [CrossRef]
- Aguero-Valverde, J.; Jovanis, P.P. Spatial Analysis of Fatal and Injury Crashes in Pennsylvania. Accid. Anal. Prev. 2006, 38, 618–625. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Abdel-Aty, M.A.; Darwiche, A.L. County-Level Crash Risk Analysis in Florida: Bayesian Spatial Modeling. Transp. Res. Rec. 2010, 2148, 27–37. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Lee, J.; Siddiqui, C.; Choi, K. Geographical Unit Based Analysis in the Context of Transportation Safety Planning. Transp. Res. Part A Policy Pract. 2013, 49, 62–75. [Google Scholar] [CrossRef]
- Quddus, M.A. Modelling Area-Wide Count Outcomes with Spatial Correlation and Heterogeneity: An Analysis of London Crash Data. Accid. Anal. Prev. 2008, 40, 1486–1497. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Quddus, M.; Ison, S. The Effects of Area-Wide Road Speed and Curvature on Traffic Casualties in England. J. Transp. Geogr. 2009, 17, 385–395. [Google Scholar] [CrossRef]
- Rahman, M.T.; Jamal, A.; Al-Ahmadi, H.M. Examining Hotspots of Traffic Collisions and Their Spatial Relationships with Land Use: A GIS-Based Geographically Weighted Regression Approach for Dammam, Saudi Arabia. ISPRS Int. J. Geo-Inf. 2020, 9, 540. [Google Scholar] [CrossRef]
- Amoh-Gyimah, R.; Saberi, M.; Sarvi, M. Macroscopic Modeling of Pedestrian and Bicycle Crashes: A Cross-Comparison of Estimation Methods. Accid. Anal. Prev. 2016, 93, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Amoh-Gyimah, R.; Sarvi, M.; Saberi, M. Investigating the Effects of Traffic, Socioeconomic, and Land Use Characteristics on Pedestrian and Bicycle Crashes: A Case Study of Melbourne, Australia. In Proceedings of the Transportation Research Board 95th Annual Meeting, Washington, DC, USA, 10–14 January 2016. [Google Scholar]
- Amoh-Gyimah, R.; Saberi, M.; Sarvi, M. The Effect of Variations in Spatial Units on Unobserved Heterogeneity in Macroscopic Crash Models. Anal. Methods Accid. Res. 2017, 13, 28–51. [Google Scholar] [CrossRef]
- Anastasopoulos, P.C.; Mannering, F.L. An Empirical Assessment of Fixed and Random Parameter Logit Models Using Crash- and Non-Crash-Specific Injury Data. Accid. Anal. Prev. 2011, 43, 1140–1147. [Google Scholar] [CrossRef] [PubMed]
- Ziakopoulos, A.; Yannis, G. A Review of Spatial Approaches in Road Safety. Accid. Anal. Prev. 2020, 135, 105323. [Google Scholar] [CrossRef] [PubMed]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Development of Planning Level Transportation Safety Tools Using Geographically Weighted Poisson Regression. Accid. Anal. Prev. 2010, 42, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y. Functional-Coefficient Spatial Autoregressive Models with Nonparametric Spatial Weights. J. Econom. 2016, 195, 134–153. [Google Scholar] [CrossRef]
- El-Basyouny, K.; Sayed, T. Urban Arterial Accident Prediction Models with Spatial Effects. Transp. Res. Rec. 2009, 2102, 27–33. [Google Scholar] [CrossRef]
- Xu, P.; Huang, H. Modeling Crash Spatial Heterogeneity: Random Parameter versus Geographically Weighting. Accid. Anal. Prev. 2015, 75, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Marek, L.; Campbell, M.; Epton, M.; Kingham, S.; Storer, M. Winter Is Coming: A Socio-Environmental Monitoring and Spatiotemporal Modelling Approach for Better Understanding a Respiratory Disease. ISPRS Int. J. Geo-Inf. 2018, 7, 432. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Xiao, L.; Xu, C.; Long, D. Integrative Analysis of Spatial Heterogeneity and Overdispersion of Crime with a Geographically Weighted Negative Binomial Model. ISPRS Int. J. Geo-Inf. 2020, 9, 60. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Qiu, A.; Kang, X.; Han, J.; Chai, Z. A CUDA-Based Parallel Geographically Weighted Regression for Large-Scale Geographic Data. ISPRS Int. J. Geo-Inf. 2020, 9, 653. [Google Scholar] [CrossRef]
- Li, Z.; Fotheringham, A.S.; Li, W.; Oshan, T. Fast Geographically Weighted Regression (FastGWR): A Scalable Algorithm to Investigate Spatial Process Heterogeneity in Millions of Observations. Int. J. Geogr. Inf. Sci. 2019, 33, 155–175. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B. Macrolevel Accident Prediction Models for Evaluating Safety of Urban Transportation Systems. Transp. Res. Rec. 2003, 1840, 87–95. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Liu, P.; Bigham, J.M.; Ragland, D.R. Using Geographically Weighted Poisson Regression for County-Level Crash Modeling in California. Saf. Sci. 2013, 58, 89–97. [Google Scholar] [CrossRef]
- Nakaya, T.; Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Poisson Regression for Disease Association Mapping. Stat. Med. 2005, 24, 2695–2717. [Google Scholar] [CrossRef] [PubMed]
- da Silva, A.R.; Rodrigues, T.C.V. Geographically Weighted Negative Binomial Regression—Incorporating Overdispersion. Stat. Comput. 2013. [Google Scholar] [CrossRef]
- Shaon, M.R.R.; Qin, X.; Shirazi, M.; Lord, D.; Geedipally, S.R. Developing a Random Parameters Negative Binomial-Lindley Model to Analyze Highly over-Dispersed Crash Count Data. Anal. Methods Accid. Res. 2018, 18, 33–44. [Google Scholar] [CrossRef]
- Shaon, M.R.R.; Schneider, R.J.; Qin, X.; He, Z.; Sanatizadeh, A.; Flanagan, M.D. Exploration of Pedestrian Assertiveness and Its Association with Driver Yielding Behavior at Uncontrolled Crosswalks. Transp. Res. Rec. 2018, 2672, 69–78. [Google Scholar] [CrossRef]
- Chen, S.; Saeed, T.U.; Alqadhi, S.D.; Labi, S. Safety Impacts of Pavement Surface Roughness at Two-Lane and Multi-Lane Highways: Accounting for Heterogeneity and Seemingly Unrelated Correlation across Crash Severities. Transp. Transp. Sci. 2019, 15, 18–33. [Google Scholar] [CrossRef]
- Venkataraman, N.S.; Ulfarsson, G.F.; Shankar, V.; Oh, J.; Park, M. Model of Relationship between Interstate Crash Occurrence and Geometrics: Exploratory Insights from Random Parameter Negative Binomial Approach. Transp. Res. Rec. 2011, 2236, 41–48. [Google Scholar] [CrossRef]
- Venkataraman, N.; Ulfarsson, G.F.; Shankar, V.N. Random Parameter Models of Interstate Crash Frequencies by Severity, Number of Vehicles Involved, Collision and Location Type. Accid. Anal. Prev. 2013, 59, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Chen, E.; Tarko, A.P. Modeling Safety of Highway Work Zones with Random Parameters and Random Effects Models. Anal. Methods Accid. Res. 2014, 1, 86–95. [Google Scholar] [CrossRef]
- Saeed, T.U.; Hall, T.; Baroud, H.; Volovski, M.J. Analyzing Road Crash Frequencies with Uncorrelated and Correlated Random-Parameters Count Models: An Empirical Assessment of Multilane Highways. Anal. Methods Accid. Res. 2019, 23, 100101. [Google Scholar] [CrossRef]
- Xin, C.; Wang, Z.; Lee, C.; Lin, P.-S. Modeling Safety Effects of Horizontal Curve Design on Injury Severity of Single-Motorcycle Crashes with Mixed-Effects Logistic Model. Transp. Res. Rec. 2017, 2637, 38–46. [Google Scholar] [CrossRef]
- Xin, C.; Wang, Z.; Lin, P.-S.; Lee, C.; Guo, R. Safety Effects of Horizontal Curve Design on Motorcycle Crash Frequency on Rural, Two-Lane, Undivided Highways in Florida. Transp. Res. Rec. 2017, 2637, 1–8. [Google Scholar] [CrossRef]
- Mannering, F.L.; Bhat, C.R. Analytic Methods in Accident Research: Methodological Frontier and Future Directions. Anal. Methods Accid. Res. 2014, 1, 1–22. [Google Scholar] [CrossRef]
- Agresti, A. Foundations of Linear and Generalized Linear Models; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-1-118-73005-8. [Google Scholar]
- Hilbe, J.M. Negative Binomial Regression; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-0-521-19815-8. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 978-0-470-85525-6. [Google Scholar]
- Imprialou, M.; Quddus, M. Crash Data Quality for Road Safety Research: Current State and Future Directions. Accid. Anal. Prev. 2019, 130, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Romero, M.; Atisso, E.; Wang, T.; Slusher, L.; Tarko, A. Using GIS to Determine Locations for Safety Improvements. Available online: https://docs.lib.purdue.edu/purduegisday/2017/allevents/1/ (accessed on 26 April 2021).
- Bíl, M.; Andrášik, R.; Sedoník, J.; Cícha, V. ROCA–An ArcGIS Toolbox for Road Alignment Identification and Horizontal Curve Radii Computation. PLoS ONE 2018, 13, e0208407. [Google Scholar] [CrossRef] [PubMed]
- Heiberger, R.M.; Holland, B. Statistical Analysis and Data Display; Springer Texts in Statistics; Springer: New York, NY, USA, 2015; ISBN 978-1-4939-2121-8. [Google Scholar]
- Elliott, A.C.; Hynan, L.S. A SAS® Macro Implementation of a Multiple Comparison Post Hoc Test for a Kruskal–Wallis Analysis. Comput. Methods Programs Biomed. 2011, 102, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Geedipally, S.R.; Pratt, M.P.; Lord, D. Effects of Geometry and Pavement Friction on Horizontal Curve Crash Frequency. J. Transp. Saf. Secur. 2019, 11, 167–188. [Google Scholar] [CrossRef]
- Himes, S.; Porter, R.J.; Hamilton, I.; Donnell, E. Safety Evaluation of Geometric Design Criteria: Horizontal Curve Radius and Side Friction Demand on Rural, Two-Lane Highways. Transp. Res. Rec. 2019, 2673, 516–525. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Oshan, T.M. Geographically Weighted Regression and Multicollinearity: Dispelling the Myth. J. Geogr. Syst. 2016, 18, 303–329. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, B.; Zhu, S. Spatiotemporal Influence of Urban Environment on Taxi Ridership Using Geographically and Temporally Weighted Regression. ISPRS Int. J. Geo-Inf. 2019, 8, 23. [Google Scholar] [CrossRef]
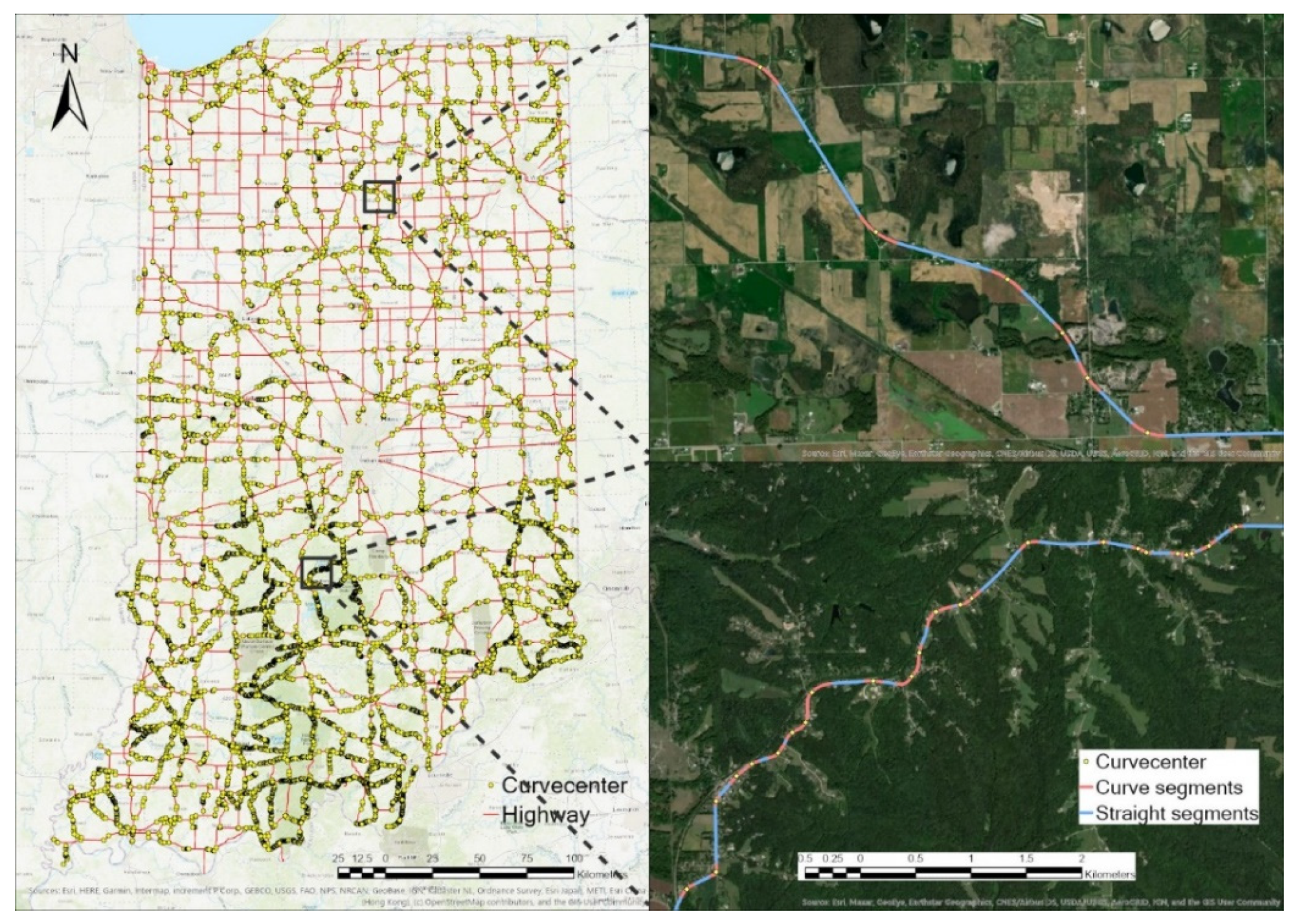
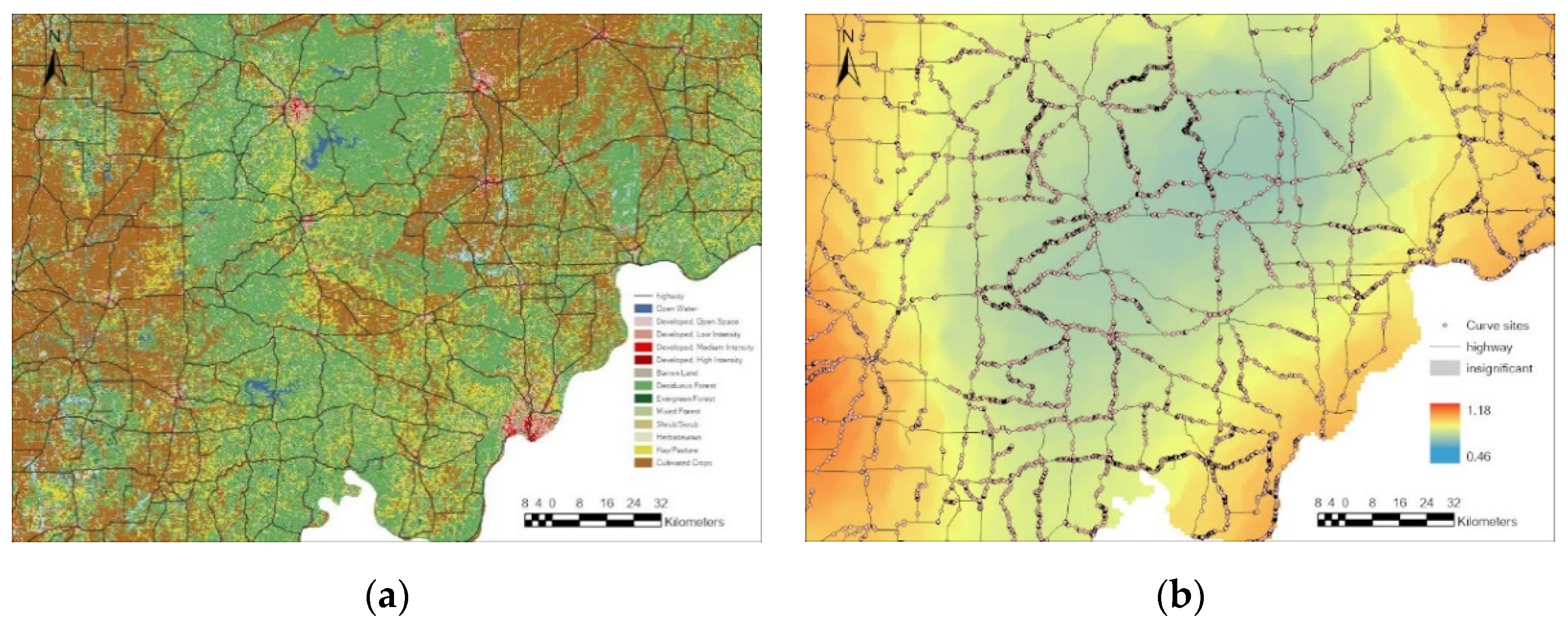
| Variables | Description | Mean | Std. dev | Min | Max |
|---|---|---|---|---|---|
| Number of crashes occurred during 2016–2018 per curve segment | 0.740 | 1.755 | 0 | 34 | |
| Radii of curve segments in meter | 354.10 | 199.61 | 25.21 | 999.64 | |
| Friction of pavement on curve segments at 40 mph | 43.80 | 15.12 | 8.20 | 104.20 | |
| Length of curve segments in meter | 104.05 | 109.92 | 30.49 | 1249.77 | |
| Mean of Annual Average Daily Traffic in 2016–2018 | 4214.16 | 5393.82 | 32.21 | 82,244.85 |
| Model | Bandwidth (km) | # of Parameter | MAD | Log Likelihood | AICc | Dispersion Parameter | Moran’s | -Value |
|---|---|---|---|---|---|---|---|---|
| NB | - | 5 | 0.881 | −9978.4 | 19,968.0 | 1.88 | 0.0769 | |
| RPNB | - | 11 | 0.847 | −9917.1 | 19,856.2 | 1.31 | 0.0753 | |
| GWPR | 15.45 | 295.1 | 0.845 | −10,805.9 | 22,219.9 | - | 0.0297 | |
| GWNBR | 34.65 | 76.5 | 0.859 | −9780.7 | 19,715.6 | - | 0.0569 | |
| GWNBRg | 76.01 | 22.7 | 0.869 | −9900.9 | 19,847.4 | 1.88 | 0.0634 |
| Model | NB | RPNB | GWPR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Min | Lwr | Med | Upr | Max | Mean | Min | Lwr | Med | Upr | Max | ||
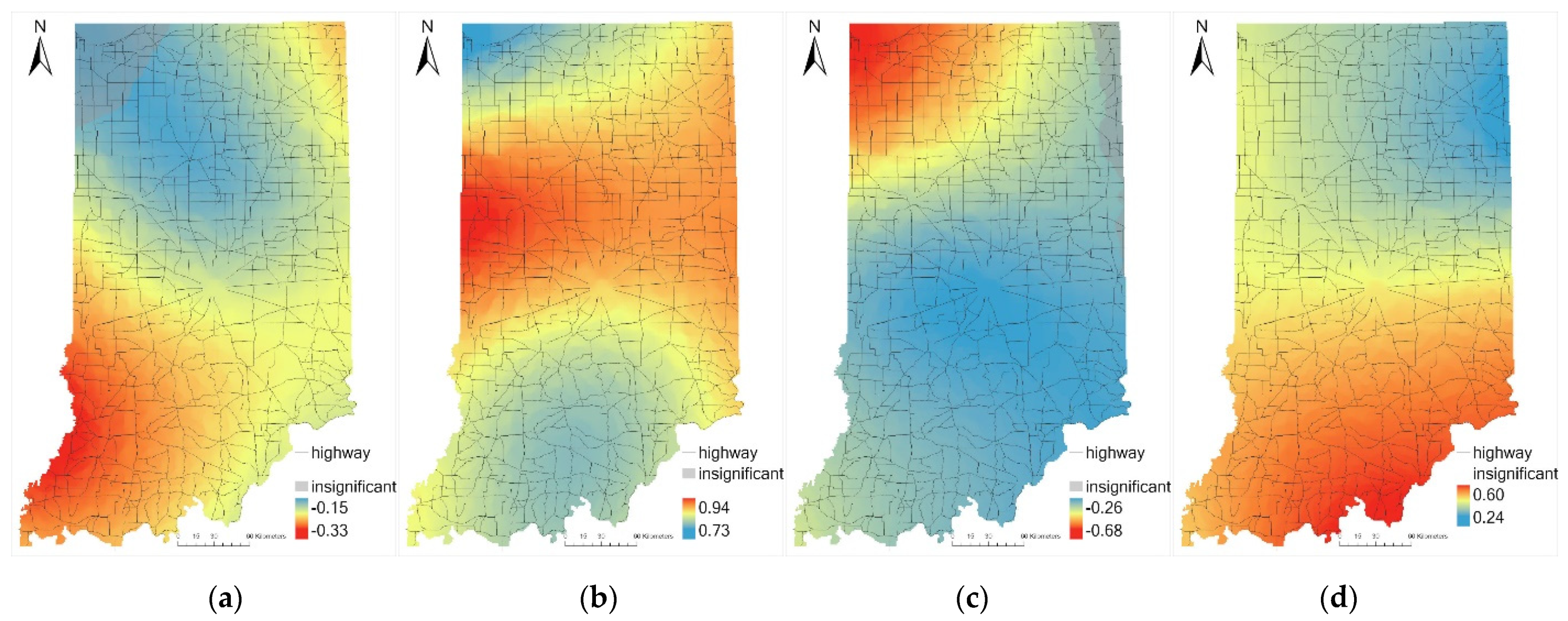
| Intercept | −5.96 | −6.25 | −6.33 | −6.26 | −6.25 | −6.23 | −5.82 | −6.14 | −22.17 | −8.21 | −6.00 | −4.32 | 3.56 |
| LOGR | −0.24 | −0.30 | −0.33 | −0.31 | −0.30 | −0.29 | −0.14 | −0.23 | −1.04 | −0.36 | −0.24 | −0.10 | 0.61 |
| LOGL | 0.87 | 0.96 | 0.94 | 0.95 | 0.96 | 0.96 | 1.07 | 0.87 | 0.137 | 0.68 | 0.85 | 1.05 | 1.98 |
| LOGF | −0.36 | −0.40 | −0.46 | −0.42 | −0.41 | −0.39 | 0.08 | −0.29 | −2.24 | −0.44 | −0.25 | −0.04 | 0.94 |
| LOGA | 0.49 | 0.48 | 0.46 | 0.48 | 0.48 | 0.49 | 0.61 | 0.47 | −0.34 | 0.35 | 0.51 | 0.61 | 1.24 |
| Model | GWNBR | GWNBRg | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Min | Lwr | Med | Upr | Max | Mean | Min | Lwr | Med | Upr | Max | |
| Intercept | −5.80 | −9.19 | −6.82 | −5.64 | −5.16 | −1.79 | −5.82 | −7.07 | −6.42 | −6.01 | −5.66 | −3.45 |
| LOGR | −0.24 | −0.55 | −0.30 | −0.25 | −0.18 | 0.04 | −0.24 | −0.33 | −0.27 | −0.24 | −0.23 | −0.15 |
| LOGL | 0.85 | 0.46 | 0.76 | 0.85 | 0.93 | 1.18 | 0.84 | 0.73 | 0.80 | 0.83 | 0.87 | 0.94 |
| LOGF | −0.31 | −0.97 | −0.33 | −0.28 | −0.24 | −0.03 | −0.33 | −0.68 | −0.34 | −0.30 | −0.27 | −0.26 |
| LOGA | 0.46 | 0.07 | 0.36 | 0.47 | 0.57 | 0.73 | 0.48 | 0.24 | 0.40 | 0.51 | 0.55 | 0.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Li, S.; Shan, J. Non-Stationary Modeling of Microlevel Road-Curve Crash Frequency with Geographically Weighted Regression. ISPRS Int. J. Geo-Inf. 2021, 10, 286. https://doi.org/10.3390/ijgi10050286
Wang C, Li S, Shan J. Non-Stationary Modeling of Microlevel Road-Curve Crash Frequency with Geographically Weighted Regression. ISPRS International Journal of Geo-Information. 2021; 10(5):286. https://doi.org/10.3390/ijgi10050286
Chicago/Turabian StyleWang, Ce, Shuo Li, and Jie Shan. 2021. "Non-Stationary Modeling of Microlevel Road-Curve Crash Frequency with Geographically Weighted Regression" ISPRS International Journal of Geo-Information 10, no. 5: 286. https://doi.org/10.3390/ijgi10050286
APA StyleWang, C., Li, S., & Shan, J. (2021). Non-Stationary Modeling of Microlevel Road-Curve Crash Frequency with Geographically Weighted Regression. ISPRS International Journal of Geo-Information, 10(5), 286. https://doi.org/10.3390/ijgi10050286






