Abstract
Research efforts focused on developing a better understanding of the evolution of mortality over time are considered to be of significant interest—not just to the demographers. Mortality can be expressed with different parameters through multiparametric prediction models. Based on the Beta Gompertz generalized Makeham (BGGM) distribution, this study aims to evaluate and map four of such parameters for 22 countries of the European Union, over the period 1960–2045. The BGGM probabilistic distribution is a multidimensional model, which can predict using the corresponding probabilistic distribution with the following parameters: infant mortality (parameter θ), population aging (parameter ξ), and individual and population mortality due to unexpected exogenous factors/events (parameters κ and λ, respectively). This work focuses on the random risk factor (λ) that can affect the entire population, regardless of age and gender, with increasing mortality depicting developments and trends, both temporally (past–present–future) and spatially (22 countries). Moreover, this study could help policymakers in the field of health provide solutions in terms of mortality. Mathematical models like BGGM can be used to achieve and highlight probable cyclical repetitions of sudden events (such as Covid-19) in different time series for different geographical areas. GIS context is used to map the spatial patterns of this estimated parameter as well as these variations during the examined period for both men and women.
1. Introduction
Fertility, mortality, and migration are the three main demographic phenomena. Mortality was the first to be studied; age and gender differences, geographical variations, as well as time fluctuations have been attracting the interest of researchers from different disciplines for more than three centuries [1]. The unprecedented reduction in mortality achieved during the 20th century intensified efforts to model this phenomenon, as mortality rates decreased at all ages, especially in the early stages of life. This important human achievement generated a great increase in the world population, as well as major changes in its age distribution. Recently, interest in mortality trends and forecasts has been renewed as policymakers, health scientists, demographers, and economists focus on changing drivers of mortality [2,3,4,5,6,7,8,9,10] and on impacts of pandemics such as COVID-19 [11,12,13].
Different probability distributions describe/approximate human mortality as a function of age [14]. The most common among them, Gompertz distributions [15,16], have been widely accepted as they describe mortality data quite well up to the age of 60–70 years. However, their reliability is not satisfactory for adults (above 70 years) and/or young people (below 30 years of age). To “improve” the distribution fitness to the actual data, a new mathematical distribution called Beta Gompertz generalized Makeham (BGGM) has been proposed [17]. The new distribution results from the combination of the above distributions with the Beta distribution. The Beta distribution has been selected for its flexibility in different datasets. Thus, tested for its good adaptation, BGGM has a higher predictive capacity for men and women, even in higher age groups.
The analysis and, consequently, the application is applied to Vital statistics data provided by Eurostat [18] and the Human Mortality Database [19] for the years from 1960 until today. The available census data were used to calculate age- and sex-specific mortality rates.
The BGGM model aims to contribute to the global scientific debate on mortality models and their suitability by actually proposing a new six-parameter mortality distribution, which seems to provide a good fit, especially at advanced ages. In other words, it presents a comparative advantage at those ages where other distributions fail to capture the observed deceleration of mortality [20].
On the prediction side, an attempt was made to approximate the BGGM distribution to the actual mortality data as much as possible. A soundly established distribution may turn out to be a useful tool for its predictive ability. Based on past experience and recent trends the extrapolation on future population data may provide insightful information that should not be neglected.
This work could benefit strategy makers in the field of health to provide solutions in terms of mortality. Mathematical models such as BGGM can be used towards achieving and highlighting possible cyclical repetitions of sudden events in different time series, such as Covid-19, for different geographical areas.
2. Materials and Methods
2.1. Construction of Mortality Models
The construction of a mortality model that evaluates the mortality pattern is based on one of the following two approaches. The first approach constructs a mortality table that describes the probability of death per age group, while the second approach describes the actual mortality pattern using a function (probability theory—BGGM).
The second approach is a method of parametric smoothing, proposed and studied by London [21] and Haberman et al. [22]. It adopts a mathematical function to describe the initial estimates of mortality rates or mortality intensity. Smoothing is performed by adjusting either one function at all ages or several functions gradually across data. Non-parametric methods are applied to mortality tables by combining data at different age values x. The main purpose of these methods is to normalize the values of mortality tables using mortality models, which are produced by methods such as generalized linear models (GLMs) or splines. (the analysis of splines methods is beyond the scope of this paper. Besides, the new distribution (BGGM) presents a good adaptation to a variety of human mortality data (spatial and temporal) without the use of additional mathematical formulas that will temporarily normalize the result. The least squares (LS) method is used to estimate the unknown parameters of the models adapted to the original data [23].
Describing the least squares method followed in this work [24], the initial estimate of mortality at age x was considered to be the value adjusted to that age. The selection of the appropriate model is done by adjusting the estimated values so that it is as near as possible to the observed values. To minimize the distance between the actual and estimated values, the method of weighted least squares [25] is applied, which is given by the following relation:
where and is the number of deaths and is the corresponding population at that age x.
Moreover, the analysis relies on mortality statistics by age and sex as provided annually by Eurostat [18] and the Human Mortality Database [19] for the years 1960–2020.
2.2. Selection of the Appropriate Mortality Model
Some examples of older laws are the laws of De Moivre [26]. De Moivre was the first one who proposed a mortality model (model mortality intensity) as a function of age,
where ω is the limit age and n is a numeric variable until 100 years old. However, this model satisfactorily described mortality only in old age. On the other hand, a law with many applications in problems of waiting, system operation, wear, devaluation, and so on (but not particularly in the study of human mortality) is the exponential law of the generalized family of exponential distributions, where its mathematical expression is as follows:
Gompertz formulated the evolution of the above law a hundred years later in 1825. The probability density function of the Gompertz (G) distribution with parameters θ and ξ, where θ, ξ > 0, is
According to this law, the intensity of mortality increases with geometric progress, i.e., it is valid,
where θ and are positive parameters. Parameter describes the normal deterioration of human life and is directly dependent on age (also referred to as the rate of aging over 70 years, mortality rate, or Gompertz inclination). Parameter x describes the lifetime (in years), while θ is affected by the course followed by the infant mortality of the population.
This law describes quite satisfactorily the empirical data of mortality of a population for at least a period of 60–70 years, but as a rule, it fails to adequately describe mortality in the extreme ages: it overestimates the possibility of death in old age and underestimates it in infancy. The main disadvantage of Gompertz’s law is that it takes into account only “natural wear” and ignores the effect of random fatality. To improve Gompertz’s law, the “first Makeham law” (1860) was proposed to reduce, if not eliminate, the disadvantages of the previous laws and to better adapt results to reality. Makeham’s first law is given by the following mathematical expression:
where λ is a parameter—constant at all ages—that examines the randomness of death that may be due to deteriorating health or some accidental risk factor and is independent of age. It describes a risk that applies to the whole population equally. The introduction of the third parameter (λ) makes the Makeham law more flexible in displaying empirical data. The probability density function (pdf) of the Gompertz–Makeham (GM) distribution with parameters θ, ξ, and λ, where θ, ξ, λ > 0, is
The corresponding hazard function is as follows:
and the cumulative distribution function is as follows:
Then, Makeham himself introduced a series of modifications to the primary mortality models, with the aim of always better adapting the statistical results to reality, to arrive at the “2nd Makeham law” or the “generalized Makeham law” or “generalized Gompertz Makeham”:
where a linear (λ + κx) part is now combined with a λ constant parameter that examines the chance of death that may be due to deteriorating health or an accidental risk factor and an unknown positive parameter that examines all time events that are of interest to the researcher and are immediate age-dependent and an exponential part .
The generalized Gompertz–Makeham (GGM) distribution has the following probability density function:
and the corresponding cumulative distribution function:
The three laws of mortality mentioned above are considered to be the main distributions that adequately describe both normal mortality resulting from the aging of the population and the probability of death related to the cause of a disease or accident. The probability density function, denoted by f(x), gives the probability of death for a person at age x, and the cumulative probability density function, denoted by F(x), is the complement of the survival function [27]. Both probability density and cumulative probability density functions are related to the hazard rate, as shown in the following equation:
The following distribution is a derivative of the mixing of the generalized Beta distribution with the generalized Gompertz–Makeham mortality law and is called the Beta Gompertz generalized Makeham distribution (BGGM).
This is the model that is used in this work to evaluate the mortality data taken by Eurostat and the Human Mortality Database, where x is age starting from 0 and going up to a maximum theoretical biological threshold (i.e., an age above which no individual can theoretically survive), and a and β are parameters of the Beta distribution. A mathematical approach to demographic trends is presented through the parameters of when applied to gender-specific European data, as provided by the Human Mortality Database (2019). The model construction and the statistical analysis of each parameter were performed in R, using the minpack.lm function [28].
2.3. Selection of Mortality Data
This current study is part of a descriptive map of the mortality of the population of the last 60 years in 22 European countries (Denmark, Finland, France, Iceland, Italy, the Netherlands, Norway, Sweden, Switzerland, Austria, Belgium, Czech Republic, Ireland, Estonia Latvia, Lithuania, Germany, Greece, Poland, Portugal, Spain, and the United Kingdom). The period covered goes from 1960 to 2020 and the mortality projection goes up to 2045. The projection analysis is based on one of the six parameters of the BGGM distribution. A previous study has in detail presented and analyzed the importance of each of the model parameters in the path of human mortality [17]. Modeling aims to capture trends in age-specific mortality rates to assess the impact of individual age groups on life expectancy and to identify potentially significant gender differences in Europe.
The estimation of the parameter λ was performed using the open-source R (www.r-project.org, accessed on 1 January 2021) and specifically the package “minpack.lm” from the CRAN digital library (Comprehensive R Archive). The suggested function from the library was nls.lm (the function that belongs to minpack.lm). The purpose of nls.lm is to minimize the sum square of the vector returned by the function “fn” (a function that returns a vector of residuals, the sum square of which is to be minimized) by a modification of the Levenberg–Marquardt algorithm. Details for this package and this algorithm are out of the scope of this work.
ESRI ArcGIS (version 10.8) was used to manipulate and process spatial data, as well as to develop final maps. The subsequent processing of the quantitative data of the parameter λ and its projection in the future was achieved using FORECAST.ETS.
3. Results
The next two tables (Table 1 and Table 2) present the descriptive statistics for parameter λ for males and females, respectively, for the whole study period for the 22 countries.

Table 1.
Descriptive statistics (male).

Table 2.
Descriptive statistics (female).
The estimate of parameter λ, as extracted from the BGGM distribution, can be visualized on maps using a color palette (blue was chosen for men and pink for women). The strong hue of each color corresponds to the negative relative position of each country, concerning the 22 European countries that participated in the analysis, each year for both sexes. On the contrary, the pale color indicates the corresponding good relative position of the country, regarding the parameter under consideration [29].
Before analyzing the random risk factor (λ), which is the core of this study, it seems appropriate to briefly describe the course of an important parameter (parameter θ). As expected, the value of parameter θ differs between the two sexes. According to Gompertz, parameter θ reflects the impact of infant mortality on the mortality function of a specific population at a specific time [30]. Its value varies with respect to the deaths that occur at the age of 0 to 1, and its trend is a first sign of the living standard of the country. A projected declining value of θ reflects an increasing life expectancy for the next period [31]. Parameter θ shows an interesting development over time, although the findings are to some extent anticipated. The analysis shows that, over the years examined, male and female values of parameter θ follow a similar path, while the former is constantly higher than the latter. During the years 1960–2000, male and female values decrease, but their difference remains almost unchanged.
Briefly, in the 1960s, 1970s, and 1980s, the Netherlands, Norway, Switzerland, and Portugal recorded high infant mortality rates for men and women, yet afterward, the relative position of each of these countries improved. From the 1990s onwards, the values of parameter θ have been following a downward trend in all countries for both sexes. Besides, during the economic recession years, from 2008 to 2015, the downward trend of infant mortality was continued, as expected. Even during the recession years, from 2008 to 2015, the downward trend of infant mortality was not interrupted.
3.1. Non Age-Related Random Risk Factor for the Whole Population (Parameter λ)
The random risk factor, which affects the entire population regardless of age and gender, in the Beta Gompertz generalized Makeham distribution is expressed through the parameter λ. By accidental risk factors, we understand all those events that may occur at any age and increase the death probability. Such events could be a war, a pandemic, or dangerous environmental phenomena with disastrous consequences (earthquake, air pollution or floods, and so on). There are indications (Figure 1) that, in most cases, a catastrophe does not affect men and women the same way, neither does it equally affect different countries. However, spatial proximity plays a decisive role in the evolution of the phenomenon, and thus in the value of parameter λ.
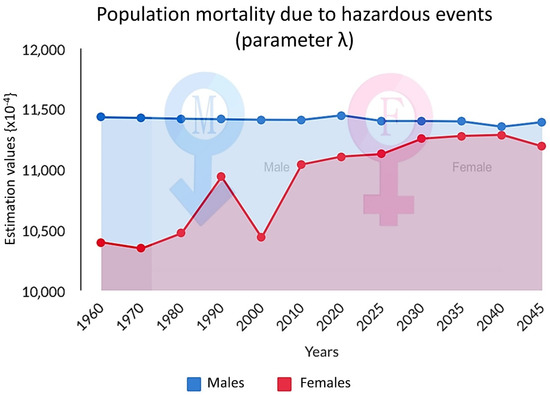
Figure 1.
The evolution of collective mortality (λ) for the 22 EU countries in the past, present, and future, for both men (males, blue) and women (females, red), for the years from 1960 to 2045.
The demographic measures that count the mortality of the population of a geographical area are called general mortality indicators, and that is what parameter λ stands for. These indicators are by nature of general coverage and concern the entire population of a country, regardless of age or sex.
The demographic and spatial evolution of mortality that affects the populations in the countries examined is of great interest to both men and women. From 1960 to 2010, the distance in the values of the parameter λ between the two sexes is large. The next four maps (Figure 2, Figure 3, Figure 4 and Figure 5) were made using the standard deviation method. This method presents how much a value varies from the mean and within ArcGIS is calculated automatically. Thus, this classification method produces class breaks by adding or subtracting one standard deviation at a time [25,32]. The parameter values were divided based on the relative standard deviations (std). These standard deviation values are presented within the following four maps.
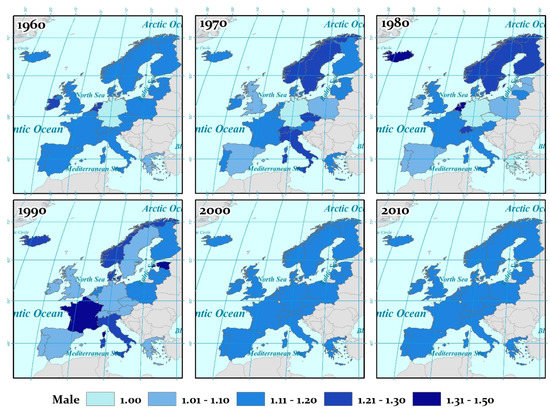
Figure 2.
The evolution of random risk factor for the 22 EU countries (parameter λ—male).
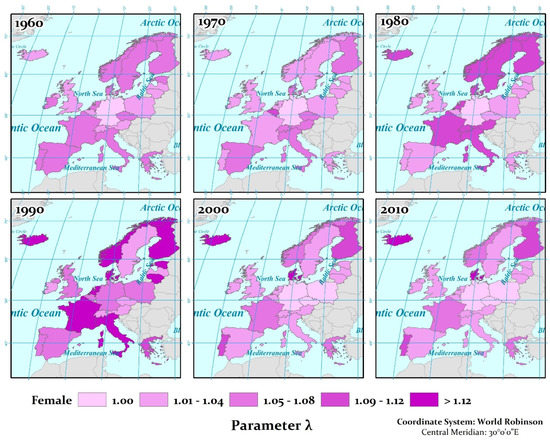
Figure 3.
The evolution of random risk factor for the 22 EU countries (parameter λ—female).
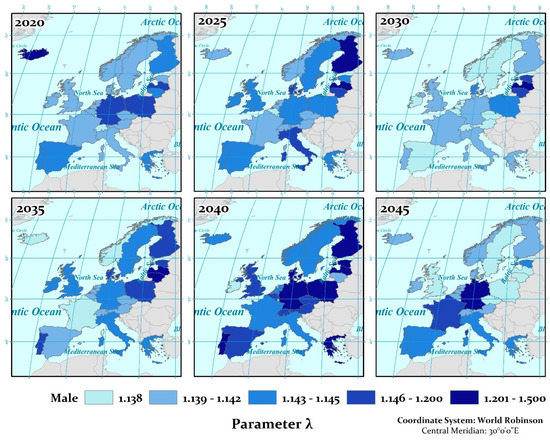
Figure 4.
Projected values of random risk factor for the 22 EU countries (parameter λ—male).
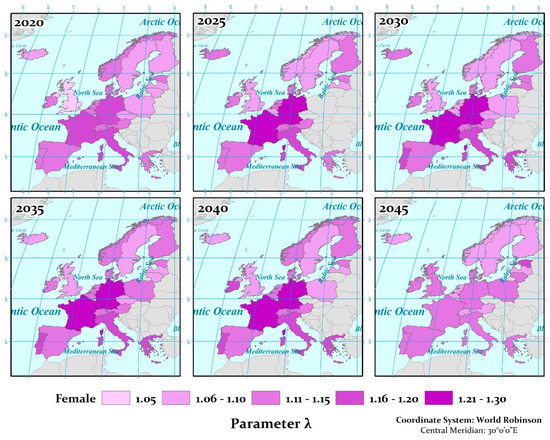
Figure 5.
The projected values of random risk factor for the 22 EU countries (arameter λ—female).
Figure 2 presents the evolution of random risk factor for the study area concerning men.
The interest, however, focuses on how parameter λ varies over time by sex in various sudden events [33]. As shown in Figure 1, although men hold a high percentage of deaths collectively, women are the ones with the highest percentage increase of 6.2% in the 50 reference years (1960–2010).
Countries such as Spain, Poland, Greece, Germany (after 1990), Latvia, and marginally Lithuania show high levels of general mortality risk (λ) in the period 1960–2010 for both men and women. The historical-social changes of these countries in that period seem to have caused an increase in the deaths of both sexes (Spain enters the 1960s after social tensions and civil strife (First Carlisle War and Spanish Civil War). The country then entered a dictatorship between 1939 and 1975, which isolated Spain until it transitioned to democracy. These intensities are reflected in the λ parameter with an increase in deaths in both sexes).
Focusing on Greece, the turbulent historical route explains the high values of parameter λ: long periods of political instability, royal dictatorship, wars, and military occupation followed by civil war and a seven-year military dictatorship. Yet, and although political stability has been established, economic downturns have not been avoided. Figure 3 presents the evolution of the random risk factor for the study area for women. During the period 1990–2000, there is a relatively small increase in female mortality in Central European countries—an observation that recovers between 2000 and 2010. However, in the Nordic countries, this is something that needs the attention of scholars, as the rates remain slightly high.
Moving on to the next chronological phase from 2010 to 2040 (Figure 1, Figure 4 and Figure 5), the change of the parameter λ shows signs of stabilization. Values of parameter λ for men and women are very close, while after 2040, the model forecasts a new opening of the “gap” between the two sexes, with a downward trend for women (Figure 5) and an upward trend for men (Figure 4), respectively.
An impressive finding of females is the big drop in collective mortality in the decade 1990–2000, which was followed by an equally high change in 2000–2010 (Figure 1). Throughout the years studied, the risk of sudden death is constantly higher for men compared with women. Moreover, during the period 2016–2021 (Figure 1), the values of λ for males increase, while the corresponding values for females decrease, aggravating the gender gap. The recent pandemic disproportionally affects men, as indicated by country-specific data.
Values of λ for males reached high levels during the Second World War across all the countries that actively participated (United Kingdom, France, Italy, and Germany), as well as during the recent economic crisis in 2007–2015 (Greece, Portugal, Italy, Spain, France, and so on). On the contrary, as the female population reacts differently from the male population in adverse conditions, female values of λ show different variations over time. In Italy, for example, fluctuations in values of λ were almost identical for men and women, except during the period of economic crisis, where λ increased sharply for men, but not for women. Focusing only on the female population of Italy, the parameter λ gave smoother results, but with a lower average and less contemplative noise from 1970 to 2013 (Figure 1).
The United Kingdom is also a country that has experienced several fluctuations in the random risk factor over time. By the year 2020, the United Kingdom increased its relative position among the examined countries. However, from the year 2025, the collective mortality rates are steadily rising, and the predominantly male population is showing signs of rising, as evidenced by the COVID-19 pandemic, with a sharp rise in deaths in both sexes.
Indicatively, France, in 2009–2012, during the period of severe economic recession, showed an increase in death rates at the collective level, with Figure 4 and Figure 5 showing a cyclical increase of the parameter in the years 2020 and beyond. Estonia is in a disadvantageous situation with strong parameter instability. Historically, since 1991, when political change occurred in the country (independence from the USSR), as well as in the most recent past (2000–2020), the country shows one of the most intense income reclassifications in the European Union, with a direct effect on the mortality rates of its population.
A general conclusion about the risk of mortality (λ) is that, eventually, the “unanticipated event” that will affect the entire population regardless of age and gender, with an increase in deaths, will always exist. Human nature will always be called upon to deal with unbalanced factors. What has to be done is to learn from the past and use acquired experience to deal with similar phenomena in the future. The models used for future forecasting (BGGM distribution) show a tendency for “cyclical repetition” of such unpleasant events, something that should be taken seriously into account by policy-makers if they are to react methodically and timely to similar conditions when they emerge. Such predictions about population mortality rates could help public health strategies and encourage the better organization of public hospitals.
The parameters α (shape) and β (scale) concern the Beta distribution and maintain the known statistical properties [34]. They do not affect the demographic properties of the distribution and are defined by initial values set according to the statistical properties of the Beta distribution [29].
3.2. Sensitivity Analysis of the Prediction Model
This section verifies the actual mortality data with the “possible” future data for a time series where the data are available. This method provides a secure simulation for now so that the data can be tested after 2020.
Based on mortality data from 1960 to 2017, the forecast model is verified (via the FORECAST.ETS function) in the years 2010–2017. The forecast, based on the BGGM distribution, yields results reflecting the trend that mortality will follow in 22 countries of the analysis for the time series 2010–2017. The mortality projection (log (mortality)—forecast) is then compared with the real (log (mortality)—actual) mortality data from the Human Mortality Database of the respective countries, for the respective period time. This method is an indication of the reliability of the forecast that will be used for the years after 2017 where data are not yet available. Figure 6 shows the mortality projection approach (red) to the actual (blue) data indicative for the countries of Greece, the Czech Republic, Estonia, France, Iceland, and Sweden.
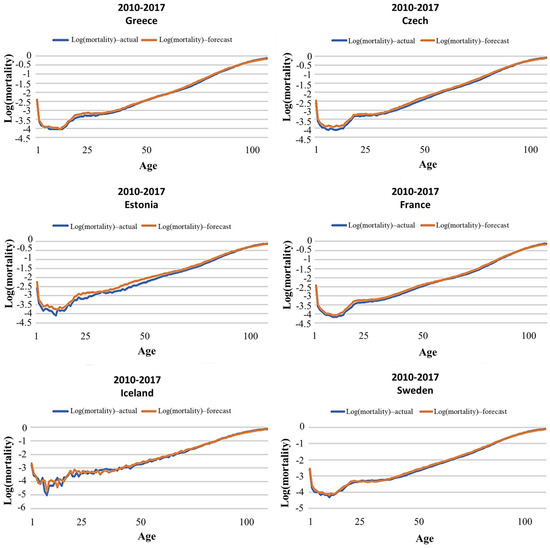
Figure 6.
Approach to the projection of mortality (red) in the real (blue) data indicative for the countries of Greece, the Czech Republic, Estonia, France, Iceland and Sweden, for the years 2010–2017.
The data for the parameters were analyzed and processed using a specific code in R for both men and women for the total of 22 European countries, which in turn can be visualized in the previous maps (Figure 2, Figure 3, Figure 4 and Figure 5) for the time moments 1960, 1970, 1980, 1990, 2000, 2010, 2020, 2025, 2030, 2035, 2040, and 2045. For the best differentiation of the results, the specific years were selected, thus indicating the changes noted by the parameter in chronological order (1960–2045).
4. Discussion
This study presented how Beta Gompertz generalized Makeham distribution parameters read/capture gender-specific mortality across European countries over a 60-year period. Each of the parameters has a specific demographic interpretation that allows the exploration of mortality from different aspects, such as infant mortality (parameter θ), population aging (parameter ξ), as well as individual (parameter κ) and collective risk factors (parameter λ). This work focused on the analysis of collective risk factors, as represented by parameter λ. To assess it, certain demographic characteristics must be taken into account. Age and gender are two of the most important of such characteristics, as they can show the composition in terms of gender and age distribution of a population, identifying its possible prospects. The importance of certain causes of death in recent years is increasing, as a result of human adoption of unhealthy practices and their exposure to frequently occurring environmental hazards [35]. Taking into account the above, chronological mortality data were used to estimate the parameters. The estimated parameters were then statistically analyzed and displayed with a time series of maps by gender.
It is already known, for both sexes in Europe, that there are more baby boys compared with baby girls who do not survive the critical age of [0, 1) years. These findings are consistent with corresponding European studies of 2008 [36]. According to them, between the sexes, an increasing male disadvantage in infant mortality has occurred in both European and non-European countries from the first half of the twentieth century onwards. This disadvantage is mainly due to the even greater vulnerability of men to prenatal mortality. Moreover, according to a 2019 [37] European study, women live longer than men in most European countries. The female advantage in longevity was observed mainly in the middle of the eighteenth century. During the twentieth century, this “gender gap” widened further owing to economic growth and improved living conditions for women.
In addition, men have proved to be more vulnerable to various exogenous factors (Figure 2 and Figure 4) and unexpected events that affect mortality in both individual and population perspectives. A higher percentage of men than women are documented to be associated with deaths caused by accidents, suicides, and exposure to many “dangerous externalities” in European countries [38]. This rate was found to be proportional to the rate of male population deaths caused by natural disasters and other harmful socioeconomic conditions [34].
Regarding the vulnerability to exogenous factors, the differences from the “nature” of the vulnerability (as a whole) are mainly identified over time with age. For men, parameter λ shows an increasing trend in overall mortality. On the contrary, for women, a stabilized “positive” trend (with low parameter values) in the mortality of the total population is reflected by each parameter (Figure 3 and Figure 5). The most common explanations for these findings are considered biological hazards, risks acquired through social roles, lifestyle and behavior, and perhaps different access to treatments and health care [39].
Surveys of 2008 highlight the ever-increasing mortality of the male population owing to unexpected events for the countries of Central Europe, as well as for the Mediterranean countries. This increase is likely to reflect the effects of the 2008 global financial crisis on mortality. An economic crisis is associated with job losses and rising unemployment rates, which tend to worsen living conditions. It is also highly associated with mortality, owing to specific causes or affecting specific groups of the population [14]. For example, a study in 2016 [40] reported that suicide deaths increased in Greece during the 2008 financial crisis, with mortality rates being the strongest among men of work age (15–64 years). Moreover, the Netherlands in the Mediterranean at that time was characterized by unexpectedly high mortality rates among women. The change in the composition of their populations of different nationalities probably played an important role in this. The Netherlands, with a focus on Greece and Italy, has proportionally absorbed the largest percentages of immigrants in Europe for decades [41]. Long-term residence in a host country, such as Greece, can lead to deteriorating health of some immigrant groups as a result of poor living conditions and health care [42].
The current work is a study of understanding the evolution of mortality over time and space. Meanwhile, the BGGM and especially the parameter λ showed that, for 2020, it recorded an unexpected event, based on its ability to make predictions/forecast. There are many paradigms of such models, for example, using splines [1] or P-splines [43], in this direction. Policymakers aiming to understand the mechanism of mortality can use all these models, together with BGGM.
5. Conclusions
It is understood that research efforts to investigate the dynamics of mortality throughout human life and its fluctuations over time can be of significant use.
The study of human mortality through mathematical models is not something new, but is a field with many expectations for the future. The parameter λ examined in the present study, throughout analysis (from 1960 to 2045), showed signs of a sometimes strong and sometimes less intense rise in mortality rates regardless of gender and age, with political, economic, health (COVID-19), and social rearrangements in the populations of the countries. This may be due to the randomness of the BGGM mathematical model used or, more realistically, because the mathematical model achieves and highlights a clear cyclical repetition of sudden events in different time series for different geographical areas. This fact needs special attention as the analysis of spatiotemporal variants of mortality can significantly contribute to the understanding of the mechanisms governing aging and mortality, as well as to the design and implementation of socio-economic strategies aimed at improving quality of life, extending life expectancy, and reducing premature mortality. Besides, valuable indications can be drawn from the projections (analysis period 2020–2045) on the demographic evolution of the population in Europe. Based on these forecasts, the historical mortality data can predict or can show governments a path to better manage their pension liabilities and distribute health budgets more rationally.
On the side of limitations, it could be mentioned that the number of parameters is higher than in other models. However, each one of those parameters has a specific demographic interpretation; this makes modeling results easy to analyze and useful for understanding age- and time-specific observations related to mortality.
Moreover, focusing on the two sexes of the Western world, their differences in mortality or health are considered complex, as they depend mainly on the biological, social, and economic context. Especially when women behave more and more like men, as inequalities in employment, access to health care, and similar family responsibilities reduce the racial gap between them.
Author Contributions
Conceptualization, Panagiotis Andreopoulos; Methodology, Panagiotis Andreopoulos, Kleomenis Kalogeropoulos, Alexandra Tragaki, and Nikolaos Stathopoulos; Analysis, Panagiotis Andreopoulos; Writing—original draft preparation, Panagiotis Andreopoulos, Kleomenis Kalogeropoulos, Alexandra Tragaki, and Nikolaos Stathopoulos; Writing—review and editing, Panagiotis Andreopoulos, Kleomenis Kalogeropoulos, Alexandra Tragaki, and Nikolaos Stathopoulos; Visualization, Kleomenis Kalogeropoulos, Nikolaos Stathopoulos; Supervision, Alexandra Tragaki. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Currie, I.D.; Durban, M.; Eilers, P.H. Smoothing and forecasting mortality rates. Stat. Model. 2004, 4, 279–298. [Google Scholar] [CrossRef]
- Gianquintieri, L.; Brovelli, M.A.; Pagliosa, A.; Dassi, G.; Brambilla, P.M.; Bonora, R.; Sechi, G.M.; Caiani, E.G. Mapping Spatiotemporal Diffusion of COVID-19 in Lombardy (Italy) on the Base of Emergency Medical Services Activities. ISPRS Int. J. Geo-Inf. 2020, 9, 639. [Google Scholar] [CrossRef]
- Huang, J.; Kwan, M.P.; Kan, Z.; Wong, M.S.; Kwok, C.Y.T.; Yu, X. Investigating the Relationship between the Built Environment and Relative Risk of COVID-19 in Hong Kong. ISPRS Int. J. Geo-Inf. 2020, 9, 624. [Google Scholar] [CrossRef]
- Niu, X.; Yue, Y.; Zhou, X.; Zhang, X. How Urban Factors Affect the Spatiotemporal Distribution of Infectious Diseases in Addition to Intercity Population Movement in China. ISPRS Int. J. Geo-Inf. 2020, 9, 615. [Google Scholar] [CrossRef]
- Antoniou, V.; Vassilakis, E.; Hatzaki, M. Is Crowdsourcing a Reliable Method for Mass Data Acquisition? The Case of COVID-19 Spread in Greece During Spring 2020. ISPRS Int. J. Geo-Inf. 2020, 9, 605. [Google Scholar] [CrossRef]
- Brito, P.L.; Kuffer, M.; Koeva, M.; Pedrassoli, J.C.; Wang, J.; Costa, F.; Freitas, A.D. The Spatial Dimension of COVID-19: The Potential of Earth Observation Data in Support of Slum Communities with Evidence from Brazil. ISPRS Int. J. Geo-Inf. 2020, 9, 557. [Google Scholar] [CrossRef]
- Liu, Y.; He, Z.; Zhou, X. Space-Time Variation and Spatial Differentiation of COVID-19 Confirmed Cases in Hubei Province Based on Extended GWR. ISPRS Int. J. Geo-Inf. 2020, 9, 536. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, R.; Liu, L.; Wu, H. Exploring Urban Spatial Features of COVID-19 Transmission in Wuhan Based on Social Media Data. ISPRS Int. J. Geo-Inf. 2020, 9, 402. [Google Scholar] [CrossRef]
- Thakar, V. Unfolding Events in Space and Time: Geospatial Insights into COVID-19 Diffusion in Washington State during the Initial Stage of the Outbreak. ISPRS Int. J. Geo-Inf. 2020, 9, 382. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, M.; Meng, C.; Claramunt, C. Risk Assessment of the Overseas Imported COVID-19 of Ocean-Going Ships Based on AIS and Infection Data. ISPRS Int. J. Geo-Inf. 2020, 9, 351. [Google Scholar] [CrossRef]
- Vatavali, F.; Gareiou, Z.; Kehagia, F.; Zervas, E. Impact of COVID-19 on Urban Everyday Life in Greece. Perceptions, Experiences and Practices of the Active Population. Sustainability 2020, 12, 9410. [Google Scholar] [CrossRef]
- Giannakis, E.; Hadjioannou, L.; Jimenez, C.; Papageorgiou, M.; Karonias, A.; Petrou, A. Economic Consequences of Coronavirus Disease (COVID-19) on Fisheries in the Eastern Mediterranean (Cyprus). Sustainability 2020, 12, 9406. [Google Scholar] [CrossRef]
- Telukdarie, A.; Munsamy, M.; Mohlala, P. Analysis of the Impact of COVID-19 on the Food and Beverages Manufacturing Sector. Sustainability 2020, 12, 9331. [Google Scholar] [CrossRef]
- Ballester, J.; Robine, J.M.; Herrmann, F.R.; Rodó, X. Effect of the Great Recession on regional mortality trends in Europe. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Gompertz, B. XXIV. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. In a letter to Francis Baily, Esq. FRS &c. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar]
- Makeham, W.M. On the law of mortality and the construction of annuity tables. J. Inst. Actuar. 1860, 8, 301–310. [Google Scholar] [CrossRef]
- Andreopoulos, P.; Bersimis, G.F.; Tragaki, A.; Rovolis, A. Mortality modeling using probability distributions. APPLICATION in Greek mortality data. Commun. Stat. Theory Methods 2019, 48, 127–140. [Google Scholar] [CrossRef]
- European Statistical Authority (Eurostat), Population Data. Available online: https://ec.europa.eu/eurostat/ (accessed on 10 November 2020).
- HMD. Mortality and Population Data. Human Mortality Database. 2019. Available online: http://www.mortality.org/ (accessed on 10 November 2020).
- Gavrilov, L.A.; Gavrilova, N.S. The Biology of Life Span: A Quantitative Approach; Harwood Academic Publishers: Warsaw, Poland, 1991. [Google Scholar]
- London, D. Graduation, the Revision of Estimates; Actex Publications: Greenland, NH, USA, 1985. [Google Scholar]
- Haberman, S. Actuarial Methods, Encyclopedia of Biostatistics, 1st ed.; Armitage, P., Colton, T., Eds.; John Wiley & Sons: New York, NY, USA, 1998; pp. 37–49. [Google Scholar]
- Chalkias, C.; Papadopoulos, A.G.; Kalogeropoulos, K.; Tambalis, K.; Psarra, G.; Sidossis, L. Geographical heterogeneity of the relationship between childhood obesity and socio-environmental status: Empirical evidence from Athens, Greece. Appl. Geogr. 2013, 37, 34–43. [Google Scholar] [CrossRef]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Amemiya, T. Advanced Econometrics; Harvard University Press: Cambridge, MA, USA, 1985. [Google Scholar]
- De Moivre, A. Annuities Upon Lives: Or, The Valuation of Annuities Upon Any Number of Lives; NewsBank Readex: Naples, FL, USA, 1725. [Google Scholar]
- Horiuchi, S.; Coale, A.J. Age patterns of mortality for older women: An analysis using the age-specific rate of mortality change with age. Math. Popul. Stud. 1990, 2, 245–267. [Google Scholar] [CrossRef]
- Elzhov, T.V.; Mullen, K.M.; Spiess, A.; Bolker, B. R interface to the Levenberg-Marquardt nonlinear least-squares algorithm found in MINPACK. Plus Support Bounds 2010, 1–2. [Google Scholar]
- Andreopoulos, P.; Polykretis, C.; Tragaki, A. Assessment and Mapping of Spatio-Temporal Variations in Human Mortality-Related Parameters at European Scale. ISPRS Int. J. Geo-Inf. 2020, 9, 547. [Google Scholar] [CrossRef]
- Jones, D.R. Mathematical Analysis of Mortality Dynamics; Technical Report; University of Liverpool: Liverpool, UK, 2013. [Google Scholar]
- Kim, D.; Saada, A. The social determinants of infant mortality and birth outcomes in Western developed nations: A cross-country systematic review. Int. J. Environ. Res. Public Health 2013, 10, 2296–2335. [Google Scholar] [CrossRef]
- Kalogeropoulos, K. The Geographical Aspect of the Geodata of the National Population Censuses. Mapping—Creation of Modern Spatial Data Infrastructures with the Use of Geoinformatics. Ph.D. Thesis, Department of Geography, Harokopio University, Athens, Greece, 2020. Available online: http://estia.hua.gr/browse/23211 (accessed on 27 April 2021).
- Lenart, P.; Kuruczova, D.; Joshi, P.K.; Bienertová-Vašků, J. Male mortality rates mirror mortality rates of older females. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zografos, K.; Balakrishnan, N. On families of beta-and generalized gamma-generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Kalogirou, S.; Tsimbos, C.; Verropoulou, G.; Kotsifakis, G. Regional mortality differentials in Greece by selected causes of death: 2006–2008. J. Maps 2012, 8, 354–360. [Google Scholar] [CrossRef]
- Drevenstedt, G.L.; Crimmins, E.M.; Vasunilashorn, S.; Finch, C.E. The rise and fall of excess male infant mortality. Proc. Natl. Acad. Sci. USA 2008, 105, 5016–5021. [Google Scholar] [CrossRef]
- Organisation for Economic Co-Operation and Development (OECD). Health at a Glance 2019: OECD Indicators; OECD Publishing: Paris, France, 2019. [Google Scholar]
- Wasserman, D.; Cheng, Q.I.; Jiang, G.X. Global suicide rates among young people aged 15–19. World Psychiatry 2005, 4, 114. [Google Scholar] [PubMed]
- Oksuzyan, A.; Juel, K.; Vaupel, J.W.; Christensen, K. Men: Good health and high mortality. Sex differences in health and aging. Aging Clin. Exp. Res. 2008, 20, 91–102. [Google Scholar] [CrossRef]
- Laliotis, I.; Ioannidis, J.P.; Stavropoulou, C. Total and cause-specific mortality before and after the onset of the Greek economic crisis: An interrupted time-series analysis. Lancet Public Health 2016, 1, e56–e65. [Google Scholar] [CrossRef]
- Lafaut, D.; Vandenheede, H.; Surkyn, J.; Coene, G. Counting the non-existing: Causes of death of undocumented migrants in Brussels-Capital Region (Belgium), 2005–2010. Arch. Public Health 2019, 77, 42. [Google Scholar] [CrossRef] [PubMed]
- Domnich, A.; Panatto, D.; Gasparini, R.; Amicizia, D. The “healthy immigrant” effect: Does it exist in Europe today? Ital. J. Public Health 2012, 9, e7532. [Google Scholar]
- Ugarte, M.D.; Goicoa, T.; Etxeberria, J.; Militino, A.F. Projections of cancer mortality risks using spatio-temporal P-spline models. Stat. Methods Med Res. 2012, 21, 545–560. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).