Production, Validation and Morphometric Analysis of a Digital Terrain Model for Lake Trichonis Using Geospatial Technologies and Hydroacoustics
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Topographic and Bathymetric Maps
3.2. DTM Production
3.2.1. DTM Interpolation
3.2.2. DTM Accuracy Analysis
- 1)
- New contours at a 5 m interval (i.e., at half the original 10 m interval) were created from the interpolated DTM (DTM_original);
- 2)
- The 5 m contours, together with the original 135 depth points, were used to create a new DTM using the Topo-to-Raster algorithm;
- 3)
- 4)
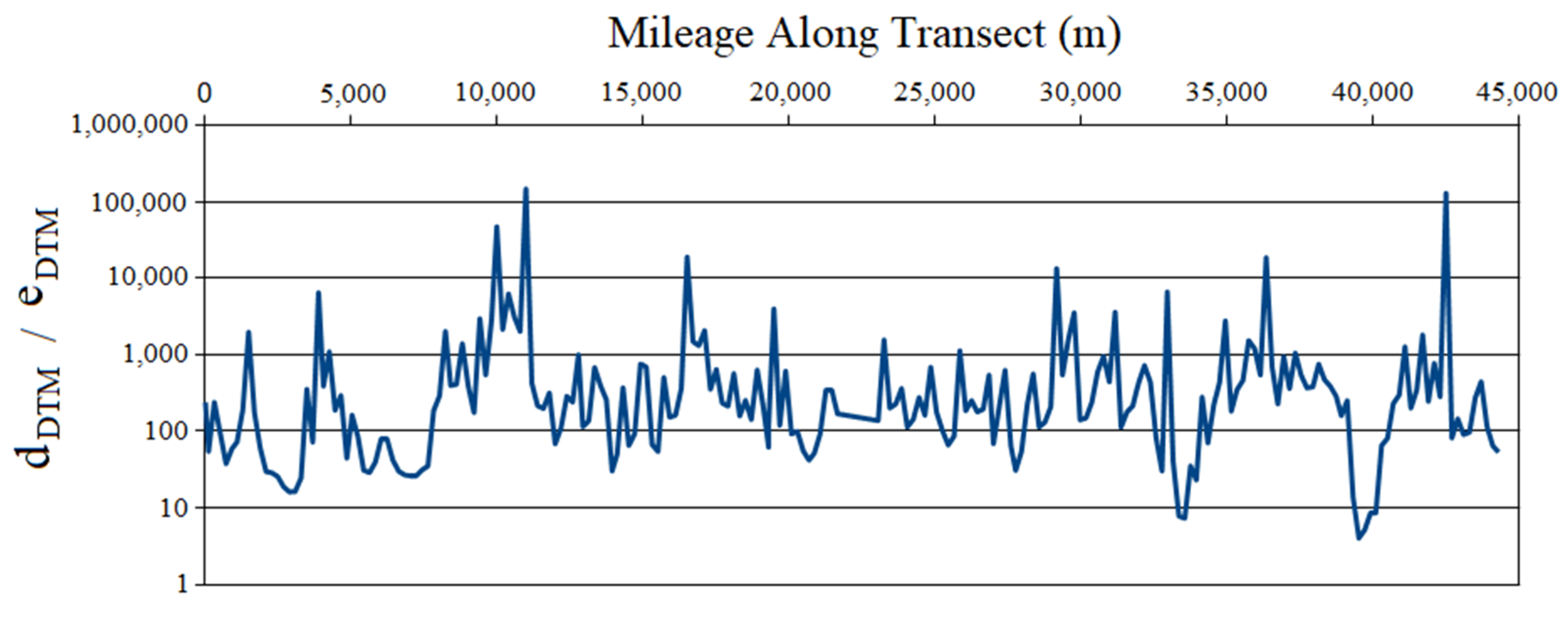
- The ratio of interpolated depth to interpolation error was calculated as a proxy for the signal-to-noise ratio and was plotted along the transect (Figure 4).
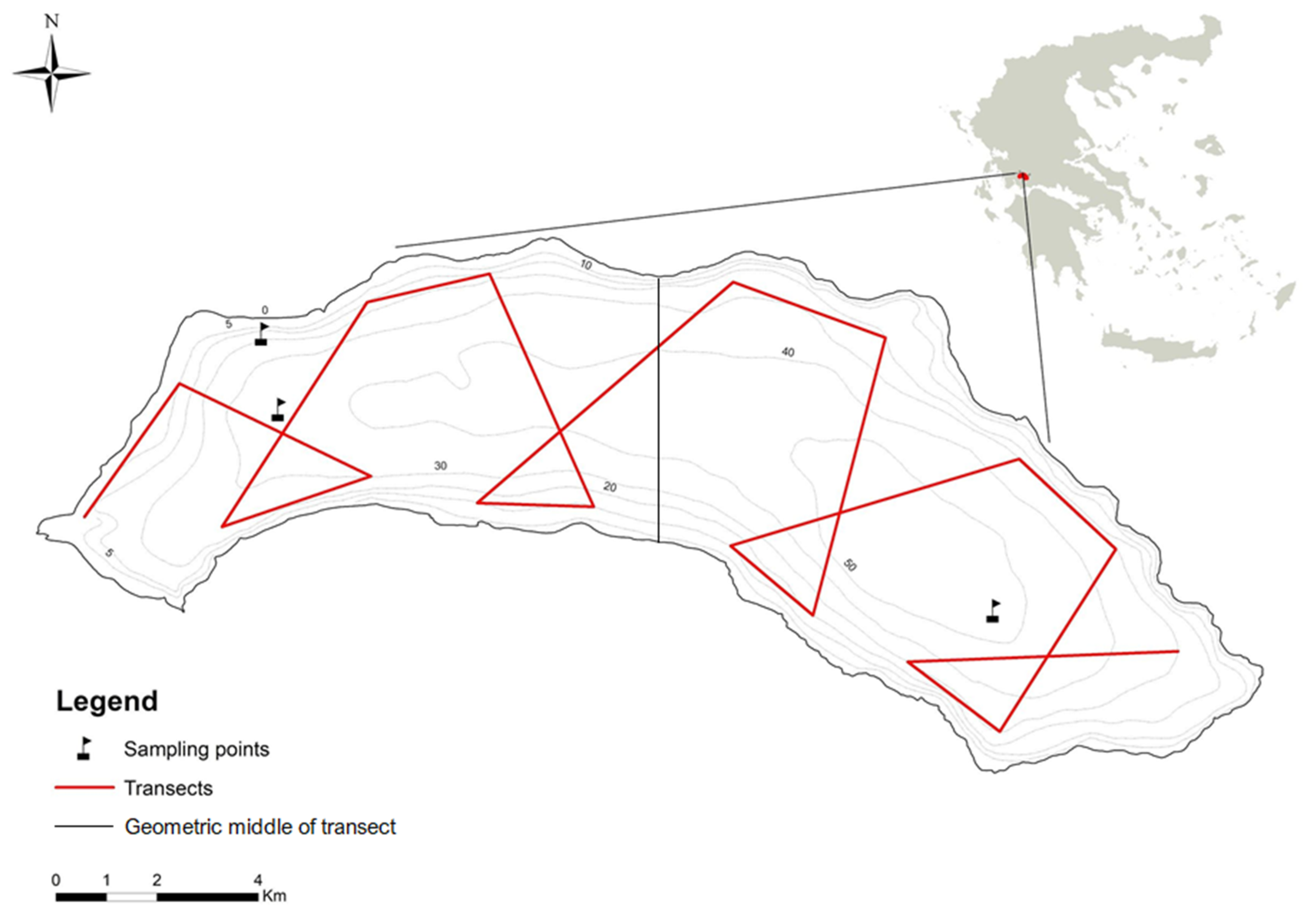
3.3. Echosoundings and GPS Data
3.3.1. Bathymetric Data Extraction from Hydroacoustic Data
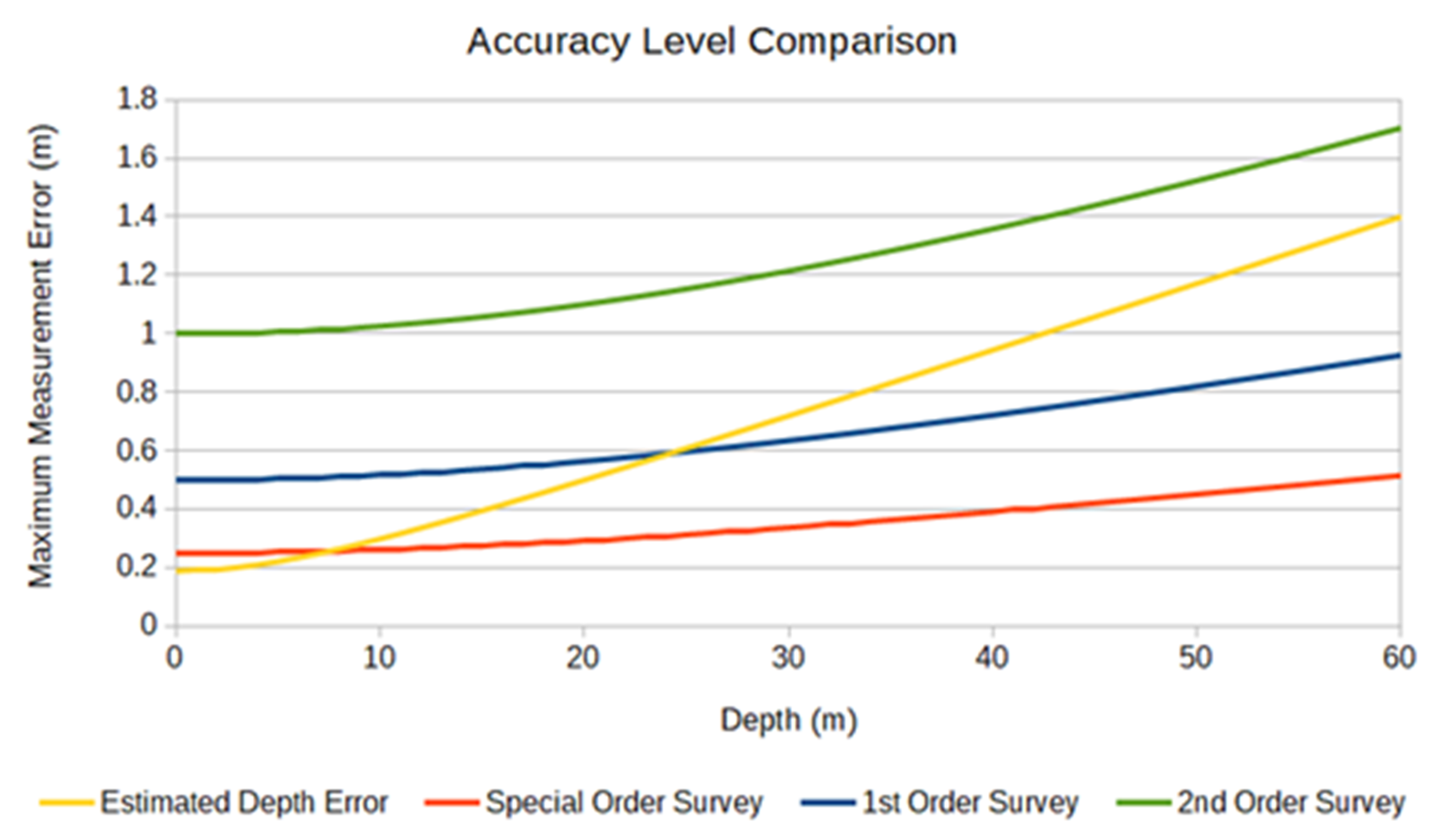
3.3.2. Echosounder Accuracy Analysis
- Horizontal Accuracy (Spatial Resolution)
- Vertical (Depth) Accuracy
- i.
- Bottom Slope
- ii.
- Sound Velocity Variations
- iii.
- Time-Dependent Variations
- iv.
- Water-Undulation-Related Variations
- v.
- Vertical Datum Error
- Overall Uncertainty
3.3.3. Data Processing
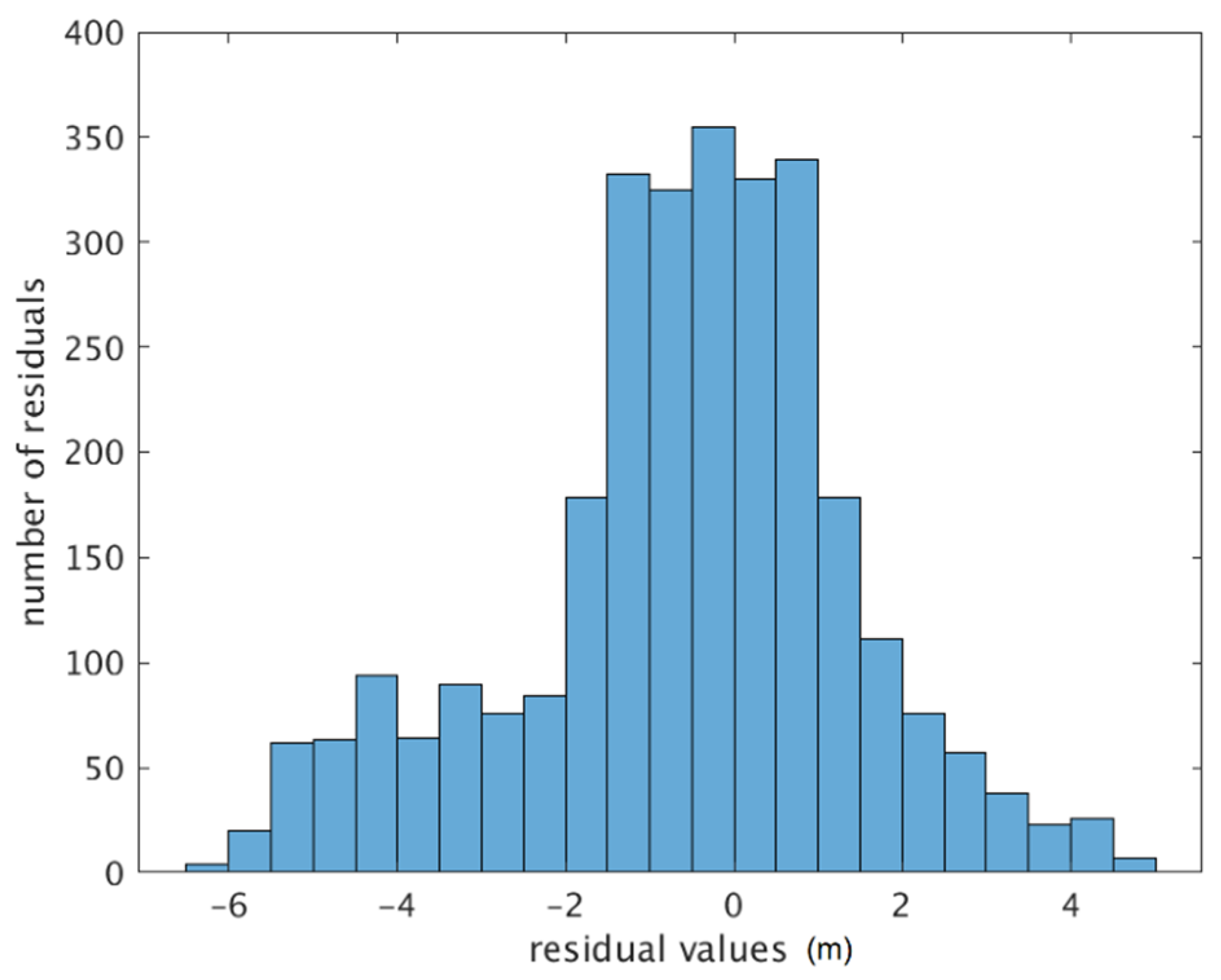
3.4. Absolute Elevation Validation
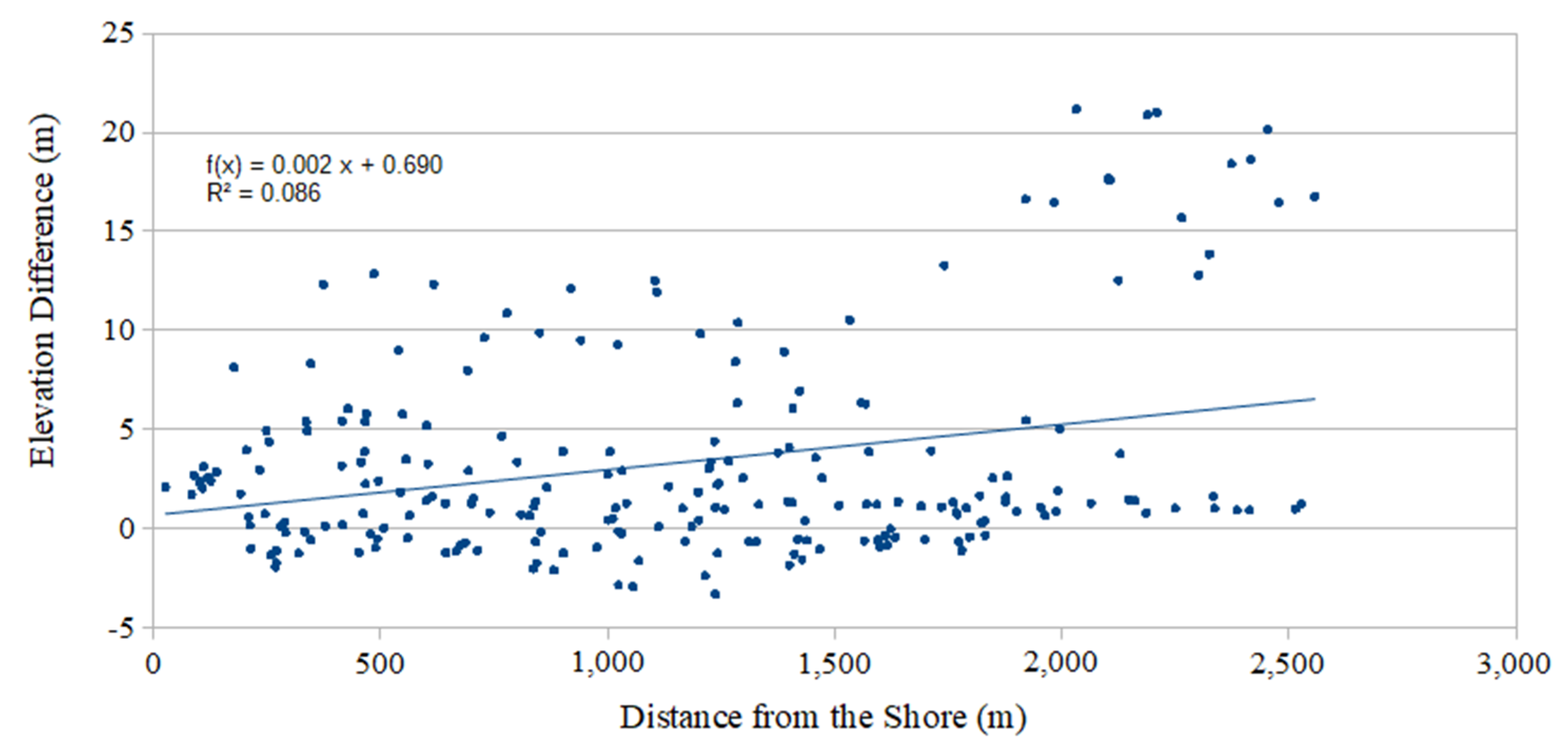
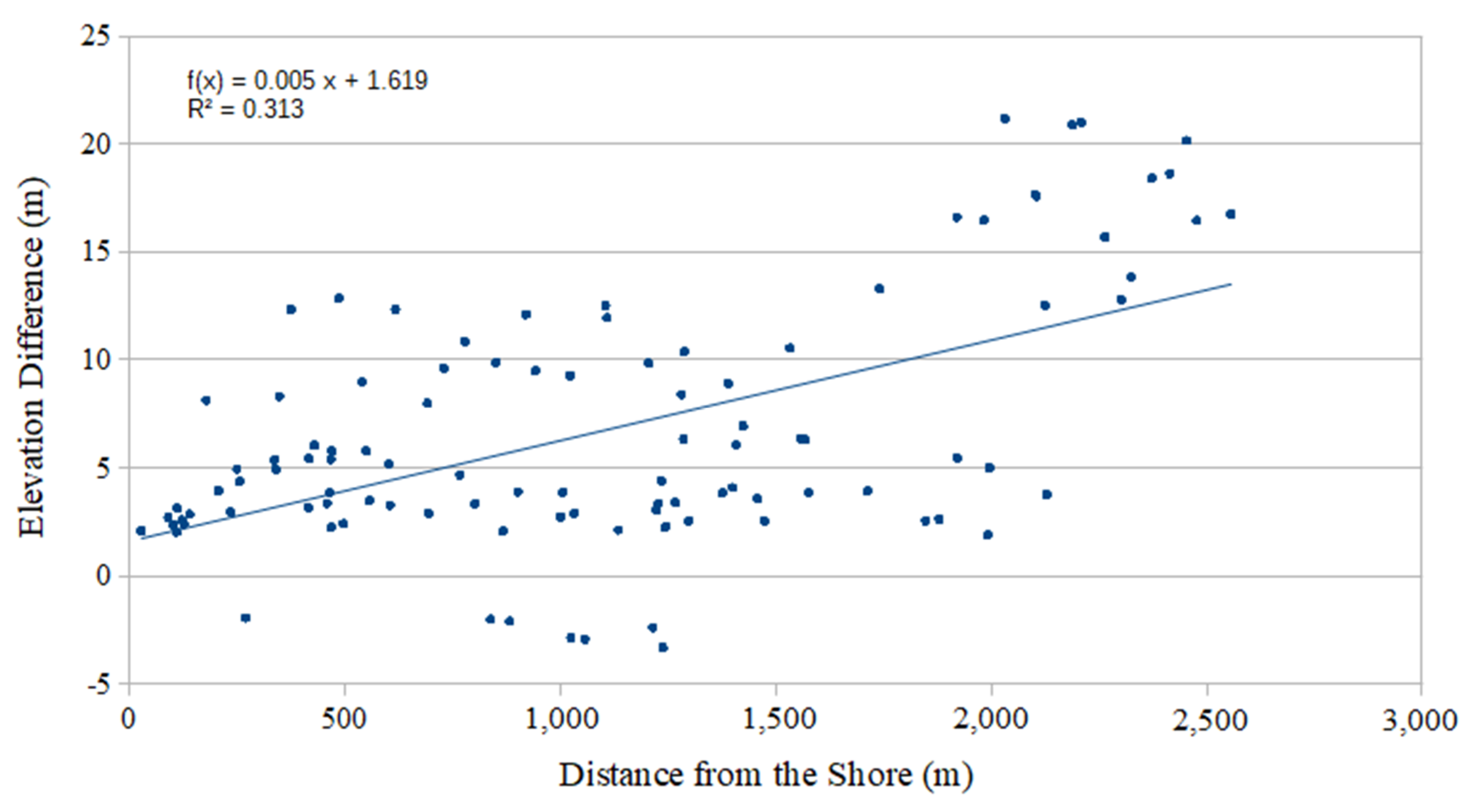
3.5. Relative Elevation Validation
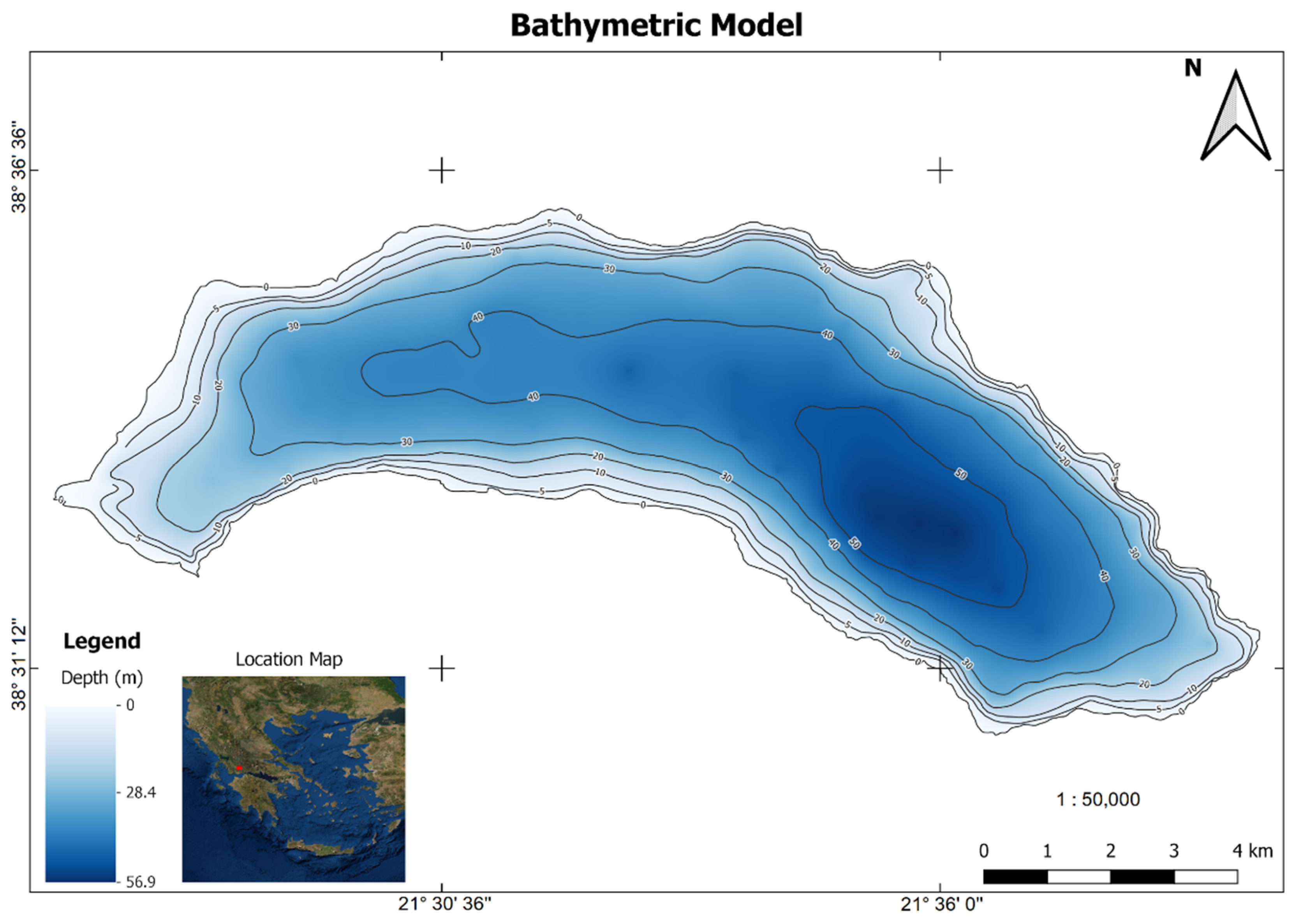
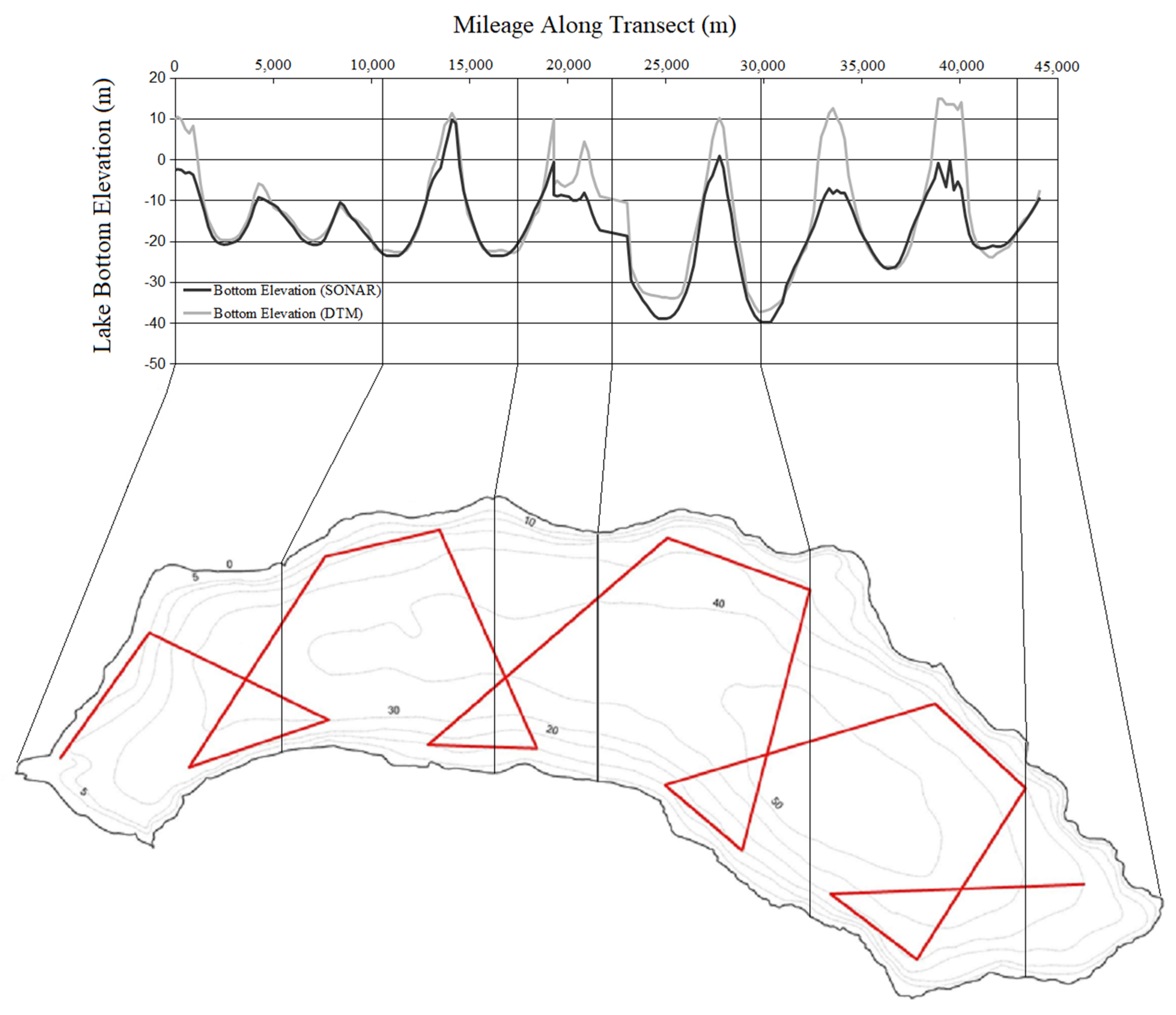
3.6. Bathymetric Model
3.7. Morphometric Analysis
4. Results
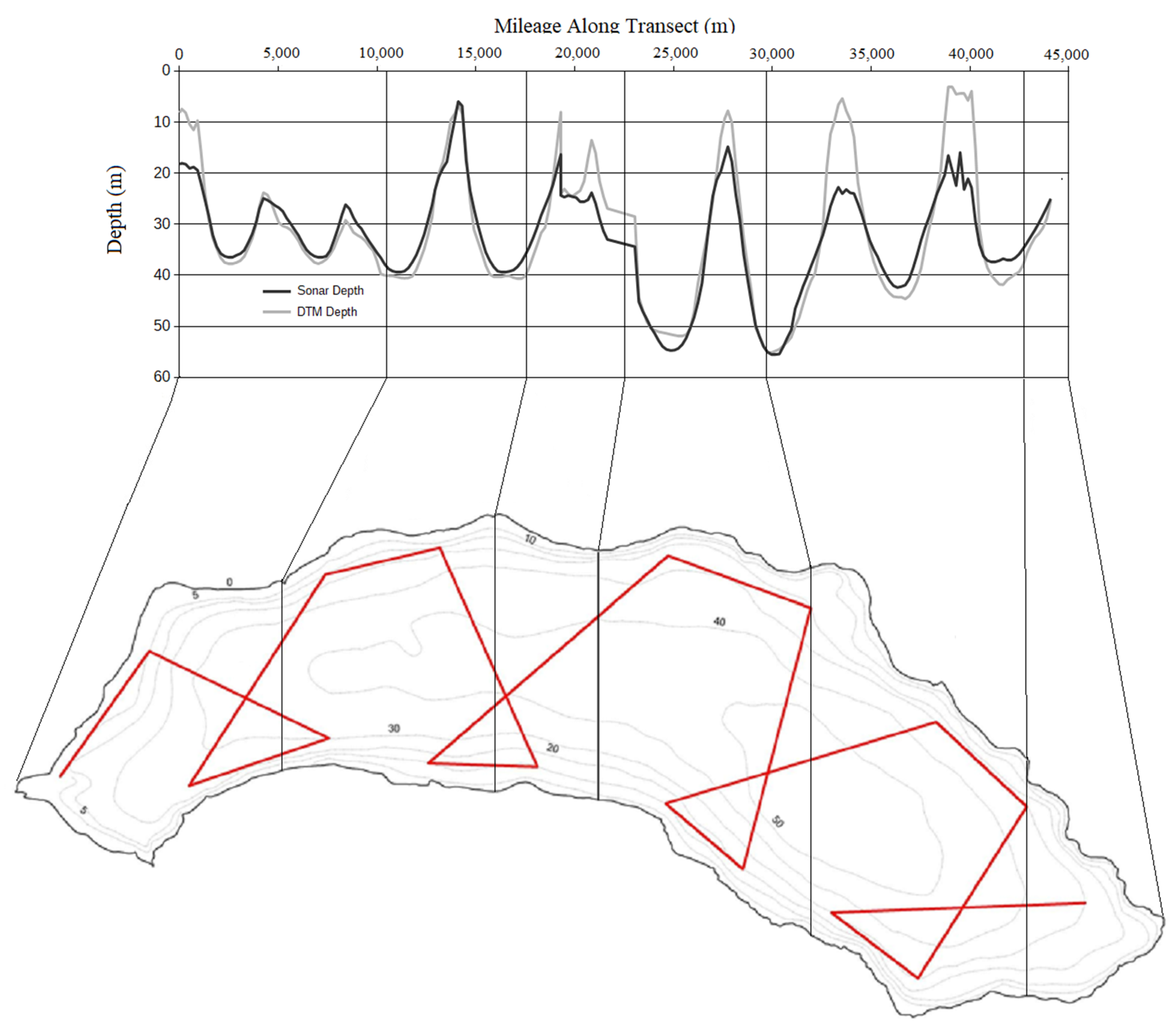
4.1. DTM
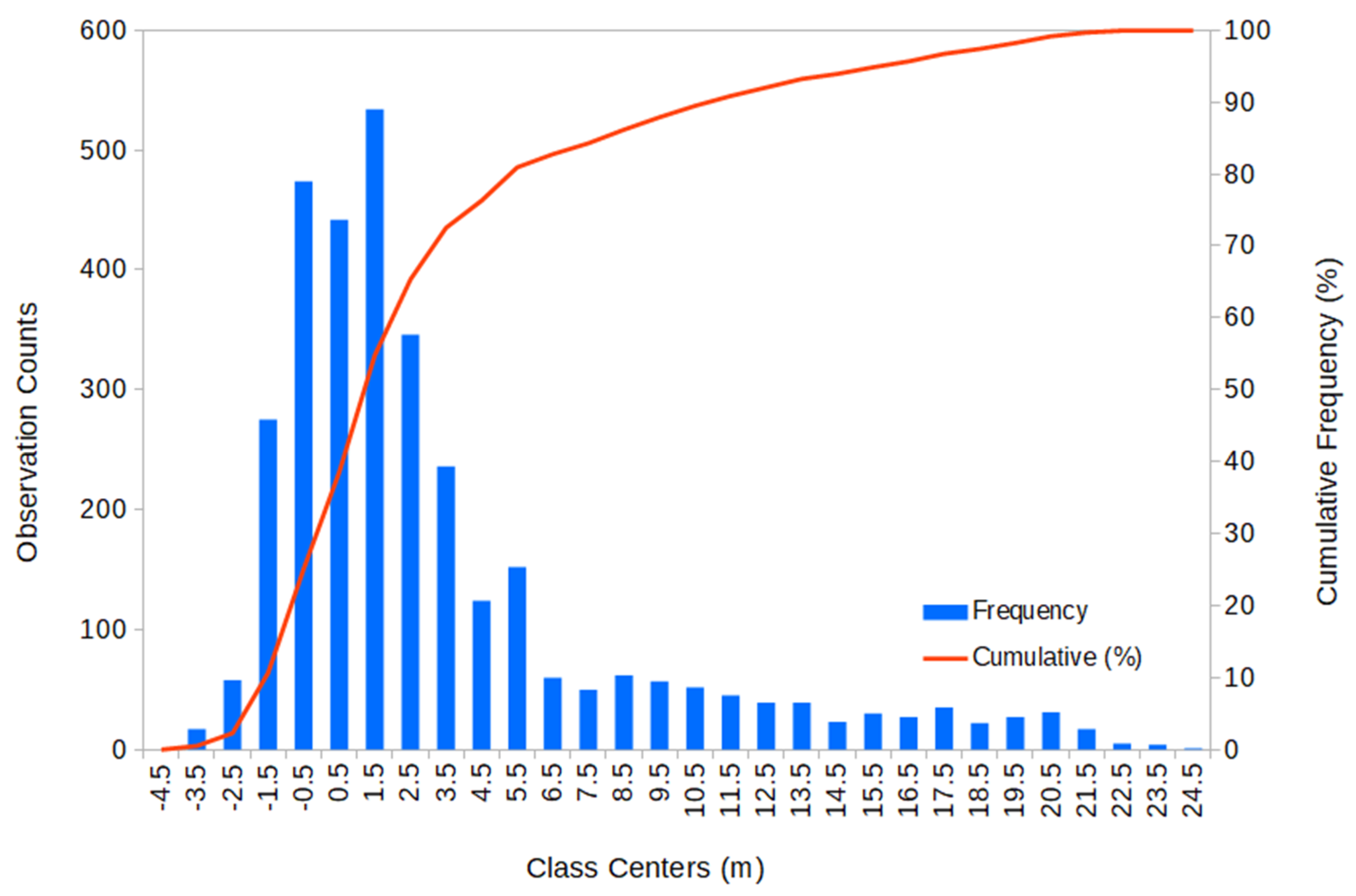
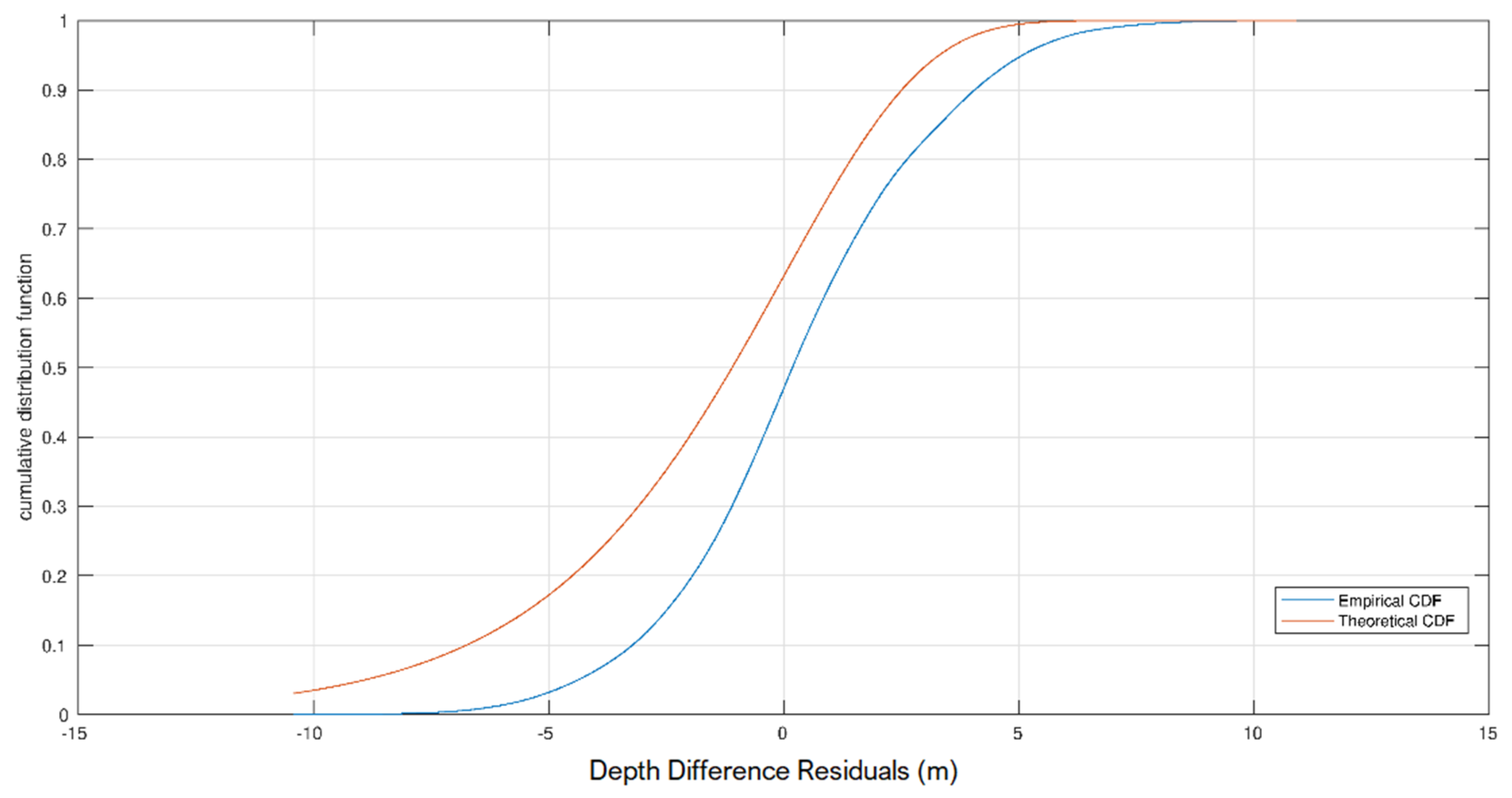
4.2. Absolute Elevation Error
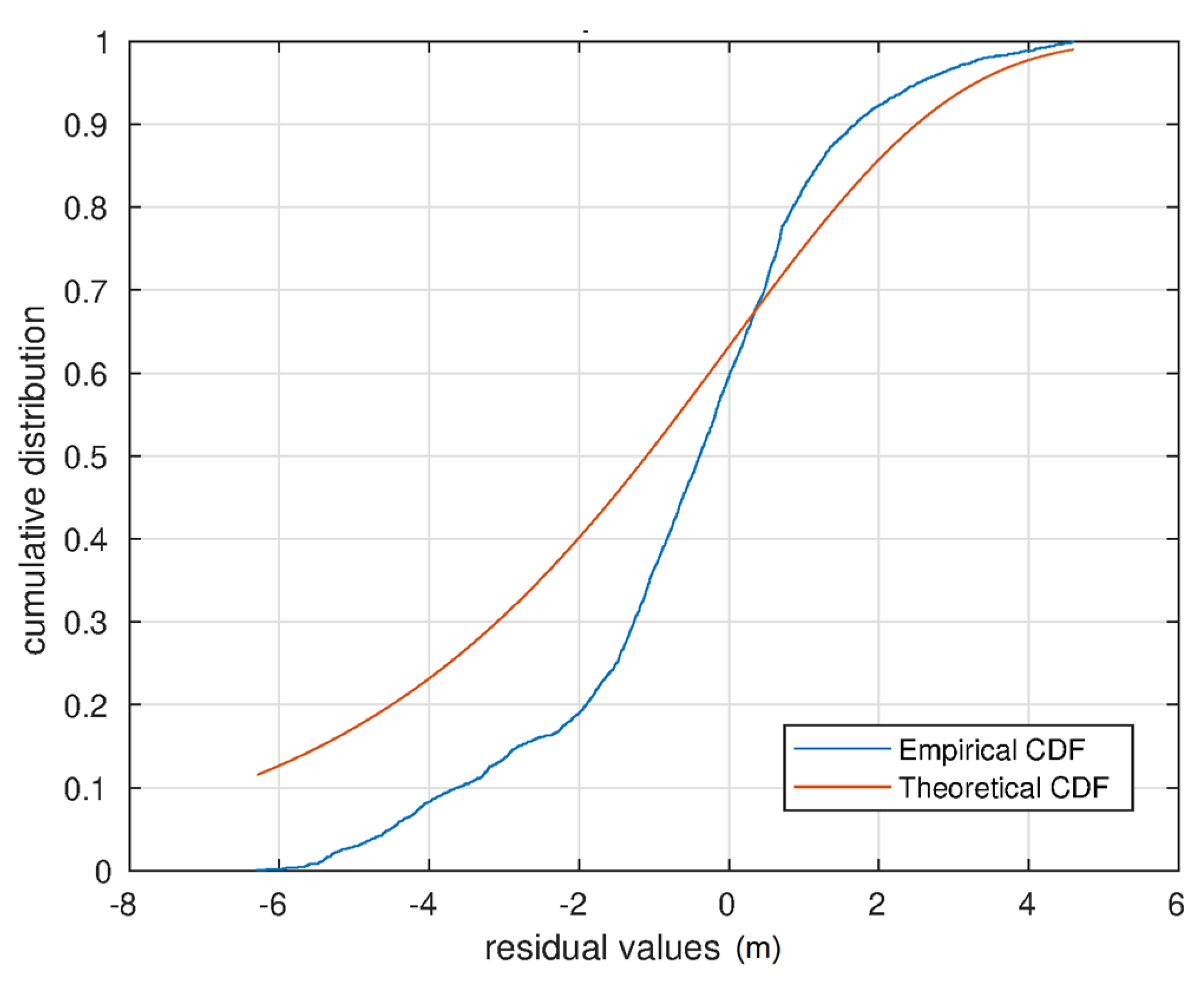
4.3. Relative Elevation Error
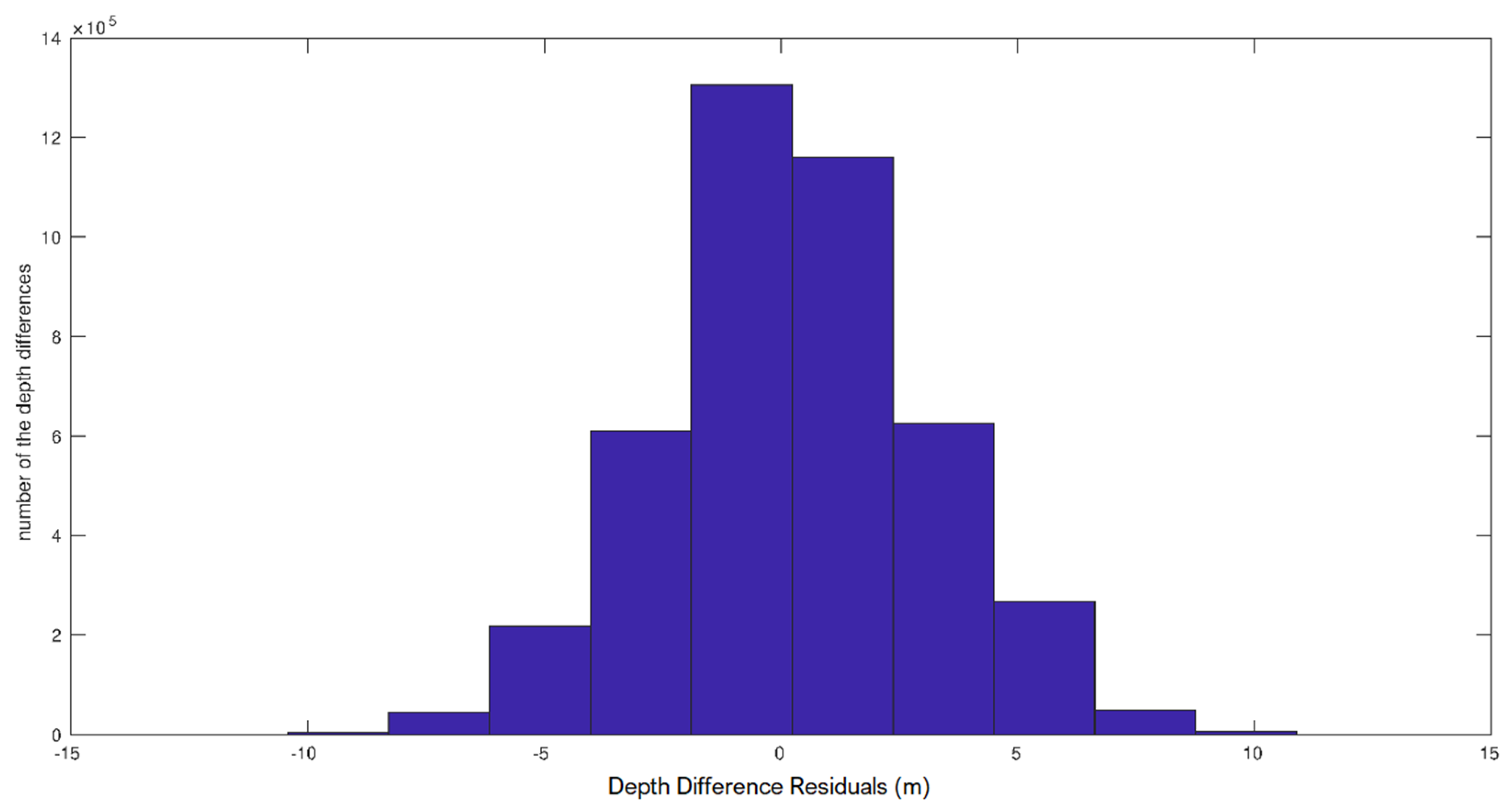
4.4. Bathymetric Model
4.5. Morphometry
4.5.1. Absolute Depth and Volume
4.5.2. Relative Depth
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 1–11. [Google Scholar] [CrossRef]
- Søndergaard, M.; Jeppesen, E. Anthropogenic impacts on lake and stream ecosystems, and approaches to restoration. J. Appl. Ecol. 2007, 44, 1089–1094. [Google Scholar] [CrossRef]
- Shanahan, T.M.; Overpeck, J.T.; Sharp, W.E.; Scholz, C.A.; Arko, J.A. Simulating the response of a closed-basin lake to recent climate changes in tropical West Africa (Lake Bosumtwi, Ghana). Hydrol. Process. Int. J. 2007, 21, 1678–1691. [Google Scholar] [CrossRef]
- Quinn, N.W.; Hanna, W.M. A decision support system for adaptive real-time management of seasonal wetlands in California. Environ. Model. Softw. 2003, 18, 503–511. [Google Scholar] [CrossRef]
- Håkanson, L. The importance of lake morphometry and catchment characteristics in limnology–ranking based on statistical analyses. Hydrobiologia 2005, 541, 117–137. [Google Scholar] [CrossRef]
- Popielarczyk, D.; Templin, T.; Łopata, M. Using the geodetic and hydroacoustic measurements to investigate the bathymetric and morphometric parameters of Lake Hancza (Poland). Open Geosci. 2015, 7, 1–16. [Google Scholar]
- Li, Z.; Zhu, Q.; Gold, C. Digital Terrain Modeling: Principles and Methodology; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Yuzugullu, O.; Aksoy, A. Generation of the bathymetry of a eutrophic shallow lake using WorldView-2 imagery. J. Hydroinform. 2014, 16, 50–59. [Google Scholar] [CrossRef]
- Abdallah, H.; Bailly, J.S.; Baghdadi, N.N.; Geours, S.N.; Fabre, F. Potential of space-borne LiDAR sensors for global bathymetry in coastal and inland waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 202–216. [Google Scholar] [CrossRef]
- Bandini, F.; Olesen, D.H.; Jakobsen, J.; Kittel, C.M.M.; Wang, S.; Garcia, M.; Gottwein, B.P. Bathymetry observations of inland water bodies using a tethered single-beam sonar controlled by an unmanned aerial vehicle. Hydrol. Earth Syst. Sci. 2018, 22, 4165–4181. [Google Scholar] [CrossRef]
- Arseni, M.; Roșu, A.; Georgescu, L.P.; Murariu, G. Single beam acoustic depth measurement techniques and bathymetric mapping for Catusa lake Galati. Ann. Univ. Dunarea Jos Galati Fascicle II Math. Phys. Theor. Mech. 2016, 39, 281–287. [Google Scholar]
- Holcombe, T.L.; Youngblut, S.; Slowey, N. Geological structure of Charity Shoal crater, Lake Ontario, revealed by multibeam bathymetry. Geo-Mar. Lett. 2013, 33, 245–252. [Google Scholar] [CrossRef]
- Popielarczyk, D.; Templin, T. Application of integrated GNSS/hydroacoustic measurements and GIS geodatabase models for bottom analysis of Lake Hancza: The deepest inland reservoir in Poland. Pure Appl. Geophys. 2014, 171, 997–1011. [Google Scholar] [CrossRef]
- De Moustier, C.; Matsumoto, H. Seafloor acoustic remote sensing with multibeam echo-sounders and bathymetric sidescan sonar systems. Mar. Geophys. Res. 1993, 15, 27–42. [Google Scholar] [CrossRef]
- Dost, R.J.J.; Mannaerts, C.M.M. Generation of lake bathymetry using sonar, satellite imagery and GIS. In Proceedings of the ESRI International User Conference GIS, Geography in Action, San Diego, CA, USA, 4–8 August 2008. [Google Scholar]
- Dimitriou, E.; Moussoulis, E. Hydrological and nitrogen distributed catchment modeling to assess the impact of future climate change at Trichonis Lake, western Greece. Hydrogeol. J. 2010, 18, 441–454. [Google Scholar] [CrossRef]
- Tafas, T.; Danielidis, D.; Overbeck, J.; Amilli, E.A. Limnological survey of the warm monomictic lake Trichonis (central western Greece); I. The physical and chemical environment. Hydrobiologia 1997, 344, 129–139. [Google Scholar] [CrossRef]
- Zacharias, I.; Dimitriou, E.; Koussouris, T. Integrated water management scenarios for wetland protection: Application in Trichonis Lake. Environ. Model. Softw. 2005, 20, 177–185. [Google Scholar] [CrossRef]
- Psilovikos, A.; Albanakis, K.; Palikaridis, C.; Vouvalidis, K. Enironmental value and importance of Lake Trichonis as the largest natural freshwater reservoir of Greece. In Proceedings of the 4th Panhellenic Geographical Conference, Athens, Greece, 12–14 October 1995; pp. 348–358. (In Greek). [Google Scholar]
- HMGS. The Basic Cartographic Scale. Hellenic Military Geographical Service. (In Greek). Available online: https://drive.google.com/file/d/1PZJpAFOZaiqgZp-aBGoaAWqspMDoS9z6/view (accessed on 4 October 2020).
- Monmonier, M. The History of Cartography, Volume 6: Cartography in the Twentieth Century, 1st ed.; University of Chicago Press: Chicago, IL, USA, 2015; Volume 6. [Google Scholar]
- Böhme, R.; Anson, R. Inventory of World Topographic Mapping Volume 3–Eastern Europe, Asia, Oceania and Antarctica. International Cartographic Association; Elsevier Applied Science: Amsterdam, The Netherlands, 1989; Volume 3. [Google Scholar]
- ESRI. How Topo to Raster Works. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/3d-analyst/how-topo-to-raster-works.htm (accessed on 31 January 2021).
- Wahba, G. Spline Models for Observational Data; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1990. [Google Scholar]
- Hengl, T. Finding the right pixel size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Perivolioti, T.M.; Frouzova, J.; Tušer, M.; Bobori, D. Assessing the Fish Stock Status in Lake Trichonis: A Hydroacoustic Approach. Water 2020, 12, 1823. [Google Scholar] [CrossRef]
- IHO. Depth Determination. In Manual on Hydrography (Publication C-13), 1st ed.; International Hydrographic Bureau: Monaco, France, 2005; p. 539. [Google Scholar]
- Tušer, M.; Balk, H.; Mrkvička, T.; Frouzová, J.; Čech, M.; Muška, M.; Kubečka, J. Validation of current acoustic dead-zone estimation methods inlakes with strongly sloped bottoms. Limnol. Oceanogr. Methods 2011, 9, 507–514. [Google Scholar]
- Chen, C.T.; Millero, F.J. The use and misuse of pure water PVT properties for lake waters. Nature 1977, 266, 707–708. [Google Scholar] [CrossRef]
- Lubbers, J.; Graaff, R. A simple and accurate formula for the sound velocity in water. Ultrasound Med. Biol. 1998, 24, 1065–1068. [Google Scholar] [CrossRef]
- Johannesson, K.A.; Mitson, R.B. Fisheries Acoustics: A Practical Manual for Aquatic Biomass Estimation. FAO Fisheries Technical Paper 240; Technical Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1983. [Google Scholar]
- Barrass, C.B.; Derrett, D.R. Heel Due to Turning. In Ship Stability for Masters and Mates, 7th ed.; Butterworth-Heinemann, Elsevier: Massachusetts, MA, USA, 2012; pp. 145–147. [Google Scholar]
- Mühll, K.V.D. Über die Bewegung tropfbarer Flüssigkeiten in Gefässen. Nach Johann Rudolf Merian. Math. Ann. 1886, 27, 575–600. [Google Scholar]
- Kalff, J. Limnology: Inland Water Ecosystems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- IHO. IHO Standards for Hydrographic Surveys (Special Publication No S-44), 6th ed.; International Hydrographic Organization: Monaco, France, 2020. [Google Scholar]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI-An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A refined conversion from normal height to orthometric height. Studia Geophys. Geod. 2006, 50, 595–606. [Google Scholar] [CrossRef]
- Glowka, K.G.; Krynski, J.; Szelachowska, M. Time variations of the gravity field over Europe obtained from GRACE data. Rep. Geod. Geoinform. 2012, 92, 175–190. [Google Scholar]
- Godah, W.; Szelachowska, M.; Krynski, J. On the analysis of temporal geoid height variations obtained from GRACE-based GGMs over the area of Poland. Acta Geophys. 2017, 65, 713–725. [Google Scholar] [CrossRef]
- Wu, F.; Zeng, A.; Ming, F. Analyzing the long-term changes in China’s National Height Datum. Adv. Space Res. 2020, 66, 1342–1350. [Google Scholar] [CrossRef]
- Bitharis, S.; Ampatzidis, D.; Pikridas, C.; Fotiou, A.; Rossikopoulos, D.; Schuh, H. The Role of GNSS Vertical Velocities to Correct Estimates of Sea Level Rise from Tide Gauge Measurements in Greece. Mar. Geod. 2017, 40, 297–314. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis, 1st ed.; Pearson: London, UK, 1977. [Google Scholar]
- Vassilakis, E.; Royden, L.; Papanikolaou, D. Kinematic links between subduction along the Hellenic trench and extension in the Gulf of Corinth, Greece: A multidisciplinary analysis. Earth Planet. Sci. Lett. 2011, 303, 108–120. [Google Scholar] [CrossRef]
- Armijo, R.; Meyer, B.; King, G.; Rigo, A.; Papanastassiou, D. Quaternary evolution of the Corinth Rift and its implications for the Late Cenozoic evolution of the Aegean. Geophys. J. Int. 1996, 126, 11–53. [Google Scholar] [CrossRef]
- Briole, P.; Rigo, A.; Caen, L.H.; Ruegg, J.C.; Papazissi, K.; Mitsakaki, C.; Balodimou, A.; Veis, G.; Hatzfeld, D.; Deschamps, A. Active deformation of the Corinth rift, Greece: Results from repeated Global Positioning System surveys between 1990 and 1995. J. Geophys. Res. 2000, 105, 605–625. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Papazachos, C.B. The Earthquakes of Greece, 3rd ed.; Ziti Publications: Thessaloniki, Greece, 2003. (In Greek) [Google Scholar]
- Benekos, G.; Parcharidis, I.; Foumelis, M.; Ganas, A. Ground deformation measurements over Lake Trichonis based on SAR interferometry. Bull. Geol. Soc. Greece 2013, 47, 1071–1080. [Google Scholar] [CrossRef][Green Version]
- Kiratzi, A.; Sokos, E.; Ganas, A.; Tselentis, A.; Benetatos, C.; Roumelioti, Z.; Serpetsidaki, A.; Andriopoulos, G.; Galanis, O.; Petrou, P. The April 2007 earthquake swarm near Lake Trichonis and implications for active tectonics in western Greece. Tectonophysics 2008, 452, 51–65. [Google Scholar] [CrossRef]
- Delibasis, N.; Carydis, P. Recent earthquake activity in Trichonis region and its tectonic significance. INGV Ann. Geophys. 1977, 30, 19–81. [Google Scholar]
- Psychogyiou, C.; Papoutsis, I.; Kontoes, C.; Poyiadji, E.; Spanou, N.; Klimis, N. Multi-temporal monitoring of slow-moving landslides in South Pindus mountain range, Greece. In Proceedings of the Fringe 2015 Workshop, Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Klimchouk, A.B. Subsidence hazards in different types of karst: Evolutionary and speleogenetic approach. Environ. Geol. 2005, 48, 287–295. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Plessa, A. Magnitude–distance relations for earthquake-induced landslides in Greece. Eng. Geol. 2000, 58, 377–386. [Google Scholar] [CrossRef]
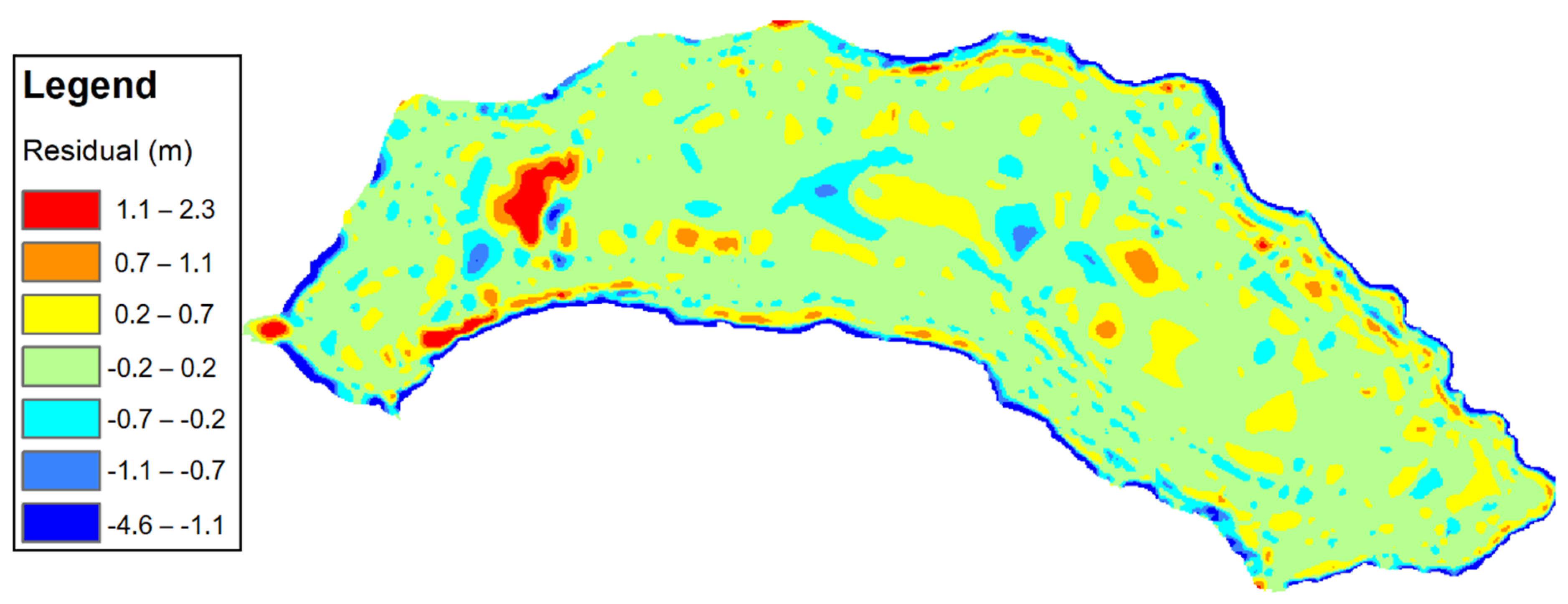






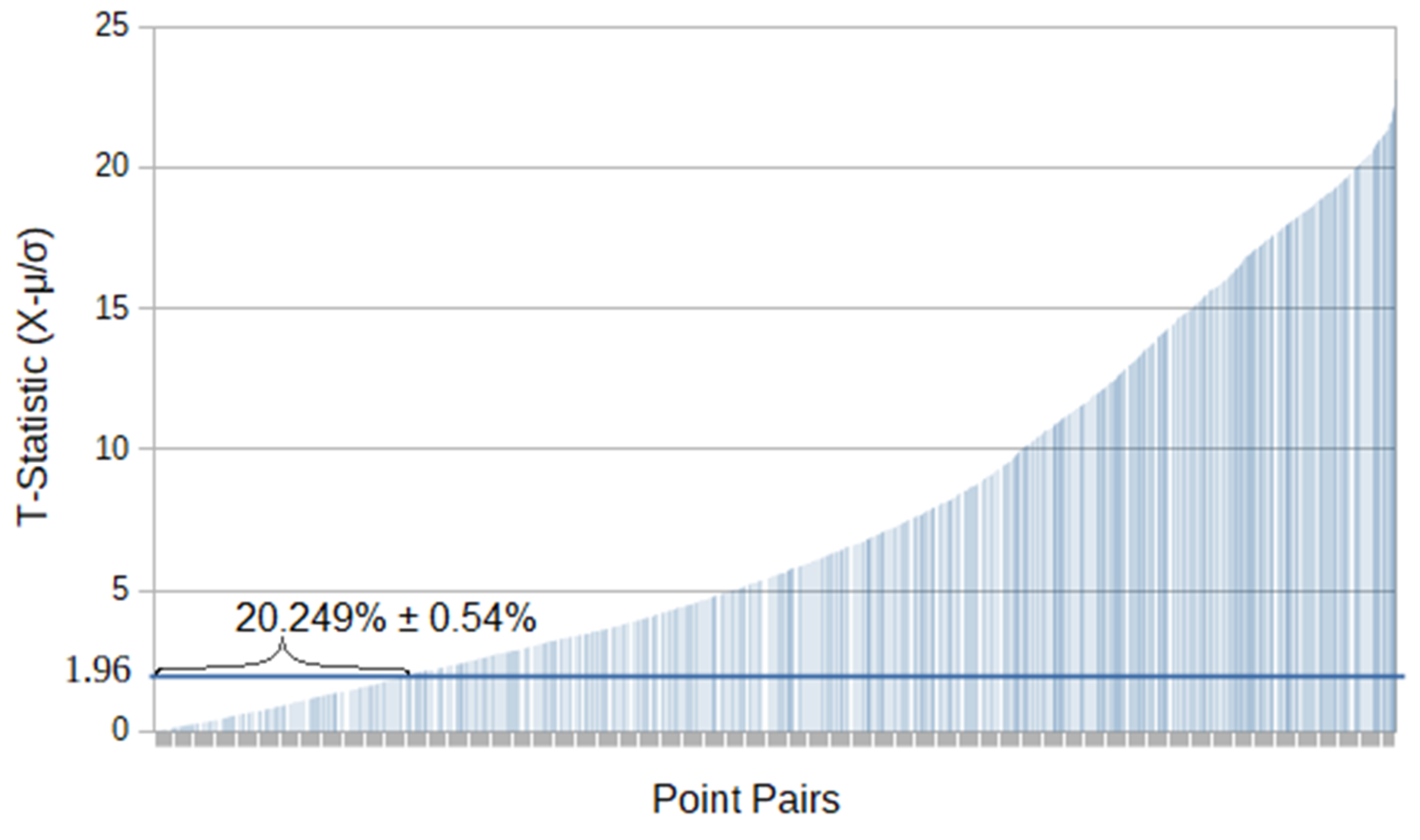
| Minimum (m) | −4.6 |
| Maximum (m) | 2.3 |
| Mean (m) | 0.0 |
| Standard Deviation (m) | 0.4 |
| Number of pixels | 136,640 |
| Statistical Measure | Value |
|---|---|
| Mean (m) | 3.39 |
| Standard Deviation (m) | 5.26 |
| RMSE (Root Mean Squared Error) (m) | 5.38 |
| RMSE 95% (m) | 3.90 |
| RMSE 90% (m) | 2.98 |
| Median (m) | 1.51 |
| NMAD (Normalized Median Absolute Deviation) (m) | 2.86 |
| (Excess) Kurtosis | 2.48 |
| Skewness | –1.71 |
| Minimum (m) | –3.93 |
| Maximum (m) | 24.05 |
| Range (m) | 27.98 |
| N (number of samples) | 3284 |
| Statistical Measure | Value |
|---|---|
| Mean (m) | 0.00 |
| Standard Deviation (m) | 7.49 |
| RMSE (Root Mean Square Error) (m) | 7.49 |
| RMSE 95% (m) | 6.20 |
| RMSE 90% (m) | 5.22 |
| Median (m) | 0.72 |
| Normalised Median Average Deviation (NMAD) (m) | 2.86 |
| (Excess) Kurtosis | 1.17 |
| Skewness | 0.04 |
| Minimum (m) | –24.80 |
| Maximum (m) | 24.67 |
| Range (m) | 49.47 |
| n (number of samples) | 3284 |
| Mean | 0.00 m |
| Median | –0.09 m |
| Minimum | –6.30 m |
| Maximum | 4.60 m |
| Standard Deviation | 2.11 m |
| Mean | 0.29 m |
| Median | 0.18 m |
| Minimum | −10.42 m |
| Maximum | 10.89 m |
| Standard Deviation | 2.81 m |
| 1st Order Surface (Plane) | |
| Coefficient of (x’) | 0.0003035 |
| Coefficient of (y’) | 0.0004229 |
| Constant Term | 2.913 m |
| Mean Error | 0.000 m |
| Median Error | –0.931 m |
| Minimum | –6.645 m |
| Maximum | 16.689 m |
| Range | 23.334 m |
| Mean Absolute Error | 3.148 m |
| RMSE | 4.331 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perivolioti, T.-M.; Mouratidis, A.; Terzopoulos, D.; Kalaitzis, P.; Ampatzidis, D.; Tušer, M.; Frouzova, J.; Bobori, D. Production, Validation and Morphometric Analysis of a Digital Terrain Model for Lake Trichonis Using Geospatial Technologies and Hydroacoustics. ISPRS Int. J. Geo-Inf. 2021, 10, 91. https://doi.org/10.3390/ijgi10020091
Perivolioti T-M, Mouratidis A, Terzopoulos D, Kalaitzis P, Ampatzidis D, Tušer M, Frouzova J, Bobori D. Production, Validation and Morphometric Analysis of a Digital Terrain Model for Lake Trichonis Using Geospatial Technologies and Hydroacoustics. ISPRS International Journal of Geo-Information. 2021; 10(2):91. https://doi.org/10.3390/ijgi10020091
Chicago/Turabian StylePerivolioti, Triantafyllia-Maria, Antonios Mouratidis, Dimitrios Terzopoulos, Panagiotis Kalaitzis, Dimitrios Ampatzidis, Michal Tušer, Jaroslava Frouzova, and Dimitra Bobori. 2021. "Production, Validation and Morphometric Analysis of a Digital Terrain Model for Lake Trichonis Using Geospatial Technologies and Hydroacoustics" ISPRS International Journal of Geo-Information 10, no. 2: 91. https://doi.org/10.3390/ijgi10020091
APA StylePerivolioti, T.-M., Mouratidis, A., Terzopoulos, D., Kalaitzis, P., Ampatzidis, D., Tušer, M., Frouzova, J., & Bobori, D. (2021). Production, Validation and Morphometric Analysis of a Digital Terrain Model for Lake Trichonis Using Geospatial Technologies and Hydroacoustics. ISPRS International Journal of Geo-Information, 10(2), 91. https://doi.org/10.3390/ijgi10020091








