Influence of Relief Degree of Land Surface on Street Network Complexity in China

Abstract

The relief degree of land surface (RDLS) was often calculated to describe the topographic features of a region. It is a significant factor in designing urban street networks. However, existing studies do not clarify how RDLS affects the distribution of urban street networks. We used a Python package named OSMnx to extract the street networks of different cities in China. The street complexity metrics information (i.e., street grain, connectedness, circuity, and street network orientation entropy) were obtained and analyzed statistically. The results indicate that street network exhibits more complexity in regions with high RDLS. Further analysis of the correlation between RDLS and street network complexity metrics indicates that RDLS presents the highest correlation with street network circuity; that is, when RDLS is higher, the routes of an urban street network is more tortuous, and the additional travel costs for urban residents is higher. This study enriches and expands research on street networks in China, providing a reference value for urban street network planning.

1. Introduction

Urban planning defines the development and construction of a city. On the basis of the principles of sustainable development, it investigates the future development of a city and rationalizes its layout [1,2]. As one of the largest urban public spaces, an urban street network is the skeleton of the urban surface, presenting social and humanitarian connotations and becoming the focus in urban planning. It plays an important role in the physical/material and informational exchange of a city with its function of connecting one area to another [3].

As cities enter the period of spatial expansion into structural optimization, the scale of the street network gradually expands [4,5,6], and the rational planning of street structures becomes increasingly significant. Topographic information provides valuable support to various urban activities, such as urban waterlogging monitoring and urban expansion planning. Viero et al. pointed out that urban waterlogging was influenced by the natural environment, including precipitation and topography, so understanding urban topography is beneficial for monitoring urban waterlogging [7]. Yang et al. planned the road construction in the Jianye District of Nanjing by using topographic information, which effectively expressed the spatial geometry and semantic features of urban roads [8]. The close relationship between topographic information and streets may be valuable in the planning of urban streets [9], because of the combination of natural factors and human activities resulting in flat topography interspersed with undulating topography [10]. Many studies have demonstrated that topography has become a non-negligible factor in street network planning. For example, Osama et al. identified street network connectivity and topography as factors affecting pedestrian safety and found that higher continuity, linearity, coverage, and slope of the street network were associated with lower crash incidence, which was useful for street network planning [11]. Daniels et al. illustrated how the natural environment (including topography) influenced network planning principles through an analysis of the Sydney, Australia, case [12]. Szajowski et al. proposed a quantitative approach to measure the importance of roads based on topography and traffic intensity, which could be a guide for road builders planning road infrastructure [13].

Regional topographic features are typically identified by using the relief degree of land surface (RDLS) as a key indicator to characterize topographic relief in a certain area [14]. RDLS is frequently used as one of the indicators of habitat suitability evaluation [15] and ecological environment evaluation [16]. It is also widely used in the fields of geological disaster evaluation [17], soil erosion sensitivity evaluation [18], and population distribution and economic development [19]. An urban street network is the basic skeleton of urban spatial form that expresses evident complexity in many aspects, including topology structure [20]. At present, it is mostly described as a topological diagram. Thereafter, mathematical models are built and metrics are calculated for urban street networks, including the alpha index, the beta index, and the gamma index [21]. These metrics provide a good description of the structural characteristics of an urban street network. Most studies on urban street network complexity have selected a single city or a smaller scale of an area as objects of study. However, a small spatial scale usually reflects only the partial/individual characteristics of an area but not its overall/common characteristics embedded into the transportation network at a larger scale. Moreover, existing studies are typically limited to applying complex network theory [22], fractal theory [23], and space syntax [24] when measuring urban street network complexity.

Boeing proposed a street network complexity analysis method based on OSMnx, a Python package developed by his team [25]. This approach used a unified OpenStreetMap data source and optimized network topology. Street networks are complex research objects; hence, the introduction of OSMnx solves the following problems, which existed in previous studies on street networks: (1) network oversimplification and the inconsistency of simplified models exert fundamental effects on the research results [26], and (2) the lack of free downloadable and easy-to-handle tools [27]. OSMnx enables the measurement of urban street network complexity through street grain, connectedness, street network orientation entropy, and circuity. In recent years, some studies on urban street networks have been conducted by using OSMnx. Yen et al. used circuity as one of the metrics to analyze three street network patterns, namely, walkable, bikeable, and drivable, in Phnom Penh, Cambodia [28]. Their results suggested that urban central areas are more favorable for walking and biking than peripheral districts. Boeing used OSMnx as a data-access tool and the street network of 100 cities as the study subject. He included street orientation entropy as a metric for quantifying street network analysis and found that US cities tended to be more grid-oriented than other cities [29]. Moreover, the large sample of an urban street network can be collected by using OSMnx, considerably facilitating the study of urban street networks. Zhao et al. compared the network characteristics of the 26 pilot cities of the ASEAN Smart City Network by downloading the drivable and walkable road networks, using OSMnx with various network metrics [30]. Boeing used OSMnx and OpenStreetMap to analyze a street network with 27,000 urban street networks in the US and shared the large-scale data he collected in a public database [31]. Zhou et al. obtained a large sample of street network patterns by using OSMnx and found that similar street network patterns exhibit a clustered form in spatial distribution [32].

The influence of topography on a street network is one of the most important indicators of transportation costs and vehicle driving performance [33,34]. Nevertheless, existing studies have not yet explored in detail how topography affects the distribution of street networks. In our study, we used OSMnx to extract the city street networks of China and quantitatively analyze the closeness of the relationship between topography and street networks by the Pearson correlation coefficient. This study enriches and complements current research on the complexity of Chinese street networks in the theoretical and applied aspects. It contributes to the understanding of the layout and development of street network patterns and their associated urban forms in China, and may also play a greater role in future urban planning.

2. Study Area and Data

2.1. Overview of Study Area

In this study, China was chosen as the study area for the following reasons. First of all, Chinese territory is vast and shows great diversity in physical geography. For instance, the topography of China is high in the west and low in the east, and is complex and diverse, forming three levels of steps from west to east: The western part of the country has the highest terrain, the Qinghai-Tibet Plateau, known as the “Roof of the World”, which is the first step, and is bounded by the Kunlun Mountains, Qilian Mountains, Hengduan Mountains and the second step; the Qinghai-Tibet Plateau east to the Daxinganling Mountains, Taihang Mountains, Wushan Mountains and Xuefeng Mountains is the second step, generally at an altitude of 1000–2000 m, mainly composed of mountains, plateaus and basins; the wide plains and hills of eastern China are the third step. Secondly, the street system has developed significantly with the growth of cities since the implementation of China’s reform and open policy [35], but few studies have described the street network patterns of Chinese cities as a whole. Thirdly, with over 300 prefectures in China, it greatly helps us to explore whether the pattern of China’s street network is limited by the topography at a macro level.

2.2. Data

The digital elevation model (DEM) data used in our study were obtained from the Geospatial Data Cloud Platform (http://www.gscloud.cn (accessed on 5 March 2021)), with an accuracy of 30 m.

Administrative boundary and road network data were downloaded, using OSMnx and collected across 34 provincial administrative units nationwide. Administrative units at the prefecture level were used as the primary statistical measure. With reference to the administrative divisions of the People’s Republic of China, the data used in our study included 4 municipalities, 2 special administrative regions, 293 prefecture-level cities, 30 autonomous prefectures, 7 districts, 3 leagues, and 30 administrative units (non-administered) at the county level under the administration of provinces (autonomous regions), along with 6 “Yuan-administered cities” and 3 cities and 13 counties in Taiwan, for a total of 391 data items.

3. Methodology

3.1. RDLS

RDLS is the degree of topographic relief above sea level for the average elevation in a given region [36]. It can be calculated by using Equation (1).

$$RDLS=\frac{ALT}{1000}+\left(Max\left(H\right)-Min\left(H\right)\right)\ast \left(1-\frac{P\left(A\right)}{A}\right)/500,$$

(1)

where RDLS is the relief degree of land surface of a region, ALT is the average altitude within the region, Max(H) is the maximum altitude within the region, Min(H) is the minimum altitude within the region, P(A) is the flat area of the region, and A is the total area of the region.

3.2. Street Network Complexity Metrics

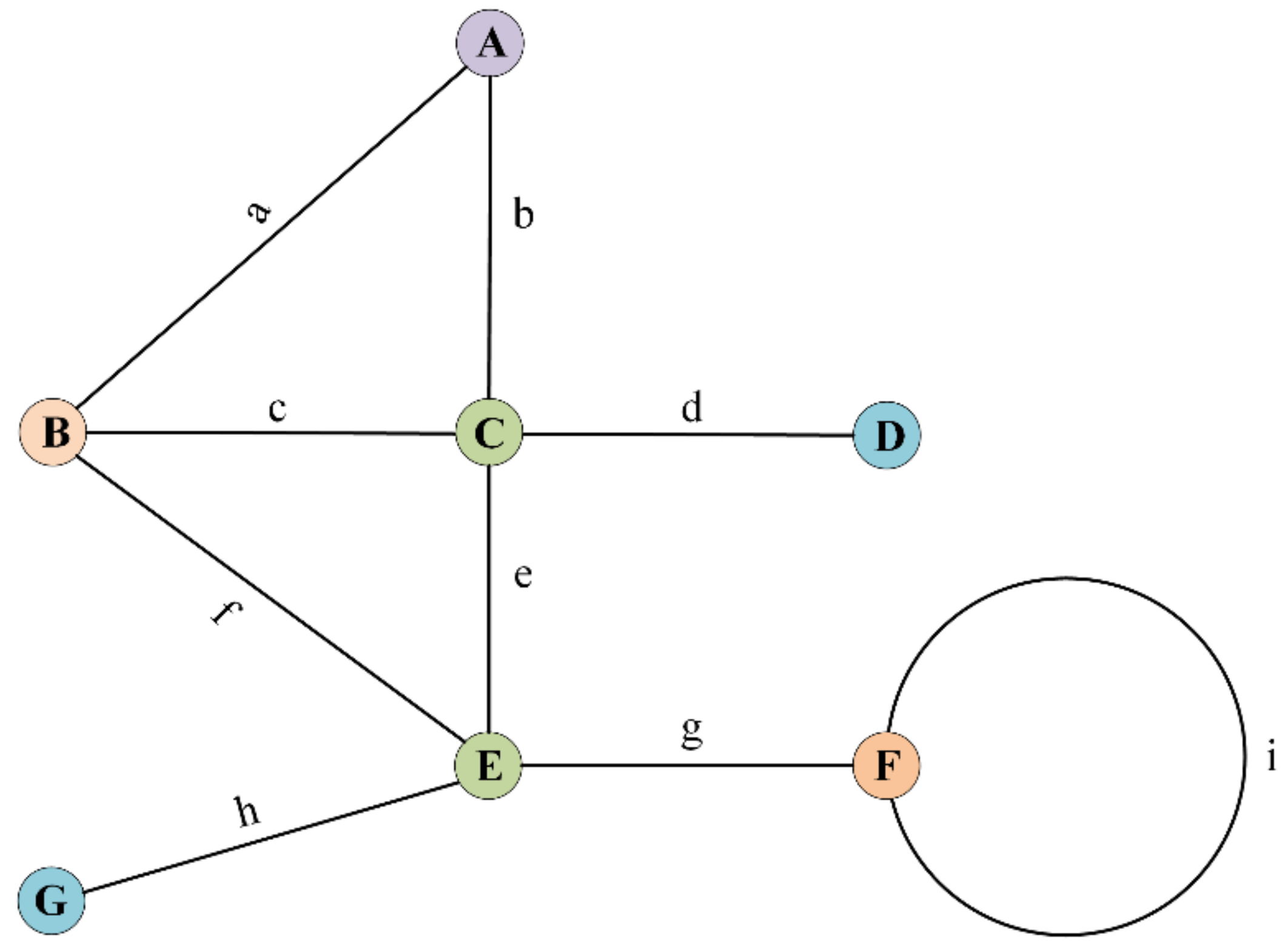
3.2.1. Grain and Connectedness

Through OSMnx, users can analyze complex street networks and calculate the statistical information and spatial measure of networks. The number of nodes, intersection count, number of edges, number of street segments, average node degree, average streets per node, counts of streets per node, proportions of streets per node, total edge length, average edge length, total street length, average street length, and self-loop proportion of street networks can be obtained. Among these parameters, the number of nodes, number of edges, intersection count, number of street segments, total edge length, and total street length measure the basic statistical information about the scale of an urban street network in general. Other metrics reflect the levels of “grain” and “connectedness” of a city street network.

Grain refers to the size of the basic unit of study area. The grid is the basic unit in a street network. The average length of the edges of a street network or the average street length reflects the grain of a street network. In our study, the average length of streets in an undirected graph was selected as the metric for measuring grain.

Connectedness indicates the degree of interconnection between basic units. In street networks, nodes are connected by streets, and streets intersect with streets to form new nodes (i.e., intersections). Figure 1 shows the basic network metrics. In this case, A, B, C, D, E, F, and G are nodes, where A, B, C, E, and F are intersection nodes, while D and G are dead ends. Moreover, a, b, c, d, e, f, g, h, and i are edges, and i is a self-looping edge. Given that two edges pass through it, node A is a two-way intersection. Similarly, nodes B and F are three-way intersections, and nodes C and E are four-way intersections. The proportion of node types (e.g., dead ends, three-way intersections, or four-way intersections) indicates the proportion of nodes in a street network with branches 1, 2, 3, 4, …, and n. The self-loop proportion refers to the proportion of edges with a single incident node. The metric “average streets per node” indicates the average number of edges passing through a node. It is frequently used to measure connectedness. In our study, the “average streets per node” in an undirected graph was selected as the metric for measuring the connectedness of a street network.

3.2.2. Circuity

Circuity refers to the degree of tortuous path. It is commonly used to measure the additional cost of travel to urban residents due to distance factors. In our study, 50,000 pairs of nodes with starting and ending points were simulated as random routes for each city and network type.

The circuity of each route was calculated by using Equation (2).

$$C=\frac{D_{net}}{D_{gc}},$$

(2)

where $C$ represents circuity, $D_{net}$ represents the distance of the shortest path between the starting and ending points of a route, and $D_{gc}$ represents the great circle distance between these nodes. Therefore, $C$ is the ratio of the network distance of the shortest path from the start to the end of each route to the great circle distance. Average circuity was selected as a metric for measuring the tortuous degree of a street network in our study.

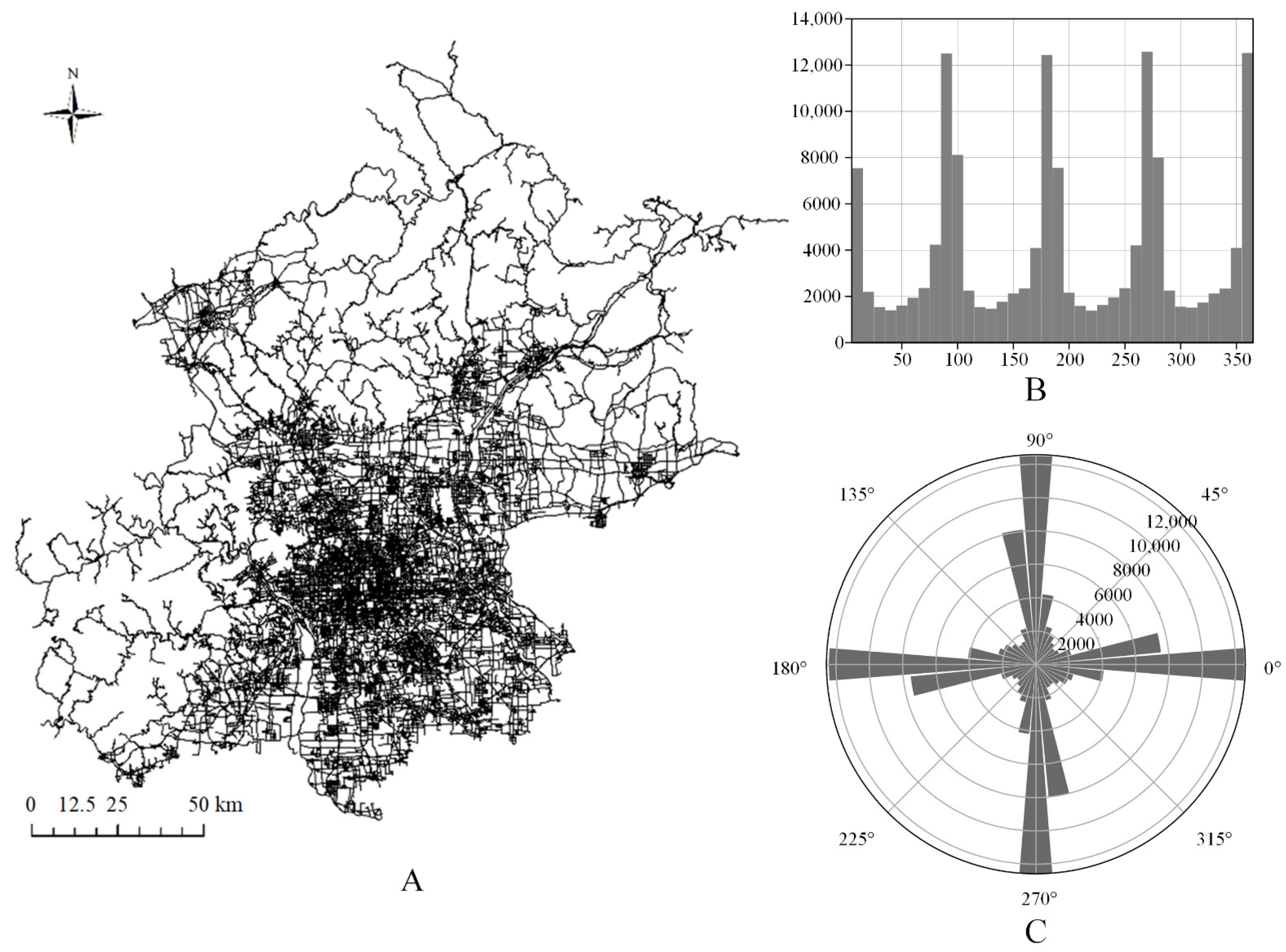
3.2.3. Street Network Orientation Entropy

Information entropy has been used in street network research: the orientation property of a street is considered the target, and street network orientation entropy is used to measure the nature of spatial order/disorder in the orientations of street networks [29].

The simplified street network orientation entropy (without considering length weighting) was calculated by using Equation (3).

$$H_o=-\sum _{i=1}^{n}P\left(o_i\right)\ln P\left(o_i\right),$$

(3)

where $n$ represents the number of bins, and each bin represents a certain range around the orientation of a street. $i$ represents the index value of a bin, $o_i$ represents the frequency of a street falling into the $i$th bin, and $P\left(o_i\right)$ represents the proportion (probability) of a street falling into the $i$th bin. Street network orientation entropy $H$, which is measured in a dimensionless unit called “nats” or the natural unit of an information bit (1 nat ≈ 1.44 bits).

A total of 36 bins with the same size were divided for street frequency statistics, with each bin having a range of 10°. Each bin was shifted by −5° to ensure that the values are distributed in the center of the bin [29]. The orientation angles of each street segment were calculated and counted in the corresponding bin. The histogram and rose illustration were obtained, using OSMnx, on the basis of the frequency of street segments in the bin. The entropy of the street orientations was calculated by using Equation (3). For example, a street network in Beijing (Figure 2A) was used to calculate the street orientation histogram and rose illustration, as shown in Figure 2B,C, respectively. From Equation (3), the highest value of the street network orientation entropy is equal to the logarithm of the number of bins n. At this moment,$P\left(o_1\right)=P\left(o_2\right)=\cdots =P\left(o_n\right)$; that is, the entropy of the street orientations is distributed perfectly in all the bins. If the number of bins is 36, then the highest entropy of the street orientation $H_{max}$ will be 3.584 nats. When all the street orientations are located in the same bin, the entropy of the street orientation will have the lowest value of 0. The entropy of the street orientation $H_G$ is 1.386 nats when all the streets are distributed in equal proportions in the bins in the east–south–west–north directions of the rose illustration.

4. Results

4.1. Spatial Distribution Characteristics of RDLS

Equation (1) was used to calculate RDLS at the municipal levels, which ranged from 0 to 17.7. The result presented evident regional differences and a clear stair-stepping characteristic in the east–west direction. Such finding is basically consistent with the three steps of China’s terrain (Figure 3).

4.2. Graduation Statistics of RDLS

In our study, the basic network metrics were calculated by using the aforementioned method. The metrics included grain ($L_S$), average circuity ($C$) and connectedness (the average streets per node ($D_S$), proportion of dead ends ($P_{DE}$), proportion of three-way intersections ($P_{3W}$), and proportion of four-way intersections ($P_{4W}$)). The street orientation histogram and rose illustration were generated by calculating the angle of street orientation. The street network orientation entropy ($H_o$) for each municipal street network in the country was calculated by using Equation (3). Finally, ALT and RDLS were obtained by using Equation (1).

Table 1. Calculation results of each index for prefecture-level cities.

	Ho	LS	C	DS	PDE	P3W	P4W	ALT	RDLS
Beijing	3.26	329	1.09	2.97	0.14	0.61	0.23	355	3.4
Tianjin	3.49	371	1.05	3	0.16	0.52	0.31	19	0.25
Shijiazhuang	2.75	328	1.06	2.93	0.17	0.56	0.27	270	2.56
Cangzhou	3.1	320	1.04	2.87	0.16	0.64	0.2	10	0.1
Hengshui	2.98	370	1.04	2.86	0.16	0.67	0.17	22	0.16
Handan	2.86	396	1.04	2.88	0.16	0.65	0.19	239	1.73
Xingtai	2.82	367	1.05	2.93	0.15	0.61	0.23	168	1.47
Baoding	3.02	543	1.07	2.92	0.15	0.61	0.23	341	2.59
Chengde	3.57	1027	1.15	2.5	0.28	0.64	0.07	936	4.72
Tangshan	3.31	636	1.06	2.8	0.21	0.56	0.22	57	0.46
Qinhuangdao	3.47	627	1.1	2.85	0.18	0.6	0.21	214	2.03
Langfang	3.12	459	1.04	2.9	0.19	0.54	0.27	11	0.41
Shenyang	3.52	576	1.06	3.1	0.11	0.58	0.29	56	0.54
…	…	…	…	…	…	…	…	…	…

provides the partial results of each metric for prefecture-level cities in China. The details of the results for all the cities can be found in the Appendix A.

China, in topography, forms a three-step “staircase” according to altitude. As shown in Figure 4, the dotted lines are the dividing lines of the three steps on the surface. All cities are divided into three categories based on the dotted lines. The street network of cities with a high street density is frequently located in the city’s administrative center [37]. Therefore, some cities that cross the dotted line are classified according to the location of their administrative center. The classification results are presented in Figure 4, with 20 cities in the first step, 127 cities in the second step, and 244 cities in the third step.

Table 2. Graduation statistics results based on RDLS.

Evaluation Factor	Measure	Statistical Content	First Step	Second Step	Third Step
topography	average altitude (m)	mean	3925.050	1252.709	227.319
		maximum	5038.000	3125.000	1389.000
		minimum	2747.000	180.000	9.000
		variance	518,533.418	364,182.764	53,705.552
	RDLS	mean	12.091	5.125	1.890
		maximum	21.270	14.560	8.390
		minimum	7.720	0.370	0.020
		variance	14.238	8.219	2.625
orientation entropy	street network orientation entropy (nat)	mean	3.540	3.454	3.432
		maximum	3.580	3.580	3.580
		minimum	3.420	2.480	2.750
		variance	0.002	0.034	0.034
grain	average street length (m)	mean	2194.400	935.425	673.882
		maximum	6882.000	2057.000	1839.000
		minimum	552.000	307.000	93.000
		variance	2,110,879.200	121,476.246	99,816.433
average circuity	average circuity	mean	1.265	1.187	1.108
		maximum	1.480	1.650	1.380
		minimum	1.110	1.000	1.030
		variance	0.012	0.016	0.004
connectedness	average streets per node	mean	2.503	2.738	2.854
		maximum	2.740	3.170	3.260
		minimum	2.120	2.250	2.360
		variance	0.022	0.027	0.026

shows the mean, maximum, minimum, and variance of street complexity-related metrics that correspond to the three steps. The mean and variance of topography, orientation entropy, grain, average circuity, and connectedness metrics were standardized by using the Z-score method. The performance of each metric in different steps was compared, as shown in Figure 5.

As shown in Figure 5, on average, the city street network in the first step exhibits the greatest RDLS, street orientation entropy, grain, and average circuity, but the lowest node connectivity. The city street network in the third step presents the smallest RDLS, street orientation entropy, grain, and path average circuity, but the highest node connectivity. For all the metrics, street network complexity exhibits the following order: first step > second step > third step. A clear correlation is also observed between street network complexity and RDLS. When evaluated in terms of grain, connectedness, circuity, and orientation entropy, the more topographic relief in a region, the higher its street network complexity.

With regard to variance, the average elevation, RDLS, and average street length of the city street network in the first step exhibit the largest dispersion, followed by that in the second step and then that in the third step. Street network orientation entropy presents the opposite degree of dispersion in the three major orders of cities, with the first step being the smallest, followed by the second step, and the third step being the largest. The urban street network in the second step has the largest dispersion in terms of circuity and average streets per node. The dispersion degree of circuity in the second step achieves the highest value, followed by that in the first step and then that in the third step. The dispersion degree of average streets per node in the three steps is ordered as follows: second step > third step > first step.

4.3. Correlation Analysis of RDLS and Street Network Complexity

Correlation analysis is a statistical analysis method for investigating the degree of correlation between two random variables in equal positions. The closeness of the relationship between two random variables (i.e., correlation) is frequently expressed by the correlation factor r. In our study, the Pearson correlation coefficient was selected for correlating RDLS with street network complexity. This coefficient is calculated by using Equation (4) [38].

$$r=\frac{{\sum }_{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{{\sum }_{i=1}^n{\left(X_i-\overline{X}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}},$$

(4)

where $X_i$ and $Y_i$ ($i$ = 1, 2, 3, …, n) represent the sample values of the random variables $X$and $Y$, respectively; and $\overline{X}$ and $\overline{Y}$ represent the sample means of the random variables $X$and $Y$, respectively.

The correlation factor has values between −1 and 1. A correlation factor of 1 indicates that the two random variables are completely linearly and positively correlated. A correlation factor of −1 indicates that the two variables are completely negatively correlated. A correlation factor of 0 indicates that the two variables are completely uncorrelated. The closer the correlation factor is to 1 (or −1), the stronger the correlation between two random variables (positive or negative correlation). Conversely, the closer the correlation factor is to 0, the weaker the correlation between two random variables.

The total proportion of intersections with two-ways and more ways that four-ways was less than 1%, and, thus, was not considered in this study. Only the proportions of dead ends, three-way intersections, and four-way intersections were selected for analysis and research. The correlation factor between street network complexity-related metrics and RDLS was calculated separately, using Equation (4). To verify the authenticity of the linear relationship between variables, we also conducted hypothesis testing on the correlation factor by using SPSS software, as shown in

Table 3. Calculation results of the correlation coefficient and hypothesis testing.

		Ho	LS	C	DS	PDE	P3W	P4W	RDLS
Ho	correlation factor	1
	sig
LS	correlation factor	0.233	1
	sig	0.000
C	correlation factor	0.490	0.461	1
	sig	0.000	0.000
DS	correlation factor	−0.481	−0.504	−0.673	1
	sig	0.000	0.000	0.000
PDE	correlation factor	0.363	0.491	0.504	−0.810	1
	sig	0.000	0.000	0.000	0.000
P3W	correlation factor	0.295	0.053	0.220	−0.156	0.187	1
	sig	0.000	0.297	0.000	0.002	0.000
P4W	correlation factor	−0.527	−0.420	−0.660	0.865	−0.622	−0.424	1
	sig	0.000	0.000	0.000	0.000	0.000	0.000
RDLS	correlation factor	0.331	0.493	0.612	−0.549	0.444	−0.012	−0.499	1
	sig	0.000	0.000	0.000	0.000	0.000	0.820	0.000

Note: Units with gray background indicate insignificant results.

.

As shown in Table 3, $H_o$ means street network orientation entropy (nat), $L_S$ means average street length (m), $C$ means average circuity, $D_S$ means average streets per node, $P_{DE}$ means proportion of dead ends, $P_{3W}$ means proportion of three-way intersections, $P_{4W}$ means proportion of four-way intersections, and RDLS means relief degree of land surface.

From the results of the hypothesis testing, we see that a majority of the variables are linearly correlated with one another and significantly correlated at the 0.01 level. Only $L_S$ and RDLS are not significantly correlated with $P_{3W}$. As indicated in Table 3, the following conclusions can be drawn for RDLS.

(1)

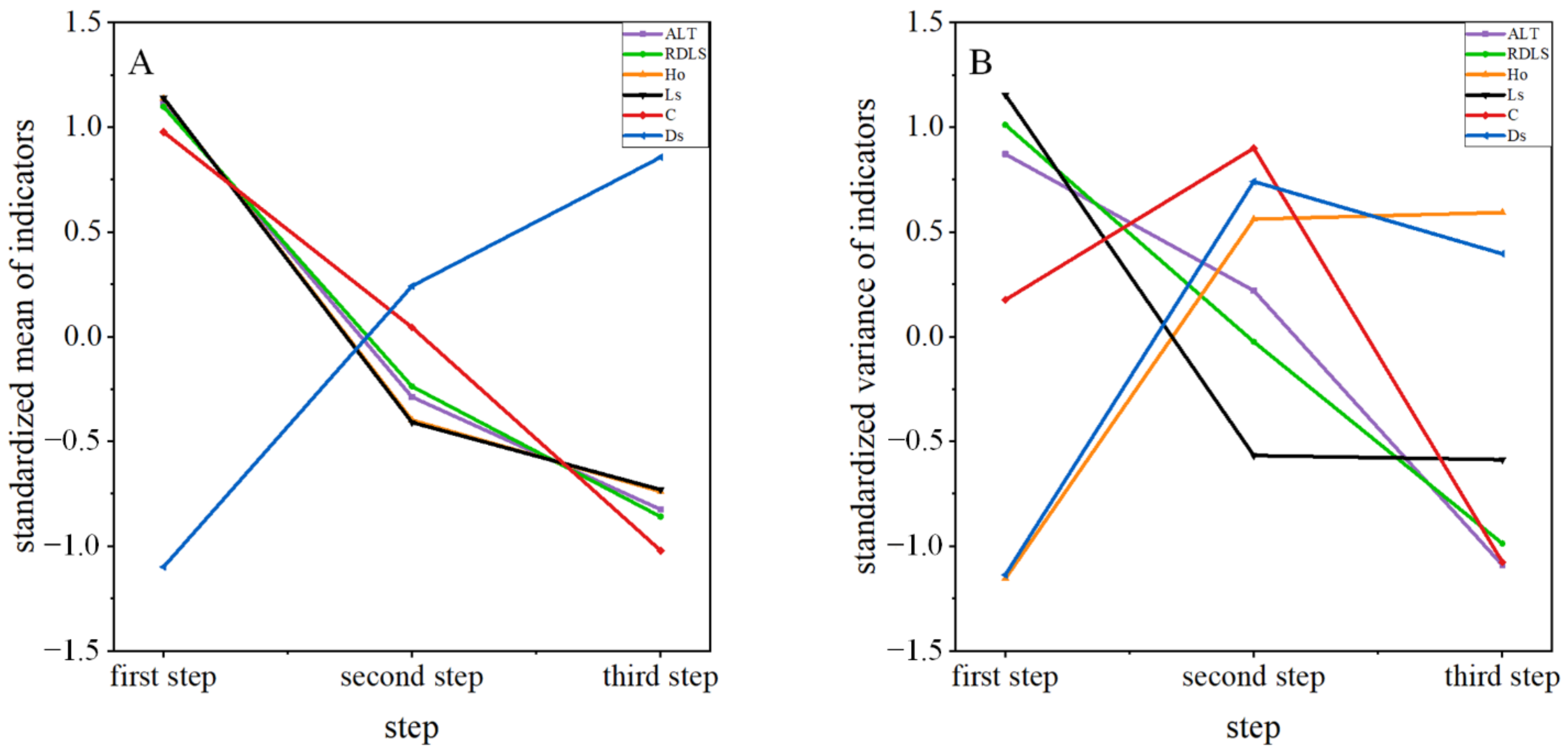
RDLS exhibits the strongest correlation with street network circuity, with a correlation coefficient of 0.612. This result illustrates that, when RDLS is greater, the urban street network is more circuitous, and the additional travel costs for urban citizens are higher.

(2)

The correlation between RDLS and average street length is 0.493, indicating that, the flatter the topography, the shorter the average street network length. The average street length is largely determined by the proportions of dead ends, three-way intersections, and four-way intersections. The correlation between RDLS and dead-end proportion is 0.444, demonstrating that more dead-end nodes exist in places with greater topographic relief. This finding is probably caused by topographic relief affecting the extension and construction of roads and leading to dead-end nodes. Three-way intersection proportion exhibits an insignificant correlation with RDLS. By contrast, four-way-intersection proportion demonstrates a larger and negative correlation with RDLS (−0.499). Increasing one branch from three-way intersection to four-way intersection enhances the effect of topography; that is, regions with large RDLS are unsuitable for the construction of four-way intersections.

(3)

The correlation between RDLS and street network orientation entropy is 0.331, exhibiting a certain correlation. That is, when RDLS is greater, the street network is more predisposed to being distributed in different directions.

5. Discussion

A quantitative approach was used in this study to capture the pattern of street networks for a whole country. Specifically, the relationship between street network and topographic relief was analyzed quantitatively. The street network is considered to be the skeleton of the country and can reflect the physical structure [39]. We used OSMnx to extract street data of different cities from OpenStreetMap. In fact, the accuracy of OpenStreetMap data is different in different cities. Larger cities usually have higher accuracy than smaller, lesser-known cities. We recommend that the accuracy of the street network data be consistent for each city in future studies.

In addition, RDLS is an important element in the description of landforms at the macroscopic scale [36]. We used a DEM with a resolution of 30 m in calculating RDLS. We believe that, the higher the DEM resolution, the more accurate the RDLS calculation results will be. The high-resolution DEM data are expected to improve the research results. Topography was shaped by the movement of the earth’s crust, and, as described in existing studies, complex topography (such as mountains or basins) can impose constraints on the orientation of streets and their associated networks [40,41]. Topography has a strong influence on the evolving direction of the urban street network [42], while fast-growing cities lead to problems, such as efficacy of land use [43] and sustainable development [44]. Analyzing the relationship between the street network and RDLS specifically may facilitate a better understanding of the layout and development of street network patterns and their associated urban forms in China. On this basis, urban designers can plan the street layout according to the local topographic features in the fast-growing cities, not only in China, but also South America and Asia.

Previous studies on urban street networks are mostly limited to small-scale areas because of the lack of tools for obtaining standardized data sources (i.e., inconvenience of data acquisition), and thus, they cannot reflect the overall characteristics of street networks at large scales. On the basis of the spatial distribution characteristics of topographic relief at the municipal level in China, we used OSMnx-based metrics of street network complexity (i.e., grain, connectedness, circuity, and street network orientation entropy) to calculate complexity metrics for each prefecture-level city. The type of road (one-way road, two-way road, etc.), the class of street (major street, minor street, etc.), etc., were not covered; thus, they can be added to relevant studies in the future.

6. Conclusions

The contributions of this study can be reflected in three aspects:

(1)

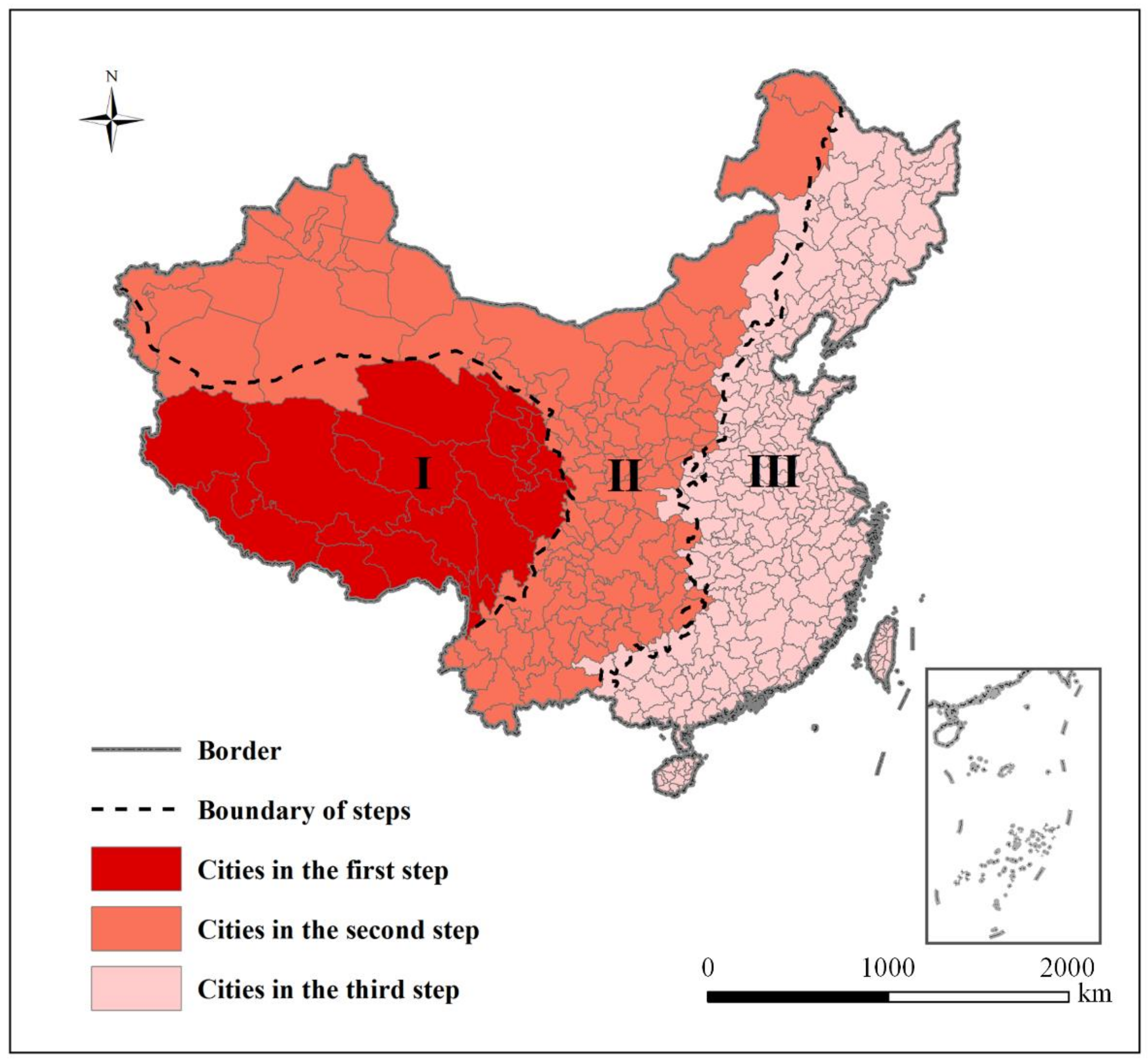
On the basis of the spatial distribution characteristics of topographic relief at the municipal level in China, we determined that the spatial distribution of topographic relief was non-uniform, and the east–west direction exhibited a pattern of “high in the west and low in the east”. This finding is generally consistent with the three steps of China’s terrain. It is also similar to the results obtained by Feng et al. [36,45].

(2)

The dividing lines of the three terrain steps were used as the boundary for classifying the metrics of municipal street networks in China. The street network complexity presented the following order: first step > second step > third step. This result indicated that, the more undulating the topography, the higher the complexity of a street network.

(3)

RDLS was significantly correlated with street network complexity metrics, including street network orientation entropy, average street length, average circuity, average streets per node, dead-end proportion, and four-way intersection proportion. Among these metrics, RDLS was positively correlated with street network orientation entropy, average street length, average circuity, and the dead-end proportion. Meanwhile, it was negatively correlated with average streets per node and the four-way intersection proportion.

This study extended the research on the correlation between topographic relief and street network to a certain extent, while complementing the research methods and results on the complexity of urban street networks in China. A higher-resolution DEM and higher-accuracy street network data will help improve the research results in future studies.