Abstract
Cities are responsible for a large share of the global energy consumption. A third of the total greenhouse gas emissions are related to the buildings sector, making it an important target for reducing urban energy consumption. Detailed data on the building stock, including the thermal characteristics of individual buildings, such as the construction type, construction period, and building geometries, can strongly support decision-making for local authorities to help them spatially localize buildings with high potential for thermal renovations. In this paper, we present a workflow for deep learning-based building stock modeling using aerial images at a city scale for heat demand modeling. The extracted buildings are used for bottom-up modeling of the residential building heat demand based on construction type and construction period. The results for DL-building extraction exhibit F1-accuracies of 87%, and construction types yield an overall accuracy of 96%. The modeled heat demands display a high level of agreement of R2 0.82 compared with reference data. Finally, we analyze various refurbishment scenarios for construction periods and construction types, e.g., revealing that the targeted thermal renovation of multi-family houses constructed between the 1950s and 1970s accounts for about 47% of the total heat demand in a realistic refurbishment scenario.
1. Introduction
With increasing urbanization, cities represent an important component for ensuring a sustainable future for our planet. A high potential for decreasing greenhouse gas emissions is credited to the building sector as buildings consume vast amounts of energy [1,2]. In Germany, buildings account for about 40% of the final energy use, and they contribute to almost a third of the country’s greenhouse gas emissions [3]. The efficiency of building standards has increased significantly over the past decades, making modern constructions very energy-efficient; however, older buildings constructed before the turn of the millennium do not meet current thermal standards [4]. The targeted refurbishment of older buildings can thus help to transform cities into more sustainable environments. For the analysis of cities’ energy use and to quantitatively evaluate the effects of building retrofitting, bottom-up urban building energy modeling (UBEM) has become a proven tool to support energy efficiency for buildings at a city scale [5,6,7]. In addition to simulation tools for modeling building energy [8], the development of a dataset on the existing building stock model (BSM) is an important task for UBEM [7]. BSMs have been successfully deployed for modeling urban building energy at various spatial scales: from local neighborhoods [9,10,11] to a city scale [12,13,14,15] and national scale [16]. Besides the modeling of current energy demands of buildings at a city scale, BSMs are most helpful for retrofit analyses [10,17]. With the increased awareness of the building sector as a major emitter of greenhouse gas, the field of UBEM has experienced increased attention in various scientific fields. For an overview of the past and current methodological developments in UBEM, readers should refer to related meta-studies in this field [2,6,8,18,19,20]. As indicated above, building stock data are crucial for UBEM because they serve as a spatial data base for bottom-up energy modeling, including relevant parameters on each building [5], as follows:
Building geometry: This is a key parameter in UBEM since the total energy demand of a building is strongly dependent on a building’s size in terms of the footprint area and floor area;
Construction type: This impacts the thermal behavior of buildings, e.g., a free-standing (semi-)detached house is more exposed to energy loss due to the higher portion of exterior walls in relation to building volume than terraced houses or multi-family houses [14,15,18,21,22,23];
Use type: Modeling of the energy demand of a building is strongly affected by its use, in terms of whether it is a residential building or a non-residential building. Non-residential buildings are much more heterogeneous in terms of thermal behavior and thus more difficult to model without specific knowledge;
Year of construction: Many thermal regulations have been introduced over the past decades, making newly constructed or refurbished buildings more efficient in their energy behavior than buildings in their original state [24].
Nowadays, the situation on data availability for building stock models in many developed countries has significantly improved over the past years: Until a few decades ago, city-scale BSMs were scarce, but recent advents in (open)geo-spatial data [25] and processing methods have increased the number of cities and countries with access to detailed data for urban planning and management, as well as energy modeling. Nevertheless, access to nation-scale building stock data remains very heterogeneous, even in the EU, where huge efforts are invested in the harmonization of national data. The discrepancy of (geo-)data availability in the EU can be evaluated by European (meta)-data platforms, such as INSPIRE (https://inspire-geoportal.ec.europa.eu/index.html) or the European Data Portal (https://www.europeandataportal.eu), revealing that few countries provide detailed BSMs at a national scale, without restrictions to public access (e.g., Belgium and The Netherlands). In some countries, the data exist, but their use is restricted to payment licenses (e.g., Germany and Austria), while no building stock data are available for other countries (e.g., Croatia and Greece). Whilst these data platforms cannot be exhaustive in terms of the existence of national data sets on building stock, they do show that there is much space for improvement in terms of data access.
In addition to official data, crowd-generated data from initiatives such as the OpenStreetMap Project (https://www.openstreetmap.org) (OSM) are constantly increasing in spatial coverage and data quality. While OSM provides a broad availability of data for building footprints in larger cities, only a few buildings include data on the building height or floor area. For Germany, for less than 5% of the buildings, the floor area is available in OSM. Furthermore, current advents in automated image analysis from remotely sensed imagery can significantly facilitate and speed-up the task of building detection: The latest advancements in big data analysis through deep learning techniques [26] have led to a paradigm shift in terms of accuracy for image analysis [27], semantic segmentation in dense urban settings [28], and city-scale building extraction [29,30]. The methods deploying convolutional neural networks (CNNs) for the semantic segmentation of individual buildings in very high resolution (VHR) imagery [29,31,32] have proven their superior performance compared to traditional image classification methods. Moreover, Microsoft® has generated almost 125 million building footprints from aerial images for the entire U.S. [33], applying deep neural networks, ResNet34, and RefineNet [34] with high accuracies of 0.85 intersection over union (IoU). In combination with height data from LiDAR or digital surface models (DSMs), CNNs have been successfully deployed for the generation of building stock models [35,36]. Therefore, compared to traditional, laborious land surveying or manually digitized building footprints, a significant increase in speed can be achieved for building stock modeling at a large scale. This makes the application of deep neural networks a promising tool for remote sensing-based building data generation in data-scarce regions.
Considering these latest developments in deep learning-based image analysis, in this paper, we will explore the capabilities of applying current deep neural networks on remote sensing data for the generation of a building stock model and analyze its applicability for urban building energy modeling at a city scale. Specifically, we apply a U-net Inceptionresnet on high resolution aerial imagery and DSM to generate a 3D building model incorporating the building geometry (footprint area and floor area) at a city scale. In a next step, we perform semantic labeling of the building construction type (semi-detached/detached houses, terraced houses, and multi-family houses) based on morphometric parameters such as the area, shape, compactness, and height etc. using a shallow machine learning approach [37,38,39,40,41]. For use type and building age, we integrate ancillary geo-data at the urban block and census data. In a final step, we perform bottom-up building energy demand modeling for each building at a city scale based on characteristic energy demand data for German buildings [42,43]. The validity of the proposed approach using remotely sensed data is evaluated with officially modeled values from the Energy Atlas (https://www.energieatlas.nrw.de).
The entire workflow is described by the city of Münster, in the Federal State of North-Rhine Westphalia (NRW) in Germany, as a case study, in order to evaluate the usability and accuracy of the proposed workflow. We selected Münster because we found an excellent open data base for NRW including aerial image data and reference data for performance evaluation in terms of a detailed LoD1 building model and modeled energy data from the Energy Atlas. The workflow, however, is designed to be applicable to other cities and geographical regions. In this way, we want to add to the existing literature by applying current deep learning methods for building stock modeling at a city scale for bottom-up modeling of the building energy demand using freely available geo-data.
The manuscript is organized as follows. Section 2 presents the used data sets and the methods employed for building stock modeling from aerial images and the modeling approach for the heat demand; the results and discussions are presented in Section 3 and Section 4, respectively; and Section 5 concludes the paper.
2. Data and Methods
The proposed workflow consists of three parts: (1) Building stock modeling from aerial images and DSM using deep neural networks (Section 2.2.1); (2) calculation of the building parameters for energy modeling (Section 2.2.2, Section 2.2.3 and Section 2.2.4); and (3) bottom-up modeling of buildings’ energy demand (Section 2.3). The overall workflow, including its three parts, is visualized in Figure 1. The study site Münster is located in the Federal State of North Rhine-Westphalia in northwestern Germany. With almost 320,000 inhabitants, the city has experienced radial urban growth over the past decades. It has a monocentric urban spatial structure with a historic city center, which is radially surrounded by urban extensions from successive construction periods. Therefore, the city morphology contains related characteristic building types, e.g., block development in the center, as well as free-standing (semi-)detached houses in the suburbs or large-area developments of industrial sites at the city fringe. In total, the study area covers 51 km2, incorporating about 14,800 residential buildings.
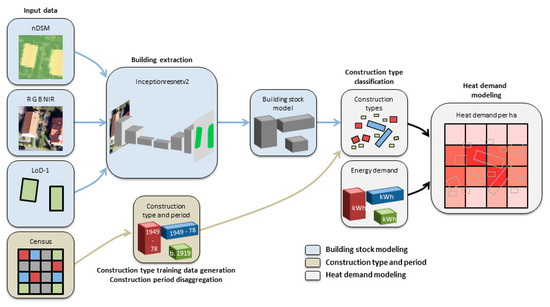
Figure 1.
Overview of the workflow of methods and data employed for building stock modeling using deep learning and orthophotos, and heat demand modeling at a city scale.
2.1. Data
For the generation of the building stock model, we deployed digital orthophotos at a 10 cm resolution and a normalized digital surface model (nDSM) at a 1 m ground sampling distance. For training and validation purposes, we relied on publicly available geodata from the open geodata portal of NRW (https://www.opengeodata.nrw.de) (Table 1). The differentiation of use type is based on urban land-use data at the level of urban blocks. For an assessment of the geometric accuracy of the generated BSM, we deployed an official LoD1 building model which was available at a national scale in standard BSM format City Geographical Markup Language (CityGML). The yearly updated dataset incorporates data on the building geometry, such as the area and height.

Table 1.
Data sets used in this study.
For data on buildings, we incorporated data from the German Census data base where, among socio-demographic parameters, data on the building age and construction type are also stored at the neighborhood level in 100 × 100 m grid cells (Figure 2). Finally, we used data from the Energy Atlas of NRW as a source for validation of the energy modeling.
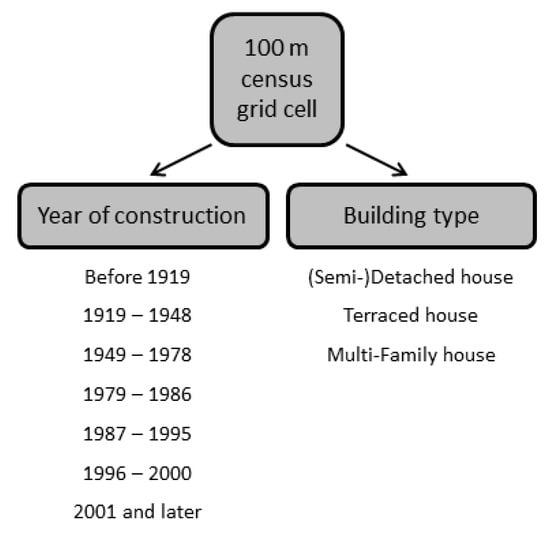
Figure 2.
Overview of detailed buildings’ data in the German Census 2011 at the 100 m grid level.
2.2. Building Stock Modeling
2.2.1. Building Extraction from Aerial Images Using Deep Learning
Semantic segmentation is the process of representing each pixel of an image with its semantic class, e.g., buildings, vegetation, etc. In recent years, the use of convolutional neural networks (CNNs) has introduced a paradigm shift for scene classification tasks. First introduced by [44], fully convolutional networks (FCNs) replace the fully connected layers of a traditional CNN with dilated convolutions for semantic segmentation. In [45], the fully convolutional approach was extended using a contracting path to capture the context and a symmetric expanding path was added for upsampling the information back to the original input image. This mirrored encoder-decoder approach allows for a fine-grained upsampling procedure and enables more recent CNNs to be applied for the task of semantic segmentation. While early networks relied on a vgg16 encoder [46], nowadays, more advanced models have been proposed. In GoogLeNet [47], also referred to as the first version of the Inception family, the CNN allows for the depth and width of the network to be increased by heavily using 1 × 1-convolutions as a way of reducing the dimensionality within the network to remove computational bottlenecks. The network makes use of Inception modules, in terms of a network-in-networks approach [48]. It combines 1 × 1, 3 × 3, and 5 × 5 filter sizes which are stacked on top of each other. This concept is further expanded in multiple versions of the Inception CNN. Through further improvements, Inception v4 [49], also referred to as Inceptionresnet, which is trained with residual connections, was introduced. This process was adapted by the ResNet architecture [50] and significantly accelerated the training of the Inceptionresnet network. The Inceptionresnet networks could also out-perform similarly expensive Inception networks without residual connections.
In this study, we propose a U-net Inceptionresnetv2 approach for building extraction. The architecture is depicted in Figure 3. The U-net architecture uses an encoder-decoder approach. During the encoder phase, the network learns feature representations, while the decoder upsamples a large number of feature channels to propagate information to higher resolution layers. Inceptionresnetv2 serves as the backbone of the U-net and is mirrored during the decoder phase. The input data consist of image patches with the dimensions 224 × 224 × 5. During the stem of the CNN, multiple convolutions and pooling operations transform a tensor of the size 28 × 28 × 320. In the second block of U-net-Inceptionresnetv2, five Inception modules of type A are repeated. The Reduction A module forms a tensor of the size 14 × 14 × 1088. The Inception module B is repeated ten times to learn more mid-level features, while in the Reduction module B, it produces a tensor of the size 7 × 7 × 2080. The Inception module C is repeated five times and the Bottleneck, representing the crossover between the encoder and decoder, of the U-net approach is reached. From there on, the decoder upsamples the learned feature representations back to the original input image, including its height and width. During the decoder phase, each block is concatenated with the upsampled tensor from the previous block. Therefore, the U-net approach contains learned feature representations not only from the upsampling with transposed convolutions, but also from skip connections of the decoder, in order to ensure a fine-grained prediction map.
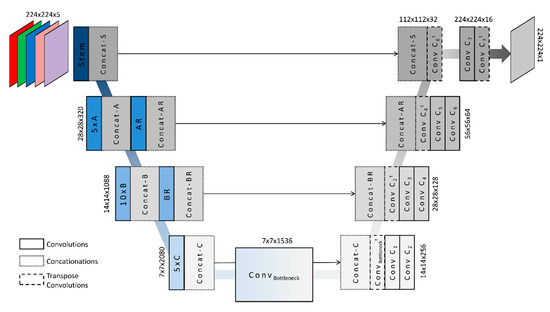
Figure 3.
Schematic representation of U-net Inceptionresnetv2.
Due to the binary setting of the task, U-net Inceptionresnetv2 was trained using binary cross entropy loss and the Adam optimizer (Adaptive Moment Estimation) [51] for loss minimization and featured approximately 62 M trainable parameters. Hyperparameter tuning resulted in the following settings: (a) For increasing the number of features, seven image augmentation algorithms were implemented (e.g., horizontal flip or blurring of image tiles); (b) class weights were set to emphasize the higher importance on buildings (1 for background and 2 for buildings) and furthermore, based on the available GPU and amount of computational time, the batch size was set to 8; and (c) for training, we set 100 epochs, but included early stopping to prevent overfitting and a decaying learning rate on the plateau was used with an initial value of 0.0001, which was dropped by a factor of 0.2 after a set patience of 2. Therefore, the network stopped learning after 10 epochs. For training U-net Inceptionresnetv2, the Orthophoto mosaic of the entire study area of the city of Münster was split into 93,417 image patches with dimensions of 224 × 224 × 5 and the Red, Green, Blue, Infrared, and nDSM height channels. Furthermore, for validation and testing, 10,000 image patches were used in spatially disjunctive regions to ensure a robust learning approach. Image patches were split with a 50% overlap in the x and y direction, resulting in four overlapping predictions for each pixel. The final output was generated using a majority operator for achieving a higher robustness. The accuracy of the derived building footprints was assessed by the intersection over union (IoU). This is defined as the size of the intersection between the ground truth and the classified map, divided by the size of the union of the sample sets. In the last step, the mean height value of all pixels from the nDSM which fall inside a building was calculated for each extracted building footprint, resulting in a city-wide LoD-1 building stock model. Small artifacts were removed by a size-based threshold and building footprints were post-processed using mathematical operators, such as closing and opening [52]. Finally, the use type was extracted based on the Federal Land-Use data at the urban block level (Table 1).
2.2.2. Building Geometry
A key parameter for modeling the energy demand is the building size. It was used in the energy model as the total floor area, which is the value of the multiplication of the footprint area by the number of floors. The number of floors was derived from the building height (Section 2.2.1) using generalized, standard floor heights from related studies for Germany [53,54]. The number of floors was then used to calculate the total floor area FA:
where is the footprint area and is the number of floors.
2.2.3. Semantic Labeling of the Construction Type
The 3D buildings generated from the preceding building extraction step were classified as one of three main construction types related to the energy demand: (a) (Semi-)detached houses (S-DH); (b) terraced houses (TH); and c) multi-family houses (MFH) (Figure 4). Classification was performed by a supervised Random Forest (RF) approach based on morphometric building features and census data [55]. Random Forest is a widely applied ensemble classifier with only very little user input and parameter tuning, which makes it very simple and straightforward to apply, and it generally yields very good accuracies [56]. For each building, 24 morphometric parameters, including simple parameters such as the area and perimeter or more complex features, were calculated. A detailed description of the morphometric features and the workflow is presented in Table 2 and in [38,57], and in [58], respectively.
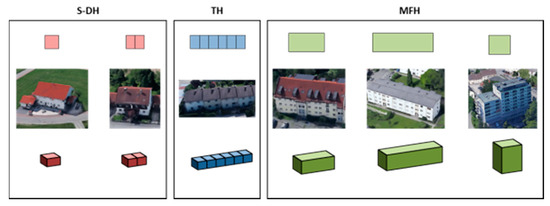
Figure 4.
Representation of building construction types in a 2D ground plan, 3D building model, and aerial images of (semi-)detached houses, terraced houses, and multi-family houses.

Table 2.
Morphometric parameters used for building type classification.
For the training and validation of the Random Forest classifier, building type information from the census was used: In a first step, homogenous census grid cells with only one building type were sought and all spatially enclosed buildings of this grid cell were allocated to this building type. The generated training and reference dataset contained 1179 buildings in total: S-DH: 702; TH: 233, and MFH: 244. The RF model was trained on these three classes and the morphometric features with 50% of the reference buildings and 50% of the reference buildings were kept for validation. In the following step, the trained RF model was applied to the entire building stock model for the study site, resulting in every residential building being allocated to one of the three classes. The settings for the Random Forest algorithm were kept at default settings, with 500 trees and the feature subset for each tree.
2.2.4. Disaggregation of the Construction Period
In addition to the building size and construction type, the construction period is considered as another piece of crucial information for building energy modeling. Data on the construction period are reported in the census data base, also at the 100 × 100 m grid level (Figure 2). In contrast to the building type, the construction period at the aggregated grid level cannot be directly associated with the individual buildings with a high level of confidence [59]. Therefore, disaggregation of the construction period was performed based on a majority vote, where each building within a grid cell was assigned with the most reported construction year for each census grid cell. In the rare cases of parity, the most recent construction year was assigned. With 52%, the majority of all 2227 grid cells in the study area reported only one construction period. Only 32% reported two classes, and for half of those grid cells, one construction year class strongly outweighed the other (15%). In 298 grid cells (13%), three construction years were reported, with one predominant class in 188 cells (8%). In only 76 (3%) of the grid cells, more than three building age classes were reported.
2.3. Building Heat Demand Modeling
Building heat demand modeling is based on the parameters building geometry (Section 2.2.1 and Section 2.2.2), use type (Section 2.2.1), construction type (Section 2.2.3), and construction period (Section 2.2.4). The method is an established workflow in UBEM which relates these individual building parameters to characteristic energy demand tables in Germany from the German Institute for Housing and Environment (IWU) [60,61]. These studies assume a characteristic building energy demand for each of the construction types ((semi-)detached houses (S-DH), terraced houses (TH), and multi-family houses (MFH)), for each construction period, and for three refurbishment scenarios: (1) Existing state; (2) usual refurbishment; and (3) advanced refurbishment (Table 3). The modeling of the building energy demand is based on the total heat demand. The specific energy demands, as reported in the IWU tables with regard to the construction period, generally largely correspond to the construction periods in the German Census. Furthermore, the characteristic energy demand is reported in the tables for various refurbishment scenarios: Existing state without any thermal renovations; usual refurbishment with partial thermal renovations of, e.g., windows; and advanced refurbishment, involving a complete thermal renovation including roof and walls. The total heat demand in kWh/a per building was modeled based on the characteristic heat demand , the floor area , and a constant (https://enev-online.org/enev_2009_volltext/enev_2009_anlage_01_anforderungen_an_wohngebaeude.pdf) for the number of floors . The heat demand is a function of construction type and construction period (see Table 3).

Table 3.
Energy demand reported as the heat demand in kWh/(m2 a) for building types, years of construction, and refurbishment scenarios (modified from [60], p. 113–115).
3. Results
In this section, results for building stock modeling (Section 3.1) and energy demand modeling (Section 3.2) are presented. Furthermore, we perform a detailed assessment of the geometric and semantic accuracies for the building model, as well as for the modeled energy demand.
3.1. Building Stock Modeling
3.1.1. Building Extraction from Aerial Images Using U-net Inecptionresnetv2
After the trained U-net Inceptionresnetv2 was applied on all 93,417 patches of the aerial image, each of the patches with the dimensions of 224 × 224 pixels was segmented into a binary classification: Buildings were labeled with ‘value 1’ and background was labeled with ‘value 0’. Examples of visual representations of extracted building footprints, reference building footprints, and aerial images are depicted in Figure 5 for various building morphologies.
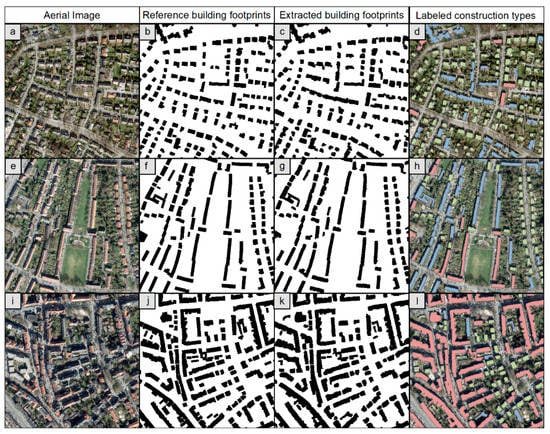
Figure 5.
Results of the building extraction using U-net Inceptionresnetv2 for various building morphologies in the city of Münster. Aerial images as input data are depicted in (a,e,i), reference building footprints from the official LoD-1 building model are shown in (b,f,j), results of building footprint extraction are presented in (c,g,k), and the result of labeled construction types is displayed in (d,h,l).
A visual comparison of the extracted building footprints and the reference building footprints revealed that, on a general level, we can observe a good agreement between the extracted building geometries and the reference data for all construction types. This observation is supported by a detailed accuracy assessment of the output, where we compared the performance of the building extraction method and the reference building footprints using standard machine learning measures of agreement, such as the precision, recall, F1-score, and intersection over union (IoU). All values report a very good performance for the building extraction: Precision of 0.88 and recall of 0.87, with F1-score of 0.87 and IoU of 0.77. In general, we found a high reliability and low errors of commission, meaning that almost 90% of the areas of the reference buildings from the official LoD-1 building model were detected (precision) and only very few buildings were generated which were not represented in the reference data (false positives).
Additionally, a detailed assessment of false positives and false negatives at the pixel level revealed that some of the reported errors in the accuracy assessment are not related to the performance of the applied U-net Inceptionresnetv2 for building extraction, but to geometric imprecision between the reference LoD-1 building footprints and the digital orthophoto (Figure 6). Since the orthophotos are not referenced to a perfect nadir, buildings are not only represented by their roofs (footprints), but also some parts of the façades that are visible, whereas reference buildings are only represented by their footprints. Therefore, for each building, a few pixels are detected as false positives and a few pixels are detected as false negatives, thus impacting the agreement between extracted buildings and reference buildings. Furthermore, small secondary buildings, e.g., in backyards or garages, are prone to false negatives because of their small areas and low heights. Figure 6 shows an example of an extracted building which is not part of the reference data but is present in the aerial image. In general, however, only very few false positives and false negatives are related to temporal inconsistencies between the data sets (Table 1) because relatively, only a few buildings are newly constructed or demolished in the time span of two years.
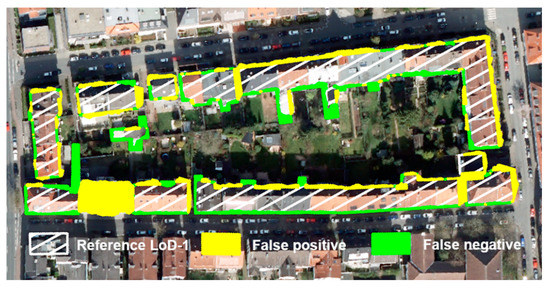
Figure 6.
False positives and false negatives due to varying geometries/inconsistencies between image data and reference data.
Another source of error is also related to the input data: The aerial images were acquired during the leaf-on season, so tree crowns covering the roofs of lower buildings impacted the building detection using U-net Inceptionresnetv2 because pixels with a high reflectance in the infrared spectrum were interpreted as vegetation.
3.1.2. Semantic Labeling of Construction Types
Based on the RF classifier and the 24 morphometric building parameters, each building in the building stock model was allocated to one of the three construction types of S-DH, TH, and MFH (Figure 5d,h,i). Compared to reference data, the accuracies of the RF classifier are reported with very high accuracies of 0.96 for the overall accuracy and a kappa value of 0.93. Per-class accuracies are reported as F1-scores of 0.98 (S-DH), 0.91 (TH), and 0.96 (MFH), indicating a good representation of the morphometric parameters for the construction types. The confusion matrix for the accuracy assessment with validation data is presented in Table 4.

Table 4.
Confusion matrix for the classification of construction types.
These quantitative performance evaluations are also supported by the graphical representation of the value range for all morphometric parameters presented as boxplots in Figure 7. For most of the parameters, the values of the construction type S-DH are significantly distinguishable from those of TH and MFH. The feature value ranges for TH and MFH are more similar; however, the building height serves as a reliable separator of these two classes. A detailed view on the importance of each morphometric parameter (Figure 8) underlines this observation, with height and volume being very relevant for the semantic labeling of construction types.
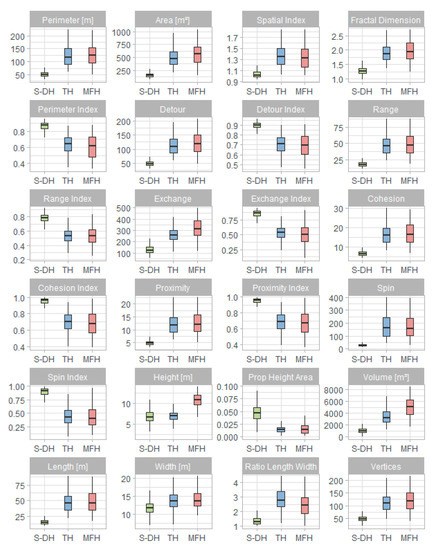
Figure 7.
Value range of the 24 morphometric parameters for the three building types.
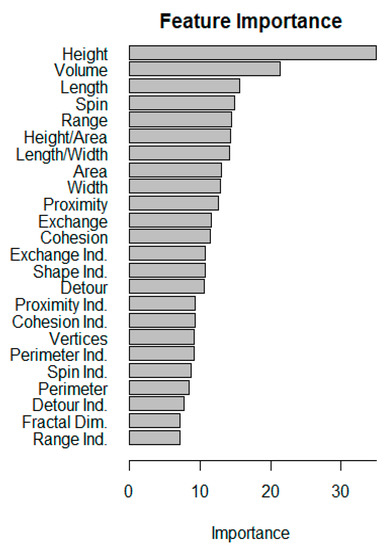
Figure 8.
Feature importance for the semantic labeling of the extracted building stock model as one of the three construction types ((semi-)detached houses (S-DH), terraced houses (TH), and multi-family houses (MFH)).
3.2. Heat Demand Modeling
3.2.1. Grid Level
The heat demand was modeled for each individual building based on tables with characteristic energy demands from Table 3 and Equation (2). The tables include characteristic heat demands for three refurbishment scenarios of existing state, usual refurbishment, and advanced refurbishment. To analyze the potential of targeted energy savings per, e.g., construction type or construction period, we used all three scenarios for retrofit analyses at a city scale. In this way, the heat demand was obtained in kWh/a for each individual building and then aggregated to 100 × 100 m grid cells (Figure 9). The figure depicts in a,b,c the area in and around the city center with large, old buildings in the existing state, without any thermal renovations. Therefore, very high heat demands are reported for this area. These are also comparatively high with usual and advanced refurbishment. The other example in d,e,f focuses on (semi-)detached houses in sub-urban developments with a significantly lower heat demand for all three refurbishment states.
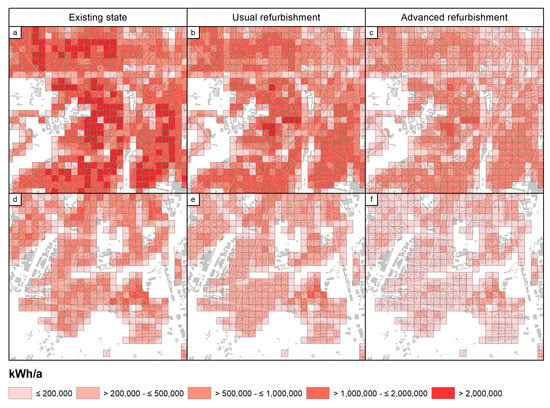
Figure 9.
Total heat demand of residential buildings per 100 × 100 m grid cell for the center of Münster (a–c) and the southern outskirts (d–f) for three refurbishment scenarios: existing state, usual refurbishment, and advanced refurbishment.
3.2.2. City Scale
While the heat demand at the 100 m grid cell level allows for a detailed analysis of areas in the city with a high energy demand, the analysis at a city scale reveals the potential for energy savings with respect to the construction types and refurbishment scenarios. Figure 10 depicts, on the left side, the mean energy demand over all buildings in the study area for each construction type with respect to the three refurbishing scenarios. While (semi-)detached houses show the lowest energy demands on average, due to lower specific energy demands (Table 3) and smaller floor areas, they actually contribute to a larger portion of the total energy demand for the entire study area because they occur more frequently than the other two building types. In terms of absolute savings due to reduced heat demands after advanced refurbishment, however, multi-family houses would contribute to the largest portion.
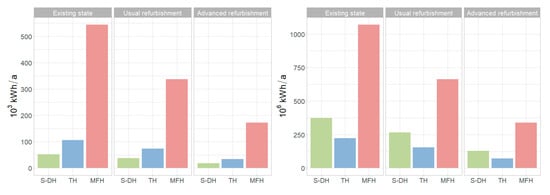
Figure 10.
Mean (left) and total (right) heat demand for all buildings in the study area.
3.2.3. Construction Type and Construction Period
In addition to the characteristic heat demand for each construction type, the construction period represents a crucial input variable for heat demand modeling. The significant variations of the specific heat demand for each construction year allow for a diversified view on the buildings’ energy demand (Figure 11). Relatively, MFH contribute the highest energy demand for the earliest construction year (before 1919); however, this is mostly because the majority of MFH have been constructed as block perimeter development around the historic city center. With a decreasing building age, it is possible to observe a converging heat demand per construction type, especially for construction periods after 1978. This year marks an important date with respect to the building energy demand because The German Thermal Insulation Ordinance—the first regulation subject to public law for energy saving—was enforced at this time [62]. The construction phase between the end of WWI until the end of the 1970’s is characterized by very high energy demands, especially for MFH. While the specific energy demand for this construction phase is not significantly higher than that for the previous construction years, this phase is characterized by a large number of newly constructed houses, resulting in a high cumulative energy demand for this period.
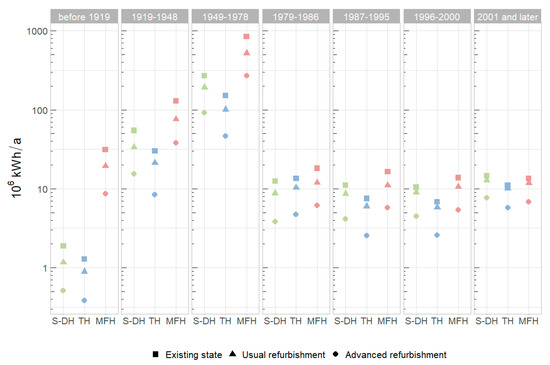
Figure 11.
The total heat demand for all buildings in the study area by construction type and construction period. Heat demand values on the ordinate are represented on a log scale.
At a city scale, we calculated a total heat demand of 1700 × 106 kWh/a for all buildings in the existing state scenario, and a reduction to 1097 × 106 kWh/a for the usual refurbishment and finally to 544 × 106 kWh/a for the advanced refurbishment. The energy savings between the refurbishment scenarios range between −35% from existing state to usual refurbishment and −50% from usual to advanced refurbishment, respectively. When the unrealistic scenario is assumed, where all buildings are still in their existing state and would undergo advanced refurbishment, 68% of the energy could be saved by the thermal renovation of all buildings. In terms of the construction type, the highest potential of total energy savings was found for multi-family houses. Up to 741 × 106 kWh/a could be saved between existing state and advanced refurbishment and 139 × 106 kWh/a for usual refurbishment to advanced refurbishment, respectively.
With regards to the construction period, the savings in energy demand were highest for buildings constructed in the 1950–1970s: A total of 1268 × 106 kWh/a was related to this construction period in the existing state scenario; 814 × 106 kWh/a in the usual refurbishment; and 407 × 106 kWh/a in the advanced refurbishment scenario.
3.2.4. Comparison with Energy Atlas NRW
The assessment of the validity of results for urban building energy modeling is considered a challenging task because real world data on the energy demand are often not accessible due to data privacy. Furthermore, there exist a great variety of different approaches for energy modeling, which means that interpretations of comparisons of two modeled data sets must be considered with caution. As a proof of concept, however, we compared the results of the heat demand modeling with the modeled heat demand for the city of Münster from the Energy Atlas of the Federal State North-Rhine Westphalia (www.energieatlas.nrw.de). The direct comparison of modeled heat demands at the 100 × 100 m grid cell level is depicted in Figure 12. The total derived heat demand from the Energy Atlas is reported to be 1268 × 106 kWh/a and for the deep learning-based building stock model, it is 1080 × 106 kWh/a, which is only about 15% lower. Furthermore, the R2 of 0.82 indicates a good agreement between the two data sets, for both very high and very low heat demands. The small number of grid cells for which our approach reports values close to zero can be mostly related to the modifiable areal unit problem (MAUP) because of the varying input geometries for the building stock model which are intersected by the borders of the 100 × 100 m grid cells. Moreover, they can be related to different spatial domains for the use type: While the Energy Atlas incorporates a differentiation of residential and non-residential buildings at the individual building level, we used land-use at the block level. Other differences in the methodologies relate to the characteristic heat demands used: In our model, we used the latest published heat demand for construction types and construction periods from the year 2011 (https://www.iwu.de/fileadmin/publikationen/gebaeudebestand/episcope/2015_IWU_LogaEtAl_Deutsche-Wohngeb%C3%A4udetypologie.pdf page 113-115). While the Energy Atlas used data from 2003 (https://www.iwu.de/fileadmin/publikationen/gebaeudebestand/2003_IWU_BornEtAl_Energieeinsparung-f%C3%BCr-31-Musterh%C3%A4user-der-Geb%C3%A4udetypologie.pdf page 7). Despite these variations between input data and methods, the good overall agreement between the two data sets is considered a proof of concept for the proposed approach using deep learning-based building stock models from orthophotos.
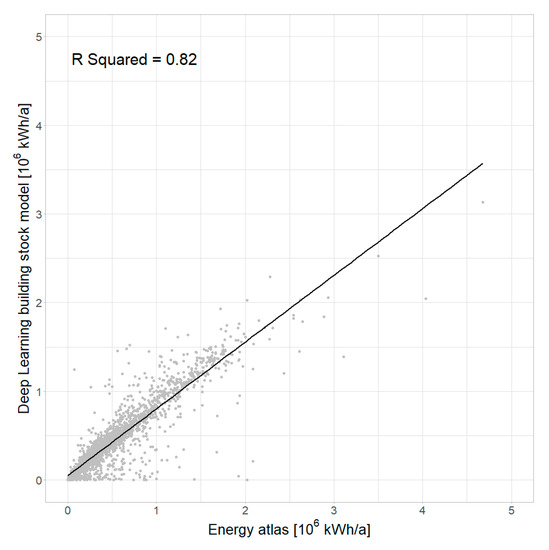
Figure 12.
Comparison of the modeled heat demand from the Energy Atlas (abscissa) and the building stock model using the proposed deep learning approach (ordinate) with the usual refurbishment scenario.
To account for the impact of the data source of the building stock model for heat demand modeling, Figure 13 depicts the modeled heat demand based on the deep learning-based building stock model and the official LoD-1 building model using the same method and characteristic heat demand for all three construction types. The comparison of both building stock data sets reports very small variations of +2.3% for S-DH, +6.6% for TH, and +0.4% for MFH, respectively.
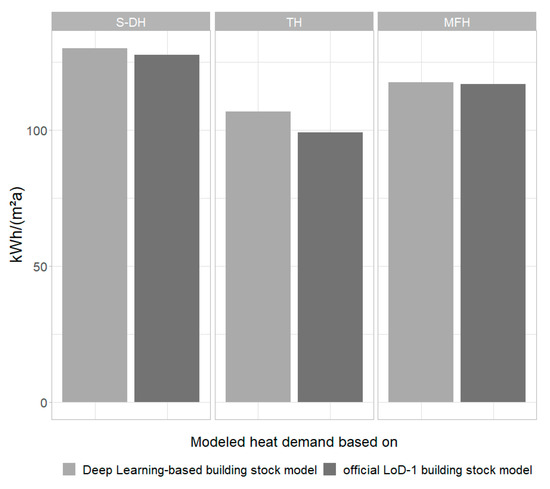
Figure 13.
Comparison of the modeled heat demand using the same method for the building stock model using the proposed deep learning approach and an official building stock model from LoD-1.
4. Discussion
With more than half of the global population living in urban areas, cities are key to sustainable development. Large parts of the final energy use and greenhouse gas emissions are credited to the buildings sector, thus putting the reduction of CO2 emissions and greener cities on the agenda of the UN Sustainable Development Goals. In particular, older buildings are prone to high energy demands for heating because of the low standards for energy efficiency at the time of construction. Therefore, a large potential is seen in building refurbishment, since the majority of the building stock in the EU was constructed before 1970 and thus before thermal regulations [4]. The ecological and economical benefit of thermal renovation is obvious—the targeted refurbishment of buildings with low thermal standards would be amortized within 15 years [3]. City-scale building stock models can help to localize areas with high retrofitting potential through urban building energy modeling. The availability of building stock models has increased over the past years for many regions of the world; however, we are still facing (geo-)data scarcity in many areas, especially in developing countries. While the manual data generation of building stock models at a city scale is an extremely laborious and time-intensive task, remote sensing data offer large-area, cost-efficient, and timely data acquisition. With the latest advent of image analysis techniques through deep learning [26], the task for information extraction from images has significantly increased in speed and accuracy. In this study, we explored the applicability of deep learning-based building stock modeling from aerial images in the context of building heat demand modeling using the example of the city of Münster in North-Rhine Westphalia.
The modeled heat demand was compared with official modeled heat demand data from the Energy Atlas NRW at the scale of a regular spatial grid of 100 × 100 m, demonstrating a very high level of agreement between both data sets, despite some minor methodological differences in the two approaches. These insights can be considered as very promising for the use of aerial images in the context of energy modeling. Nevertheless, we identified some potential for improvements of the proposed workflow. The first aspect relates to the process of building stock modeling, where the geometric resolution of the input data plays a significant role in obtaining high accuracies in building extraction. Especially for regions with a poor coverage of high resolution orthophotos, the recent advent of satellite technology offering geometric image resolutions of 15 cm will facilitate the task of appropriate data acquisition for data-scarce regions. The outcomes of the proposed approach using U-net Inceptionresnetv2 for building extraction demonstrated very high accuracies in comparison with detailed reference data, with an F1-score of 0.87. While the building extraction method generates very good results, some deviations from the reference data can be assigned to off-nadir images. Additionally, the geometric generalization of building footprints, as proposed by [33], can help to increase the quality of the extracted buildings.
While the proposed workflow has been demonstrated for the city of Münster to analyze its general feasibility, it is designed to be generally applicable to other regions with regards to ancillary data. For German regions, all incorporated data for building stock modeling are available at a national scale: High resolution orthophotos and DSM; census data; and land-use data. Used reference data from IWU for heat demand modeling is fully transferable at a national scale and thus directly applicable to other German cities. The possibilities for transferability of the workflow to other countries are directly related to available input data: High resolution remote sensing data in the form of orthophotos or aerial images are widely available for almost all areas of the world. Data on land-use for the identification of residential buildings can be substituted for other European countries with data from the European Urban Atlas (https://land.copernicus.eu/local/urban-atlas). For other countries, land-use data from the OpenStreetMap project have been successfully incorporated to assign land-use to buildings [63]. Another crucial data set for modeling of the energy demand, however, is the construction period of the building. While the German Census provides this information on the grid-level at 100 × 100 m, related studies have modeled this information from historic map data [64] geometric and spatial features [59].
Urban building energy modeling is an interdisciplinary and important field of research. In this study, we applied current deep learning methods for building stock modeling as input data for heat demand modeling with the aim of applying remote sensing data facilitating the generation of crucial data on buildings at a city scale. For future research on urban heat demand modeling, precise data on real energy consumption at the building level would significantly increase the accuracy of related models, e.g., in the form of smart meter data [65]. Such kinds of data could also foster the applicability of current approaches in cross-border analyses, which are currently limited to reference energy demand values [66].
5. Conclusions
Considering climate change and the important role of urban areas for future development, humankind is seeking new opportunities to reduce CO2 and greenhouse gas emissions. New data sources such as very high-resolution remote sensing imagery and cutting-edge technologies such as deep neural networks can help cities and urban planners to reduce their energy consumption and thus contribute to making urban areas ‘greener’. In this current era of big data, we need fast and accurate data analysis methods to transform the ever-increasing data into relevant information to support urban planning and management. We can also observe that huge gaps still exist between data requirements of local or national decision-makers and the information needed to implement sustainable development targets. The study presented in this paper can contribute to narrowing this gap using Earth observation data for generating detailed input data for urban building energy modeling.
Author Contributions
Conceptualization, Michael Wurm, Ariane Droin, Thomas Stark, Hannes Taubenböck, Wolfgang Sulzer, and Christian Geiß; methodology, Michael Wurm, Ariane Droin, and Thomas Stark; data Curation, Michael Wurm, Ariane Droin, and Thomas Stark; writing—original draft preparation, Michael Wurm, Ariane Droin, Thomas Stark, Hannes Taubenböck, Wolfgang Sulzer, and Christian Geiß; funding acquisition, Hannes Taubenböck and Michael Wurm. All authors have read and agreed to the published version of the manuscript.
Funding
This study received funding from the German Ministry of Economic Affairs and Energy within the 6th Energy Research Programme of the Federal Government/Applied Energy Research under the funding code O20E-SY 48192 ANSWER-Kommunal.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank Nils Dering from Landesamt für Natur, Umwelt und Verbraucherschutz Nordrhein-Westfalen (LANUV) for the provision of reference data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Environment Agency. Trends and Projections in Europe 2015. Tracking Progress towards Europe’s Climate and Energy Targets; European Environment Agency: Luxembourg, 2015.
- Silva, M.; Oliveira, V.; Leal, V. Urban Form and Energy Demand: A Review of Energy-Relevant Urban Attributes. J. Plan. Lit. 2017, 32, 346–365. [Google Scholar] [CrossRef]
- BPIE—Buildings Performance Institute Europe. Renovating Germany’s Building Stock. An Economic Appraisal from the Investors’ Perspective. Available online: http://bpie.eu/wp-content/uploads/2016/02/BPIE_Renovating-Germany-s-Building-Stock-_EN_09.pdf (accessed on 24 November 2020).
- EC—European Commission. Building Stock Characteristics. Available online: https://ec.europa.eu/energy/en/eu-buildings-factsheets-topics-tree/building-stock-characteristics (accessed on 24 November 2020).
- Hong, T.; Chen, Y.; Luo, X.; Luo, N.; Lee, S.H. Ten Questions on Urban Building Energy Modeling. Build. Environ. 2020, 168, 106508. [Google Scholar] [CrossRef]
- Reinhart, C.F.; Cerezo Davila, C. Urban Building Energy Modeling—A Review of a Nascent Field. Build. Environ. 2016, 97, 196–202. [Google Scholar] [CrossRef]
- Chen, Y.; Hong, T.; Luo, X.; Hooper, B. Development of City Buildings Dataset for Urban Building Energy Modeling. Energy Build. 2019, 183, 252–265. [Google Scholar] [CrossRef]
- Sola, A.; Corchero, C.; Salom, J.; Sanmarti, M. Simulation Tools to Build Urban-Scale Energy Models: A Review. Energies 2018, 11, 3269. [Google Scholar] [CrossRef]
- Rosser, J.F.; Long, G.; Zakhary, S.; Boyd, D.S.; Mao, Y.; Robinson, D. Modelling Urban Housing Stocks for Building Energy Simulation Using CityGML EnergyADE. ISPRS Int. J. Geo-Inf. 2019, 8, 163. [Google Scholar] [CrossRef]
- Fonseca, J.A.; Nguyen, T.-A.; Schlueter, A.; Marechal, F. City Energy Analyst (CEA): Integrated Framework for Analysis and Optimization of Building Energy Systems in Neighborhoods and City Districts. Energy Build. 2016, 113, 202–226. [Google Scholar] [CrossRef]
- Estevam Schmiedt, J.; Cerra, D.; Dahlke, D.; Dill, S.; Ge, N.; Göttsche, J.; Haas, A.; Heiden, U.; Israel, M.; Kurz, F.; et al. Remote Sensing Techniques for Building Models and Energy Performance Studies of Buildings. Available online: https://www.researchgate.net/publication/318283747_Remote_sensing_techniques_for_building_models_and_energy_performance_studies_of_buildings (accessed on 24 November 2020).
- Mastrucci, A.; Baume, O.; Stazi, F.; Leopold, U. Estimating Energy Savings for the Residential Building Stock of an Entire City: A GIS-Based Statistical Downscaling Approach Applied to Rotterdam. Energy Build. 2014, 75, 358–367. [Google Scholar] [CrossRef]
- Österbring, M.; Mata, É.; Thuvander, L.; Mangold, M.; Johnsson, F.; Wallbaum, H. A Differentiated Description of Building-Stocks for a Georeferenced Urban Bottom-up Building-Stock Model. Energy Build. 2016, 120, 78–84. [Google Scholar] [CrossRef]
- Kaden, R.; Kolbe, T.H. City-Wide Total Energy Demand Estimation of Buildings Using Semantic 3D City Model and Statistical Data. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2013, II-2/W1, 163–171. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.P. Estimation of the Building Energy Use Intensity in the Urban Scale by Integrating GIS and Big Data Technology. Appl. Energy 2016, 183, 182–192. [Google Scholar] [CrossRef]
- Evans, S.; Liddiard, R.; Steadman, P. 3DStock: A New Kind of Three-Dimensional Model of the Building Stock of England and Wales, for Use in Energy Analysis. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 227–255. [Google Scholar] [CrossRef]
- Chen, Y.; Hong, T.; Piette, M.A. Automatic Generation and Simulation of Urban Building Energy Models Based on City Datasets for City-Scale Building Retrofit Analysis. Appl. Energy 2017, 205, 323–335. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I. Modeling of End-Use Energy Consumption in the Residential Sector: A Review of Modeling Techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Y.; Cetin, K.; Eom, J.; Wang, Y.; Chen, G.; Zhang, X. Modeling Urban Building Energy Use: A Review of Modeling Approaches and Procedures. Energy 2017, 141, 2445–2457. [Google Scholar] [CrossRef]
- Johari, F.; Peronato, G.; Sadeghian, P.; Zhao, X.; Widén, J. Urban Building Energy Modeling: State of the Art and Future Prospects. Renew. Sustain. Energy Rev. 2020, 128, 109902. [Google Scholar] [CrossRef]
- Nouvel, R.; Mastrucci, A.; Leopold, U.; Baume, O.; Coors, V.; Eicker, U. Combining GIS-Based Statistical and Engineering Urban Heat Consumption Models: Towards a New Framework for Multi-Scale Policy Support. Energy Build. 2015, 107, 204–212. [Google Scholar] [CrossRef]
- Krüger, A.; Kolbe, T.H. Buildings Analysis for Urban Energy Planning Using Key Indicators on Virtual 3D City Models. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, XXXIX-B2, 145–150. [Google Scholar] [CrossRef]
- Beck, A.; Long, G.; Boyd, D.S.; Rosser, J.F.; Morley, J.; Duffield, R.; Sanderson, M.; Robinson, D. Automated Classification Metrics for Energy Modelling of Residential Buildings in the UK with Open Algorithms. Environ. Plan. B Urban Anal. City Sci. 2020, 47, 45–64. [Google Scholar] [CrossRef]
- Aksoezen, M.; Daniel, M.; Hassler, U.; Kohler, N. Building Age as an Indicator for Energy Consumption. Energy Build. 2015, 87, 74–86. [Google Scholar] [CrossRef]
- Alhamwi, A.; Medjroubi, W.; Vogt, T.; Agert, C. OpenStreetMap Data in Modeling the Urban Energy Infrastructure: A First Assessment and Analysis. In Proceedings of the 9th International Conference on Applied Energy, ICAE2017, Cardiff, UK, 21–24 August 2017. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Wurm, M.; Stark, T.; Zhu, X.X.; Weigand, M.; Taubenböck, H. Semantic Segmentation of Slums in Satellite Images Using Transfer Learning on Fully Convolutional Neural Networks. ISPRS J. Photogramm. Remote Sens. 2019, 150, 59–69. [Google Scholar] [CrossRef]
- Stiller, D.; Stark, T.; Wurm, M.; Dech, S.; Taubenbock, H. Large-Scale Building Extraction in Very High-Resolution Aerial Imagery Using Mask R-CNN. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 22–24 May 2019; pp. 1–4. [Google Scholar]
- Wu, G.; Shao, X.; Guo, Z.; Chen, Q.; Yuan, W.; Shi, X.; Xu, Y.; Shibasaki, R. Automatic Building Segmentation of Aerial Imagery Using Multi-Constraint Fully Convolutional Networks. Remote Sens. 2018, 10, 407. [Google Scholar] [CrossRef]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an Edge: Improving Semantic Image Segmentation with Boundary Detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Zhang, W.; Zhang, C.; Li, W.; Zhao, T. Semantic Segmentation of Urban Buildings from VHR Remote Sensing Imagery Using a Deep Convolutional Neural Network. Remote Sens. 2019, 11, 1774. [Google Scholar] [CrossRef]
- Microsoft US Building Footprints. Available online: https://github.com/Microsoft/USBuildingFootprints (accessed on 24 November 2020).
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation. arXiv 2016, arXiv:1611.06612. [Google Scholar]
- Huang, J.; Zhang, X.; Xin, Q.; Sun, Y.; Zhang, P. Automatic Building Extraction from High-Resolution Aerial Images and LiDAR Data Using Gated Residual Refinement Network. ISPRS J. Photogramm. Remote Sens. 2019, 151, 91–105. [Google Scholar] [CrossRef]
- Bittner, K.; Cui, S.; Reinartz, P. Building Extraction from Remote Sensing Data Using Fully Convolutional Networks. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2017, XLII-1/W1, 481–486. [Google Scholar] [CrossRef]
- Henn, A.; Römer, C.; Gröger, G.; Plümer, L. Automatic Classification of Building Types in 3D City Models: Using SVMs for Semantic Enrichment of Low Resolution Building Data. Geoinformatica 2012, 16, 281–306. [Google Scholar] [CrossRef]
- Wurm, M.; Schmitt, A.; Taubenbock, H. Building Types’ Classification Using Shape-Based Features and Linear Discriminant Functions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1901–1912. [Google Scholar] [CrossRef]
- Belgiu, M.; Tomljenovic, I.; Lampoltshammer, T.; Blaschke, T.; Höfle, B. Ontology-Based Classification of Building Types Detected from Airborne Laser Scanning Data. Remote Sens. 2014, 6, 1347–1366. [Google Scholar] [CrossRef]
- Du, S.; Zhang, F.; Zhang, X. Semantic Classification of Urban Buildings Combining VHR Image and GIS Data: An Improved Random Forest Approach. ISPRS J. Photogramm. Remote Sens. 2015, 105, 107–119. [Google Scholar] [CrossRef]
- Aubrecht, C.; Steinnocher, K.; Hollaus, M.; Wagner, W. Integrating Earth Observation and GIScience for High Resolution Spatial and Functional Modeling of Urban Land Use. Comput. Environ. Urban Syst. 2009, 33, 15–25. [Google Scholar] [CrossRef]
- Monien, D.; Strzalka, A.; Koukofikis, A.; Coors, V.; Eicker, U. Comparison of Building Modelling Assumptions and Methods for Urban Scale Heat Demand Forecasting. Future Cities Environ. 2017, 3, 2. [Google Scholar] [CrossRef]
- Zirak, M.; Weiler, V.; Hein, M.; Eicker, U. Urban Models Enrichment for Energy Applications: Challenges in Energy Simulation Using Different Data Sources for Building Age Information. Energy 2020, 190, 116292. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv 2015, arXiv:1411.4038. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2014, arXiv:1312.4400. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press, Inc.: Orlando, FL, USA, 1982. [Google Scholar]
- Wurm, M.; Taubenböck, H.; Schardt, M.; Esch, T.; Dech, S. Object-Based Image Information Fusion Using Multisensor Earth Observation Data over Urban Areas. Int. J. Image Data Fusion 2011, 2, 121–147. [Google Scholar] [CrossRef]
- Wurm, M.; Goebel, J.; Wagner, G.G.; Weigand, M.; Dech, S.; Taubenböck, H. Inferring Floor Area Ratio Thresholds for the Delineation of City Centers Based on Cognitive Perception. Environ. Plan. B Urban Anal. City Sci. 2019, 239980831986934. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Cernadaseva, E.; Barro, S.; Amorim, D. Do We Need Hundreds of Classifiers to Solve Real World Classification Problems? JMRS 2014, 15, 3133–3181. [Google Scholar]
- Angel, S.; Parent, J.; Civco, D.L. Ten Compactness Properties of Circles: Measuring Shape in Geography: Ten Compactness Properties of Circles. Can. Geogr. Géographe Can. 2010, 54, 441–461. [Google Scholar] [CrossRef]
- Droin, A.; Wurm, M.; Sulzer, W. Semantic Labelling of Building Types. A Comparison of Two Approaches Using Random Forest and Deep Learning. Available online: https://www.researchgate.net/publication/339800032_Semantic_labelling_of_building_types_A_comparison_of_two_approaches_using_Random_Forest_and_Deep_Learning (accessed on 24 November 2020).
- Garbasevschi, O.; Estevam Schmiedt, J.; Verma, T.; Lefter, I.; Korthals Altes, W.K.; Droin, A.; Schiricke, B.; Wurm, M. Spatial Factors Influencing Building Age Prediction and Implications for Urban Energy Modelling. Comput. Environ. Urban Syst. under review.
- IWU—Institut für Wohnen und Umwelt (German Institute for Housing and Environment). Deutsche Gebäudetypologie. Beispielhafte Maßnahmen Zur Verbesserung Der Energieeffizienz von Typischen Wohngebäuden—Zweite Erweirter Auflage; Institut für Wohnen und Umwelt: Darmstadt, Germany, 2015. [Google Scholar]
- Loga, T.; Stein, B.; Diefenbach, N. TABULA Building Typologies in 20 European Countries—Making Energy-Related Features of Residential Building Stocks Comparable. Energy Build. 2016, 132, 4–12. [Google Scholar] [CrossRef]
- BBSR—Bundesinstitut für Bau-, Stadt- und Raumforschung. Thermal Insulation Ordinance 1977. Available online: https://www.bbsr-energieeinsparung.de/EnEVPortal/EN/Archive/ThermalInsulation/1977/1977_node.html (accessed on 24 November 2020).
- Stiller, D.; Wurm, M.; Stark, T.; dAngelo, P.; Stebner, K.; Dech, S.; Taubenbock, H. Spatial Parameters for Transportation: A Multi-Modal Approach for Modelling the Urban Spatial Structure Using Deep Learning and Remote Sensing. J. Transp. Land Use, under review.
- Rosser, J.F.; Boyd, D.S.; Long, G.; Zakhary, S.; Mao, Y.; Robinson, D. Predicting Residential Building Age from Map Data. Comput. Environ. Urban Syst. 2019, 73, 56–67. [Google Scholar] [CrossRef]
- Wang, Z.; Crawley, J.; Li, F.G.N.; Lowe, R. Sizing of District Heating Systems Based on Smart Meter Data: Quantifying the Aggregated Domestic Energy Demand and Demand Diversity in the UK. Energy 2020, 193, 116780. [Google Scholar] [CrossRef]
- Ballarini, I.; Corgnati, S.P.; Corrado, V. Use of Reference Buildings to Assess the Energy Saving Potentials of the Residential Building Stock: The Experience of TABULA Project. Energy Policy 2014, 68, 273–284. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).