Abstract
Parallel kinematic machines (PKMs) have demonstrated their potential in many applications when high stiffness and accuracy are needed, even at micro- and nanoscales. The present paper is focused on the functional design of a parallel platform providing high accuracy and repeatability in full spatial motion. The hexaglide architecture with 6-PSS kinematics was demonstrated as the best solution according to the specifications provided by an important Italian company active in the field of micro-positioning, particularly in vacuum applications. All the steps needed to prove the applicability of such kinematics at the microscale and their inherent advantages are presented. First, the kinematic model of the manipulator based on the study’s parametrization is provided. A global conditioning index (GCI) is proposed in order to optimize the kinetostatic performance of the robot, so that precise positioning in the required platform workspace is guaranteed avoiding singular configurations. Some numerical simulations demonstrate the effectiveness of the study. Finally, some details about the realization of a physical prototype are given.
1. Introduction
The ability to change the orientation and position of a sample with high precision has become an indispensable requisite in many applications, ranging from testing of microelectronic components, to assembly of optoelectronic components, to measurements in extreme environments such as ultra-high vacuums, to exposure to cryogenic radiation and temperature typical of synchrotrons, and more. These functions are normally performed by robotic platforms with limited workspace and a small range of rotation. Compliant devices often fulfill such requirements allowing precise movements only in a subdomain of the typically required six degrees of freedom, as is well documented in [1,2,3,4,5,6,7]. Parallel kinematic machines (PKMs) are usually preferred to serial devices because of their intrinsic features, such as stiffness, positioning accuracy, and repeatability. Many examples of commercial devices based on parallel kinematics architectures can be found in industry, especially in the measurement sector.
The most widely used PKM in such fields is the Gough–Stewart platform [8], which has been commercially proposed in many sizes in order to respond to different application domains. Many examples of hexapods, whose operating principle is used to orient and manipulate microelectronic components, can be found in the scientific literature [9,10,11]. The main drawback of these manipulators, shared by most of the PKMs, is the limited workspace caused by the fixed location of both active and passive joints at the base frame, with which the legs of the manipulator are connected.
This limit can be overcome by a well-known mechanism from École Polytechnique Fédérale of Zürich, which takes the name of Hexaglide for its particular architecture. It belongs to the family of Hexapods, with six legs and six actuated rails at the fixed base [12]. In fact, the mechanical solution of having six parallel rails at the base can significantly extend the manipulator workspace, at least in one direction, providing a sort of extruded volume. One of the benefits could be the possibility of combining classic operations of pick and place, exploiting the whole length of the rails and covering a large workspace, to specific alignment and assembly tasks, for instance those typical of the microelectronics industry, in reduced sections of the rails by repeating them in several parallel workstations.
There are many examples in the literature of Hexaglide PKMs, but some of them are conceived with a different arrangement of the actuated rails at the base frame, for instance along the edges of an equilateral triangle [13] or in a star configuration [14], or even in more complex configurations [15,16], losing the ability to translate the entire mechanics in a prevalent direction. On the contrary, other studies are focused on their parallelism [17,18], but the proposed mechanical designs are oriented towards large machines where accuracy and repeatability are not the main objectives.
The present work proposes the functional design of a Hexaglide manipulator aimed at precision applications in the electronics and measurement sectors, with the aim of revealing a new potential use by showing its kinematic performance when designed for carrying out microscale tasks. Therefore, the first part of the paper is focused on the kinematics modeling of the manipulator, whereas the rest of the paper proposes an optimization procedure that, starting from one of its multiple inverse kinematics solutions, results in a functional design that fulfills the specifications set by an industrial manufacturer. Finally, a prototype designed with the aforementioned procedure is shown. Such prototype is based on a different inverse kinematics solution that is subject to a confidentiality agreement and currently cannot be disclosed.
2. Design Specifications
The design specifications of the Italian manufacturer concern the kinematic and static performance required by the manipulator. They result from a market analysis in the microelectronics sector, as previously indicated. These can be summarized as follows:
- overall dimensions of mm ,
- translation of mm along the x-, y- and z-directions, respectively,
- translation resolution of about m, repeatability of m, maximum speed of 5 mm/s,
- rotation range of about x-, y- and z-axes,
- rotation resolution of about , repeatability of ,
- payload of kg.
3. The Hexaglide Kinematics
As already mentioned in the previous sections, one of the most suitable kinematic architectures that can meet such desired specifications is the Hexaglide. Six actuated sliders, equally oriented in a given direction of the fixed base, provide the manipulator with a main direction of translation. A typical configuration of the manipulator is obtained with six rigid legs of constant length, and a hexagonal or triangular moving platform according to the connection of the legs in a 6-6 [19] or 6-3 scheme [20] by means of spherical joints, as shown in Figure 1. Six of the twelve spherical joints, the ones at the base or the others at the moving platform, can be replaced by universal joints for a non-under-constrained version of the manipulator, avoiding the spin of the legs about their axis. It is often preferred that there is a reduction of the rails at the frame with three units, where two sliders move in pairs [21,22,23].
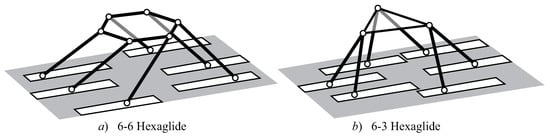
Figure 1.
Functional solutions for the Hexaglide manipulator.
3.1. Model Parametrization
The pose of the moving platform of a manipulator is typically defined by means of a homogeneous transformation expressed in terms of a matrix, called in the following. It involves the rotation matrix between the mobile reference system , placed on the moving platform, and the fixed reference system , located at the base frame, and the relative position vector amongst their origins. The two reference systems and other important geometric data related to the Hexaglide are shown in Figure 2. The rotation matrix is also interpreted in this work as a sequence of roll, pitch, and yaw elemental rotations, namely a matrix multiplication of the form , with obvious meanings of terms. The well-established study’s parametrization can be conveniently used in the implementation of calculation routines in order to avoid representation singularities for :
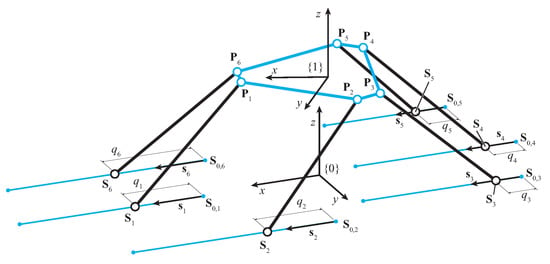
Figure 2.
Kinematic scheme of the 6-PSS Hexaglide.
The eight study parameters, here gathered in the vector , are constrained by the study quadric:
with
Moreover, the following constraint normalization equation must hold in order to avoid a projective transformation:
with
The full inverse transformations are also given for the sake of completeness:
where stands for the element of matrix at the ith row and jth column.
The position of the lower spherical joints is parametrized as follows:
where is the variable position of the attachment point of the ith leg on the frame, corresponding to the ith spherical joint center, driven by the actuated prismatic joints at the base, is the fixed point on each slider that corresponds to when in the home position, is the unit vector giving the direction of the linear sliding, and is the ith actuated joint variable. All the can be gathered in the actuated joint vector . The generality of the expression can be noted, where can still be different for each prismatic joint.
The ith leg can be represented by vector whose expression is given by
where is its constant length and is the unit vector giving its direction from to .
Finally, the moving platform, whose geometric scheme is shown in Figure 3, is parametrized by means of two parameters: r is the radius of a circle, on which the six centers of the upper spherical joints lie, and is the semi-central angle of the circular sector between pairs of points, namely . Such arrangement is motivated by the need to avoid the perfect hexagonal symmetry of singular configurations inside the manipulator workspace, while maintaining a certain symmetry. Matrix in (1) can be used to find the absolute coordinates of each point in the fixed reference frame when the coordinates in the moving reference frame are known:
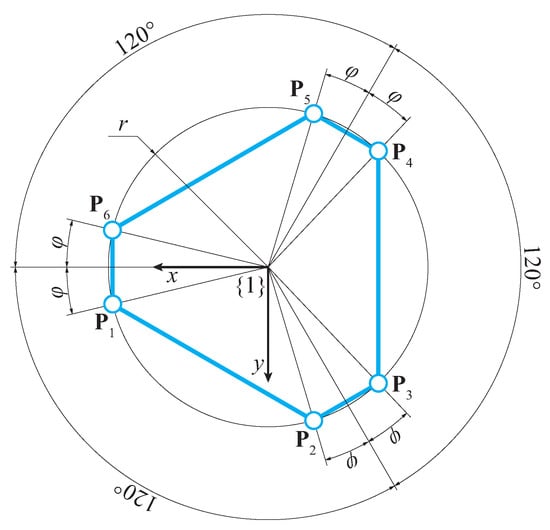
Figure 3.
Geometric scheme of the moving platform.
From here on, all vectors are considered written in the fixed frame, unless explicitly stated.
3.2. Inverse Position Kinematics (IPK)
The mapping from the pose coordinates of the moving platform to the actuated joint displacements along the six linear axes can easily be obtained if the rigid body constraint is imposed to the length of the legs of the manipulator. It consists of the following expression:
with
The subscript i is related to the ith leg according to the notation shown in Figure 4. The resulting system of equations is given by as many constraints as the number of legs, with the addition of the study quadric and the normalization equation :
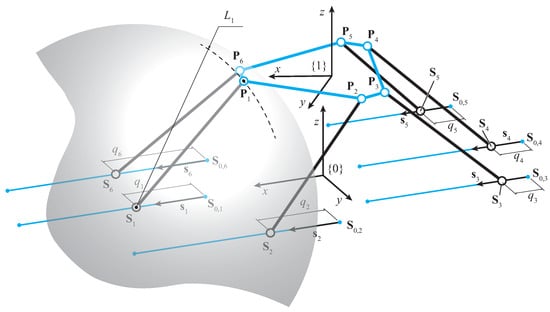
Figure 4.
Constraint manifold of the ith leg.
The expressions of points and are given by Equations (7) and (9), respectively. As expected, the system provides two inverse kinematics solutions for each leg, whose expression in compact form is given by:
where is the ith vector resulting from the following expression:
Both solutions in Equation (12) are acceptable and provide theoretical inverse kinematic solutions for the Hexaglide, if all combinations are taken into account. Therefore, a selection routine for the best solution that meets the design specifications, together with the best kinematic performance, is required. Some geometrical and physical assumptions can be made: the zero configuration for each slider, namely the absolute position of each point at the fixed base, can be associated to one end of the relative actuated rail, whereas the other end corresponds to the maximum stroke , providing an always positive or at least null . Moreover, the legs of the manipulator must never reach a vertical configuration during its operation. Such condition is required to avoid singularities, as shown in the following section about differential kinematics. The foregoing assumptions are summarized as follows:
with as large as desired and directed along the x-axis of the fixed frame .
3.3. Direct Position Kinematics (DPK)
The mapping from the actuated joint vector to the pose coordinates of the moving platform expressed by vector , or analogously given by matrix , is more complex than the inverse problem, as expected for PKMs. It can be demonstrated that in this case such problem has 40 solutions and numerical approaches are often preferred to closed-form models because of their easier software implementation. Numerical solutions depend on initial conditions and it is not generally easy to converge to the right solution among the many possibilities. As an initial condition, a matrix based on an identity matrix and an arbitrary position vector inside the manipulator workspace, or alternatively a starting Cartesian vector , is chosen. The algorithm conceived to solve the problem consists of the following steps:
- Input: vector ;
- a discrete sequence of actuated joint vectors, regulated by the index k, is obtained by means of a linear interpolation ranging from to , with resulting from the IPK of ;
- an iterative Newton–Raphson algorithm, this time regulated by the index i, is progressively used for each of the sequence to evaluate the vector that verifies the constraint manifold in (11) with a desired level of accuracy, each iteration starting from the previous solution ;
- Output: vector of study parameters or directly if a matrix form is preferred.
In more detail, at each iteration of step 3, a new estimate of the solution is sought by means of the aforementioned Newton–Raphson algorithm:
where and are:
3.4. Differential Kinematics
The Jacobian matrix of the manipulator, which maps the Cartesian velocity vector of the moving platform from the actuated joint velocity vector , is presented in the classic partitioned form:
where with the angular velocity and the linear velocity of the moving platform, and . The expression of the matrices and , called respectively the geometric and analytical Jacobians of the manipulator, are obtained by making use of kinematic torsors:
where is the six-dimensional kinematic torsor related to the ith actuated prismatic joint and is the dual torsor to passive joints of each ith leg. When the square matrix has full rank, the full Jacobian matrix can be found as:
A look at the components of the matrices and in (18) allows identification of the singular configurations of the manipulator. The two matrices lose rank according to the following conditions:
- when any pair of reciprocal torsors and (with ) satisfies the relation ;
- when is verified at least for one of the ith legs.
4. Optimization Problem
An objective function is defined with the aim of maximizing the kinematic performance of the manipulator, laying the foundation for a geometrical optimization. One of the most frequently used tools in kinematic optimization problems is the condition number of the Jacobian matrix. However, besides not being a finite index, it merges the kinematic characteristics of different natures when applied to full motion manipulators. It follows that two sub-matrices extracted from matrix related to angular and linear velocities independently seem more suitable for a guided optimization, instead of using the full Jacobian matrix [24]. Two indexes result from this partitioning:
where is the matrix given by the first three rows of and analogously by the second three. The terms and represent the minimum and maximum eigenvalues of the matrices inside the round brackets. The two condition numbers in (20) are local indexes and have the property of being confined in the range , with isotropic and singular conditions revealed by the upper and lower extremes respectively. Further useful indexes with global properties can be defined if the condition numbers in (20) are integrated on the manipulator workspace W [25], where the latter in the present case refers to the desired workspace defined in Section 2:
Finally, an objective function based on (21) and tailored to meet the design specifications can be defined as:
where the weights and are in the range and can be adjusted according to kinematic needs and respecting the relationship , favoring translation over rotation performance if required, or other combinations. As highlighted in (22), function depends on , namely the y and z coordinates of the relative position vector between frames and in the home configuration of the manipulator, and the yaw rotation about the vertical z axis. The home configuration is defined as the central configuration of the manipulator, from which the required translations and rotations can be performed without incurring singularities, with a horizontal top surface of its moving platform. This latter condition is assumed for practical reasons, in fact the top surface can be used as a horizontal support plane, narrowing the study only to rotations about the z axis. At this stage of the study, the x coordinate between frames and is arbitrary, therefore, a variability of is not taken into account. Finally, the vector in (22) collects all the geometric parameters of the manipulator that a user wants to optimize. In the present case, with reference to Section 3, it is defined as:
with the y-position of the ith slider with respect to the fixed frame represented by and all the legs considered with equal length . It can be noted that and do not participate in the optimization process because the respective linear guides are the most external along the y-direction and are confined within the maximum range of 350 mm already mentioned in Section 2.
Geometric Optimization
A preliminary study about the expected overall size of the manipulator was carried out. The design specifications of Section 2 allow limitation of the range of variability of some geometrical parameters, so that optimization results are effectively constrained around an arbitrary initial configuration taken as a first guess. Eventually, they are checked again after all parameters are optimized.
The maximum height of the moving reference frame with respect to the fixed frame is limited to 200 mm, leaving the remaining millimeters to mechanically design the moving platform. According to the results of the kinematic study in Section 3.4, a maximum tilt of for each leg from the horizontal plane is considered in order to be sufficiently far from singular configurations. It follows that a hypothesized length for the legs is 210 mm, as shown in Figure 5a. In addition, the unit vectors of the legs must be as far as possible from being parallel, suggesting a staggered disposition of the linear guides at the base. Their first attempt arrangement is shown in Figure 5b, with a distance of 300 mm between the external guides in order to take into account their physical dimensions.
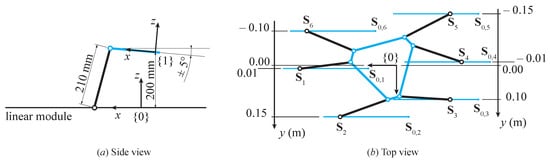
Figure 5.
Preliminary design: (a) side view, (b) top view.
The choice of a first guess value for the geometric parameters of the moving platform is due to technical reasons: on the one hand, the maximization of the free surface where a load can be placed, and, on the other hand, the need for enough space to realize a physical connection of the legs with the platform. Their values are: and mm, where the subscript 0 has the meaning of the initial value of the optimization procedure.
As already mentioned, the home position of the sliders along the x-direction, corresponding to the home configuration of the moving platform, is defined only after the optimization of the other geometric parameters. In fact, the zero of each slider can be placed so that the actual home position falls in the center of the available stroke of the sliders.
The objective function in (22) collects information from the robot about its whole required workspace volume. However, as expected by virtue of the particular features of the Hexaglide along a specific direction, the study of is narrowed to a single cross-section of the workspace: without loss of generality the condition is chosen. This assumption is justified by the behavior of the manipulator that does not depend on the translation in the x-direction, but only on the maximum dimension of the sliders and their initial position. A range of mm and mm in the y- and z-directions, respectively, and rotations of about all Cartesian axes are considered (see Section 2).
The pre-sizing values of the optimization parameters, together with their assumed lower and upper range limits, are shown in Table 1. Their values result from a preliminary analysis (a sort of Monte Carlo method) of the objective function subject to discrete variations of the parameters in their admissible range. Values of the objective function above allow a large number of combinations of parameters to be excluded from the study. A further refinement around the most promising combinations allows the choosing of the initial values gathered in Table 1, approximated to whole numbers, with a corresponding of about . Rotations greater than five degrees for in Table 1 are justified by the search of its home configuration value, around which the required range of can be obtained with the best kinematic performance. A similar approach is followed for the other design parameters.

Table 1.
Initial values, lower and upper limits of the optimization parameters.
The optimization procedure is repeated 10 times iteratively, each time providing the result obtained in the previous step as starting point, in order to improve the local minimum point of the objective function. This method is necessary because of the sensitivity of the problem to initial conditions.
5. Optimization Results
The geometrical parameters and the home position coordinates summarized in Table 1 are processed by means of the Matlab Optimization Toolbox by MathWorks. A constrained minimization problem is tackled in order to find the required optimal values according to the minimization of the function proposed in (22), with equal weights . Hard constraints are imposed on Equation (11), while soft constraints are imposed on the variability of vector , ensuring that Cartesian y and z translations together with x and y rotations in their required ranges are satisfied. Another important soft constraint ensures that none of the six legs exceeds the maximum tilt of , a less stringent condition with respect to the one mentioned in the previous sections, in order to give more flexibility to the optimum search. Table 2 shows each calculation step progressively as rows increase. It is easy to verify that, after the first few steps, the variability of parameters tends to decrease and results stabilize around some reference values, with quite a small deviation. Finally, a of about is obtained, derived from a slow progressive increase at each step of the optimization process.

Table 2.
Optimized values of geometric parameters and home configuration.
Resulting design values are highlighted in the last row of Table 2, where an approximation of figures to average and more practical values is proposed, remembering that better conditions are associated with smaller values of . Some important information about the home configuration is already available from the optimization procedure, for instance vector in (22) is now completely known. However, the absolute position of the actuated carriages in the home configuration is only partially defined, knowing their y and z components (see Figure 5, Table 2 with for ). Their x components can be obtained from the application of the inverse kinematics algorithm proposed in (12), where the Cartesian pose of the moving platform is assigned: , , together with the remaining parameters in Table 2. A null value can be also assigned to the components of . Such choice allows the absolute x position of the carriages to be found with respect to the fixed reference frame when all the linear guides at the platform base are perfectly side by side. Ultimately, the absolute coordinates of the points, for , in the home configuration become:
with values in meters. In (24) only the x coordinates result from a computation, and this justifies the figures down to a tenth of a millimeter. In order to locate the points to their actual position and to maximize the admissible travel in the x-direction, their zero position must be placed so that:
6. Kinematic Performance
Once the optimal geometric dimensions are determined, a further step towards the definition of the mechanical elements can be done by defining the linear modules at the fixed base. The Hercules Stages HLS-M-185-DC-Arom1Vpp by Vacuum Fab Srl with a coreless DC motor, a linear optical scale with a nm resolution, a stroke of 185 mm, and an actuation force of 212 N are used. If an ultra-high vacuum application is the target, RodRail eXtreme linear translation stages, produced by the same manufacturer, with a stroke of 190 mm and a repeatability of 1 m in a vacuum, can be used instead.
A map of the Cartesian positioning errors obtained by virtue of the nameplate data of the linear stages is shown in Figure 6 on a vertical yz-plane (), covering the manipulator workspace. The white dot represents the Cartesian home configuration of the platform inside its workspace. A fixed orientation is considered in all Cartesian positions, the same as the home configuration, namely , and . The map in Figure 6 is coherent with the one of the determinants of the Jacobian matrix shown in Figure 7, obtained by analyzing the expression in (19) inside the manipulator workspace. In fact, where the value of the determinant is small, the manipulator in the relative Cartesian position is less prone to errors due to uncertainties in the displacement of the linear modules.
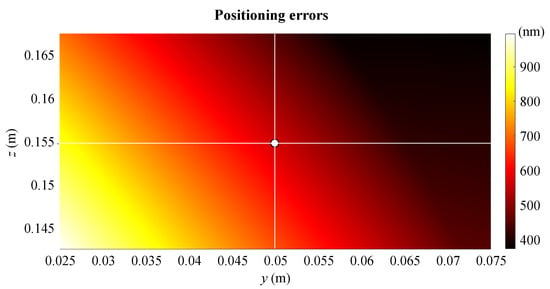
Figure 6.
Map of the Cartesian positioning errors (fixed orientation: , , ).
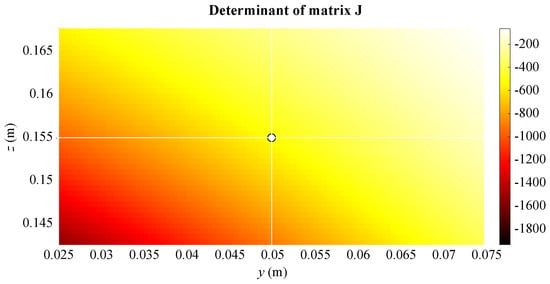
Figure 7.
Map of the determinant of (fixed orientation: , , ).
The maximum absolute value of positioning error obtained in the center of the workspace is about 0.6 m. Such value is the worst possible considering every direction and any combination of errors for the actuated carriages, but it significantly reduces according to the direction chosen, even by an order of magnitude. If the first three rows of the Jacobian matrix are considered instead of the second three, orientation errors can be investigated. Figure 8 shows a trend analogous to the other map, where an error in the center of the workspace of about degrees can be read, related to the worst condition. Other studies could be proposed taking into account a change of orientation of the moving platform with a fixed Cartesian position, but results are quite similar to the ones already proposed and do not really add more insight. Finally, a force polyhedron can be evaluated in static conditions to show if the manipulator meets the requirement of a kg payload. Figure 9 refers to the static performance in terms of Cartesian forces in every direction when the manipulator is in its home configuration and no torques are provided at the end effector. The maximum force magnitude is about 800 N, whereas the minimum is about 80 N, but it is easy to verify that the highest performance is related to almost vertical directions, allowing the weight of the mechanical parts of the manipulator to be borne as well as the required payload. Eventually, it can be concluded that the obtained results almost entirely meet the specifications of Section 2.
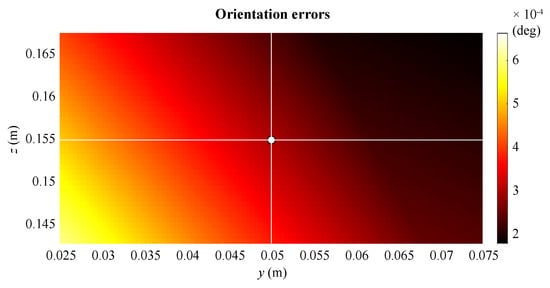
Figure 8.
Map of the orientation errors (around the given orientation , , ).
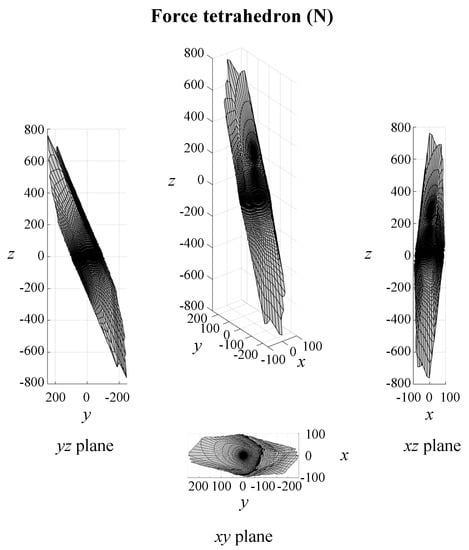
Figure 9.
Static force performance in home configuration.
7. Conclusions
In this study we proposed a compact version of a Hexaglide parallel manipulator, commissioned by an Italian company operating in the micro-positioning sector. The main feature of the manipulator is its ability to exploit a Cartesian direction along which the entire mechanism can move without inner relative motions, with the aim of serving a few stations arranged for different mechatronic tasks. All the steps needed to functionally design a high-precision manipulator were addressed. The effect of commercial linear modules on the Cartesian positioning errors of the manipulator were investigated. The resolution of their sensors allows a high repeatability to be achieved along the sliding direction of the prismatic rails and high performance along the other directions, whose worst condition is still less than a micrometer for translations and less than a thousandth of a degree for rotations. Tailored linear modules with a longer stroke can be used to increase the workspace of the manipulator, while preserving the other kinetostatic features. Finally, all key functional design information of the manipulator has been given to prototype a compact Hexaglide.
An even more compact design can be obtained with a different leg tilt and similar stages with a shorter stroke of 150 mm, as shown in Figure 10 for a prototype of another confidential version of the Hexaglide by Vacuum Fab Srl. Figure 10 also shows the mechanical solution that can be used for the twelve spherical joints, based on a magnetic principle with self-centering. Preliminary tests on such a prototype have demonstrated a repeatability for linear and angular movements of about m and better than , respectively.

Figure 10.
Prototype of a more compact version of the Hexaglide manipulator with similar performance by Vacuum Fab Srl.
Author Contributions
Conceptualization, L.C. and M.-C.P.; methodology, L.C. and M.-C.P.; software, E.L. and F.D.; formal analysis, L.C. and G.P.; investigation, L.C. and G.P.; resources, M.-C.P.; data curation, G.P. and M.-C.P.; writing—original draft preparation, M.-C.P.; writing—review and editing, G.P.; supervision, M.-C.P. and G.G.; project administration, G.G.; funding acquisition, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ahn, C.; Seo, T.; Kim, J.; Kim, T.-W. High-tilt parallel positioning mechanism development and cutter path simulation for laser micro-machining. Comput. Aided Des. 2007, 39, 218–228. [Google Scholar]
- Shimizu, Y.; Peng, Y.; Kaneko, J.; Azuma, T.; Ito, S.; Gao, W.; Lu, T.-F. Design and construction of the motion mechanism of an XY micro-stage for precision positioning. Sens. Actuators A Phys. 2013, 201, 395–406. [Google Scholar]
- Zhang, D.; Li, X.; Ni, M.; Li, P.; Dong, L.; Rui, D.; Zhang, J. Design of 6 degree-of-freedom micro-positioning mechanism for optical elements. In Proceedings of the IEEE 13th International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017. [Google Scholar]
- Xiao, R.; Shao, S.; Xu, M.; Jing, Z. Design and Analysis of a Novel Piezo-Actuated XYθz Micropositioning Mechanism with Large Travel and Kinematic Decoupling. Adv. Mater. Sci. Eng. Hindawi 2019, 2019, 5461725. [Google Scholar]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Zhong, Y. Modelling and analysis of a three-revolute parallel micro-positioning mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1273–1286. [Google Scholar]
- Palpacelli, M.-C.; Palmieri, G.; Callegari, M. A Redundantly Actuated 2-Degrees-of-Freedom Mini Pointing Device. J. Mech. Robot. 2012, 4, 031012. [Google Scholar]
- Palmieri, G.; Callegari, M.; Carbonari, L.; Palpacelli, M.C. Mechanical design of a mini pointing device for a robotic assembly cell. Meccanica 2015, 50, 1895–1908. [Google Scholar]
- Lin, L.-C.; Tsay, M.-U. Modeling and control of micropositioning systems using Stewart platforms. J. Robot. Syst. 2000, 17, 17–52. [Google Scholar]
- Liu, Z.; Cai, C.; Yang, M.; Zhang, Y. Testing of a MEMS Dynamic Inclinometer Using the Stewart Platform. Sensors 2019, 19, 4233. [Google Scholar]
- Mura, A. Multi-dofs MEMS displacement sensors based on the Stewart platform theory. Microsyst. Technol. 2012, 18, 575–579. [Google Scholar]
- Shi, H.; Duan, X.; Su, H. Optimization of the workspace of a MEMS hexapod nanopositioner using an adaptive genetic algorithm. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Rehsteiner, F.; Neugebauer, R.; Spiewak, S.; Wieland, F. Putting Parallel Kinematics Machines (PKM) to Productive Work. Ann. CIRP 1999, 48, 345–350. [Google Scholar]
- Bernal, J.; Campa, R.; Soto, I. Kinematics and dynamics modeling of the 6-3-PUS-type Hexapod parallel mechanism. J. Mech. Sci. Tech. 2018, 32, 4555–4570. [Google Scholar]
- Giberti, H.; La Mura, F.; Resmini, G.; Parmeggiani, M. Fully Mechatronical Design of an HIL System for Floating Devices. Robotics 2018, 7, 39. [Google Scholar]
- Nabavi, S.N.; Shariatee, M.; Enferadi, J.; Akbarzadeh, A. Parametric design and multi-objective optimization of a general 6-PUS parallel manipulator. Mech. Mach. Theory 2020, 152, 103913. [Google Scholar]
- Guo, J.; Wang, D.; Fan, R.; Chen, W.; Zhao, G. Kinematic calibration and error compensation of a hexaglide parallel manipulator. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 215–225. [Google Scholar]
- Dong, W.; Du, Z.; Xiao, Y.; Chen, X. Development of a parallel kinematic motion simulator platform. Mechatronics 2013, 23, 154–161. [Google Scholar]
- Spiewak, S.A.; Ludwick, S.J.; Hauer, G. A Test Setup for Evaluation of Harmonic Distorsions in Precision Inertial Sensors. J. Manuf. Sci. Eng. 2013, 135, 021015. [Google Scholar]
- Gao, F.; Li, W.; Zhao, X.; Jin, Z.; Zhao, H. New kinematic structures for 2-, 3-, 4-, and 5-DOF parallel manipulator designs. Mech. Mach. Theory 2002, 37, 1395–1411. [Google Scholar]
- Liu, C.H.; Huang, K.-C.; Wang, Y.-T. Forward position analysis of 6-3 Linapod parallel manipulators. Meccanica 2012, 47, 1271–1282. [Google Scholar]
- Abtahi, M.; Pendar, H.; Alasty, A.; Vossoughi, G. Kinematics and Singularity Analysis of the Hexaglide Parallel Robot. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008. [Google Scholar]
- Yen, P.-L.; Ke, Z.-W.; Lu, T.-S.; Lu, C.-W. Development of a New Safety-Enhanced Surgical Robot Using the Hexaglide Structure. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, The Hague, The Netherlands, 10–13 October 2004. [Google Scholar]
- Kong, M.; Zhang, Y.; Sun, L.; Du, Z. Analysis of a New Workspace of the Hexaglide as a Motion Simulator for Fuel Tanker Trucks. In Proceedings of the International Conference on Mechatronics, Kumamoto, Japan, 8–10 May 2007. [Google Scholar]
- Merlet, J.P. Jacobian, Manipulability, Condition Number, and Accuracy of Parallel Robots. ASME J. Mech. Des. 2006, 128, 199–206. [Google Scholar]
- Gosselin, C.; Angeles, J. A Global Performance Index for the Kinematic Optimization of Robotic Manipulators. ASME J. Mech. Des. 1991, 113, 220–226. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).