The Effect of the Optimization Selection of Position Analysis Route on the Forward Position Solutions of Parallel Mechanisms
Abstract
1. Introduction
2. The Optimization Selection Criteria for the Position Analysis Route (PAR)
2.1. Optimization Criteria for PAR
2.2. Procedures of Optimization Selection of PAR
- i.
- ii.
- If there are several optional first loops with the same minimum constraint degree Δ, the loop with the smallest of the NIDE ξmin should be selected as the first loop. In this way, the number of position equations required to solve the loop positions can be minimized, which is exactly equal to ξmin.
- iii.
- If there are both planar SKC(s) and space SKC(s) in a PM, the FPS should be started from the planar SKC(s) first, and then the space SKC(s) should be analyzed. This is because the NIDE of the planar mechanism loop is always the smallest, i.e., ξ = 3.
3. Basic Formulas for Topological Characteristics Analysis
3.1. Analysis of the POC Set
- —POC set generated by the ith joint.
- —POC set generated by the end link of the ith chain.
- —POC set generated by the moving platform of PM.
3.2. Determining the DOF
- F—DOF of PM.
- fi—DOF of the ith joint.
- v—number of independent loops, and v = m − n + 1.
- m, n—number of all joints and links of the whole PM, respectively.
- —number of independent displacement equations (NIDE) of the jth loop.
- —POC set generated by the sub-PM formed by the former j branches.
- —POC set generated by the end link of (j + 1)th sub-chains.
3.3. Determining the Coupling Degree
- —number of joints contained in the jth SOCj.
- —the number of actuated joints in the jth SOCj.
4. Case Studies
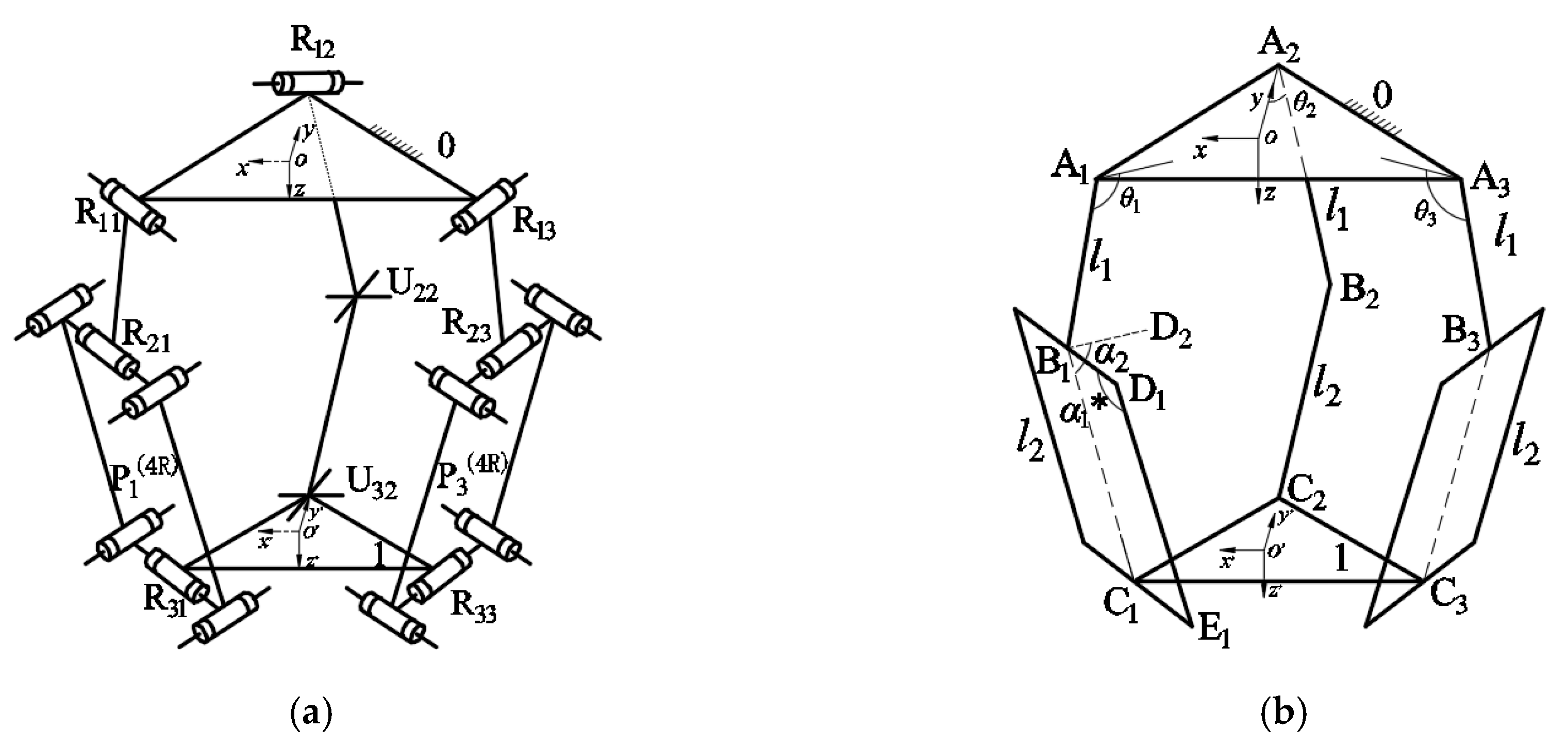
4.1. Three-Translation PM (3T-CU)
4.1.1. Topology Analysis
4.1.2. Position Analysis
4.2. Three-Translation PM (Delta-CU)
4.2.1. Topological Analysis
4.2.2. Position Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kinzel, G.L.; Chang, C. The analysis of planar linkage using a modular approach. Mech. Mach. Theory 1984, 19, 165–172. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Generation and forward displacement analysis of RPR-PR-RPR analytic planar parallel manipulators. J. Mech. Des. 2001, 8, 2195–2304. [Google Scholar]
- Pennock, G.R.; Hasan, A. A Polynomial Equation for a Coupler Curve of the Double Butterfly Linkage. J. Mech. Des. 2002, 124, 39–46. [Google Scholar] [CrossRef]
- Husain, M.; Waldron, K.J. Direct Position Kinematics of the 3-1-1-1 Stewart Platforms. J. Mech. Des. 1994, 116, 1102–1107. [Google Scholar] [CrossRef]
- Wampler, C.W. Forward displacement analysis of general six-in-parallel sps (Stewart) platform manipulator using soma coordinates. Mech. Mach. Theory 1996, 31, 311–337. [Google Scholar] [CrossRef]
- Husty, M.L. Algorithm for Solving the direct kinematic of Stewart-Gough-Type platforms. Mech. Mach. Theory 1996, 31, 365–380. [Google Scholar] [CrossRef]
- Rojas, N.; Thomas, F. On closed-form Solutions to the position analysis of Baranov trusses. Mech. Mach. Theory 2012, 50, 179–196. [Google Scholar] [CrossRef]
- Yang, T.; Liu, A.; Shen, H.; Hang, L.; Luo, Y.; Jin, Q. Theory and Appication of of Robot Mechanism Topology; Science Press: Beijing, China, 2012. [Google Scholar]
- Yang, T.; Liu, A.; Shen, H.; Hang, L.; Luo, Y.; Jin, Q. Topology Design of Robot Mechanisms; Springer: Singapore, 2018. [Google Scholar]
- Shen, H. Research on Forward Position Solutions for 6-SPS Parallel Mechanisms Based on Topology Structure Analysis. Chin. J. Mech. Eng. 2013, 49, 70–80. [Google Scholar] [CrossRef]
- Shen, H.; Chablat, D.; Zen, B.; Li, J.; Wu, G.; Yang, T. A Translational Three-Degrees-of-Freedom Parallel Mechanism with Partial Motion Decoupling and Analytic Direct Kinematics. J. Mech. Robot. 2020, 12, 1–7. [Google Scholar] [CrossRef]
- Shen, H.; Yang, T.; Li, J.; Zhang, D.; Deng, J.; Liu, A. Evaluation of Topological Properties of Parallel Manipulators Based on the Topological Characteristic Indexes. Robotica 2020, 38, 1381–1399. [Google Scholar] [CrossRef]
- Shen, H.; Xu, Q.; Li, J.; Yang, T. The Effect of the Optimal Route Selection on the Forward Position Solutions of Parallel Mechanisms. In Advances in Mechanism and Machine Science; Springer: Cham, Switzerland, 2020; pp. 450–458. [Google Scholar]
- Li, J.; Shen, H.; Meng, Q.; Deng, J. A delta-CU—Kinematic analysis and dimension design. In Proceedings of the 10th International Conference on Intelligent Robotics and Applications, Wuhan, China, 16–18 August 2017; Springer: Cham, Switzerland, 2017; pp. 371–382. [Google Scholar]
- Shen, H.; Wang, Y.; Wu, G.; Meng, Q. Stiffness Analysis of a Semi-symmetrical Three-Translation Delta-CU Parallel Robot. In Proceedings of the 6th IFToMM International Symposium on Robotics and Mechatronics, ISRM 2019, Taipei, Taiwan, 28 October–3 November 2019. [Google Scholar]
- Shen, H.; Xu, Q.; Li, J.; Wu, G.; Yang, T.-L. The Effect of Selection of Virtual Variable on the Direct Kinematics of Parallel Mechanisms. In New Trends in Mechanism and Machine Science; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Shen, H.; Ji, H.; Xu, Z.; Yang, T. Design, Kinematic Symbolic Solution and Performance Evaluation of a New Three Translation Mechanism. Trans. Chin. Soc. Agric. Mach. 2020, 51, 397–407. [Google Scholar]
- Shen, H.; Zhu, Z.; Meng, Q.; Wu, G.; Deng, J. Kinematics and Stiffness Modeling Analysis of a Spatial 2T1R Parallel Mechanism with Zero Coupling Degree. Trans. Chin. Soc. Agric. Mach. 2020, 51, 411–420. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Xu, Q.; Li, J.; Yang, T.-l. The Effect of the Optimization Selection of Position Analysis Route on the Forward Position Solutions of Parallel Mechanisms. Robotics 2020, 9, 93. https://doi.org/10.3390/robotics9040093
Shen H, Xu Q, Li J, Yang T-l. The Effect of the Optimization Selection of Position Analysis Route on the Forward Position Solutions of Parallel Mechanisms. Robotics. 2020; 9(4):93. https://doi.org/10.3390/robotics9040093
Chicago/Turabian StyleShen, Huiping, Qing Xu, Ju Li, and Ting-li Yang. 2020. "The Effect of the Optimization Selection of Position Analysis Route on the Forward Position Solutions of Parallel Mechanisms" Robotics 9, no. 4: 93. https://doi.org/10.3390/robotics9040093
APA StyleShen, H., Xu, Q., Li, J., & Yang, T.-l. (2020). The Effect of the Optimization Selection of Position Analysis Route on the Forward Position Solutions of Parallel Mechanisms. Robotics, 9(4), 93. https://doi.org/10.3390/robotics9040093




