A New Soft RCC Device with Pneumatic Regulation

Abstract

The work described in this paper aims at exploiting the characteristic of a special deformable actuator with rolling membranes to realize a device with defined Remote Center of Compliance (RCC). Starting from theoretical approaches to the definition of the RCC, the authors propose a novel and simple formulation that can be applied to the soft actuator to determine its RCC. The position of the device’s RCC was determined by creating an asymmetry on the geometry of the device along its axis, i.e., by imposing a longitudinal displacement to the piston with respect to the membranes’ rest condition. FEM simulations of the device behavior were carried out and a first formulation describing the placement of the RCC by varying the operating pressure was found. Finally, a comparison of the theoretical model and FEM results is presented, validating the proposed formulation.

1. Introduction

The concept of the Remote Center of Compliance (RCC) has been investigated by researchers for a number of years and has been used in simple applications, such as inserting a peg in the hole [1]. The RCC is a localized point in the geometrical representation of a device, in which the application of external forces (or torques) produces a displacement related only to the applied external action (force or torque). Its position strongly depends on the geometry and the stiffness of the system and its components. Drake introduces the RCC as “a point in which an applied force causes only a lateral displacement while an applied moment causes only a rotation” [2]. Drake was one of the first researchers who investigated the properties of the compliance center, proposing mechanical systems with architectures capable of positioning it according to the work to be performed.

In the literature, the typical task used to describe the RCC is the insertion of a peg into a hole that can occur during an assembly operation [3,4]. If a misalignment between the peg and the hole axes occurs, and if the device is developed with the RCC concept (with the RCC placed at the physical end of the peg), the compliance of the system enables the peg to spontaneously re-align its axis with the hole axis without using any force sensory feedback. Aiming to completely automate the assembly functions in industries, this type of device is relevant to several applications: clearance fits, bearings in housings, shafts in bearings, mounting splines, or inserting screws into threaded cavities [5].

Several studies have highlighted that placing the center of compliance on the tip of the shaft avoids unwanted conditions, such as jamming or wedging [6,7]. Sorli and Govi [8] studied contact forces during insertion, making a comparison between different passive compliance designs. They analyzed different cases according to the initial position of the peg (1-point contact or 2-point contact), and for each derived a model capable of estimating optimal insertion parameters. They showed how an RCC system requires a lower insertion force. In [9], elastomeric shear pads are chosen instead of beams, which constitute the classical components of devices for applications with an RCC. This arrangement allows a lower lateral stiffness to be obtained to more quickly compensate for the misalignment of the device. However, the material properties of the elastomeric shear pads must be taken into account because they strongly influence the final placement of the center.

In many applications, the RCC position is fixed, which means that different RCC devices must be used for different peg lengths. In [10], an adjustable RCC device is presented, and the advantages and disadvantages of this type of device are outlined [11]. In particular, some of the errors of the axis misalignment between peg and hole may not be compensated for. In a structure with a constant stiffness and an established geometry, the position of the RCC is defined and fixed, which implies that the device can be used only for that specific task [12]. Practical solutions to change the position of the compliance center have been designed, including the improvement made along the axis of elastomeric shear pads [13]. By adjusting the insertion depth of a rod in a hole, a variable number of layers is clamped. In this way, lateral stiffness is controlled and different positions of the center of compliance are achieved.

Recently, Camilo et al. [14] presented a deep reinforcement learning approach for the variable compliance control for robotic peg-in-hole assembly, defining the RCC position using software rather than hardware. In Zhang et al. [15], the peg–hole disassembly was presented using active compliance, and, in particular, a quasi-static analysis of peg–hole disassembly with a compliant manipulator was performed. In Lai LJ et al. [16] a formulation of the RCC was proposed based on the stiffness matrix approach. In [17] a system device to align an array was presented, and in [18] a set of flexural hinges was used to create a RCC architecture for assembly operations.

In all of the presented systems, the RCC is defined for devices with compliant beams and elastic parts (e.g., flexural hinges and shear pads). In this paper, the authors attempted to apply the RCC concept to a new linear variable stiffness pneumatic actuator, which was presented for the first time in [19], and named for convenience using the acronym PATuCCo (Pneumatic Actuator with Tunable-Compliance Constraint). To date, a large number of variable stiffness actuators have been developed but, in general, stiffness is controllable only in the same direction of the actuation [20,21,22,23,24,25]. In [19], the authors proposed a novel pneumatic actuator with tunable compliance that is able to modify the general stiffness of its internal constraints due to the use of rolling diaphragm seals for separating the actuator’s chambers. Actuators with rolling deformable membranes have been recently used in soft robotics applications [26]. In this field, the possibility to modify the general stiffness of the soft actuator may lead to the realization of RCC devices with configurable characteristics, opening new frontiers in the field of soft robotics.

To apply the RCC concept to the novel soft actuator presented in [19], the specific constitutive characteristics of our system, which are distinctly different from those of the classical system considered for defining the RCC theory (shown in [27]), obliged us to find a novel formulation of the RCC for the soft actuators. This work is a first step in this direction.

2. RCC Formulation and Adaptation to PATuCCo Actuator

2.1. Remote Center of Compliance (RCC)

Ciblak and Lipkin designed a system consisting of an upper and a lower plate assumed to be rigid and connected by n linkages treated as beams and set out in a truncated-conical arrangement [27]. They considered these lateral beams to be the only compliant elements of the system. A simple sketch of the section of a truncated cone is shown in Figure 1, where E is the center of compliance, E_i is the midpoint of the i-th beam, P is the origin of the reference frame, and O is the geometrical center of the structure.

The complete formulation for the position of the RCC was developed in [27] and, with reference to Figure 1, leads to the following formula:

$${\overline{PE}}_y= \frac{q\left({\lambda }_x+{\lambda }_z\right)\cos \alpha }{{\lambda }_{x}co{s}^2\alpha +{\lambda }_z+{\lambda }_{y}si{n}^2\alpha }$$

(1)

where λ_x, λ_y, and λ_z are the values of linear stiffness along the X, Y, and Z axes, respectively. The other parameters are shown in Figure 1.

As reported in [27] and with reference to Figure 1, Equation (1) allows the calculation of the position of point E, which is the device’s RCC. If a force is applied to the point E, the system will have a displacement without rotation, as shown in Figure 2.

2.2. Pneumatic Actuator with Tunable-Compliance Constraint (PATuCCo)

In [19], Muscolo and Fontana proposed a novel pneumatic actuator with tunable-compliance constraint (PATuCCo); a sketch of this soft actuator is shown in Figure 3.

A sliding piston in a cylinder is surrounded by 2 membranes (upper and lower in Figure 3) arranged in such a way to form a pressure chamber. The pressure (p) inside this chamber is modified to change the compliance of the constraints of the whole system. The cylinder and the piston are both composed of two heads and one middle belt. The belt of the cylinder has a small radial hole for air supply to the pressure chamber, which is delimited by an upper and lower membrane fixed to the belt of the piston and cylinder.

If the cylinder is fixed to the frame, when the piston is moved in the axial direction, membranes roll on the surface of the piston and the cylinder. The advantage of an actuator having two rolling diaphragm seals, instead of classical bearings, is its ability to perform a movement with reduced friction. Unlike a large portion of the variable stiffness systems presented in the literature, where the impedance has the same direction as the actuation [20,21,22], in this design it is possible also to adjust the compliance in the not-actuated directions. This is achieved by modifying the pressure p in the chamber A, while the actuation is modifying the pressure p_B in the chamber B. An actuator that is able to modify its compliance in the not-actuated directions (as in the cases of those presented in this paper and in [19]) presents greater advantages compared to the classical actuators with (or without) variable stiffness in the same direction of the actuation [20,21,22]. These advantages mainly consist in the reduced sensitivity to external perturbations and the ability to be reconfigured.

The characteristics of our actuator with variable stiffness can increase the number of applications in which particular sensitivity and adaptability to the environment are required. In particular, the ability to vary the compliance not only along the direction of actuation, but also in the transversal direction, makes 3D control of the whole mechanical characteristic of the device possible, allowing its use in applications such as precise assembly operations.

3. RCC Formula for the PATuCCo Actuator

Our objective is to apply the RCC concept to the PATuCCo system to identify its center of compliance when geometric properties or stiffness vary. In particular, in the PATuCCo actuator, it is possible to potentially change the position of the RCC by regulating the pressure in the membrane’s chamber and moving the piston along its stroke.

A characteristic which permitted the Remote Compliance Center (RCC) point to be defined in [27] is the asymmetry of the system shown in Figure 1. In [2], Drake noted how the geometry of the system is important in the RCC determination. In particular, it may be noted how the system of the Figure 1 is symmetric with respect to the longitudinal Y axis but asymmetric with respect to a transversal axis which passes from O. However, the existence of a defined RCC (point E in Figure 1) is also due to the convergence of beams to point P.

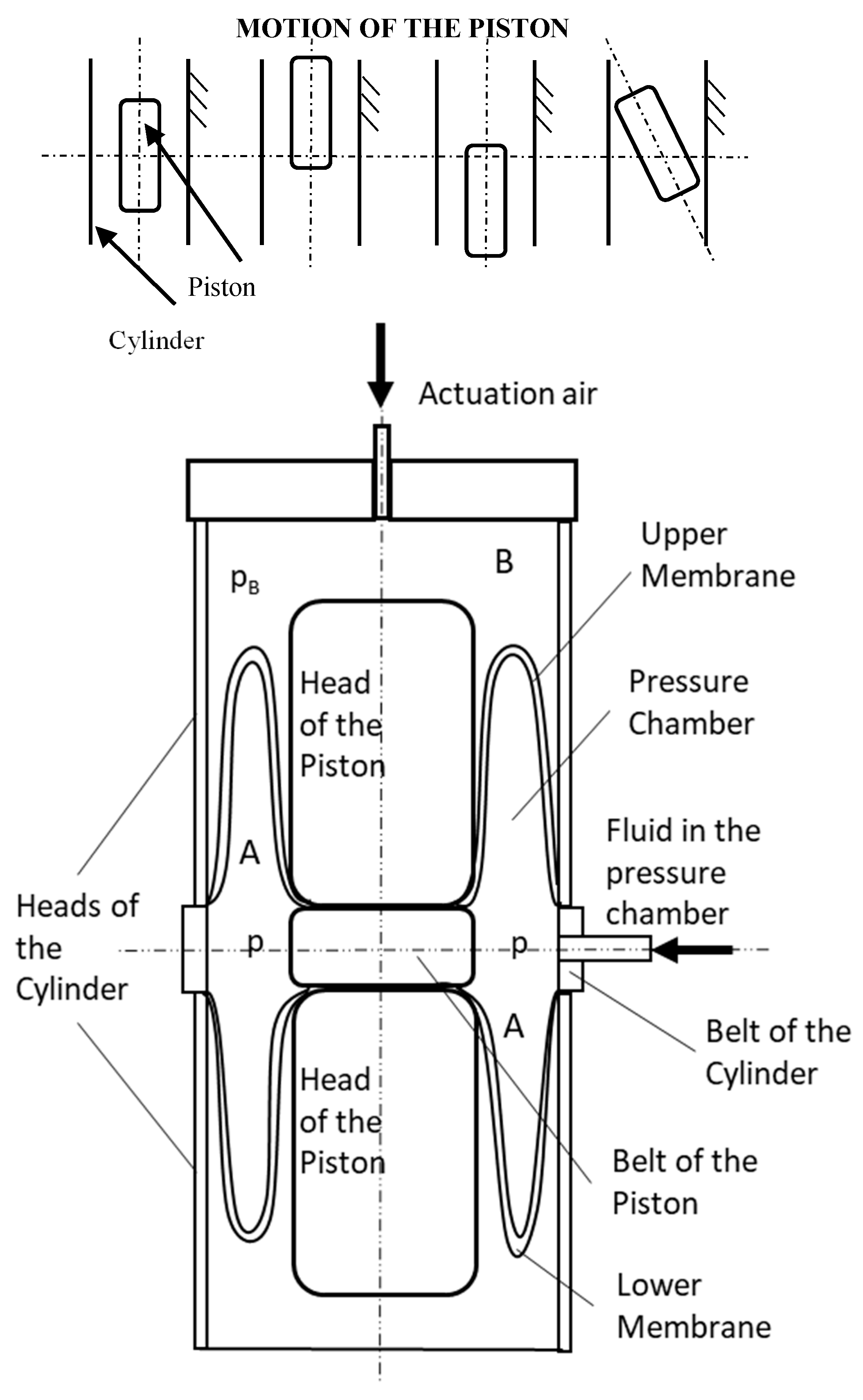
In the PATuCCo actuator shown in Figure 3, it may be shown how the system is symmetric with respect to the axis of the piston and the cylinder, but also with respect to any transversal axis which passes from the belt of the piston and cylinder. To determine a RCC for the PATuCCo actuator in a given position, it is necessary to create and define a corresponding asymmetry with respect to a transversal axis.

Due to the difficulty in predicting the elastic behavior of the membranes, the task of identifying the RCC position in the proposed system shown in Figure 3 is complex. To obtain a design which resembles Lipkin’s system, it is possible to longitudinally displace the piston (actuating the chamber B) to create an asymmetrical configuration. This also avoids the coincidence of the center of compliance with the center of the actuator.

The RCC identification accuracy is influenced by the dimensional characteristics of the whole system and by the dimensional and constitutive characteristics of the membranes. The asymmetrical configuration via the longitudinal displacement is differed by modifying one of these parameters.

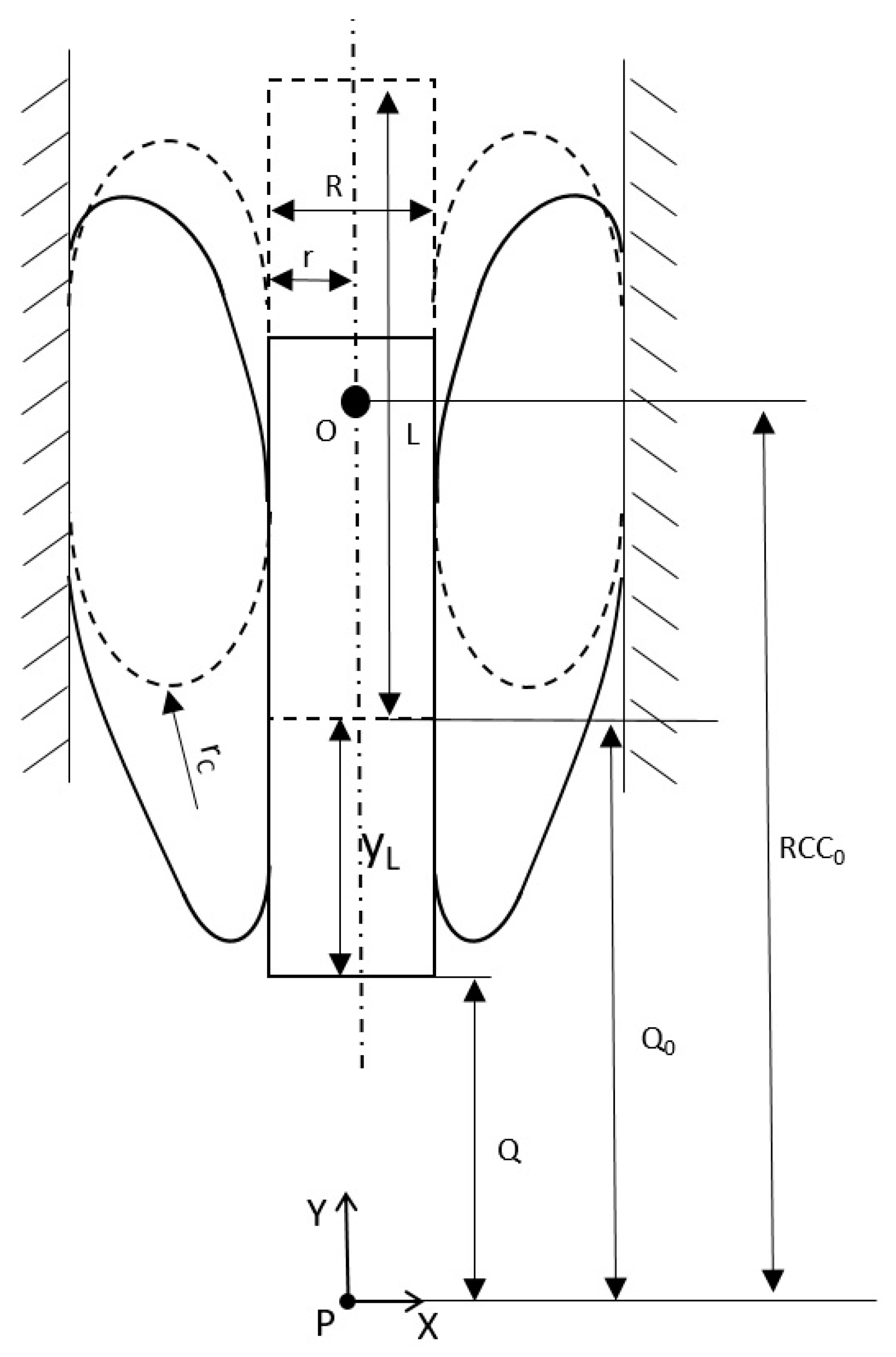
Figure 4 shows the model of the PATuCCo system in the initial condition (dotted line) and when an y_L displacement is imposed on the piston (continuous line). The reference frame X, Y, Z is positioned as in the scheme of Figure 1, and is fixed to the external cylinder. If y_L increases (or Q decreases), the RCC of the device moves along the Y axis of the piston with an almost linear trend. A first formulation to calculate the RCC was empirically derived by the authors of this paper, by analyzing the results of the real device shown in [19]:

$$RCC=RC{C}_0+\left[\frac{\left(b-p\right)}{a}\right]\times \left(Q-Q_0\right)$$

(2)

where

$$RC{C}_0=Q_0+L/2$$

(3)

$$Q=Q_0-y_L$$

(4)

Q₀ and RCC₀ are the initial positions, respectively, of the piston tip and the compliance center, with respect to the used reference frame centered in P, as shown in Figure 4; y_L is the displacement imposed on the piston; p is the actual pressure inside the chamber; L is the length of the piston; a and b are constant pressure values, which are empirically determined.

4. FEM Analysis of the PATuCCo actuator

The behavior of the system was simulated using FEM analysis. Figure 5a shows the used PATuCCo CAD model. The simulations were performed imposing 10 values of y_L (from 1 to 10 mm) and applying a force of 5 N perpendicular to the Y axis at five different points on the piston (see Figure 5b). Simulations were carried out considering 5 values of pressure in the chamber from 0.2 to 1 bar. More trials were also undertaken using 1.5 and 2 bar, highlighting how the membrane buckles (or passes in other configurations) under such conditions. Piston and belts are made of aluminum, whereas membranes are made of silicon and modelled as hyper-elastic materials using the Mooney–Rivlin model:

$$\psi =c_1\left(I_1-3\right)+c_2\left(I_2-3\right)$$

(5)

where $\psi$ is the strain energy function, $c_1$ and $c_2$ are constants, and $I_1$ and $I_2$ are, respectively, the first and the second invariant [25,28]. All of the simulations were performed with: $c_1=0.25 \mathrm{MPa}$, $c_2=0 \mathrm{MPa}$, $density=1000 \mathrm{kg}/{\mathrm{m}}^3$. In our simulations, boundary conditions were chosen in correspondence with Figure 3, in which the cylinder is the fixed frame and the piston is free to move, being connected to the cylinder by means of the upper and lower membranes. In particular, the external belt of Figure 5a represents the belt of the cylinder shown in Figure 3 and was fixed to the frame. The external sides of the upper and lower membranes (in contact with the cylinder) are modelled as a carriage/vertical sliding motion (i.e., one degree of freedom). The same approach was used for the modelling of the internal sides of the membranes (in contact with the piston). This configuration approximates the behavior of the PATuCCo system schematized in Figure 3. A scheme of the constraints used in the FEM model of the membrane is shown in Figure 5c.

In the simulations, the following values were used: Q₀ = 80 mm, L = 100 mm, r = 10 mm, R = 17 mm, r_c = 3.5 mm, thickness of the membrane = 1 mm, a = 0.8744, and b = 0.7205.

5. Results and Discussion

The RCC of the FEM simulation was obtained for each Q value (or y_L displacement) using the following procedure:

(1)

Increasing values of the longitudinal displacement y_L of the piston tip are imposed (see Figure 4);

(2)

At each y_L, a transversal load (parallel to X axis) is applied to different points of the piston, producing a motion of the axis of the piston in the XY plane (translation and rotation);

(3)

The system’s RCC is individuated as the point of the applied load that produces a pure translation (parallel to X axis) of the axis of the piston without rotation.

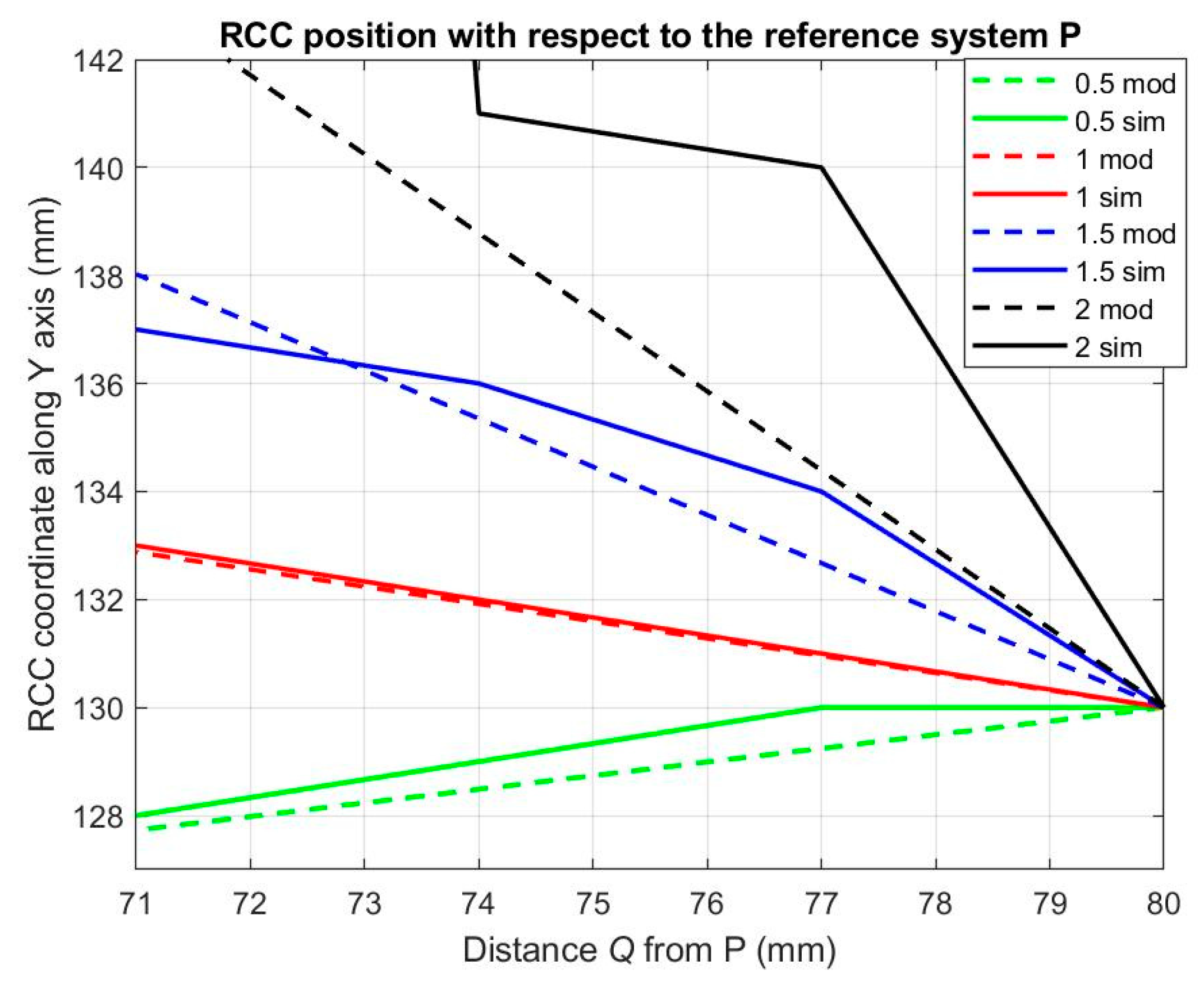
Figure 6 shows the comparison between the RCC position calculated with the empirical model of Formulation (2) (mod in Figure 6) and obtained by the FEM simulation (sim in Figure 6), for a pressure range from 0.2 to 1 bar.

Figure 7 shows the same comparison between the RCC position calculated with the Formulation (2) (mod in Figure 7) and obtained by the FEM simulation (sim in Figure 7), but with a pressure range from 0.5 to 2 bar.

The graphs of Figure 6 and Figure 7 underline how the empirical Model (2) is highly effective for describing the behavior of the whole system for a chamber pressure up to 1 bar, whereas, for pressure greater than 1 bar, Formulation (2) is not able to describe the behavior of the system. After analyzing the results, it emerged that, at higher pressure values (the buckling of membranes may occur or other configurations of the whole system may be created), the nonlinearities of the system are more evident and the simple linear Formulation (2) cannot predict the RCC position.

The errors from the comparison between the FEM simulation and the empirical model were used to optimize the a and b gains of Equation (2), using the MATLAB tool. These gains will be optimized in future experimental tests.

Figure 8 shows the trend of the stiffness of the whole system when a force F_X = 5 N is applied to the piston and the pressure varies from 0.5 to 2 bar. Figure 8 shows that after 1 bar the stiffness of the whole system also decreases if the pressure increases, thus highlighting the buckling of the membranes or the transformation of the whole system in other configurations.

In a real-life scenario, a soft actuator must be used in the functional operation ranges, excluding all buckling cases (which must be studied in future works). The commercial rolling diaphragm seals are produced using hyper-elastic membranes reinforced with fibers. To increase the performance and avoid the buckling condition, this solution should also be adopted for the future production of the PATuCCo actuator.

Figure 9 shows the results obtained if a linear force Fx of 5 N is applied at five different points equally spaced along the Y axis as shown in Figure 5b. It may be noted that when the piston is still in its original position (Q = Q₀ = 80 mm and y_L = 0 mm), the RCC is in the center of the piston (130 mm with respect to the reference system) for every pressure value. Consistent with the previous results, the stiffness is greater for a pressure of 1 bar, which corresponds to smaller rotations for the same point at which the force is applied, whereas, as expected, the graphs relating to 2 bar are unreliable for the reasons explained above. The maximum stiffness is in the geometrical center of the system.

In Figure 10, the results show how the linear stiffness of the whole system varies as a function of the y_l displacement. In particular, if the displacement increases (y_l = 3 mm, y_l = 6 mm, y_l = 9 mm in Figure 10) the stiffness will increase its value more for a lower (0.5 bar) then a higher value (1.5 bar) of pressure.

6. Conclusions

In this work, an original variable Remote Center of Compliance (RCC) device obtained from a novel soft pneumatic actuator was studied. The device is equipped with a particular structure that also allows varying its stiffness in the not-actuated directions. The position of the RCC was determined by studying the symmetrical constraints of the device, as performed by past works on RCC, and a simple formulation based on the device characteristics and the operating pressures was proposed. Comparison with FEM analysis demonstrated the effectiveness of this formulation for the pressure range 0.2–1 bar. While keeping in mind the original characteristics of our device, its performance was compared with that of some of the RCC devices described in the literature. Ciblak and Lipkin [27] conducted a FEM simulation of their system, evaluating a stiffness of about 131 N/mm with a lateral displacement of the RCC point of about 5.08 mm. The variable RCC device proposed by Zhao et al. [29] presents a lateral stiffness of the device of 133.3 N/mm, which is able to modify the longitudinal RCC position from 42 to 160 mm. Our proposed device is softer because, in the current configuration, the lateral stiffness can vary between 4 and 15 N/mm. However, a significant increase could be achieved using membranes with a textile reinforcement, which is less subject to the buckling phenomenon. In addition, the regulation range of the RCC position, which currently varies between 125 and 221 mm, can be widened with the use of more performing membranes. Ultimately, the results of this work demonstrate the feasibility of soft RCC devices, highlighting possible new scenarios in the field of soft robotics. In the near future it is planned to create several prototypes, in various configurations, to evaluate their characteristics and verify the effectiveness of the empirical model.