Simulation of an Autonomous Mobile Robot for LiDAR-Based In-Field Phenotyping and Navigation
Abstract
1. Introduction
2. Materials and Methods
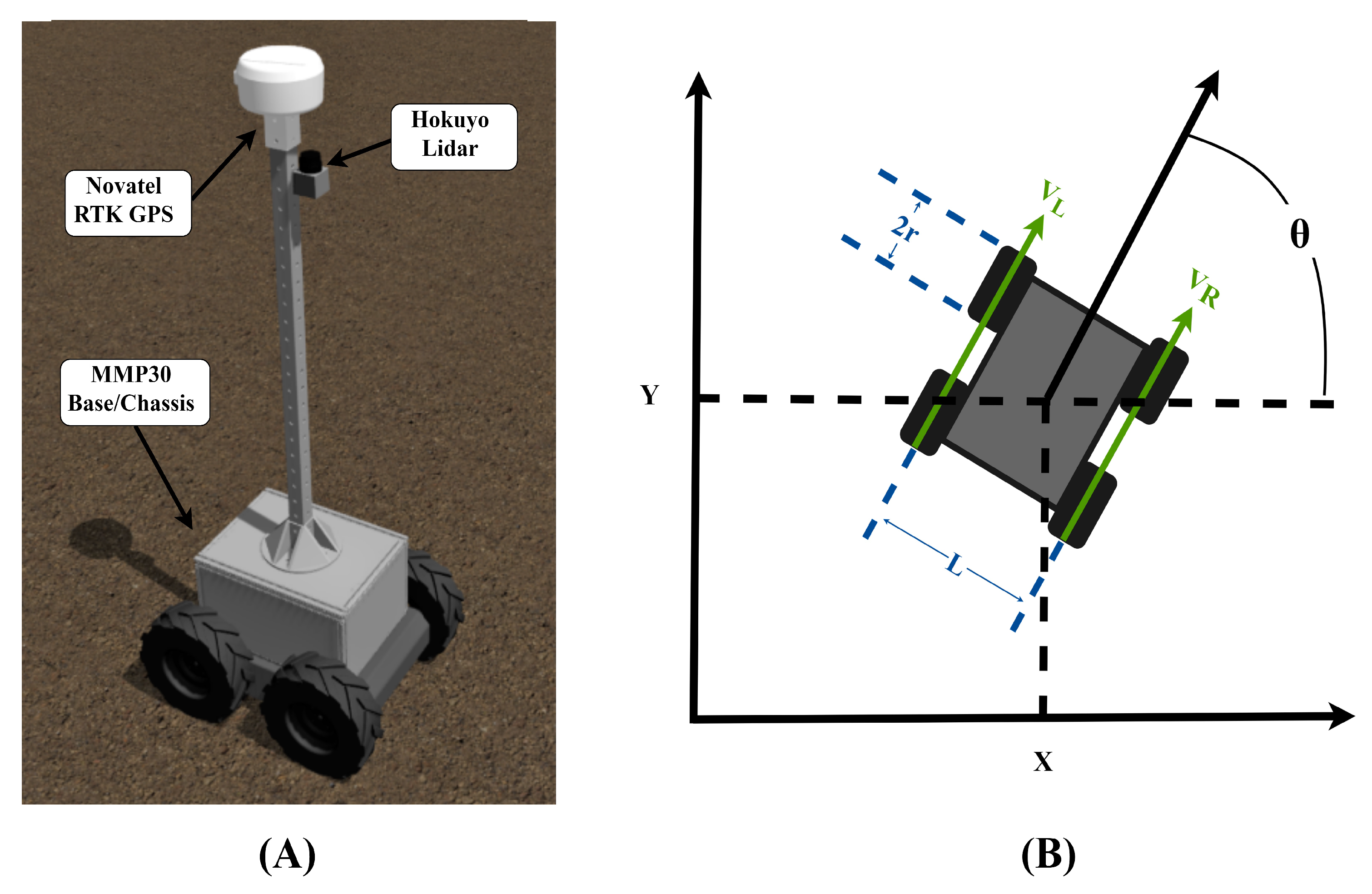
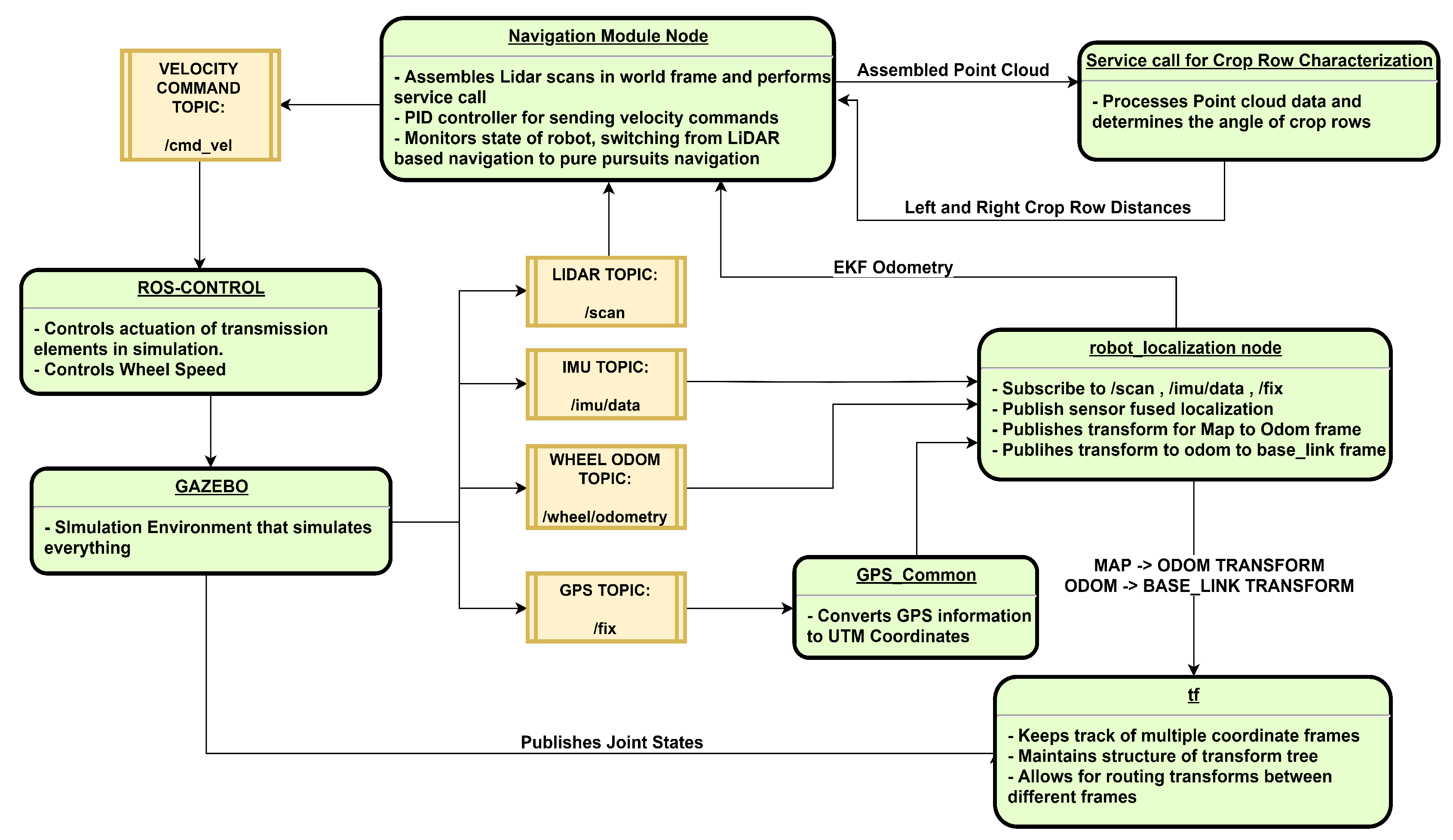
2.1. ROS Mobile System Overview
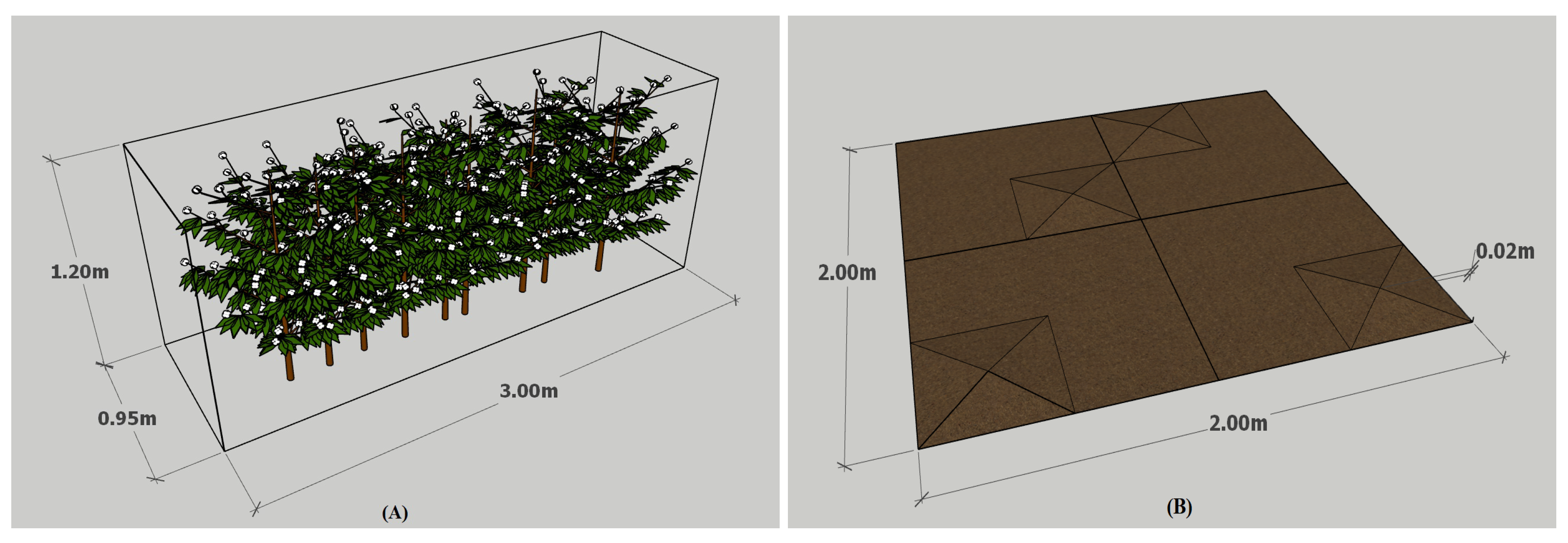
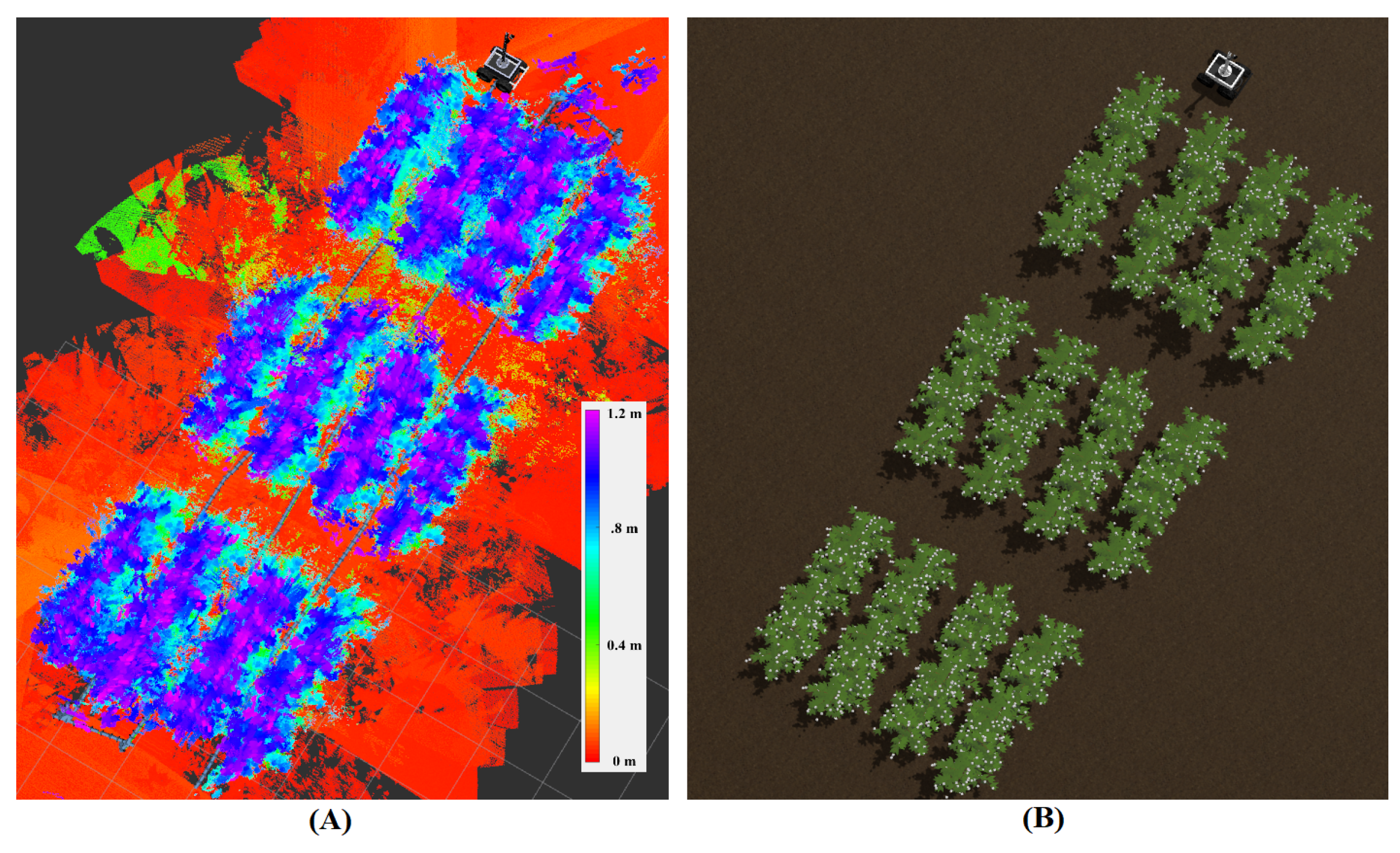
2.2. Simulation World
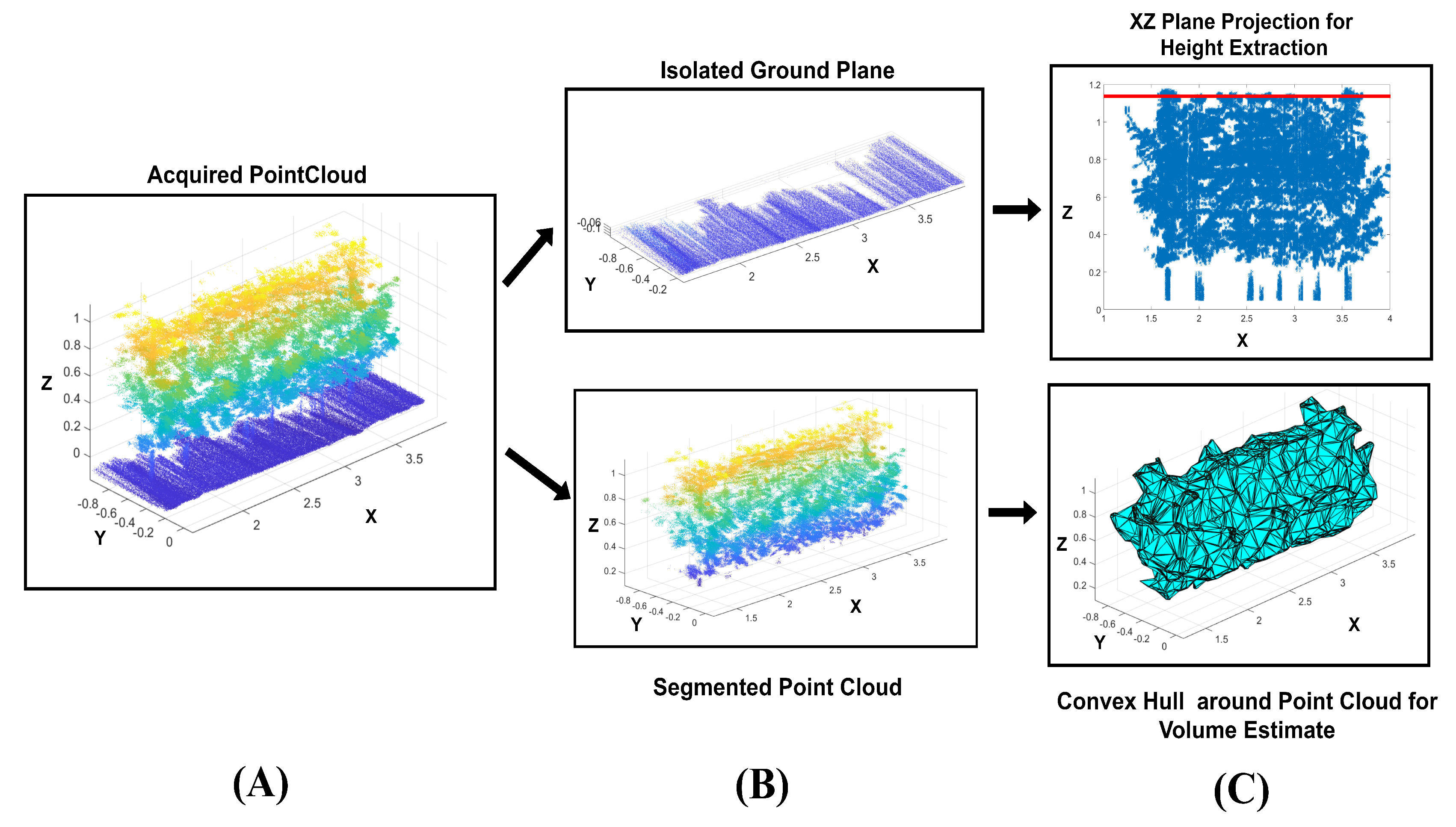
2.3. Experiment/Analysis Phenotypic Analysis
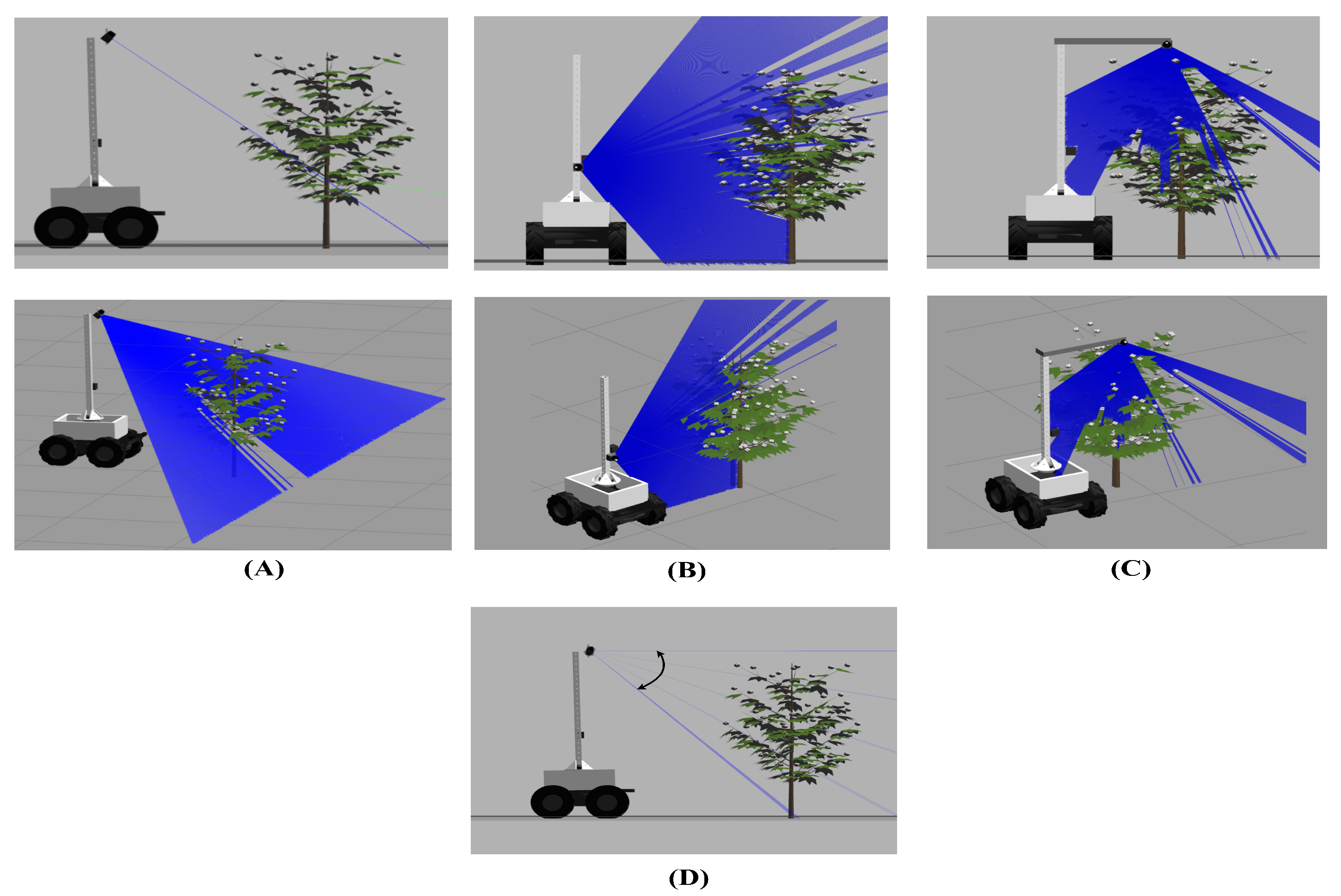
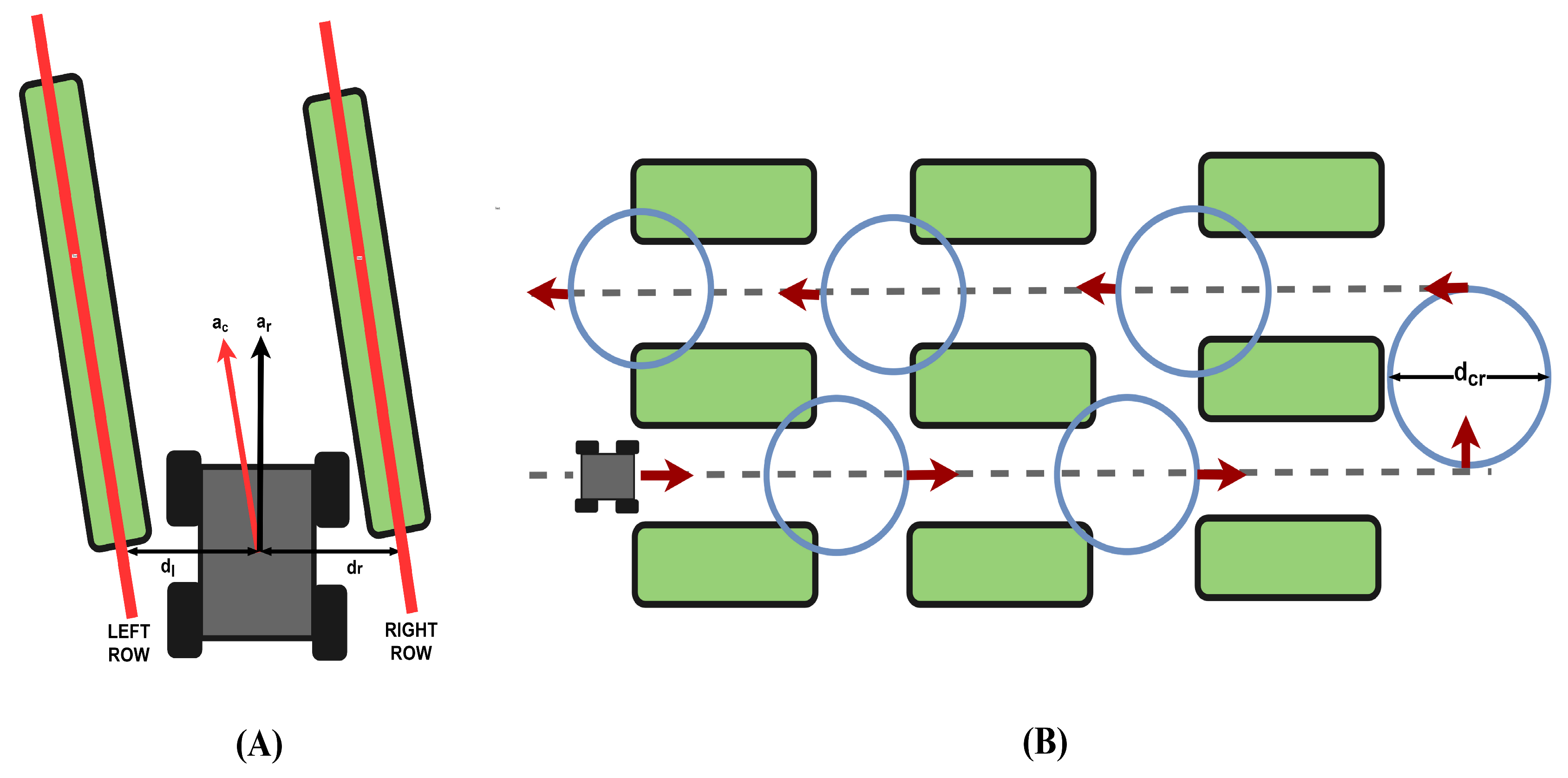
LiDAR Configurations
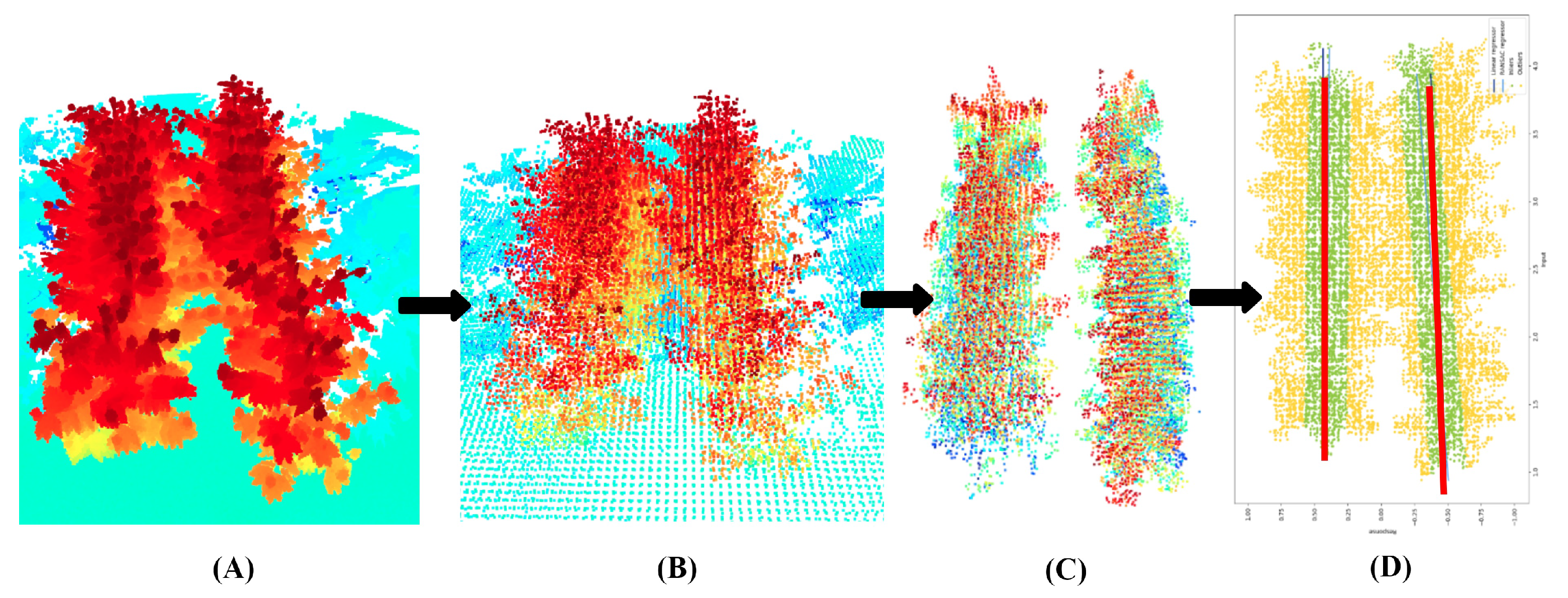
2.4. Experiment/Analysis Nodding LiDAR Configuration for Navigation Through Cotton Crops
LiDAR Processing Strategy
2.5. ROS Node Structure
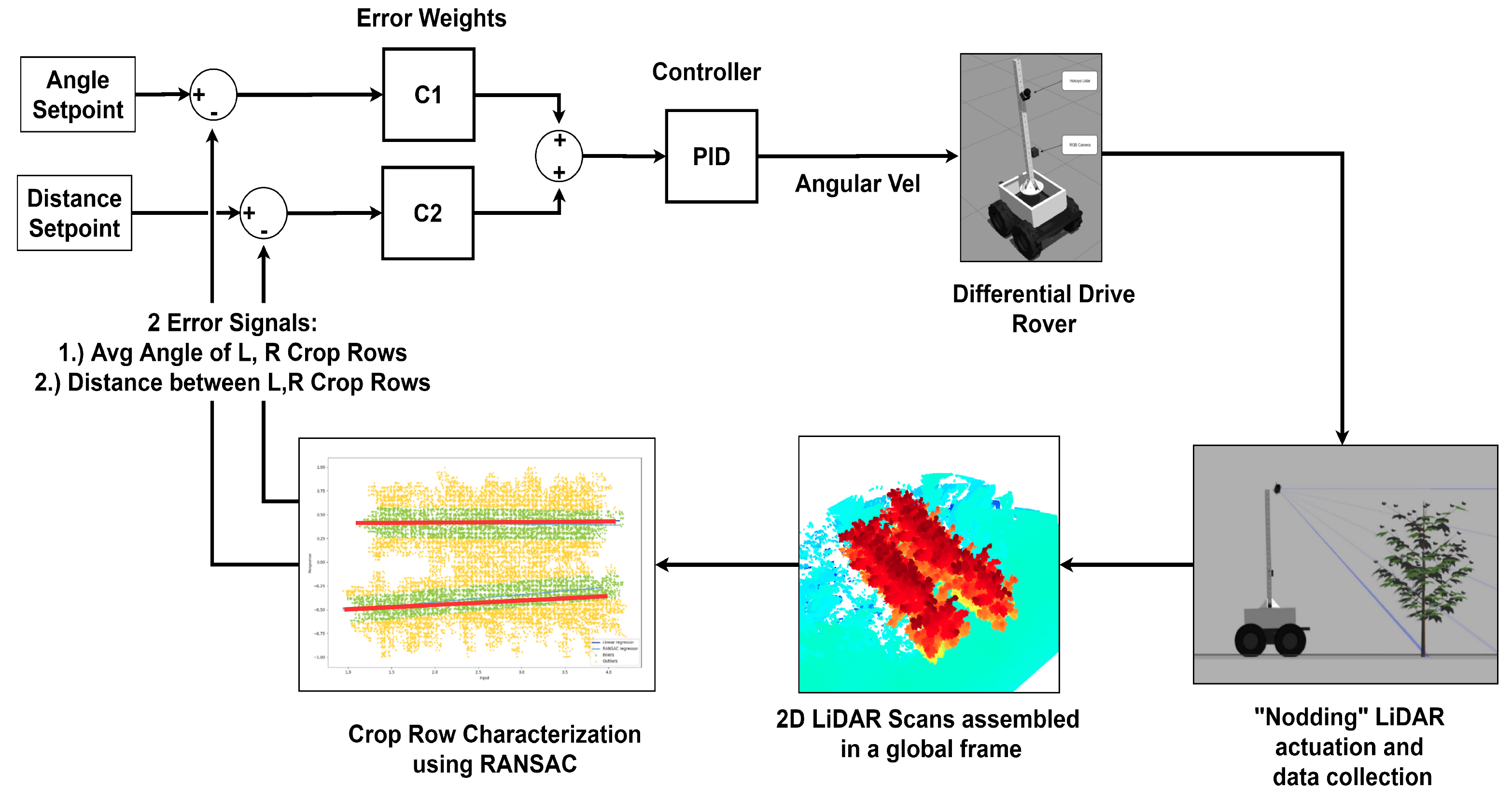
2.5.1. Control Loop for Crop Row Navigation
2.5.2. Complete Navigation Algorithm
| Algorithm 1: Complete Navigation Algorithm |
 |
3. Results and Discussion
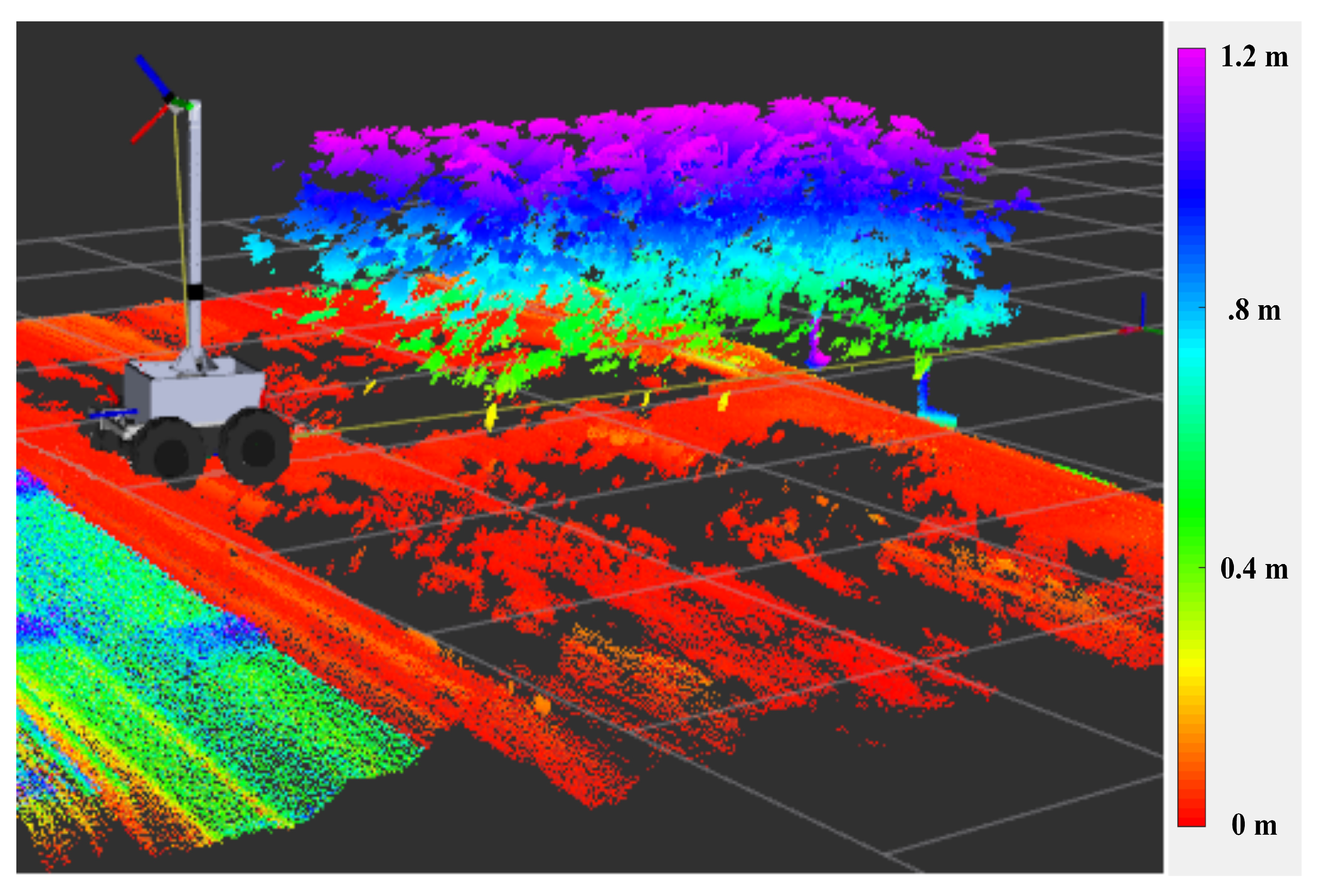
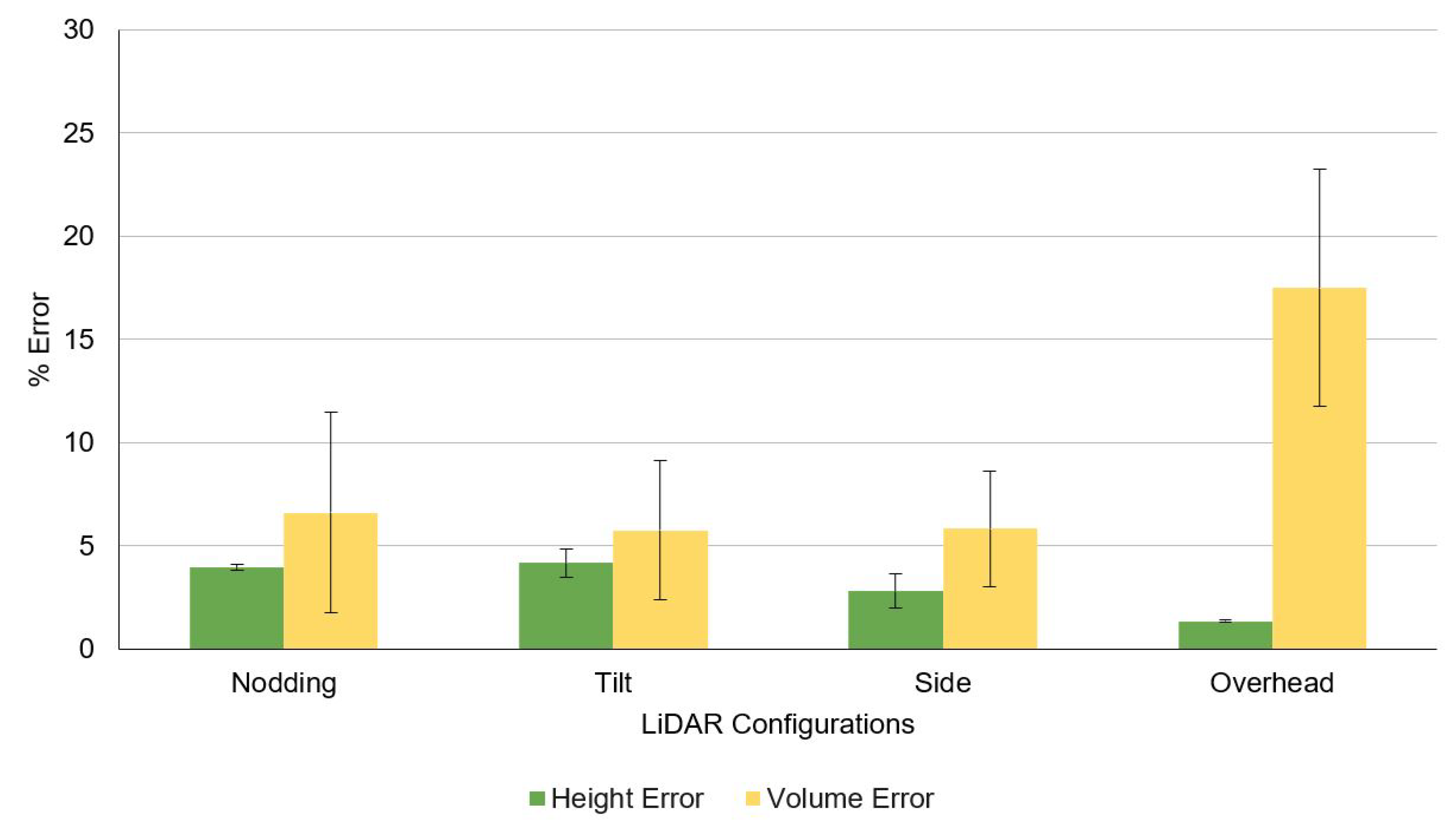
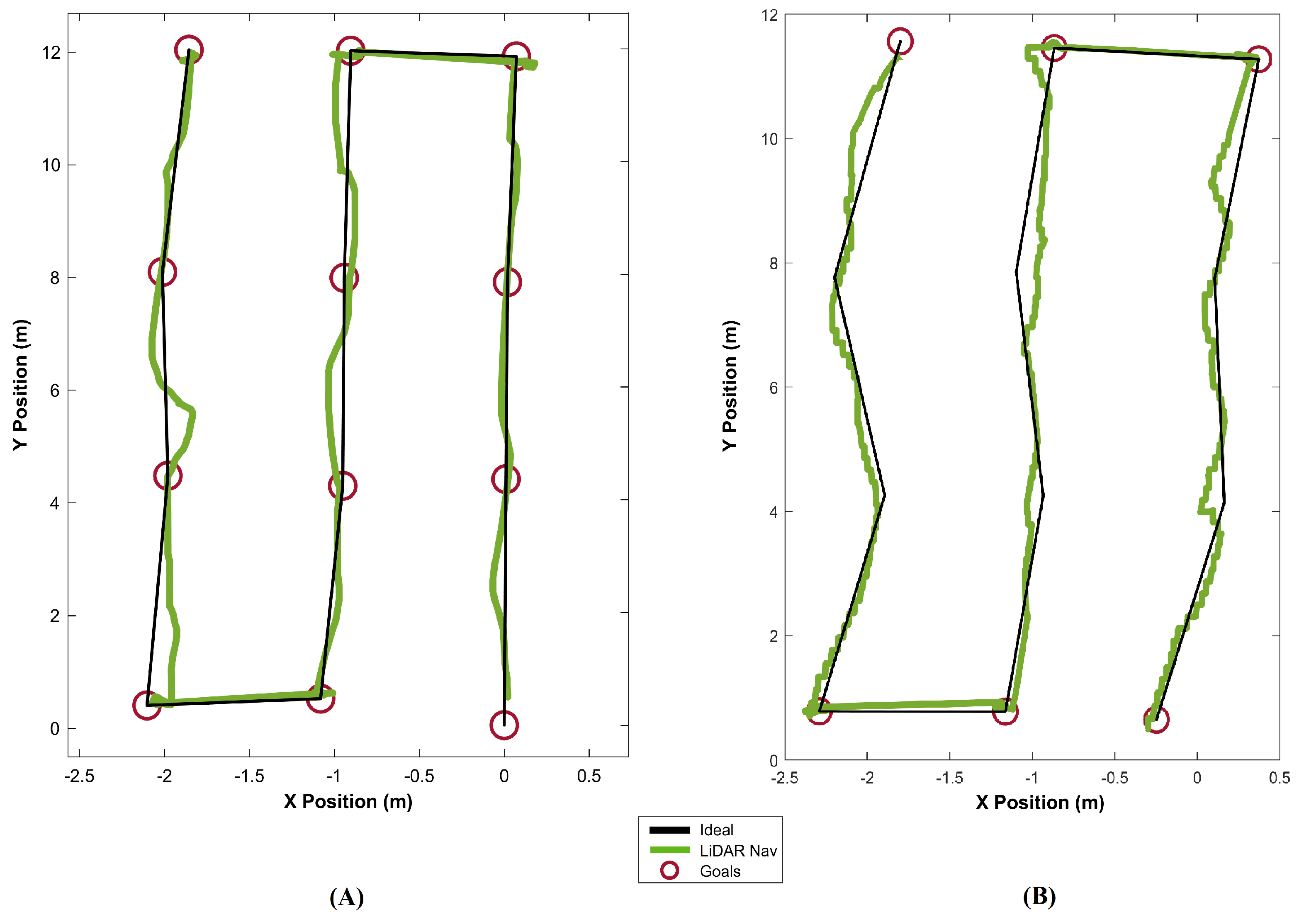
3.1. Phenotyping and Navigation Results
3.2. Discussion and Future Work
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Campbell, Z.C.; Acosta-Gamboa, L.M.; Nepal, N.; Lorence, A. Engineering plants for tomorrow: How high-throughput phenotyping is contributing to the development of better crops. Phytochem. Rev. 2018, 17, 1329–1343. [Google Scholar] [CrossRef]
- Jannink, J.L.; Lorenz, A.J.; Iwata, H. Genomic selection in plant breeding: From theory to practice. Brief. Funct. Genom. 2010, 9, 166–177. [Google Scholar] [CrossRef] [PubMed]
- Fiorani, F.; Schurr, U. Future scenarios for plant phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Furbank, R.T.; Tester, M. Phenomics – technologies to relieve the phenotyping bottleneck. Trends Plant Sci. 2011, 16, 635–644. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Lin, Y.; Wang, Z.; Yao, Y.; Zhang, Y.; Wu, L. Validation of a low-cost 2D laser scanner in development of a more-affordable mobile terrestrial proximal sensing system for 3D plant structure phenotyping in indoor environment. Comput. Electron. Agric. 2017, 140, 180–189. [Google Scholar] [CrossRef]
- Pabuayon, I.L.B.; Sun, Y.; Guo, W.; Ritchie, G.L. High-throughput phenotyping in cotton: A review. J. Cotton Res. 2019, 2, 18. [Google Scholar] [CrossRef]
- Sun, S.; Li, C.; Paterson, A.H. In-Field High-Throughput Phenotyping of Cotton Plant Height Using LiDAR. Remote Sens. 2017, 9, 377. [Google Scholar] [CrossRef]
- Sun, S.; Li, C.; Paterson, A.H.; Jiang, Y.; Xu, R.; Robertson, J.S.; Snider, J.L.; Chee, P.W. In-field High Throughput Phenotyping and Cotton Plant Growth Analysis Using LiDAR. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Wu, F.; Pang, S.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. Stem–Leaf Segmentation and Phenotypic Trait Extraction of Individual Maize Using Terrestrial LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1336–1346. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Paterson, A.H. High throughput phenotyping of cotton plant height using depth images under field conditions. Comput. Electron. Agric. 2016, 130, 57–68. [Google Scholar] [CrossRef]
- Zotz, G.; Hietz, P.; Schmidt, G. Small plants, large plants: The importance of plant size for the physiological ecology of vascular epiphytes. J. Exp. Bot. 2001, 52, 2051–2056. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Grift, T.E. A LIDAR-based crop height measurement system for Miscanthus giganteus. Comput. Electron. Agric. 2012, 85, 70–76. [Google Scholar] [CrossRef]
- Jimenez-Berni, J.A.; Deery, D.M.; Rozas-Larraondo, P.; Condon, A.G.; Rebetzke, G.J.; James, R.A.; Bovill, W.D.; Furbank, R.T.; Sirault, X.R.R. High Throughput Determination of Plant Height, Ground Cover, and Above-Ground Biomass in Wheat with LiDAR. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Llop, J.; Gil, E.; Llorens, J.; Miranda-Fuentes, A.; Gallart, M. Testing the Suitability of a Terrestrial 2D LiDAR Scanner for Canopy Characterization of Greenhouse Tomato Crops. Sensors 2016, 16, 1435. [Google Scholar] [CrossRef]
- White, J.W.; Andrade-Sanchez, P.; Gore, M.A.; Bronson, K.F.; Coffelt, T.A.; Conley, M.M.; Feldmann, K.A.; French, A.N.; Heun, J.T.; Hunsaker, D.J.; et al. Field-based phenomics for plant genetics research. Field Crops Res. 2012, 133, 101–112. [Google Scholar] [CrossRef]
- Vidoni, R.; Gallo, R.; Ristorto, G.; Carabin, G.; Mazzetto, F.; Scalera, L.; Gasparetto, A. ByeLab: An Agricultural Mobile Robot Prototype for Proximal Sensing and Precision Farming. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; p. V04AT05A057. [Google Scholar] [CrossRef]
- Bietresato, M.; Carabin, G.; D’Auria, D.; Gallo, R.; Ristorto, G.; Mazzetto, F.; Vidoni, R.; Gasparetto, A.; Scalera, L. A tracked mobile robotic lab for monitoring the plants volume and health. In Proceedings of the 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar]
- French, A.; Gore, M.; Thompson, A. Cotton phenotyping with lidar from a track-mounted platform. In Proceedings of the SPIE Commercial + Scientific Sensing and Imaging, Baltimore, MD, USA, 17 May 2016; Volume 9866. [Google Scholar]
- Mueller-Sim, T.; Jenkins, M.; Abel, J.; Kantor, G. The Robotanist: A ground-based agricultural robot for high-throughput crop phenotyping. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3634–3639. [Google Scholar] [CrossRef]
- Reiser, D.; Vázquez-Arellano, M.; Paraforos, D.S.; Garrido-Izard, M.; Griepentrog, H.W. Iterative individual plant clustering in maize with assembled 2D LiDAR data. Comput. Ind. 2018, 99, 42–52. [Google Scholar] [CrossRef]
- Harchowdhury, A.; Kleeman, L.; Vachhani, L. Coordinated Nodding of a Two-Dimensional Lidar for Dense Three-Dimensional Range Measurements. IEEE Rob. Autom. Lett. 2018, 3, 4108–4115. [Google Scholar] [CrossRef]
- Bosse, M.; Zlot, R.; Flick, P. Zebedee: Design of a Spring-Mounted 3-D Range Sensor with Application to Mobile Mapping. IEEE Trans. Rob. 2012, 28, 1104–1119. [Google Scholar] [CrossRef]
- Mousazadeh, H. A technical review on navigation systems of agricultural autonomous off-road vehicles. J. Terramech. 2013, 50, 211–232. [Google Scholar] [CrossRef]
- Bonadies, S.; Gadsden, S.A. An overview of autonomous crop row navigation strategies for unmanned ground vehicles. Eng. Agric. Environ. Food 2019, 12, 24–31. [Google Scholar] [CrossRef]
- Bakker, T.; Asselt, K.; Bontsema, J.; Müller, J.; Straten, G. Systematic design of an autonomous platform for robotic weeding. J. Terramech. 2010, 47, 63–73. [Google Scholar] [CrossRef]
- Nagasaka, Y.; Saito, H.; Tamaki, K.; Seki, M.; Kobayashi, K.; Taniwaki, K. An autonomous rice transplanter guided by global positioning system and inertial measurement unit. J. Field Rob. 2009, 26, 537–548. [Google Scholar] [CrossRef]
- Blackmore, B.; Griepentrog, H.W.; Nielsen, H.; Nørremark, M.; Resting-Jeppesen, J. Development of a deterministic autonomous tractor. In Proceeding of the CIGR International Conference, Beijing, China, 11–14 November 2004. [Google Scholar]
- Yang, L.; Noguchi, N. Development of a Wheel-Type Robot Tractor and its Utilization. IFAC Proc. Volumes 2014, 47, 11571–11576. [Google Scholar] [CrossRef]
- Ollero, A.; Heredia, G. Stability analysis of mobile robot path tracking. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; pp. 461–466. [Google Scholar]
- Samuel, M.; Hussein, M.; Mohamad, M.B. A review of some pure-pursuit based path tracking techniques for control of autonomous vehicle. Int. J. Comput. Appl. 2016, 135, 35–38. [Google Scholar] [CrossRef]
- Normey-Rico, J.E.; Alcalá, I.; Gómez-Ortega, J.; Camacho, E.F. Mobile robot path tracking using a robust PID controller. Control Eng. Pract. 2001, 9, 1209–1214. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, Z.; Zhao, Z.; Chen, B.; Hu, L.; Wu, X. Design of DGPS navigation control system for Dongfanghong X-804 tractor. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2009, 25, 139–145. [Google Scholar] [CrossRef]
- Reina, G.; Milella, A.; Rouveure, R.; Nielsen, M.; Worst, R.; Blas, M.R. Ambient awareness for agricultural robotic vehicles. Biosyst. Eng. 2016, 146, 114–132. [Google Scholar] [CrossRef]
- Rovira-Más, F.; Chatterjee, I.; Sáiz-Rubio, V. The role of GNSS in the navigation strategies of cost-effective agricultural robots. Comput. Electron. Agric. 2015, 112, 172–183. [Google Scholar] [CrossRef]
- Pedersen, S.; Fountas, S.; Have, H.; Blackmore, B. Agricultural robots—system analysis and economic feasibility. Precision Agric. 2006, 7, 295–308. [Google Scholar] [CrossRef]
- Malavazi, F.B.P.; Guyonneau, R.; Fasquel, J.B.; Lagrange, S.; Mercier, F. LiDAR-only based navigation algorithm for an autonomous agricultural robot. Comput. Electron. Agric. 2018, 154, 71–79. [Google Scholar] [CrossRef]
- Higuti, V.A.H.; Velasquez, A.E.B.; Magalhaes, D.V.; Becker, M.; Chowdhary, G. Under canopy light detection and ranging-based autonomous navigation. J. Field Rob. 2019, 36, 547–567. [Google Scholar] [CrossRef]
- Velasquez, A.; Higuti, V.; Borrero GUerrero, H.; Valverde Gasparino, M.; Magalhães, D.; Aroca, R.; Becker, M. Reactive navigation system based on H∞ control system and LiDAR readings on corn crops. Precis. Agric. 2019. [Google Scholar] [CrossRef]
- Blok, P.M.; van Boheemen, K.; van Evert, F.K.; IJsselmuiden, J.; Kim, G.H. Robot navigation in orchards with localization based on Particle filter and Kalman filter. Comput. Electron. Agric. 2019, 157, 261–269. [Google Scholar] [CrossRef]
- Shamshiri, R.; Hameed, I.; Karkee, M.; Weltzien, C. Robotic Harvesting of Fruiting Vegetables, A Simulation Approach in V-REP, ROS and MATLAB; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Fountas, S.; Mylonas, N.; Malounas, I.; Rodias, E.; Hellmann Santos, C.; Pekkeriet, E. Agricultural Robotics for Field Operations. Sensors 2020, 20, 2672. [Google Scholar] [CrossRef] [PubMed]
- Le, T.D.; Ponnambalam, V.R.; Gjevestad, J.G.O.; From, P.J. A low-cost and efficient autonomous row-following robot for food production in polytunnels. J. Field Rob. 2020, 37, 309–321. [Google Scholar] [CrossRef]
- Habibie, N.; Nugraha, A.M.; Anshori, A.Z.; Ma’sum, M.A.; Jatmiko, W. Fruit mapping mobile robot on simulated agricultural area in Gazebo simulator using simultaneous localization and mapping (SLAM). In Proceedings of the 2017 International Symposium on Micro-NanoMechatronics and Human Science (MHS), Nagoya, Japan, 3–6 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Grimstad, L.; From, P. Software Components of the Thorvald II Modular Robot. Model. Identif. Control A Nor. Res. Bull. 2018, 39, 157–165. [Google Scholar] [CrossRef]
- Sharifi, M.; Young, M.S.; Chen, X.; Clucas, D.; Pretty, C. Mechatronic design and development of a non-holonomic omnidirectional mobile robot for automation of primary production. Cogent Eng. 2016, 3. [Google Scholar] [CrossRef]
- Weiss, U.; Biber, P. Plant detection and mapping for agricultural robots using a 3D LiDAR sensor. Rob. Autom. Syst. 2011, 59, 265–273. [Google Scholar] [CrossRef]
- Hector_gazebo_plugins–ROS Wiki. Available online: http://wiki.ros.org/hector_gazebo_plugins (accessed on 31 May 2020).
- MasayasuIwase. Scanning Rangefinder Distance Data Output/UTM-30LX Product Details | HOKUYO AUTOMATIC CO., LTD. Available online: https://www.hokuyo-aut.jp/search/single.php?serial=169 (accessed on 31 May 2020).
- Kragh, M.; Jørgensen, R.N.; Pedersen, H. Object Detection and Terrain Classification in Agricultural Fields Using 3D LiDAR Data. In Proceedings of the International Conference on Computer Vision Systems, Copenhagen, Denmark, 6–9 July 2015; pp. 188–197. [Google Scholar]
- Shamshiri, R.; Hameed, I.; Pitonakova, L.; Weltzien, C.; Balasundram, S.; Yule, I.; Grift, T.; Chowdhary, G. Simulation software and virtual environments for acceleration of agricultural robotics: Features highlights and performance comparison. Int. J. Agric. Biol. Eng. 2018, 11, 15–31. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, J.; Xu, R.; Sun, S.; Li, C. Simulation of an Autonomous Mobile Robot for LiDAR-Based In-Field Phenotyping and Navigation. Robotics 2020, 9, 46. https://doi.org/10.3390/robotics9020046
Iqbal J, Xu R, Sun S, Li C. Simulation of an Autonomous Mobile Robot for LiDAR-Based In-Field Phenotyping and Navigation. Robotics. 2020; 9(2):46. https://doi.org/10.3390/robotics9020046
Chicago/Turabian StyleIqbal, Jawad, Rui Xu, Shangpeng Sun, and Changying Li. 2020. "Simulation of an Autonomous Mobile Robot for LiDAR-Based In-Field Phenotyping and Navigation" Robotics 9, no. 2: 46. https://doi.org/10.3390/robotics9020046
APA StyleIqbal, J., Xu, R., Sun, S., & Li, C. (2020). Simulation of an Autonomous Mobile Robot for LiDAR-Based In-Field Phenotyping and Navigation. Robotics, 9(2), 46. https://doi.org/10.3390/robotics9020046





