Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments
Abstract
1. Introduction
- We propose an approach using simple cell-to-cell mapping [19] to find a joint trajectory of multiple bouncing robots for covering a known environment.
- We also present an algorithm to generate the collision-free and overlapping trajectories of multiple robots that monitor some regions of interest in an environment persistently.
2. Related Work
2.1. Coverage
2.2. Persistent Monitoring
3. Preliminaries
3.1. Motion Model
3.2. Cell-to-Cell Mapping
3.3. Problem Formulation
4. Approach
4.1. Finding a Joint Trajectory of Multiple Robots for Coverage
| Algorithm 1: MultiRobotCoverage () |
 |
4.2. Generating Periodic Groups for Persistent Monitoring of Target Regions
| Algorithm 2: PersistentBehavior() |
 |
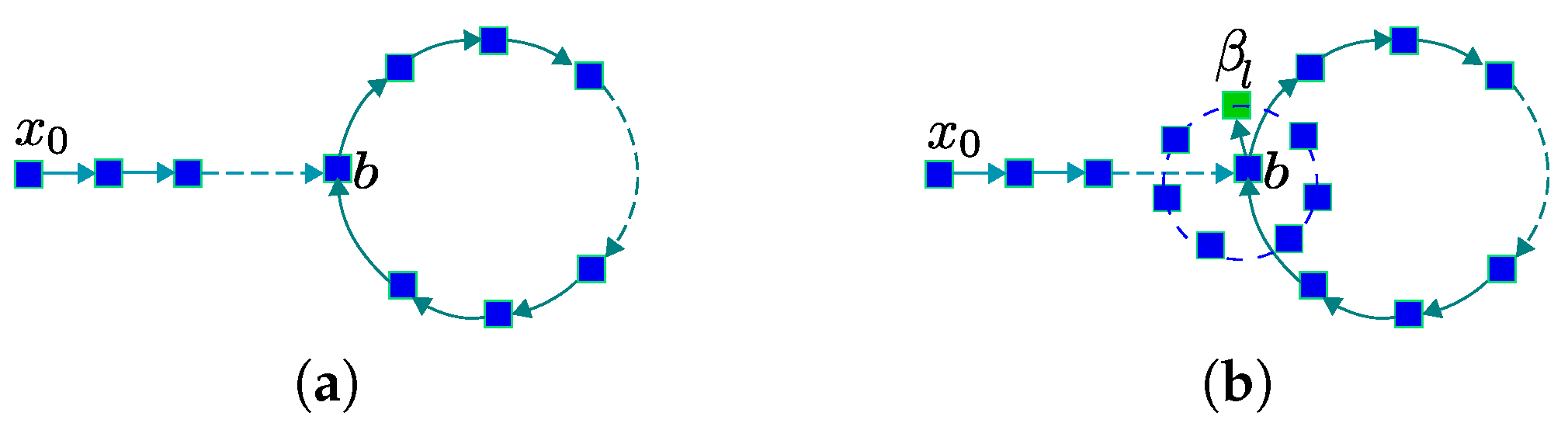
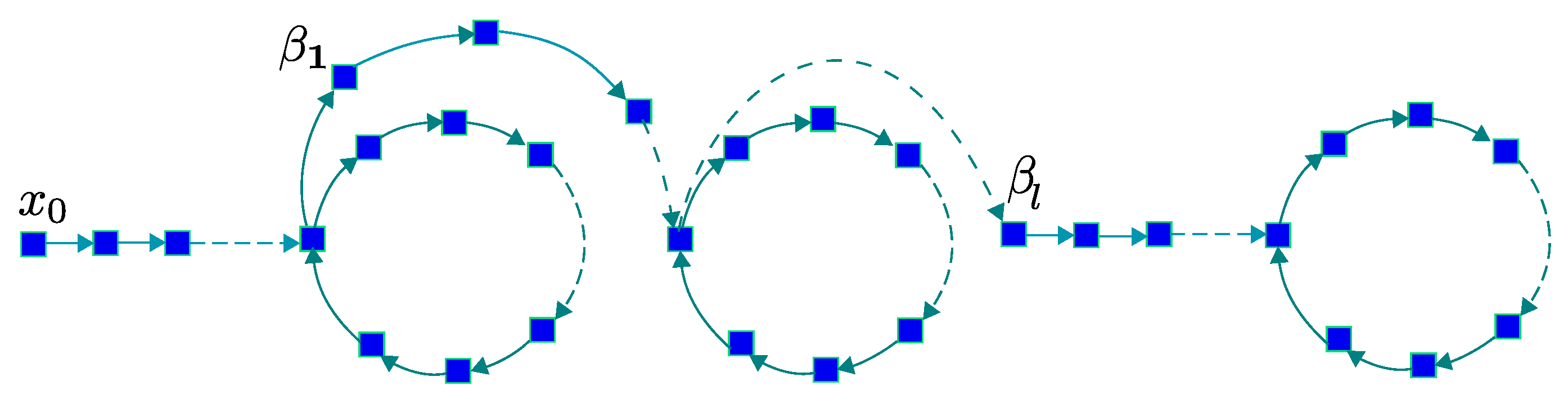
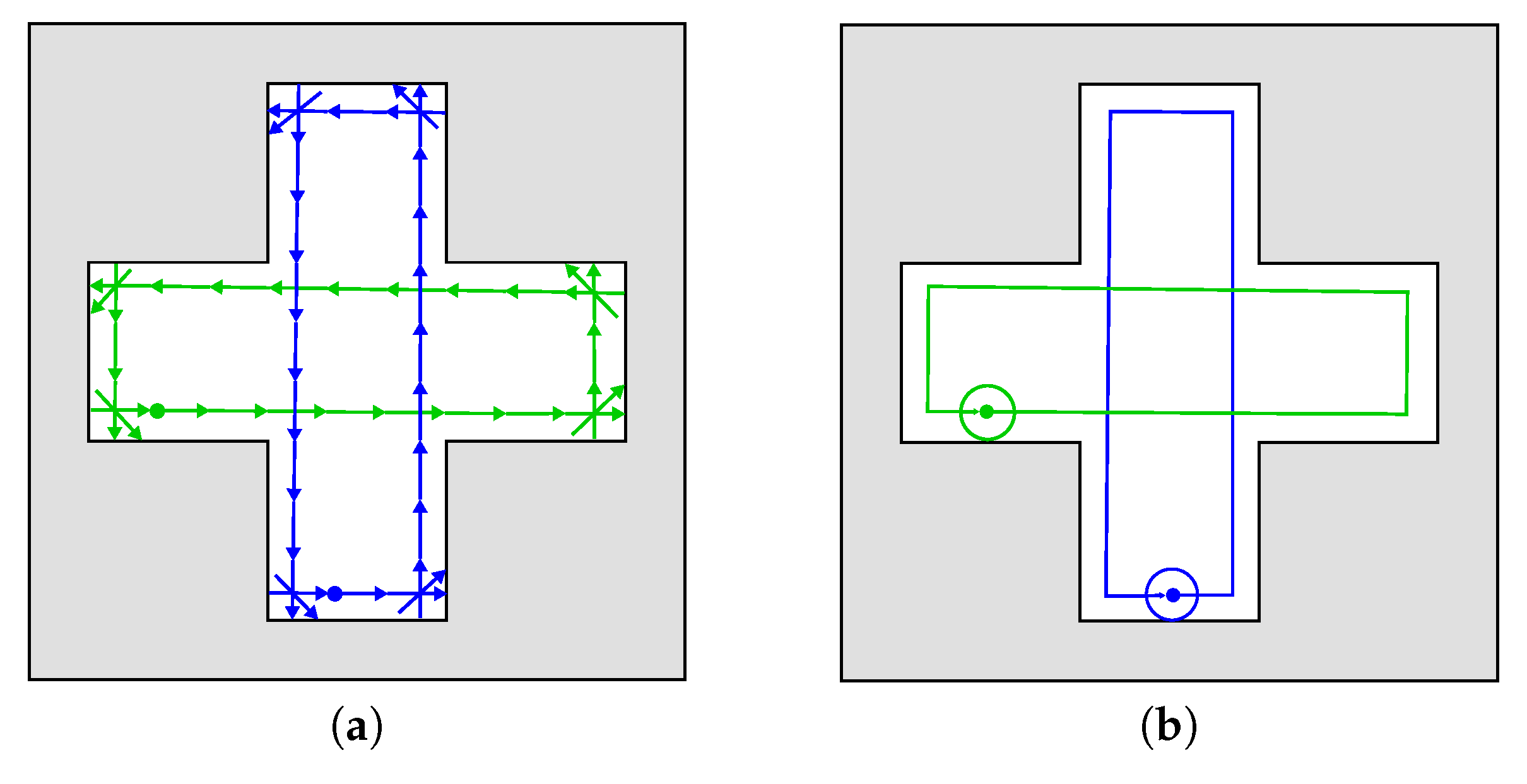
- If b is both the initial cell and the ending cell of the sequence (the first scenario of Figure 5a), all cells starting from the initial cell of the sequence till the end of the sequence are classified as periodic cells and they form the periodic group.
- If b is not the initial cell of this sequence (the second scenario of Figure 5b), then after determining the first b-th position in this sequence, which is , all cells starting from the -th cell until the end of the sequence are classified as periodic cells. However, all cells ranging from the initial cell of the sequence to the -th cell are classified as transient cells, and they form the transient trajectory.
5. Simulations and Experiments
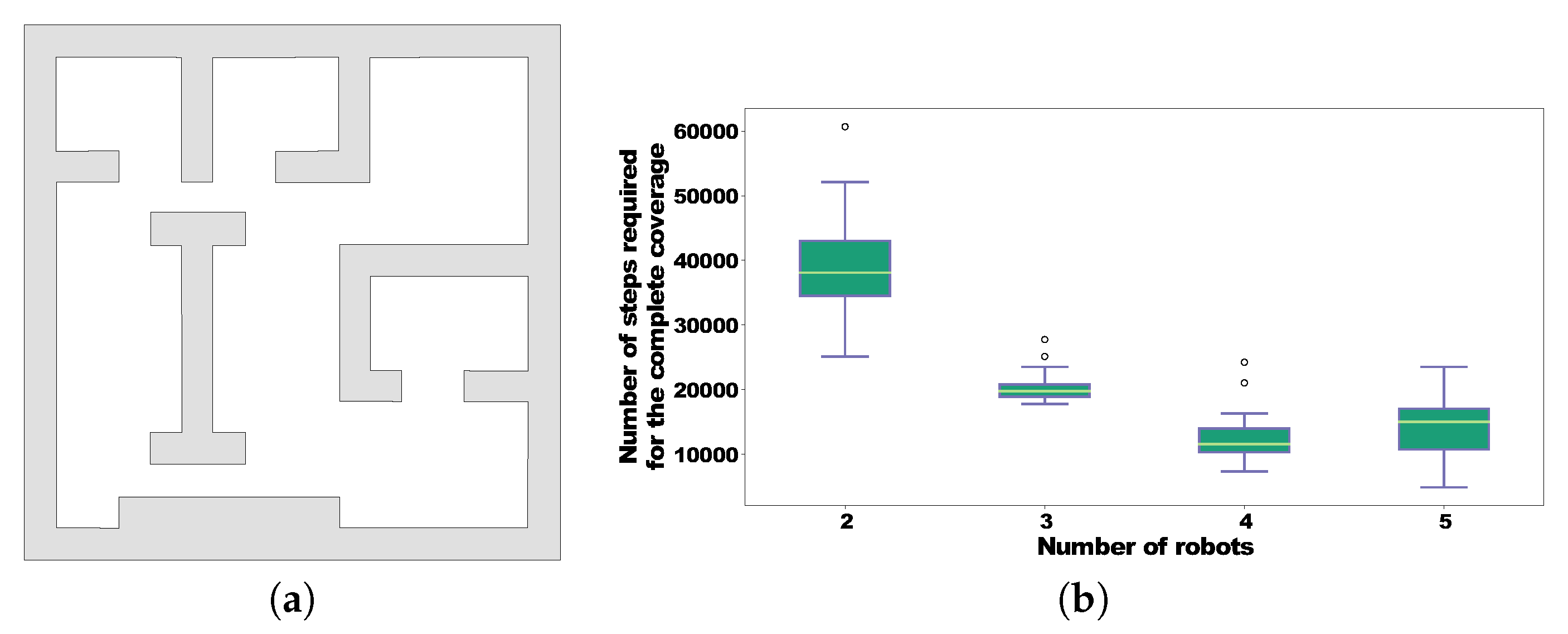
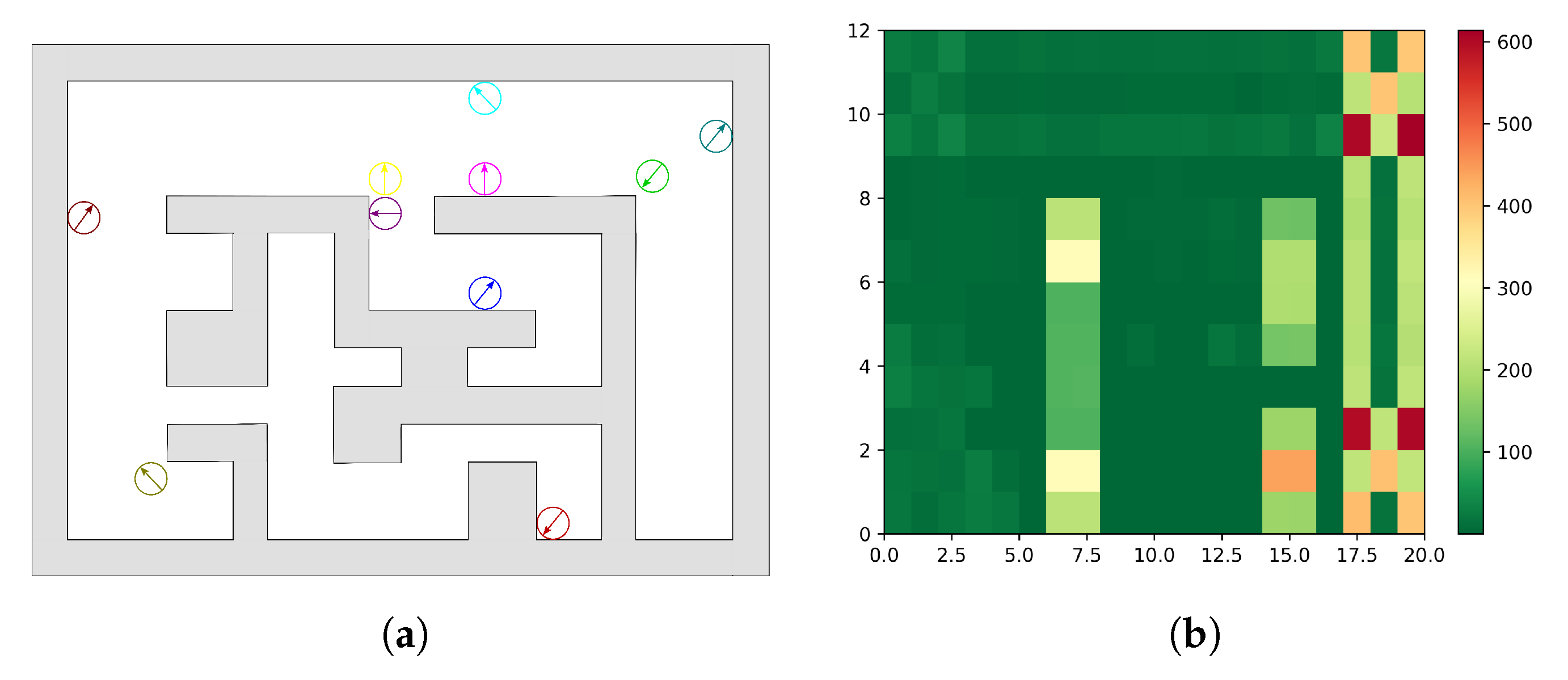
5.1. Results of a Joint Trajectory of Multiple Robots for Coverage
5.2. Results of Persistent Monitoring of Target Regions
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Alam, T.; Reis, G.M.; Bobadilla, L.; Smith, R.N. A Data-Driven Deployment Approach for Persistent Monitoring in Aquatic Environments. In Proceedings of the IEEE International Conference on Robotic Computing (IRC), Laguna Hills, CA, USA, 31 January–2 February 2018; pp. 147–154. [Google Scholar]
- Mulgaonkar, Y.; Makineni, A.; Guerrero-Bonilla, L.; Kumar, V. Robust aerial robot swarms without collision avoidance. IEEE Robot. Autom. Lett. 2017, 3, 596–603. [Google Scholar] [CrossRef]
- Nilles, A.Q.; Pervan, A.; Berrueta, T.A.; Murphey, T.D.; LaValle, S.M. Information Requirements of Collision-Based Micromanipulation. In Proceedings of the Workshop on the Algorithmic Foundations of Robotics (WAFR), Oulu, Finland, 21–23 June 2020. [Google Scholar]
- O’Kane, J.M.; LaValle, S.M. Localization with limited sensing. IEEE Trans. Robot. 2007, 23, 704–716. [Google Scholar] [CrossRef]
- Alam, T.; Bobadilla, L.; Shell, D.A. Space-efficient filters for mobile robot localization from discrete limit cycles. IEEE Robot. Autom. Lett. 2018, 3, 257–264. [Google Scholar] [CrossRef]
- Stavrou, D.; Panayiotou, C. Localization of a simple robot with low computational-power using a single short range sensor. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 729–734. [Google Scholar]
- Erickson, L.H.; Knuth, J.; O’Kane, J.M.; LaValle, S.M. Probabilistic localization with a blind robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Pasadena, CA, USA, 19–23 May 2008; pp. 1821–1827. [Google Scholar]
- Bobadilla, L.; Martinez, F.; Gobst, E.; Gossman, K.; LaValle, S.M. Controlling wild mobile robots using virtual gates and discrete transitions. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 743–749. [Google Scholar]
- Alam, T.; Bobadilla, L.; Shell, D.A. Minimalist robot navigation and coverage using a dynamical system approach. In Proceedings of the IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 10–12 April 2017; pp. 249–256. [Google Scholar]
- Lewis, J.S.; O’Kane, J.M. Guaranteed navigation with an unreliable blind robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 5519–5524. [Google Scholar]
- Mastrogiovanni, F.; Sgorbissa, A.; Zaccaria, R. Robust navigation in an unknown environment with minimal sensing and representation. IEEE Trans. Syst. Man Cybern. 2009, 39, 212–229. [Google Scholar] [CrossRef] [PubMed]
- Tovar, B.; Guilamo, L.; LaValle, S.M. Gap navigation trees: Minimal representation for visibility-based tasks. In Proceedings of the Workshop on the Algorithmic Foundations of Robotics (WAFR), Zeist, The Netherlands, 11–13 July 2004; pp. 425–440. [Google Scholar]
- Nilles, A.Q.; Becerra, I.; LaValle, S.M. Periodic trajectories of mobile robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3020–3026. [Google Scholar]
- Nilles, A.Q.; Ren, Y.; Becerra, I.; LaValle, S.M. A visibility-based approach to computing nondeterministic bouncing strategies. In Proceedings of the Workshop on the Algorithmic Foundations of Robotics (WAFR), Merida, Mexico, 9–11 December 2018; pp. 89–104. [Google Scholar]
- Choset, H. Coverage for robotics–A survey of recent results. Ann. Math. Artif. Intell. 2001, 31, 113–126. [Google Scholar] [CrossRef]
- Karapetyan, N.; Benson, K.; McKinney, C.; Taslakian, P.; Rekleitis, I. Efficient multi-robot coverage of a known environment. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1846–1852. [Google Scholar]
- Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decomposition. In Field and Service Robotics; Springer: London, UK, 1998; pp. 203–209. [Google Scholar]
- Soltero, D.E.; Smith, S.L.; Rus, D. Collision avoidance for persistent monitoring in multi-robot systems with intersecting trajectories. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 3645–3652. [Google Scholar]
- Hsu, C.S. A theory of cell-to-cell mapping dynamical systems. J. Appl. Mech. 1980, 47, 931–939. [Google Scholar] [CrossRef]
- Hsu, C.S. Cell-To-Cell Mapping: A Method of Global Analysis for Nonlinear Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 64. [Google Scholar]
- Burridge, R.R.; Rizzi, A.A.; Koditschek, D.E. Sequential composition of dynamically dexterous robot behaviors. Int. J. Robot. Res. 1999, 18, 534–555. [Google Scholar] [CrossRef]
- Alam, T. A Dynamical System Approach for Resource-Constrained Mobile Robotics. Ph.D. Thesis, Florida International University, Miami, FL, USA, 2018. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Experimental investigation on coverage performance of a chaotic autonomous mobile robot. Robot. Auton. Syst. 2013, 61, 1314–1322. [Google Scholar] [CrossRef]
- Gabriely, Y.; Rimon, E. Spanning-tree based coverage of continuous areas by a mobile robot. Ann. Math. Artif. Intell. 2001, 31, 77–98. [Google Scholar] [CrossRef]
- Agmon, N.; Hazon, N.; Kaminka, G.A. The giving tree: Constructing trees for efficient offline and online multi-robot coverage. Ann. Math. Artif. Intell. 2008, 52, 143–168. [Google Scholar] [CrossRef]
- Hazon, N.; Kaminka, G.A. On redundancy, efficiency, and robustness in coverage for multiple robots. Robot. Auton. Syst. 2008, 56, 1102–1114. [Google Scholar] [CrossRef]
- Zheng, X.; Jain, S.; Koenig, S.; Kempe, D. Multi-robot forest coverage. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Edmonton, AB, Canada, 2–6 August 2005; pp. 3852–3857. [Google Scholar]
- Fazli, P.; Davoodi, A.; Pasquier, P.; Mackworth, A.K. Complete and robust cooperative robot area coverage with limited range. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 5577–5582. [Google Scholar]
- Fazli, P.; Davoodi, A.; Mackworth, A.K. Multi-robot repeated area coverage. Auton. Robots 2013, 34, 251–276. [Google Scholar] [CrossRef]
- Fazli, P.; Mackworth, A.K. The effects of communication and visual range on multi-robot repeated boundary coverage. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), College Station, TX, USA, 5–8 November 2012; pp. 1–8. [Google Scholar]
- Smith, S.L.; Rus, D. Multi-robot monitoring in dynamic environments with guaranteed currency of observations. In Proceedings of the IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 514–521. [Google Scholar]
- Smith, S.L.; Schwager, M.; Rus, D. Persistent robotic tasks: Monitoring and sweeping in changing environments. IEEE Trans. Robot. 2012, 28, 410–426. [Google Scholar] [CrossRef]
- Lan, X.; Schwager, M. Planning periodic persistent monitoring trajectories for sensing robots in gaussian random fields. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 2415–2420. [Google Scholar]
- Yu, J.; Schwager, M.; Rus, D. Correlated orienteering problem and its application to persistent monitoring tasks. IEEE Trans. Robot. 2016, 32, 1106–1118. [Google Scholar] [CrossRef]
- Akella, S.; Hutchinson, S. Coordinating the motions of multiple robots with specified trajectories. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 11–15 May 2002; pp. 624–631. [Google Scholar]
- Snape, J.; Van Den Berg, J.; Guy, S.J.; Manocha, D. Independent navigation of multiple mobile robots with hybrid reciprocal velocity obstacles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), St. Louis, MO, USA, 10–15 October 2009; pp. 5917–5922. [Google Scholar]
- Cassandras, C.G.; Lin, X.; Ding, X. An optimal control approach to the multi-agent persistent monitoring problem. IEEE Trans. Autom. Control 2013, 58, 947–961. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006; Available online: http://lavalle.pl/planning/ (accessed on 1 June 2020).
- Van Der Spek, J.A.W. Cell Mapping Methods: Modifications and Extensions. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1994. [Google Scholar]

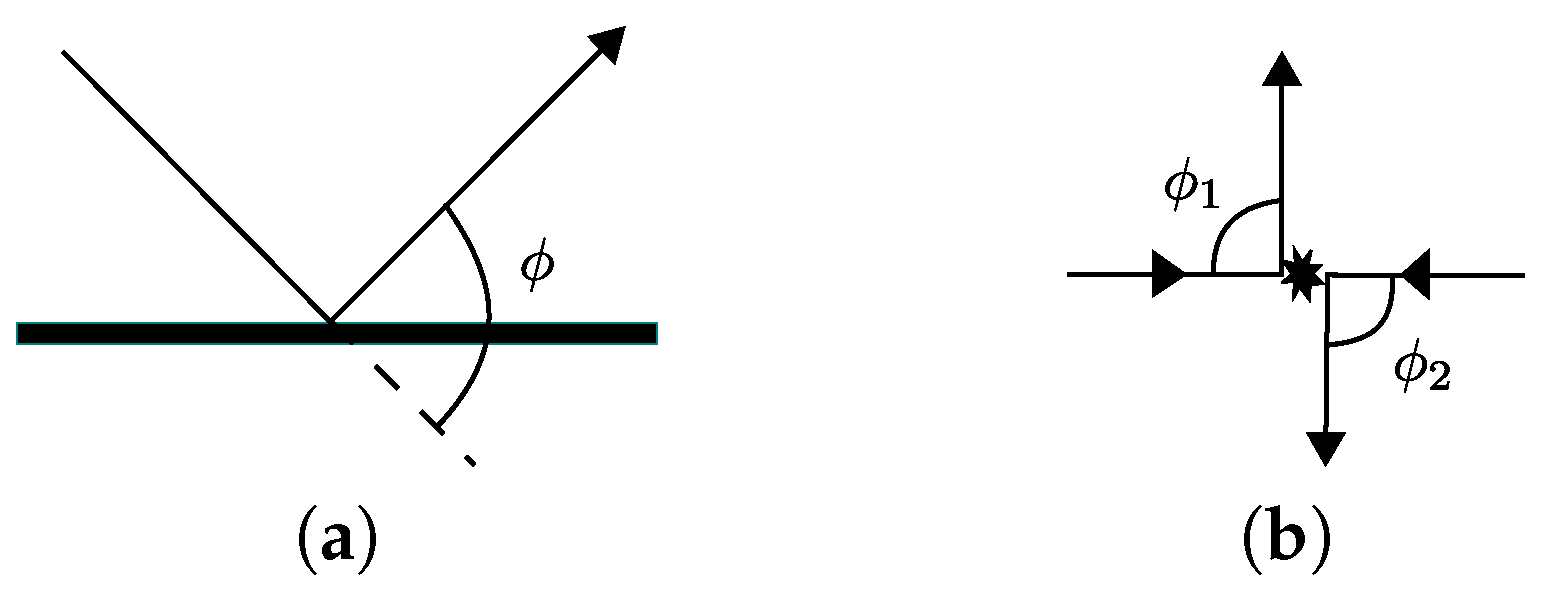





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, T.; Bobadilla, L. Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments. Robotics 2020, 9, 47. https://doi.org/10.3390/robotics9020047
Alam T, Bobadilla L. Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments. Robotics. 2020; 9(2):47. https://doi.org/10.3390/robotics9020047
Chicago/Turabian StyleAlam, Tauhidul, and Leonardo Bobadilla. 2020. "Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments" Robotics 9, no. 2: 47. https://doi.org/10.3390/robotics9020047
APA StyleAlam, T., & Bobadilla, L. (2020). Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments. Robotics, 9(2), 47. https://doi.org/10.3390/robotics9020047




