Model-Based Grasping of Unknown Objects from a Random Pile
Abstract
1. Introduction
2. Related Work
2.1. Grasping Strategies Based on Machine Learning
2.2. Grasping Strategies Resorting to Pile Interaction
2.3. Geometric Properties
3. Testbed
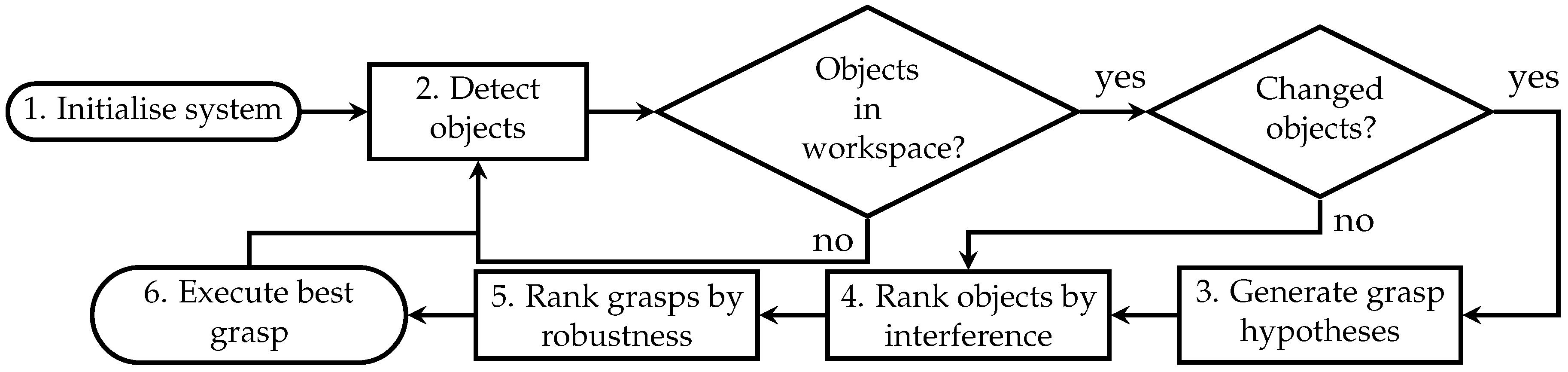
4. Proposed Algorithm
- Initialise system: Standard initialisation of software and hardware, that is, connection to the robotic manipulator, the gripper, the 3D camera, trajectory planning service and launch of GUI.
- Detect objects: Using the RGB-D output of the 3D camera, detect the objects in the robot workspace.
- Generate grasp hypotheses: Several grasp hypotheses are generated for each shape of object inferred from the vision system.
- Rank of objects by interference: A sorting function allows to sort the objects according to the likelihood of collision when attempting to grasp them.
- Rank grasps by robustness: Among the interference-free objects, the best grasp pose is chosen according to a criterion referred to as the robustness of static equilibrium [10].
- Execute best grasp: Send a command to the robot to effectuate the grasp.
4.1. Detect Objects
- (a)
- Object extraction: The objects are distinguished by eliminating the regions that match the table top color and that lie on or below the height of the table top. In order to avoid the elimination of thin objects, the background colour is carefully chosen. A binary image is created after the elimination where the black colour represents the eliminated background and a white colour represents the objects. The image is then used to extract a list of contours of the objects. Each contour includes an ordered list of the outermost pixel values surrounding the corresponding objects. If there is a hole in an object such as in a roll of tape, another list of pixel values is generated for the hole. Each pixel is converted into Cartesian coordinates using PCL.
- (b)
- Object segmentation: The above method only works when the objects are scattered over the workspace. When the objects overlap, the algorithm perceives them as one single object. To distinguish between overlapping objects, a watershed algorithm is applied as an additional step in the object extraction, providing a segmentation (see Figure 3). Due to the dependency on grayscale images, the algorithm tends to result in over segmentation of objects composed of multiple colours. This does affect the success rate of the algorithm, as there is an increased risk of detecting small objects where none exists. On the other hand, under-segmentation brings the risk of conflating neighbouring objects. This often leads to failed grasps when they are attempted near the interface between the two objects that are detected as one. There appears to be a trade-off between over- and under-segmentation, and we found empirically that some over-segmentation gave the best results, although the vision system was still susceptible to some errors.
4.2. Grasp Hypotheses
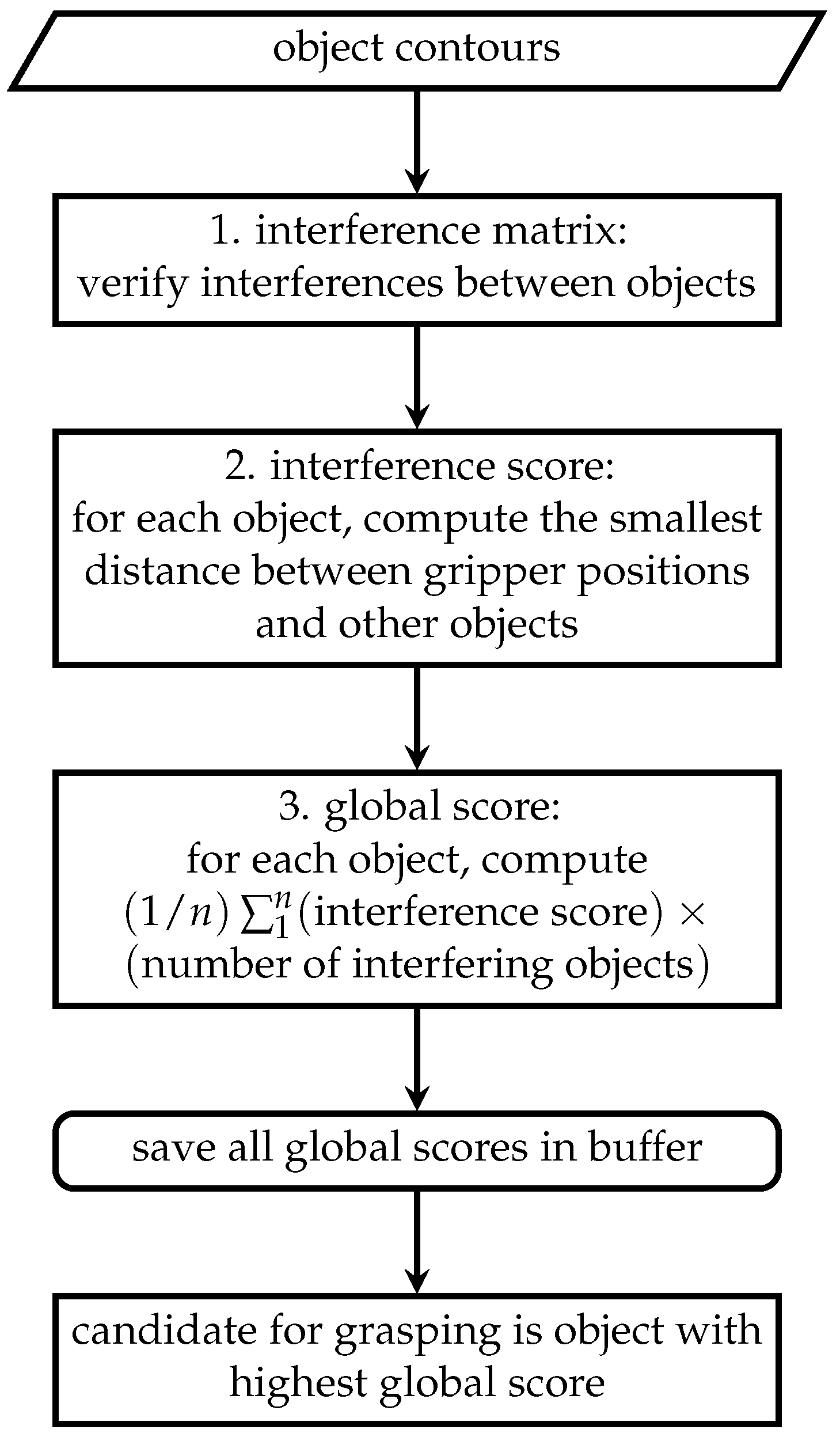
4.3. Interference Ranking
- Interference matrix: A symmetric matrix is defined to describe the potential interferences between objects. In this matrix, each row (and column) corresponds to one of the objects detected from the scene. Thus, entry of the interference matrix is a value representing the likelihood of avoiding a collision with object j when attempting to grasp object i.The entry is one whenever the two objects are separated by less than the width (in the plane) and the depth (in the vertical Z direction) of the gripper, and zero otherwise. The Python package Shapely is used to offset the -plane contour of a given object by one gripper width and to determine if there are intersections with the other objects. This operation is done for all objects.
- Interference score: For all grasping hypotheses for a given object, the minimal distance between the fingers and the surrounding other objects is calculated. The smallest distance is retained for the score. If the finger is free from interference, the score is the positive distance whereas if the finger has an interference with an object, the score is the negative of the distance of penetration of one into the other.
- Global score: The interference score of each object is averaged and multiplied by the number of interfering objects (the interference matrix). For exemple, an object with five grasping hypotheses surrounded by three objects will have the interference score averaged on the five grasping hypotheses and multiplied by three, the number of interfering objects. The objective of this calculation is to maximize the global score of the objects that can provide more space.
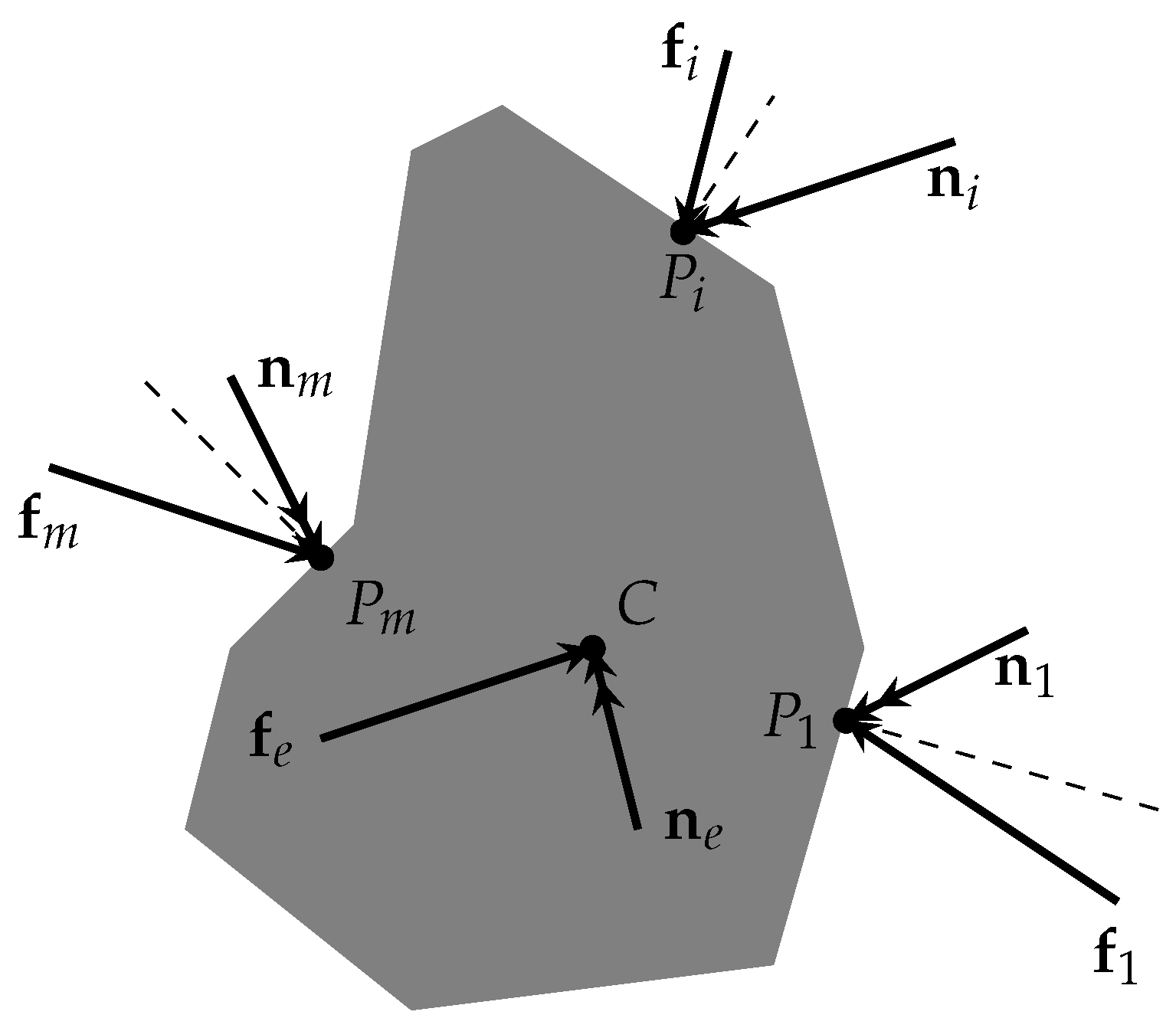
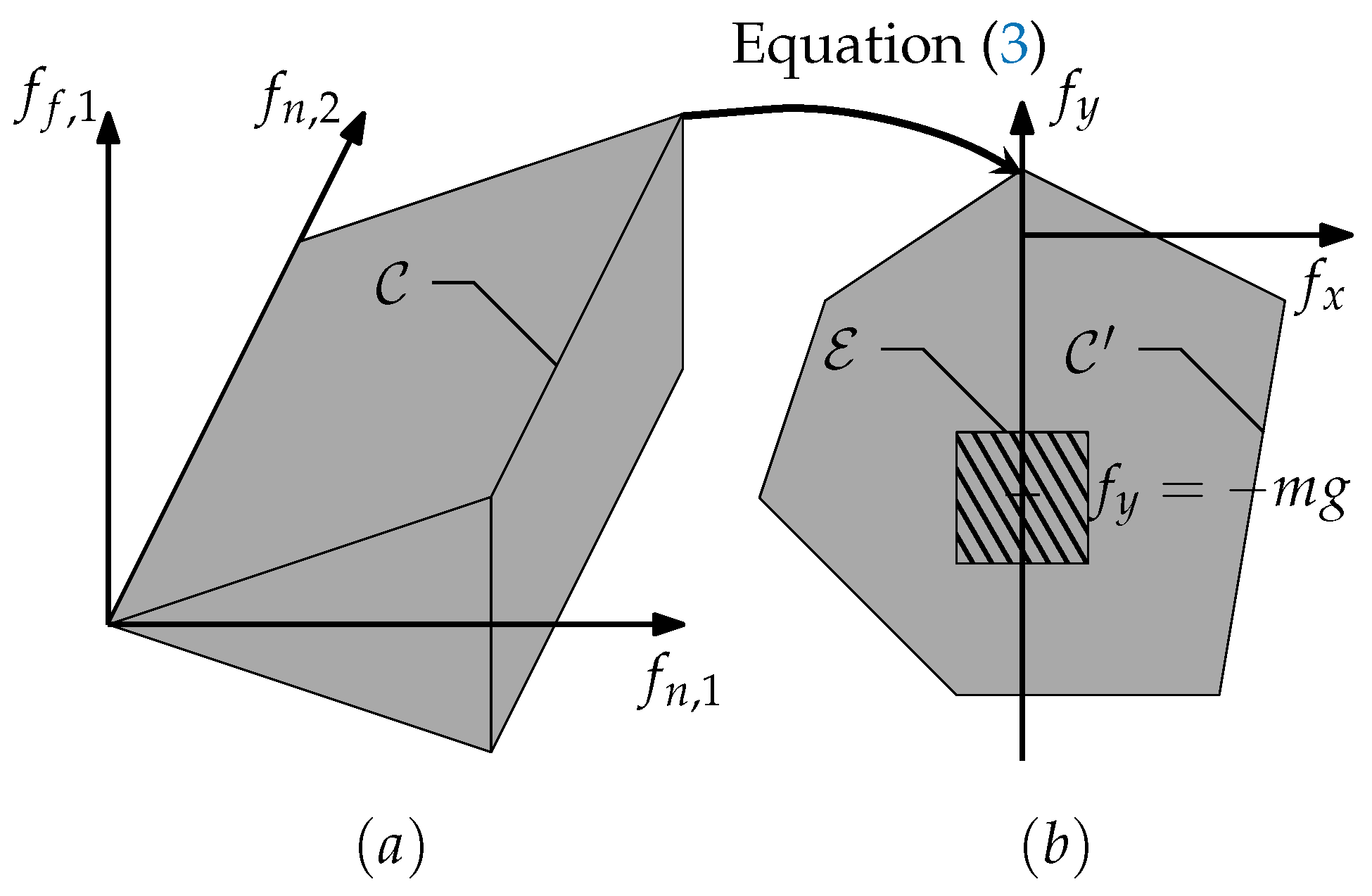
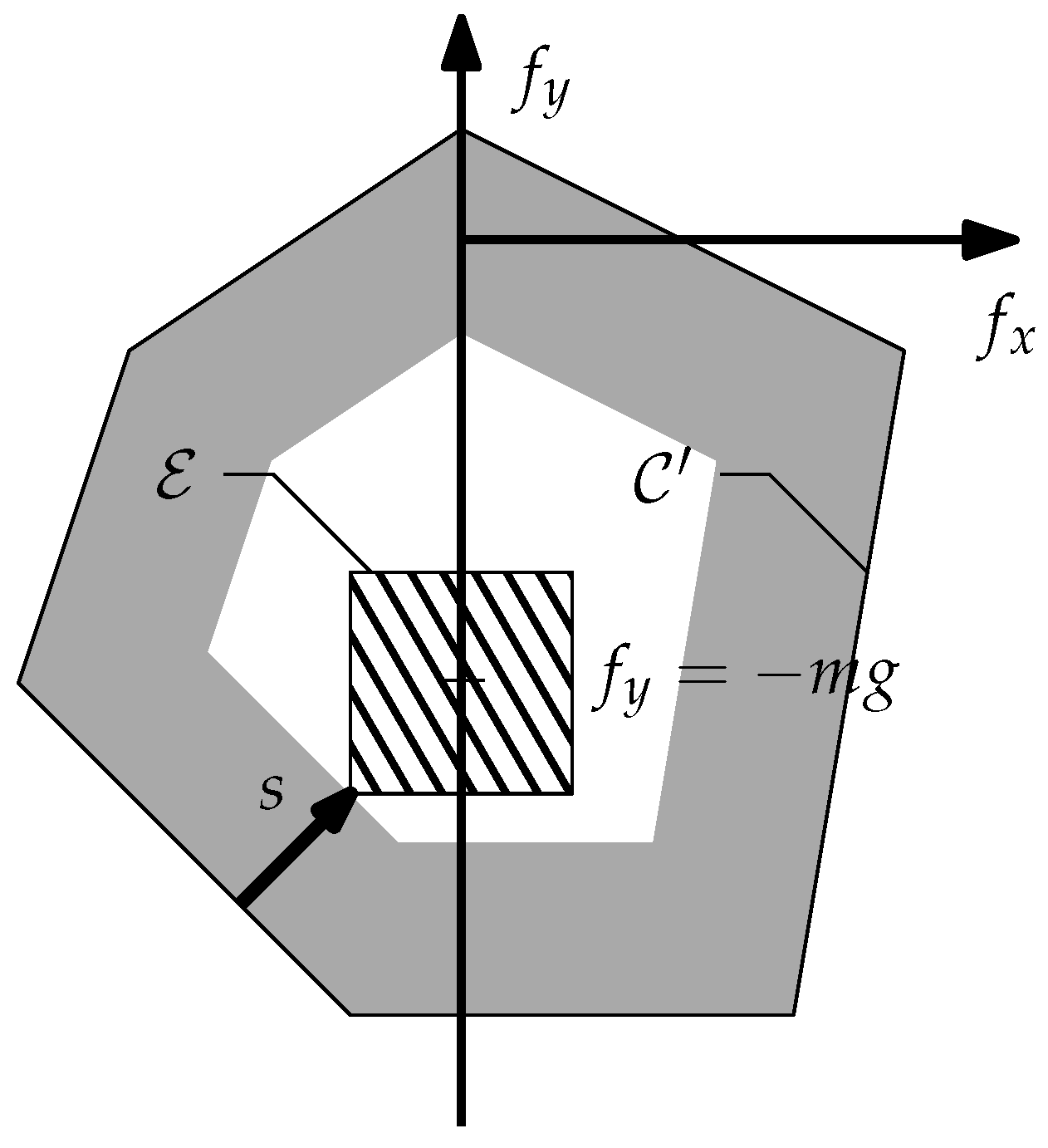
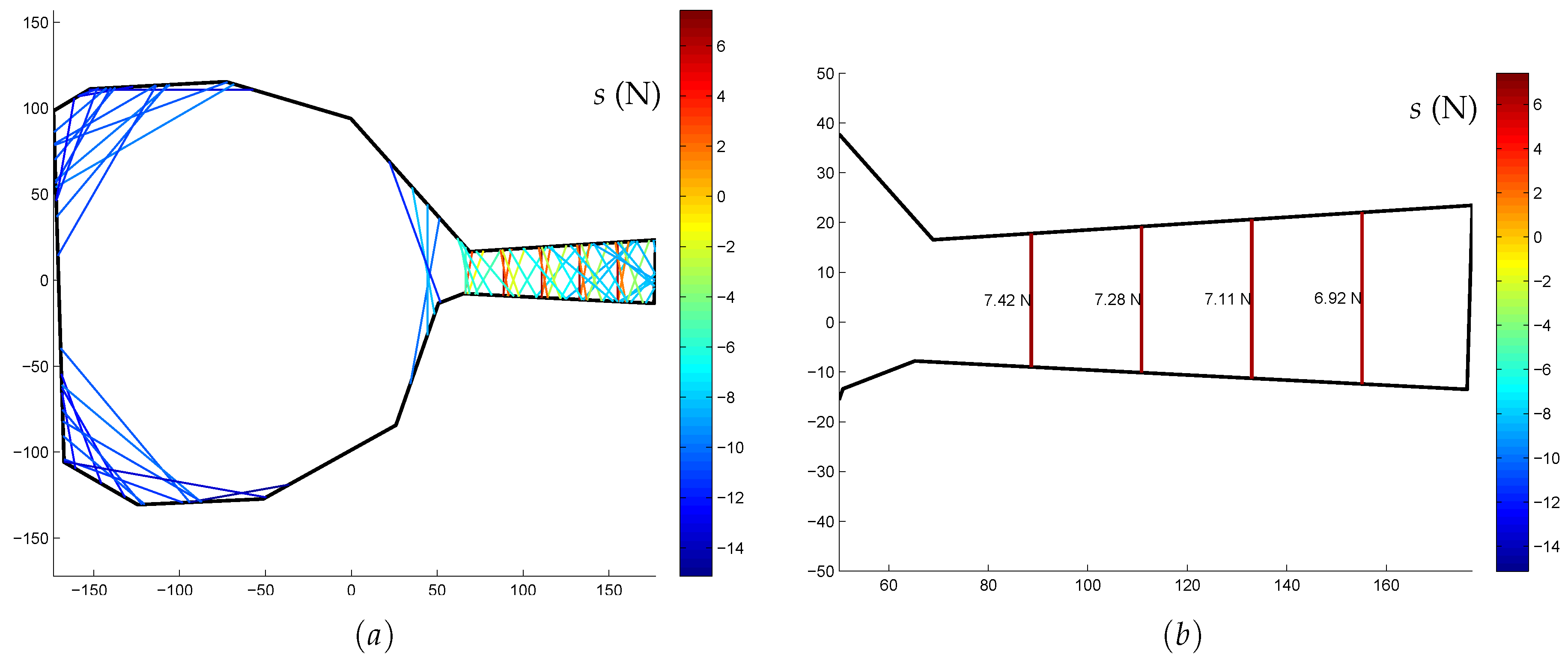
4.4. Grasp Robustness Ranking
5. Experimental Tests and Results
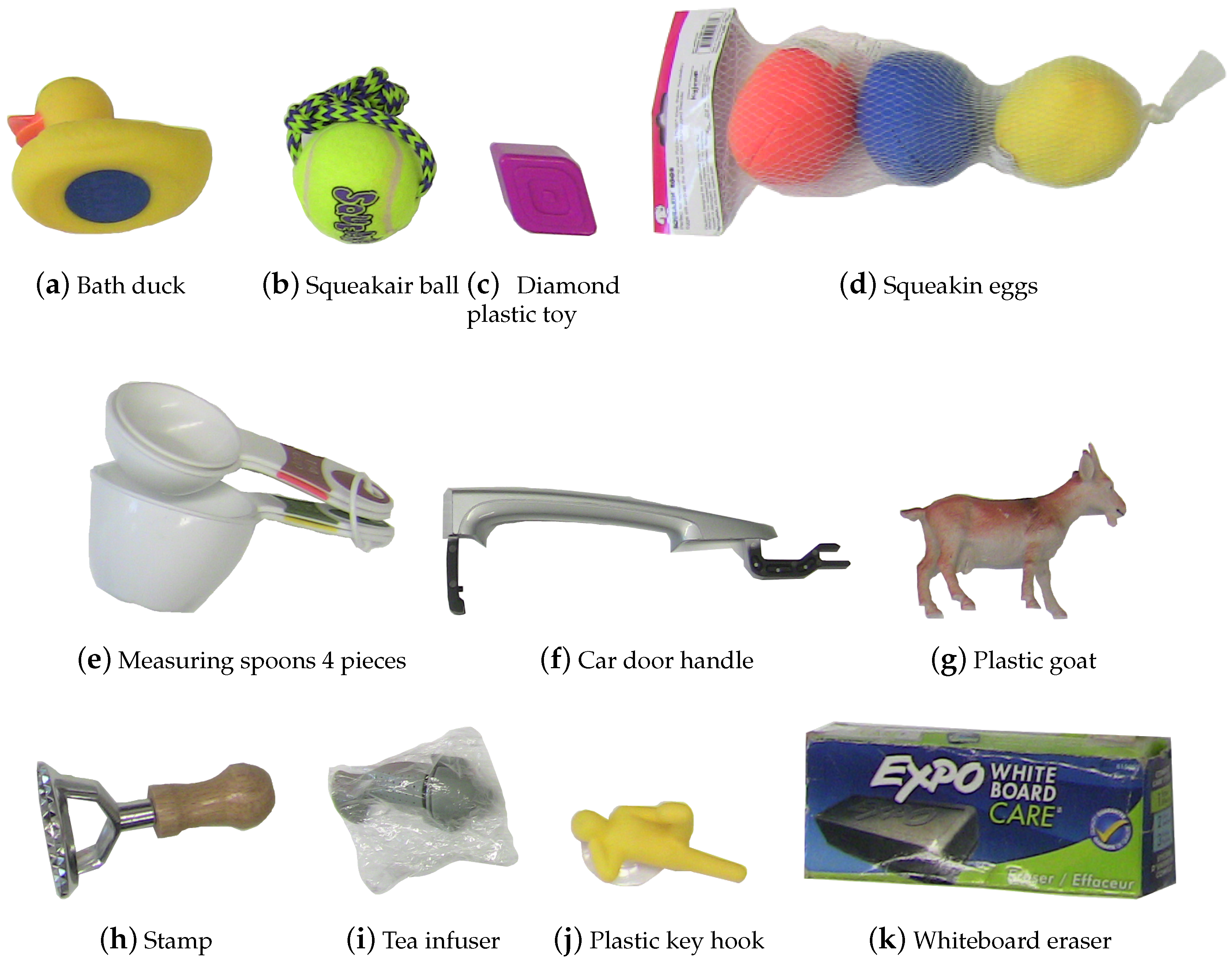
5.1. Protocol
- No object is grasped by the gripper;
- Only one object is grasped by the gripper;
- Two or more objects are grasped by the gripper.
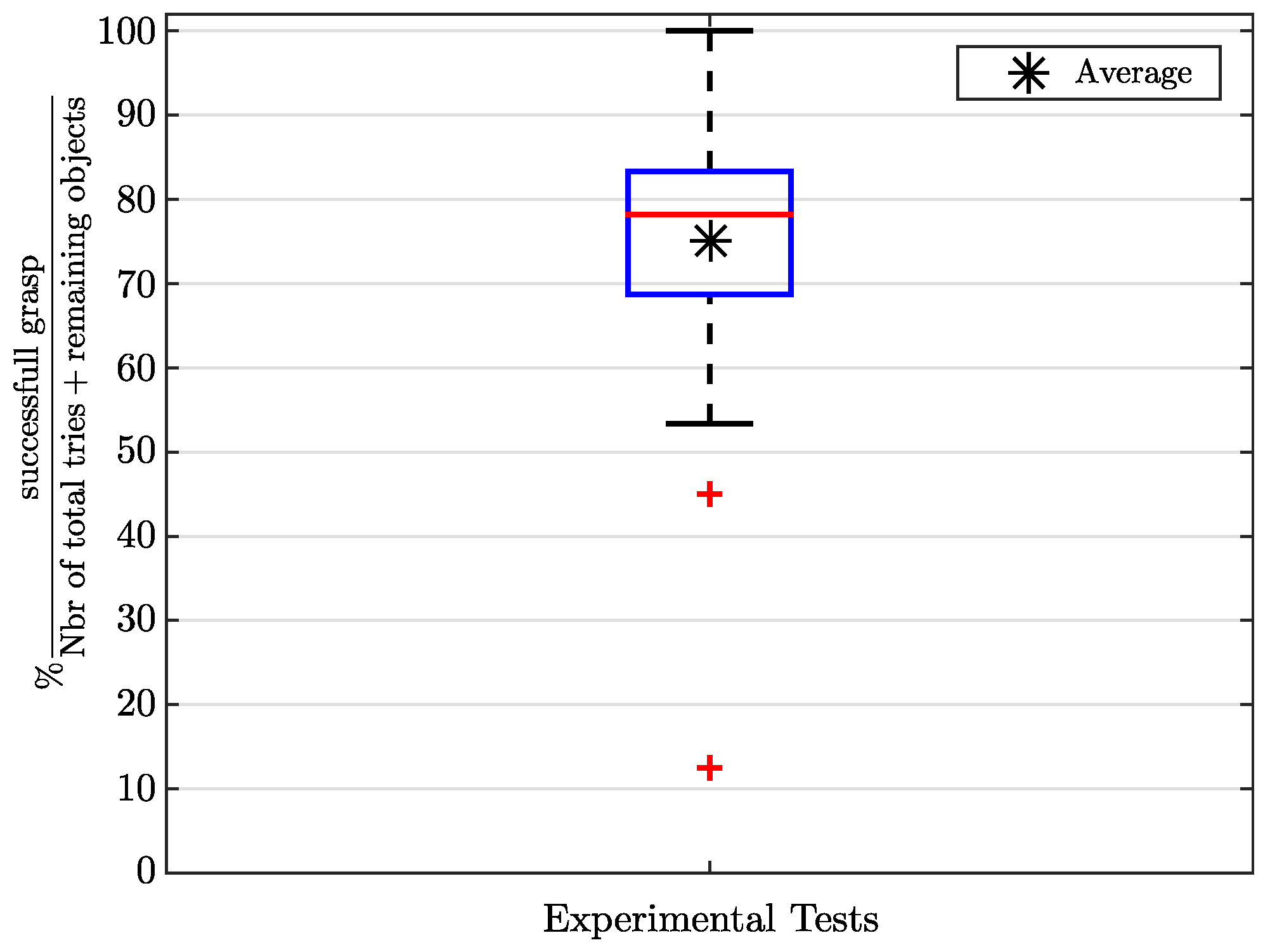
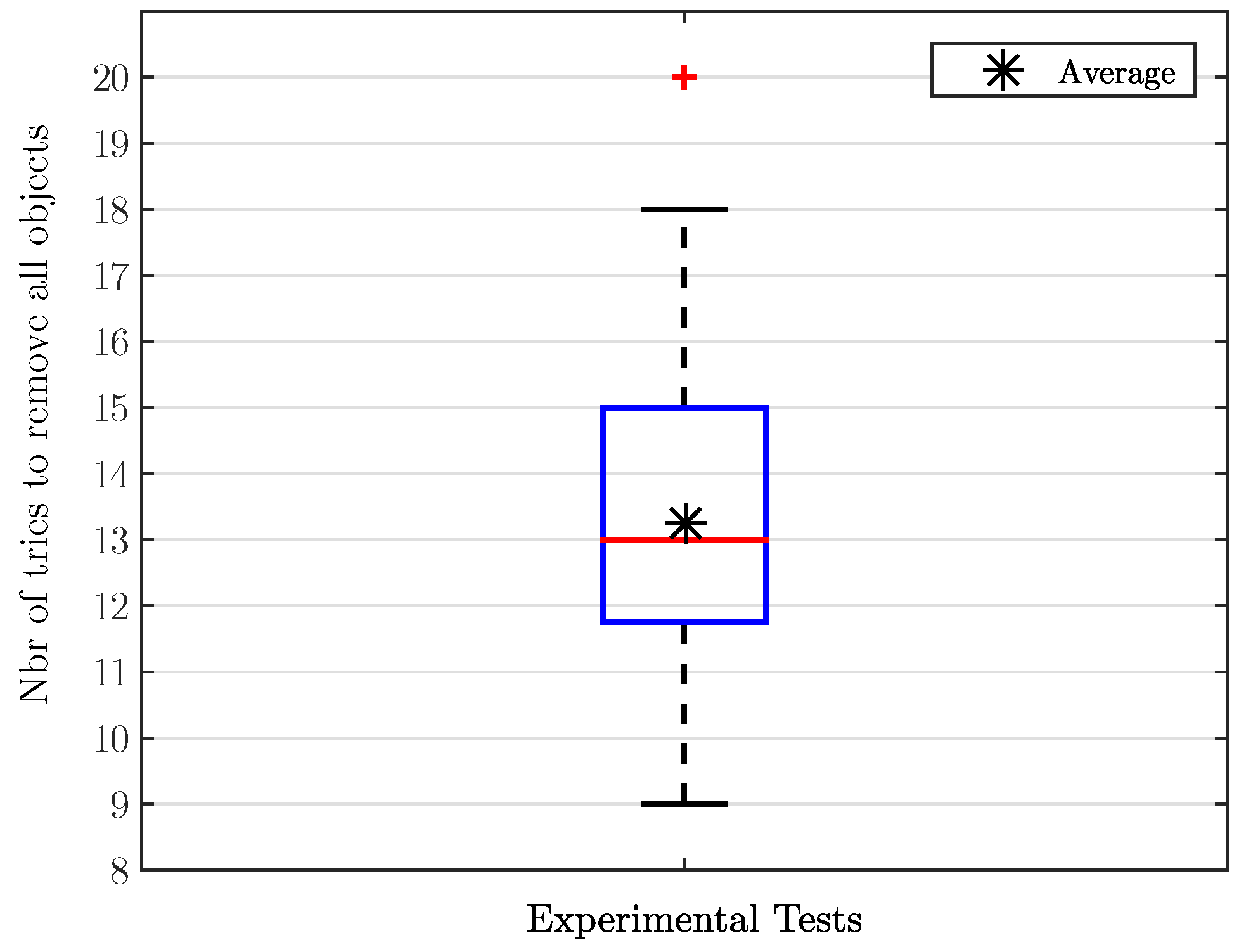
5.2. Results
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ikeuchi, K.; Horn, B.K.P.; Nagata, S.; Callahan, T.; Feingold, O. Picking up an object from a pile of objects. In Robotics Research: The First International Symposium; MIT Press: Cambridge, MA, USA, 1984; pp. 139–162. [Google Scholar]
- Buchholz, D. Bin-Picking: New Approaches for a Classical Problem; Studies in Systems, Decision and Control; Springer: Heidelberg, Germany, 2015; Volume 44. [Google Scholar]
- Eppner, C.; Deimel, R.; Álvarez Ruiz, J.; Maertens, M.; Brock, O. Exploitation of Environmental Constraints in Human and Robotics Grasping. Int. J. Robot. Res. 2015, 34, 1021–1038. [Google Scholar] [CrossRef]
- Bohg, J.; Morales, A.; Asfour, T.; Kragic, D. Data-driven grasp synthesis—A survey. IEEE Trans. Robot. 2014, 30, 289–309. [Google Scholar] [CrossRef]
- Roa, M.A.; Suárez, R. Grasp quality measures: Review and performance. Auton. Robot. 2015, 38, 65–88. [Google Scholar] [CrossRef]
- Sahbani, A.; El-Khoury, S.; Bidaud, P. An overview of 3D object grasp synthesis algorithms. Robot. Auton. Syst. 2012, 60, 326–336. [Google Scholar] [CrossRef]
- Aleotti, J.; Caselli, S. Interactive teaching of task-oriented robot grasps. Robot. Auton. Syst. 2010, 58, 539–550. [Google Scholar] [CrossRef]
- Pedro, L.M.; Belini, V.L.; Caurin, G.A. Learning how to grasp based on neural network retraining. Adv. Robot. 2013, 27, 785–797. [Google Scholar] [CrossRef]
- Zheng, Y. An efficient algorithm for a grasp quality measure. IEEE Trans. Robot. 2013, 29, 579–585. [Google Scholar] [CrossRef]
- Guay, F.; Cardou, P.; Cruz-Ruiz, A.L.; Caro, S. Measuring how well a structure supports varying external wrenches. In New Advances in Mechanisms, Transmissions and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 385–392. [Google Scholar]
- Roa, M.A.; Argus, M.J.; Leidner, D.; Borst, C.; Hirzinger, G. Power grasp planning for anthropomorphic robot hands. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 563–569. [Google Scholar]
- Nieuwenhuisen, M.; Droeschel, D.; Holz, D.; Stückler, J.; Berner, A.; Li, J.; Klein, R.; Behnke, S. Mobile bin picking with an anthropomorphic service robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2327–2334. [Google Scholar]
- El Khoury, S.; Sahbani, A. Handling Objects by Their Handles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’08), Nice, France, 22–26 September 2008; pp. 58–64. [Google Scholar]
- Kehoe, B.; Berenson, D.; Goldberg, K. Toward cloud-based grasping with uncertainty in shape: Estimating lower bounds on achieving force closure with zero-slip push grasps. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 576–583. [Google Scholar]
- Fischinger, D.; Weiss, A.; Vincze, M. Learning grasps with topographic features. Int. J. Robot. Res. 2015, 34, 1167–1194. [Google Scholar] [CrossRef]
- Eppner, C.; Höfer, S.; Jonschkowski, R.; Martín-Martín, R.; Sieverling, A.; Wall, V.; Brock, O. Four Aspects of Building Robotic Systems: Lessons from the Amazon Picking Challenge 2015. In Proceedings of the Robotics: Science and Systems XII, Ann Arbor, MI, USA, 18–22 June 2016. [Google Scholar]
- Saxena, A.; Wong, L.L.S.; Ng, A.Y. Learning Grasp Strategies with Partial Shape Information. In Proceedings of the 23rd National Conference on Artificial Intelligence (AAAI’08), Chicago, IL, USA, 13–17 July 2008; Volume 3, pp. 1491–1494. [Google Scholar]
- Saxena, A.; Driemeyer, J.; Ng, A.Y. Robotic grasping of novel objects using vision. Int. J. Robot. Res. 2008, 27, 157–173. [Google Scholar] [CrossRef]
- Katz, D.; Venkatraman, A.; Kazemi, M.; Bagnell, J.A.; Stentz, A. Perceiving, learning, and exploiting object affordances for autonomous pile manipulation. Auton. Robot. 2014, 37, 369–382. [Google Scholar] [CrossRef]
- Fischinger, D.; Vincze, M. Empty the basket-a shape based learning approach for grasping piles of unknown objects. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 2051–2057. [Google Scholar]
- Pinto, L.; Gupta, A. Supersizing self-supervision: Learning to grasp from 50k tries and 700 robot hours. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3406–3413. [Google Scholar]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2016, 37, 421–436. [Google Scholar] [CrossRef]
- Ten Pas, A.; Platt, R. Using geometry to detect grasp poses in 3d point clouds. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2018; pp. 307–324. [Google Scholar]
- Van Hoof, H.; Kroemer, O.; Peters, J. Probabilistic segmentation and targeted exploration of objects in cluttered environments. IEEE Trans. Robot. 2014, 30, 1198–1209. [Google Scholar] [CrossRef]
- Katz, D.; Kazemi, M.; Bagnell, J.A.; Stentz, A. Clearing a pile of unknown objects using interactive perception. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 154–161. [Google Scholar]
- Chang, L.; Smith, J.R.; Fox, D. Interactive singulation of objects from a pile. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 3875–3882. [Google Scholar]
- Gupta, M.; Sukhatme, G.S. Using manipulation primitives for brick sorting in clutter. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 3883–3889. [Google Scholar]
- Hermans, T.; Rehg, J.M.; Bobick, A. Guided pushing for object singulation. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 4783–4790. [Google Scholar]
- Eppner, C.; Brock, O. Grasping unknown objects by exploiting shape adaptability and environmental constraints. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4000–4006. [Google Scholar]
- Buchholz, D.; Kubus, D.; Weidauer, I.; Scholz, A.; Wahl, F.M. Combining visual and inertial features for efficient grasping and bin-picking. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 875–882. [Google Scholar]
- Bouchard, S.; Gosselin, C.; Moore, B. On the Ability of a Cable-Driven Robot to Generate a Prescribed Set of Wrenches. ASME J. Mech. Robot. 2010, 2, 011010. [Google Scholar] [CrossRef]
- Pollard, N.S. Parallel Algorithms for Synthesis of Whole-Hand Grasps. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Albuquerque, NM, USA, 25–25 April 1997; pp. 373–378. [Google Scholar]
- Borst, C.; Fischer, M.; Hirzinger, G. Grasp Planning: How to Choose a Suitable Task Wrench Space. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), New Orleans, LA, USA, 26 April–1 May 2004; pp. 319–325. [Google Scholar]
- Pozzi, M.; Malvezzi, M.; Prattichizzo, D. On Grasp Quality Measures: Grasp Robustness and Contact Force Distribution in Underactuated and Compliant Robotic Hands. IEEE Robot. Autom. Lett. 2017, 2, 329–336. [Google Scholar] [CrossRef]
- Bonilla, M.; Farnioli, E.; Piazza, C.; Catalano, M.; Grioli, G.; Garabini, M.; Gabiccini, M.; Bicchi, A. Grasping with Soft Hands. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 581–587. [Google Scholar]




| Nbr of Tests | Nbr of Grasped Objects | % |
|---|---|---|
| 1 | 2 | 18.2 |
| 1 | 8 | 72.7 |
| 2 | 9 | 81.8 |
| 7 | 10 | 90.9 |
| 39 | 11 | 100 |
| total: 50 tests |
| Nbr of Experimental Tests | |||
|---|---|---|---|
| Double Grasping | Failed Grasping | ||
| Nbr of occurrences | 0 | 35 | 5 |
| 1 | 12 | 13 | |
| 2 | 3 | 7 | |
| 3 | - | 8 | |
| 4 | - | 8 | |
| 5 | - | 6 | |
| 6 | - | 1 | |
| 7 | - | 1 | |
| 10 | - | 1 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sauvet, B.; Lévesque, F.; Park, S.; Cardou, P.; Gosselin, C. Model-Based Grasping of Unknown Objects from a Random Pile. Robotics 2019, 8, 79. https://doi.org/10.3390/robotics8030079
Sauvet B, Lévesque F, Park S, Cardou P, Gosselin C. Model-Based Grasping of Unknown Objects from a Random Pile. Robotics. 2019; 8(3):79. https://doi.org/10.3390/robotics8030079
Chicago/Turabian StyleSauvet, Bruno, François Lévesque, SeungJae Park, Philippe Cardou, and Clément Gosselin. 2019. "Model-Based Grasping of Unknown Objects from a Random Pile" Robotics 8, no. 3: 79. https://doi.org/10.3390/robotics8030079
APA StyleSauvet, B., Lévesque, F., Park, S., Cardou, P., & Gosselin, C. (2019). Model-Based Grasping of Unknown Objects from a Random Pile. Robotics, 8(3), 79. https://doi.org/10.3390/robotics8030079






