Trajectory Analysis for the MASAR: A New Modular and Single-Actuator Robot

Abstract

Single-actuator mobile robots offer the benefits of low energy consumption, low weight and size, and low cost, but their motion is typically only one-dimensional. By using auxiliary binary mechanisms that redirect and channel the driving force of their only actuator in different ways, it is possible for these robots to perform higher-dimensional motions, such as walking straight, steering, or jumping, with only one motor. This paper presents the MASAR, a new Modular And Single-Actuator Robot that carries a single motor and several adhesion pads. By alternately releasing or attaching these adhesion pads to the environment, the proposed robot is able to pivot about different axes using only one motor, with the possibility of performing concave plane transitions or combining with other identical modules to build more complex reconfigurable robots. In this paper, we solve the planar trajectory tracking problem of this robot for polygonal paths made up of sequences of segments, which may include narrow corridors that are difficult to traverse. We propose a locomotion based on performing rotations of 180°, which we demonstrate to be the minimum-time solution for long trajectories, and a near-optimal solution for shorter ones.

1. Introduction

Single-Actuator Mobile Robots (SAMR) are robots with the ability to explore environments with relatively high freedom using only one motor. The most direct consequences and advantages of using a single actuator are savings in costs, energy consumption, size, and weight. Due to these advantages, SAMR robots are especially appropriate for applications that require energy autonomy, miniaturization, and navigation in difficult-to-access areas, with the purpose of performing inspection, cleaning, reconnaissance or search-and-rescue tasks, among others [1].

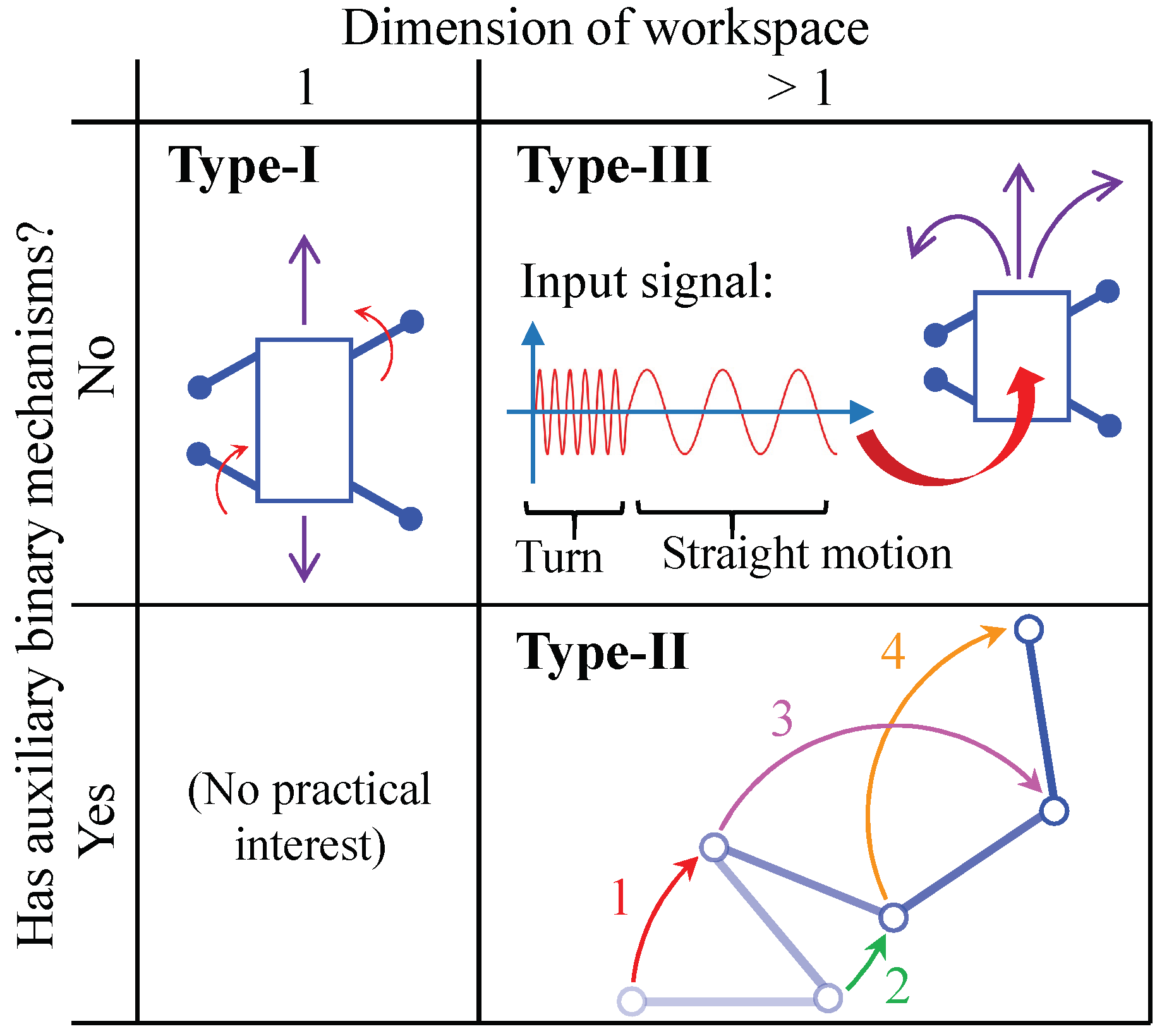
Most SAMR robots reported in the specialized literature can be classified into one of three main types (type-I, type-II, or type-III), depending on two criteria: the dimension of their workspace, and the existence of auxiliary binary mechanisms that help the robot to change the direction of motion. This classification, which we propose in this paper, is illustrated in Figure 1.

Type-I SAMR are robots that use a single actuator to control their motion along a one-dimensional workspace, with no additional mechanisms. For example, the authors in [2] presents an octopod that can walk forward or backwards along a straight line by means of a single motor and a system of cams that synchronize the motion of all its eight legs. Similarly, the authors in [3,4] present two climbing robots that can vertically climb using a single actuator each. Another single-actuator climbing robot is presented in [5]; this robot swings a pendulum to dynamically climb the vertical space between two walls by bouncing between these walls. The authors in [6] present a robot that can climb or move along a straight line by using a wave-like locomotion generated by a single motor. Type-I SAMR robots can only move along one dimension. In order for these robots to be able to change the direction of their motion and control their motion in higher-dimensional workspaces (e.g., plane or space), it would be necessary to equip them with additional motors [4,6], and thus they would no longer be single-actuator mobile robots.

According to Figure 1, type-II SAMR have workspaces with dimensions higher than one, i.e., they are not constrained to move along a straight line only, but they can typically control their position and orientation in a plane. In addition to having a main continuous actuator, type-II SAMR are characterized by having also some additional binary mechanisms that allow the robot to modify its topology, changing in this way the effect that its single main actuator exerts on the overall motion of the robot. In other words: strictly speaking, type-II SAMR robots should be called “Single-Actuator Mobile Robots...with auxiliary binary actuators” (nevertheless, some authors of these robots regard them as single-actuated). Thanks to these auxiliary binary actuators, the driving force generated by the only continuous actuator of the robot can be channeled as required, e.g., to produce straight motion, to change the direction of motion, to jump, etc. Note that these auxiliary binary actuators do not necessarily need to be motors or actuators in the usual sense of the term, but they can simply be electromagnets, suction cups, or clutches that engage or disengage two mobile parts of some internal mechanism of the robot, in order to transmit the driving force of the only continuous actuator to different mechanisms and modify the overall motion of the mobile robot.

Some examples of type-II SAMR robots can be found in the literature. For example, the authors in [7] present a mobile robot with two variable-radius wheels driven by a single motor such that, when activating a clutch, this motor also displaces the center of mass of the robot along its main shaft, which modifies the relative radii of the wheels and produces a change in the direction of motion due to differential drive kinematics. The authors in [8,9] propose snake-like robots powered by a single tendon-driven actuator each robot. These robots are made up of several segments rigidly connected by welded joints such that, when applying an electric current to some of these welds, can temporarily melt them in order to modify the geometry of the robots. By selectively melting these welded joints and actuating their only motor, these robots can move along straight lines, change their direction in a plane, or perform out-of-plane motions. Finally, the authors in [10] present the DynaRoACH robot, which is inspired by cockroaches and has a single actuator to move along straight lines. This robot can also turn by modifying the relative stiffness of its legs through shape-memory alloys. Similarly, the DASH robot [11] is a single-motor hexapod that can steer or walk straight by respectively introducing or removing small asymmetries between its legs, by means of shape-memory alloys.

Type-III SAMR typically are under-actuated mobile robots that use a single actuator and lack auxiliary binary mechanisms, and they are able to control their motion in more than one dimension. Usually, these robots will perform some type of motion or other (e.g., moving along a straight line, turning, jumping...) depending on the characteristics (amplitude, sign, frequency...) of the input signal applied to its only actuator. For example: [12] presents a robot that swims over water surfaces, this robot is driven by a single actuator that produces straight motion when excited at constant frequency, whereas it modifies the direction of motion when being excited at different frequencies during each semi-period. The authors in [13] develop a micro-robot made up of a single piezoelectric actuator that makes the robot move in straight lines or turn left/right depending on the natural frequency at which this actuator is excited. A similar cubic robot is presented in [14], where the robot can move straight or turn by exciting its only actuator (a dielectric elastomer resonator) at different resonant frequencies. Zuliani et al. [15] developed an origami hand that can adopt different configurations (with different fingers extended or folded) depending on the excitation frequency of its only actuator. Although this is not a mobile robot, the idea might be exploited to build small and lightweight single-actuated legged origami robots. In [16], a spherical robot is proposed, which is able to either move straight or steer by rotating its only internal motor at constant or alternating velocity, respectively. The authors in [1] present a single-actuated hexapod robot whose legs have different stiffnesses; this robot will walk in straight lines or turn left/right depending on the shape of the velocity profile introduced to its only motor. Ribas et al. [17] designed a single-motor tricycle robot that can steer and move forward describing undulatory trajectories by pivoting alternatively about each of the rear wheels, similar to our robot proposed in the present paper. The front wheel of this tricycle can freely steer, displacing the instantaneous center of rotation from one rear wheel to the other by inverting the spin of the motor. In [18], a robot consisting of a single large wheel with only one motor is presented: if this motor oscillates between two limit positions, the robot rolls along a straight line. If the motor overcomes one of such limits, then a spring is compressed and its elastic energy is suddenly released, which produces the jump of the robot to overcome steps and other obstacles. Finally, the authors in [19,20] present jumper robots that can perform different movements using only one motor: jumping (by compressing springs), standing up after the jump, modifying the direction of the next jump, or panning a camera mounted on the robot. These robots will perform some or other motions depending on the amplitude and sign of the rotation of their only motors.

Comparing the three types of SAMR robots identified, generally one of the main drawbacks of type-III SAMR is that it may be difficult to precisely control their motion [1], since it largely depends on their under-actuated dynamics. On the contrary, it is relatively easy to precisely control the motion of type-II SAMR robots by using their auxiliary binary actuators. Type-I robots are usually simpler but they can only move along one dimension. Note that the bottom-left cell in the classification table of Figure 1 is empty because it would not have much practical interest to design SAMR robots that have auxiliary binary mechanisms but can only move along one-dimensional workspaces (the purpose of these binary mechanisms is precisely to increase the dimension of the workspace).

Acknowledging the higher simplicity and flexibility of type-II SAMR robots, this paper presents the MASAR: a new Modular And Single-Actuator Robot that explores two-dimensional environments by rotating about binary pivots that are alternately adhered to the environment or detached as required, as illustrated schematically in the bottom-right cell of Figure 1. Contrary to previous type-II SAMR, the proposed robot is capable of performing concave transitions between orthogonal planes, which makes it especially suitable for exploring indoor environments delimited by floors, walls, and ceilings. In addition, the proposed robot can combine with other identical modules in order to form more complex modular reconfigurable robots. This paper focuses on the trajectory analysis of the proposed robot, in order to follow polygonal paths composed of chains of straight segments that may include narrow sections that constrain the movements of the robot.

This paper is organized as follows. First, Section 2 presents the proposed MASAR robot. Then, Section 3 solves its path tracking problem in the case of polygonal paths with narrow sections that must be traversed. Next, Section 4 illustrates the proposed path tracking solution with some examples and experiments that deepen into the problem. Finally, Section 5 presents the conclusions and future work.

2. MASAR: A New Modular And Single-Actuator Robot

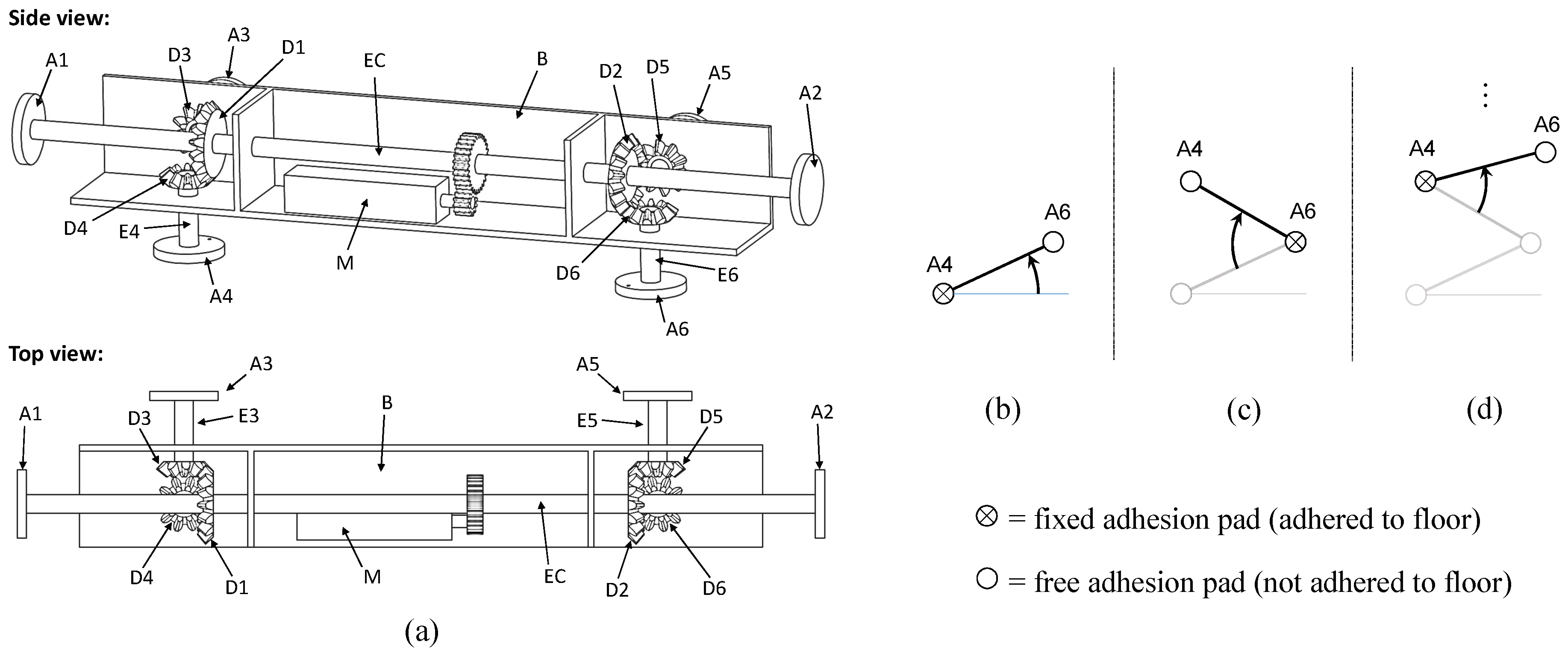
This section presents a new type-II SAMR robot, whose trajectory analysis is the main focus of the present paper. This robot is depicted in Figure 2a, and it has been called MASAR, which is the acronym of “Modular And Single-Actuator Robot”. MASAR is patented with Ref. number ES2684377 and priority date 31 March 2017.

As illustrated in Figure 2a, MASAR has a main body B rigidly attached to a single motor M that drives a central shaft EC that can rotate with respect to body B. At each side of the motor M, there is a mechanism comprised of three bevel gears with mutually orthogonal and intersecting axes: gears D1, D3, D4 to the left of M, and gears D2, D5, D6 to the right. Gears D3, D4, D5, D6 are connected to respective small shafts E3, E4, E5, E6 that can rotate with respect to the main body B; these axes have adhesion pads A3, A4, A5, A6 at their ends (see Figure 2a). Likewise, the central shaft EC has adhesion pads A1, A2 at both ends.

According to the classification of Figure 1, MASAR is a type-II SAMR robot because it has several binary adhesion pads (A1, A2, A3...), each of which may be ON or OFF (i.e., adhered to the environment or not adhered to it, respectively). The locomotion of this robot is as follows. Assume that the robot is initially resting on the floor through pads A4 and A6, as in the previous Figure 2a. Assume also that only pad A4 is ON (i.e., adhered to the floor). When actuating motor M in this situation, since A4 is rigidly adhered to the floor, the central shaft EC (and the whole robot, as a consequence) will rotate about the axis of E4, since the bevel gear D1 will roll on gear D4, which is static because A4 is adhered to the floor. This motion is illustrated in Figure 2b, which represents schematically a top view of the robot. After rotating the robot about E4, the adhesion pad A6 would be turned ON, whereas A4 would be turned OFF, and powering the motor in that case would produce the rotation of the whole robot about axis E6, as indicated in Figure 2c. By alternately turning ON and OFF pads A4 and A6, the robot would walk on the floor describing some desired trajectory (see Figure 2d or Figure 1).

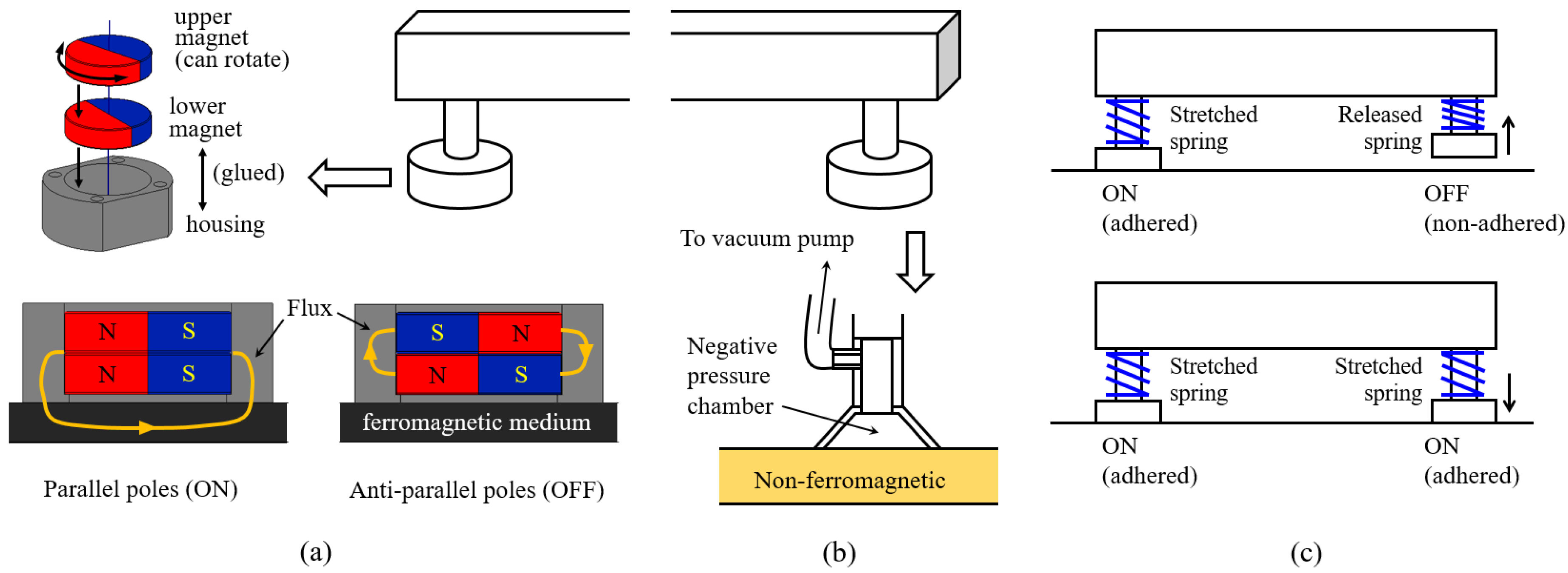
Regarding the adhesion pads, the technology to implement them should not be different from other adhesion technologies generally used in climbing robots. Of all adhesion technologies used in climbing robots [21], magnetic and pneumatic technologies are the most mature and widely used ones, and these should be the adhesion technologies used for the adhesion pads of the MASAR robot. The choice to use one or another technology will depend on the medium on which the robot moves:

• If the MASAR robot is used for exploring industrial infrastructures, made of ferromagnetic materials, then the best choice will be magnetic adhesion, preferably switchable permanent magnets [22]. As illustrated in Figure 3a, switchable magnets are made of cylindrical and diametrically magnetized permanent magnets embedded inside a ferromagnetic housing such that, by rotating by 180°, one of the magnets with respect to the other using a micromotor, their magnetic poles remain parallel or anti-parallel, recirculating the magnetic flux either through the ferromagnetic medium (ON state: producing the adhesion to it) or internally through the housing (OFF state: canceling adhesion). Switchable magnets have many advantages over classical electromagnets [23], such as lower energy consumption (power is only needed for switching the adhesion state, instead of continuously draining power to remain attached), higher adhesion forces per unit mass, and higher safety (in the event of power failure, permanent magnets will not detach). Examples of binary switchable magnets were developed in [22] for a climbing biped robot.
• If the environment where the MASAR robot moves is not ferromagnetic, such as domestic environments, then magnetic adhesion is not feasible and active pneumatic adhesion should be used instead. Active pneumatic adhesion requires using suction cups inside which a negative pressure is produced by means of a vacuum pump (Figure 3b). Thus, in case pneumatic adhesion was required, each MASAR robot will have to carry a small vacuum pump in addition to a battery to power the pump and other elements of the robot, as in the robot presented in [24].

Independently of the adhesion technology used for the adhesion pads, it is clear from Figure 2 that the OFF adhesion pad will rub against the floor, which may hinder the motion of the robot in case the floor is not sufficiently smooth (e.g., pad A6 will rub when it rotates about pad A4 in Figure 2b). If necessary, this can be overcome by introducing an additional translational articulation to each adhesion pad, such that each pad remains retracted when OFF (just the minimum distance necessary to prevent rubbing against the floor), but it is slightly extended when ON, to guarantee that it makes contact with the floor (see Figure 3c). This may be implemented with electromagnets or other specifically designed mechanisms, which are commanded by the very same ON/OFF signal that activates or deactivates the adhesion of the pad to the environment. The concrete definition of this system is part of ongoing and future work, together with the development of a prototype of the proposed robot.

A similar robot that also uses the mode of locomotion shown in Figure 2b–d was developed in [25] for autonomous cleaning of glass windows. In [25], two opposite pads similar to our pads A4 and A6 are simultaneously powered by the same motor by means of a belt mechanism with parallel axes, whereas our robot uses the bevel-gear mechanisms with concurrent axes depicted in Figure 2a. In addition to this difference, our robot also has two additional differences with respect to the one described in [25]:

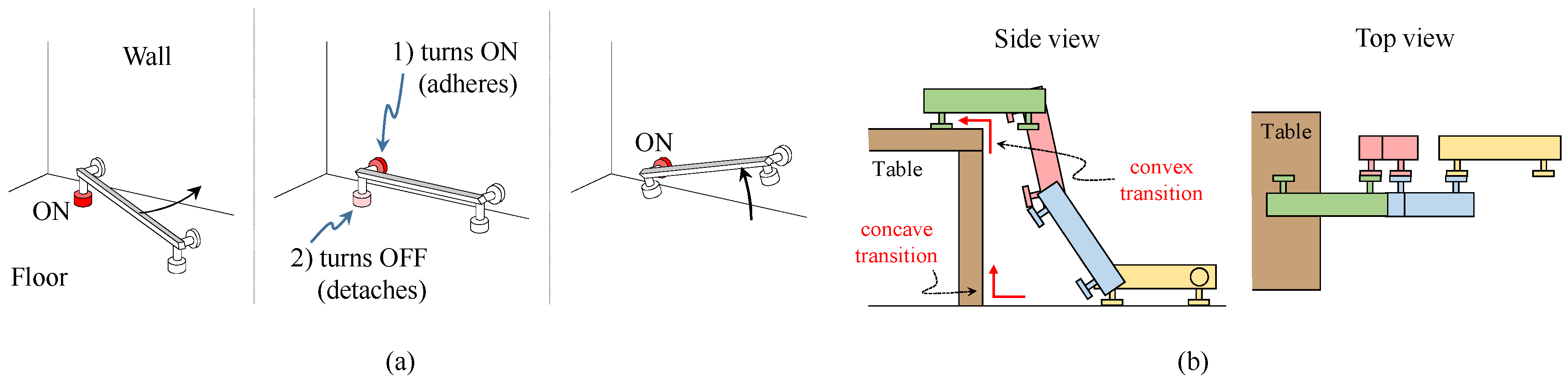
• MASAR can perform concave plane transitions, such as those necessary for traversing between a vertical wall and the floor/ceiling or between different walls (see Figure 4a). This is thanks to the arrangement of adhesion pads at orthogonal faces of our robot, as shown in Figure 2a. Accordingly, this allows MASAR to climb walls and autonomously explore three-dimensional environments made up of the concave intersection of orthogonal planes (such as domestic indoor environments delimited by walls, ceilings and floors) using only one motor. Note that, in order for the MASAR robot to perform a concave transition, it should place its lateral adhesion pads on the new plane, but this is possible only if the distance between the robot and the new plane is appropriate. However, this is not a problem since the MASAR robot can finely adjust its position and orientation in the plane by performing small rotations about alternate pivots, attaining a position that enables the aforementioned transitions.
• Our robot is modular, in the sense that several identical MASAR modules can be combined (joining their adhesion pads) in order to form multi-degree freedom of manipulators able to complete tasks more complex than a single module can complete. This idea is illustrated in Figure 4b, which shows a team of four MASAR modules working together to form a serial arm that can climb to a table. Note that a single module would be unable to climb the table on its own, since this would require a convex transition between the table leg and the tabletop, which a single module cannot perform (a single module can only perform concave transitions, such as those between the floor and the leg of the table).

Finally, regarding the potential applications of the proposed MASAR robot, its locomotion mode (Figure 2b–d) makes it especially suitable for cleaning tasks, as the similar robot proposed in [25]: these robots move by “sweeping” their bodies rotating about their extreme points, so placing sponges [25] or some other cleaning device at their base (between the adhesion pads) takes advantage of this sweeping motion to clean the plane in which they move (floor, wall, or ceiling). In this aspect, these robots would act as “mobile” versions of the wiper washer of a car. Another possible application is inspection or surveillance of industrial facilities. In any case, as illustrated in Figure 4b, the MASAR robot has also been designed as a modular reconfigurable robot, in which several identical MASAR modules can cooperate and combine in order to complete more advanced tasks than a single module can do. One of the most attractive features of modular reconfigurable robots is their potential to solve a myriad of different tasks by simply disassembling and reassembling in a different way, adapting their formation to the environment or task at hand [26]. For this reason, at the moment, we prefer not to limit the potential applications of the proposed robot by focusing on a concrete application, but we prefer to keep the applications of this robot quite open and focus on its analysis and design without limiting it to a concrete application, to explore the future possibilities that the MASAR robot has to offer both as an individual module and as plurality of collaborating modules.

3. Trajectory Following

This section approaches three planar trajectory following problems of the proposed robot. Assuming that the trajectory to follow is polygonal, made up of a sequence of segments obtained from, e.g., an A* algorithm, the problems to solve are the following:

• How to make the robot follow a polygonal path without obstacles that constrain the motion of the robot, i.e., there is no restriction on the amplitude of the rotations that the robot can perform.
• How to make the robot go through a narrow path or corridor, which restricts the amplitude of its rotations.
• Combination of both previous problems, solving a set of segments which may contain narrow sections.

These three problems will be solved in the following sections from a purely geometric and deterministic perspective, assuming that both the location of the robot and the trajectory to follow are known. This will allow us to focus on the analysis of the optimality of the proposed solutions, in Section 4.

3.1. Problem 1: Following Unconstrained Polygonal Paths

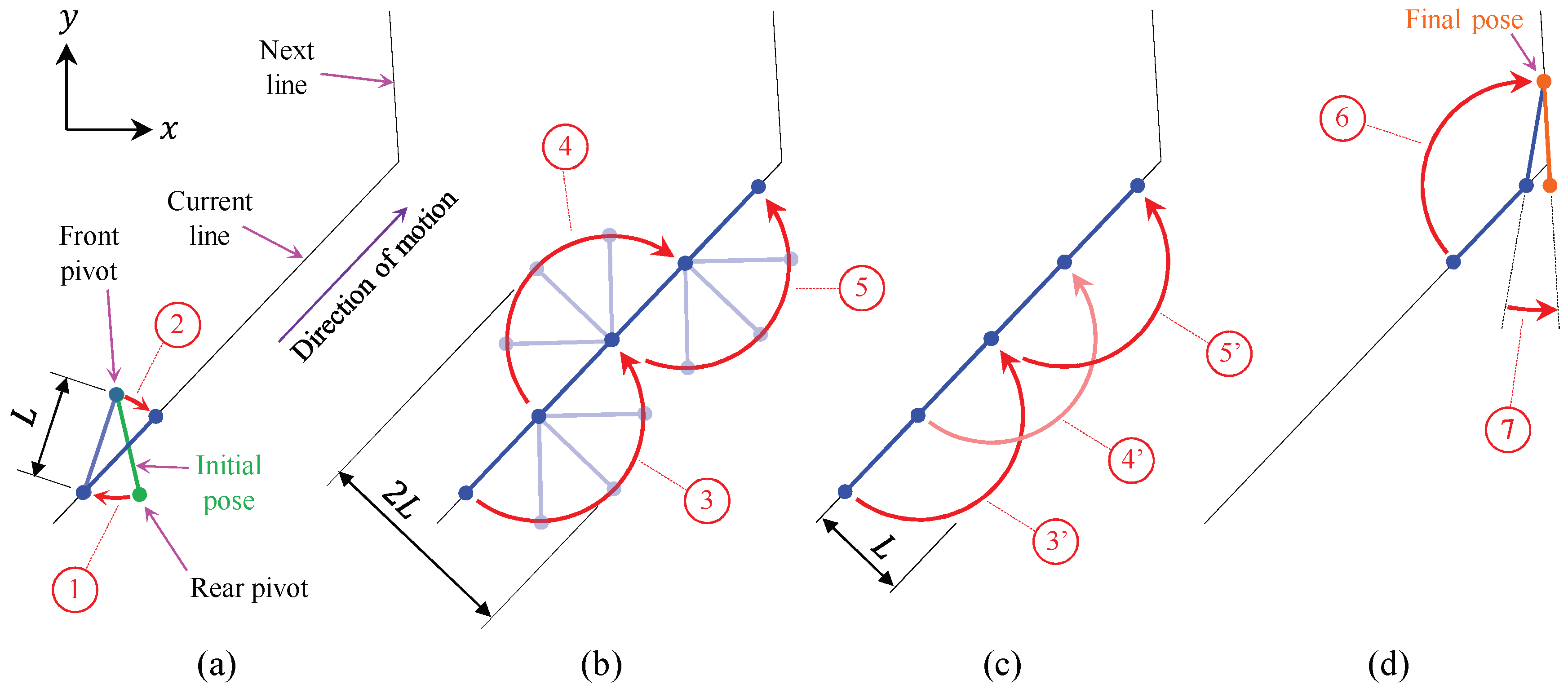
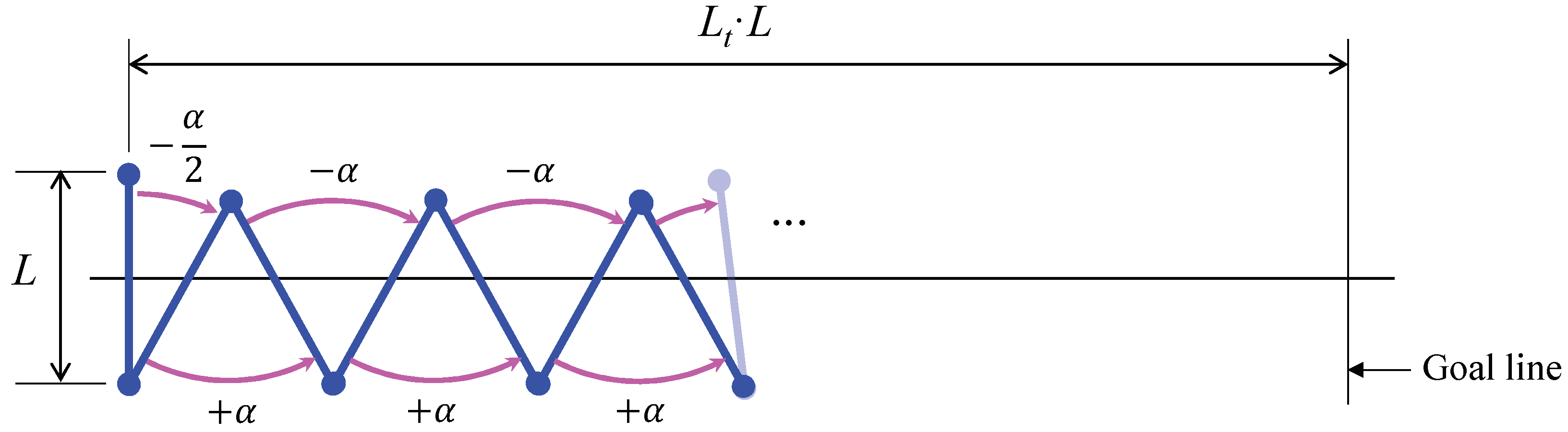
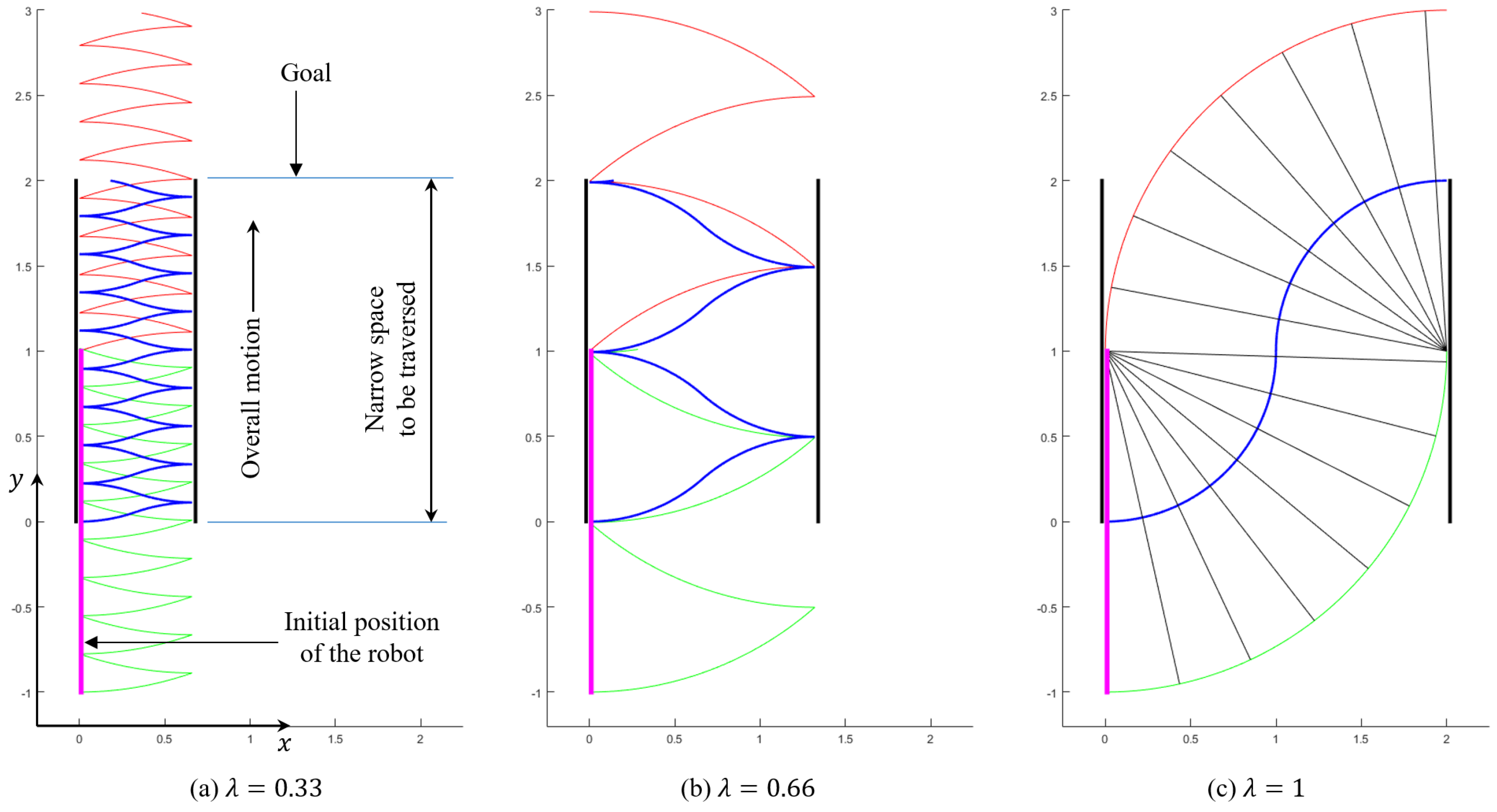
The first decision to make is the gait that the robot should use for following straight trajectories that have no restrictions that is, paths with no obstacles or collisions that may constrain the amplitude of the rotations of the robot (at most, only changes of direction are found). If the motion of the robot is not constrained, then the most reasonable gait for the robot should be based on 180° turns, since they achieve a maximum displacement along the direction of the trajectory and reduce overall time. This choice is illustrated in Figure 5b,c, and will be further discussed in Section 4.1.

We assume that, at the beginning of the polygonal path, the robot starts with any orientation, and with its middle point placed on the first straight segment of the path. If this was not the case, it will simply be necessary to rotate the robot around any of its pivots until its center point intersects this segment—or, in case the center point does not intersect the initial segment, a virtual segment may be defined between the center of the robot and the closest point of the first actual segment of the trajectory, continuing then, as explained next, without any changes.

To start the movement that traverses each segment using 180° turns, the robot must be completely aligned with the straight line. In general, the pivots may not be initially on the line. Therefore, two rotations are required for reaching the desired initial pose, as explained next.

3.1.1. Initial Reorientation

As mentioned before, initially, it may be possible that both pivots are not on the line; in that case, the robot must re-orient itself to align with the straight line, with both pivots on it. Two rotations will be needed, as illustrated in Figure 5a: one rotation about the front pivot (i.e., the one closest to the end of the segment to traverse) and another about the rear pivot.

The first rotation, considered as initial re-orientation and identified in Figure 5a by the number 1, is based on the search of a point on the line whose distance to the front pivot is equal to the length L of the robot. This point is found solving the intersection between the line and the circle centered at the front pivot and with radius L.

After computing the intersection point, through the law of cosines, we calculate the value of the rotation angle 1 (shown in Figure 5a), which places the rear pivot on the line by rotating the whole robot about the front pivot. Considering the straight line as a vector, with its end at the goal of the motion, if the front pivot is located to the right of this vector, the rotation angle will be positive (counter-clockwise). Otherwise, it will be negative (clockwise), as in Figure 5a.

After this rotation, a second re-orientation is produced in order to completely align the robot with the line. The second rotation is about the rear pivot (which is already placed on the line) and is identified in Figure 5a by rotation number 2. The angle to rotate will simply be the angle formed between the robot and the x-axis, minus the angle formed between the line and the x-axis.

3.1.2. Straight Motion and Change of Direction

When the robot is completely on the line, the movement along it can begin. As we previously argued, this movement is based on 180° rotations about alternating pivots, alternating the sign of the rotation with each pivot change, as illustrated by rotations {3,4,5} in Figure 5b. Alternatively, the sign of the rotations may remain constant during the motion, as shown by rotations {3’,4’,5’} in Figure 5c. If this sign is switched together with the pivots (Figure 5b), the trajectory is more symmetric with respect to the line to be followed, but it requires twice the space than by keeping the sign of the rotations (Figure 5c) constant, measuring this space in the direction perpendicular to the line. If there are no space limitations, either gait shown in Figure 5b,c would be valid.

After performing a certain number of 180° rotations, when the front pivot is sufficiently close to the end of the current line, the robot considers that it has reached the end of the line and starts a sequence of movements for moving to the next straight line (Figure 5d). The first movement places the rear pivot of the robot on the next line by rotating about the front pivot. The angle to rotate in this case (angle 6 in Figure 5d) is determined by finding again the intersection point between the new line and a circle centered at the front pivot and with radius L.

Finally, in order to completely align the robot with the new line, it must be rotated by angle 7 of Figure 5d about the front pivot (which lies already on the new line). This final angle is again computed as the difference of the angles formed by the robot and the line with the x-axis. When this change of direction is over, the robot will be able to continue along the new line with the described locomotion: performing 180° turns until the end of the new line is reached, then changing again the direction of motion, etc., until the end of the whole polygonal path is reached.

3.2. Problem 2: Traversing Narrow Corridors

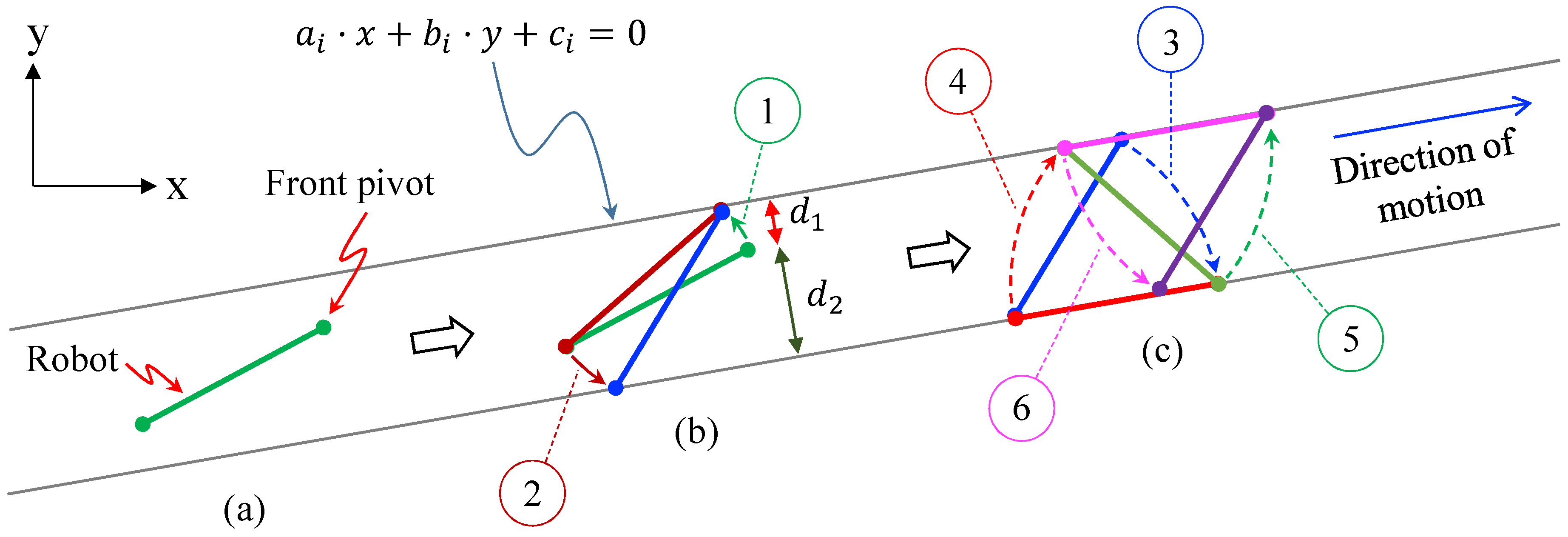
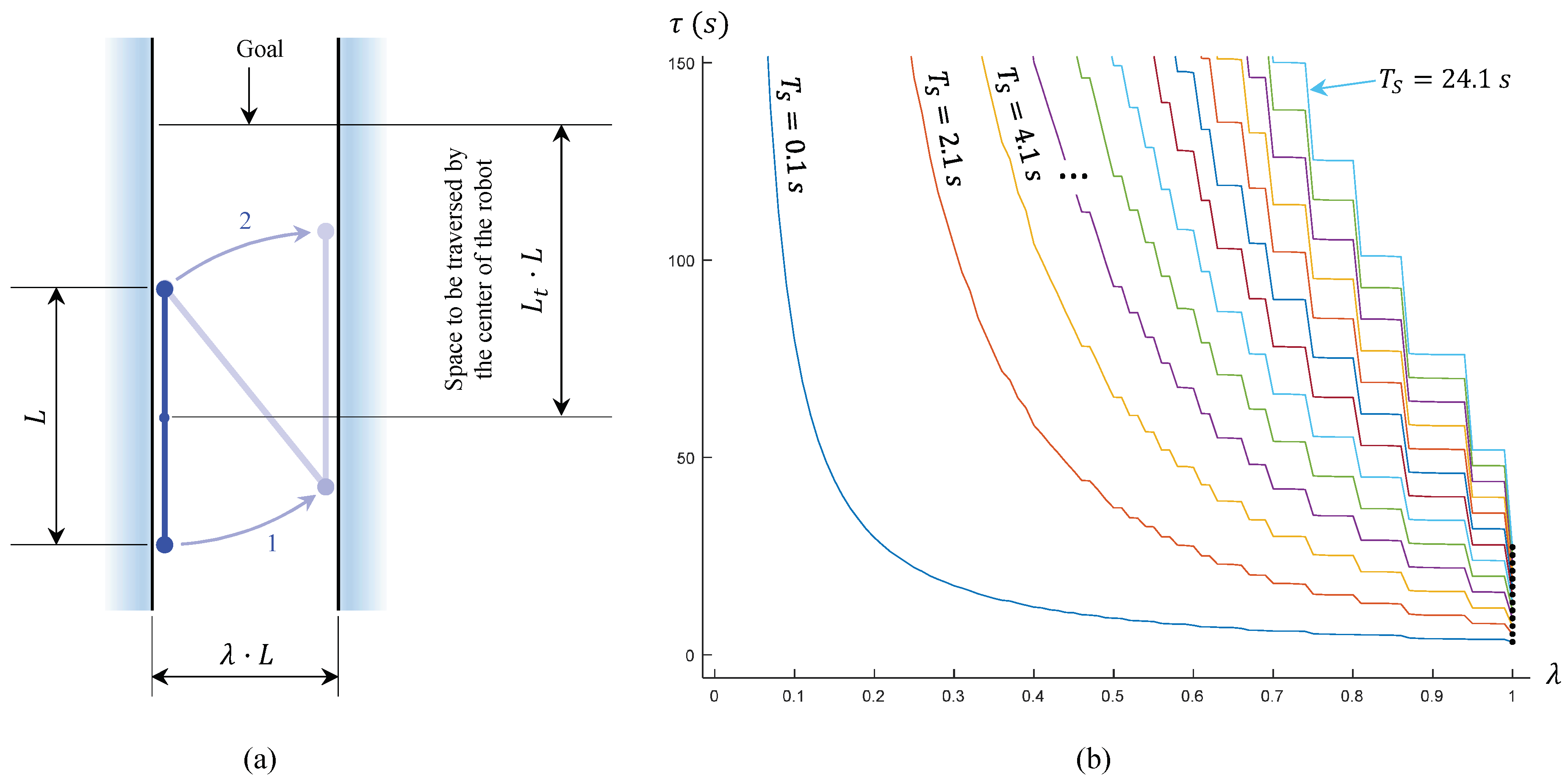
This section focuses on solving those situations where the robot needs to traverse a narrow corridor defined by two parallel walls (Figure 6), such that the separation between these walls is smaller than the length L of the robot (otherwise, the robot would be able to traverse the corridor by employing the locomotion illustrated in Figure 5c). Note that these walls may be actual physical walls, but also virtual walls defined artificially for safety reasons, so that the robot does not collide with other obstacles whose shape may be more involved.

In this scenario, the robot cannot perform complete rotations of 180° and it must use an alternative locomotion, which we explain next. In order to perform the optimal locomotion to traverse a narrow corridor, it will be necessary to perform an initial reorientation of the robot first, so that each pivot is placed on a different wall of the corridor, as explained next.

3.2.1. Initial Maneuvering inside the Narrow Corridor

The fastest and more efficient motion for going through a narrow corridor is the one in which the robot moves by placing its whole body alternately on a different wall, as illustrated in Figure 6c. This motion is the best option since it achieves the maximum displacement in the direction of the corridor during each step. To achieve this motion, the robot must start with each pivot placed on a different wall. The main objective of this sub-section is to determine the pair of rotations that the robot must perform (with each rotation about a different pivot) to reach the desired initial pose (Figure 6b).

This process begins by looking for the shortest distance $min(d_1,d_2)$ from each wall to the front pivot of the robot:

$$d_i=\frac{|a_i·x_{\mathit{front}}+b_i·y_{\mathit{front}}+c_i|}{\sqrt{a_i^2+b_i^2}},$$

(1)

where each wall $i\in \{1,2\}$ is modeled by a line defined by its implicit equation $a_i·x+b_i·y+c_i=0$. Once the calculation is done, the shortest distance identifies the wall closest to the front pivot, which must be moved to that wall by rotating about the rear pivot (rotation number 1 in Figure 6b). This rotation is determined by finding the intersection between the closest wall and a circle centered at the rear pivot and with radius L (where L is the length of the robot). After obtaining this intersection point, the law of cosines is applied for obtaining the desired angle that the robot must be rotated about the rear pivot in order to place the front pivot at the calculated intersection point.

When this point is reached by the front pivot, the same process needs to be done again for placing the rear pivot on the opposite wall, this time rotating about the front pivot (rotation 2 in Figure 6b).

3.2.2. Movement along the Corridor

After each pivot of the robot lies on a different wall, the robot proceeds to move inside the corridor, until reaching its end. This movement is accomplished by rotating always by the same angle, which is the angle formed between the robot and the walls when the robot has each pivot placed on a different wall. As explained before, this is the optimal rotation for advancing along the narrow corridor since it produces the maximum advance along the direction of the corridor in a single rotation. The fixed pivot must be switched after each rotation, whereas the sign of the rotation must be switched every two rotations. This process is illustrated in Figure 6c, with a sequence of rotations {3,4,5,6}.

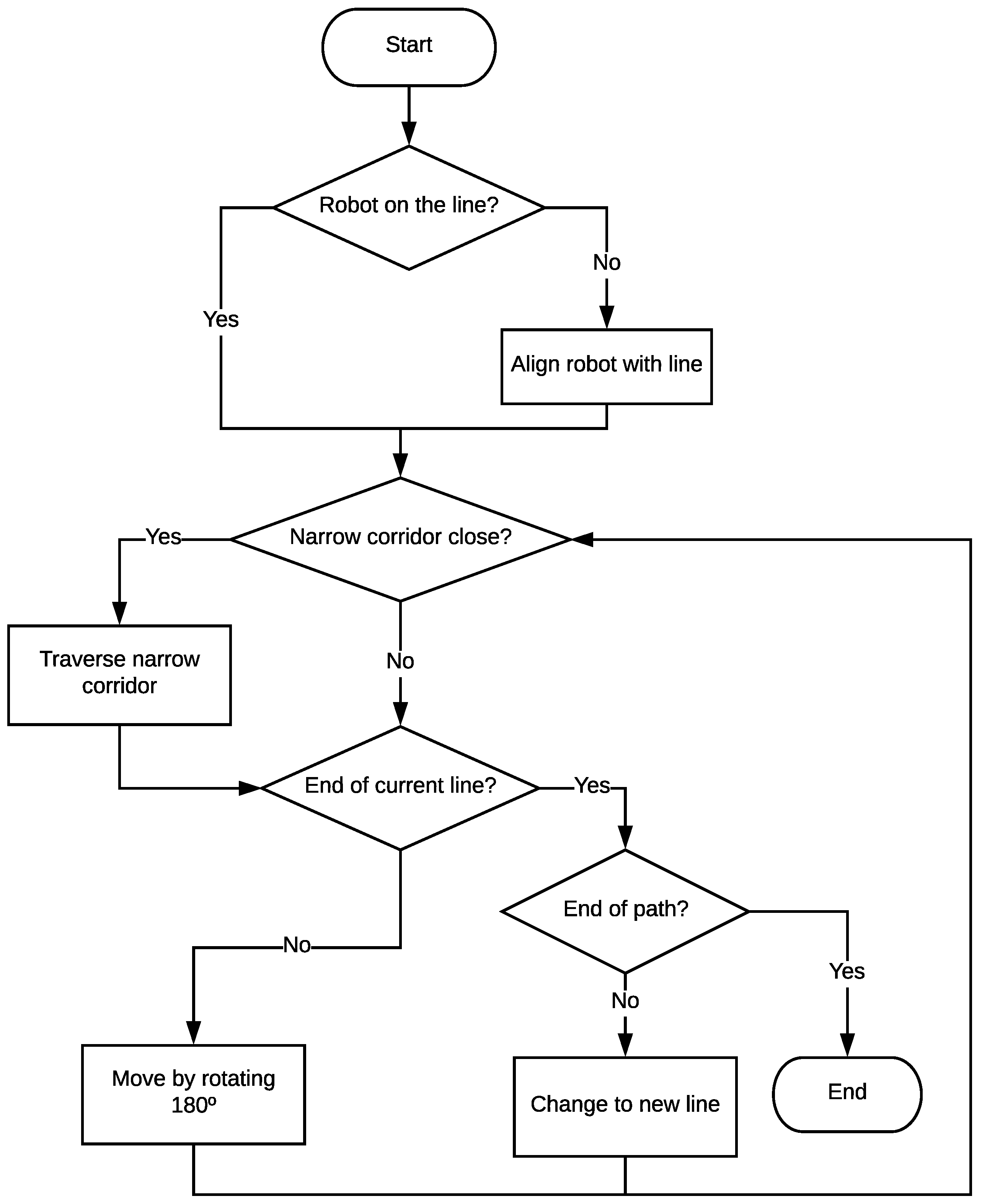
3.3. Problem 3: Combination of Both Problems

After explaining the previous two problems (following obstacle-free polygonal trajectories in Section 3.1, and traversing narrow corridors in Section 3.2), this section analyzes the combined scenario, in which the robot must follow a polygonal trajectory that has narrow sections. This combination of the two problems is based on an online management by the robot while moving, i.e., as it proceeds along the trajectory, if the robot finds a narrow corridor, a change of direction, or obstacle-free lines, it will perform some or other relevant actions defined in previous subsections. The algorithm used by the robot to manage the different possibilities is illustrated graphically in the flow diagram shown in Figure 7. This flow diagram describes how the different methods and procedures presented in Section 3 are “activated” and executed as the robot advances along the trajectory and encounters an obstacle-free straight segment, a narrow corridor, or a change of line.

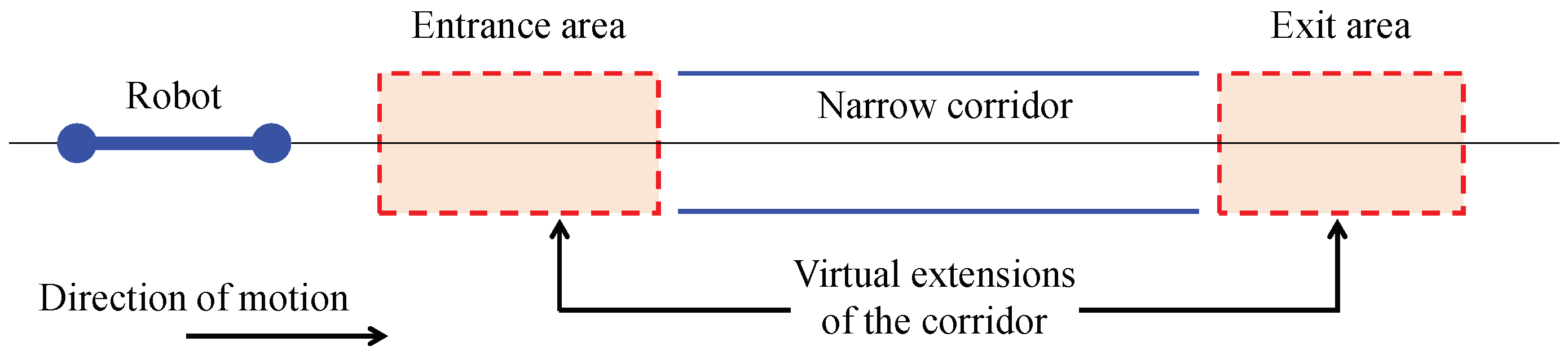
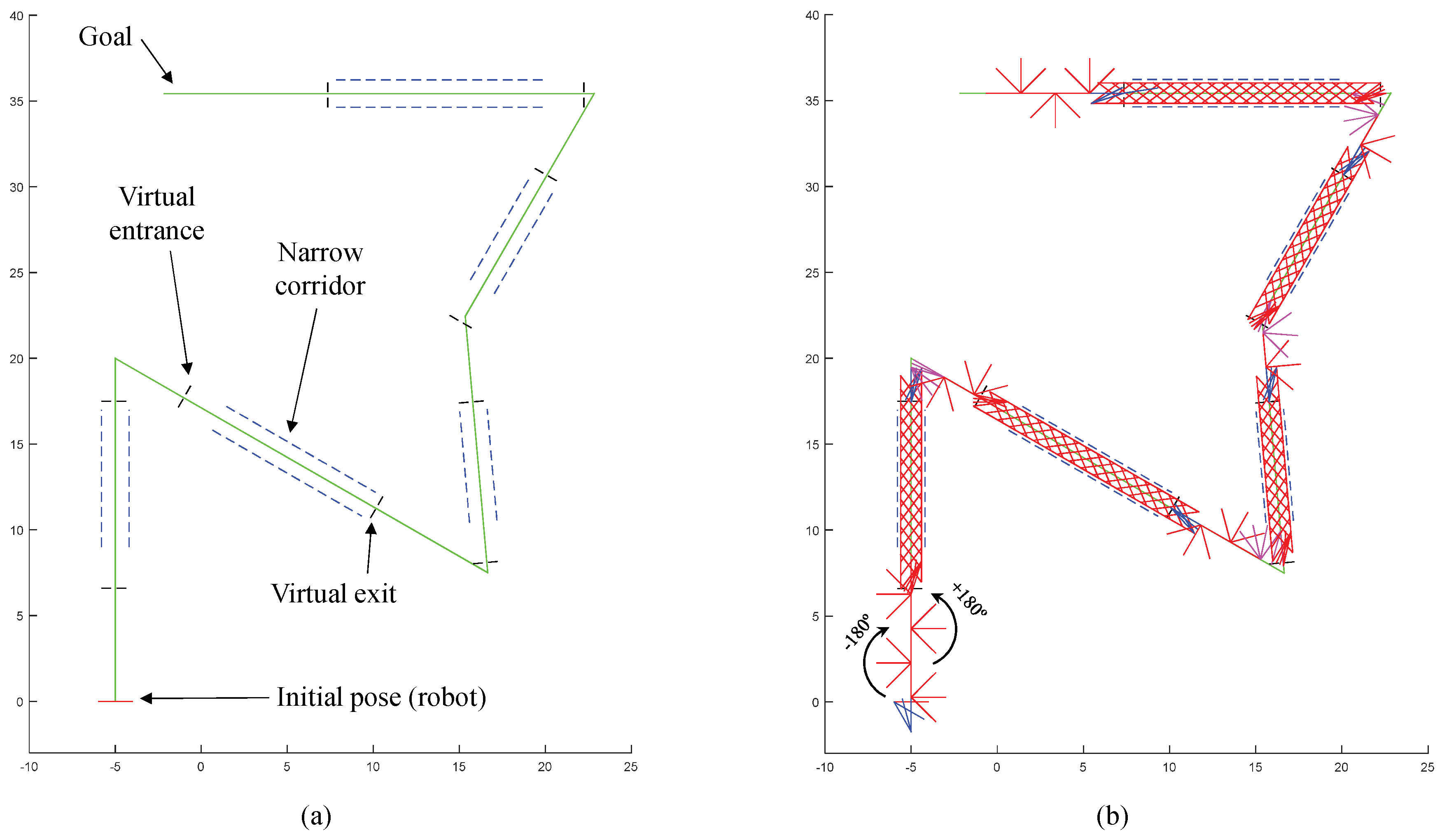
At this point, it is important to specify how the robot is able to face narrow corridors, that is, how it enters and leaves them. In order to solve this situation, virtual narrow areas are defined both at the beginning and at the end of the corridor. These virtual areas will be virtual extensions of the real corridor, as illustrated in Figure 8.

On the one hand, in order to enter the corridor, when the front pivot enters the first virtual area (denoted by “Entrance area” in Figure 8), the robot will understand that the corridor is near. Then, it will behave as if it was already inside of the corridor: the robot will perform the corresponding movements for placing its pivots on each virtual wall (as in Figure 6b), and, afterwards, it will move forward using the gait of Figure 6c, even if it is still in the virtual entrance of the corridor. In this way, it is guaranteed that the robot will not try to approach the entrance of the corridor by performing wide rotations of 180°, which may produce the collision with the walls of the corridor before entering it.

On the other hand, for leaving the corridor, a similar procedure is followed. This time the robot understands that the narrow corridor is “safely” finished when its rear pivot leaves the second virtual area (denoted by “Exit area” in Figure 8). Finally, once the robot is completely out, it performs the sequence of movements shown in Figure 5a in order to completely align with its current straight line, and continue traversing the path.

4. Experiments and Discussion

This section presents some simulation experiments to illustrate and analyze the problems and solutions proposed in the previous section, as well as deepen some aspects of these solutions.

4.1. Experiment 1: Comparison of Gaits

In Section 3.1, we argued that the most efficient gait for the MASAR robot to follow obstacle-free straight trajectories would be by performing 180° turns, since this gait maximizes the traversed distance (along the direction of the line to follow) in a single rotation. Here, we will analyze the optimality of this choice in more detail, by studying the overall time $\tau$ required by this robot to complete a straight-line trajectory of length $L_t$ times the length of the robot, depending on the angle $\alpha$ rotated by the robot during each step. As Figure 9 illustrates, we assume that the robot starts at the beginning of this trajectory and orthogonal to it. First, the robot rotates $-\alpha /2$ about one pivot, and then it starts to rotate $+\alpha$ or $-\alpha$ about alternating pivots, until the end of the straight trajectory is attained (we consider that the trajectory is completed when the center of the robot crosses the goal line parallel to the initial orientation of the robot). We compute the overall time $\tau$ necessary for completing this straight trajectory as follows:

$$\tau ={\tau }_S+{\tau }_R.$$

(2)

${\tau }_S$ is the overall time that the robot spends switching the adhesion states of its pivots during the whole trajectory. This time can be computed as follows:

$${\tau }_S=T_S·M\left(\alpha \right),$$

(3)

where $T_S$ is the time necessary for adhering to the previously released pivot plus releasing the previously adhered pivot. Note that, for a safe operation of the robot, the previously adhered pivot should be released only after the previously released pivot has been adhered sufficiently to the surface, to guarantee that the robot will always remain sufficiently adhered to the environment through at least one pivot. If the adhesion state of the pads of the robot changes simultaneously (or in the wrong order), the robot may temporarily lose control of its motion (and fall down, if it was climbing). In the case of adhesion devices that take some time to switch their adhesion states (such as switchable magnets [22]), in order to save time, it may be possible to partially overlap the attaching and detaching processes of both pivots without compromising the stability of the adhesion, instead of executing these processes sequentially. In any case, here we will not need to specify the precise sequence to switch the adhesion states of the pivots of the MASAR robot: it will suffice to model this process through the overall time $T_S$ necessary to complete it.

In (3), $M\left(\alpha \right)$ is the total number of times that the pivots change their adhesion states along the whole trajectory. Note that M will depend on $\alpha$: it is intuitive to think that small rotations ($\alpha$ small) will require a higher number of pivot changes, whereas wider rotations ($\alpha$ large) will require fewer pivot changes. This will be quantified later, through some simulation examples. Finally, note also that ${\tau }_S$ is a “dead” time where the robot is not moving at all: it is just switching the adhesion state of its adhesion units.

On the contrary, ${\tau }_R$ is the overall time spent by the robot rotating, in order to advance and reach the end of the straight trajectory. ${\tau }_R$ is computed as follows:

$${\tau }_R=\frac{\alpha }{2\omega }+\sum _{i=1}^{N\left(\alpha \right)}\frac{\alpha }{\omega }+\frac{{\alpha }_{\mathit{final}}}{\omega }=\frac{\alpha }{\omega }\left(\frac{1}{2}+N\left(\alpha \right)+\kappa \right),$$

(4)

where $\omega$ is the angular velocity of the rotations of the robot about its fixed pivot, which we assume constant. All angles $\alpha$ involved in (4) are taken to be positive. In (4):

• The first term [$\alpha /\left(2\omega \right)$] is the time necessary for performing the initial rotation of $-\alpha /2$.
• The second term (the sum of N terms) is the time necessary to perform all the integer rotations of $+\alpha$ and $-\alpha$ necessary to (almost) reach the end of the straight trajectory. $N\left(\alpha \right)$ is the total number of these rotations of angle $\pm \alpha$, counting both positive and negative rotations. Note that N depends on $\alpha$.
• Finally, the third term $({\alpha }_{\mathit{final}}/\omega )$ is the time necessary for performing one last rotation of ${\alpha }_{\mathit{final}}$ so that the center of the robot reaches the end of the trajectory. This is necessary since, generally, the end of the trajectory will not be exactly reached after performing an integer number of rotations of angle $\alpha$: a final rotation ${\alpha }_{\mathit{final}}=\kappa ·\alpha$ (with $\kappa \in [0,1]$) will be necessary.

Substituting (3) and (4) into (2) yields the expression of the overall trajectory time $\tau$ in terms of $\alpha$:

$$\tau =T_S·M\left(\alpha \right)+\frac{\alpha }{\omega }\left(\frac{1}{2}+N\left(\alpha \right)+\kappa \right),$$

(5)

which can be rewritten as follows:

$$\tau =\frac{1}{\omega }\left[\left(T_S·\omega \right)·M\left(\alpha \right)+\alpha \left(\frac{1}{2}+N\left(\alpha \right)+\kappa \right)\right]=\frac{1}{\omega }\left[\eta ·M\left(\alpha \right)+\alpha \left(\frac{1}{2}+N\left(\alpha \right)+\kappa \right)\right].$$

(6)

According to Equation (6), for a given relative length $L_t$ of the straight path to be traversed (which affects implicitly the values of M and N), the optimal value of $\alpha$ that minimizes the overall time $\tau$ depends solely on the product $\eta =T_S·\omega$ (the first factor $1/\omega$ will only scale the optimal value of the time $\tau$, but it will not affect the optimal value of $\alpha$). $\eta$ has an interesting physical meaning: it is the angle that the robot would be able to rotate if it employed the switching time $T_S$ to rotate about one pivot, instead of switching the adhesion states of its pivots. $\eta$ acts effectively as a weight that gives more importance to one objective (minimize the time spent switching the adhesion states of the pivots) or the other (minimize the time spent rotating about the pivots).

In what follows, we will perform some simulations to analyze the dependence of (6) on $\alpha$. To that end, we will set $\omega$ constant to 1 rad/s for simplicity, and we will vary the switching time $T_S$ to analyze its effects on the merit function $\tau$. Alternatively, if one wanted to avoid setting $\omega$ to some arbitrary value, Equation (6) may be rewritten as follows:

$$\tau ·\omega =\eta ·M\left(\alpha \right)+\alpha \left(\frac{1}{2}+N\left(\alpha \right)+\kappa \right).$$

(7)

In this case, the merit function is the product $\tau ·\omega$, whose shape depends only on $\eta$ and avoids setting $\omega$ to some arbitrary numeric value. However, while $\tau$ has an intuitive and useful physical interpretation (it is the overall time needed by the robot to complete the trajectory), $\tau ·\omega$ is not so intuitive or useful: it would represent the angle that the robot would rotate if it was continuously rotating about one of its fixed pivots, during the whole time that it would otherwise employ to complete the trajectory. For this reason, the next tests will consider $\tau$ of (6) as the merit function, with $T_S$ as a variable parameter and $\omega =1$.

4.1.1. Completing a Short Trajectory

In order to illustrate the previous analysis, let us consider a straight trajectory $L_t=5$ times longer than the robot. Figure 10a shows a graph with the time $\tau$ required for completing this trajectory as a function of $\alpha$, for different switching times $T_S$. This graph was obtained after simulating the trajectory in Matlab for each value of $T_S$ and $\alpha$. Figure 10b,c show the contribution of the two components that add up to the overall time $\tau$: the total number $M\left(\alpha \right)$ of times that pivots are switched, and the time ${\tau }_R$ that the robot spends rotating about its pivots along the whole trajectory. According to these figures, the dependence of M on $\alpha$ is U-shaped, i.e.: M increases for small (near 0°) and large (near 360°) values of $\alpha$, while it decreases for intermediate values. As for ${\tau }_R$, it increases with $\alpha$.

Figure 11 shows some discrete postures adopted by the robot during the trajectory, as well as the continuous trajectories described by its pivots (in red and green) and by the center of the robot (in blue), which is the point of interest in this experiment (the objective is that the center of the robot crosses the horizontal line $y=10$, departing from the origin). In this figure, the robot is two-units long, whereas the trajectory has 10 units of length. According to Figure 11, the trajectory described by the robot is quite straight when using small values for $\alpha$, whereas larger values yield more “curly” trajectories. Note that, for $\alpha >$ 180°, the center of the robot goes back during some parts of the movement, which is counterproductive since the objective is to reach the horizontal line $y=10$.

As it can be observed in Figure 10a, $\tau \left(\alpha \right)$ has steps or discontinuities because both of its components $M\left(\alpha \right)$ and ${\tau }_R\left(\alpha \right)$ have them. These steps are explained as follows:

• The steps in M are due to the fact that, for similar values of $\alpha$ falling in some intervals, the number of times that pivots must be switched to reach the end of the trajectory will be constant.
• The steps in ${\tau }_R$ are due to the fact that, for some (large) values of $\alpha$, the curly trajectory described by the center of the robot becomes almost tangent to the goal horizontal line $y=10$, such that an additional arc must be described between the point of tangency and the goal line in order to reach the goal. This is illustrated in Figure 11d,e, between $\alpha =$ 231° and $\alpha =$ 232°, two angles between which ${\tau }_R$ suffers a steep change (Figure 10c). The time required to perform this additional arc accounts for the sudden increase in ${\tau }_R$ observed in Figure 10c.

As it will be shown later, these steps disappear when the length $L_t$ of the trajectory increases: in that case, $\tau \left(\alpha \right)$ becomes much smoother. Note that, in the graph of Figure 10a, $\tau$ has small positive slopes between successive steps, i.e., it is not exactly constant between these steps (unlike M), due to the contribution of ${\tau }_R$, which increases with $\alpha$.

Returning to the graph of Figure 10a, this graph represents the minimum of $\tau$ for each time $T_S$ by a small black dot, which is attained for the optimal angle ${\alpha }^{*}$. According to this figure, for small switching times $T_S\approx 0.1$ s (i.e., for fast adhesion mechanisms that have small attachment/detachment times), the optimal angle ${\alpha }^{*}$ is about 60°, and this optimal angle quickly increases with $T_S$ until it stabilizes at ${\alpha }^{*}=$ 131° for sufficiently large values of $T_S$ (which would be the case of adhesion devices that take some time to switch between their adhesion states, such as switchable permanent magnets [22]).

Finally, note that, according to Figure 10a, the optimal value of ${\alpha }^{*}$, which minimizes the overall trajectory time $\tau$, is below 180° $\forall T_S$, despite the fact that 180° was chosen as the “optimal” rotation for the trajectory-following algorithm described in Section 3.1. However, it will be shown next that, for sufficiently long trajectories, the asymptotic optimal angle indeed is 180°. In any case, note that $\alpha =$ 180° is always a good choice despite not being the optimum, since the time $\tau$ obtained for $\alpha =$ 180° is only slightly higher than the minimum time obtained for the optimal ${\alpha }^{*}$, $\forall T_S$.

4.1.2. Completing Long Trajectories

Figure 12 shows the variation of time $\tau$ with $\alpha$ and $T_S$ for longer trajectories. Figure 12a,b show the times for trajectories 50 and 1000 times longer than the robot, respectively. First, note that the graph of $\tau$ has become smoother when increasing the length of the trajectory by a factor of 10 (compare Figure 10a and Figure 12a), and these steps have practically disappeared for a sufficiently long trajectory (Figure 12b).

As for the optimal angles ${\alpha }^{*}$ that minimize $\tau$, for $L_t=50$, the optimal angle stabilizes at ${\alpha }^{*}=$ 164° for $T_S>8$ s approximately, whereas it stabilizes at ${\alpha }^{*}=$ 178° for $T_S>50$ s for the longest trajectory ($L_t=1000$). (Again, the minimum $\tau$ for each $T_S$ is represented by a small black dot in Figure 12, as it was done previously in Figure 10a.) By comparing Figure 10a and Figure 12a,b, it can be observed that the optimum angle ${\alpha }^{*}$ tends to 180° when both the length of the trajectory and the switching time $T_S$ increase sufficiently. In the practice, the switching time $T_S$ and/or the length of the trajectory will be much smaller than in Figure 12. However, even in that case, as it was stated previously, the use of $\alpha =$ 180° is always a good choice despite being suboptimal, since the previous figures show that the times $\tau$ necessary to complete the trajectory with $\alpha =$ 180° are only slightly higher than the minimum time obtained when using the optimal angle ${\alpha }^{*}$, for all $T_S$ and $L_t$. Therefore, for simplicity, instead of adapting the optimal gait angle $\alpha$ of the MASAR robot to the length of the trajectory or the switching time $T_S$, we will adopt the asymptotically optimal solution$\alpha =$ 180° for the gait of the robot in all cases, which justifies this choice for the algorithm presented in Section 3.1 for following polygonal, obstacle-free trajectories.

4.2. Experiment 2: Time Necessary to Traverse a Narrow Corridor

While the previous experiment dealt with the first stage of the trajectory-following algorithm proposed in Section 3 (i.e., tracking straight trajectories by using rotations of 180°), this second experiment will analyze the second part of the aforementioned algorithm, which is focused on traversing narrow corridors that constrain the motion of the robot and prevent it from performing such wide 180° rotations. The problem analyzed here is illustrated in Figure 13a: we assume that the robot begins initially with both pivots placed on one of the walls of the narrow corridor. Then, it begins to apply the gait described in Section 3.2, in which the robot places alternately one pivot on each wall or both pivots on the same wall, as illustrated in Figure 13a. In this experiment, we will analyze the time spent by the robot to traverse the narrow corridor using this gait, assuming that the length of the corridor is $L_t$ times the length of the robot (see Figure 13a). The objective is that the center of the robot traverses a distance of $L_t$ times its length, in the direction of the corridor.

In this case, unlike in the previous experiments, the angle rotated by the robot in each step is not a variable parameter, but it is the angle between the walls of the corridor and the robot, when it has one pivot on each wall. Instead, we will analyze next how the time $\tau$ necessary to traverse the corridor depends on the ratio $\lambda$ of the width of the corridor and the length of the robot. This ratio $\lambda$ will be between 0 and 1. We exclude the case $\lambda >1$ because, in that case, the robot can traverse the corridor using the gait illustrated previously in Figure 5c without colliding with the walls of the corridor, a gait by which the robot rotates 180° about alternating pivots, without alternating the sign of successive rotations.

Figure 13b shows the variation of the time $\tau$ with $\lambda$ and $T_S$ for a corridor whose length equals that of the robot, i.e., $L_t=1$. In this case, the overall time $\tau$ is computed similar to the previous experiment, i.e., $\tau$ accounts both for the time spent by the robot switching the adhesion state of its pivots, and the time spent rotating about each pivot (assuming a unit angular speed $\omega =1$ rad/s), during the whole trajectory until the center of the robot reaches the end of the corridor. As Figure 13b shows, the time $\tau$ decreases when the width of the narrow corridor increases, attaining the minimum time when this width equals the length of the robot ($\lambda =1$), which is the limit case beyond which the robot would be able to traverse the corridor with the gait illustrated in Figure 5c, as stated earlier. In this experiment, the minimum time is always attained for $\lambda =1$, independently of the switching time $T_S$. In addition, in this experiment, as in the previous one, the graph of $\tau$ versus $\lambda$ presents some steps or discontinuities, which disappear when increasing the length $L_t$ of the corridor to be traversed, obtaining smoother graphs. However, unlike in the previous experiment, in this case, increasing the length of the trajectory does not affect the position of the minimum time $\tau$, which is always attained for $\lambda =1$.

Finally, to further illustrate this experiment, Figure 14 shows the trajectory described by the center of the robot (in blue) and the pivots (red and green) for traversing the narrow corridor, for different values of $\lambda$ (discrete postures of the robot along the motion are only shown for $\lambda =1$, for clarity of representation). Note that the robot needs to perform many pivot changes for narrow corridors (Figure 14a), as well as many rotations, which justifies the higher values of $\tau$ observed in Figure 13b for small $\lambda$. In the limit of $\lambda =1$ (Figure 14c), which is the fastest case according to Figure 13b, the robot only needs to perform the following three steps: (1) rotate +90° about the upper pivot, (2) switch the adhesion state of the pivots, and (3) rotate −90° about the other pivot. The time required to perform these three steps would be [$\pi /\left(2\omega \right)+T_S+\pi /\left(2\omega \right)=\pi /\omega +T_S$]. Since $\lambda =1$, the width of the corridor equals the length of the robot and the corridor can be traversed with a single rotation of 180° about the upper pivot, which would take a time equal to [$\pi /\omega$], i.e., the time $T_S$ necessary to switch the pivots is avoided. Thus, the fastest gait for traversing narrow corridors (a gait which occurs for corridors nearly as wide as the length of the robot) always takes more time than the gait based on rotations of 180°, which, in comparison, saves at least $T_S$ seconds for every $L_t$ units of corridor that need to be traversed.

4.3. Experiment 3: Example Path

The algorithm illustrated in Figure 7, which achieves the tracking of polygonal trajectories with narrow sections as described throughout Section 3, is applied next to the example trajectory illustrated in Figure 15a. This trajectory is composed of five segments with narrow sections in all of them. Figure 15a shows the robot in its starting pose as a small red segment. In addition, this figure represents the start and end of the virtual extensions of the narrow corridors, at their entrances and exits. The robot must move from its starting position to the end of the path near point $(0,35)$.

Figure 15b shows the result of executing the proposed trajectory tracking algorithm. This figure shows some discrete postures attained by the robot during the trajectory, clearly illustrating the locomotion based on 180° rotations, as well as the gait proposed in Section 3.2 for traversing narrow corridors. In addition, it can be seen in Figure 15b how the robot starts to move as if it was inside the corridor after its front pivot invades the virtual extension at the entrance of the corridor, and it switches again to normal motion (based on 180° rotations) when its rear pivots leave the virtual extension at the exit of the corridor. Some of the basic movements or maneuvers described in Section 3 are represented in Figure 15b in different colors: maneuvers for aligning with the segments of the trajectory are represented in blue, whereas changes of line are represented in magenta. A video of the simulation of Figure 15 accompanies this paper, which shows the motion of the robot and the transitions between different maneuvers (traversing straight line or narrow corridor, change of line, etc.) as the robot follows the desired trajectory (See Supplementary Materials).

5. Conclusions and Future Work

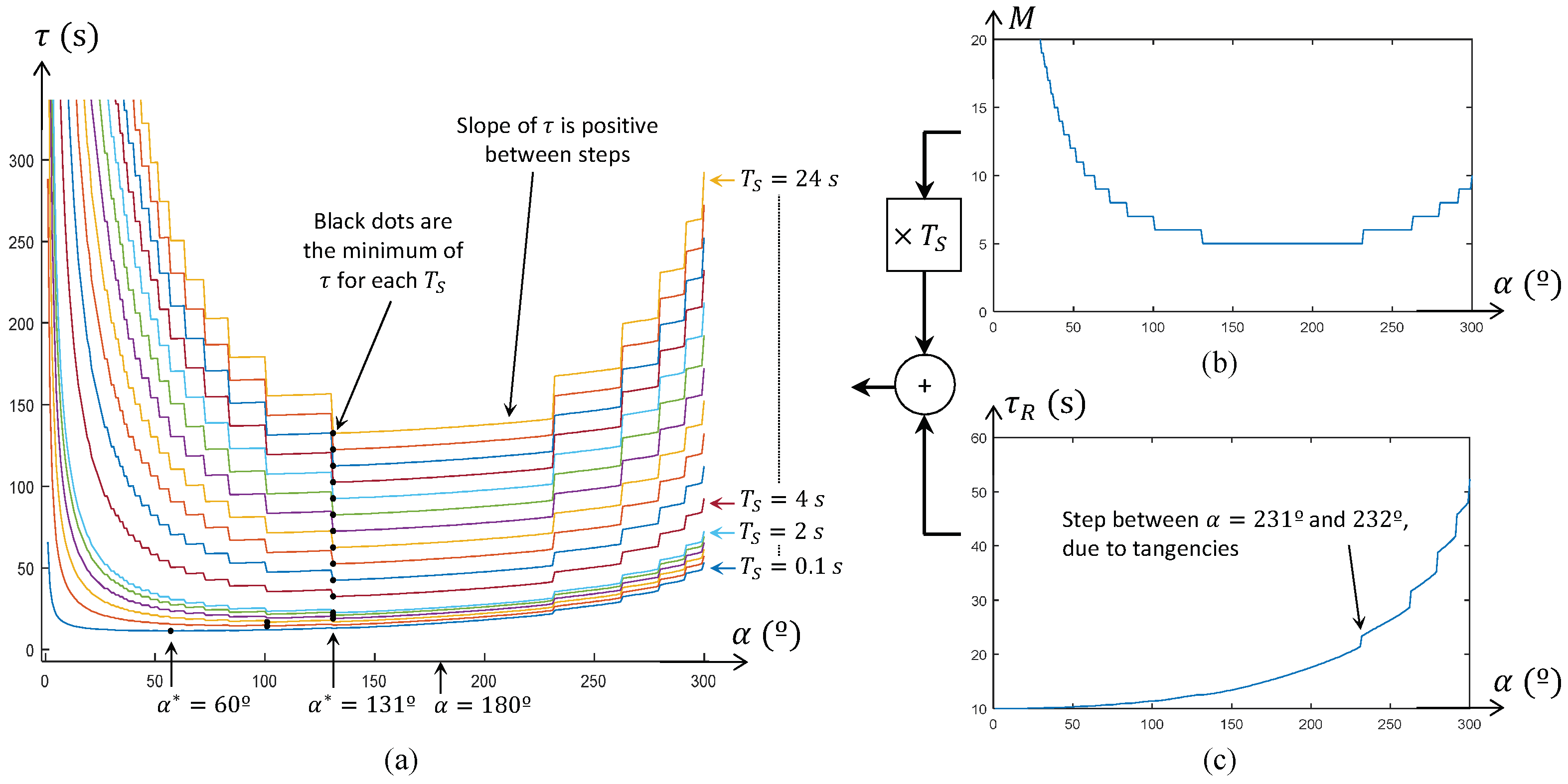
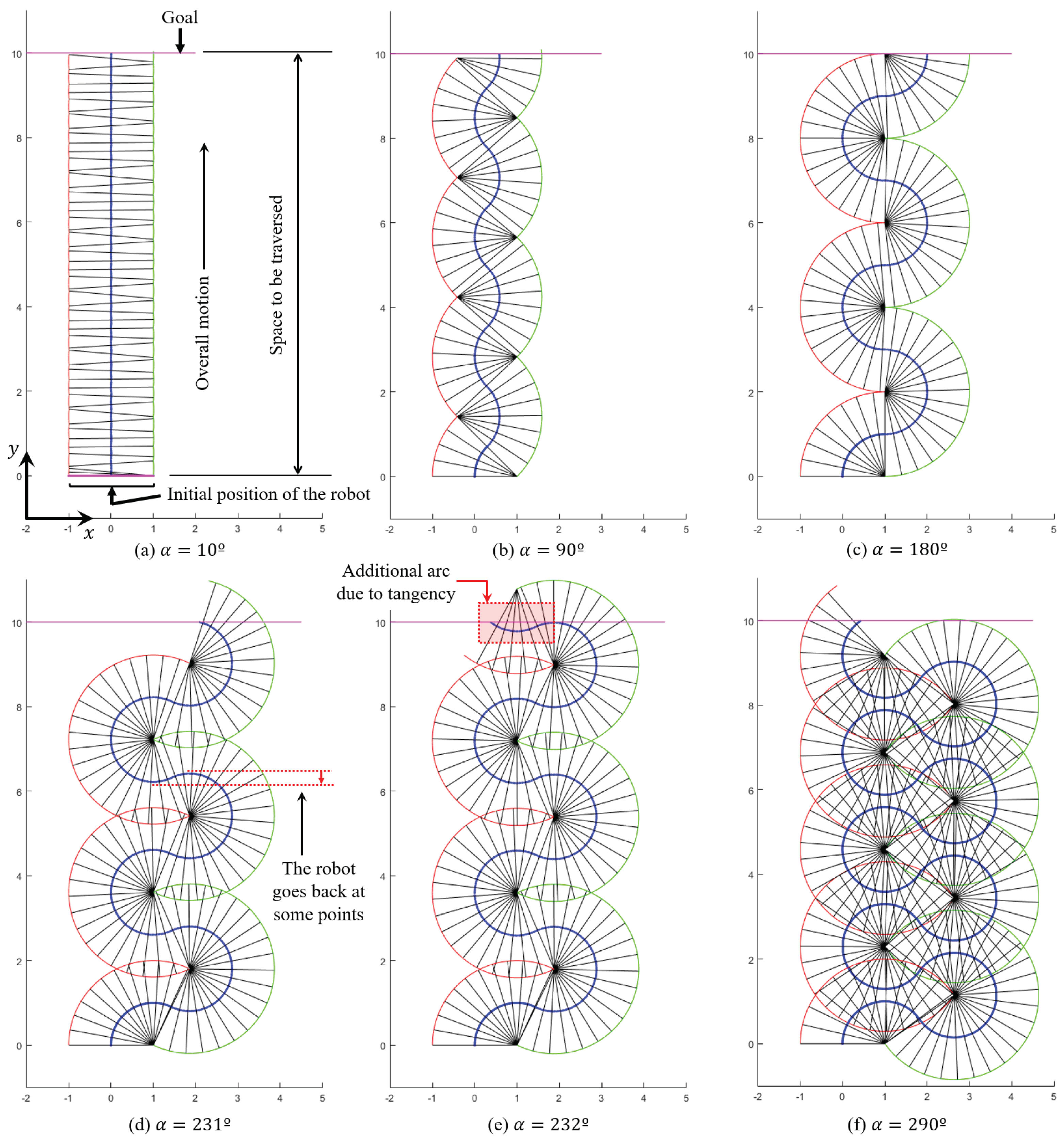
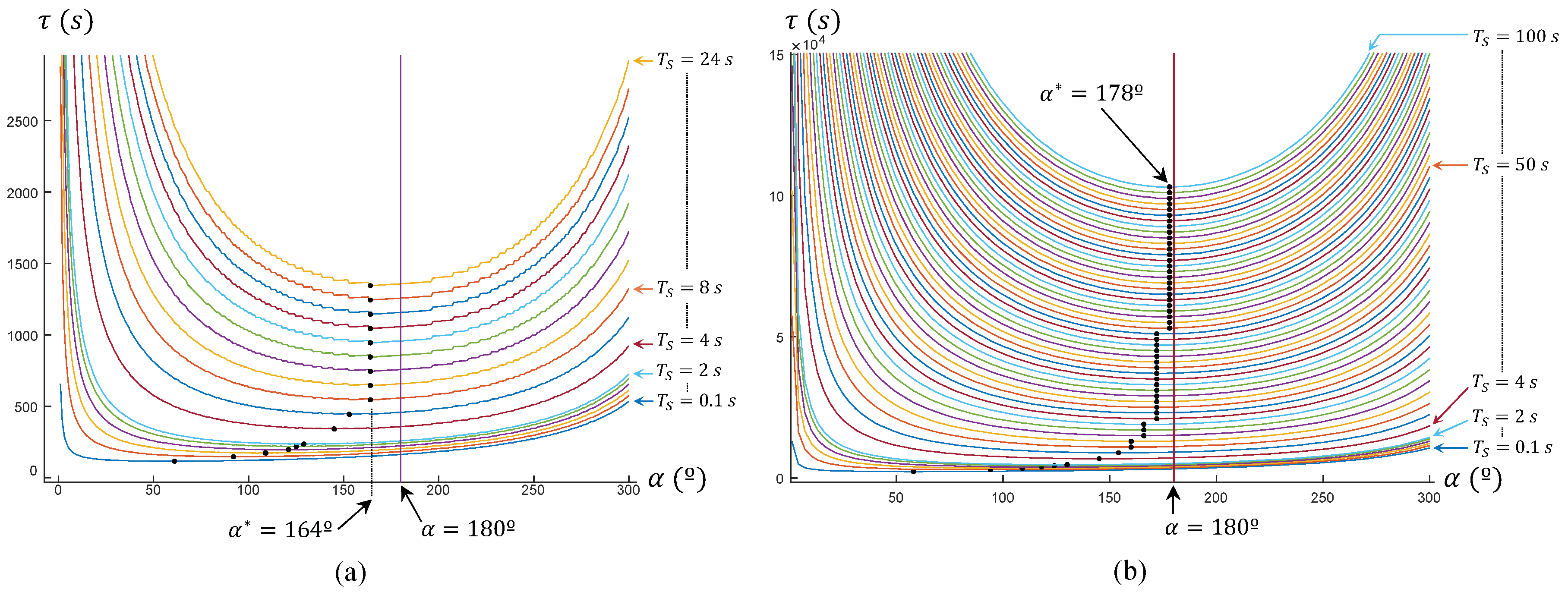
In this paper, we have described the MASAR robot: a new Modular And Single-Actuator Robot. This robot is a type-II SAMR since it has binary adhesion pads that can be adhered or detached from the environment in order to produce the rotation of the robot about different axes, achieving in this way two- or three-dimensional motions using only one continuous actuator. In this paper, we have geometrically solved the planar trajectory tracking problem of this robot when following polygonal trajectories that may have narrow sections that constrain the amplitude of the rotations of the robot. The proposed gait consists in performing 180° rotations when there is no risk of collision between the robot and obstacles of the environment, in order to maximize the distance traveled in a single step. We have shown that, for the MASAR robot, performing rotations of 180° minimizes the time necessary for traversing long trajectories when the time required to switch the adhesion state of the pivots is high. For shorter trajectories and/or pivots that switch their adhesion state quickly, a gait based on rotations of 180° may not be the optimal one, yet it is very close to it. When inside narrow corridors, the proposed gait consists of rotating the robot until both pivots touch the walls of the corridor, since this also maximizes the distance traveled in a single step, subject to the narrowness of the corridor. The analysis of the proposed robot in narrow corridors, however, has shown that this is not the optimal scenario for this robot, since its locomotion mode requires high times to traverse excessively narrow corridors. This can be considered the worst-case scenario in which the proposed robot would need to work, and for this reason it has been analyzed in this paper. Thus, the MASAR robot is most suitable to environments that allow wider rotations for the robot.

Regarding the trajectory-following problem analyzed in this paper, it was addressed from a purely geometric/kinematic perspective, and it assumed polygonal trajectories with narrow sections. In a practical implementation, we may have trajectories with other arbitrary shapes and obstacles, and a purely geometric approach may be insufficient when considering uncertainties of the map or location of the robot, as well as error in tracking of the trajectory (e.g., the robot may not be perfectly aligned with the linear segments of the trajectory, such that the successive rotations of 180° would need to be corrected slightly). In order to cope with all these factors, as part of ongoing and near future work, we are currently approaching the trajectory-following problem of the MASAR robot from a closed-loop control perspective, departing from its velocity model and designing feedback controllers that allow the tracking of arbitrary trajectories, in a similar way to the solutions proposed in [27] for a differential-drive two-wheeled mobile robot, optimizing time, distance, or energy consumption [28]. Other ongoing and future tasks to address are: the analysis of trajectories that include concave plane transitions (Figure 4a), the analysis of the MASAR robot as a modular reconfigurable robot able to perform more complex motions by combining with identical modules (Figure 4b), and the construction and validation of a prototype of the robot, including the adhesion pads that allow a single module to walk or combine with identical modules (Figure 3).

6. Patents

The MASAR robot was patented by the authors in Spain, with patent number ES2684377 and priority date 31 March 2017.