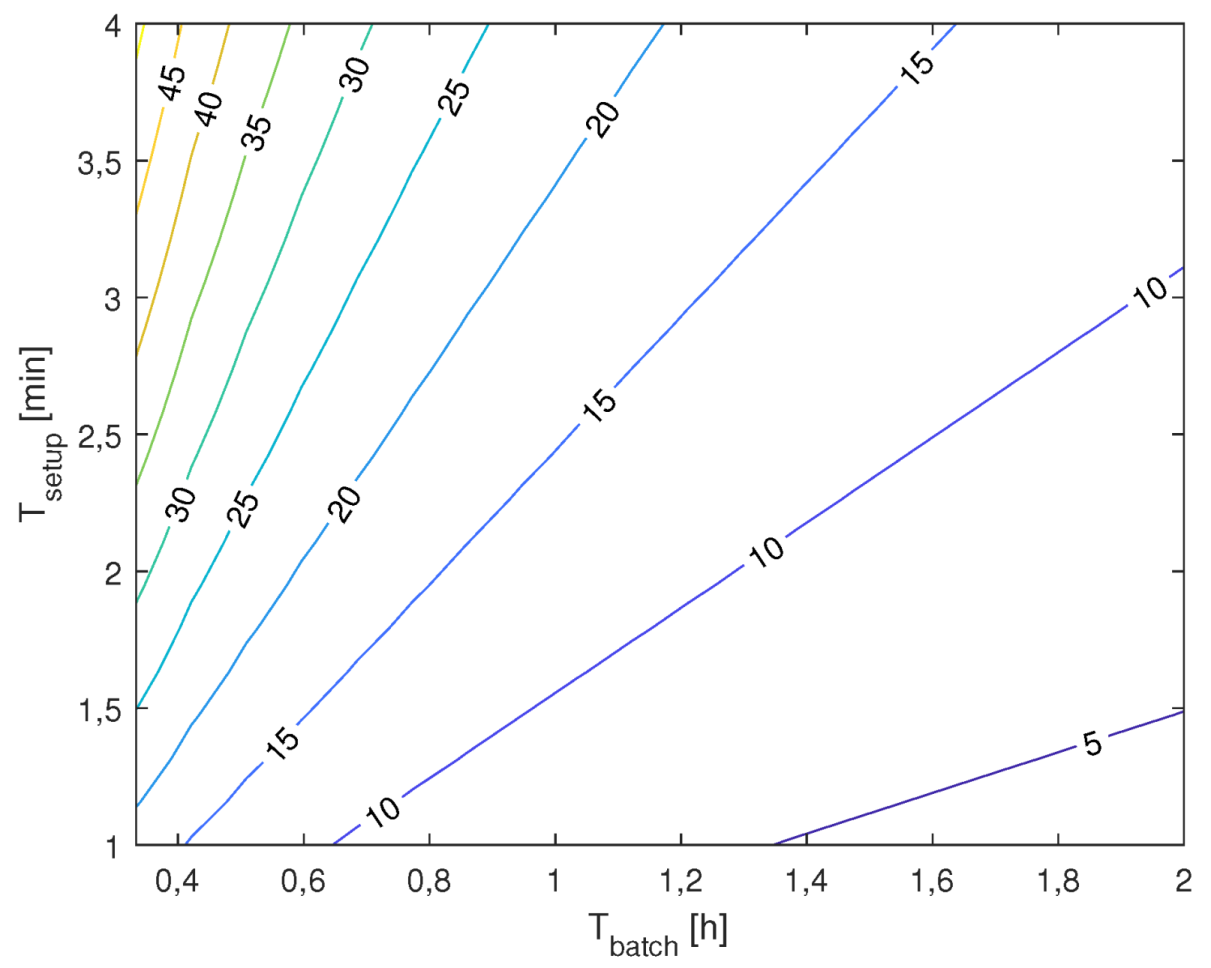
The system considered is generally composed of an input belt, a suitable sequence of hoppers and an output belt. In this paper, we just focus on these devices, assuming that the system is fed by a bowl feeder with limited capability that delivers the kits to a packing machine. The maximum throughput of the feeder is set to
, measured from the case study line. The motion of the pieces between a device and the subsequent is assumed to be a free falling motion, and is assumed that the discharging feed rate is infinite, that is, the pieces move together as a bulk from one hopper to its successor. The falling time can be so calculated as:
where
h is the distance between two devices, here set to 200 mm and
g the gravity acceleration, assumed 9.81
. We assumed that the pieces are delivered evenly spaced of a distance
d by the superior belt with speed
, so that the time delay between two subsequent pieces falls is:
The proposed case study inspired the
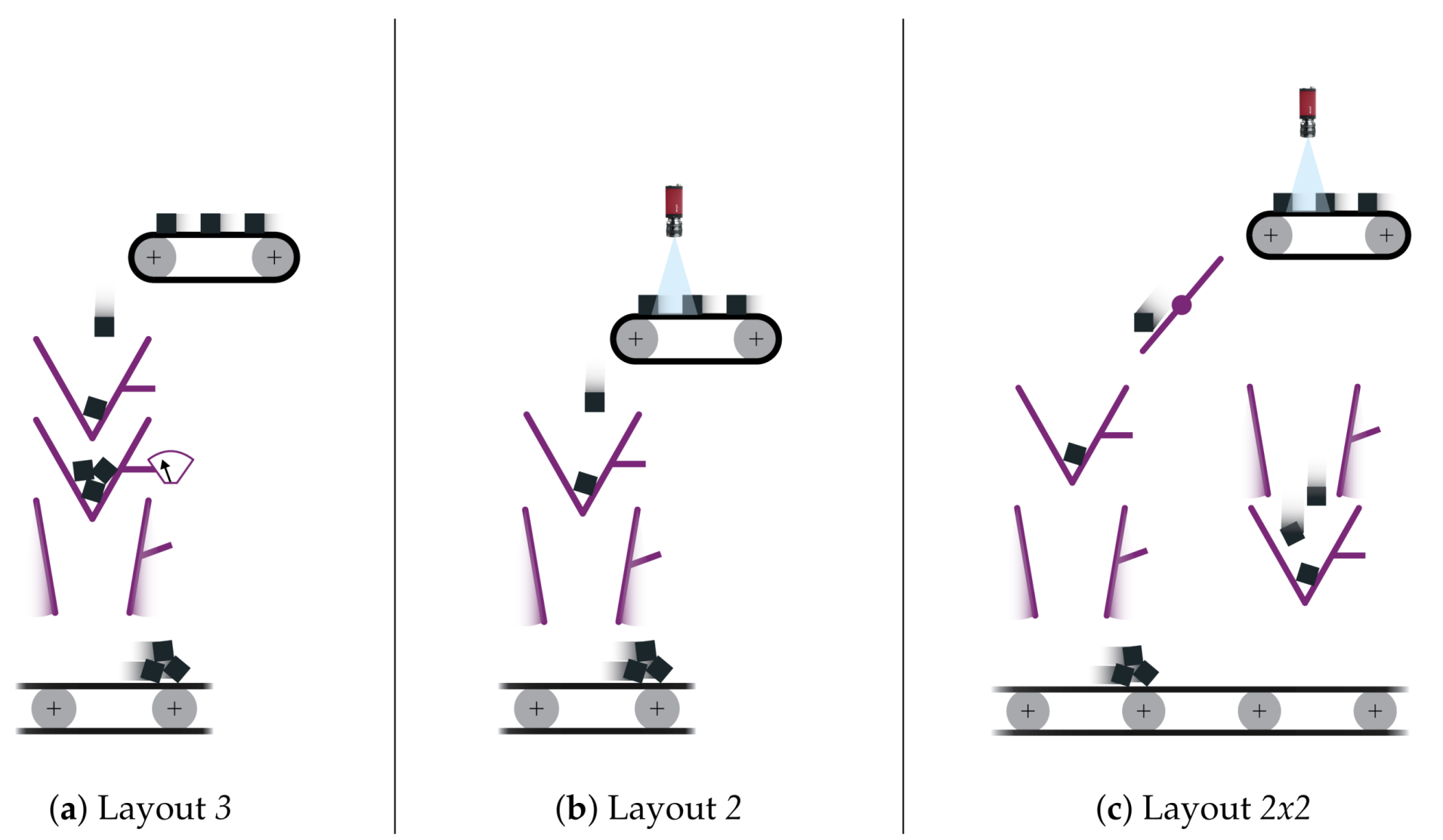
3 configuration, which is assumed to be the starting point of the study. In this configuration, the weighing hopper is needed to perform the quality inspection, verifying if the correct number of pieces has been delivered by the superior belt, in order to avoid defective kits in output. Such weighing device is equipped with a load cell used to estimate the weight, which provides a raw electrical signal. The main constraint in achieving high accuracy is a superimposed noise, which is eliminated thanks to a filter. However a trade-off between the measurement time and a high precision estimation has to be accepted. Thus the weighing time needed to obtain a stable measurement tends to become the bottleneck of the system, preventing it from reaching high efficiency and saturating the input devices. The
2 configuration addresses the problem eliminating the weighing device and replacing it with a vision system, capable of performing in its place the quality inspection. This solution is depicted in
Figure 6b, and since it does not contemplate the use of a weighing device, it is not affected by the aforementioned trade-off, allowing to perform a 100% quality control ignoring the weighing time and to discard single components instead of a full batch recognized as defective by the weighing device at the end of the sequence.
2.2.2. Simulation
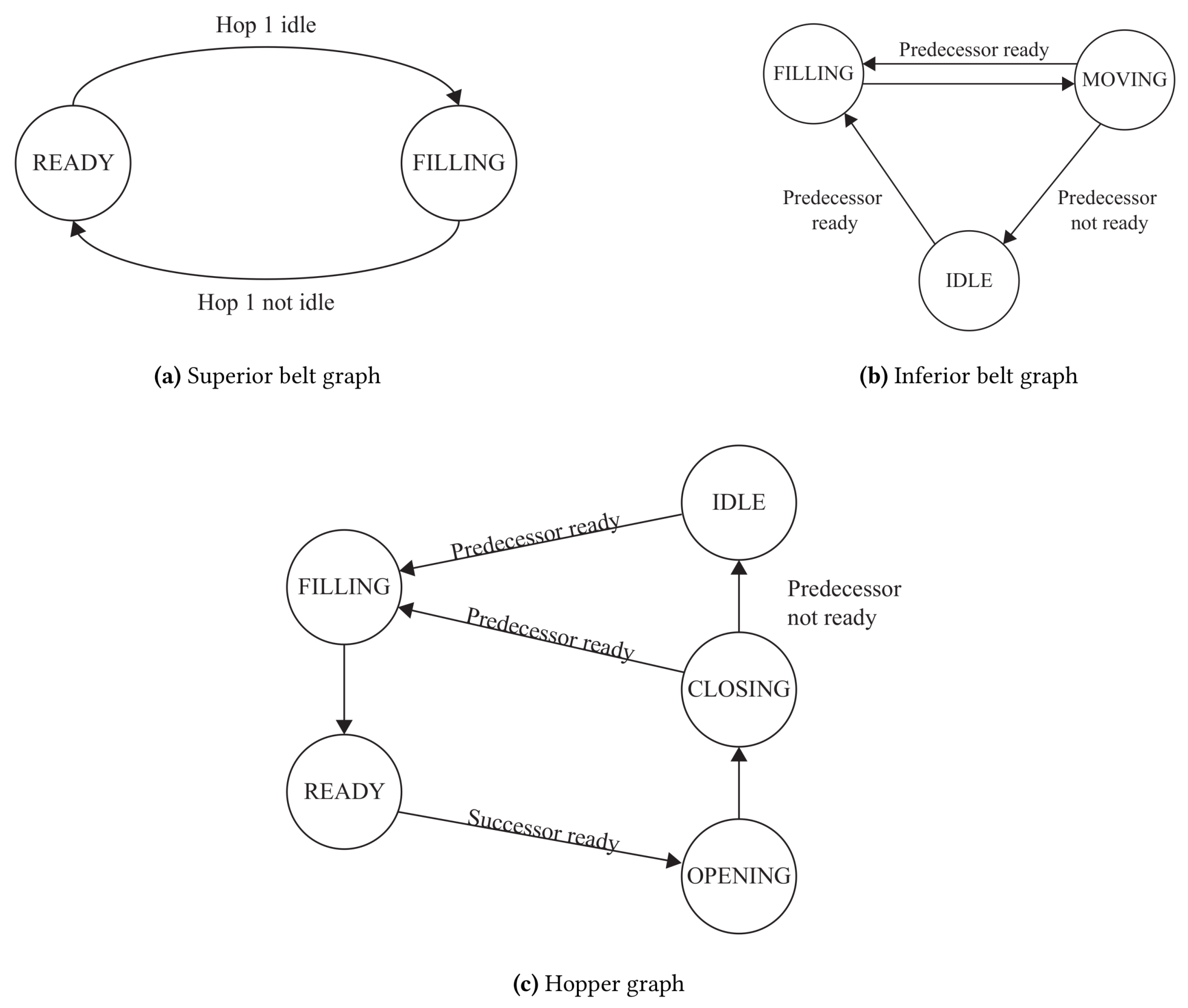
A simulation of the configurations was performed with a finite state machine, which uploads the states of the different devices over time. Since the simulation is affected by transient and/or random effects, considered as random variations on the parameters, it could be used as a reference for the proposed model; moreover, it provides for further data, such as the task scheduling and the availability of the feeders. Each device is linked to its predecessor and its successor with the relationships illustrated in
Figure 9, which describes the transition between states. The superior belt is the input device of the system and switches just between two states,
ready and
filling, with a logic described in
Figure 9a. It interacts only with the first hopper, so its state depends only on the state of this device. The generic hopper switches between many states,
filling, idle, weighing, ready, closing and
opening. The non weighing hopper presents the same graph without the state
weighing. The generic hopper can be related to one other hopper or a belt, referred as
predecessor if it is in a previous position on the feeding chain or
successor if it is in a next position on the feeding chain. Its graph is depicted in
Figure 9c. The inferior belt, that is, the output device of the system, can switch between the states
filling, moving and
idle. The
moving state is due to the need of simulate the time required from the output belt of the case study line to switch between two subsequent position. The states are described in detail in
Table 4. Each transition is due to the change of state of an adjacent device or for the expiration of the time needed for a specific action (e.g., the opening and closing movement of a hopper).
The transition logic just described was implemented into a Matlab script in order to perform time varying simulations of the system. To reflect the effect of the uncertainties on the process in a real environment we introduced some random variation of the parameters of the simulation. A random variation in the interval [−0.1 s, +0.1 s] was added to to simulate the dynamic effect of the components falling on the weighing hopper and a Gaussian distribution ( mm; mm ) of the components spacing on the input belt was assumed to simulate some variability in the bowl feeder feeding rate.
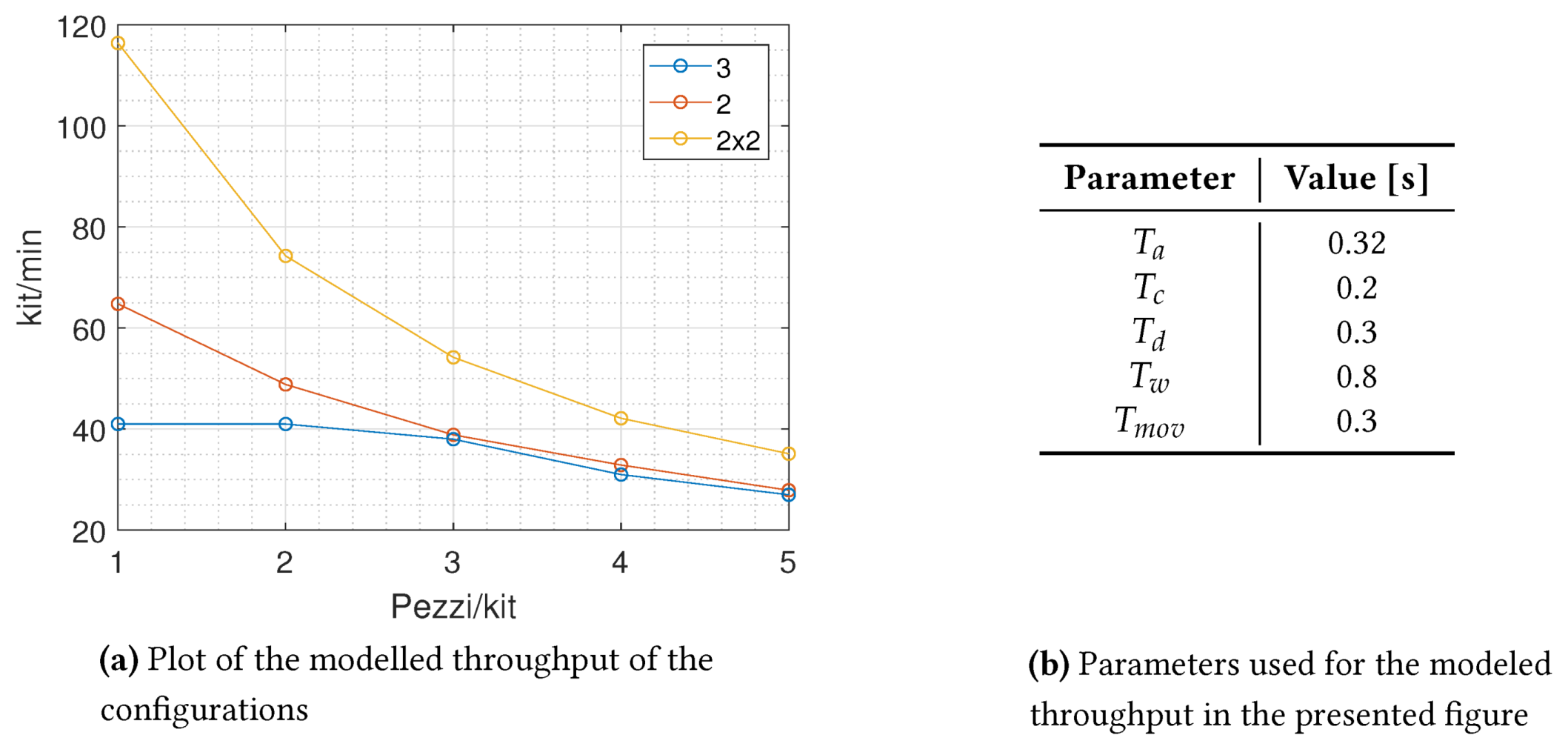
A further simulation with the same parameters in
Figure 7 was performed and the throughput for the three configurations is shown in
Figure 10. The relative error between the model prediction and the simulated throughput was calculated and presented in
Table 5. The values state a good agreement between the model and the simulation, except for the tendency of overestimate the throughput, which can be seen from the negative mean error.
One output of the simulation is the state of any device in every moment, which could be used to plot the state chart of the devices, like the one reported in
Figure 11, plotted for the values
s,
s and
.
The
availability is the ratio of run time to planned production time. With the data used to plot such state charts was also possible to evaluate the availability for the devices as:
where
A is the availability,
RT is the run time, i.e., the time the device did not spend in ready or idle state, and
PPT is the planned production time, i.e., the total time the device is used.
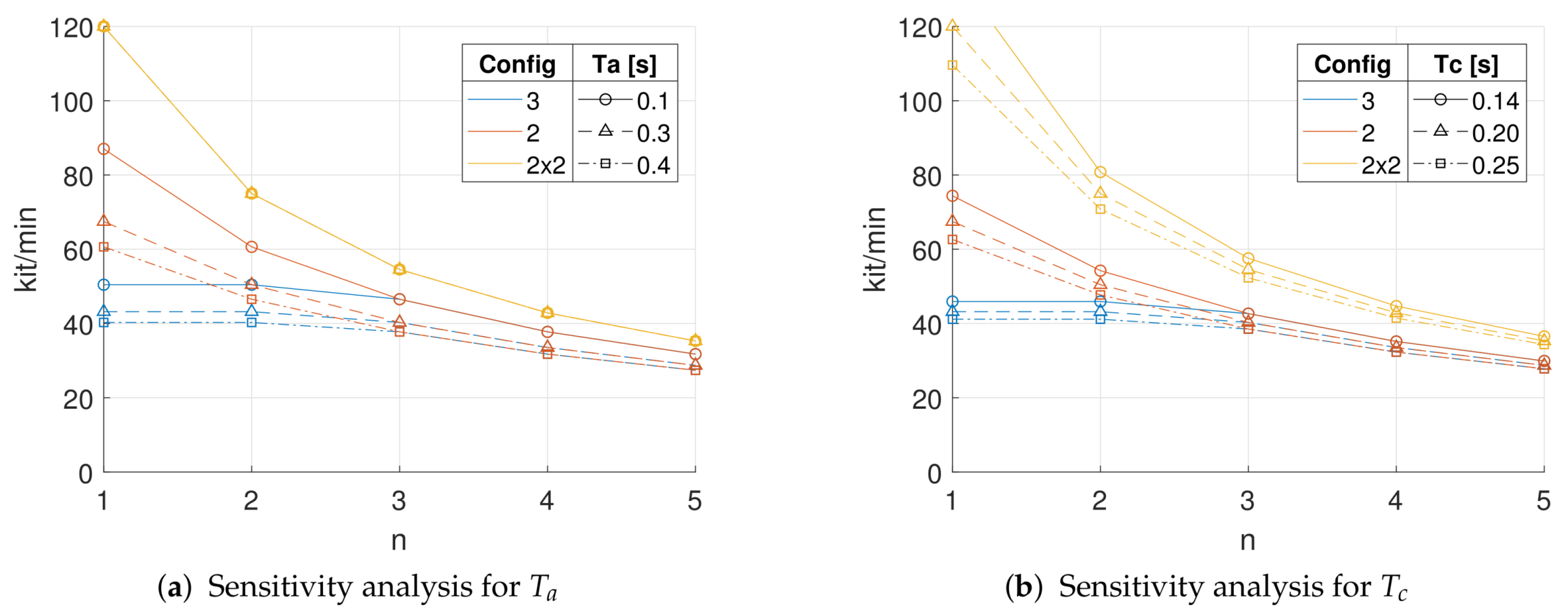
In
Figure 12 we can see the results of the simulations performed varying the opening and closing time of the hoppers to understand their influence on the system. To the left the data calculated with a
s, while to the right the data related to
s. The resulting plot shows that the opening time of the hoppers slightly affects the performance of the system, which decreases with low kit size, due to the increasing frequency of opening/closing operations. The worsening interests mainly the
3 and
2 configurations, but not change substantially the comparison between the configurations, therefore from now on we will refer indistinctly to the plot to the left or to the right column in
Figure 12. The plot
Figure 12b shows that the
A of the superior belt for the
2x2 configuration (yellow solid line) is 1 for any kit size considered. It should be noted that only the
2x2 configuration is able to reach this value, which mean the saturation of the superior belt. For a kit size equal to 1 the inferior belt is close to saturation. From the plot in
Figure 12d we can see that the kit throughput of the
2x2 configuration rises with the decrease of the kit size.
Figure 12f is the product of the kit throughput, that is, the plot in
Figure 12d, and the kit size.
The
A of the superior belt for the
2 configuration, as can be seen in plot
Figure 12b, starts from values near to 0.82 and drops for decreasing kit size. From the plot
Figure 12d is clear that its performance is worse than the
2x2 configuration but outperforms the
3 configuration for a low kit size (1 and 2). Finally the
A of the superior belt for the
3 configuration, as can be seen from the plot
Figure 12b, is similar to the one of the
2 configuration, but for decreasing kit size it shows a heavier drop. From the plot
Figure 12d is clear that for a kit size lower or equal than 2 the throughput of the system is stable, due to the saturation of the weighing feeder. This means a reduction of component throughput, as can be seen from plot
Figure 12f. It is to be noticed that all the plots in
Figure 12 are of minor importance for small kit sizes, due to the assumption made in the introduction that the feeding of low quantity components is addressed with the development of a flexible robotic workcell.
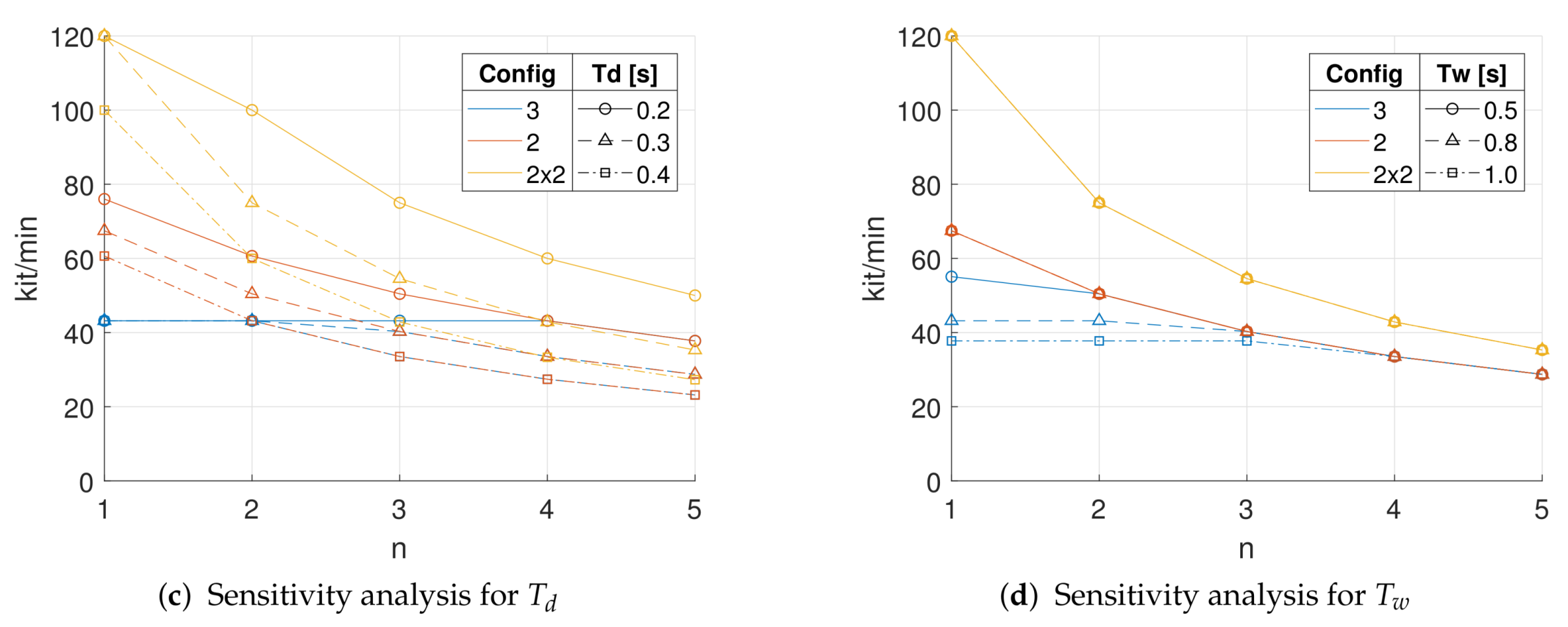
Figure 13 depicts the behavior of the system for different
. The left column of plots is defined for
s, while the right column is defined for
s, the last taken from the case study line. From
Figure 13b it is clear that the
2x2 configuration is strongly affected by a slower belt and its
A drops for a kit size smaller than one. The dashed yellow line shows that for that kit size the inferior belt starts to be saturated and cannot accept higher throughput, causing a decrease in the
A of the previous devices. It is noticeable that the
3 and the
2 configuration in the two cases are almost not affected by the time required by the inferior belt to perform a shift, as we can see from the comparison between
Figure 13c,d.
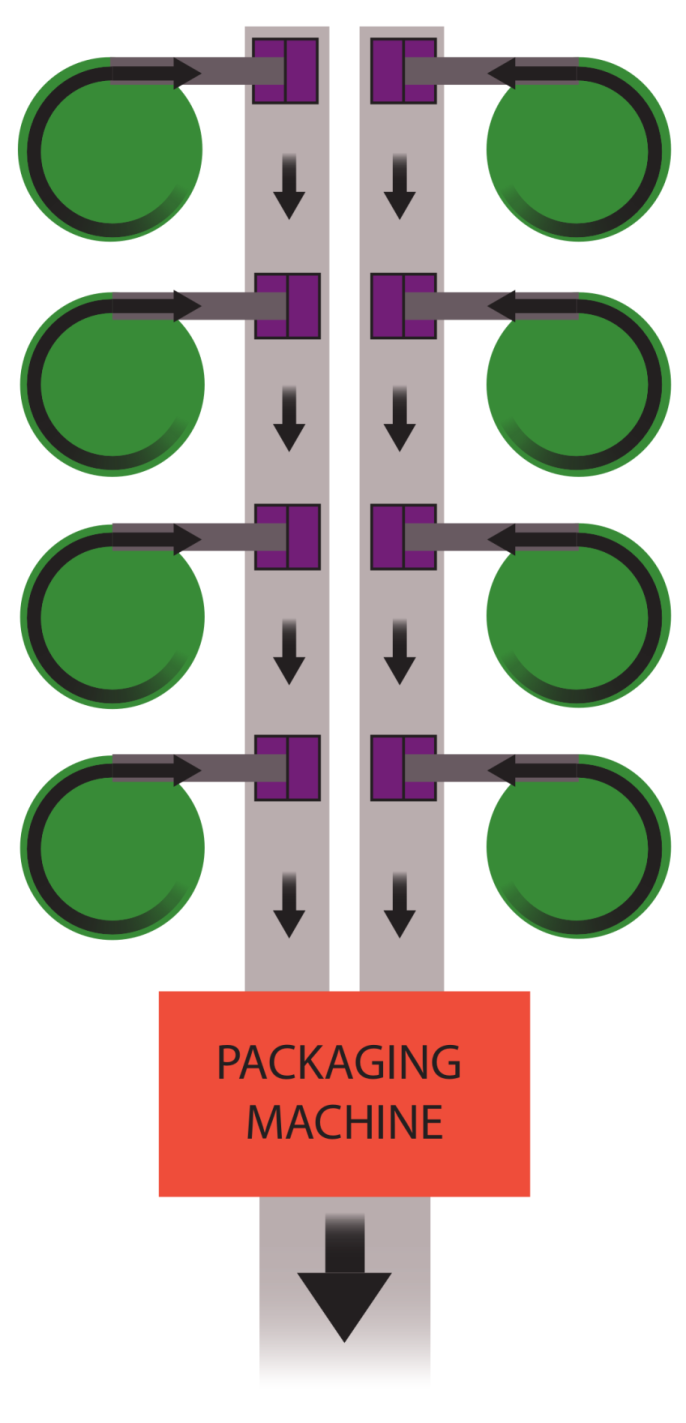
It is important to notice that the
2x2 configuration would be capable of feed two inferior belts as depicted in
Figure 1, so that the
would be approximately half compared to the other two configurations. The comparison between the configurations would make the
2x2 configurations even more valuable.
2.2.3. Vision Inspection System
In the Industrial Robotics Laboratories at the University of Padua a prototype of the vision quality inspection system placed onto the superior belt was developed. The system is composed by a AVT
Pike F032-b camera, triggered by a Sick
DRS61 incremental encoder. The belt’s width is 400 mm, its speed is set equal to 200 mm/s. The pieces are put on the conveyor belt and they run on the backlighted area, while the camera acquires images, as illustrated in
Figure 14c.
The matrix Pike camera is used as a quasi-linear camera, acquiring 6 lines at a time. It is synchronized with the belt thanks to the encoder. The acquisition is performed by a C++ algorithm which stores one hundred acquisition into a buffer and then send all the content of the buffer to Matlab, where is performed the image elaboration and then controlled the air blow to discard defective pieces.
The image processing consists in a sum of the pixel intensity value performed by row, obtaining the profile illustrated in
Figure 14b. A check on the length of the piece was used to detect defects, but further works could lead to the development of more sophisticated methods, thanks to the clear profile of the objects obtained with this setup.
It is really important to notice that with the introduction of a vision inspection system that is able to discard the wrong or defective pieces, the retooling also becomes easier. In fact, bowl feeders require an amount of pieces higher than the actual production lot to be handled, in order to guarantee a uniform output flow [
16]. This leads to high retooling time, due to the need to empty the feeder of the previous lots, before filling it with the new components. The vision inspection system could lead, together with the adoption of a flexible feeder, to a dynamic lot change, removing the need to empty the feeder and letting the vision inspection system discard the previous components.