Mechanical and Control Design of an Industrial Exoskeleton for Advanced Human Empowering in Heavy Parts Manipulation Tasks
Abstract
1. Introduction
1.1. Industrial Exoskeletons Design Solutions
1.2. Exoskeletons Control Solutions
1.3. Paper Contribution
2. Task Specifications & Exoskeleton’s Design Guidelines
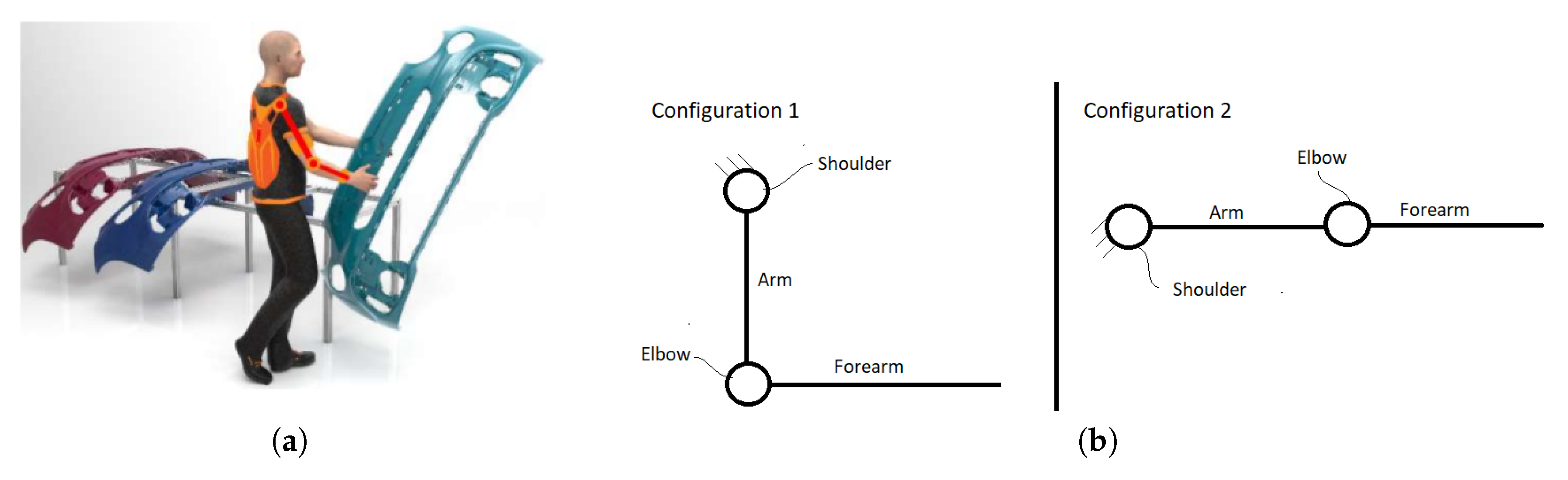
2.1. Task Description
- Configuration 1: The arm is extended along the operator’s trunk and the elbow configuration is flexed;
- Configuration 2: The shoulder is flexed of and the upper limb is completely extended. This is the most critical configuration considering the required motor torques.
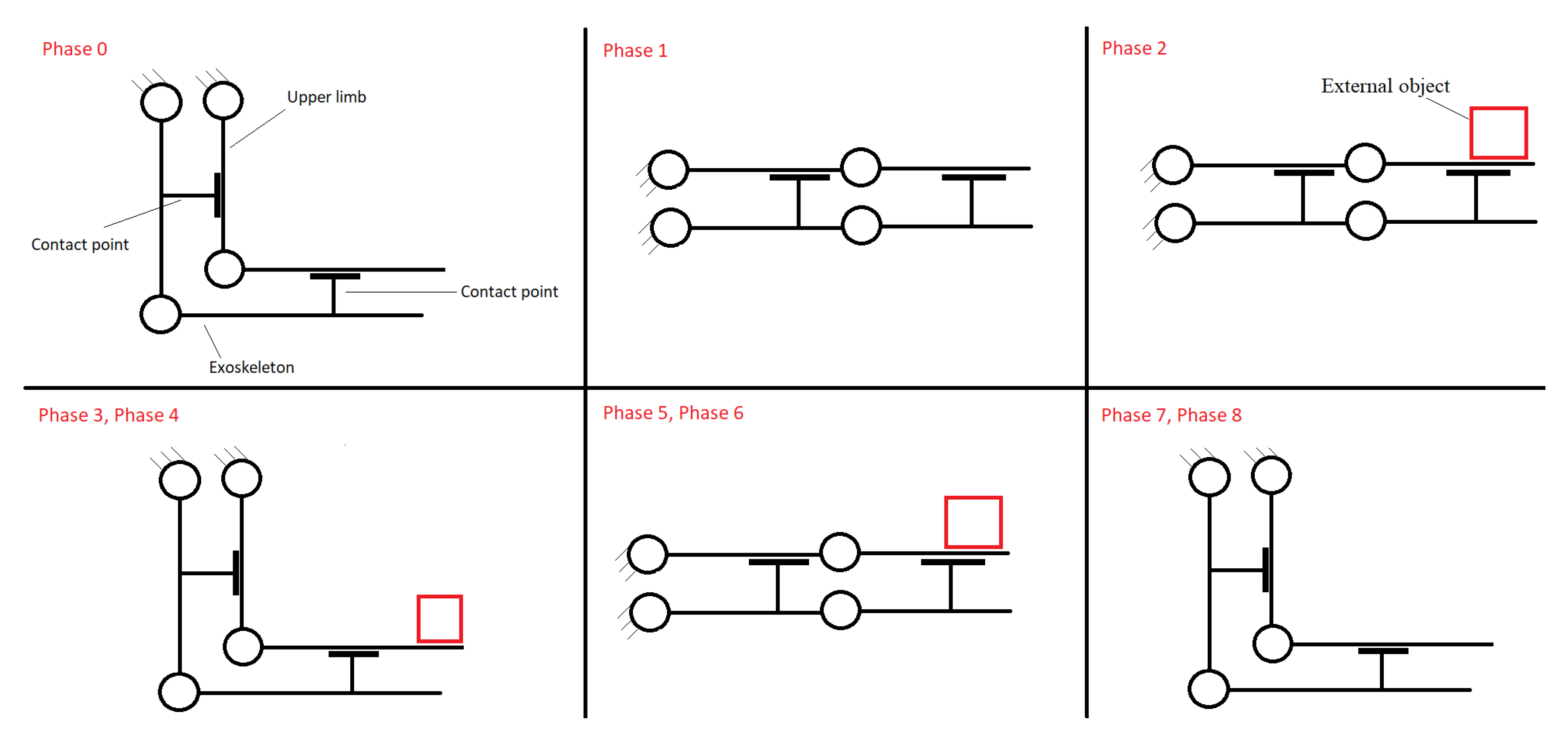
- phase 0: the operator configures the upper limbs in configuration 1 and the exoskeleton is turned on;
- phase 1: the operator moves the upper limbs without the external load, in order to grasp the object (critical configuration 2);
- phase 2: the operator grasps the object (critical configuration 2);
- phase 3: the operator moves back to configuration 1 carrying the part;
- phase 4: the operator transports the object maintaining upper limbs in configuration 1;
- phase 5: the operator lifts the external object up to the critical configuration 2 to release the part;
- phase 6: the operator releases the object staying in the critical configuration 2;
- phase 7: the operator moves back in configuration 1 without the part;
- phase 8: exoskeleton assistance is turned off (configuration 1).
2.2. Exoskeleton Specifications
- kinematics;
- torque requirements;
- weight and size of the designed device;
- human safety;
- economic affordability.
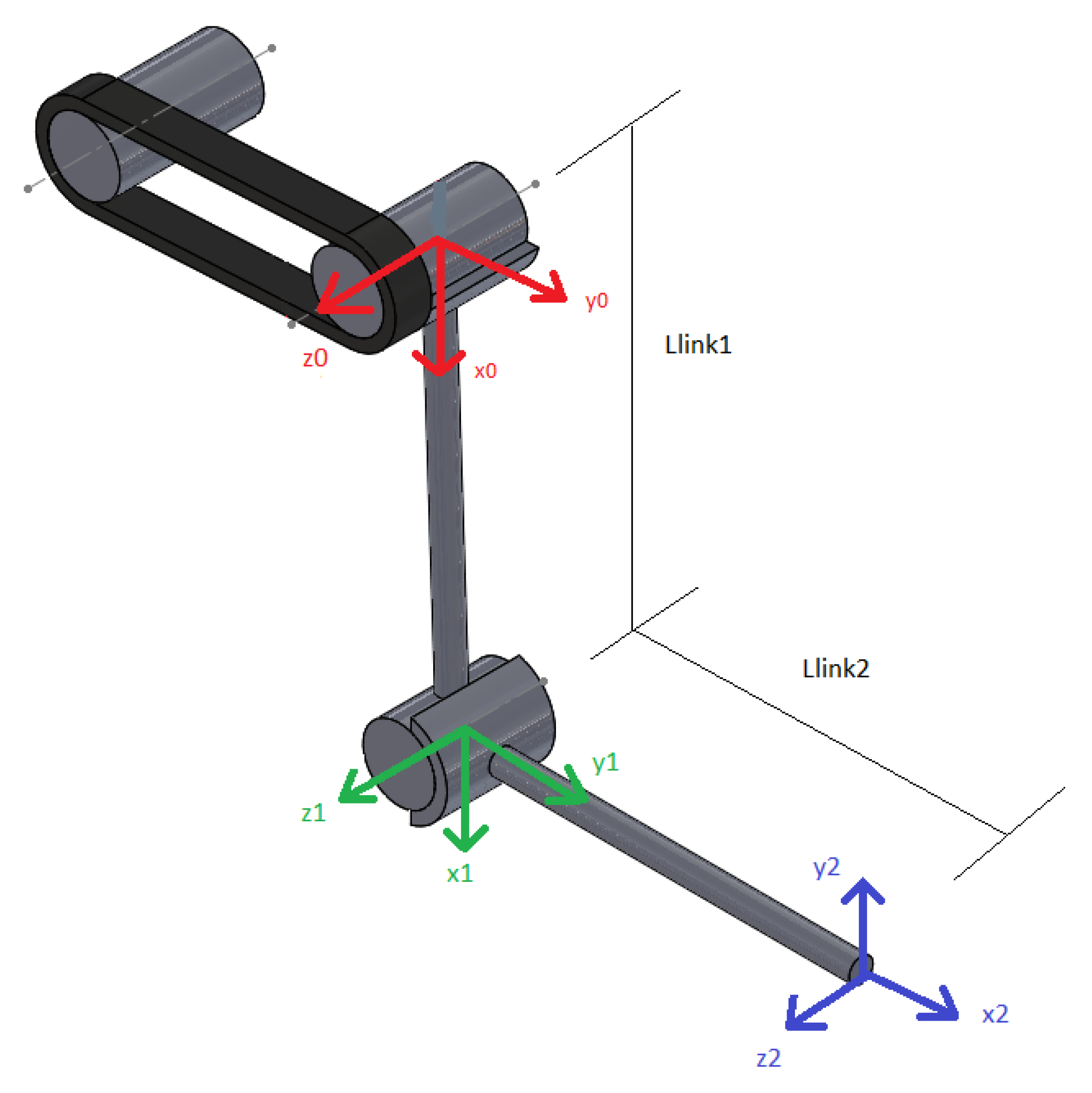
2.2.1. Kinematics
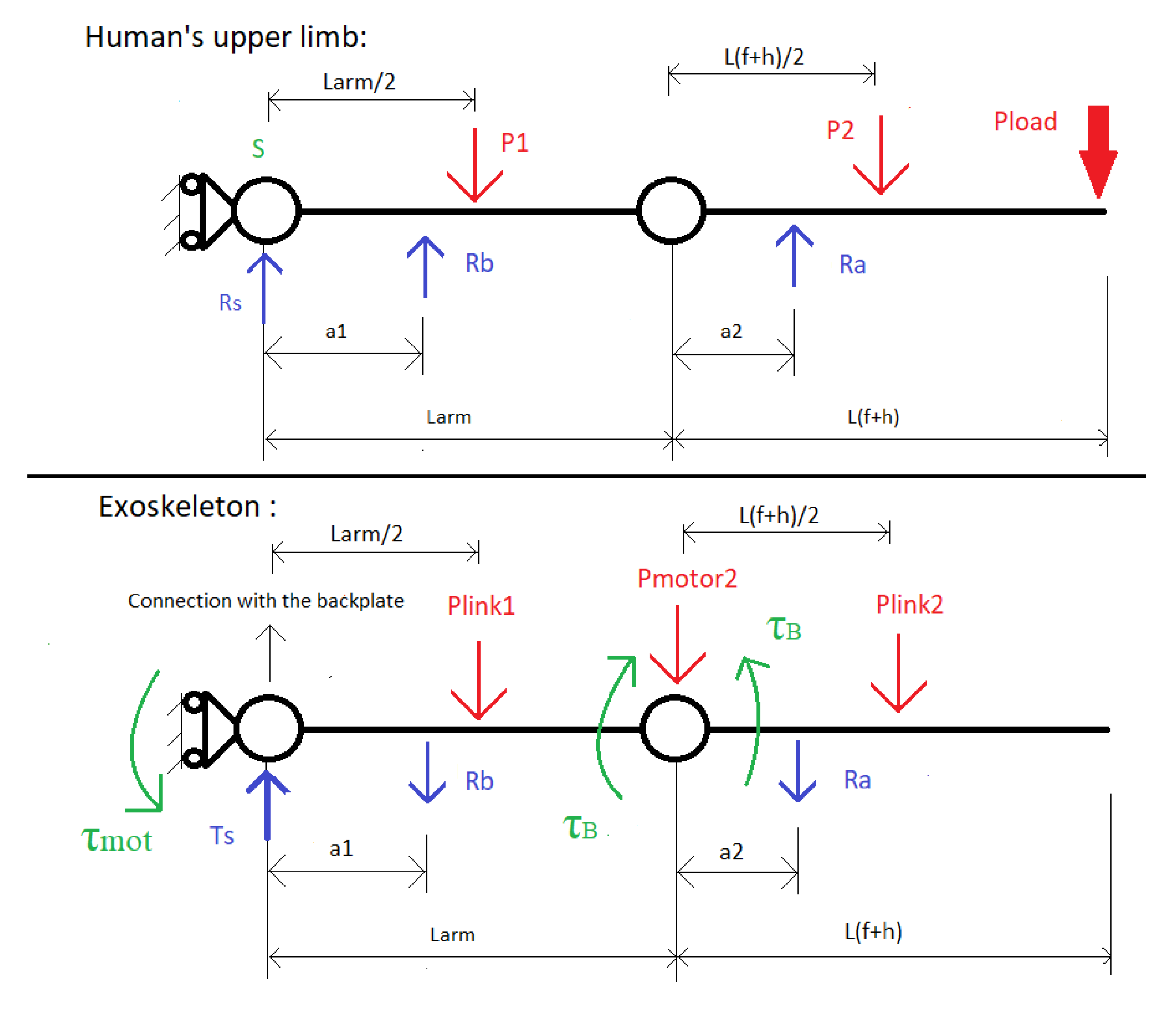
2.2.2. Torque Requirements
- : interaction force between the forearm and the exoskeleton;
- : interaction force between the arm and the exoskeleton;
- : vertical reaction force of the shoulder;
- : application point of the force;
- : application point of the force;
- : human’s arm length;
- : human’s forearm and hand;
- : weight of the forearm exoskeleton link applied in the middle of the link;
- : weight of the elbow motor;
- : weight of the arm link applied in the middle of the link;
- : torque of the elbow motor to support the joint;
- : torque of the shoulder motor to support the joint;
- : vertical reaction force of the support connecting the exoskeleton link to the back-plate.
- cm.
- kg.
- m.
- m.
- kg ( N).
- kg ( N).
2.2.3. Weight and Size of the Designed Device
2.2.4. Human Safety
2.2.5. Economic Affordability
3. Exoskeleton Modeling & Design
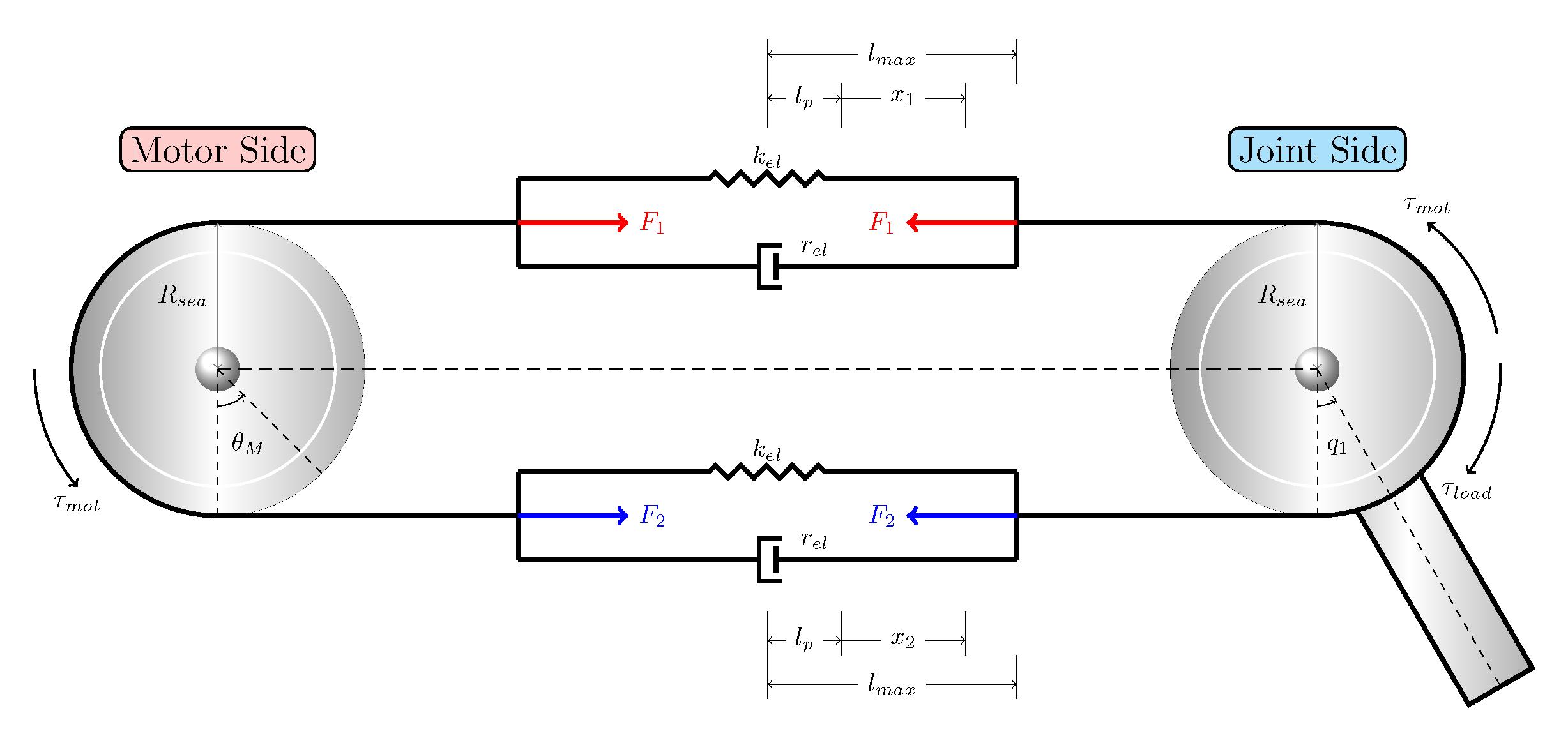
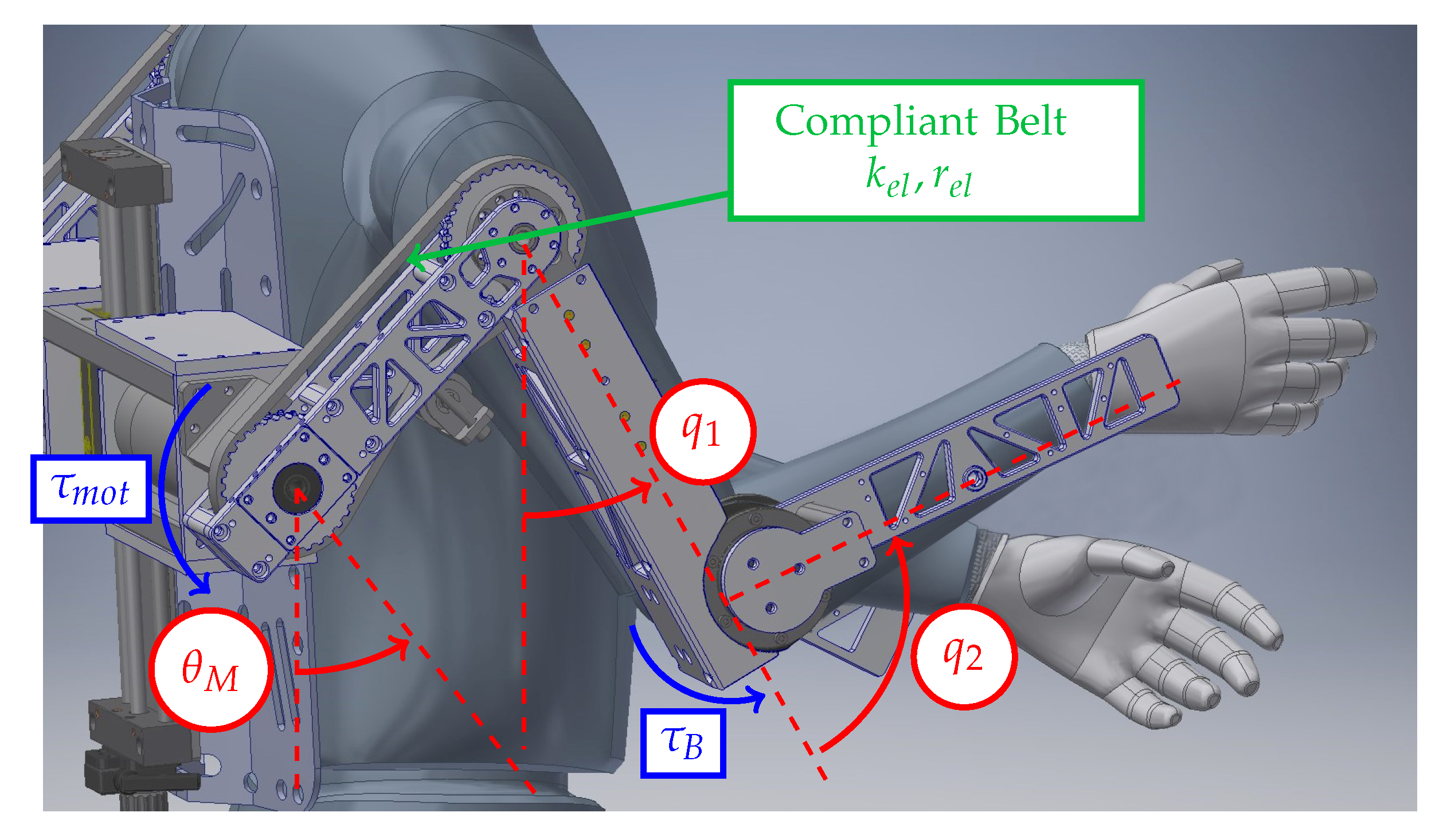
3.1. Compliant Shoulder Joint Actuation Modeling
3.2. Exoskeleton Dynamic Model
- is the vector of the DoFs ;
- is the system inertia matrix;
- is the Coriolis and centrifugal vector;
- is the gravitational vector;
- is the vector of friction forces;
- is the system elasticity vector;
- is the system damping vector;
- is the vector of applied torques at the actuated joints;
- is the transposed extended Jacobian matrix;
- is the vector of external forces applied by the human and/or external load.
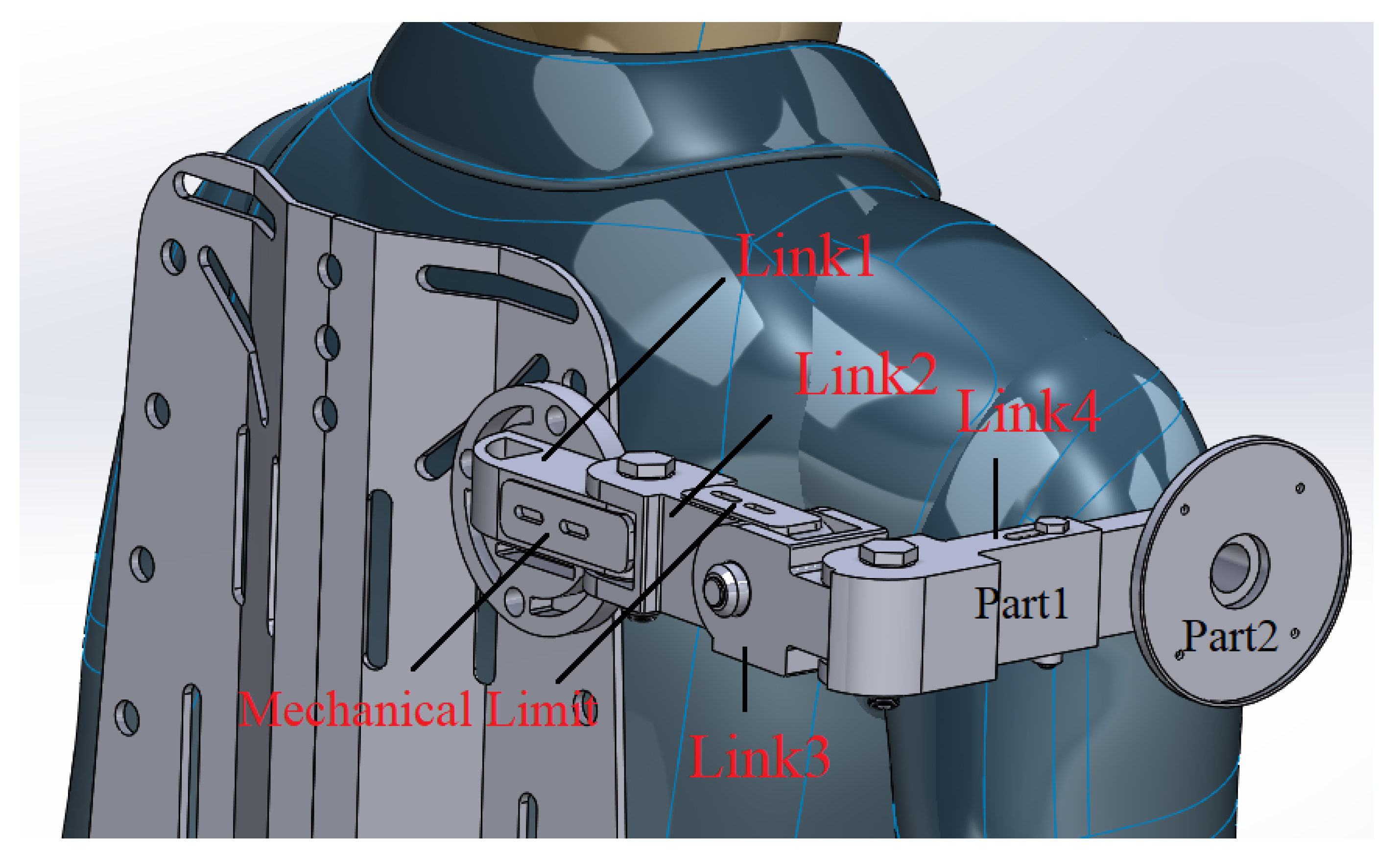
3.3. Compliant Shoulder Joint Design
3.4. Design Solution
3.4.1. Brushless Motor Maxon EC60 FLAT/MILE/PM72
- speed reducer IMS PM 72 C Ø72 mm, 4 stage, ratio 305:1.
- EC60 flat, brushless, with Hall sensors.
- encoder Maxon MILE, 1-1024 pulses, 3 differential channels.
- nominal torque Nm.
3.4.2. Transmission
3.4.3. Elbow Actuator
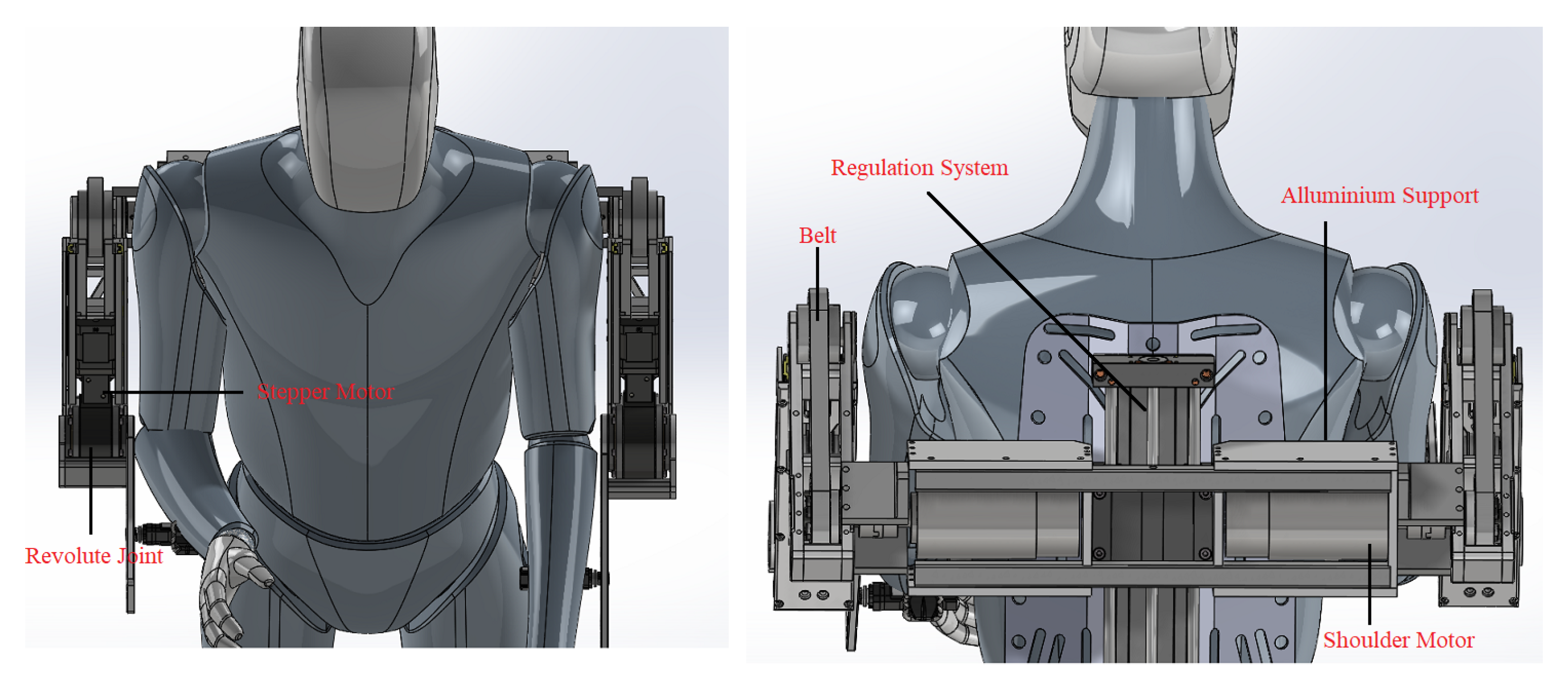
3.4.4. Exoskeleton CAD
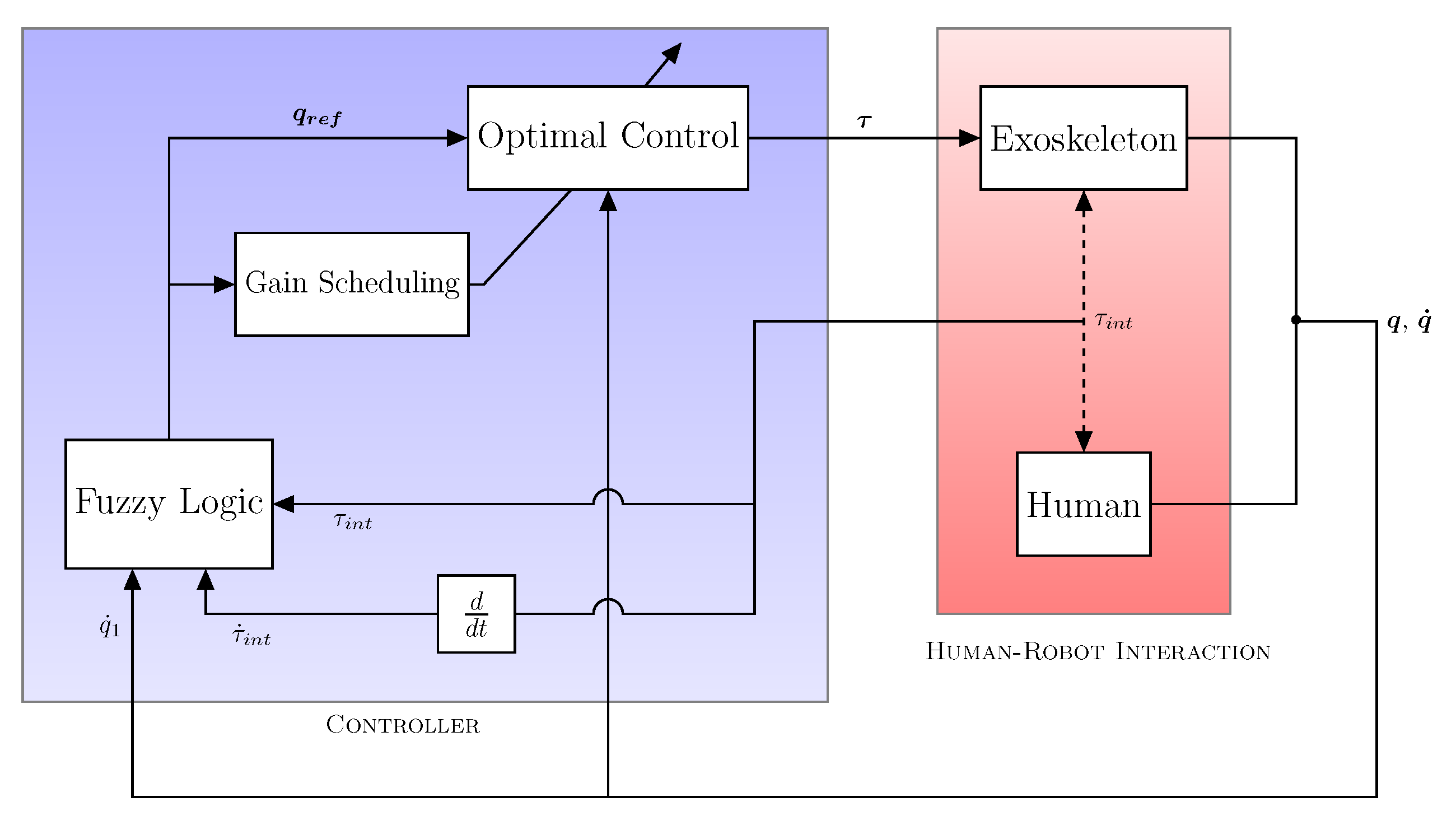
4. Industrial Exoskeleton Control
4.1. Problem Formulation
4.2. Optimal Control Design
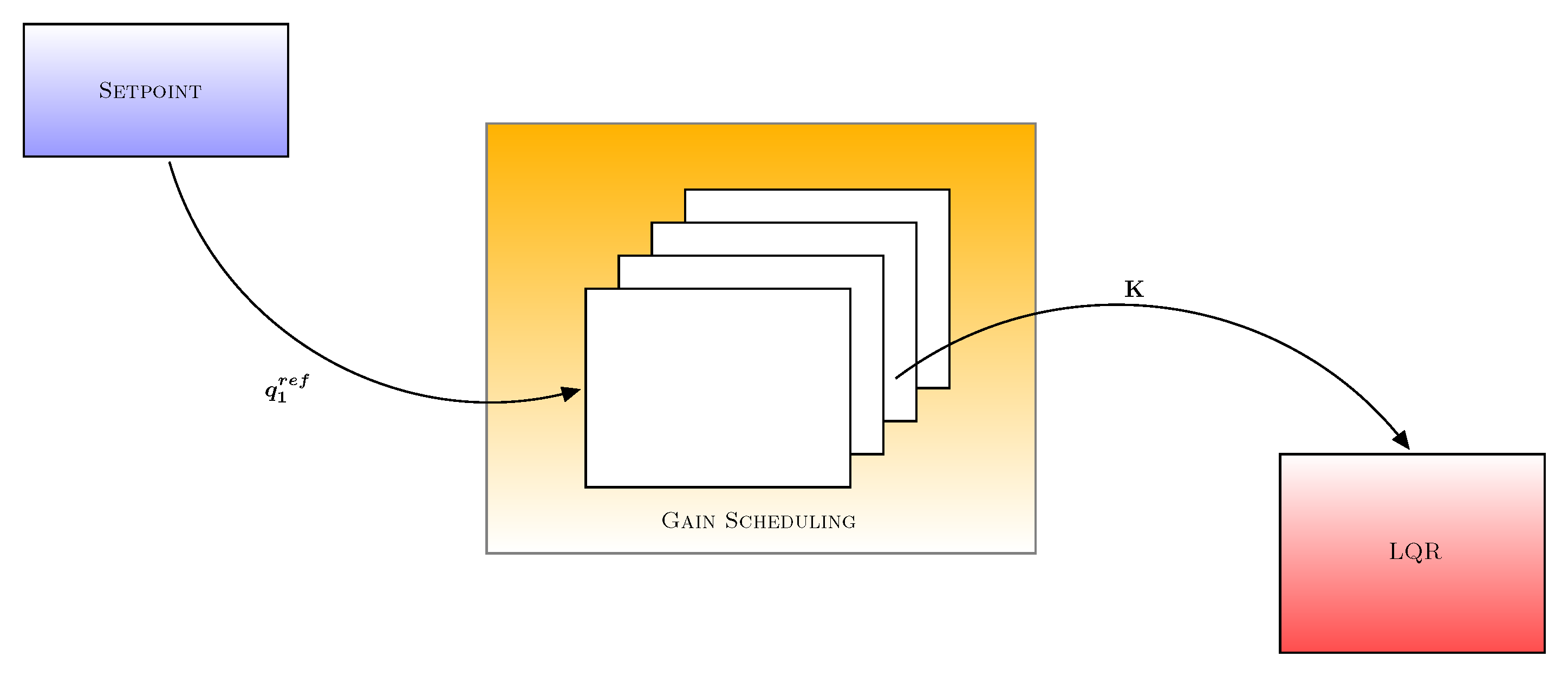
4.3. Gain Scheduling Control Design
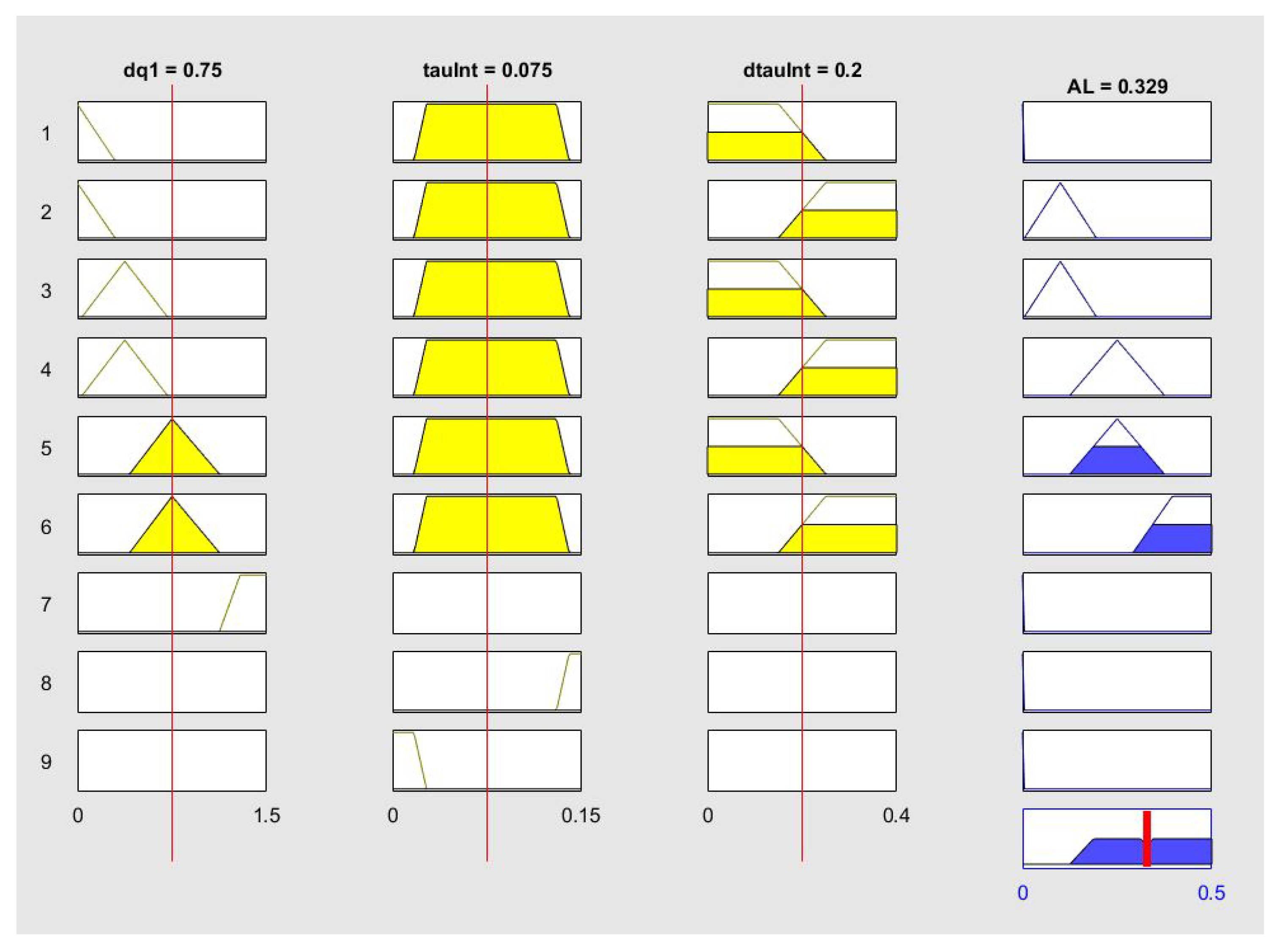
4.4. Empowering Fuzzy Controller Design
4.4.1. Membership Functions
4.4.2. Rule Base
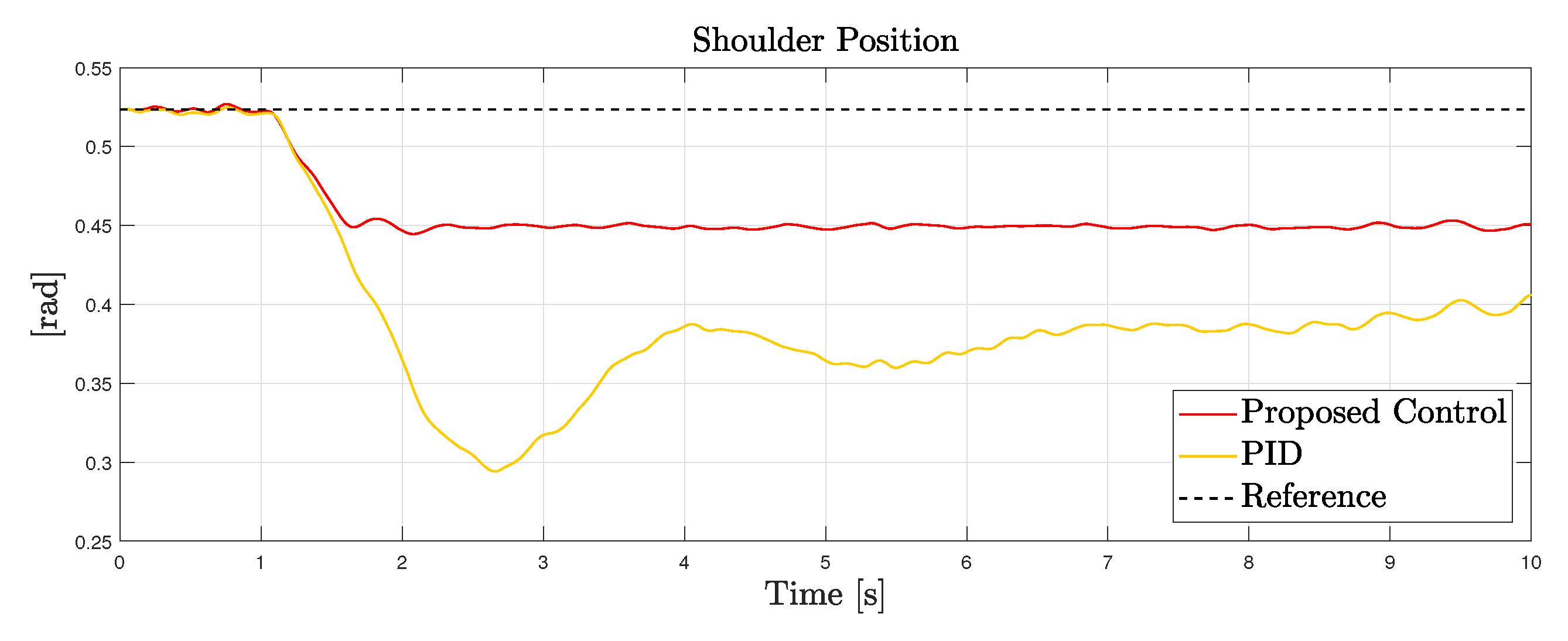
5. Simulation Validation
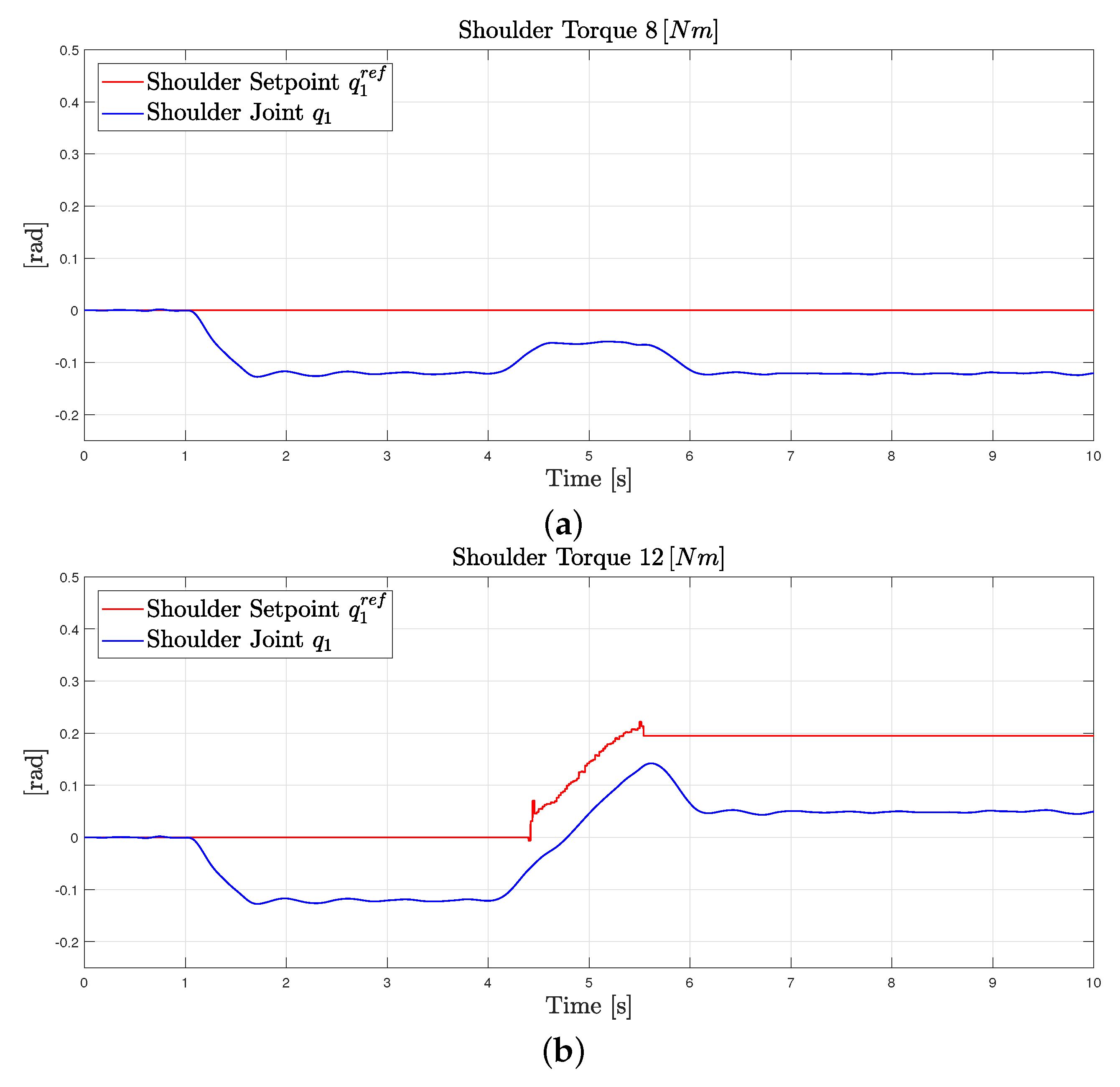
5.1. Empowering Human in Lifting Task
5.2. (Partially) Unknown Part Manipulation Task
6. Discussion
7. Conclusions
8. Current and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pons, J.; Rocon, E.; Ruiz, A.; Moreno, J. Upper-limb robotic rehabilitation exoskeleton: Tremor suppression. In Rehabilitation Robotics; Itech Education and Publishing: Vienna, Austria, 2007; pp. 453–470. [Google Scholar]
- Lo, H.S.; Xie, S.Q. Exoskeleton robots for upper-limb rehabilitation: State of the art and future prospects. Med. Eng. Phys. 2012, 34, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Jha, P.; Savla, K.; Shah, D. Exoskeleton Arm. In Proceedings of the 2018 International Conference on Smart City and Emerging Technology (ICSCET), Mumbai, India, 5 January 2018; pp. 1–6. [Google Scholar]
- Bogue, R. Exoskeletons—A review of industrial applications. Ind. Robot Int. J. 2018, 45, 585–590. [Google Scholar] [CrossRef]
- De Looze, M.P.; Bosch, T.; Krause, F.; Stadler, K.S.; O’Sullivan, L.W. Exoskeletons for industrial application and their potential effects on physical work load. Ergonomics 2016, 59, 671–681. [Google Scholar] [CrossRef] [PubMed]
- Stadler, K.S.; Scherly, D. Exoskeletons in industry: Designs and their potential. In Proceedings of the AUTSYM 2017-8th International Symposium on AUTOMATICCONTROL, Wismar, Germany, 21–22 September 2017; ZHAW Zürcher Hochschule für Angewandte Wissenschaften: Winterthur, Switzerland, 2017. [Google Scholar]
- Bosch, T.; van Eck, J.; Knitel, K.; de Looze, M. The effects of a passive exoskeleton on muscle activity, discomfort and endurance time in forward bending work. Appl. Ergon. 2016, 54, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Spada, S.; Ghibaudo, L.; Gilotta, S.; Gastaldi, L.; Cavatorta, M.P. Investigation into the applicability of a passive upper-limb exoskeleton in automotive industry. Procedia Manuf. 2017, 11, 1255–1262. [Google Scholar] [CrossRef]
- Noonee. Available online: https://www.noonee.com/ (accessed on 8 July 2019).
- ESOSCHELETRO MATE. Available online: https://www.comau.com/it/mate (accessed on 8 July 2019).
- Work Safer with EksoVest. Available online: https://eksobionics.com/eksoworks/ (accessed on 8 July 2019).
- Levitate. Available online: https://www.levitatetech.com/ (accessed on 8 July 2019).
- Imagine If the Human Body Was Not Limited by Its Physical Abilities? Available online: https://www.skelex.com/ (accessed on 8 July 2019).
- Gopura, R.; Bandara, D.; Kiguchi, K.; Mann, G.K. Developments in hardware systems of active upper-limb exoskeleton robots: A review. Robot. Auton. Syst. 2016, 75, 203–220. [Google Scholar] [CrossRef]
- Sylla, N.; Bonnet, V.; Colledani, F.; Fraisse, P. Ergonomic contribution of ABLE exoskeleton in automotive industry. Int. J. Ind. Ergon. 2014, 44, 475–481. [Google Scholar] [CrossRef]
- Stadler, K.S.; Altenburger, R.; Schmidhauser, E.; Scherly, D.; Ortiz, J.; Toxiri, S.; Mateos, L.; Masood, J. Robo-mate an exoskeleton for industrial use—Concept and mechanical design. In Advances in Cooperative Robotics; World Scientific: Singapore, 2017; pp. 806–813. [Google Scholar]
- Ebrahimi, A. Stuttgart Exo-Jacket: An exoskeleton for industrial upper body applications. In Proceedings of the 2017 10th International Conference on Human System Interactions (HSI), Ulsan, Korea, 17–19 July 2017; pp. 258–263. [Google Scholar]
- Li, R.Y.M.; Ng, D.P.L. Wearable Robotics, Industrial Robots and Construction Worker’s Safety and Health. In International Conference on Applied Human Factors and Ergonomics; Springer: Cham, Switzerland, 2017; pp. 31–36. [Google Scholar]
- Huysamen, K.; de Looze, M.; Bosch, T.; Ortiz, J.; Toxiri, S.; O’Sullivan, L.W. Assessment of an active industrial exoskeleton to aid dynamic lifting and lowering manual handling tasks. Appl. Ergon. 2018, 68, 125–131. [Google Scholar] [CrossRef]
- Atoun. Available online: http://atoun.co.jp/products (accessed on 8 July 2019).
- Innophys. Available online: https://innophys.jp/? (accessed on 8 July 2019).
- Sankai, Y. HAL: Hybrid assistive limb based on cybernics. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2010; pp. 25–34. [Google Scholar]
- Sarcos. Available online: https://www.sarcos.com/products/guardian-xo/ (accessed on 8 July 2019).
- Vanderborght, B.; Albu-Schäffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Vitiello, N.; Cempini, M.; Crea, S.; Giovacchini, F.; Cortese, M.; Moisè, M.; Posteraro, F.; Carrozza, M.C. Functional design of a powered elbow orthosis toward its clinical employment. IEEE/ASME Trans. Mechatron. 2016, 21, 1880–1891. [Google Scholar] [CrossRef]
- Bianchi, M.; Cempini, M.; Conti, R.; Meli, E.; Ridolfi, A.; Vitiello, N.; Allotta, B. Design of a series elastic transmission for hand exoskeletons. Mechatronics 2018, 51, 8–18. [Google Scholar] [CrossRef]
- Yu, H.; Huang, S.; Chen, G.; Pan, Y.; Guo, Z. Human–robot interaction control of rehabilitation robots with series elastic actuators. IEEE Trans. Robot. 2015, 31, 1089–1100. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y.; Chen, G.; Yu, H. Adaptive human–robot interaction control for robots driven by series elastic actuators. IEEE Trans. Robot. 2016, 33, 169–182. [Google Scholar] [CrossRef]
- Fernández, J.; Sprengel, H.; Mallwitz, M.; Zipper, M.; Yu, B.; Bargsten, V. Designing modular series-elastic actuators for safe human-robot collaboration in industrial settings. In Advances in Cooperative Robotics, Proceedings of the 19th International Conference on Clawar 2016, London, UK, 12–14 September 2016; World Scientific: Singapore, 2016; p. 135. [Google Scholar]
- Lenzi, T.; Vitiello, N.; De Rossi, S.M.M.; Roccella, S.; Vecchi, F.; Carrozza, M.C. NEUROExos: A variable impedance powered elbow exoskeleton. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1419–1426. [Google Scholar]
- Kim, B.; Deshpande, A.D. An upper-body rehabilitation exoskeleton Harmony with an anatomical shoulder mechanism: Design, modeling, control, and performance evaluation. Int. J. Robot. Res. 2017, 36, 414–435. [Google Scholar] [CrossRef]
- Abdallah, I.B.; Bouteraa, Y.; Rekik, C. Design and development of 3d printed myoelectric robotic exoskeleton for hand rehabilitation. Int. J. Smart Sens. Intell. Syst. 2017, 10, 341–366. [Google Scholar] [CrossRef]
- Bowers, M.; Goldfarb, N.; Jagetia, A.; Khajuriwala, R.; Kumar, A.; Lam, B.; Shah, N. Design of a Low Cost Robotic System to Aid in the Rehabilitation of Stroke Patients. 2017. Available online: https://adjagetia.github.io/Documents/design-low-cost.pdf (accessed on 8 July 2019).
- Anam, K.; Al-Jumaily, A.A. Active exoskeleton control systems: State of the art. Procedia Eng. 2012, 41, 988–994. [Google Scholar] [CrossRef]
- Noda, T.; Sugimoto, N.; Furukawa, J.; Sato, M.A.; Hyon, S.H.; Morimoto, J. Brain-controlled exoskeleton robot for BMI rehabilitation. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 21–27. [Google Scholar]
- Li, Z.; Wang, B.; Sun, F.; Yang, C.; Xie, Q.; Zhang, W. sEMG-based joint force control for an upper-limb power-assist exoskeleton robot. IEEE J. Biomed. Health Inform. 2014, 18, 1043–1050. [Google Scholar] [PubMed]
- Secciani, N.; Bianchi, M.; Meli, E.; Volpe, Y.; Ridolfi, A. A novel application of a surface ElectroMyoGraphy-based control strategy for a hand exoskeleton system: A single-case study. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419828197. [Google Scholar] [CrossRef]
- Li, Z.; Huang, Z.; He, W.; Su, C.Y. Adaptive impedance control for an upper limb robotic exoskeleton using biological signals. IEEE Trans. Ind. Electron. 2017, 64, 1664–1674. [Google Scholar] [CrossRef]
- Yu, W.; Rosen, J.; Li, X. PID admittance control for an upper limb exoskeleton. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 1124–1129. [Google Scholar]
- Ryser, F.; Bützer, T.; Held, J.P.; Lambercy, O.; Gassert, R. Fully embedded myoelectric control for a wearable robotic hand orthosis. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 615–621. [Google Scholar]
- Ding, Y.; Galiana, I.; Siviy, C.; Panizzolo, F.A.; Walsh, C. IMU-based iterative control for hip extension assistance with a soft exosuit. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweeden, 16–21 May 2016; pp. 3501–3508. [Google Scholar]
- Langtree, I. Height Chart of Men and Woman in Different Countries. Canada: Disabled. 2018. Available online: https://www.disabled-world.com/calculators-charts/height-chart.php (accessed on 1 December 2017).
- Walpole, S.C.; Prieto-Merino, D.; Edwards, P.; Cleland, J.; Stevens, G.; Roberts, I. The weight of nations: An estimation of adult human biomass. BMC Public Health 2012, 12, 439. [Google Scholar] [CrossRef] [PubMed]
- Legnani, G.; Palmieri, G. Fondamenti di Meccanica e Biomeccanica del Movimento; CittàStudi: Milano, Italy, 2016. [Google Scholar]
- Lens, T.; Kirchhoff, J.; von Stryk, O. Dynamic modeling of elastic tendon actuators with tendon slackening. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 779–784. [Google Scholar]
- Roveda, L.; Pallucca, G.; Pedrocchi, N.; Braghin, F.; Tosatti, L.M. Iterative learning procedure with reinforcement for high-accuracy force tracking in robotized tasks. IEEE Trans. Ind. Inform. 2017, 14, 1753–1763. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tao, C.W.; Taur, J.S.; Chen, Y. Design of a parallel distributed fuzzy LQR controller for the twin rotor multi-input multi-output system. Fuzzy Sets Syst. 2010, 161, 2081–2103. [Google Scholar] [CrossRef]
- Roveda, L.; Haghshenas, S.; Prini, A.; Dinon, T.; Pedrocchi, N.; Braghin, F.; Tosatti, L.M. Fuzzy impedance control for enhancing capabilities of humans in onerous tasks execution. In Proceedings of the 2018 15th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 26–30 June 2018; pp. 406–411. [Google Scholar]
- Drive for Real-World Robots. Available online: https://www.anybotics.com/anydrive-robotic-actuator/ (accessed on 30 July 2019).
- EUROBENCH. Available online: http://eurobench2020.eu/ (accessed on 30 July 2019).
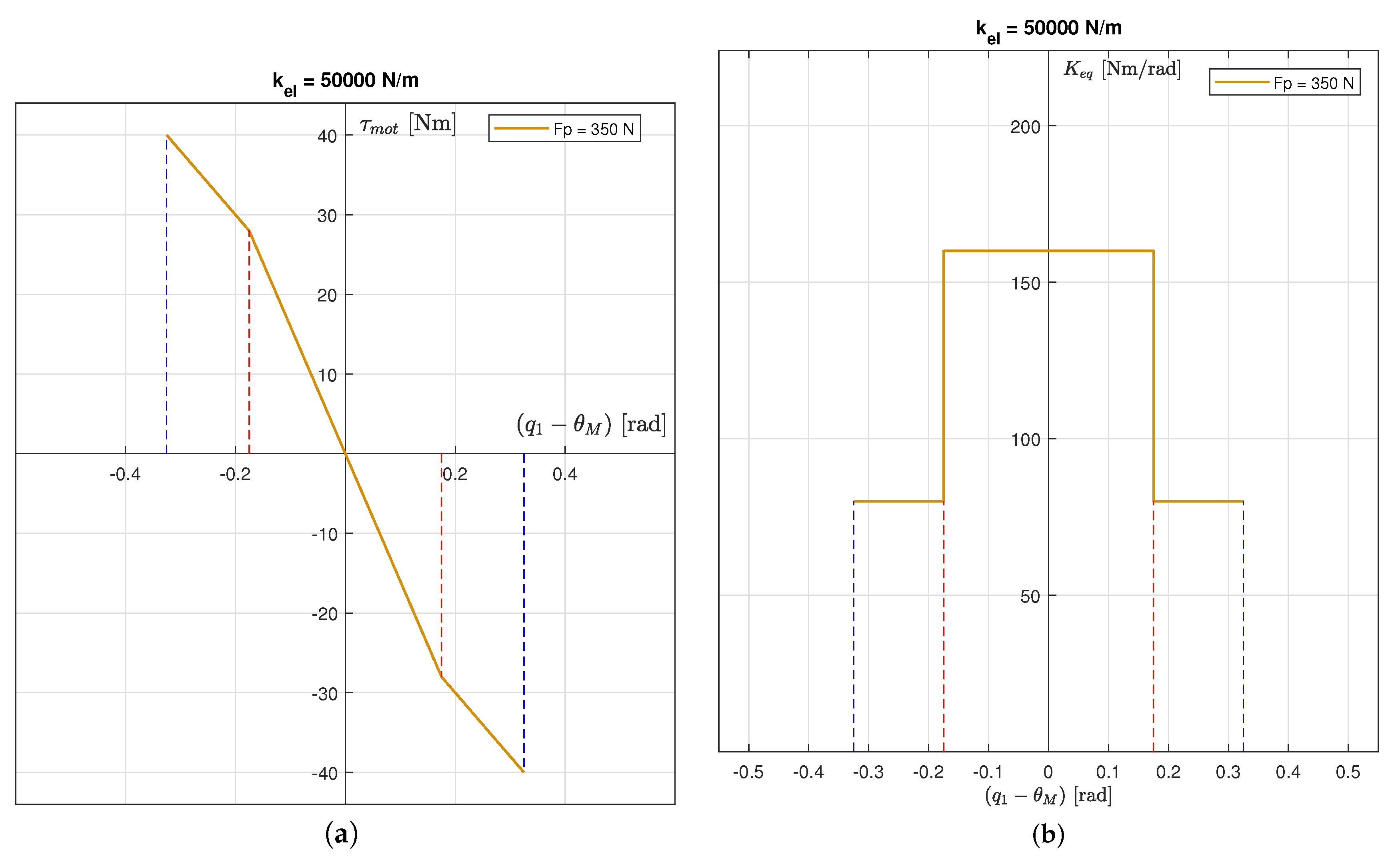

| r | d | ||
|---|---|---|---|
| 0 | 0 | ||
| 0 | 0 |
| N | N | N | N | Nm | Nm |
|---|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauri, A.; Lettori, J.; Fusi, G.; Fausti, D.; Mor, M.; Braghin, F.; Legnani, G.; Roveda, L. Mechanical and Control Design of an Industrial Exoskeleton for Advanced Human Empowering in Heavy Parts Manipulation Tasks. Robotics 2019, 8, 65. https://doi.org/10.3390/robotics8030065
Mauri A, Lettori J, Fusi G, Fausti D, Mor M, Braghin F, Legnani G, Roveda L. Mechanical and Control Design of an Industrial Exoskeleton for Advanced Human Empowering in Heavy Parts Manipulation Tasks. Robotics. 2019; 8(3):65. https://doi.org/10.3390/robotics8030065
Chicago/Turabian StyleMauri, Alessandro, Jacopo Lettori, Giovanni Fusi, Davide Fausti, Maurizio Mor, Francesco Braghin, Giovanni Legnani, and Loris Roveda. 2019. "Mechanical and Control Design of an Industrial Exoskeleton for Advanced Human Empowering in Heavy Parts Manipulation Tasks" Robotics 8, no. 3: 65. https://doi.org/10.3390/robotics8030065
APA StyleMauri, A., Lettori, J., Fusi, G., Fausti, D., Mor, M., Braghin, F., Legnani, G., & Roveda, L. (2019). Mechanical and Control Design of an Industrial Exoskeleton for Advanced Human Empowering in Heavy Parts Manipulation Tasks. Robotics, 8(3), 65. https://doi.org/10.3390/robotics8030065








