Vacuum-Actuated Bending for Grasping
Abstract
1. Introduction
2. Actuator Structure and Construction
3. Actuator Kinematics
3.1. Mechanical Behavior of Cellular Solids
3.2. Composite Bending
4. Results
4.1. Setup
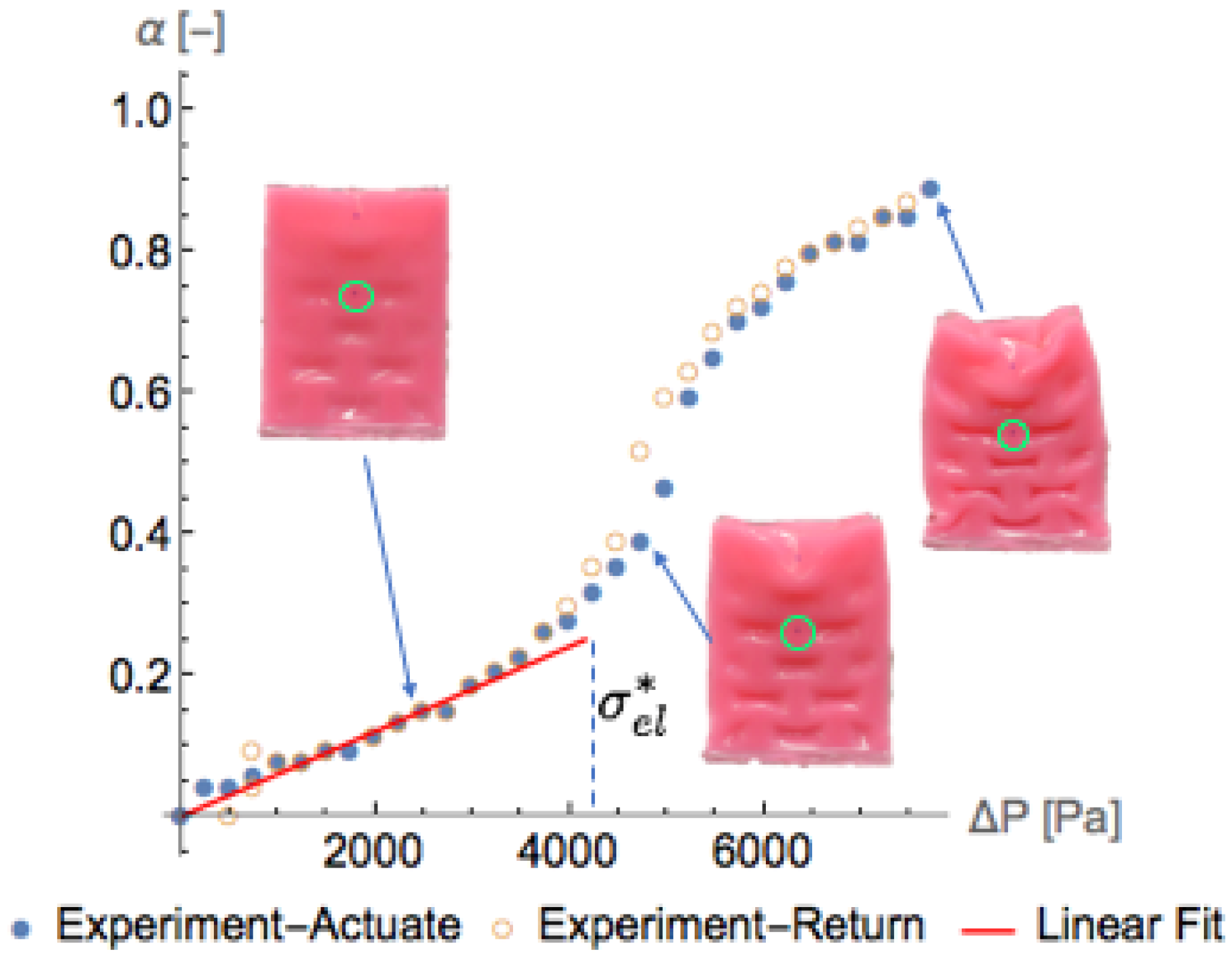
4.2. Cellular Solid Characterization
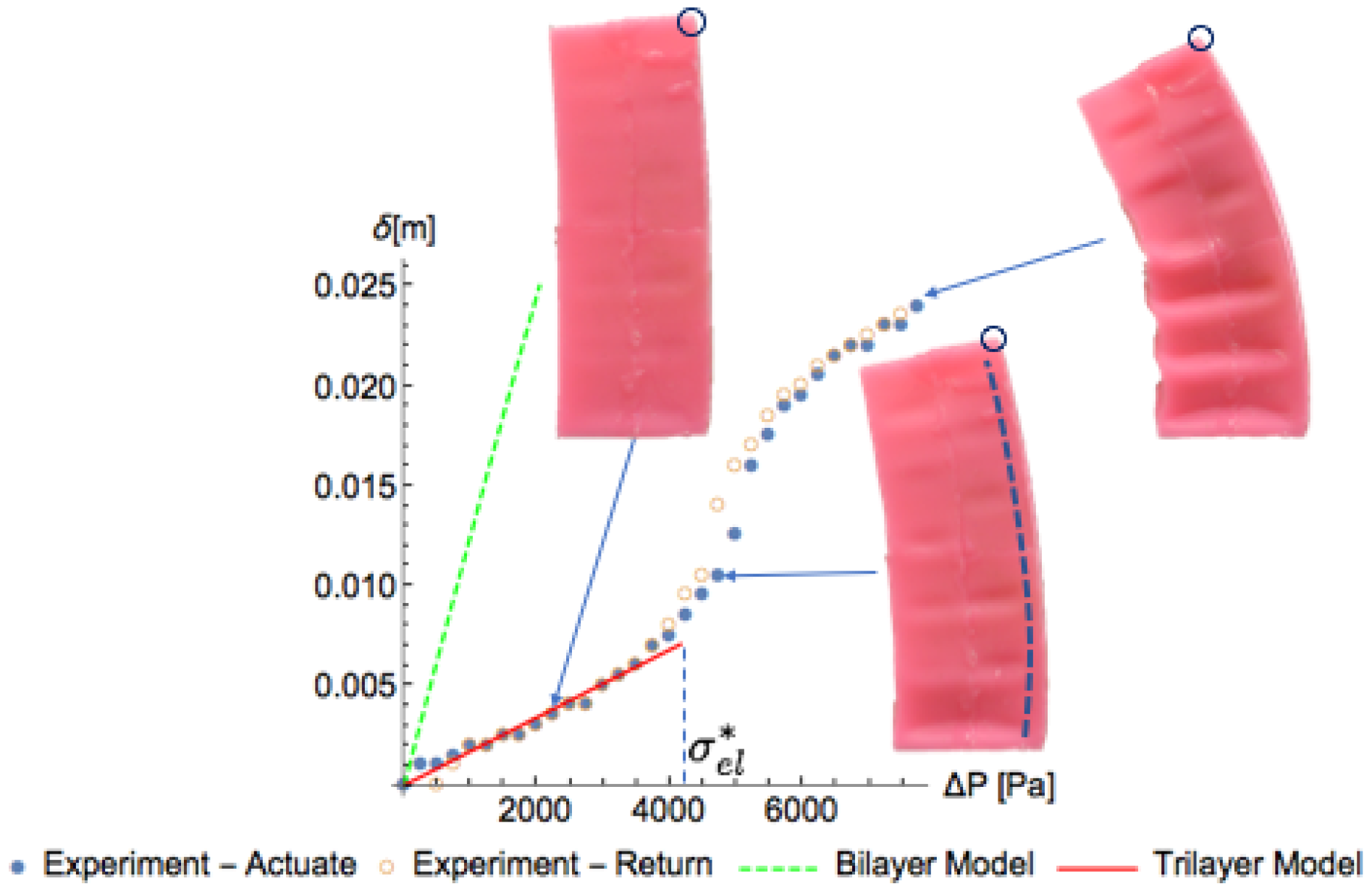
4.3. Displacement
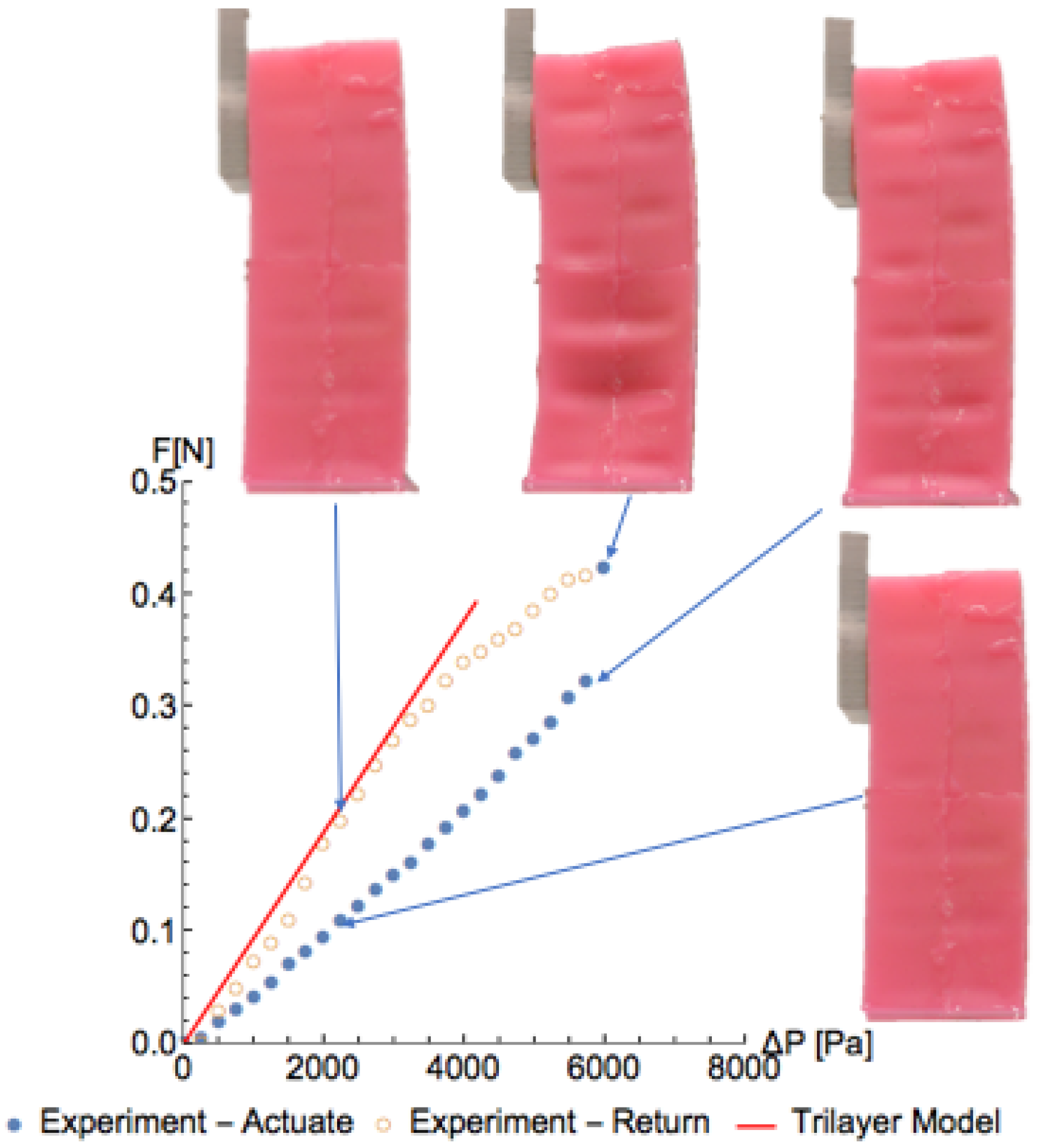
4.4. Force Generation
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marchese, A.D.; Onal, C.D.; Rus, D. Autonomous soft robotic fish capable of escape maneuvers using fluidic elastomer actuators. Soft Robot. 2014, 1, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [PubMed]
- Morrow, J.; Shin, H.S.; Phillips-Grafflin, C.; Jang, S.H.; Torrey, J.; Larkins, R.; Dang, S.; Park, Y.L.; Berenson, D. Improving Soft Pneumatic Actuator fingers through integration of soft sensors, position and force control, and rigid fingernails. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5024–5031. [Google Scholar]
- Homberg, B.S.; Katzschmann, R.K.; Dogar, M.R.; Rus, D. Haptic identification of objects using a modular soft robotic gripper. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1698–1705. [Google Scholar]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft robotics for chemists. Angew. Chem. 2011, 123, 1930–1935. [Google Scholar] [CrossRef]
- Lu, N.; Kim, D.H. Flexible and stretchable electronics paving the way for soft robotics. Soft Robot. 2014, 1, 53–62. [Google Scholar] [CrossRef]
- Cianchetti, M.; Ranzani, T.; Gerboni, G.; Nanayakkara, T.; Althoefer, K.; Dasgupta, P.; Menciassi, A. Soft robotics technologies to address shortcomings in today’s minimally invasive surgery: The STIFF-FLOP approach. Soft Robot. 2014, 1, 122–131. [Google Scholar] [CrossRef]
- Bertoldi, K.; Boyce, M.C.; Deschanel, S.; Prange, S.; Mullin, T. Mechanics of deformation-triggered pattern transformations and superelastic behavior in periodic elastomeric structures. J. Mech. Phys. Solids 2008, 56, 2642–2668. [Google Scholar] [CrossRef]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative Poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef] [PubMed]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Florijn, B.; Coulais, C.; van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 2014, 113, 175503. [Google Scholar] [CrossRef] [PubMed]
- Mullin, T.; Deschanel, S.; Bertoldi, K.; Boyce, M.C. Pattern transformation triggered by deformation. Phys. Rev. Lett. 2007, 99, 084301. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, J.T.; Shan, S.; Bertoldi, K. Compaction through buckling in 2D periodic, soft and porous structures: Effect of pore shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, J.T.; Bertoldi, K. Relating pore shape to the non-linear response of periodic elastomeric structures. J. Mech. Phys. Solids 2014, 64, 351–366. [Google Scholar] [CrossRef]
- Taylor, M.; Francesconi, L.; Gerendás, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low porosity metallic periodic structures with negative Poisson’s ratio. Adv. Mater. 2014, 26, 2365–2370. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.; Perdigou, C.; Chen, E.R.; Bertoldi, K.; Reis, P.M. Buckling-induced encapsulation of structured elastic shells under pressure. Proc. Natl. Acad. Sci. USA 2012, 109, 5978–5983. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Verma, M.; So, J.H.; Mosadegh, B.; Keplinger, C.; Lee, B.; Khashai, F.; Lossner, E.; Suo, Z.; Whitesides, G.M. Buckling Pneumatic Linear Actuators Inspired by Muscle. Adv. Mater. Technol. 2016, 1. [Google Scholar] [CrossRef]
- Lazarus, A.; Reis, P.M. Soft actuation of structured cylinders through auxetic behavior. Adv. Eng. Mater. 2015, 17, 815–820. [Google Scholar] [CrossRef]
- Yang, D.; Mosadegh, B.; Ainla, A.; Lee, B.; Khashai, F.; Suo, Z.; Bertoldi, K.; Whitesides, G.M. Buckling of elastomeric beams enables actuation of soft machines. Adv. Mater. 2015, 27, 6323–6327. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Verma, M.S.; Lossner, E.; Stothers, D.; Whitesides, G.M. Negative-Pressure Soft Linear Actuator with a Mechanical Advantage. Adv. Mater. Technol. 2017, 2, 1600164. [Google Scholar] [CrossRef]
- Bowick, M.; Cacciuto, A.; Thorleifsson, G.; Travesset, A. Universal negative Poisson ratio of self-avoiding fixed-connectivity membranes. Phys. Rev. Lett. 2001, 87, 148103. [Google Scholar] [CrossRef] [PubMed]
- Shukla, A.; Karki, H. Application of robotics in offshore oil and gas industry—A review Part II. Robot. Auton. Syst. 2016, 75, 508–524. [Google Scholar] [CrossRef]
- Galloway, K.C.; Becker, K.P.; Phillips, B.; Kirby, J.; Licht, S.; Tchernov, D.; Wood, R.J.; Gruber, D.F. Soft robotic grippers for biological sampling on deep reefs. Soft Robot. 2016, 3, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Property; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Timoshenko, S. Analysis of bi-metal thermostats. JOSA 1925, 11, 233–255. [Google Scholar] [CrossRef]
- Christophersen, M.; Shapiro, B.; Smela, E. Characterization and modeling of PPy bilayer microactuators: Part 1. Curvature. Sens. Actuators B Chem. 2006, 115, 596–609. [Google Scholar] [CrossRef]
- Shapiro, B.; Smela, E. Bending actuators with maximum curvature and force and zero interfacial stress. J. Intell. Mater. Syst. Struct. 2007, 18, 181–186. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]

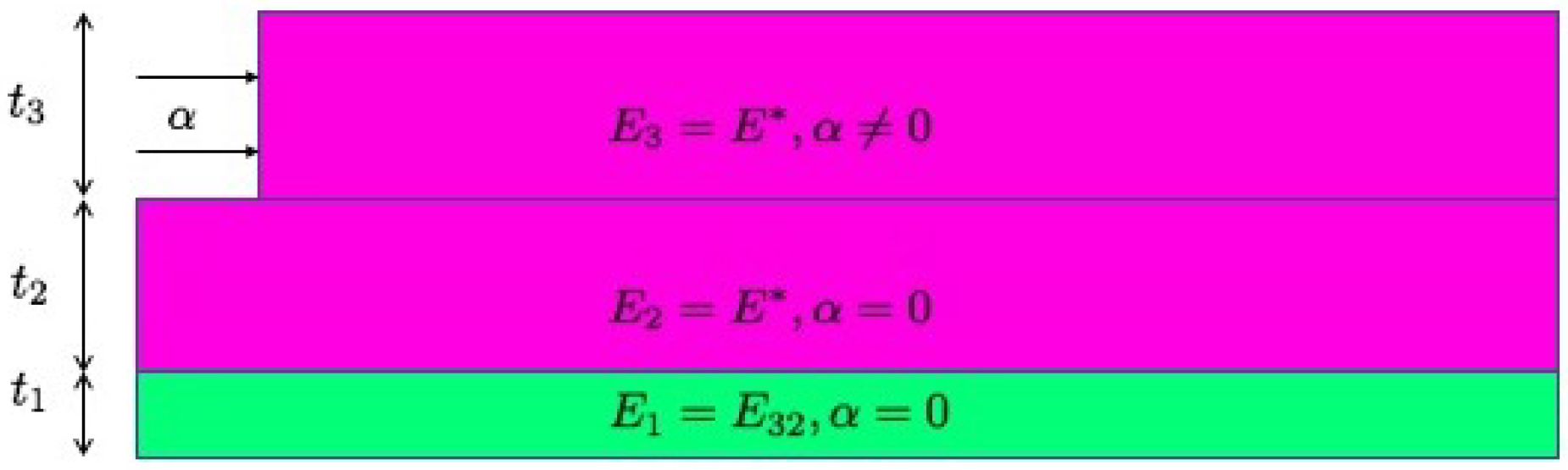

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, J.T.; Wicks, N. Vacuum-Actuated Bending for Grasping. Robotics 2018, 7, 73. https://doi.org/10.3390/robotics7040073
Miller JT, Wicks N. Vacuum-Actuated Bending for Grasping. Robotics. 2018; 7(4):73. https://doi.org/10.3390/robotics7040073
Chicago/Turabian StyleMiller, Jay T., and Nathan Wicks. 2018. "Vacuum-Actuated Bending for Grasping" Robotics 7, no. 4: 73. https://doi.org/10.3390/robotics7040073
APA StyleMiller, J. T., & Wicks, N. (2018). Vacuum-Actuated Bending for Grasping. Robotics, 7(4), 73. https://doi.org/10.3390/robotics7040073





