Model-Free Gradient-Based Adaptive Learning Controller for an Unmanned Flexible Wing Aircraft
Abstract
:1. Introduction
- An online adaptive learning control approach is proposed to solve the challenging weight-shift control problem of flexible wing aircraft. The approach uses model-free control structures and gradient-based solving value functions. This serves as a model-free solution framework for the classical Action Dependent Dual Heuristic Dynamic Programming problems.
- The work handles many concerns associated with implementing value and policy iteration solutions for ADDHP problems, which either necessitate partial knowledge about the system dynamics or involve difficulties in the evaluations of the associated solving value functions.
- The relation between a modified form of Bellman equation and the Hamiltonian expression is developed to transfer the gradient-based solution framework from the Bellman optimality domain to an alternative domain that uses Hamilton–Jacobi–Bellman expressions. This duality allows for a straightforward solution setup for the considered ADDHP problem. This is supported by a Riccati development that is equivalent to solving the underlying Bellman optimality equation.
- The proposed solution that is based on the combined-costate structure is implemented using a novel policy iteration approach. This is followed by an actor-critic implementation that is free of the computational expensive matrix inverse calculations.
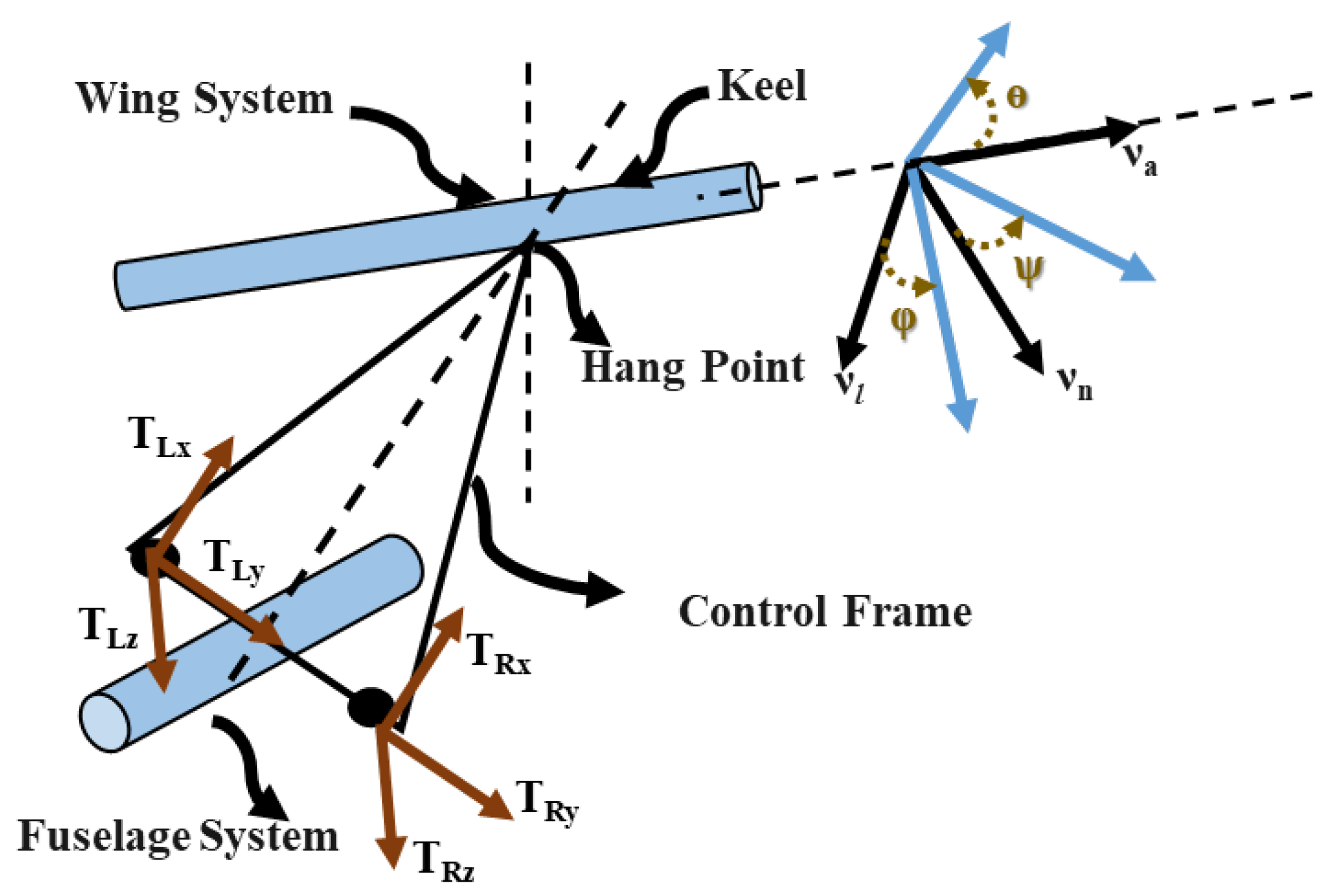
2. Control Mechanism of a Flexible Wing Aircraft
- The hang strap works as a kinematic constraint between the decoupled wing/fuselage systems.
- The fuselage system is assumed to be a rigid body connected to the wing system via a control triangle and a hang strap.
- The force components applied on the control bar are the input control signals.
- External forces, such as the aerodynamics and gravity, the associated moments, and the internal forces, are evaluated for both fuselage and wing systems.
- The fuselage’s pitch–roll–yaw attitudes and pitch–roll–yaw attitude rates are referred to the wing’s frame of motion through kinematic transformations.
- The complete aerodynamic model of the aircraft is reduced by substituting for the internal forces at the hang strap using the action/reaction laws.
- The pilot’s frames of motion (i.e., longitudinal and lateral states) are referred to the respective wing’s frames of motion.
3. Optimal Control Problem
3.1. Bellman Equation Formulation
3.2. Model-Based Policy Formulation
3.3. Model-Free Policy Formulation
| Algorithm 1 Value Iteration Gradient-based Solution |
|
| Algorithm 2 Policy Iteration Gradient-based Solution |
|
4. Hamiltonian-Jacobi–Bellman Formulation
4.1. The Hamiltonian Mechanics
4.2. Hamiltonian–Bellman Solutions Duality
5. The Adaptive Learning Solution and Riccati Development
5.1. Model-Free Gradient-Based Solution
| Algorithm 3 Online Policy Iteration Process |
|
5.2. Riccati Development
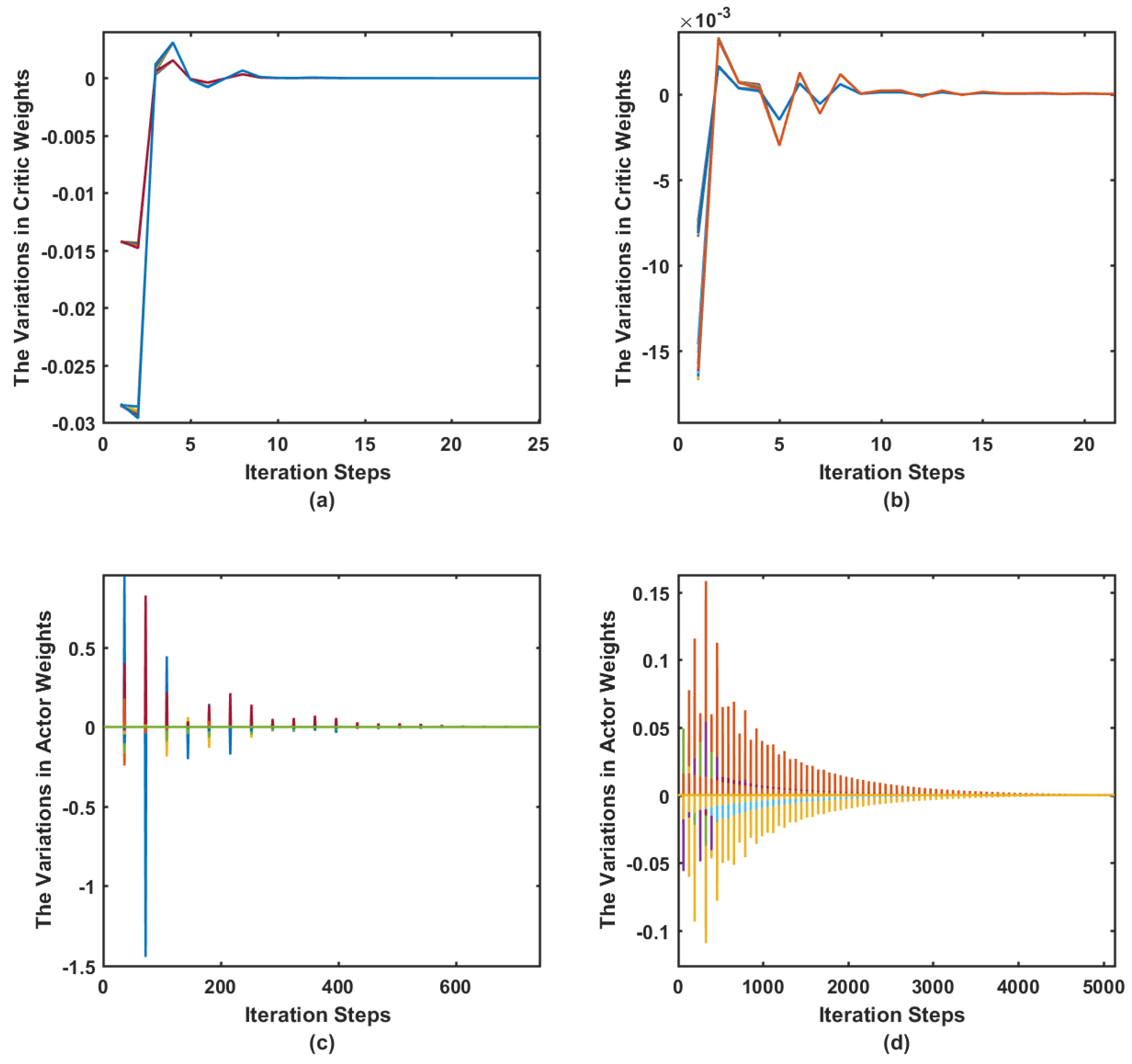
6. Adaptive Critics Implementations
6.1. Actor-Critic Neural Networks Implementation
| Algorithm 4 Online Model-Free Actor-Critic Neural Network Solution |
|
7. Simulation Results
7.1. Simulation Parameters
7.2. Simulation Case I
| The state space matrices for the longitudinal decoupled dynamics and are
|
7.3. Simulation Case II
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Variables | |
| , , | Axial, lateral, and normal velocities in the wing’s frame of motion. |
| , , | Pitch, roll, and yaw angles in the wing’s frame of motion. |
| , , | Pitch, roll, and yaw angle rates in the wing’s frame of motion. |
| , , | Pitch, roll, and yaw angles of the fuselage relative to the wing’s frame of motion. |
| , , | Pitch, roll, and yaw angle rates of the fuselage relative to the wing’s frame of motion. |
| Right and left internal forces on the control bar. | |
| Subscripts | |
| X, Y, and Z Cartesian components of , respectively. | |
| Abbreviations | |
| ADP | Adaptive Dynamic Programming |
| ADDHP | Action Dependent Dual Heuristic Dynamic Programming |
| DHP | Dual Heuristic Dynamic Programming |
| HJB | Hamilton–Jacobi–Bellman |
| RL | Reinforcement Learning |
References
- Bertsekas, D.; Tsitsiklis, J. Neuro-Dynamic Programming, 1st ed.; Athena Scientific: Belmont, MA, USA, 1996. [Google Scholar]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavior Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Werbos, P. Neural Networks for Control and System Identification. In Proceedings of the 28th Conference on Decision and Control, Tampa, FL, USA, 13–15 December 1989; pp. 260–265. [Google Scholar]
- Miller, W.T.; Sutton, R.S.; Werbos, P.J. Neural Networks for Control: A Menu of Designs for Reinforcement Learning Over Time, 1st ed.; MIT Press: Cambridge, MA, USA, 1990; pp. 67–95. [Google Scholar]
- Werbos, P. Approximate Dynamic Programming for Real-time Control and Neural Modeling. In Handbook of Intelligent Control: Neural, Fuzzy, and Adaptive Approaches; Chapter 13; White, D.A., Sofge, D.A., Eds.; Van Nostrand Reinhold: New York, NY, USA, 1992. [Google Scholar]
- Howard, R.A. Dynamic Programming and Markov Processes; Four Volumes; MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Abouheaf, M.; Lewis, F. Dynamic Graphical Games: Online Adaptive Learning Solutions Using Approximate Dynamic Programming. In Frontiers of Intelligent Control and Information Processing; Chapter 1; Liu, D., Alippi, C., Zhao, D., Zhang, H., Eds.; World Scientific: Singapore, 2014; pp. 1–48. [Google Scholar]
- Blake, D. Modelling The Aerodynamics, Stability and Control of The Hang Glider. Master’s Thesis, Centre for Aeronautics—Cranfield University, Silsoe, UK, 1991. [Google Scholar]
- Cook, M.; Spottiswoode, M. Modelling the Flight Dynamics of the Hang Glider. Aeronaut. J. 2005, 109, I–XX. [Google Scholar] [CrossRef]
- Cook, M.V.; Kilkenny, E.A. An experimental investigation of the aerodynamics of the hang glider. In Proceedings of the an International Conference on Aerodynamics, London, UK, 15–18 October 1986. [Google Scholar]
- De Matteis, G. Response of Hang Gliders to Control. Aeronaut. J. 1990, 94, 289–294. [Google Scholar] [CrossRef]
- de Matteis, G. Dynamics of Hang Gliders. J. Guid Control Dyn. 1991, 14, 1145–1152. [Google Scholar] [CrossRef]
- Kilkenny, E.A. An Evaluation of a Mobile Aerodynamic Test Facility for Hang Glider Wings; Technical Report 8330; College of Aeronautics, Cranfield Institute of Technology: Cranfield, UK, 1983. [Google Scholar]
- Kilkenny, E. Full Scale Wind Tunnel Tests on Hang Glider Pilots; Technical Report; Cranfield Institute of Technology, College of Aeronautics, Department of Aerodynamics: Cranfield, UK, 1984. [Google Scholar]
- Kilkenny, E.A. An Experimental Study of the Longitudinal Aerodynamic and Static Stability Characteristics of Hang Gliders. Ph.D. Thesis, Cranfield University, Silsoe, UK, 1986. [Google Scholar]
- Vrancx, P.; Verbeeck, K.; Nowe, A. Decentralized Learning in Markov Games. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 976–981. [Google Scholar]
- Webros, P.J. A Menu of Designs for Reinforcement Learning over Time. In Neural Networks for Control; Miller, W.T., III, Sutton, R.S., Werbos, P.J., Eds.; MIT Press: Cambridge, MA, USA, 1990; pp. 67–95. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Si, J.; Barto, A.; Powell, W.; Wunsch, D. Handbook of Learning and Approximate Dynamic Programming; The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Prokhorov, D.; Wunsch, D. Adaptive Critic Designs. IEEE Trans. Neural Netw. 1997, 8, 997–1007. [Google Scholar]
- Abouheaf, M.; Lewis, F.; Vamvoudakis, K.; Haesaert, S.; Babuska, R. Multi-Agent Discrete-Time Graphical Games And Reinforcement Learning Solutions. Automatica 2014, 50, 3038–3053. [Google Scholar]
- Lewis, F.; Vrabie, D.; Syrmos, V. Optimal Control, 3rd ed.; John Wiley: New York, NY, USA, 2012. [Google Scholar]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Abouheaf, M.; Lewis, F. Approximate Dynamic Programming Solutions of Multi-Agent Graphical Games Using Actor-critic Network Structures. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–8. [Google Scholar]
- Abouheaf, M.; Lewis, F.; Mahmoud, M.; Mikulski, D. Discrete-time Dynamic Graphical Games: Model-free Reinforcement Learning Solution. Control Theory Technol. 2015, 13, 55–69. [Google Scholar]
- Abouheaf, M.; Gueaieb, W. Multi-Agent Reinforcement Learning Approach Based on Reduced Value Function Approximations. In Proceedings of the IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Ottawa, ON, Canada, 5–7 October 2017; pp. 111–116. [Google Scholar]
- Widrow, B.; Gupta, N.K.; Maitra, S. Punish/reward: Learning with a Critic in Adaptive Threshold Systems. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 455–465. [Google Scholar] [CrossRef]
- Webros, P.J. Neurocontrol and Supervised Learning: An Overview and Evaluation. In Handbook of Intelligent Control: Neural, Fuzzy, and Adaptive Approaches; White, D.A., Sofge, D.A., Eds.; Van Nostrand Reinhold: New York, NY, USA, 1992; pp. 65–89. [Google Scholar]
- Busoniu, L.; Babuska, R.; Schutter, B.D. A Comprehensive Survey of Multi-Agent Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part C 2008, 38, 156–172. [Google Scholar]
- Abouheaf, M.; Mahmoud, M. Policy Iteration and Coupled Riccati Solutions for Dynamic Graphical Games. Int. J. Digit. Signals Smart Syst. 2017, 1, 143–162. [Google Scholar]
- Lewis, F.L.; Vrabie, D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst. Mag. 2009, 9, 32–50. [Google Scholar]
- Vrabie, D.; Lewis, F.; Pastravanu, O.; Abu-Khalaf, M. Adaptive Optimal Control for Continuous-Time Linear Systems Based on Policy Iteration. Automatica 2009, 45, 477–484. [Google Scholar]
- Abouheaf, M.I.; Lewis, F.L.; Mahmoud, M.S. Differential graphical games: Policy iteration solutions and coupled Riccati formulation. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 1594–1599. [Google Scholar]
- Asma Al-Tamimi, F.L.L.; Abu-Khalaf, M. Model-Free Q-Learning Designs for Linear Discrete-Time Zero-Sum Games with Application to H-infinity Control. Automatica 2007, 43, 473–481. [Google Scholar]
- Bahare Kiumarsi, F.L.L. Actor–Critic-Based Optimal Tracking for Partially Unknown Nonlinear Discrete-Time Systems. IEEE Trans. Neural Netw. Learn. Syst. 2105, 26, 140–151. [Google Scholar]
- Kiumarsi, B.; Vamvoudakis, K.G.; Modares, H.; Lewis, F.L. Optimal and Autonomous Control Using Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2042–2062. [Google Scholar]
- Cook, M.V. The Theory of the Longitudinal Static Stability of the Hang-glider. Aeronaut. J. 1994, 98, 292–304. [Google Scholar] [CrossRef]
- Ochi, Y. Modeling of the Longitudinal Dynamics of a Hang Glider. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, American Institute of Aeronautics and Astronautics, Kissimmee, FL, USA, 5–9 January 2015; pp. 1591–1608. [Google Scholar]
- Ochi, Y. Modeling of Flight Dynamics and Pilot’s Handling of a Hang Glider. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, American Institute of Aeronautics and Astronautics, Grapevine, TX, USA, 9–13 January 2017; pp. 1758–1776. [Google Scholar]
- Sweeting, J. An Experimental Investigation of Hang Glider Stability. Master’s Thesis, College of Aeronautics, Cranfield University, Silsoe, UK, 1981. [Google Scholar]
- Cook, M. Flight Dynamics Principles; Butterworth-Heinemann: London, UK, 2012. [Google Scholar]
- Kroo, I. Aerodynamics, Aeroelasticity and Stability of Hang Gliders; Stanford University: Stanford, CA, USA, 1983. [Google Scholar]
- Spottiswoode, M. A Theoretical Study of the Lateral-directional Dynamics, Stability and Control of the Hang Glider. Master’s Thesis, College of Aeronautics, Cranfield Institute of Technology, Cranfield, UK, 2001. [Google Scholar]
- Cook, M.V. (Ed.) Flight Dynamics Principles: A Linear Systems Approach to Aircraft Stability and Control, 3rd ed.; Aerospace Engineering; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
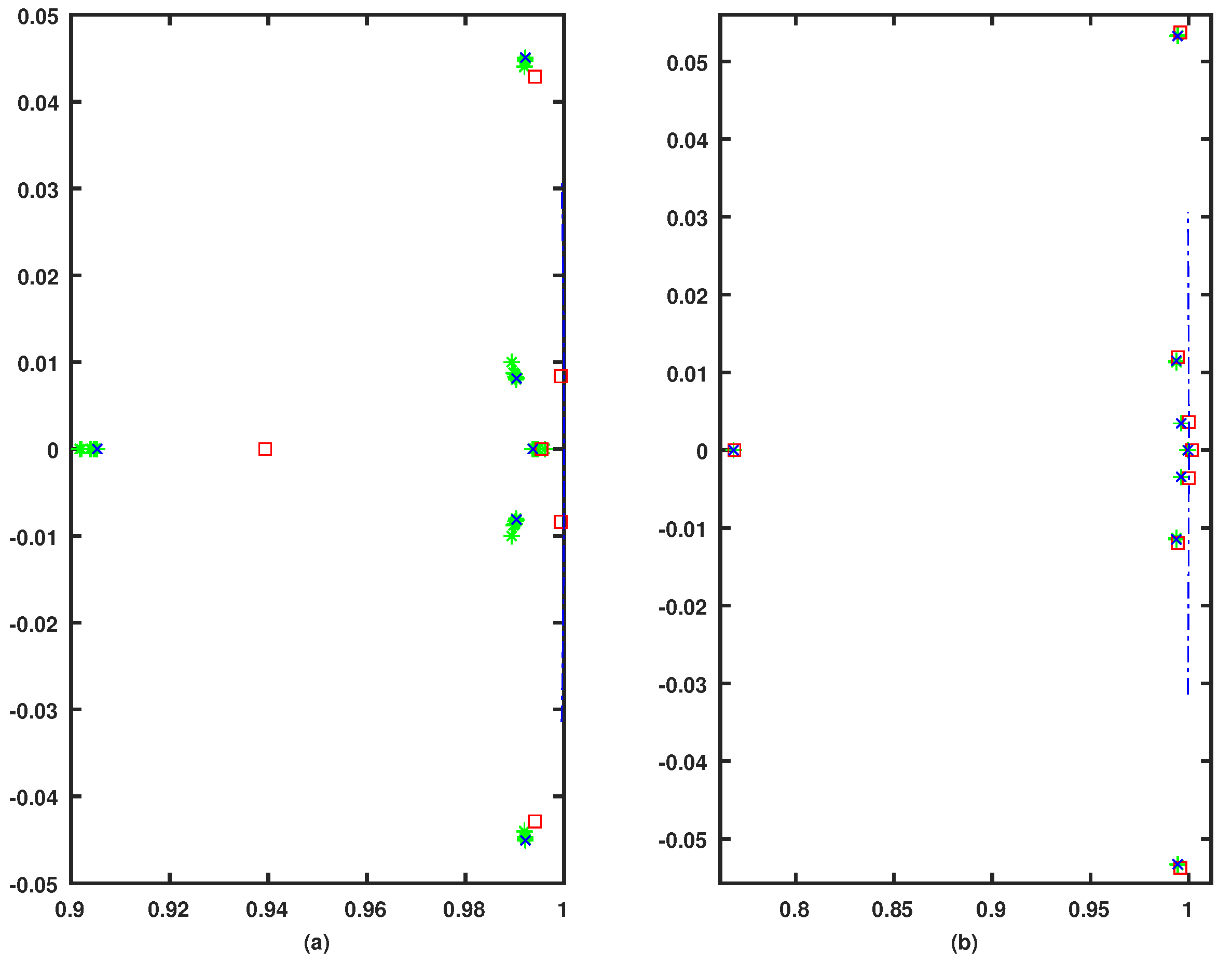
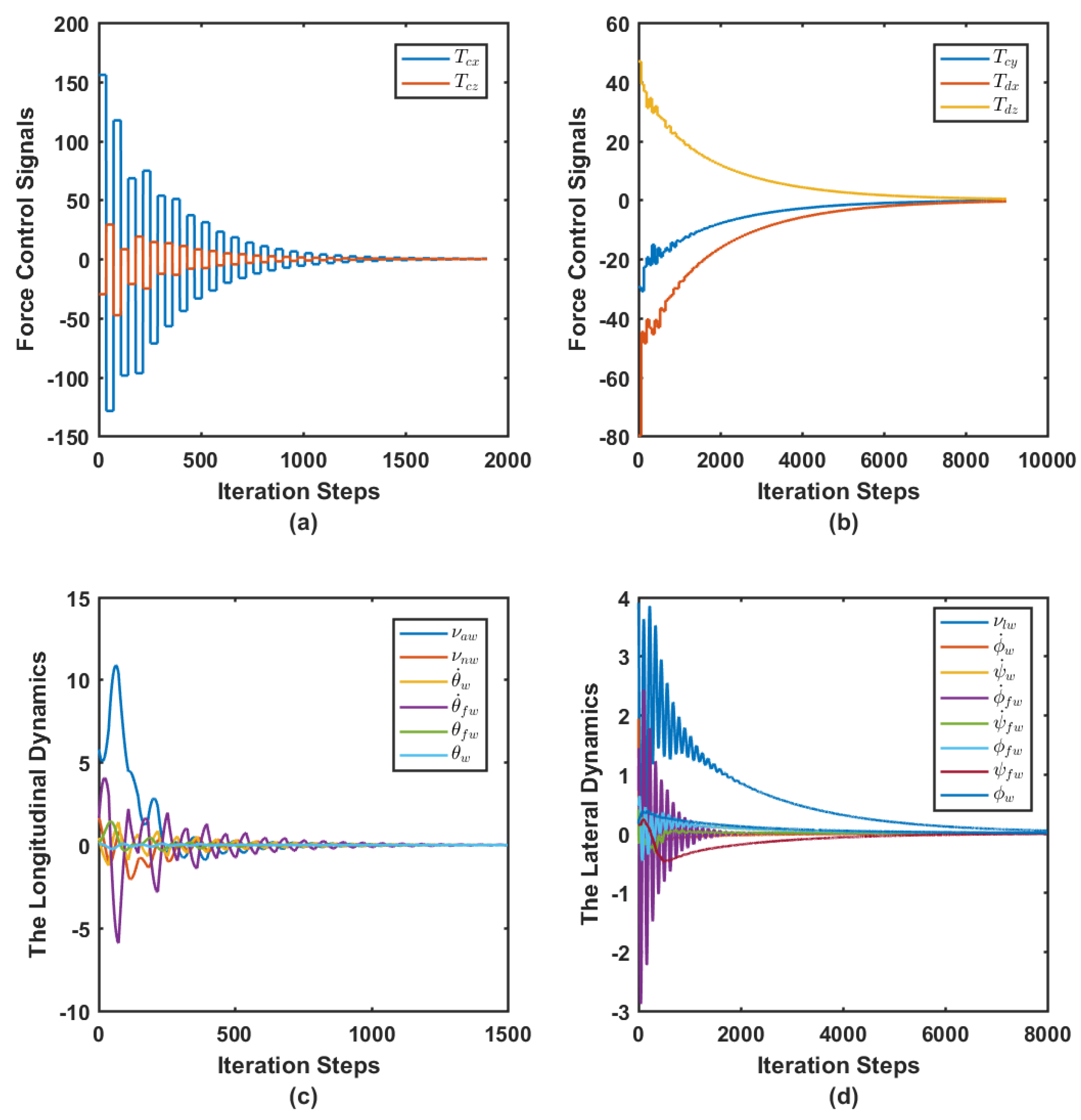
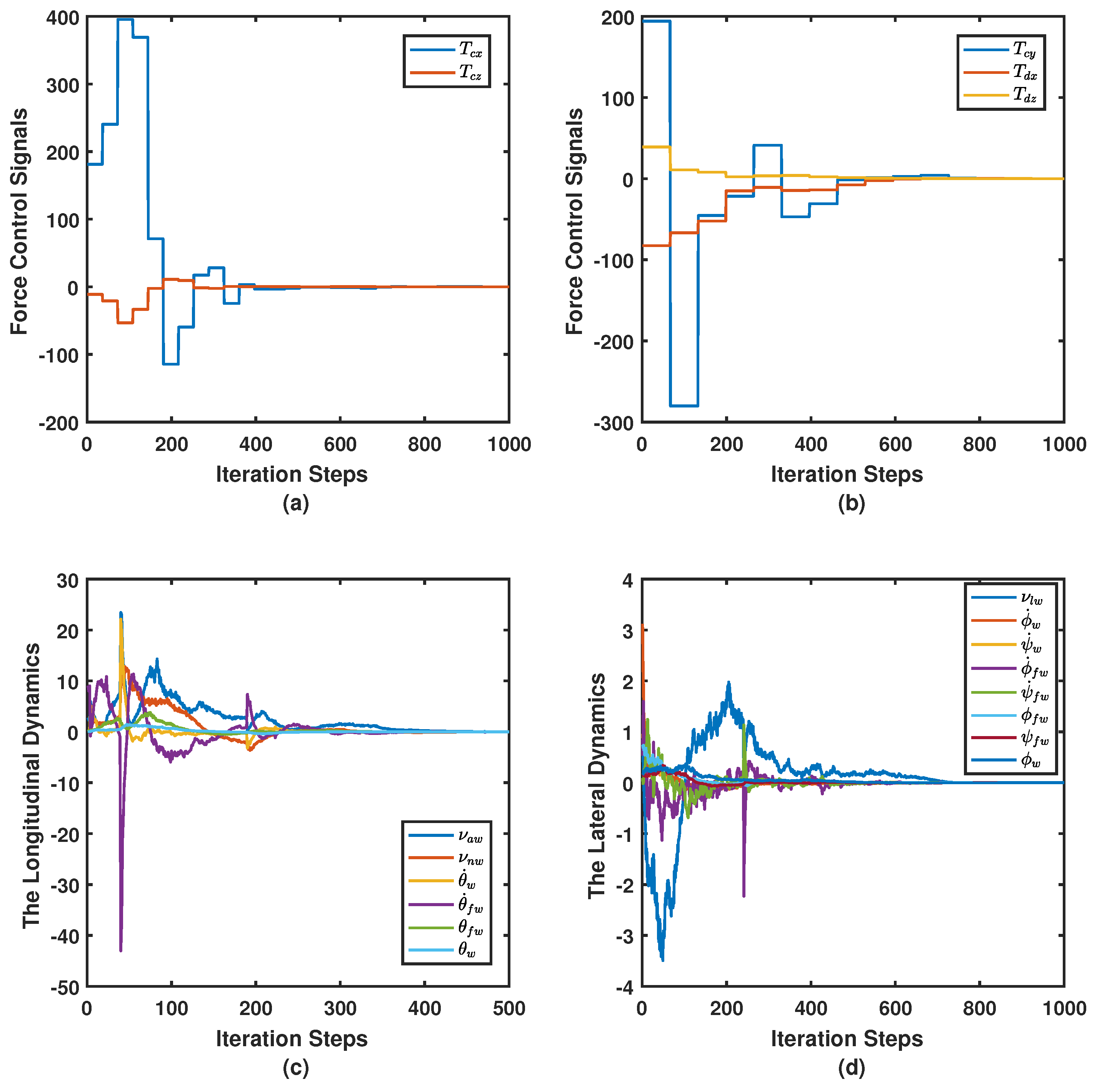
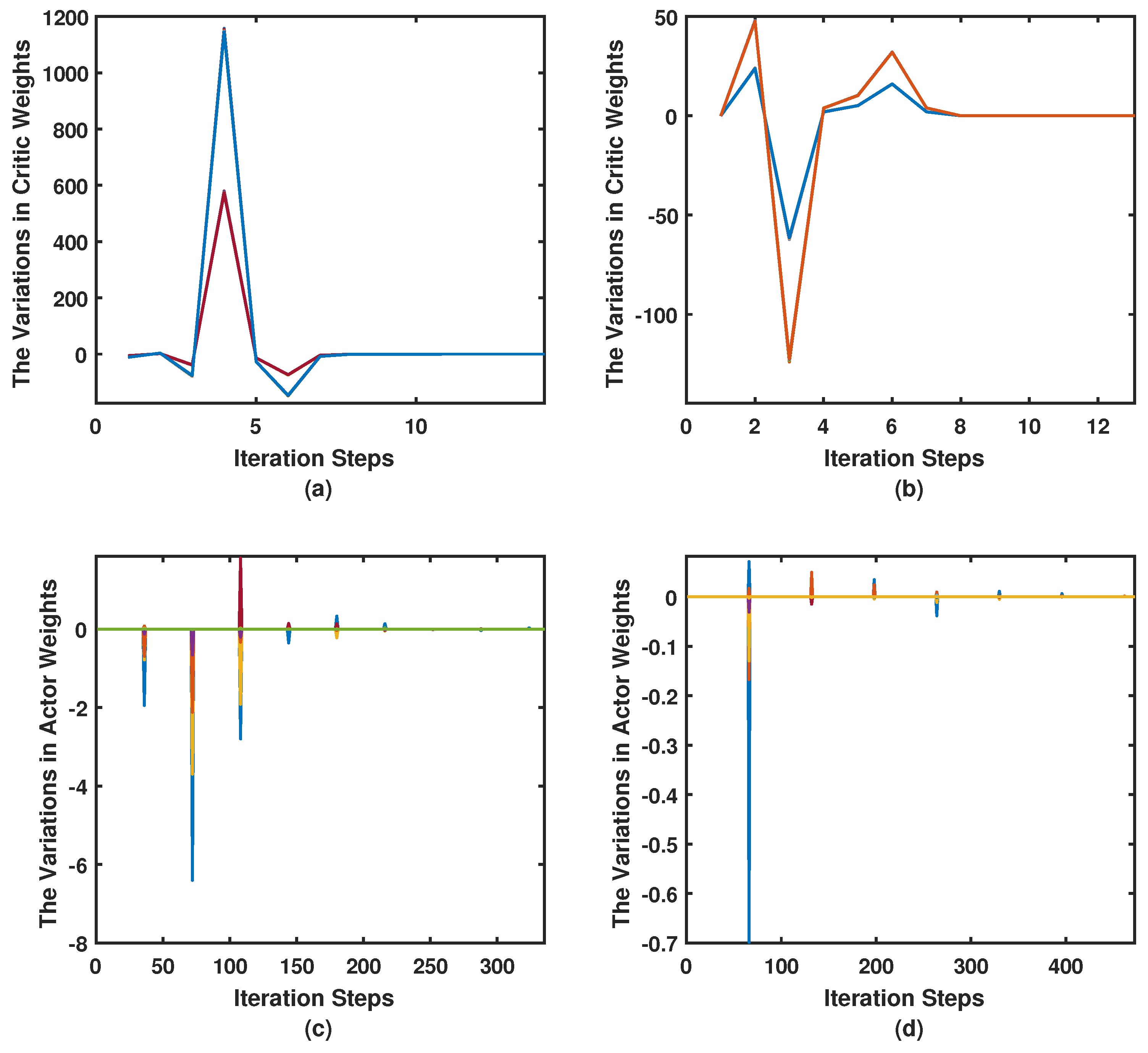
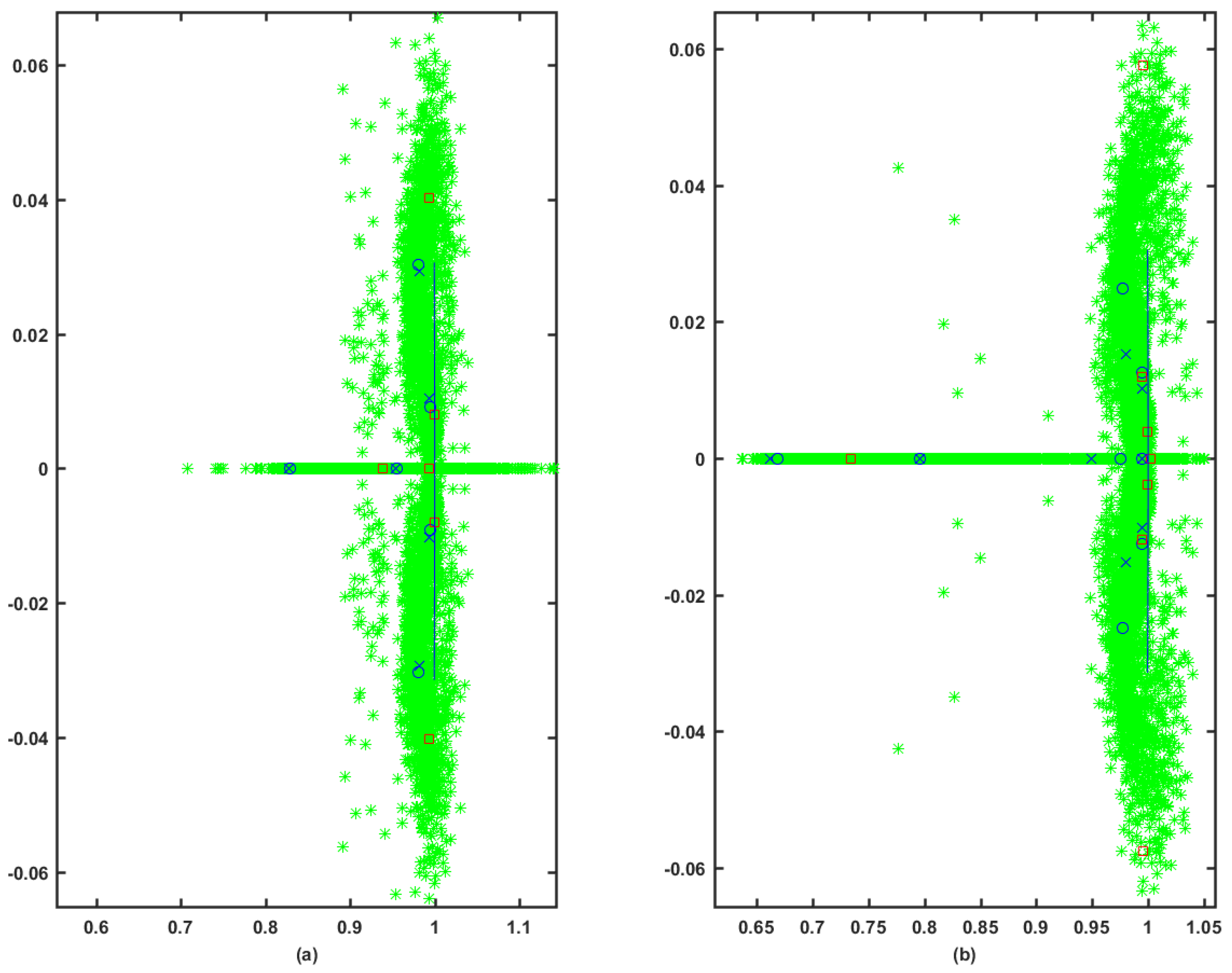
| Longitudinal Dynamics | |
| Open-Loop System | |
| Closed-Loop system | |
| Lateral Dynamics | |
| Open-Loop System | |
| Closed-Loop system | |
| Longitudinal Dynamics | |
|---|---|
| Open-Loop System | |
| (Disturbed System) | |
| Closed-Loop System | |
| (Riccati Solution) | |
| Closed-Loop System | |
| (Model-Free Solution) | |
| Lateral Dynamics | |
| Open-Loop System (Disturbed System) | |
| Open-Loop System (Riccati Solution) | |
| Closed-Loop system (Model-Free Solution) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abouheaf, M.; Gueaieb, W.; Lewis, F. Model-Free Gradient-Based Adaptive Learning Controller for an Unmanned Flexible Wing Aircraft. Robotics 2018, 7, 66. https://doi.org/10.3390/robotics7040066
Abouheaf M, Gueaieb W, Lewis F. Model-Free Gradient-Based Adaptive Learning Controller for an Unmanned Flexible Wing Aircraft. Robotics. 2018; 7(4):66. https://doi.org/10.3390/robotics7040066
Chicago/Turabian StyleAbouheaf, Mohammed, Wail Gueaieb, and Frank Lewis. 2018. "Model-Free Gradient-Based Adaptive Learning Controller for an Unmanned Flexible Wing Aircraft" Robotics 7, no. 4: 66. https://doi.org/10.3390/robotics7040066
APA StyleAbouheaf, M., Gueaieb, W., & Lewis, F. (2018). Model-Free Gradient-Based Adaptive Learning Controller for an Unmanned Flexible Wing Aircraft. Robotics, 7(4), 66. https://doi.org/10.3390/robotics7040066





