Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey

Abstract

Autonomous/unmanned driving is the major state-of-the-art step that has a potential to fundamentally transform the mobility of individuals and goods. At present, most of the developments target standalone autonomous vehicles, which can sense the surroundings and control the vehicle based on this perception, with limited or no driver intervention. This paper focuses on the next step in autonomous vehicle research, which is the collaboration between autonomous vehicles, mainly vehicle formation control or vehicle platooning. To gain a deeper understanding in this area, a large number of the existing published papers have been reviewed systemically. In other words, many distributed and decentralized approaches of vehicle formation control are studied and their implementations are discussed. Finally, both technical and implementation challenges for formation control are summarized.

1. Introduction

A driverless vehicle is a next big innovation in the transport industry. Many automotive companies are now working on five levels of autonomy [1]. Most of these companies are doing research on developing the fifth level of autonomous car and set to launch their cars in upcoming years. The introduction of fully autonomous vehicles will perhaps constitute the largest change to everyday transportation in living memory and is predicted to deliver a wide range of environmental, social and economic benefits [2]. Moreover, the United Kingdom has launched several projects to develop this technology further and created a Centre for Connected and Autonomous Vehicles (CCAV) [3].

A vehicle formation control or vehicle platooning is an important part of traffic management because of several benefits such as improved safety, fuel efficiency, mileage, a time needed to travel and reduced road congestion. Vehicles on the road usually follow another vehicle and form a platoon-based formation. For the human-operated vehicle, a platoon based formation is simple and can be seen every day. However, for connected autonomous vehicles (CAV), they must stay in the lanes and follow nearby vehicles by maintaining safe distance and velocity. The aim of the platoon formation control is to confirm that all vehicles in a platoon move at the same speed while maintaining a desired formation shape or geometry, which is stated by a desired inter-vehicle spacing strategy [4]. Therefore, for autonomous vehicles, forming a platoon formation requires specific algorithms, controllers and strategies consisting of longitudinal and lateral control.

Furthermore, for a formation control, vehicles need to communicate with each other; therefore, information sharing plays a vital role in the overall operation. This overall operation can be called collaboration within vehicles. A collaboration depends on sensing and information sharing within a vehicular network. The challenge here is to make these two operations, i.e. sensing and information sharing, autonomous to achieve desired control. Therefore, as autonomous vehicles are being developed, the next problem of collaboration between vehicles in dynamic environment needs to be addressed. The solution to these problems will secure the future of the CAVs. Figure 1 shows a summary of current approachs and methods used for formation control.

In the leader-follower approach, a leader is assigned to the multi-robot formation and remaining robots are the followers. In this approach, a leader follows its desired trajectory while follower robots track the position of the leader. There are three kinds of leader in this approach, namely static leader, dynamic leader and virtual leader. The advantage of this approach is the reduced tracking errors and can be analysed using standard control techniques [5]. Another benefit is that only the leader is responsible for planning trajectories and followers must follow the coordinates of the leader; therefore, it results in a simple controller. In terms of disadvantage, a leader’s fault can penalise the whole formation and feedback from followers to a leader is generally not applied in this approach.

In the behaviour-based approach, each individual robot shows several behaviours based on sensory inputs such as obstacle avoidance, goal seeking and formation keeping where final control is derived from the weighting of the relative importance of each behaviour. There are main four methods in this approach, namely motor scheme, potential field, swarm intelligence and flocking. This approach can be defined as a structured network of such interacting behaviours where the final action of each robot is derived by the behaviour coordinator. The behaviour coordinator multiplies the output of each behaviour by its relative weight, then summing and normalizing the results. One advantage of this approach is that it can operate in the unknown and dynamic environment because it is a parallel, real-time and distributed method, requiring less information sharing [5]. Its another advantage is that each behaviour has its physical meaning and the formation feedback can be incorporated into group dynamics by coupling the outputs of each individual behaviour. This method has some disadvantage such as the need to deriving a mathematical model of group dynamics, studying the convergence of specific formation, and guaranteeing the stability of the whole formation [6].

In the virtual structure approach, a virtual rigid structure is derived that represents a form of agents. Then, the desired motion of the virtual rigid structure is given, and agents’ motion is derived from the given rigid structure. Finally, to track the agents, a tracking controller for each individual agent is derived in which the formation is maintained by minimising the error between the virtual structure and the current agent position. In this approach, the desired trajectory is not assigned to the single agent, but it is shared by the whole formation team. In terms of advantage, this approach is easy to prescribe the coordinated behaviour for the whole group [5]. In terms of disadvantage, this approach is centralized, therefore, a single point of failure can crash the whole system. Furthermore, heavy communication and computation burden is concentrated on the centralized location, which may degrade the overall system performance [7].

The rest of this paper organised as follows. Some preliminaries are discussed in Section 2 to help readers to understand several concepts in the multi-robot systems. In Section 3, the leader-follower approach is presented, including the literature on vehicle platooning and formation controller design. The behaviour-based approach is described in Section 4, including motor schema-based method, potential field method, flocking and swarm intelligence based method for vehicle formation control. Section 5 analyses the virtual structure approach and resultant formation controllers. Finally, a number of technical and implementation challenges are discussed in Section 6.

2. Preliminaries

In this section, the fundamental concepts which are frequently used in formation control are covered such as communication topologies, graph theory and consensus. A consensus control theory is used to study the interaction between a group of dynamical agents. A tool commonly used to analyse consensus control strategies is the graph theory, whereas the communication topologies indicate a potential interaction between neighbouring agents and are described by the graph.

2.1. Topologies

To attain formation control, information sharing with other robots is a key task in the multi-robot system. Therefore, topologies are implemented in the vehicle platooning to address the information sharing problem. These topologies are responsible for the information exchange flow which describes how the vehicles in a platoon exchange information with each other. There are different types of communication topologies to choose from, and some of them are shown in Figure 2.

In Figure 2, several leader–follower topologies are presented. Here, topology A is the predecessor following (PF) topology, topology B is the predecessor–leader following (PLF) topology, topology C is the bidirectional (BD) topology, topology D is the bidirectional-leader (BDL) topology, topology E is the two-predecessor following (TPF) topology and topology F is the two-predecessor–leader following (TPFL) topology. Note that these topologies are for single platoon formation. During platoon operation, several scenarios can take place such as interaction between multiple platoons or loss of communication under existing topology. Therefore, dynamic or switching topologies should be considered for platoon stability and mobility [9,10]. Here, dynamic or switching topology means that the topology of platoon formation switch into a different topology over time.

2.2. Algebraic Graph Theory

Graph theory is used in the multi-robot formation control for the information exchange between autonomous robots, to perform the stability analysis of the formation, and to achieve consensus. The topologies discussed previously are modelled as a graph where robots can be represented as nodes of a graph and intersections such as sensing and communication can be represented as edges of the graph. Here, two basic graph theories are presented, directed graph or diagraph and undirected graph. More information on graph theory can be found in these books [11,12].

A diagraph is called strongly connected if there is a directed path from every node to every other node. A diagraph g is defined as pair $(V,E)$, where V denotes the set of nodes and $E\subseteq VxV$ denotes the set of ordered pairs of the nodes, called edges. It is assumed that there is no self-edge, i.e., $(i,i)\notin E$ for any $i\in V$. The set of neighbours of $i\in V$ is defined as a set $N_i:=j\in V:(i,j)\in E$. A directed path of g is an edge sequence of the form $(v_{i_1},v_{i_2}),(v_{i_2},v_{i_3}),\dots ,(v_{i_{k-1}},v_{i_k})$. If $(i,j)\in E$, j is called a parent of i and i is called a child of j. A tree is a directed graph where a node, called the root, has no parent and the other nodes have exactly one parent. A spanning tree of a directed graph is a directed tree containing every node of the graph.

Given a directed graph $g=(V,E)$, where $w_{ij}$ is a real number associated with $(i,j)$ for $i,j\in V$ and assume that $w_{ij}>0$ if $(i,j)\in E$ and $w_{ij}=0$, otherwise. The Laplacian matrix $L=\left[l_{ij}\right]\in {\mathbb{R}}^{\left|v\right|x\left|v\right|}$ of g is defined as:

$$l_{ij}=\left\{\begin{array}{cc}{\sum }_{k\in N_i}{w}_{ik},\hfill & \mathrm{if}i=j,\hfill \\ -w_{ij},\hfill & \mathrm{if}i\ne j.\hfill \end{array}\right.$$

(1)

An undirected graph is called connected if there is a path between any distinct pair of nodes. Let g be a directed graph such that $(i,j)\in E$ if and only if $(j,i)\in E$ and $w_{ij}=w_{ji}$ for all $(i,j)\in E$. Then, g is said to be undirected. The Laplacian matrix L of g is symmetric and positive semi-definite. If g is connected, the second smallest eigenvalue of L is positive. Furthermore, the Laplacian matrix L can be defined as, $L=D-A$. Here, D is the degree matrix and A is the adjacency matrix.

2.3. Consensus in Multi-Robot Systems

In multi-robot systems, reaching a consensus can be considered as one of the important requirements where autonomous vehicles can reach an agreement to form a formation by sharing information locally with their neighbour vehicles. Generally, convergence to a common value is called consensus, and this depends on communication between autonomous vehicles. Analysing emergent of consensus behaviour as a result of local interactions among mobile agents who share information only with their neighbours according to some designed distributed protocols is a critical issue. A consensus is helpful in several ways such as:

• Alignment (Pointing in the same direction),
• Synchronization (Agreeing on the same time),
• Distributed Estimation (Agreeing on the estimation/measurement of the distributed quantity),
• Rendezvous (Meeting at a common point).

Earlier, a consensus problem was targeted by a first-order dynamical system [13,14]. Afterwards, the second order consensus where all agents are governed by second-order dynamics, position and velocity, and the third-order consensus where all agents are governed by third-order dynamics, position, velocity and acceleration, have attracted much of the interest and several publications target second-order and third-order consensus to derive sufficient and necessary conditions to reach consensus.

An analysis on second-order consensus algorithms was carried out using algebraic graph theory and it concluded that the real and imaginary parts of the eigenvalues of the Laplacian matrix have a key role in reaching consensus [15]. Moreover, the effect of communication delay was investigated in this study and it was shown that the second-order consensus can be achieved in the multi-agent systems with a directed spanning tree only when the time delay is less than a critical value. Another study proposed a second-order consensus protocol for multi-agent systems with synchronous intermittent information feedback and directed topology [16]. In this study, algebraic theory and Lyapunov control approach were used for the analysis and proved that second-order consensus can be reached if the general algebraic connectivity of the communication topology is larger than a threshold value and each agent communicates with its neighbours frequently enough as the network evolves.

A third-order consensus of a dynamic system containing position, velocity and acceleration was studied for the case of an undirected graph [17] and directed networks [18] using algebraic graph theory in a theoretical study. In these papers, necessary and sufficient conditions for consensus was established in terms of scaling strength and the eigenvalues of the Laplacian matrix. Moreover, a consensus problem for the second-order multi-agent and third-order multi-agent systems were considered in which this heterogeneous system was converted into an equivalent error system for the stability analysis [19]. In this study, both fixed and switching topologies were considered and a consensus was achieved by obtaining sufficient and necessary conditions based on Markovian jump system theory.

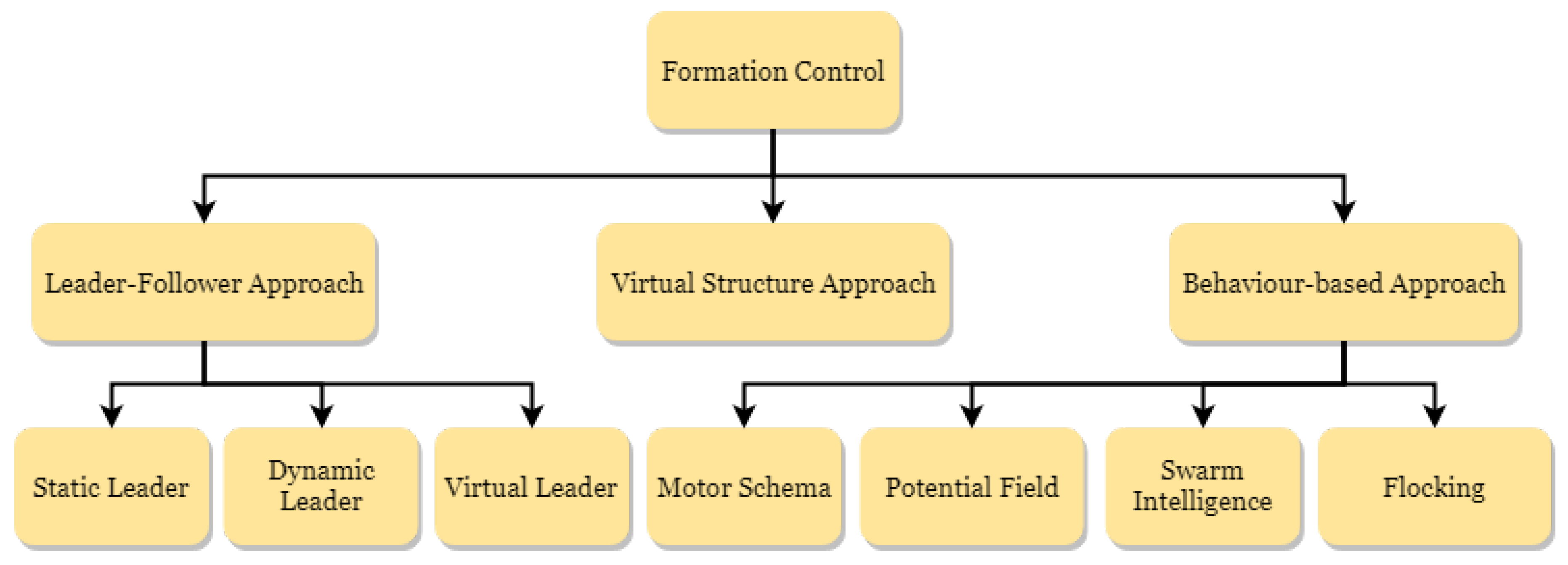
3. Leader–Follower Approach

The leader–follower control is a widely adopted formation approach. In this approach, a leader robot can be implemented in three ways: a static leader where leader robot does not change, a virtual leader where a software leader is employed, and a dynamic leader where leadership changes depending on the situation. Furthermore, a communication topology, responsible for the information exchange between robots, plays a vital role in the leader–follower approach. For the controller design, most of the literature discusses longitudinal control. However, lateral control is equally important for the navigation of autonomous vehicles in the structured environment. Once the formation is attained, the stability analysis of the formation is carried out using string stability analysis. In the leader–follower approach, consensus is said to be reached on each sum of a position vector and an inter-vehicle separation vector and the information flow is itself a directed spanning tree [20].

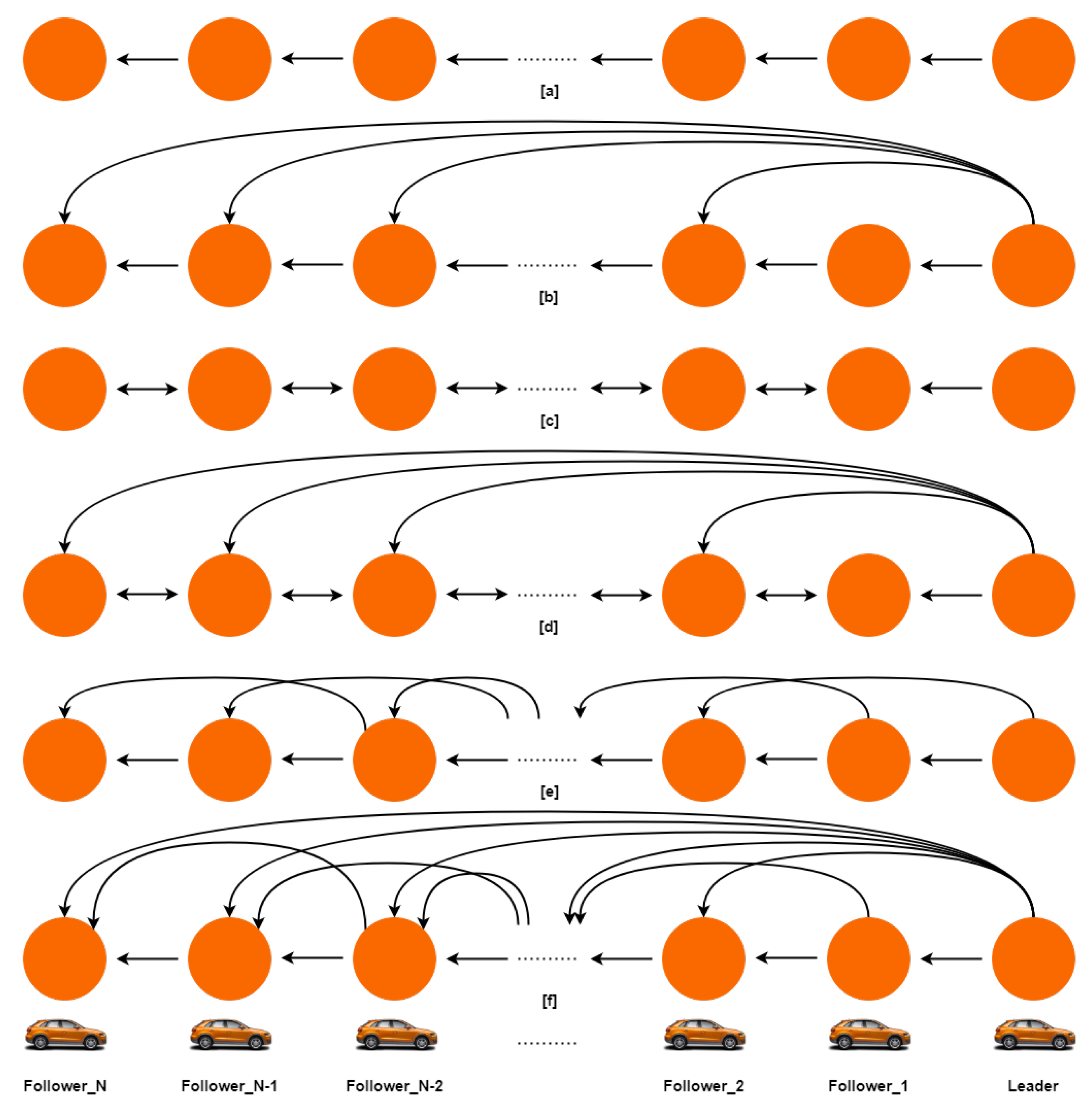
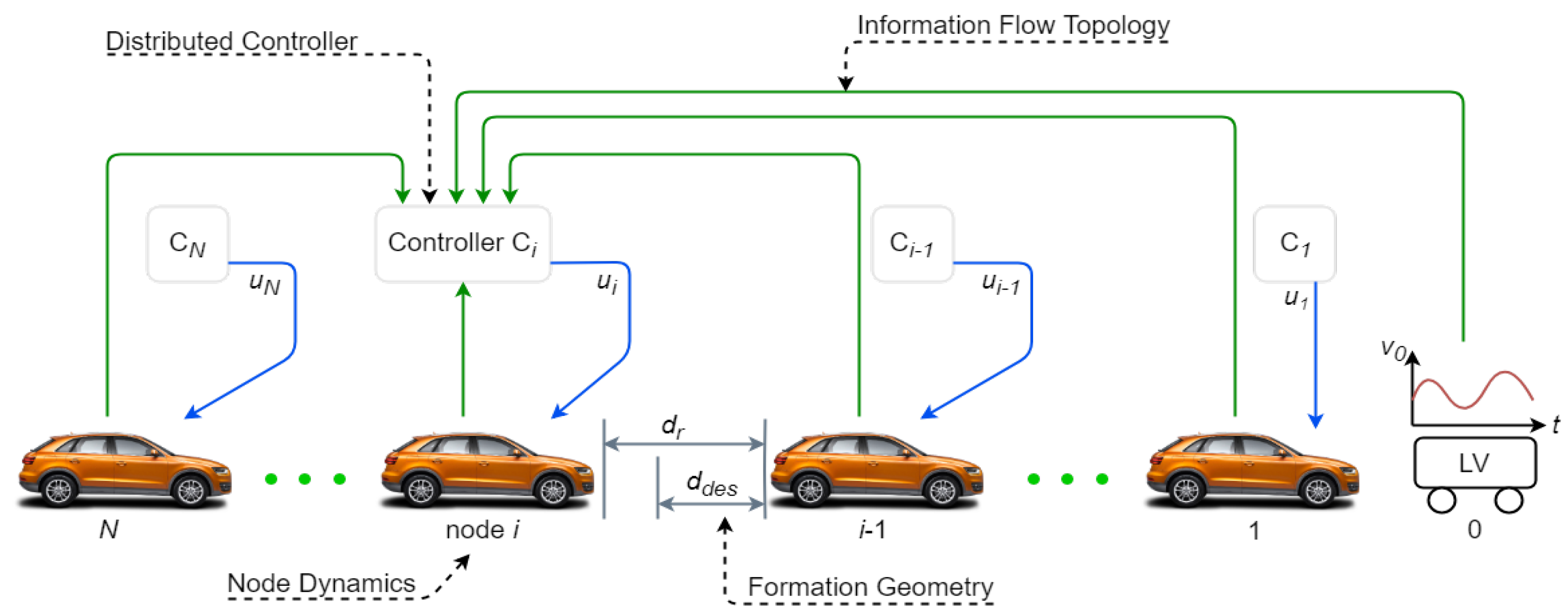
3.1. Leader–Follower Formation Controllers

A leader–follower formation tracking control of the autonomous vehicles was achieved on a straight path proving that recursive implementation of a cascaded system inspired controller leads to a spanning-tree communication topology [21]. In this article, the authors recommended working on switching communication topologies to measure the performance of the formation-tracking controller. In another paper, a leader–follower semi-centralized approach was employed for the formation control of the robots using the Hungarian method [22]. In this study, during the first phase, robots selected a leader and moved following the leader and during the second phase, a formation was given a centre and robots moved referring to the centre establishing a formation around the centre such as square, circle and triangle formations.

Several controllers were developed for the formation control of the multiple vehicles targeting a leader–follower tracking problem such as feedback linearization controller for formation maintenance, an adaptive controller to achieve ideal control due to inaccurate relative distance and a robust adaptive controller to cope with the external interference [23]. In this study, the stability of the system was confirmed through the Lyapunov method. Moreover, a virtual leader was employed for the distributed formation control of multiple nonholonomic wheeled mobile robots [24]. Here, the global position from the virtual leader was not supplied to each follower robot, but followers were able to exchange information with their neighbour robots. In this study, a distributed kinematic controller was proposed to achieve consensus and an adaptive dynamic controller was designed to maintain the stability of the kinematic error system. Another publication proposed a decentralized leader–follower tracking-agreement controller which used relative velocity and position measurement of the actual robot, with respect to a leader robot [25]. Here, virtual reference vehicle was used for the reference trajectory generation and resultant angular and linear velocities were communicated to the leader robot. Moreover, Lyapunov’s direct method was employed to establish global asymptotic stability.

An active vision-based adaptive leader–follower formation control was achieved in the absence of communication [26]. In this study, a follower robot was tracking the features of a leader robot through a camera and two controllers were developed: a formation controller to maintain formation and a camera controller to provide visual measurements. Furthermore, a vision-based leader–follower formation control was achieved by developing a neural-dynamic optimization-based nonlinear model predictive control (MPC) [27]. In this study, a camera on follower robot was employed to track the features and to measure state and velocity of the leader robot. A vision-based localization and leader–follower formation control was studied for the nonholonomic mobile robots [28]. In this work, a necessary condition for observability was derived and an extended Kalman filter was employed to estimate inter-robot distance.

Another publication used a GQ($\lambda$) algorithm, a gradient-based off-policy temporal-difference learning algorithm [29], to achieve leader–follower formation control. In this work, a static line follower was implemented where a leader robot moved without requiring advanced path planning and map recognition, whereas follower robots tried to learn how to follow the robot directly in front of them [30]. In the leader–follower approach, controlling throttle and brake of the follower vehicles is mandatory to regulate the follower vehicle’s speed and position with respect to the leader vehicle. Using longitudinal control of the vehicle, a reinforcement learning based neural dynamic programming method, an actor-critic algorithm with three layers of neural networks was developed to learn near optimal throttle and brake control policy for the follower vehicle. In this work, vehicle’s speed and distance were input to the network, whereas output was the desired action, throttle or break [31]. In this study, the authors recommended doing experiments on real vehicles.

A platoon formation control can be viewed as a leader–follower approach. It has attracted several research studies and confirmed its application to practical on-road traffic scenarios by developing robust controllers. One publication presented the platoon formation framework and divided this framework into four components, node dynamics, information flow topology, a distributed controller, and formation geometry as shown in Figure 3 [32]. In this framework, node dynamics describe the behaviour of an individual platoon vehicle, information flow topology defines the information exchange between each vehicle inside the platoon, the distributed controller implements the feedback control via neighbouring vehicle’s information and formation geometry maintains desired inter-vehicle distance in a platoon.

3.2. Second-Order Dynamics

A second-order consensus of multiple inertial agents was achieved for a leader–follower network in the presence of communication loss and delays. In this work, a necessary and sufficient condition was given and proved that, if damping and stiffness gains are chosen appropriately, the exponential consensus can be achieved [33]. A second-order feedback-based control protocol was developed to form a platoon formation under the non-lane-discipline road to show that proposed controller can reach a consensus state under sufficient convergence time [34]. Here, convergence means that the longitudinal gap can converge to the desired distance, the lateral gap can converge to zero, and the velocity can converge to the desired speed. In this paper, network topology was evaluated under different initial states by putting vehicles at different positions and the stability of the platoon was analysed using the Lyapunov technique.

Once the platoon formation is attained, it is important to keep track of the performance of formation. To study or maintain this formation, a string stability analysis is used. It is an important part to evaluate the behaviour of the platoon formation. A string stability analysis is the process of attenuating the disturbance along the vehicle string or platoon and is evaluated by considering amplification of signals such as the distance error, the velocity, the acceleration, or the control effort in the vehicle string as the vehicle index increases [35]. Moreover, the CAV technology relies on wireless communication between autonomous vehicles. Therefore, there might be a case when communication is delayed or communication link introduces time-varying delay over the vehicular network. Thus, the resultant effects might affect the stability of the platoon formation. Therefore, to study the stability of such developed controllers is the fundamental requirement [36].

In a theoretical study, a distributed control protocol to achieve platoon formation in the presence of heterogeneous time-varying delay was demonstrated by achieving a second-order consensus where string stability was achieved by using a Lyapunov–Razumikhin theorem [37]. The resultant architecture provided guaranteed stability of the platoon in the presence of disturbances. In an experimental study, a previously designed control protocol in [37] was applied to the three-vehicle platoon. Here, convergence to the desired spacing policy and robustness with time-varying communication topology were achieved under two scenarios, vehicle joining or leaving a platoon and loss of communication links [38]. In this study, a velocity and acceleration fluctuation were attenuated downstream the string of vehicles by the proposed algorithm to accomplish string-stability requirements.

The effects of wireless communication on string stability were studied for cooperative adaptive cruise control (CACC) using several parameters. One study presented the modelling and string stability analysis method for the vehicle platooning by considering parameters like time-varying transmission intervals and delays [39], whereas a subsequent study discussed the design trade-off between the specification for the vehicle following controller, network performance and string stability performance criteria by considering parameters like sampling, constant network delay and zero-order hold (ZOH) for a string stability of the platoon [35].

A distributed consensus-based reconfigurable control approach for the vehicle platooning was proposed considering heterogeneous vehicles and time-varying delays [40]. In this study, the Lyapunov–Razumikhin theorem was used to attain the string stability and a proposed controller was tested using the real dynamics of heterogeneous vehicles. In this paper, the convergence analysis was performed to check the performance of platoon maintenance and transient manoeuvres. In another publication, a study was conducted to analyse the influence of switching topology on the stability of a platoon of heterogeneous vehicles moving in a rigid formation [41]. In this study, the Krasovskii-based method proved to be more effective against communication delay compared to the Razumikhin-based approach.

Moreover, a local and improved second-order consensus control algorithms were applied to a cooperative car-following model where a local algorithm provided stability and an improved algorithm used local traffic information and downstream traffic information to smooth the traffic perturbation [42]. In this study, the authors recommended working on a third-order system by adding actuator lags and sensing delay. In another theoretical study, a consensus control was applied to a multi-platoon cooperative driving with consideration of the realistic inter-vehicle communication using IEEE 802.11p standard [43]. The proposed consensus algorithm considered the position and velocity data and acceleration was determined by the state difference between vehicle and its neighbouring vehicles. However, to achieve an equilibrium state, the authors recommended working on getting acceleration data, which means achieving a third-order consensus.

3.3. Third-Order Dynamics

A distributed control algorithm was developed to achieve a third-order consensus of a vehicular platoon network in the presence of time-varying heterogeneous delays [44]. In this work, acceleration errors due to time delay were taken into consideration to improve control reactivity and Lyapunov–Krasovskii function was constructed for the stability analysis. In another paper, a controller for emergency braking was presented for collision avoidance in a platoon. In this third-order dynamical model, a centralized control methodology of the heterogeneous platoon method was investigated [45]. Here, both Lyapunov–Razumikhin and Lyapunov–Krasovskii theorems were applied to construct a common Lyapunov function for a constant time headway strategy. Moreover, a third-order distributed protocol for a heterogeneous vehicle platooning under time-varying delays and switching topologies was presented [46]. Here, the stability of the closed-loop vehicular network was achieved using the Lyapunov–Krasovskii theorem and stability under a switched topology was achieved using the Lyapunov–Razumikhin theorem.

A virtual leader scheme was considered for multiple vehicle platoons to guarantee both inter-platoon internal stability and string stability in the presence of communication and parasitic delays [47]. In this study, it was assumed that each leader in the inter-platoon network is in communication with preceding and subsequent leaders; therefore, resulting topology was bidirectional virtual leader-following. Furthermore, stability analysis was performed by decoupling the closed-loop dynamics.

3.4. Platoon Management

Vehicle platoon can result in multiple formation operations such as several platoons working in the same environment; therefore, multi-platoon management such as inter-platoon and intra-platoon management is a necessity. To address the multi-platoon management, a leader–follower approach was employed and several algorithms were proposed to tackle issues such as inter-platoon position management, intra-platoon position management, platoon joining manoeuvres management and extra spacing for secure manoeuvring [48]. In another article, a platoon management protocol was developed for the autonomous vehicles to perform basic manoeuvres such as merge, split and lane change [49]. In this study, some basic platoon scenarios were addressed such as leader leave, follower leave and vehicle entry. Here, the information sharing was achieved through single-hop message broadcasting and finite-state machine approach.

Moreover, considering the longitude control of the autonomous vehicles, a vehicle controller was proposed for a platoon management in a simulation study [50]. In this study, the effects of acceleration, inter-platoon speed, and inter-platoon distance and space errors were analysed using the developed controller. Another study proposed a distributed controller for the multi-lane heterogeneous vehicles [51]. This controller was based on Laplacian control consisting of a lateral controller for staying in the lane and longitudinal controller for desired inter-vehicle distance. This graph-based controller was able to adapt the shape of the curvilinear road shape.

As autonomous vehicles emerge on the road, they will have to interact with other human-operated vehicles. Therefore, the interaction between autonomous vehicles and the presence of human-operated vehicles on roads needs to be studied. One publication studied this interaction by applying second-order consensus control to a vehicle platoon in a single lane roadway [52]. This study proposed a unified multiclass model for a heterogeneous platoon that analyses the system steady-state errors and transient-state performance. Furthermore, a controller was developed to obtain string stability in vehicle platoon using feedback linearization and further extended to attain merging of a two string of vehicles using time-gap and velocity profiles [53]. Here, input to the controller was given by time-gap and velocity profiles and string stability analysis was studied for both velocity tracking errors and time-gap tracking errors. Figure 4 shows the operation of autonomous vehicle platoon.

4. Behaviour-Based Approach

4.1. Basic Principles

Behavioural control is used to achieve coordinated control of a multi-robot system in an unknown or dynamic environment. The behaviour-based approach serves best when the real world cannot be accurately modelled or characterized. This approach provides the autonomy to the system to navigate in complex or cluttered environments by avoiding the offline path planning and using sensors to obtain instantaneous information of the environment. Furthermore, an environment for the autonomous vehicles is full of uncertainty and is also unpredictable, noisy, and dynamic. Therefore, a behaviour-based architecture is the answer to overcoming these difficulties by enabling real-time processing, relying heavily on sensing without constructing potentially erroneous global world models [55].

Behaviour-based robots are highly autonomous, mechanically imprecise, equipped with few computational resources, improve through learning, are programmed with software re-use, and integrated into the environment [56]. The basic principles of the behaviour-based control can be described as follows [57]:

• Behaviours are implemented as control laws, either in software or hardware, as a processing element or as a procedure.
• Each behaviour can take inputs from the robot’s sensors and/or from other modules in the system, and send outputs to the robot’s effectors and/or to other modules.
• Many different behaviours may independently receive input from the same sensors and output action commands to the same actuators.
• Behaviours are encoded to be relatively simple, and are added to the system incrementally.
• Behaviours are executed concurrently, not sequentially, in order to exploit parallelism and speed of computation, as well as the interaction dynamics among behaviours and between behaviours and the environment.

In order to enable formation behaviour in a multi-robot system, each robot should maintain certain distance and angle to other robots. For line or platoon formation, each robot should be able to move forward and backward and turn left and right to maintain desired velocity and position. The consensus in behaviour-based approach is said to be achieved on each deviation vector between the actual vehicle location and the desired vehicle location and the information flow forms a bi-directional ring topology [20].

A hierarchical architecture consisting of a behaviour module, velocity tuning module and the supervisory module was proposed for the multi-robot formation control [58]. Here, the behaviour module was responsible for the formation keeping and obstacle avoidance tasks and implemented using a fuzzy logic technique. The supervisory module was implemented using a fuzzy neural network and used to derive the final output from formation keeping and obstacle avoidance task. The velocity module was responsible for velocity tuning and handled by the fuzzy inference system. Moreover, the behaviour-based approach for the formation control of a swarm robot was proposed using a fuzzy logic controller [59]. In this study, obstacle avoidance and formation keeping behaviours were implemented.

4.2. Motor Schema-Based Control

Motor schemas used for mobile robots are sequences of action that accomplish a goal-directed behaviour. Rather than representing the simplest elementary actions available to the robot, such as a simple command to a robot actuator, schemas and motion primitives represent a higher-level abstraction of robot actions, such as avoiding obstacles, avoiding robot, maintaining formation, and moving to goal. These schemas and motion primitives define control policies that are encoded with only a few parameters and serve as the basis set, or movement vocabulary, of the robot. Such primitives are sufficient for generating the robot’s entire repertoire of motions via the combination of schemas or primitives [60].

A number of formation shapes such as line, column, diamond, and wedge were considered by implementing several motor schemas such as move-to-goal, avoid-static obstacle, avoid-robot and maintain-formation [61]. These schemas were used to implement the overall behaviour for a robot to move to a goal location while avoiding obstacles and collisions with other robots and remaining in the formation. In this study, a comparison between three formation position determination techniques, unit-centre-references, leader-referenced and neighbour-referenced were carried out and advantages and disadvantages were discussed regarding these three techniques. In another study, a distributed layered formation control framework to guide the robots as a whole in an unknown environment by avoiding obstacles and collision between robots was developed [62]. In this study, a leader–follower approach for formation control and behaviour-based approach for obstacle avoidance was implemented and dynamic role switching of the leader was proposed.

The formation of the swarm of robots was considered where two important formation control problems, efficient initial formation and formation control while avoiding obstacles were solved [63]. For initial formation control, a classification-based target searching algorithm was proposed. Here, the formation control while avoiding obstacles was attained by implementing five different behaviours such as moving to the goal, avoiding obstacles, wall-following, avoiding robot, and formation keeping. Another article proposed a decentralized behaviour-based formation control and obstacle avoidance algorithm for multiple robots in which information exchange was considered only between neighbouring robots [64]. In this study, collision avoidance was obtained by determining the avoidance angle using the distance between obstacles as well as the formation generation behaviour being obtained by selecting the leader robot and determining the location in the formation using locations of other mobile robots and formation matrix.

4.3. Artificial Potential Field

In the artificial potential field (APF) method, the mobile robots have two fields generated by the goal and obstacles in search spaces. These two fields are the repulsive force field generated by obstacles and the attractive force field generated by goals. These forces are stronger close to the obstacles or goal and have less effect at a distance. In this method, the goal location gains an attractive force to it, while the obstacles produce a repulsive force on robots. The resultant forces (the sum of all forces) of the fields on the robots are used to determine the robots’ motion and speed and the direction of travel while avoiding a collision.

APF is proved to be a good algorithm for obstacle avoidance and is employed for the formation problem. In a simulation based study, an algorithm was developed for formation control and obstacle avoidance using second-order consensus control and a modified APF method where both fixed and switching topology were considered [65]. In another paper, an APF approach was employed for the cooperative merging manoeuvre using a longitudinal control scheme [66]. In this study, a single controller was able to perform the different tasks such as vehicle following, gap closing, obstacle avoidance and platoon merging.

Formation generation through virtual nodes was proposed where a robot converges to virtual nodes under the velocity matching to attain formation [67]. In this study, a distributed formation control algorithms were proposed to guarantee the stability of the formation using a Lyapunov approach meaning that robots converge to a desired position under the velocity matching, thus maintaining the formation. In this paper, four algorithms were proposed for the formation control and they are formation connection control algorithm, collision avoidance algorithm, obstacle avoidance algorithm and target tracking algorithm. In formation connection control, the attractive force fields are created to drive free robots to move towards their desired positions. For collision avoidance, a local repulsive force field was created. For obstacle avoidance, the rotational force field was combined with the repulsive force field surrounding the obstacle to drive the robot to escape obstacles without collisions. For target tracking, a leader robot is selected based on minimum distance from target and then the leader leads the formation to track the moving target.

An adaptive approach for formation control of a swarm of multi-robots was proposed using a potential field method and artificial neural networks (ANN) [68]. In this study, three potential fields were considered: obstacle field, swarm robots field and target field as well as ANN were implemented to optimize the parameters of the potential field method. Another study proposed a distributed hybrid control architecture based on APF and MPC for the vehicle merge and platoon split operations [69]. In this method, an APF model was established capable of describing the mutual effect and collaboration between a vehicle and its surrounding environment and then an MPC controller incorporating APF was presented to accomplish the path planning and motion control synchronously.

A two-stage formation tracking controller was proposed for mobile robots with limited sensing ranges by incorporating bump functions with potential function and using the backstepping technique [70]. Here, robots’ heading and velocity were used as a control input for the task of position tracking and collision avoidance during the first stage and robots’ angular velocity was used as a control input to stabilize the error between the actual robot heading and its immediate value at the origin.

4.4. Flocking

Flocking describes the behaviour of a group of flying birds, schooling of fish or swarming behaviour of insects. Flocking control mainly includes three behaviours: collision avoidance also known as separation, velocity matching also known as alignment, and flock centering also known as cohesion [71]. Here, velocity matching is a vector quantity, referring to the combination of heading and speed. Collision avoidance is a separation behaviour to avoid overcrowding and collision with each other, whereas flock centering makes robots be near the center of the flock or nearby flockmates.

The flocking problem could be viewed as a subcase of the formation control problem, requiring robots to move together along some path in the aggregate, but with only minimal requirements for paths taken by specific robots [72]. Compared with flocking, formations are stricter, requiring robots to maintain certain relative positions as they move through the environment. Therefore, this section considers flocking and formation control for multiple mobile robot systems.

One paper established a connection between formation control and flocking behaviour for multiple nonholonomic kinematic agents using algebraic graph theory and Lyapunov stability analysis [73]. Here, it was shown that when inter-agent formation objectives cannot occur simultaneously in the state-space then, under certain assumptions, the agents’ velocity vectors and orientations converge to a common value at steady state, under the same control strategy that would lead to a feasible formation. Furthermore, using LaSalle’s invariance principle, it was proved that agents converge to the desired configuration and all agents have a common orientation.

Inspired from the flocking behaviour, an algorithm for nonholonomic vehicles was derived to realise the application of flocking control in structured environments such as roads and highways [74]. In this paper, a virtual vehicle was employed to linearise the nonholonomic car model and LaSalle’s invariance principles were utilized to prove the convergence of the entire system. Furthermore, simulation results showed that multiple cars were able to achieve steady formation. In another publication, a distributed formation control algorithm was proposed for a multiple wheeled mobile robot in a free space environment [75]. In this work, LaSalle’s invariance principles were used for the stability analysis. Moreover, simulation results showed that the proposed method can achieve a desired shape of the formation while keeping the same velocity and heading angle.

A single control architecture was derived for the formation control of mobile robots consisting of three controllers: path planning, flocking and formation controllers [76]. In this work, flocking provided the asymptotic stability for formation control and formation shape was achieved by a synchronizing velocity vector of individual vehicles. In another publication, considering the problem of decentralized flocking and global formation building of the group of wheeled robots, a randomized decentralized navigation algorithm was presented where autonomous vehicles move in the same direction with the same speed, thus forming a formation [77]. Here, each robot did not know a priori its position in the desired configuration, and the robots attained consensus on their positions via local information exchange. In this paper, a consensus for formation building was achieved through variables of speed, heading and mass centre of the formation.

4.5. Swarm Intelligence

Swarm robotics refers to the application of swarm intelligence techniques where a desired collective behaviour emerges from the local interactions of robots with one another and with their environment. Swarm intelligence has great potential for implementation in vehicular traffic of the CAVs due to their ability to control the group of robots. There are numbers of algorithms inspired by swarm intelligence. References in

Table 1. Theoretical detail of algorithms and their survey papers.

Algorithms	Algorithm Details	Survey Papers
Particle Swarm Optimization (PSO)	[78,79]	[80,81]
Ant Colony Optimization (ACO)	[82]	[83]
Artificial Bees Colony Optimization (ABCO)	[84,85]	[86]
Artificial Fish Swarm Algorithm (AFSA)	[87,88]	[89]
Bacteria Foraging Optimization (BFO)	[90]	[91]
Glowworm Swarm Optimization (GSO)	[92]	[93]
Firefly Algorithm (FA)	[94]	[95]
Bat Algorithm (BA)	[96]	[97]
Grey Wolf Optimizer (GWO)	[98]	[99]

include comprehensive detail on the original algorithms and their survey papers. Note that there are a modified, hybrid and advanced version of these basic algorithms and used in many fields besides mobile robotics. Each of these algorithms have their own mathematical models and can be assessed through references provided in Table 1.

4.5.1. Exploration and Exploitation

To achieve good performance from the algorithms, a balance between exploration and exploitation process is an important requirement that depends on algorithms’ parameters. Exploration is the process to explore the search space efficiently on a global scale, whereas exploration can generate the diverse solution far from the current solution [100,101]. The advantage of exploration is the ability to achieve global optimality and to avoid getting trapped in a local mode. The disadvantage of exploration is the slow convergence, and it is computationally expensive because many new solutions can be far from global optimality. On the other hand, exploitation is a local search process and uses local information; therefore, a new solution generated by the exploitation is better than the existing ones. The advantage of exploitation is the high convergence rate—however, at the cost of getting trapped in a local optimum. Therefore, more exploration and a little bit of exploitation results in a slow convergence and more exploitation and little bit of exploration results in a fast convergence, but chances of finding a true global optimality are low [100]. Thus, this balance depends on algorithm parameters setting and tuning as shown in

Table 2. The balance between exploration and exploitation can be handled by these parameters.

Algorithms	Algorithm Parameters
PSO	Inertia Weight, w
ACO	Pheromone evaporation rate (Good at exploring)
ABCO	Distance between food source (Good at exploring)
AFSA	Visual and step
BFO	Run length
GSO	Euclidean Distance
FA	Attractiveness (Good at exploring)
BA	Frequency, loudness and pulse emission rates
GWO	a and A

.

4.5.2. Swarm Intelligence and Formation Control

A piece of literature on the implementation of swarm intelligence based algorithms in robot formation control is limited. PSO is one of the first algorithms and implemented most compared to other swarm intelligence based algorithms. A formation and coordination task was carried out using PSO where ground robots were simulated for the forest fire scenario [102]. Here, the simulation results showed that, with an adequate set of parameters, it was possible to get satisfactory strategic positions for a multi-robot system’s operation using PSO. Moreover, cooperative PSO and distributed receding horizon control (RHC) scheme were incorporated for multi-robot formation control in which robots were able to track a reference trajectory while maintaining formation [103].

In another publication, a distributed MPC scheme incorporating cooperative PSO was proposed for multi-robot formation control problem [104]. In this study, the Nash equilibrium strategy was considered and robots were able to track the reference path while maintaining the triangle formation. Furthermore, a hybrid approach of control parametrization and time discretization (CPTD) and PSO was proposed for formation reconfiguration of multiple wheeled robots [105]. In this study, a group of three ground robots were tested for the proposed algorithm.

A research was conducted on the intelligent vehicle navigation problems for path planning and vehicle guiding to the target position [106]. In this work, a vehicle dynamic method and PSO were employed for the testing of behaviour coordination problems such as lane keeping, lane changing and overtaking. Moreover, a cooperative driving and vehicle platooning problem were addressed using PSO by proposing algorithms for platoon reorganisation and platoon control [107]. In this article, vehicles can choose to accelerate to join in the preceding platoon or decelerate to depart from the current platoon.

A distributed and dynamic graph-based formation control approach was presented for vehicles to join, leave, or change lanes without affecting the stability of the convoy. Here, PSO was implemented to optimize the parameters of the control law (lane keeping and obstacle avoidance) and to reduce the overall formation control errors [108]. In this paper, a vision sensor was used for the lane keeping and LIDAR was used for the obstacle avoidance. In another study, a consensus algorithm and PSO were employed to maintain formation and explore the unknown static environment [109]. Here, a consensus algorithm was based on graph theory, and positions were shared to achieve consensus.

ACO was used to address the reformation problem in the multi-agent system in which recursion algorithm was proposed to reduce the distance travelled by each agent during reformation process [110]. Moreover, ACO was implemented for the formation control of swarm robots by implementing ants and pheromone level as software agents [111,112,113]. Here, the first agent calculates the location of the conceptual barycentre of the formation and all the locations for the robots to occupy, whereas the second agent physically drives the robots to the locations to compose the formation.

In a comparative study, a formation control and obstacle avoidance problems were studied using BFO and PSO in which BFO resulted in good formation performance with low computation time and PSO produced optimal trajectory but avoided the formation [114]. BA was used for the formation reconfiguration of multi-robot systems in which the CPTD method was applied to convert time optimal formation reconfiguration problem into a parameter optimization problem [115]. Here, BA was used to get the control law. In this study, a comparison was made between three different methods: BA-CPTD, CPTD and line-of-sight in which BA-CPTD was able to derive a better result.

In another study, inspired from the swarm intelligence, a decentralized platooning concept was proposed for CAV platooning where a spring-mass-damper system was considered for platoon formation and evolution [116]. In this study, a platoon formation was achieved via three zones: attractive, alignment and repulsion zone.

5. Virtual Structure Approach

5.1. Basic Principles

A virtual structure approach is targeted to address the problem of maintenance of a geometric configuration during movement in cooperative robotics. As per [117], a virtual structure is a collection of elements, e.g., robots, which maintain a (semi) rigid geometric relationship to each other and to a frame of reference. The merit of virtual structure approach can be described as follows [117]:

• Capability of achieving high-precision control.
• Inherently fault tolerant during the failure of robots by maintaining formation.
• No need to elect leader robot.
• Reconfigurable for different kinds of virtual structures with no modification.
• Can be implemented in a distributed fashion with no increase in communications from a centralized implementation.
• No explicit functional decomposition.

Inspired form the above-mentioned centralized method, a decentralized virtual structure approach was proposed to achieve the following characteristics [7]:

• A decentralized framework for a large number of agents/robots and for a strict limitation on inter-vehicle communication.
• Integration of formation feedback in the framework to improve group robustness.
• Ability to prescribe a group manoeuvre directly in the framework.
• A framework to guarantee high precision for maintaining formation during manoeuvre.

In this decentralized approach, each robot in the formation instatiates a local copy of the coordination vector in the virtual structure framework. The local instatiation of the coordination vector in each robot is then synchronized by communication with its neighbours using a bidirectional ring topology. Regarding consensus in a decentralized virtual structure approach, it is said to be reached on each instantiation of the virtual structure states and the information flow forms a bidirectional ring topology [20].

5.2. Virtual Structure Controllers

A vehicle convoy is formed when multiple CAVs collaborate over multiple lanes by maintaining a pre-designed formation. To control this type of convoy, a virtual structure approach was adopted by separating the convoy control problem into a high-level virtual structure control problem and a low-level vehicle control problem [118]. Here, the MPC controller was developed to generate reference trajectories by considering longitudinal and lateral offsets and a nonlinear MPC controller was implemented for autonomous driving by integrating lane-keeping and collision avoidance behaviours. Another publication proposed the architecture of adaptable virtual structure formation control by developing a formation tracking controller for the nonholonomic mobile robots to track the time-varying formation configurations [119]. In this work, two controllers were derived, a tracking controller to achieve stable tracking control performance during the transitions between two formation configurations and a formation controller to generate online formation reference and make robots converge to a given formation pose.

A stabilising control method was proposed using the flexible virtual structure approach that ensured the non-collision among the agents in formation and preserved a desired shape configuration [120]. In this work, three control laws were used to perform multi-robot navigation, a formation keeping and inter-robot collision avoidance law, an attractive control law to guarantee the convergence to the desired final configuration and an obstacle avoidance law. Moreover, a controller was developed to solve the problem of formation control of multiple wheeled mobile robots by guaranteeing that the derivative of the Lyapunov candidate is a negative definite meaning that the controller is robust against to disturbances [121]. In this work, a triangular formation was achieved on a circular track using three robots.

A formation control strategy was proposed for nonholonomic intelligent vehicles based on virtual structures approach and consensus technique [122]. Here, formation control was achieved by employing target tracking and formation tracking strategies. A target tracking strategy was responsible for tracking the target points of the virtual structure and formation control strategy was responsible for tracking the trajectory by collecting velocity and pose messages. The developed controller was able to improve the convergence speed and increase the stability of the system by employing the leader-following consensus protocol.

6. Remaining Challenges

6.1. Technical Challenges

Here, several technical challenges are presented that needs to be solved to implement the CAV technology. These challenges play a vital role when developing algorithms for the collaboration between the autonomous vehicles.

6.1.1. Communication

A wireless communication is a critical factor in CAV operation. Usually, a vehicle transmits messages containing speed data, sensor readings and current position to other vehicles and this is done using broadcasting or multicasting and by employing handshaking protocol. A wireless communication can increase errors due to not transmitting and receiving messages on time. Furthermore, a wrong message received at the wrong time can result in the error. So far, the problems with communication between autonomous vehicles have included missing messages, wrong messages, garbage contents, failure of the communication device, and delay in transmission. To solve this problem, a communication topology should be targeted towards connecting at least two vehicles during poor bandwidth or bad weather. Furthermore, sensors can be used to guide vehicles during complete communication loss such as sensor-based navigation.

6.1.2. Error Accumulation

An error can increase when transmitting messages to other vehicles. If a vehicle has a noisy, false positive or false negative sensory data, then it will get transmitted to the second vehicle. The second vehicle will add its own noisy, false positive or false negative sensory data and will transmit to the third one. This results in an error accumulation thus coordination between autonomous vehicles cannot be achieved. One way to minimize the error accumulation would be to compare vehicle’s sensor data with other vehicles’ sensor data and to use string stability analysis.

6.1.3. Deadlock and Livelock

A deadlock and livelock situation may arise during the behaviour-based navigation of multiple autonomous vehicles [123,124]. A deadlock refers to an autonomous vehicle transition when few or many robots are unable to move physically. In this situation, an autonomous vehicle has outstanding operations to complete, but no operation can make progress. Deadlock can arise at the intersections or to avoid a collision when each operation has acquired a shared resource (a free lane to move) that another operation needs. Therefore, no vehicle can move since all vehicles are waiting for a shared resource which is being held by another vehicle. A livelock is similar to a deadlock situation. In this situation, robots move to allocate shared resource but fall back to the same situation repeatedly, thus making no meaningful progress. A livelock can arise at the intersections where all vehicles keep moving back and forth by staying at the same location. Therefore, a resultant algorithm should be able to address these issues.

6.1.4. Limit on Maximum Scalability

The maximum scalability refers to the number of maximum autonomous vehicles any multi-robot system or network can employ. The multi-robot algorithms must be scalable, but a limit on the scalability should be considered as an important parameter. This limit can have a significant impact on the working principles of the CAVs. A higher limit can impose significant drawbacks such as:

• Communication loss or delay due to a time taken for a signal or message to transmit in a large vehicular network.
• Errors accumulation as explained above.
• Higher time to derive decision (consensus control) at every situation and moment.

Moreover, setting an upper limit will create multiple multi-robot systems interacting with each other. These systems should be able to work together by cooperating with each other.

6.1.5. Cybersecurity

A security of such networks is another challenge that needs to be solved. Basically, CAVs are a collection of networked sensors and computers connected wirelessly to other vehicles and infrastructure; therefore, this network must be safe from online attacks by the intruders or hackers.

6.2. Implementation Challenges

Here, several implementation challenges are presented that needs to be addressed for the CAV operation. These challenges play a vital role when evaluating developed algorithms for the autonomous vehicles.

6.2.1. Platoon Formation

A platoon based formation control is useful when vehicles need to maintain distance from each other and in the traffic conditions. A dynamic platooning should be targeted by addressing several scenarios such as:

• If any vehicle leaves the formation or joins another platoon, other vehicles should rearrange their position to maintain the formation by feeling the gap in the formation.
• If a leader leaves the platoon, then it should not affect the formation but a subsequent vehicle inside the platoon should take the role of the leader.
• This platoon based formation can also have a fixed number of vehicles that can be allowed and, if the number increases, then another platoon should be created for autonomous vehicles.
• The above discussed problems can be extended to the multi-lane platoon and two-way traffic platoon formation.
• Moreover, different platoons and vehicles inside the platoon should share information with each other. This is helpful for other vehicles to join another platoon.

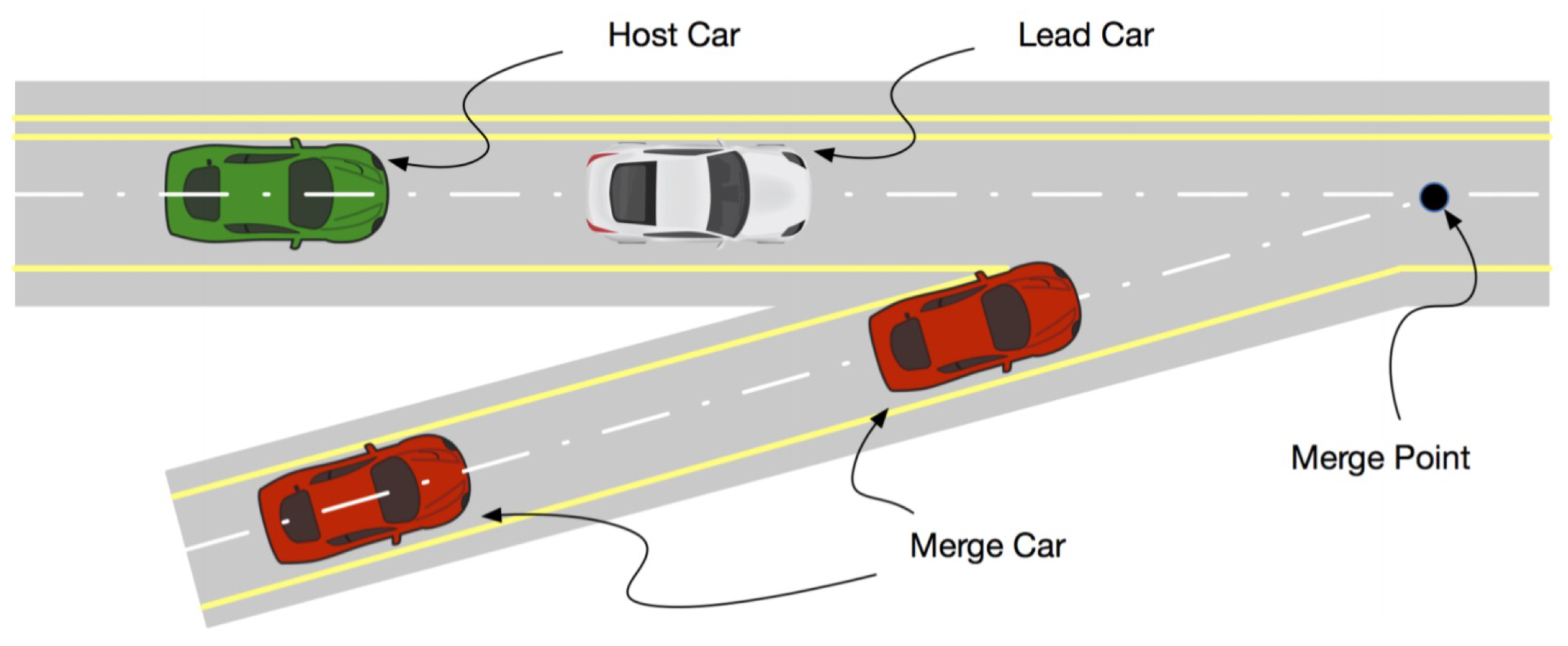
6.2.2. Lane Merge and Change

Lane merging and changing of the vehicles is another key area to target which requires cooperation between vehicles in uncoordinated traffic environment as shown in Figure 5. For these operations, estimating other vehicles’ intention and information sharing between vehicles plays a vital role.

6.2.3. Emergency Vehicle Response

Giving way to emergency vehicles such as ambulances and police vehicles is another challenge that requires developing specific controllers for autonomous vehicles. If these vehicles encounter existing vehicle formations, then what should be the behaviour of the formation and vehicles inside the formations. Currently, human drivers stop by the side and give way to emergency vehicles. This same behaviour needs to be implemented for the CAVs.

6.2.4. Intersection Management

All CAVs need to face various intersections, roundabouts or junctions during their journey. These junctions can have different structures as shown in Figure 6. Vehicles arriving and leaving at these intersections should cooperate at the intersection crossing by deciding which vehicle should leave first. Furthermore, traffic during the intersection crossing would be higher; therefore, deadlock and livelock situations need to be addressed for this scenario. Regarding the vehicle formation, some vehicles might join new roads as per their destinations; therefore, new platoons should be formed just after crossing the intersection.

7. Conclusions

In this paper, many academic publications are reviewed to understand the current developments on CAV technology, including controller design and stability analysis. The leader–follower approach is found to be used by many researchers for the vehicle platooning problem. A second-order consensus control is widely targeted to reach the consensus, whereas third-order consensus control is a growing field. Furthermore, the string stability theorem is used to evaluate the platoon formation performance. It can be observed that simulation work is completed to prove the derived controllers and theories and few publications target actual implementation on mobile robots.

Moreover, the challenges discussed in this paper require extensive testing before implementing the CAV technology for general uses. Whatever approach one chooses to implement out of these discussed methods, these challenges remains the same and need to be solved. On the other hand, the application challenges provide a good ground to analyse the developed algorithms. After reviewing the vehicle formation control field using several approaches, it can be concluded that:

• Few controllers and algorithms in a leader–follower approach targets third-order consensus control and real robot experiments. Furthermore, a dynamic role changing leader should be targeted in a leader–follower approach.
• Considering the swarm intelligence based algorithms, it can be observed that they can handle a population of robots, but they do not offer formation control ability; therefore, new parameters or another algorithm should be implemented along with these algorithms.
• A machine learning approach is not applied to the formation control problem compared to other techniques and deep learning remains unexplored for multi-robot formation control problems.