Robot Learning from Demonstration in Robotic Assembly: A Survey
Abstract
:1. Introduction
1.1. Robotic Assembly
1.2. Learning from Demonstration
1.3. Outline
2. Research Problems in Robotic Assembly
2.1. Pose Estimation
2.2. Force Estimation
2.3. Assembly Sequence
2.4. Assembly with Screwing
3. Demonstration Approach
3.1. Kinesthetic Demonstration
3.2. Motion-Sensor Demonstration
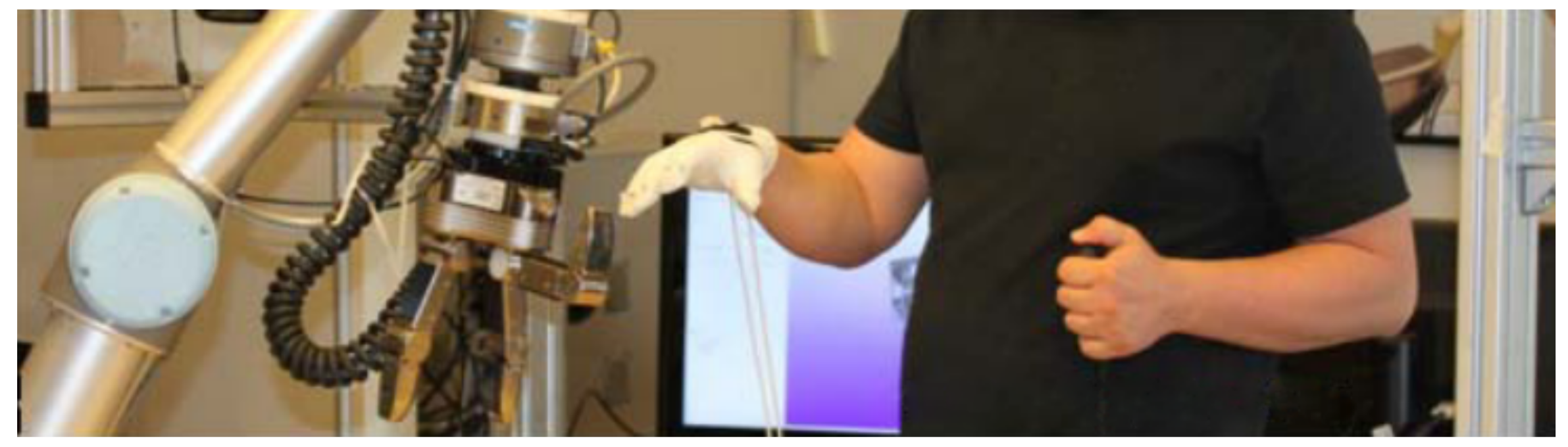
3.3. Teleoperated Demonstration
4. Feature Extraction
4.1. Hidden Markov Models
4.2. Dynamic Movement Primitives
4.3. Gaussian Mixture Models
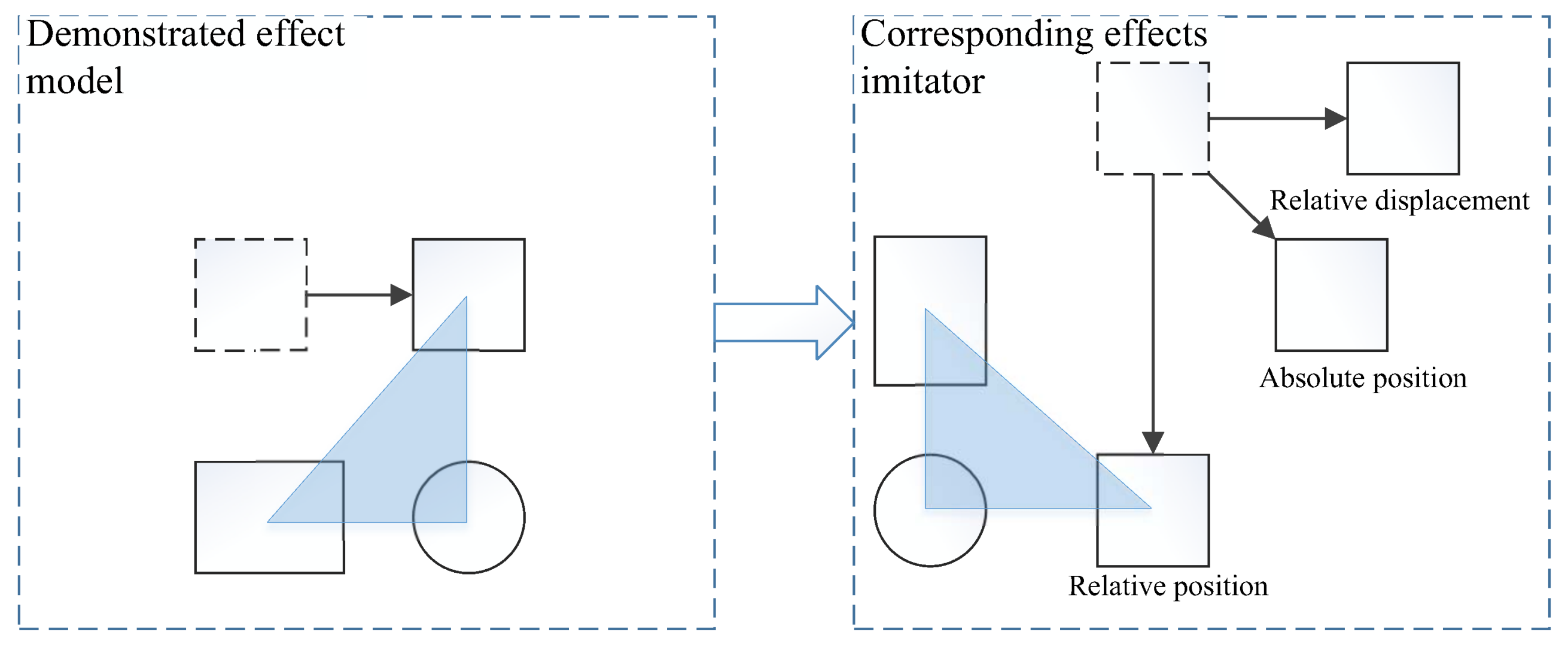
5. Metric of Imitation Performance
5.1. Weighted Similarity Measure
5.2. Generic Similarity Measure
5.3. Combination of Metrics
6. Conclusions and Discussion
- Learning from insufficient data. LfD aims at providing non-experts an easy way to teach robots practical skills, although usually, the quantity of demonstrations is not numerous. However, the demonstration in robotic assembly may contain noise. Due to the lack of some movement features and the intuitive nature of interacting with human demonstrators, it becomes hard for the non-expert users to use LfD. Requiring non-experts to demonstrate one movement in a repetitive way is not a good solution. Future research work on how to generalize through a limited number of feature samples is needed.
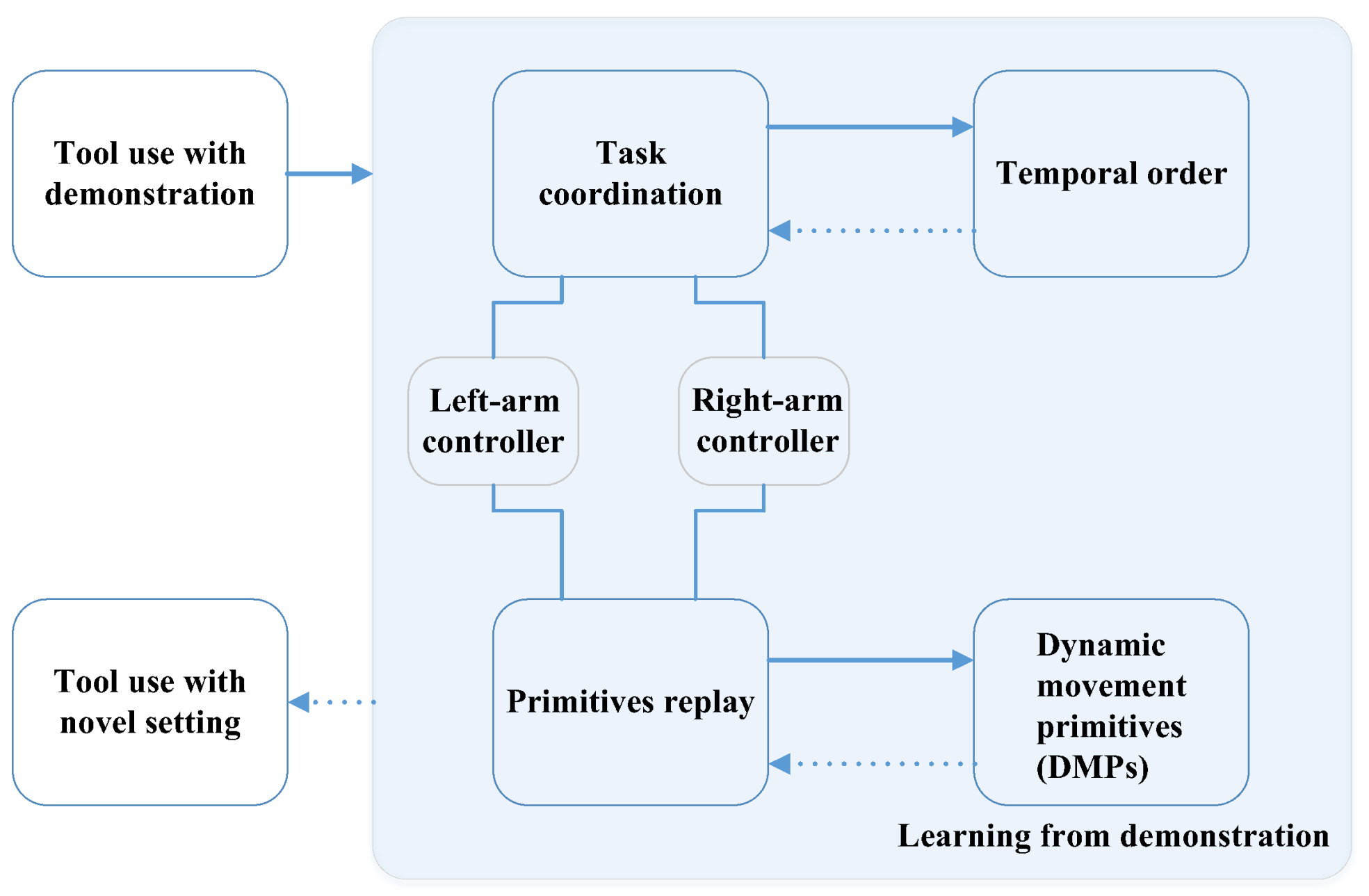
- Incremental learning. The robot can learn a skill from a demonstrator, or learn several skills from different demonstrations. The study on incremental learning is still very limited during the past research. The skills that the robot has learned are parallel, not progressive or incremental. DMPs are fundamental learning blocks that can be used to learn more advanced skills, while these skills cannot be used to learn more complicated skills. Incremental learning features should be given more attention for robotic assembly in the future research.
- Effective demonstration. When the demonstrator executes any assembly actions, the robot tries to extract the features from the demonstration. In most cases, the learning process is unidirectional, lacking timely revision, leading to less effective learning. The most popular approaches adopted in LfD systems are reward functions. However, the reward functions only give the evaluation of the given state, and no desirable information on which demonstration can be selected as the best example. One promising solution is that the human demonstrator provides timely feedback (for example, through a GUI [19]) on the robot’s actions. More research on how to provide such effective feedback information is another aspect of future work.
- Fine assembly. Robotics assembly aims at enormously promoting industry productivity and helping workers on highly repeated tasks, especially in ’light’ industries, such as the assembly of small parts. The robots have to be sophisticated enough to handle more complicated and more advanced tasks instead of being limited to the individual subskills of assembly, such as inserting, rotating, screwing and so on. Future research work on how to combine the subskills into smooth assembly skills is desired.
- Improved evaluation. A standardized set of evaluation metrics is a fundamentally important research area for future work. Furthermore, improved evaluation metrics help the learning process of imitation by providing a more accurate and effective goal in LfD. The formalization of evaluation criteria would also facilitate the research and development of the extended general-purpose learning systems in robotic assembly.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. HMM
- Hidden state SThe states (for example, ) are the actual hidden states in HMM which satisfy the Markov characteristics and cannot be directly observed.
- Observable state OThe observable state O is associated with the hidden state and can be directly observed. (For example, and so on, the number of observable states is not necessarily the same as hidden states.)
- Initial state probability matrixis the probability matrix of hidden state at the initial moment . (For example, given , , , then the initial state probability matrix .)
- Hidden state transition probability matrix AMatrix A defines the transition probabilities between different states of HMM, where , which means given the time t and state , the state is with probability P at time .
- Observable state transition probability matrix BAssume that N is the number of hidden states, and M is the number of observable states, then: , which means that given the time t and hidden state , the observed state is with probability P.
Appendix A.2. DMP
Appendix A.3. GMM
References
- Krüger, J.; Lien, T.K.; Verl, A. Cooperation of human and machines in assembly lines. CIRP Ann.-Manuf. Technol. 2009, 58, 628–646. [Google Scholar] [CrossRef]
- Hu, S.; Ko, J.; Weyand, L.; ElMaraghy, H.; Lien, T.; Koren, Y.; Bley, H.; Chryssolouris, G.; Nasr, N.; Shpitalni, M. Assembly system design and operations for product variety. CIRP Ann. 2011, 60, 715–733. [Google Scholar] [CrossRef]
- Knepper, R.A.; Layton, T.; Romanishin, J.; Rus, D. IkeaBot: An autonomous multi-robot coordinated furniture assembly system. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 855–862. [Google Scholar] [CrossRef]
- Suárez-Ruiz, F.; Pham, Q.C. A framework for fine robotic assembly. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 421–426. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, L.; Song, Y.; Nemec, B.; Ude, A.; Buch, A.G.; Krüger, N.; Savarimuthu, T.R. Fast programming of Peg-in-hole Actions by human demonstration. In Proceedings of the 2014 International Conference on Mechatronics and Control (ICMC), Jinzhou, China, 3–5 July 2014; pp. 990–995. [Google Scholar] [CrossRef]
- Kramberger, A.; Gams, A.; Nemec, B.; Chrysostomou, D.; Madsen, O.; Ude, A. Generalization of orientation trajectories and force–torque profiles for robotic assembly. Robot. Auton. Syst. 2017, 98, 333–346. [Google Scholar] [CrossRef]
- Kim, Y.L.; Song, H.C.; Song, J.B. Hole detection algorithm for chamferless square peg-in-hole based on shape recognition using F/T sensor. Int. J. Precis. Eng. Manuf. 2014, 15, 425–432. [Google Scholar] [CrossRef]
- Kramberger, A.; Piltaver, R.; Nemec, B.; Gams, M.; Ude, A. Learning of assembly constraints by demonstration and active exploration. Ind. Robot Int. J. 2016, 43, 524–534. [Google Scholar] [CrossRef]
- Nottensteiner, K.; Sagardia, M.; Stemmer, A.; Borst, C. Narrow passage sampling in the observation of robotic assembly tasks. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 130–137. [Google Scholar] [CrossRef]
- Jain, R.K.; Majumder, S.; Dutta, A. SCARA based peg-in-hole assembly using compliant IPMC micro gripper. Robot. Auton. Syst. 2013, 61, 297–311. [Google Scholar] [CrossRef]
- Abu-Dakka, F.J.; Nemec, B.; Kramberger, A.; Buch, A.G.; Krüger, N.; Ude, A. Solving peg-in-hole tasks by human demonstration and exception strategies. Ind. Robot Int. J. 2014, 41, 575–584. [Google Scholar] [CrossRef]
- Tang, T.; Lin, H.C.; Zhao, Y.; Fan, Y.; Chen, W.; Tomizuka, M. Teach industrial robots peg-hole-insertion by human demonstration. In Proceedings of the 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 488–494. [Google Scholar] [CrossRef]
- Savarimuthu, T.R.; Buch, A.G.; Schlette, C.; Wantia, N.; Rossmann, J.; Martinez, D.; Alenya, G.; Torras, C.; Ude, A.; Nemec, B. Teaching a Robot the Semantics of Assembly Tasks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 1–23. [Google Scholar] [CrossRef]
- Nemec, B.; Abu-Dakka, F.J.; Ridge, B.; Ude, A.; Jorgensen, J.A.; Savarimuthu, T.R.; Jouffroy, J.; Petersen, H.G.; Kruger, N. Transfer of assembly operations to new workpiece poses by adaptation to the desired force profile. In Proceedings of the 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 November 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Peternel, L.; Petrič, T.; Babič, J. Robotic assembly solution by human-in-the-loop teaching method based on real-time stiffness modulation. Autonom. Robots 2018, 42, 1–17. [Google Scholar] [CrossRef]
- Laursen, J.S.; Schultz, U.P.; Ellekilde, L.P. Automatic error recovery in robot-assembly operations using reverse execution. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1785–1792. [Google Scholar] [CrossRef]
- Laursen, J.S.; Ellekilde, L.P.; Schultz, U.P. Modelling reversible execution of robotic assembly. Robotica 2018, 1–30. [Google Scholar] [CrossRef]
- Dogar, M.; Spielberg, A.; Baker, S.; Rus, D. Multi-robot grasp planning for sequential assembly operations. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 193–200. [Google Scholar] [CrossRef]
- Mollard, Y.; Munzer, T.; Baisero, A.; Toussaint, M.; Lopes, M. Robot programming from demonstration, feedback and transfer. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1825–1831. [Google Scholar] [CrossRef]
- Wan, W.; Harada, K. Integrated assembly and motion planning using regrasp graphs. Robot. Biomim. 2016, 3, 18. [Google Scholar] [CrossRef] [PubMed]
- Lambrecht, J.; Kleinsorge, M.; Rosenstrauch, M.; Krüger, J. Spatial programming for industrial robots through task demonstration. Int. J. Adv. Robot. Syst. 2013, 10, 254. [Google Scholar] [CrossRef]
- Thorndike, E.L. Animal Intelligence. Experimental Studies; Macmillan: London, UK, 1911; Volume 39, p. 357. [Google Scholar] [CrossRef]
- Bakker, P.; Kuniyoshi, Y. Robot see, robot do: An overview of robot imitation. In Proceedings of the AISB96 Workshop on Learning in Robots and Animals, Kobe, Japan, 12–17 May 2009; pp. 3–11. [Google Scholar]
- Rozo, L.; Jiménez, P.; Torras, C. A robot learning-from-demonstration framework to perform force-based manipulation tasks. Intell. Serv. Robot. 2013, 6, 33–51. [Google Scholar] [CrossRef] [Green Version]
- Mataric, M.J. Getting humanoids to move and imitate. IEEE Intell. Syst. Their Appl. 2000, 15, 18–24. [Google Scholar] [CrossRef]
- Billard, A.; Calinon, S.; Dillmann, R.; Schaal, S. Robot Programming by Demonstration. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1371–1394. [Google Scholar] [CrossRef]
- Pastor, P.; Hoffmann, H.; Asfour, T.; Schaal, S. Learning and generalization of motor skills by learning from demonstration. In Proceedings of the ICRA’09. IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 763–768. [Google Scholar] [CrossRef]
- Krüger, N.; Ude, A.; Petersen, H.G.; Nemec, B.; Ellekilde, L.P.; Savarimuthu, T.R.; Rytz, J.A.; Fischer, K.; Buch, A.G.; Kraft, D. Technologies for the fast set-up of automated assembly processes. KI-Künstliche Intell. 2014, 28, 305–313. [Google Scholar] [CrossRef]
- Aleotti, J.; Caselli, S.; Reggiani, M. Toward programming of assembly tasks by demonstration in virtual environments. In Proceedings of the 12th IEEE International Workshop on Robot and Human Interactive Communication, Millbrae, CA, USA, 2 November 2003; pp. 309–314. [Google Scholar] [CrossRef]
- Suomalainen, M.; Kyrki, V. A geometric approach for learning compliant motions from demonstration. In Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots, Birmingham, UK, 15–17 November 2017; pp. 783–790. [Google Scholar] [CrossRef]
- Stenmark, M.; Topp, E.A. From demonstrations to skills for high-level programming of industrial robots. In AAAI Fall Symposium Series: Artificial Intelligence for Human-Robot Interaction; AAAI: Arlington, VA, USA, 2016; pp. 75–78. [Google Scholar]
- Takamatsu, J.; Ogawara, K.; Kimura, H.; Ikeuchi, K. Recognizing assembly tasks through human demonstration. Int. J. Robot. Res. 2007, 26, 641–659. [Google Scholar] [CrossRef]
- Rozo, L.; Calinon, S.; Caldwell, D.; Jiménez, P.; Torras, C. Learning collaborative impedance-based robot behaviors. In Proceedings of the Twenty-Seventh AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 11–18 July 2013; Volume 1, p. 1. [Google Scholar]
- Dantam, N.; Essa, I.; Stilman, M. Linguistic transfer of human assembly tasks to robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 237–242. [Google Scholar] [CrossRef]
- Argall, B.D.; Chernova, S.; Veloso, M.; Browning, B. A survey of robot learning from demonstration. Robot. Auton. Syst. 2009, 57, 469–483. [Google Scholar] [CrossRef]
- Liu, Q.; Li, R.; Hu, H.; Gu, D. Extracting semantic information from visual data: A survey. Robotics 2016, 5, 8. [Google Scholar] [CrossRef]
- Choi, C.; Taguchi, Y.; Tuzel, O.; Liu, M.Y.; Ramalingam, S. Voting-based pose estimation for robotic assembly using a 3D sensor. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 1724–1731. [Google Scholar] [CrossRef]
- Zeng, A.; Yu, K.T.; Song, S.; Suo, D.; Walker, E.; Rodriguez, A.; Xiao, J. Multi-view self-supervised deep learning for 6d pose estimation in the amazon picking challenge. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, Singapore, 29 May–3 June 2017; pp. 1383–1386. [Google Scholar] [CrossRef]
- Schmitt, R.; Cai, Y. Recognition of dynamic environments for robotic assembly on moving workpieces. Int. J. Adv. Manuf. Technol. 2014, 71, 1359–1369. [Google Scholar] [CrossRef]
- Sarić, A.; Xiao, J.; Shi, J. Reducing uncertainty in robotic surface assembly tasks based on contact information. In Proceedings of the IEEE Workshop on Advanced Robotics and its Social Impacts (ARSO), Evanston, IL, USA, 11–13 September 2014; pp. 94–100. [Google Scholar] [CrossRef]
- Likar, N.; Nemec, B.; Žlajpah, L.; Ando, S.; Ude, A. Adaptation of bimanual assembly tasks using iterative learning framework. In Proceedings of the IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, South Korea, 3–5 November 2015; pp. 771–776. [Google Scholar] [CrossRef]
- Wahrburg, A.; Zeiss, S.; Matthias, B.; Ding, H. Contact force estimation for robotic assembly using motor torques. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Taipei, Taiwan, 18–22 August 2014; pp. 1252–1257. [Google Scholar] [CrossRef]
- Jasim, I.F.; Plapper, P.W. Contact-state modeling of robotic assembly tasks using Gaussian mixture models. Procedia CIRP 2014, 23, 229–234. [Google Scholar] [CrossRef]
- Stolt, A.; Linderoth, M.; Robertsson, A.; Johansson, R. Force controlled robotic assembly without a force sensor. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 1538–1543. [Google Scholar] [CrossRef]
- Suomalainen, M.; Kyrki, V. Learning compliant assembly motions from demonstration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, South Korea, 9–14 October 2016; pp. 871–876. [Google Scholar] [CrossRef]
- Navarro-Gonzalez, J.; Lopez-Juarez, I.; Rios-Cabrera, R.; Ordaz-Hernández, K. On-line knowledge acquisition and enhancement in robotic assembly tasks. Robot. Comput.-Integr. Manuf. 2015, 33, 78–89. [Google Scholar] [CrossRef]
- Peternel, L.; Petric, T.; Babic, J. Human-in-the-loop approach for teaching robot assembly tasks using impedance-control interface. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1497–1502. [Google Scholar] [CrossRef]
- Bahubalendruni, M.R.; Biswal, B.B.; Kumar, M.; Nayak, R. Influence of assembly predicate consideration on optimal assembly sequence generation. Assem. Autom. 2015, 35, 309–316. [Google Scholar] [CrossRef]
- Liang, Y.S.; Pellier, D.; Fiorino, H.; Pesty, S. Evaluation of a Robot Programming Framework for Non-Experts using Symbolic Planning Representations. In Proceedings of the 26th IEEE International Symposium on Robot and Human Interactive Communication, Lisbon, Portugal, 28 August 2017. [Google Scholar] [CrossRef]
- Hersch, M.; Guenter, F.; Calinon, S.; Billard, A. Dynamical System Modulation for Robot Learning via Kinesthetic Demonstrations. IEEE Trans. Robot. 2008, 24, 1463–1467. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Reinforcement learning of motor skills with policy gradients. Neural Netw. 2008, 21, 682–697. [Google Scholar] [CrossRef] [PubMed]
- Mistry, M.; Mohajerian, P.; Schaal, S. An exoskeleton robot for human arm movement study. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 4071–4076. [Google Scholar] [CrossRef]
- Albu-Schäffer, A.; Ott, C.; Hirzinger, G. A Unified Passivity-based Control Framework for Position, Torque and Impedance Control of Flexible Joint Robots. Int. J. Robot. Res. 2007, 26, 23–39. [Google Scholar] [CrossRef]
- Hyon, S.H.; Hale, J.G.; Cheng, G. Full-Body Compliant Human–Humanoid Interaction: Balancing in the Presence of Unknown External Forces. IEEE Trans. Robot. 2007, 23, 884–898. [Google Scholar] [CrossRef]
- Calinon, S.; Guenter, F.; Billard, A. On learning the statistical representation of a task and generalizing it to various contexts. In Proceedings of the International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; Volume 37, pp. 2978–2983. [Google Scholar] [CrossRef]
- Calinon, S.; Guenter, F.; Billard, A. On Learning, Representing, and Generalizing a Task in a Humanoid Robot. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2007, 37, 286–298. [Google Scholar] [CrossRef]
- Ye, G.; Alterovitz, R. Demonstration-Guided Motion Planning. Springer Tracts Adv. Robot. 2017, 291–307. [Google Scholar] [CrossRef]
- Li, W.; Fritz, M. Teaching robots the use of human tools from demonstration with non-dexterous end-effectors. In Proceedings of the IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, South Korea, 3–5 November 2015; pp. 547–553. [Google Scholar] [CrossRef]
- Moeslund, T.B.; Hilton, A.; Krüger, V. A survey of advances in vision-based human motion capture and analysis. Comput. Vis. Image Underst. 2006, 104, 90–126. [Google Scholar] [CrossRef]
- Riley, M.; Ude, A.; Atkeson, C.G. Methods for motion generation and interaction with a humanoid robot: Case studies of dancing and catching. In Proceedings of the Workshop Interactive Robot and Entertainment, Pittsburgh, PA, USA, 30 April–1 May 2000; pp. 35–42. [Google Scholar]
- Pollard, N.S.; Hodgins, J.K.; Riley, M.J.; Atkeson, C.G. Adapting human motion for the control of a humanoid robot. In Proceedings of the ICRA’02 IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 2, pp. 1390–1397. [Google Scholar] [CrossRef]
- Ude, A.; Atkeson, C.G.; Riley, M. Programming full-body movements for humanoid robots by observation. Robot. Auton. Syst. 2004, 47, 93–108. [Google Scholar] [CrossRef]
- Ruchanurucks, M.; Nakaoka, S.; Kudoh, S.; Ikeuchi, K. Humanoid robot motion generation with sequential physical constraints. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA, Orlando, FL, USA, 15–19 May 2006; pp. 2649–2654. [Google Scholar] [CrossRef]
- Skoglund, A.; Iliev, B.; Palm, R. Programming-by-Demonstration of reaching motions—A next-state-planner approach. Robot. Auton. Syst. 2010, 58, 607–621. [Google Scholar] [CrossRef]
- Acosta-Calderon, C.A.; Hu, H. Robot imitation: Body schema and body percept. Appl. Bionics Biomech. 2005, 2, 131–148. [Google Scholar] [CrossRef]
- Kulić, D.; Ott, C.; Lee, D.; Ishikawa, J.; Nakamura, Y. Incremental learning of full body motion primitives and their sequencing through human motion observation. Int. J. Robot. Res. 2012, 31, 330–345. [Google Scholar] [CrossRef]
- Kulic, D.; Nakamura, Y. Scaffolding online segmentation of full body human-motion patterns. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS, Nice, France, 22–26 September 2008; pp. 2860–2866. [Google Scholar] [CrossRef]
- Kuklinski, K.; Fischer, K.; Marhenke, I.; Kirstein, F.; aus der Wieschen, M.V.; Solvason, D.; Kruger, N.; Savarimuthu, T.R. Teleoperation for learning by demonstration: Data glove versus object manipulation for intuitive robot control. In Proceedings of the 6th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), St. Petersburg, Russia, 6–8 October 2014; pp. 346–351. [Google Scholar] [CrossRef]
- Edmonds, M.; Gao, F.; Xie, X.; Liu, H.; Qi, S.; Zhu, Y.; Rothrock, B.; Zhu, S.C. Feeling the force: Integrating force and pose for fluent discovery through imitation learning to open medicine bottles. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar] [CrossRef]
- Tzafestas, C.S. Teleplanning by human demonstration for VR-based teleoperation of a mobile robotic assistant. In Proceedings of the 10th IEEE International Workshop on Robot and Human Interactive Communication, Paris, France, 18–21 September 2001; pp. 462–467. [Google Scholar] [CrossRef]
- Chong, N.Y.; Kotoku, T.; Ohba, K.; Komoriya, K.; Tanie, K. Exploring interactive simulator in collaborative multi-site teleoperation. In Proceedings of the 10th IEEE International Workshop on Robot and Human Interactive Communication, Paris, France, 18–21 September 2001; pp. 243–248. [Google Scholar] [CrossRef]
- Makiishi, T.; Noborio, H. Sensor-based path-planning of multiple mobile robots to overcome large transmission delays in teleoperation. In Proceedings of the 1999 IEEE International Conference on Systems, Man, and Cybernetics, Tokyo, Japan, 12–15 October 1999; Volume 4, pp. 656–661. [Google Scholar] [CrossRef]
- Chen, J.; Zelinsky, A. Programing by Demonstration: Coping with Suboptimal Teaching Actions. Int. J. Robot. Res. 2003, 22, 299–319. [Google Scholar] [CrossRef]
- Bohren, J.; Papazov, C.; Burschka, D.; Krieger, K.; Parusel, S.; Haddadin, S.; Shepherdson, W.L.; Hager, G.D.; Whitcomb, L.L. A pilot study in vision-based augmented telemanipulation for remote assembly over high-latency networks. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3631–3638. [Google Scholar] [CrossRef]
- Argall, B.D.; Browning, B.; Veloso, M. Learning robot motion control with demonstration and advice-operators. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 399–404. [Google Scholar] [CrossRef]
- Sweeney, J.D.; Grupen, R. A model of shared grasp affordances from demonstration. In Proceedings of the 7th IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 27–35. [Google Scholar] [CrossRef]
- Calinon, S.; Evrard, P.; Gribovskaya, E.; Billard, A.; Kheddar, A. Learning collaborative manipulation tasks by demonstration using a haptic interface. In Proceedings of the International Conference on Advanced Robotics, ICAR, Munich, Germany, 22–26 June 2009; pp. 1–6. [Google Scholar]
- Dong, S.; Williams, B. Motion learning in variable environments using probabilistic flow tubes. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1976–1981. [Google Scholar] [CrossRef] [Green Version]
- Peters, R.A.; Campbell, C.L.; Bluethmann, W.J.; Huber, E. Robonaut task learning through teleoperation. In Proceedings of the ICRA’03. IEEE International Conference on Robotics and Automation, Taipei, Taiwa, 14–19 September 2003; Volume 2, pp. 2806–2811. [Google Scholar] [CrossRef]
- Tanwani, A.K.; Calinon, S. Learning Robot Manipulation Tasks With Task-Parameterized Semitied Hidden Semi-Markov Model. IEEE Robot. Autom. Lett. 2016, 1, 235–242. [Google Scholar] [CrossRef]
- Pardowitz, M.; Knoop, S.; Dillmann, R.; Zollner, R.D. Incremental Learning of Tasks From User Demonstrations, Past Experiences, and Vocal Comments. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2007, 37, 322–332. [Google Scholar] [CrossRef]
- Breazeal, C.; Aryananda, L. Recognition of affective communicative intent in robot-directed speech. Autonom. Robots 2002, 12, 83–104. [Google Scholar] [CrossRef]
- Calinon, S.; Guenter, F.; Billard, A. Goal-directed imitation in a humanoid robot. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, ICRA 2005, Barcelona, Spain, 18–22 April 2005; pp. 299–304. [Google Scholar] [CrossRef]
- Nicolescu, M.; Mataric, M.J. Task learning through imitation and human-robot interaction. In Imitation and Social Learning in Robots, Humans and Animals: Behavioural, Social and Communicative Dimensions; Cambridge University Press: Cambridge, UK, 2007; pp. 407–424. [Google Scholar]
- Demiris, J.; Hayes, G. Imitative Learning Mechanisms in Robots and Humans; University of Edinburgh, Department of Artificial Intelligence: Edinburgh, UK, 1996. [Google Scholar]
- Muhlig, M.; Gienger, M.; Hellbach, S.; Steil, J.J.; Goerick, C. Task-level imitation learning using variance-based movement optimization. In Proceedings of the ICRA’09. IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1177–1184. [Google Scholar] [CrossRef]
- Asfour, T.; Azad, P.; Gyarfas, F.; Dillmann, R. Imitation learning of dual-arm manipulation tasks in humanoid robots. Int. J. Humanoid Robot. 2008, 5, 183–202. [Google Scholar] [CrossRef]
- Breazeal, C.; Scassellati, B. Robots that imitate humans. Trends Cogn. Sci. 2002, 6, 481–487. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Schaal, S. Movement imitation with nonlinear dynamical systems in humanoid robots. In Proceedings of the ICRA’02 IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 2, pp. 1398–1403. [Google Scholar] [CrossRef]
- Billard, A.; Matarić, M.J. Learning human arm movements by imitation: Evaluation of a biologically inspired connectionist architecture. Robot. Auton. Syst. 2001, 37, 145–160. [Google Scholar] [CrossRef]
- Schaal, S.; Ijspeert, A.; Billard, A. Computational approaches to motor learning by imitation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2003, 358, 537–547. [Google Scholar] [CrossRef] [PubMed]
- Ude, A.; Gams, A.; Asfour, T.; Morimoto, J. Task-Specific Generalization of Discrete and Periodic Dynamic movement primitives. IEEE Trans. Robot. 2010, 26, 800–815. [Google Scholar] [CrossRef]
- Breazeal, C.; Berlin, M.; Brooks, A.; Gray, J.; Thomaz, A.L. Using perspective taking to learn from ambiguous demonstrations. Robot. Auton. Syst. 2006, 54, 385–393. [Google Scholar] [CrossRef]
- Demiris, Y. Prediction of intent in robotics and multi-agent systems. Cognit. Process. 2007, 8, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Breazeal, C.; Gray, J.; Berlin, M. An embodied cognition approach to mindreading skills for socially intelligent robots. Int. J. Robot. Res. 2009, 28, 656–680. [Google Scholar] [CrossRef]
- Jansen, B.; Belpaeme, T. A computational model of intention reading in imitation. Robot. Auton. Syst. 2006, 54, 394–402. [Google Scholar] [CrossRef]
- Chella, A.; Dindo, H.; Infantino, I. A cognitive framework for imitation learning. Robot. Auton. Syst. 2006, 54, 403–408. [Google Scholar] [CrossRef]
- Trafton, J.G.; Cassimatis, N.L.; Bugajska, M.D.; Brock, D.P.; Mintz, F.E.; Schultz, A.C. Enabling effective human-robot interaction using perspective-taking in robots. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2005, 35, 460–470. [Google Scholar] [CrossRef]
- Pook, P.K.; Ballard, D.H. Recognizing teleoperated manipulations. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; Volume 2, pp. 578–585. [Google Scholar] [CrossRef]
- Yang, J.; Xu, Y.; Chen, C.S. Hidden Markov model approach to skill learning and its application to telerobotics. IEEE Trans. Robot. Autom. 1994, 10, 621–631. [Google Scholar] [CrossRef]
- Hovland, G.E.; Sikka, P.; McCarragher, B.J. Skill acquisition from human demonstration using a hidden markov model. In Proceedings of the 1996 IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 3, pp. 2706–2711. [Google Scholar] [CrossRef]
- Lee, C.; Yangsheng, X. Online, interactive learning of gestures for human/robot interfaces. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 2982–2987. [Google Scholar] [CrossRef]
- Tso, S.K.; Liu, K.P. Hidden Markov model for intelligent extraction of robot trajectory command from demonstrated trajectories. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT ’96), Shanghai, China, 2–6 December 1996; pp. 294–298. [Google Scholar] [CrossRef]
- Yang, J.; Xu, Y.; Chen, C.S. Human action learning via hidden Markov model. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 1997, 27, 34–44. [Google Scholar] [CrossRef]
- Rybski, P.E.; Voyles, R.M. Interactive task training of a mobile robot through human gesture recognition. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 664–669. [Google Scholar] [CrossRef]
- Voyles, R.M.; Khosla, P.K. A multi-agent system for programming robots by human demonstration. Integr. Comput. Aided Eng. 2001, 8, 59–67. [Google Scholar]
- Inamura, T.; Toshima, I.; Nakamura, Y. Acquiring motion elements for bidirectional computation of motion recognition and generation. In Experimental Robotics Viii; Springer: Berlin/Heidelberg, Germny, 2003; pp. 372–381. [Google Scholar]
- Dixon, K.R.; Khosla, P.K. Learning by observation with mobile robots: A computational approach. In Proceedings of the ICRA’04. 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 1, pp. 102–107. [Google Scholar] [CrossRef]
- Inamura, T.; Kojo, N.; Sonoda, T.; Sakamoto, K.; Okada, K. Intent imitation using wearable motion-capturing system with online teaching of task attention. In Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots, Tsukuba, Japan, 5 December 2005; pp. 469–474. [Google Scholar] [CrossRef]
- Lee, D.; Nakamura, Y. Stochastic Model of Imitating a New Observed Motion Based on the Acquired Motion Primitives. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4994–5000. [Google Scholar] [CrossRef]
- Lee, D.; Nakamura, Y. Mimesis Scheme using a Monocular Vision System on a Humanoid Robot. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 2162–2168. [Google Scholar] [CrossRef]
- Calinon, S.; D’halluin, F.; Sauser, E.; Caldwell, D.; Billard, A. A probabilistic approach based on dynamical systems to learn and reproduce gestures by imitation. IEEE Robot. Autom. Mag. 2010, 17, 44–54. [Google Scholar] [CrossRef]
- Lee, K.; Su, Y.; Kim, T.K.; Demiris, Y. A syntactic approach to robot imitation learning using probabilistic activity grammars. Robot. Auton. Syst. 2013, 61, 1323–1334. [Google Scholar] [CrossRef]
- Niekum, S.; Chitta, S.; Barto, A.; Marthi, B.; Osentoski, S. Incremental Semantically Grounded Learning from Demonstration. Robot. Sci. Syst. 2013, 9. [Google Scholar] [CrossRef]
- Kulić, D.; Takano, W.; Nakamura, Y. Incremental Learning, Clustering and Hierarchy Formation of Whole Body Motion Patterns using Adaptive Hidden Markov Chains. Int. J. Robot. Res. 2008, 27, 761–784. [Google Scholar] [CrossRef]
- Chernova, S.; Veloso, M. Confidence-based policy learning from demonstration using gaussian mixture models. In Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems, Honolulu, HI, USA, 14–18 May 2007; p. 233. [Google Scholar] [CrossRef]
- Cohn, D.A.; Ghahramani, Z.; Jordan, M.I. Active learning with statistical models. Adv. Neural Inf. Process. Syst. 1995, 705–712. [Google Scholar] [CrossRef]
- González-Fierro, M.; Balaguer, C.; Swann, N.; Nanayakkara, T. Full-Body Postural Control of a Humanoid Robot with Both Imitation Learning and Skill Innovation. Int. J. Humanoid Robot. 2014, 11, 1450012. [Google Scholar] [CrossRef] [Green Version]
- Alissandrakis, A.; Nehaniv, C.L.; Dautenhahn, K.; Saunders, J. Evaluation of robot imitation attempts: comparison of the system’s and the human’s perspectives. In Proceedings of the 1st ACM SIGCHI/SIGART conference on Human-robot interaction, Salt Lake City, UT, USA, 2–3 March 2006; pp. 134–141. [Google Scholar] [CrossRef]
- Kuniyoshi, Y.; Yorozu, Y.; Inaba, M.; Inoue, H. From visuo-motor self learning to early imitation—A neural architecture for humanoid learning. In Proceedings of the International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 3132–3139. [Google Scholar] [CrossRef]
- Billard, A.; Epars, Y.; Calinon, S.; Schaal, S.; Cheng, G. Discovering optimal imitation strategies. Robot. Auton. Syst. 2004, 47, 69–77. [Google Scholar] [CrossRef]
- Lopes, M.; Santos-Victor, J. A developmental roadmap for learning by imitation in robots. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2007, 37, 308–321. [Google Scholar] [CrossRef]
- Billard, A.G.; Calinon, S.; Guenter, F. Discriminative and adaptive imitation in uni-manual and bi-manual tasks. Robot. Auton. Syst. 2006, 54, 370–384. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–38. [Google Scholar]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Hu, H. Robot Learning from Demonstration in Robotic Assembly: A Survey. Robotics 2018, 7, 17. https://doi.org/10.3390/robotics7020017
Zhu Z, Hu H. Robot Learning from Demonstration in Robotic Assembly: A Survey. Robotics. 2018; 7(2):17. https://doi.org/10.3390/robotics7020017
Chicago/Turabian StyleZhu, Zuyuan, and Huosheng Hu. 2018. "Robot Learning from Demonstration in Robotic Assembly: A Survey" Robotics 7, no. 2: 17. https://doi.org/10.3390/robotics7020017
APA StyleZhu, Z., & Hu, H. (2018). Robot Learning from Demonstration in Robotic Assembly: A Survey. Robotics, 7(2), 17. https://doi.org/10.3390/robotics7020017





