1. Introduction
Endowing robots with human-like abilities to perform motor skills in a smooth and natural way is one of the important goals of robotics. A promising way to achieve this is by creating robots that can learn new skills by themselves, similarly to humans. However, acquiring new motor skills is not simple and involves various forms of learning.
Over the years, the approaches for teaching new skill to robots have evolved significantly, and currently, there are three well-established types of approaches:
direct programming,
imitation learning and
reinforcement learning. All of these approaches are still being actively used, and each one has its own advantages and disadvantages and is preferred for certain settings, as summarized in
Table 1. The bottom row in
Table 1 indicates our prediction about a hypothetical future approach, predicted based on extrapolation from the existing approaches, as explained in
Section 10.
The ultimate goal of these approaches is to give robots the ability to learn, improve, adapt and reproduce tasks with dynamically changing constraints. However, these approaches differ significantly from one another:
Direct programming: This is the lowest-level approach, but it is still being actively used in industrial settings, where the environment is well-structured and complete control over the precise movement of the robot is crucial. We add it for completeness, although it is not really a teaching method; hence, we classify it as programming. Industrial robots are usually equipped with the so-called teach pendant—a device that is used to manually set the desired robot positions.
Imitation learning: This approach is called
learning instead of
programming, in order to emphasize the active part that the agent (the robot) has in the process. This approach is also known as
programming by demonstration [
1] or
learning from demonstration [
2]. There are three main methods used to perform demonstrations for imitation learning:
- -
Kinesthetic teaching: This is the process of manually moving the robot’s body and recording its motion [
3]. This approach usually works only for smaller, lightweight robots and in combination with a gravity-compensation controller, in order to minimize the apparent weight of the robot. However, nevertheless, since the robot’s inertia cannot be effectively reduced, it is not practical for bigger robots. Kinesthetic teaching could be performed in a continuous way, recording whole trajectories, or alternatively, it could be performed by recording discrete snapshots of the robot’s state at separate time instances, such as in keyframe-based teaching of sequences of key poses [
4].
- -
Teleoperation: This is the process of remotely controlling the robot’s body using another input device, such as a joystick or a haptic device. This approach shares many similarities with kinesthetic teaching in terms of advantages and disadvantages. One big difference is that with teleoperation, the teacher can be located in a geographically distant location. However, time delays become an issue as the distance increases (e.g., teleoperating a Mars rover would be difficult). Similarly to kinesthetic teaching, only a limited number of degrees of freedom (DoFs) can be controlled at the same time. Furthermore, with teleoperation, it is more difficult to feel the limitations and capabilities of the robot than by using kinesthetic teaching. As an advantage, sometimes the setup could be simpler, and additional information can be displayed at the interface (e.g., forces rendered by the haptic device).
- -
Observational learning: In this method, the movement is demonstrated using the teacher’s own body and is perceived using motion capture systems or video cameras or other sensors. It is usually needed to solve the correspondence problem [
5],
i.e., to map the robot’s kinematics to that of the teacher.
The simplest way to use the demonstrations is to do a simple record-and-replay, which can only execute a particular instance of a task. However, using smart representation of the recorded movement in appropriate frame of reference (e.g., using the target object as the origin), it is possible to have somewhat adaptable skill to different initial configurations, for simple (mostly one-object) tasks. Based on multiple demonstrations that include variations of a task, the robot can calculate correlations and variance and figure out which part of a task is important to be repeated verbatim and which part is acceptable to be changed (and to what extent). Imitation learning has been successfully applied many times for learning tasks on robots, for which the human teacher can demonstrate a successful execution [
3,
6].
Reinforcement learning (RL): This is the process of learning from trial-and-error [
7], by exploring the environment and the robot’s own body. The goal in RL is specified by the
reward function, which acts as positive reinforcement or negative punishment depending on the performance of the robot with respect to the desired goal. RL has created a well-defined niche for its application in robotics [
8,
9,
10,
11,
12,
13,
14]. The main motivation for using reinforcement learning to teach robots new skills is that it offers three previously missing abilities:
- -
to learn new tasks, which even the human teacher cannot physically demonstrate or cannot directly program (e.g., jump three meters high, lift heavy weights, move very fast, etc.);
- -
to learn to achieve optimization goals of difficult problems that have no analytic formulation or no known closed form solution, when even the human teacher does not know what the optimum is, by using only a known cost function (e.g., minimize the used energy for performing a task or find the fastest gait, etc.);
- -
to learn to adapt a skill to a new, previously unseen version of a task (e.g., learning to walk from flat ground to a slope, learning to generalize a task to new previously unseen parameter values, etc.). Some imitation learning approaches can also do this, but in a much more restricted way (e.g., by adjusting parameters of a learned model, without being able to change the model itself).
Reinforcement learning also offers some additional advantages. For example, it is possible to start from a “good enough” demonstration and gradually refine it. Another example would be the ability to dynamically adapt to changes in the agent itself, such as a robot adapting to hardware changes—heating up, mechanical wear, growing body parts, etc.
Table 1.
Comparison of the main robot teaching approaches.
Table 1.
Comparison of the main robot teaching approaches.
| Approach/method for teaching the robot | Computational complexity | Advantages | Disadvantages |
|---|
| Difficult for the teacher |
|---|
| Existing approaches | Direct programming Manually specifying (programming) the robot how to move each joint | Lowest | Complete control of the movement of the robot to the lowest level | Time-consuming, error-prone, not scalable, not reusable |
| High |
| Imitation learning | Kinesthetic teaching and Teleoperation Directly move the robot’s limbs or teleoperate to record the movement | Low | No need to manually program, can just record and replay movements | Cannot perform fast movements; can move usually only one limb at a time; the robot has to be lightweight |
| Medium |
| Observational learning Demonstrate the movement using the teacher’s own body; perceive the movement using motion capture systems or video cameras | Medium | Easy and natural to demonstrate; also works for bimanual tasks or even whole-body motion | Correspondence problem caused by the different embodiment; the teacher must be able to do the task; often requires multiple demonstrations that need to be segmented and time-aligned |
| Low |
| Reinforcement learning Specify a scalar reward function evaluating the robot’s performance that needs to be maximized; no need to demonstrate how to perform the task; the robot discovers this on its own | Higher | Robot can learn tasks that even the human cannot demonstrate; novel ways to reach a goal can be discovered | No control over the actions of the robot; robot has only indirect information about the goal; need to specify reward function, policy parameterization, exploration magnitude/strategy, initial policy |
| Lower |
| Hypothetical | “Goal-directed learning” (predicted via extrapolation) Only specifying the goal that the robot must achieve, without evaluating the intermediate progress | Highest | The easiest way to specify (e.g., using NLP); robot has direct knowledge of the goal | No control of the movement of the robot; must know what the goal is and how to formally define it |
| Lowest |
This paper provides a summary of some of the main components for applying reinforcement learning in robotics. We present some of the most important classes of learning algorithms and classes of policies. We give a comprehensive list of challenges for effective policy representations for the application of policy-search RL to robotics and provide three examples of tasks demonstrating how the policy representation may address some of these challenges. The paper is a significantly improved and extended version of our previous work in [
15]. The novelties include: new experimental section based on robotic archery task; new section with insights about the future of RL in robotics; new comparison of existing robot learning approaches and their respective advantages and disadvantages; an expanded list of challenges for the policy representation and more detailed description of use cases.
The paper does not propose new algorithmic strategies. Rather, it summarizes what our team has learned from a fairly extensive base of empirical evidence over the last 4–5 years, aiming to serve as a reference for the field of robot learning. While we may still dream of a general purpose algorithm that would allow robots to learn optimal policies without human guidance, it is likely that these are far off. The paper describes several classes of policies that have proved to work very well for a wide range of robot motor control tasks. The main contribution of this work is a better understanding that the design of appropriate policy representations is essential for RL methods to be successfully applied to real-world robots.
The paper is structured as follows. In
Section 2, we present an overview of the most important recent RL algorithms that are being successfully applied in robotics. Then, in
Section 3, we identify numerous challenges posed by robotics on the RL policy representation, and in
Section 4, we describe the state-of-the-art policy representations. To illustrate some of these challenges, and to propose adequate solutions to them, the three consecutive
Section 5,
Section 6 and
Section 7, give three representative examples for real-world application of RL in robotics. The examples are all based on the same RL algorithm, but each faces different policy representation problems and, therefore, requires different solutions. In
Section 8, we give a summary of the three tasks and compare them to three other robot skill learning tasks. Then, in
Section 9, we give insights about the future perspective directions for RL based on these examples and having in mind robotics, in particular, as the application. Finally, in
Section 10, we discuss potential future alternative methods for teaching robots new tasks that might appear. We conclude with a brief peek into the future of robotics, revealing, in particular, the potential wider need for RL.
2. State-of-the-Art Reinforcement Learning Algorithms in Robotics
Robot systems are naturally of high-dimensionality, having many degrees of freedom (DoF), continuous states and actions and high noise. Because of this, traditional RL approaches based on MDP/POMDP/discretized state and action spaces have problems scaling up to work in robotics, because they suffer severely from the curse of dimensionality. The first partial successes in applying RL to robotics came with the function approximation techniques, but the real “renaissance” came with the policy-search RL methods.
In policy-search RL, instead of working in the huge state/action spaces, a smaller policy space is used, which contains all possible policies representable with a certain choice of policy parameterization. Thus, the dimensionality is drastically reduced and the convergence speed is increased.
Until recently,
policy-gradient algorithms (such as Episodic Natural Actor-Critic eNAC [
16] and Episodic REINFORCE [
17]) have been a well-established approach for implementing policy-search RL [
10]. Unfortunately, policy-gradient algorithms have certain shortcomings, such as high sensitivity to the learning rate and exploratory variance.
An alternative approach that has gained popularity recently derives from the Expectation-Maximization (EM) algorithm. For example, Kober
et al. proposed in [
18] an episodic RL algorithm, called PoWER (
policy learning by weighting exploration with the returns). It is based on the EM algorithm and, thus, has a major advantage over policy-gradient-based approaches: it does not require a learning rate parameter. This is desirable, because tuning a learning rate is usually difficult to do for control problems, but critical for achieving good performance of policy-gradient algorithms. PoWER also demonstrates superior performance in tasks learned directly on a real robot, by applying an importance sampling technique to reuse previous experience efficiently.
Another state-of-the-art policy-search RL algorithm, called
PI^2 (
policy improvement with path integrals), was proposed by Theodorou
et al. in [
19], for learning parameterized control policies based on the framework of stochastic optimal control with path integrals. They derived update equations for learning to avoid numerical instabilities, because neither matrix inversions nor gradient learning rates are required. The approach demonstrates significant performance improvements over gradient-based policy learning and scalability to high-dimensional control problems, such as control of a quadruped robot dog.
Several search algorithms from the field of stochastic optimization have recently found successful use for iterative policy improvement. Examples of such approaches are the cross-entropy method (CEM) [
20] and the covariance matrix adaptation evolution strategy (CMA-ES) [
21]. Although these algorithms come from a different domain and are not well-established in RL research, they seem to be a viable alternative for direct policy search RL, as some recent findings suggest [
22].
3. Challenges for the Policy Representation in Robotics
Only having a good policy-search RL algorithm is not enough for solving real-world problems in robotics. Before any given RL algorithm can be applied to learn a task on a robot, an appropriate policy representation (also called policy encoding) needs to be devised. This is important, because the choice of policy representation determines what in principle can be learned by the RL algorithm (i.e., the policy search space), analogous to the way a hypothesis model determines what kind of data a regression method can fit well. In addition, the policy representation can have significant influence on the RL algorithm itself, e.g., it can help or impede the convergence or influence the variance of the generated policies.
However, creating a good policy representation is not a trivial problem, due to a number of serious
challenges posed by the high requirements from a robotic system, such as:
smoothness—the policy representation needs to encode smooth, continuous trajectories, without sudden accelerations or jerks, in order to be safe for the robot itself and also to reduce its energy consumption. In some rare cases, though, such as in bang-bang control, sudden changes might be desirable;
safety—the policy should be safe, not only for the robot (in terms of joint limits, torque limits, work space restrictions, obstacles, etc.), but also for the people around it;
gradual exploration—the representation should allow gradual, incremental exploration, so that the policy does not suddenly change by a lot; e.g., in state-action-based policies, changing the policy action at only a single state could cause a sudden dramatic change in the overall behavior of the system when following this new branch of the policy, which is not desirable neither for the robot, nor for the people around it. In some cases, though, a considerable step change might be necessary, e.g., a navigation task where a robot needs to decide whether to go left or right to avoid an obstacle;
scalability—to be able to scale up to high dimensions and for more complex tasks; e.g., a typical humanoid robot nowadays has well above 50 DoF;
compactness—despite the high DoF of robots, the policy should use very compact encoding, e.g., it is impossible to directly use all points on a trajectory as policy parameters;
adaptability—the policy parameterization should be adaptable to the complexity and fidelity of the task, e.g., lifting weights vs. micro-surgery;
multi-resolution—different parts of the policy parameterization should allow different resolution/precision;
unbiasedness—the policy parameterization should work without prior knowledge about the solution being sought and without restricting unnecessarily the search scope for possible solutions;
prior/bias—whenever feasible, it should be possible to add prior information (also called bias) in order to jump-start policy search approaches, as illustrated in some of the use cases in this paper;
regularization—the policy should allow one to incorporate regularization to guide the exploration towards desired types of policies;
time-independence—this is the property of a policy not to depend on precise time or position, in order to cope with unforeseen perturbations;
embodiment-agnostic—the representation should not depend on any particular embodiment of the robot, e.g., joint-trajectory based policies cannot be transferred to another robot easily;
invariance—the policy should be an invariant representation of the task (e.g., rotation-invariant, scale-invariant, position-invariant, etc.);
correlations—the policy should encapsulate correlations between the control variables (e.g., actuator control signals), similar to the motor synergies found in animals;
globality—the representation should help the RL algorithm to avoid local minima;
periodicity—to be able to represent easily periodic/cyclic movements, which occur often in robotics (e.g., for locomotion—different walking gaits, for manipulation—wiping movements, etc.);
analyzability—facility to visualize and analyze the policy (e.g., proving its stability by poles analysis, etc.);
multi-dimensionality—to be able to use efficiently high-dimensional feedback without the need to convert it into a scalar value by using a weighted sum of components;
convergence—to help the RL algorithm to converge faster to the (possibly local) optima.
A good policy representation should provide solutions to all of these challenges. However, it is not easy to come up with such a policy representation that satisfies all of them. In fact, the existing state-of-the-art policy representations in robotics cover only subsets of these requirements, as highlighted in the next section.
4. State-of-the-Art Policy Representations in Robotics
Traditionally, explicit time-dependent approaches, such as cubic splines or higher-order polynomials, were used as policy representations. These, however, are not autonomous, in the sense that they cannot cope easily with perturbations (unexpected changes in the environment). Currently, there are a number of efficient state-of-the-art representations available to address this and many of the other challenges mentioned earlier. We give three examples of such policy representations below:
Guenter
et al. explored in [
23] the use of the
Gaussian Mixture Model (GMM) and
Gaussian Mixture Regression (GMR) to respectively compactly encode a skill and reproduce a generalized version of it. The model was initially learned by demonstration through
expectation-maximization techniques. RL was then used to move the Gaussian centers in order to alter the reproduced trajectory by regression. It was successfully applied to the imitation of constrained reaching movements, where the learned movement was refined in simulation to avoid an obstacle that was not present during the demonstration attempts.
Kober and Peters explored in [
24] the use of
Dynamic Movement Primitives (DMP) [
25] as a compact representation of a movement. The DMP framework was originally proposed by Ijspeert
et al. [
26] and further extended in [
25,
27]. In DMP, a set of attractors is used to reach a target, whose influence is smoothly switched along the movement. The set of attractors is first learned by imitation, and a proportional-derivative controller is used to move sequentially towards the sequence of targets. RL is then used to explore the effect of changing the position of these attractors. The proposed approach was demonstrated with pendulum swing-up and ball-in-a-cup tasks [
28]. One of the first uses of motion primitives was in the work of Peters
et al. for a ball-batting experiment using the eNAC algorithm [
29].
Pardo
et al. proposed in [
30] a framework to learn coordination for simple rest-to-rest movements, by taking inspiration of the motor coordination, joint synergies and the importance of coupling in motor control [
31,
32,
33]. The authors suggested to start from a basic representation of the movement by considering point-to-point movements driven by a proportional-derivative controller, where each variable encoding the task is decoupled. They then extended the possibilities of movement by encapsulating coordination information in the representation. RL was then used to learn how to efficiently coordinate the set of variables, which were originally decoupled.
Although these policy representations work reasonably well for specific tasks, neither one of them manages to address all of the challenges listed in the previous section, but only a different subset. In particular, the challenges of correlations, adaptability, multi-resolution, globality, multi-dimensionality and convergence are rarely addressed by the existing policy representations.
In the following three sections. we give three concrete examples of tasks that pose such rarely-addressed challenges for the policy representation, and we propose some possible solutions to them. The three examples are: pancake flipping task, bipedal walking energy minimization task and archery-based aiming task. In all examples, the same EM-based RL algorithm is used (PoWER), but different policy representations are devised to address the specific challenges of the task at hand. Videos of the three presented robot experiments are available online at:
http://kormushev.com/research/videos/.
5. Example A: Pancake Flipping Task
This example addresses mainly the
correlations,
compactness and
smoothness challenges described in
Section 3. We present an approach allowing a robot to acquire new motor skills by learning the couplings across motor control variables. The demonstrated skill is first encoded in a compact form through a modified version of DMP, which encapsulates correlation information. RL is then used to modulate the mixture of dynamical systems initialized from the user’s demonstration via weighted least-squares regression. The approach is evaluated on a torque-controlled seven-DoF Barrett WAMrobotic arm. More implementation details can be found in [
13].
5.1. Task Description
The goal of the pancake flipping task is to first toss a pancake in the air, so that it rotates 180°, and then to catch it with the frying pan. Due to the complex dynamics of the task, it is unfeasible to try learning it directly with
tabula rasa RL. Instead, a person presents a demonstration of the task first via kinesthetic teaching, which is then used to initialize the RL policy. The experimental setup is shown in
Figure 1.
Figure 1.
Experimental setup for the pancake flipping task. A torque-controlled seven-DoF Barrett WAM robot learns to flip pancakes in the air and catch them with a real frying pan attached to its end-effector. Artificial pancakes with passive reflective markers are used to evaluate the performance of the learned policy.
Figure 1.
Experimental setup for the pancake flipping task. A torque-controlled seven-DoF Barrett WAM robot learns to flip pancakes in the air and catch them with a real frying pan attached to its end-effector. Artificial pancakes with passive reflective markers are used to evaluate the performance of the learned policy.
The pancake flipping task is difficult to learn from multiple demonstrations, because of the high variability of the task execution, even when the same person is providing the demonstrations. Extracting the task constraints by observing multiple demonstrations is not appropriate in this case for two reasons:
when considering such skillful movements, extracting the regularities and correlations from multiple observations would be difficult, as consistency in the skill execution would appear only after the user has mastered the skill;
the generalization process may smooth important acceleration peaks and sharp turns in the motion. Therefore, in such highly dynamic skillful tasks, early trials have shown that it was more appropriate to select a single successful demonstration (among a small series of trials) to initialize the learning process.
A common missing part of most existing policy representations is the lack of any coupling between the different variables. To address this problem, we propose an approach that builds upon the works above by taking into consideration the efficiency of DMP to encode a skill with a reduced number of states and by extending the approach to take into consideration local coupling information across the different variables.
5.2. Proposed Compact Encoding with Coupling
The proposed approach represents a movement as a superposition of basis force fields, where the model is initialized from weighted least-squares regression of demonstrated trajectories. RL is then used to adapt and improve the encoded skill by learning optimal values for the policy parameters. The proposed policy parameterization allows the RL algorithm to learn the coupling across the different motor control variables.
A demonstration consisting of
T positions,
x in 3D, velocities,
, and accelerations,
, is shown to the robot. By considering flexibility and compactness issues, we propose to use a controller based on a mixture of
K proportional-derivative systems:
The above formulation shares similarities with the DMP framework. The difference is that the non-linear force of DMP is considered as resulting from a set of virtual springs, adding local corrective terms to swiftly react to perturbations [
34]. Here, we extend the use of DMP by considering synergy across the different motion variables through the association of a full matrix,
, with each of the
K primitives (or states) instead of a fixed
gain.
The superposition of basis force fields is determined in Equation (
1) by an implicit time dependency, but other forms of activation weights can also be used. For example, we showed in [
35] that the representation in Equation (
1) could also be used with activation weights based on spatial inputs instead of temporal inputs, used to encode reaching behaviors modulated by the position of objects.
Similarly to DMP, a decay term defined by a canonical system,
, is used to create an implicit time dependency,
, where
s is initialized with
and converges to zero. We define a set of Gaussians,
, in time space,
, with centers,
, equally distributed in time, and variance parameters,
, set to a constant value inversely proportional to the number of Gaussians. This set is used as a set of Gaussian basis functions. The scalar,
α, is fixed depending on the duration of the demonstrations. The weights are defined by:
In Equation (
1),
is a set of full stiffness matrices, which we refer to as
coordination matrices. Using the full coordination matrices (not only their diagonal elements) allows us to consider different types of synergies across the variables, where each state/primitive encodes local correlation information. Both attractor vectors,
, and coordination matrices,
, in Equation (
1) are initialized from the observed data through weighted least-squares regression (see [
13] for details).
5.3. Experiment
Custom-made artificial pancakes are used, whose position and orientation are tracked in real-time by a reflective marker-based NaturalPoint OptiTrack motion capture system.
The return of a
rollout,
τ (also called trial), is calculated from the time-step reward,
. It is defined as a weighted sum of two criteria (orientational reward and positional reward), which encourage successful flipping and successful catching of the pancake:
where
are weights,
is the moment when the pancake passes, with a downward direction, the horizontal level at a fixed height,
, above the frying pan’s current vertical position,
is the initial orientation of the pancake (represented by a unit vector perpendicular to the pancake),
is the orientation of the pancake at time,
,
is the position of the pancake center at time,
,
is the position of the frying pan center at time,
, and
is the maximum reached altitude of the pancake. The first term is maximized when the pancake’s orientation (represented as a normal vector) at time,
, points in the opposite direction of the initial orientation, which happens in a successful flip. The second term is maximized when the pancake lands close to the center of the frying pan.
To learn new values for the coordination matrices, the RL algorithm PoWER is used. The policy parameters, , for the RL algorithm are composed of two sets of variables: the first set contains the full coordination matrices, , with the positional error gains in the main diagonal and the coordination gains in the off-diagonal elements; the second set contains the vectors, , with the attractor positions for the primitives.
5.4. Experimental Results
In practice, around 60 rollouts were necessary to find a good policy that can reproducibly flip the pancake without dropping it.
Figure 2 shows a recorded sample rollout from the RL exploration, during which the pancake rotated fully 180° and was caught successfully with the frying pan. The video frame sequence from a successful 180° flipping rollout is shown in
Figure 3.
It is interesting to notice the up-down bouncing of the frying pan towards the end of the learned skill, when the pancake has just fallen inside of it. The bouncing behavior is due to the increased compliance of the robot during this part of the movement. This was produced by the RL algorithm in an attempt to catch the fallen pancake inside the frying pan. Without it, if a controller is too stiff, it would cause the pancake to bounce off from the surface of the frying pan and fall out of it. Such unintentional discoveries made by the RL algorithm highlight its important role for achieving adaptable and flexible robots.
In summary, the proposed policy parameterization based on superposition of basis force fields demonstrates three major advantages:
it provides a mechanism for learning the couplings across multiple motor control variables, thus addressing the correlations challenge;
it highlights the advantages of using correlations in RL for reducing the size of the representation, thus addressing the compactness challenge;
it demonstrates that even fast, dynamic tasks can still be represented and executed in a safe-for-the-robot manner, addressing the smoothness challenge.
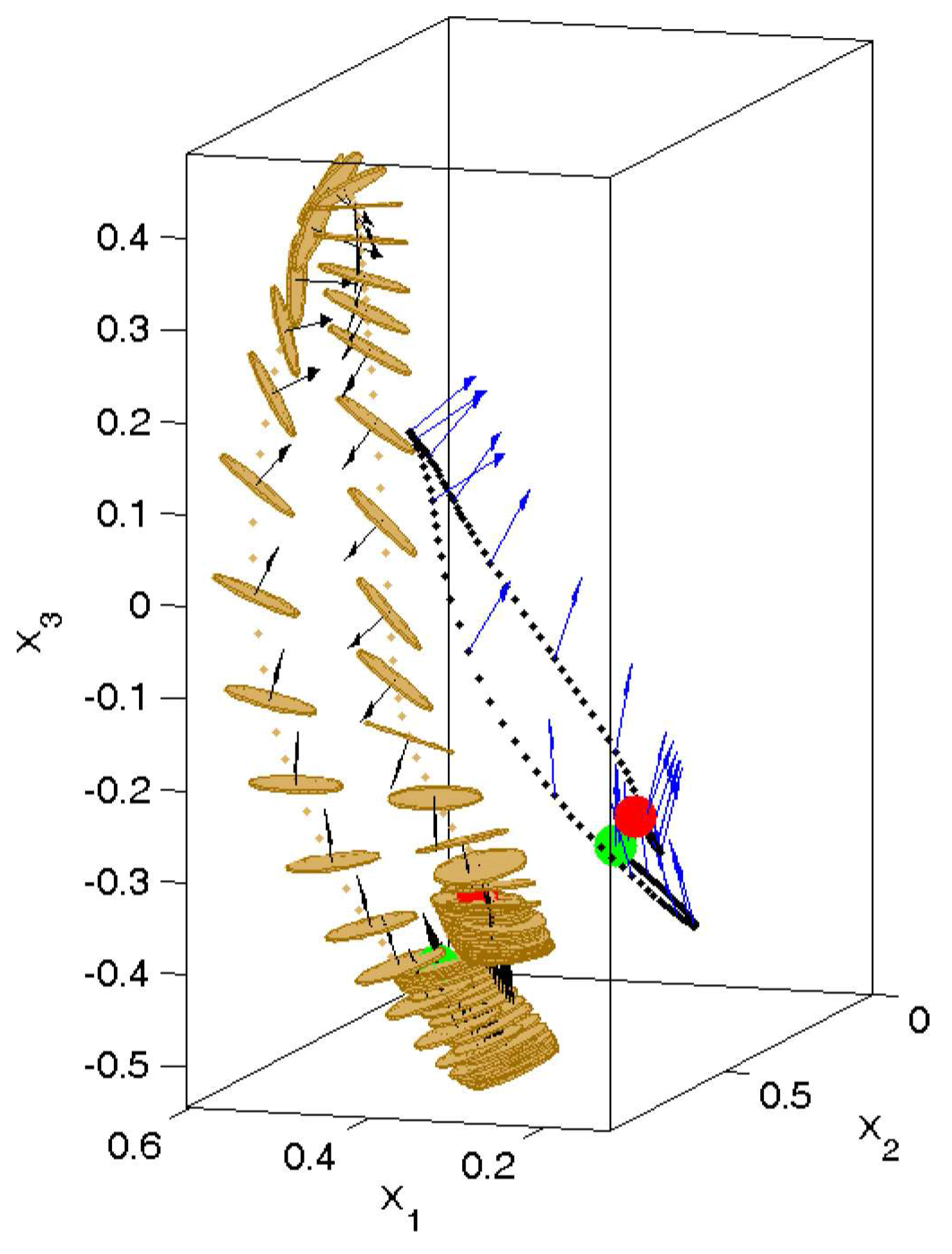
Figure 2.
Visualization of a real-world pancake flipping rollout (trial) performed by the robot. The pancake (in yellow) was successfully tossed and caught with the frying pan, and it rotated 180° (for better visibility of the pancake’s trajectory, the frying pan is not displayed here). The trajectory of the end-effector is displayed with black dots and its orientation (represented by the normal vector) with blue arrows. The normal vectors perpendicular to the pancake are shown with black arrows.
Figure 2.
Visualization of a real-world pancake flipping rollout (trial) performed by the robot. The pancake (in yellow) was successfully tossed and caught with the frying pan, and it rotated 180° (for better visibility of the pancake’s trajectory, the frying pan is not displayed here). The trajectory of the end-effector is displayed with black dots and its orientation (represented by the normal vector) with blue arrows. The normal vectors perpendicular to the pancake are shown with black arrows.
Figure 3.
Sequence of video frames showing a successful pancake flipping, performed on the WAM robot.
Figure 3.
Sequence of video frames showing a successful pancake flipping, performed on the WAM robot.
6. Example B: Bipedal Walking Energy Minimization Task
In this example, we address mainly the
adaptability,
multi-resolution and
globality challenges described in
Section 3. Adaptive resolution methods
in state space have been studied in RL before (see e.g., [
36]). They address the pitfalls of discretization during reinforcement learning and show that in high dimensions, it is better if the learning is not planned uniformly over the state space. For example, in [
37], Moore
et al. employed a decision-tree partitioning of state-space and applied techniques from game-theory and computational geometry to efficiently and adaptively concentrate high resolution on critical areas.
However, in the context of RL, adaptive resolution
in policy parameterization remains largely unexplored, so far. To address this challenge, we present a policy parameterization that can evolve dynamically, while the RL algorithm is running without losing information about past experience. We show that the gradually increasing representational power of the policy parameterization helps to find better policies faster than a fixed parameterization. The particular problem at hand is an energy minimization problem for a bipedal walking task. More implementation details can be found in [
38].
6.1. Energy Minimization Problem
Recent advances in robotics and mechatronics have allowed for the creation of a new generation of passively-compliant robots, such as the humanoid robot, COMAN(derived from the cCubbipedal robot [
39]), shown in
Figure 4.
Figure 4.
The experimental setup for the bipedal walking energy minimization task, showing a snapshot of the lower body of the compliant humanoid robot, COMAN, during one walking rollout.
Figure 4.
The experimental setup for the bipedal walking energy minimization task, showing a snapshot of the lower body of the compliant humanoid robot, COMAN, during one walking rollout.
Such robots have springs that can store and release energy and are essential for reducing the energy consumption and for achieving mechanical power peaks. However, it is difficult to manually engineer an optimal way to use the passive compliance for dynamic and variable tasks, such as walking. For instance, the walking energy minimization problem is very challenging, because it is nearly impossible to be solved analytically, due to the difficulty in modeling accurately the properties of the springs, the dynamics of the whole robot and various nonlinearities of its parts. In this section, we apply RL to learn to minimize the energy consumption required for walking of this passively-compliant bipedal robot.
The vertical center of mass (CoM) movement is a crucial factor in reducing the energy consumption. Therefore, the proposed RL method is used to learn an optimal vertical trajectory for the center of mass (CoM) of the robot to be used during walking, in order to minimize the energy consumption. In order to apply RL in robotics to optimize the movement of the robot, first, the trajectory needs to be represented (encoded) in some way. This particular experiment is based on cubic splines. Similar approaches have been investigated before in robotics under the name
via-points [
40,
41,
42].
However, there is a problem with applying a fixed policy parameterization RL to such a complex optimization problem.
6.2. Problems with Fixed Policy Parameterization
In policy-search RL, in order to find a good solution, the policy parameterization has to be powerful enough to represent a large enough policy space, so that a good candidate solution is present in it. If the policy parameterization is too simple, with only a few parameters, then the convergence is quick, but often a sub-optimal solution is reached. If the policy parameterization is overly complex, the convergence is slow, and there is a higher possibility that the learning algorithm will converge to some local optimum, possibly much worse than the global optimum. The level of sophistication of the policy parameterization should be just the right amount, in order to provide both fast convergence and a good enough solution.
Deciding what policy parameterization to use and how simple/complex it should be is a very difficult task, often performed via trial-and-error manually by the researchers. This additional overhead is usually not even mentioned in reinforcement learning papers and falls into the category of “empirically tuned” parameters, together with the reward function, decay factor, exploration noise, weights, etc. Since changing the policy parameterization requires restarting the learning from scratch, throwing away all accumulated data, this process is slow and inefficient. As a consequence, the search for new solutions often cannot be done directly on a real-world robot system and requires, instead, the use of simulations, which are not accurate enough.
6.3. Evolving Policy Parameterization
To solve this problem, we propose an approach that allows us to change the complexity of the policy representation dynamically, while the reinforcement learning is running, without losing any of the collected data and without having to restart the learning. We propose a mechanism that can incrementally “evolve” the policy parameterization as necessary, starting from a very simple parameterization and gradually increasing its complexity and, thus, its representational power. The goal is to create an adaptive policy parameterization, which can automatically “grow” to accommodate increasingly more complex policies and get closer to the global optimum.
A very desirable side effect of this is that the tendency of converging to a sub-optimal solution will be reduced, because in the lower-dimensional representations, this effect is less exhibited, and gradual increasing the complexity of the parameterization helps us not to get caught in a poor local optimum. A drawback of such an approach is that an informed initialization would be harder, depending on the expressive power of the initial parameterization.
The main difficulty to be solved is providing backward compatibility, i.e., how to design the subsequent policy representations in such a way that they are backward-compatible with the previously collected data, such as past rollouts and their corresponding policies and rewards. One of the simplest representations that have the property of backward compatibility are the geometric splines. For example, if we have a cubic spline with K knots, and then we increase the number of knots, we can still preserve the shape of the generated curve (trajectory) by the spline. In fact, if we put one additional knot between every two consecutive knots of the original spline, we end up with knots and a spline that coincides with the original spline. Based on this, the idea we propose is to use the spline knots as a policy parameterization and use the spline backward compatibility property for evolving the policy parameterization without losing the previously collected data.
The proposed technique for evolving the policy parameterization can be used with any policy-search RL algorithm. For this particular implementation, we use PoWER, due to its low number of parameters that need tuning. Different techniques can be used to trigger the increase in the number of knots of the spline representation. For this example, we used a fixed, pre-determined trigger, activating at regular time intervals.
6.4. Evaluation of Evolving Policy Parameterization
In order to evaluate the proposed evolving policy parameterization, we conduct a function approximation experiment. The goal is to compare the proposed method with a conventional fixed policy parameterization method that uses the same reinforcement learning algorithm as a baseline.
For this experiment, the reward function is defined as follows:
where
is the return of a rollout (the policy-generated trajectory),
τ, and
is the (unknown to the learning algorithm) function that the algorithm is trying to approximate.
Figure 5.
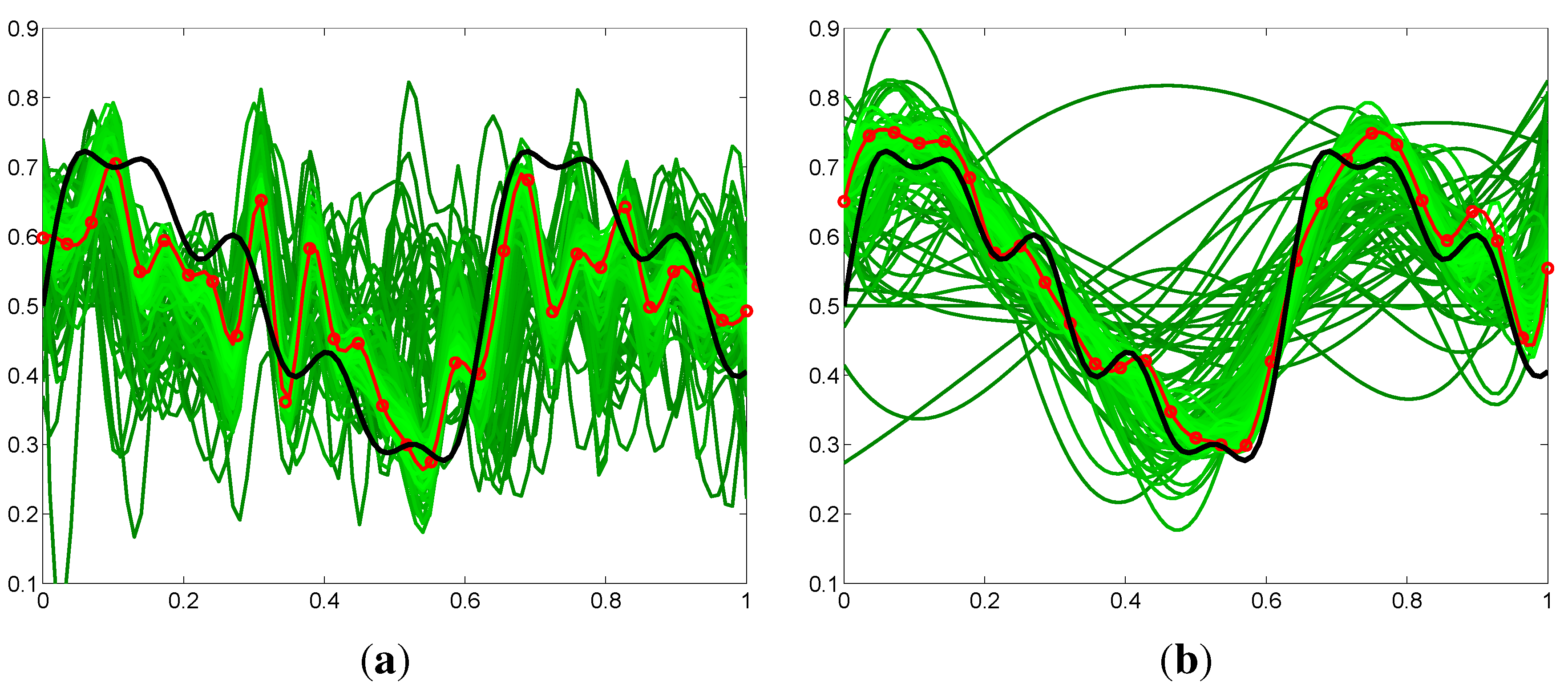
Comparison of the policy output from RL with fixed policy parameterization (30-knot spline) versus evolving policy parameterization (from four- to 30-knot spline). In black, the unknown to the algorithm global optimum, which it is trying to approximate. In green, all the rollouts performed during the learning process. In red, the current locally-optimal discovered policy by each reinforcement learning (RL) algorithm. Due to the lower policy-space dimensionality at the beginning, the evolving policy parameterization approaches the shape of the globally-optimal trajectory much faster. The fixed policy parameterization suffers from inefficient exploration, due to the high dimensionality, as well as from overfitting problems, as seen by the high-frequency oscillations of the discovered policies. (a) Fixed policy parameterization; (b) Evolving policy parameterization.
Figure 5.
Comparison of the policy output from RL with fixed policy parameterization (30-knot spline) versus evolving policy parameterization (from four- to 30-knot spline). In black, the unknown to the algorithm global optimum, which it is trying to approximate. In green, all the rollouts performed during the learning process. In red, the current locally-optimal discovered policy by each reinforcement learning (RL) algorithm. Due to the lower policy-space dimensionality at the beginning, the evolving policy parameterization approaches the shape of the globally-optimal trajectory much faster. The fixed policy parameterization suffers from inefficient exploration, due to the high dimensionality, as well as from overfitting problems, as seen by the high-frequency oscillations of the discovered policies. (a) Fixed policy parameterization; (b) Evolving policy parameterization.
Figure 5 shows a comparison of the generated policy output produced by the proposed evolving policy parameterization method, compared with the output from the conventional fixed policy parameterization method.
Figure 6 shows that the convergence properties of the proposed method are significantly better than the conventional approach.
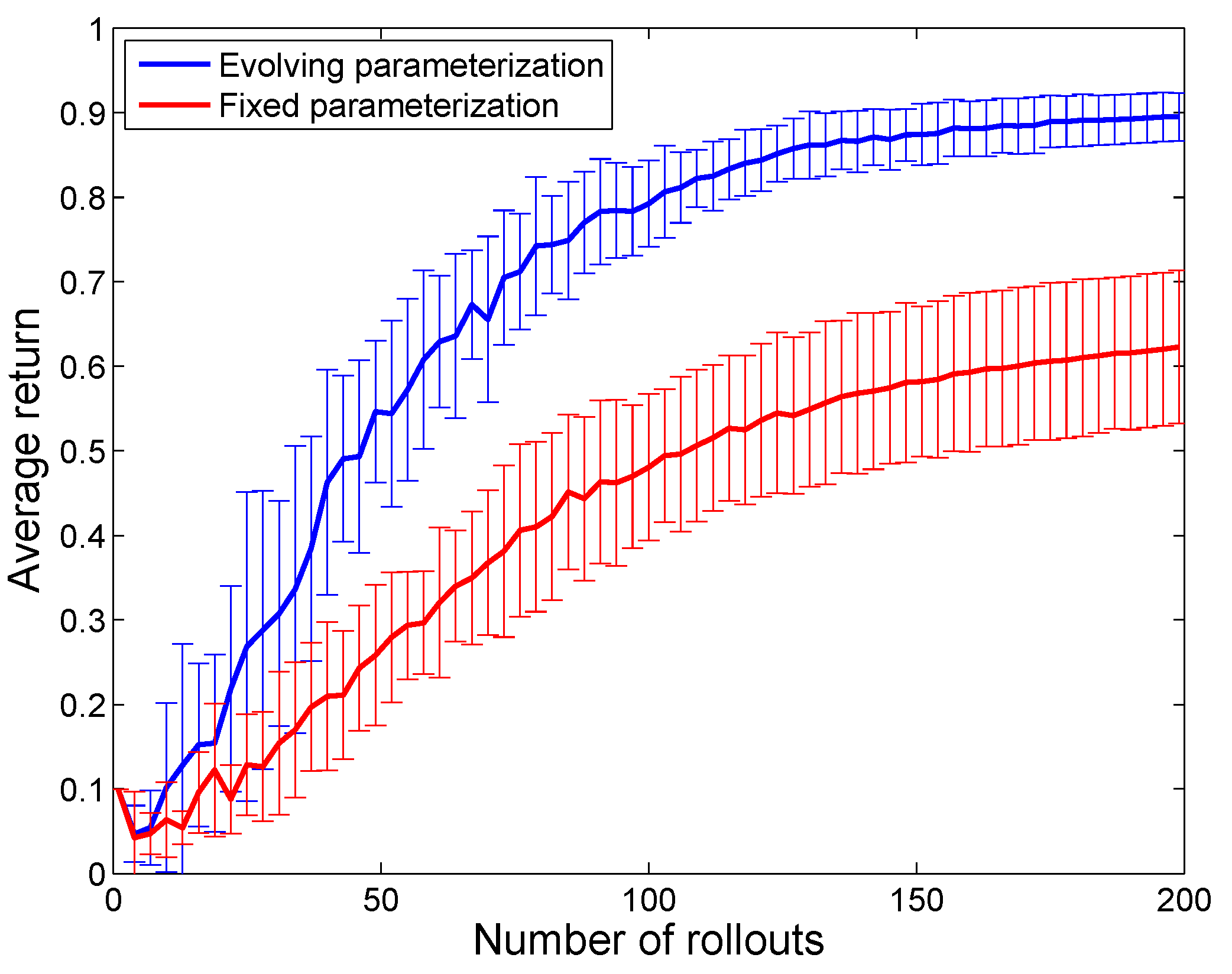
Figure 6.
Comparison of the convergence of the RL algorithm with fixed policy parameterization (30-knot spline) versus evolving policy parameterization (from four- to 30-knot spline). The results are averaged over 20 runs of each of the two algorithms. The standard deviation is indicated with error bars. In addition to faster convergence and higher achieved rewards, the evolving policy parameterization also achieves lower variance compared to the fixed policy parameterization.
Figure 6.
Comparison of the convergence of the RL algorithm with fixed policy parameterization (30-knot spline) versus evolving policy parameterization (from four- to 30-knot spline). The results are averaged over 20 runs of each of the two algorithms. The standard deviation is indicated with error bars. In addition to faster convergence and higher achieved rewards, the evolving policy parameterization also achieves lower variance compared to the fixed policy parameterization.
6.5. Bipedal Walking Experiment
For the real-world bipedal walking experiment, we use the lower body of the passively-compliant humanoid robot, COMAN, which has 17 DoF. The experimental setup is shown in
Figure 4.
To generate trajectories for the robot joints, we use a custom variable-height bipedal walking generator. Given the z-axis CoM trajectory provided by the RL, we use the ZMP (Zero Moment Point) concept for deriving the x- and y-axis CoM trajectories.
To calculate the reward, we measure the actual electrical energy used by the motors of the robot. The return of a rollout,
τ, depends on the average electric energy consumed per walking cycle and is defined as:
where
J is the set of joints whose energy consumption we try to minimize,
is the accumulated consumed electric energy for the motor of the
j-th individual joint of COMAN and
k is a scaling constant. To reduce the effect of noise on the measurement, for each rollout, the robot walks for 16 s (from time
to
), which corresponds to eight steps (
walking cycles).
The learning converged after 150 rollouts. The total cumulative distance traveled by the robot during our experiments was 0.5 km. The discovered optimal policy by the RL algorithm, for which the lowest energy consumption was achieved, consumes 18% less energy than a conventional fixed-height walking, which is a significant improvement.
In summary, the proposed evolving policy parameterization demonstrates three major advantages:
it achieves faster convergence and higher rewards than the fixed policy parameterization, using varying resolution for the policy parameterization, thus addressing the adaptability and multi-resolution challenges;
it exhibits much lower variance of the generated policies, addressing the gradual exploration challenge;
it helps to avoid local minima, thus addressing the globality challenge.
The described approach has been successfully applied also to other robot locomotion tasks, such as learning to optimize the walking speed of a quadruped robot [
43].
7. Example C: Archery-Based Aiming Task
This example addresses mainly the
multi-dimensionality and
convergence speed challenges described in
Section 3. We show that RL in combination with regression yields an extremely fast-converging algorithm, and we demonstrate it in practice using the iCubhumanoid robot to quickly learn the skill of archery.
The goal of this example is to develop an integrated approach allowing the humanoid robot, iCub, to learn the skill of archery. After being instructed how to hold the bow and release the arrow, the robot learns by itself to shoot the arrow in such a way that it hits the center of the target. Two learning algorithms are introduced and compared to learn the bi-manual skill: one with Expectation-Maximization-based reinforcement Learning and one with chained vector regression, called the Augmented Reward Chained Regression (ARCHER) algorithm. Both algorithms are used to modulate and coordinate the motion of the two hands, while an inverse kinematics controller is used for the motion of the arms. The approach is evaluated on the humanoid robot, iCub, where only the upper body is used for the experiment (38 DoF). The image processing part recognizes where the arrow hits the target and is based on Gaussian Mixture Models for color-based detection of the target and the arrow’s tip. More implementation details can be found in [
14].
7.1. Description of the Archery Task
The archery task is challenging because: (1) it involves bi-manual coordination; (2) it can be performed with slow movements of the arms and using small torques and forces; (3) it requires using tools (bow and arrow) to affect an external object (target); (4) it is an appropriate task for testing different learning algorithms and aspects of learning, because the reward is inherently defined by the high-level description of the task goal; (5) it involves integration of image processing, motor control and learning parts in one coherent task.
The focus of this task is on learning the bi-manual coordination necessary to control the shooting direction and velocity in order to hit the target. Two learning algorithms are introduced and compared: one with Expectation-Maximization-based reinforcement Learning and one with chained vector regression. Both algorithms are used to modulate and coordinate the motion of the two hands, while an inverse kinematics controller is used for the motion of the arms. We propose solutions to the learning part, the image processing part used to detect the arrow’s tip on the target and the motor control part of the archery training.
In the following two subsections, we introduce two different learning algorithms for the archery training. The focus of the proposed approach falls on learning the bi-manual coordination for shooting the arrow with a desired direction and velocity.
7.2. Learning Algorithm 1: PoWER
As a first approach for learning the bi-manual coordination needed in archery, we use the state-of-the-art EM-based RL algorithm, PoWER, by Kober
et al. [
18]. We selected the PoWER algorithm, because it does not need a learning rate (unlike policy-gradient methods) and also because it can be combined with importance sampling to make better use of the previous experience of the agent in the estimation of new exploratory parameters.
PoWER uses a parameterized policy and tries to find values for the parameters that maximize the expected return of rollouts (also called trials) under the corresponding policy. For the archery task, the policy parameters are represented by the elements of a 3D vector corresponding to the relative position of the two hands performing the task.
We define the return of an arrow shooting rollout,
τ, to be:
where
is the estimated 2D position of the center of the target on the target’s plane,
is the estimated 2D position of the arrow’s tip and
is Euclidean distance.
7.3. Learning Algorithm 2: ARCHER
For a second learning approach, we propose a custom algorithm developed and optimized specifically for problems like the archery training, which has a smooth solution space and prior knowledge about the goal to be achieved. We will refer to it as the ARCHER algorithm (Augmented Reward Chained Regression). The motivation for ARCHER is to make use of richer feedback information about the result of a rollout. Such information is ignored by the PoWER RL algorithm, because it uses scalar feedback, which only depends on the distance to the target’s center. ARCHER, on the other hand, is designed to use the prior knowledge we have on the optimum reward possible. In this case, we know that hitting the center corresponds to the maximum reward we can get. Using this prior information about the task, we can view the position of the arrow’s tip as an augmented reward. In this case, it consists of a two-dimensional vector giving the horizontal and vertical displacement of the arrow’s tip with respect to the target’s center. This information is obtained by the image processing algorithm in
Section 7.4 during the real-world experiment. Then, ARCHER uses a chained local regression process that iteratively estimates new policy parameters, which have a greater probability of leading to the achievement of the goal of the task, based on experience, so far.
Each rollout, , where , is initiated by input parameters, , which is the vector describing the relative position of the hands and is produced by the learning algorithms. Each rollout has an associated observed result (considered as a two-dimensional reward), , which is the relative position of the arrow’s tip with respect to the target’s center, . The unknown function, f, is considered to be non-linear due to air friction, wind flow, friction between the bow and the arrow, etc.
Without loss of generality, we assume that the rollouts are sorted in descending order by their scalar return calculated by Equation (
6),
i.e.,
,
i.e., that
is the closest to
. For convenience, we define vectors,
and
. Then, we represent the vector,
, as a linear combination of vectors using the
N best results:
Under the assumption that the original parameter space can be linearly approximated in a small neighborhood, the calculated weights,
, are transferred back to the original parameter space. Then, the unknown vector to the goal parameter value,
, is approximated with
as a linear combination of the corresponding parameter vectors using the same weights:
In a matrix form, we have , where W contains the weights, , and U contains the collected vectors, , from the observed rewards of N rollouts. The least-norm approximation of the weights is given by , where is the pseudoinverse of U. By repeating this regression process when adding a new couple, , to the dataset at each iteration, the algorithm refines the solution by selecting at each iteration the N closest points to . ARCHER can thus be viewed as a linear vector regression with a shrinking support region.
The ARCHER algorithm can also be used for other tasks, provided that: (1) a priori knowledge about the desired target reward is known; (2) the reward can be decomposed into separate dimensions; and (3) the task has a smooth solution space.
7.4. Image Processing Algorithm
The problem of detecting where the target is and what is the relative position of the arrow with respect to the center of the target is solved by image processing. We use color-based detection of the target and the tip of the arrow based on the Gaussian Mixture Model (GMM). Two separate GMM models are fitted to represent the target’s and arrow’s color characteristics in YUVcolor space. After each shot, the reward vector, , is calculated as , where is the estimated center of the arrow and is the estimated center of the target.
7.5. PoWER vs. ARCHER (RL vs. Regression)
The two proposed learning algorithms (PoWER and ARCHER) are first evaluated in a simulation experiment. The trajectory of the arrow is modeled as a simple ballistic trajectory, ignoring air friction, wind velocity,
etc. A typical experimental result for each algorithm is shown in
Figure 7. A comparison of the convergence of the two algorithms is shown in
Figure 8. The ARCHER algorithm clearly outperforms the PoWER algorithm for the archery task. This is due to the use of 2D feedback information, which allows ARCHER to make better estimations/predictions of good parameter values, and to the prior knowledge concerning the maximum reward that can be achieved. PoWER, on the other hand, achieves reasonable performance despite using only 1D feedback information.
Based on the results from the simulated experiment, the ARCHER algorithm was chosen to conduct the following real-world experiment:
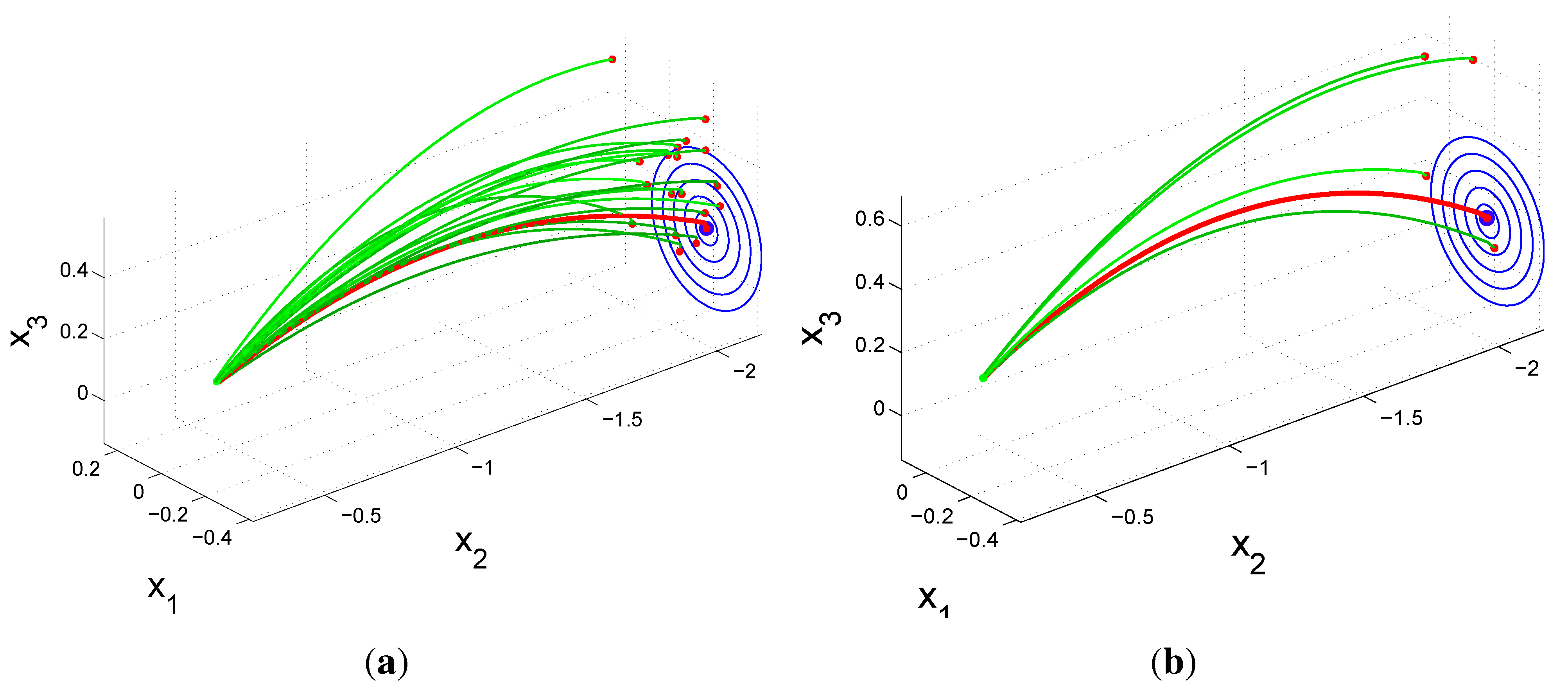
Figure 7.
Simulation of archery. Learning is performed under the same starting conditions with two different algorithms. The red trajectory is the final rollout. (a) The PoWER algorithm needs 19 rollouts to reach the center; (b) The ARCHER algorithm needs five rollouts to do the same.
Figure 7.
Simulation of archery. Learning is performed under the same starting conditions with two different algorithms. The red trajectory is the final rollout. (a) The PoWER algorithm needs 19 rollouts to reach the center; (b) The ARCHER algorithm needs five rollouts to do the same.
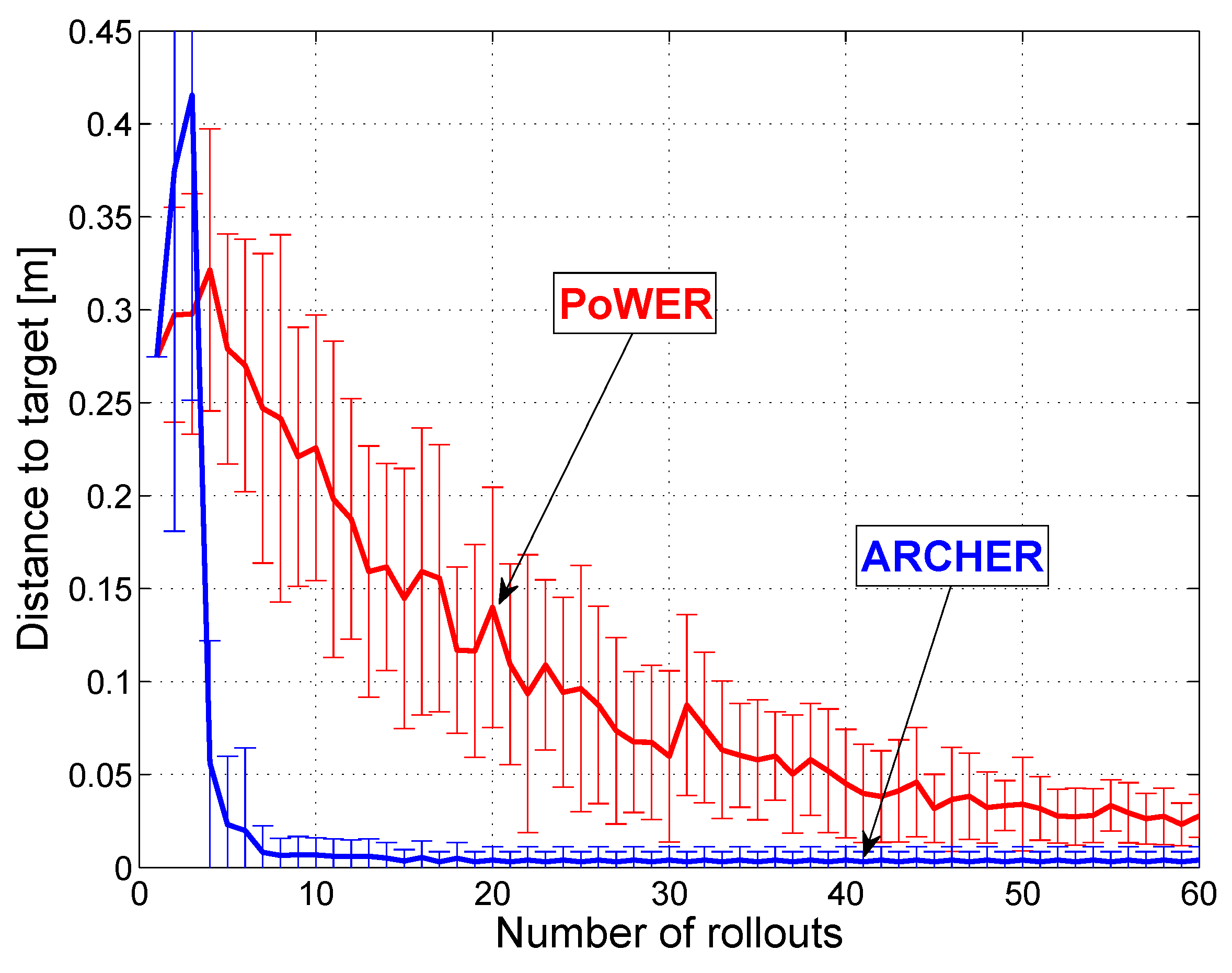
Figure 8.
Comparison of the speed of convergence for the PoWER and ARCHER algorithms. Statistics are collected from 40 learning sessions with 60 rollouts in each session. The first three rollouts of ARCHER are done with large random exploratory noise, which explains the big variance at the beginning.
Figure 8.
Comparison of the speed of convergence for the PoWER and ARCHER algorithms. Statistics are collected from 40 learning sessions with 60 rollouts in each session. The first three rollouts of ARCHER are done with large random exploratory noise, which explains the big variance at the beginning.
7.6. Experimental Results on the iCub Robot
The real-world robot experimental setup is shown in
Figure 9. The experiment was conducted with iCub [
44]. The iCub is an open-source robotic platform with dimensions comparable to a three and a half year-old child (about 104cm tall), with 53° of freedom (DOF) distributed on the head, torso, arms, hands and legs.
Figure 9.
Experimental setup for the archery task. A position-controlled 53-DOF humanoid robot, iCub, learns to shoot arrows using a bow and learns to hit the center of the target using the RL algorithm and visual feedback from a camera. Real-world experiment using the iCub. The distance between the target and the robot is 2.2 m. The diameter of the target is 50 cm.
Figure 9.
Experimental setup for the archery task. A position-controlled 53-DOF humanoid robot, iCub, learns to shoot arrows using a bow and learns to hit the center of the target using the RL algorithm and visual feedback from a camera. Real-world experiment using the iCub. The distance between the target and the robot is 2.2 m. The diameter of the target is 50 cm.
In the experiment, we used the torso (three DoF), arms (seven DoF each) and hands (nine DoF each). The thick blue arrow shows the relative position of the two hands, which is controlled by the learning algorithm during the learning sessions.
To robot’s arms are controlled using inverse kinematics solved as an optimization under an inequality constraints problem. The posture of the iCub’s arms and the grasping configuration for the bow and the arrow are shown in
Figure 9. During the experiment, while the robot is learning, between every trial shot, it is adjusting the relative position and orientation of the two hands, which, in turn, controls the direction and speed of the arrow. The desired relative position between the two hands is given by the learning algorithm before each trial. The orientation of the two hands is calculated in such a way that the bow is kept vertical.
The real-world experiment was conducted using the proposed ARCHER algorithm and the proposed image processing method. During the real experiments, the ARCHER algorithm needed less than 10 rollouts to converge to the center.
For the archery task, we can conclude that a local regression algorithm, like ARCHER, performs better than a state-of-the-art RL algorithm. The experiments show significant improvement in terms of speed of convergence, which is due to the use of a multi-dimensional reward and prior knowledge about the optimum reward that one can reach.
8. Summary and Comparison of the Robot Learning Tasks
Table 2 summarizes the high-level properties of the three presented RL problems (rows 1–3). In addition, a comparison is made with three other robot skill learning problems (rows 4–6) in which, also, the goal is to learn motor skills. Based on the empirical results about the best-performing approach in each of these particular situations, the following conclusions can be drawn:
Reinforcement learning is well suited for highly-dynamic tasks, where there is a clear measure about the success of the task;
Imitation learning works well for slow tasks, which are easy to demonstrate and which do not have a clear optimal way of execution;
Regression-based learning performs well in cases when the goal is known in advance, and it is possible to exploit a multi-dimensional feedback in the learning algorithm.
Table 2.
Comparison of the three presented RL problems (rows 1–3) with three other robot skill learning problems (rows 4–6). DMP, Dynamic Movement Primitives; CoM, center of mass.
Table 2.
Comparison of the three presented RL problems (rows 1–3) with three other robot skill learning problems (rows 4–6). DMP, Dynamic Movement Primitives; CoM, center of mass.
| No. | Task | Dimensionality | Task dynamics | Noise and uncertainty | Best performing approach |
|---|
| 1 | Pancake flipping | High (positions and stiffness for each attractor) | Very high | High | RL + DMP |
| 2 | Walking optimization | Medium (continuous trajectory of CoM) | High | High | RL + evolving policy |
| 3 | Archery | Low (relative pose of hands) | Low (static shooting pose) | Medium | Regression |
| 4 | Ironing [3] | Medium (pose of end-effector) | Low
(slow movement) | Low | Imitation learning + DMP |
| 5 | Whiteboard cleaning [6] | Medium (pose and force at end-effector) | Low
(slow movement, medium forces) | Medium |
| 6 | Door opening [3] | Medium (pose and force at end-effector) | Low
(slow movement, high forces) | Medium |
9. The Future of Reinforcement Learning in Robotics
What does the future hold for RL in robotics? This seems difficult to predict for RL, but it is relatively easier to predict the near-future trend for robotics. Robotics is moving towards higher and higher DoF robots, having more nonlinear elements, variable passive compliance, variable damping, flexible joints, reconfigurability, fault tolerance, independence, power autonomy, etc. Robots will be progressively going out of the robot labs and into everyday life.
As the robot hardware complexity increases to higher levels, the conventional engineering approaches and analytical methods for robot control will start to fail. Therefore, machine learning (and RL, in particular) will inevitably become a more and more important tool to cope with the ever-increasing complexity of the physical robotic systems. Furthermore, the future RL candidates will have to address an ever-growing number of challenges accordingly.
10. Beyond Reinforcement Learning
Turning back to
Table 1, in the bottom row, we have made a prediction, based on extrapolation of the trend in the existing approaches for teaching robots. The result of this extrapolation has lead us to a hypothetical approach that we call
goal-directed learning. For example, a goal could be “throw the basketball through the hoop”, and it could actually be specified as human-readable text and require natural language processing to understand it. Note that this is different from unsupervised learning, where there is not any goal specified by a teacher, but the system is performing self-organization.
The hypothetical goal-directed learning could be “emulated” using the existing RL methods, but it would be extremely inefficient. For instance, it would be similar to learning how to play chess based on only terminal reward (win, lose or draw) without the possibility to assess any intermediate chessboard configurations. This means that in goal-directed learning, novel mechanisms should be invented to autonomously guide the exploration towards the goal, without any help from a human teacher, and extensively using a bias from the previous experience of the agent.
Another promising direction is to move towards semantics, where the robot will have direct knowledge about the goal and the meaning of achieving it. This is contrary to the current approaches, where the robot never has any direct information about the goal of the task, and it blindly executes trajectories without realizing their outcome and meaning in the real world.
Ideally, the robot should be aware of what it is doing, what the goal is and should be able to evaluate its own partial incremental progress by itself, using a self-developed internal performance metric. This is a far more natural mechanism for self-improvement than the currently employed method of providing an externally-imposed reward function.
11. Conclusions
We summarized the state-of-the-art for RL in robotics, in terms of both algorithms and policy representations. We identified a significant number of the existing challenges for policy representations in robotics. Three examples for extensions of the capabilities of policy representations on three real-world tasks were presented: pancake flipping, bipedal walking and archery aiming. In these examples, we proposed solutions to six rarely-addressed challenges in policy representations: correlations, adaptability, multi-resolution, globality, multi-dimensionality and convergence. Finally, we attempted to have a peek into the future of RL and its significance to robotics.