An Improved Reinforcement Learning System Using Affective Factors
Abstract
:1. Introduction
2. An Improved Q Learning
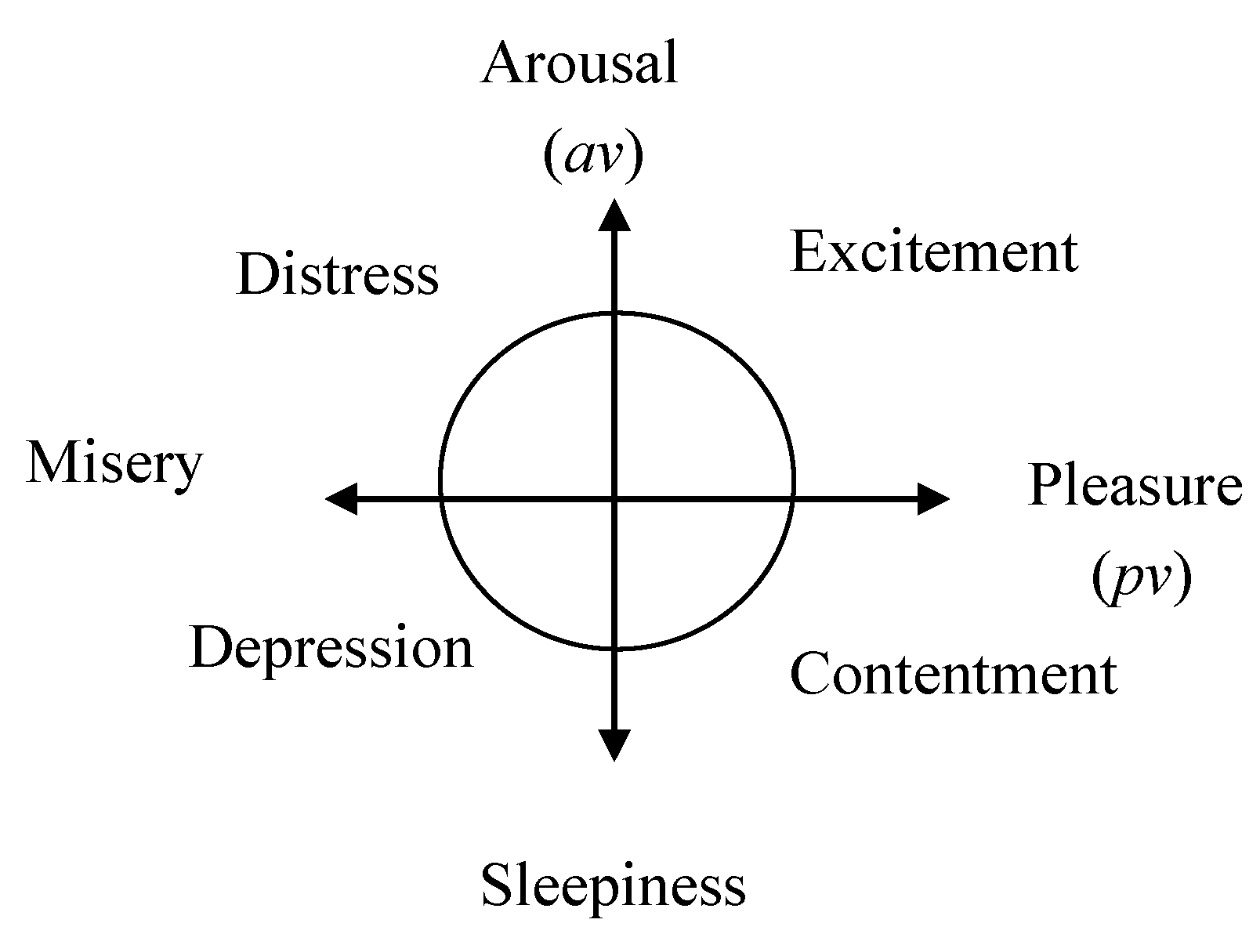
2.1. Russell’s Affect Model
2.2. Emotion Function





- Rule A: Pleasure pvi(e) concerns with the distance between the agent i, i ∈ {1,2,…,N} and the goal (Equation (5)) if the situation e means that the goal is perceived .
- Rule B: Arousal avi(e) increases when the eliciting situation is continued (Equation (4)).
- Rule C: Emotion state Emoi(e) (Equations (1–3)) of agent i in the eliciting situation e is expressed by the multiplication of Pleasurepvi(e) or pvj(e) (Equation (5)) and Arousal avi(e) or avj(e) (Equation (4)).
- Rule D: Emotion state Emoi(e) is constructed and changed by stimuli from objects and events: perceiving the goal or other agents dynamically (Equations (1–5)).
2.3. A Motivation Function


2.4. Policy to Select an Action

2.5. Learning Algorithm
- Step 1
- Initialize Qi(s,a) = 0; avi = 0 for each agent i, i ∈ {1,2,…,N} and all obserable states s ∈ S and actions.
- Step 2
- Repeat following in each episode.
- (1)
- Return to the initial state.
- (2)
- Repeat the following until the final state.
- Observe the state si ∈ S of the environment, judge the situation ei ∈ E if the goal or other agents appear in perceivable area, calculate emotion Emoi(e) and motivation Mi(s, Emoi(e), a) at the state si and situation ei of each selectable actions, select an action ai ∈ A according to the stochastic policy (Equation (8)).
- Execute the action ai; observe a reward r and next state si’.
- Renew Qi(s,a) according to Equation (6).
- (3)
- si ← si’
- Step 3
- Stop if episodes are repeated enough.
3. Computer Simulation
3.1. Definition of Pursuit Problem
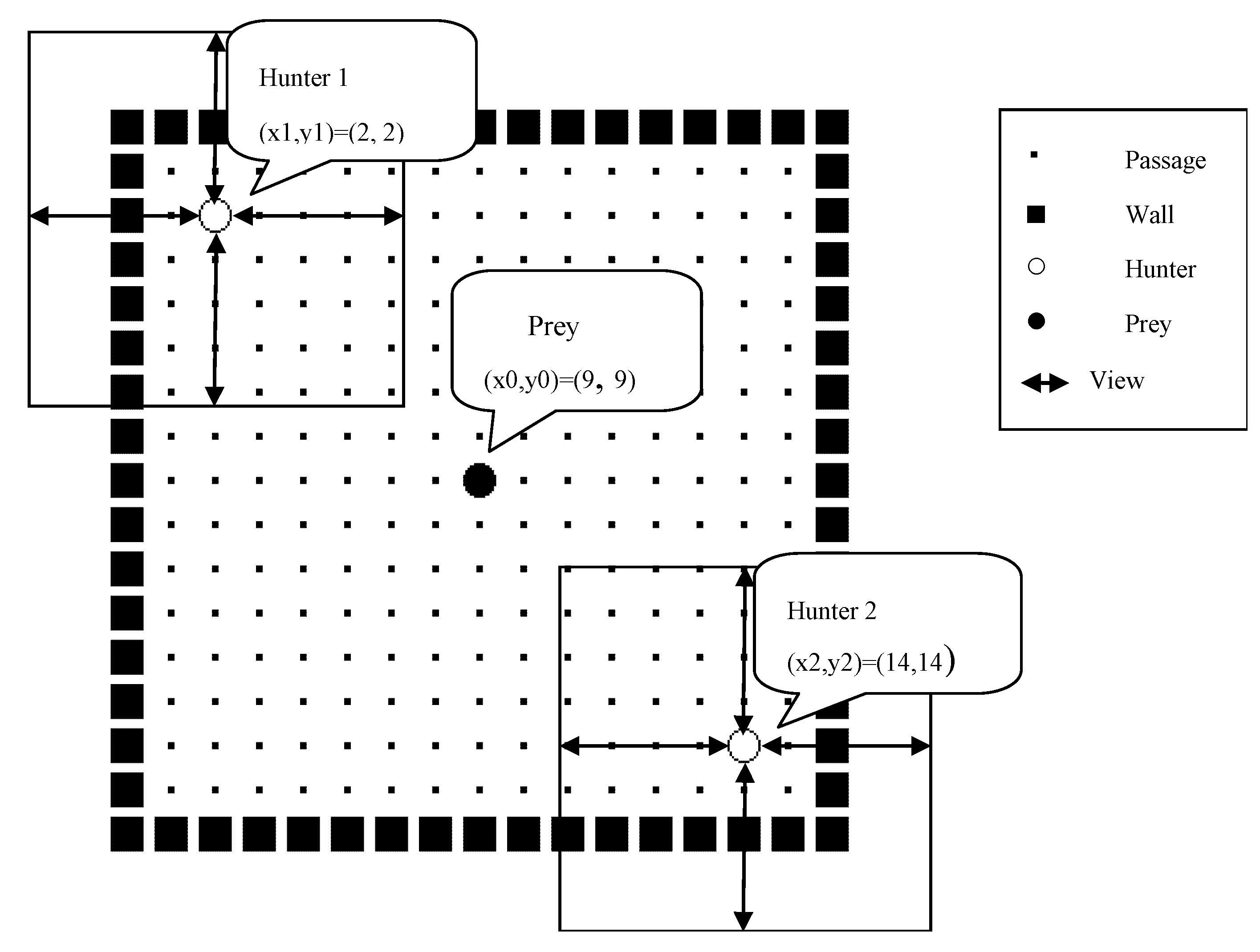
| Description | Symbol | Value |
|---|---|---|
| Episode limitation | Episode | 200 times |
| Exploration limitation in one episode | step | 10,000 steps |
| Size of the environment | X × Y | 17 × 17 grids |
| Threshold (depth) of perceive field | Depth | 4 grids |
| Number of hunter | i | 2, 3, 4 |
| Number of action/situation | a/e | 4 |
| Parameter | Symbol | Q learning | Proposed method |
|---|---|---|---|
| Learning rate | α | 0.9 | 0.9 |
| Damping constant | γ | 0.9 | 0.9 |
| Temperature (initial value) | T | 0.99 | 0.994 |
| Reward of prey captured by 2 hunters | r1 | 10.0 | 10.0 |
| Reward of prey captured by 1 hunter | r2 | 1.0 | 1.0 |
| Reward of one step movement | r3 | −0.1 | −0.1 |
| Reward of wall crash | r4 | −1.0 | −1.0 |
| Parameter | Symbol | Value |
|---|---|---|
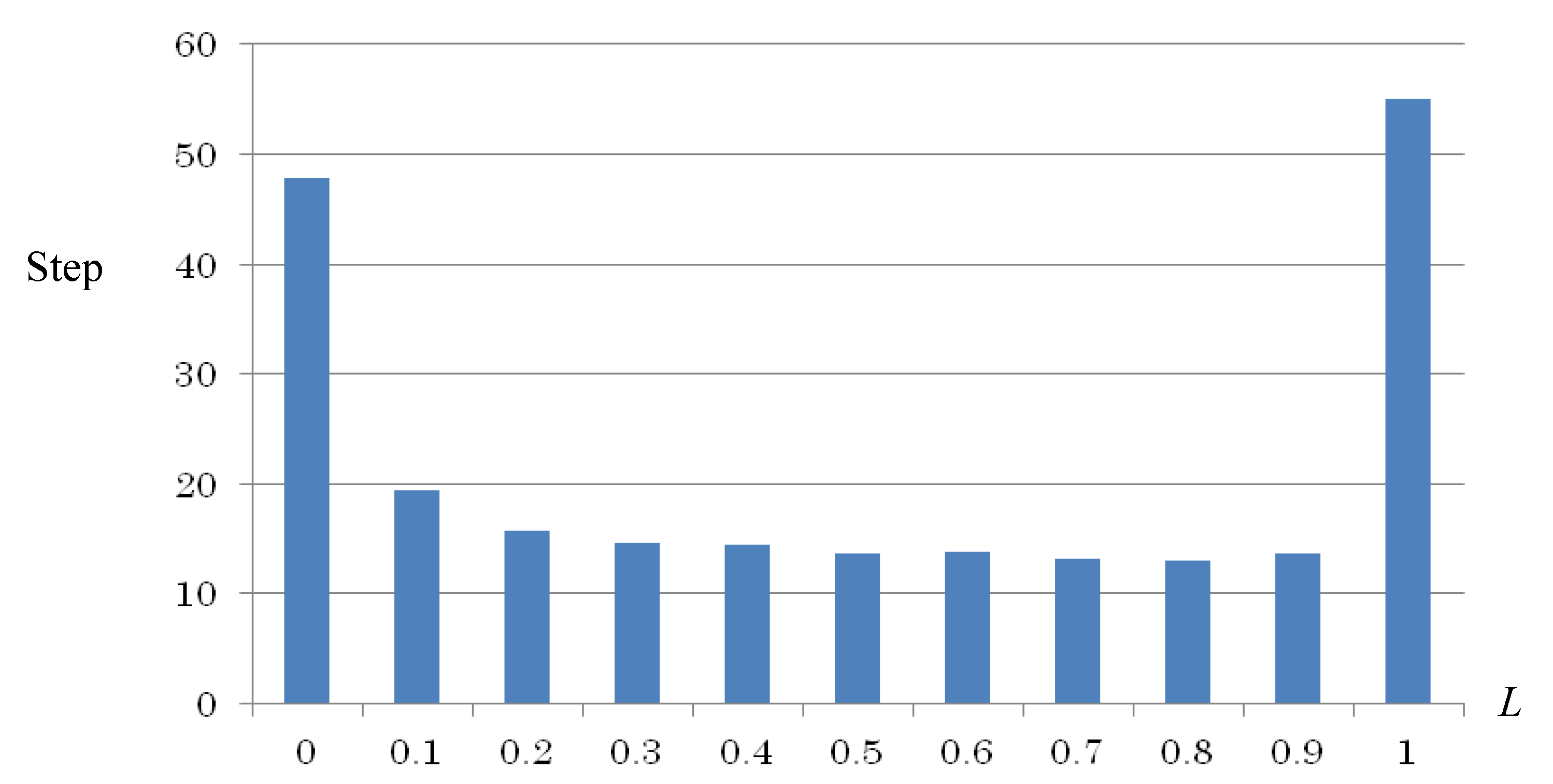
| Coefficient of Emo | L | 0.5 |
| Coefficient of Pleasure | Pv | 200.0 |
| Initial value of Arousal | Av | 1.0 |
| Modification of Arousal | Δav | 0.01 |
| Constant of Gaussian function | σ | 8.0 |
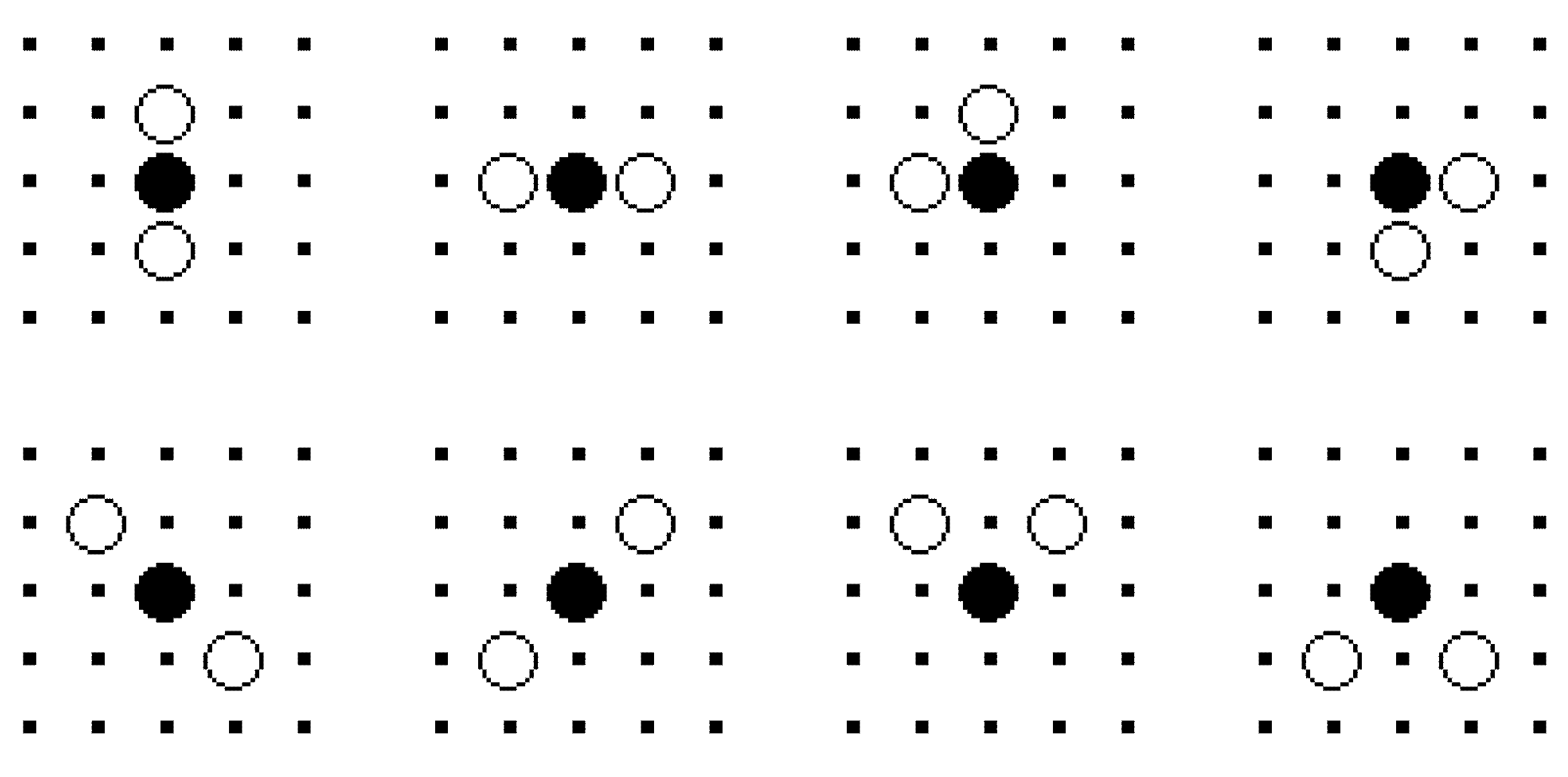
3.2. Results of Simulation with a Static Prey
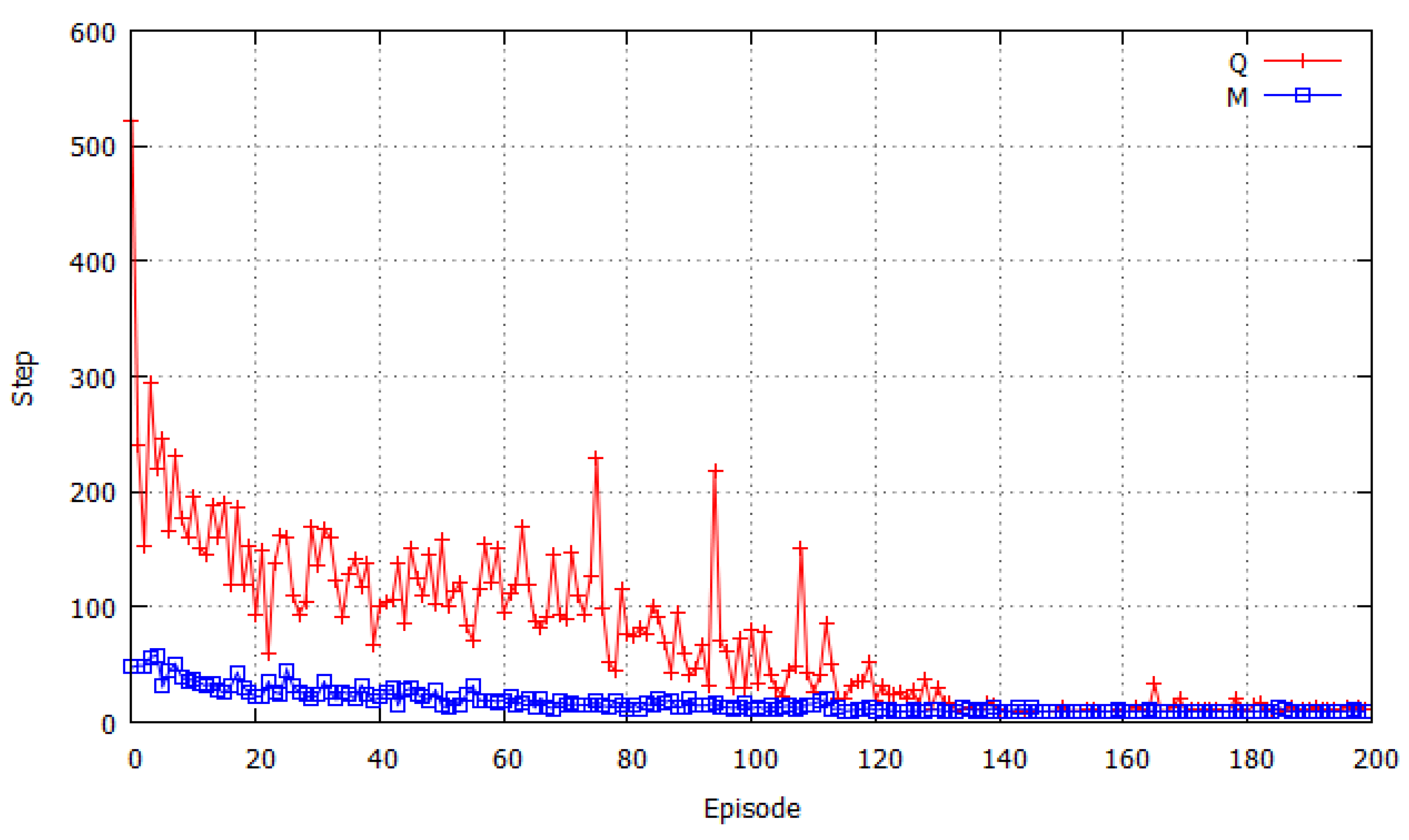
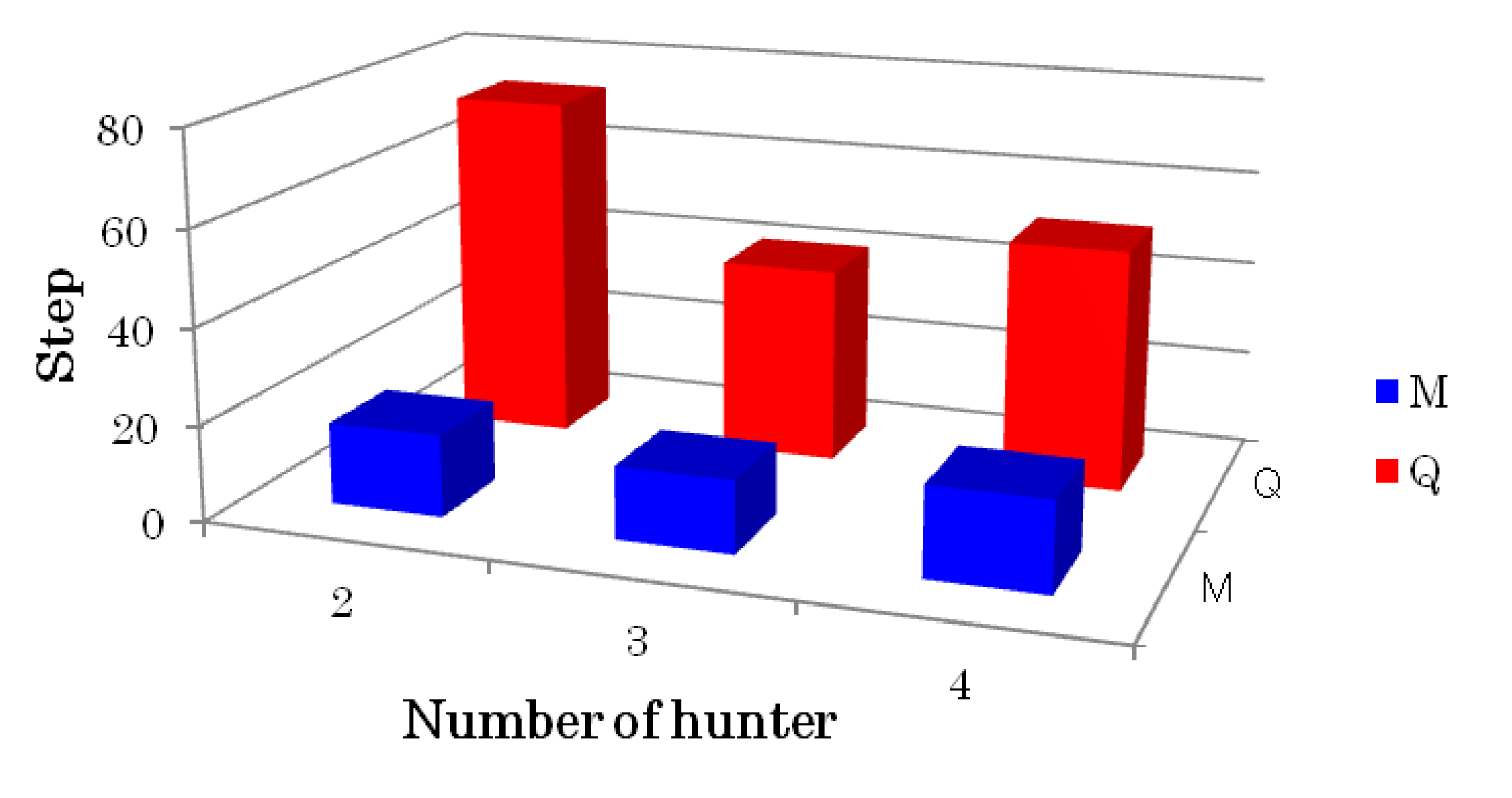
| Number of hunter | Q learning | Proposed method |
|---|---|---|
| 2 | 72.9 | 17.1 |
| 3 | 41.1 | 15.0 |
| 4 | 50.7 | 18.6 |
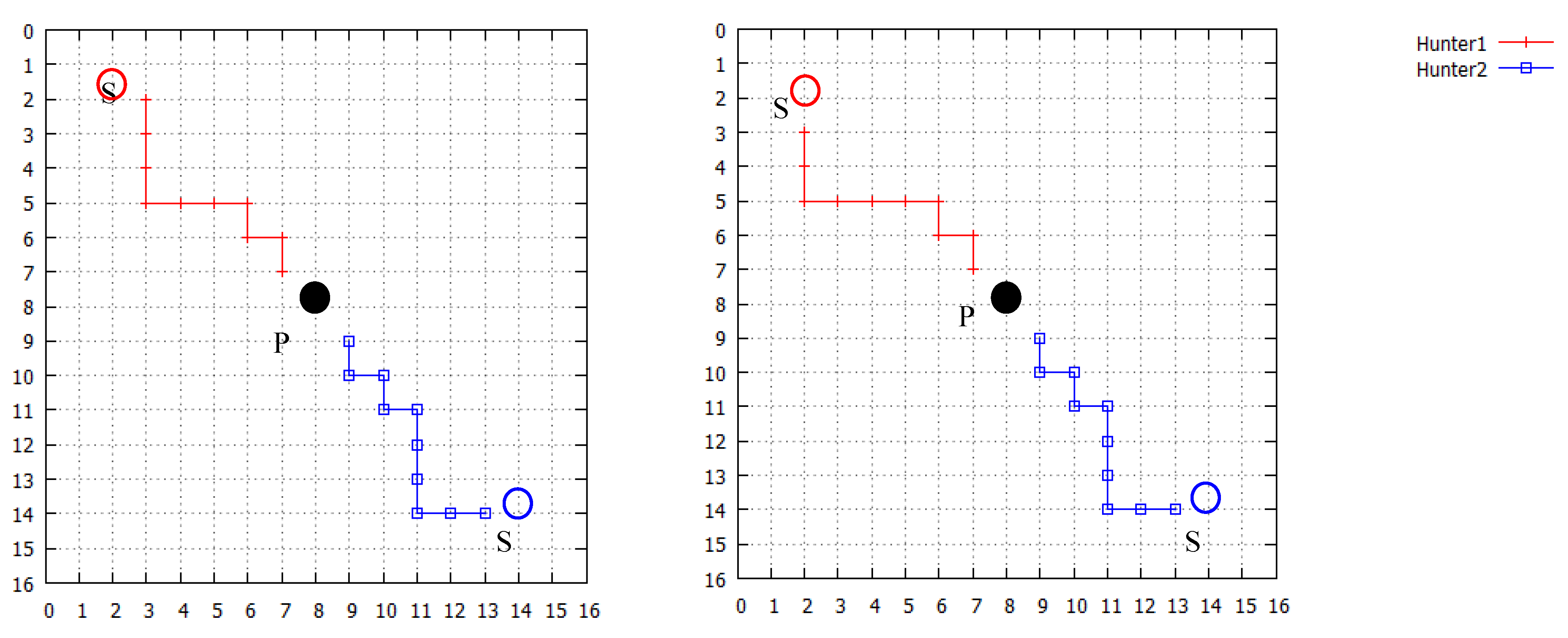
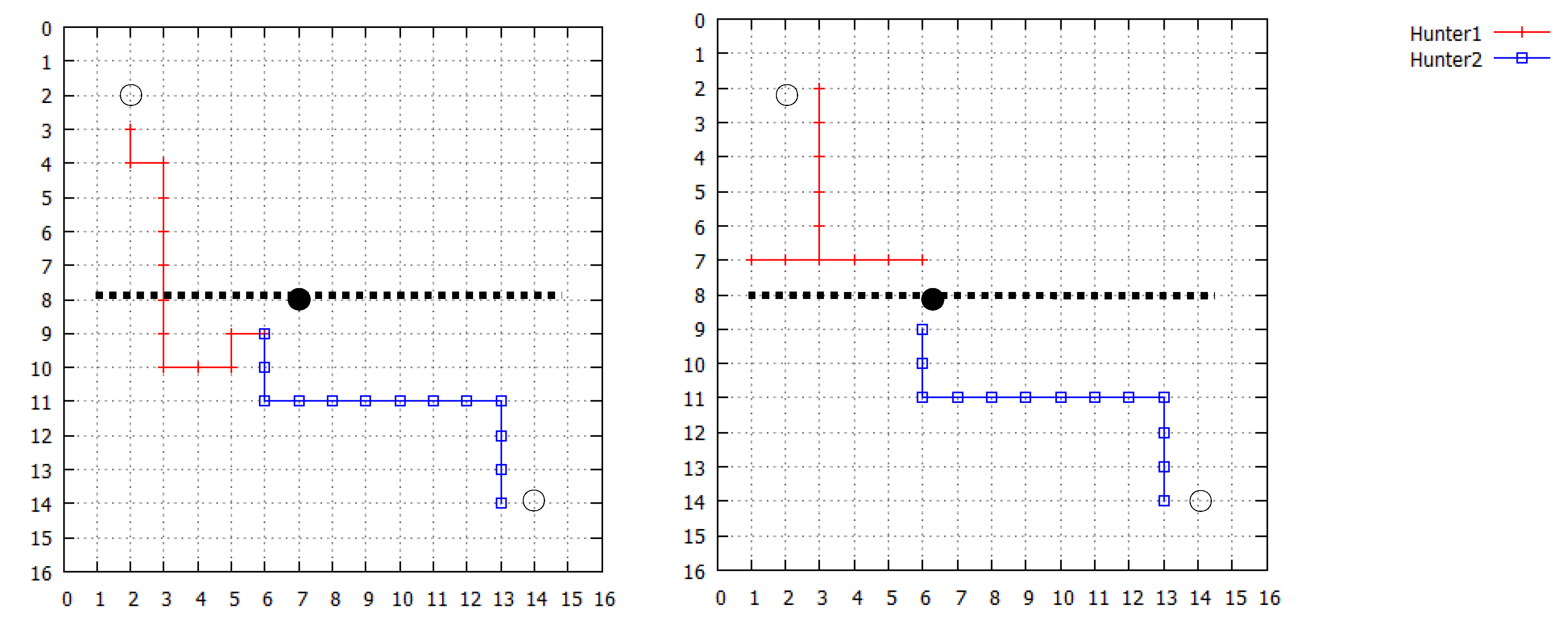
3.3. Results of Simulation with a Dynamic Prey
| Parameter | Symbol | QL | Proposed method |
|---|---|---|---|
| Learning rate | α | 0.9 | 0.9 |
| Damping constant | γ | 0.9 | 0.9 |
| Temperature (initial value) | T | 0.99 | 0.99 |
| Reward of prey captured by 2 hunters | r1 | 10.0 | 10.0 |
| Reward of prey captured by 1 hunter | r2 | 1.0 | 1.0 |
| Reward of one step movement | r3 | −0.1 | −0.1 |
| Reward of wall crash | r4 | −1.0 | −1.0 |
| Coefficient of Emo | L | - | 0.5 |
| Coefficient of Pleasure | Pv | - | 10.0 |
| Initial value of Arousal | Av | - | 1.0 |
| Modification of Arousal | Δav | - | 0.1 |
| Constant of Gaussian function | σ | - | 8.0 |

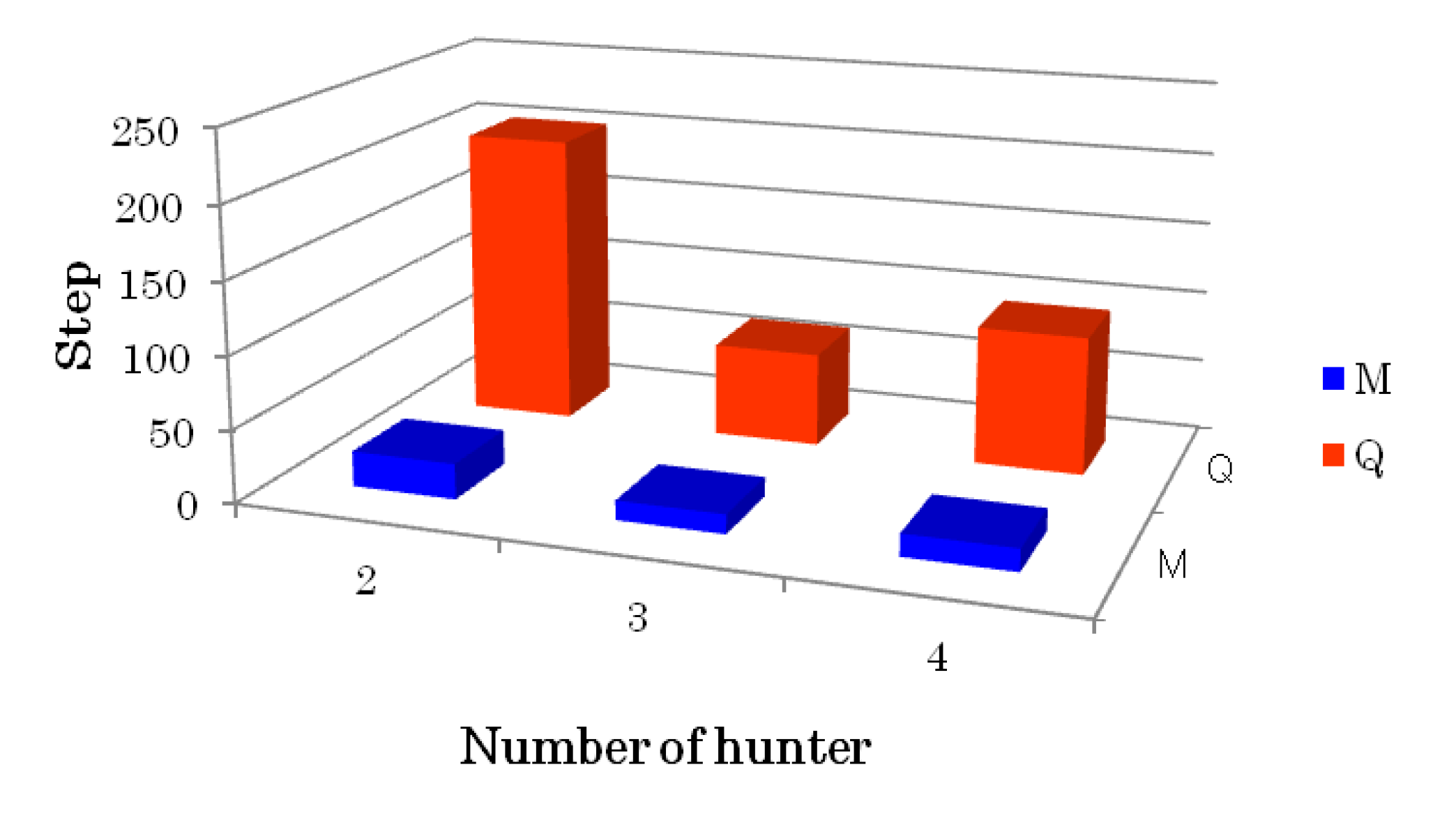
| Number of hunter | Q learning (QL) | Proposed model (DEM) |
|---|---|---|
| 2 | 202.7 | 24.4 |
| 3 | 65.1 | 13.3 |
| 4 | 96.0 | 15.3 |
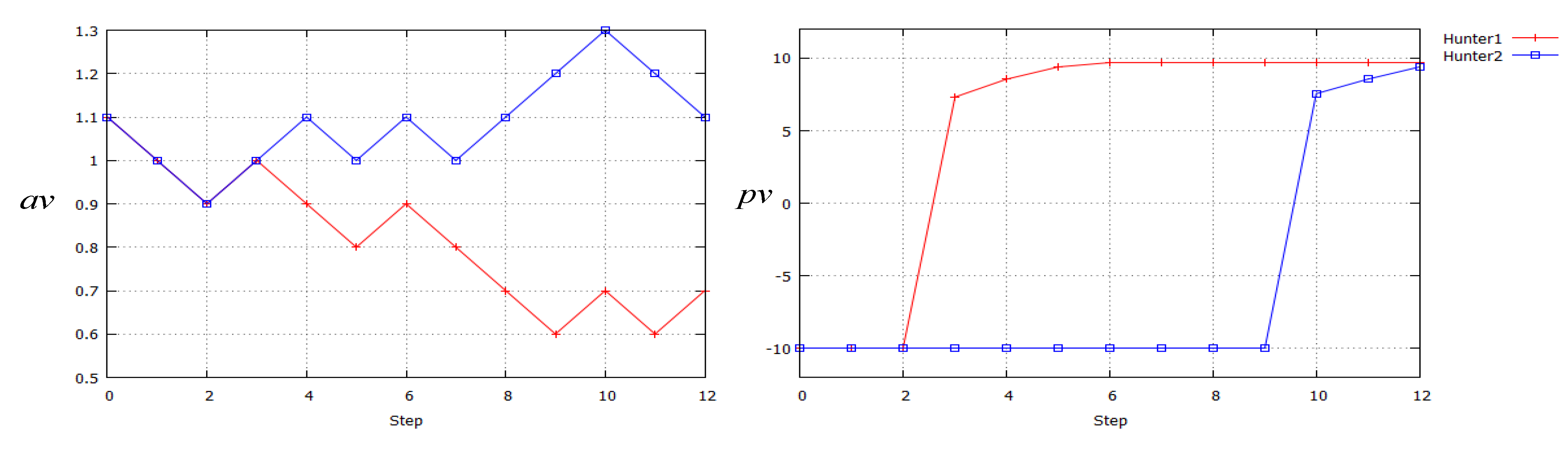
4. Discussions
5. Conclusions and Future Works
Acknowledgments
Conflict of Interest
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; The MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Doya, K. Metalearning and neuromodulation. Neural Netw. 2002, 15, 495–506. [Google Scholar] [CrossRef]
- Asada, M.; Uchibe, E.; Hosoda, K. Cooperative behavior acquisition for mobile robots in dynamically changing real worlds via vision-based reinforcement learning and development. Artif. Intell. 1999, 110, 275–292. [Google Scholar] [CrossRef]
- Kollar, T.; Roy, N. Trajectory optimization using reinforcement learning for map exploration. Int. J. Robot. Res. 2008, 27, 175–196. [Google Scholar] [CrossRef]
- Jouffe, L. Fuzzy inference system learning by reinforcement learning. IEEE Trans. Syst. Man Cybern. B 1998, 28, 338–355. [Google Scholar] [CrossRef]
- Obayashi, M.; Nakahara, N.; Kuremoto, T.; Kobayashi, K. A robust reinforcement learning using concept of slide mode control. Artif. Life Robot. 2009, 13, 526–530. [Google Scholar] [CrossRef]
- Kuremoto, T.; Obayashi, M.; Yamamoto, A.; Kobayashi, K. Predicting Chaotic Time Series by Reinforcement Learning. In Proceedings of the 2nd International Conference on Computational Intelligence, Robotics, and Autonomous Systems, Singapore, 15–18 December 2003.
- Kuremoto, T.; Obayashi, M.; Kobayashi, K. Nonlinear prediction by reinforcement learning. Lect. Note. Comput. Sci. 2005, 3644, 1085–1094. [Google Scholar]
- Kuremoto, T.; Obayashi, M.; Kobayashi, K. Forecasting Time Series by SOFNN with Reinforcement Learning. In Proceedings of the 27th Annual International Symposium on Forecasting, Neural Forecasting Competition (NN3), New York, NY, USA, 24–27 June 2007.
- Kuremoto, T.; Obayashi, M.; Kobayashi, K. Neural forecasting systems. In Reinforcement Learning, Theory and Applications; Weber, C., Elshaw, M., Mayer, N.M., Eds.; InTech: Vienna, Austria, 2008; pp. 1–20. [Google Scholar]
- Kuremoto, T.; Obayashi, M.; Kobayashi, K.; Adachi, H.; Yoneda, K. A Reinforcement Learning System for Swarm Behaviors. In Proceedings of IEEE World Congress Computational Intelligence (WCCI/IJCNN 2008), Hong Kong, 1–6 June 2008; pp. 3710–3715.
- Kuremoto, T.; Obayashi, M.; Kobayashi, K. Swarm behavior acquisition by a neuro-fuzzy system and reinforcement learning algorithm. Int. J. Intell. Comput. Cybern. 2009, 2, 724–744. [Google Scholar] [CrossRef]
- Kuremoto, T.; Obayashi, M.; Kobayashi, K.; Adachi, H.; Yoneda, K. A neuro-fuzzy learning system for adaptive swarm behaviors dealing with continuous state space. Lect. Notes Comput. Sci. 2008, 5227, 675–683. [Google Scholar]
- Kuremoto, T.; Obayashi, M.; Kobayashi, K. An improved internal model for swarm formation and adaptive swarm behavior acquisition. J. Circuit. Syst. Comput. 2009, 18, 1517–1531. [Google Scholar] [CrossRef]
- Sycara, K.P. Multi-agent systems. Artif. Intell. Mag. 1998, 19, 79–92. [Google Scholar]
- Mataric, J. Reinforcement learning in multi-robot domain. Auton. Robot. 1997, 4, 77–93. [Google Scholar] [CrossRef]
- Makar, R.; Mahadevan, S. Hierarchical multi agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2000, 12, 345–352. [Google Scholar]
- Kobayashi, K.; Kurano, T.; Kuremoto, T.; Obayashi, M. Cooperative behavior acquisition using attention degree. Lect. Notes Comput. Sci. 2012, 7665, 537–544. [Google Scholar]
- Barto, A.G.; Sutton, R.S.; Anderson, C.W. Neuron-like adaptive elements that can solve difficult learning control problems. IEEE Trans. Syst. Man. Cybern. 1983, 13, 834–846. [Google Scholar]
- Sutton, R.S. Learning to predict by the method of temporal difference. Mach. Learn. 1988, 3, 9–44. [Google Scholar]
- Watkins, C.; Dayan, P. Technical note: Q-learning. Mach. Learn. 1992, 8, 55–68. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. Adv. Neural Inf. Process. 2000, 12, 1008–1014. [Google Scholar]
- LeDoux, J.E. The Emotional Brain: The Mysterious Underpinnings of Emotional Life; Siman & Schuster: New York, NY, USA, 1996. [Google Scholar]
- Greenberg, L. Emotion and cognition in psychotherapy: The transforming power of affect. Can. Psychol. 2008, 49, 49–59. [Google Scholar] [CrossRef]
- Sato, S.; Nozawa, A.; Ide, H. Characteristics of behavior of robots with emotion model. IEEJ Trans. Electron. Inf. Syst. 2004, 124, 1390–1395. [Google Scholar] [Green Version]
- Kusano, T.; Nozawa, A.; Ide, H. Emergent of burden sharing of robots with emotion model (in Japanese). IEEJ Trans. Electron. Inf. Syst. 2005, 125, 1037–1042. [Google Scholar] [Green Version]
- Larsen, R.J.; Diener, E. Promises and problems with the circumplex model of emotion. In Review of Personality and Social Psychology; Clark, M.S., Ed.; Sage: Newbury Park, CA, USA, 1992; Volume 13, pp. 25–59. [Google Scholar] [Green Version]
- Russell, J.A. A circumplex model of affect. J. Personal. Soc. Psychol. 1980, 39, 1161–1178. [Google Scholar] [CrossRef]
- Kuremoto, T.; Obayashi, M.; Kobayashi, K.; Feng, L.-B. Autonomic behaviors of swarm robots driven by emotion and curiosity. Lect. Notes Comput. Sci. 2010, 6630, 541–547. [Google Scholar]
- Kuremoto, T.; Obayashi, M.; Kobayashi, K.; Feng, L.-B. An improved internal model of autonomous robot by a psychological approach. Cogn. Comput. 2011, 3, 501–509. [Google Scholar] [CrossRef]
- Russell, J.A.; Feldman Barrett, L. Core affect, prototypical emotional episodes, and other things called emotion: Dissecting the elephant. J. Personal. Soc. Psychol. 1999, 76, 805–819. [Google Scholar] [CrossRef]
- Russell, J.A. Core affect and the psychological construction of emotion. Psychol. Rev. 2003, 110, 145–172. [Google Scholar] [CrossRef]
- Wundn, W. Outlines of Psychology; Wilhem Englemann: Leipzig, Germany, 1897. [Google Scholar]
- Ortony, A.; Clore, G.; Collins, A. The Cognitive Structure of Emotions; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Jaakkola, T.; Singh, S.P.; Jordan, M.I. Reinforcement learning algorithm for partially observable Markov decision problems. Adv. Neural Inf. Process. Syst. 1994, 7, 345–352. [Google Scholar]
- Agogino, A.K.; Tumer, K. Quicker Q-Learning in Multi-Agent Systems. Available online: http://archive.org/details/nasa_techdoc_20050182925 (accessed on 30 May 2013).
- Augustine, A.A.; Hemenover, S.H.; Larsen, R.J.; Shulman, T.E. Composition and consistency of the desired affective state: The role of personality and motivation. Motiv. Emot. 2010, 34, 133–143. [Google Scholar] [CrossRef]
- Watanabe, S.; Obayashi, M.; Kuremoto, T.; Kobayashi, K. A New Decision-Making System of an Agent Based on Emotional Models in Multi-Agent System. In Proceedings of the 18th International Symposium on Artificial Life and Robotics, Daejeon, Korea, 30 January–1 February 2013; pp. 452–455.
- Aleksander, I. Designing conscious systems. Cogn. Comput. 2009, 1, 22–28. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kuremoto, T.; Tsurusaki, T.; Kobayashi, K.; Mabu, S.; Obayashi, M. An Improved Reinforcement Learning System Using Affective Factors. Robotics 2013, 2, 149-164. https://doi.org/10.3390/robotics2030149
Kuremoto T, Tsurusaki T, Kobayashi K, Mabu S, Obayashi M. An Improved Reinforcement Learning System Using Affective Factors. Robotics. 2013; 2(3):149-164. https://doi.org/10.3390/robotics2030149
Chicago/Turabian StyleKuremoto, Takashi, Tetsuya Tsurusaki, Kunikazu Kobayashi, Shingo Mabu, and Masanao Obayashi. 2013. "An Improved Reinforcement Learning System Using Affective Factors" Robotics 2, no. 3: 149-164. https://doi.org/10.3390/robotics2030149
APA StyleKuremoto, T., Tsurusaki, T., Kobayashi, K., Mabu, S., & Obayashi, M. (2013). An Improved Reinforcement Learning System Using Affective Factors. Robotics, 2(3), 149-164. https://doi.org/10.3390/robotics2030149