An AI Approach to Markerless Augmented Reality in Surgical Robots

Abstract

This paper examines the integration of markerless augmented reality (AR) within the da Vinci Surgical Robot, utilizing artificial intelligence (AI) for improved precision. The main challenge in creating AR for these systems is the small size (5 mm diameter) of the cameras used. Traditional camera-calibration approaches produce significant errors when used for miniature cameras. Further, the use of external markers can be obstructive and inaccurate in dynamic surgical environments. The study focuses on overcoming these limitations of traditional AR methods by employing advanced neural networks for camera calibration and real-time image processing. We demonstrate the use of a dense neural network to reduce the total projection error by directly learning the mapping of a 3D point to a 2D image plane. The results show a median error of 7 pixels (1.4 mm) when using a neural network, as compared to an error of 50 pixels (10 mm) when using a more traditional approach involving camera calibration and robot kinematics. This approach not only enhances the accuracy of AR for surgical procedures but also offers a more seamless integration with existing robotic platforms. These research findings underscore the potential of AI in revolutionizing AR applications in medical robotics and other teleoperated systems, promising efficient and safer interventions.

1. Introduction

Surgical robots have been adopted by many major hospitals in the United States due to the minimally invasive procedures, increased accuracy, and shorter operating times associated with these robots, factors which allow the patients to recover faster from their surgeries [1,2]. This growth in robot-assisted surgery (RAS) has in turn spurred an increase in research in this field in various aspects such as integration with Artificial Intelligence [3], natural language integration [4,5], augmented and virtual reality, etc. [4,6,7]. Augmented reality (AR) provides a unique interface for the surgeon as it can neatly overlay relevant information on the surgical scene without compromising any information of value. Moreover, AR can play crucial roles in surgical planning, localization of tumors, and recording procedures for educational purposes and for the training of new surgeons.

Despite its potential, the integration of AR into surgical systems faces significant challenges, particularly in achieving high tracking accuracy. The problem stems from cascading errors that propagate from inverse kinematics, in which small errors in the determination of joint angles can cause a significant error in the end-effector positions of the cameras or tools. The small stereo baseline in the endoscopic cameras adds an additional challenge to minimizing the errors in camera calibration. Several methods have been explored by various researchers to address this issue, such as addition of external fiducial markers and more comprehensive calibration, but these add an additional complexity to the surgical scene.

Neural networks have been shown to learn patterns with high accuracy, given enough training data and careful training. De Backer et al. [8] showed the use of AI to extract nonorganic items (including tools) using video images. In contrast, this paper explores the use of neural networks to learn the location of an object in an image, given the 3D position of the object and the 2D images from the camera. The innovation in our proposed solution is a neural network-based registration system capable of accurately mapping 3D world points to 2D image points, thereby significantly enhancing the precision, and potentially the refresh rates, of AR systems. Our registration system can map a 3D world point to the image plane without additional markers and the need for extensive manual calibration of the stereo camera and accurate robot kinematics.

The integration of Artificial Intelligence (AI) with augmented reality for surgical robotics represents an innovative solution used to overcome the existing limitations in tracking accuracy. This research not only aims to improve the field of robot-assisted surgery but also holds promise for improving surgical training methods and overall patient care outcomes.

2. Background

In the domain of surgical robotics, the integration of augmented reality (AR) has been a subject of considerable interest and research. A thorough review of AR for surgical robotics applications is provided in [9]. We provide a targeted background, focusing on the da Vinci Surgical Robot, augmented reality in surgical settings, camera calibration, and neural networks, in order to support the main innovations of this paper.

The da Vinci Surgical Robot, developed by Intuitive Surgical, has been a revolutionary addition to the field of surgical robotics. This system, approved by the FDA in 2000, is composed of three primary components: a surgeon console, a patient cart, and a vision cart. The surgeon console is equipped with hand controllers and stereo vision, offering a 3D perspective of the patient [10]. A research toolkit has also been created, and has significantly enhanced research efforts [6,11]. Several research groups have been working on addressing errors in the augmented reality associated with surgical robots. In 2018, Qian et al. [12] used tags as fiducial markers to reduce projection errors in a head-mounted display. These tags are attached to the tools and objects that need to be tracked, which then provide information on the object’s pose with respect to the camera. Using this, the error was reduced to 4.27 mm, with a standard deviation of 2.09 mm. Liu et al. [13] show how a marker-based image guidance system can help in cochlear implants. The use of markers, however, comes with limitations, such as a more cluttered operating scene, since markers are often rigid. Markers also limit flexibility, since augmenting new areas in the scene would require additional markers and calibration. Markerless AR is a technique that has been studied in order to overcome these challenges by utilizing robot kinematics to determine the pose and orientation of the object with respect to the camera [14]. Pandya et al. [15] show the feasibility of a markerless AR for neurosurgery with an error of approximately 2.75 mm. In 2019, Kalia et al. [16] used a custom calibration rig to calibrate the endoscopic camera of the da Vinci surgical robot, which reduced the error to 3 mm. The calibration rig was 3D-printed, and a fourth-order polynomial was then used to fit the curve and interpolate the camera parameters at different positions. A gradient descent-based optimization was then used to further reduce the error. The use of such extensive steps to reduce the error in markerless AR makes for a cumbersome approach.

2.1. Camera Calibration

In robotics and computer vision, camera calibration is essential for accurate image interpretation. This process involves the definition of intrinsic parameters like focal length and principal point, extrinsic parameters detailing the camera’s position and orientation, and distortion parameters that account for lens imperfections. The calibration method developed by Zhang [17] in 2000, which utilizes a checkerboard pattern, remains a standard approach for camera calibration, especially for stereo camera systems. Accurate camera calibration is vital for effective AR implementation in surgical robotics, for which precision is critical.

2.2. Neural Networks

The rise of neural networks, particularly in deep learning, has been transformative in the field of machine learning, finding applications in areas like image recognition and autonomous vehicles. These networks, modeled after the human brain, learn from data through backpropagation and gradient descent algorithms. In minimally invasive surgeries, deep learning has been increasingly employed for tasks like tool segmentation and trajectory analysis, demonstrating significant reductions in error rates and enhancing the overall efficiency of surgical procedures [18].

There has been a rise in the application of deep learning in minimally invasive surgeries [19]. Several methods have been developed to segment tools in a surgical scene using convolutional neural networks [20,21,22], and other studies have made use of the kinematics data along with images for trajectory segmentation [23]. A recent study in 2019 at UC Berkeley utilized a combination of deep learning and random forest to determine 3D points given 2D pixel locations for the use case of medical debridement [24].

In summary, the technological landscape of surgical robotics has been marked by significant advancements in the da Vinci Surgical Robot, AR, camera calibration, and neural networks. These developments not only highlight the current state of surgical robotics but also point towards future directions in the enhancement of the precision and efficiency of robot-assisted surgeries.

3. Methods

The following methodology is used to compute the tooltip location in the image frame. To replicate this work, the user must properly prepare the training data, choose the appropriate threshold for testing, and use an appropriate neural network. These steps are discussed in the following sections.

3.1. Data Preparation

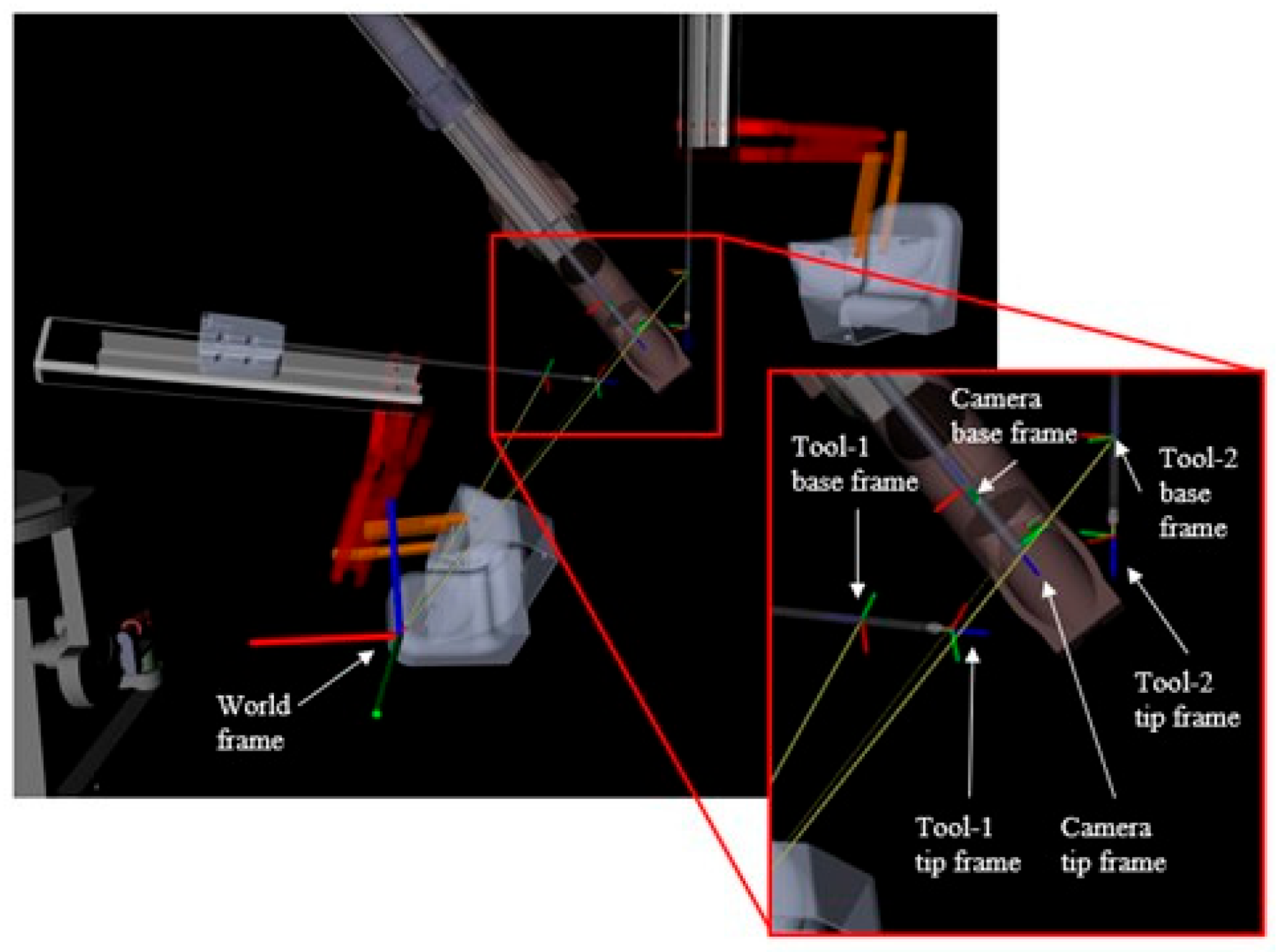
Successful training of a neural network requires large amounts of clean, labelled data. This was obtained by meticulously collecting data, utilizing the dVRK system [11]. Since the objective is to map a 3D world location to a 2D image plane, the dataset was curated to collect the positions of the patient-side manipulators (PSMs), the camera arm, and the pixel location of the PSMs in the endoscopic stereo camera views. The data was then labelled using image processing techniques. The labels were further optimized to reduce any errors in the ground truth data. The dVRK system publishes the location and joint angles of all the robot arms with respect to a predefined reference frame. The tooltip locations are defined with respect to each tool’s base frame and the camera location is defined with respect to the camera base frame, as seen in Figure 1. These data were published by the dVRK at 100 Hz, and the camera images were published at 10 Hz.

3.1.1. Data Collection

The data was collected by subscribing to the Robot Operating System (ROS) topics that publish the Cartesian pose of the patient-side manipulators and the camera arm. To acquire the endoscopic camera images, a simple ROS node was created that reads the image and publishes it over ROS. The publishing rate of the images was set to 10 Hz to reduce the data size and remove redundancies. Images published at 30 Hz would have frames that would be identical to previous frames and would add no additional information. The data was stored in ROS bag files, with each file consisting of 3 min of messages in which both tools (PSMs) were moved around manually. The tools were moved in such a way that they covered the majority of the working envelope. The autocamera algorithm [25] ensured that the camera followed the tools and the tooltips remained in the field of view. This allowed us to capture more than 10,000 different tool and camera positions throughout the working envelope. The difference in the publish rates was addressed by using the ROS ‘ApproximateTimeSynchronizer’ which uses an adaptive algorithm to group messages that are published within a specified time tolerance [26]. The time tolerance for this dataset was set to 10 ms.

Data labelling was automated by coloring the tips of the tools with red and green and using image processing techniques to locate them. To detect the tooltips in the image, a 3 × 3 Gaussian filter was used to blur the image, and a hue–saturation–value (HSV) mask was used to segment the red and green tips. A contour was then fitted over the segmented tips, and the centroids were extracted as the pixel positions of the tools. Figure 2 shows the raw image from the endoscopic camera, the results of HSV filtering, and the centroids overlaid on the raw images. OpenCV 4.6.0 and Python3 (version 3.7) were used for all image processing.

3.1.2. Threshold Optimization

To automatically optimize the segmentation of tooltips, we developed an optimization method to refine the HSV values used for accurate segmentation. From a dataset of over 10,000 images, we selected 50 images in which the tooltips—one red and one green—were clearly visible. For each of these images, we manually clicked and recorded the ground truth coordinates of the red and green tips. Using an HSV thresholding program, we segmented the tooltips and formulated an objective function to quantify the error between the HSV-segmented positions (${\mathrm{x}}_{\mathrm{h}\mathrm{s}\mathrm{v}},{\mathrm{y}}_{\mathrm{h}\mathrm{s}\mathrm{v}})$ and the ground truth positions $({\mathrm{x}}_{\mathrm{g}\mathrm{t}},{\mathrm{y}}_{\mathrm{g}\mathrm{t}})$. The objective function was defined as the square root sum of the squared errors:

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left(\mathrm{H},\mathrm{S},\mathrm{V}\right)=\sum _{i=1}^{50}\sqrt[ ]{{[\left({\mathrm{x}}_{\mathrm{g}\mathrm{t},\mathrm{i}}-{\mathrm{x}}_{hsv,\mathrm{i}}\right)}^2+{\left({\mathrm{y}}_{\mathrm{g}\mathrm{t},\mathrm{i}}-{\mathrm{y}}_{hsv,\mathrm{i}}\right)}^2}]$$

(1)

This error function was minimized using the Nelder–Mead optimization algorithm [27], which iteratively adjusted the HSV values to minimize the differences between the ground truth and the segmented positions. The optimization process can be expressed as

$$({\mathrm{H}}^{\mathrm{*}},{\mathrm{S}}^{\mathrm{*}},{\mathrm{V}}^{\mathrm{*}})=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\left\{\mathrm{H},\mathrm{S},\mathrm{V}\right\}}{\min }\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left(\mathrm{H},\mathrm{S},\mathrm{V}\right)$$

(2)

where $\left({\mathrm{H}}^{*}, {\mathrm{S}}^{*}, {\mathrm{V}}^{*}\right)$are the optimal HSV parameters that minimize the error. These optimized parameters were then applied to the entire dataset to extract the corresponding tooltip pixels. Each segmented result was manually validated to ensure accuracy. The final dataset, consisting of 2D tip coordinates, was subsequently used to train a neural network to map the 3D positions of the tools (extracted from ROS topics) to their corresponding 2D positions in the images. The result of the HSV based detection in a frame can be seen above in Figure 2.

3.2. Dense Network

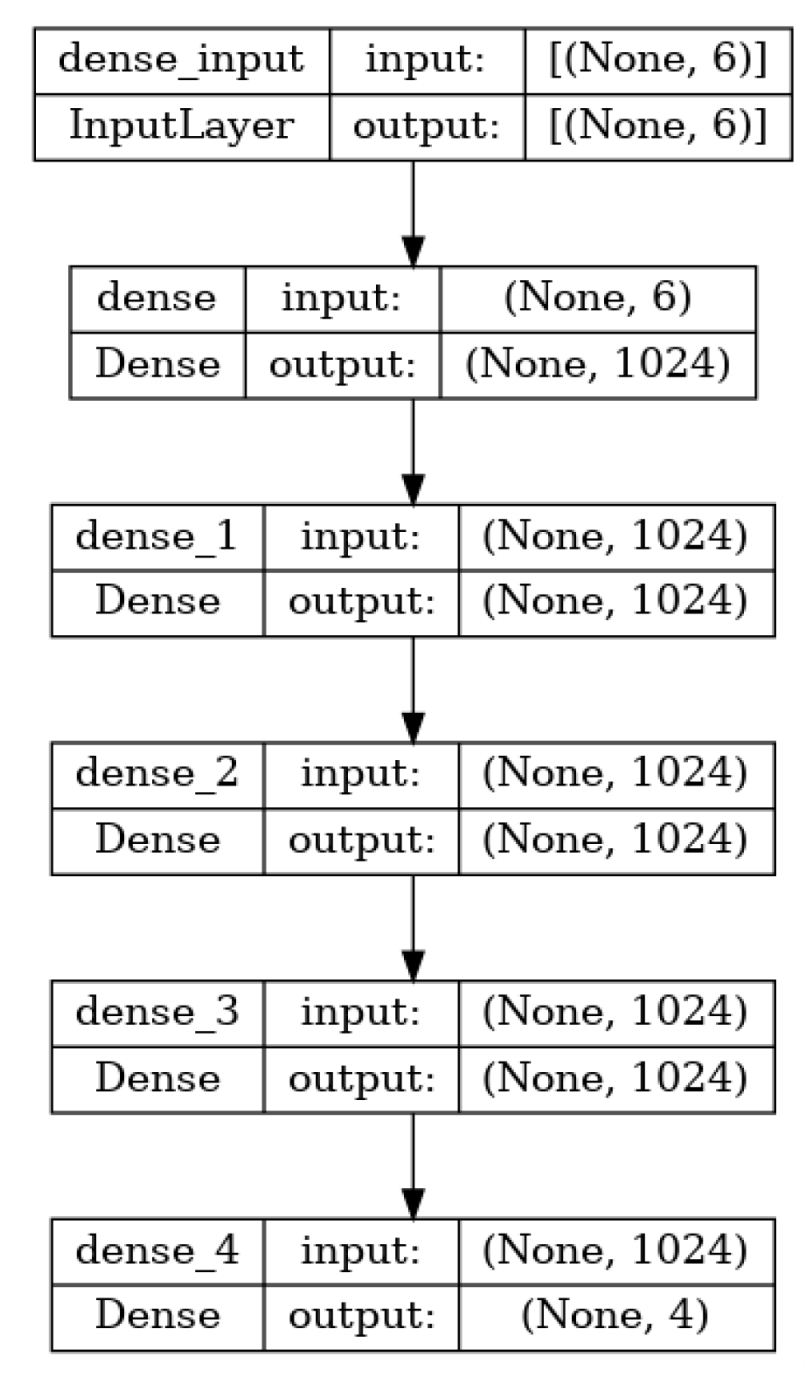
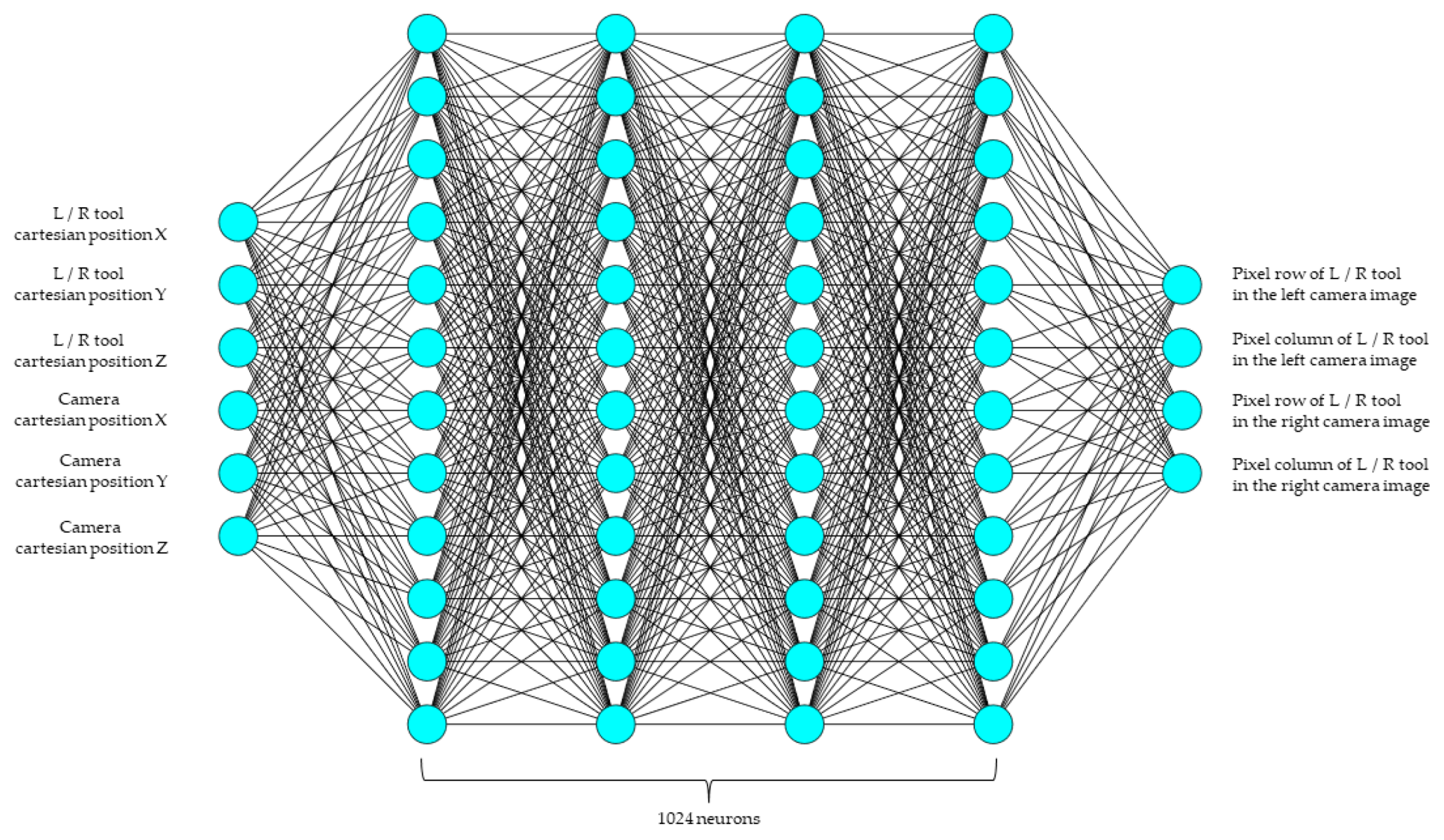
The dense network provides a simple yet powerful method for learning a function that can map the points on an image. These networks also serve as a baseline used to compare other networks. The network trained for this study has six inputs, corresponding to the x, y, and z positions of the tool and the camera. The system learns the mapping of a point in 3D space to its corresponding pixel location. Four hidden layers with 1024 neurons each were used, and the output had four neurons, corresponding to the pixel locations (row, column) for the left and right cameras. All of the hidden layers had a rectified linear unit (ReLU) activation function. An overview of the architecture is shown in Figure 3 and Figure 4 below. Mean square error was used as the loss function, since the prediction of pixel location is treated as a regression problem. The Adam optimizer was used for training and the MSE loss was reduced to 4 × 10⁻⁴.

3.3. Integrating Camera Calibration

To improve the accuracy of the dense network, calibrated camera parameters were added to the network input. The endoscopic camera was calibrated with a checkerboard pattern with a size of 8 × 8, with each square measuring 5 mm in length. The resulting projection of 3D points using the intrinsic matrix, extrinsic matrix, and distortion values were added as inputs to the dense network. The hidden layers and the output layers remained unchanged while the input layer contained more neurons, to accommodate the projected points.

4. Results

4.1. Network Results

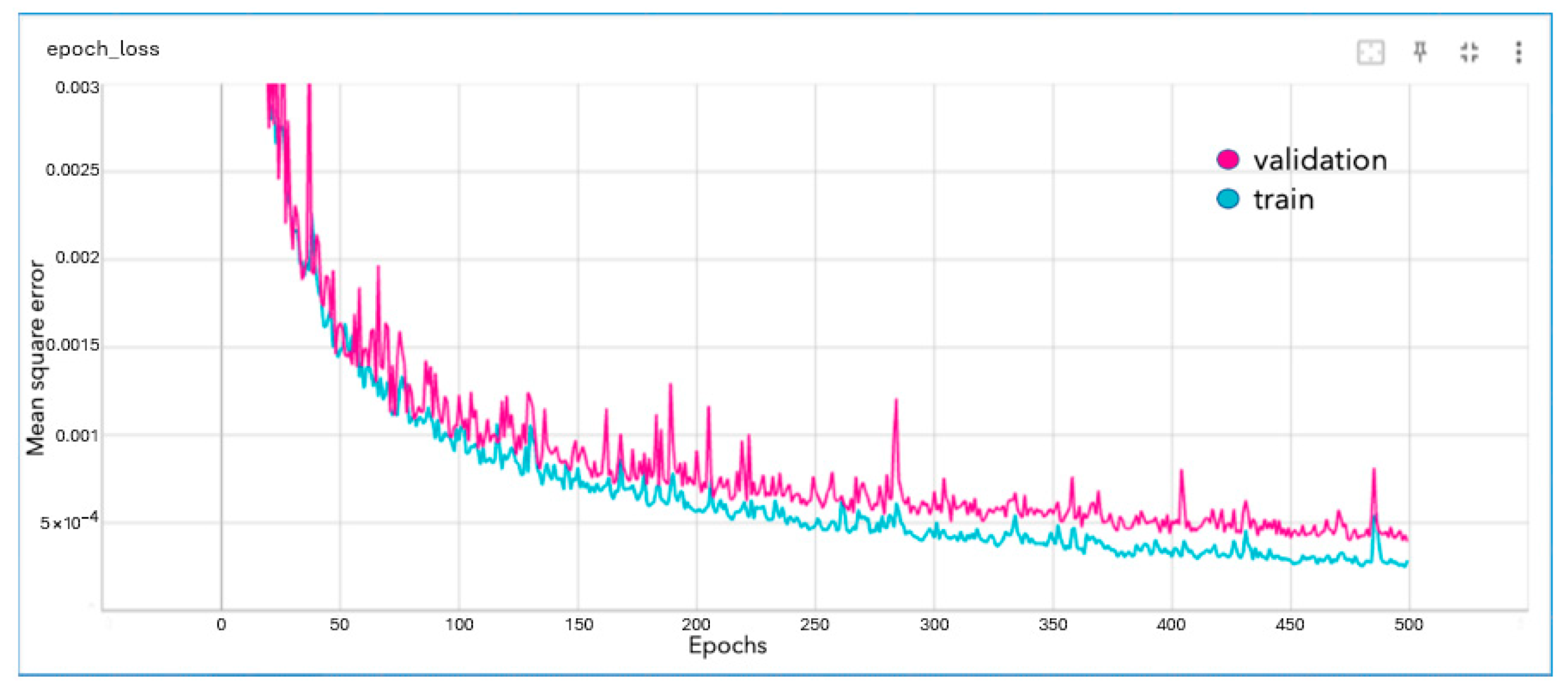
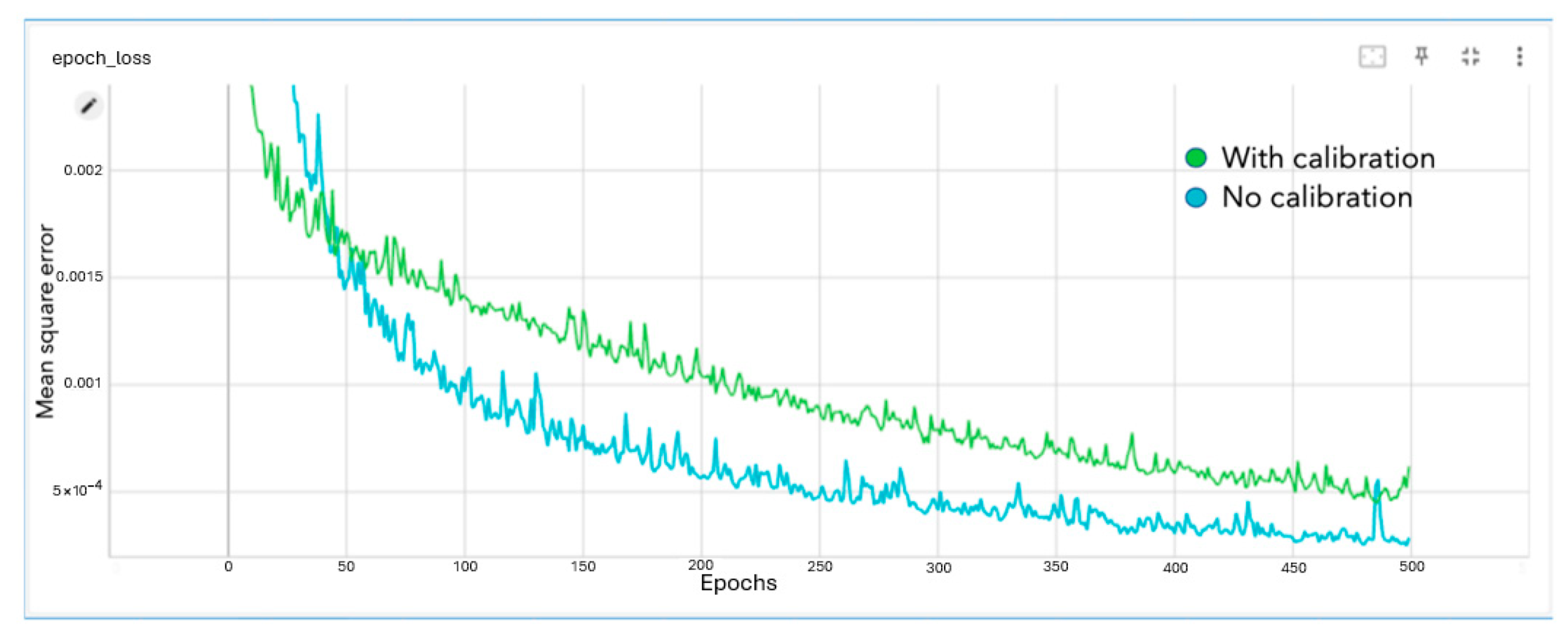
The dense network was able to reduce the mean square error to approximately 4 × 10⁻⁴ pixels. The network trained for 500 epochs. The loss graph for the network, where the mean square error is in pixels, is given below in Figure 5.

The comparison of the training loss with and without calibration parameters added is shown below.

As seen in Figure 6, adding calibration data to the dense network did not improve the performance. The error converged to a higher value, indicating the reduced accuracy of the model.

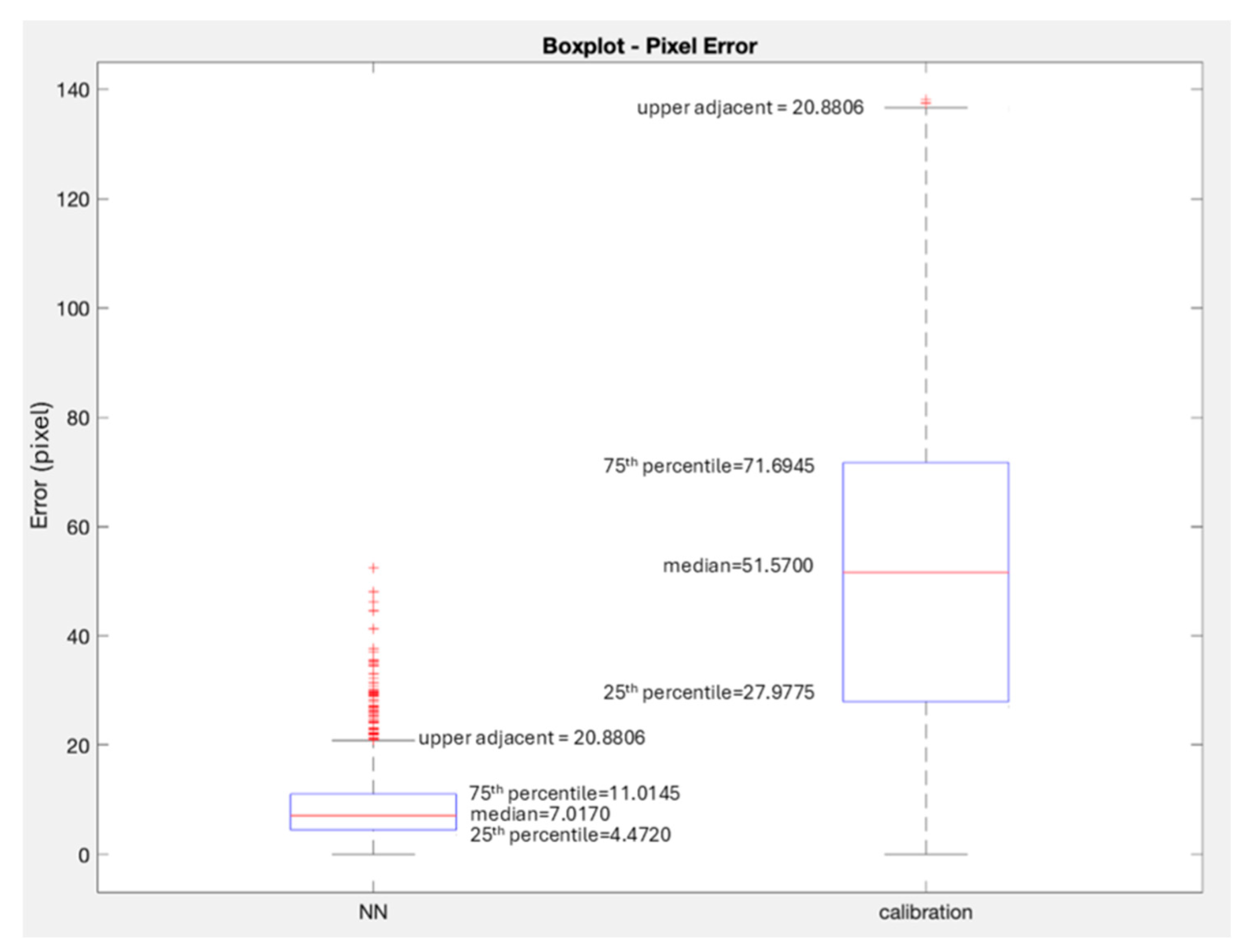
Figure 7 plots the median error as observed using the neural network-based approach, and a robot kinematics/camera-calibration-based approach that is commonly used in augmented reality.

4.2. Tooltip Projection Comparison

To compare the performance of our neural network-based projection method with the traditional method involving camera calibration and kinematics, we selected a subset of 1000 image frames from the test dataset. For each frame, we inferred the 2D pixel location of the tooltips using both methods. The traditional method used intrinsic and extrinsic calibration parameters and the robot’s forward kinematics to project the tooltip into the image plane. The neural network method took as inputs the 3D positions of the tool and camera to directly predict the 2D tooltip location.

For quantitative assessment, we compared both predicted positions to the manually verified HSV-segmented ground truth pixel locations. The projection error was calculated as the Euclidean distance in pixels. The results show that the neural network approach performs consistently better, with a median error of 7 pixels (1.4 mm), compared to 50 pixels (10 mm) for the traditional method.

Figure 8 shows the projection results for the tooltips for a typical frame of camera feed with both of the tooltips in view. The left image shows tooltip positions that are directly inferred from the 3D positions using the trained dense network—note, no camera calibration was used. The only inputs to the neural network are the positions of the end-effectors. The right image shows the traditional approach using camera calibration and robot kinematics. Both images visualize the predicted 2D pixel locations overlaid on the stereo endoscopic feed. The Supplemental Video demonstrates the projection of tooltips over time using both methods, highlighting the stability and feasibility of the neural network approach.

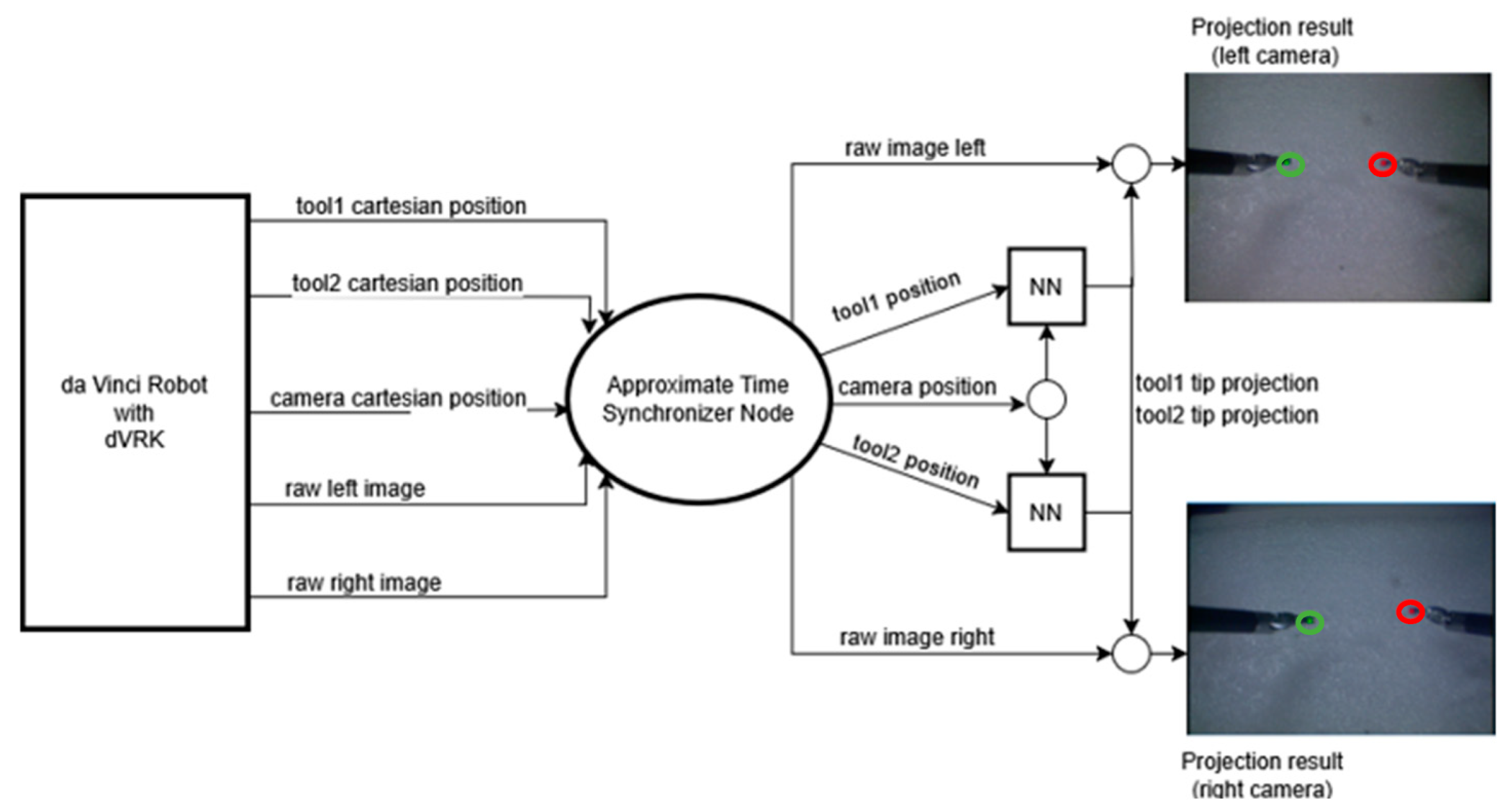
4.3. Integration with dVRK

The trained network was then integrated with the Robot Operating System (ROS) to interface with the daVinci system. Figure 9 shows the integrated architecture. The ROS topics corresponding to the tools and the camera positions were input to the Approximate Time Synchronizer to synchronize the rate of publishing. The left and right tool positions, along with the camera position, were then input to the neural network to obtain the pixel locations. The two neural network boxes in the diagram are shown to illustrate that the inference was performed separately for the left and the right tool.

The unoptimized inference speed was measured at 5 ms with CUDA enabled on a machine with an NVIDIA RTX 3080Ti. The total system latency, including ROS overhead, was measured at 20 ms, which is two times slower than the speed at which the tooltip positions are published.

5. Discussion

Central to this study is the exploration of neural networks to significantly reduce the AR projection error, a critical factor in enhancing the accuracy and reliability of robot-assisted surgical procedures. A considerable amount of emphasis was placed on data collection and cleaning to ensure that the training data was reliable and accurate. The automation of the labeling process for the tooltips was further verified by manually processing each image, as the HSV-based optimization method is sensitive to lighting changes and prone to misclassifications in such conditions.

The key finding of this research is the significant reduction in projection error achieved through the implementation of a neural network-based supervised learning approach. A median error of 7 pixels was observed, and to assess accuracy in millimeters, we randomly selected 40 images and manually measured the end-effector length (in pixels), which was determined (with a caliper) to be 5 mm. Using these measurements, we calculated the pixel-to-millimeter ratio. This ratio was then applied to estimate the average difference in millimeters across the entire dataset, resulting in an accuracy of 1.4 mm. This is a marked improvement compared to the minimum error of 3 mm in current state-of-the-art markerless AR systems for the da Vinci robot. This result is particularly noteworthy, as it signifies the neural network’s capability to accurately map the complex 3D-to-2D point relations that are inherent in high-precision surgical AR applications.

The addition of projected points using camera calibration and robot kinematics confounds the working of the neural network. We hypothesize that with the addition of the pixel positions received from camera calibration, the network must learn to compensate for the errors in projection while also learning the mapping of the point to the image plane. The added complexity results in a hinderance to the model’s performance rather than improving it.

In delving into the specifics of these results, it becomes apparent that the neural network model successfully circumvents the traditional complexities associated with camera calibration and robot kinematics. By directly learning the mapping between the 3D world points and the 2D image plane, the neural network model negates the need for intricate calibration and adjustments typically required in AR systems. This simplification not only streamlines the integration process but also enhances the overall robustness and reliability of the AR system within the surgical setting.

6. Conclusions and Future Work

In this paper, we present the application of neural network-based supervised learning to implement markerless augmented reality (AR) in surgical robots. This study successfully demonstrated that neural networks have the potential to substantially reduce errors in AR projection. One notable achievement of this research is the attainment of a median error of 1.4 mm, a considerable improvement over the existing state-of-the-art markerless AR systems for the da Vinci robot, which have a minimum kinematic error margin of about 3 mm. What sets this approach apart is its ability to circumvent the complexities and potential inaccuracies associated with robot kinematics and camera calibration. Although this system was demonstrated with the daVinci system, any system that controls the camera with a robot, and utilizes methods to compute the pose for each of the tools used, will be able to use these methods.

However, the application of neural networks in this context is not without its challenges. It demands rigorous data collection and meticulous training, underlining the importance of precision in the initial stages of system development. Moreover, the model’s inference speed emerges as a critical factor in its practical application. The rapid evolution of hardware capabilities, particularly in the realms of GPU acceleration and computational efficiency, is essential to harness the full potential of neural networks in surgical AR.

Looking ahead, this research opens avenues for further enhancements. There is ample scope for reducing error margins with more extensive training data and refinement of the neural network model’s architecture. Exploring the possibilities offered by recurrent neural networks could address specific challenges related to tools’ dynamic movements during surgeries. Additionally, integrating neural networks with other methodologies, such as random forests, could lead to even greater accuracy in AR projections. One weakness of the current system is that the kinematic chain considered for the AR projection stops at the base joint of the PSMs. There are additional setup joints in the system which would need to be incorporated to obtain a full kinematic model of the system, and these must be incorporated in an OR-ready system. Hence, the current system still needs additional research and development to reach clinical relevance. We estimate that the current system implementation is at LoCR 2 in the scale of clinical realism [28].

The integration of AR into surgical robots extends beyond mere technical improvements. It holds the potential to revolutionize the functionality and usability of surgical robots. Envisioning a future in which AR is combined with features like drawing tools for surgeon training, or natural language interfaces, reveals possibilities that can significantly enhance the surgeon’s experience and the overall effectiveness of robot-assisted procedures.

In conclusion, this paper not only underscores the capabilities of neural networks in enhancing the precision of AR in surgical robotics but also lays the groundwork for future innovations in this field. The successful reduction of projection error in AR applications paves the way for more accurate, efficient, and advanced robot-assisted surgeries, ultimately contributing to improved surgical outcomes and patient care. Achieving sub-millimeter accuracy is still an open research problem for augmented reality in surgical robots. The work presented in this paper is a step in that direction.