Abstract
Gesture recognition based on conventional machine learning is the main control approach for advanced prosthetic hand systems. Its primary limitation is the need for feature extraction, which must meet real-time control requirements. On the other hand, deep learning models could potentially overfit when trained on small datasets. For these reasons, we propose a hybrid Linear Discriminant Analysis–convolutional neural network (LDA-CNN) framework to improve the gesture recognition performance of sEMG-based prosthetic hand control systems. Within this framework, 1D-CNN filters are trained to generate latent representation that closely approximates Fisher’s (LDA’s) discriminant subspace, constructed from handcrafted features. Under the train-one-test-all evaluation scheme, our proposed hybrid framework consistently outperformed the 1D-CNN trained with cross-entropy loss only, showing improvements from 4% to 11% across two public datasets featuring hand gestures recorded under various limb positions and arm muscle contraction levels. Furthermore, our framework exhibited advantages in terms of induced spectral regularization, which led to a state-of-the-art recognition error of 22.79% with the extended 23 feature set when tested on the multi-limb position dataset. The main novelty of our hybrid framework is that it decouples feature extraction in regard to the inference time, enabling the future incorporation of a more extensive set of features, while keeping the inference computation time minimal.
1. Introduction
Myoelectric gesture recognition translates sEMG signals into a limited set of discrete hand gestures that fulfill most daily user’s needs and is featured in various commercial prosthetic hands [1,2,3]. Hand gesture recognition systems are typically based on classical machine learning and deep learning. Classical machine learning models, such as Linear Discriminant Analysis (LDA) [4], Quadratic Discriminant Analysis (QDA) [5], and Support Vector Machine (SVM) [6,7], are the predominant approaches for sEMG-based hand gesture recognition, due to their computational efficiency and intuitive interpretations, making them suitable for use in prosthetic systems [1,8]. Manual feature extraction is essential for identifying discriminative information in sEMG signals [2]. Advancements in deep learning have enabled the ability to recognize hand gestures from raw sEMG signals by directly extracting discriminative features. Over the years, a variety of deep learning architectures have been proposed for sEMG-based gesture recognition, including 1D-CNN [9], 2D-CNN [10], an LSTM-CNN hybrid [11], multi-stream 1D-CNNs [9,12], multi-stream 1D-CNN-LSTM [9], and Transformer-based models [13,14].
While early research on sEMG hand gesture recognition showed promising results [4,10,12], a significant limitation was that the recognition performance was evaluated in limited settings. As sEMG gesture classifiers only perform effectively in conditions where the signals’ characteristic are closely similar [15], there has been a shift toward addressing the non-stationarities of sEMG signals, particularly for conditions not encountered during training. The most straightforward approach is to gather more data across diverse conditions [6]. Other potential solutions include incorporating additional modalities, such as inertial measurement units (IMUs) [16], pressure-based force myography (pFMG) [17], and RGB [18,19], or depth cameras [20]. Another approach is the use of feature engineering to enhance the robustness of myoelectric hand gesture classifiers [6,7,21]. However, such solutions can increase the user training burden or system complexity, further reducing prosthesis user acceptance.
Notably, previous studies have consistently shown that LDA improves recognition performance in the presence of sEMG non-stationarity. Vidovic, Hwang, Amsüss, Hahne, Farina, and Müller [5] found that over five days, LDA provided up to 10% more stable performance than QDA. Similarly, Phinyomark, et al. [22] observed that over 21 days, LDA reduced the recognition errors by 8% to 20% compared to QDA and the random forest algorithm. Lorrain et al. [23] found that LDA improved the recognition performance by 8% to 35% compared to a Gaussian Kernel SVM in the presence of transient sEMG signals. Al-Timemy, Khushaba, Bugmann, and Escudero [6] reported that LDA consistently achieved the lowest recognition error compared to random forest, Naive Bayes, and kNN across all feature sets, under varying contraction forces.
Despite progress in the field, sEMG-based hand gesture recognition still faces many challenges, especially when dealing with the non-stationary nature of sEMG signals. The performance of classical machine learning methods, while being the default approach in regard to commercial products due to their proven robustness [24], is heavily dependent on the choice of the input feature set [22,25]. Feature engineering often leads to complex and non-parallelizable computations, making their deployment on wearable devices for prosthetic control more difficult. Deep learning, on the other hand, is often regarded as a universal approximator that relies on a small number of standardized, parallelizable operations [26]. However, the robustness of deep learning for myoelectric hand gesture recognition under dynamic conditions has not been clinically validated. In our previous work, we found no significant performance difference between LDA and deep CNNs when evaluating gestures recorded under unseen conditions [27]. Since LDA is not only a classification method, but also a dimensionality reduction technique, and given its demonstrated robustness in previous studies [5,22,27], we hypothesize that LDA’s discriminant subspace (or Fisher’s representation) serves as a highly compressed and rich form of representation. We further hypothesize that a deep CNN can approximate this representation, thereby bypassing the need for explicit temporal feature extraction during inference.
In light of this observation, we propose a hybrid CNN-LDA framework in this study. In regard to this framework, a 1D-CNN is used to extract the temporal features, so that the model’s latent representation approximates Fisher’s discriminant subspace of the LDA classifier. The novelty of our framework is that the feature extraction occurs only during the training stage, while, during inference, the model predicts hand gestures directly from raw sEMG signals.
Our proposed LDA-CNN framework can be viewed as a form of feature-level knowledge distillation, which is considered richer than conventional class probability-based (response based) knowledge distillation [28]. Zeng et al. [29] introduced a cross-modality, response-based knowledge distillation approach that transfers information from ultrasound to the sEMG modality. They first trained a hand gesture recognition model using only ultrasound data, which was then used as the teacher model. The student model for the sEMG modality was subsequently trained jointly with the ultrasound teacher model to capture cross-modal knowledge. In another study, Wei et al. [30] proposed using a generative adversarial network (GAN) to distill the relationship between sEMG and IMU modalities. During inference, the pseudo-IMU data generated by the GAN are combined with sEMG signals to enhance recognition performance. Unlike most prior work that distills knowledge from a teacher deep neural network [28,29,30], our method distills knowledge from Fisher’s discriminant subspace. Traditionally, Fisher’s discriminant subspaces are computed analytically using methods such as Singular Value Decomposition or Eigenvalue Decomposition [31], which are prone to numerical instability. In contrast, deep learning models are typically trained using mini-batch optimization frameworks [32]. By leveraging deep learning to approximate Fisher’s representation, our method introduces a spectral regularization effect that mitigates the numerical instability associated with the direct computation of Fisher’s subspace.
Our proposed framework is tested on two public datasets: one with hand gestures recorded for five different upper limb positions [7] and one with hand gestures recorded under three different levels of contraction force [6]. Our investigation focuses on the ‘train-one-test-all’ validation scheme. In regard to this scheme, only three repetitions recorded under a single condition (either one limb position or one contraction force) are used for training. The testing dataset includes both the training conditions and novel conditions that were not used during training, better aligning with real-world operating conditions of prosthetic hand systems. The contributions from our proposed framework include:
- Highlighting the robustness of Fisher’s representation for sEMG gesture recognition under dynamic conditions (multi-limb positions and contraction forces);
- Highlighting the problem of overfitting in regard to deep CNNs trained with cross-entropy on a limited dataset;
- Improving sEMG hand gesture recognition under dynamic conditions through the knowledge distillation of manual sEMG features in Fisher’s discriminative subspace as deep convolutional weights;
- Applying gradient-based optimization of the CNN optimization framework to address the numerical instability of LDA Rayleigh–Ritz quotient for large feature sets;
- Ensuring the system’s real-time robustness to avoid perceptible user delays by utilizing fast GPU computation.
2. Materials and Methods
2.1. Benchmark Datasets
2.1.1. Multiple Limb Position Hand Gesture Dataset
The Multiple Limb-Position Dataset (Limb.Pos. dataset [7], Figure 1) comprises recordings of eight hand gestures, performed under five distinct limb positions, namely P1 through P5, by 11 intact subjects (9 males and 2 females). The gestures include four wrist movements, flexion, extension, pronation, and supination, and three active hand movements, pinch grip, power grip, and open hand, plus one inactive gesture of resting. However, this investigation excluded the resting hand gesture for two reasons: (1) it can be detected via changes in the sEMG amplitude [33], and (2) to further analyze the impact of the covariate shift on the detection rate of active gestures. The sEMG signals were captured using seven Delsys DE 2.x electrodes and amplified by a Delsys Bagnoli amplifier, with a gain of 1000. These signals were then converted to a digital format, at 4 kHz, using the BNC-2090 ADC module. The dataset was preprocessed by the dataset recording author, using a bandpass filter ranging from 20 to 450 Hz and a 50 Hz notch filter to eliminate power line interference. To further reduce the processing time, we also downsampled the sEMG signal to 2 kHz.
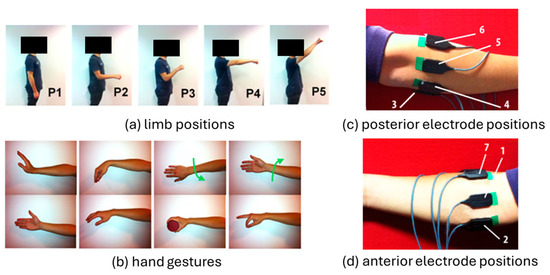
Figure 1.
(a) Five limb positions (P1–P5), (b) eight hand gestures, and (c,d) electrode placements from Limb.Pos. dataset [7].
2.1.2. Amputee sEMG Multi-Contraction Forces Dataset
The Amputee sEMG Multi-Contraction Force Dataset (Amp.Force. dataset [6], Figure 2) includes sEMG recordings from nine unilateral transradial volunteers, each with varying types of amputation and different familiarity with prosthetic systems. The primary objective of the use of this dataset is to explore the impact of covariate shifts in the response to changes in the contraction force. This is of significant practical importance, as many commercial prosthetic systems employ proportional control based on muscle force [34]. The sEMG signals were recorded using eight pairs of Ag/AgCl sEMG electrodes, positioned on the stump of the amputated upper limb. The sEMG signal was recorded at 2 kHz, then preprocessed using a 4th order Butterworth filter, with cutoff frequencies set at 20 Hz and 500 Hz. The participants performed six hand gestures, thumb flexion, index flexion, fine pinch, tripod grip, hook grip, and spherical grip, with each gesture repeated 5 to 8 times. The contraction forces were categorized into three levels, low, moderate, and high, and maintained for 8 to 12 s, during each gesture repetition. Additionally, the participants received feedback on the sEMG amplitude to ensure accurate perception of the invoked muscle force.
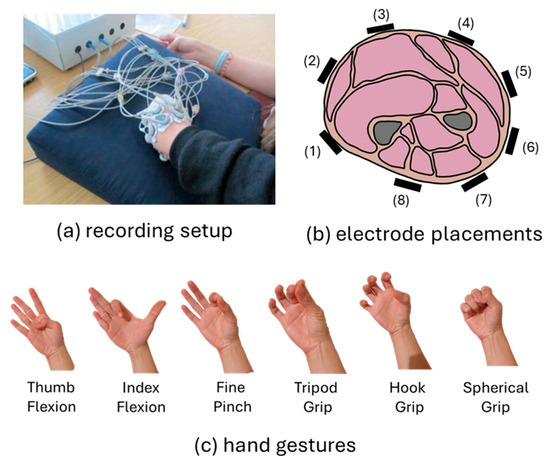
Figure 2.
(a) Recording setup, (b) electrode placements and (c) recorded hand gestures from Amp.Force. dataset [6].
2.2. sEMG Feature Extraction
Figure 3 illustrates the forward generation process of an sEMG signal. The surface EMG (sEMG) signal represents the summation of the electrical activity from all the active muscle fiber action potentials (MFAPs) within the detection volume of the electrodes [35]. These MFAPs are generated by motor neuron activation and propagate through biological tissues, where they are subject to distortion caused by tissue impedance and noise, before reaching the skin surface [2,36]. The level of muscle force generated is regulated by the central nervous system through two primary mechanisms: the number of recruited motor units and the firing rate of these motor units [2,37].
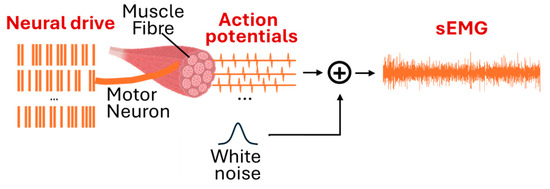
Figure 3.
The generation process of an sEMG signal.
The general goal of sEMG-based muscle–machine interfaces is to solve the inverse problem of the forward generation process, specifically to infer the underlying neural drive from the recorded sEMG signal. However, this has been proven to be a challenging and underdetermined problem, particularly when dealing with sparse sEMG signals. To address this, heuristic feature extraction methods are often employed, with sEMG features designed to reflect the physiological mechanisms involved in sEMG signal generation. In general, sEMG features reflect either the signal’s energy or its frequency components. Among these, the signal energy and amplitude (low-pass filtered sEMG signals, mean absolute value) are the most commonly used features, as they are associated with both motor unit recruitment and rate coding mechanisms during the sEMG generation process [37]. Frequency-based features, such as the power spectrum, autoregressive coefficients, and the zero-crossing rate, provide more detailed analysis of rate coding [37], the spatial relationship between the electrodes and motor units [35], and muscle fatigue conditions [38]. These frequency-based features have also been found to be more robust in regard to confounding factors, such as changes in the contraction force [6,39] and limb position [7]. Moreover, since each sEMG feature is typically designed to capture a limited aspect of the signal, combining multiple features often leads to improved performance in myoelectric hand gesture recognition compared to using a single feature [22,25].
Building on previous research [7,22,40,41], this study directly utilized eight distinct feature sets, including a new set proposed here, comprising 23 robust sEMG features shown to facilitate sEMG gesture recognition, without connecting them to neuromuscular mechanisms in regard to gesture recognition, which would possibly lead to the capturing of features that are not physiologically valid or relevant. Additionally, seven commonly used and robust feature sets were employed. Each feature set was extracted using a window size of 512 samples (equivalent to 256 ms), with a step size of 50 samples (25 ms).
- Our proposed extended 23 sEMG feature set (Ext-23): Mean Frequency (mnf), Cepstrum Coefficient (cc), Power Spectrum Ratio (psr), Marginal of Discrete Wavelet Transform (mdwt), Slope Sign Change (ssc), Auto-Regressive Coefficient (ar), and time-domain power spectral moments (TD-PSR), mean absolute value slope (mavs), Histogram of EMG (hemg), mean absolute value (mav), Zero Crossing (zc), Waveform Length (wl), Root Mean Square (rms), Integral Absolute Value (iav), Difference Absolute Standard Deviation Value (dasdv), Average Amplitude Change (aac), Log Detector (log), Willison Amplitude (wamp), Myopulse Percentage Rate (myop), V-Order (v), variance (var), Log variance (logvar), and Maximum Fractal Length (mfl).
Other robust feature sets used for benchmarking purposes are as follows:
- Atzori’s feature set: rms, mdwt, hemg, mav, wl, ssc, and zc;
- Du’s feature set: iav, var, wamp, wl, ssc, and zc;
- Hudgins’ feature set: mav, wl, ssc, and zc;
- Time-domain power spectral moments (TD-PSR): a set of features that are robust to changes in arm position and contraction force frequency domain features extracted directly from the time domain;
- Phinyomark’s feature set: mav, wl, wamp, zc, mavs, ar, mnf, and psr;
- Robust Time-Domain 8 (TD8) [25]: aac, dasdv, mfl, myop, ssc, wamp, wl, and zc;
- Robust Time-Domain 8 with Autoregressive Coefficients (TD8-ARs) [25]: aac, dasdv, mfl, myop, ssc, wamp, wl, zc, and ar.
2.3. Linear Discriminant Analysis and Fisher’s Representation
LDA (or Fisher’s Discriminant Analysis) is the most commonly used technique for sEMG-based gesture recognition, due to its low computational footprint and its parametric and generative nature. Given a dataset consisting of samples as column vectors of dimension , where each sample corresponds to one of the classes. Additionally, LDA further assumes that data belonging to class is of multivariate Gaussian distribution and the covariance of all the classes is equal, i.e., . Then, the probability that a sample belongs to class is determined as [42]:
where is the prior probability that a sample belongs to class . Samples are assigned to the class that has the highest posteriori:
where the classification outlined by (1) and (2) naturally gives rise to a linear decision boundary [42,43]. Additionally, centroids in the dimensional input feature space are contained in the subspace of dimensional when the dataset is zero-centered [42]. Hence, the data can be projected onto this subspace without losing either discriminant information or distribution based on a Gaussian assumption. This subspace is the discriminant subspace. The discriminant subspace where can be solved by optimizing the Rayleigh–Ritz quotient:
where denotes matrix trace operations, and and are the between class and within class covariance matrices, respectively [31]. The optimization objective from (3) is equivalent to:
which can be interpreted as finding directions that maximize the between-class variance, while maintaining unitary intra-class variance. Fisher’s representation is defined as the projection of the sample vector onto , and is expressed as:
2.4. Hybrid CNN-LDA Framework for End-to-End sEMG-Based Hand Gesture Recognition
Here, we introduce a novel hybrid approach combining CNN and LDA to enhance sEMG-based hand gesture recognition, even under unseen conditions, by approximating Fisher’s representation. To this end, we study a simple and straightforward 1D-CNN. The general framework is illustrated in Figure 4, and the detailed configuration of the 1D-CNN model is presented in Table 1. A key feature of the proposed framework is that manual feature extraction occurs only during the training phase. During inference, the hand gestures are predicted directly from the raw sEMG signals. Overall, the model consists of three main components: (1) deep feature extraction, (2) Fisher’s approximation, and (3) hand gesture classification (Table 1).
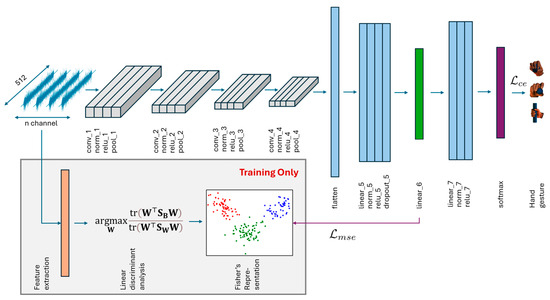
Figure 4.
Illustration of the hybrid CNN-LDA framework for end-to-end sEMG-based hand gesture recognition, with manual feature extraction and Fisher’s representation used only during the CNN training stage.

Table 1.
Components of 1D convolutional neural network. Fisher’s approx. refers to Fisher’s approximator layers and clf. refers to classifier layers; k, ch, and strd denote filter kernel size, number of filters, and stride, respectively.
To optimize the model parameters, we employed cross-entropy loss, denoted as , for the discriminative training and mean squared error, , for the reconstruction loss in approximating Fisher’s representation. The cross-entropy loss quantifies the dissimilarity between the predicted probability distribution of a sample belonging to class and the ground truth distribution. is given by:
where represents the true class label in a one-hot encoded vector, and denotes the predicted probability for class , as determined by the softmax function. By minimizing the cross-entropy loss, the model is trained to assign higher probabilities to the correct class and lower probabilities to the incorrect classes. To align the latent representation from the CNN with Fisher’s representation, we minimize the mean squared error (MSE) loss between the output from the linear_6 layer and the features in Fisher’s representation. This step forces the CNN to learn a latent representation that closely resembles Fisher’s discriminant representation. The MSE loss, , frequently used in regression tasks, is defined as:
Here, is the number of samples, is the reference value in Fisher’s subspace, and is the corresponding latent representation produced by the CNN. The combined loss function of and is defined as:
- Cross-entropy CNN (CNN-CE, ), where the CNN parameters are learned by minimizing the .
- Fusion CNN-LDA (CNN-CEMSE, ), which simultaneously optimizes both the and during training.
- Fisher’s approximator (CNN-MSE, ). This model is trained to minimize the loss exclusively to obtain a latent representation closely aligned with Fisher’s representation. After the model is trained, the weight of the convolution layers up to linear_6 are frozen, and the remaining layers are retrained with cross-entropy loss.
The training and inference of the CNN-CE are both end-to-end processes, using raw sEMG data, while the CNN-CEMSE and CNN-MSE require manual feature extraction during training only. All the 1D-CNN variants were trained using stochastic gradient descent for 60 epochs, with a mini-batch size of 128, a learning rate of 0.01, a weight decay of 0.01, and a dropout rate of 0.2 to further prevent overfitting.
2.5. Training and Testing Dataset Partitioning
To evaluate the generalization capability of our proposed framework for hand gesture recognition under conditions not encountered during training, we adopted the “train-one-test-all” evaluation scheme. Specifically, the classifiers were trained on hand gestures from a single condition. For testing, the hand gestures from all the available conditions are included. For example, train on P1 test on (P1 to P5) or train on medium force test on (low, medium, high). The training dataset included the first three repetitions from the recorded condition, while the testing dataset comprised all subsequent repetitions of the hand gestures across every recorded condition. This “train-one-test-all” approach helps minimize the user training burden by reducing the amount of data needed.
2.6. Statistical Tests
Where applicable, statistical tests were conducted. Due to the high degree of non-normality in the recognition error results, non-parametric tests were used. Our experiments were designed based on a repeated measures setting, where the result from each individual subject was considered as a single measurement. First, the Friedman test, a non-parametric alternative to the repeated measures ANOVA, was conducted to verify the presence of significant differences between at least two groups. When significant differences were confirmed by the Friedman test, Wilcoxon signed-rank tests with Bonferroni correction were then applied to identify the specific pairs with significant differences. The significance level was set at .
3. Results
3.1. Robustness of Fisher’s Representation for Hand Gesture Recognition Under Dynamic Conditions Using the TD8-AR Feature Set
Here, we demonstrate the efficacy of Fisher’s representation by comparing the recognition error rates of different classifiers in the original feature space and after their transformation into Fisher’s discriminant subspace. Seven of the most commonly used classifiers for hand gesture recognition were included in this demonstration, namely LDA, SVM with Linear Kernel, QDA, k-nearest neighbor (k-NN), nearest centroid (CEN), random forest (RF), logistic regression with quadratic kernel (lr quadratic), and multi-layer perceptron (MLP). Furthermore, to demonstrate the impact of the MLP size, we increased the number of hidden layers from one to six, with each layer having 100 perceptrons.
Overall, transforming the data into Fisher’s discriminant subspace reduced the recognition error across all the classifiers. In regard to the Limb.Pos. dataset results, the recognition error of the LDA classifier was 24.31% (Figure 5a). For the SVM, the recognition error in the original feature space was 26.46%, which increased to 29.32% when the data was transformed into the LDA subspace. For the QDA, k-NN, and CEN, using the original feature space, the recognition errors all exceeded 30%, with the CEN reaching as high as 38.9%. However, transforming the data into Fisher’s discriminant subspace reduced the errors to around 25%. With MLP (Figure 5b), the recognition errors consistently stayed above 30% in the original feature space, ranging from 33.48% for one layer to 31.18% for six layers; however, when transformed into Fisher’s subspace, the recognition errors dropped consistently to under 28%.
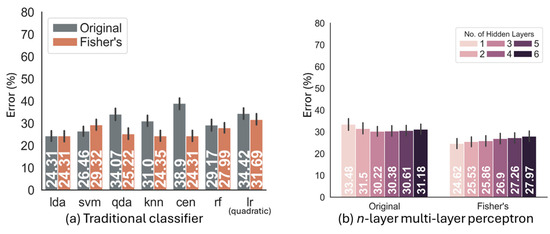
Figure 5.
Comparison of recognition error (%) based on the Limb.Pos. dataset using the original TD8-AR feature space and transformed into Fisher’s discriminant space for (a) seven traditional classifiers and (b) -layers MLP.
The results based on the Amp.Force. dataset are shown in Figure 6, where the recognition error for the LDA is 27.3% (Figure 6a). Transforming the data into Fisher’s discriminant subspace reduced the recognition errors to approximately 28% for all the classifiers, with the CEN showing a large reduction of 34.09%. For MLP (Figure 6b), in the original feature space, the recognition error increased from 45.13% with one hidden layer to 46.8% with six hidden layers. When transformed into Fisher’s discriminant subspace, the recognition error decreased by 17% to approximately 28.41–1.11% higher than that of the LDA.
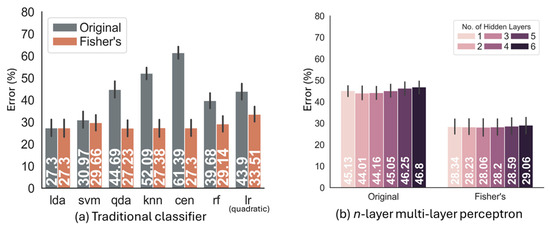
Figure 6.
Comparison of recognition error (%) based on the Amp.Force. dataset using the original TD8-AR feature space and transformed into Fisher’s discriminant subspace for (a) seven traditional classifiers and (b) -layers MLP.
3.2. Recognition Performance of Hybrid Frameworks in Regard to Hand Gesture Recognition Under Dynamic Conditions
3.2.1. Results Based on Limb.Pos. Dataset
Figure 7 presents the recognition errors across eight feature sets based on the Limb.Pos. dataset. The Friedman statistical test identified statistically significant differences between at least one pair of classification methods among all the feature sets (). Except for Ext-23, all the feature sets, when trained with the LDA classifier, had significantly lower errors compared to the CNN-CE, which had an error of 34.32% (). In regard to LDA, the TD8 feature set recorded the lowest recognition error at 23.81%, outperforming the state-of-the-art TD-PSR [7] set by 0.53%. Meanwhile, the LDA and TD8-AR set raised the recognition error from TD8 by 0.5% to 24.31%. In regard to the hybrid CNN-LDA framework, the CNN-MSE consistently exhibited lower recognition errors and reconstruction losses than the CNN-CEMSE, with statistically significant differences observed in the recognition errors of the DU, TD-PSR, and TD8 feature sets (). When trained with the Ext-23 feature set, the CNN-MSE achieved state-of-the-art performance, with a 22.79% error rate, significantly outperforming the LDA based on the same feature set (). It is also observed that Fisher’s reconstruction loss was relatively high ( ) based on the Ext-23 feature set for both the CNN-MSE and CNN-CEMSE.
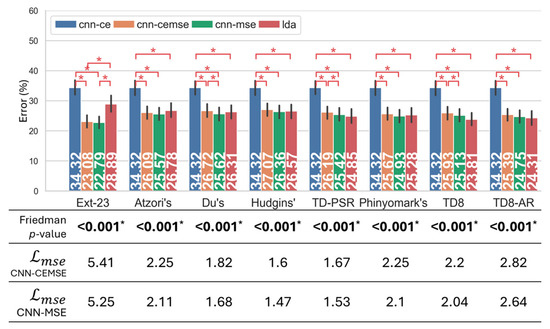
Figure 7.
Comparison of the performance based on Limb.Pos. dataset between 8 different feature sets and 4 classification approaches in terms of recognition error (%), the result of Friedman statistical test with Fisher’s reconstruction loss by the CNN-CEMSE and CNN-MSE; * indicates statistical significance ().
Figure 8 illustrates the recognition errors based on the Ext-23 feature set across 11 subjects, where performance variations by subject were clearly observed. For the CNN-CE, trained end-to-end using the raw sEMG signals, the recognition errors ranged from 25.15% for S9 to as high as 48.27% for S7. Training the LDA model on the Ext-23 feature set did not guarantee enhanced recognition performance over the CNN-CE for all the subjects; notably, the LDA model’s error for S10 was 41.5%, 11.5% higher than the CNN-CE. In contrast, the CNN-CEMSE and CNN-MSE significantly reduced the errors across all the subjects compared to the CNN-CE, with the lowest errors recorded for S9 of 13.29% and 13.4%, respectively, for the CNN-CEMSE and CNN-MSE.
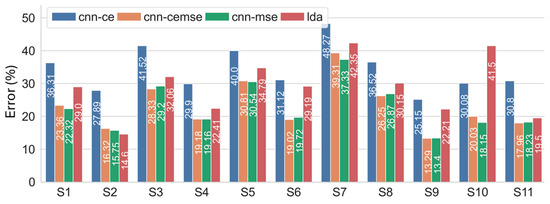
Figure 8.
Recognition error (%) for each subject, averaged over all the train–test limb position combinations, using four classification approaches, namely CNN-CE, CNN-CEMSE, CNN-MSE, and LDA, using Ext-23 feature set.
In Figure 9, we can see that the CNN-CEMSE, along with the CNN-MSE and LDA, successfully reduced the recognition error compared to the CNN-CE based on all the train–test combinations, using the Ext-23 feature set. When trained and tested on the same P3 limb position, the CNN-CEMSE achieved the most substantial reduction in the recognition error, decreasing by 6.8% from 8.8% to just 2.0%. When trained and tested on different limb positions, specifically when trained on P3 and tested on P4, the CNN-MSE showed the largest reduction in the recognition errors, decreasing from CNN-CE’s 44% to 24.87%. On average, the LDA achieved the lowest error of 2.6% in the same limb position train–test evaluation, marking a 4% improvement over the CNN-CE. While in the case where the tested limb positions differed from the training ones, the CNN-MSE returned the lowest recognition error decrease of 27.71–13.53% compared to the CNN-CE and 7.75% compared to the LDA. Table 2 highlights the recognition performance of our proposed hybrid method compared with other deep end-to-end machine learning approaches for myoelectric hand gesture recognition. By enforcing the linear_6 latent representation to approximate Fisher’s representation of the Ext-23 feature set, our proposed CNN-LDA framework based on the CNN-MSE achieved the lowest recognition error across all the evaluation metrics.
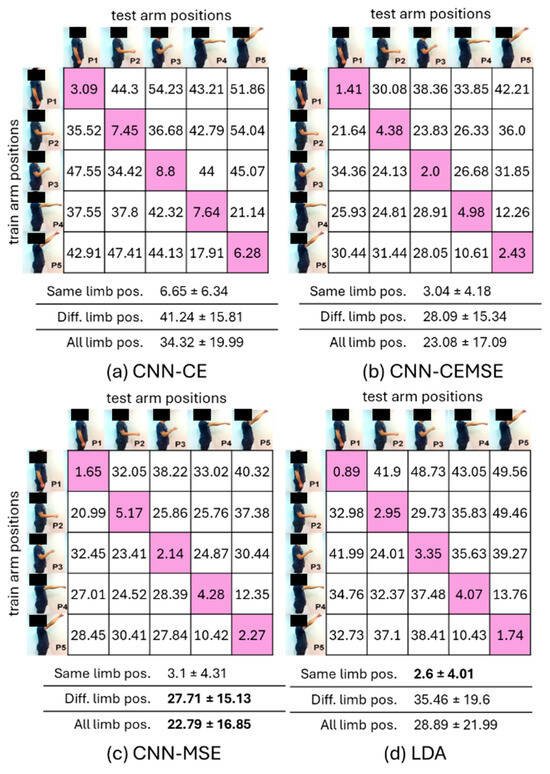
Figure 9.
Average inter-limb position recognition error across all 11 subjects with four classification approaches and the Ext-23 feature set: (a) CNN-CE, (b) CNN-CEMSE, (c) CNN-MSE, and (d) LDA. Bold values denote the lowest recognition errors.

Table 2.
Performance comparison of our proposed hybrid CNN-LDA framework (CNN-MSE) with other deep end-to-end architectures for myoelectric hand gesture recognition based on Limb.Pos. dataset.
3.2.2. Results Based on Amp.Force. Dataset
Figure 10 shows the recognition error based on the Amp.Force. dataset for all eight feature sets. The Friedman statistical test confirmed that there were significant differences between at least one pair of classification methods across all the feature sets (). In regard to the LDA classifier, TD8-AR, Phinyomark’s, and the Ext-23 feature sets were effective when subject to changes in the contraction force, with recognition errors of 27.3%, 27.44%, and 28.85%, respectively. Additionally, significant differences between the LDA and CNN-CE were confirmed in regard to these feature sets (). In contrast, the recognition error exceeded 32% for all the remaining feature sets, including the TD-PSR. The CNN-CEMSE and CNN-MSE consistently reduced the recognition errors across all the features compared to the CNN-CE, although the performance differences in regard to the LDA varied depending on the feature set. For the Ext-23 feature set, the CNN-CEMSE and CNN-MSE recorded recognition errors of 29.76% and 29.79%, respectively, each showing a 0.8% increase compared to the LDA. In contrast, when trained on Phinyomark’s and the TD8-AR feature sets, the CNN-CEMSE and CNN-MSE showed recognition errors more than 3% higher than the LDA.
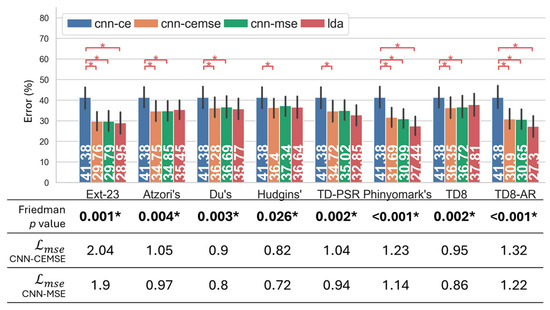
Figure 10.
Comparison based on Amp.Force. dataset between 8 different feature sets and 4 classification approaches in terms of (top) recognition error (%) (bottom) result of Friedman statistical test with Fisher’s reconstruction loss by the CNN-CEMSE and CNN-MSE; * indicates statistical significance ().
Regarding the recognition errors averaged across all training–testing contraction combinations for each subject (Figure 11), the CNN-CEMSE, CNN-MSE, and LDA effectively reduced the errors for every subject compared to the CNN-CE. S6 experienced substantial performance improvements using the CNN-MSE and LDA, achieving recognition errors of 16.7% and 14.22%, respectively, over a 20% reduction compared to the CNN-CE. Noticeably, for S8, both the CNN-MSE and CNN-CEMSE reduced the recognition error by over 10% compared to the CNN-CE and by more than 5% compared to the LDA.
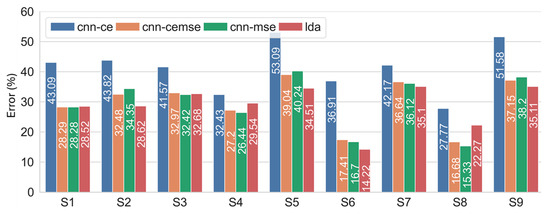
Figure 11.
Recognition error (%) for each subject based on Amp.Force. dataset, averaged over all train–test contraction force combinations, using four classification approaches, namely CNN-CE, CNN-CEMSE, CNN-MSE, and LDA, using Ext-23 feature set.
As shown in Figure 12, the CNN-CEMSE, CNN-MSE, and LDA effectively reduced the recognition errors across all the combinations of trained and tested contraction forces compared with the CNN-CE. Notably, the LDA returned the lowest recognition error of 4.11% when trained and tested on the same level of contraction force (Figure 12d), with the most substantial reduction observed of 14.5% when trained and tested on high contraction force levels compared with the CNN-CE. The CNN-CEMSE obtained the lowest recognition error of 40.25% when tested on contraction forces that differed from those used in training (Figure 12b). Table 3 showcases the end-to-end recognition performance of our proposed hybrid CNN-LDA framework (CNN-MSE) compared with other deep learning methods, based on the Amp.Force. dataset. It was observed that our proposed framework successfully reduced the recognition error across all the evaluation metrics.

Figure 12.
Average inter-contraction force recognition error across all 9 subjects with four classification approaches and the Ext-23 feature set: (a) CNN-CE, (b) CNN-CEMSE, (c) CNN-MSE, and (d) LDA. Bold values denote the lowest recognition errors.

Table 3.
Performance comparison of our proposed hybrid CNN-LDA framework (CNN-MSE) with other deep end-to-end architectures for myoelectric hand gesture recognition, based on Amp.Force. dataset.
3.3. The Effect of Hyperparameter Balancing MSE and Cross-Entropy Loss
As shown in Figure 13, we have studied the effect of the hyperparameter in Equation (8) on the recognition error across two public datasets. It is observed that when , minimal changes in the recognition performance are seen based on both datasets. However, when the cross-entropy loss starts to become the dominant training loss (), an increase in recognition error is observed based on both datasets, highlighting the adverse effects of cross-entropy loss.
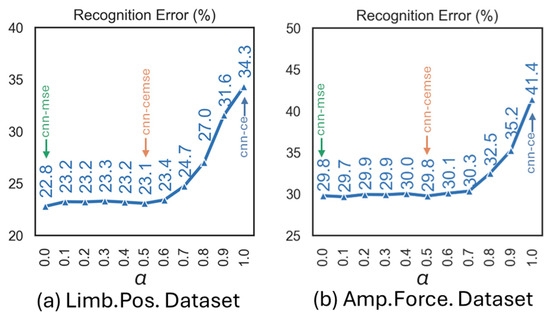
Figure 13.
The effect of in Equation (8) on recognition accuracy of (a) Limb.Pos. dataset and (b) Amp.Force. dataset, using Ext-23 feature set.
3.4. Evaluation of CNN Training Convergence and Latent Representation
Figure 14 and Figure 15 show comprehensive analysis, comparing three deep CNN training approaches with the conventional LDA, specifically focusing on the Ext-23 feature set. Regarding overall recognition performance, from the 30th epoch onward, the performance of the three CNN models converged, as indicated by minimal reductions in the recognition error (Figure 14a and Figure 15a), based on both datasets. Additionally, the CNN-MSE converged faster than the CNN-CEMSE, based on both datasets, with no signs of overfitting observed at the 60th epoch.
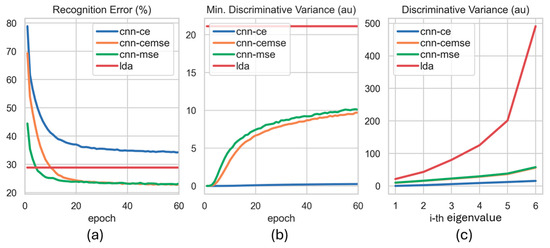
Figure 14.
Training convergence in terms of (a) recognition error, (b) smallest eigenvalue, and (c) eigenvalue at 60 epochs for CNN-CE, CNN-CEMSE, CNN-MSE, and LDA, based on the Limb.Pos. dataset and the Ext-23 feature set.
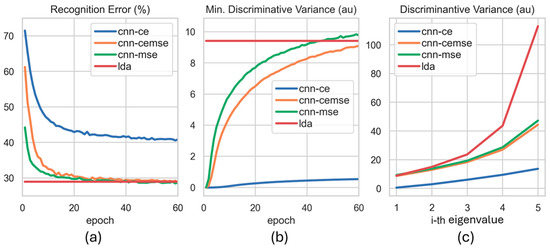
Figure 15.
Training convergence in terms of (a) recognition error, (b) smallest eigenvalue, and (c) eigenvalue at 60 epochs for CNN-CE, CNN-CEMSE, CNN-MSE, and LDA, based on the Amp.Force. dataset and the Ext-23 feature set.
Interesting insights were revealed by examining the eigenvalues of the CNN latent representation for the linear_6 layer (Figure 14b,c and Figure 15b,c). The smallest or the first discriminant eigenvalue represents the variance in the most challenging direction for classifying hand gestures. In regard to both datasets, the first eigenvalue of the CNN-CE data exhibited a minimal increase during training (Figure 14b and Figure 15b). However, when using Fisher’s reconstruction loss (), the first eigenvalue of the CNN-MSE and CNN-CEMSE noticeably rises, with the CNN-MSE surpassing the LDA starting from epoch 50th, based on the Amp.Force. dataset (Figure 15b). In regard to the Limb.Pos. dataset, the first eigenvalue of the CNN-MSE and CNN-CEMSE remained smaller than that of the LDA even after 60 epochs. Additionally, the CNN-MSE consistently achieved higher first eigenvalues than the CNN-CEMSE, based on both datasets. With the LDA classifier, significant disparities between the largest and smallest eigenvalues in the embedded space were also observed (Figure 14c and Figure 15c). By approximating Fisher’s representation, both the CNN-MSE and CNN-CEMSE mitigated the extreme eigenvalues of the LDA, demonstrating a spectral regularization effect.
To further analyze the spectral regularization effect of our proposed framework, we utilized T-SNE (t-distributed Stochastic Neighbor Embedding, as shown in Figure 16) to illustrate the data embedded in linear_6 and referenced Fisher’s representation. T-SNE is a machine learning technique that enables visualization of high-dimensional data by reducing the dimensionality of a dataset, while preserving the relative distance between the datapoints. It is evident that there is substantial displacement in the Limb.Pos. dataset (Figure 16a), particularly in regard to the wrist extension and wrist flexion, where the cluster formed by the CNN-MSE and LDA is entirely non-overlapped. In regard to the Amp.Force. dataset (Figure 16b), although not as pronounced as in the Limb.Pos. dataset, there is clear presence of cluster shifts in the spherical grip and thumb flexion data.

Figure 16.
T-SNE visualization of embedded representation of CNN-MSE linear_6 and Fisher’s representation on (a) S1 trained on P2 limb position based on Limb.Pos. dataset and (b) S1 trained on moderate contraction force based on Amp.Force. dataset.
3.5. Comparison of Inference Time
To demonstrate the suitability of our proposed frameworks for the real-time control of prosthetic devices or for other muscle/human–machine interface applications, we evaluated the inference time of our proposed CNN-LDA framework. The inference time was tested on a computer that was equipped with an Intel(R) Core(TM) i7-8750H CPU and an NVIDIA GeForce RTX 2070 GPU. Table 4 presents the inference time for the Amp.Force. dataset. The inference time for the LDA was consistently low, at 0.19 ms per frame, regardless of the input feature set. Feature extraction varied in regard to computation duration, ranging from 0.49 ms per frame using TD-PSR to 16.95 ms per frame using the Ext-23 feature set. By decoupling feature extraction during inference, our CNN-LDA framework offered low real-time processing, at 1.72 ms per frame, for the CNN-CEMSE, CNN-MSE, and CNN-CE.

Table 4.
Comparison of inference time between classical LDA with manual feature extraction and the CNN-LDA framework; * CNN includes CNN-CEMSE, CNN-MSE, and CNN-CE.
4. Discussion
We have employed the train-one-test-all evaluation scheme to assess the generalization performance of the framework, which is better aligned with real-world conditions. We first highlighted the robustness of the LDA, showing that it consistently outperformed other algorithms in regard to the train-one-test-all evaluation scheme. Notably, the LDA trained with manual feature extraction demonstrated superior performance, not only over traditional machine learning algorithms (Figure 5 and Figure 6), but also over deep 1D convolutional neural networks trained end-to-end with only cross-entropy loss (CNN-CE) (Figure 7 and Figure 10). Furthermore, since the LDA functions as both a classifier and a dimensionality reduction method, transforming the data in regard to Fisher’s discriminant subspace significantly reduced the classification error for all the traditional machine learning algorithms.
There are a few possible underlying reasons that may explain this finding. Most machine learning classifiers, except for LDA and QDA, are primarily point based, wherein decision boundaries can be significantly affected by data outliers [44,45]. Algorithms, such as k-NN and SVMs, place high emphasis on hard-to-classify data points [42]. Neural networks trained with cross-entropy have a tendency to heavily penalize incorrect predictions, leading to severe overfitting in regard to outliners [44]. In contrast, the LDA and QDA assume normally distributed data within each class, and their decision boundaries are determined by overall data distributions rather than individual points [43]. Although similar, gesture recognition performance of the LDA and QDA differs significantly, with the QDA showing an over 10% higher error than the LDA (Figure 5a and Figure 6a). While the LDA assumes that all classes have the same variance, leading to a linear decision boundary, the QDA relaxes this homoscedasticity assumption, resulting in a more complex quadratic decision boundary [42]. It has been shown that a simple linear mapping function is effective not only in regard to discrete hand gesture recognition tasks [5], but also in regard to proportional control problems [46,47]. Moreover, gesture consistency varies with the subject’s expertise [48,49], and data cluster shifts are expected even under the same conditions [50,51]. Our findings further confirm that the LDA effectively accommodates gestures under new conditions. As a dimensionality reduction method, the LDA’s Fisher discriminant subspace is linked to muscle synergy [52], wherein muscle groups coordinate together during movement. We hypothesize that the LDA preserves spatial information related to electrode placement, facilitating an effective muscle/human–machine interface. In related research, [53] proposed a force tolerance model based on muscle synergy reconstruction loss, akin to the LDA’s method of assigning hand gestures with the highest probability, as shown in Equation (2).
Based on improved recognition accuracy from transforming sEMG features into Fisher’s discriminant subspace, we proposed a novel CNN-LDA framework to approximate Fisher’s representation. We tested two variants of our hybrid CNN-LDA framework, the CNN-CEMSE and CNN-MSE, using eight feature sets, across two public datasets. Our results indicate that both variants effectively lowered the recognition error compared to a naive CNN-CE, with improvement ranges from 7% to 11% based on the Limb.Pos. dataset and 4% to 11% based on the Amp.Force. dataset. Notably, based on the Limb.Pos. dataset, we achieved a state-of-the-art performance with the Ext-23 feature set (Figure 7), recording the lowest error of 22.79% with the CNN-MSE, a 2.06% improvement over the TD-PSR [7]. However, based on the Amp.Force. dataset, the CNN-LDA and Ext-23 feature set combination did not achieve state-of-the-art results, with recognition errors 1% higher than the Ext-23 feature set with the LDA, and 2.4% higher than the LDA with Phinyomark’s and TD8-AR features (Figure 10). Yet, the result of the CNN-LDA with the Ext-23 feature set remains competitive, showing overall improvements over most of the tested pipelines (Figure 10) and a minimal inference time (Table 4).
Our novel CNN-LDA framework provides many practical features that are suitable for myoelectric-based applications. For every feature set, the relatively high reconstruction error ( > 0.8, Figure 7 and Figure 10) induced the spectral regularization effect based on the discriminant eigenvalue structure for linear_6 (Figure 14c and Figure 15c), with a cluster shift in terms of the wrist movements being clearly observable in the t-SNE visualization (Figure 16a). However, since a state-of-the-art performance was achieved based only on the Limb.Pos. dataset using the Ext-23 feature set, further research is needed to understand the relationship between the discriminant eigenvalue structure and generalizability.
The Ext-23 feature set is a concatenation of all the individual features from other effective feature sets, without applying any formal feature selection process. While feature selection can potentially improve recognition performance, even for out-of-distribution hand gestures [25], it is generally a costly and time-consuming process, often requiring manual intervention. Moreover, the resulting feature set is not guaranteed to be generalizable across different datasets. For instance, the TD8 feature set was derived using the Minimum Redundancy Maximum Relevance technique, based on the Limb.Pos. dataset [25]. When trained with the LDA, the TD8 feature set achieved a recognition error of 23.81%, based on the Limb.Pos. dataset (Figure 7). However, based on the Amp.Force. dataset (Figure 10), the same TD8 feature set resulted in the highest recognition error of 37.81%. Moreover, Wei, Dai, Wong, Hu, Kankanhalli, and Geng [41] proposed a multiview deep learning architecture for sEMG-based hand gesture recognition, wherein each input view corresponds to a different sEMG feature set. While the work of Wei, Dai, Wong, Hu, Kankanhalli, and Geng [41] requires explicit computation of each individual feature during inference, our framework does not, resulting in a constant inference time regardless of the feature choice (Table 4). Additionally, by decoupling feature extraction during inference, our CNN-LDA framework enables future integration of robust but computationally intensive features, such as Sample Entropy or Empirical Mode Decomposition [22,54].
Our results also highlighted that cross-entropy loss adversely affected myoelectric hand gesture recognition. As shown in Figure 5 and Figure 6, MLP trained on the original TD8-AR feature space with cross-entropy loss increased the recognition error compared to the LDA, ranging from 6% to 20%. Moreover, the CNN-CEMSE increased the reconstruction loss across all the features (Figure 7 and Figure 10) and reduced the smallest eigenvalue (Figure 14b and Figure 15b). Moreover, the CNN-CE exhibited only a negligible increase in the smallest eigenvalue as the training converged (Figure 14b,c and Figure 15b,c). This observation aligns with related machine learning findings that cross-entropy favors easily classified classes [44] and is sensitive to noisy datasets [55,56].
In this work, we focused solely on hand gesture recognition using a single modality: the sEMG signal. Multi-modal sensory fusion, i.e., combining sEMG signals with additional sensory inputs, such as pFMG [17,57,58], IMU [30,59], or RGB [18,19], and depth cameras [20], has shown promising results in regard to enhancing sEMG-based hand gesture recognition under dynamic conditions. In general, multi-modal fusion can be approached in two ways. The first concerns sensory complementarity, wherein the sEMG signal is paired with another modality to enhance recognition, as is common with pFMG and IMU [17,59]. The second approach leverages additional modalities to provide contextual information, such as on the arm position [60], usage scenarios [59], grasped object types [18], or wrist orientation [19]. In future work, we aim to explore multi-modal sensing in greater depth to further improve recognition performance under dynamic conditions.
As shown in Figure 7 and Figure 10, recognition performance varies depending on the feature set used. Currently, feature selection is often performed heuristically, typically by combining high-performing features, based on classification accuracy [22] or the ANOVA F-score [25]. However, in our previous study, we observed that criteria, such as the ANOVA F-score, become less reliable under novel conditions [25]. Moreover, there is a lack of detailed analysis on the impact of sEMG signals under dynamic conditions, with only a few notable studies addressing this issue [6,7,38,39]. We believe that a deeper investigation into this impact would be beneficial for developing highly robust and intuitive prosthetic hand control interfaces.
5. Conclusions
We have demonstrated that the LDA and Fisher’s discriminant subspace achieved an optimal hand gesture recognition performance under the train-one-test-all evaluation scheme across both the Limb.Pos. and Amp.Force. datasets. Based on this observation, we have proposed a CNN-LDA hybrid framework that approximates Fisher’s representation from raw EMG signals. The results from two different public datasets consistently demonstrated that our CNN-LDA hybrid framework outperformed multiple deep learning architectures, trained end-to-end with cross-entropy loss only. When trained with the Ext-23 feature set, our CNN-LDA framework achieved a state-of-the-art recognition error of 22.79%, based on the Limb.Pos. dataset, using the CNN-MSE variant. Additionally, the CNN-LDA framework’s imperfect reconstruction of Fisher’s representation induced a spectral regularization effect, preventing the occurrence of extreme values of discriminant eigenvalues. By highlighting the robustness of the LDA subspace in regard to sEMG signal covariate shifts and demonstrating that leveraging Fisher’s representation can effectively guide CNN training, our framework serves as a foundation for the future development of effective muscle–machine interfaces using deep learning.
Author Contributions
H.L.: Conceptualization, Methodology, Software, Writing—Original Draft, Formal Analysis, Visualization. M.i.h.P. and G.M.S.: Resources, Supervision, Writing—Review and Editing. G.A.: Conceptualization, Resources, Writing—Review and Editing, Supervision, Funding Acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this article was made possible through financial support from the ARC Centre of Excellence for Electromaterials Science (Grant No. CE140100012), the ARC-Discovery Project (DP210102911), and the University of Wollongong.
Institutional Review Board Statement
Ethical approval was not required for this study as it only uses publicly available datasets.
Data Availability Statement
The dataset used in this manuscript is publicly accessible at https://www.rami-khushaba.com/biosignals-repository (accessed on 1 June 2024).
Acknowledgments
During the preparation of this work the author(s) used ChatGPT 4.0 and Quillbot in order to enhance the writing quality. After using this tool/service, the author(s) reviewed and edited the content as needed, and take full responsibility for the content of the published article.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN-CE | Cross-Entropy CNN (α = 1) |
| CNN-CEMSE | Fusion CNN-LDA (α = 0.5) |
| CNN-MSE | Fisher’s approximator (α = 0) |
| LDA | Linear Discriminant Analysis |
| SVMs | Support Vector Machines |
| QDA | Quadratic Discriminant Analysis |
| kNN | K-nearest neighbor |
| CEN | Nearest centroid |
| LR-quadratic | Logistic Regression with Quadratic Kernel |
| TD8 | Robust Time-Domain 8 |
| TD8-ARs | Robust Time-Domain 8 with Autoregressive Coefficients |
| TD-PSR | Time-domain power spectral moments |
References
- Cordella, F.; Ciancio, A.L.; Sacchetti, R.; Davalli, A.; Cutti, A.G.; Guglielmelli, E.; Zollo, L. Literature review on needs of upper limb prosthesis users. Front. Neurosci. 2016, 10, 209. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Gu, Y.; Thakor, N.V.; Liu, H. Improving the functionality, robustness, and adaptability of myoelectric control for dexterous motion restoration. Exp. Brain Res. 2019, 237, 291–311. [Google Scholar] [CrossRef] [PubMed]
- Kyranou, I.; Vijayakumar, S.; Erden, M.S. Causes of performance degradation in electromyographic pattern recognition in upper limb prostheses. Front. Neurorobotics 2018, 12, 58. [Google Scholar] [CrossRef] [PubMed]
- Hargrove, L.J.; Scheme, E.J.; Englehart, K.B.; Hudgins, B.S. Multiple binary classifications via linear discriminant analysis for improved controllability of a powered prosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Vidovic, M.M.-C.; Hwang, H.-J.; Amsüss, S.; Hahne, J.M.; Farina, D.; Müller, K.-R. Improving the robustness of myoelectric pattern recognition for upper limb prostheses by covariate shift adaptation. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 961–970. [Google Scholar] [CrossRef]
- Al-Timemy, A.H.; Khushaba, R.N.; Bugmann, G.; Escudero, J. Improving the performance against force variation of EMG controlled multifunctional upper-limb prostheses for transradial amputees. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 650–661. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Takruri, M.; Miro, J.V.; Kodagoda, S. Towards limb position invariant myoelectric pattern recognition using time-dependent spectral features. Neural Netw. 2014, 55, 42–58. [Google Scholar] [CrossRef]
- Smith, L.H.; Hargrove, L.J.; Lock, B.A.; Kuiken, T.A. Determining the optimal window length for pattern recognition-based myoelectric control: Balancing the competing effects of classification error and controller delay. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 19, 186–192. [Google Scholar] [CrossRef]
- Le, H.; Spinks, G.M.; in Het Panhuis, M.; Alici, G. Cross-day myoelectric gesture recognition with hybrid multistream CNN-bidirectional LSTM. In Proceedings of the 2025 IEEE International Conference on Mechatronics (ICM’25), Wollongong, Australia, 28 February–2 March 2025. [Google Scholar]
- Atzori, M.; Cognolato, M.; Müller, H. Deep learning with convolutional neural networks applied to electromyography data: A resource for the classification of movements for prosthetic hands. Front. Neurorobotics 2016, 10, 9. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, B.; Zhao, Y. Dynamic gesture recognition based on LSTM-CNN. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2446–2450. [Google Scholar]
- Wei, W.; Wong, Y.; Du, Y.; Hu, Y.; Kankanhalli, M.; Geng, W. A multi-stream convolutional neural network for sEMG-based gesture recognition in muscle-computer interface. Pattern Recognit. Lett. 2019, 119, 131–138. [Google Scholar] [CrossRef]
- Zabihi, S.; Rahimian, E.; Asif, A.; Mohammadi, A. Light-weight CNN-attention based architecture for hand gesture recognition via electromyography. In Proceedings of the ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Zabihi, S.; Rahimian, E.; Asif, A.; Mohammadi, A. Trahgr: Transformer for hand gesture recognition via electromyography. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 4211–4224. [Google Scholar] [CrossRef] [PubMed]
- Betthauser, J.L.; Hunt, C.L.; Osborn, L.E.; Masters, M.R.; Levay, G.; Kaliki, R.R.; Thakor, N.V. Limb position tolerant pattern recognition for myoelectric prosthesis control with adaptive sparse representations from extreme learning. IEEE Trans. Biomed. Eng. 2017, 65, 770–778. [Google Scholar] [CrossRef] [PubMed]
- Tchantchane, R.; Zhou, H.; Zhang, S.; Alici, G. A review of hand gesture recognition systems based on noninvasive wearable sensors. Adv. Intell. Syst. 2023, 5, 2300207. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, H.; Tchantchane, R.; Alici, G. Hand gesture recognition across various limb positions using a multi-modal sensing system based on self-adaptive data-fusion and convolutional neural networks (CNNs). IEEE Sens. J. 2024, 24, 18633–18645. [Google Scholar] [CrossRef]
- Deshmukh, S.; Khatik, V.; Saxena, A. Robust Fusion Model for Handling EMG and Computer Vision Data in Prosthetic Hand Control. IEEE Sens. Lett. 2023, 7, 6004804. [Google Scholar] [CrossRef]
- Cirelli, G.; Tamantini, C.; Cordella, L.P.; Cordella, F. A Semiautonomous Control Strategy Based on Computer Vision for a Hand–Wrist Prosthesis. Robotics 2023, 12, 152. [Google Scholar] [CrossRef]
- Castro, M.N.; Dosen, S. Continuous semi-autonomous prosthesis control using a depth sensor on the hand. Front. Neurorobotics 2022, 16, 814973. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Al-Timemy, A.; Kodagoda, S.; Nazarpour, K. Combined influence of forearm orientation and muscular contraction on EMG pattern recognition. Expert. Syst. Appl. 2016, 61, 154–161. [Google Scholar] [CrossRef]
- Phinyomark, A.; Quaine, F.; Charbonnier, S.; Serviere, C.; Tarpin-Bernard, F.; Laurillau, Y. EMG feature evaluation for improving myoelectric pattern recognition robustness. Expert. Syst. Appl. 2013, 40, 4832–4840. [Google Scholar] [CrossRef]
- Lorrain, T.; Jiang, N.; Farina, D. Influence of the training set on the accuracy of surface EMG classification in dynamic contractions for the control of multifunction prostheses. J. Neuroeng. Rehabil. 2011, 8, 25. [Google Scholar] [CrossRef]
- Franzke, A.W.; Kristoffersen, M.B.; Bongers, R.M.; Murgia, A.; Pobatschnig, B.; Unglaube, F.; van der Sluis, C.K. Users’ and therapists’ perceptions of myoelectric multi-function upper limb prostheses with conventional and pattern recognition control. PLoS ONE 2019, 14, e0220899. [Google Scholar] [CrossRef] [PubMed]
- Le, H.; Spinks, G.M.; in Het Panhuis, M.; Alici, G. Feature significance and generalizability of myoelectric hand gesture recognition under varying limb positions. In Proceedings of the 2025 IEEE International Conference on Mechatronics (ICM’25), Wollongong, Australia, 28 February–2 March 2025. [Google Scholar]
- Akkad, G.; Mansour, A.; Inaty, E. Embedded deep learning accelerators: A survey on recent advances. IEEE Trans. Artif. Intell. 2023, 5, 1954–1972. [Google Scholar] [CrossRef]
- Le, H.; in Het Panhuis, M.; Spinks, G.M.; Alici, G. The effect of dataset size on EMG gesture recognition under diverse limb positions. In Proceedings of the 2024 10th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), Heidelberg, Germany, 1–4 September 2024; pp. 303–308. [Google Scholar]
- Moslemi, A.; Briskina, A.; Dang, Z.; Li, J. A Survey on Knowledge Distillation: Recent Advancements. Mach. Learn. Appl. 2024, 18, 100605. [Google Scholar] [CrossRef]
- Zeng, J.; Sheng, Y.; Yang, Y.; Zhou, Z.; Liu, H. Cross modality knowledge distillation between A-mode ultrasound and surface electromyography. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Wei, W.; Ren, L.; Zhou, M.; Ma, Z.; Zhao, K.; Xu, X. Improving unimodal sEMG-based pattern recognition through multimodal generative adversarial learning. IEEE Trans. Instrum. Meas. 2025, 74, 2523520. [Google Scholar] [CrossRef]
- Ghojogh, B.; Karray, F.; Crowley, M. Fisher and kernel fisher discriminant analysis: Tutorial. arXiv 2019, arXiv:1906.09436. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Drapała, J.; Brzostowski, K.; Szpala, A.; Rutkowska-Kucharska, A. Two stage EMG onset detection method. Arch. Control Sci. 2012, 22, 427–440. [Google Scholar] [CrossRef]
- Jiang, N.; Englehart, K.B.; Parker, P.A. Extracting simultaneous and proportional neural control information for multiple-DOF prostheses from the surface electromyographic signal. IEEE Trans. Biomed. Eng. 2008, 56, 1070–1080. [Google Scholar] [CrossRef]
- Fuglevand, A.J.; Winter, D.A.; Patla, A.E.; Stashuk, D. Detection of motor unit action potentials with surface electrodes: Influence of electrode size and spacing. Biol. Cybern. 1992, 67, 143–153. [Google Scholar] [CrossRef]
- Farina, D.; Merletti, R.; Stegeman, D. Biophysics of the generation of EMG signals. In Electromyography: Physiology, Engineering, and Noninvasive Applications; Wiley: Hoboken, NJ, USA, 2004; pp. 81–105. [Google Scholar] [CrossRef]
- Fuglevand, A.J.; Winter, D.A.; Patla, A.E. Models of recruitment and rate coding organization in motor-unit pools. J. Neurophysiol. 1993, 70, 2470–2488. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Kim, J. Electromyography-signal-based muscle fatigue assessment for knee rehabilitation monitoring systems. Biomed. Eng. Lett. 2018, 8, 345–353. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Zhang, D.; Sheng, X.; Li, S.; Zhu, X. Invariant surface EMG feature against varying contraction level for myoelectric control based on muscle coordination. IEEE J. Biomed. Health Inform. 2014, 19, 874–882. [Google Scholar] [CrossRef] [PubMed]
- Phinyomark, A.; Phukpattaranont, P.; Limsakul, C. Feature reduction and selection for EMG signal classification. Expert. Syst. Appl. 2012, 39, 7420–7431. [Google Scholar] [CrossRef]
- Wei, W.; Dai, Q.; Wong, Y.; Hu, Y.; Kankanhalli, M.; Geng, W. Surface-electromyography-based gesture recognition by multi-view deep learning. IEEE Trans. Biomed. Eng. 2019, 66, 2964–2973. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Ghojogh, B.; Crowley, M. Linear and quadratic discriminant analysis: Tutorial. arXiv 2019, arXiv:1906.02590. [Google Scholar] [CrossRef]
- Dorfer, M.; Kelz, R.; Widmer, G. Deep linear discriminant analysis. arXiv 2015, arXiv:1511.04707. [Google Scholar] [CrossRef]
- Frénay, B.; Verleysen, M. Classification in the presence of label noise: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 845–869. [Google Scholar] [CrossRef]
- Hahne, J.M.; Biessmann, F.; Jiang, N.; Rehbaum, H.; Farina, D.; Meinecke, F.C.; Müller, K.-R.; Parra, L.C. Linear and nonlinear regression techniques for simultaneous and proportional myoelectric control. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 269–279. [Google Scholar] [CrossRef]
- Jiang, N.; Vujaklija, I.; Rehbaum, H.; Graimann, B.; Farina, D. Is accurate mapping of EMG signals on kinematics needed for precise online myoelectric control? IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 22, 549–558. [Google Scholar] [CrossRef]
- Bunderson, N.E.; Kuiken, T.A. Quantification of feature space changes with experience during electromyogram pattern recognition control. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 239–246. [Google Scholar] [CrossRef]
- Stuttaford, S.A.; Dyson, M.; Nazarpour, K.; Dupan, S.S. Reducing motor variability enhances myoelectric control robustness across untrained limb positions. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 32, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, D.; Sheng, X.; Zhu, X. Quantification and solutions of arm movements effect on sEMG pattern recognition. Biomed. Signal Process. Control 2014, 13, 189–197. [Google Scholar] [CrossRef]
- Radmand, A.; Scheme, E.; Englehart, K. A characterization of the effect of limb position on EMG features to guide the development of effective prosthetic control schemes. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 662–667. [Google Scholar]
- Vinjamuri, R.; Patel, V.; Powell, M.; Mao, Z.-H.; Crone, N. Candidates for synergies: Linear discriminants versus principal components. Comput. Intell. Neurosci. 2014, 2014, 373957. [Google Scholar] [CrossRef] [PubMed]
- Teng, Z.; Xu, G.; Liang, R.; Li, M.; Zhang, S. Evaluation of synergy-based hand gesture recognition method against force variation for robust myoelectric control. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2345–2354. [Google Scholar] [CrossRef]
- Al-Timemy, A.H.; Bugmann, G.; Outram, N.; Escudero, J. Single channel-based myoelectric control of hand movements with Empirical Mode Decomposition. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 6059–6062. [Google Scholar]
- Zhang, Z.; Sabuncu, M. Generalized cross entropy loss for training deep neural networks with noisy labels. arXiv 2018, arXiv:1805.07836. [Google Scholar] [CrossRef]
- Feng, L.; Shu, S.; Lin, Z.; Lv, F.; Li, L.; An, B. Can cross entropy loss be robust to label noise? In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 2206–2212. [Google Scholar]
- Zhou, H.; Le, H.T.; Zhang, S.; Phung, S.L.; Alici, G. Hand gesture recognition from surface electromyography signals with graph convolutional network and attention mechanisms. IEEE Sens. J. 2025, 25, 9081–9092. [Google Scholar] [CrossRef]
- Oyemakinde, T.T.; Kulwa, F.; Peng, X.; Liu, Y.; Cao, J.; Deng, X.; Wang, M.; Li, G.; Samuel, O.W.; Fang, P. A novel sEMG-FMG combined sensor fusion approach based on an attention-driven CNN for dynamic hand gesture recognition. IEEE Trans. Instrum. Meas. 2025, 747, 2533413. [Google Scholar] [CrossRef]
- Samuel, O.W.; Li, X.; Geng, Y.; Asogbon, M.G.; Fang, P.; Huang, Z.; Li, G. Resolving the adverse impact of mobility on myoelectric pattern recognition in upper-limb multifunctional prostheses. Comput. Biol. Med. 2017, 90, 76–87. [Google Scholar] [CrossRef]
- Scheme, E.; Fougner, A.; Stavdahl, Ø.; Chan, A.D.; Englehart, K. Examining the adverse effects of limb position on pattern recognition based myoelectric control. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 6337–6340. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).