Kriging-Variance-Informed Multi-Robot Path Planning and Task Allocation for Efficient Mapping of Soil Properties

Abstract

One of the most commonly performed environmental explorations is soil sampling to identify soil properties of agricultural fields, which can inform the farmer about the variable rate treatment of fertilisers in precision agriculture. However, traditional manual methods are slow, costly, and yield low spatial resolution. Deploying multiple robots with proximal sensors can address this challenge by parallelising the sampling process. Yet, multi-robot soil sampling is under-explored in the literature. This paper proposes an auction-based multi-robot task allocation that efficiently coordinates the sampling, coupled with a dynamic sampling strategy informed by Kriging variance from interpolation. This strategy aims to reduce the number of samples needed for accurate mapping by exploring and sampling areas that maximise information gained per sample. The key innovative contributions include (1) a novel Distance Over Variance (DOV) bid calculation for auction-based multi-robot task allocation, which incentivises sampling in high-uncertainty, nearby areas; (2) integration of the DOV bid calculation into the cheapest insertion heuristic for task queuing; and (3) thresholding of newly created tasks at locations with low Kriging variance to drop those unlikely to offer significant information gain. The proposed methods were evaluated through comparative simulated experiments using historical soil compaction data. Evaluation trials demonstrate the suitability of the DOV bid calculation combined with task dropping, resulting in substantial improvements in key performance metrics, including mapping accuracy. While the experiments were conducted in simulation, the system is compatible with ROS and the ‘move_base’ action client to allow real-world deployment. The results from these simulations indicate that the Kriging-variance-informed approach can be applied to the exploration and mapping of other soil properties (e.g., pH, soil organic carbon, etc.) and environmental data.

1. Introduction

Managing soil health is one of the most essential practices in agriculture and sports ground management (e.g., golf and football). These industries have seen increasing digitisation and automation to enable more precise land management, utilising its potential to reduce inputs, waste, and environmental harms, while simultaneously increasing soil health and crop yields [1]. The mapping of soil properties is critical to precision land management [2], allowing for localised soil management to address spatially variable deficiencies [3]. There are governmental financial incentives for farmers to map their soils and demonstrate the maintenance of soil health, such as the United States Department of Agriculture’s “Environmental Quality Incentives Program”, the EU (European Union)’s “Common Agricultural Policy”, and the “Sustainable Farming Initiative” of the United Kingdom’s Department for Environment Food and Rural Affairs [4,5,6], which provide additional commercial motivation for high-resolution soil mapping.

In this work, the soil compaction dataset of [7] is resampled in a multi-robot simulation to demonstrate these developments, as multiple bespoke automated penetrometers have not yet been developed to facilitate this experiment with real robots. This work contributes novel multi-robot coordination methods, which incorporate information from Kriging interpolation to estimate the soil property map and inform multi-robot path planning. It investigates whether these improve performance across several metrics of mapping and coordination accuracy and efficiency, in comparative simulated experiments. Auction-based MRTA and other such market-based MRTA approaches have been popular and effective in multi-robot exploration [8]. These experiments compare the effectiveness of SSI (Sequential Single-Item) auction-based MRTA (multi-robot task allocation), an existing method effective in dynamic task environments such as that of our dynamic sampling [9], with our coordination contributions detailed at the end of this section.

Soil compaction, i.e., increased soil density and reduced porosity due to pressure or vibration [10], is one property of interest in measuring soil health, which we map in this work to demonstrate a proposed multi-robot soil mapping system. High soil compaction is most commonly caused by the pressure on the soil surface from the operation of heavy machinery. It impedes the ability of crops to penetrate the soil with their roots, with negative effects on yields [11]. Excess compaction also causes a lower concentration of SOM (soil organic matter), making the soil less effective at sequestering CO₂ [12]. Treatment of soil compaction often involves deep tillage, with the machinery used for this tillage requiring large quantities of fossil fuels [13]. As such, a higher resolution mapping of soil compaction could reduce CO₂ emissions by allowing more localised tillage.

Efficient and accurate high-resolution mapping of such soil properties (e.g., soil pH, electrical conductivity and SOC) requires optimised exploration due to significant spatial variations in these properties. Fentanes et al. [14] used OK (Ordinary Kriging) interpolation [15], which is widely used to interpolate geospatial data, to predict soil property measurements at locations where samples have not yet been taken, using a limited number of recorded samples as input. OK produces a variance value for each of its predictions, a metric of the prediction’s uncertainty. Relatively high Kriging variance can indicate areas that are likely to provide the highest information gain, and most decrease the uncertainty of the OK’s predictions. The authors of [14] use this Kriging variance for IPP (informative path planning) in a single-robot mapping of soil compaction, using the output of OK to direct a Thorvald outdoor robot [16] with a bespoke penetrometer to navigate to and sample at a location where the Kriging variance is highest. Although this work looks at soil compaction data, information-driven dynamic sampling of other soil properties from large areas can also utilise the Kriging interpolation and Kriging variance approach.

This IPP was later extended to multiple robots in [17], generating sampling tasks at multiple positions for each new measured sample, and the new interpolation that follows. This work contributes further extensions to this multi-robot greedy NBV (Next Best View) IPP approach and presents methods of additionally informing auction-based MRTA (multi-robot task allocation) using Kriging variance, allowing sampling tasks to be delegated more efficiently. We expect that the system demonstrated effectively mapping soil compaction here can be applied to efficient mapping of other soil properties, and possibly spatial data from other areas of environmental monitoring or inspection.

The core contributions of this work are:

• DOV (Distance Over Variance)—A Kriging-variance-informed bid calculation for auction-based MRTA.
• Integration of the DOV bid calculation into the cheapest insertion heuristic [18].
• Thresholding of tasks at low Kriging variance locations at the point of task creation.

This work also validates these IPP and task allocation contributions in a simulated experimental evaluation. A free and open-source ROS implementation and simulation of this multi-robot soil mapping system is available at github.com/laurencejbelliott/ROS_multi-robot_soil_mapping_sim (accessed on 28 May 2025).

The remainder of this paper is organised as follows. Section 2 presents existing work related to this. Section 3 introduces the proposed multi-robot coordination system, with details of the different bid calculation approaches and heuristics used. The experimental setup is explained in Section 4. This is followed by the outcomes of the empirical evaluations in Section 5 and concluding discussions in Section 6.

2. Related Work

This work combines three specific areas of research, namely the proximal sensing of soil properties, informative path planning to optimise the exploration process, and multi-robot task allocation for efficient coordination between the robots in allocating and executing the exploration tasks. Related works from these areas are discussed in this section, with the key papers listed in Table 1.

2.1. Automated Soil Properties Mapping

2.1.1. Aerial Sensing

Although multi-robot soil mapping is underexplored in the academic literature, there are numerous existing methods of automated mapping of soil properties, each capable of measuring or predicting a different set of properties and having unique strengths and limitations. One of the earliest of these methods is aerial sensing, using imagery captured by sensors or cameras on satellites in orbit of Earth, or UAVs flying within the earth’s atmosphere. The data captured by these satellites are typically low in spatial resolution but are captured continuously, allowing for high temporal resolution. Some of these data are open access, such as that of the EU’s Sentinel satellites [19]. RGB image data from satellites have been used to accurately estimate crop biomass [20], and NDVI (Normalised Difference Vegetation Index) [21], a metric of crop health. Data from hyperspectral sensors, mounted on satellites or on UAVs (Unmanned Ariel Vehicles) and UGVs (Unmanned Ground Vehicles), has facilitated accurate prediction of pH, SOM, clay content [22], and soil moisture [23]. Microwave sensing has been used to directly measure soil moisture [24].

While UAVs can map a large area in a short time, this speed comes at the expense of resolution, as higher resolution mapping requires reduced distance to the ground, which also reduces the coverage speed. Measurements cannot be obtained below the soil surface, which can also be obscured by a crop’s canopy. It is not presently possible to remotely capture such a gamut of soil properties as on-the-ground probe sensors can, with remote sensing largely limited to prediction or proxy measurements from vision sensors, e.g., visual indices such as NDVI and hyperspectral Physiological Reflectance Index (PRI) [25]. Prediction of soil properties from aerial imagery often involves machine learning models such as Random Forest [23] and neural networks trained on aerial multispectral or hyperspectral imagery [26].

2.1.2. Wireless Sensor Networks

It is important to note that some soil properties cannot be accurately measured or predicted by remote sensing, and those that cannot be estimated at depths below the soil surface using these sensing methods [22,27]. WSNs (Wireless Sensor Networks) offer more direct continuous sensing of soil properties at or below the soil surface, typically using TDR (Time Domain Reflectometry). However, the costs of WSNs scale linearly with their spatial resolution, making high-resolution mapping of large areas prohibitively expensive. Despite this, WSNs are gaining industrial adoption, with commercial solutions available from companies such as Soil Scout [28] and Agrovista [29].

Table 1. Key papers in related work.

Reference	Key Contribution and Description
Fentanes et al. [14] (2018)	Demonstrated 3D soil compaction mapping using the Thorvald outdoor mobile robot [16]. Used Ordinary Kriging (OK) interpolation to predict measurements at unsampled locations and OK variance to direct a single robot (Thorvald) with a bespoke automated penetrometer to sample the location with the highest Kriging variance, informing its path planning.
Fentanes et al. [30] (2020)	Presented an informative path planning (IPP) method based on Kriging variance for single-robot soil moisture mapping. The robot navigates to the location with the highest uncertainty (Kriging variance) after each new measurement and interpolation. This greedy Next Best View (NBV) adaptive sampling method is extended in the current work to multiple robots by creating sampling tasks at the highest Kriging variance locations.
Roberts-Elliott et al. [17] (2022)	Extended the IPP approach described in [30] to multiple robots, generating new sampling tasks after each new measured sample and subsequent interpolation.
Schneider et al. [9] (2015)	Evaluated auction-based multi-robot task allocation (MRTA) algorithms for dynamic task environments, finding Sequential Single-Item (SSI) auction to be effective. Dynamic task environments are characteristic of informative path planning where tasks are not known beforehand and new tasks are created continuously. The current work compares against and extends the SSI auction approach.
Rosenkrantz et al. [18] (1977)	Proposed the cheapest insertion heuristic, which is implemented as an optional feature in the current work’s coordinator for use in calculating the bid function and the insertion index of tasks added to robots’ task queues. This heuristic calculates the cost of a robot traversing its task queue when a new task is inserted at different indices, selecting the insertion that results in the lowest cost increase. The current work integrates its bespoke DOV bid function into this heuristic.

Table 1. Key papers in related work.

Reference	Key Contribution and Description
Fentanes et al. [14] (2018)	Demonstrated 3D soil compaction mapping using the Thorvald outdoor mobile robot [16]. Used Ordinary Kriging (OK) interpolation to predict measurements at unsampled locations and OK variance to direct a single robot (Thorvald) with a bespoke automated penetrometer to sample the location with the highest Kriging variance, informing its path planning.
Fentanes et al. [30] (2020)	Presented an informative path planning (IPP) method based on Kriging variance for single-robot soil moisture mapping. The robot navigates to the location with the highest uncertainty (Kriging variance) after each new measurement and interpolation. This greedy Next Best View (NBV) adaptive sampling method is extended in the current work to multiple robots by creating sampling tasks at the highest Kriging variance locations.
Roberts-Elliott et al. [17] (2022)	Extended the IPP approach described in [30] to multiple robots, generating new sampling tasks after each new measured sample and subsequent interpolation.
Schneider et al. [9] (2015)	Evaluated auction-based multi-robot task allocation (MRTA) algorithms for dynamic task environments, finding Sequential Single-Item (SSI) auction to be effective. Dynamic task environments are characteristic of informative path planning where tasks are not known beforehand and new tasks are created continuously. The current work compares against and extends the SSI auction approach.
Rosenkrantz et al. [18] (1977)	Proposed the cheapest insertion heuristic, which is implemented as an optional feature in the current work’s coordinator for use in calculating the bid function and the insertion index of tasks added to robots’ task queues. This heuristic calculates the cost of a robot traversing its task queue when a new task is inserted at different indices, selecting the insertion that results in the lowest cost increase. The current work integrates its bespoke DOV bid function into this heuristic.

2.1.3. Ground-Based Robotic Solutions

Outdoor ground-based mobile robots can be equipped with proximal sensors to capture soil property data at a very high spatial resolution, through hyperspectral imagery or probe sensor measurements, compared to UAV and satellite visual remote sensing which suffer from poor image resolution [31]. Compared with WSN measurements, ground robots can vary the number of sampling points [30] and change the spatial resolution of the sampling as necessary. An example of this can be seen in [32], which creates a multi-layered map from composites of stereo RGB, Visible/Near Infrared (VIS-NIR), and thermal images. The thermal and VIS-NIR images are projected onto the point cloud from the stereo camera to enrich them with the same depth information that a stereo camera brings to its RGB imagery. This high-resolution 3D map includes surface readings of the soil temperature and NDVI.

Being able to capture and predict soil properties from high-resolution hyperspectral imagery is useful, but the unique advantage of ground-based outdoor robots compared to other methods of automated soil sensing is their ability to measure soil properties more directly and at variable depths below the soil surface using probe sensors. This extra dimension enables the mapping of soil properties in 3D, as demonstrated by 3D mapping of soil compaction by [14], using the Thorvald agricultural robot platform equipped with an automated penetrometer at sampling locations informed by Kriging variance.

2.2. Informative Path Planning

Informative path planning algorithms aim to produce paths that avoid collisions and optimize one or more particular objectives [33]. Ref. [30] presents an informative path-planning method based on the Kriging variance, a measure of the uncertainty of predictions made by OK interpolation. A single ground-based Thorvald robot mapping soil moisture, after each new measurement and subsequent OK interpolation, navigates to the location where this uncertainty metric is highest to perform its next soil moisture measurement. We extend this greedy Next Best View (NBV) adaptive sampling method described in their work, creating sampling tasks at the x highest Kriging variance locations, where x is the number of robots. This multi-robot Kriging-variance-based informative path planning is described in more detail in Section 3.1.

2.3. Multi-Robot Coordination

SSI (Sequential Single-Item) auction was identified as the most effective of a set of auction-based MRTA algorithms tested for dynamic task environments in [9]. Dynamic task environments are produced by informative path-planning, as tasks are not known a priori and new tasks are continually created throughout the sampling mission. Auction-based MRTA also has the benefit of allowing for domain-specific information to be encoded in its bid calculation to better inform task allocation [34,35], agnostic of the particular auction-based task allocation algorithm used. We utilise this by designing a Kriging-variance-informed bid calculation to further incentivise sampling in areas of high information gain and use it to extend the cheapest insertion heuristic [18]. The cheapest insertion heuristic calculates the cost of a robot traversing a queue of tasks in sequence, given the insertion of a prospective task at the index which will contribute the lowest increase in this cost. Our bespoke bid function and its use in combination with the cheapest insertion heuristic is described in more detail in Section 3.2.

3. Methodology

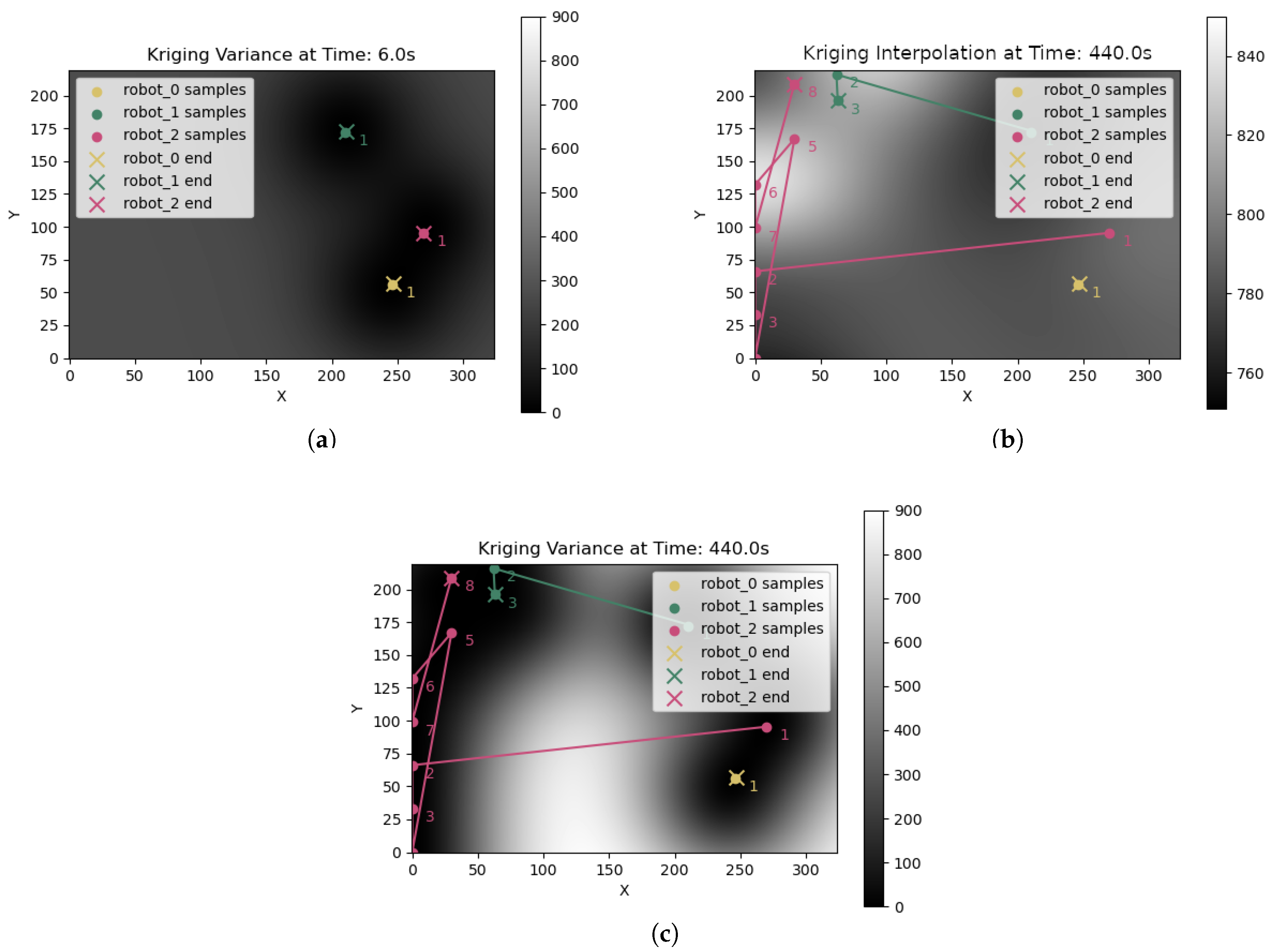
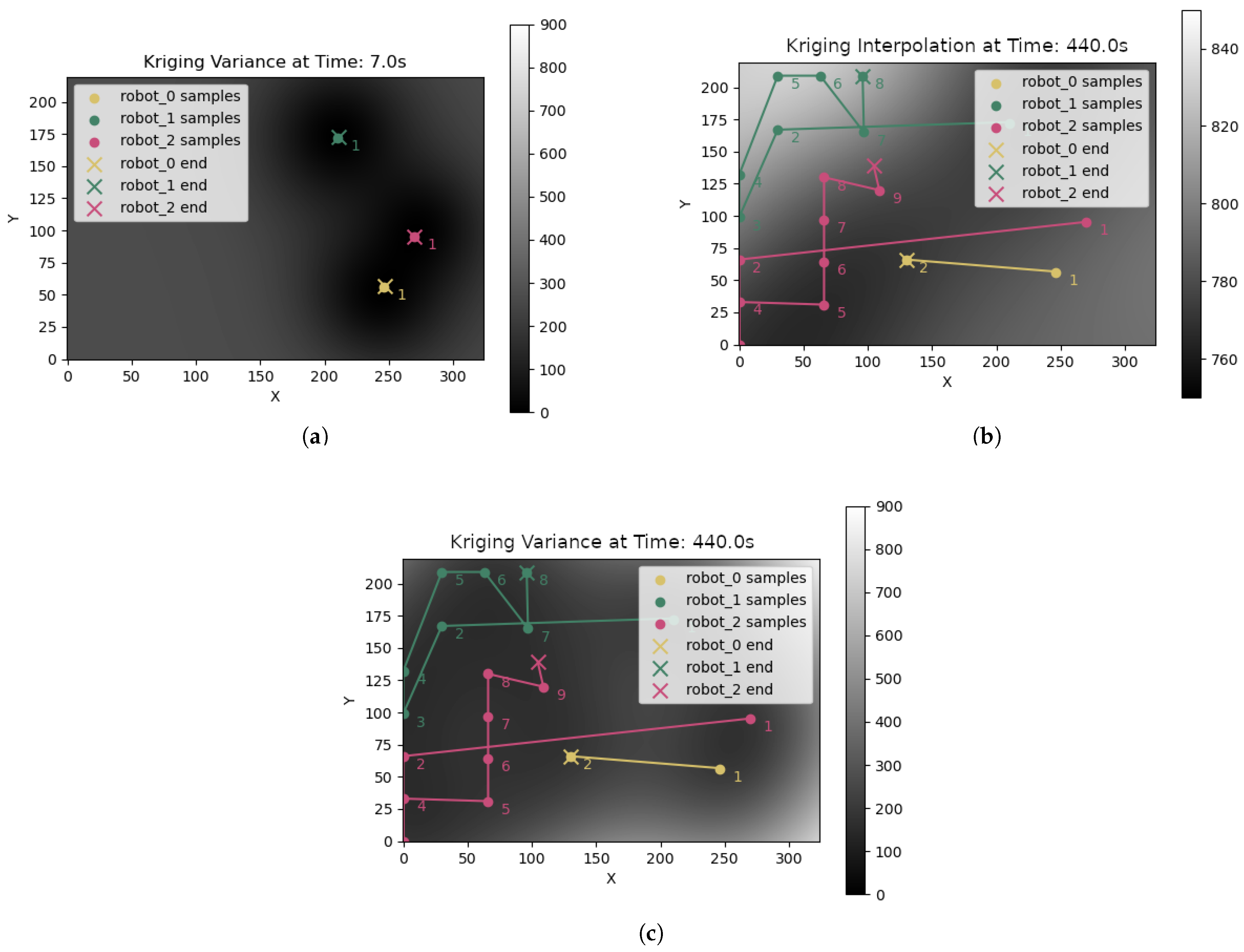
3.1. Multi-Robot Informative Path Planning from Kriging Variance

In this work, we consider that the environment is partitioned into a course-grain “sampling grid” pattern with square-shaped cells, similar to the standard geological mapping approaches. We use this grid structure to reduce the chances of multiple sampling tasks in close proximity by limiting to a maximum of one sampling task in each grid cell. In this grid pattern, the cell’s side $cel{l}_{dim}$ of each of this grid’s cells is calculated as

$$cel{l}_{dim}=\lfloor \sqrt{{\displaystyle \frac{\left(w·h\right)}{N_c}}}\rfloor$$

(1)

where w and h are the width and height of the environment being sampled, and $N_c$ is the approximate total number of cells in the grid pattern, resulting in cells of area $A={cel{l}_{dim}}^2$. These cells are created in rows, starting in the north-western (top left) corner of the environment, and are cropped where they intersect with the limits of the environment. In the data considered in this work, the environment was divided into 64 grid cells ($N_c=64$).

Our multi-robot soil mapping system uses a centralised coordinator as a proof of concept for easier Kriging interpolation to identify the task locations and as the fixed auctioneer for the task allocation auctions. With the task allocation already based on auctions, the Kriging interpolation could be easily decentralised with each robot interpolating independently and a consensus process propagating and converging the information across the robotic fleet. The coordinator is responsible for performing the Kriging interpolation and broadcasting new sampling tasks at the locations with high Kriging interpolation values. We extend the greedy NBV adaptive sampling method described in [30], creating sampling tasks at the $N_r$ highest Kriging variance locations, where $N_r$ is the number of robots, after each round of interpolation. These tasks are allocated using SSI auctions, with each robot storing its allocated tasks in a FIFO (First-In-First-Out) task queue. This results in multi-robot exploration of the unknown distribution of the target soil property, seeking to measure and map this accurately from a limited number of samples which maximally contribute to the map’s information gain.

Initial sampling tasks are created at the robots’ initial positions, as a minimum of three samples are required for Kriging interpolation. This assumes a team of at least three robots is engaged in the sampling. If fewer robots are used, the initial three sampling tasks are created in their initial positions and random positions within the environment.

Before these created tasks are allocated using auction-based MRTA, we “drop” new sampling tasks where the Kriging variance at the task’s position is less than the median of the Kriging variance matrix. This is intended to reduce the incidence of robots being allocated sampling tasks that are unlikely to significantly reduce the uncertainty of the Kriging interpolation of the soil property being mapped.

3.2. Bid Calculation for Allocation of Soil Sampling Tasks

3.2.1. Distance over Variance (DOV) Bid Function for Auction-Based Multi-Robot Task Allocation

In this work, the SSI auction approach is used as the MRTA algorithm to reduce the computational complexities associated with combinatorial auctions. A general approach in such auction-based methods is to use the Euclidean distance between the robot and the task location as the bid value. However, to select a task that will improve the information gain with minimal navigation, we propose a bespoke bid calculation we term “DOV (Distance Over Variance)”, calculated as

$$\mathrm{DOV}={\displaystyle \frac{\sqrt{{(x_r-x_t)}^2+{(y_r-y_t)}^2}}{V{x}_t,y_t}}$$

(2)

where $(x_r,y_r)$ is the robot’s position, $(x_t,y_t)$ is the task’s position, and V is the 2D Kriging variance matrix produced by the most recent Kriging interpolation.

This bid calculation divides the Euclidean distance between the robot and the task by the Kriging variance at the task’s position, incentivising sampling in nearby areas where the interpolation has high uncertainty, and is therefore expected to result in the highest information gain with minimal navigation of the robot.

3.2.2. Cheapest Insertion Heuristic

The cheapest insertion heuristic proposed in [18] is implemented as an optional feature within the coordinator, and when enabled, is used in calculating the bid function. In a robot’s bid calculation, for each possible insertion of the currently auctioned task into its task queue, the cost is calculated for the robot traversing from its current position, to the sampling position in the first task in the robot’s queue, and then iteratively from that task’s sampling position to the sampling position of the next task in the queue, until this cost is calculated for the whole queue. When using the DOV bid function, the cost of traversing from one position to another is calculated as the Euclidean distance between the two positions, divided by the Kriging variance at the second position.

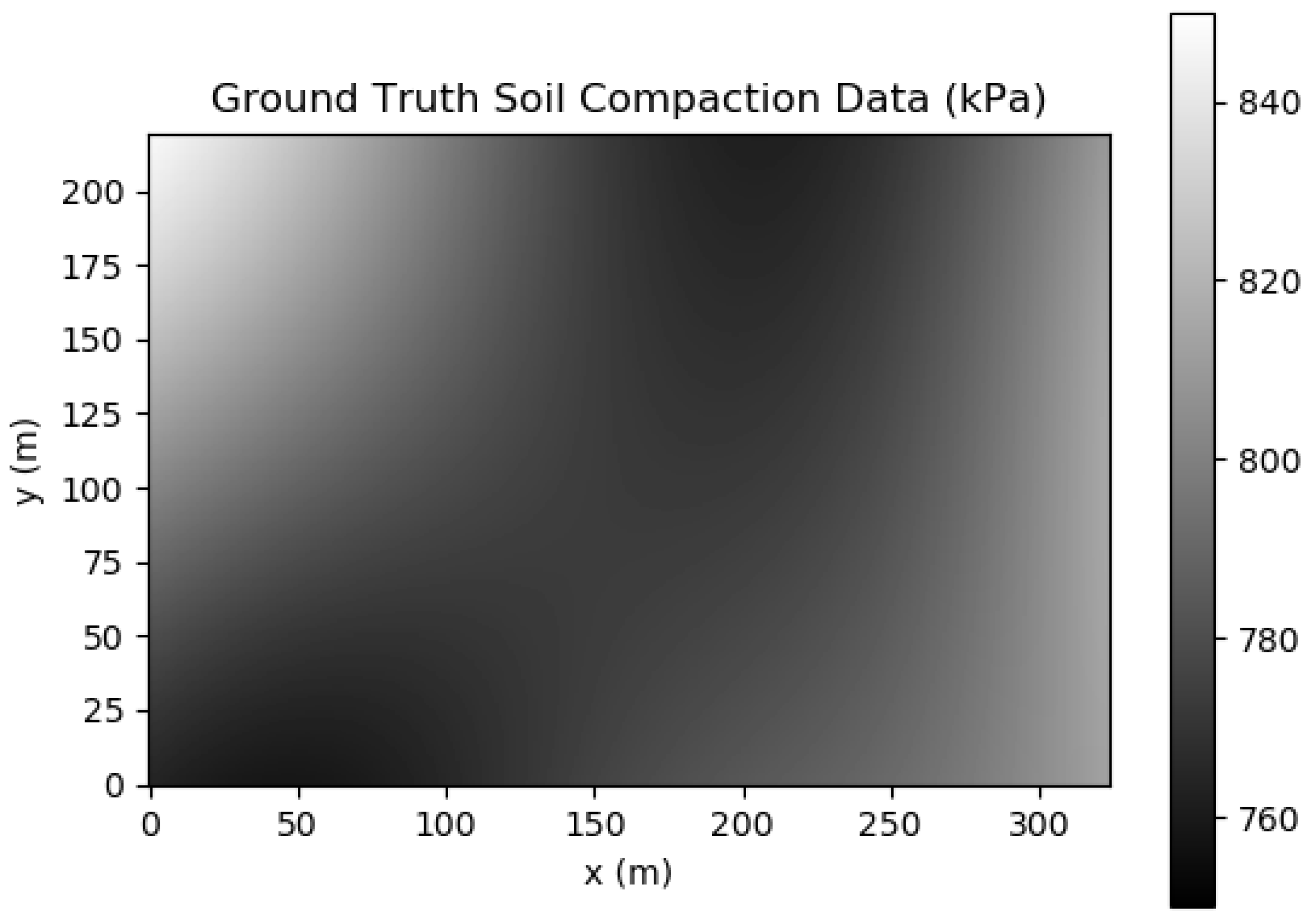
3.3. Abstract ROS Simulation of Multi-Robot Soil Compaction Mapping

Historical soil compaction data [7], sampled from an arable field by a single Saga Robotics Thorvald robot [16] in a grid pattern using a bespoke automated penetrometer, was interpolated using OK to create a ground truth soil compaction distribution, pictured in Figure 1, for re-sampling by multiple simulated robots. We consider a fleet of three ground-based outdoor wheeled robots. However, larger robotic fleets can be considered. The robots are simulated using the multi-robot simulator included in ‘move_base_abstract’ [36]. This simulator represents robots with a high level of abstraction, not modelling collisions, sensors, complex physics simulation, or 3D graphics, to enable faster-than-realtime simulation of systems that do not require these features. It models only time and the poses and navigation of an arbitrary number of robots. It uses a drop-in replacement of the standard ‘move_base’ robot navigation in ROS to move the robots to positions along a straight line to their goal according to their maximum speed and acceleration, enabling faster-than-real-time simulations.

4. Experimental Design

Eight auction configurations of the multi-robot soil properties mapping system were tested in the simulation:

• ED—Euclidean distance as the bid value.
• EDCI—Euclidean distance as the bid value with the cheapest insertion heuristic.
• EDTD—Euclidean distance as the bid value with task dropping.
• EDCITD—Euclidean distance as the bid value with the cheapest insertion heuristic and task dropping.
• DOV—Distance Over Variance as the bid value.
• DOVCI—Distance Over Variance as the bid value with the cheapest insertion heuristic.
• DOVTD—Distance Over Variance as the bid value with task dropping.
• DOVCITD—Distance Over Variance as the bid value with the cheapest insertion heuristic and task dropping.

Thirty trials of simulated 3-robot soil compaction mapping were conducted for each of these configurations. Each trial ran with a time budget of 480 s of simulation time so that the performance of the system could be measured at the end of this time, and compared between configurations using a number of performance metrics and testing of statistically significant differences between the values of these metrics across different configurations. The robot’s maximum speed was set at 2 m/s considering the fast locomotion systems in many agricultural robots and an open field environment. From the start of their movement, they accelerate at 0.1 m/s² until they reach their maximum speed.

The robots’ starting locations within the simulated field environment were randomly generated. The trial number, incrementing from one to 30 in each batch of 30 trials run for each configuration of the system, was used as a seed for this random number generation, so that trial 1 of 30 in the ED trials, for example, had the three robots start at the same locations as they did in trial 1 of 30 in the trials run for DOV, and the other configurations tested.

Values of different performance metrics, listed below, were calculated at the end of each trial. The arrow, next to the metric name, indicates if a high value (↑) or a low value (↓) is preferred for that metric.

• Kriging RMSE (Root Mean Squared Error) (↓)—The RMSE between the Kriging interpolation of soil compaction produced from the samples taken by the multi-robot sampling, and the ground truth soil compaction data. A lower value indicates a more accurate interpolation.
• Max task queue length (↓)—The maximum length measured across all of the robots’ task queues. A lower value indicates more efficient task allocation, as task positions are reached and tasks are executed more quickly, avoiding a large backlog of queued tasks.
• Mean TA (task allocation) equality (↑)—A metric that measures how equally distributed tasks are between the robot team. This equality E is calculated using the equal allocation proportion

  $$e={\displaystyle \frac{1}{N_r}}$$

  (3)

  where $N_r$ is the number of robots. With this, we can calculate

  $$E=1-|e-{\displaystyle \frac{T_i}{{\sum }_{r=1}^{\#\left(T\right)}{T}_r}}|$$

  (4)

  where T is the set of task counts for all robots (please note that $\#\left(T\right)$ is used to denote the cardinality of T, to distinguish it from the notation for absolute distance), indexed by robot ID r, and i is the ID of the robot we are calculating the TA equality for.
  This TA equality is calculated for each robot, and the mean is taken to represent the equality of TA for the whole team. Values closer to 1 indicate more equal task allocation, and values closer to 0 show a less equal task allocation.
• Mean Kriging variance (↓)—The mean of the Kriging variance matrix generated from the most recent Kriging interpolation. Lower values indicate less overall uncertainty in the estimates of the interpolation.
• Mean task completion time (seconds) (↓)—The mean time taken to execute a sampling task, across all robots and tasks, measured from the beginning of robot navigation towards the task, to task completion following the measurement of the task’s sample. Lower values indicate more efficient task allocation, with robots allocated tasks they are capable of completing in a shorter time.
• Number of samples (↑)—The total number of samples of soil compaction measured by the robot team. A high value is considered to be the best value, as the trials are run for a specific time. If the trials are run for an arbitrary time until the Kriging variance comes below a threshold value, a low value would be ideal for this metric.
• Total distance travelled (metres) (↓)—The total distance travelled by the robot team, measured in metres. A lower value is preferred as complete coverage of the environment is not desired, but rather a time-efficient exploration and mapping of the soil property distribution from sampling “hot spots” that provide high information gain. This metric is also a proxy for the energy expenditure and soil compaction contribution of the multi-robot system, and so a lower total distance corresponds to reduced energy requirements and environmental impacts.
• Total idle time (seconds) (↓)—The total time that robots within the team have spent idle (stationary, without any current or queued tasks). A low value is considered to be the best here, assuming maximum utilisation. However, if the number of samples is smaller for the same number of robots, the idle time can be high.
• Total robot tasks count—The total number of sampling tasks allocated to the robot team. A lower or higher value may be preferable depending on whether tasks are being executed efficiently. This should be viewed in conjunction with the maximum task queue length, as a high total task count in combination with a high maximum task queue length indicates that more tasks are being created than the robots can complete before being allocated subsequent tasks.
• Earliest Time Where RMSE < 0.75 × STD (seconds) (↓)—The earliest time in the sampling mission where Kriging RMSE is less than ${\displaystyle \frac{3}{4}}$ of the standard deviation (STD) of the ground truth soil compaction data. This serves as an optimisation indicator for the mapping, as the RMSE of predictions being significantly below the STD of the ground truth demonstrates that the model captures the variability of the data it is estimating [37,38]. Lower values in this metric indicate an earlier acquisition of an accurate soil property map, and thus a more time-efficient mapping.

5. Simulated Experiment Results

Thirty trials of simulated 3-robot soil compaction mapping were conducted for each of the eight different task allocation configurations. Each trial ran with a time budget of 480 s of simulation time. Figure 2 shows the screenshot of the rViz window with the robot positions during the mission (yellow, green, and red arrows) and the background shows a heatmap of soil compaction interpolated using OK from the sampling completed so far.

Figure 3a shows the Kriging-interpolated soil compaction at 439.0 s and Figure 3b shows the corresponding Kriging variance at the next iteration at 440.0 s for future allocations when DOVTD strategy was used. The routes taken by each robot are highlighted with sampling locations. It can be clearly observed that the Kriging variance is extremely low near the sampled locations. The task locations and allocations are different for the eight configurations based on the initial locations of the robots, bid calculation and task queue maintenance strategies. This can be seen by comparing Figure 3 with Figure 4, which shows the Kriging interpolated soil compaction values (a), Kriging variance (b), and the colour-coded routes take by each robot when DOVCITD strategy was used.

Mean and standard deviation were calculated from each metric described in Section 4 at the end of the 8-min time budget given to the sampling, across 30 trials within each configuration of the multi-robot soil mapping system. These summary statistics can be found in

Table 2. Mean and standard deviation ($\sigma$) of performance metrics calculated from 30 trials in each of the 8 configurations of the multi-robot soil mapping system tested in simulation. The best and second-best value for each metric is highlighted in green and yellow, respectively.

	ED	EDCI	EDTD	EDCITD	DOV	DOVCI	DOVTD	DOVCITD —
Kriging RMSE (Root Mean Squared Error)	17.46 ± 13.9	17.11 ± 9.44	16.85 ± 20.17	15.41 ± 8.98	19.13 ± 16.33	17.09 ± 9.92	12.88 ± 4.74	20.41 ± 18.41 —
Max task queue length	11.8 ± 4.28	6.87 ± 2.4	8.76 ± 4.77	5.83 ± 1.78	8.93 ±65 3.76	5.2 ± 1.54	5.47 ± 3.25	3.3 ± 1.37 —
Mean TA equality	0.78 ± 0.05	0.78 ± 0.03	0.81 ± 0.09	0.81 ± 0.04	0.8 ± 0.05	0.8 ± 0.03	0.83 ± 0.06	0.84 ± 0.05 —
Mean Kriging variance	339.68 ± 127.94	352.65 ± 158.21	347.76 ± 156.15	340.45 ± 135.26	398.21 ± 160.69	336.17 ± 122.24	335.26 ± 145.38	280.36 ± 121.05 —
Mean task completion time (seconds)	28.16 ± 10.67	36.33 ± 13.28	24.71 ± 8.57	40.25 ± 11.02	36.95 ± 9.45	43.03 ± 5.73	31.93 ± 10.91	38.76 ± 10.01 —
Number of samples	20.43 ± 14.54	16.8 ± 2.82	16.03 ± 3.01	16.4 ± 2.13	15.87 ± 2.3	15.53 ± 2.01	14.23 ± 3.04	15.43 ± 2.1 —
Total idle time (seconds)	318.6 ± 529.65	139.57 ± 112.15	324.75 ± 230.95	217.29 ± 190.79	185.51 ± 142.27	205.7 ± 149.11	416.08 ± 308.98	455.05 ± 250.52 —
Total robot tasks count	45.87 ± 10.08	42.93 ± 8.14	33.41 ± 10.12	35.07 ± 6.86	40.47 ± 6.32	38.17 ± 5.58	26.43 ± 8.68	27.87 ± 7.76 —
Earliest Time Where RMSE < 0.75 × STD (seconds)	360.37 ± 123.82	348.35 ± 102.7	329.57 ± 108.2	368.36 ± 87.51	306.6 ± 113.26	271.55 ± 96.33	290.48 ± 109.29	269.51 ± 84.15 —

. D’Agostino and Pearson’s normality test [39] was run for each performance metric and configuration of the system, on the values observed for the given metric in the last second of each simulated trial in the given configuration.

This normality testing was used to determine whether parametric or non-parametric significance tests would be more appropriate for comparing performance between different configurations of the system across the recorded metrics. It was found that per-configuration observations for all metrics were normally distributed, except for Kriging RMSE and “Earliest Time Where RMSE < 0.75 × STD”. It was thus decided that significance testing would first investigate, for each performance metric, using the Kruskal–Wallis [40] test for Kriging RMSE and ‘Earliest Time Where RMSE < 0.75 × STD’, and ANOVA [41] for the other metrics, whether there was a statistically significant difference between the means of these metrics between different configurations of the multi-robot soil mapping system.

ANOVA and Kruskal–Wallis tests showed a significant difference in the means of all performance metrics across the tested configurations of the system, except for Kriging variance. This could be explained by the very high standard deviation seen in Table 2, which suggests that the initial positions of the robots may have a significant impact on the Kriging variance. This may be due to the ground truth soil compaction distribution, pictured in Figure 1, having relatively small “hot spots” of high soil compaction, which could be measured and accounted for in Kriging interpolation immediately in cases where one or more robots start sampling within these areas of interest.

Following the ANOVA and Kruskal–Wallis tests, Tukey’s HSD (Honestly Significant Difference) test [42] was conducted within each metric comparing every pair of configurations. For the metrics “Kriging RMSE” and “Earliest Time Where RMSE < 0.75 × STD”, non-parametric Wilcoxon signed-rank tests [43] were used instead. These tests were more appropriate given that the data for these metrics was not normally distributed.

The configuration of the system that resulted in the lowest mean Kriging RMSE, a key metric of the accuracy of the mapping, after 480 s of simulation time, was DOVTD. Wilcoxon signed-rank tests showed that DOVTD performed significantly better for Kriging RMSE than DOV, DOVCI, and EDCI. This indicates that the “task dropping”, introduced in Section 3.1, results in improved interpolation accuracy within a time-limited mapping when used in conjunction with the DOV bid calculation, and more effectively improves interpolation accuracy than using DOV with the cheapest insertion integration (DOVCI).

In Wilcoxon signed-rank tests comparing “Earliest Time Where RMSE < 0.75 × STD” between pairs of conditions, DOVCITD produces an accurate map significantly earlier than any method that uses the traditional Euclidean distance (ED) bid calculation. It does not achieve this significantly earlier than the other methods that incorporate the DOV bid calculation; however, these other methods are not able to produce an accurate map significantly earlier than all ED-based methods. This suggests that the DOV bid calculation is the most important contribution of this work in terms of its effect on the speed of achieving an accurate interpolation, but its combination with the additional contributions is necessary for this accuracy to be achieved significantly earlier than all ED-based methods.

One limitation of the SSI auction-based task allocation used in this system is that some robots can be under-utilised, sitting idle without any tasks in their task queues. This unfairness in task allocation can be observed when some robots’ initial positions are further from regions of high Kriging variance, where tasks are created by the IPP, than the initial positions of other robots. DOVCITD was found to best address this, out of the eight configurations tested, achieving the highest mean TA equality and the lowest max task queue size. This demonstrates a more even distribution of tasks, which is supported by Tukey’s HSD tests showing that DOVCITD had a significantly lower mean for the max task queue length metric than DOV, ED, EDTD, EDCI, and EDCITD.

Another important metric is the total distance travelled, a proxy of the energy expended by the system and the compaction that the operation of the robots on the soil surface contributes. It is a key indicator of task allocation efficiency, as efficient MRTA should minimise the distance between robots and their allocated tasks, balancing this with minimising the time required to produce an accurate interpolation in the DOV bid calculation.

EDTD resulted in the lowest mean for this metric but was not significantly lower than that of the DOVTD, which scored second lowest. Given DOVTD’s superior interpolation accuracy and not significantly lower total distance, it may be argued that DOVTD represents a more acceptable trade-off between interpolation accuracy and energy consumption and soil compaction resulting from the system than other configurations tested.

6. Conclusions

This work has presented novel contributions in IPP and MRTA, including thresholding of sampling tasks at the point of task creation using median Kriging variance, the DOV bid calculation, and integration of DOV within the cheapest insertion heuristic for a multi-robot soil sampling system. This approach has wider applications in other ground sampling, where Kriging interpolations are used traditionally. A free and open-source ROS coordinator and simulation has been developed to implement and test these contributions, individually, and in combination, and against the baseline Euclidean distance bid calculation.

The Kriging-variance-informed MRTA contributions presented in this work, i.e., DOV bid calculation in conjunction with the dropping of tasks at low Kriging variance locations, was found to produce the most accurate maps of soil compaction of all configurations of the multi-robot soil mapping system tested in simulated experiments. Significance testing described in Section 5 demonstrated that the task-dropping feature significantly improved this interpolation accuracy when combined with DOV. DOVTD was also found to not be significantly worse than the best-performing configurations for TA equality, task completion time, and total distance travelled. While DOVTD produced the most accurate maps at the end of the sampling, DOVCITD was found to achieve a reasonably accurate map in the shortest average time through comparison of the optimisation indicator “Earliest Time Where RMSE < 0.75 × STD” with other methods tested.

The integration of DOV into the cheapest insertion also produced the most equal allocation of tasks, addressing an issue observed in some trials where one robot would be assigned very few sampling tasks and be underutilised. Future work may investigate alternative solutions to this task allocation inequality, such as limiting the size of each robot’s task queue, and test whether this improves the system’s performance. The coordinator’s ROS compatibility, and use of the move_base action client to direct robot navigation, should allow it to be deployed and tested as a real-world multi-robot system with relative ease. The multi-robot mapping of spatial data demonstrated here can easily be applied to other soil properties and even spatial data from other applications within environmental monitoring and inspection. Future work may investigate its effectiveness in the exploration and mapping of other distributions of spatial data.