Real Time MEMS-Based Joint Friction Identification for Enhanced Dynamic Performance in Robotic Applications
Abstract
1. Introduction
- The proposed method does not rely on the sequential, joint-by-joint friction analysis often performed on serial robots; therefore, it is applicable not only to serial kinematic chains but also to parallel chains.
- The identification process is carried out in real time on multi-axis systems during normal motion tasks and without using specially designed trajectories.
- Focus is placed on the uncertain friction and PDS parameters, as the masses are already known.
- In particular, a rarely considered source of uncertainty, namely, the actual value of each PDS torque conversion gain, is explicitly considered in the proposed formulation.
- Finally, the stiction regime is detected using accelerometric and gyroscopic measures and excluded from the identification process, as the velocity-based friction model is not applicable in those conditions.
- The development of a low-cost solution for a real-time friction identification architecture, based on MEMS IMUs applicable to multi-DOF serial and parallel mechanisms alike;
- The theoretical analysis and subsequent compensation of the effects of uncertain PDS parameters;
- An empirical and comparative demonstration of the benefits achievable with the proposed measurement, identification, and control architecture in realistic, high-speed pick-and-place motion cycles.
- An experimental characterization of the frictional phenomena on a high stiffness 5R parallel kinematic robot that also includes an analysis of the effects of temperature both on friction and on its identification.
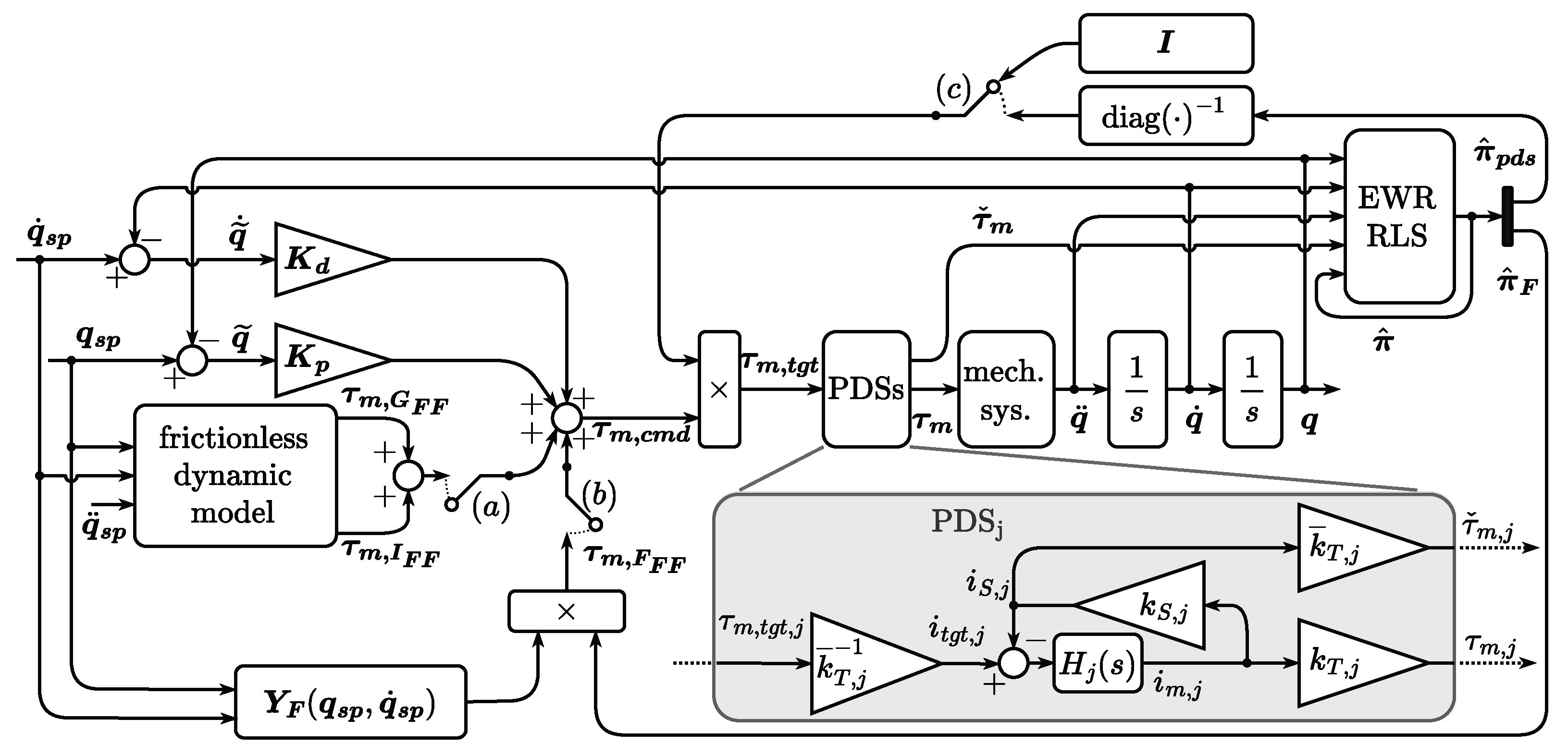
2. Methods
- Computational efficiency, as the Woodbury–Sherman–Morrison formula can then be used to avoid matrix inversions altogether;
- Storage efficiency, as new data points are processed at once to yield a running estimate of the unknown parameters and then overwritten;
- Immediate usability of the estimated parameters within the robot’s control system;
- Ability to track slow changes in the parameters (such as those caused, for example, by temperature variations) thanks to the exponentially decaying weighting of the data points;
- Uniqueness of the solution at each iteration.
- A pure Proportional Derivative (PD) feedback controller (switch closed and and open);
- A Computed Torque Controller (CTC) in which the frictionless dynamics are accounted for by the a priori model (switches and closed and open);
- An Adaptive Controller (AC) in which the results of the friction identification framework are also inserted (switches , , and closed).
3. Results and Discussion
3.1. Case Study Description
5R Robot Model
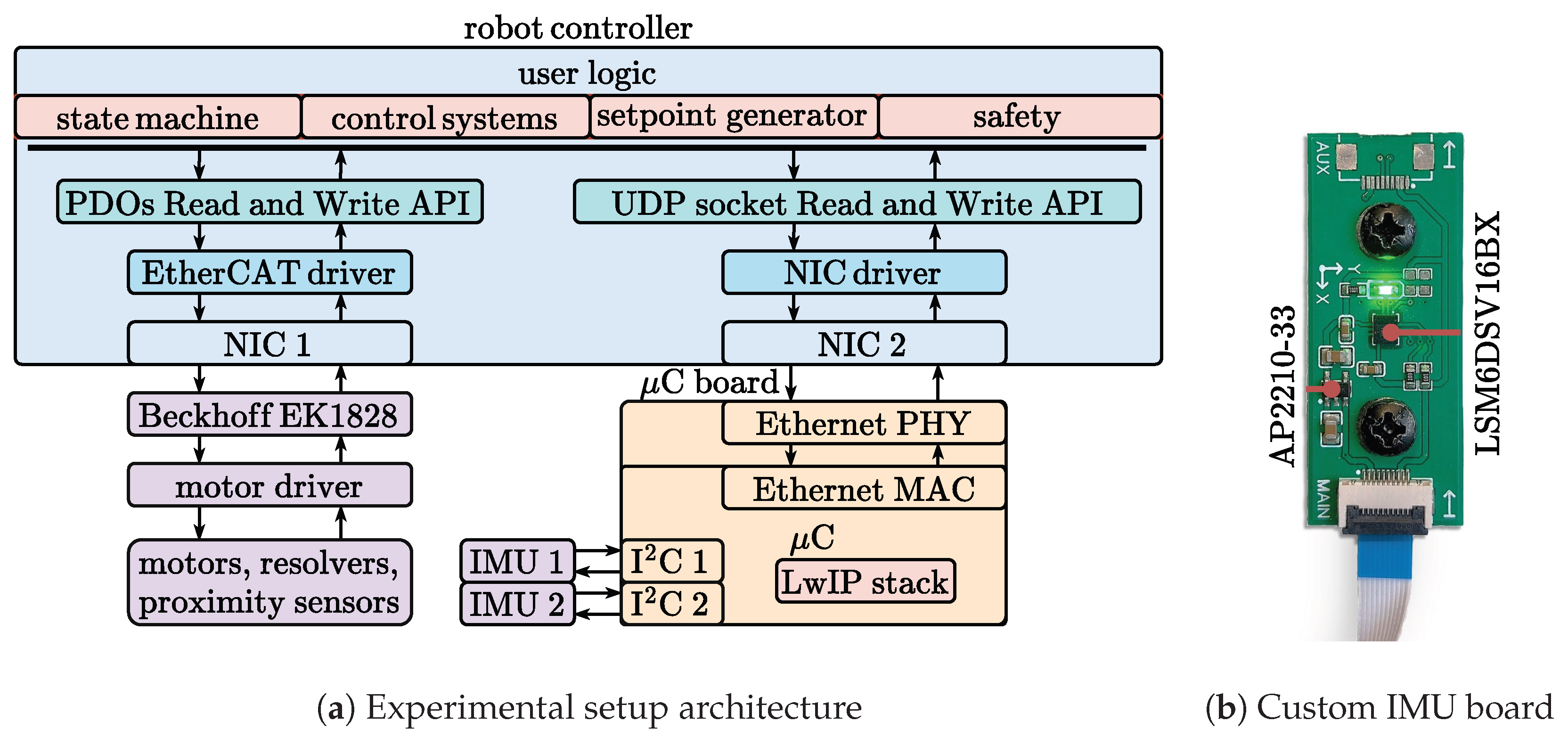
3.2. Experimental Setup
- A desktop equipped with two Network Interface Cards (NICs) and serving as the robot controller;
- A Beckhoff EK1828 EtherCAT head;
- A Copley Control Accelnet BE2-090-20-R dual-axis motor driver operating in torque mode and acting as an EtherCAT subordinate device;
- Two Mavilor BLS55 Brushless AC motors whose resolvers are used by the driver to generate virtualized rotary encoder signals;
- Two proximity sensors used in the zeroing phase;
- An STM32 F439ZI microcontroller (μC) capable of Ethernet connectivity and equipped with two I2C interfaces set to Fast Mode operation;
- Two ST LSM6DSV16BX triaxial IMUs with an integrated I2C interface, each mounted on the custom board depicted in Figure 3b; the other notable component mounted on the PCB is the AP2210-33 voltage regulator, which was selected due to its high power supply rejection ratio.
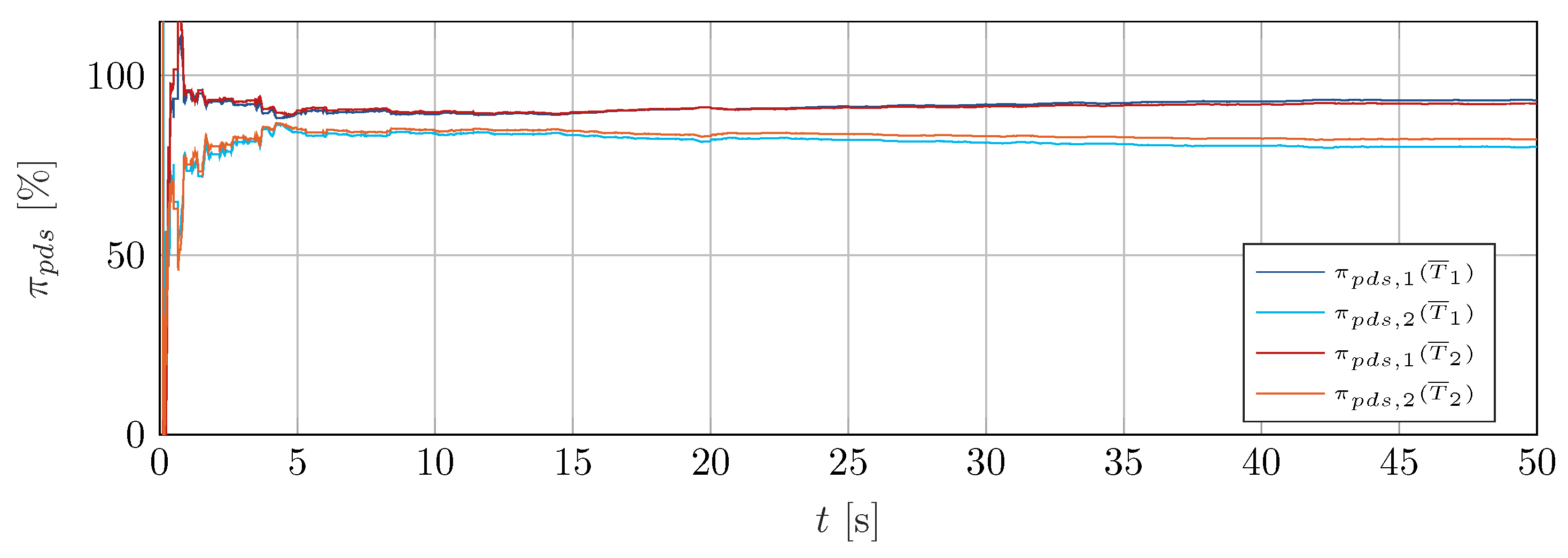
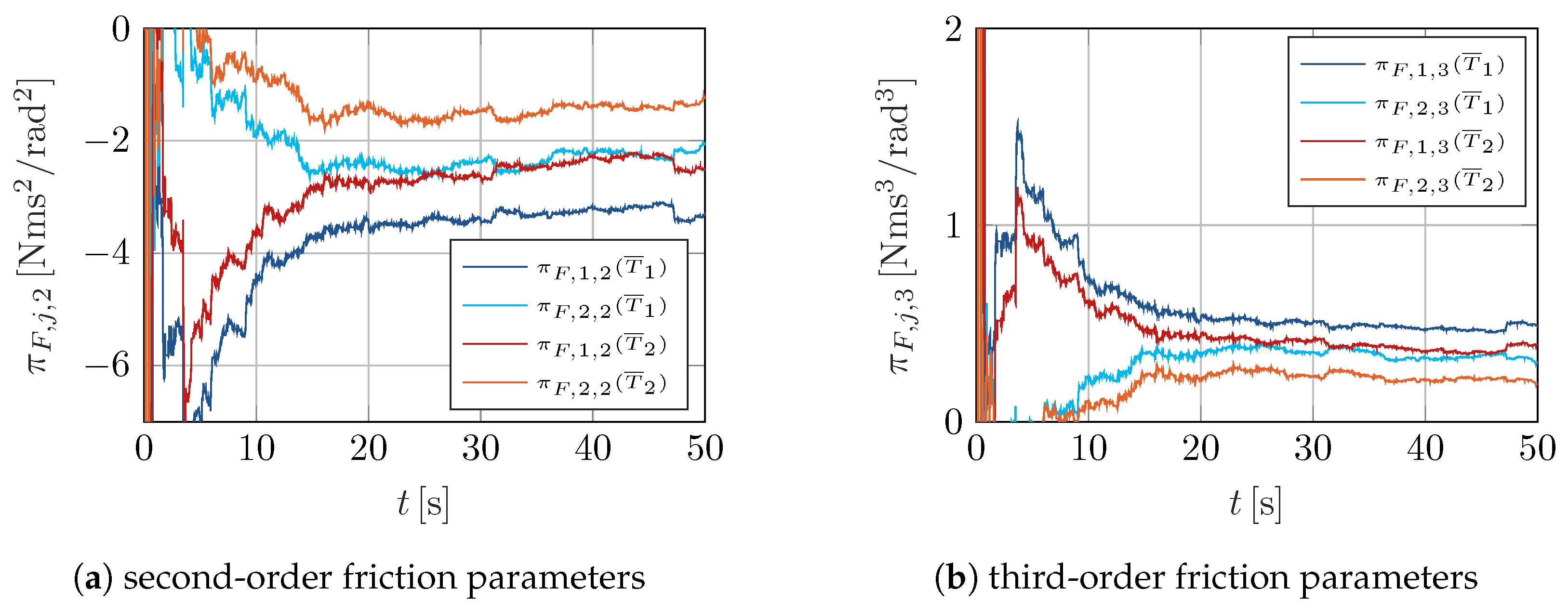
3.3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Righettini, P.; Strada, R.; Cortinovis, F. General Procedure for Servo-Axis Design in Multi-Degree-of-Freedom Machinery Subject to Mixed Loads. Machines 2022, 10, 454. [Google Scholar] [CrossRef]
- Righettini, P.; Strada, R.; Cortinovis, F. Neural Network Mapping of Industrial Robots’ Task Times for Real-Time Process Optimization. Robotics 2023, 12, 143. [Google Scholar] [CrossRef]
- Righettini, P.; Strada, R.; Cortinovis, F. Experimental Evaluation of Centralized Control Strategies on a 5R Robot. Mech. Mach. Sci. 2024, 163 MMS, 334–342. [Google Scholar] [CrossRef]
- Righettini, P.; Strada, R.; Cortinovis, F.; Tabaldi, F.; Santinelli, J.; Ginammi, A. An Experimental Investigation of the Dynamic Performances of a High Speed 4-DOF 5R Parallel Robot Using Inverse Dynamics Control. Robotics 2024, 13, 54. [Google Scholar] [CrossRef]
- Márton, L.; Van Der Linden, F. Temperature dependent friction estimation: Application to lubricant health monitoring. Mechatronics 2012, 22, 1078–1084. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; Parker, R. Effects of lubrication on gear performance: A review. Mech. Mach. Theory 2020, 145, 103701. [Google Scholar] [CrossRef]
- Lontin, K.; Khan, M. Interdependence of friction, wear, and noise: A review. Friction 2021, 9, 1319–1345. [Google Scholar] [CrossRef]
- Al-Bender, F.; De Moerlooze, K. Characterization and modeling of friction and wear: An overview. Int. J. Sustain. Constr. Des. 2011, 2, 19–28. [Google Scholar] [CrossRef]
- Kato, K. Wear in relation to friction - A review. Wear 2000, 241, 151–157. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Gu, J.; Wang, Z. Influences of preload on the friction and wear properties of high-speed instrument angular contact ball bearings. Chin. J. Aeronaut. 2018, 31, 597–607. [Google Scholar] [CrossRef]
- Farhat, N.; Mata, V.; Page, A.; Daz-Rodríguez, M. Dynamic simulation of a parallel robot: Coulomb friction and stick-slip in robot joints. Robotica 2010, 28, 35–45. [Google Scholar] [CrossRef]
- Hao, L.; Pagani, R.; Beschi, M.; Legnani, G. Dynamic and friction parameters of an industrial robot: Identification, comparison and repetitiveness analysis. Robotics 2021, 10, 49. [Google Scholar] [CrossRef]
- Luo, R.; Yuan, J.; Hu, Z.; Du, L.; Bao, S.; Zhou, M. Lie-theory-based dynamic model identification of serial robots considering nonlinear friction and optimal excitation trajectory. Robotica 2024, 42, 3552–3569. [Google Scholar] [CrossRef]
- Karahan, O.; Karci, H. Swarm Intelligence Based Nonlinear Friction and Dynamic Parameters Identification for a 6-DOF Robotic Manipulator. J. Intell. Robot. Syst. Theory Appl. 2023, 108, 19. [Google Scholar] [CrossRef]
- Chaoui, H.; Sicard, P.; Lakhsasr, A.; Schwartz, H. Neural network based model reference adaptive control structure for a flexible joint with hard nonlinearities. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Ajaccio, France, 4–7 May 2004; Volume 1, pp. 271–276. [Google Scholar] [CrossRef]
- Chaoui, H.; Sicard, P.; Gueaieb, W. ANN-based adaptive control of robotic manipulators with friction and joint elasticity. IEEE Trans. Ind. Electron. 2009, 56, 3174–3187. [Google Scholar] [CrossRef]
- de Wit, C.; Lischinsky, P.; Åström, K.; Olsson, H. A New Model for Control of Systems with Friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- de Wit, C.C.; Lischinsky, P. Adaptive Friction Compensation with Dynamic Friction Model. IFAC Proc. Vol. 1996, 29, 2078–2083. [Google Scholar] [CrossRef]
- Azizi, Y.; Yazdizadeh, A. Passivity-based adaptive control of a 2-DOF serial robot manipulator with temperature dependent joint frictions. Int. J. Adapt. Control Signal Process. 2019, 33, 512–526. [Google Scholar] [CrossRef]
- Piatkowski, T. Dahl and LuGre dynamic friction models - The analysis of selected properties. Mech. Mach. Theory 2014, 73, 91–100. [Google Scholar] [CrossRef]
- Swevers, J.; Al-Bender, F.; Ganseman, C.; Prajogo, T. An integrated friction model structure with improved presliding behavior for accurate friction compensation. IEEE Trans. Autom. Control 2000, 45, 675–686. [Google Scholar] [CrossRef]
- Lampaert, V.; Swevers, J.; Al-Bender, F. Modification of the Leuven integrated friction model structure. IEEE Trans. Autom. Control 2002, 47, 683–687. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Zhang, Z.; Hu, X.; Zhang, W. Experimental comparison of five friction models on the same test-bed of the micro stick-slip motion system. Mech. Sci. 2015, 6, 15–28. [Google Scholar] [CrossRef]
- Lampaert, V.; Swevers, J.; Al-Bender, F. Experimental comparison of different friction models for accurate low-velocity tracking. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2002; pp. 1121–1126. [Google Scholar]
- Sun, Y.H.; Chen, T.; Wu, C.; Shafai, C. Comparison of four friction models: Feature prediction. J. Comput. Nonlinear Dyn. 2016, 11, 031009. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. On the adaptive control of robot manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar] [CrossRef]
- Slotine, J.J.; Li, W. Composite adaptive control of robot manipulators. Automatica 1989, 25, 509–519. [Google Scholar] [CrossRef]
- Spong, M.; Ortega, R. On Adaptive Inverse Dynamics Control of Rigid Robots. IEEE Trans. Autom. Control 1990, 35, 92–95. [Google Scholar] [CrossRef]
- Odry, A.; Fullér, R.; Rudas, I.; Odry, P. Kalman filter for mobile-robot attitude estimation: Novel optimized and adaptive solutions. Mech. Syst. Signal Process. 2018, 110, 569–589. [Google Scholar] [CrossRef]
- Dai, F.; Gao, X.; Jiang, S.; Guo, W.; Liu, Y. A two-wheeled inverted pendulum robot with friction compensation. Mechatronics 2015, 30, 116–125. [Google Scholar] [CrossRef]
- Pei, Y.; Kleeman, L. Mobile robot floor classification using motor current and accelerometer measurements. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC), Auckland, New Zealand, 22–24 April 2016; pp. 545–552. [Google Scholar] [CrossRef]
- Pang, G.; Liu, H. Evaluation of a low-cost MEMS accelerometer for distance measurement. J. Intell. Robot. Syst. Theory Appl. 2001, 30, 249–265. [Google Scholar] [CrossRef]
- Georgy, J.; Karamat, T.; Iqbal, U.; Noureldin, A. Enhanced MEMS-IMU/odometer/GPS integration using mixture particle filter. GPS Solut. 2011, 15, 239–252. [Google Scholar] [CrossRef]
- Kada, B.; Munawar, K.; Shaikh, M.; Hussaini, M.; Al-Saggaf, U. UAV Attitude Estimation Using Nonlinear Filtering and Low-Cost Mems Sensors. IFAC-PapersOnLine 2016, 49, 521–528. [Google Scholar] [CrossRef]
- Euston, M.; Coote, P.; Mahony, R.; Kim, J.; Hamel, T. A complementary filter for attitude estimation of a fixed-wing UAV. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 340–345. [Google Scholar] [CrossRef]
- Min, F.; Wang, G.; Liu, N. Collision detection and identification on robot manipulators based on vibration analysis. Sensors 2019, 19, 1080. [Google Scholar] [CrossRef]
- Pucher, F.; Gattringer, H.; Müller, A. Collision detection for flexible link robots using accelerometers. IFAC-PapersOnLine 2019, 52, 514–519. [Google Scholar] [CrossRef]
- Birjandi, S.; Fortunic, E.; Haddadin, S. Evaluation of Robot Manipulator Link Velocity and Acceleration Observer. IFAC-PapersOnLine 2023, 56, 292–299. [Google Scholar] [CrossRef]
- Xu, T.; Fan, J.; Fang, Q.; Wang, S.; Zhu, Y.; Zhao, J. A novel virtual sensor for estimating robot joint total friction based on total momentum. Appl. Sci. 2019, 9, 3344. [Google Scholar] [CrossRef]
- Jin, M.; Kang, S.; Chang, P. Robust compliant motion control of robot with nonlinear friction using time-delay estimation. IEEE Trans. Ind. Electron. 2008, 55, 258–269. [Google Scholar] [CrossRef]
- Kou, B.; Huang, Y.; Wang, P.; Ren, D.; Zhang, J.; Guo, S. A New Parameter Identification Method for Industrial Robots with Friction. Machines 2022, 10, 349. [Google Scholar] [CrossRef]
- Roveda, L.; Bussolan, A.; Braghin, F.; Piga, D. Robot joint friction compensation learning enhanced by 6D virtual sensor. Int. J. Robust Nonlinear Control 2022, 32, 5741–5763. [Google Scholar] [CrossRef]
- Tadese, M.; Yumbla, F.; Yi, J.S.; Lee, W.; Park, J.; Moon, H. Passivity Guaranteed Dynamic Friction Model with Temperature and Load Correction: Modeling and Compensation for Collaborative Industrial Robot. IEEE Access 2021, 9, 71210–71221. [Google Scholar] [CrossRef]
- Nevmerzhitskiy, M.; Notkin, B.; Vara, A.; Zmeu, K. Friction Model of Industrial Robot Joint with Temperature Correction by Example of KUKA KR10. J. Robot. 2019, 2019, 6931563. [Google Scholar] [CrossRef]
- Afrough, M.; Hanieh, A. Identification of Dynamic Parameters and Friction Coefficients: Of a Robot with Planar Serial Kinemtic Linkage. J. Intell. Robot. Syst. Theory Appl. 2019, 94, 3–13. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Wang, X. Sensorless force estimation for industrial robots using disturbance observer and neural learning of friction approximation. Robot.-Comput.-Integr. Manuf. 2021, 71, 102168. [Google Scholar] [CrossRef]
- Khishtan, A.; Kim, S.; Lee, J. A hybrid model in a nonlinear disturbance observer for improving compliance error compensation of robotic machining. Robot. -Comput.-Integr. Manuf. 2025, 92, 102887. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, W.; Liu, T.; Zhang, Z.; Lu, W.; Wang, L.; Zheng, Y.; Lin, Z. Online identification of inertial parameters of a robot with partially combined links using IMU sensing. Mechatronics 2023, 94, 103023. [Google Scholar] [CrossRef]
- Patel, A.; Ferdowsi, M. Current sensing for automotive electronics - A survey. IEEE Trans. Veh. Technol. 2009, 58, 4108–4119. [Google Scholar] [CrossRef]
- Renner, A.; Wind, H.; Sawodny, O. Online payload estimation for hydraulically actuated manipulators. Mechatronics 2020, 66, 102322. [Google Scholar] [CrossRef]
- Cochrane, C.; Lenahan, P. Real time exponentially weighted recursive least squares adaptive signal averaging for enhancing the sensitivity of continuous wave magnetic resonance. J. Magn. Reson. 2008, 195, 17–22. [Google Scholar] [CrossRef]











| 180 | 250 | 250 | 250 | 250 |
| , [kg m2] | , [kg m2] | , [kg m2] | , [kg m2] | , [kg] | , [kg] | [kg] |
|---|---|---|---|---|---|---|
| 0.292 | 0.292 | 0.030 | 0.036 | 2.32 | 2.78 | 2.72 |
| 210 | 1680 | 25,200 | −25,200 |
| Model | Model | Model | Model | Model | |
|---|---|---|---|---|---|
| considered joints | all | active only | active only | active only | active only |
| polynomial order | 4 | 4 | 3 | 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Righettini, P.; Legnani, G.; Cortinovis, F.; Tabaldi, F.; Santinelli, J. Real Time MEMS-Based Joint Friction Identification for Enhanced Dynamic Performance in Robotic Applications. Robotics 2025, 14, 36. https://doi.org/10.3390/robotics14040036
Righettini P, Legnani G, Cortinovis F, Tabaldi F, Santinelli J. Real Time MEMS-Based Joint Friction Identification for Enhanced Dynamic Performance in Robotic Applications. Robotics. 2025; 14(4):36. https://doi.org/10.3390/robotics14040036
Chicago/Turabian StyleRighettini, Paolo, Giovanni Legnani, Filippo Cortinovis, Federico Tabaldi, and Jasmine Santinelli. 2025. "Real Time MEMS-Based Joint Friction Identification for Enhanced Dynamic Performance in Robotic Applications" Robotics 14, no. 4: 36. https://doi.org/10.3390/robotics14040036
APA StyleRighettini, P., Legnani, G., Cortinovis, F., Tabaldi, F., & Santinelli, J. (2025). Real Time MEMS-Based Joint Friction Identification for Enhanced Dynamic Performance in Robotic Applications. Robotics, 14(4), 36. https://doi.org/10.3390/robotics14040036







