SCARA Assembly AI: The Synthetic Learning-Based Method of Component-to-Slot Assignment with Permutation-Invariant Transformers for SCARA Robot Assembly
Abstract
1. Introduction
2. Related Works
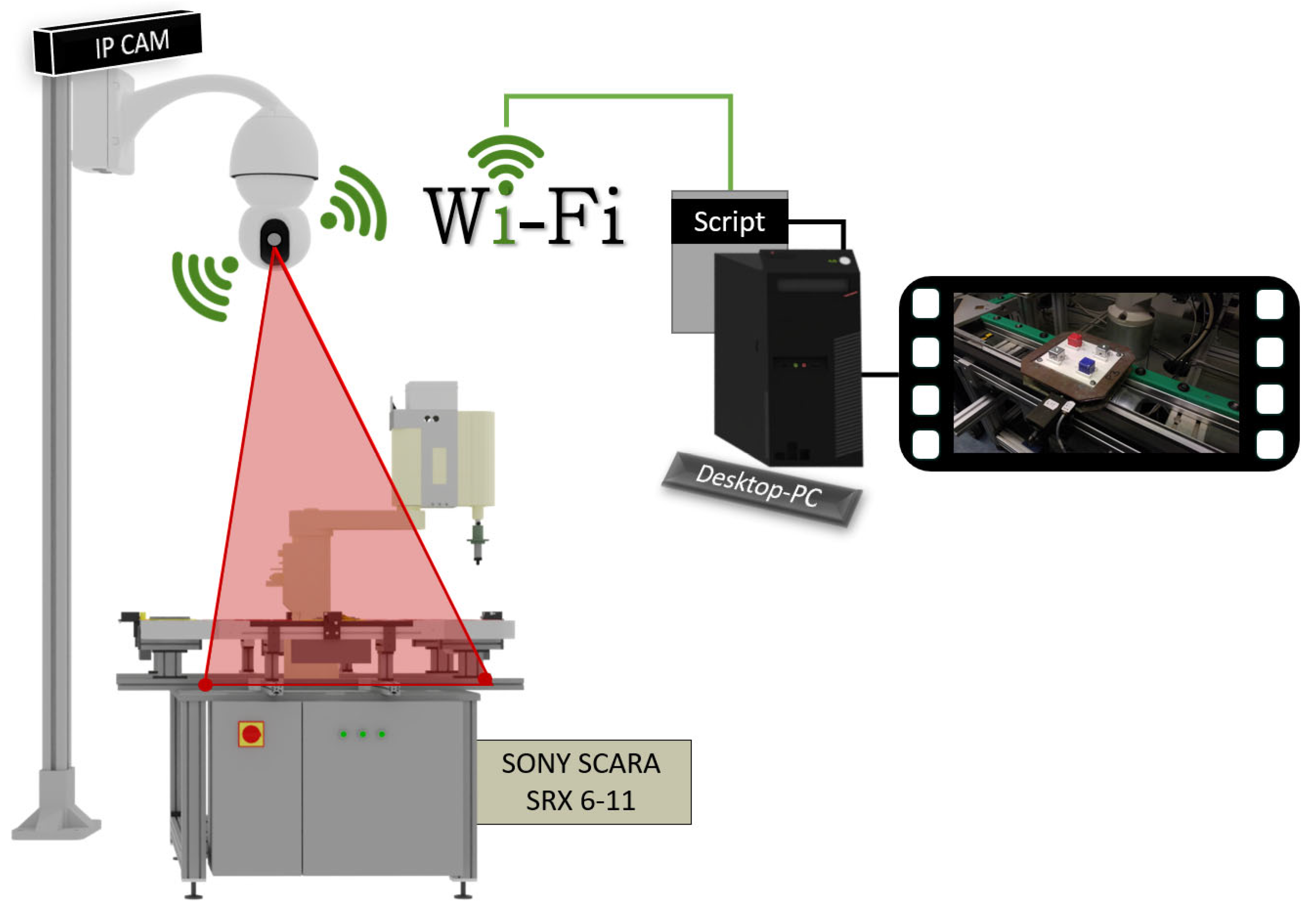
3. SONY SCARA—SRX-611 Robot Unit
| Arm Length | Workspace | Maximum Speed | Repeatability | ||||
|---|---|---|---|---|---|---|---|
| 1. Axis | 350 mm | 1. Axis | 220° | - | - | - | - |
| 2. Axis | 250 mm | 2. Axis | ±150° | - | - | - | - |
| - | - | Z. Axis | 150 mm | Z axis | 770 mm/sec | Z axis | ±0.02 mm |
| - | - | R. Axis | ±360° | R axis | 1150/sec | R axis | ±0.03 mm |
4. Problem Foundation
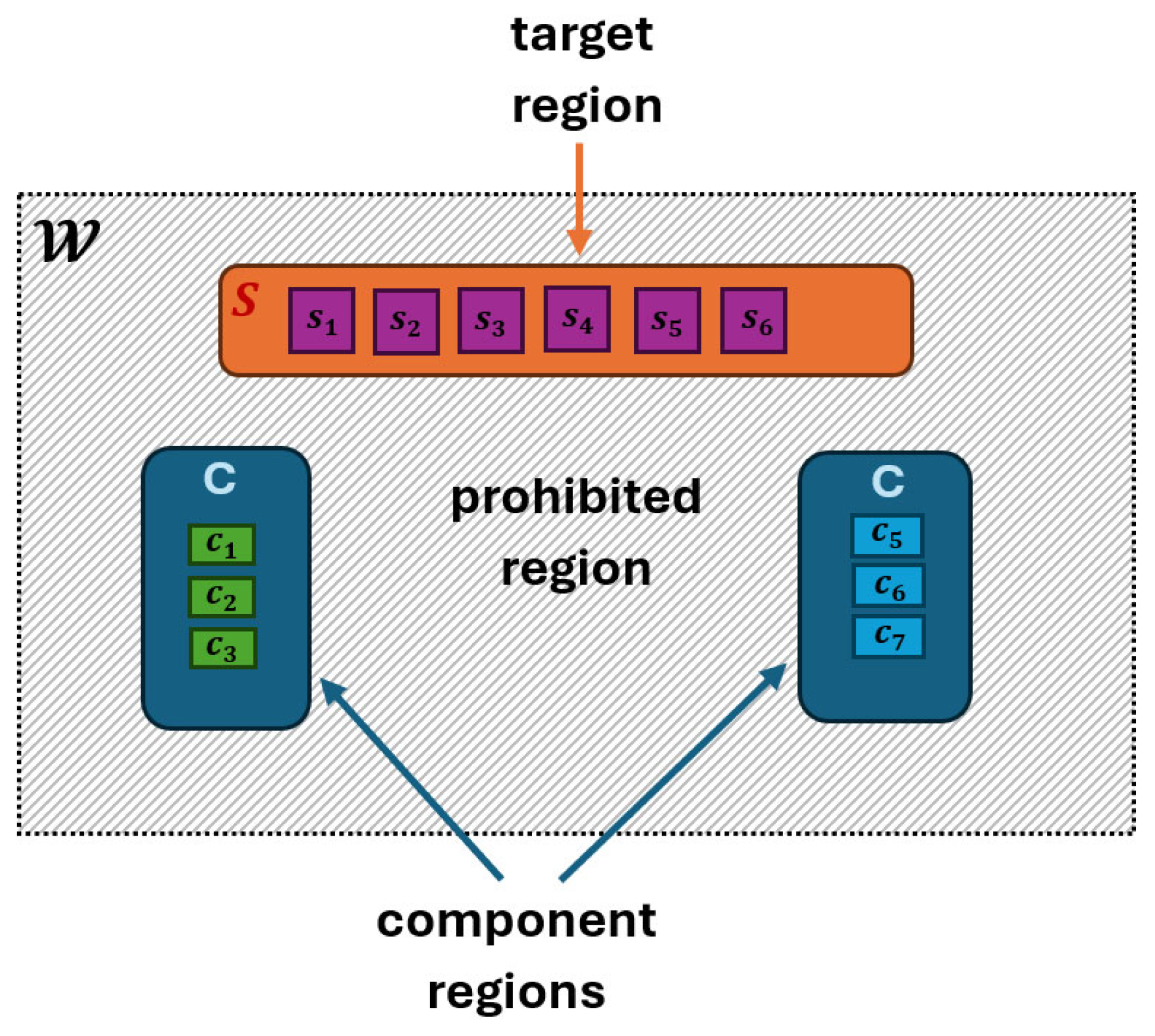
4.1. The Spatial Workspace of Robot Arm
4.2. The Components-Slot Assignment
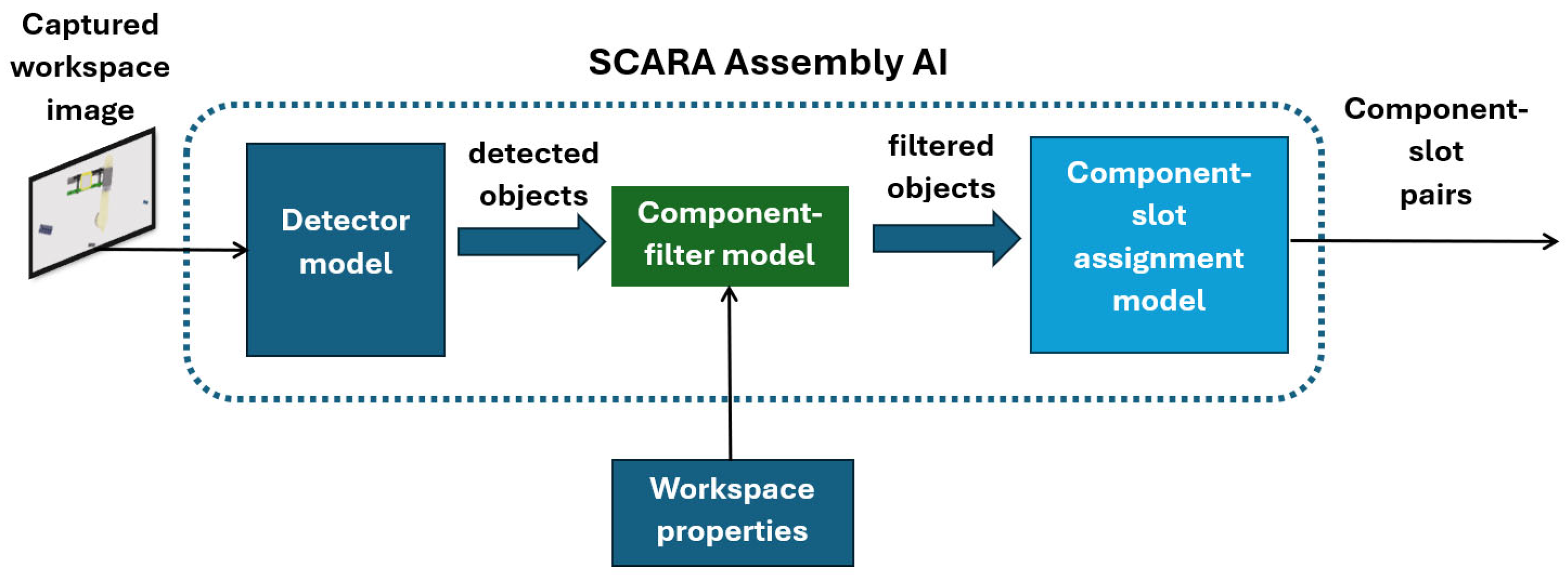
5. The Proposed Method
5.1. The Concept of the Method
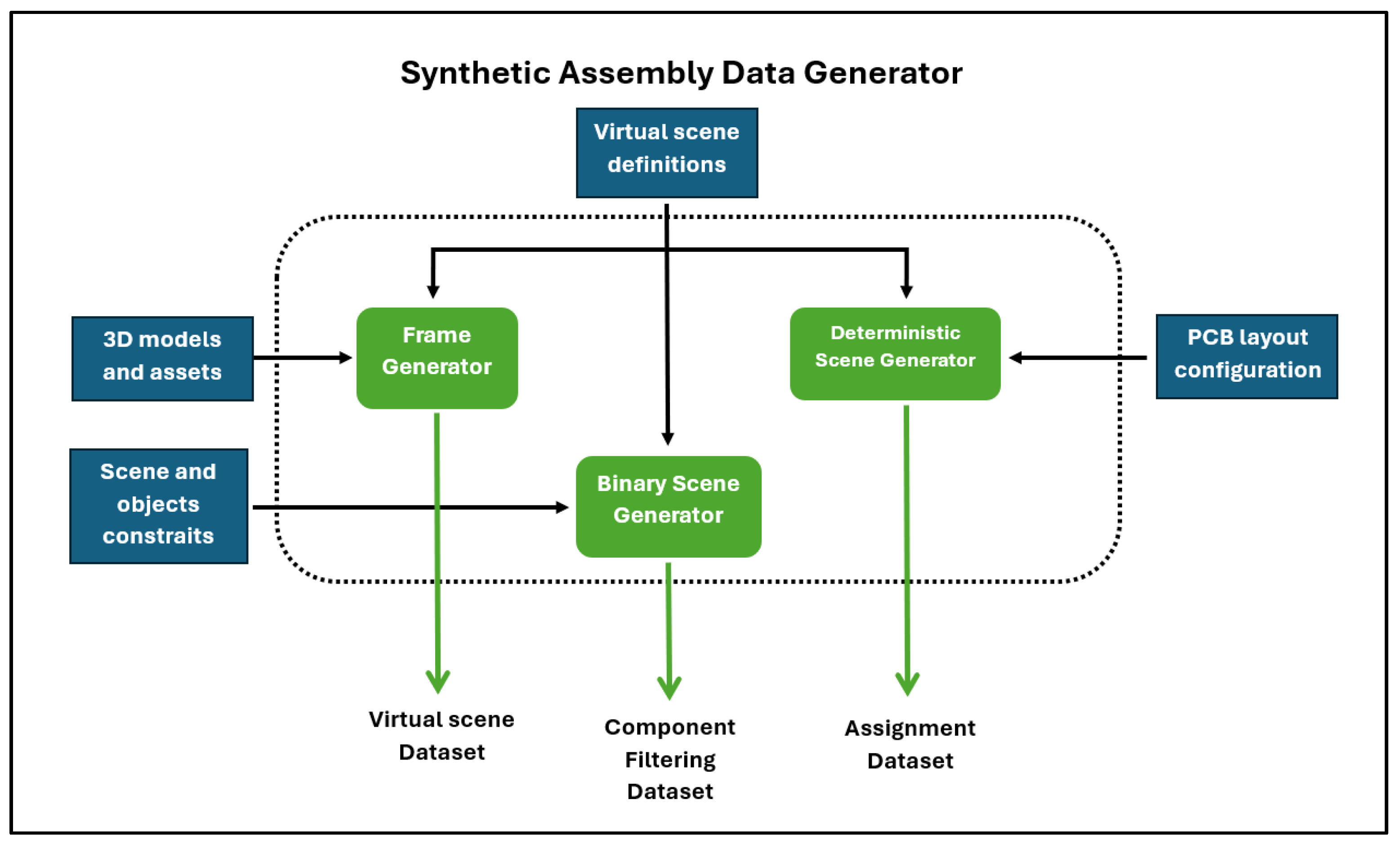
5.2. Synthetic Data Generation
5.3. Details of Detector Model
5.4. Details of Component Filter Model
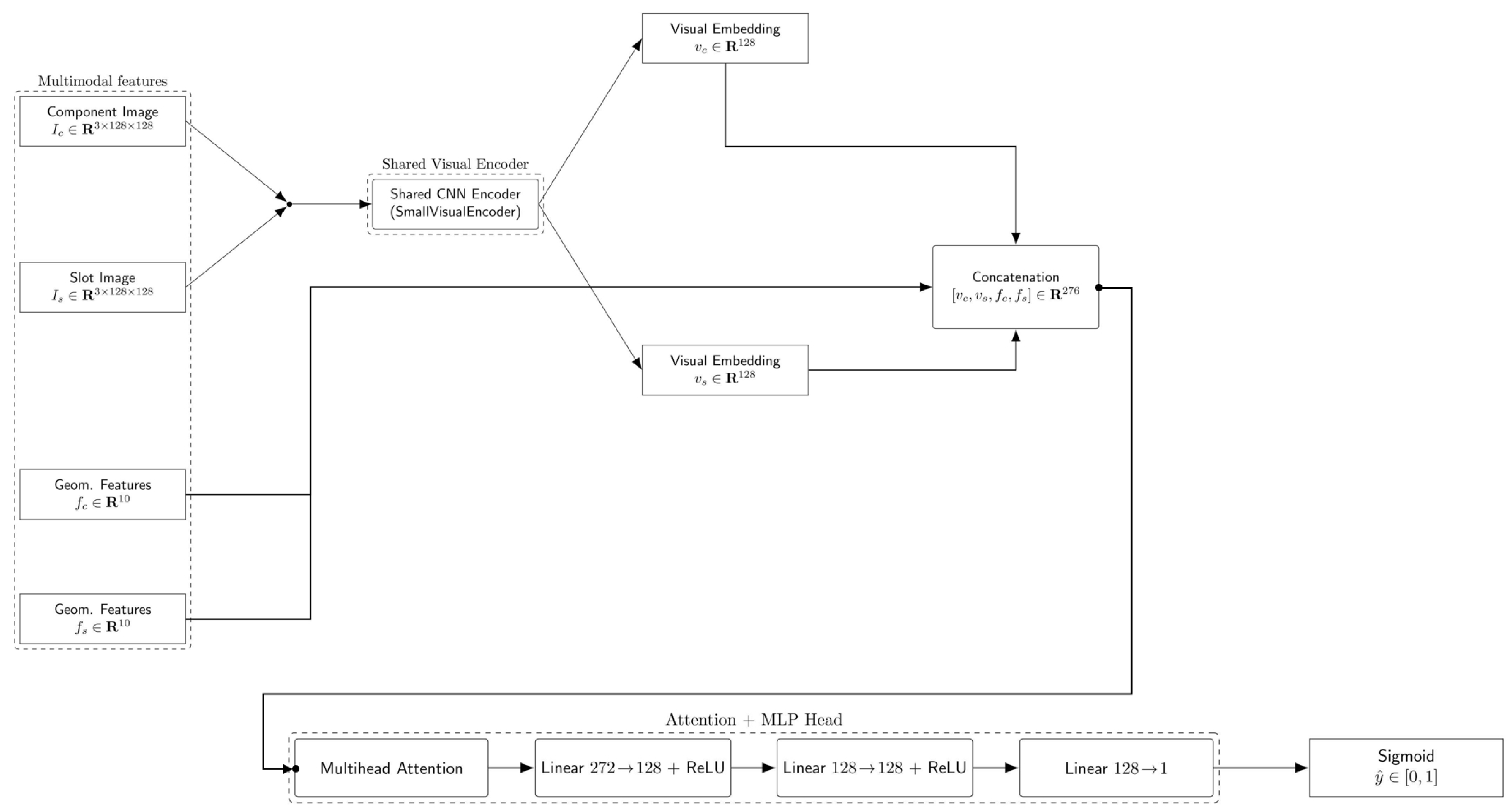
5.5. Details of Assignment Model
6. Training and Validation of the Models
6.1. Datasets
6.2. The Detector Model
6.3. The Component Filter Model
6.4. The Assignment Model
7. Simulation in NVIDIA Omniverse Platform and Real-World Validation
7.1. Omniverse Simulation Framework
7.2. SONY SRX-611 SCARA Robot Digital-Twin
- MOVE, MVS, MVL (point-to-point, linear, and arc motion execution).
- Fine-tuning speed, acceleration, and deceleration.
- Storing movement points and coordinates.
- Input and output commands (grippers and feeders).
- Wait function, waiting for a specific signal.
- Label and Jump, program flow control.
- IF, THEN, ELSE logical decisions based on input signals.
- LOOK: Performing repetitive tasks and cycles
7.3. Visual Inference, Performance and Real-World Evaluation
| Algorithm 1: SCARA Assembly AI method |
 |
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain Randomization for Transferring Deep Neural Networks from Simulation to the Real World. arXiv 2017, arXiv:1703.06907. [Google Scholar] [CrossRef]
- NVIDIA Corporation. NVIDIA Omniverse Platform—A Simulation and Collaboration Framework for 3D Workflows; NVIDIA Developer: Santa Clara, CA, USA, 2024; Available online: https://developer.nvidia.com/nvidia-omniverse (accessed on 4 October 2025).
- NVIDIA Corporation. Omniverse Replicator: Synthetic Data Generation Framework; NVIDIA Developer: Santa Clara, CA, USA, 2024; Available online: https://developer.nvidia.com/omniverse/replicator (accessed on 4 October 2025).
- Kaigom, E.G. Potentials of the Metaverse for Robotized Applications in Industry 4.0 and Industry 5.0. Procedia Comput. Sci. 2024, 232, 1829–1838. [Google Scholar] [CrossRef]
- Pasanisi, D.; Rota, E.; Ermidoro, M.; Fasanotti, L. On Domain Randomization for Object Detection in Real Industrial Scenarios Using Synthetic Images. Procedia Comput. Sci. 2023, 217, 816–825. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian Method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Yu, T.; Ma, J.; Yang, H.; Xu, C.; Wang, Z.; Liu, J. Deep Graph Matching with Channel-Independent Embedding and Hungarian Attention. In Proceedings of the International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Garcia-Najera, A.; Brizuela, C.A. PCB Assembly: An Efficient Genetic Algorithm for Slot Assignment and Component Pick and Place Sequence Problems. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation (CEC’05), Edinburgh, UK, 2–5 September 2005; pp. 1485–1492. [Google Scholar] [CrossRef]
- Ahmadi, R.; Osman, I.H. Component Allocation for Printed Circuit Board Assembly Using Modular Placement Machines. Int. J. Prod. Res. 2002, 40, 3545–3562. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Ji, P. Optimizing feeder arrangement of a PCB assembly machine for multiple boards. In Proceedings of the 2010 IEEE International Conference on Industrial Engineering and Engineering Management, Macao, China, 7–10 December 2010; pp. 2343–2347. [Google Scholar] [CrossRef]
- Li, W.; Xu, A.; Wei, M.; Zuo, W.; Li, R. Deep Learning-Based Augmented Reality Work Instruction Assistance System for Complex Manual Assembly. J. Manuf. Syst. 2024, 73, 307–319. [Google Scholar] [CrossRef]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-Real Transfer of Robotic Control with Dynamics Randomization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar] [CrossRef]
- James, S.; Davison, A.J.; Johns, E. Transferring End-to-End Visuomotor Control from Simulation to Real World for Robotic Manipulation. In Proceedings of the 1st Conference on Robot Learning (CoRL 2017), Mountain View, CA, USA, 13–15 November 2017; pp. 334–343. [Google Scholar]
- Zhang, S.; Wang, Y.; Chen, Q. Research on Robotic Peg-in-Hole Assembly Method Based on Deep Reinforcement Learning. Appl. Sci. 2025, 15, 2143. [Google Scholar] [CrossRef]
- Mena, G.E.; Belanger, D.; Linderman, S.; Snoek, J. Learning Latent Permutations with Gumbel–Sinkhorn Networks. arXiv 2018, arXiv:1802.08665. [Google Scholar] [CrossRef]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching with Graph Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2020, Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Kim, J.; Kosiorek, A.R.; Choi, S.; Teh, Y.W. Set Transformer: A Framework for Attention-Based Permutation-Invariant Neural Networks. In Proceedings of the 36th International Conference on Machine Learning (ICML 2019), Long Beach, CA, USA, 9–15 June 2019; pp. 3744–3753. [Google Scholar] [CrossRef]
- Zhou, W.; Yi, X.; Zhou, C.; Li, C.; Ye, Z.; He, Q.; Gong, X.; Lin, Q. Feature Importance Evaluation-Based Set Transformer and KAN for Steel Plate Fault Detection. IEEE Trans. Instrum. Meas. 2025, 74, 3555113. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the 16th European Conference on Computer Vision (ECCV 2020), Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar] [CrossRef]
- Jia, C.; Liu, H.; Wang, X.; Zhang, Y.; Zhang, Z.; Zhang, L. DETRs with Hybrid Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2023), Vancouver, BC, Canada, 17–24 June 2023; pp. 19702–19712. [Google Scholar] [CrossRef]
- Calzada-Garcia, A.; Victores, J.G.; Naranjo-Campos, F.J.; Balaguer, C. A Review on Inverse Kinematics, Control and Planning for Robotic Manipulators with and Without Obstacles via Deep Neural Networks. Algorithms 2025, 18, 23. [Google Scholar] [CrossRef]
- Calzada-Garcia, A.; Victores, J.G.; Naranjo-Campos, F.J.; Balaguer, C. Inverse Kinematics for Robotic Manipulators via Deep Neural Networks: Experiments and Results. Appl. Sci. 2025, 15, 7226. [Google Scholar] [CrossRef]
- Bouzid, R.; Gritli, H.; Narayan, J. ANN Approach for SCARA Robot Inverse Kinematics Solutions with Diverse Datasets and Optimisers. Appl. Comput. Syst. 2024, 29, 24–34. [Google Scholar] [CrossRef]
- Cheah, C.C.; Wang, D.Q. Region Reaching Control of Robots: Theory and Experiments. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 974–979. [Google Scholar] [CrossRef]
- SCARA Robots: Robot Hall of Fame. Available online: http://www.robothalloffame.org/inductees/06inductees/scara.html (accessed on 23 December 2024).
- PARO QE 01 31-6000; Manual of the Modular Conveyor. PARO AG: Subingen, Switzerland, 2016.
- Kapusi, T.P.; Erdei, T.I.; Husi, G.; Hajdu, A. Application of Deep Learning in the Deployment of an Industrial SCARA Machine for Real-Time Object Detection. Robotics 2022, 11, 69. [Google Scholar] [CrossRef]
- Falcon, W.; The PyTorch Lightning Team. PyTorch Lightning: A Lightweight PyTorch Wrapper for High-Performance AI Research. In Proceedings of the NeurIPS 2019 Workshop on ML Systems, Vancouver, WA, Canada, 13 December 2019; Available online: https://www.pytorchlightning.ai (accessed on 4 October 2025).
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2014), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2015), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NeurIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2017), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the European Conference on Computer Vision (ECCV 2016), Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2017), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. Object Detection with Transformers: A Review. arXiv 2023, arXiv:2306.04670. [Google Scholar] [CrossRef]
- Li, F.; Zhang, H.; Liu, S.; Guo, J.; Ni, L.; Zhang, C.; Ni, B.; Wang, L.; Lu, H.; Hu, H.; et al. DN-DETR: Accelerate DETR Training by Introducing Query DeNoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2022), New Orleans, LA, USA, 19–24 June 2022; pp. 13619–13627. [Google Scholar] [CrossRef]
- Lv, W.; Song, G.; Yu, H.; Ma, C.; Pang, Y.; Zhang, C.; Wei, Y. DINO: DETR with Improved DeNoising Anchor Boxes for End-to-End Object Detection. In Proceedings of the International Conference on Learning Representations (ICLR 2023), Kigali, Rwanda, 1–5 May 2023. [Google Scholar] [CrossRef]
- Wei, Y.; Lv, W.; Ma, C.; Liu, Y.; Zhang, C.; Zhang, Y.; Pang, Y.; Song, G. RT-DETR: Real-Time DETR with Efficient Hybrid Encoder. arXiv 2023, arXiv:2304.08069. [Google Scholar] [CrossRef]
- Zhao, Y.; Lv, W.; Xu, S.; Wei, J.; Wang, G.; Dang, Q.; Liu, Y.; Chen, J. DETRs Beat YOLOs on Real-time Object Detection. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 16965–16974. [Google Scholar] [CrossRef]
- Jocher, G. YOLOv8: Real-Time Object Detection and Instance Segmentation. Ultralytics. 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 5 November 2025).
- Yu, T.; Wang, R.; Yan, J.; Li, B. Learning Deep Graph Matching via Channel-Independent Embedding and Hungarian Attention. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; Available online: https://api.semanticscholar.org/CorpusID:214361872 (accessed on 23 November 2025).
- Hodaň, T.; Haluza, P.; Obdržálek, Š.; Matas, J.; Lourakis, M.; Zabulis, X. T-LESS v2: An RGB-D Dataset for 6D Pose Estimation of Texture-less Objects. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 880–888. [Google Scholar] [CrossRef]
- Hinterstoisser, S.; Lepetit, V.; Ilic, S.; Holzer, S.; Bradski, G.; Konolige, K.; Navab, N. Model-Based Training, Detection and Pose Estimation of Texture-less 3D Objects in Heavily Cluttered Scenes. In Proceedings of the 14th Asian Conference on Computer Vision (ACCV), Daejeon, Republic of Korea, 5–9 November 2012. [Google Scholar] [CrossRef]
- Tyree, S.; Tremblay, J.; To, T.; Cheng, J.; Mosier, T.; Smith, J.; Birchfield, S. 6-DoF Pose Estimation of Household Objects for Robotic Manipulation: An Accessible Dataset and Benchmark. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; Available online: https://github.com/swtyree/hope-dataset (accessed on 10 November 2025).
- NVIDIA Corporation. vMaterials 2: Physically-Based Material Library for NVIDIA Omniverse. Available online: https://developer.nvidia.com/vmaterials (accessed on 4 November 2025).
- NVIDIA Corporation. Omniverse Dome Light HDRI Environment Package. Available online: https://developer.nvidia.com/omniverse (accessed on 10 November 2025).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Pixar Animation Studios. Universal Scene Description (USD) Specification; Pixar: Emeryville, CA, USA, 2016; Available online: https://openusd.org/release/intro.html (accessed on 3 October 2025).
- NVIDIA Corporation. Omniverse Isaac Sim: Robotics Simulation Platform; NVIDIA Developer: Santa Clara, CA, USA, 2024; Available online: https://developer.nvidia.com/isaac-sim (accessed on 4 October 2025).
- Pixar Animation Studios. USD Xform Schema—Transforming Prims; Pixar: Emeryville, CA, USA, 2016; Available online: https://openusd.org/release/api/class_usd_geom_xform.html (accessed on 3 October 2025).


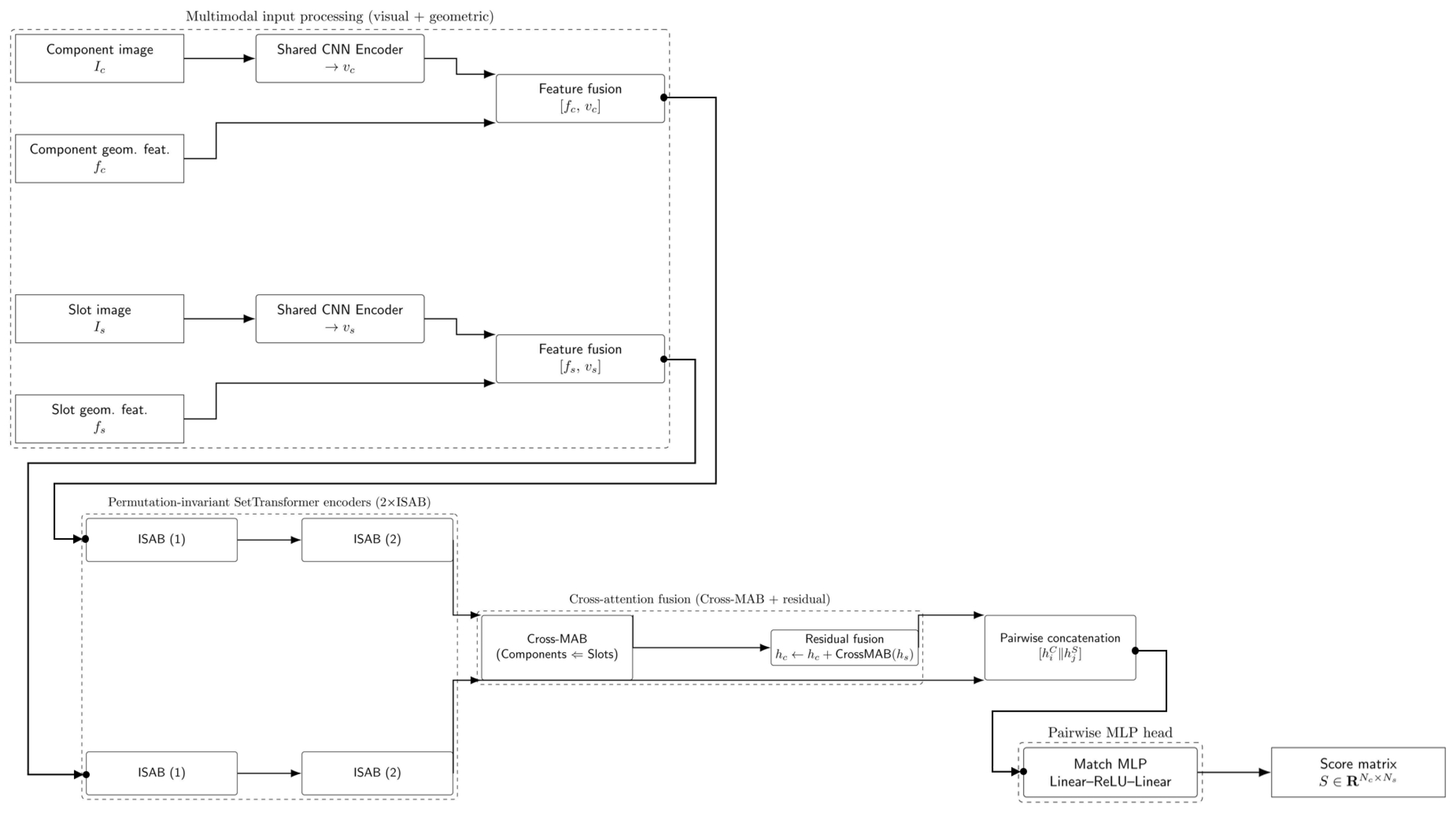

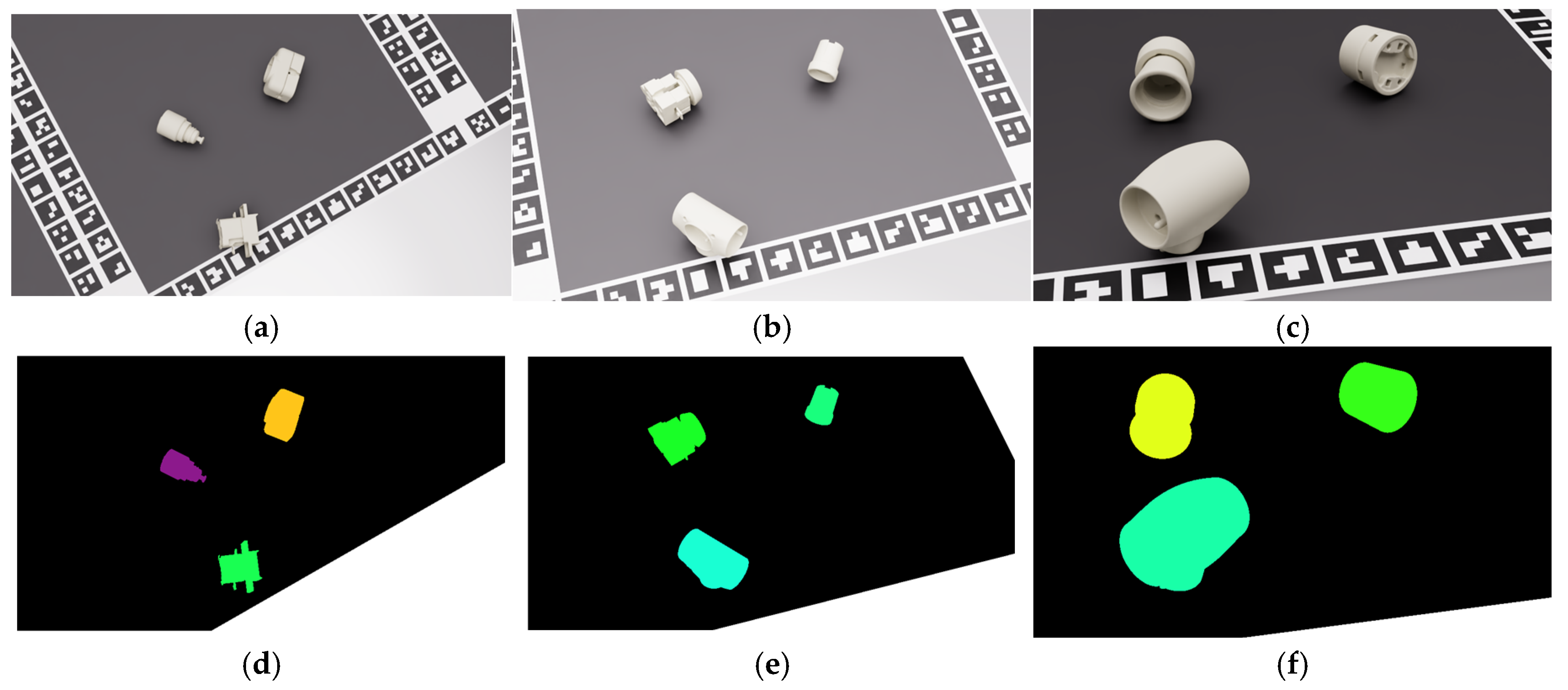

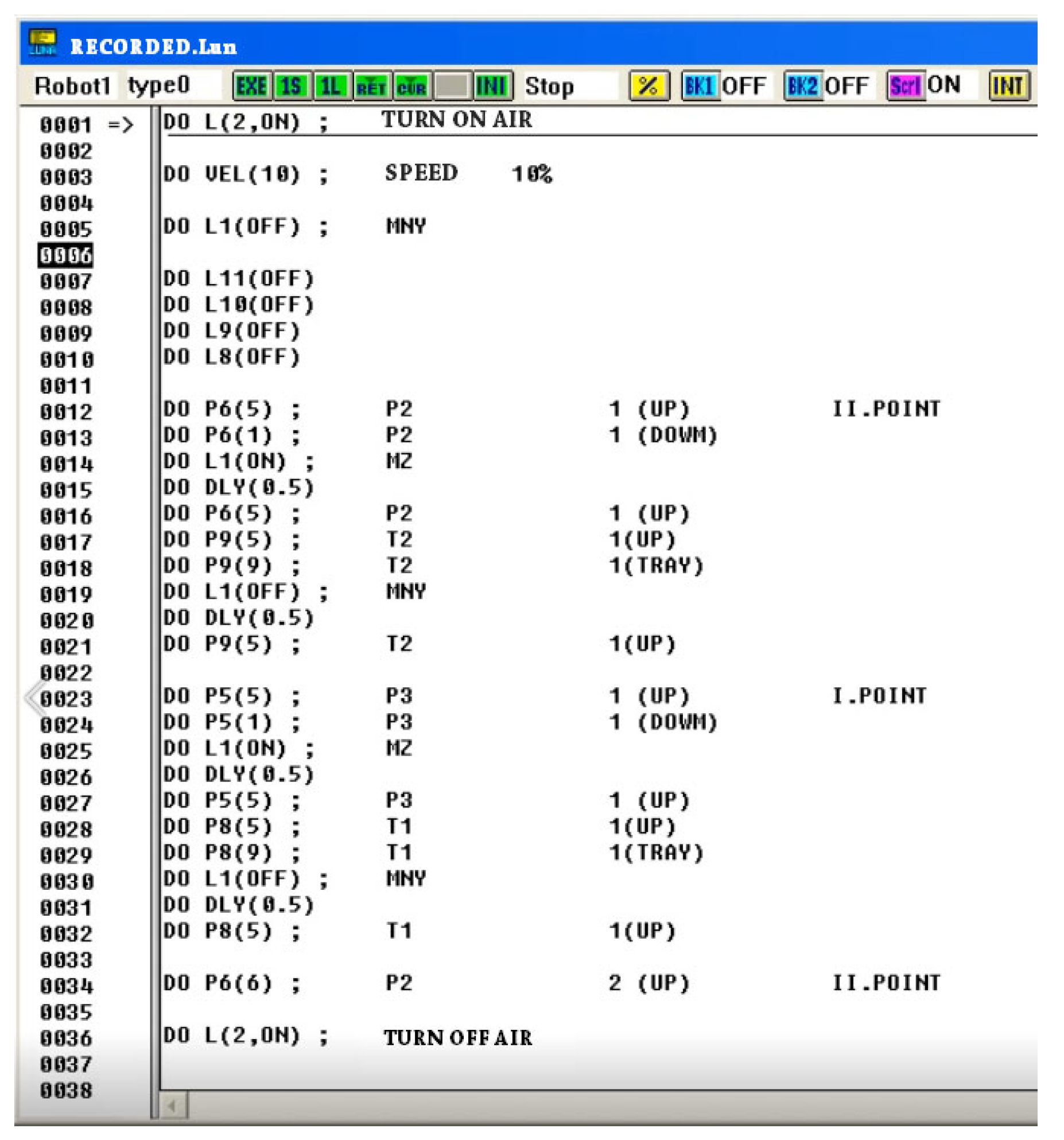
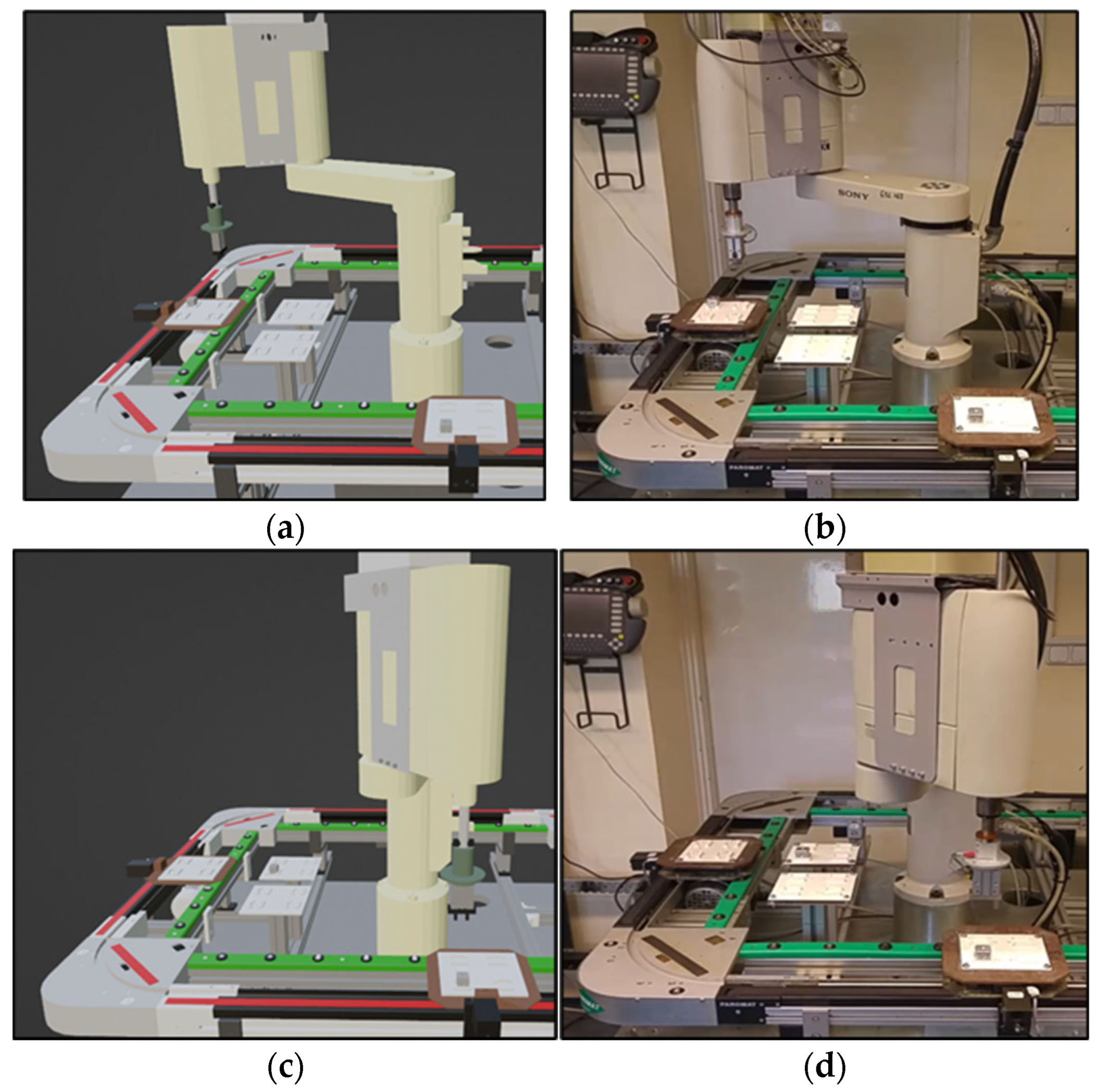
| Category | Name | Parameters |
|---|---|---|
| Illumination variation | RandomBrightnessContrast | brightness_limit = 0.2, contrast_limit = 0.2, |
| Sensor noise | GaussNoise | var_limit = (10, 50), mean = 0, |
| Motion/focus blur | MotionBlur, GaussianBlur | blur_limit = 5, |
| Color shift/illumination temperature | HueSaturationValue | hue_shift_limit = 10, sat_shift_limit = 15, val_shift_limit = 10, p = 0.3 |
| RGB channel misalignment | RGBShift | r_shift_limit = 10, g_shift_limit = 10, b_shift_limit = 10 |
| Compression artifacts | ImageCompression | quality_lower = 40, quality_upper = 90 |
| Parameter | Default Value(s) |
|---|---|
| Epochs | 100 |
| Batch size | 16 |
| Image size (imgsz) | 640 |
| Optimizer | Adam |
| Initial learning rate (lr0) | 0.00025 (backbone: 0.000025) |
| Momentum/betas | (0.9, 0.999) |
| Weight decay | 0.05 |
| Warmup steps | about 1000 iterations |
| LR scheduler | cosine decay |
| Loss weights | cls = 1.0, bbox = 5.0, GIoU = 2.0 |
| PSNR | YOLOv8-Nano-Seg | YOLOv8-Small-Seg | YOLOv11-Nano-Seg | YOLOv11-Small-Seg | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prec. | Recall. | mAP50 | mAP50–95 | Prec. | Recall. | mAP50 | mAP50–95 | Prec. | Recall. | mAP50 | mAP50–95 | Prec. | Recall. | mAP50 | mAP50–95 | |
| ∞ | 0.976 | 0.92 | 0.97 | 0.906 | 0.96 | 0.92 | 0.97 | 0.914 | 0.991 | 0.953 | 0.982 | 0.915 | 0.989 | 0.963 | 0.984 | 0.932 |
| 34.10 | 0.592 | 0.501 | 0.534 | 0.428 | 0.719 | 0.573 | 0.675 | 0.667 | 0.369 | 0.276 | 0.315 | 0.307 | 0.724 | 0.720 | 0.769 | 0.726 |
| 28.21 | 0.2431 | 0.263 | 0.223 | 0.216 | 0.399 | 0.319 | 0.309 | 0.0299 | 0.244 | 0.212 | 0.224 | 0.212 | 0.441 | 0.470 | 0.426 | 0.421 |
| 22.48 | 0.0431 | 0.0163 | 0.0223 | 0.0216 | 0.019 | 0.0032 | 0.011 | 0.009 | 0.043 | 0.001 | 0.022 | 0.021 | 0.004 | 0.007 | 0.002 | 0.002 |
| Rank | Learning Rate | Hidden Dim | Embed Dim | Cnn Base | Cnn Layers | Cnn Drop | Mlp Drop | Optimizer | Val Acc |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 7.33 × 10−6 | 128 | 128 | 4 | 4 | 0.077 | 0.274 | Adam | 0.979 |
| 2 | 4.64 × 10−5 | 32 | 16 | 4 | 2 | 0.013 | 0.121 | AdamW | 0.967 |
| 3 | 2.81 × 10−5 | 32 | 128 | 16 | 3 | 0.031 | 0.152 | AdamW | 0.963 |
| 4 | 1.02 × 10−6 | 128 | 128 | 32 | 2 | 0.046 | 0.225 | Adam | 0.942 |
| 5 | 9.93 × 10−6 | 64 | 16 | 32 | 3 | 0.212 | 0.207 | Adam | 0.929 |
| Parameter | Range/Options | Sampling Type |
|---|---|---|
| Learning rate | 1 × 10−6–5 × 10−6 | Log-uniform |
| Hidden dimension | (32, 64, 128) | Categorical |
| CNN embedding | (16, 64, 128) | Categorical |
| CNN layers | 2–4 | Integer |
| Dropout (CNN/MLP) | 0.0–0.3 | Uniform |
| Optimizer | {Adam, AdamW} | Categorical |
| Experiment Type | Variable Parameters | Fixed Parameters | Purpose | Runs |
|---|---|---|---|---|
| α-Sensitivity | α ∈ {0.0, 0.25, 0.5,0.75 1.0,1.5,2.0} | lr_core = 5 × 10−5, lr_vis = 1 × 10−5, Optimizer = Adam | Soft Hungarian Loss sensitivity analysis. | 8 |
| Model-variant comparison | hidden_dim ∈ {256, 384, 512}; embedding_dim ∈ {128, 192}; num_heads ∈ {8, 16}; num_inds ∈ {32, 64} | α = 1.0, lr_core = 5 × 10−5, lr_vis = 1 × 10−5 | Capacity and architectural sensitivity evaluation | 3 |
| Generalization test | Layouts and component types unseen during training; random rotation ± 15°; partial occlusion masks | Fixed model = best configuration (α = 1.0, hidden = 384) | Tests cross-layout and cross-category generalization. | 3 |
| Failure-case analysis | Qualitative inspection of top-N incorrect predictions | Fixed best model | Identifies typical mismatches between visually similar parts or overlapping slots. | qualitative |
| Method | Approach Type | Precision | Accuracy | Recall | F1-Score |
|---|---|---|---|---|---|
| Rule-based Hungarian | Deterministic cost-matrix matching using IoU and centroid distance | 0.060 | 0.031 | 0.031 | 0.041 |
| Hungarian Attention | Visual-feature-weighted Hungarian matching (non-learned attention) | 0.820 | 0.764 | 0.746 | 0.781 |
| Proposed Set Transformer and Soft Hungarian Loss | Learned visual-geometric matching with permutation-invariant transformer | 0.966 | 0.924 | 0.914 | 0.942 |
| α | Accuracy | Precision | Recall | F1-Score | Best Val Loss | Epoch to Converge |
|---|---|---|---|---|---|---|
| 0.0 | 0.749 | 0.721 | 0.845 | 0.763 | 0.442 | 18 |
| 0.25 | 0.858 | 0.872 | 0.903 | 0.899 | 0.342 | 16 |
| 0.5 | 0.929 | 0.955 | 0.892 | 0.923 | 0.197 | 15 |
| 0.75 | 0.916 | 0.968 | 0.911 | 0.920 | 0.211 | 14 |
| 1.0 | 0.947 | 0.979 | 0.942 | 0.955 | 0.274 | 15 |
| 1.5 | 0.924 | 0.943 | 0.876 | 0.911 | 0.282 | 15 |
| 2.0 | 0.918 | 0.959 | 0.910 | 0.937 | 0.237 | 15 |
| Model Variant | Hidden Dim | Embedding Dim | Heads | Induced Points | Parameters (M) | Val. F1 (%) | Memory (MB) | Inference Time (ms) |
|---|---|---|---|---|---|---|---|---|
| V1 (Light) | 256 | 128 | 8 | 32 | 3.7 | 0.854 ± 0.126 | 14.69 | 3.42 |
| V2 (Balanced) | 384 | 128 | 16 | 64 | 8.0 | 0.878 ± 0.4 | 32.036 | 3.67 |
| V3 (Extended) | 512 | 256 | 16 | 64 | 14.2 | 0.941 ± 0.22 | 56.79 | 3.97 |
| Test Condition | Description | Precision | Recall | F1-Score | Accuracy | Comments |
|---|---|---|---|---|---|---|
| Unseen layout | Completely new PCB topology, same component set | 0.802 | 0.714 | 0.764 | 0.782 | Maintains stable performance; moderate sensitivity to spatial rearrangement. |
| Unseen components | New component categories excluded from training | 0.966 | 0.812 | 0.898 | 0.911 | High precision; recall slightly reduced due to unseen geometric shapes. |
| Rotated/partial views | Random 10–15° rotation and 20% occlusion | 0.909 | 0.846 | 0.878 | 0.892 | Robust to rotation and partial occlusion; minor degradation under stronger distortions. |
| Failure Type | Description | Example Cause | Impact on Prediction |
|---|---|---|---|
| Geometric similarity | Components with nearly identical bounding-box shapes and aspect ratios (e.g., identical capacitors) | Visual embeddings insufficiently discriminative | False-positive matches between visually similar parts |
| Partial occlusion | Component partially hidden by other object or viewpoint | Missing features in the visible region | Decreased recall; occasional slot mismatch |
| Rotational ambiguity | Symmetric components rotated by 180° produce similar features | Orientation feature underrepresented | Wrong slot assigned despite correct region |
| Clustered layouts | Multiple components densely arranged within small area | Overlapping receptive fields in attention | Assignment confusion among neighboring slots |
| Texture overdominance | Visual encoder overweights texture compared to geometry | Texture randomization insufficient | Misclassification of visually noisy samples |
| Module | Operation | Time [ms] | Comment |
|---|---|---|---|
| Detector (YOLOv8s-Seg) | Object detection and instance segmentation | 4.2 ± 0.2 | Primary perception stage |
| Crop extraction | ROI slicing from detected masks | 0.5 ± 0.1 | Torch tensor-based cropping |
| Visual Filter Network | Dummy vs. valid classification | 1.5 ± 0.4 | Lightweight attention-based CNN |
| Assignment Network | Component–slot pairing | 3.7 ± 0.5 | SetTransformer with Soft Hungarian Loss |
| Inverse Kinematics (IK) | Angle computation for (c,s) pairs | 0.7 ± 0.2 | Trigonometric forward pass |
| Total | Full pipeline inference | 12.0 ± 1.0 | ≈85 FPS on RTX 4060 Ti |
| Test Condition | Environment | Throughput (FPS) | Latency (ms/Frame) | Accuracy [%] | ΔAcc vs. Nominal [%] | Notes |
|---|---|---|---|---|---|---|
| Normal lighting | Omniverse | 62 | 16 | 97.9 | – | Reference |
| Brightness +20% | Omniverse | 62 | 16 | 96.3 | –1.6 | Robust |
| Motion blur | Omniverse | 61 | 16–17 | 93.8 | –4.1 | Slight degradation |
| HSV shift | Omniverse | 61 | 16–17 | 92.2 | –5.7 | Color perturbation |
| Real-world Tapo feed | Physical | 62 | 16 | 96.9 | –1.0 | Consistent performance |
| Module | Environment | Key Metric | Performance | Remarks |
|---|---|---|---|---|
| Detection (YOLOv8s-Seg) | Omniverse and Real | Accuracy | 97.9% | Stable under domain transfer |
| Filter Network | Synthetic only | Accuracy | 97.4% | Robust to visual noise |
| Assignment Network | Synthetic and Real | Accuracy | 96.9% | Best at α = 1.0 configuration |
| Simulation inference | Omniverse | Latency/Throughput | 16 ms/≈62 FPS | Real-time capable |
| Real-world test | SCARA SRX-611 | Success rate | 98% | Physical validation on robot hardware |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapusi, T.P.; Erdei, T.I.; Abdullah, M.; Husi, G.; Hajdu, A. SCARA Assembly AI: The Synthetic Learning-Based Method of Component-to-Slot Assignment with Permutation-Invariant Transformers for SCARA Robot Assembly. Robotics 2025, 14, 175. https://doi.org/10.3390/robotics14120175
Kapusi TP, Erdei TI, Abdullah M, Husi G, Hajdu A. SCARA Assembly AI: The Synthetic Learning-Based Method of Component-to-Slot Assignment with Permutation-Invariant Transformers for SCARA Robot Assembly. Robotics. 2025; 14(12):175. https://doi.org/10.3390/robotics14120175
Chicago/Turabian StyleKapusi, Tibor Péter, Timotei István Erdei, Masuk Abdullah, Géza Husi, and András Hajdu. 2025. "SCARA Assembly AI: The Synthetic Learning-Based Method of Component-to-Slot Assignment with Permutation-Invariant Transformers for SCARA Robot Assembly" Robotics 14, no. 12: 175. https://doi.org/10.3390/robotics14120175
APA StyleKapusi, T. P., Erdei, T. I., Abdullah, M., Husi, G., & Hajdu, A. (2025). SCARA Assembly AI: The Synthetic Learning-Based Method of Component-to-Slot Assignment with Permutation-Invariant Transformers for SCARA Robot Assembly. Robotics, 14(12), 175. https://doi.org/10.3390/robotics14120175








