Cable-Driven End-Effector Robots for Gait Rehabilitation: A Review and Future Research Directions

Abstract

Robot-Assisted Gait Training (RAGT) has emerged as a promising approach to improve motor recovery for stroke survivors. Among RAGT devices, exoskeletons offer precise joint actuation, but they are costly, mechanically complex and present risks related to joint misalignment. End-effector systems present a more affordable and simpler alternative, but face limitations in workspace and adaptability for assist-as-needed therapy. Cable-Driven End-Effector Gait Rehabilitation Robots (CDEGRs) combine the strengths of both approaches, offering low inertia, flexible configurations, and scalable designs. This review systematically examines the current landscape of CDEGRs, encompassing their kinematic classifications, control strategies, and platform configurations. Unlike previous reviews that broadly addressed exoskeletons or upper-limb rehabilitation devices, this work provides a focused and detailed analysis of lower-limb end-effector systems. In doing so, it identifies persistent gaps in design and control frameworks and highlights future research directions toward more efficient and clinically validated CDEGR architectures.

1. Introduction

Stroke is a leading cause of long-term disability worldwide, with more than 50% of survivors not regaining full functional independence [1]. Restoring walking ability is a critical component of neurorehabilitation, as mobility is essential for personal autonomy and quality of life [2]. Traditional gait rehabilitation methods include task-oriented training [3], resistance exercises [4], and treadmill walking assisted by therapists using body weight support devices [5]. However, these approaches are labor-intensive and are often limited by the availability of trained personnel.

Robot-Assisted Gait Training (RAGT) has emerged as a promising solution to enhance traditional rehabilitation by reducing therapists workload and providing consistent and repeatable movement patterns [6]. RAGT systems are typically classified into two categories: exoskeletons and end-effector robots. Exoskeletons directly activate joints through wearable rigid structures aligned with the patient’s limbs [7,8,9,10], while end-effector systems apply forces at attachment points, such as the foot or ankle, to guide limb trajectories [11].

Although exoskeletons offer fine control over joint-level motion and high kinematic fidelity, they are associated with several drawbacks: high cost, mechanical complexity, and safety risks related to joint misalignment [12,13,14,15,16]. Furthermore, these systems often do not produce significantly better rehabilitation outcomes compared to simpler alternatives [17]. In contrast, end-effector devices are more affordable, mechanically simpler, and allow for natural joint motion. However, they are limited by the reduced workspace, constrained motion flexibility—primarily due to the need for precise control and adaptation to patient-specific forces and movements [18]—and insufficient support for assist-as-needed therapy [19].

To address these limitations, recent research has introduced cable-driven end-effector gait rehabilitation robots (CDEGR), a subclass of RAGT systems that use tensioned cables to actuate limb movement. CDEGRs offer several advantages over traditional rigid link devices, including low inertia, adaptable geometry, and simplified mechanical design [20,21]. These features enable greater compliance and reconfigurability, which is especially beneficial in patient-specific rehabilitation contexts.

Despite the growing interest in cable-driven architectures, to our knowledge, no comprehensive review has systematically examined the design, control strategies, platform configurations, and experimental validation of CDEGRs. Previous reviews have either focused on upper-limb end-effector systems and exoskeletons [18], or have considered cable-driven rehabilitation devices with a broad scope that includes both lower- and upper-limb applications [22]. Similarly, other works have compared cable-driven robots mainly from the perspective of general control strategies, without a detailed analysis of gait-oriented end-effector systems [23]. In contrast, this review provides a focused and in-depth examination of CDEGRs, emphasizing their mechanical design principles, control frameworks, and experimental validation. Finally, we identify existing limitations and outline key research opportunities to guide the development of next-generation CDEGRs.

This article is organized as follows. Section 2 presents the methodology used for the systematic review, including selection criteria and data extraction procedures. Section 3 outlines the clinical stages of gait rehabilitation and their implications for robot control. Section 4 introduces a classification framework for CDEGRs, covering degrees of freedom, platform configurations, wrench feasibility, and control strategies. Section 5 reviews and compares existing CDEGR platforms based on their mechanical design, control implementations, and experimental validation. Section 6 presents a comparative overview of CDEGRs in terms of workspaces, complexity, adaptability, and clinical proficiency. Finally, Section 7 concludes the article by summarizing key insights, identifying persistent challenges, and suggesting future research directions.

2. Method

This systematic review was conducted to comprehensively evaluate the current state of CDEGRs for gait rehabilitation, focusing on their design architectures, control strategies, and clinical applicability. The methodology adhered to the Preferred Reporting Items for Systematic Reviews and Meta-Analyzes (PRISMA) guidelines to ensure a rigorous and transparent approach.

A systematic literature search was performed across multiple electronic databases, including PubMed, IEEE Xplore, Scopus, and Web of Science, to identify relevant studies published up to July 2025. The search strategy employed a combination of controlled vocabulary (e.g., MeSH terms) and free-text terms related to cable-driven robots, gait rehabilitation, and control strategies. Key search terms included: “cable-driven robot”, “end-effector robot”, “gait rehabilitation”, “lower limb rehabilitation,” “control strategies”, “impedance control”, and “optimization techniques”. Boolean operators (AND, OR) were used to combine terms, and filters were applied to limit results to peer-reviewed articles, conference proceedings, and technical reports published in English. Additional studies were identified through manual searches of reference lists from relevant articles and reviews.

Studies were included if they met the following criteria: (1) focused on cable-driven end-effector robots specifically designed for gait or lower limb rehabilitation, (2) described platform configurations, control strategies, or experimental validations, (3) included technical details on system design or performance metrics, and (4) were published in peer-reviewed journals, conference proceedings, or reputable technical reports. Exclusion criteria considered studies that: (1) focused on upper limb rehabilitation without relevance to lower limb applications, (2) lacked technical details on CDEGR systems, or (3) were non-English publications or non-peer-reviewed sources.

The selection process involved two stages. First, titles and abstracts were screened independently by two reviewers to assess their relevance based on the inclusion and exclusion criteria. Second, full-text articles of potentially eligible studies were retrieved and evaluated for final inclusion. Discrepancies between reviewers were resolved through discussion or consultation with a third reviewer.

Data were extracted systematically using a standardized template to ensure consistency. Extracted information included: (1) study characteristics (author, year, publication type), (2) CDEGR platform details, (3) control strategies, (4) rehabilitation stage targeted, (5) experimental validation, and (6) reported limitations and future research directions. Data extraction was performed independently by two reviewers, with cross-verification to minimize errors.

Due to the heterogeneity of study designs and outcomes, a narrative synthesis was employed to summarize the findings. Studies were categorized based on platform configurations (e.g., 1L, 2L, IL), control strategies, and rehabilitation stages. Key themes, such as anchor point optimization, cable tension management, and human-robot interaction, were analyzed to identify trends, gaps, and challenges in CDEGR development. Where applicable, quantitative data (e.g., workspace feasibility, tracking error, force distribution metrics) were summarized to provide insights into system performance. Limitations of current systems and proposed future research directions were synthesized to guide the development of next-generation CDEGRs.

As this review involved no human or animal subjects, ethical approval was not required. However, the review considered the ethical implications of CDEGRs. For example, safety in human-robot interactions and the need for clinical validation are part of the analysis of study limitations and future directions.

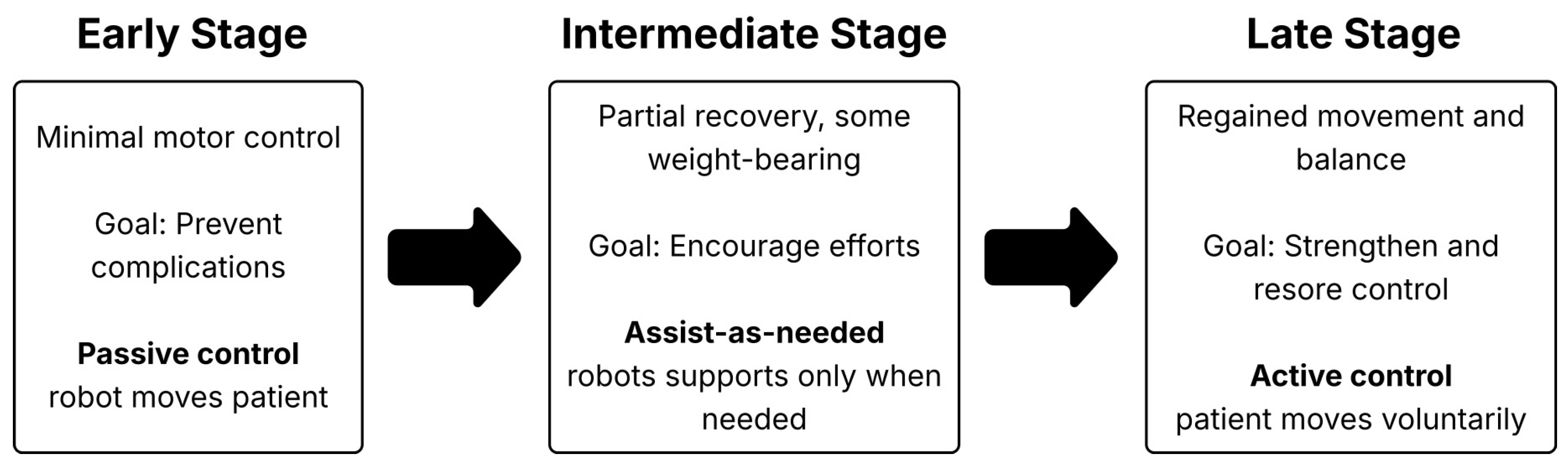
3. Rehabilitation Stages

Rehabilitation after a neurological injury can be divided into three stages: early-stage, intermediate-stage, and late-stage.

In the early stage, corresponding to the acute or subacute post-injury period, patients exhibit minimal voluntary motor function and are often unable to support their body weight. The main therapeutic goal is to prevent secondary complications, such as muscle atrophy, joint contractures, and circulatory problems, while initiating neuromuscular activation [24,25]. Robotic systems at this stage operate in a fully passive mode, where the robot completely guides the patient’s limbs. CDEGRs must offer safe and smooth passive trajectories, typically with low Degrees of Freedom (DoFs) and position-based controllers.

During the intermediate stage, patients regain partial motor control and begin to carry some or all of their body weight. The control objective shifts to assist-as-needed therapy, in which robotic assistance is provided only when the patient is unable to complete a movement voluntarily [26]. This promotes active engagement and accelerates neuromotor recovery [27]. CDEGRs in this phase benefit from adaptive control strategies (e.g., variable impedance, or force-modulated Proportional-Integral-Derivative (PID) control). Electromyography (EMG) or Inertial Measurement Units (IMUs) are also integrated to support real-time interaction [28].

In the late stage, patients regain functional gait patterns, balance, and coordination. Consequently, the focus shifts to active rehabilitation, where the robot provides minimal guidance to promote voluntary muscle activation [29]. Robots used at this stage must support high DoFs motion tracking [30] and be equipped with advanced control algorithms capable of seamlessly switching between passive and active training modes. This adaptability enables smooth transitions between assistance levels while maintaining patient participation and safety [26].

Figure 1 summarizes the stages of the rehabilitation process and their associated control objectives.

4. Classification of CDEGRs

The design of CDEGRs varies widely across the literature, reflecting differences in kinematics, cable routing, and control philosophy. To enable systematic comparison, this section reviews CDEGRs according to four main criteria: DoFs, platform and anchor-point configuration, wrench-feasible workspace, and control strategy. Each criterion is examined in the following subsections to highlight its role in shaping robot functionality and rehabilitation performance.

4.1. Degrees of Freedom

DoFs refer to the number of independent movements that the CDEGR can execute [31], and they are usually represented by the amount of Rotations (R) and Translations (T) the robot is capable of. For example, a CDEGR with 2R3T has 5-DoFs with 2 rotational and 3 translational movements.

Since cables can only generate pulling forces, at least two cables are needed to manipulate the platform along a single axis. Then, to fully control a CDEGR, it is crucial to understand the relationship between the number of cables and the DoFs. For this purpose, Ming and Higuchi introduced the concept of redundancy level r [32], which quantifies the difference between the number of cables and the number of DoFs of the moving platform. In this context, the moving platform corresponds to the end-effector, which is attached to the patient’s leg and whose position and orientation are controlled through the cables. The redundancy level is defined by the following equation:

$$r=m-n.$$

(1)

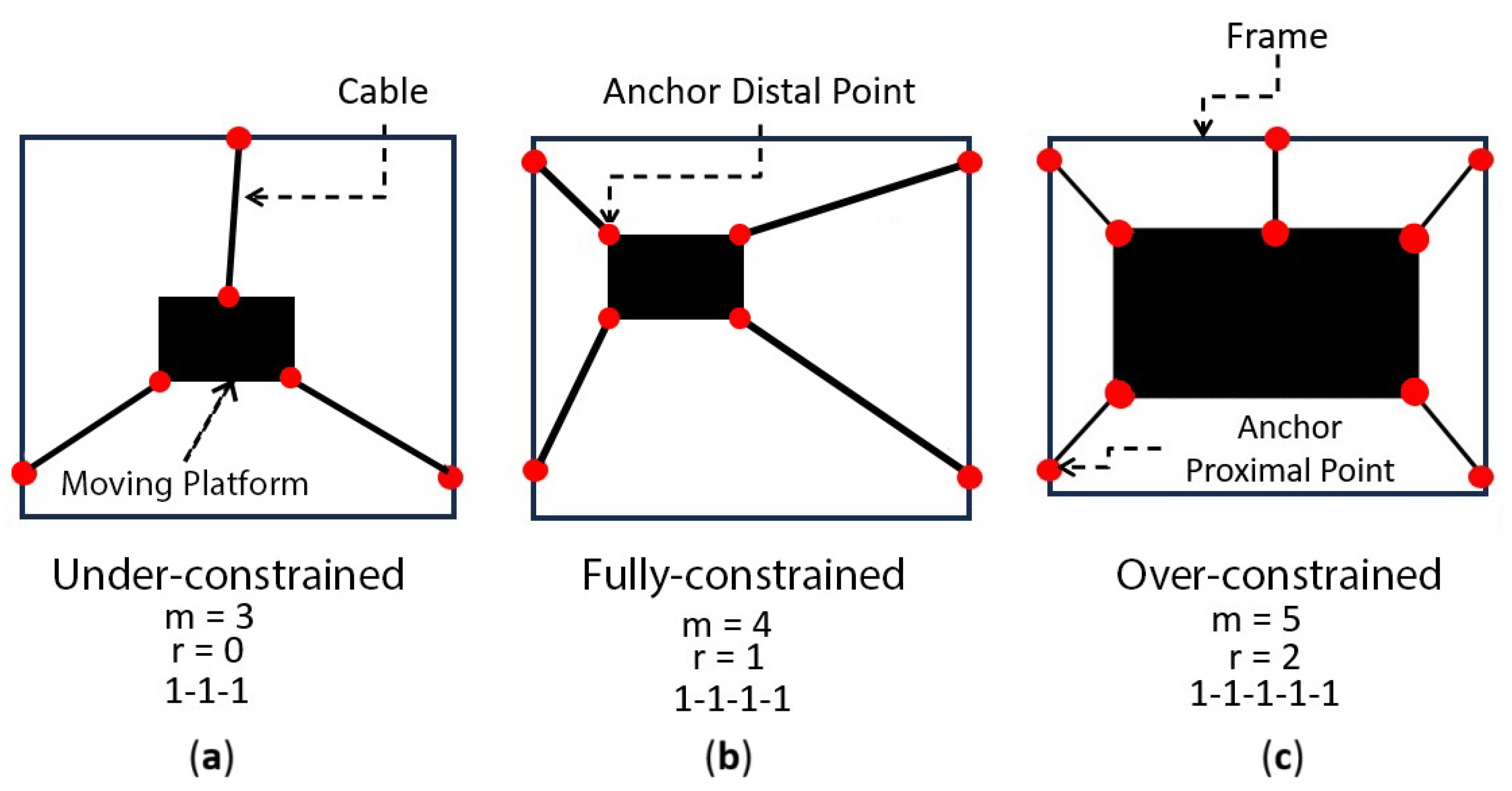
Here, m represents the number of cables and n denotes the number of DoFs of the end-effector. A redundancy level equal to or less than zero ($r\le 0$) is termed under-constrained. Which implies that the position of the end-effector requires an external force to be in equilibrium [33]. A special case occurs when $r=0$; in this scenario, gravity is the only external force required. Figure 2a presents an example of an under-constrained CDEGR. All under-constrained configurations are inherently prone to singularities [31].

When $r=1$, the CDEGR becomes fully constrained, which means that all DoFs of the end-effector are directly governed by the actuators without external forces (Figure 2b). This configuration ensures a unique mapping between actuator inputs and the pose of the end-effector, eliminating internal singularities within the workspace and improving the kinematic stability [34,35].

When $r>1$, the manipulator becomes over-constrained (Figure 2c), meaning it has more cables than the DoFs of the end-effector. This redundancy improves the wrench-feasible workspace and enhances stiffness, contributing to greater robustness against external disturbances [36]. However, it also introduces additional complexity in actuation and control, particularly in the management of internal tensions, a challenge known as the force distribution problem [37].

4.2. Platform Configuration and Anchor Points

In addition to the number of cables, the placement of cable attachment points is a key kinematic design parameter, as it directly affects the system’s capacity to achieve the desired DoFs [38]. Cables connected to the fixed structure or frame are named Anchor Proximal Points (APP), while those connected to the end-effector are termed Anchor Distal Points (ADP).

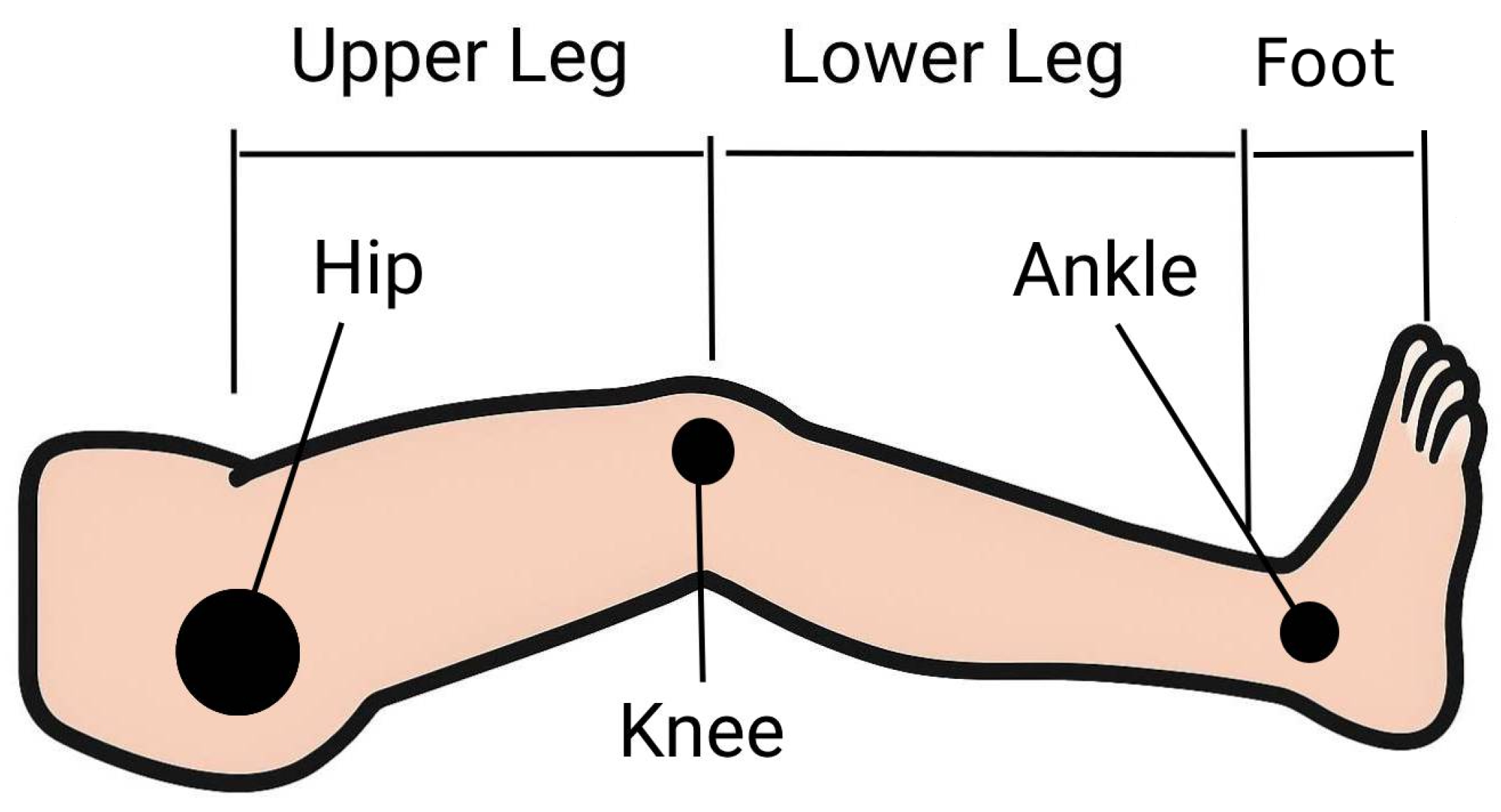
Hyphen notation is commonly employed in cable-driven robots to specify the number of cables attached to each ADP. For example, the configuration 1-1-1-1, depicted in Figure 2c, indicates that the robot consists of four ADPs, each with a single attached cable. However, since the robot can be connected to various sections of the lower extremity, the applicability of this notation for CDEGRs is limited. To overcome this, the proposed notation extends the conventional format by specifying not only the number and distribution of anchor points but also the corresponding leg segment to which each is attached. Thus, the leg segmentation illustrated in Figure 3 is adopted, which divides the human leg into three primary segments according to the anatomy of the skeletal and muscular systems. The segment containing the femur and thigh muscles is designated as the upper leg (U), the segment comprising the tibia and fibula is referred to as the lower leg (L), and the foot is denoted as (F). Consequently, a 1-1-1-1 configuration with end effectors attached to the lower leg would be denoted as 1-1-1-1L.

In cases where multiple end effectors are attached to different segments of the lower limb, a forward slash (/) is used to distinguish the target segments. For example, a robot with two end effectors in the upper leg and three in the lower leg is indicated as 2U/3L. This notation is also used to represent multiple DoFs in different sections of the leg; for example, 2TU/1TL indicates that the upper leg has two translational DoFs, while the lower leg has one translational DoF. More examples of platform configurations are presented in Figure 4.

4.3. Wrench Feasible Evaluation

Cable-driven robots are constrained by the unilateral nature of cable tension, as cables can only pull. This limitation poses challenges in maintaining static equilibrium and achieving a feasible set of controllable force distributions, called the wrench, at the end effector. For any given pose, the cable tensions must remain within physically admissible bounds, typically strictly positive and within specified tension limits. Ensuring this requires careful placement of the cable anchor points [39].

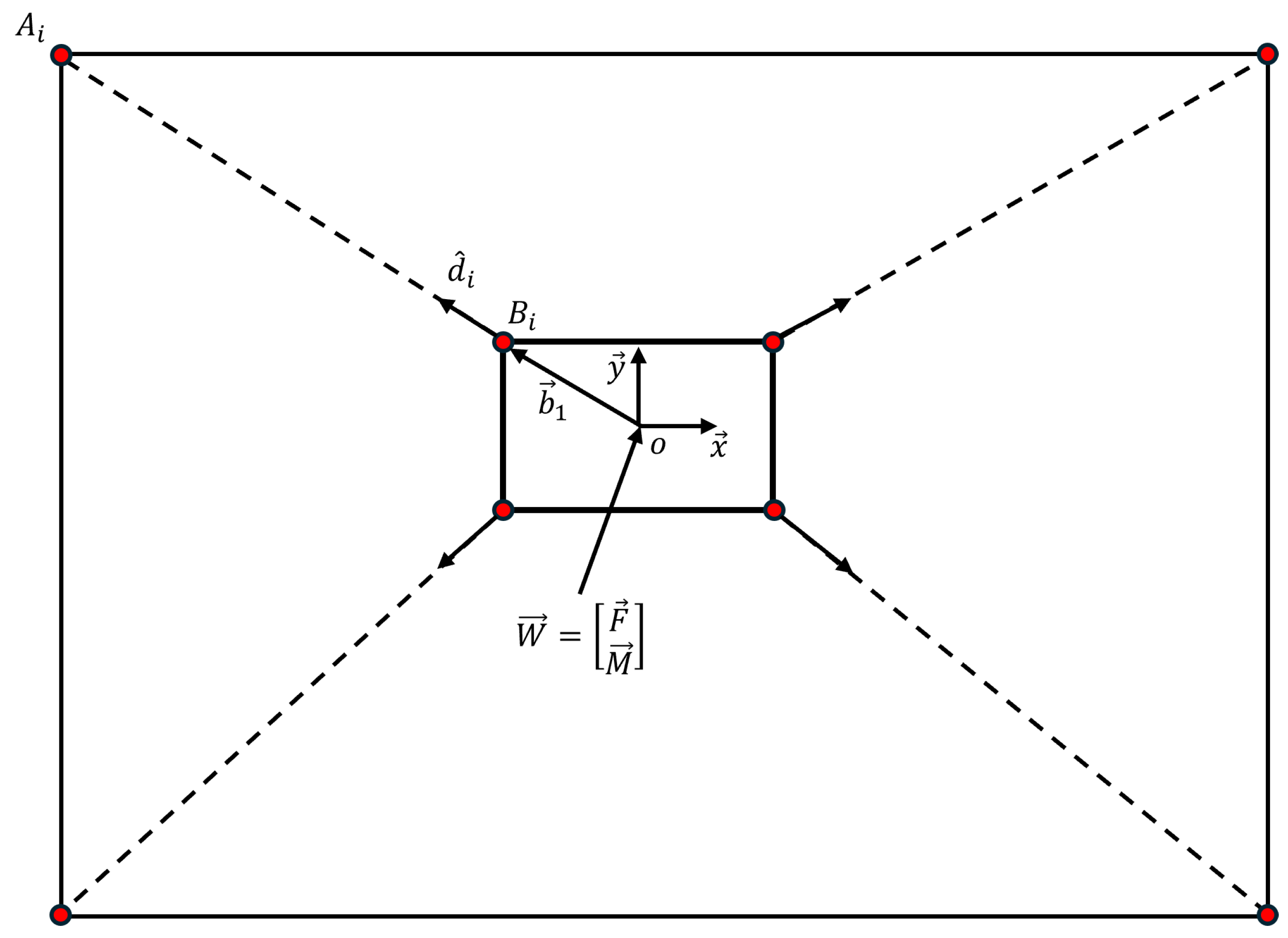
A common approach for evaluating the feasibility of a configuration is through wrench space analysis, which examines the set of wrenches (forces and moments) that the robot can generate at the end effector, given feasible cable tensions. To establish the relationship between the cable tensions and the wrench, consider Figure 5, which represents an acting wrench on a cable-driven robot. In this figure, the acting wrench $\overrightarrow{w}$ is represented by a vector of forces and moments, as presented below:

$$\overrightarrow{w}=\left[\begin{array}{c}\overrightarrow{F}\\ \overrightarrow{M}\end{array}\right].$$

(2)

To counteract this wrench, the robot exerts tension through the cables. The tension vector ${\overrightarrow{\tau }}_i$ acting on each i cable is given by:

$${\overrightarrow{\tau }}_i={\widehat{d}}_i{\tau }_i,$$

(3)

where ${\tau }_i$ is the magnitude and direction of the tension; and ${\widehat{d}}_i$ represents a unit vector along the cable, obtained by applying the following equation:

$${\widehat{d}}_i={\displaystyle \frac{B_i{A}_i}{\parallel B_i{A}_i\parallel }}.$$

(4)

Each i cable has an APP $A_i$ and an ADP $B_i$. Thus, the tensions required to counteract $\overrightarrow{F}$ satisfy the static equilibrium equation as follows:

$$\sum _i^m{\widehat{d}}_i{\tau }_i=-\overrightarrow{F}.$$

(5)

Similarly, to counteract $\overrightarrow{M}$, we consider the moment generated by the tensions on the moving platform, which is given by ${\overrightarrow{b}}_i\times \overrightarrow{\tau }$. Where $\overrightarrow{b_i}$ is a vector that represents the distance between the point at which the torque is applied to the corresponding ADP $B_i$. Thus, the tensions required to counteract $\overrightarrow{M}$ solve the following equation:

$$\sum _i^m{\overrightarrow{b}}_i\times {\widehat{d}}_i{\tau }_i=-\overrightarrow{M}.$$

(6)

Grouping both Equations (5) and (6) into a single equation, we obtain:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\sum _i^m{\widehat{d}}_i\\ \sum _i^m{\overrightarrow{b}}_i\times {\widehat{d}}_i\end{array}\right]\left[\begin{array}{c}{\tau }_1\\ ⋮\\ {\tau }_m\end{array}\right]& =-\left[\begin{array}{c}\overrightarrow{F}\\ \overrightarrow{M}\end{array}\right]\hfill \\ \hfill {\mathbf{J}}^{\mathrm{T}}\overrightarrow{\tau }& =-\overrightarrow{w}\hfill \end{array}$$

(7)

where $\mathbf{J}$ is the Jacobian matrix and $\overrightarrow{\tau }$ is a vector containing all the cable tensions. Equation (7) is used to verify whether the tensions generated by the cables are capable of counteracting the required wrench. The region in which Equation (7) is satisfied is called the wrench-feasible region. Each ${\tau }_i$ in Equation (7) is constrained to ${\tau }_{min}<{\tau }_i<{\tau }_{max}$. The limit ${\tau }_{min}$ is used to assure positive tension and avoid sagging. While the limit ${\tau }_{max}$ is used to avoid breaking the cable [40,41]. In addition to torque limits, several other factors can restrict the severance of the feasible wrench, such as cable interference (crossing), loss of rank in the Jacobian matrix [42], or the joint limitations of the user [43]. 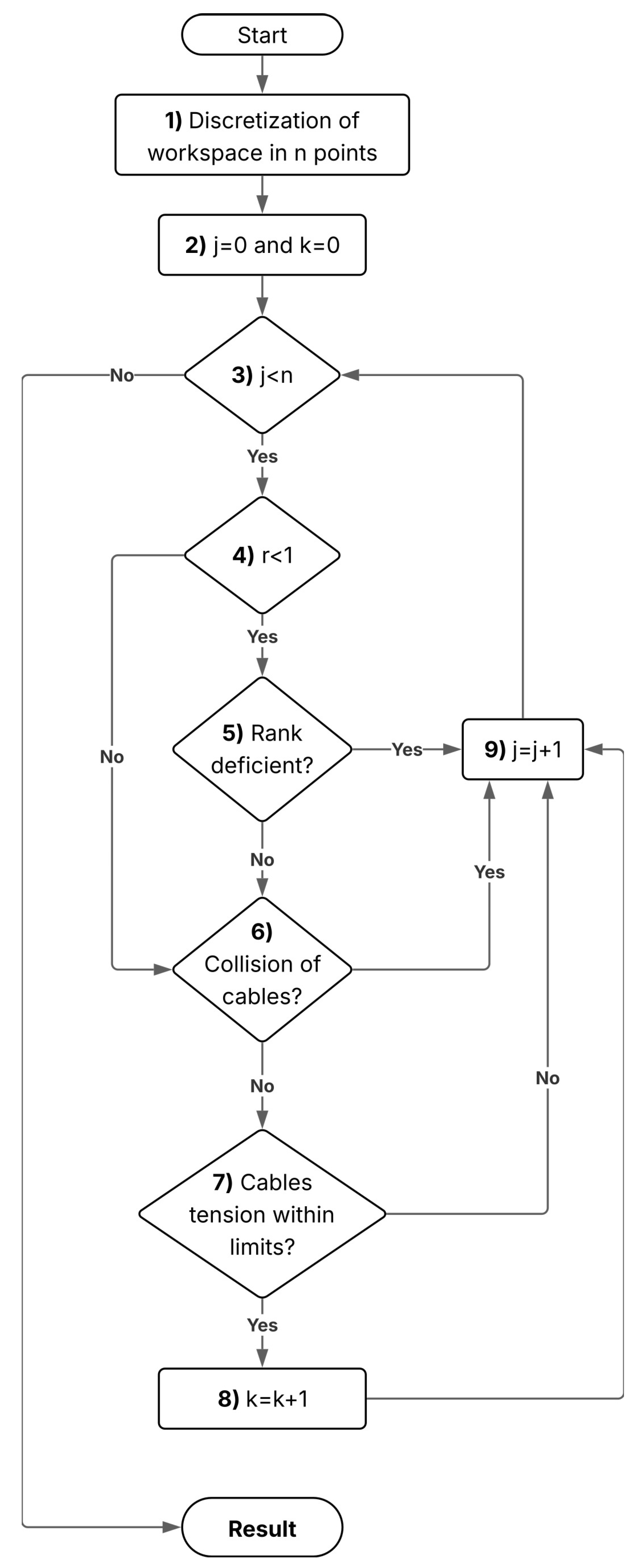In the literature, the standard procedure for evaluating the wrench-feasible region is illustrated in the flow diagram in Figure 6. Each step of the algorithm is described below:

• Discretizations of the workspace: This step seeks to identify the desired positions of the robot. The definition depends on the specific requirements of the rehabilitation task and the DoFs. For example, Zou et al. used a discretization in $x,y,\theta$ for a 3-DOF CDEGR [42]. The defined workspace is discretized evenly into $n_p$ points.
• Initialize counters $j=0$ and $k=0$: Given that the desired positions were discretized into $n_p$ points in Step 1, this step initializes two counters: j refers to the index of the current position under evaluation, while k counts the number of positions that satisfy all requirements (e.g., no cable collisions, feasible tension, etc.).
• Start workspace evaluation: This step begins a loop that iterates through each discretized position until the counter j reaches $n_p$.
• Evaluate redundancy level: This step determines the redundancy level of the robot. If the redundancy level is less than one, the CDEGR may encounter singularities; in this case, a rank evaluation must be performed in the next step.
• Rank evaluation: For the current position, the algorithm evaluates the rank of the Jacobian matrix $\mathbf{J}$. A rank-deficient matrix indicates a singular configuration, meaning that the robot cannot generate the required wrench at that pose [44].
• Cable collision check: Effective collision avoidance strategies are essential for maintaining cable tension within safe operational limits [45]. A commonly used method relies on geometric tests to determine whether a cable segment intersects any convex polyhedron representing an obstacle region. In this context, the user or the end-effector is modeled as an obstacle. Each plane of the polyhedron is tested using scalar product conditions; a collision is detected if the cable segment violates all plane inequalities [46].
• Calculation of cable tensions: Several methods are commonly used to compute cable tensions in rehabilitation robots. These methods vary in complexity and application. The most common techniques used in CDEGRs are linear programming and quadratic programming, presented below:
  • Linear programming: In this approach, the cable tension computation is formulated as a linear system subject to inequality constraints [47]:

    $$\begin{array}{cccc}\hfill & \underset{\overrightarrow{\tau }\in {\mathbb{R}}^m}{min}\hfill & \hfill & {\mathbf{1}}^{\mathrm{T}}\overrightarrow{\tau }\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & {\mathbf{J}}^{\mathrm{T}}\overrightarrow{\tau }=-\overrightarrow{w}\hfill \\ \hfill & \hfill & & {\overrightarrow{\tau }}_{min}\le \overrightarrow{\tau }\le {\overrightarrow{\tau }}_{max}\hfill \end{array}$$

    (8)

    The idea behind this optimization problem is to minimize the sum of tensions on each cable; that way, we ensure a reduction in the energy consumption required to actuate the end-effector [48].
  • Quadratic programming: As an alternative to linear programming, this approach formulates the cable tension computation as a quadratic optimization problem that minimizes the squared 2-norm of the tension vector. Although computationally more demanding, it overcomes some of the limitations associated with linear formulations and results in smoother, more evenly distributed cable forces [49]:

    $$\begin{array}{cccc}\hfill & \underset{\overrightarrow{\tau }\in {\mathbb{R}}^m}{min}\hfill & \hfill & {\parallel \overrightarrow{\tau }\parallel }_2^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & {\mathbf{J}}^{\mathrm{T}}\overrightarrow{\tau }=-\overrightarrow{w}\hfill \\ \hfill & \hfill & & {\overrightarrow{\tau }}_{min}\le \overrightarrow{\tau }\le {\overrightarrow{\tau }}_{max}\hfill \end{array}$$

    (9)

    This formulation promotes stable and continuous cable force distributions, which are advantageous for real-time control and improved user comfort. While linear programming is a convex optimization method with a continuous feasible region, its use of a linear objective function can lead to abrupt changes in the optimal solution, particularly under varying external wrenches. This behavior arises from the geometric nature of the 1-norm, which tends to favor sparse solutions located at the vertices of the feasible region [50]. Consequently, small perturbations in input parameters may cause the optimal tension distribution to switch suddenly between extreme points, leading to practical discontinuities in the control output. In contrast, minimizing the 2-norm yields smoother, more robust tension profiles that are generally preferred for achieving continuous and stable control in cable-driven systems.
• Increment counter k: If all conditions are satisfied, the current point is considered feasible, and the counter k is incremented by one.
• Increment counter j: This counter is incremented regardless of feasibility, allowing the algorithm to continue evaluating the next position in the discretized workspace.
• Results: Once all positions have been evaluated, the algorithm determines the fraction of the workspace that is feasible based on the ratio $k/n_p$.

Implementing this algorithm creates opportunities to integrate optimization techniques aimed at selecting anchor point locations that comply with additional design constraints, such as maximizing the distance between the cables and the patient [51]. The primary objective of these studies is to determine the optimal robot configuration and the set of design parameters that ensure favorable tension distributions along prescribed trajectories, while also minimizing the overall volume of the system [52]. For instance, Hamida et al. employed genetic algorithms to achieve these multi-objective goals. However, in the specific context of CDEGRs, anchor point optimization has received relatively little attention. A notable exception is the work of Cao et al., who applied a particle swarm optimization approach to address this challenge [53].

4.4. Control Strategies in CDEGRs

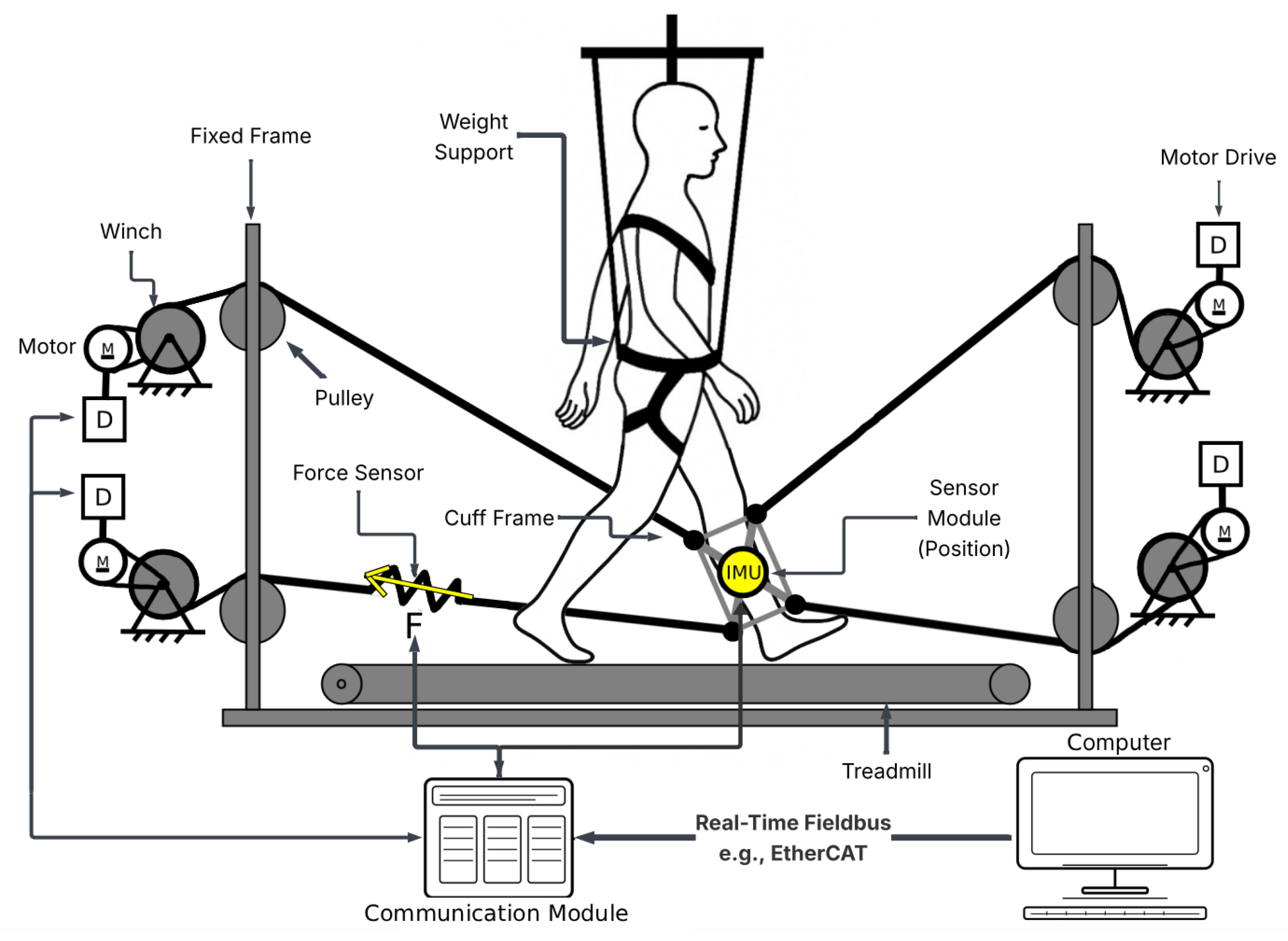
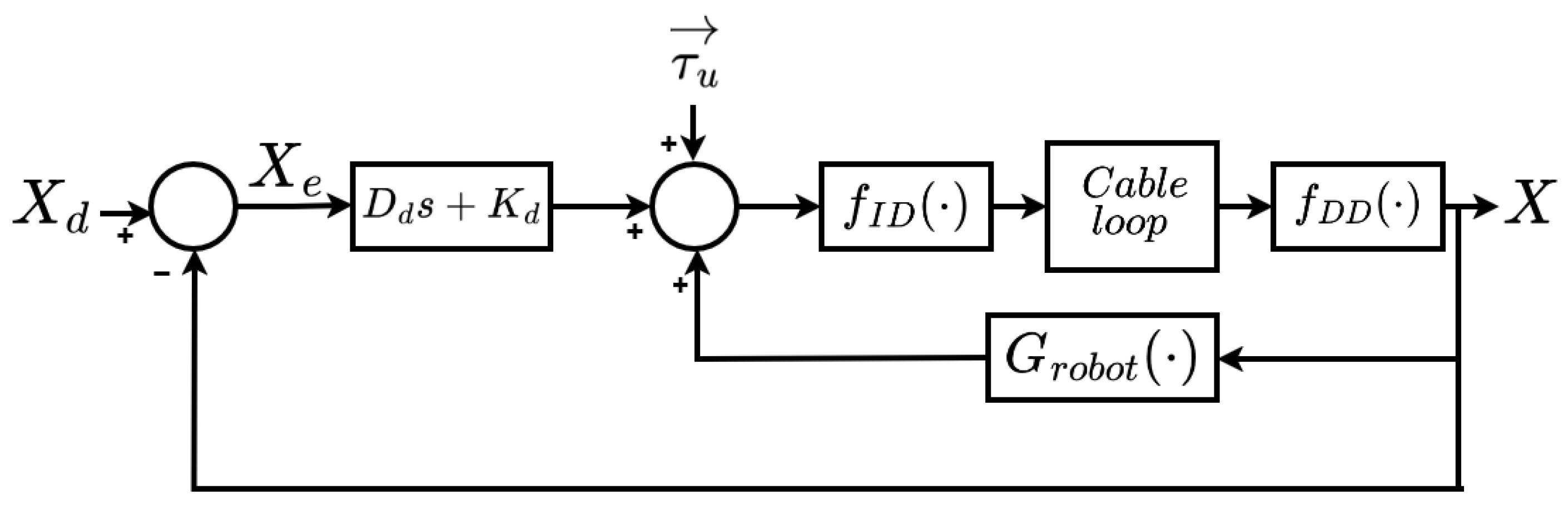
Control strategies in CDEGRs play a critical role in ensuring precise end-effector motion, continuous cable tension, adaptive assistance, and overall system stability. As illustrated in Figure 7, these strategies operate within a closed-loop architecture that connects the patient, sensors, controller, and actuators. Sensor modules such as IMUs and load cells provide real-time feedback on kinematic and dynamic variables, enabling the controller to regulate motor-driven cables and apply appropriate assistive forces through the cuff frame. The choice of control approach—whether PID, impedance, or sliding mode control—is guided by the rehabilitation objectives and the patient’s stage of recovery [54]. The following sections review the main control strategies commonly implemented in CDEGRs, emphasizing their biomechanical relevance and control performance.

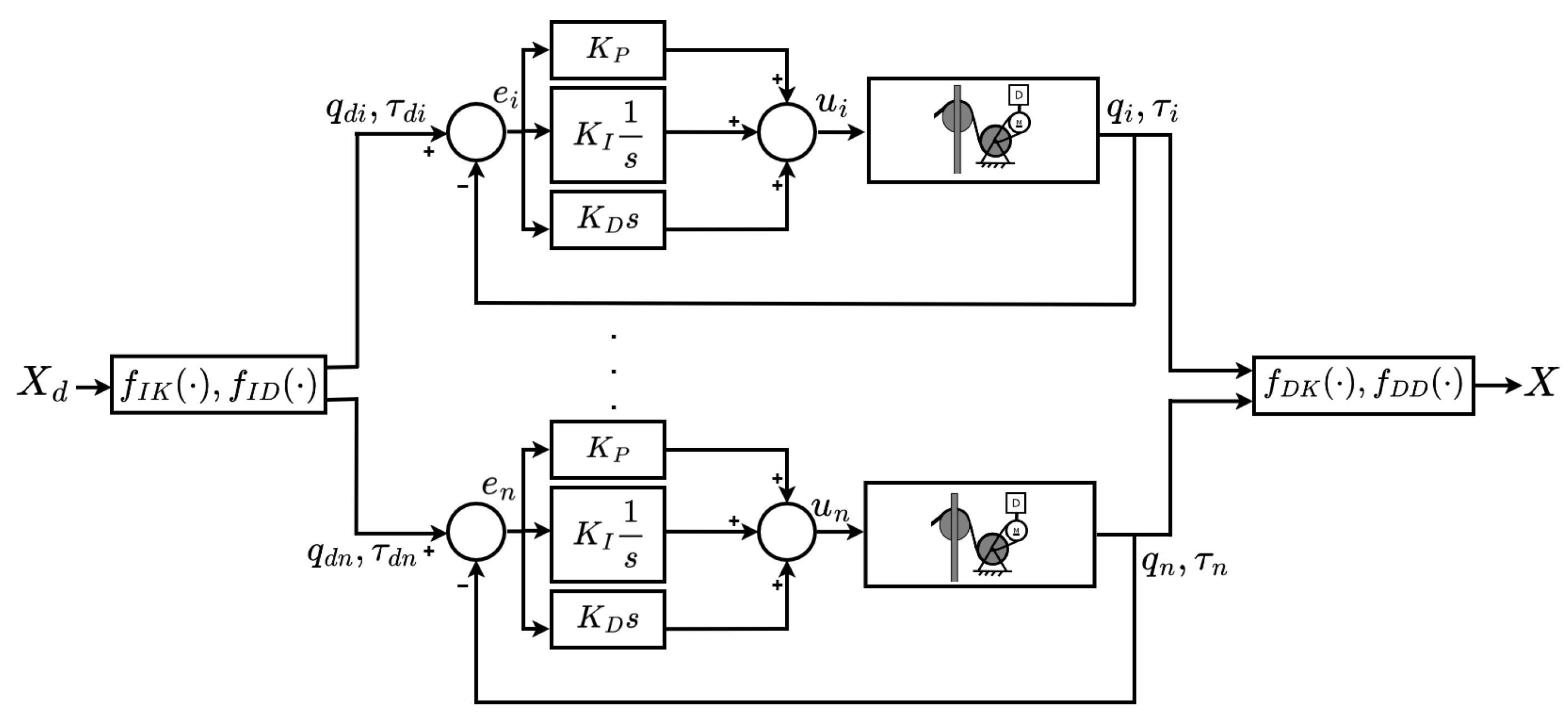
4.4.1. PID Control

PID control remains widely implemented in CDEGRs due to its conceptual simplicity, ease of implementation, and acceptable tracking performance. In this approach, the desired end-effector trajectory ${\mathit{X}}_d$ is mapped to the corresponding desired cable lengths ${\mathit{q}}_d$ through the robot’s inverse kinematics:

$${\mathit{q}}_d=f_{\mathrm{IK}}\left({\mathit{X}}_d\right)$$

(10)

where $f_{\mathrm{IK}}(·)$ denotes the inverse kinematics function and ${\mathit{q}}_d$ represents the target cable lengths. The actual cable lengths are denoted by $\mathit{q}$. The cable-space tracking error is defined as

$$\mathbf{e}={\mathit{q}}_d-\mathit{q}$$

This error is regulated by the classical PID control law:

$$\mathbf{u}=K_P\mathbf{e}+K_I{\int }_0^t\mathbf{e}\left(\tau \right)d\tau +K_D{\displaystyle \frac{d\mathbf{e}}{dt}},$$

(11)

where $\mathbf{u}$ denotes the actuator command, and $K_P$, $K_I$, and $K_D$ represent the proportional, integral, and derivative gain matrices, respectively. We can track the position of the end-effector by means of the direct kinematics:

$$\mathit{X}=f_{\mathrm{DK}}\left(\mathit{q}\right)$$

(12)

Figure 8 illustrates the block diagram of the PID control implementation for CDEGRs. In this figure, $f_{DD}(·)$ and $f_{ID}(·)$ represent the direct and inverse dynamics, respectively; As this formulation also enables the PID to be applied for cable tension control, where each cable’s force (${\tau }_{di}$) is individually regulated.

A representative implementation is found in Wu et al. [55], where a cable-driven rehabilitation system applies assistive and resistive forces based on position and velocity errors during the swing phase of gait. The system maintained acceptable tracking accuracy in subjects with Spinal Cord Injury (SCI). Participants reported no discomfort, and controller gains were manually tuned to user tolerance, ensuring a basic level of safety.

Despite its widespread use, PID control presents notable limitations. It does not explicitly compensate for the nonlinear and time-varying dynamics of human–robot interaction, such as joint impedance variability, cable elasticity, or patient-specific gait characteristics. Its gains are typically tuned heuristically and lack adaptability to evolving rehabilitation needs or individual responses. Furthermore, the absence of model-based compensation leads to degraded performance under disturbances or uncertainties, which are common in real-world gait training scenarios.

Performance also decreases as the number of cables increases. For example, Qin et al. [56] reported average tracking errors rising from 20 mm (three cables) to 40 mm (four cables), underscoring the difficulty of coordinating redundancy without model-based optimization. By contrast, the CaLT system demonstrated consistently low ankle trajectory deviations (10.7 ± 3.4 mm at baseline vs. 10.5 ± 3.0 mm with assistance) and stable peak swing-phase velocities. This robustness is partly due to its 1-DoF design, which simplifies PID control. A rigid ankle bar is used to guide the motion of the limb in a single direction, reducing cable-induced nonlinearities and stabilizing force transmission [55].

Force-based PID controllers are also limited by phase lag and reduced responsiveness, as they lack anticipatory dynamics [57]. To address this, some studies incorporate feedforward compensation for velocity-related disturbances [58], achieving up to 45% error reduction compared to classical force-based PID schemes [59].

Finally, compared to more advanced approaches such as impedance or sliding-mode control, PID controllers often result in higher interaction forces and reduced compliance [60]. Some implementations have attempted to overcome these issues by incorporating disturbance observers that estimate nonlinear error dynamics and compensate for unmodeled disturbances, sometimes with the aid of additional sensors [61]. However, such methods have thus far been limited to relatively simple 1-DoF CDEGRs, restricting their applicability to more complex rehabilitation tasks.

4.4.2. Impedance Control

In impedance control, the wrench generated by the cables reacts to deviations from the trajectory followed by the user. However, to avoid discomfort, the controller does not enforce strict trajectory tracking. Instead, it generates a wrench proportional to the deviations in the position and velocity of the end effector [62]. The general formulation of impedance control is given by:

$$\overrightarrow{w}=G_{\mathrm{robot}}\left(\mathit{X}\right)+{\mathbf{D}}_d{\dot{\mathit{X}}}_e+{\mathbf{K}}_d{\mathit{X}}_e+{\overrightarrow{\tau }}_u$$

(13)

Here, $G_{\mathrm{robot}}$ represents the gravitational wrench of the robot as a function of the end-effector pose $\mathit{X}$. In practice, since the velocity of the end effector is relatively low, Coriolis and inertial effects are often neglected [63]. The trajectory error is defined as:

$${\mathit{X}}_e={\mathit{X}}_d-\mathit{X}$$

(14)

and the velocity error is as follows:

$${\dot{\mathit{X}}}_e={\dot{\mathit{X}}}_d-\dot{\mathit{X}}$$

(15)

The matrices ${\mathbf{D}}_d$ and ${\mathbf{K}}_d$ are diagonal matrices containing the virtual damping and stiffness coefficients, respectively. These parameters define the impedance characteristics of the controller. Finally, the term ${\overrightarrow{\tau }}_u$ is a feedforward component that compensates for nonlinearities in the cables [64]. The impedance controller block diagram is presented in Figure 9.

This formulation defines the principle of impedance control, allowing the robot to interact compliantly with the patient by modulating its dynamic response to deviations from the intended motion [65]. Here, the Cable Loop represents the PID force control loop for each cable, as shown in Figure 8.

Beyond the classical formulation, dynamic variations of the impedance coefficients have been proposed to improve the stability of the human–robot coupled system, typically implemented through neural networks trained in simulation [66,67,68]. Although these approaches have shown promising results, they remain largely confined to simulated environments and require validation in real-world scenarios. Similarly, fuzzy logic algorithms have been investigated to enhance impedance control performance [69]. Preliminary hardware tests have demonstrated coordinated and smooth interaction between users and exoskeletons. However, these methods still require more extensive evaluation before they can be considered viable for clinical rehabilitation.

4.4.3. Sliding Mode Control

Sliding Mode Control (SMC) offers a robust alternative for controlling CDEGR systems, particularly when addressing model uncertainties, patient variability, and external disturbances [70]. The primary objective is to ensure that the patient’s joint trajectories follow the desired motion despite modeling inaccuracies or unpredictable interactions [71].

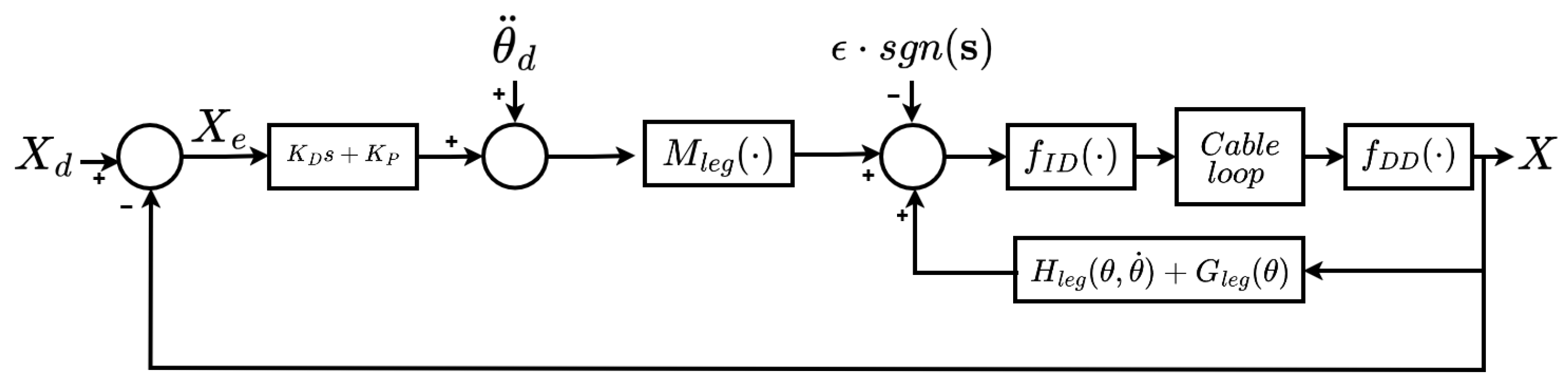
SMC defines a sliding surface that combines position and velocity errors:

$$\mathbf{s}={\dot{\mathit{X}}}_e+K{\mathit{X}}_e,$$

(16)

where ${\mathit{X}}_e={\mathit{X}}_d-\mathit{X}$ is the end-effector trajectory error, ${\dot{\mathit{X}}}_e={\dot{\mathit{X}}}_d-\dot{\mathit{X}}$ is the velocity error, and $K\in {\mathbb{R}}^{n\times n}$ is a positive definite gain matrix that shapes the convergence dynamics.

To drive the system toward the sliding surface and maintain it there, the control input $\overrightarrow{w}$ is defined as:

$$\overrightarrow{w}=M_{\mathrm{leg}}({\ddot{\mathsf{\theta }}}_d+K_D{\dot{\mathit{X}}}_e+K_P{\mathit{X}}_e)+H_{\mathrm{leg}}(\mathsf{\theta },\dot{\mathsf{\theta }})+G_{\mathrm{leg}}\left(\mathsf{\theta }\right)-ϵ·\mathrm{sgn}\left(\mathbf{s}\right),$$

(17)

where:

• $M_{\mathrm{leg}}$ is the inertia matrix of the human leg model.
• $H_{\mathrm{leg}}(\mathsf{\theta },\dot{\mathsf{\theta }})$ represents the Coriolis and centrifugal effects of the leg.
• $G_{\mathrm{leg}}\left(\mathsf{\theta }\right)$ is the gravitational force vector.
• $\mathsf{\theta },\dot{\mathsf{\theta }},\ddot{\mathsf{\theta }}$ are the joint positions, velocities, and accelerations of the leg, while ${\ddot{\mathsf{\theta }}}_d$ is the desired joint acceleration.
• $\mathit{ϵ}\in {\mathbb{R}}^n$ is a diagonal gain matrix that balances convergence speed, mitigates chattering, and compensates for dynamic uncertainties in the leg model.
• $K_P$ and $K_D$ are PD terms.

Once the system reaches the sliding surface, the tracking error dynamics reduce to a first-order linear system:

$${\dot{\mathit{X}}}_e+K{\mathit{X}}_e=0,$$

(18)

ensuring the exponential convergence of the tracking error to zero. Figure 10 presents the block diagram of the general implementation of the SMC.

A major drawback of SMC is the chattering effect, which can cause high-frequency oscillations in the control input. This may lead to actuator wear, energy inefficiency, and discomfort during physical human–robot interaction. Various techniques have been proposed to mitigate this problem, including continuous approximations, boundary layers, and higher-order sliding modes [72]. For instance, a composite sliding-mode reaching law combining smooth and power-exponential functions was proposed to reduce chattering and shorten convergence time during the start-up phase. However, performance gains have been modest, with convergence speed improving by only about 1% compared to standard approaches [73]. Without proper mitigation, SMC often requires stronger actuators to handle the effects of discontinuous control signals [70].

Designing and tuning SMC controllers also remain complex, particularly when incorporating disturbance observers or adaptive mechanisms to manage real-time uncertainties and patient-specific dynamics [74].

To address these limitations, recent research has explored intelligent and adaptive enhancements to classical SMC. Brahmi et al. proposed an adaptive super-twisting SMC strategy for an upper-limb rehabilitation exoskeleton, integrating impedance control with an online-trained Radial Basis Function Neural Network (RBFNN) [75]. The RBFNN estimated the user’s target hand position in real time using sensor data, and this prediction was integrated into an impedance model governing the desired robot behavior. The adaptive SMC ensured robust trajectory tracking while mitigating chattering through higher-order control and online gain adaptation. Unlike conventional SMC, which requires prior knowledge of uncertainty bounds, this approach dynamically estimated them via an adaptive law, simplifying tuning and improving real-time performance. The complete control architecture was implemented and validated in the MARSE exoskeleton with human subjects, demonstrating accurate tracking, smooth torque profiles, and effective human–robot interaction. Although originally designed for upper-limb applications, this architecture represents a promising direction for lower-limb CDEGR systems, where robust compliance, disturbance rejection, and intention tracking are equally critical.

Similarly, Wang et al. developed a Fuzzy Sliding Mode Variable Admittance (FSMVA) controller for a cable-driven lower-limb rehabilitation robot [76]. Their scheme combined fuzzy logic with SMC to reduce chattering and incorporated a safety evaluation module that adapted admittance parameters in real time based on system state and clinical input. Although this approach improved adaptability and robustness, it was tested only on a prosthetic limb and did not integrate human–robot interaction or intention estimation, making it a partial yet relevant step toward interactive CDEGR systems.

One advantage of SMC is the possibility of implementing synovial control. Synovial control refers to the compensation of internal forces within the human joint or other external disturbances. It is particularly relevant for patients with lower limb dysfunction who may experience increased friction during joint motion [77]. This control strategy is achieved by adding an additional term to the sliding surface s [78]. The added term satisfies the Lyapunov stability criteria, thereby guaranteeing system stability.

In particular, cable-driven architectures stand to benefit from adaptive estimation and impedance shaping offered by RBFNN-enhanced SMC, which can help address challenges such as cable elasticity, modeling uncertainty, and the need for smooth force delivery under dynamic gait conditions.

5. Review of Cable-Driven End-Effector Gait Rehabilitation Robots

This section reviews the platform configurations according to the classifications presented in Section 4. To this end,

Table 1. Comparison of Platform Configurations Based on Rehabilitation Stages and Control Strategies.

Platform Configuration	DOF	Redundancy Level	Stages of Rehabilitation			Control			Validation On				Article
			Early	Intermediate	Late	Impedance	PID	SMC	Plaftorm	Dummy	Healthy Users	Clinical Subjects
1-1-1-1L	1R2TL	1		X			X		X				[57]
				X			X				X		[56]
4L	2TL	2		X	X		X		X				[59]
				X	X				X				[79]
				X		X		X		X			[76]
				X	X	X					X		[80]
1U/1L	1RU/1RL	0	X				X				X	X	[81]
1L	1R	0	X				X				X		[61]
2U/2L	1RU/1RL	2		X	X		X				X		[58]
			X	X	X		X		X				[82]
1-1-1F	1R2TL	0		X						X			[44]
2L	2TL	0	X	X		X	X		X	X	X		[65]
3L	2TL	1	X								X		[83]
				X	X		X		X				[84]

provides a comparative overview of various CDEGR platforms. For each platform, the table includes the corresponding rehabilitation stage, the control strategy used, and whether human-robot experiments have been conducted.

To complement Table 1, Figure 4 visually illustrates the different CDEGR configurations. Besides,

Table 2. Comparison of Control Strategies.

Article	Control Strategy			Measured Variable(s)				Sensor(s)
	Impedance	PID	SMC	Motor Speed	Cable Tension(s)	Displacement of Cable	Position
[57]		X		X				Encoder
					X			S-beam load cell
[56]		X				X		Draw-wire
[59]		X		X				Photoelectric encoder
					X			Canister load cell
[76]	X		X	X				Photoelectric encoder
					X			Canister load cell
						X		Draw-wire
							X	Infrared
[80]	X				X			S-beam load cell
						X		Draw-wire
[81]		X		X				Encoder
					X			Spring deformation
							X	Encoder
[61]		X		X				Encoder
					X			S-beam load cell
							X	Encoder
[58]		X		X				Encoder
					X			S-beam load cell
[82]		X			X			Load cell
[65]	X	X		X				Encoder
					X		X	Load cell

and

Table 3. Validation of Control Strategies.

Article	Validation
	Metric(s)	Error
[57]	Phase lag in force curve	At 0.5 Hz and 1 Hz: negligible. At 2 Hz: 6°. At 5 Hz: 20°
[56]	Error in displacement curve	Cables near the knee exhibit higher error peaks (∼50 mm) in the swing phase
[59]	Mean Error (ME) and maximum error in force curve	At 1 Hz: 0.2602 N and 0.3501 N. At 5 Hz: 0.2892 N and 0.4806 N. At 10 Hz: 0.3120 N and 0.5824 N
[76]	ME and RMS of trajectory	Total RMS: 5.54 mm. Total ME: 2.65 mm. ME active training: 0.97 mm. ME passive training: 3.86 mm.
[80]	Mean and standard deviation of force control accuracy. RMS of position.	Control accuracy: $6.4\pm 0.56N$. RMS position: 0.025 m.
[81]	RMS and Mean Absolute Error (MEA) of joint angles ($q_1$ and $q_2$). RMS and MEA of cable lengths ($l_1$ and $l_2$).	Joint angles: RMS of 3.19° for $q_1$ and 4.65° for $q_2$. MEA of: 5.44% for $q_1$ and 18.47% for $q_2$. Cable lengths: RMS of 11.5mm for $l_1$ and 25.5 mm for $l_2$. MEA of: 0.97% for $l_1$ and 1.70% for $l_2$
[58]	ME of force curve	Static: force tracking of 5.3% and 5.7%. Dynamic: force tracking of 14.8% and 11.6%. Force control of 9.6% and 8.4%.
[82]	Surplus force reduction rate	1 Hz: 95.05%, 2 Hz: 93.15%, 3 Hz: 90.85%, 4 Hz: 89.18%, 5 Hz: 87.19%, 6 Hz: 87.17%.

present a comparison of each article found in terms of their implemented control strategies, the errors encountered, and the types of errors.

In the following discussion, each platform is examined in detail, highlighting its advantages and limitations to identify areas where further research is needed to improve human-robot interaction.

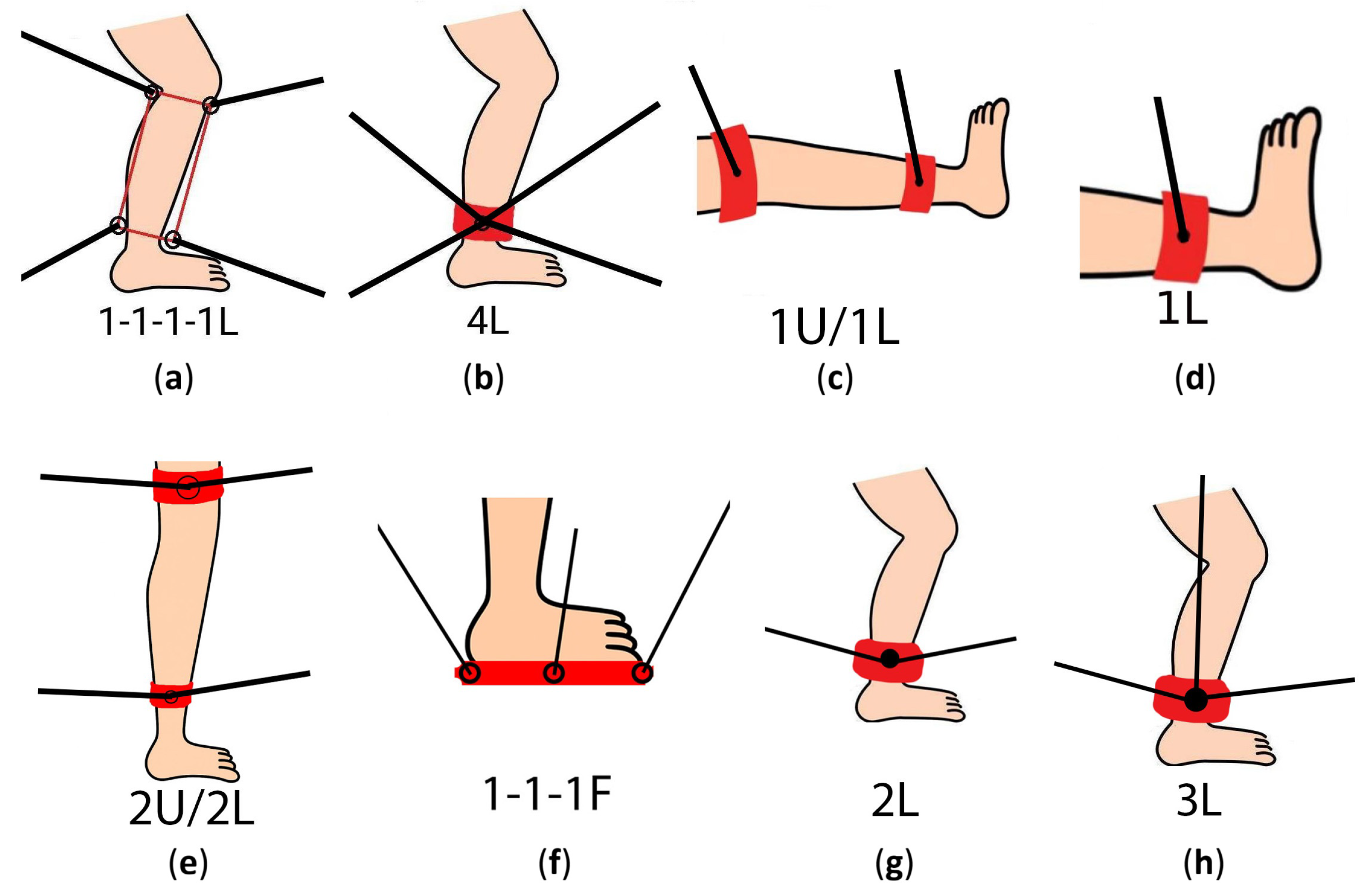
5.1. 1-1-1-1L Platform

Two implementations of the 1-1-1-1L (Figure 4a) in CDEGR were found, one by Qin et al. [56] and Zou et al. [57]. In both cases, the control strategies are based on PID approaches, either in composite form or augmented with feedforward and phase-lead compensation. Although these offer basic tracking capabilities, they depend on fixed parameters and lack the adaptability required to respond to patient-specific dynamics, external disturbances, and variations in cable tension. To overcome these shortcomings, future implementations should explore more advanced control strategies, such as impedance control or SMC. Furthermore, the absence of integrated sensors (cable tension sensors, force sensors, IMUs, or EMG) limits real-time feedback and restricts the system’s ability to provide intention-aware or assist-as-needed guidance [85]. Another fundamental constraint is purely planar actuation: because motion is confined to the sagittal plane, the robot cannot detect or correct out-of-plane deviations due to hip abduction, pelvic rotation, or misalignment of the limb. These limitations highlight the need for future developments that incorporate multimodal sensing, adaptive and model-informed control strategies, and robust 3D tracking to ensure safe, personalized, and effective rehabilitation.

5.2. 4L Platform

The 4L platform (Figure 4b) is a CDEGR system composed of four cables typically attached to the ankle. Unlike the 1-1-1-1L configuration, which enables full 3T1R control, the 4L platform sacrifices rotational mobility to control only the three translational DoFs. This simplification results in a kinematically over-constrained system that offers improved stability, enhanced force controllability, and the potential for a larger workspace. In addition, by properly orienting the cable attachment points, the system can selectively counteract disturbances in the sagittal plane.

Various control strategies have been proposed for this platform. One study introduced a compound controller that combines integral feedback, phase-lead compensation, and feedforward control, achieving accurate force tracking in both passive and active modes. However, its reliance on a linear actuator model and the absence of testing with human subjects limit its clinical applicability [59]. Another approach used a FSMVA guided by a safety index $S_{\mathrm{index}}$, which dynamically adjusts impedance parameters based on real-time evaluations of cable tension distribution, the geometry of the workspace, and the velocity of the end effector. Although mathematically robust, this method has not yet been validated with human subjects [76]. A common limitation of CDEGRs is the pseudo-drag phenomenon, where slack or low tension leads to unsafe or inaccurate movement of the limb. To address this, the authors proposed a novel bionic muscle cable that incorporates an elastic element in parallel with the driving cable, inspired by the Hill muscle model. This design ensures continuous tension, improving safety and motion stability without relying solely on complex control strategies [79]. Finally, a cable-driven platform combined impedance control with a kinetic compensation layer that provided phase-specific support computed from inverse dynamics. Although force tracking was accurate (root-mean-square error (RMS) ≈ 6.4 N), the user exhibited reduced muscle activity in the lower limb under kinetic compensation, as indicated by an EMG analysis during the experiment. Besides, the system exhibited inaccuracies due to medial-lateral leg movements or slight cuff shifts. However, the platform appears to be well suited for mid-stage gait rehabilitation. As in previous studies, validation was limited to a single unimpaired subject [80].

5.3. 1U/1L Platform

The 4L CDEGR system (see Figure 4c) is a 2-DoF bedside rehabilitation platform designed to facilitate supine stepping exercises for early-stage lower limb rehabilitation. To date, the only reported implementation of this specific architecture is the AirStep platform detailed in [81].

The AirStep platform utilizes two cables per leg connected via adjustable pulleys and mass-spring counterbalancing mechanisms to minimize gravitational effort during motion. Its mechanical simplicity, low cost (~$3000), and portability make it suitable for bedside use in early-stage rehabilitation. The device allows for three operational modes: (i) passive counterbalance mode, (ii) therapist-assisted mode, and (iii) motor-assisted mode using a single servo motor for bilateral hip motion.

From a control perspective, the system is based on an analytical kinematic and kinetostatic model. Hip trajectories are tracked via a PD controller, using reference trajectories generated from cubic-spline interpolation of motion capture (MoCap) data. Although only the hip joint is actively actuated, the knee motion is supported by weight compensation without direct actuation. The overall control strategy is semiactive, lacking adaptive or impedance-based feedback.

Kinematic validation using MoCap showed strong agreement between the sagittal plane and 3D joint angles, with RMS errors of 3.2° for the hip and 4.6° for the knee. Cable length estimates were accurate within a 1–2% relative error. Kinetostatic validation demonstrated near-zero required assistance forces in healthy subjects, confirming effective gravitational compensation. Minor discrepancies were attributed to unmodeled friction and imperfections in cable routing.

AirStep’s capabilities were evaluated through both laboratory tests and pilot clinical trials. Tests with healthy subjects revealed gait trajectories that resemble running patterns, with symmetric stance/swing phases (52/48%). Pilot testing with two individuals with SCI confirmed the feasibility, showing an increased range of motion when motor assistance was combined with spinal cord stimulation and foot vibration. Although the evaluation remains preliminary, the results support the potential of the device for personalized, low-cost, and scalable early-stage gait therapy.

5.4. 1L Platform

The 1L CDEGR, as illustrated in Figure 4d, is a 1-DoF assistive device developed to support straight leg raise exercises for lower limb rehabilitation. The only implementation of this architecture has been reported in [61]. The actuation system is based on a wire-driven Series Elastic Actuator (SEA), which integrates a compact planetary gearbox with an inline elastic spring to estimate cable tension. The interaction force is measured indirectly through spring deformation, which is captured by a high-resolution encoder. This eliminates the need for external force sensors and minimizes system complexity.

The SEA is capable of delivering up to 1.7 Nm of assistive torque (assuming a leg weight of 5 kg)—sufficient to overcome the gravitational load of an average adult leg while maintaining a force resolution of 1 g and a control bandwidth of 20 Hz. According to the authors, this bandwidth is adequate for typical human limb dynamics, as it allows the system to maintain high linearity in force measurement. However, this performance may be affected by the gear ratio [86].

The control strategy incorporates a human force observer to estimate the torque exerted by the patient in real time, and a human work observer to quantify mechanical work as an indicator of rehabilitation effort. The assist torque is dynamically adjusted according to the patient’s capacity and is applied through a robust control loop that includes a disturbance observer and PD-based feedback control. The disturbance observer compares the expected actuator behavior based on the model with actual sensor readings to infer disturbances.

Despite its effective implementation and portability, the device is limited to unidirectional actuation and a single DoF, restricting its use to simple flexion-extension tasks. In addition, experimental validation remains preliminary, and no trials have been conducted in clinical patients. Future work should evaluate its long-term therapeutic benefits through well-designed clinical protocols.

5.5. 2U/2L Platform

The 2U2L platform is illustrated in Figure 4e. In reported applications, it consists of four wire-driving modules mounted in a planar configuration above a treadmill. The system is designed to support various rehabilitation modes: passive, active, and assist-as-needed.

Two control approaches have been implemented and evaluated on this platform. Both strategies employ PID-based architectures enhanced with feedforward compensation. One study proposed a multiloop force control architecture that integrates integral, phase-lead, and velocity feedforward components, along with a surplus force compensator based on the structural invariance principle [82]. This principle functions as a feedforward mechanism to suppress disturbances arising from the voluntary movement of the limbs, achieving surplus force reductions that exceed 90% for sinusoidal inputs up to 3 Hz at a speed of 0.3 m/s. The second approach focused on simulation-assisted controller tuning and frequency domain design, achieving mean force-tracking errors below 10% during walking at 0.2 m/s. The authors report that the inclusion of a velocity-feedforward lead compensator in this implementation not only improved tracking accuracy but the user comfort [58]. In particular, only this latter strategy was tested with real patients, underscoring its potential for clinical application.

Despite its strengths, several limitations have been identified. Principally, unilateral cable configuration causes off-sagittal loading, which can introduce lateral force components and cause discomfort, particularly at the cuff interface. In addition, the platform has not yet been validated under realistic, irregular limb trajectories, and its effective workspace has not yet been fully characterized. Future research should enhance biomechanical adaptability by adding an additional cable to improve force vector alignment and control redundancy.

5.6. 1-1-1F

The 1-1-1F configuration is composed of three cables that move a 6-DoF footplate, making the system under-constrained (see Figure 4f). The only known physical implementation of this platform is presented by Wang et al. [44].

Although the study does not implement a formal control strategy, the authors validate through simulation and experimental testing that the platform can generate the required torques at given spatial positions and along predefined trajectories. Validation relies on dynamic equilibrium analysis, and disturbances are introduced using external weights to evaluate the stability of the system.

The prototype occupies a large physical space, with the fixed pulley anchor points located approximately 2 m apart. This footprint makes the platform impractical for typical clinical or home settings. Furthermore, due to the under-constrained nature of the system, the robot’s performance is highly dependent on the mass and inertia of the patient’s leg, which can significantly affect both the reachable workspace and the dynamical stability.

Despite these limitations, the 1-1-1F system stands out as the only known cable-driven platform specifically designed to actuate the foot. This is particularly interesting for achieving more localized and detailed rehabilitation interventions, such as ankle mobility restoration or balance control training. For broader applications or more demanding dynamic scenarios, it is plausible that future implementations will require additional cables attached directly to the foot to improve control precision, robustness, and safety.

5.7. 2L Platform

To our knowledge, the ROMRES platform is the only reported example of a 2L CDEGR (see Figure 4g). In this configuration, a single-limb segment is actuated around 1-DoF using just two cables attached to vertically movable pulleys (elevators) on either side. This arrangement maintains the directionality of the applied force and the mechanical advantage throughout the entire range of motion, achieving bidirectional actuation and flexibility in the workspace without requiring additional cables or complex routing [65].

The control strategy is centered around impedance control, enabling compliant interaction through state-dependent virtual stiffness and damping parameters. A state machine governs transitions between passive, active-assisted, and spasticity exercise modes based on real-time measurements of joint angles and interaction forces. In particular, spasticity is detected when the robot attempts to move the limb in a given direction but encounters a sustained high-magnitude force in the opposite direction, typically exceeding a preset threshold. This condition is interpreted as velocity-dependent involuntary resistance, which causes the robot to reverse its movement direction to align with the patient’s muscle response and prevent discomfort [65].

Additional control layers include PD controllers for elevator positioning, a cable tension controller to avoid slack, and a disturbance observer to mitigate friction and improve force sensitivity. The disturbance observer estimates the difference between the actual motor torque and the ideal torque predicted by a simplified dynamic model based on pulley inertia and angular acceleration. By calculating the residual torque and applying a compensating control signal, the system achieves improved tracking accuracy, particularly in low-torque scenarios [65].

Experimental validation with a motorized dummy arm and a healthy human subject demonstrated effective tracking of joint trajectories and accurate detection of user-applied forces, with successful transitions between rehabilitation modes. However, limitations such as the 1-DoF planar assumption, the dependence on noisy Micro-Electro-Mechanical System (MEMS) accelerometer sensors, and the absence of tests with neurologically impaired patients suggest the need for further clinical validation. However, ROMRES represents a promising and practical solution for multi-joint rehabilitation, emphasizing adaptability, ease of use, and responsive control.

5.8. 3L Platform

The 3L CDEGR, illustrated in Figure 4h, is designed to operate in a supine configuration. In this architecture, one cable is typically fixed while the other two are mounted on motorized pulley units equipped with adjustable APPs, enabling the robot to adapt its geometry in response to changing task demands and cable tension directions. Zhang et al. [83] developed a platform with servo-driven APPs to improve workspace coverage and optimize tension routing. Their system employed a feedforward trajectory planning strategy that combined a quintic polynomial with an adaptive S-shaped velocity profile. Two performance metrics were introduced: the trajectory smoothness index ($S_1$), based on the integrated squared jerk, and the energy consumption index ($S_2$), based on the square of the accelerations of the routing cable. Lower values of these indices correspond to smoother motion and reduced actuator effort. In experimental trials, the hybrid planning method achieved the best performance among the strategies tested, with $S_1=5.83$ and $S_2=27.89$. However, the system relied entirely on open loop control, using only encoder-derived cable lengths, with no active cable tension control or feedback. Although validated on a healthy subject, issues such as signal jitter and pulley slippage affected performance, and the lack of compliance modeling or real-time adaptation limits its clinical applicability.

Wang et al. [84], who developed another 3L CDEGR platform, proposed a related approach. In this work, two rigid chain motion planning strategies were introduced and evaluated using a dynamic stability index that incorporates cable tension uniformity, stiffness analysis, and velocity smoothness. Although the study provides a thorough mechanical analysis and includes an experimental evaluation under artificial loads and disturbances, it is based on open-loop control and does not involve testing with human subjects. Real-time adaptation, patient feedback, and physiological variability are not addressed, which limits the practical safety and effectiveness of the system. Despite these limitations, both the 3L CDEGRs platforms contribute valuable insights into the design space of cable-driven rehabilitation robots, serving as testbeds for evaluating planning strategies and performance metrics such as $S_1$, $S_2$, and stability indices under different configurations.

6. Discussion

A comparative overview of CDEGRs is provided in

Table 4. Advantages and disadvantages of CDEGR moving platforms: Workspace and Complexity.

Platform	Workspace	Complexity
1-1-1-1L	Adv.: Simple sagittal-plane motion. Disadv.: No out-of-plane control.	Adv.: Very low mechanical and control complexity. Disadv.: PID only, limited sensing.
4L	Adv.: 3D translational control, larger workspace. Disadv.: No rotational DOF.	Adv.: Supports advanced control, improved stability. Disadv.: Over-constrained, needs tension management.
1U/1L	Adv.: Enables supine stepping, hip–knee sagittal range. Disadv.: Workspace confined to early-stage exercises.	Adv.: Low-cost, portable system. Disadv.: Semi-active, lacks adaptive control.
1L	Adv.: Suitable for flexion– extension tasks. Disadv.: Single DOF only.	Adv.: Simple design with SEA sensing. Disadv.: Limited versatility.
2U/2L	Adv.: Bilateral workspace coverage. Disadv.: Off-sagittal discomfort.	Adv.: Allows advanced force control. Disadv.: Complex tuning, unilateral configuration.
1-1-1F	Adv.: Direct foot actuation. Disadv.: Under-constrained, large footprint.	Adv.: Unique focus on distal segment. Disadv.: High sensitivity to leg inertia.
2L	Adv.: Bidirectional actuation with 2 cables. Disadv.: Limited to 1-DOF planar tasks.	Adv.: Simple yet flexible (movable pulleys). Disadv.: Dependent on noisy MEMS sensors.
3L	Adv.: Configurable geometry, adaptable workspace. Disadv.: lack of compliance modeling limits applicability.	Adv.: Good testbed for planning/control studies. Disadv.: Pulley slippage, limited robustness.

and

Table 5. Advantages and disadvantages of CDEGR moving platforms: Medical proficiency.

Platform	Medical Proficiency
1-1-1-1L	Adv.: Low cost, early-stage trials. Disadv.: Narrow therapeutic scope.
4L	Adv.: Promising for mid-stage rehab. Disadv.: slight cuff shifts limited the accuracy.
1U/1L	Adv.: Pilot trials show feasibility. Disadv.: No advanced gait correction.
1L	Adv.: Portable, individualized training. Disadv.: No patient trials yet.
2U/2L	Adv.: Tested with patients in walking tasks. Disadv.: Irregular gait trajectories may limits its implementation.
1-1-1F	Adv.: Potential for localized rehab (ankle, foot). Disadv.: No clinical feasibility demonstrated.
2L	Adv.: Adaptive impedance useful for spasticity detection. Disadv.: Only validated in healthy/dummy trials.
3L	Adv.: Smooth trajectories in healthy users. Disadv.: No patient validation yet.

. Table 4 presents a comparison of platforms in terms of workspace and complexity, while Table 5 focuses on medical proficiency. The following subsections synthesize these findings.

6.1. Workspace Versus Complexity

As summarized in Table 4, the simplest platforms (1-1-1-1L and 1L) operate with reduced workspace but minimal mechanical and computational complexity. Their planar or single-DoF designs are straightforward to implement and cost-effective, making them attractive for proof-of-concept studies or early-stage rehabilitation. However, their inability to address out-of-plane deviations restricts their usefulness in realistic gait training. By contrast, more advanced systems (4L and 2U/2L) expand the feasible workspace to three translational DoFs and improve force controllability. Yet, this increase in workspace coverage introduces greater complexity in cable routing, redundancy management, and control design. These comparisons indicate that achieving larger workspaces often comes at the cost of mechanical and computational simplicity.

6.2. Adaptability and Control Strategies

Table 4 also shows that most early configurations rely on PID controllers with fixed gains, thus limiting their adaptability to patient-specific variability. In contrast, redundant platforms such as the 4L, 2U/2L, and 2L systems support more sophisticated control schemes, including impedance or sliding mode control. These strategies improve compliance, safety, and adaptability during assist-as-needed therapy, but they require precise sensing and careful tuning. The lack of multimodal integration (e.g., EMG or inertial sensors) remains a bottleneck for intention-aware control. Therefore, while complex platforms are technically capable of adaptive rehabilitation, their potential has not yet been fully realized in practice.

6.3. Clinical Proficiency and Translation

From the medical perspective summarized in Table 5, most systems have only been tested with healthy users or mechanical dummies. Only the 2U/2L platform has progressed to partial patient validation, and even in this case, adaptability to irregular gait remains limited. Unique designs such as the 1-1-1F, which targets the foot, or the 3L, which offers reconfigurable geometries, contribute important insights but lack clinical demonstration. This gap emphasizes the need for structured validation pipelines, moving from healthy-subject trials to patient studies and eventually to long-term clinical assessments. Without such evidence, technical advances in workspaces or control strategies cannot be translated into therapeutic benefits.

6.4. Future Directions

The synthesis across Table 4 and Table 5 suggests several priorities for future work. First, reconfigurable anchor points or mobile pulleys could expand the functional workspace without exacerbating redundancy management. Second, adaptive controllers must be supported by multimodal sensing to provide intention-aware and patient-specific assistance. Third, designs must balance simplicity and affordability with sufficient functionality to be clinically meaningful, especially in low-resource settings. Finally, standardized protocols for evaluating CDEGR platforms are urgently needed to enable consistent comparison and accelerate clinical translation.

In summary, simplicity ensures feasibility and safety; however, the long-term clinical impact will depend on integrating advanced control and sensing into scalable designs validated in patients.

7. Conclusions

This review examined the state of the art in CDEGRs, with a focus on their design architectures, control strategies, redundancy configurations, and clinical validation. Although numerous platforms have been proposed and tested on mechanical dummies or healthy users, only one system has been successfully evaluated in clinical subjects. This platform—characterized by a low number of DoF and a simple configuration—illustrates a key insight: simplicity remains a critical enabler of safety and feasibility in real-world rehabilitation.

The main challenge of CDEGRs lies in their mechanical and computational complexity. Unlike rigid-link robots, cable-driven systems must deal with multiple nonlinearities, including cable elasticity, sagging, hysteresis, and singularities. These factors require precise models and sophisticated real-time control, which can significantly increase the cost of the platform. Most systems rely on PID control schemes, which are inadequate for tasks requiring adaptive or intention-aware behavior. One area for improvement is the communication infrastructure: no studies report using high-performance fieldbus systems, such as EtherCAT. While EtherCAT enables high-speed control loops and deterministic communication, it often requires a C++ implementation and deeper embedded integration, thereby increasing overall system complexity and development costs.

Another limitation is the workspace. Many CDEGRs operate within constrained sagittal-plane regions and are limited in their ability to accommodate full gait trajectories, particularly in the late stages of rehabilitation. Increasing the number of cables to expand the workspace introduces the risk of cable interference and complexity in redundancy management. To address this, we believe that mobile pulleys represent a promising direction, as they allow dynamic reconfiguration of anchor points without adding cables, thereby enhancing workspace coverage while minimizing interference.

Finally, the limited ability of current systems to provide smooth and stable transitions throughout rehabilitation stages remains a barrier to clinical translation. Most platforms are designed with a fixed control paradigm and struggle to adapt dynamically to the evolving needs of the patient.