A Control System Design and Implementation for Autonomous Quadrotors with Real-Time Re-Planning Capability

Abstract

Real-time (re-)planning is crucial for autonomous quadrotors to navigate in uncertain environments where obstacles may be detected and trajectory plans must be adjusted on-the-fly to avoid collision. In this paper, we present a control system design for autonomous quadrotors that has real-time re-planning capability, including the hardware pipeline for the hardware–software integration to realize the proposed real-time re-planning algorithm. The framework is based on a modified version of the PX4 Autopilot and a Raspberry Pi 5 companion computer. The planning algorithm utilizes minimum-snap trajectory generation, taking advantage of the differential flatness property of quadrotors, to realize computationally light, real-time re-planning using an onboard computer. We first verify the control system and the planning algorithm through simulation experiments, followed by implementing and demonstrating the system on hardware using a quadcopter.

1. Introduction

The advent of quad- and multi-rotor vehicles, including electric Vertical Take-Off and Landing (eVTOL) aircraft, has drastically impacted the landscape of aerial mobility [1]. These versatile vehicles are increasingly employed in various domains, ranging from recreational activities and commercial delivery services to critical applications in search and rescue operations and for urban air mobility [2]. The distinctive capabilities of quadrotors and eVTOLs, such as vertical takeoff, hovering, and precise maneuverability, position them as pivotal components in the future of aerial transportation and logistics. However, maximizing their potential requires advanced and robust control systems, with real-time trajectory optimization and (re-)planning remaining paramount challenges [3].

Control and real-time trajectory planning methods have been gaining extensive interest as the rapid advancement of sensing and computing technologies is making data and computational resources increasingly accessible [4]. Real-time trajectory optimization is crucial to ensuring the safe and efficient operation of these aerial vehicles [5] and for planetary exploration [6]. Unlike traditional fixed-wing aircraft [7], quad- and multi-rotor vehicles must constantly adjust their flight paths to maintain stability and respond to dynamic environmental conditions [8]. This demands an advanced level of computational power and intelligent algorithms capable of processing myriad inputs in real-time. Factors such as wind speed [9], presence of obstacles, payload variations, and energy consumption need to be continuously evaluated to optimize the flight trajectory for safety, efficiency, and mission success [10]. Moreover, for UAV applications, there is a clear desire to push for higher degrees of autonomy that allow automated decision-making and adaptability in fast-paced environments, where reaction time becomes critical. As several researchers have already demonstrated [11,12], online trajectory planning and optimization for quadrotor UAVs is not only feasible but is required for operating large fleets of these vehicles, especially in uncertain environments where the mission profile must evolve as more information is collected during the flights.

A critical component enabling UAS autonomy and collision avoidance is navigation and perception [13,14]. Although these topics are not covered in this work, they are paramount to the success of any autonomous vehicle and are separate research fields on their own. The complexity of real-time trajectory optimization lies in its requirement to balance multiple objectives while adhering to the physical and operational constraints of the vehicle [15]. For instance, eVTOL aircraft, designed for urban air mobility, must navigate through densely populated areas, requiring precise control to avoid collisions and minimize noise pollution [16]. These vehicles often operate on limited battery power, making their energy efficiency a critical design factor [17]. Real-time optimization algorithms must, therefore, integrate advanced techniques from control theory and sensor fusion to adapt to ever-changing conditions and ensure optimal performance [18].

Many researchers have studied collision-free trajectory optimization problems. A two-step online trajectory planning framework for a quadrotor in indoor environments with obstacles is given in [19]. The framework in [19] relies on the differential flatness property of quadrotors, employs RRT* and Line-of-Sight (LOS) algorithms to obtain the initial set of collision-free waypoints, and reduces the size of the input dataset used for trajectory optimization, but it does not consider solving optimal time-allocation problems. Time-optimal planning for an agile quadrotor flight with model predictive contouring control and moving obstacles was investigated in [20]. Receding-horizon lattice-based motion planning with dynamic obstacle avoidance was investigated in [21]. A trajectory optimization and replanning framework for a micro air vehicle in cluttered environments was proposed in [22]. The boundary-RRT* algorithm for drone collision avoidance and interleaved path re-planning was presented in [23].

This research provides further insight into the feasibility and benefits of full trajectory replanning. More specifically, the contributions of this paper are as follows:

1.

We consider differential flatness-based minimum-snap trajectory optimization with a time-allocation optimization step for obtaining the initial solution and global online fixed-time, on-demand replanning for obstacle avoidance.

2.

We integrate the full-state feed-forward generated from the reference trajectory with the feedback control. This kinematics-based full-state (including attitude and torque) feedforward is generated directly from the reference minimum-snap trajectory, thus reducing the required control effort. More importantly, this feature is integrated within the PX4 Autopilot.

3.

We report our test results in a high-fidelity simulation environment. The results demonstrate the ability of the proposed replanning framework to successfully avoid previously unknown obstacles by re-generating a new mission profile in an automated manner.

4.

We also provide a hardware pipeline integration overview (using a modified version of the PX4 Autopilot and a Raspberry Pi5 companion computer) and algorithm implementation details. We demonstrate successful collision avoidance in hardware flight experiments using a custom-built quadrotor in our indoor flight test facility.

The paper is organized as follows. Section 2 briefly reviews the vehicle dynamics, control system architecture, trajectory optimization method, and the proposed online replanning strategy. This section also outlines the key elements required for hardware integration and implementation of the proposed real-time replanning method. Section 3 is divided into two parts: Section 3.1 describes the simulation results obtained using a 6-DOF non-linear quadrotor model; Section 3.2 reports the results of the flight test using the methods outlined in Section 2 and implemented on the actual hardware. Section 4 concludes the paper.

2. Methods

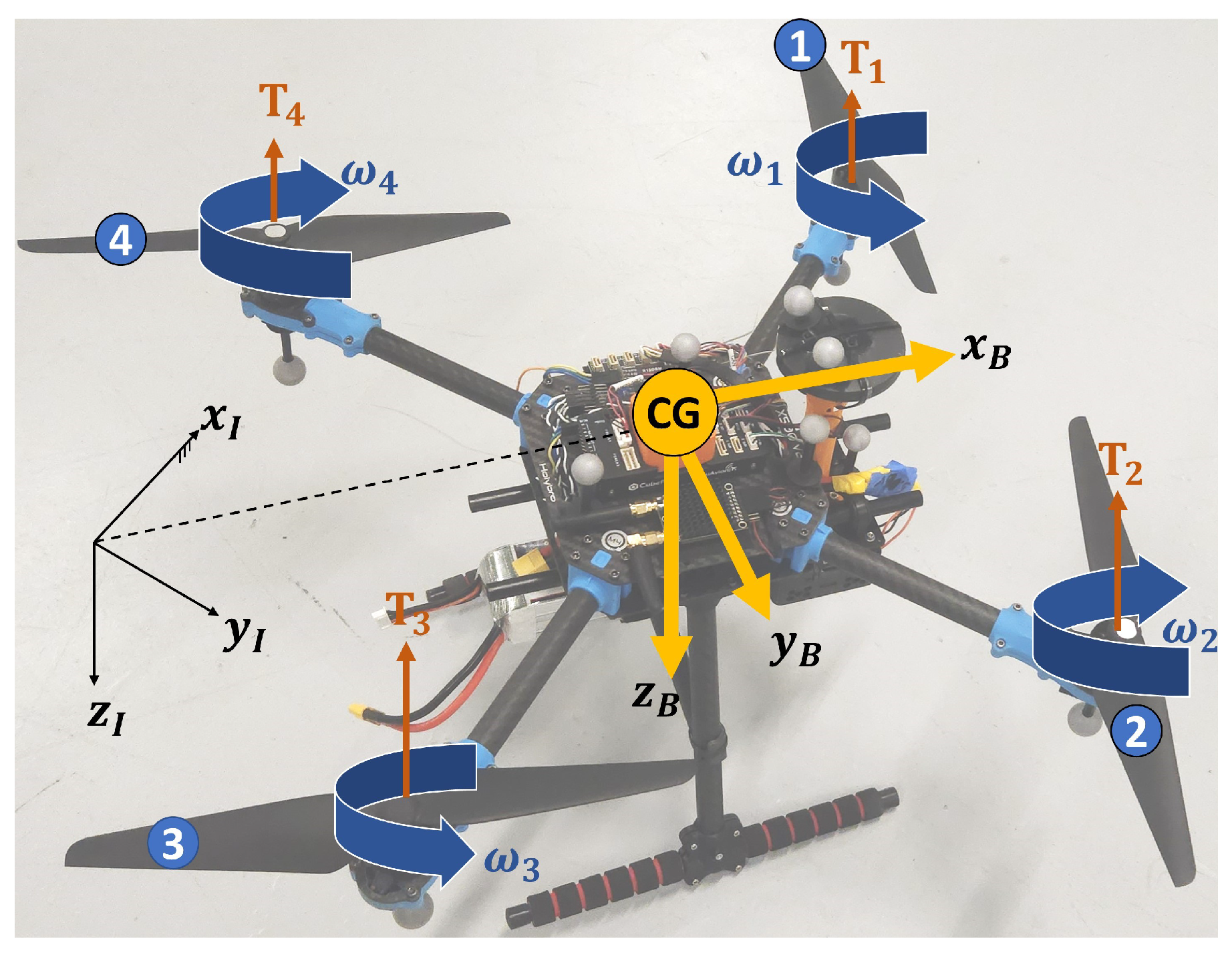
2.1. Vehicle Dynamics

We consider a standard ‘✕’ frame configuration quadrotor under rigid-body dynamics. Let the position and velocity vectors of the center of mass of the body frame relative to the inertial frame (subscript ‘I’) be ${\mathit{R}}_I={[x,y,z]}^{\top }$, ${\mathit{V}}_I={[v_x,v_y,v_z]}^{\top }$, respectively. The angular velocity vector of the body frame relative to the inertial frame (when expressed in the body frame) is defined as $\mathrm{\Omega }={[p,q,r]}^{\top }$. The attitude of the vehicle is expressed using quaternion as $\mathit{q}={[q_0,q_1,q_2,q_3]}^{\top }$, with $q_0$ denoting the scalar component [24]. For some intermediate calculations and visualizations, the attitude is represented with the ‘3-2-1’ Euler angle sequence, which is defined by three sequential rotations about the orthogonal axes of the body frame $\mathrm{\Theta }={[\varphi ,\theta ,\psi ]}^{\top }$. Euler angles denote rotation about the body $x_B$ axis (with roll angle $\varphi$), $y_B$ axis (with pitch angle $\theta$) and $z_B$ axis (with yaw angle $\psi$) [9].

Figure 1 shows the schematics of the quadrotor, the definitions of the frames of references and the positive sense of rotation of the propellers. The numbering convention starts at 1, from the left-front motor, and increments by 1 in a clockwise manner. Let the state vector be ${\mathit{X}}^{\top }=[{\mathit{R}}_I^{\top },{\mathit{V}}_I^{\top },{\mathit{q}}^{\top },{\mathrm{\Omega }}^{\top }]$. The Six-Degree-of-Freedom (6DoF) rigid-body dynamics can be written as [24]

$${\dot{\mathit{R}}}_I={\mathit{V}}_I,{\dot{\mathit{V}}}_I={\displaystyle \frac{1}{m}}\left({\mathit{F}}_g+R_{\mathrm{B}2\mathrm{I}}\left(\mathit{q}\right)\left(\mathit{T}+{\mathit{F}}_{\mathrm{aero}}\right)\right),$$

(1)

$$\dot{\mathrm{\Omega }}=I_B^{-1}\left(-\mathrm{\Omega }\times I_B\mathrm{\Omega }-{\mathit{M}}_{\mathrm{gyro}}+\mathit{M}\right),$$

(2)

$$\dot{\mathit{q}}={\displaystyle \frac{1}{2}}{\omega }_{\mathrm{sq}}\mathit{q},$$

(3)

$${\omega }_{\mathrm{sq}}=\left[\begin{array}{cccc}0& -p& -q& -r\\ p& 0& r& -q\\ q& -r& 0& p\\ r& q& -p& 0\end{array}\right],$$

(4)

$$R_{\mathrm{B}2\mathrm{I}}\left(\mathit{q}\right)=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& q_0^2-q_1^2+q_2^2-q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_0{q}_1)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right],$$

(5)

where m is the constant total mass of the vehicle, g is gravitational acceleration, ${\mathit{F}}_g={[0,0,mg]}^{\top }$ denotes the gravitational force, $R_{\mathrm{B}2\mathrm{I}}\left(\mathit{q}\right)$ is the transformation matrix from the body frame to the inertial frame. The constant moment of the inertia matrix of the vehicle is denoted as $I_B$. In Equation (2), $\mathit{M}\in {\mathbb{R}}^3$ denotes the control torque vector produced by the propellers given in Equation (11). Total thrust, $\mathit{T}\in {\mathbb{R}}^3$, is expressed as

$$\mathit{T}=\left(\sum _{i=1}^4{T}_i\right)\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]=b\left(\sum _{i=1}^4{\omega }_i^2\right)\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right],$$

(6)

where thrust output of each propeller, $T_{\mathrm{i}}$, is related to the square of the motor angular velocity, ${\omega }_i$, by a constant coefficient, b, and is written as

$$T_{\mathrm{i}}=b{\omega }_i^2,\mathrm{for}i=1,\cdots ,4.$$

(7)

It is assumed that all motors have the same performance. The total moment of inertia of the rotary part of the electric motor, with the propeller attached to it, is denoted as $I_r$, and the gyroscopic torque, ${\mathit{M}}_{\mathrm{gyro}}$, due to all motors, is expressed as

$${\mathit{M}}_{\mathrm{gyro}}=\sum _{i=1}^4\left(\mathrm{\Omega }\times \left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\right)I_r{\omega }_i{(-1)}^i.$$

(8)

The aerodynamic forces and torques due to wind and turbulence were modeled as

$${\mathit{F}}_{\mathrm{aero}}=C{T}_z{\mathit{V}}_{\mathrm{rel}}\mathrm{with}C={\left[\begin{array}{ccc}0.04& 0.04& 0.0\end{array}\right]}^{\top },$$

(9)

where $T_z$ is the thrust component along the body-fixed z-axis [9]. Note that $T_z$ is negative by the definition (see Equation (12)), which results in a negative aerodynamic force consistent with the drag force.

The relative velocity of the vehicle was calculated as ${\mathit{V}}_{\mathrm{rel}}={\mathit{V}}_B-{\mathit{V}}_{\mathrm{wind}}$, where velocity expressed in the body frame is defined as ${\mathbf{V}}_B=R_{\mathrm{B}2\mathrm{I}}^{\top }{\mathbf{V}}_I$, and the wind velocity is denoted as ${\mathbf{V}}_{\mathrm{wind}}$, which is mapped into the body frame. The wind velocity is modeled using a combination of the Dryden wind turbulence model [25], the wind shear model and the horizontal wind model, all readily available in the Simulink^® Aerospace Toolbox. All simulations assume 1 m/s reference wind speed at 6 m altitude, coming ${38}^{\circ }$ from north. Wind speed at different altitudes is assumed to increase up to 3 m/s. It is assumed that wind changes its direction to ${55}^{\circ }$ from north. However, all simulations assume low-altitude flight (below 3 m). The discrete Dryden wind turbulence model (MIL-F-8785C) assumes a 100 m scale length for medium (and high) altitudes and $0.3$ m and $0.1$ s for reference wing span and discrete filter sample rate. We also used the following noise seed for turbulence generation: [23,341; 23,342; 23,343; 23,344], which allows for reproducing the simulation results reported in Section 3.

Reactive torque due to each electric motor and its propeller is related to the square of the speed of rotation, with a constant coefficient k, and is expressed as

$$Q_i=k{\omega }_i^2,\mathrm{for}i=1,\cdots ,4.$$

(10)

Let h and l denote the roll and pitch moment arms, respectively. The total torque vector due to propellers can be written as

$$\begin{array}{c}\hfill \mathit{M}=\left[\begin{array}{c}{M}_x\\ M_y\\ M_z\end{array}\right]=\left[\begin{array}{c}bh(-{\omega }_1^2-{\omega }_2^2+{\omega }_3^2+{\omega }_4^2)\\ bl({\omega }_1^2-{\omega }_2^2-{\omega }_3^2+{\omega }_4^2)\\ k({\omega }_1^2-{\omega }_2^2+{\omega }_3^2-{\omega }_4^2)\end{array}\right].\end{array}$$

(11)

Combining Equations (6) and (11) defines the control vector, $\mathit{U}$, which can be written as

$$\mathit{U}=\left[\begin{array}{c}{T}_z\\ M_x\\ M_y\\ M_z\end{array}\right]=\left[\begin{array}{cccc}-b& -b& -b& -b\\ -bh& -bh& bh& bh\\ bl& -bl& -bl& bl\\ k& -k& k& -k\end{array}\right]\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right].$$

(12)

The motor dynamics are modeled using a first-order low-pass filter with a time constant of $0.05$ s. No additional disturbances or uncertainty (due to sensor noise) have been considered at this stage. The vehicle model has been simulated using Matlab^® and Simulink^® (R2023a) using a fixed-time-step Rk4 integration scheme (update rate is 200 Hz).

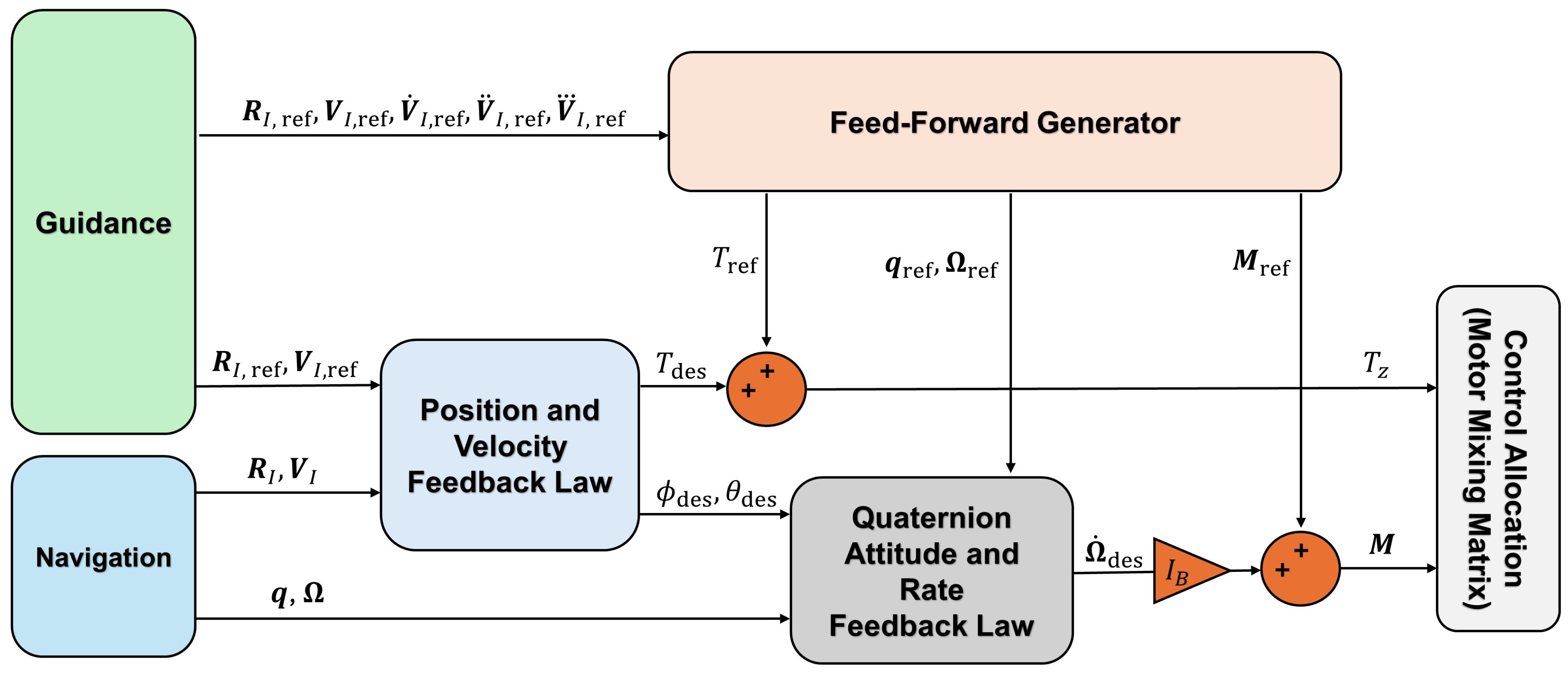
2.2. Control System Architecture

The flight control system of the quadrotor is based on a classical cascaded structure, with rotational and translational motion feedback loops [26].

Let $\mathrm{\Delta }\left(·\right)$ denote the tracking error between the state and the reference (e.g., $\mathrm{\Delta }{\mathit{R}}_I={\mathit{R}}_{I,\mathrm{ref}}-{\mathit{R}}_I$). The feedback control law for the translational motion is defined as

$$\begin{array}{cc}\hfill {\overline{\mathit{U}}}_I& ={\mathbb{P}}_P\mathrm{\Delta }{\mathit{R}}_I+{\mathbb{P}}_D{\displaystyle \frac{d}{dt}}\left(\mathrm{\Delta }{\mathit{R}}_I\right)+{\mathbb{P}}_I{\int }_{t_0}^{t_f}\mathrm{\Delta }{\mathit{R}}_{I}dt,\hfill \\ \hfill T_{\mathrm{des}}& =m{\overline{\mathit{U}}}_I^{\top }{R}_{B2I}^{\top }{[0,0,-1]}^{\top },\hfill \end{array}$$

(13)

where ${\overline{\mathit{U}}}_I$ is a virtual control vector, and $T_{\mathrm{des}}$ is the desired thrust, which is calculated as a vertical component of the virtual control vector and scaled by mass, m. In Equation (13), ${\mathbb{P}}_P$, ${\mathbb{P}}_D$ and ${\mathbb{P}}_I$ are 3 by 3 diagonal gain matrices. We can define the desired attitude using the first two components of the virtual control vector, reference roll, ${\varphi }_{\mathrm{ref}}$, and pitch, ${\theta }_{\mathrm{ref}}$, as

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{des}}={\varphi }_{\mathrm{ref}}+[-{\overline{\mathit{U}}}_x,{\overline{\mathit{U}}}_y,0]R_{B2I}^{\top }{[1,0,0]}^{\top },\\ \hfill {\theta }_{\mathrm{des}}={\theta }_{\mathrm{ref}}+[-{\overline{\mathit{U}}}_x,{\overline{\mathit{U}}}_y,0]R_{B2I}^{\top }{[0,1,0]}^{\top },\end{array}$$

(14)

which defines the desired roll and pitch Euler angles as a combination of the reference roll, pitch, and feedback from the translational controller. To calculate the attitude feedback error, we consider two components. First, we define a desired tilt-angle quaternion representation, ${\mathit{q}}_{\varphi ,\theta }$, using the desired roll, desired pitch, and the current heading angle. The desired heading quaternion, ${\mathit{q}}_{\psi }$ is obtained from the reference heading angle, current roll, and pitch angles. Next, the attitude error is calculated as:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{\mathit{q}}_{\varphi ,\theta }& ={\mathit{q}}^{-1}\otimes {\mathit{q}}_{\varphi ,\theta }\mathrm{\Delta }{\mathit{q}}_{\psi }={\mathit{q}}^{-1}\otimes {\mathit{q}}_{\psi },\hfill \\ \hfill \mathrm{\Delta }\mathit{q}& =\pm \sqrt{\left({\left[[0,1,0,0]\mathrm{\Delta }{\mathit{q}}_{\varphi ,\theta },[0,0,1,0]\mathrm{\Delta }{\mathit{q}}_{\varphi ,\theta },[0,0,0,1]\mathrm{\Delta }{\mathit{q}}_{\psi }\right]}^{\top }\right)},\hfill \end{array}$$

(15)

where we can separately calculate tilt and heading errors using the quaternion product symbol, ⊗, and conjugate of the current attitude, ${\mathit{q}}^{-1}$. Since the quaternion vector, $\mathit{q}$, is normalized, we can directly extract the axis components representing roll, pitch, and yaw errors. Finally, we apply an element-wise signed square root, $\pm \sqrt{·}$, given that the relationship between torque and motor speed is quadratic. The quaternion feedback law has been adopted from [27,28]. Let $\mathrm{\Delta }\mathrm{\Omega }=\mathrm{\Omega }-{\mathrm{\Omega }}_{\mathrm{ref}}$. The rotational/attitude motion feedback loop can be summarized as

$${\dot{\mathrm{\Omega }}}_{\mathrm{des}}={\mathbb{A}}_P\mathrm{\Delta }\mathit{q}\pm {\mathbb{A}}_D\sqrt{\mathrm{\Delta }\mathrm{\Omega }},$$

(16)

where ${\mathbb{A}}_P$ and ${\mathbb{A}}_D$ are 3 by 3 diagonal gain matrices. The total commanded thrust and torque is a combination of the desired (feedback-corrected) outputs and feed-forward reference directly calculated from the reference trajectory as

$$\begin{array}{c}\hfill T_z=T_{\mathrm{des}}+T_{\mathrm{ref}},\mathit{M}=I_B{\dot{\mathrm{\Omega }}}_{\mathrm{des}}+{\mathit{M}}_{\mathrm{ref}}.\end{array}$$

(17)

All reference values (i.e., ${\mathit{R}}_{\mathrm{I},\mathrm{ref}}$, ${\mathit{V}}_{\mathrm{I},\mathrm{ref}}$, ${\mathrm{\Theta }}_{\mathrm{ref}}$, ${\mathrm{\Omega }}_{\mathrm{ref}}$${\mathit{M}}_{\mathrm{ref}}$, and $T_{\mathrm{ref}}$) can be directly obtained from the smooth trajectory reference due to the differential flatness property of quadrotors. The reader is referred to [28] for more details regarding the analytic derivation of the reference thrust and torque from the minimum-snap trajectory solution. The control system with all inputs from guidance and navigation modules is shown in Figure 2. Feedback control and the control-allocation (motor mixing) matrix have all been implemented in Simulink, autogenerated into C, and compiled with the rest of the PX4 autopilot, replacing its built-in control- and allocation-related modules. For more details, please refer to Section 2.5.

Although the control system outlined in Figure 2 appears to be similar to the one implemented in PX4 Autopilot^® (v1.12.3), the key differences, presented in this paper, lie in the feed-forward signals generated from the reference trajectory (for all states) and its integration with the feedback control. The PX4 Autopilot^® incorporates some feed-forward capabilities; however, it is primarily generated internally, but the control system is not directly related to the trajectory. In other words, the feedforward path in PX4 Autopilot^® is achieved through a set of heuristically tuned gains and internal (to the feedback control) calculations. However, in this work, we use kinematics-based full-state (including attitude and torque) feedforward signals generated directly from the reference trajectory. Thus, the ideal, open-loop simulation, with a feedforward path (and only feed-forward path) active, has been simulated to successfully execute the entire reference trajectory. In such cases, feedback control is only needed when the internal model deviates from the truth, thus reducing the required control effort.

2.3. Minimum-Snap Trajectory Optimization

Consider a trajectory, which is shown as a dashed red line in Figure 3. The trajectory is characterized by a set of waypoints and multiple intervals. Each interval is parameterized by a polynomial as

$$P(t,TO{F}_{\mathrm{i}},{\mathit{p}}_{\mathrm{i}})=a_0+a_1{\displaystyle \frac{t}{TO{F}_{\mathrm{i}}}}+a_2{\left({\displaystyle \frac{t}{TO{F}_{\mathrm{i}}}}\right)}^2+a_3{\left({\displaystyle \frac{t}{TO{F}_{\mathrm{i}}}}\right)}^3+\cdots +a_9{\left({\displaystyle \frac{t}{TO{F}_{\mathrm{i}}}}\right)}^9,$$

(18)

where ${\mathit{p}}_i={\left[a_0,a_1,a_2,a_3,\cdots ,a_9\right]}^{\top }$ is a vector of coefficients defining the i-th segment, $TO{F}_i$ is the total time of flight allocated to the i-th segment, and $t\in [0,TO{F}_{\mathrm{i}}]$ is the current time (since the start of each interval).

We proceed by formulating an optimization problem with the objective function written to minimize the total squared snap (the fourth derivative of P) as

$$\underset{{\mathit{p}}_{\mathrm{i}}}{\mathrm{minimize}}J=\sum _{i=1}^{n_{\mathrm{int}}}{\int }_{t_0=0}^{t_f=TO{F}_{\mathrm{i}}}{\left[{\displaystyle \frac{d^4}{d{t}^4}}P(t,TO{F}_{\mathrm{i}},{\mathit{p}}_{\mathrm{i}})\right]}^{2}dt=\sum _{i=1}^{n_{\mathrm{int}}}{\mathit{p}}_{\mathrm{i}}^{\top }{\mathbb{Q}}_{\mathrm{i}}\left(TO{F}_{\mathrm{i}}\right){\mathit{p}}_{\mathrm{i}},$$

(19)

$$\mathrm{s}.\mathrm{t}.{\mathbb{A}}_{\mathrm{i}}{\mathit{p}}_{\mathrm{i}}={\mathit{d}}_{\mathrm{i}},\mathrm{for}\mathrm{i}\in \{1,\cdots ,n_{\mathrm{int}}\},$$

(20)

where the matrix ${\mathbb{A}}_{\mathrm{i}}$ maps the vector of design variables, ${\mathit{p}}_{\mathrm{i}}$, to the constraint vector, ${\mathit{d}}_{\mathrm{i}}$. The matrix ${\mathbb{Q}}_{\mathrm{i}}$ maps the vector of design variables ${\mathit{p}}_{\mathrm{i}}$ to the integral of $P(t,TO{F}_{\mathrm{i}},{\mathit{p}}_{\mathrm{i}})$, and $TO{F}_{\mathrm{i}}$ is the time allocated to the i-th segment (in a multi-segment trajectory) such that $0\le t\le TO{F}_{\mathrm{i}}$. Note that $TO{F}_{\mathrm{i}}$ is assumed to be fixed and known. If more than one segment is used, time is allocated externally for each interval with a total of $n_{\mathrm{int}}$ (number of intervals) such that a time allocation vector can be formed as $\mathit{TOF}={[TO{F}_1,\cdots ,TO{F}_{{\mathrm{n}}_{\mathrm{int}}}]}^{\top }$. Figure 3 shows a schematic summarizing the trajectory parametrization definitions. The red markers denote the input set of waypoints and the dashed red curve denotes the computed solution (reference trajectory). This convention is used in all trajectory plots.

The cost function, given in Equation (19), has the physical meaning of minimizing power consumption along the trajectory. This formulation allows us to obtain rapid, high-fidelity solutions for the full state of the quadrotor along the entire trajectory. The solution procedure is explained in detail in [29]. In this work, the time-allocation problem is solved off-board (only once) to obtain optimal time distribution (ratios) between all segments. A fixed-time minimum-snap problem is solved onboard (online). The reason for considering a fixed-time minimum-snap formulation is that the problem defined by Equations (19) and (20) can be solved analytically and without resorting to any numerical methods (i.e., there is no need to solve a quadratic programming problem online).

For the purpose of online re-planning, we have to keep track of the most recent trajectory solution defined by the optimal time allocation vector, $\mathit{TOF}$, and polynomial coefficients that define the entire trajectory (segment-wise). Additionally, resolving and obtaining a more refined solution in case re-planning is necessary, and the input boundary conditions (waypoints) are also needed.

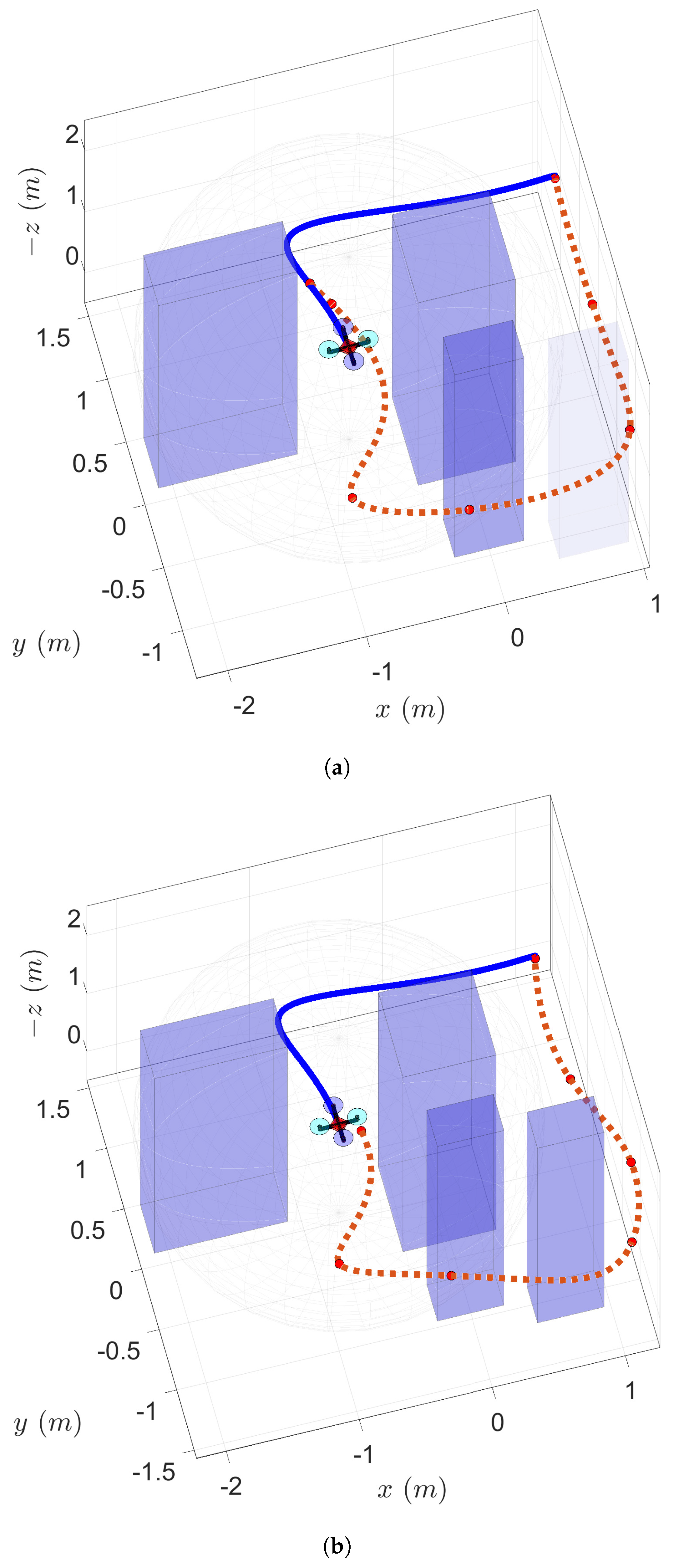
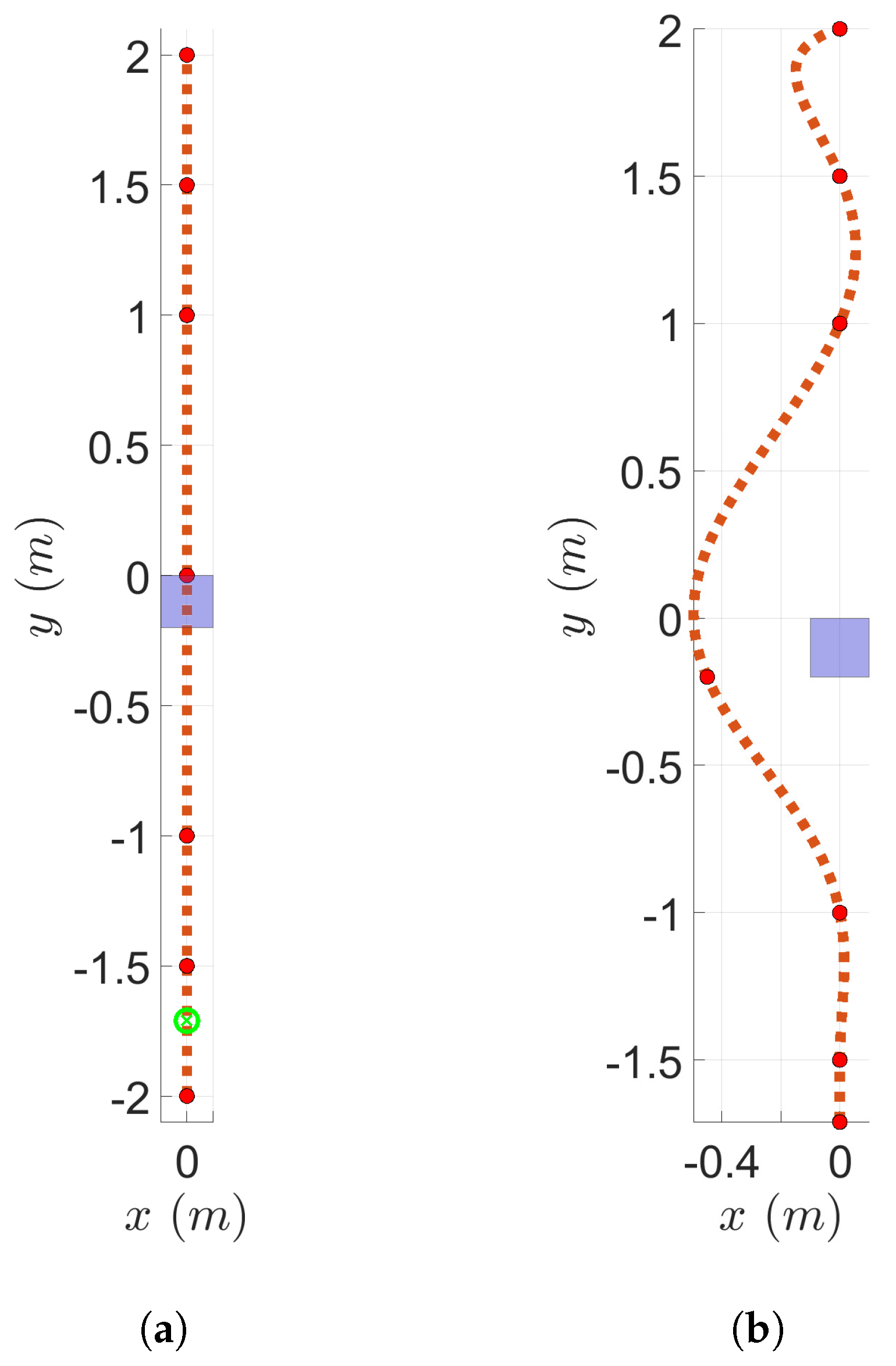
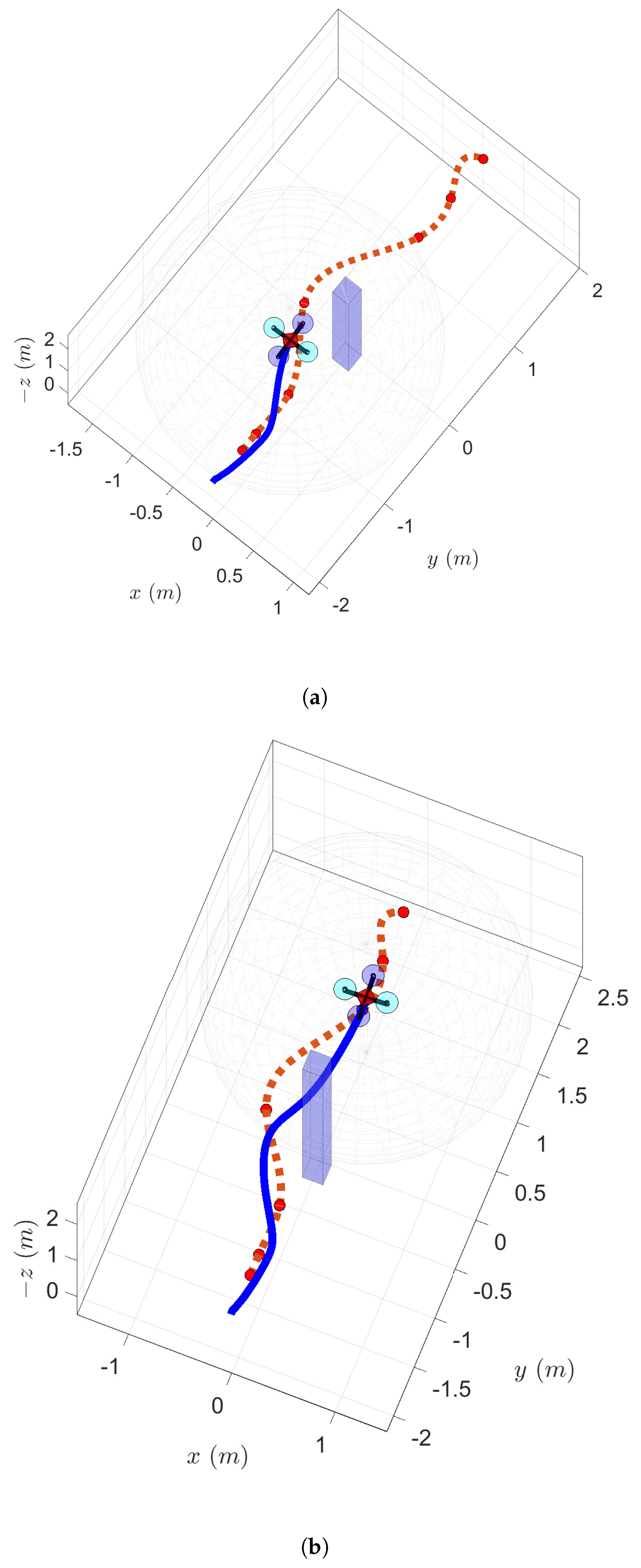
2.4. Online Re-Planning Strategy

In this work, we assume that the vehicle can detect static obstacles and draw a bounding box around each one of them. Once an obstacle is detected, a previously computed trajectory solution may not be valid anymore and can result in a collision. Therefore, any collision has to be checked and, if needed, a new feasible (i.e., collision-free) trajectory has to be recomputed while accounting for the changes in the locations of the obstacles.

While we have assumed perfect knowledge of the locations and dimensions of the obstacles, the scenario that we consider is as follows: while still on the ground, we assume that the vehicle is not sent into a completely unknown environment and a collision-free multi-segmented trajectory exists. This collision-free trajectory is defined by an initial set of waypoints based on the information of a finite number of obstacles. This initial scenario is considered to compute an end-to-end, minimum-snap trajectory (offline). This assumption is considered reasonable since most of the time the UAVs are sent to an already mapped environment (e.g., a payload delivery mission in an urban environment), where buildings and large obstacles are known a priori and a feasible trajectory can be defined (and computed) ahead of time. Certainly, if the environment is perfectly known and static, a globally optimal trajectory can be computed; but unexpected obstacles will change the environment, which warrants the need for a re-planning algorithm.

To present a practical mission scenario, we consider a situation where a small set of obstacles has not been accounted for during the initial planning phase. These obstacles are detected by the onboard sensors during the execution of the mission. The obstacle-detection problem is not the focus of this work [30]. However, to represent the obstacle-detection process, a set of virtual obstacles are stored onboard, but they are not considered by the planning algorithm until they have been detected. Specifically, the obstacle information (i.e., location and size) is made available to the re-planning algorithm only when one of the boundaries of the bounding box around the obstacle crosses a safety sphere around the vehicle. The diagram for the proposed re-planning algorithm is depicted in Figure 4.

The process starts (offline or before executing the mission) by solving a time-allocation problem using the unconstrained quadratic minimum-snap optimization problem outlined in Section 2.3 to obtain the optimal time-allocation vector, $\mathit{TOF}$, for the entire trajectory. This step is performed only once with the initially available data (i.e., obstacles are not considered at this step). Note that the time-allocation problems result in non-convex optimization problems [31]. Upon obtaining a solution, the vehicle executes the planned mission. The re-planning event is triggered for each newly detected obstacle, and the most recent set of waypoints and its respective solution (polynomial coefficients and time allocation vector) are modified in the following manner:

1.

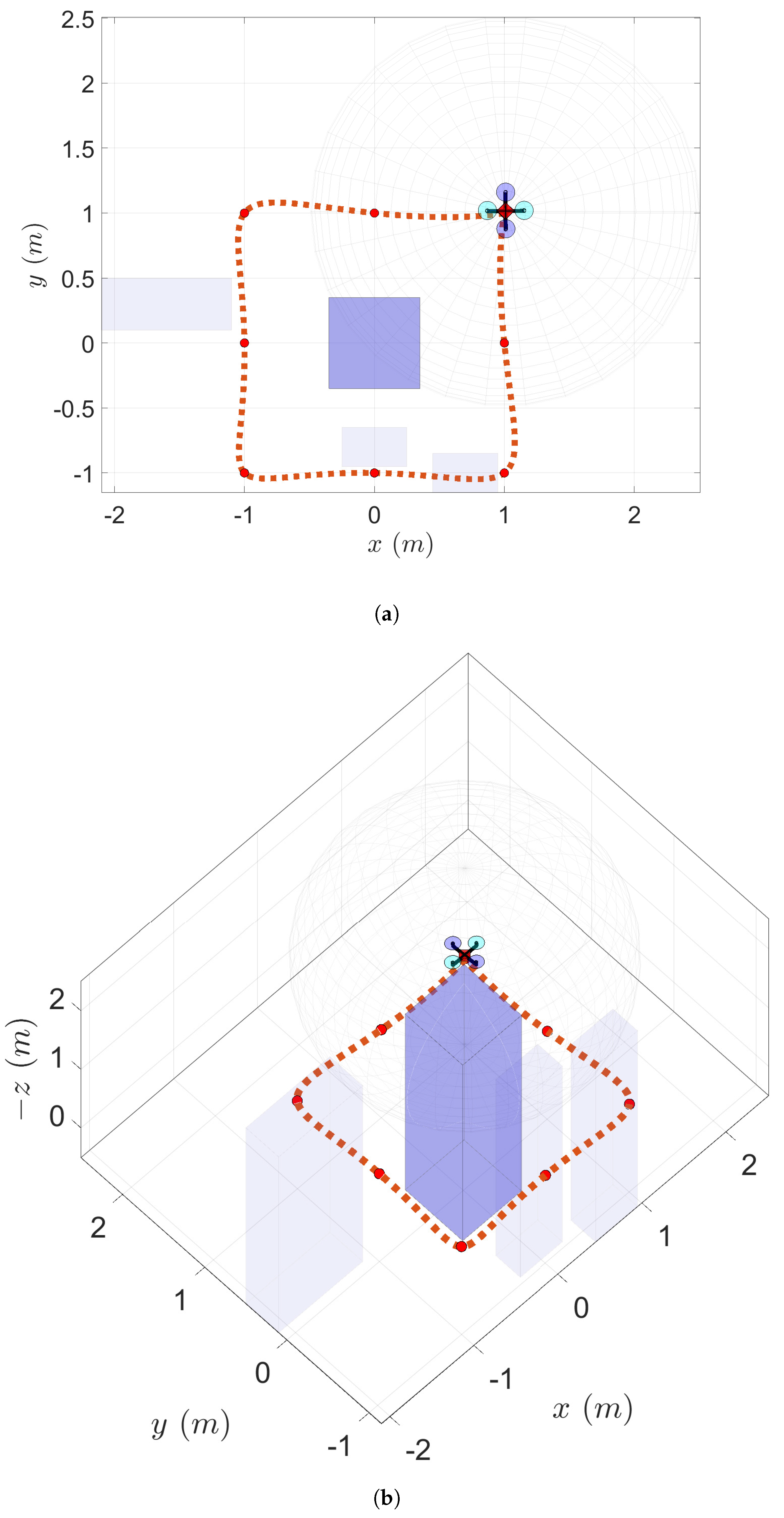
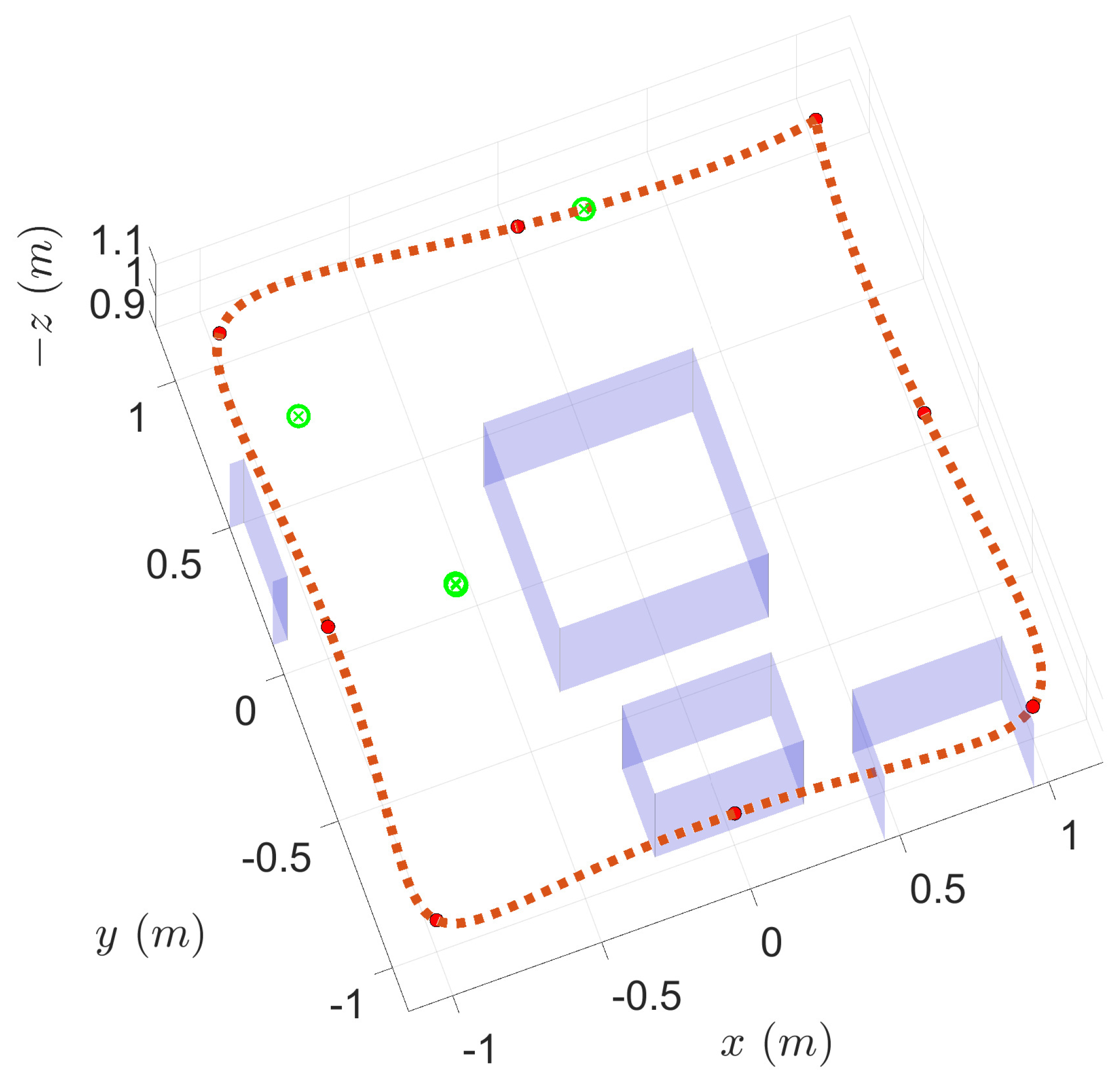
Waypoint pruning. The latest set of waypoints is modified based on whether any of the waypoints are within an obstacle or not. In other words, the old set of waypoints may no longer be feasible and must be pruned. Since we have assumed that we know all the parameters of the obstacles once they are detected, and obstacles are assumed to be convex (rectangle), we only need to check whether each of the waypoints is inside any of the bounding boxes and mark the waypoint as infeasible. No trajectory optimization is performed at this step, and the initial set of enforced waypoints and associated segment time is reduced for future calculations.

2.

Collision avoidance through updating/introducing waypoints. The latest set of coefficients is evaluated to obtain a discrete trajectory. The trajectory ahead is then checked for collision with all available obstacles. If a collision is detected, the discrete trajectory is used to determine the segment that lies inside the bounding box and estimate a single point outside its boundaries that will result in a collision-free minimum-snap trajectory (without computing it). This additional point is added to the latest set of (pruned) waypoints. As a result, the initial set of enforced boundary conditions (waypoints) may increase (by one).

3.

Time allocation update. If any of the previous steps resulted in any modifications to the most recent set of waypoints, the time allocation vector, $\mathit{TOF}$, must be updated accordingly. Since solving an optimal time-allocation problem is time-consuming, and we have assumed this algorithm must be executed in real-time, we have adopted velocity-based heuristics. In essence, we already keep track of the time allocation vector, $\mathit{TOF}$, and we only need to update the modified/new segments. First, we compute the average speed with the most recent set of waypoints and time-allocation vector (from the previous iteration). We use the Euclidean distance between two consecutive waypoints (e.g., A and B), and the total time allocated for this segment is used to estimate the average speed. We also keep track of the changes made so far (during this iteration) and mark segment(s) that have been modified/introduced (e.g., by introducing point C). The time allocated for all the newly introduced segments (e.g., A to C and C to B) is estimated assuming the same average speed as for the old segment (e.g., A to B). If any of the old waypoints are removed (e.g., point A, point B, or both), the same average speed is assumed for the new segment(s).

4.

Reference trajectory update. If prior steps have led to any modification to the most recent set of waypoints and time allocation vector, the fixed-time unconstrained quadratic minimum-snap optimization problem is resolved using the modified set of inputs. Although the solution is analytic, it may not be ready immediately, so it is scheduled as a separate process to be computed in parallel using a companion computer. While the new solution is being computed, the most recent (old) set of polynomial coefficients is used to provide references to the control system, and all further collision detection is paused until the new solution is ready. This logic is adopted to provide the least interruption to the trajectory execution process and to minimize computational loads. Once the new solution is ready, it replaces the most recently computed one, and the entire algorithm above is allowed to resume.

As noted, the above algorithm does not assume fixed times for segments and uses prior solutions to recursively update the trajectory through waypoint and time modifications. The initial time-allocation problem (solved offline or in-flight, but prior to main mission execution) is used to obtain globally optimal times for all segments, and subsequent iterations of the algorithm above recompute the entire trajectory ahead to account for any changes. Contrary to [32], we do not assume uniform time distribution at any point (since it leads to a suboptimal solution) for the unconstrained quadratic minimum-snap optimization problem. We exploit the known feature [26,33] of the minimum-snap trajectories, where no optimization is required when the input set of waypoints (and their boundary conditions) remain unmodified and only the total time for the entire trajectory is adjusted.

2.5. Hardware Implementation and Deployment

We have developed a hardware deployment framework to validate the proposed methodology using real hardware experiments. The hardware validation pipeline is shown in Figure 5 and consists of three major components: (1) ground control station (GCS), (2) onboard companion computer, and (3) flight control stack.

The primary role of the ground control station is straightforward—it provides an interface for the human operator to issue high-level commands to the vehicle and monitor the flight performance. Specifically, in the scenarios that are considered in this work, the operator has control over the flight modes (e.g., manual/autonomous flights) and the ability to terminate the autonomous mission at any time during the mission. The ground control station is a Windows 10 desktop computer that also processes the incoming data from the OptiTrack motion capture (MOCAP) system and relays the data to the vehicle. All experiments are conducted in the Aero-Astro Computational and Experimental (ACE) Lab indoor flight facility at Auburn University. All communication with the vehicle is established wirelessly via a single 900 Hz RFD900x-US telemetry radio pair, utilizing the MAVLINK [34] messaging protocol. The backbone of the communication software is the KGroundControl software, also developed in the ACELAB (refer to Appendix B for more details regarding the specific code used in this work).

A Raspberry Pi 5 is used as the companion computer on board the vehicle. It communicates with the Pixhawk^® Cube Orange flight control board via a direct wired (UART) connection and with the GCS via a wireless link. All wired and wireless communications are implemented through the MAVLINK protocol. The communication rate between the companion computer and the autopilot was set to 100 Hz for all time-critical data, which was necessary for the control system. The data rate for the motion capture and related data was set to 40 Hz, as per the PX4 documentation. To simplify the communication pipeline and keep only one telemetry link, all communications are routed through the autopilot board, which forwards all the necessary data to the companion computer and receives back the most up-to-date guidance solution. The task of the companion computer is to provide the most up-to-date reference solution, defined by position, heading angle, and their derivatives up to snap (included) evaluated at the current timestamp. The flight control firmware (PX4 Autopilot^®) provides the companion computer with the most recent estimated state of the vehicle (e.g., position, velocity, attitude), as well as the current flight state of the vehicle (e.g., armed state and flight mode). The rest of the telemetry is relayed by the autopilot to the GCS for real-time flight monitoring and data-logging purposes.

The companion computer has a simple internal state machine, with the following internal states. (1) Idle (standby): the replanning capabilities are considered inactive. Therefore, the trajectory is not updated and the output reference to the flight controller is kept at the last active (valid) output. (2) Active: once issued, it always defines the start of the mission (both in time and global position) and executes the replanning routine, as outlined in Section 2.4. As noted, all mission-related communications are achieved via fixed-size data packets, such that the required data throughput is minimized. We note that all mission data are stored and handled by the companion computer. This was primarily done to minimize the complexity of the required modifications to the PX4^® firmware.

All navigation and flight control processes are handled by the Pixhawk^® Cube Orange board running PX4 Autopilot^® firmware. The authors are fully aware of the built-in autonomous capability of the PX4^® and native solutions for the companion computer-PX4 bridges (e.g., ROS). Unfortunately, the existing (stock) PX4^® firmware does not allow providing a custom feedforward input without major modification of the firmware. In this work, we attempted to use the rapid Matlab^®–Simulink^® deployment tools made available by MathWorks to deploy the control law outlined in Section 2.2. The existing hardware deployment pipeline of Simulink^® allows significant simplification of flight control deployment directly, without the need to write your own implementation in C++. However, at the time of writing, several key challenges in the aforementioned pipeline exist, which have been addressed in this work.

The PX4^® [35] is a deeply embedded robotics middleware and programming environment, which revolves around multithreaded publish–subscribe architecture. The public data structures, or uORB topics, are made available within PX4^® for all of its internal modules (e.g., state estimator, attitude controller, etc.) through this publish–subscribe framework, and Simulink^® provides an interface for accessing uORB topics from the auto-generated code deployed from Simulink. Unfortunately, the number of uORB topics that can be reliably accessed from Simulink^® is limited to 4, and more uORB topics are needed to obtain all the information required by the control system. The authors have used all Matlab^® releases from R2022b to R2023b, and all have this issue (all require PX4^® version v1.12.3); the R2024a has not yet been released at the time of writing. It is also important to note that this limitation does not exist in R2022a, but it required PX4^® v1.10.2, which had its limitations and was not feasible. The ACE Lab has developed a similar pipeline on PX4^® v1.10.2 and deployed it on a tilt-wing aircraft, as outlined in [36]. In this work, however, we used R2023a along with a modified version of the PX4^® v1.12.3.

The simplest solution to the aforementioned uORB limitation was to use an existing (but previously unused) topic (we chose a “debug array” topic and created two new instances of it) and pack all the required data into it. This way, we can limit the number of uORB publish and subscribe calls to 2: one for outbound data (control system outputs) and one for inbound data (all required inputs to the controller from PX4). For this solution to work properly, a new PX4^® module is created and all the inbound/outbound messages are handled internally: all required data are collected from other uORB topics and packed into the inbound message, and the same process but in reverse is performed on the outbound message. Although completely unnecessary for the quadrotor, all actuation has been implemented through CAN (controller area network), which was also only partially supported in PX4^® and not supported in Simulink^®. The CAN implementation for actuator control was chosen since we plan to consider vehicles that require more PWM outputs than are supported by Pixhawk^® boards.

As a side note, the MOCAP data are not used directly by the flight control system but are provided to the PX4^® as a “vision position estimate” MAVLINK message and handled by an extended Kalman filter, which is a standard procedure for improving the accuracy of the PX4^® for indoor experiments. Additionally, to simplify outdoor flights, testing, and validation, PX4^® firmware had to be further updated to include additional parameters that were not originally considered in stock PX4^®. This step was performed to grant remote access to an exposed set of parameters (like control system gains), without any need to regenerate and recompile anything. All custom codes were written in C++, including the GCS, companion computer functionality, and modifications to the PX4. The remaining parts of the model have been auto-generated from the Simulink^® model. The hardware deployment and simulation are the exact same Simulink^® model, which also includes the message serialization and parsing. The flight control system is executed at a fixed update frequency of 200 Hz, without any differentiation between attitude and position feedback loops (translational and rotational controllers are executed sequentially at the same update frequency).

3. Results

3.1. Simulation Results

All figures follow the same color and marker conventions: blue solid lines denote the state of the vehicle executing the dashed red reference trajectory. The red markers show the waypoints used for obtaining the reference solution. Blue rectangular boxes denote the obstacles that must be avoided.

As the first validation step, we have considered a simulated environment with five virtual obstacles. All obstacles are assumed to be within the blue bounding boxes, as shown in Figure 6, where transparency indicates whether the obstacle was detected by the vehicle or not. The mission considers a square-like flight plan, with the reference trajectory solution (dashed red) respecting an initial set of waypoints (9 red dots, with start and end points matching).

The initial trajectory is a collision-free one with respect to the central obstacle only, while other obstacles were placed such that they are either directly on the trajectory or close enough to create a potential collision (Figure 6a shows a top-down view of Figure 6b). Please note that the calculations are based on a North-East-Down (NED) coordinate system, but the z-axis was flipped for visualization purposes. The initial trajectory solution assumes 10 s for the entire mission.

The initial (offline) optimal trajectory solution is shown in Figure 7, with all four future replanning locations marked with a green marker. As previously mentioned, the proposed algorithm does not assume a set replanning rate and re-solves the trajectories only when necessary. In this particular case, the replanning events are triggered by the appearance of new obstacles that violate proximity constraints (bounding box around the obstacle). The time instances, for replanning events, are 1.27 s, 2.96 s, 3.48 s, and 3.51 s relative to the start time of the mission.

The new/replanned trajectories are shown in Figure 8, Figure 9, Figure 10 and Figure 11. Note that the last two replanning events happen very closely to each other because the third replanning event has led to a solution that violates the proximity boundary along the newly formed interval. However, since we are recursively checking the most recently computed solution with all detected obstacles, this possible collision was resolved in a timely manner (and automatically).

It is also important to clarify that these results are the process of post-processing and the number of replanning events, timing, sequence, or any other information is not known a priori and is the result of applying the proposed replanning algorithm. Once the mission starts, the flight plan can be updated if needed. The state time history is shown with a blue solid line on all figures. Once the first obstacle enters the radius of the detection sphere, the replanning algorithm becomes aware of it and automatically decides whether the existing trajectory is collision-free and updates it or not.

As it is shown in Figure 12 and following the re-planning algorithm in Figure 4, the reference just before the obstacle was detected, is marked as dangerous, and a new solution has to be regenerated, as can be seen in Figure 12. This process is repeated for every other obstacle in an automated manner.

An important distinction of the proposed method is that the entire trajectory (and not just the nearest interval) ahead of the vehicle is recomputed; thus, the entire flight path ahead and time to reach each waypoint are also adjusted. As can be seen from Figure 13, Figure 14 and Figure 15, the regenerated solution considers only part of the mission that has not been flown yet, thus reducing the computational burden as the vehicle is approaching the final waypoint.

We would like to highlight that this test scenario has been specifically designed to illustrate replanning for mission scenarios, when not only the initial reference trajectory is no longer collision-free but also some of the waypoints have to be moved outside the boundaries of the obstacles, entirely removed or added such that the re-generated trajectory is a collision-free one.

Although the reference trajectory in Figure 13 appears to be sharp, the 3D plot does not show how fast the turn was supposed to be made. It turns out that at that point in time, given the current knowledge, the optimal solution was to come close to a full stop and then move toward a new direction (almost reverse the approach direction).

Please note that although the shape of the (position) trajectory appears to be sharp, it does not represent a sharp maneuver for the quadrotor. Please also recall that all boundary conditions, except for positions at the waypoints and initial/final waypoints, are free and are optimized as part of the re-planning algorithm.

3.2. Experimental Validation/Results

To validate the proposed framework, a simple scenario has been considered. As shown in Figure 16, the initial mission profile is a straight 4-m-long line, all along the y-axis, with the initial total flight time set to 10 s. The initial solution with time allocation was computed onboard, in-flight, and takes 3 s on average for this mission. While this time allocation solution is being computed, the companion computer guides the vehicle to the first waypoint by solving the fixed-time minimum snap trajectory optimization problem.

The exact computational times are case-by-case dependent and are not deterministic when multiple problems are solved in parallel on the same CPU. It was found that issues related to matrix inversion can all be removed if all missions are mapped to precisely the last 10 s. Once the solutions are obtained, the path and all derivatives along the minimum-snap trajectory can be evaluated for the actual mission duration (if not already 10 s). That is, the same trajectory can be recovered when solving in scaled and non-scaled time units, with all boundary conditions and derivates matching [26].

We have considered only one virtual obstacle at the center of the coordinate system. The goal here is to validate the algorithm on a real vehicle that is shown in Figure 1 for conducting the experiments. The key challenge is that the system cannot be paused at any instance of time to solve a trajectory (which was the case for the simulation).

In this case, the companion computer algorithm was configured to output the most recent trajectory solution while (asynchronously) computing the new, collision-free mission update. That is, the “old” mission profile is reused, even if it will result in a collision, until a new solution becomes available and replaces it. If replanning was already initiated and was not yet completed, no further obstacle detection or replanning is triggered. Although this may be invalid when multiple, especially moving, obstacles are present, such simplification does not affect this simple scenario where the trajectory should be replanned only once (since there is only one obstacle).

The initial (offline) optimal trajectory solution is shown in Figure 17, with one replanning location marked with a green marker. The replanning event is triggered by the appearance of a single obstacle that is placed such that it violates proximity constraints (bounding box around the obstacle). The replanning event occurs at 3.42 s relative to the start time of the mission. The replanned trajectory is shown in Figure 17. Note that replanning required automatically removing the infeasible point and placing a new waypoint that resulted in a collision-free reference path, as shown in Figure 18. For this simple scenario, no additional replanning was needed.

The flight results demonstrate the successful application of the proposed method. Once the obstacle was detected, the entire mission was re-planned (Figure 19) and updated to avoid the obstacle. As is shown in Figure 19, the vehicle could follow the commanded reference and complete the avoidance maneuver autonomously. However, some noticeable errors in tracking are present and will have to be resolved.

We emphasize that the entire mission ahead is replanned, and new waypoints are used to solve a fixed-time minimum snap trajectory optimization problem. This approach is different from the one in [12] that restricts the updated solution to finding a single interval (or connecting arc) between the current reference and some future reference behind the obstacle, essentially merging back to the global optimal trajectory, which was computed previously.

In our work, the subsequent reference trajectory is also optimized, accounting for the collision avoidance detour and, therefore, is by definition, more optimal than the combination of two different solutions (one being the global solution that was computed without the detected obstacle).

The developed pipeline streamlines the development of path-planning algorithms in simulated environments for all validation and verification purposes. The same pipeline can be leveraged for operating a large class of vehicles with many actuation systems and for real-world experiments.

4. Conclusions

We present a control system design for autonomous quadrotors that has real-time re-planning capability, including the hardware pipeline for the hardware–software integration to realize the proposed real-time re-planning algorithm. The framework is based on a modified version of the PX4 Autopilot and a Raspberry Pi 5 companion computer.

The planning algorithm utilizes minimum-snap trajectory generation, taking advantage of the differential flatness property of quadrotors, to realize computationally-light, real-time re-planning using an onboard computer. We first verify the control system, including the planning algorithm with simulation experiments, and then implement and showcase the system on hardware.

We assumed that the mission was already designed given all available data at that time, but the obstacles were placed at locations such that replanning was required. This work successfully demonstrated an online trajectory replanning and optimization framework for handling uncertain scenarios where obstacles are not known at the start of the mission and must be accounted for during flight and in real-time.

The results are presented for quadrotor vehicles both in simulation and in an experimental setting. The simulation environment considers aerodynamic drag, wind, turbulence, and actuator dynamics. The experimental results are demonstrated using a modified PX4 Autopilot firmware that included full feedforward control using minimum-snap trajectories and a companion computer (RPi 5).

The results clearly show that the vehicle is capable of avoiding obstacles in real-time if provided with a reliable and accurate obstacle-detection capability. In this article, we have focused on motion-planning problems subject to static obstacles. Extending the approach to handle dynamic obstacles will be investigated in our future work.