Abstract
Our study presents a novel design for a cable-driven robotic arm, emphasizing low cost, low inertia movement, and long-term cable durability. The robotic arm shares similar specifications with the UR5 robotic arm, featuring a total of six degrees of freedom (DOF) distributed in a 1:1:1:3 ratio at the arm base, shoulder, elbow, and wrist, respectively. The three DOF at the wrist joints are driven by a cable system, with heavy motors relocated from the end-effector to the shoulder base. This repositioning results in a lighter cable-actuated wrist (weighing 0.8 kg), which enhances safety during human interaction and reduces the torque requirements for the elbow and shoulder motors. Consequently, the overall cost and weight of the robotic arm are reduced, achieving a payload-to-body weight ratio of 5:8.4 kg. To ensure good positional repeatability, the shoulder and elbow joints, which influence longer moment arms, are designed with a direct-drive structure. To evaluate the design’s performance, tests were conducted on loading capability, cable durability, position repeatability, and manipulation. The tests demonstrated that the arm could manipulate a 5 kg payload with a positional repeatability error of less than 0.1 mm. Additionally, a novel cable tightener design was introduced, which served dual functions: conveniently tightening the cable and reducing the high-stress concentration near the cable locking end to minimize cable loosening. When subjected to an initial cable tension of 100 kg, this design retained approximately 80% of the load after 10 years at a room temperature of 24 °C.
1. Introduction
Robotic arms have been increasingly utilized in various human activities. In fields involving manipulation, the end-effectors of these arms are used to maneuver robotic grippers or hands in spatial environments [1,2,3] for numerous tasks, such as lifting heavy objects [4], handling deformable materials [5,6,7,8], healthcare systems [9,10,11], food processing, farming, agriculture [12,13,14,15], and industrial production lines [16,17,18,19]. These robotic arms can achieve highly accurate movements through the use of rigid linkages driven by motors positioned at each hinge joint [16,17,18]. For example, the UR5 robotic arm, developed by Universal Robots, is renowned as a collaborative industrial robot arm that operates with six degrees of freedom (DOF) and achieves 0.1 mm repeatability when performing tasks at a distance of 0.85 m from its base’s centerline. The UR5 weighs over 20 kg and can lift a maximum payload of 5 kg, resulting in a payload-to-weight ratio of approximately 1:4. Despite being among the most precise robotic arms available, the UR5’s wrist is relatively heavy and bulky due to the three motors integrated into this section. Additionally, mounting a motor at each joint significantly increases the arm’s moving inertia, even without any payload. Placing the motors closer to the base reduces the robot arm’s energy consumption during task execution. However, the increased moving inertia may lead to unsafe interactions or unexpected outcomes in its surrounding environment. These challenges persist in other robotic products such as those from ABB, Denso, Kuka, and Fanuc.
The limitations of the aforementioned robotic arms can be addressed by the designs of the next generation of soft robots, which incorporate soft materials or flexible mechanisms into their structures. For example, Louis in [20] proposed a soft-hybrid humanoid robot arm with a fabric thermoplastic polyurethane actuator for the shoulder, elbow, and wrist joints, enabling movement in the upper arm and forearm. A soft robotic arm introduced in [21] features an omnidirectional actuator created through multi-material 3D printing. An invasive surgery robot arm was designed using a series of connected soft Pneunet segments [22]. Another design combined suction cups with a Pneunet structure to create an octopus-inspired soft robotic arm with sensing capabilities as presented in [23]. Shape memory polymers (SMAs) or origami structures were used to control the movements of other soft robotic arms, such as an octopus arm [24] and an elephant-like arm [25]. Additionally, numerous robot arms with soft body structures actuated by air pressure or hydraulics were developed in [26,27,28,29,30], respectively. While these soft robotic arms offer enhanced safety, adaptability, and flexibility, achieving high repeatability under heavy payloads remains a significant challenge.
1.1. Related Works
Cable-driven systems are increasingly used to drive the links and joints of robotic arms, where one motor controls the back-and-forth movement of each link or joint through a pair of cables. The ends of these cables are secured to the link or joint and to a pulley attached to the motor shaft, allowing the motor’s force output to be transmitted effectively. This mounting scheme enables optimal positioning of the motors on the robotic arms, minimizing the arm’s moment of inertia. Furthermore, the structures of the links and joints become more compact and lighter than those of conventional robotic arms, as they only need to support the cables instead of heavy motors. In other words, cable-driven systems provide significant advantages, allowing robotic arms to achieve faster accelerations within workspaces [31,32,33,34] while ensuring safer interactions.
Cable-driven robotic arms are widely used in both soft and traditional robotics. Most soft cable-driven arms feature continuum mechanisms with circular cross-section bodies supported by a single flexible backbone at the center. These soft bodies consist of multiple discs driven by multiple cables [30,35,36,37,38,39]. While these soft arms are highly flexible and effective for handling light objects or in surgical applications, they struggle with heavier loads. Traditional cable-driven robotic arms address this issue by providing higher stiffness in each link and joint. For example, AMBIDEX [40] and other robotic arms [41,42] have seven degrees of freedom (DOF), with three at the wrist, one at the elbow, and three at the shoulder, where each joint is operated by a motor that transfers torque through the cables. Although these arms are designed to achieve low moving inertia, the wrist mechanisms are often complex and bulky, limiting their ability to handle lateral payloads and heavy objects. Our previous work [43] introduced a cable-driven robotic arm with five DOF, featuring a lightweight body and low moment of inertia. However, the robotic arms in previous works [40,41,43] required re-tensioning after short-term use due to the lack of a cable-tightening mechanism capable of generating sufficient holding force at each end of the cable.
1.2. Research Concept
To address the identified problem, we developed a low-cost design for a novel cable-driven robotic arm that features a lightweight body with low inertia, durable cable tension, and good pose repeatability. This robotic arm has six degrees of freedom (DOF), including one at the shoulder, one at the base, one at the elbow, and three at the wrist (see Figure 1). To keep the design cost effective, the arm utilizes a frame-like structure made from thin carbon fiber plates. Additionally, a suction-cup gripper is attached to the end-effector of the wrist for testing and manipulation demonstrations. In this design, all motors are positioned near the shoulder joint to counterbalance the payload held by the gripper. Six Dyneema cables, arranged in three pairs, are used to drive the movements of the 3-DOF wrist. In the past, the durability test for cable-driven robots was rarely mentioned, so we primarily focused on it. The novelty of our work lies in the following points:
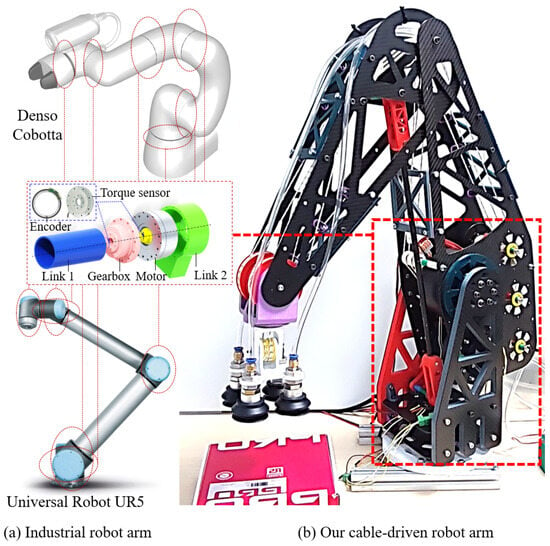
Figure 1.
(a) Drawbacks of industrial collaborative robot arms consisting of direct-drive joints in handling heavy load and generating low-inertia interaction. (b) Our solution of a cable-driven robot arm. In this inset picture, the encoder and torque sensor may be located before or after the gearbox.
- Robot arm: We design a low-cost cable-driven robotic arm with six degrees of freedom (DOF) at the same scale as the UR5 robotic arm. Our proposed design targets to manipulate a 5 kg payload. The arm’s body is lightweight, allowing for operation with low movement inertia. Unlike many previous designs where all six DOF are cable-actuated, our approach employs a hybrid design. Only the three DOF in the wrist joints are driven by a cable system. To ensure good pose repeatability, the shoulder and elbow joints, which influence longer moment arms, were designed with a direct-drive structure.
- The wrist: The design relocates the three motors driving the three DOF of the wrist closer to the shoulder, with the actuation remotely transmitted by three pairs of cables. As a result, the wrist weighs only 0.8 kg, allowing for safer human interactions and reducing the torque requirements for the elbow and shoulder motors. This reduction in torque requirements also leads to a decrease in the overall cost and weight of the robotic arm.
- Decoupling system: The design ensures that the length of each cable remains constant when the forearm and wrist rotate around their hinge joints. Compared with [40], our design achieves less vibration as the cables move due to no compensating spring in our decoupling mechanism. Additionally, the cable is wound around the tightening pulley approximately 10 times before reaching the termination point, which enhances the creep performance of the cable and improves the durability of the cable tension.
- This mechanism enables tighter cable adjustments with greater durability and allows users to re-tension cables after a period of use. This feature enhances reliability and maintains the operational accuracy of the robotic arm. It represents a novel improvement compared with [40,41,43,44], where cable ends were secured with bolts.
- Counterbalance design: We enhance the capability of the shoulder motor in lifting heavy loads. It is a novelty compared with [40,41].
2. Design of Cable-Driven Robot Arm
As depicted in Figure 2, the design of our robotic arm features six degrees of freedom (DOF) distributed across key clusters: the base, shoulder, upper arm, elbow, forearm, and wrist, with a distribution ratio of 1:1:0:1:0:3. Each cluster can rotate around its neighboring cluster via a hinge-like structure, which constitutes the primary motion of the robotic arm. For simplicity, we will sequentially focus on the details of the robotic arm, covering the main frame, wrist, cable tightening mechanism, and decoupling mechanism.
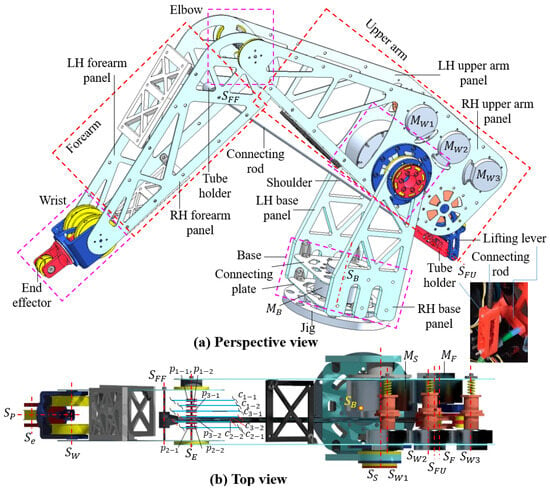
Figure 2.
A 3D design of the cable-driven robot arm with different views: (a) perspective view, and (b) top view. The dash-line boxes show the boundaries of the main cluster structures in the robot arm. , are respectively the center lines of the joints: elbow, tube holders at the forearm, tube holders at the upper arm, wrist, end-effector, and pinion wrist. Concurrently, are in turn the center lines of the motor shafts: base , shoulder , forearm , and wrist .
2.1. Main Frame
This minor section presents the structure of the main frame encompassing the clusters: the base, shoulder, upper arm, elbow, and forearm. The main frame comprises three pairs of parallel panels each used for the design of the base, upper arm, and forearm (i.e., base panels, upper arm panels, and forearm panels, respectively). Moreover, each of these panels is designated as an LH (left-hand) or RH (right-hand) panel, depending on whether it is located on the left or right side of the robotic arm as viewed from the end-effector.
At the bottom of the base panels, near the jig, two parallel spacing plates are fixedly mounted in a rectangular box configuration. These spacing plates position and clamp the front and back faces of the base motor (), specifically RMD-X8-S2 (My Actuator). The output shaft of is secured to the jig surface. In other words, the robotic arm rotates around the jig, while the motor operates.
At the top of the base panels, farther from the jig, there is a pattern of holes for mounting the output shaft of the shoulder motor (), specifically, the RMD X10-S2. The front end of this motor is secured to the LH upper arm panel, while its rear end is connected to the RH upper arm panel using bolts and spacers. When operates, the arm, excluding the base cluster, rotates around the center line , which is aligned with the motor shaft.
Additionally, the upper arm panels are equipped with four motors: one forearm motor (RMD X10, referred to as ) and three wrist motors (RMD X6-S2, referred to as , , and ). These motors are mounted on one side of the shoulder motor (), opposite the elbow, to counterbalance the inertia generated on the other side of . Motors , , and are aligned in a straight line on the RH upper arm panel, opposite the location of . This layout ensures that the center of gravity of the upper arm remains low during operation. The output shaft of is locked with a lifting lever that has a hinge shaft for connecting with a tube holder. A composite tube, with its ends secured to the tube holders on the lifting lever and the forearm, acts as a connecting rod to transmit the pushing or pulling forces from . In Figure 2, the four-segment lines formed by , , , and always create a parallelogram as the arm moves.
The LH- and RH-upper arm panels differ in characteristics due to the varying locations of the five motors, whereas the forearm panels are symmetrical. The elbow cluster features a shaft with a center line, , which connects the forearm panels to the upper arm panels in pairs (see Figure 2). When the motor operates, the pushing/pulling forces are transmitted through the connecting rod to the shaft , causing the forearm to rotate around . Additionally, the elbow serves as a transition region for routing the cables between the wrist and the shoulder. In this design, six elbow pulleys, labeled as , each with a radius , are mounted on the elbow shaft to support one cable from each group . For simplicity, an arbitrary cable pair (referred to as a branch) is denoted as , with its branches , where and , . Compared to the previous work in [40], the elbow in our design is more compact, having simplified multiple links and joints into a single hinge joint. Hence, our design reduces assembly errors and provides additional space for incorporating sensors to track elbow rotation.
The forearm features a structure similar to that described in [43]. It consists of a pair of V-shaped panels interconnected by two spacing plates. This design stabilizes the long robot arm under heavy external loads. The plate frame optimizes the structure to reduce the robot’s body weight, simplifies the assembly process, and lowers the machining costs.
2.2. Wrist
As in Figure 3 and Figure 4, the wrist cluster connects to the forearm panels via a hinge joint located at the far end from the elbow. This joint features a ring shaft that aligns with two ring gears and the bores of the forearm panels along line . The wrist achieves three rotational degrees of freedom (DOF) through a differential gear mechanism [43] driven by the cable system . The differential gear mechanism includes two ring gears that mesh with a pinion gear, and it has a symmetrical structure relative to the center line . As the ring gears rotate, they induce corresponding rotations in the pinion gear around and/or , depending on the direction and speed of the driving gears. The pinion gear meshes with the ring gears and is mounted on a U-shaped wrist bracket that rotates around . The other end of the pinion gear connects to the end-effector via a hinge joint that rotates around the pinion shaft, with its center line at . The wrist’s end-effector is a solid block that does not involve gearing transmission. It has a through-bore at each end for mounting on the pinion gear at and for attaching external modules such as a gripper.
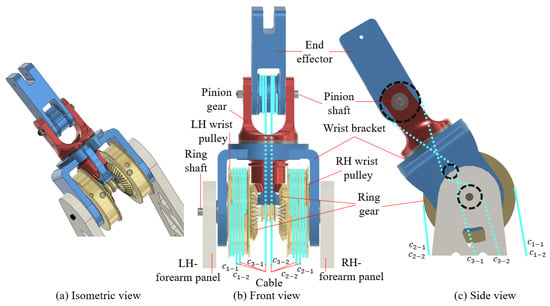
Figure 3.
Schematic illustration of the 3-DOF differential-gear wrist design with (a) isometric view, (b) front view, and (c) side view. Six cables are labeled as .
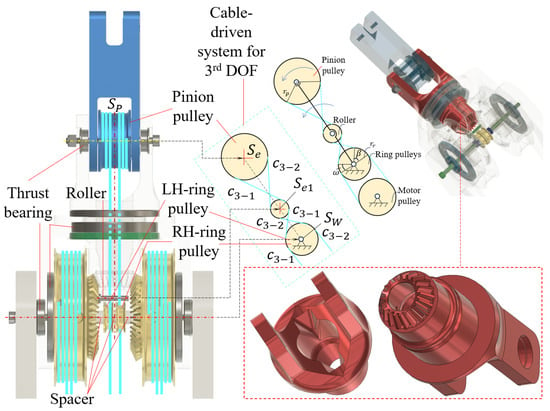
Figure 4.
Illustration of the inside structure and the decoupling mechanism in the 3-DOF differential-gear wrist.
To drive all DOF of the wrist cluster, we use the cable system including six cable branches connecting from the wrist to the motors . One end of each cable branch is wound more than three rounds before being locked on the pulley structure and merged onto the hub surfaces of the pulley gear and end-effector (see Figure 3 and Figure 4). Additionally, the pairs , and are respectively mounted to the LH-wrist pulley, RH-wrist pulley, and the pinion pulley to generate back and forth rotation for their respective pulleys.
2.3. Cable Tightening Mechanism
After leaving the wrist cluster, all cables pass over the elbow pulleys (see Figure 2), traverse through a decoupling mechanism, and then end at a cable tightening mechanism (also known as a cable tightener) mounted on the output shafts of motors , , and .
The working principle of the cable tightener is based on the locking mechanism of a gear coupler as in Figure 5. Each cable tightener encompasses two pulleys, male and female, that can slide and rotate around a connecting shaft. Each of these pulleys has one ending surface with a circular pattern of right-triangle teeth located right at the peripheral circle (aka ring teeth). After being mounted to the motor shaft with its center line or or , the remaining ending surface of the male and female pulleys, having a toothless structure, is locked with the motor shaft and touched with a spring lock, respectively. At the detachment stage, the female pulley can rotate and slide along the connecting shaft, while the male pulley only rotates together with its belonging motor shaft. At the attachment stage, the female pulley moves towards the male one until their ring teeth completely mesh together. Simultaneously, the spring lock generates a compressing force to restrict the loosening in this attachment. At this stage, the right-triangle teeth lock one rotational direction of the female pulley, while the remaining direction of the rotation is braked by the friction integrated from the teeth mesh and the spring lock. In Figure 5a), each pulley has a hexagonal head fitting with an external spanner tool, which facilitates users to clamp and rotate the pulleys in the case of requiring strong torques.
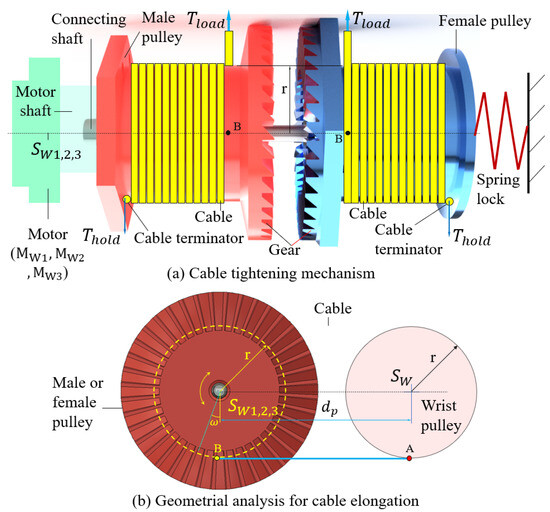
Figure 5.
Schematic illustration of the cable tightening mechanism (a) and the principle of adjusting the cable tension (b). A yellow-dash circle line presents the hub surface of the pulley and means , or . The models in this figure are also applied for both wrist and pinion pulleys. The cable is assumed to be locked in the wrist pulley and the male/female pulley, while A and B are the first contact points between the cable and the pulleys.
The hub surface of each pulley is a smooth cylinder that has enough length for winding multiple rounds of one cable branch . For each cable tightener, the cable branch, for example, from the outside arrives and contacts the male pulley at B on the back surface, while those of are at B at the front surface of the female pulley (see Figure 5a)). These cables are then wound multiple rounds around their belonging pulleys before being locked at the cable terminators. This mounting method allows the pair of cables to pull and release simultaneously in both rotational directions. In our initial prototypes, the cable tends to loosen at the cable terminating point due to the high-stress concentration as well as high clamping force at the terminating end. As a result, the cable loosens over a relatively short time of 10–15 min. To improve the durability of the cable tension, we incorporated our cable tightening mechanism such that the cable would complete about 10 turns on the pulley before reaching the terminating point. This will significantly reduce the cable tension force near the terminating point and further reduce the maximum creep stress at the terminating point. At contact point B, the cable bears a tension that gradually reduces over the cable rounds around the pulley. This decrement is affected by the frictional loss at the contact position between the cable and the pulley. Hence, reaches a minimum value at the contact point between the cable and the terminator i.e., (i.e., holding tension). This claim was validated in our experiment (see Figure 6a)), as quickly dropped by increasing the number of cable rounds on the pulley. With two rounds on the pulleys, retained 16÷20% of , whereas this ratio was reduced to less than 4% as the number of rounds increased to higher than 2. Let be the frictional coefficient between the cable and the pulley and be the total angle swept by all rounds of the cable (e.g., = 2 as the cable winds one round on the pulley), and we have the following relation.
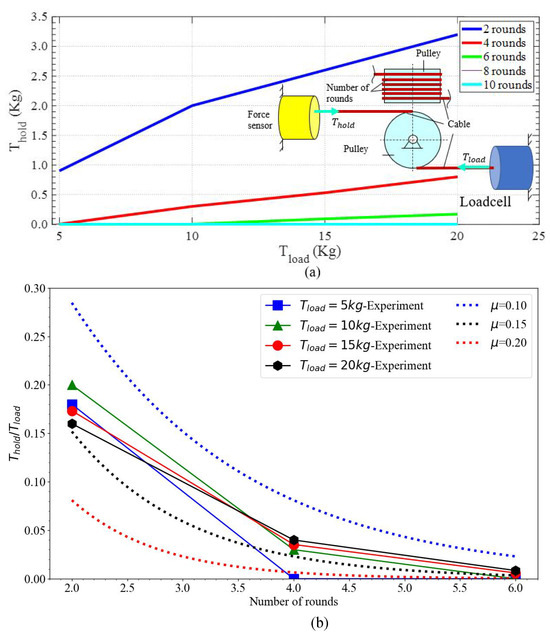
Figure 6.
Experimental relation between the and (a) and the ratio of on the pulley over two variants and the number of rounds (b). In graph (a), the pulley with a diameter of 32 mm, the load cell, and the force sensor are clamped. Also, the cable made from Dyneema material has a diameter of 2 mm. The cable is wound many rounds on the pulley hub surface. is set at the load cell, while is measured at the force sensor. In (b), the ratio of in experiments is shown in the solid lines, and the dot lines show the interpolations from such data over different values of .
Since and in Equation (1) are always positive, is smaller than , which can theoretically validate our previous claim. Also, drops quickly when the product of enlarges. was always smaller than and reached zero when the number of rounds increased. As the number of rounds reached four rounds, dropped to zero at all values of . The correlation between the and in Equation (1) is also charted in Figure 6b with the variants = 0.1, 0.15, 0.2 and the number of rounds 2, 4, 6 ( = ). is close to zero when the value of is higher than 4 rounds. Therefore, the more cable rounds are wound on the pulley, the closer is to zero, which prevents the cable from loosening over long-term usage. Based on the test result, the value for the contact between the Dyneema cable and the plastic pulley is approximated to 0.15.
Besides locking the cables, the cable-tightening mechanism in Figure 5 serves in the tensioning of the cables. For the simplest model, we consider AB as a rectangle with its edge lengths , and the wrist pulley (also applied for the pinion pulley) is clamped in place (see Figure 5). As the male pulley rotates in the clockwise direction with an angle , the cable generates a greater contact length with this pulley. In other words, the length BA has to be longer than its origin with an elongation . If we neglect any slippage between the cable and the pulley, the cable elongation in this situation is estimated as follows:
where r, k are, respectively, the radius of the pulley, the total number of teeth, and the rotational angle ( =j 2/k, ()). From Equation (2), a small increment in the angle significantly enlarges the elongation and the cable tension, which facilitates the users to adjust the cable tension by a slight rotation on each pulley.
2.4. Decoupling Mechanism
To transfer the force from the wrist motor to the wrist or pinion pulley, each end of every cable is locked at the wrist pulley or the cable tightener, and each cable must lean on one elbow pulley (see Figure 7). This mounting scheme generates the variation in the length for all cables with their length as the forearm rotates around the elbow joint according to [43,45]. Normally, one spring is inserted along the cable to compensate for the length variation [40,46], elastic cable [47], variable stiffness joint [48], compliant mechanism [49], and Bowden cables [50], or one motor directly compensates for them [38]. In this paper, let us suppose the rotational angle of the elbow joint and the wrist are , and , respectively. When rotating the forearm at to reach a new value of , the length changes with an amount of depending on the rotational direction of the forearm. It generates a jumping increment or a falling decrease in the cable tension. In the case of tension increment, two cable ends of each branch loosen to compensate for the extra tension, causing damage or fatigue on the system. In contrast, as the tension decreases, the motor cannot drive wrist/pinion pulleys with high repeatability due to the tension loss along the cable.
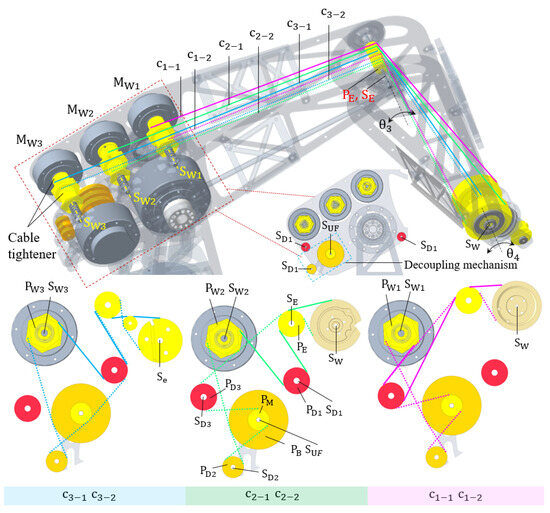
Figure 7.
Front-view illustration of cable layout in the robot arm. are, respectively, the motors driving the shoulder joint, forearm, and wrist. are the pulleys, respectively, elbow, minor, base, planar, direct 1, and direct 2, with their center lines . Inset images covered by the green-dash lines and red-dash lines show the front view of the cable layout at the elbow and the decoupling mechanism, respectively.
To eliminate the given problem, we propose a decoupling mechanism to maintain the cable length constantly whenever the forearm rotates around the elbow. As shown in Figure 7, the decoupling includes three pulleys: base and minor , with their bores being coincident with , and direct pulley , with its center line . Concurrently, the radius of triples in length with that of , . The working principle of this mechanism was also depicted in [43]. For each pair of cables , one branch is mounted on the decoupling mechanism and always generates an extra amount in its length of . Simultaneously, the remaining branch without traversing the decoupling mechanism generates an amount of . Hence, for each pair , having a length of = , we have the length variation as follows:
When the right-hand side of Equation (3) becomes zero or , the length variation in each cable is eliminated.
Equation (3) and the decoupling mechanism are applied to constantly maintain the length for all cables. However, due to traversing different structures, the cable requires one extra structure to balance its entire length . Back to Figure 3 and Figure 4, the pinion gear has a different design at each end, i.e., the gear transmission and a hinge joint connecting with the end-effector via a pinion shaft. A big hole at the pinion gear’s center line is designed for threading the cable from the LH and RH ring pulleys to the pinion pulley. When such cable branches drive the pinion pulley, the end-effector rotates around the pinion shaft. To maintain the cable tensions in , we hang those on the rollers between the pinion shaft and the ring shaft according to the mounting scheme with being on one straight line. Also, the relative locations of these points are fixed on the pinion gear. When the wrist bracket anti-clockwise rotates around the ring shaft with an angle , the angles and , resulting in the deviations of the cable length : , . In this scenario, the pinion pulley needs to rotate an angle of to eliminate such deviations on each cable.
3. Kinetics of the Robot Arm
The previous section depicted the structural design and the functions of each cluster in the robot arm. This section builds a kinematic model for the robot arm based on the main parameters relating to its joints and geometry.
Our robot arm comprises six DOF with six completely rotational joints. Let us embed one Cartesian coordinate system for each joint of the arm as shown in Figure 8, where is coincident with the center lines of shafts or motors, is the rotational angle between two connecting links around , and i is among . In the front view, we connect two sequential joints by one straight-segment line to identify the Denavit–Hartenberg parameters for the arm and obtain them as built in Table 1. In this scenario, the entities , a, and are the offset along the previous z axis to the common normal of the current link, the length of the common normal of the link, and the angle about the common normal from the previous z axis to the next one, respectively.
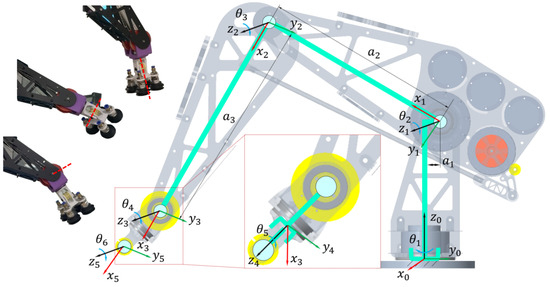
Figure 8.
Kinematics analysis of the cable-driven robot arm with six DOF. Inset images show the rotations of the wrist along three axes indicated by red-dash lines. The range of motion of each joint is = (°). can reach a full round and only a half round rotation if is zero and non-zero, respectively.

Table 1.
D-H parameters of the robot arm.
Let matrix be a homogeneous transformation depicting a motion relation between two consecutive links i and i+1, which is annotated from A1 to A6 for link 1 to link 6. Hence, matrix can be determined as follows:
Hence, the position and the direction of the end-effector link can be estimated as follows:
with
By replacing Equation (4) into (6), we obtain that is a 4 × 4 matrix over variations , a. Then, the left-hand side of Equation (5) can be calculated in Equation (7):
The matrix elements in Equation (7) are determined in Table 2. Hence, with the given parameters of the robot arm’s geometry, we can calculate the position and direction of the end-effector in the coordinate system of .

Table 2.
Deployment of elements in matrix M.
4. Results
4.1. Fabrication
The fabricated robot arm is illustrated in Figure 9. The panels are flat plates, each with a thickness of 2 mm, made from carbon fiber composite material. These plates are not only lightweight but also cost effective and quickly fabricated using CNC cutting. To further optimize the arm’s weight, a carbon fiber tube with a cross-section of 8 × 10 mm diameter is used to construct the connecting rod. The wrist’s differential gear consists of a set of two-ring bevel gears with a module of 1.5, made from polybutylene plastic. This material enables the gears to handle heavy loads without requiring lubrication. The pulleys are equipped with internal bearings and are covered with Polyoxymethylene (POM) plastic. Other components, such as the pinion gear, wrist bracket, end-effector, and cable tensioners, are made from PLA and PETG plastics, using Joseph Prusa and Ultimaker S5 printers. All cables mounted on this robot arm, denoted as , are made from Dyneema fiber with a 2 mm diameter cross-section.

Figure 9.
Fabrication and assembling processes for making the robot arm.
4.2. Electrical Design
As shown in Figure 10, the actuator system of our cable-driven robot arm includes six RMD-X Series (Myactuator) servo motors, which are known for their high precision and compact pancake design. For driving the base, forearm, and shoulder, we use the following motors: RMD-X8-S2 for the base and forearm, and RMD-X10-S2 for the shoulder. To accommodate fast motion and manage smaller torques, the wrist is driven by a unit consisting of three RMD-X6 motors aligned in a straight line. The entire actuator system is powered by a 48-volt power supply. The motors communicate via a CAN bus network, which enables high-speed data transfer at 500 kbps between motor components.
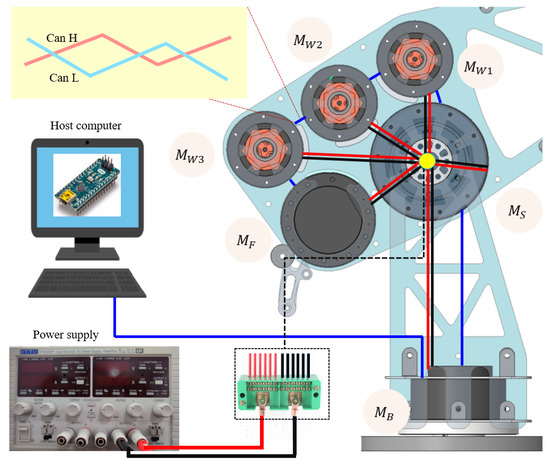
Figure 10.
Electrical design and controlling system for the cable-driven robot arm.
The CAN bus network directly connects to a host computer to transfer specific tasks that are run by the motors. The programming code, written in Arduino script, is compiled and uploaded to the CAN bus network using an Arduino Nano. Additionally, a 120 terminal resistor is connected in parallel to the CAN bus network to enhance communication reliability. The robot arm’s position (), velocity (), and torque () are controlled through auto-tuning PID controllers in feedback closed loops.
4.3. Testing Configuration of the Robot Arm
In this section, experiments are conducted on the fabricated robot arm to evaluate its configurations and performance. The evaluations include loading tests (see Figure 11), cable durability assessments (see Figure 11), repeatability tests (see Figure 12), and manipulation capabilities at the end.

Figure 11.
Setting up experiments for testing the cable loosening in static payload of 100 kg (a) and dynamic payload of 2 kg (b) with (b-1), (b-2), and (b-3), respectively, for rotating around .
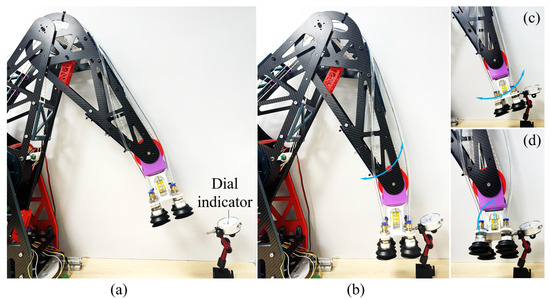
Figure 12.
Setting up experiments for testing the repeatability of the arm (a) and the wrist: (b), (c) and (d) for rotating around , respectively. In this figure, the grasped object is a box sucked and manipulated by a suction-cup gripper.
4.3.1. Loading Test
The loading test is one of the most important evaluations for our cable-driven robot arm, which is to evaluate the capability of the arm in loading the heaviest object in safety conditions such as a highly stable structure, less vibration, and no crack. For safety, the loads, the objects hooked to the end-effector of the robot arm, used in this test comprise 1 kg rice bags each [43]. The setting up for the load test can be referred from [43], where the motors , , , , and , generate torque to lift and move the object back and forth between two positions. The success and failure results are illustrated in Table 3. The wrist can hold and rotate the object up to 5 kg in a range of at all levels of the motor speed. Since the distance between the object (payload) and the elbow joint is very long, the energy requirement to lift the forearm becomes much higher than that of the wrist. Thus, to reach the same ultimate positions, the motor needs to run at higher speed levels to compensate for the loading energy in the case of increasing the payload.

Table 3.
Load testing at elbow.
4.3.2. Cable Durability Test
Cable durability is crucial for ensuring the stable operation of the robot arm over time. Typically, the cable tension decreases after extended use. This section evaluates the durability of the cables in the robot arm over a period and predicts the retained tension several months into the future.
The experimental setup for the cable loosening test on the wrist pulleys and the cable tightener is shown in Figure 11. The wrists serially rotate around axes in two cases: without payload and with a 2 kg payload gripped by a suction cup gripper attached to the end-effector. We use a tension meter to measure the cable tension for the cable at 0.1, 2, 4, 6, 8.5, 10, 13, 19, and 24 h after finishing the setting up. Additionally, two pulleys have ten rounds of cables wound, representing the model of the cable tightener, with one locked to a jig frame and the other attached to a 100 kg S load cell. It aims to test the cable tension after 28 days.
When lifting the 2 kg payload, the cable tension gradually reduces by 9.1, 14.3, and 16.9% in the case of RH-, pinion, and LH-wrist pulleys, respectively, after 4 h (see Figure 13). Then, after 10 h, such decrements slightly decrease by less than 1% over a whole day. The cable behavior can be characterized by two phases: elastic and plastic. In the current phase, we are testing 3D-printed prototypes for the wrist, which exhibit some deformation under payload after several initial hours of operation. Following this stage, the cables become more stable in the arm, resulting in only slight decreases in tension until the end of the trial. Interpolation curves for these scenarios are modeled using two different functions to represent each phase: linear for the elastic phase and logarithmic for the plastic phase. Based on these models, the predicted rate of cable tension loss after six months of continuous operation (24 × 182.5 h) is estimated to be 22.45% for the RH-wrist, 39.7% for the pinion, and 36.3% for the LH-wrist.
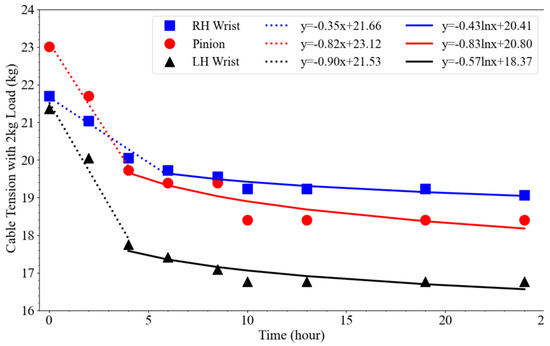
Figure 13.
Evaluation of the cable loosening under 2 kg dynamic payload. The value of each dot point indicates the measurement value of the tension, and the dot and solid lines show the interpolation of the real test data over time.
In Figure 14, the cable tension gradually decreases over time, by 7.5% after 28 days. Based on the interpolation curve, the cable tension will lose 9.67% after six months, and 20.4% after 10 years at a room temperature of 24 °C of continuous usage.
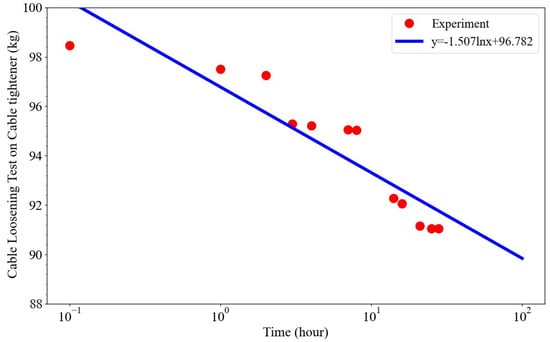
Figure 14.
Cable durability test on the cable tightener with 10 wound rounds on its hub surface under 100 kg static payload setting-up. The blue curve indicates the interpolating function from the experimental data (red markers).
4.3.3. Repeatability
Repeatability is crucial for ensuring the effectiveness of a cable-driven robot arm in practical applications. This section presents the measurements used to evaluate the position repeatability of our robot arm. In the experiment, a dial indicator is mounted on a platform using a magnetic base. The end-effector of the robot arm is then controlled to make contact with the probe of the indicator, allowing data to be recorded. The tests are conducted over ten iterations to assess the repeatability of the robot arm as shown in Figure 12. The repeatability tests include four separate measurements to assess the repeatability at each joint and degree of freedom (DOF) of the robot arm: the wrist and the six DOF of the arm.
As illustrated in Table 4, the deviation in this test of the six DOF arm is 0.005 mm with the maximum and minimum values of 0.4 and 0.35 mm, respectively. Also, the deviations in the cases of the LH and RH wrists are slightly different by 0.007 and 0.006 mm, respectively. The repeatability test of combining the ring gears of the wrist (LH and RH wrists) reach a zero standard deviation. The error is highest when only a single wrist pulley is turning due to the high friction. However, such errors decrease significantly when both pulleys move due to the two pulleys overcoming the friction better. Most of the errors are from the wrist pulleys, as there is no significant increase in errors when we add the additional three DOF for the elbow, and two shoulder motors. This is because these three DOF are direct drives instead of the cable-driven system.

Table 4.
Repeatability test for the wrist and the arm in 15 times trial (unit mm).
A gripper equipped with four rubber suction cups is mounted on the end-effector of the robot arm to evaluate its performance in manipulating various objects, including a filament box, heavy box, foam sheet, pneumatic-joint box, storage box, and component bag (see Figure 15). Each manipulation task is carried out in three phases: approaching and gripping the object, lifting and moving it, and finally placing and releasing it. The vacuum required for each suction cup is generated by a pump controlled by an Arduino microcontroller. The robot arm successfully manipulates all objects without any failures during the trials.
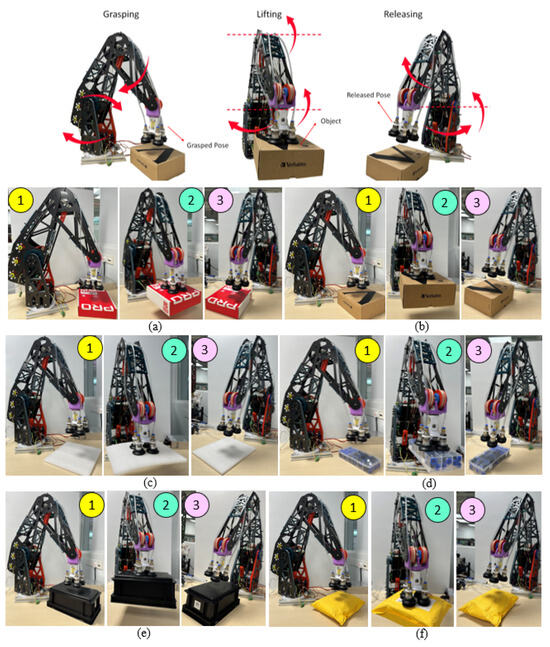
Figure 15.
Demonstration of the cable-driven robot arm in manipulating the objects (a) filament box, (b) heavy box, (c) foam sheet, (d) pneumatic-joint box, (e) storing box, and (f) component bag. (1), (2), and (3) are the phases of the experiments following the order of sucking, lifting, moving, and releasing.
Compared to other robot arms with similar upper arm and forearm scales, our robot arm demonstrates excellent repeatability and achieves a higher payload-to-body weight ratio of 5:8.4 kg. Additionally, the wrist and forearm contribute to safer interactions due to their lightweight design (the wrist and forearm each weigh 0.8 kg, representing approximately % of the total arm weight of 8.4 kg) and low inertia during movement (see Figure 16a)). The robot arm’s weight is concentrated at the upper arm, which accounts for roughly 50% of the total weight. This design helps counterbalance the arm during operation and reduces overall inertia. Furthermore, the total cost of our robot arm is approximately USD 3.5k, achieved by streamlining the fabrication process and selecting cost-effective materials (see Figure 16b)). Consequently, our robot arm is more affordable than other commercial robot arms with similar specifications. To improve the robot configuration in the future work, some encoders are considered to enhance the accuracy for the motions of robot joints. The bionic skin or tactile skin sensors [51,52,53] are useful for safety interaction thanks to sensing touch on the robot arm. The FEM methods such as [54] is meaningful to optimize the panel design and weight of the robot frame.
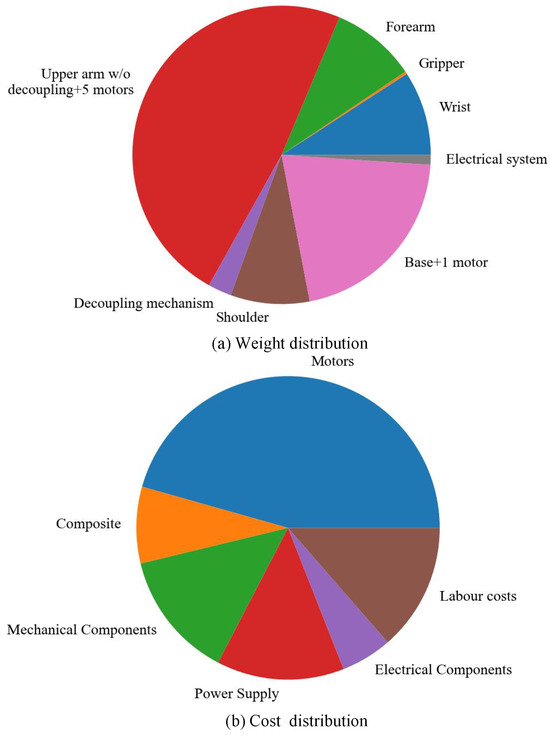
Figure 16.
Weight distribution (a) and cost distribution of our robot arm after fabrication (b).
5. Conclusions
This paper presents the development of a six-DOF cable-driven robot arm capable of manipulating a 5 kg payload at a distance of 400 mm from the elbow centerline. The novel design of the cable tightener significantly enhances cable durability, extending the service life of the arm. The incorporation of differential gears for the three DOF at the wrist improves the arm’s ability to lift heavy payloads with high repeatability. The arm’s repeatability during operation is within 0.1 mm, making it well suited for handling delicate and precise tasks. The optimization of composite panels contributes to a higher payload-to-body weight ratio and reduced inertial momentum during movement. Additionally, the robot arm is cost effective, making it suitable for a wide range of industrial and other applications.
6. Patents
The cable tightener depicted in Section 2C had a patent filed in Germany with a registered number of 102023135269.5 on 15 December 2023.
Author Contributions
V.P.N.—concept, design, modeling, experiment, and writing, S.B.D. and B.Z.—Fabrication, data analysis, experiment and writing, W.T.C.—concept, design, funding acquisition, writing, revision and proofreading, B.S.H. and H.Y.A.W.—writing, revising and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Agency for Science, Technology and Research (A*STAR) under its IAF-ICP Programme I2001E0067 and the Schaeffler Hub for Advanced Research at NTU.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- AboZaid, Y.A.; Aboelrayat, M.T.; Fahim, I.S.; Radwan, A.G. Soft robotic grippers: A review on technologies, materials, and applications. Sens. Actuators A Phys. 2024, 372, 115380. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Dhyan, S.B.; Mai, V.; Han, B.S.; Chow, W.T. Bioinspiration and Biomimetic Art in Robotic Grippers. Micromachines 2023, 14, 1772. [Google Scholar] [CrossRef] [PubMed]
- Qu, J.; Yu, Z.; Tang, W.; Xu, Y.; Mao, B.; Zhou, K. Advanced Technologies and Applications of Robotic Soft Grippers. Adv. Mater. Technol. 2024, 9, 2301004. [Google Scholar] [CrossRef]
- Goh, G.L.; Goh, G.D.; Toh, W.; Lee, S.; Li, X.; Sunil; Lim, J.Y.; Li, Z.; Sinha, A.K.; Yeong, W.Y.; et al. A 3D Printing-Enabled Artificially Innervated Smart Soft Gripper with Variable Joint Stiffness. Adv. Mater. Technol. 2023, 8, 2301426. [Google Scholar] [CrossRef]
- Lv, N.; Liu, J.; Jia, Y. Dynamic Modeling and Control of Deformable Linear Objects for Single-Arm and Dual-Arm Robot Manipulations. IEEE Trans. Robot. 2022, 38, 2341–2353. [Google Scholar] [CrossRef]
- Van Nguyen, P.; Ho, V.A. Wet Adhesion of Soft Curved Interfaces with Micro Pattern. IEEE Robot. Autom. Lett. 2021, 6, 4273–4280. [Google Scholar] [CrossRef]
- Hofer, M.; Zughaibi, J.; D’Andrea, R. Design and Control of an Inflatable Spherical Robotic Arm for Pick and Place Applications. Actuators 2021, 10, 299. [Google Scholar] [CrossRef]
- Nguyen, P.V.; Ho, V.A. Grasping Interface with Wet Adhesion and Patterned Morphology: Case of Thin Shell. IEEE Robot. Autom. Lett. 2019, 4, 792–799. [Google Scholar] [CrossRef]
- Yang, S.; Xu, S. Accuracy of autonomous robotic surgery for single-tooth implant placement: A case series. J. Dent. 2023, 132, 104451. [Google Scholar] [CrossRef]
- Xu, Z.; Xiao, Y.; Zhou, L.; Lin, Y.; Su, E.; Chen, J.; Wu, D. Accuracy and efficiency of robotic dental implant surgery with different human-robot interactions: An in vitro study. J. Dent. 2023, 137, 104642. [Google Scholar] [CrossRef]
- Trute, R.J.; Zapico, C.S.; Christou, A.; Layeghi, D.; Craig, S.; Erden, M.S. Development of a Robotic Surgery Training System. Front. Robot. AI 2022, 8, 773830. [Google Scholar] [CrossRef] [PubMed]
- Kaleem, A.; Hussain, S.; Aqib, M.; Cheema, M.J.M.; Saleem, S.R.; Farooq, U. Development Challenges of Fruit-Harvesting Robotic Arms: A Critical Review. AgriEngineering 2023, 5, 2216–2237. [Google Scholar] [CrossRef]
- Morar, C.A.; Doroftei, I.A.; Doroftei, I.; Hagan, M.G. Robotic applications on agricultural industry. A review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 997, 012081. [Google Scholar] [CrossRef]
- Yoshida, T.; Onishi, Y.; Kawahara, T.; Fukao, T. Automated harvesting by a dual-arm fruit harvesting robot. ROBOMECH J. 2022, 9, 19. [Google Scholar] [CrossRef]
- Nguyen, V.P. Picking food by robot hand with tree-frog like pad in various wet conditions. Eng. Res. Express 2024, 6, 015086. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Xu, W.; Wang, L.; Zhou, Z. Robot learning towards smart robotic manufacturing: A review. Robot. Comput.-Integr. Manuf. 2022, 77, 102360. [Google Scholar] [CrossRef]
- Barosz, P.; Gołda, G.; Kampa, A. Efficiency Analysis of Manufacturing Line with Industrial Robots and Human Operators. Appl. Sci. 2020, 10, 2862. [Google Scholar] [CrossRef]
- Weidemann, C.; Mandischer, N.; van Kerkom, F.; Corves, B.; Hüsing, M.; Kraus, T.; Garus, C. Literature Review on Recent Trends and Perspectives of Collaborative Robotics in Work 4.0. Robotics 2023, 12, 84. [Google Scholar] [CrossRef]
- Nguyen, P.V.; Nguyen, P.N.; Nguyen, T.; Le, T.L. Hybrid robot hand for stably manipulating one group objects. Arch. Mech. Eng. 2022, 69, 375–391. [Google Scholar] [CrossRef]
- Hernandez-Barraza, L.; Kalil-Khan, A.; Yeow, R.C.H. A bioinspired modular soft robotic arm. Eng. Res. Express 2023, 5, 015021. [Google Scholar] [CrossRef]
- Ouyang, W.; He, L.; Albini, A.; Maiolino, P. A Modular Soft Robotic Arm with Embedded Tactile Sensors for Proprioception. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics (RoboSoft), Edinburgh, UK, 4–8 April 2022; pp. 919–924. [Google Scholar]
- Zhang, Y.; Liao, J.; Chen, M.; Li, X.; Jin, G. A multi-module soft robotic arm with soft actuator for minimally invasive surgery. Int. J. Med Robot. Comput. Assist. Surg. 2023, 19, e2467. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Yuan, F.; Liu, J.; Tian, L.; Chen, B.; Fu, Z.; Mao, S.; Jin, T.; Wang, Y.; He, X.; et al. Octopus-inspired sensorized soft arm for environmental interaction. Sci. Robot. 2023, 8, eadh7852. [Google Scholar] [CrossRef]
- Deshpande, S.; Almubarak, Y. Octopus-Inspired Robotic Arm Powered by Shape Memory Alloys (SMA). Actuators 2023, 12, 377. [Google Scholar] [CrossRef]
- Tang, S.; Tang, K.; Wu, S.; Xiao, Y.; Liu, S.; Yi, J.; Wang, Z. Performance enhancement of the soft robotic segment for a trunk-like arm. Front. Robot. AI 2023, 10, 1210217. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y. Path planning and intelligent control of a soft robot arm based on gas-structure coupling actuators. Front. Mater. 2022, 9, 1052538. [Google Scholar] [CrossRef]
- Rao, P.; Peyron, Q.; Lilge, S.; Burgner-Kahrs, J. How to Model Tendon-Driven Continuum Robots and Benchmark Modelling Performance. Front. Robot. AI 2021, 7, 630245. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Wen, L. An Opposite-Bending-and-Extension Soft Robotic Manipulator for Delicate Grasping in Shallow Water. Front. Robot. AI 2019, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Su, H. Pneumatic Soft Robots: Challenges and Benefits. Actuators 2022, 11, 92. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, T.; Zhu, S. Simplified dynamical model and experimental verification of an underwater hydraulic soft robotic arm. Smart Mater. Struct. 2022, 31, 075011. [Google Scholar] [CrossRef]
- Qian, S.T. A Review on Cable-driven Parallel Robots. Chin. J. Mech. Eng. 2018, 31, 66. [Google Scholar] [CrossRef]
- Lum, G.; Yeo, S. Design and motion control of a cable-driven dexterous robotic arm. In Proceedings of the 2010 IEEE Conference on Sustainable Utilization and Development in Engineering and Technology, Kuala Lumpur, Malaysia, 20–21 November 2010. [Google Scholar]
- Wang, Y.; Yang, G.; Zheng, T.; Shen, W.; Fang, Z.; Zhang, C. Tension reduction method for a modular cable-driven robotic arm with co-shared cables. Intell. Serv. Robot. 2022, 15, 3410–3425. [Google Scholar] [CrossRef]
- Yuan, H.; Li, Z. Workspace analysis of cable-driven continuum manipulators based on static model. Robot. Comput.-Integr. Manuf. 2018, 49, 240–252. [Google Scholar] [CrossRef]
- Yeshmukhametov, A.; Koganezawa, K.; Yamamoto, Y. A Novel Discrete Wire-Driven Continuum Robot Arm with Passive Sliding Disc: Design, Kinematics and Passive Tension Control. Robotics 2019, 8, 51. [Google Scholar] [CrossRef]
- Wei, D.; Zhou, J.; Zhu, Y.; Ma, J.; Ma, S. Axis-space framework for cable-driven soft continuum robot Zou2017control via reinforcement learning. Commun. Eng. 2023, 2, 61. [Google Scholar] [CrossRef]
- Tang, J.; Tao, H.; Zhuang, X.; Cheng, Y.; Xiao, H.; Xu, K.; Ding, X. Design and analysis of cable-driven robotic arm with variable stiffness modular joint. In Proceedings of the 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO), Jinghong, China, 5–9 December 2022; pp. 1843–1848. [Google Scholar]
- Yang, K.; Yang, G.; Zhang, C.; Chen, C.; Zheng, T.; Cui, Y.; Chen, T. Cable Tension Analysis Oriented the Enhanced Stiffness of a 3-DOF Joint Module of a Modular Cable-Driven Human-Like Robotic Arm. Appl. Sci. 2020, 10, 8871. [Google Scholar] [CrossRef]
- Chen, Q.; Qin, Y.; Li, G. QPSO-MPC based tracking algorithm for cable-driven continuum robots. Front. Neurorobot. 2022, 16, 1014163. [Google Scholar] [CrossRef]
- Choi, K.; Park, F.C. A hybrid dynamic model for the AMBIDEX tendon-driven manipulator. Mechatronics 2020, 69, 102398. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, T.; Chen, J.; Xu, W.; Wei, H.; Song, Y.; Guan, Y. A modular cable-driven humanoid arm with anti-parallelogram mechanisms and Bowden cables. Front. Mech. Eng. 2023, 18, 6. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Lee, W.W.; Liu, T.; Teng, X.; Zheng, Y.; Li, Q. A Robust Model Predictive Controller for Tactile Servoing. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 13848–13854. [Google Scholar]
- Nguyen, V.P.; Bohra Dhyan, S.; Hoang, C.C.; Siew Han, B.; Tan, J.Y.; Tuck Chow, W. Mitigate Inertia for Wrist and Forearm Towards Safe Interaction in 5-DOF Cable-Driven Robot Arm. In Proceedings of the 2023 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Seattle, WA, USA, 28–30 June 2023; pp. 215–220. [Google Scholar]
- Nguyen, V.P.; Chow, W.T. Wiring-Claw Gripper for Soft-Stable Picking up Multiple Objects. IEEE Robot. Autom. Lett. 2023, 8, 3972–3979. [Google Scholar] [CrossRef]
- Jiang, S.; Hua, D.; Wang, Y.; Ju, F.; Yin, L.; Chen, B. Design and modeling of motion-decoupling mechanism for cable-driven joints. Adv. Mech. Eng. 2018, 10, 1687814018777428. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Dhyan, S.B.; Han, B.S.; Chow, W.T. Universally Grasping Objects with Granular—Tendon Finger: Principle and Design. Micromachines 2023, 14, 1471. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.V.; Sunil, D.B.; Chow, W.T. Soft-stable interface in grasping multiple objects by wiring-tension. Sci. Rep. 2020, 13, 21537. [Google Scholar] [CrossRef]
- Goh, G.L.; Huang, X.; Toh, W.; Li, Z.; Lee, S.; Yeong, W.Y.; Ng, T.Y. Joint angle prediction for a cable-driven gripper with variable joint stiffness through numerical modeling and machine learning. Int. J. AI Mater. Des. 2024, 1, 62. [Google Scholar] [CrossRef]
- Liu, T.; Hao, G. Design of a Cylindrical Compliant Linear Guide with Decoupling Parallelogram Mechanisms. Micromachines 2022, 13, 1275. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, S.K.; Yang, G.; Yeo, S.H.; Lin, W.; Chen, I.M. Self-Calibration of a Biologically Inspired 7 DOF Cable-Driven Robotic Arm. IEEE/ASME Trans. Mechatron. 2008, 13, 66–75. [Google Scholar] [CrossRef]
- Gaoyu, L.; Wei-Hsin, L. A self-powered magnetoelectric 3D tactile sensor with adjustable sensitivity for robot arms. Sensors Actuators Phys. 2024, 374, 115455. [Google Scholar]
- Van Nguyen, P.; Pham, V.C.; Tan, Y.; Ho, V.A. Toward a Tactile Ontology for Semantic Interoperability of the Tactile Internet. In Proceedings of the 2022 IEEE 16th International Conference on Semantic Computing (ICSC), Laguna Hills, CA, USA, 26–28 January 2022; pp. 115–118. [Google Scholar]
- Zou, L.; Ge, C.; Wang, Z.J.; Cretu, E.; Li, X. Novel Tactile Sensor Technology and Smart Tactile Sensing Systems: A Review. Sensors 2017, 17, 2653. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Lee, J. Load-Carrying Capacity of Ultra-Thin Shells with and without CNTs Reinforcement. Mathematics 2022, 10, 1481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).