1. Introduction
Algorithms for 6D pose estimation of objects are fundamental modules of any robotic system for logistic applications where the relocation of items is a task of primary relevance. One of the most challenging material-handling tasks is the pick-and-place of items characterized by a high variability of object instances in appearance and dimensions. Food handling is a logistic scenario where such a challenge arises, demonstrating an increasing interest of food industries in autonomous solutions, especially in packaging systems, in the last decade [
1]. The related challenges include making robotic manipulators able to first localize in space objects of variable shape and dimensions, such as fruits and vegetables, and then carefully grasp them without any damage. Although several solutions for pick-and-place tasks have already been developed, dealing with delicate food makes the problem more challenging as explained in [
1,
2,
3]. Indeed, although the 6D pose estimation algorithms based on RGB-only images (such as [
4,
5]) devised so far can localize objects with no variability in appearance and size with great accuracy, they cannot localize different instances of the same object, such as fresh fruits, which greatly differ in appearance and dimensions; this is still an open problem, and some solutions based on deep learning have been proposed in some works such as [
6,
7]. Besides the localization problem, the existing technology typically used to pick items in the industry could be unsuitable for grasping delicate fruits without damaging them. Existing solutions are based on two main approaches, the use of soft grippers [
8] and tactile sensors [
9]. The former ones are difficult to control in a precise way, while the latter ones require proper algorithms for the interpretation of tactile data and their correlation to the grasping force [
3]. As demonstrated by the approach used by humans to manipulate fresh fruits, the best way to avoid deteriorating food is controlling the force used for grasping it; therefore, grippers equipped with tactile sensors seem to be a great replacement for the suction cup usually adopted in industrial practice.
The localization of the object to grasp is usually achieved by adopting a pose estimation algorithm based on deep learning techniques, able to recognize objects in a cluttered scene and estimate their position and orientation in the space. This is a common feature of all the examined methods [
4,
5,
10,
11,
12,
13].
Here, we classify the existing 6D pose estimation algorithms into two main categories: the pure learning methods, based on an end-to-end approach, and the hybrid ones, which combine deep learning techniques with geometrical approaches, thus exploiting additional knowledge to improve the accuracy of the estimated pose. Concerning the pure learning approach, PoseNet proposed in [
13] is one of the first end-to-end 6D pose estimation models, based on convolutional neural networks (CNNs) and RGB data only, and it regresses the camera pose in both indoor and outdoor scenarios. By exploiting the same input, Deep-6DPose in [
4] extends the instance segmentation network Mask R-CNN [
14] with an end-to-end regression-based pose estimation branch to jointly detect, segment, and recover the 6D pose of a target object without any post-refinement algorithm. In order to improve the pose estimation performance in complex environments, several works exploit RGB-D data, thus directly elaborating both the depth and the corresponding RGB image. The authors of [
12,
15,
16] propose an efficient RGB-D dense (pixel-wise) approach to fuse the two data sources individually processed. On the other hand, the approaches developed in [
10,
17] regress the eight corners of the 3D cuboid enclosing a known object and use the Perspective-n-Point (PnP) solver [
18] to retrieve the corresponding 6D pose, thus realizing a hybrid 6D pose estimation algorithm. Moreover, the methods presented in [
19,
20] employ a least-squares fitting algorithm [
21] instead of PnP to retrieve the final 6D pose given the keypoints on the object surface. Other hybrid solutions, such as [
11], exploit a pose refinement stage based on geometrical approaches, such as the Iterative Closest Point (ICP) algorithm [
22], to improve the accuracy of the pose arising from a deep learning technique.
In this article, which extends the conference paper [
23], we present an extensive experimental comparison between a pure deep learning method based on the widely used DenseFusion deep neural network [
12] and the hybrid method, originally proposed in [
23], resulting from a combination of the RGB-only algorithm Deep Object Pose Estimation (DOPE) [
10] with a geometric pose refinement algorithm based on the availability of the depth map. The same algorithm is also used in a more sophisticated manipulation task including non-prehensile manipulation actions in [
24]. Moreover, besides comparing two pose estimation methods with two fruit types, while the conference paper considered apples only, we add new experiments with the following objectives: highlighting how both the position and orientation of detected fruits are relevant to the grasping action, quantifying the noise level and sensitivity to the lighting conditions of the two compared methods.
The presented comparison is carried out by testing the robotic fruit picking not only with the apples used in the former conference paper but also with other fresh fruits. To avoid damage to the fruits, the slipping avoidance grasp control algorithm described in [
2] is added to the overall robotic pipeline. Exploiting the 6D contact wrench measurements arising from a parallel gripper equipped with the SUNTouch force/tactile sensors [
3], the aforementioned control algorithm computes the minimum grasp force required to lift the object, whose weight is unknown.
Figure 1 shows the overall setup of the robotic picking solution.
The test results prove that both methods can address the problem of dimension variability but with differing performance. Indeed, the experimental results of several picking tests of various types of fruits with similar appearances but different dimensions show that the robotic picking system has a better grasp success rate with the proposed 6D pose hybrid estimation algorithm than with the state-of-the-art purely deep learning method. The paper presents a final discussion on the accuracy of the compared methods and a deep analysis of all their pros and cons.
2. Materials and Methods
The deep learning methods to address the pose estimation problem can be divided into 2 groups: the ones that use only RGB images and the ones that add to that information the depth map. In general, RGB models are attractive thanks to their simplicity since no fusion is required to merge multiple data sources and the sensor is a standard RGB camera, making these methods quite cheap (see [
5,
10,
25]). On the other hand, they may suffer a loss in accuracy from the lack of the geometrical information given by the depth channel, especially in the case of occlusions or high-intensity light conditions. Furthermore, the recent availability of relatively cheaper depth sensors has increased the attention on RGBD models [
11,
12,
16,
20], which, at the cost of a more complex architecture, usually are more accurate and less sensitive to occlusion and lighting conditions. To investigate the 2 methodologies, we choose one model for each category, namely DOPE [
10] and DenseFusion [
12]; both are selected thanks to their effectiveness in solving the pose estimation problem and for having inspired several subsequent models such as [
20] or [
26].
To make DOPE able to correctly detect objects that differ in terms of size from the model used during the training, in [
23], we realize a hybrid solution by combining DOPE with a geometric algorithm that exploits the depth map without fusing it with the RGB image as it happens in DenseFusion.
2.1. DenseFusion
The DenseFusion network is an
instance-level pose estimator, which directly regresses the pose, as a translation vector and a quaternion, of instances of known objects from RGB-D images. The methods also require the point cloud models during training but not in the inference stage. The architecture of the model (see
Figure 2) can be divided into 4 main components in series: the first one performs instance segmentation on the input RGB image, isolating the pixels belonging to each instance of the object of interest in the scene; in the second component, the cropped RGB image and the masked point cloud are passed to the feature extraction module, which generates both pixel-wise and global features; the third component performs the pose prediction based on each of the input features; and the last component is an optional refinement module that improves the prediction coming from the previous component. The dense fusion processing is carried out during the feature extraction phase, and it consists of concatenating each feature (related to the same pixel) coming from the CNN and the PointNet modules. As for the global feature, it is computed by applying an average pooling stage to the output of a fully connected Multi Layer Perceptron (MLP) network, that takes as inputs all the dense features. The pose predictor module processes one feature for each segmented pixel and estimates a pose for each of them. It follows that there is one estimated pose for each segmented pixel, and therefore a mechanism to select the final pose is needed. The network training has a twofold objective. The first one aims at minimizing the mean distance between the corresponding points in the actual object’s point cloud and the one transformed by the regressed pose; the second one aims at learning a score for each prediction that measures how confident the network is. The final pose is simply chosen as the one that has the maximum score.
It is worth noting that the network used for the real robotic grasp is trained on synthetic data only, in contrast to the original work in [
12], which used classical benchmarks as LineMOD in [
27] and YCB-video in [
11] for both training and testing.
2.2. DOPE + Pose Refinement
The
instance-level level neural network DOPE works only on RGB images and assumes to know the size of the object to recognize at inference time. With reference to
Figure 3, DOPE is characterized by a two-stage architecture that first regresses nine keypoints of the object in the image plane. These keypoints are functional to the estimation of the eighth vertices and the centroid of the 3D cuboid enclosing the object. The keypoints are estimated by a deep CNN and a Greedy Algorithm (GA) necessary to associate keypoints to a single object. The second stage, exploiting the knowledge of the camera intrinsic parameters and the known cuboid dimensions of the recognized object, uses the standard PnP algorithm [
18] to retrieve the 6D pose of the object. This separation between regression and pose retrieving is an attractive feature of the architecture because the network will learn only the object’s appearance feature and not the camera parameters too. It follows that the network parameters do not depend on the camera used to make the inference, unlike other end-to-end pose-estimation algorithms such as DenseFusion or [
11]. However, if a scaled version of the CAD model used for the training were shown to the network, the estimated position would be affected by an error proportional to the scale difference between CAD and real object. Indeed, estimating the position of a scaled version of the trained object using a single RGB image is an ill-posed problem since we cannot establish whether we are looking at a smaller object nearest to the camera or at a bigger one farthest from the camera. To overcome this limitation and successfully use DOPE to recognize and localize objects of different scales as shown in the last part of the scheme of
Figure 3, we exploit the camera depth measures by employing the pose refinement algorithm presented in [
23], and here summarized for the reader’s convenience. The algorithm consists of jointly translating and scaling the CAD model of the object (used by the network) in a virtual world without altering its representation in the image plane so that the virtual depth map of the object and the real one are best overlapped.
Let
and
be the position and unit quaternion estimated by DOPE with respect to the camera frame, respectively. We can place the CAD model (used by the network) in a virtual world at the same pose with respect to a virtual camera and capture the corresponding virtual depth map. Using the geometric relations reported in (
1) and (
2) (more details can be found in [
23]), for a given scalar value
, we can translate the CAD in the new position
and to scale it into the updated cuboid dimensions
(starting from the original ones
) such that the RGB image is the same but the depth map is different. Therefore, we can solve an optimization problem to compute the optimal
such that the depth map coming from the RGB-D sensor and the one rendered are best overlapped. Once the
is computed, we can retrieve the refined position
and the refined cuboid dimensions
entering with this value in Equations (
1) and (
2):
Figure 4 shows the pose estimation of an apple smaller than the CAD model used for training DOPE and the resulting one after the pose refinement. The bigger apple (under the table) has the same dimensions as the CAD model and generates the same RGB image of the actual smaller apple (on the table). As expected, the position estimated by DOPE is such that the object is located under the table due to the size mismatch, but our refinement is able to correct not only its position but also its dimensions.
2.3. Robotic Fruit Picking
To successfully pick the fresh fruit, we adopt the robotic pipeline described in detail in [
23], whose architecture is illustrated in
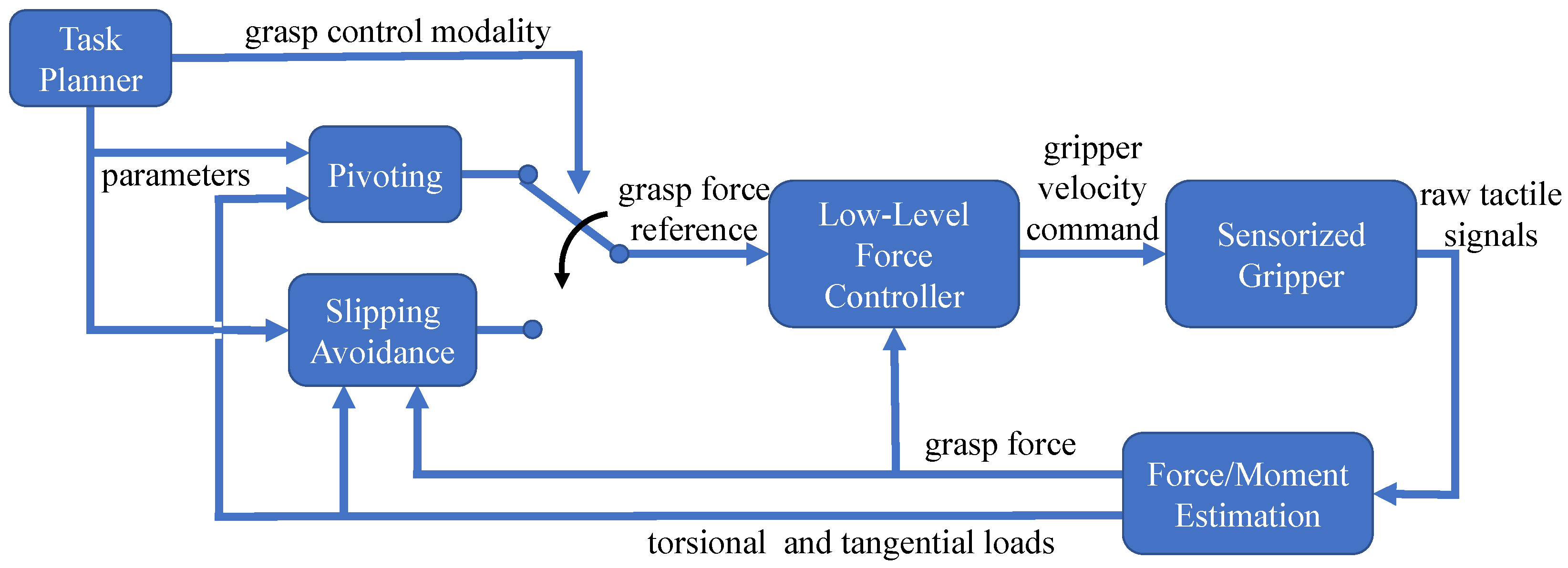
Figure 5. The pipeline is composed of a vision component for the Equation6D pose estimation algorithm (which is one of the two methods being compared), a motion-planning module, used to bring the robot gripper in a collision-free grasp pose, and a grasp-force controller for parallel grippers, which exploits tactile measures to grasp the delicate items, avoiding any deformation or damage. The motion-planning module and the grasp-force controller are briefly described in the next subsections. In
Section 3, we report the experimental results of the robotic pipeline when the objects to pick are apples or limes.
2.4. Grasp Control
The target objects are fresh fruits to be handled with care to avoid their damage; thus, the grasping force should be the lowest one that permits lifting with no slippage.
This challenging task is carried out by the model-based grasp force controller in [
2] that will be here briefly described for the readers’ convenience. The control law enables two modalities,
slipping avoidance and
pivoting (see
Figure 6). In both cases, the algorithm outputs a grasp force reference tracked by a low-level force controller. To grasp the fruits, we use only the slipping avoidance modality.
The grasp force
is computed as a superposition of two contributions, a static contribution
and a dynamic one
. The object motion is modeled as a planar slider, i.e., a rigid object that moves in a plane and can be described as a pure rotation about the instantaneous Center of Rotation (CoR) with angular velocity
. In particular,
is the minimum force that avoids slippage in static conditions; it exploits the Limit Surface concept [
28], and it is based on the measured tangential and torsional loads estimated by the fingertip tactile sensors.
When the loads are time-varying (e.g., during the lifting), the static contribution is not enough, as the maximum friction decreases as the rate of the variation in the load increases [
29]. Such a condition is modeled by the LuGre dynamic friction model [
30]. The dynamic contribution
is based on a slippage velocity observer exploiting a dynamic model that combines the LuGre dynamics with the Limit Surface concept.
is computed by applying a linear control law that brings the estimated slippage velocity to zero. The interested reader can find more details on the control design and its stability property in [
30].
2.5. Motion Planning
To improve the safety of the overall pick-and-place task and avoid collisions with obstacles in the working scene, we adopt the RRT* planning algorithm, powered by the open-source motion planning library OMPL [
31] and directly integrated into the MoveIt! [
32] platform. Given the pick-and-place poses, we plan from the pre-grasp pose to the post-place one by appropriately alternating the plans in joint and Cartesian spaces. In the end, the overall task is executed by the robot only if the motion planner has successfully found the sequence of the required trajectories. Finally, to make the robot aware of the surrounding obstacles, we exploit the point cloud from the depth camera to reconstruct the corresponding OctoMap [
33].
2.6. Grasping Strategy
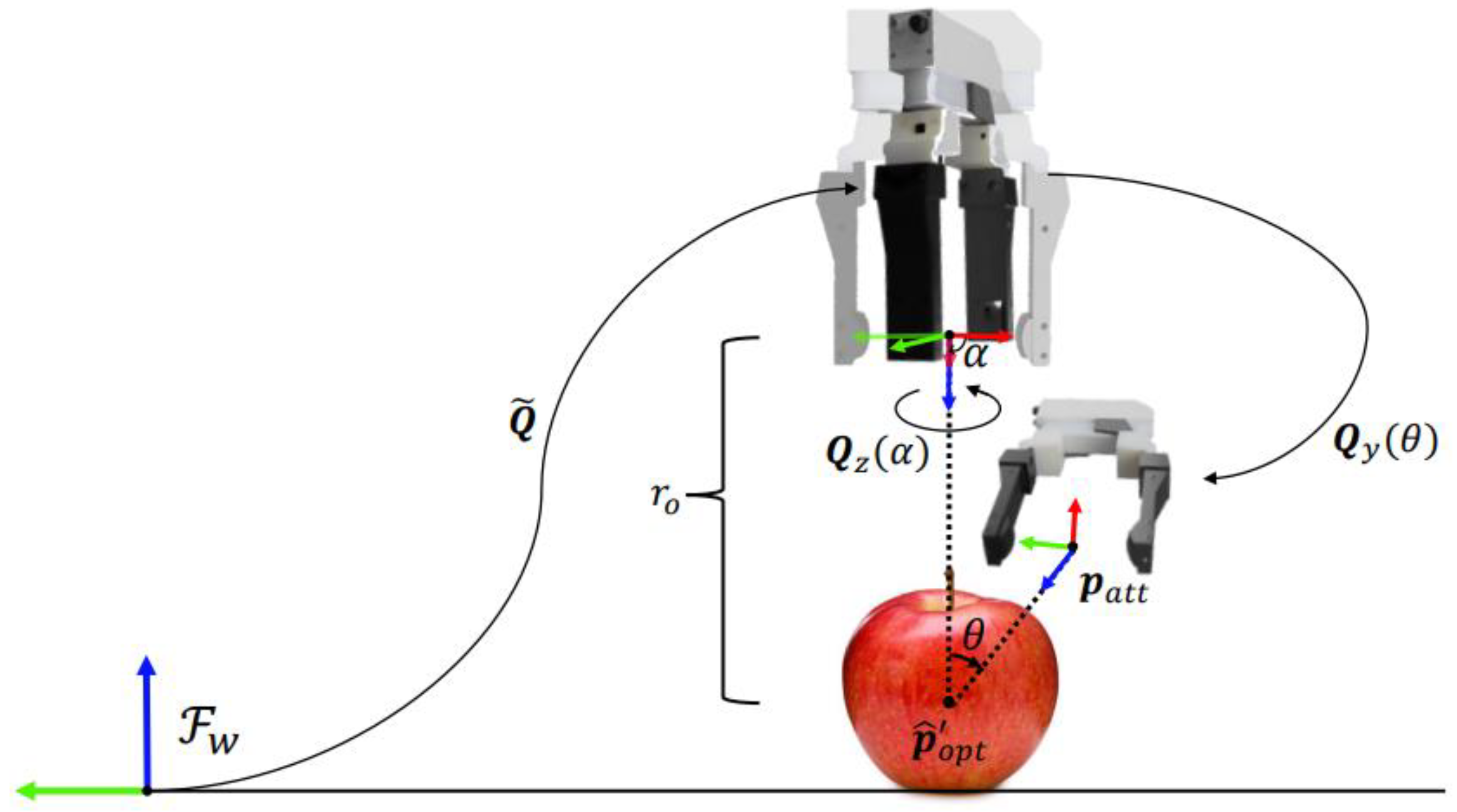
Given the estimated pose of the target object, a suitable grasp pose has to be defined depending not only on the object’s shape but also on the obstacles of the scene. Therefore, to ensure a successful grasp, we adopt the grasp strategy described in [
23], which is well suited for the fruits under consideration, i.e., apples and limes, which have a practically spherical shape. Indeed, referring to
Figure 7, the strategy consists of sampling a sphere of radius
centered at the estimated position of the target object
. In particular, the positions are computed by varying the rotation angle about the
z axis of the object frame (assumed aligned to the axis of symmetry)
and those about the gripper sliding vector
, while the orientations arise from the quaternion product
, where
is used to align the approach vector of the end-effector frame with the
z axis of the world frame, and
and
represent the elementary rotation about the
z and
y axes of the corresponding angles, respectively.
3. Results
The following experimental tests aim to evaluate whether and with what accuracy the two selected algorithms estimate the 6D pose of apples and limes of various sizes, different from those of the CAD model used during the training phase. The pick-and-place tasks are performed using the seven-axis robot Yaskawa Motoman SIA5F, equipped with the RGB-D Intel Realsense D435i camera mounted on a WSG32 gripper. This latter is sensorized with the SUNTouch force/tactile fingers [
3] that provide a
tactile map and are calibrated to estimate the full contact wrench at 500 Hz between 0.5 and 8 N with an accuracy of 0.2 N. The gripper accepts finger velocity commands updated at 50 Hz to control the grasp force. The CAD model of the apple used to train DOPE and DenseFusion is enclosed in a cuboid with dimensions in meters
, where, according to the orientation of the CAD frame,
m represents the apple height. Moreover, the CAD model of the lime is enclosed in a cuboid with dimensions
, where
m represents the lime height.
3.1. Dataset Generation and Training of the Models
Both models are trained on synthetic datasets using the CAD models described above. In order to ensure a suitable variability among all the images, the datasets of both limes and apples are generated by randomizing several elements, such as the background and the relative orientation of the camera, the light intensity, and the type and the number of distractors, as well as the number of instances of the object of interest. This randomization is inspired by works such as [
10,
34,
35,
36], which show the effectiveness of using simulated data to train deep learning algorithms for real-world tasks such as grasping, drone flight, and object recognition. The same works also suggest that, through domain randomization and/or adaptation, the generalizability of the network can be improved; if the training set is built with a large number of synthetic images that represent the same objects in very different configurations or if only a few real images are injected into the synthetic dataset, the network is forced to learn only the highly important features from the training images due to the high variability of the dataset.
The software used to generate the data is NViSII [
37], which also provides the APIs to store the annotations in JSON format. Regarding the apples, the generated dataset contains 120 k frames, 30% of which are used as the validation set and the remaining part as the training set. The training procedure of DenseFusion takes 51 epochs with a learning rate of
, a batch size of 32, and a refine margin (the distance margin below which the refinement training starts) of 9 mm. Instead, DOPE is trained for 120 epochs with a batch size of 116 and a learning rate of
. For limes, the dataset contains about 5 k frames, 20% of which are used for the validation and the remaining for the training phase. DenseFusion is trained for 277 epochs with a learning rate of
and a batch size of 32, while DOPE requires 232 epochs with a batch size of 116 and a learning rate of
. Note that, even if the lime dataset is much smaller than the apple one, each frame of the former contains a higher number of object instances than the latter one as the sample frames in
Figure 8 demonstrate.
Training and testing are both implemented on a workstation equipped with a GPU NVIDIA Titan V GV100 and an Intel Core i9-7980XE processor at 2.60 GHz. The OS used is Ubuntu 20.04 LTS. The reason why the two networks are trained for different epochs is that, to carry out a complete comparison, we decide to allocate the same training time to both to assess which one, with a given amount of training time, performs better. The allotted training time is 72 h, which is enough to have a satisfactory convergence of the loss function, whereas the inference rates of DenseFusion and DOPE are about 20 Hz and 15 Hz, respectively.
3.2. Comparison of the Two Methods
The comparison of the two methods is carried out in three experimental tests by employing the robotic pipeline described in the previous section. In the first test, the quantitative results are provided in terms of two metrics.
The first one is aimed at evaluating the pose accuracy. Considering that we express all the estimated poses in a reference frame with the origin located on the table surface and the
z axis pointing in the upward direction, to evaluate the pose accuracy along the
z direction, we define the ground truth equal to the half of each fruit height
h, which corresponds to
for apples and
for limes. Therefore, we define the
centroid error metric as the difference between
and the
z coordinate of the estimated frame. The second metric is the
grasp success rate defined as the ratio between the number of successful fruit grasps and the total number of attempts. A grasp is successful if the fruit is picked and lifted without dropping or damaging it; the damage is evaluated by means of visual inspection. For this experimental test, we select five apples (see
Figure 9) and two limes (see
Figure 10) such that all of them have great variability in terms of dimensions compared to the CAD models used in the model training.
Regarding the centroid error, we evaluate the results obtained with each apple and each lime in location 3, indicated in
Figure 9 and
Figure 10, respectively.
Table 1 shows a first rough comparison of the two proposed algorithms highlighting the centroid error metric. Regarding the apples, the accuracy of the estimated position along the
z direction seems to be unaffected by the dimension variability for both the proposed methods. Therefore, both methods might be able to provide a position accurate enough to allow a successful grasp. Instead, regarding limes, unlike DOPE + Pose Refinement (PR), DenseFusion does not provide a position that allows us to grasp the fruits since the resulting
z component of the estimated position is mostly above the centroid of the object.
The results of the comparison in terms of grasp success rates are computed on three repetitions of each grasp attempt for each apple and each lime approximately placed in the five locations with different orientations on the table that the robot is fixed to, shown in
Figure 9 and
Figure 10, respectively, for a total of 105 grasp attempts for each pose estimation algorithm.
Table 2 shows the corresponding results obtained by using DenseFusion and DOPE + PR, respectively. These more accurate experiments show that DOPE + Pose Refinement significantly outperforms DenseFusion (which uses its refinement method too): regarding the apples, we obtain a 68% overall grasp success rate for the latter and an 88% grasp success rate for the former; for the limes, we obtain a 40% overall grasp success rate for DenseFusion and a 100% grasp success rate for DOPE + Pose Refinement. The success rates achieved by DenseFusion for limes being slightly worse than those achieved for the apples could be explained by the small dimensions of the selected limes (even smaller than Apple 5), which require a higher accuracy of the estimated pose to be picked correctly.
The second experimental test is devoted to assessing the sensitivity of the two pose estimation methods to lighting conditions by evaluating the grasp success rate metric. To this aim, additional fruits are selected, i.e., a big and a small apple and a big and a small lime.
Figure 11 shows the four fruits and the four locations selected for the grasp attempts that are repeated three times by approximately placing each fruit in each location with a random orientation, for a total of 48 grasp attempts for each pose estimation algorithm. Note that the two locations on the taller box are subject to a brighter illumination than those on the lower box, where the fruits are overshadowed.
Table 3 shows the grasp success rates obtained in the second test. The two pose estimation methods show a different sensitivity to the lighting conditions. The performance of both the algorithms deteriorates for the overshadowed fruits, but DenseFusion is more affected by non-optimal lighting conditions.
A third experimental test is performed with the specific objective of comparing the two methods in the estimation of the orientation of fresh fruits. An apple is placed in a fruit punnet in the three different orientations shown in
Figure 12. This arrangement is chosen for a twofold reason; first, to keep the apple in a stable position with different orientations, and second, because it is representative of a common situation in practice. Again, the evaluation is carried out indirectly through the grasp success rate computed on three repetitions of each orientation. We perform the experiment with the apple only because the limes are too small to be grasped without collisions in a cluttered fruit punnet.
Figure 13 clearly shows that the gripper orientations planned to grasp the apple are significantly different for each of the three apple orientations, demonstrating that the estimation of the full 6D pose is relevant to the grasp. The results reported in
Table 4 confirm that DOPE + PR generally outperforms DenseFusion.
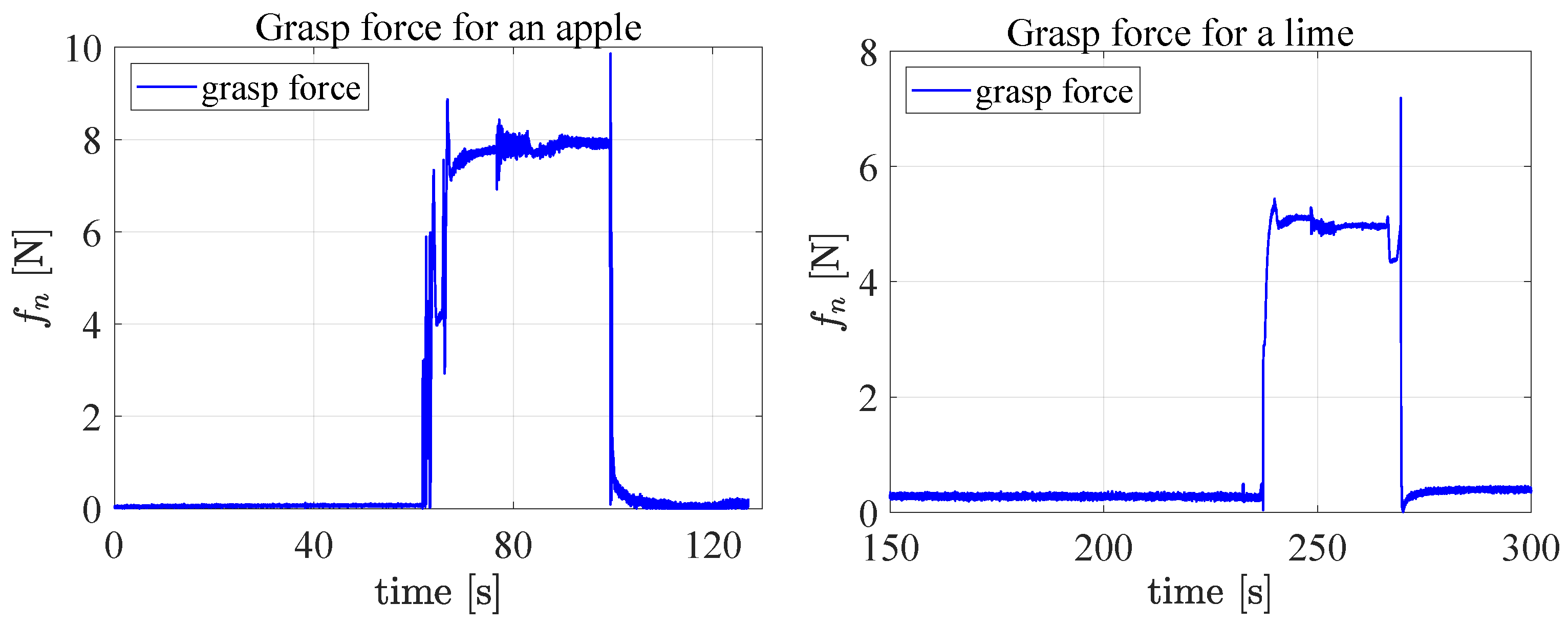
By observing the failure cases in more detail, we can argue that the failures of the DenseFusion method are mainly due to the low accuracy in the pose estimation, as it can be appreciated in the attached video at minute 1:12–1:43 and at minute 8:36–8:45, where, even if MoveIt! successfully plans the grasps of the fruit, the task fails due to the error in the
plane or to an orientation error, respectively. Instead, the DOPE + PR failures are mainly due to the inaccurate estimation of the object scale since they all happen during the planning phase because of the collisions of the fingers with the support table. The video also shows a pick-and-place experiment with some limes and apples in a crate, where the robot has to place them in separate bowls. With reference to this experiment,
Figure 14 (left) and
Figure 14 (right) show the trend of the grasp force computed by the grasp controller and applied by the sensorized fingers to an apple and a lime, respectively. As expected, lifting the apple requires a higher force than lifting the lime because it is lighter than the apple.
A final evaluation is performed to assess the noise level of the pose estimated by the two algorithms being compared. An apple and a lime are placed first on the left box (good lighting) and then on the right shelf (bad lighting) in
Figure 11. The standard deviations of the estimated pose components are reported in
Table 5. It is quite evident how the lighting conditions affect the noise level in both algorithms but the pose components estimated by DenseFusion are generally more noisy.
4. Discussion
Besides the differences in terms of accuracy of the estimated pose and grasp success rate, the compared methods also differ in terms of the resources needed and complexity. In particular, we find that DenseFusion needs more training time to make estimations accurate enough to be used in a real grasp experiment.
This is due to two main reasons:
DenseFusion is a modular architecture, which rigidly separates the segmentation pipeline from the pose estimation one. Hence, if on one hand, this enhances the scalability and the interpretability of the entire model, on the other hand, this also implies that two different (and usually large) networks must be trained, one that provides the segmentation masks and one that implements the pose estimation. This could significantly increase the training time if the two networks cannot be trained in parallel and makes the joint optimization of the whole method more difficult.
Since the refiner is a deep network too, it must be trained as well as the main pipeline, with the further condition that its training cannot start until the main network has converged, as otherwise it will not learn useful information, i.e., the refiner and the main network cannot be trained in parallel. This increases the total training time.
The modular nature of DenseFusion also requires that the network has to be deployed on hardware that is more powerful (and expensive) since it requires more memory usage to run the inference because two models have to be loaded into the VRAM at the same time. Of course, this could be mitigated by using simpler segmentation networks, but the accuracy of the masks greatly impacts the overall performance of the estimator, so a careful trade-off must be chosen. Another feature of the DenseFusion architecture is that it is quite noisy, in the sense that the estimated pose has a considerable degree of variability. This fact could be explained by the decision to make a direct regression on the input images, which means that the network has to learn a strongly non-linear function that maps the 2D information (the ones in the image space) to 3D space (position and orientation); therefore, especially for the orientation, even very slight changes in the input could produce very different outputs in the final prediction. DOPE, on the other hand, applies a keypoint-based regression, mapping 2D information (the RGB image) to 2D keypoints (the corners and the centroid), so the function to be learned is simpler, and the pose is less noisy. Another consequence of performing a direct regression on the images is that the network might suffer a considerable drop in performance if the camera parameters used for training are not exactly the same as the ones used during the inference stage: making 6D predictions directly on the images causes the network, during the training phase, to specialize too much on the particular characteristics of the images coming from a specific camera, indirectly learning also the intrinsics, distortions, and all those parameters tightly linked to the camera used to construct the dataset. On the other hand, DOPE (and all methods using a keypoint-based regression) does not suffer from this, thanks to the following features:
It usually has an initial normalization and resizing stage that makes all objects look identical, independent of the camera used;
The network outputs keypoints in the rectified space only;
Some kind of algorithm is used to transform these keypoints in 3D and obtain the final pose.
In this framework, the camera parameters are only used in the first stage to rectify the image and in the final stage to obtain the final pose; the whole network is trained and makes predictions on normalized images. The main advantage is obviously that once trained on a dataset, the algorithm is very resilient to changes in the camera parameters to the point that even a different camera could in principle be used for inference, while a network that directly makes the regression should be retrained if the two cameras have very different parameters. Finally, only one disadvantage of the proposed post-refinement algorithm can be highlighted in comparison with DenseFusion. Indeed, the proposed post refinement algorithm used to enhance DOPE in terms of dimension variability, requires more time than DenseFusion to retrieve the estimated pose due to the virtual depth map generation and the comparison with the real one at each iteration of the optimization problem. The optimization time might be reduced depending on the solver parameters and the required accuracy. Nevertheless, the inference time is less important than the accuracy of the estimated pose given the specific use case, when the pose estimation is performed only at the planning time.