PRF: A Program Reuse Framework for Automated Programming by Learning from Existing Robot Programs

Abstract

This paper explores the problem of automated robot program generation from limited historical data when neither accurate geometric environmental models nor online vision feedback are available. The Program Reuse Framework (PRF) is developed, which uses expert-defined motion classes, a novel data structure introduced in this work, to learn affordances, workspaces, and skills from historical data. Historical data comprise raw robot joint trajectories and descriptions of the robot task being completed. Given new tasks, motion classes are then used again to formulate an optimization problem capable of generating new open-loop, skill-based programs to complete the tasks. To cope with a lack of geometric models, a technique to learn safe workspaces from demonstrations is developed, allowing the risk of new programs to be estimated before execution. A new learnable motion primitive for redundant manipulators is introduced, called a redundancy dynamical movement primitive, which enables new end-effector goals to be reached while mimicking the whole-arm behavior of a demonstration. A mobile manipulator part transportation task is used throughout to illustrate each step of the framework.

1. Introduction

Most industrial robots in operation today are programmed to complete repetitive tasks in highly structured environments, such as material handling, painting, and welding, through a combination of manual online and offline programming methods [1]. Meanwhile, manufacturing is moving towards a paradigm of increased agility and rapid reconfiguration to cope with changing demands under Industry 4.0, rendering traditional brittle programming methods excessively time-consuming and labor-intensive, and emphasizing the need for more automated programming solutions.

Most industrial robot tasks are composed of sequences of simple behaviors, often broadly called skills. This insight has led to great interest in the area of skill-based programming, in which skills are leveraged to accelerate manual programming through human–machine interfaces [2,3,4] or sequenced automatically [5,6,7,8]. In the latter case, vision sensing, precise environmental models, or both are required, which may not be realistic in practice. The industry has been slow to adopt this widespread vision, partly due to worker privacy concerns [9,10], but also because most industrial robots still operate in structured environments. Additionally, suitable environmental models may not be available in practice, especially in smaller enterprises in which online, pendant-based programming is the norm.

Recent deep learning approaches have successfully solved a variety of robotic tasks by effectively leveraging rich datasets [11,12,13,14,15]. However, in practice, historical data currently collected from industrial robots rarely go beyond joint trajectories, which are largely repetitive and thus not sufficiently diverse for deep learning methods. In contrast, learning from demonstration (LfD) methods, originally developed to generalize human demonstrations, are far more data-efficient [16,17]. LfD skills are likewise more suitable for generalizing the most common industrial robot tasks, in which a task variation that a robot may experience is limited to arrangements of manipulated objects. However, LfD skills typically encode only the motion of a skill, with limited learning of the affordance selection (such as grasp targets) and task constraints (such as workspace bounds). This work develops a method to simultaneously learn affordances, workspaces, and skills from demonstrations.

To enable automated, skill-based robot programming with minimal environmental knowledge and limited data, the Program Reuse Framework (PRF) is proposed (Figure 1). At the core of the framework is a set of motion classes: expert-designed templates, each defining the learning and reuse of a distinct behavior. A historical dataset of demonstrations, containing robot programs and task metadata such as object poses, is assumed to be given. An offline module learns affordances, workspaces, and skills from the historical dataset. Then, when a new task is specified, an online skill planning module uses the motion class set and the learned affordances, workspaces, and skills to generate a new program to accomplish the task. The primary contributions of this work are as follows:

• An approach to workspace learning from demonstration, in which learned volumetric workspace constraints are used for program safety quantification in the absence of environmental models;
• The development of the redundancy dynamical movement primitive, a learnable motion generator for redundant manipulator skills that encodes and generalizes whole-arm motion to new task space goals;
• The introduction of motion classes, which are expert-designed templates for learning from historical data demonstrations and generating new skill-based programs.

An example mobile manipulator part transportation task is used throughout this work to illustrate an application of each component of the framework. The remainder of this paper is organized as follows. A review of related work is given in Section 2, followed by preliminaries, a formal problem statement, and the illustrative example definition in Section 3. Section 4 introduces both learnable workspaces and redundancy DMPs, and provides an experimental comparison in terms of generalization safety. In Section 5, the offline learning approach is detailed. Section 6 formulates the risk-minimizing, skill-based program generation approach; results of the full framework’s generalization performance are also included. Finally, a discussion is provided in Section 7 and concluding remarks are given in Section 8.

2. Related Work

2.1. Skill-Based Programming

Constraint-based programming approaches focus on the generation of robot motion based on careful definitions of task constraints. The Task Frame Formalism [18] provided an early framework for mapping simple task constraints to force and position control commands using user-provided templates. Later work like iTASC [19] and eTaSL [20] introduced more detailed, formal languages to specify complex tasks and available sensor streams, from which feedback controllers are automatically synthesized for sensor-based execution. Other work recontextualized constraint-based programming in terms of skills: user-defined, semantically meaningful actions with associated motion generators [21,22]. Other skill-based approaches generally consist of expert-defined skills with a variety of approaches to compose them [5,6,7,23]. Many skill-based programming approaches are designed for non-experts to design new programs in a modular way with intuitive graphical user interfaces [2] or even mixed reality [4]. Recent work has emphasized the correctness verification of skill-based programs [24] and automatic synthesis of sensor-based skill sequences suitable for execution in Robot Operating System (ROS) 2 [8]. A skill-based programming approach that emphasizes open-loop execution without vision feedback is presented in [25]; a Unified Programming Framework is introduced that enables a user to flexibly alternate between offline programming with a preexisting skill library and online programming by demonstration. In [26], an augmented reality-based programming interface is developed, with an emphasis on intuitive programming with sensor-based skills. In each approach, accurate world models, runtime perception, or manual design are required for program generation. The focus has been on programming with preexisting skills rather than how skills are learned or encoded.

The most similar work to our approach is [5], in which tasks are defined as desired world states and skills are carefully designed for intuitive use by both non-experts and automated planners. However, skills are realized at runtime by motion planners, which require precise world models and vision. In contrast, the presented work focuses on leveraging a historical dataset to solve a more constrained problem, in which neither explicit environmental models nor vision sensors are available during learning or at runtime. Moreover, we introduce motion classes as expert-designed templates for robot motion, similar to other skill templates that contain symbolic and/or physical constraints [18,19,20,27]. Motion classes enable both structured learning from demonstrations as well as the construction of new programs.

2.2. Skill Learning

While skill-based programming architectures often operate on existing skill libraries, the ability to learn skills expands a robot’s capabilities while reducing programming effort. Deep learning has been widely adopted to enable automated acquisition of a variety of complex skills, encoded as neural networks, including cable insertion [12], bin picking [11], rapid robot rehoming [15], deformable object manipulation [14], and even general manipulation from natural language commands [13]. Deep learning algorithms are commonly implemented with mature open-source Python libraries like Meta’s Pytorch [28] or Google’s TensorFlow [29]. However, deep learning methods can be challenging for non-experts to successfully deploy in practice [30] and are generally sample-inefficient [31]. As such, many deep learning-based approaches rely on simulation for the majority of training [11,12,14], or otherwise require expensive data collection in the real world [13].

Other methods utilize less data, albeit for more specialized skills. Learning from demonstration (LfD) methods enable encoding demonstrations with low-dimensional, yet highly expressive, models. See [32] for an overview of common models, along with libraries for Python, MATLAB, and C++. Perhaps the most prominent LfD model is the dynamical movement primitive (DMP) [16,33,34], which encodes skills using as few as a single demonstration. DMPs have long served as learnable motion generators for skills [35,36]. When more diverse demonstrations are available, statistical models based on DMPs [37] or Gaussian mixture models (GMMs) [17] can be leveraged for greater generalizability to task variation, such as rearrangements of key objects. Skills may also be acquired through a small number of task iterations in the real world when skill models are sufficiently low-dimensional, including DMPs [38], radial basis functions [21], or reach-avoid controllers [39]. In this work, we interpret existing robot programs in a historical dataset as demonstrations and leverage LfD models to efficiently learn specialized skills from limited, low-diversity data.

In order to effectively deploy learned skills, they must be appropriately parameterized for new tasks, such as end-effector goal selection for picking skills. Task-parameterized DMPs and GMMs [17] build task-conditioned skill parameter distributions from multiple demonstrations, while other methods enable runtime goal selection through multiple task iterations [6,38]. With a rich, multimodal demonstration dataset, as in RT-1 [13], both skills and vision-based goals are jointly learned from vision-based demonstrations, allowing flexible execution at runtime for new object configurations. Our framework learns skills and task-conditioned goals, or affordances, from historical data. In contrast, however, we do not assume the historical dataset was generated with the intention of learning and thus we do not expect sufficiently diverse examples to build statistical models. Moreover, new programs are generated for execution without vision feedback, so iterative methods are not suitable.

2.3. Geometric Constraint Learning

Demonstrations implicitly respect the constraints of a task, although constraints can be encoded in different ways. Prior work has investigated how geometric constraints can be inferred from demonstrations consisting only of state trajectories [40]. Later work focused on the inclusion of vision-based tracking during demonstrations to learn more complex geometric task constraints for multi-step tasks, but did not consider obstacle avoidance at runtime [41]. Other work developed a framework for learning infeasible states by assuming demonstrations are optimal and comparing them to optimal trajectories without constraints [40]. More recent work likewise assumes optimal demonstrations to build probabilistic obstacle models [42]. In practice, robot programs generated manually with traditional methods cannot be assumed to be optimal.

Our work is most similar to [41], which develops a framework to learn geometric constraints from demonstrations, including task space regions (TSRs) [43]. TSRs are volumes in $SE\left(3\right)$ that describe volumetric end-effector constraints. In contrast, we focus on learning volumes in ${\mathbb{R}}^3$ that define safe whole-arm workspaces, which enable the safety quantification of new trajectories generated by learned skills.

3. Preliminaries and Problem Setup

3.1. Automated Planning

Task-level planning can be accomplished by several planning algorithms, such as those described in [44], e.g., GraphPlan [45,46]. A state variable planning domain is a tuple $\Sigma =(\mathbb{S},\mathbb{A},{\Phi }_{\Sigma })$, consisting of a symbolic state space $\mathbb{S}$, action space $\mathbb{A}$, and state transition function ${\Phi }_{\Sigma }:\mathbb{S}\times \mathbb{A}\to \mathbb{S}$. State variables in a set $SV$ are symbolic terms of the form $\mathsf{name}(b_1,\dots ,b_{n_p})\in SV$ where $\mathbf{b}=\langle b_i\rangle$ are parameters from a set of symbolic names $\mathbb{B}$. A symbolic state $s\in \mathbb{S}$ is a set of atomic formulas involving state variables in $SV$. To form a set of actions $\mathbb{A}$, action templates$\alpha =(\mathsf{head},\mathsf{pre},\mathsf{eff})$ are first introduced, where head is a symbolic expression containing variable arguments, and pre and eff represent the preconditions and effects of $\alpha$ in the form of atomic formulas on state variables.

An action $a\in \mathbb{A}$ is constructed by parameterizing an action template with valid symbolic names, $a=\alpha \left(\mathbf{b}\right)$. In this sense, an action a is a concrete version of an action template $\alpha$, and the particular symbolic names $\mathbf{b}$ in an action are referred to as concrete parameters. The function ${\Phi }_{\Sigma }$ obeys the preconditions and effects of actions: $s_1\in {\Phi }_{\Sigma }(s_0,a_0)\iff a_0.\mathsf{pre}\in s_0\mathrm{and}{a}_0.\mathsf{eff}\in s_1$. Given a state variable planning domain $\Sigma$, an initial state $s_0$, and a goal state $s_g$, a sequence of actions, or action plan, $\mathbf{a}=\langle a_i\rangle$ can be constructed by a planning algorithm if such a plan exists.

3.2. Dynamical Movement Primitives

The dynamical movement primitive (DMP) is a motion model for LfD, encoding demonstrations as dynamical systems. Building upon the original formulation of DMPs [33], later extensions included a proper treatment of rotation trajectories [47]; the latter formulation is briefly summarized next. The purpose of a DMP is to encode the simultaneous motion of multiple robot coordinates as the solution to a forced dynamical system. A canonical system is first introduced for the phase variable $\zeta$, whose exponential decay $\tau \dot{\zeta }=-{\alpha }_{\zeta }\zeta$ from 1 to 0 is used to synchronize all other systems without explicit time dependence. The same time constant $\tau$ is used for all systems and is used to scale their convergence. The following system describes stable attraction of a position coordinate $\mathrm{p}\in {\mathbb{R}}^{n_{\mathrm{p}}}$ to a goal ${\mathrm{p}}_g$ from any initial $\mathrm{p}\left(0\right)$ subject to a forcing term $f_{\mathrm{p}}\left(\zeta \right)$:

$$\begin{array}{cc}\hfill \tau \dot{z}& ={\alpha }_z({\beta }_z({\mathrm{p}}_g-\mathrm{p})-z)+f_{\mathrm{p}}\left(\zeta \right)\hfill \\ \hfill \tau \dot{\mathrm{p}}& =z.\hfill \end{array}$$

(1)

Here, z is the scaled time derivative of $\mathrm{p}$ with $z\left(0\right)=0$. By selecting ${\beta }_z={\alpha }_z/4$, the response of (1) is critically damped and exponentially converges to $\mathrm{p}={\mathrm{p}}_g$ and $z=0$ if $f_{\mathrm{p}}\left(\zeta \right)\equiv 0$.

Equivalently, the following system from [47] describes an attraction to a rotation goal ${\mathrm{R}}_g\in SO\left(3\right)\subset {\mathbb{R}}^{3\times 3}$ from $\mathrm{R}\left(0\right)$ subject to forcing term $f_{\mathrm{R}}\left(\zeta \right)$:

$$\begin{array}{cc}\hfill \tau \dot{\eta }& ={\alpha }_z({\beta }_{z}log\left({\mathrm{R}}_g{\mathrm{R}}^{\top }\right)-\eta )+f_{\mathrm{R}}\left(\zeta \right)\hfill \\ \hfill \tau \dot{\mathrm{R}}& =\widehat{\eta }\mathrm{R}\hfill \end{array}$$

(2)

where $\eta =\tau \omega$ for angular velocity $\omega$. The forcing terms $f_{\mathrm{p}}\left(\zeta \right)$ and $f_{\mathrm{R}}\left(x\right)$ are commonly defined as follows:

$$f_F\left(\zeta \right)=D_F{\displaystyle \frac{{\sum }_{i=1}^{n_g}{w}_i^F{\psi }_i\left(\zeta \right)}{{\sum }_{i=1}^{n_g}{\psi }_i\left(\zeta \right)}}\zeta ,$$

(3)

for $F\in \{\mathrm{p},\mathrm{R}\}$, where $D_{\mathrm{p}}=diag({\mathrm{p}}_g-\mathrm{p}\left(0\right))$ and $D_{\mathrm{R}}=diag(log\left({\mathrm{R}}_g\mathrm{R}{\left(0\right)}^{\top }\right))$ with $D_{\mathrm{p}}\in {\mathbb{R}}^{n_{\mathrm{p}}\times n_{\mathrm{p}}}$ and $D_{\mathrm{R}}\in {\mathbb{R}}^{3\times 3}$. The same $n_g$ Gaussian bases ${\psi }_i\left(\zeta \right)=exp(-{\tilde{\psi }}_i{(\zeta -{\overline{\psi }}_i)}^2)$ are used for both forcing terms with centers ${\overline{\psi }}_i=exp(-{\alpha }_{\zeta }{\displaystyle \frac{i-1}{n_g-1}})$ and widths ${\tilde{\psi }}_i={\displaystyle \frac{2}{{\overline{\psi }}_{i+1}-{\overline{\psi }}_i}}$ for all $i\in [1,n_g]$, evenly spacing the bases in phase $\zeta$ [48].

By selecting weights $w_i^{\mathrm{p}}$ and $w_i^{\mathrm{R}}$ appropriately, the response of (1) and (2) can be shaped as desired, such as to mimic a demonstration in an LfD context. Without loss of generality, consider only position DMPs (1): by substituting values from a demonstration $\mathrm{p}\left(t\right)$ into (1), taking $\tau$ as the duration, and rearranging, $f_{\mathrm{p}}\left(\zeta \right)$ can be taken as a target value for regression in (3) for $F=\mathrm{p}$ to solve for a matrix of weights ${\mathbf{w}}^{\mathrm{p}}={\left[w_i^{\mathrm{p}}\right]}_{i=1}^{n_g}$. Then, to reach a new goal ${\tilde{\mathrm{p}}}_g$ from a new initial position $\tilde{\mathrm{p}}\left(0\right)$ in a new duration $\tilde{\tau }$, the new values are substituted into (1) and (3) to generate a new trajectory $\tilde{\mathrm{p}}\left(t\right)$ of duration $\tilde{\tau }$ that is a spatially and temporally scaled version of the demonstration $\mathrm{p}\left(t\right)$. A locally weighted regression for efficiently solving for ${\mathbf{w}}^{\mathrm{p}}$ is given in [16]. For notational convenience, we introduce the following:

Train : y(t) → w

(4)

Integrate : (₀y, g, w) → y(t)

(5)

for a generic coordinate y (position or rotation), where Train (4) maps a demonstration to a set of trained DMP weights $\mathbf{w}$, and Integrate (5) maps an initial condition ${}_{0}y$, goal g, and a set of DMP weights $\mathbf{w}$ to a new trajectory $y\left(t\right)$. Temporal scaling is not critical to this work and is omitted for clarity.

3.3. Problem Statement

In this work, we consider a robot with configuration $q\in Q\subset {\mathbb{R}}^{n_{\mathrm{a}}}$ that has been manually programmed to complete tasks $\mathcal{T}$ in environments without explicit geometric models. A task description $\mathcal{T}$ contains only the poses of task-relevant objects, but not their geometric models, representing the minimal data available in a manual programming regime. Each program–task pair $d=\left(q\right(t),\mathcal{T})$ is interpreted as a demonstration and stored in a historical dataset $\mathbf{D}=\left\{d\right\}$.

The present work considers a mobile manipulator performing part transportation tasks. The robot is equipped with a mobile base with $q_{\mathrm{m}}\in Q_{\mathrm{m}}\subset {\mathbb{R}}^3$ (a parameterization of $SE\left(2\right)$), a manipulator with $q_{\mathrm{a}}\in Q_{\mathrm{a}}\subset {\mathbb{R}}^{n_{\mathrm{a}}}$, and a gripper with $q_{\mathrm{g}}\in Q_{\mathrm{g}}$, forming a configuration $q={\left[q_{\mathrm{m}}^{\top }{q}_{\mathrm{a}}^{\top }{q}_{\mathrm{g}}^{\top }\right]}^{\top }$. The robot is assumed to be equipped with minimal, supplier-provided sensing. A laser scanner is available for the mobile base to navigate safely between work locations. However, the arm operates at each work location without visual feedback, as it is manually programmed. Thus, the safety of new trajectories cannot be guaranteed explicitly. The arm and mobile base have known home configurations $q_{\mathrm{a},H}$ and $q_{\mathrm{m},H}$, respectively. We denote the pose of a frame A with respect to B as ${}^{B}T_A\in SE\left(3\right)$. When the reference frame is omitted, the world origin frame o is assumed.

A part transportation task (PTT) involves transporting a part p from location ${\ell }_1$ to location ${\ell }_2$. Both ${\ell }_1$ and ${\ell }_2$ represent work locations such as a manufacturing machine, buffer, or other environment in which the arm may operate. The initial part pose is $T_{p,0}$ and the goal part pose is $T_{p,g}$. The static locations are at poses $T_{{\ell }_1}$ and $T_{{\ell }_2}$, respectively. Altogether, a PTT is specified with the tuple

$$\mathcal{T}=(T_{p,0},T_{p,g},T_{{\ell }_1},T_{{\ell }_2}).$$

(6)

Throughout this work, we denote a member of a tuple using a leading superscript, such as ${}^{\mathcal{T}}T_{p,0}$ or ${}^{\mathcal{T}}T_{{\ell }_1}$ in (6). The poses of the mobile base frame b and end-effector frame e are computed using known forward kinematics, respectively: $T_b={\mathcal{F}}_{\mathrm{m}}\left(q_{\mathrm{m}}\right)$ and ${}^{b}T_e={\mathcal{F}}_{\mathrm{a}}\left(q_{\mathrm{a}}\right)$. The physical state encodes the configuration of both the robot and the part as $\mathrm{x}={\left[q^{\top }{}_{\vee }T_p^{\top }\right]}^{\top }$, where ${}_{\vee }M\in {\mathbb{R}}^{nm}$ is a vectorization of a matrix $M\in {\mathbb{R}}^{n\times m}$.

The precise problem considered in this work is as follows. Given a historical dataset $\mathbf{D}$ of task–program pairs and a new task $\mathcal{T}$, find a new program $q\left(t\right)$ to solve $\mathcal{T}$ while maximizing safety. The following assumptions are made:

(A1)

Geometric models of the robot are known, but those of parts and locations are not;

(A2)

$\mathcal{T}$ precisely describes the poses of parts p and locations ${\ell }_1$, ${\ell }_2$.

3.4. Illustrative Example Description

In this section, we introduce a concrete problem domain that will serve as an illustrative example throughout the development of this work (Figure 2). The mobile manipulator under consideration is a Kuka KMR iiwa, composed of an omnidirectional mobile platform, $Q_{\mathrm{m}}\subset {\mathbb{R}}^3$, and a manipulator with $n_{\mathrm{a}}=7$ axes. The manipulator is redundant, meaning that an $SE\left(3\right)$ end-effector goal can be realized by a non-singleton subset of $Q_{\mathrm{a}}\subset {\mathbb{R}}^7$, enabling greater programming flexibility than a robot with six or fewer axes. Attached to the end of the manipulator is a parallel jaw gripper, $Q_{\mathrm{g}}=\{0,1\}$, with 0 and 1 indicating an open and closed state, respectively.

The robot operates at threes types of locations: a computer numerically controlled milling machine (CNC), a 3D printer (Printer), and a simple table (Table). The robot transports two types of parts: $\mathrm{Part}1$ and $\mathrm{Part}2$. The robot has a set of manually generated programs for some tasks involving the transport of parts $p\in \{\mathrm{Part}1,\mathrm{Part}2\}$ between locations ${\ell }_1,{\ell }_2\in \{\mathrm{CNC},\mathrm{Printer},\mathrm{Table}\}$. Note that a task may involve transportation between two instances of the same location, such as between two CNC machines, ${\ell }_1={\mathrm{CNC}}_1$ and ${\ell }_2={\mathrm{CNC}}_2$, each with the same geometry.

The executions of manual programs $q\left(t\right)$ to solve tasks $\mathcal{T}$ form the historical dataset $\mathbf{D}=\{d=(q\left(t\right),\mathcal{T}\left)\right\}$. Within this dataset, affordances in two forms are implicitly encoded: approaches, describing possible base poses with respect to different locations, and grasps, describing possible gripper poses with respect to different parts. Furthermore, the programs $q\left(t\right)$ provide trajectory examples, from which affordances, workspaces, and skills can be learned. The presented work formalizes a methodology for generalizing a historical program dataset $\mathbf{D}$ to new tasks $\mathcal{T}$ by learning feasible affordances, safe workspaces, and skills, which enable the generation of new programs $q\left(t\right)$ with quantified risk.

4. Learning and Safe Generalization within Unmodeled Workspaces

This section details two parts of our strategy to handle new program generation in unmodeled workspaces. First, a method to learn volumetric workspaces from demonstrations is given in Section 4.1. Then, a novel motion primitive formulation for redundant manipulators is given in Section 4.2. Finally, the performance of the new motion primitive formulation is compared to existing motion primitives in Section 4.3.

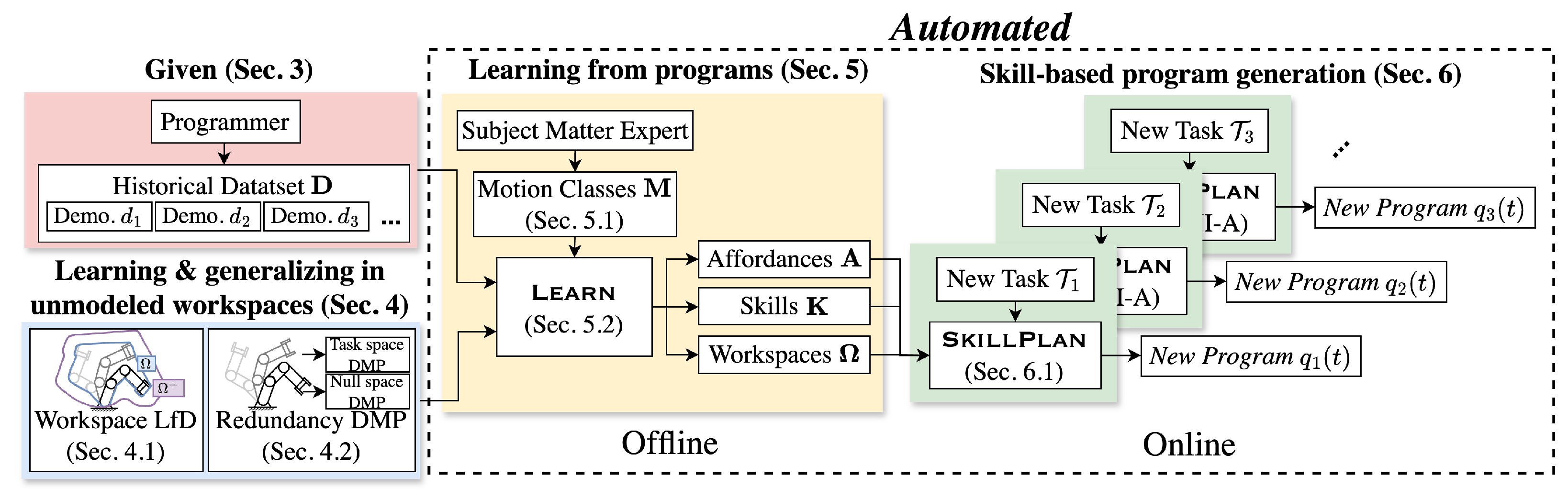
4.1. Workspace Learning from Demonstration

While demonstrations are commonly used to train skills capable of generalization, bounds on their generalizability are not commonly considered. In this section, we show how the same demonstration trajectories used for skill learning can be used to build sets capable of certifying the safety of new trajectories.

Consider a robot with $n_l$ links, including end-effectors, mobile platforms, and other attachments. Each link’s volumetric geometries can be expressed as compact sets ${\lambda }_j\left(q\right)\in {\mathcal{C}}^3$∀$j\in [1,n_l]$, where ${\mathcal{C}}^3\subset \mathcal{P}\left({\mathbb{R}}^3\right)$ is the set of compact subsets of ${\mathbb{R}}^3$. The complete volume occupied by the robot at any configuration q, $\Lambda \left(q\right)\in {\mathcal{C}}^3$, can then be expressed by the union of all link geometries (we represent link geometries as meshes and use Trimesh [49] for operations like mesh concatenation):

$$\Lambda \left(q\right)=\bigcup _{j=1}^{n_l}{\lambda }_j\left(q\right).$$

(7)

Meanwhile, suppose that a set of control points are sampled from the surface $\partial {\lambda }_j\left(q\right)$ of each link and collected in sets $c_j\left(q\right)\subset \partial {\lambda }_j\left(q\right)$. Then, the full set of control points at a configuration is given by the union of link control points:

$$C\left(q\right)=\bigcup _{j=1}^{n_l}{c}_j\left(q\right).$$

(8)

To measure the distance between a point $\mathbf{x}\in {\mathbb{R}}^3$ and the boundary of a compact set $\mathcal{S}\in {\mathcal{C}}^3$, a signed distance function (we use Pytorch Volumetric for SDF computation between meshes [50]) is used, where $\mathrm{SDF}(\mathbf{x},\mathcal{S})\le 0\forall \mathbf{x}\in \mathcal{S}$ and $\mathrm{SDF}(\mathbf{x},\mathcal{S})=0$ for surface points $\mathbf{x}\in \partial \mathcal{S}$. From this point-dependent SDF, we introduce a configuration-dependent SDF (C-SDF), similar to [51]:

$$\varphi (q,\mathcal{S})=\underset{\mathbf{x}\in C\left(q\right)}{min}\mathrm{SDF}(\mathbf{x},\mathcal{S})$$

(9)

which finds the minimum clearance between the robot control points and the set $\mathcal{S}$.

Now, consider a robot programmed to operate at a location ℓ with static obstacle geometry ${\mathcal{O}}_{\ell }\subset {\mathbb{R}}^3$, resulting in a set of demonstration trajectories $Q^d=\left\{q^d\left(t\right)\right\}$ which are collision-free, meaning

$$\underset{q\in q^d\left(t\right)}{min}\varphi (q,{\mathcal{O}}_{\ell })>0\forall q^d\left(t\right)\in Q^d.$$

(10)

Gathering all configurations across the trajectory set $Q^d$ yields the set of known safe configurations:

$$Q_{\ell }^{\mathrm{safe}}=\bigcup _{q^d\left(t\right)\in Q^d}{q}^d\left(t\right).$$

(11)

The safe configuration set is robot-specific, but we can consider the robot links at each configuration, which sweep through ${\mathbb{R}}^3$ to construct a generic safe Cartesian workspace:

$${\Omega }_{\ell }=\bigcup _{q\in Q_{\ell }^{\mathrm{safe}}}\Lambda \left(q\right).$$

(12)

With the safe workspace ${\Omega }_{\ell }$, we can certify the safety of any trajectory $q\left(t\right)$ executed at location ℓ without knowledge of ${\mathcal{O}}_{\ell }$. First, since the demonstrations are collision-free, we know that ${\mathcal{O}}_{\ell }$ and ${\Omega }_{\ell }$ do not intersect: ${\mathcal{O}}_{\ell }\cap {\Omega }_{\ell }=\varnothing$. Then, we know that the obstacle set ${\mathcal{O}}_{\ell }$ must be a subset of the complement of ${\Omega }_{\ell }$: ${\mathcal{O}}_{\ell }\subset {\overline{\Omega }}_{\ell }$. Therefore, a sufficient condition for safety of a trajectory $q\left(t\right)$ at a location ℓ is

$$\underset{q\in q\left(t\right)}{min}\varphi (q,{\overline{\Omega }}_{\ell })>0\Rightarrow \underset{q\in q\left(t\right)}{min}\varphi (q,{\mathcal{O}}_{\ell })>0.$$

(13)

In other words, if the robot trajectory does not enter the complement of the safe workspace, it cannot enter the obstacle set.

On its own, (13) does not admit much flexibility in the design of new trajectories, as even the safe demonstrations $q^d\left(t\right)\in Q^d$ operate at the boundary of ${\Omega }_{\ell }$. Instead, we leverage domain knowledge about the construction of the demonstrations to enlarge ${\Omega }_{\ell }$. Guidelines regarding the minimum clearance between robot trajectories and workspace obstacles are common, specified by enterprise policies and industry standards, such as ISO 10218 2011-2 [52] and ANSI/RIA R15.06 [53]. Suppose that demonstrations used to construct $Q_{\ell }^{\mathrm{safe}}$ are known to have been generated using a standard, conservative minimum clearance of $r_{\ell }^d$, so $\varphi (q,{\mathcal{O}}_{\ell })>r_{\ell }^d$$\forall q\in Q_{\ell }^{\mathrm{safe}}$. Further suppose that a less conservative $r_{\ell }<r_{\ell }^d$ represents the true acceptable clearance. Thus, a dilated safe workspace ${\Omega }_{\ell }^{+}$ can be formed:

$${\Omega }_{\ell }^{+}={\Omega }_{\ell }\oplus {\mathcal{B}}_{{ϵ}_{\ell }}\left(0\right),$$

(14)

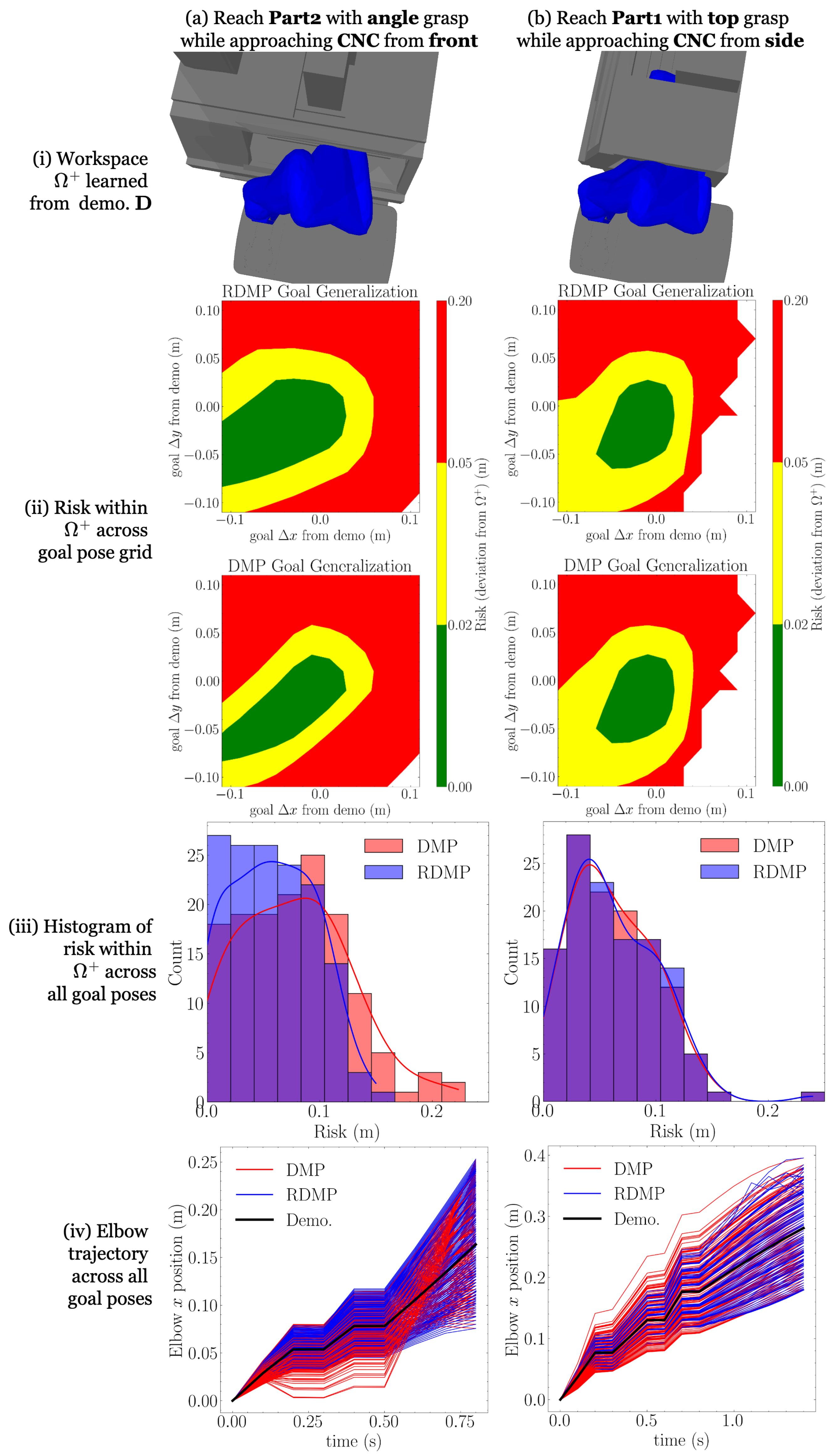
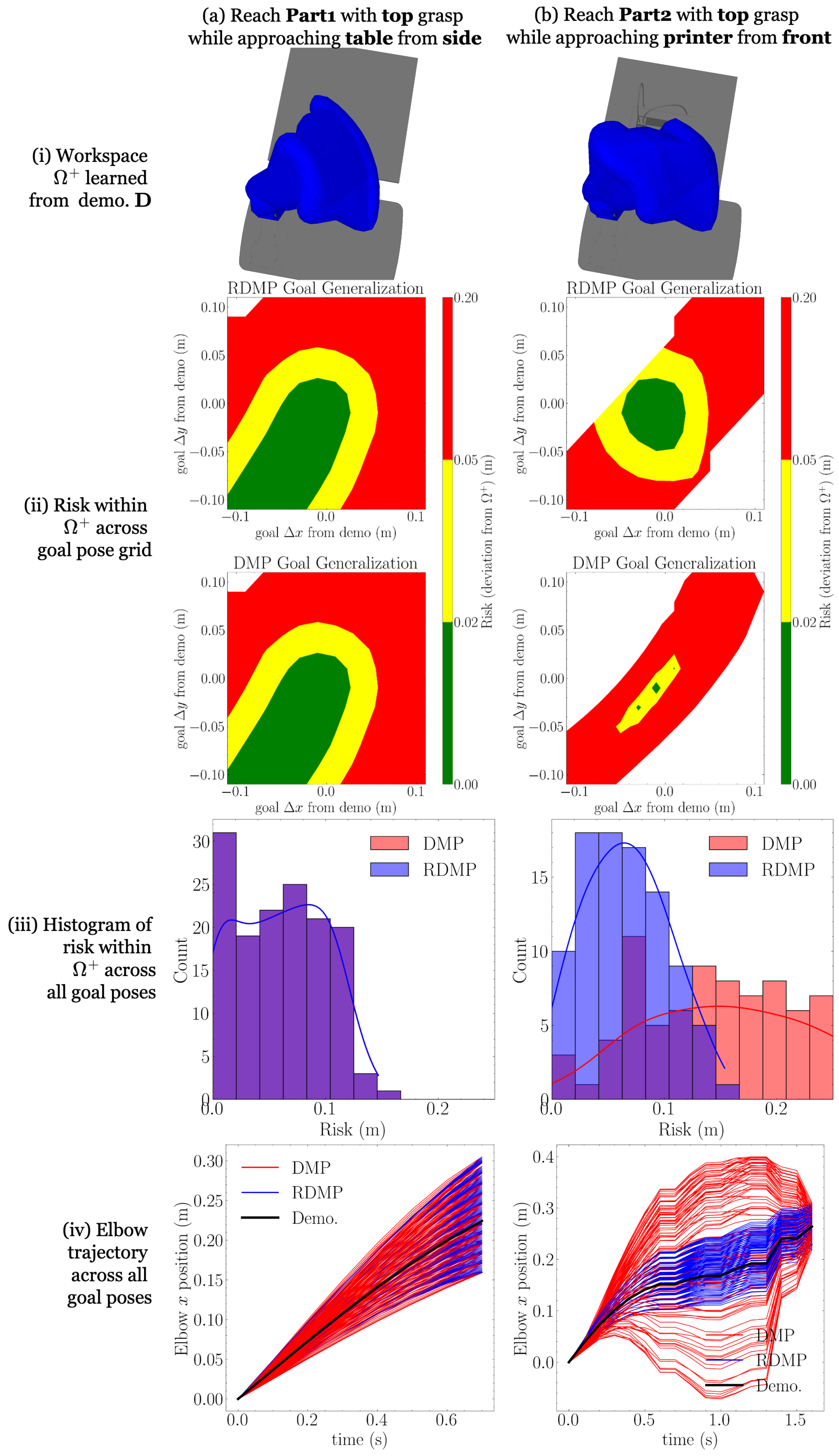
where ${\mathcal{B}}_{{ϵ}_{\ell }}\left(0\right)$ is a ball of radius ${ϵ}_{\ell }=r_{\ell }^d-r_{\ell }$ centered at 0, and ⊕ is the Minkowski sum. A planar illustration of the safe workspace and its dilation is given in Figure 1. Following a similar argument as above, we know that the obstacle set ${\mathcal{O}}_{\ell }$ is still a disjoint from the dilated safe workspace ${\Omega }_{\ell }^{+}$: ${\mathcal{O}}_{\ell }\subset {\overline{\Omega }}_{\ell }^{+}$. Thus, we have a sufficient condition similar to (13) that is less restrictive:

$$\underset{q\in q\left(t\right)}{min}\varphi (q,{\overline{\Omega }}_{\ell }^{+})>0\Rightarrow \underset{q\in q\left(t\right)}{min}\varphi (q,{\mathcal{O}}_{\ell })>0.$$

(15)

Note that trajectories that do not satisfy (15) are not necessarily unsafe; their safety is simply uncertain. A reasonable heuristic is to assume that the probability of obstacle collision increases the farther trajectories travel outside of the dilated safe workspace (or, equivalently, how far they travel inside its complement). Therefore, we define the risk of a trajectory as

$$\mathcal{R}(q\left(t\right),{\Omega }_l^{+})=\eta \left(-\underset{q\in q\left(t\right)}{min}\varphi (q,{\overline{\Omega }}_{\ell }^{+})\right),$$

(16)

where $\eta$ is a monotonically increasing function with $\eta \left(\mathsf{x}\right)=0$ for $\mathsf{x}\le 0$. $\eta$ can represent either conservative risk functions, like $\eta \left(\mathsf{x}\right)\propto {\displaystyle \frac{\mathsf{x}}{1-\mathsf{x}}}$, or more relaxed ones, like $\eta \left(\mathsf{x}\right)\propto \mathsf{x}$. In all experiments in this paper, we use $\eta \left(\mathsf{x}\right)=max(\mathsf{x},0)$.

For notational convenience, we hereafter refer to the above procedure of mapping a demonstration trajectory set $\left\{q^d\left(t\right)\right\}$ at a location ℓ to its dilated safe workspace as

LearnWorkspace : {q^d(t)} → Ω_ℓ⁺.

(17)

4.2. Redundancy Dynamical Movement Primitives

Goals for manipulator tasks are most naturally expressed as end-effector goals $g\in SE\left(3\right)$. DMPs trained in task space allow the straightforward specification of goals in $SE\left(3\right)$; however, task space DMPs cannot encode the full motion of redundant robots, resulting in ambiguous joint space solutions. On the other hand, DMPs learned in joint space capture a demonstration’s full motion; however, joint space DMPs do not encode the whole-arm Cartesian behavior. Joint space DMPs also require inverse kinematics for $SE\left(3\right)$ goals to obtain joint space goals $q_g\in Q_{\mathrm{a}}$, which are ambiguous for redundant robots.

To learn the full motion of a redundant manipulator given new task space goals, the redundancy DMP (RDMP) is introduced. During training, a joint space demonstration trajectory $q^d\left(t\right)\in {\mathbb{R}}^{n_{\mathrm{a}}}$ is separated into task space $({\mathrm{p}}^d\left(t\right),{\mathrm{R}}^d\left(t\right))$ and a compact null space representation ${\gamma }^d\left(t\right)\in {\mathbb{R}}^{6-n_{\mathrm{a}}}$, all of which are encoded as individual DMPs. Then, given a new task space goal $g=({\mathrm{p}}_g,{\mathrm{R}}_g)\in SE\left(3\right)$, both task space and null space DMPs are simultaneously integrated to generate a new trajectory $q\left(t\right)$ to reach g while preserving both task space and null space characteristics. The details of the compact null space representation are presented next.

4.2.1. Compact Null Space Representation

The manipulator Jacobian $J\left(q\right)\in {\mathbb{R}}^{6\times n_{\mathrm{a}}}$ maps instantaneous joint space velocities $\dot{q}\in {\mathbb{R}}^{n_{\mathrm{a}}}$ at a particular configuration q to the instantaneous task space twist $V={\left[v^{\top }{\omega }^{\top }\right]}^{\top }$, composed of linear velocity $v\in {\mathbb{R}}^3$ and angular velocity $\omega \in {\mathbb{R}}^3$. The forward and inverse velocity kinematics, respectively, are

$$\begin{array}{cc}\hfill V& =J\left(q\right)\dot{q}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \dot{q}& =J^{+}\left(q\right)V+N\left(q\right)\xi \hfill \end{array}$$

(19)

where $J^{+}\left(q\right)$ is the Moore–Penrose pseudoinverse of $J\left(q\right)$. $N\left(q\right)=I-J^{+}\left(q\right)J\left(q\right)\in {\mathbb{R}}^{n_{\mathrm{a}}\times n_{\mathrm{a}}}$ is the null space projection matrix, which projects any $\xi \in {\mathbb{R}}^{n_{\mathrm{a}}}$ into $ker\left(J\right(q\left)\right)$, generating null space motion, meaning zero task space velocity, as $J\left(q\right)N\left(q\right)\xi =0\forall \xi$.

For a particular $\dot{q}$, $N\left(q\right)\xi \in {\mathbb{R}}^{n_{\mathrm{a}}}$ represents the component of $\dot{q}$ contributing to null space motion, and can be computed by substituting (18) into (19) and rearranging:

$$N\left(q\right)\xi =\dot{q}-J^{+}\left(q\right)J\left(q\right)\dot{q}=N\left(q\right)\dot{q}.$$

(20)

Thus, (18)–(20) describe a one-to-one mapping between joint space velocity $\dot{q}\in {\mathbb{R}}^{n_{\mathrm{a}}}$ and $(V,N\left(q\right)\dot{q})\in {\mathbb{R}}^{6+n_{\mathrm{a}}}$. However, since $rank\left(J\left(q\right)\right)=6<n_{\mathrm{a}}$, null space motion describes motion along an $(n_{\mathrm{a}}-6)$-dimensional manifold within $Q_{\mathrm{a}}$. As such, we can represent null space velocity more compactly in $n_{\mathrm{a}}-6$ dimensions. Let $M\left(q\right)\in {\mathbb{R}}^{n_{\mathrm{a}}\times (n_{\mathrm{a}}-6)}$ be a matrix whose columns are the orthonormal bases of $N\left(q\right)$, obtained from singular value decomposition (SVD). Then, any null space motion $N\left(q\right)\xi$ can be expressed as

$$N\left(q\right)\xi =M\left(q\right)\dot{\gamma },$$

(21)

where $\dot{\gamma }\in {\mathbb{R}}^{n_{\mathrm{a}}-6}$ is a compact null space velocity. Rearranging (21) and substituting (20), the compact null space velocity can be computed from $\dot{q}$ by

$$\begin{array}{cc}\hfill \dot{\gamma }& =M^{+}\left(q\right)N\left(q\right)\dot{q}.\hfill \end{array}$$

(22)

Therefore, at a configuration q, a joint velocity $\dot{q}\in {\mathbb{R}}^{n_{\mathrm{a}}}$ can be represented uniquely with $(V,\dot{\gamma })\in {\mathbb{R}}^{n_{\mathrm{a}}}$. The quantity $\dot{\gamma }$ represents a redundant robot’s speed along its $n_{\mathrm{a}}-6$ null space manifold given its current configuration q and joint velocity $\dot{q}$. Note that RDMPs are not suitable for demonstrations that come close to kinematic singularities in $Q^{\mathrm{a}}$, where $rank\left(J\right(q\left)\right)<6$ as the null space computation becomes numerically unstable. However, since singularities pose other challenges, including loss of manipulability, manually generated robot programs are unlikely to contain them.

4.2.2. Training and Integrating RDMPs

In this section, we explain the RDMP implementations of Train (4) and Integrate (5). First, consider TrainRDMP (Algorithm 1). Given a joint space demonstration $q^d\left(t\right)$, corresponding task space Cartesian trajectories ${\mathrm{p}}^d\left(t\right)$ and ${\mathrm{R}}^d\left(t\right)$ are computed from forward kinematics and trained to weights ${\mathbf{w}}^{\mathrm{p}}$ and ${\mathbf{w}}^{\mathrm{R}}$, respectively. Compact null space motion is computed using (22) and integrated over time with ${\gamma }^d\left(0\right)=0$ to form a demonstration ${\gamma }^d\left(t\right)$ which is treated as a position DMP (1) and trained to ${\mathbf{w}}^{\gamma }$. Additionally, the integrated ${\gamma }^d\left(t\right)$ has no obvious physical meaning and thus new values cannot sensibly be chosen when the DMP is later integrated for reuse, so the original goal ${\gamma }_g={\gamma }^d(-1)$ is likewise recorded. Altogether, the RDMP weight vector is

Algorithm 1 TrainRDMP$\left(q\right(t\left)\right)$

1: Compute forward kinematics over trajectory $q\left(t\right)$ of duration $\overline{t}$ sampled at $\Delta t$: 2: $\mathrm{p}\left(t\right),\mathrm{R}\left(t\right)\leftarrow \mathcal{F}\left(q\left(t\right)\right)\forall t\in \{0,\Delta t,2\Delta t,\dots ,\overline{t}\}$ 3: Compute null space trajectory: 4: for $t\in \{0,\Delta t,2\Delta t,\dots ,\overline{t}\}$ do 5:     Compute null space matrix: 6:     $N\leftarrow I-J^{+}\left(q\left(t\right)\right)J\left(q\left(t\right)\right)$          ▹ note: $rank\left(N\right)=n_{\mathrm{a}}-6$ 7:     Apply Singular Value Decomposition to the null space matrix: 8:     $\mathit{U},\Sigma ,{\mathit{V}}^{\top }\leftarrow$SVD$\left(N\right)$ 9:     Form orthonormal bases from the first $n_{\mathrm{a}}-6$ columns of $\mathit{U}$: 10:     $M\leftarrow {\mathit{U}}_{1:n_{\mathrm{a}}-6}$ 11:     Compute null space velocity: 12:     $\dot{\gamma }\left(t\right)\leftarrow M^{+}N\dot{q}\left(t\right)$ 13: Compute $\gamma \left(t\right)$ from integration of $\dot{\gamma }\left(t\right)$ 14: Set null space goal as final trajectory value: ${\gamma }_g=\gamma \left(\overline{t}\right)$ 15: Train DMPs with (4): 16: ${\mathbf{w}}^{\mathrm{p}}\leftarrow$Train$\left(\mathrm{p}\right(t\left)\right)$ 17: ${\mathbf{w}}^{\mathrm{R}}\leftarrow$Train$\left(\mathrm{R}\right(t\left)\right)$ 18: ${\mathbf{w}}^{\gamma }\leftarrow$Train$\left(\gamma \right(t\left)\right)$ 19: return ${\mathbf{w}}^{\mathrm{RDMP}}\leftarrow {\left[{\left({\mathbf{w}}^{\mathrm{p}}\right)}^{\top }{\left({\mathbf{w}}^{\mathrm{R}}\right)}^{\top }{\left({\mathbf{w}}^{\gamma }\right)}^{\top }{\gamma }_g\right]}^{\top }$

$${\mathbf{w}}^{\mathrm{RDMP}}={\left[\begin{array}{cccc}{\left({\mathbf{w}}^{\mathrm{R}}\right)}^{\top }& {\left({\mathbf{w}}^{\mathrm{p}}\right)}^{\top }& {\left({\mathbf{w}}^{\gamma }\right)}^{\top }& {\gamma }_g^{\top }\end{array}\right]}^{\top }.$$

(23)

Then, given an initial configuration $q_0$ and goal pose $g\in SE\left(3\right)$, the task space and null space DMPs are simultaneously integrated to generate a new trajectory $q\left(t\right)$, shown in IntegrateRDMP (Algorithm 2). In Section 4.3, RDMPs are compared to traditional DMPs in terms of generating lower-risk trajectories during generalization.

Algorithm 2 IntegrateRDMP$({}_{0}y,g,{\mathbf{w}}^{\mathrm{RDMP}})$

1: ${\mathbf{w}}^{\mathrm{p}},{\mathbf{w}}^{\mathrm{R}},{\mathbf{w}}^{\gamma },{\gamma }_g\leftarrow {\mathbf{w}}^{\mathrm{RDMP}}$ 2: $q\left(0\right)\leftarrow {}_{0}y\in Q$ 3: ${\mathrm{p}}_0,{\mathrm{R}}_0\leftarrow \mathcal{F}\left(q\left(0\right)\right)$ 4: ${\mathrm{p}}_g,{\mathrm{R}}_g\leftarrow g\in SE\left(3\right)$ 5: Integrate task space and null space DMPs with (5) for duration $\overline{t}$ and sampled at $\Delta t$: 6: $\mathrm{p}\left(t\right)\leftarrow$Integrate$({\mathrm{p}}_0,{\mathrm{p}}_g,{\mathbf{w}}^{\mathrm{p}})$ 7: $\mathrm{R}\left(t\right)\leftarrow$Integrate$({\mathrm{R}}_0,{\mathrm{R}}_g,{\mathbf{w}}^{\mathrm{R}})$ 8: $\gamma \left(t\right)\leftarrow$Integrate$({\gamma }_0,{\gamma }_g,{\mathbf{w}}^{\gamma })$ 9: Compute angular velocity and form task space velocity: 10: $\omega \left(t\right)\leftarrow logm{\left(\dot{\mathrm{R}}\left(t\right)\right)}^{\vee }\forall t\in \{0,\Delta t,2\Delta t,\dots ,\overline{t}\}$   ▹${·}^{\vee }$ lowers skew-sym. matrix to ${\mathbb{R}}^3$ 11: $V\left(t\right)={\left[\dot{\mathrm{p}}{\left(t\right)}^{\top }\omega {\left(t\right)}^{\top }\right]}^{\top }\forall t\in \{0,\Delta t,2\Delta t,\dots ,\overline{t}\}$ 12: Compute compact null space velocity $\dot{\gamma }\left(t\right)$ through numerical differentiation of $\gamma \left(t\right)$ 13: Compute joint space trajectory: 14: for $t\in \{0,\Delta t,2\Delta t,\dots ,\overline{t}\}$ do 15:     Compute null space matrix: 16:     $N\leftarrow I-J^{+}\left(q\left(t\right)\right)J\left(q\left(t\right)\right)$               ▹ note: $rank\left(N\right)=n_{\mathrm{a}}-6$ 17:     Apply Singular Value Decomposition to the null space matrix: 18:     $\mathit{U},\mathbf{\Sigma },{\mathit{V}}^{\top }\leftarrow$SVD$\left(N\right)$ 19:     Form orthonormal bases from the first $n_{\mathrm{a}}-6$ columns of $\mathit{U}$: 20:     $M\leftarrow {\mathit{U}}_{1:n_{\mathrm{a}}-6}$ 21:     Compute joint velocity and integrate joint configuration: 22:     $\dot{q}\leftarrow J^{+}\left(q\left(t\right)\right)V\left(t\right)+M\dot{\gamma }\left(t\right)$ 23:     $q(t+\Delta t)\leftarrow q\left(t\right)+\dot{q}\Delta t$ 24: return $q\left(t\right)$

4.3. Illustrative Example: DMP and RDMP Risk during Generalization

To compare the performance of DMPs and RDMPs in the context of the PRF, we compare the risk (16) of DMP- and RDMP-generated trajectories with the same initial conditions and goal, where the risk’s workspace, DMP, and RDMP are trained on the same demonstrations. To generate example demonstrations, we consider the four location approaches outlined in Section 3.4. Results for all examples are shown in Figure 3i–iv and Figure 4i–iv corresponding to comparison metrics.

4.3.1. Approach

The following procedure is followed for each example to generate the comparison metrics. A part is located at a fixed, nominal pose near the center of each location. One of the part’s grasps is chosen and used to define an end-effector goal pose $g^d$. A collision-free demonstration trajectory $q^d\left(t\right)$ is generated from an initial configuration ${}_{0}y=q_{\mathrm{a},H}$ using a standard (we use RRT-connect [54], implemented in [55], for demonstration trajectory generation) motion planner. A workspace is constructed, LearnWorkspace, where $\left\{q^d\left(t\right)\right\}\to {\Omega }^{+}$ (17) and a demonstration relaxation of $ϵ=0.02$ m is used for workspace dilation (14); workspaces are illustrated in Figure 3i and Figure 4i.

Next, both a DMP and an RDMP are trained on $q^d\left(t\right)$: Train$\left(q^d\left(t\right)\right)\to {\mathbf{w}}^{\mathrm{DMP}}$ (4) and TrainRDMP$\left(q^d\left(t\right)\right)\to {\mathbf{w}}^{\mathrm{RDMP}}$ (Algorithm 1). Then, new goals $\left\{g_i\right\}$ are selected along a uniform horizontal grid centered at $g^d$. For each new goal $g_i$, an RDMP trajectory is generated from IntegrateRDMP$(q_{\mathrm{a},H},g_i,{\mathbf{w}}^{\mathrm{RDMP}})\to q_i^{\mathrm{RDMP}}\left(t\right)$ (Algorithm 2). Using the final RDMP configuration as the DMP goal, a DMP trajectory is likewise generated from Integrate$(q_{\mathrm{a},H},q_i^{\mathrm{RDMP}}(-1),{\mathbf{w}}^{\mathrm{DMP}})\to q_i^{\mathrm{DMP}}\left(t\right)$ (5). From the RDMP and DMP trajectories for each goal $g_i$, the corresponding risks are computed (16): $\mathcal{R}(q_i^{\mathrm{RDMP}}\left(t\right),{\Omega }^{+})$ and $\mathcal{R}(q_i^{\mathrm{DMP}}\left(t\right),{\Omega }^{+})$. The corresponding risks are displayed as contour plots in Figure 3ii and Figure 4ii. Note that missing values correspond to kinematically unreachable goals. Then, for each primitive, the risks are aggregated across all goals and displayed as histograms in Figure 3iii and Figure 4iii.

Finally, to help explain the differences in risk during generalization, we need to understand how DMPs and RDMPs differ in their reproduction of whole-arm motion. As a low-dimensional encoding of whole-arm motion, we select the fourth link, or elbow, of the robot (Figure 2). From the demonstration $q^d$ and all generalized trajectories $\left\{q_i^{\mathrm{DMP}}\left(t\right)\right\}$ and $\left\{q_i^{\mathrm{DMP}}\left(t\right)\right\}$, the x coordinate trajectory of the elbow link is computed and plotted in Figure 3iv and Figure 4iv.

4.3.2. Analysis

From the risk contours in Figure 3ii and Figure 4ii, we observe that the risk of the RDMP trajectories is the same or lower than that of DMP trajectories for the same goals. In examples (b) and (c), we see similar behavior between the RDMPs and DMPs, while the differences are more drastic in (a) and (d). From the risk histograms in Figure 3iii and Figure 4iii, we observe the same phenomenon without spatial dimensions: the RDMP histograms are similar or have a lower mean compared to the DMP histograms.

To explain the risk, we examine the elbow trajectories (Figure 3iv and Figure 4iv), which represent one dimension of whole-arm motion. In each case, we observe that RDMP trajectories remain closer to the demonstration than DMP trajectories, despite reaching the same joint configuration goals. The most dramatic deviations are in the examples in Figure 3a and Figure 4b, which correspond to the greater difference in risks seen in Figure 3ii–iii and Figure 4ii–iii. As the elbow deviates farther from the demonstration, the whole robot arm is moving farther outside of the safe workspace, so this relationship is sensible. When true workspace geometry is unmodeled and deviations from safe workspaces should be minimized, RDMPs appear to enable safer adaptation to a wider range of goals.

5. Learning from Programs

5.1. Motion Classes and Skills

This section details the specification of motion classes (MCs), a data structure that allows a subject-matter expert (SME) to define distinct behaviors that are salient for a particular class of tasks. A motion class serves as a bridge from the semantic description of a behavior to concrete methods of extracting examples of the behavior from demonstrations and generating new instances of the behavior.

To describe general functions that generate robot trajectories $q\left(t\right)$ given endpoint constraints, we first define a motion generator as

$$\pi :{}_{0}y,g\to q\left(t\right)$$

(24)

which maps an initial condition ${}_{0}y$ and goal g to a trajectory $q\left(t\right)$. Motion generators with learnable parameters $\mathbf{w}$ are denoted as ${\pi }^{\mathbf{w}}$ (e.g., DMP integration (5)). ${\pi }^{\varnothing }$ is used to denote an empty motion generator, which is learnable but whose parameters have not yet been learned, thus serving as a template. A motion generator without learnable parameters, such as a motion planner, is considered fixed and denoted as ${\pi }^{\square }$.

A motion class (MC) is defined as

m = (f_r, f_a, f_w, f_o, SEGMENT, α, π, 𝕐, 𝔾, Φ_x) ∈ M,

(25)

where

• $f_r$, $f_a$, $f_w$, and $f_o$ define the robot, affordance, workspace, and origin reference frames of a motion class m;
• segment$:d\to {\left\{{(\tilde{q}\left(t\right),T_{f_r},T_{f_a},T_{f_w},T_{f_o})}_i\right\}}_{i=1}^{N_m}$ identifies all $N_m$ instances of m in a demonstration $d=\left(q\right(t),\mathcal{T})$, consisting of a robot trajectory segment $\tilde{q}\left(t\right)$ and reference frame poses during each instance;
• $\alpha =(\mathsf{head},\mathsf{pre},\mathsf{eff})$ is an action template, describing m symbolically;
• $\pi ({}_{0}y,g)=\langle {\pi }_i({}_{0}y,g)\rangle$ is a sequence of fixed or empty motion generators describing m physically, parameterized by a single pair $({}_{0}y,g)$;
• $\mathbb{Y}(\mathrm{x},\mathcal{T},\mathbf{b})$ and $\mathbb{G}(\mathrm{x},\mathcal{T},\mathbf{b})$ define the admissible initial conditions ${}_{0}y$ and goals g as functions of physical state $\mathrm{x}$, task $\mathcal{T}$, and symbolic names $\mathbf{b}$;
• ${\Phi }_{\mathrm{x}}:\mathrm{x},g\to {\mathrm{x}}^{\prime }$ is a state transition function defining the discrete evolution of the physical state $\mathrm{x}$ as a result of m with goal $g\in \mathbb{G}(\mathrm{x},\mathcal{T},\mathbf{b})$.

Items $f_r$, $f_a$, $f_w$, $f_o$, and segment are used during the learning of affordances, workspaces, and skills from $\mathbf{D}$ (Section 5.2), while items $\alpha$, $\mathit{\pi }$, $\mathbb{Y}$, $\mathbb{G}$, and ${\Phi }_{\mathrm{x}}$ are used to formulate constraints and generate motion during the generation of new programs (Section 6.1). All SME-defined motion classes are collected in the set $\mathbf{M}$. Concrete examples of motion classes for mobile manipulator part transportation are given in Section 5.3: $\mathsf{Pick}$, $\mathsf{Place}$, and $\mathsf{Move}$.

Next, a skill $\kappa$ is defined as

$$\kappa =(m,\mathit{\pi }),$$

(26)

where $\mathit{\pi }=\langle {\pi }_i\rangle$ is a motion generator sequence comprising fixed or learned motion generators ${\pi }_i$. As such, a skill $\kappa$ is semantically defined by ${}^{\kappa }m$ and can generate motion with ${}^{\kappa }\mathit{\pi }$. Skill learning is covered in Section 5.2, in which a skill library $\mathbf{K}$ is constructed from $\mathbf{D}$ using $\mathbf{M}$.

Given an initial condition ${}_{0}y$ and goal g, a parameterized skill is denoted as $k=\kappa ({}_{0}y,g)$, analogous to an action defined as a parameterized action template, $a=\alpha \left(\mathbf{b}\right)$. A parameterized skill generates a trajectory by concatenating the trajectories yielded by its motion generators:

$$q\left(t\right)\leftarrow k=\kappa ({}_{0}y,g)=\bigcup _{{\pi }_i\in {}^k\mathit{\pi }}{\pi }_i({}_{0}y,g),$$

(27)

where the operator ← is used to indicate the execution of the parameterized skill k and the union operator ∪ is overloaded in this context to indicate trajectory concatenation. Planning with skills is covered in Section 6.1.

Finally, an SME may define how related skills can share a subset of their motion generators. For example, the motion classes $\mathsf{Pick}$ and $\mathsf{Place}$ defined in Section 5.3 are differentiated only by gripper action. Thus, $\mathsf{Pick}$ skills learned from $\mathbf{D}$ can be used to generate $\mathsf{Place}$ skills, and vice versa. The SME-defined function share$:\mathbf{K}\to {\mathbf{K}}^{\prime }$ encodes these relationships and enables the construction of an expanded skill set ${\mathbf{K}}^{\prime }\supset \mathbf{K}$.

5.2. Learning from Programs as Demonstrations

The process for applying a motion class set $\mathbf{M}$ to a historical dataset of demonstrations $\mathbf{D}$ to learn a set of affordances $\mathbf{A}$, skills $\mathbf{K}$, and workspaces $\mathbf{\Omega }$ is detailed in Learn (Algorithm 3). For each demonstration d, ^msegment extracts learning-relevant data from d (line 7), which is computed in the following ways.

First, on line 9, the affordance pose ${}^{f_a}T_{f_r}=T_{f_a}^{-1}{T}_{f_r}$ (e.g., end-effector frame $f_r$ and part frame $f_a$ for grasps) is computed and added to the affordance set  ${}^{f_a}\mathrm{A}_{f_r}$.

Next, on line 11, the workspace in the origin frame $f_o$ is computed using LearnWorkspace (17) and then transformed into the workspace frame (e.g., the frame of a machine ℓ to which the workspace belongs) using  ${}^{f_w}T_{f_o}=T_{f_w}^{-1}{T}_{f_o}$, and then added to the $f_w$ workspace set ${\Omega }_{f_w}^{+}$.

Then, on lines 13–16, a skill is built and added to the skill set ${\mathrm{K}}_m$. If ^m$\mathit{\pi }$ contains a learnable motion generator ${\pi }^{\varnothing }$, then the extracted trajectory segment $\tilde{q}\left(t\right)$ is used to Train a DMP with (4). The resulting weights $\mathbf{w}$ form a new motion generator ${\pi }^{\mathbf{w}}$ which replaces ${\pi }^{\varnothing }$ in $\mathit{\pi }$ and the new skill is formed $\kappa =(m,\mathit{\pi })$. Otherwise, if ^m$\mathit{\pi }$ contains only fixed motion generators, then $\kappa =(m,\mathit{\pi })$ is built directly. Note that since $\mathbf{K}$ is a set, duplicate skills are not stored.

Finally, affordance, workspace, and skill sets are built. The skill set is expanded by sharing motion generators among compatible skills, as defined in share. The final sets are then returned by Learn. In the next section, these learned sets are used to synthesize new programs.

Algorithm 3 Learn$(\mathrm{historical}\mathrm{dataset}\mathbf{D},\mathrm{motion}\mathrm{class}\mathrm{set}\mathbf{M}$)

1: for $m\in \mathbf{M}$ do 2:     Extract $f_r,f_a,f_w\leftarrow m$ 3:     Initialize ${}^{f_a}\mathrm{A}_{f_r}\leftarrow \varnothing$, ${\Omega }_{f_w}^{+}\leftarrow \varnothing$, ${\mathrm{K}}_m\leftarrow \varnothing$ 4: for $d=\left(q\right(t),\mathcal{T})\in \mathbf{D}$ do 5:     for $m\in \mathbf{M}$ do 6:         Extract $f_r,f_a,f_w,f_o,$segment, $\mathit{\pi }\leftarrow m$ 7:         for $(\tilde{q}\left(t\right),T_{p_r},T_{f_a},T_{f_w},T_{f_p},T_{f_o})\in$segment$\left(d\right)$ do 8:            Learn affordance: 9:            ${}^{f_a}\mathrm{A}_{f_r}\leftarrow {}^{f_a}\mathrm{A}_{f_r}\cup \left\{T_{f_a}^{-1}{T}_{f_r}\right\}$ 10:            Learn workspace and transform into workspace frame: 11:            ${\Omega }_{f_w}^{+}\leftarrow {\Omega }_{f_w}^{+}\cup \{T_{f_w}^{-1}{T}_{f_o}$LearnWorkspace$\left(\tilde{q}\left(t\right)\right)\}$ 12:            Learn skill, if possible: 13:            if $\mathit{\pi }$ contains a learnable motion generator ${\pi }^{\varnothing }$ then 14:                $\mathbf{w}\leftarrow$Train$\left(\tilde{q}\left(t\right)\right)$ 15:                Replace ${\pi }^{\varnothing }\in \mathit{\pi }$ with ${\pi }^{\mathbf{w}}$ 16:            ${\mathrm{K}}_m\leftarrow {\mathrm{K}}_m\cup \{\kappa =(m,\mathit{\pi })\}$ 17: Build sets: 18: $\mathbf{A}\leftarrow \left\{{}^{f_a}\mathrm{A}_{f_r}\right\}$, $\mathbf{\Omega }\leftarrow \left\{{\Omega }_{f_w}^{+}\right\}$, $\mathbf{K}\leftarrow \left\{{\mathrm{K}}_m\right\}$ 19: Expand skill set: 20: $\mathbf{K}\leftarrow$share$\left(\mathbf{K}\right)$ 21: return affordance set $\mathbf{A}$, skill set $\mathbf{K}$, workspace set $\mathbf{\Omega }$

5.3. Illustrative Example: Motion Class Design

In this section, the process of specifying a set of motion classes is illustrated using the example described in Section 3.4.

5.3.1. Motion Generators

The mobile manipulator described in Section 3.4 is capable of safely planning and executing base trajectories using a built-in laser scanner for localization and obstacle avoidance. A fixed motion generator ${\pi }_{\mathrm{BaseMove}}^{\square }({}_{0}y,g)$ is introduced to represent this capability, for an initial and final base pose ${}_{0}y,g\in {\mathbb{R}}^3$.

Moreover, the robot’s gripper is force-controlled with boolean commands. To represent this capability, a fixed motion generator ${\pi }_{\mathrm{Grip}}^{\square }({}_{0}y,g)$ is introduced, where ${}_{0}y,g\in \{0,1\}$ with 0 and 1 corresponding to “open” and “close,” respectively.

Finally, the robot’s redundant manipulator is manually programmed to pick and place parts in a variety of workspace locations safely. For new tasks, we want to generalize the safe workspace trajectories contained in $\mathbf{D}$. As such, a learnable motion generator for arm motion is introduced:

$${\pi }_{\mathrm{ArmRDMP}}^{\mathbf{w}}({}_{0}y,g)=IntegrateRDMP({}_{0}y,g,\mathbf{w}),$$

(28)

where ${}_{0}y\in Q_{\mathrm{a}}$ and $g\in SE\left(3\right)$.

5.3.2. Planning Domain

To describe the symbolic constraints of motion classes in the form of preconditions and effects, a planning domain must be specified. Primarily, the symbolic state representation of a part transportation task must describe the proximity of the robot, part, and locations between which the part can be transported. As such, state variables are introduced, $SV=\{\mathsf{at},\mathsf{robAt},\mathsf{holding}\}$. Additionally, to enable states to be defined as atomic formulae on state variables, a set of symbolic names are defined as $\mathbb{B}=\{\mathsf{True},\mathsf{False},\mathsf{None},p_1,\dots ,{\ell }_1,\dots \}$.

5.3.3. Motion Classes

The expected behaviors in a part transportation task are $\mathsf{Pick}$, $\mathsf{Place}$, and $\mathsf{Move}$. Using the motion generators and planning domain specified above, the motion classes are specified next. Note that the physical state here is $\mathrm{x}={\left[q^{\top }{}_{\vee }T_p^{\top }\right]}^{\top }$ with a configuration $q={\left[q_{\mathrm{m}}^{\top }{q}_{\mathrm{a}}^{\top }{q}_{\mathrm{g}}^{\top }\right]}^{\top }$ as introduced in Section 3.3.

First, $\mathsf{Pick}$ is introduced below. The moving robot frame is the end-effector e with respect to the robot base frame b as it approaches a part p at a workspace ℓ (line 1). Before picking part p from location ℓ, the robot and p must both be at ℓ and the robot must be holding nothing (line 2). After picking the part, p is no longer at ℓ, and the robot now holds p (line 3). segment identifies within $q\left(t\right)$ temporally proximal arm motions between which the gripper closes, which it identifies as instances of $\mathsf{Pick}$ (line 4). The motion generator sequence encodes an arm motion, followed by gripper closing, following by a reversal of the same arm motion, indicated by the notation ¬ (line 5). A $\mathsf{Pick}$ is assumed to always begin from a home configuration $q_{\mathrm{a},H}$ (line 6), while the goal is confined to a known grasp in ${}^e\mathrm{A}_p$ (line 7). Finally, the application of $\mathsf{Pick}$ results in a new physical state $\mathrm{x}$ with an unchanged base pose and arm configuration; however, the gripper is closed and the part pose is defined by the selected goal g and the end-effector pose ${\mathcal{F}}_{\mathrm{a}}\left(q_{\mathrm{a}}\right)$ (line 8).

$\mathsf{Pick}(\mathrm{part}p,\mathrm{location}\ell )$ 1: $f_r,f_a,f_w,f_o=e,p,\ell ,b$ 2: ${}^{\alpha }\mathsf{pre}=\{\mathsf{at}(p,\ell )=\mathsf{True},\mathsf{robAt}(\ell )=\mathsf{True},\mathsf{holding}\left(\right)=\mathsf{None}\}$ 3: ${}^{\alpha }\mathsf{eff}=\{\mathsf{at}(p,\ell )=\mathsf{False},\mathsf{robAt}(\ell )=\mathsf{True},\mathsf{holding}\left(\right)=p\}$ 4: segment 5: $\mathit{\pi }=\langle {\pi }_{\mathrm{ArmRDMP}}^{\varnothing }({}_{0}y,g),{\pi }_{\mathrm{Grip}}(0,1),\neg {\pi }_{\mathrm{ArmRDMP}}^{\varnothing }({}_{0}y,g)\rangle$ 6: $\mathbb{Y}(\mathrm{x},\mathcal{T})=\left\{q_{\mathrm{a},H}\right\}$ 7: $\mathbb{G}(\mathrm{x},\mathcal{T})=\{T_b^{-1}{T}_p{}^{p}T_e\mid {}^{p}T_e\in {}^p\mathrm{A}_e\}$ 8: ${\Phi }_{\mathrm{x}}(\mathrm{x},g)={\left[{}_{\vee }T_b^{\top }{q}_{\mathrm{a}}^{\top }1{}_{\vee }\left(T_b{\mathcal{F}}_{\mathrm{a}}\left(q_{\mathrm{a}}\right)g^{-1}{T}_b^{-1}{T}_p\right)^{\top }\right]}^{\top }$

Next, the $\mathsf{Place}$ motion class is defined in a similar way to $\mathsf{Pick}$. Preconditions and effects are reversed (lines 2–3). Instead of closing, the segment function looks for the gripper opening (line 4), and likewise in the motion generator sequence (line 5). The initial condition is the same (line 6), but the goal is constrained by the part goal pose $T_{p,g}$ rather than affordances (line 7). After a $\mathsf{Place}$, the next physical state $\mathrm{x}$ has the same base pose and arm configuration; however, the gripper opens and the part pose is defined by the goal selection (line 8).

$\mathsf{Place}(\mathrm{part}p,\mathrm{location}\ell )$ 1: $f_r,f_a,f_w,f_o=e,p,\ell ,b$ 2: ${}^{\alpha }\mathsf{pre}=\{\mathsf{at}(p,\ell )=\mathsf{False},\mathsf{robAt}(\ell )=\mathsf{True},\mathsf{holding}\left(\right)=p\}$ 3: ${}^{\alpha }\mathsf{eff}=\{\mathsf{at}(p,\ell )=\mathsf{True},\mathsf{robAt}(\ell )=\mathsf{True},\mathsf{holding}\left(\right)=\mathsf{None}\}$ 4: segment 5: $\mathit{\pi }=\langle {\pi }_{\mathrm{ArmRDMP}}^{\varnothing }({}_{0}y,g),{\pi }_{\mathrm{Grip}}(1,0),\neg {\pi }_{\mathrm{ArmRDMP}}^{\varnothing }({}_{0}y,g)\rangle$ 6: $\mathbb{Y}(\mathrm{x},\mathcal{T})=\left\{q_{\mathrm{a},H}\right\}$ 7: $\mathbb{G}(\mathrm{x},\mathcal{T})=\left\{T_b^{-1}{T}_{p_g}{T}_p^{-1}{T}_b^{-1}{\mathcal{F}}_{\mathrm{a}}\left(q_{\mathrm{a}}\right)\right\}$ 8: ${\Phi }_{\mathrm{x}}(\mathrm{x},g)={\left[{}_{\vee }T_b^{\top }{q}_{\mathrm{a}}^{\top }0{}_{\vee }\left(T_{b}g{\mathcal{F}}_{\mathrm{a}}{\left(q_{\mathrm{a}}\right)}^{-1}{T}_b^{-1}{T}_p\right)^{\top }\right]}^{\top }$

Finally, the $\mathsf{Move}$ motion class describes the motion of the robot base frame b with respect to the origin o as it approaches ${\ell }_1$ in a workspace likewise defined at the origin o (line 1). The preconditions and effects describe the robot moving from ${\ell }_0$ to ${\ell }_1$ (lines 2–3). segment identifies all periods of base motion in $q\left(t\right)$ as instances of $\mathsf{Move}$. The motion generator sequence comprises a single ${\pi }_{\mathrm{BaseMove}}^{\square }({}_{0}y,g)$ (line 5). The initial condition is the initial base pose $T_b$ (line 6) while the goal is confined to a known stance defined in ${}^{{\ell }_1}\mathrm{A}_b$ (line 7). After a $\mathsf{Move}$, the next physical state $\mathrm{x}$ has a base pose coincident with the goal, unchanged arm and gripper configurations, and a conditional part pose. If the gripper is open ($q_{\mathrm{g}}=0$), then the part pose is unchanged; otherwise, the part is assumed to be rigidly attached to the robot during base motion (line 8).

$\mathsf{Move}(\mathrm{location}{\ell }_0,\mathrm{location}{\ell }_1)$ 1: $f_r,f_a,f_w,f_o=b,{\ell }_1,o,o$ 2: ${}^{\alpha }\mathsf{pre}=\{\mathsf{robAt}\left({\ell }_0\right)=\mathsf{True},\mathsf{robAt}\left({\ell }_1\right)=\mathsf{False}\}$ 3: ${}^{\alpha }\mathsf{eff}=\{\mathsf{robAt}\left({\ell }_0\right)=\mathsf{False},\mathsf{robAt}\left({\ell }_1\right)=\mathsf{True}\}$ 4: segment 5: $\mathit{\pi }=\langle {\pi }_{\mathrm{BaseMove}}^{\square }({}_{0}y,g)\rangle$ 6: $\mathbb{Y}(\mathrm{x},\mathcal{T})=\left\{T_b\right\}$ 7: $\mathbb{G}(\mathrm{x},\mathcal{T})=\{T_{{\ell }_1}{}^{{\ell }_1}T_b\mid {}^{{\ell }_1}\mathrm{A}_b\}$ 8: ${\Phi }_{\mathrm{x}}(\mathrm{x},g)={\left[{}_{\vee }g^{\top }{q}_{\mathrm{a}}^{\top }{q}_{\mathrm{g}}{}_{\vee }\left([(1-q_{\mathrm{g}})I+q_{\mathrm{g}}g{T}_b^{-1}]T_p\right)^{\top }\right]}^{\top }$

With the motion class set $\mathbf{M}=\{\mathsf{Pick},\mathsf{Place},\mathsf{Move}\}$, applying Learn (Algorithm 3) to $\mathbf{D}$ yields an affordance set $\mathbf{A}$, workspace set $\mathbf{\Omega }$, and skill set $\mathbf{K}=\{{\mathrm{K}}_{\mathsf{Pick}},{\mathrm{K}}_{\mathsf{Place}},{\mathrm{K}}_{\mathsf{Move}}\}$. Since the only learnable motion generators are instances of ${\pi }_{\mathrm{ArmRDMP}}^{\varnothing }$, we know that ${\mathrm{K}}_{\mathsf{Move}}=\left\{(\mathsf{Move},\langle {\pi }_{\mathrm{BaseMove}}^{\square }\rangle )\right\}$ has a single element, while ${\mathrm{K}}_{\mathsf{Pick}}$ and ${\mathrm{K}}_{\mathsf{Place}}$ contain as many elements as instances of $\mathsf{Pick}$ and $\mathsf{Place}$, respectively, with each containing ${\pi }_{\mathrm{ArmRDMP}}^{\mathbf{w}}$ with a unique $\mathbf{w}$. Note that $\mathsf{Pick}$ and $\mathsf{Place}$ are only physically differentiated by gripper action. Therefore, the share$:\mathbf{K}\to {\mathbf{K}}^{\prime }$ function can be simply defined as duplicating all skills $\kappa \in {\mathrm{K}}_{\mathsf{Pick}}$, replacing ${\pi }_{\mathrm{Grip}}(0,1)$ terms with ${\pi }_{\mathrm{Grip}}(1,0)$, adding them to ${\mathrm{K}}_{\mathsf{Place}}$, and doing the reverse for all $\kappa \in {\mathrm{K}}_{\mathsf{Place}}$.

6. Skill-Based Program Generation

6.1. Program Generation from Skill-Based Planning

This section presents an approach to generating a new program $q\left(t\right)$ that drives the robot to complete a task $\mathcal{T}$. Our skill-based planning approach involves two steps: task planning followed by skill planning.

In the first step, an action plan $\mathbf{a}={\langle a_i\rangle }_{i=1}^N$ is constructed to solve $\mathcal{T}$ symbolically. In specifying a motion class set $\mathbf{M}$ and the action templates therein, an expert implicitly defines a planning domain $\Sigma =(\mathbb{S},\mathbb{A},{\Phi }_{\Sigma })$. From a task description $\mathcal{T}$, the initial $s_0$ and goal $s_g$ symbolic states can be constructed. Then, an automated task planner [44] constructs an action plan $\mathbf{a}$ to solve $\mathcal{T}$.

In the second step, each action $a_i$ is physically realized by a parameterized skill $k_i={\kappa }_i({}_{0}y_i,g_i)$ to form a skill plan $\mathbf{k}={\langle {\kappa }_i({}_{0}y_i,g_i)\rangle }_{i=1}^N$. Then, the new program trajectory is constructed by the concatenation of individual skill trajectories $q_i\left(t\right)\leftarrow k_i={\kappa }_i({}_{0}y_i,g_i)$:

$$q\left(t\right)\leftarrow \bigcup _{i\in [1,N]}{\kappa }_i({}_{0}y_i,g_i).$$

(29)

The skills ${\kappa }_i$ must be selected from the known skill set $\mathbf{K}$ along with initial conditions ${}_{0}y_i$ and goals $g_i$ in a way that is safe and feasible. Recall that an action is an action template parameterized by concrete symbolic arguments, $a_i={}^{m_i}\alpha \left({\mathbf{b}}_i\right)$. Thus, the action plan $\mathbf{a}$ can be rewritten as a motion class sequence and symbolic name sequence $\mathbf{a}={\langle {}^{m_i}\alpha \left({\mathbf{b}}_i\right)\rangle }_{i=1}^N$.

For each step i, the motion class $m_i$ provides constraints on initial conditions ${}_{0}y_i\in {}^{m_i}\mathbb{Y}({\mathrm{x}}_i,{\mathbf{b}}_i,\mathcal{T})$ and goals $g_i\in {}^{m_i}\mathbb{G}({\mathrm{x}}_i,{\mathbf{b}}_i,\mathcal{T},\mathbf{A})$, which constrain goal selection based on learned affordances to ensure physical feasibility, such as mobile base stances and part grasps. Motion classes also encode discrete state transitions ${\mathrm{x}}_{i+1}={}^{m_i}\Phi _{\mathrm{x}}({\mathrm{x}}_i,{\mathbf{b}}_i,g_i,\mathcal{T})$, enabling a state estimate ${\mathrm{x}}_i$ to be available for other constraints in each step i. Note that the initial and final states ${\mathrm{x}}_0$ and ${\mathrm{x}}_N$ are available directly from $\mathcal{T}$. For risk calculation (16), ${}^{m_i}f_w$ allows selection of the relevant workspace ${\Omega }_{{}^{m_i}f_w}^{+}\in \mathbf{\Omega }$. Altogether, skill planning is formulated as the following optimization problem, SkillPlan:

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}{\kappa }_0,\dots ,{\kappa }_{N-1}\\ {}_{0}y_0,\dots ,{}_{0}y_{N-1}\\ g_0,\dots ,g_{N-1}\end{array}}{min}& {\mathcal{J}}_{\mathcal{R}}=\underset{i\in [0,N-1]}{max}\mathcal{R}(q_i\left(t\right),{\Omega }_{{}^{m_i}f_w}^{+})\hfill \\ \hfill \mathrm{subject}\mathrm{to}& q_i\left(t\right)\leftarrow {\kappa }_i({}_{0}y_i,g_i)\hfill \\ \hfill & {\kappa }_i\in {\mathrm{K}}_{m_i},i=0,\dots ,N-1\hfill \\ \hfill & {}_{0}y_i\in {}^{m_i}\mathbb{Y}({\mathrm{x}}_i,{\mathbf{b}}_i,\mathcal{T}),i=0,\dots ,N-1\hfill \\ \hfill & g_i\in {}^{m_i}\mathbb{G}({\mathrm{x}}_i,{\mathbf{b}}_i,\mathcal{T},\mathbf{A}),i=0,\dots ,N-1\hfill \\ \hfill & {\mathrm{x}}_{i+1}={}^{m_i}{\Phi }_{\mathrm{x}}({\mathrm{x}}_i,{\mathbf{b}}_i,g_i,\mathcal{T}),i=0,\dots ,N-1\hfill \\ \hfill & {\mathrm{x}}_0\mathrm{and}{\mathrm{x}}_N\mathrm{given}.\hfill \end{array}$$

(30)

The problem (30) can only be formulated if the task $\mathcal{T}=(T_{p,0},T_{p,g},T_{{\ell }_1},T_{{\ell }_2})$ is symbolically feasible with respect to $\mathbf{M}$, $\mathbf{A}$, $\mathbf{K}$, and $\mathbf{\Omega }$, meaning

• The affordance sets ${}^{{\ell }_1}\mathrm{A}_b,{}^{{\ell }_2}\mathrm{A}_b,{}^p\mathrm{A}_e\in \mathbf{A}$ are nonempty;
• The skill sets ${\mathrm{K}}_{\mathsf{Pick}},{\mathrm{K}}_{\mathsf{Place}},{\mathrm{K}}_{\mathsf{Move}}\in \mathbf{K}$, are nonempty;
• The workspaces ${\Omega }_{{\ell }_1}^{+},{\Omega }_{{\ell }_2}^{+}\in \mathbf{\Omega }$ are nonempty.

If a task is symbolically feasible, then the problem (30) can be formulated. If (30) has a local minimizer with acceptable risk, then the task $\mathcal{T}$ is also physically feasible and (30) yields a skill plan $\mathbf{k}={\langle {\kappa }_i({}_{0}y_i,g_i)\rangle }_{i=1}^N$ that physically solves $\mathcal{T}$.

As (30) involves simultaneous optimization of a nonlinear objective ${\mathcal{J}}_{\mathcal{R}}$ over discrete variables $k_i$ and continuous variables like ${}_{0}y_i,g_i,$ and ${\mathrm{x}}_i$, it is a mixed-integer nonlinear program, which is NP-hard. However, (30) can be greatly simplified for particular motion class sets, as shown in Section 6.2.

6.2. Illustrative Example: Skill Planning

While SkillPlan (30) is, in general, a mixed-integer nonlinear program, it can be simplified by considering a specific motion class set. Given the motion class set $\mathbf{M}$ defined in Section 5.3, a minimum-length action plan is

$$\begin{array}{c}\hfill \mathbf{a}=\langle \mathsf{Move}({\ell }_0,{\ell }_1),\mathsf{Pick}(p,{\ell }_1),\mathsf{Move}({\ell }_1,{\ell }_2),\\ \hfill \mathsf{Place}(p,{\ell }_2),\mathsf{Move}({\ell }_2,{\ell }_0)\rangle .\end{array}$$

(31)

Since ${\pi }_{\mathrm{BaseMove}}^{\square }$ can safely move between locations, its execution and resulting risk computation can be neglected from the planning loop. Moreover, while ${}_{0}y_i$ and $g_i$ are continuous decision variables in general in (30), the sets ${}^m\mathbb{Y}$ and ${}^m\mathbb{G}$ defined in each $m\in \mathbf{M}$ describe discrete sets. Therefore, SkillPlan (30) can be reduced to a grid search on base stances ${}^{{\ell }_1}\mathrm{A}_b$ and ${}^{{\ell }_2}\mathrm{A}_b$, grasp poses ${}^p\mathrm{A}_e$, and skills ${\kappa }_{\mathsf{Pick}}$ and ${\kappa }_{\mathsf{Place}}$, which is given in SkillPlan-PTT (Algorithm 4). The algorithm loops over all pick and place skills as well as all possible end-effector goal poses, as defined by affordances, and finds the combination with the lowest risk.

Algorithm 4 SkillPlan-PTT$(\mathcal{T},\mathbf{A},\mathbf{K},\mathbf{\Omega }$)

1: Extract $p,{\ell }_1,{\ell }_2,T_{p,0},T_{p,g},T_{{\ell }_1},T_{{\ell }_2}$ from $\mathcal{T}$ 2: Extract grasps ${}^p\mathrm{A}_e$ and stances  ${}^{{\ell }_1}\mathrm{A}_b,{}^{{\ell }_2}\mathrm{A}_b$ from $\mathbf{A}$ 3: Extract safe workspaces ${\Omega }_{{\ell }_1}^{+}$, ${\Omega }_{{\ell }_2}^{+}$ from $\mathbf{\Omega }$ 4: Extract ${\mathrm{K}}_{\mathsf{Pick}}$, ${\mathrm{K}}_{\mathsf{Place}}$ from $\mathbf{K}$ 5: Initialize solution set $\mathtt{solu}\leftarrow \varnothing$ 6: for ${}^{{\ell }_1}T_b,{}^{{\ell }_2}T_b,{}^{p}T_e,{\kappa }_{\mathsf{Pick}},{\kappa }_{\mathsf{Pick}}\in {}^{{\ell }_1}\mathrm{A}_b\times {}^{{\ell }_2}\mathrm{A}_b\times {}^p\mathrm{A}_e\times {\mathrm{K}}_{\mathsf{Pick}}\times {\mathrm{K}}_{\mathsf{Place}}$ do 7:     $T_{\mathsf{Pick}}\leftarrow {}^{b}T_{p,0}{}^{p}T_e$ 8:     $T_{\mathsf{Place}}\leftarrow {}^{b}T_{p,\mathrm{g}}{}^{p}T_e$ 9:     $q_{\mathsf{Pick}}\left(t\right)\leftarrow {\kappa }_{\mathsf{Pick}}(q_{\mathrm{a},H},T_{\mathsf{Pick}})$ 10:     $q_{\mathsf{Place}}\left(t\right)\leftarrow {\kappa }_{\mathsf{Place}}(q_{\mathrm{a},H},T_{\mathsf{Place}})$ 11:     $r_{\mathsf{Pick}}\leftarrow \mathcal{R}(q_{\mathsf{Pick}}\left(t\right),{\Omega }_{{\ell }_1}^{+})$ 12:     $r_{\mathsf{Place}}\leftarrow \mathcal{R}(q_{\mathsf{Place}}\left(t\right),{\Omega }_{{\ell }_2}^{+})$ 13:     $\mathcal{J}\leftarrow max\{r_{\mathsf{Pick}},r_{\mathsf{Place}}\}$ 14:     Store solution $\mathtt{solu}\leftarrow \mathtt{solu}\cup \{\mathcal{J},q_{\mathsf{Pick}}\left(t\right),q_{\mathsf{Place}}\left(t\right)\}$ 15: Obtain optimal $q_{\mathsf{Pick}}^{*}\left(t\right),q_{\mathsf{Place}}^{*}\left(t\right)$ with lowest ${\mathcal{J}}^{*}$ from $\mathtt{solu}$ 16: return $q_{\mathsf{Pick}}^{*}\left(t\right)$, $q_{\mathsf{Pick}}^{*}\left(t\right)$, ${\mathcal{J}}^{*}$

6.3. Illustrative Example: End-to-End Learning and Planning Performance

In this section, we evaluate the end-to-end performance of the PRF by estimating the number of solvable tasks for a given number of demonstrations. Since there are an uncountable number of possible tasks and demonstrations, we restrict part poses and location poses to fixed, nominal values for tractability. To aid analysis, we introduce a final structure, the afforded task ${\mathcal{T}}^{\mathrm{A}}$:

$${\mathcal{T}}^{\mathrm{A}}=(\mathcal{T},{}^{{\ell }_1}T_b,{}^{{\ell }_2}T_b,{}^{p}T_e)$$

(32)

which appends a set of specific affordances (approaches ${}^{{\ell }_1}T_b$ and ${}^{{\ell }_2}T_b$ and grasp ${}^{p}T_e$) to a given task $\mathcal{T}$.

The objective of this study is to take a demonstration set $\mathbf{D}$, learn from it using Learn$(\mathbf{D},\mathbf{M})\to \mathbf{A},\mathbf{K},\mathbf{\Omega }$, and then apply the outputs to SkillPlan-PTT$(\mathcal{T},\mathbf{A},\mathbf{K},\mathbf{\Omega })$ to count how many tasks $\mathcal{T}$ are solvable.

6.3.1. Approach

For the illustrative example outlined in Section 3.4, there are a total of 18 unique tasks, assuming nominal part and location poses. There are also 64 unique afforded tasks, as there are multiple ways to perform each task considering the various approaches and grasps. Each afforded task can be realized by an infinite variation in demonstrations, but for tractability, we generate exactly one demonstration for each afforded task. Thus, for our complete demonstration set $\mathbf{D}$, its size is $\left|\mathbf{D}\right|=64$. Following the same procedure as in Section 4.3.1, demonstrations are generated using motion planners that have access to the true geometric models of the robot’s environment, ensuring that the historical datasets $\mathbf{D}$ are safe and feasible.

Since $\mathbf{D}$ contains demonstrations of every possible task, it is also capable of solving all tasks. Here, we adopt a Monte Carlo approach, in which we simulate multiple episodes of learning, with each episode representing a random sequence in which demonstrations are learned, checking the number of feasible tasks in each episode step.

Starting each episode i at step $j=0$ with an empty demonstration set ${\mathbf{D}}_{i,j}=\varnothing$, we randomly select a demonstration from $\mathbf{D}$ to append to ${\mathbf{D}}_{i,j}$. Then, we learn from the current set: Learn$({\mathbf{D}}_{i,j},\mathbf{M})\to {\mathbf{A}}_{i,j},{\mathbf{K}}_{i,j},{\mathbf{\Omega }}_{i,j}$. After learning, we iterate over all 18 tasks and attempt to solve each with SkillPlan-PTT$(\mathcal{T},{\mathbf{A}}_{i,j},{\mathbf{K}}_{i,j},{\mathbf{\Omega }}_{i,j})\to \mathcal{J}$. We store all feasible tasks (and corresponding afforded tasks from the inner loop of SkillPlan-PTT) and advance to the next episode step $j+1$.

During each episode step, we count three types of feasible tasks: physically feasible tasks, physically feasible afforded tasks, and symbolically feasible afforded tasks. As in Section 6.1, physical feasibility indicates an acceptable risk, computed by (16) using learned workspaces $\Omega$. Meanwhile, symbolic feasibility merely indicates any return value from the planner. These three counts are collected since they represent different levels of abstraction. For a task or afforded task to be physically feasible, it depends strongly on the nature of the demonstrations and specifics of the environment in which the demonstration was performed. On the other hand, symbolic feasibility captures the most basic rate of learning, abstracted from the demonstrations or environments themselves.

6.3.2. Analysis

Figure 5 captures the results of the Monte Carlo simulation with 50 episodes. The shaded regions represent the range over the episodes while the dark lines represent the mean across episodes in each step. We observe that all episodes eventually converge to solving all (afforded) tasks, and do so with fewer than half the total number of demonstrations even in the worst scenario.

In the afforded task simulations (Figure 5a), we see that all afforded tasks become symbolically feasible far earlier than physically feasible. This gap is the result of the geometry of the available demonstrations; more circuitous demonstrations result in larger safe workspaces (permitting more task variation) while more direct demonstrations result in smaller workspaces. In the physical task simulations (Figure 5b), we observe that all 18 tasks become physically feasible with between two and seven demonstrations. This indicates that some sequences of demonstrations are more informative than others. The case with two demonstrations encodes workspaces and affordances for all locations and parts, enabling a significant multiplication of 18 tasks from only two demonstrations.

7. Discussion

7.1. Applicability

The PRF is designed to automate the programming of new tasks given a historical dataset of existing robot programs. The PRF is well suited for situations in which robots are manually programmed to complete repetitive tasks that do not require online vision feedback, do not have accurate CAD models of the environment, and are occasionally reconfigured to operate at different locations and with different parts. The PRF uses historical data across all tasks for which a robot has been programmed and generates programs for new tasks that result from reconfigurations. The PRF trades the labor of robot programming for the labor of motion class design, allowing an SME to embed knowledge of robot behaviors that are both task-relevant and known to be present in the historical dataset. As shown in Section 6.3, the PRF is capable of solving a large number of new tasks with a modest historical dataset by leveraging a set of well-designed motion classes.

However, the PRF is not suitable in all situations. Generalization is only possible for new tasks that are reconfigurations of tasks covered in the historical dataset. It also must be possible for new tasks to be completed with behaviors contained in the historical dataset, and those behaviors must be appropriately encoded as motion classes. For instance, the robot in our illustrative example (Section 3.4) is used for part transportation; the PRF would not be capable of generalizing the historical data from this robot for a machining task. Additionally, generalization depends on the diversity of the historical data. From Figure 5b, we see that a historical dataset with two demonstrations can generalize to between 2 and 18 tasks. If the two demonstrations are very similar, they cannot generalize significantly. For example, the demonstration tasks may be (1) transport Part1 between one CNC and another CNC and (2) transport Part2 between one CNC and another CNC; as a result, no tasks involving a Printer or Table are feasible. On the other hand, if the two demonstration tasks are diverse—(1) transport Part1 from a CNC to a Printer and (2) transport Part2 from a Printer to a Table—then all 18 tasks become feasible.

7.2. Study Limitations

Although we demonstrate the application of the PRF for a part transportation task, our study does not cover the entire range of situations for which the PRF may be used nor does it include hardware implementation. Our emphasis on learning manipulator motion skills was motivated by the ubiquity of such behavior across industrial robots, but does not capture behavior involving forceful environmental interaction, such as machining. Furthermore, one would expect the hardware implementation of the PRF to include other practical considerations. For one, the robot’s geometric model must accurately capture the real robot’s geometry, including any end-of-arm tooling that may not be included in the robot’s standard manufacturer-provided model, as the geometry is critical for both workspace construction and safety verification. Additionally, real robot control systems are imperfect: controllers for both robot arms and mobile bases track reference trajectories with some error. Future studies should focus on both a wider range of robot tasks as well as experimental validation on real robots.

8. Conclusions

This paper considers the problem of automatically generating robot programs for new tasks when neither geometric environmental models nor vision feedback are available. The Program Reuse Framework (PRF) is defined for generating programs to solve new tasks through structured learning from a historical dataset of programs for similar tasks, which are interpreted as demonstrations. The PRF aims to maximize the utility of data collected from the existing industry to solve similar tasks without traditional manual programming.

To cope with unmodeled environments, an approach to learning safe workspaces from demonstrations is given. The approach leverages link geometries and assumptions on minimum clearance to construct safe workspace sets, from which a risk metric is defined. Workspaces are currently learned from demonstrations alone, limiting generalization, so the safe, active exploration of unknown or partially known workspaces will be explored. Additionally, the problem of on-demand sensing introduced in [39] will be developed further and integrated with the PRF to handle new tasks that deviate significantly from the historical dataset without relying on continuous sensing.

A novel dynamical movement primitive variant tailored to redundant manipulators is developed, called the RDMP, which generalizes to new end-effector goals while maintaining whole-arm motion characteristics. RDMPs were found to outperform DMPs in most cases in terms of minimizing risk while generalizing to new goals, more effectively constraining arm motion to within learned workspaces. Presently, RDMPs simply replay learned null space trajectories during integration, limiting generalization to new goals and environments. In practice, this means that RDMPs are only valid near their demonstration goal. Further development will consider how the null space goal can be modulated given new end-effector goals with the objective of increasing the range of generalization goals.

To enable structured learning of affordances, workspaces, and skills from a limited historical dataset, expert-designed motion classes are defined. Moreover, to enable the generation of new programs, motion classes also define a set of constraints suitable for formulation of a risk-minimizing plan optimization. Presently, new tasks are only feasible within the PRF if programs in the historical dataset contain explicit reference to the parts and locations involved in new tasks. Future work will consider how task infeasibility can prompt users for additional information, such as part or location models, from which affordances and workspaces can be inferred.