Abstract
The technology used for the 3D printing of buildings from concrete is currently a very relevant and developing topic and appears to be especially advantageous in terms of sustainable production. An important aspect of the sustainability assessment is the energy efficiency of the printing robots. Printing robots consume a significant amount of energy when printing. It is important to analyse this energy thoroughly and to be able to predict it in order to optimise the movement and control of printing robots to reduce energy consumption. In that paper, we analyse in detail the energy consumption of printing robots, which has not yet been thoroughly investigated in the context of 3D printing building applications. We present a methodology to develop an energy consumption model for a printing robot, specifically developed and optimized for this technology. Our methodology incorporates an innovative approach to determine reduced-efficiency maps, allowing for the inclusion of difficult-to-measure drive efficiency parameters in the model. This results in a comprehensive model of the energy consumption of the printing robot, reflecting its operating characteristics in a real-world environment. An open control system of the printing robot is used for the measurement of energy quantities, and specially developed software tools are introduced. We also present the first direct comparison of the energy consumption of different printing robots when following a uniform printing trajectory. The comparison is made based on the presented methodology to obtain and compare actual energy data from workplaces with printing robots. The methodology combines measured data with energy simulations from ABB RobotStudio, enabling energy comparisons between industrially articulated robots and real printing robots, including the ABB IRB4600, the gantry printing robot, and the printing robot. The experiments clearly demonstrate that the kinematic structure of printing robots significantly affects their energy consumption in 3D printing concrete. Based on the conducted methodologies and analyses, we identify key aspects of energy consumption of printing robots in 3D Construction Printing or 3D Concrete Printing (3DCP) technology. In doing so, we bring a new perspective and provide a basis for further research and development in this previously understudied area.
1. Introduction
Over the last few years, the field of the 3D printing of building structures has seen significant progress, bringing innovations in the form of efficient use of concrete mixes and automated robotic technologies. Additive manufacturing based on the extrusion of cement-based material, referred to as 3D Construction Printing or 3D Concrete Printing (3DCP), not only increases the efficiency of the construction process but also emphasizes key aspects such as energy savings, optimization of material resources, and environmental friendliness.
In [1], it was found that the production of a prefabricated bathroom unit using industrial robots (IRs) and 3DCP technology resulted in a 25.4% reduction in total cost, 85.9% reduction in CO2 emissions, and 87.1% reduction in energy consumption compared to a prefabricated structure produced using conventional methods. In [2], a thorough study was conducted to investigate the environmental impact of 3DCP technology for four different scenarios of 1 m2 concrete wall construction methods. The study shows that 3DCP technology significantly reduces the adverse environmental and global warming impacts compared to conventional construction methods.
3DCP technology uses robotic systems that operate with high precision and repeatability, resulting in efficient energy use and minimized waste. This paper deals with the development of an energy consumption model for a printing robot developed for 3DCP technology. The paper also presents a comparison of the energy consumption of the printing robots of different kinematic structures when they move along a uniform printing trajectory. The paper also presents a methodology for obtaining the efficiency maps of the individual actuators of the printing robot, which are crucial for determining the real energy consumption of the printing robot for 3DCP technology.
The paper is organised as follows: Background and related work is found in Section 2. Section 3 presents an analysis of robotic systems designed for 3DCP and discusses in detail the consumption of the printing robot. Section 4 describes the process of modelling the consumption of the printing robot. This part of the work elaborates on the kinematics and dynamics of the printing robot and concludes with a subsection on the linearization of the dynamics and inverse dynamic identification model (IDIM). Section 5 is devoted to experiments to verify the results on the printing robot and other real workplaces. Section 6 presents a new method for determining reduced efficiency maps of printing robot drives. The results for the energy consumption of different types of robots are presented in Section 7 and future work summarizing the energy consumption issue is presented in the last section, Section 8.
2. Background and Related Work
2.1. Robotic Systems Used in 3DCP Technology
For large-format 3D printers, industrial robotic arms or gantry robots are most commonly encountered [3]. For example, the CREATE research group at the University of Southern Denmark, which is researching new design and manufacturing strategies, uses a robotic cell incorporating a six-axis ABB IRB 6650S robot for 3DCP technology. The robot has a maximum reach of 3.3 m, a payload capacity of 125 kg, and a total weight (including cables) of 2250 kg [4]. In [5], researchers from ETH Zurich even combined the advantages of both systems and installed a six-axis ABB IRB 4600 robotic arm on a three-axis Güdel gantry robot near the ceiling. This solution increased the horizontal and vertical working space of the robotic arm. The article does not provide information about the robot itself, but according to the catalogue data, the ABB IRB 4600-40 robot has a maximum reach of 2.55 m, a payload of 40 kg and a total robot weight of 465 kg. The authors state that this solution can print objects up to 3.5 m high.
The use of industrial robotic arms for 3DCP technology seems obvious, as industrial robotic arms are available in a wide range of working ranges and load capacities and are widely used in automated production lines. Thanks to advanced software, they are easy to use and simultaneously offer high precision and dynamics. In addition, robot manufacturers themselves are now responding to robot-based additive manufacturing (RBAM) technology and often offer their own software add-ons that allow the 3D printing process to be at least partially automated. For example, ABB’s RobotStudio commercial robot programming and simulation software optionally includes a 3D Printing PowerPac add-on module that allows importing G-code and translating it into robot commands [6]. When using gantry robots, G-code can usually be directly implemented due to the custom computer numerical control (CNC) kernel. Commercial software (e.g., Ansys, Netfabb, 3DS, Cura) can be used to create a set of printing parameters in order to optimize the deposition process [7].
Although the use of industrial robots for 3DCP technology is advantageous mainly because of the user-friendliness and thus, the possible fast integration into the production process, 3DCP technology brings a number of specific requirements for printing robots that are not fully respected. Printing is currently often performed by conventional industrial robots that are not optimized for this application, which can result in, among other things, a higher power consumption that needs to be included in the overall consumption of the 3DCP printing technology.
2.2. Methods for Determining Robot Consumption Models
To be able to predict and possibly optimize the energy consumption of robots, a robot power consumption model needs to be established. Currently, there are a number of approaches for developing a robot power consumption model, which can be broadly divided into direct and indirect approaches. Direct approaches are based on direct measurements of power consumption on a real robot at different configurations and parameters (affecting power consumption) of the robot in its workspace. Indirect approaches are based on mathematical analysis/simulation leading to the determination of the robot consumption as a function of the input trajectory.
2.3. Direct Approaches for Determining Robot Energy Consumption
A representative of the first group is, e.g., the paper [8], where the optimal position/configuration of the robotic arm is determined in terms of minimizing the energy consumption required to compensate for gravitational forces. A 2D power map is constructed based on power measurements at different robot configurations. Based on the constructed energy map, it should be possible to determine the optimal region of the robot workspace where the robot consumes less energy. However, the mapping process is very time-consuming, as many experiments need to be performed and lengthy motion parameters and path planning need to be set. In [9], the quantities related to the energy consumption of a highly loaded industrial robot (KUKA KR210 R2700 with a nominal load of 210 kg) are measured. A measuring instrument for indirect power measurement is presented, consisting of Chauvin Arnoux PAC 22 current clamps, Testec TT-SI 9002 active differential probes, and Acquisition module Data Translation DT9826. In that paper, energy consumption maps were constructed based on experiments to find non-trivial energy-optimal motion parameters for a given cycle time. It is shown that a rational choice of velocity and acceleration parameters can lead to energy savings of more than 50%. In [10], temperature and variable payload parameters were also investigated in comparison to the standard operating parameters of the Kawasaki ZZX130L industrial robot. The aim of the paper was to determine which of the investigated operating parameters contributes most to energy consumption. The measurements were made directly through the robot controller, which had built-in functions to measure the current of each axis of the robot. The statistical analysis of the data was performed in that paper, and this analysis found that the linear velocity and acceleration make a significant contribution to the energy consumption in the first three joints of the Kawasaki robot. This contribution accounts for almost 95% of the total energy consumption. The remaining energy consumption is attributed to other factors such as payload and temperature.
2.4. Indirect Approaches for Determining Robot Energy Consumption
In indirect approaches, the most common approach to calculating energy consumption is based on the energy simulation model of the robot, where the energy consumption model can be obtained in different ways. In [11], the energy consumption model is obtained from a digital model of the industrial robot Motoman MH5L. The digital model was created using the CATIA Systems Dynamic Behavior Modelling (DBM) simulation tool based on the open-source language Modelica. In [12], the dynamic/energy consumption model is obtained through a graphically oriented computational approach using Solidworks CAD software and MATLAB/Simulink simulation environment with SimMechanics and SimPowerSystems libraries. A model of the KUKA KR5 industrial robot representing the mechanical structure and permanent magnet synchronous motor (PMSM) drives of the robot was created, from which the robot energy-consumption equations were subsequently evaluated. Other methods have in common the use of the linear dependence of the inertial parameters with respect to the robot dynamic model to obtain the dynamic/energy consumption model and use a parametric identification experiment to determine the inertial and friction parameters. In [13], a methodology for on-site non-invasive identification using a three-phase CA8335 Qualistar electrical network analyser is presented. From the obtained parametric dynamic model, the total power is then calculated and compared with the total power obtained from simulation through ABB RobotStudio. The systematic methodology is verified on an ABB IRB1600 industrial robot, and the obtained power model is used for subsequent trajectory optimization in terms of power. The software-simulated power obtained through ABB Robot Studio is also used in [14] to identify the inertial parameters and model the energy consumption of the robot. Compared to classical identification methods, where the measured torque of each axis of the robot is used to identify the inertial parameters, here, a stepwise identification based on simulated power data is used. This methodology appears to be advantageous for industrial robots with closed-loop control systems that do not allow direct torque/current measurements. The results are demonstrated here in a simulation of an ABB IRB 1200 robot in the RobotStudio environment. However, the accuracy of this method is directly proportional to the accuracy of the digital robot model. The energy modelling method based on the digital twin of the KUKA KR6 R700 industrial robot is presented in [15]. In that paper, a standard experiment is conducted to identify the dynamic parameters of the robot based on the direct measurement of actuator moments and motion data by the robot control system. Subsequently, the identification of the dynamic parameters was performed using the least squares method. The obtained dynamic parameters are used to create a physical energy consumption model of the robot, based on which a digital twin of the robot is created. Energy consumption can be predicted according to the energy consumption model based on the digital twin.
2.5. Considering Robot Energy Consumption in the Context of 3DCP Technology
From the above literature, there are a number of approaches to developing energy consumption models for robots. These are generally focused on determining the power consumption of robotic arms used in industry, but publications focusing on specific applications can also be found. For example, in [16], an energy-efficiency analysis of a robotic system for laser processing technology is performed. In [17], research on energy consumption analysis of robotic arms used in manufacturing processes is presented. However, there is very little information regarding the power consumption of robotic systems used for 3DCP technology. Several publications dealing with additive manufacturing in the construction industry mention the power consumption of robotic systems, but only very marginally. In [4], the amount of energy required to operate a robotic arm for the purpose of the Life Cycle Inventory of 3DCP technology was determined based on technical data available from manufacturers and using the Pareto principle. In [18], the robot power consumption for Mesh Mould technology was determined based on the battery capacity that powers the robot and the amount of time the robot can operate without being connected to the power grid.
2.6. Summary
In this context, the paper addresses the issue of modelling energy consumption in printing robots and builds on previous research by the authors. A power consumption model is developed for a unique printing robot called Printing Mantis, the design, development and description of which can be found in [19,20]. Due to the open control system of the printing robot, the design and testing of which can be found in [21], the creation of the energy consumption model is very time-efficient. It is possible to use direct readout of the torques, velocities, and positions of the individual robot axes along with direct readout of the power consumption using only the control system. The paper also presents a study comparing the effect of robots’ kinematic structure on power consumption during printing. This comparison is made both by simulation using ABB RobotStudio (RobotStudio 2024.1.1) for possible comparison with the six-axis robots used for 3DCP technology and by measurement on real devices. Specifically, we call the aforementioned unique printing robot Printing Mantis and the classic gantry robot TestBed, which was built during our proof-of-concept studies for 3DCP technology. More information regarding the gantry robot TestBed and its SW can be found in [22]. To the best of the authors’ knowledge, no study can be found in the current literature dealing with the modelling of the consumption of robotic systems for 3DCP technology and comparing the different kinematic structures of the robotic systems used for this technology. Therefore, we would like to fill this gap and present a study addressing the issue of power consumption modelling for 3DCP technology. At the same time, the paper presents a new methodology for creating reduced efficiency maps of individual robot actuators for a more objective evaluation of their power consumption. The uniqueness of this methodology lies in the use of an identification experiment for the parametric identification of dynamic parameters during which the power consumption quantities of individual actuators are also recorded to enable the subsequent creation of efficiency maps.
3. Power Analysis of 3DCP Robotic System
Robotic systems designed for 3DCP technology contain, in addition to the printing robot itself, a number of components that contribute to a greater or lesser extent to the overall consumption of robotic systems. This section seeks to analyse the impact of the individual components of a 3DCP robotic system containing the unique Printing Mantis robot on its overall energy consumption.
3.1. Energy Flow of the Printing Mantis
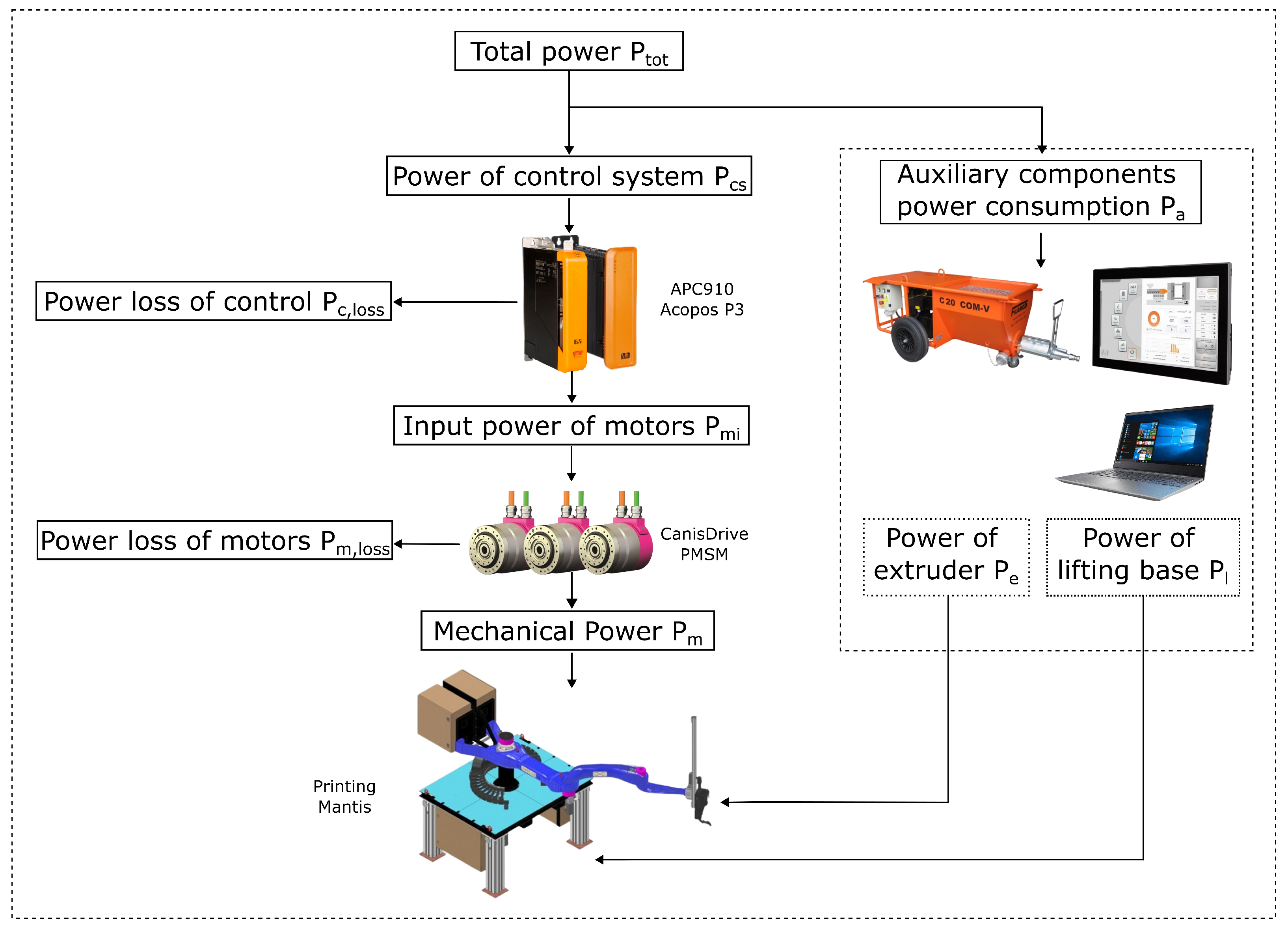
The power flow structure can be considered one of the key things to ensure the reliable and efficient operation of robots. The power flow (Figure 1) from the power supply is divided into two main branches, the power of the control system , and the auxiliary components’ power consumption, labeled . The main branch includes the robot control system of the APC910 and the Acopos P3 servo amplifiers for controlling each axis of the robot. The is generated on them. The energy is transferred from the servo amplifiers and the driving system to the PMSM drives of the CanisDrive robot with harmonic gears. The losses due to friction, heat, dissipation, etc., on the drive train are referred to as . The last part of the main branch of the energy flow is the mechanic power at the shaft , which is generated by the motion of the Printing Mantis.
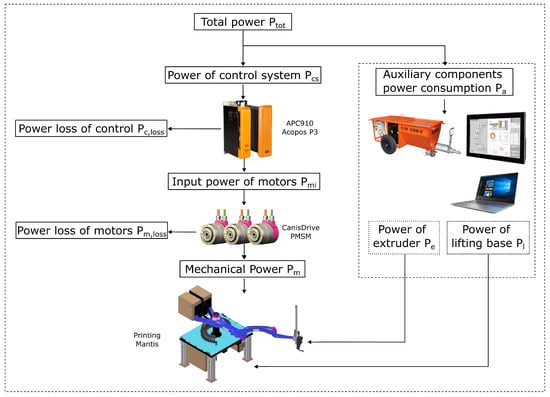
Figure 1.
Energy flow of the Printing Mantis.
The second part of the branch contains devices that usually run simultaneously with the robotic arm, for example, the pump for the concrete mix, the HMI panel for controlling the printing robot, the extruder, the drives for the base of the robotic arm, or the computer for measuring quantities during printing or interacting with the control system.
3.2. Mechanical, Electrical Power and Energy Consumption of Robot Drives
Nowadays, 3DCP technology is often used for relatively massive industrial robots with large ranges, where PMSM motors are used almost exclusively as drives for individual axes. This is no different for the Printing Mantis robot. PMSM motor technology delivers high power with reduced energy consumption and thus contributes to a high efficiency of 83–92% [23]. However, it must be taken into account that this efficiency can only be counted on at nominal values.
In the field of energy consumption (EC) and EC modelling, terms such as power, power input and energy consumption are often used. However, it is important to distinguish between the terms “mechanical power” and “electrical power” when determining the power to move the individual links of a robot arm. Mechanical power represents the power required to overcome the inertial resistance and friction in the joints of the robotic manipulator. As the joint accelerates, the motor provides mechanical power to the system. Otherwise, when the joint decelerates, the motor acts as a generator, converting the kinetic energy of the joint motion into electrical energy. This energy is most often dissipated in the braking resistor, where it is converted to heat. Mechanical power can be calculated as the product of torque and angular velocity. It therefore gives us the power of the drive on the shaft. The total mechanical power, sometimes referred to as Total Power, is then given by the sum of the mechanical powers of the individual axes of the robotic manipulator. In contrast, electrical power indicates the power input to the actuators and is defined as follows:
where n is the number of drives, is the quadrature component of the stator current, is the quadrature component of the stator voltage, is the directive component of the stator current and is the directive component of the stator voltage.
Electrical power can also be formulated in terms of mechanical power, where electrical power corresponds to the product of torque and angular velocity of the individual drive divided by efficiency.
where and are mechanical and electrical efficiencies, which are affected by a number of factors. Mechanical efficiency is influenced, for example, by losses in the gearing mechanisms, friction in the individual axis fits, etc. Electrical efficiency is influenced by a number of factors, but in particular by losses in the motor. However, in a simplified way, the overall efficiency of a given axis can be calculated as the ratio of the mechanical power to the electrical power input
where is mechanical power, defined as
Based on this assumption, efficiency maps are created; see Section 6. The total efficiency is determined as
where the total mechanical power can be defined as
The total energy consumption of the motors is then given by
This article focuses on two main aspects. The first is the assessment of the mechanical power of printing robots in following a uniform printing trajectory. The aim is to compare how different kinematic structures of printing robots affect their mechanical power in terms of 3DCP application. The second aspect is to develop a comprehensive energy consumption model for the unique Printing Mantis robot.
4. Modelling the Energy Consumption of a Printing Robot
When modelling the energy consumption of a robot, it is usually based on a mathematical model of the mechanical structure of the robot, and therefore, kinematic and dynamic relationships must be taken into account. While the kinematic parameters of the robot are usually known with high accuracy, the dynamic parameters are usually not fully known and need to be determined in some way. In energy modelling, so-called parametric identification is very often used to determine the dynamic parameters. The problem of the identification of inertial parameters of robots is very extensive and is addressed in a number of publications [24,25,26,27,28,29,30,31]. It is collectively referred to as the robot identification problem (RIP). The off-line identification of inertial parameters corresponds to the requirements of robot energy modelling, where an energy consumption model is first needed to predict the robot’s power consumption. The most common approach to offline identification of dynamic parameters is the inverse dynamic identification model with ordinary least squares estimation (IDIM-OLS) [26]. This approach is also used in publications dealing with robot energy modelling issues mentioned in Section 4.3. This method is based on the assumption of a linear mapping between joint torques and dynamic parameters. The IDIM-OLS method and its various variants, such as the weighted least squares IDIM-WOLS method, suffer from several drawbacks. These drawbacks include a lack of robustness to noise and a strong dependence on the conditionality of the robot trajectory [27]. Despite these advantages, this method is still considered efficient and easy to implement, and for this reason, it is used in this paper.
The following subsections give an overview and show the specific key points of the mathematical description of the robot leading to the development of the energy consumption model of the Printing Mantis robot.
4.1. Kinematics of the Printing Mantis Printing Robot
The Printing Mantis robot is based on an extension of the Selective Compliance Articulated Robot Arm (SCARA) structure, with the extension consisting of the addition of an extra rotary link. The added degree of freedom leads to an increase in the kinematic and dynamic flexibility of the mechanism. It allows for better manipulability and the ability to reconfigure the robot axes without having to stop when a printed curve has a sharp break [20,21]. However, the redundant character of the printing robot results in the ambiguity of solving the inverse kinematics problem. In general, the inverse kinematics problem of the printing robot has infinitely many solutions. As it is known to describe the motion of robotic manipulators, two descriptive coordinate systems are most commonly used, namely the task space coordinate system and the configuration joint coordinate system. The description of the end effector in the task space coordinate system, along with the problem of solving the inverse kinematics problem of this robot, is addressed in [20]. In this paper, the joint coordinate systems are used for the purpose of energy consumption evaluation. This is because the joint coordinates are also the coordinates of the equations of motion. To generate these equations, it is necessary to perform transformations between the joint coordinate systems using Denavit–Hartenberg (DH) frames. The transformation describing the kinematic relations is defined in the form of a specific matrix according to the classical DH approach as follows:
where and , , a and this transformation matrix represents the transformation relation between two neighbour DH frames (coordinate systems of two neighbouring robot arm links).
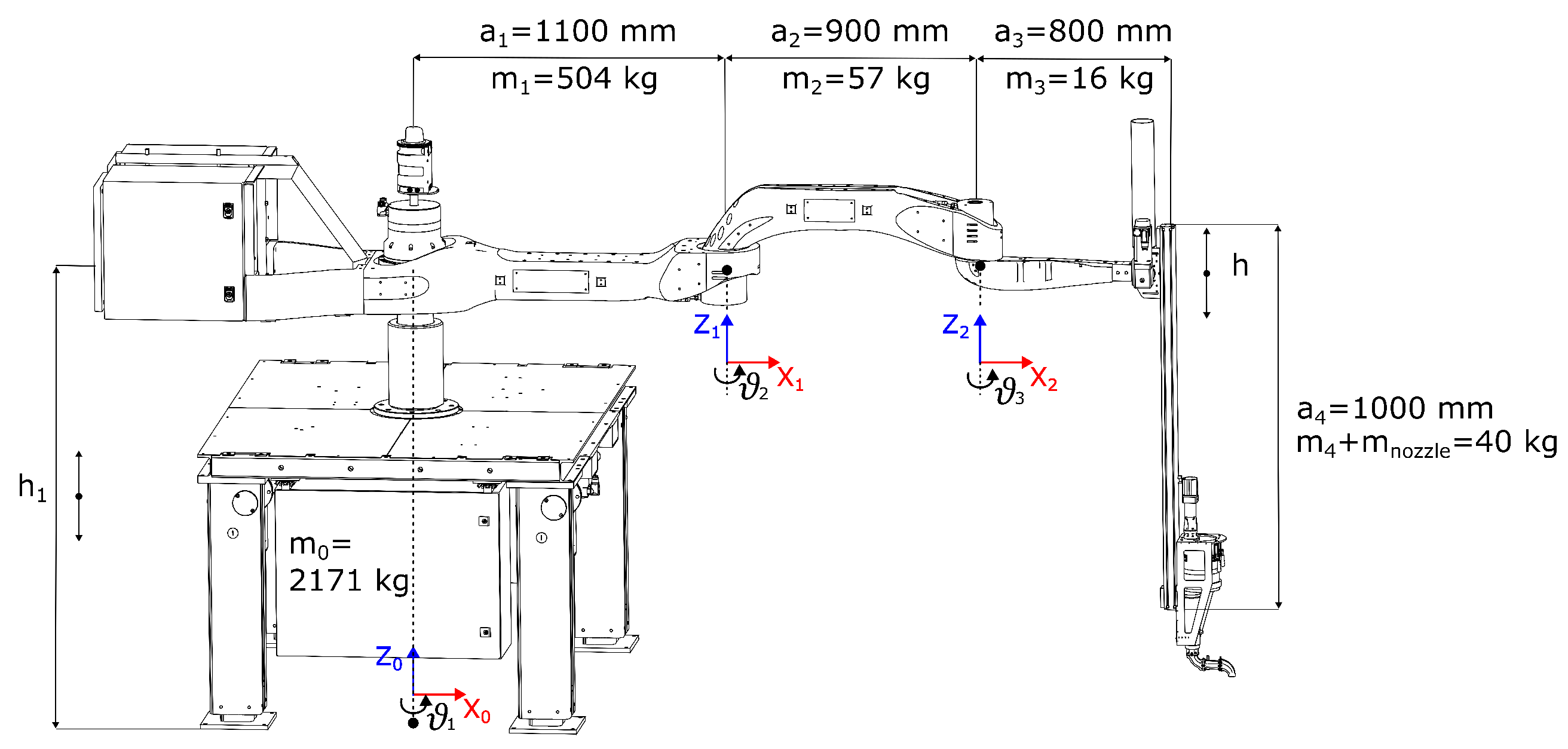
The individual DH parameters of the printing robot are demonstrated in Figure 2, where the kinematic structure of the printing robot can be seen. The printing robot has a total of four degrees of freedom (DOFs) + 1 DOF in the form of the robot base extension. The printing robot system therefore has a total of five DOFs. However, only three DOFs, represented by the three articulated joints of the horizontal arm links, are significant for the movement during the printing process; see Section 4.2. The remaining two DOFs are used for additional vertical linear guidance. The first linear guidance is implemented in the last vertical link of the robot (denoted as h), which carries the print head. This guide ensures regular strokes of the thickness of the print layer. The second linear guide (denoted as h1) is an extension of the robot base, which is used to adjust the print height. In this way, it allows the robot’s print area to be extended in the vertical plane. This connection is not an essential part of the robot. For example, if the robot is placed on a mobile platform, this connection can be fully replaced by a vertically extendable platform. This platform can then carry the entire robot. For this reason, this connection is not included in the energy consumption model of the printing robot. This is due to the need for an objective comparison of the power consumption with different robots, as discussed in Section 7.2. They would have to be equipped with a similar base to extend the printing range in the vertical plane.
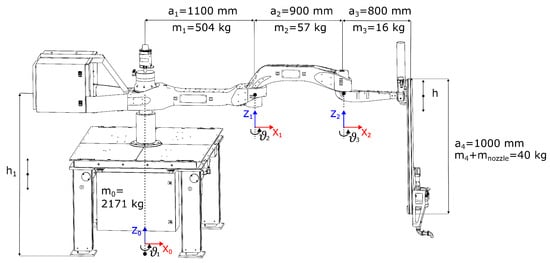
Figure 2.
Denavit–Hartenberg parameters for the Printing Mantis robot.
For this reason, and in order to objectively compare the power consumption with different robots, see Section 5.2.3, which would also have to be equipped with a similar base to increase the printing range in the vertical plane; this connection is not included in the power model of the printing robot.
4.2. Dynamics of the Printing Mantis Printing Robot
When deriving the differential equations of the printing robot, a reduced version of the robot was considered, and the differential equations were derived only for the first three rotational axes of the robot. This was performed under the assumption that the printing robot moves mainly in the horizontal plane during printing, where the first three axes of the robot have exclusive influence on the resulting motion. The last translational axis of the robot only serves to move the print head when printing the next print layer, and it is blocked most of the time (except for the stroke to the next print layer) by an electronic brake, and as a result, its effect on the overall consumption is minimal. Moreover, considering only the first three axes for energy consumption model generation is not uncommon in industrial robots (IRs) [10,14]. According to [14], the first three joints of the robot, counted from the base link, are responsible for approximately 80% of all energy consumed by IRs. A Euler Lagrange approach based on Lagrange equations of the second type, defined as
where n is the number of degrees of freedom (DOF) and scalar functions , is the so-called Lagrange function, where K is kinetic energy, P is the potential energy, values are so-called generalized forces/torques that have not been included in the potential energy P and values are generalized joint variables. According to the above assumption that the robot moves mostly horizontally, the potential energy is therefore zero. The Lagrange function is then represented only by the kinetic energy, which can be expressed by
where is the inertia/mass matrix of the robotic manipulator, which is symmetric and positive-definite.
By substituting Equation (10) into the Lagrange function, performing the appropriate partial derivatives necessary for Equation (9), and applying the physical parameters of the robot, the equations of motion can be constructed. For the articulated robot under consideration, the generalized coordinates are identical to the articulated coordinates = and the generalized force effects correspond directly to the input torques = , the equation of motion in matrix form is then
where are joint angles, velocities and accelerations; is a vector of torques acting on appropriate joints; is the matrix of Coriolis and centrifugal forces; and is the vector of friction forces.
Although friction is a complex nonlinear phenomenon and there are nonlinear friction models such as the Stribeck and LuGre models [28], a model that includes only Coulomb and viscous friction is an acceptable simplification for many robotic applications. In this paper, a conventional model of Coulomb and viscous friction is considered in the form of
where and are diagonal matrices with viscous and Coulomb friction coefficients corresponding to individual joints.
It can be noticed that Equation (12) does not include the term corresponding to the gravitational torques vector obtained as the gradient of the total potential energy P of the robot. This term is equal to zero according to the above assumption.
4.3. Linearization of Dynamics and Inverse Dynamic Identification Model (IDIM)
It is well known that the dynamic model (11) is linear with respect to the dynamic parameters and can always be rewritten in the following form [24]
where is the regressor matrix of known kinematic variables and their functions, while is a vector of unknown inertial and friction parameters. The estimation of these parameters, namely the identification of the dynamic parameters of the robot, can be considered as an inverse kinematics problem. In real conditions, due to uncertainties caused by measurement noise and modelling errors, the actual torque differs from the torque τL by an error e, which is defined as
and Equation (13) becomes
Equation (15) then represents the Inverse Dynamic Identification Model (IDIM).
4.3.1. Base Inertia Parameters
Each link of the robot is represented by a rigid body, which is generally described by the 10 inertial parameters, with the following 13 parameters in the case of considering actuator moments of inertia and friction coefficients:
where are principal moments; , are denoted products of inertia of link i; , , are the coordinates of the centre of gravity considered relative to the i-th link frame; is the link mass; is inertia of the actuator and transmission system and and are the coefficients of viscous and Coulomb friction, respectively.
These 13 parameters are also referred to as standard dynamic parameters. In the dynamic model of a particular robot, some of the standard dynamic parameters have no effect and cannot be easily identified. Some standard parameters occur only in fixed combinations with others, which means that the corresponding columns of the regressor matrix show a linear dependence and these parameters can only be identified together. A set of independent groups of dynamical parameters, called base inertial parameters, can be identified, which are sufficient for a complete description of the robot dynamics. The vector of base parameters can be obtained heuristically or by making a set of modifications in the symbolic expression of Equation (16) [29], or by numerical methods, based, for example, on QR decomposition [25]. This numerical method is implemented in the very useful Benchmark for Identification of Robot Dynamics (BIRDY) [30], which was used in this paper to determine the base inertia parameters.
4.3.2. Excitation Trajectory
Roughly speaking, robot identification can be formulated as the task of finding the values of that ensure that the dynamics of the model best match the actual behaviour of the robot when following an exciting trajectory. Due to its advantageous properties, a widely used excitation trajectory in the form of a finite Fourier series was used for the purpose of identifying the inertial parameters of the robots [24,31]. As explained in [24], each joint trajectory is a combination of and functions, i.e., a finite Fourier series.
where L is the selected number of harmonics, is the selected signal frequency, and the coefficients , and should be calculated through an optimization procedure.
The frequency in the excitation trajectory must be high enough to stimulate the robot’s inertial parameters but, at the same time, should avoid resonant frequencies of the robot structure. The individual coefficients have been optimized similarly to [21] in order to reduce the condition number of the observation matrix, which is used as an optimization criterion in many studies [14,21,24,31]. The smaller the condition number, the higher the quality of parameter identification. More details about the specific optimization process can be found in [21].
4.3.3. Least Squares (LS)
During the tracking of the excitation trajectory by the robot, N samples of joint torques and positions of individual joints are collected, and the joint velocities and accelerations are computed using the central difference method with zero-shift Butterworth filtering [26,30]. Equation (15) can then be rewritten to
where is the sampled vector of torques; is the sampled matrix of W, referred to as observation matrix, and is the sampled vector of . Solving the identification Equation (18) essentially corresponds to solving an overdetermined system of equations, where we have more equations than search parameters (we have a set of measurements that is larger than the number of search parameters). Thus, it is an overdetermined system, and one can use, for example, the least squares method to solve it. The estimated parameters can be expressed as
5. Experiments
5.1. Experimental Verifications of EC Models
The first part of the experiment consists of an experiment to determine the parameters and verify the energy consumption model of the Printing Mantis printing robot. The experimental setup consists of the Printing Mantis robot and its open control system based on an industrial PLC. A more detailed description of this workstation is given in the following Section 5.2.1. This system is complemented with tools allowing us to measure the power consumption of the drives of the printing robot for the possible verification of the developed energy consumption model.
5.1.1. Tools for Measuring the 3DCP Robot’s Power Consumption
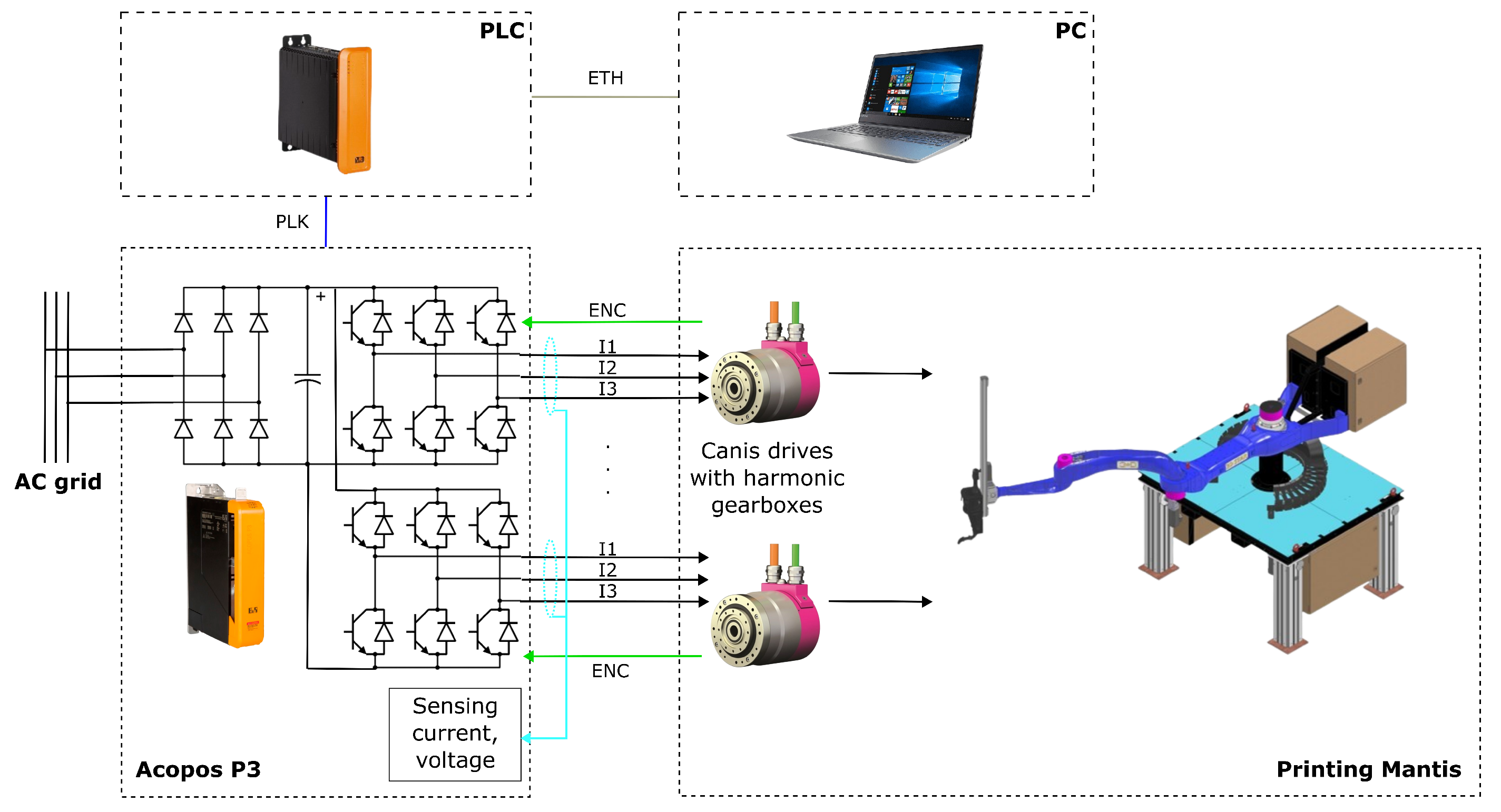
For the verification of the created model of the Printing Mantis robot, it was necessary to develop software that allows cyclic parameter readings. Specifically, it was necessary to obtain motor terminal power (MTP) values according to the formula in (1). Thanks to the possibility of measuring parameters directly from the APC control system or from Acopos servo amplifiers, there is no need to apply current probes and voltmeters to the measurement system. The control system also provides indirect motor torque measurement. The tools used to measure power are documented in Figure 3.
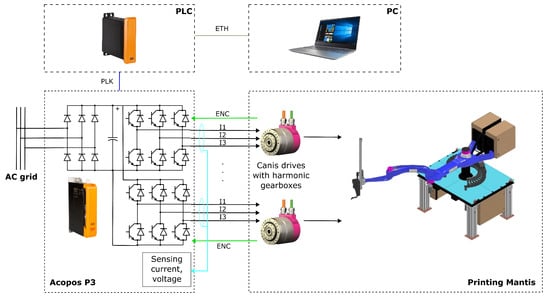
Figure 3.
Block diagram for measuring the power input from APC910.
5.1.2. Parameter Identification and Energy Consumption Modelling of Printing Mantis
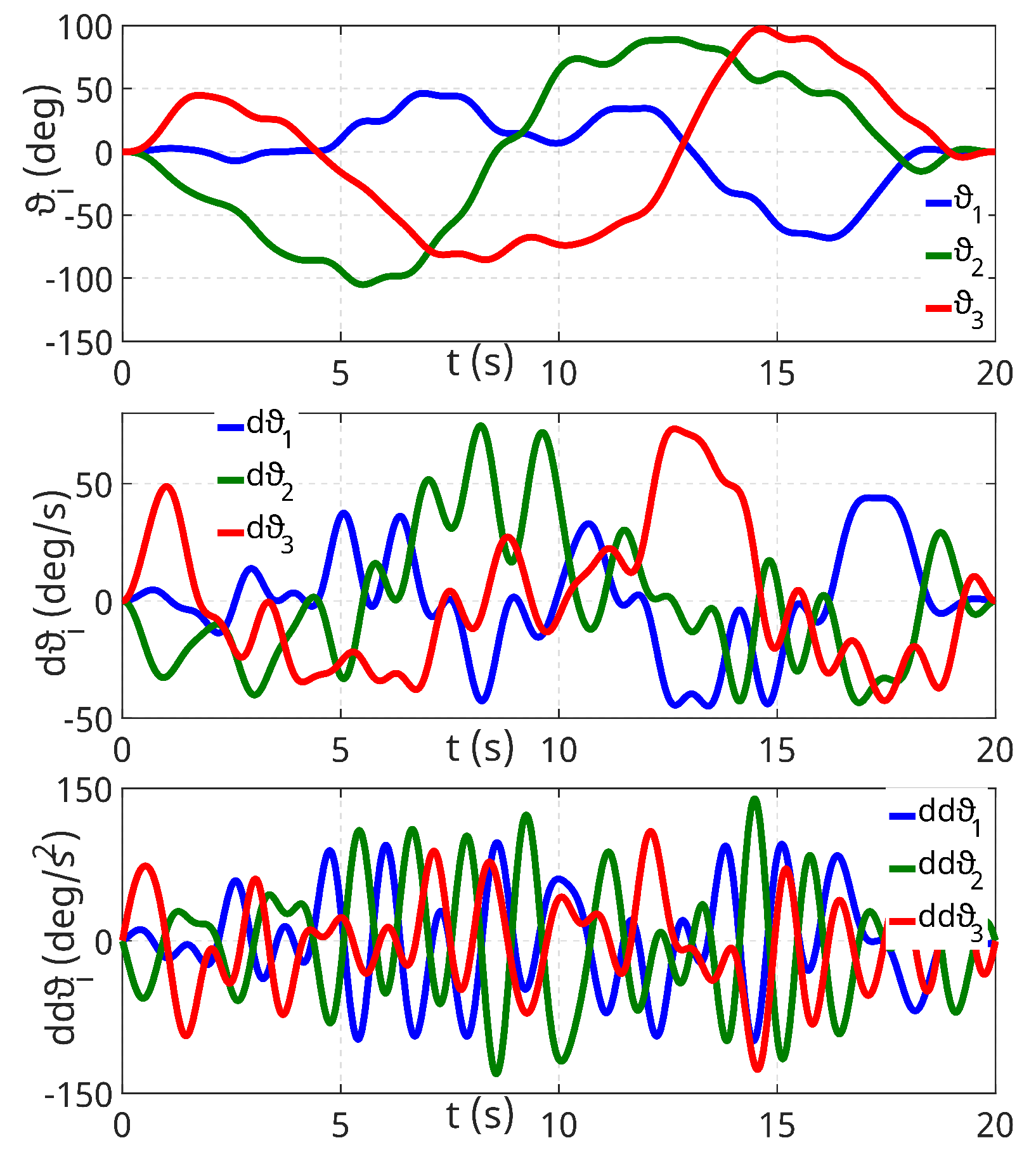
To parametrically identify the inertial parameters of the Printing Mantis robot, a classical experiment was performed; see Section 4.3.3. In contrast to the classical experiment, the power input of the individual joint motors was measured simultaneously and subsequently used to determine the reduced efficiency maps; see Section 6. In the Matlab/Simulink environment, two trajectories were designed according to Formula (17) for identification and validation purposes. The fundamental frequency of the excitation trajectories was chosen to be 20 Hz, and five Fourier series entries were used. The optimized excitation trajectory of each axis is demonstrated in Figure 4. We gratefully used the BIRDY [30] tool and the QR decomposition implemented therein to determine the base inertia coefficients. The data were sampled at a frequency of 2.5 kHz.
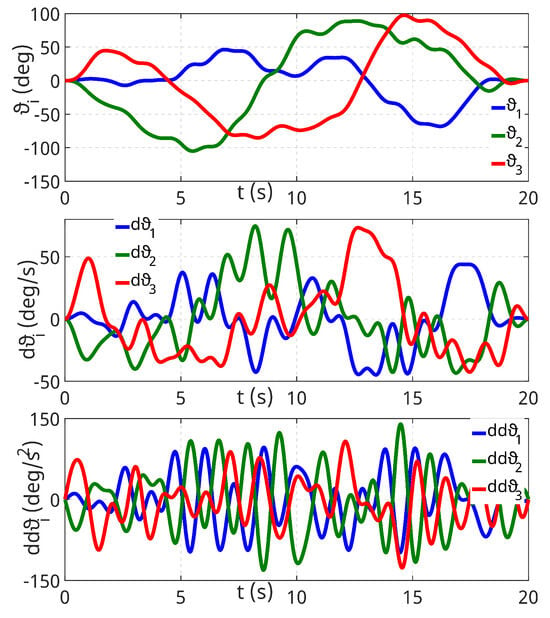
Figure 4.
Optimized excitation trajectory.
Table 1 documents each group of parameters in symbolic form, including their estimated values.

Table 1.
Estimated base inertia parameters.
5.1.3. Parameter Verification
Subsequently, the correctness of the parameters of the energy consumption model was verified by predicting the torque and the power of each joint of the robot. This power was calculated according to the mechanical power formula using a validation trajectory. Furthermore, it was compared with the power calculated from the measured data when the robot moved along the validation trajectory. Since the energy consumption depends on the time-integrated power, the prediction and measurement of the energy consumption (in the form of mechanical power) were performed using Formulas (20) respectively (21) for further validation.
In practice, the measurement of energy consumption is performed by approximating the integral formula using discrete sampling.
where n is the number of samples and is the sampling period (0.4 ms). The relative error between the predicted and measured energy consumption while moving along the validation trajectory of each joint is then determined by Formula (22).
5.2. Comparison of Energy Consumption
5.2.1. Experimental Robotic Workstations for Energy Consumption Comparison
As outlined in the introduction, the paper aims to provide a comparison of the effect of the kinematic structures of printing robots on their power consumption during printing. Two real experimental workstations and one virtual workstation created in the ABB RobotStudio environment were used to enable the comparison of power consumption.
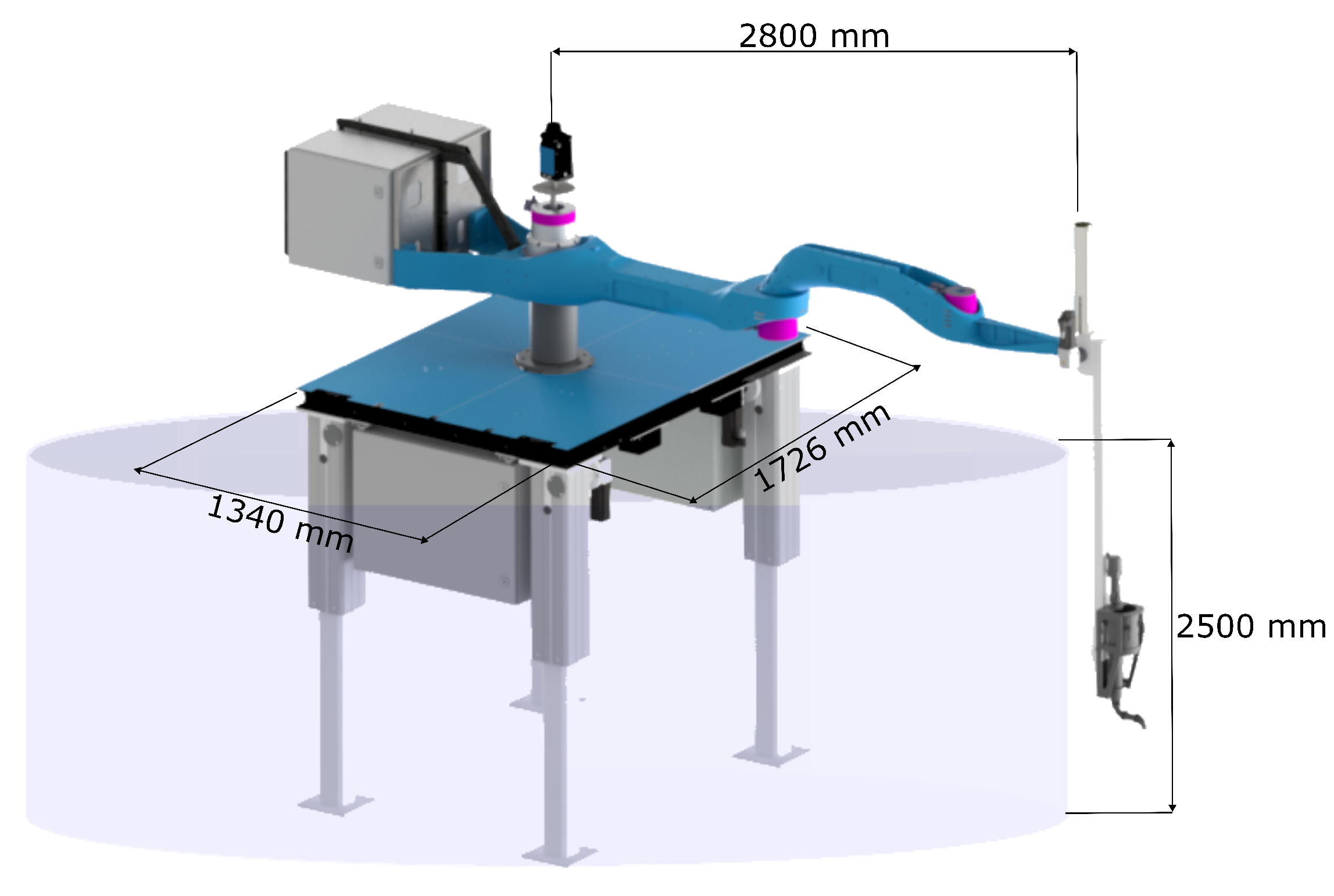
The first workstation is a workstation with a unique printing robot Printing Mantis, which has a working area with a diameter of 5.6 m (r = 2.8 m) and a height of 2.5 m and weighs nearly 620 kg without the robot base. Figure 5 demonstrates the workspace of the Printing Mantis robot. It is a very robust design that guarantees an endpoint positioning accuracy of 3 mm, which is of sufficient accuracy for 3DCP technology [32].
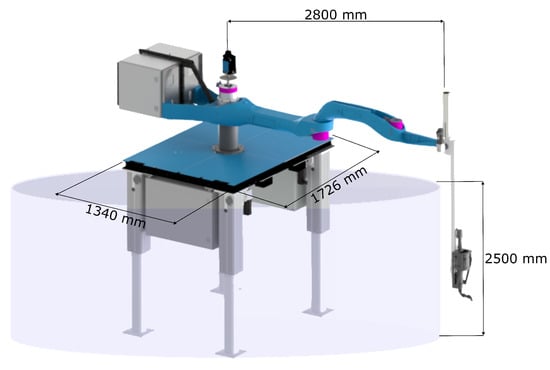
Figure 5.
Printing Mantis workspace.
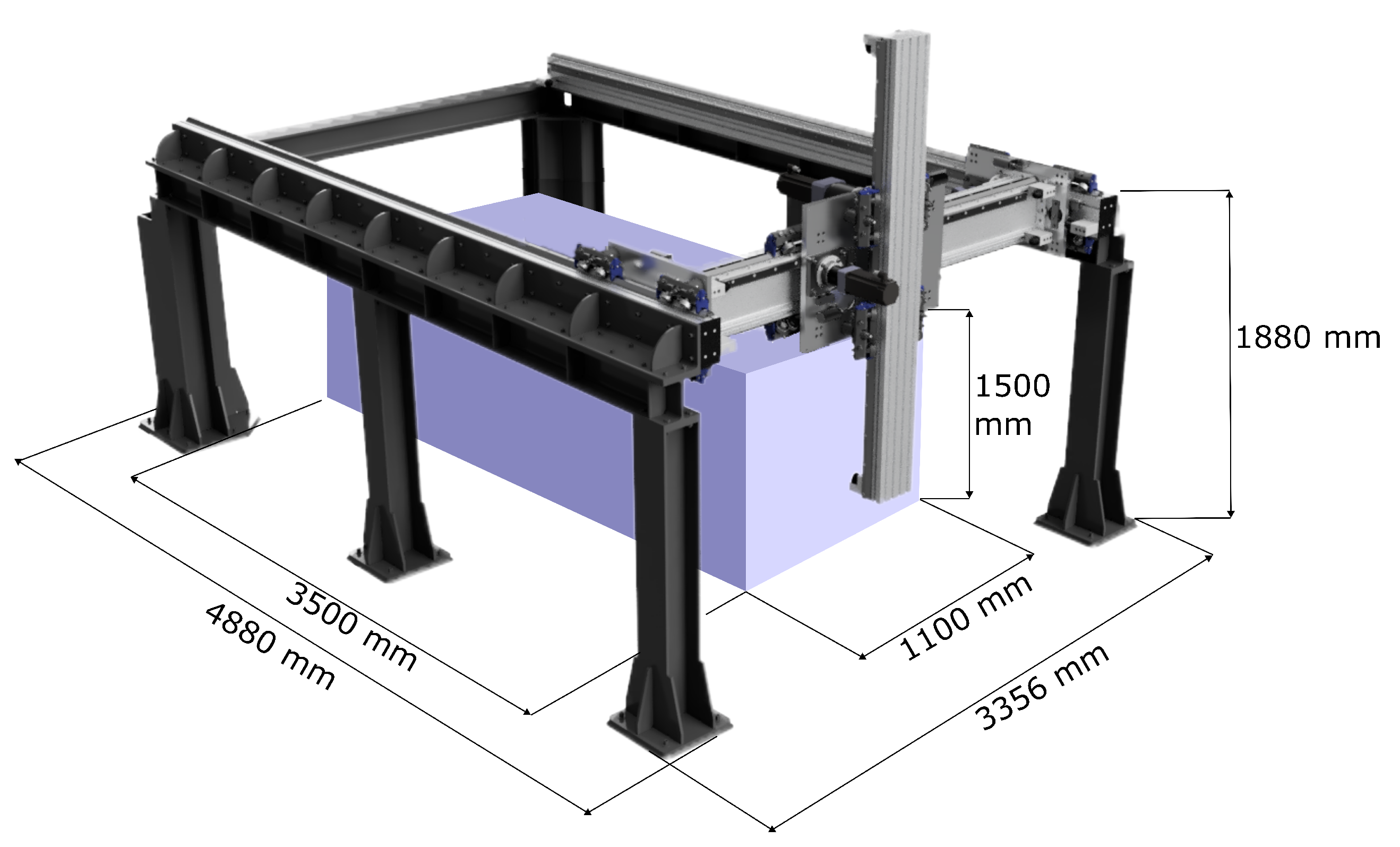
The second experimental workstation used to compare the energy consumption when moving along an identical print trajectory is the workstation with the gantry robot TestBed. Testbed is a representative of the gantry kinematic structure, which nowadays is very often used for 3D printing technology. TestBed has a cuboid-shaped workspace with dimensions of 1.1 × 1.5 × 3.5 m (w × h × d) and has a very robust construction. It weighs 2.5 t and achieves 5 mm accuracy when printing. Figure 6 demonstrates the gantry work area of the TestBed printer.
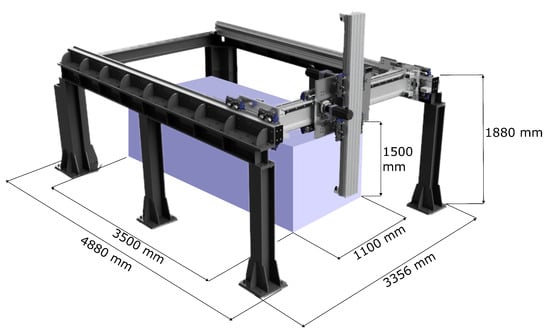
Figure 6.
TestBed, gantry printer workspace.
The last (virtual) workstation is a robotic workstation with a virtual model/controller of an ABB IRB4600 industrial robot created through the ABB RobotStudio programming/simulation environment. This robot is selected based on the working range and load capacity close to the Printing Mantis robot. It is also the specific robot used for the 3DCP application; see Section 2 [5]. The built-in simulation tool Signal analyser is used to determine the robot’s power consumption while moving along the printing trajectory, which allows the monitoring of the individual simulated robot signals in the form of positions and velocities of the robot end effector but also allows recording the Total Power consumption. The created robot workstation in the Robot Studio environment with the ABB IRB 4600 robot is documented in Figure 7. The real design of the Testbed and Printing mantis robotic workstations are documented in Figure 8 and Figure 9.
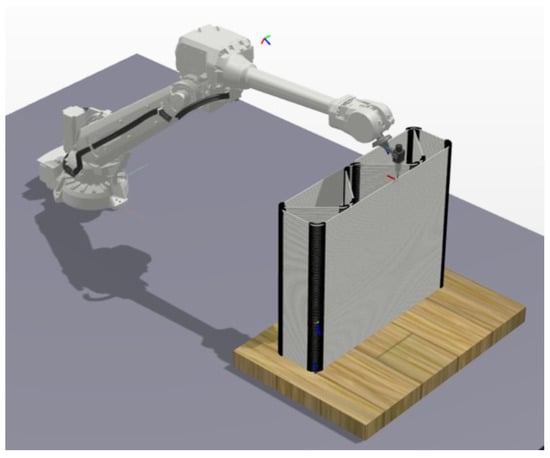
Figure 7.
ABB IRB4600 experimental working station.

Figure 8.
Experimental workstation TestBed.

Figure 9.
Experimental workstation Printing Mantis.
5.2.2. Uniform Trajectory Design
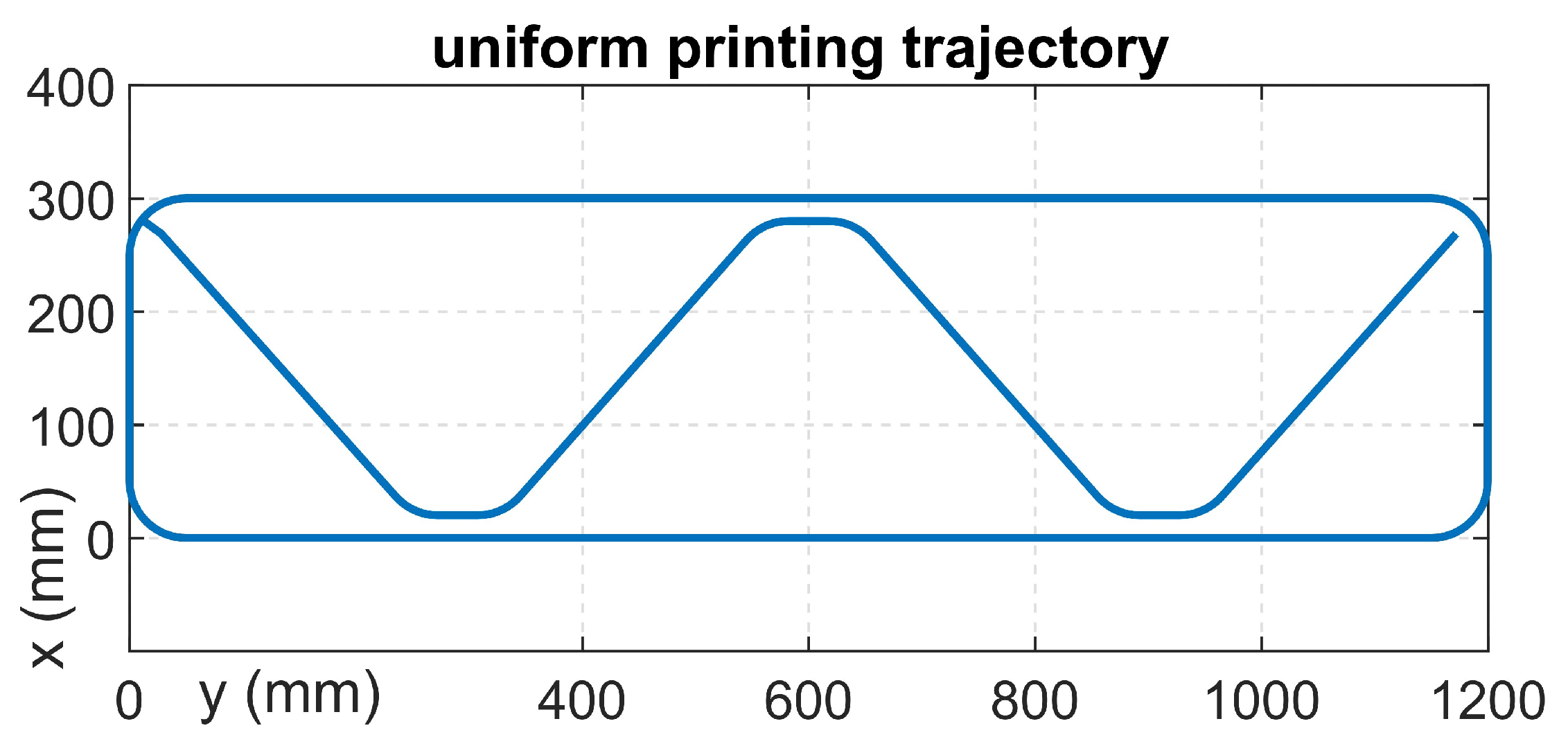
A uniform trajectory representing a simplified wall plan with a length of 1200 mm and a width of 300 mm was designed in order to compare the energy consumption during printing of this trajectory by the robots presented in Section 5.2.1. The trajectory-design procedure consisted of creating a CAD model of the printed wall and then converting the model in STL format into a G-code containing the coordinates of the endpoints and the parameters for the temporal parameterization of the motion path. The time parameterization was performed to match a constant print path speed of 125 mm/s. This print speed was chosen based on printing experience. At this point, the print data in G-code format, in the case of the TestBed gantry printer, could be directly uploaded to the CNC core-based control system. For the virtual workstation containing the ABB industrial robot, RobotStudio® 3D Printing PowerPac was used to enable the automated import of printed objects and the automatic generation of robot commands from standard G-code files. In the case of the unique Printing Mantis robot, the conversion of print data from G-code to the robot’s Cartesian coordinates was accomplished using a custom G-code interpreter, and the inverse kinematics problem was solved using an automatic code generator using Matlab/Simulink [21]. Figure 10 demonstrates the uniform print trajectory in absolute Cartesian coordinates.
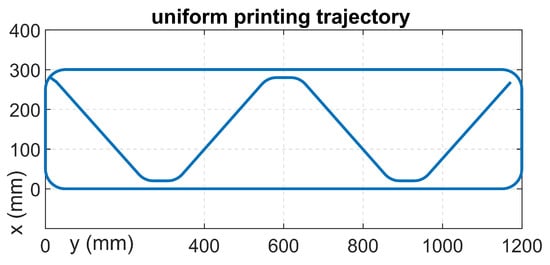
Figure 10.
Uniform printing trajectory.
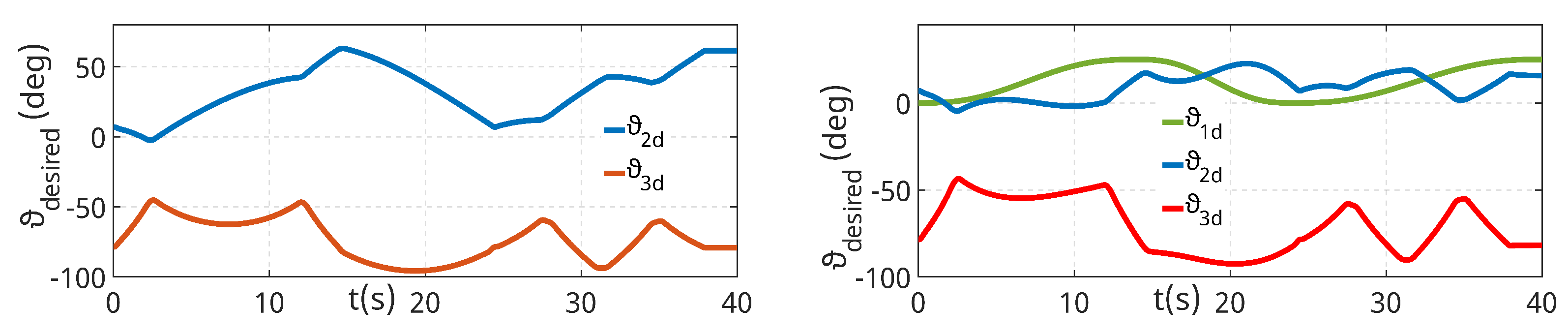
For maximum objectivity, two different configurations of the Printing Mantis printing robot are also considered. The first configuration represents the most common configuration for printing in the form of the movement of the second and third joints at a constant value of the first joint (selected ). The second configuration is chosen to account for the motion of all three joints of the robot. Moreover, the trajectory of the first joint is intentionally intensified in order to illustrate the energetically disadvantageous scenario of the possible choice of this motion. Figure 11 demonstrates the uniform trajectory in the joint coordinates of the Printing Mantis robot for the first case, . The second figure represents the uniform printing trajectory in joint coordinates for the case with the motion of all axes.
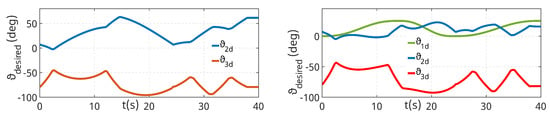
Figure 11.
Joint trajectories corresponding to the uniform print trajectory.
5.2.3. Energy Consumption Comparison Experiment
In order to compare the energy consumption of the different printing robots, two experiments were performed during which the individual robots moved along a uniform printing trajectory. The first experiment consisted of moving the robots along a trajectory representing a simplified wall plan; see Figure 10. This trajectory corresponds to a single print layer. The data from the experiment were used to compare the overall instantaneous power of each robot.
The second experiment consisted of the movement of robots along a trajectory in the form of a printed wall of identical ground plan but with a wall height of 1 m. This corresponds to 100 print layers. The data from this experiment were used to compare the total energy of the robots. This experiment was included mainly to objectively compare the power consumption with an articulated six-axis robot. When we solely compare actual power, bias in the results might arise due to the selected initial robot configuration. As the robot moves through 100 layers (see Figure 12), the robot configuration changes, and this ensures that the comparison is not only in one robot configuration. For the experimental workstations/robots Printing Mantis and the gantry robot Testbed, the power and joint torques and joint speeds were measured. These quantities were then used to calculate the powers and energies using the Equations (2) and (20). Measurements were made directly through the control system described in Section 5.2.1. An example of energy consumption testing can be seen in the video—see Figure 13—which shows the robots moving along a trajectory in the form of a printed wall [33].

Figure 12.
3DCP printed wall.

Figure 13.
Energy consumption comparison experiment (see video in [33]).
5.3. Verification of a Comprehensive Power Consumption Model of a Printing Robot
The last experiment consisted of the verification of the methodology for the determination of the reduced efficiency maps, which is presented in Section 6. During the experiment, the Printing Mantis robot moved along the printing trajectory described in Section 5.2.2, and the data for the calculation of the mechanical power were sampled together with the data of the electrical power input of each joint. Subsequently, the electrical power inputs were calculated from the mechanical powers via Equations (2) and (3). The verification of the comprehensive model of electrical power consumption was performed by comparing the calculated power inputs with the measured power inputs.
6. New Methodology for Determining Reduced-Efficiency Maps of Printing Robot Drives
As already outlined in Section 3.1, for the creation of a comprehensive robot power consumption model, it is important to consider both the electrical and mechanical efficiency of the robot arm drives. Determining the efficiency of robotic arm drives is very difficult in practice, as motor efficiency data are often not available even from the manufacturers themselves. Mechanical efficiency is a very complex effect influenced by a number of factors that are difficult to describe mathematically. One way to obtain the efficiencies of drive components is to use the results of simulations with complex mathematical models of drives. The creation of such models is quite challenging because many of the parameters entering the model are difficult to trace or even unknown. Another option for determining the efficiency is to perform a special experiment during which the efficiency is measured [34]. This method requires special equipment in the form of a measuring bench equipped with a load motor, torque sensors, speed sensors, etc., and is quite time-consuming. The motors need to be measured at different speeds and loads. This method results in so-called efficiency maps for each drive [35]. An efficiency map is a contour plot that shows the efficiency of a given drive as a function of speed and torque. This graph illustrates the maximum efficiency for different combinations of speed and torque and is a useful tool for visualizing the operating points of a motor drive according to a defined drive cycle.
However, the described experimental method for efficiency determination is almost inapplicable in practice for robotic arms. This experiment would require disassembling the robotic arm and measuring its individual actuators with a measuring apparatus. For these reasons, we present here a new method for determining reduced-efficiency maps of robotic arm actuators. This methodology uses an identification experiment to determine the inertial parameters. In addition, during the robot motion along the excitation trajectory, the individual axis inputs are measured against the measured positions, velocities and torques. From these inputs, the efficiencies are then calculated, and reduced efficiency maps for the individual robot actuators are generated. From these maps, or from the data framework for creating the maps, the efficiencies of individual robot actuators can then be determined for any desired print trajectory. A search algorithm is used to determine the efficiencies, which takes as inputs the desired velocities and estimated torques for the desired trajectory. The efficiencies found can then be used for a comprehensive power consumption model supplemented by the prediction of the electrical power input of each drive.
6.1. The Process of Determining Reduced-Efficiency Maps and Predicting Electrical Power Inputs
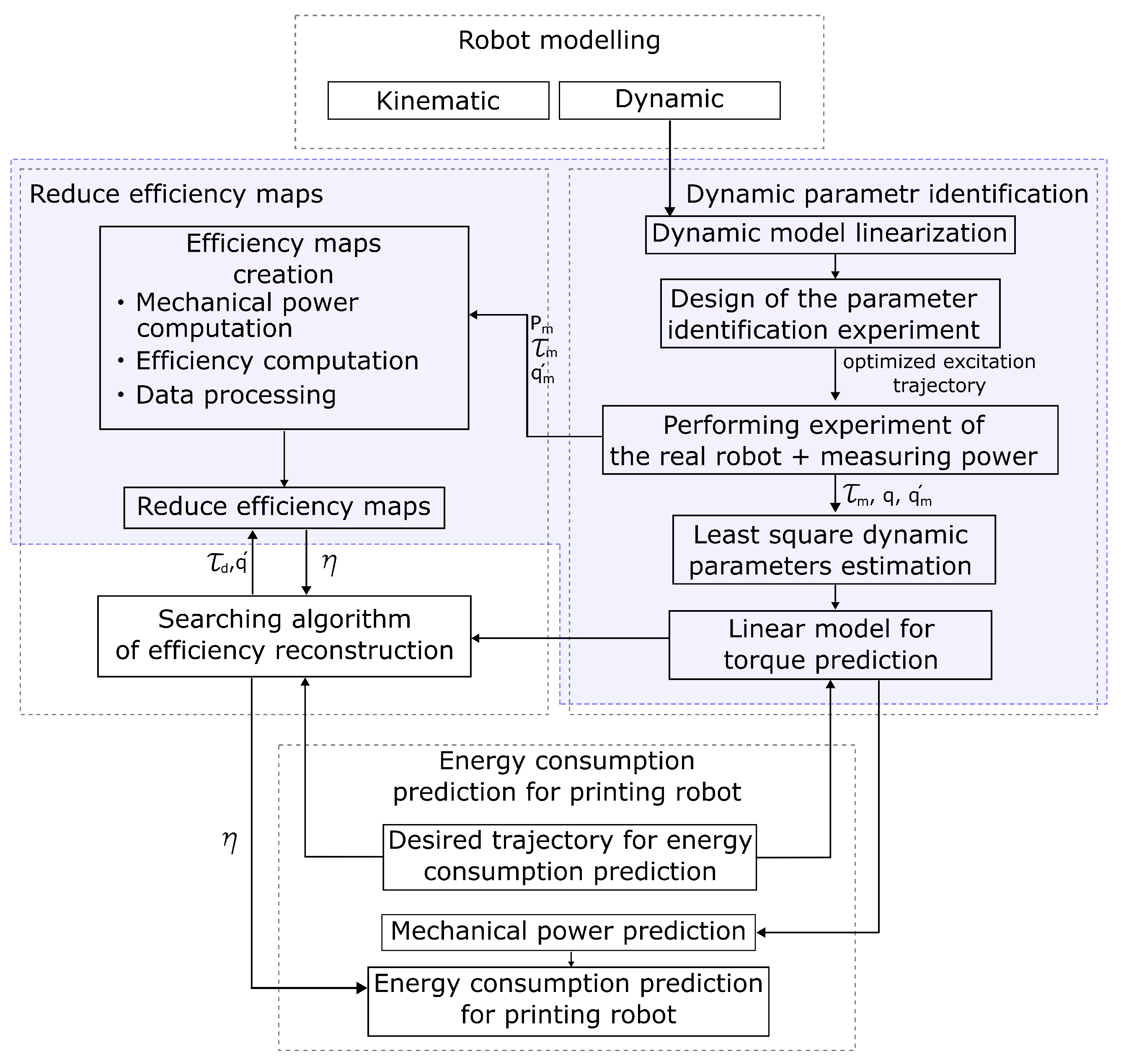
The whole process of determining the efficiency maps leading up to the actual prediction of the electrical power consumption of the robot arm actuators is summarized in the conceptual steps shown in Figure 14. The dashed boxes in the diagram represent the main stages of the procedure, and the arrows indicate the order of the steps and the flow of information. Moreover, the quantities between the blocks are designed to intuitively represent the outputs and inputs of the previous and next blocks, respectively. As can be seen from the diagram, the initial stages of the methodology for determining the efficiency maps and predicting the electrical power are identical to those of a classical identification experiment. The blue boxes in Figure 14 are executed only once during the identification experiment.
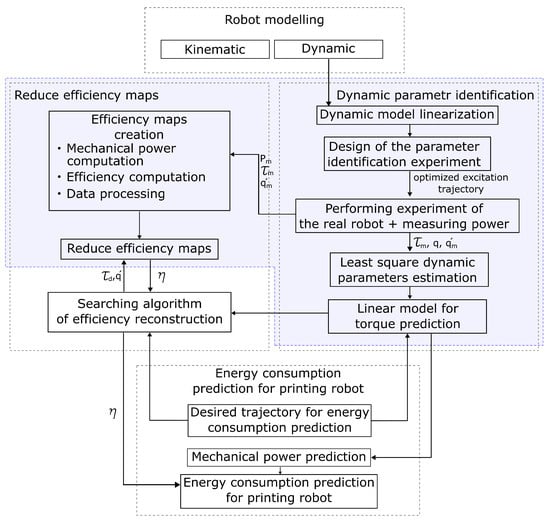
Figure 14.
Schematic representation of the methodology for determining efficiency maps and the complex robot consumption model.
6.1.1. Classical Identification Procedure Supplemented by Power Input Measurement
First, a kinematic and dynamic model of the printing robot is derived, assuming that only the geometric parameters of the robot are known. Based on the linear dependence between the dynamic parameters and the dynamic model of the robot, the dynamic model is converted into an Inverse Dynamic Identification Model (IDIM). For identification purposes, the printing robot is excited using a suitable excitation trajectory defined during the design phase of the parametric identification experiment. The selected motion is implemented, and the IDIM variables, along with the electrical power, are sampled using the available tools (see Section 5.1.1). At this stage, the diagram is divided into two branches.
The first branch continues the classical identification methodology consisting of the least squares estimation of the dynamic parameters, leading to the completion of a “linear dynamic model”. Based on this model, individual joint torques can be predicted from the desired trajectory data. The second branch presents the steps leading to the creation of reduced efficiency maps of the actuators of the printing robot.
6.1.2. Creation of Reduced Efficiency Maps
The required set of variables obtained by sampling during the robot motion along the excitation trajectory in the form of is used to calculate the overall efficiency of the individual actuators. First, the mechanical power of the individual actuators is calculated based on the relation (4). From these mechanical powers and the measured power inputs, the total efficiencies of the individual axes of the printing robot are calculated. Based on the computed efficiencies and the measured joint torques and joint speeds, the so-called reduced efficiency maps are created, and the created data framework can be used for subsequent power input prediction. Since the measured signals are noisy and, in the case of measured electrical power, peaks are present in the signal, which are highly undesirable, a data processing stage needs to be included in the process.
6.1.3. Data Processing
The main goal of data processing is to derive all the required de-noised experimental variables and to get rid of the present peaks in the electrical power variables. It has been shown that the best results are achieved by two-step data processing, whereby the first phase of data processing takes place after the efficiency calculation (block efficiency map creation in Figure 14). The second phase of data processing takes place only during the actual prediction of the power consumption. It has proven to be convenient to proceed by calculating efficiencies directly from the raw data and then processing only these calculated efficiency values. The processing of the efficiency data takes place in two steps. The first step consists of removing peaks from the efficiencies (which are indirectly present from the measured electrical power). The peaks are evaluated as values from the data that are greater than three scaled median absolute deviations (MADs) from the median. The Matlab function isoutlier is used for this purpose. In the second step, the missing data need to be filled with some “suitable value”. Filling in the missing data using linear interpolation implemented by the Matlab function fillmissing proved to be sufficient. The efficiency data thus obtained should still be filtered with a Butterworth low-pass filter in both the forward and backward directions using Matlab’s filtfilt function before the actual creation of the efficiency maps, thus removing noise without adding a phase shift to the signal. This completes the first stage of data processing. The second phase of data processing takes place at the power prediction stage.
6.2. Prediction of Energy Consumption for Printing Robots
As can be seen in the diagram that demonstrates the figure (robot modelling Figure 14), the steps for predicting energy consumption run in parallel in two branches. In the first branch, based on the input data in the form of the desired print trajectory, the torques are predicted using the created “linear dynamic model”. The mechanical power from these torques is calculated via Equation (4). To clarify, the print data must first be converted using the G-code interpreter into the robot’s Cartesian system. Subsequently, inverse kinematics or inverse differential kinematics are used for the desired values of joint rotations, velocities and accelerations (see Section 5.2.2). In the second branch, a search algorithm is used to find the corresponding efficiencies.
6.2.1. Searching Algorithm of Efficiency Reconstruction
To reconstruct the efficiencies for a desired print trajectory, a search algorithm is needed to find the efficiency maps in the dataset based on the input data. The input data to the algorithm are the predicted joint torques and joint velocities providing the desired print trajectory velocity. The search algorithm then searches the efficiency map dataset and selects efficiencies from the dataset based on the closest joint torque and velocity values found. The search algorithm uses the Matlab function pdist2 to return the distance between each pair of observations in X and Y. The use of a standardized Euclidean metric was found to be sufficient, removing the problem of a possible different range of input joint moments and velocities.
6.2.2. Energy Consumption Prediction
Once the efficiencies and predicted mechanical powers have been found, all that remains is to determine the energy consumption based on the electrical power Formulas (2) and (5). It is then appropriate to carry out a second data processing stage, which consists of removing the peaks and then filtering the predicted electrical power inputs in a similar way to what is described in Section 6.1.3. This is how the whole methodology for the determination of efficiency maps and the prediction of electrical power inputs can be described. It should be noted that the blue-bordered part visible in Figure 14 is only executed once during the identification experiment. This shows that the process of determining the reduced efficiency maps is very time-efficient compared to the classical procedure. The reduced efficiency maps for each axis of the Printing Mantis robot are shown in Appendix A Figure A1.
7. Presentation and Discussion of the Experimental Results
In the first part of this section, results concerning the energy consumption model of the Printing Mantis robot are presented. First, the results of the comparison of the actual power when the robot moves along a validation trajectory are presented, followed by a comparison using energies.
In the second part, results from the comparison of energy consumption during the movement of different printing robots along a uniform printing trajectory are presented. The comparison is again made first on actual power and then using energies.
The last section shares results from a new methodology for determining efficiency maps leading to a comprehensive model of printing robot energy consumption. The comparison is made while the robot is moving along the printing trajectory, and the effect of considering efficiency on the total power is discussed.
7.1. Results of the Energy Consumption Model of the Printing Robot
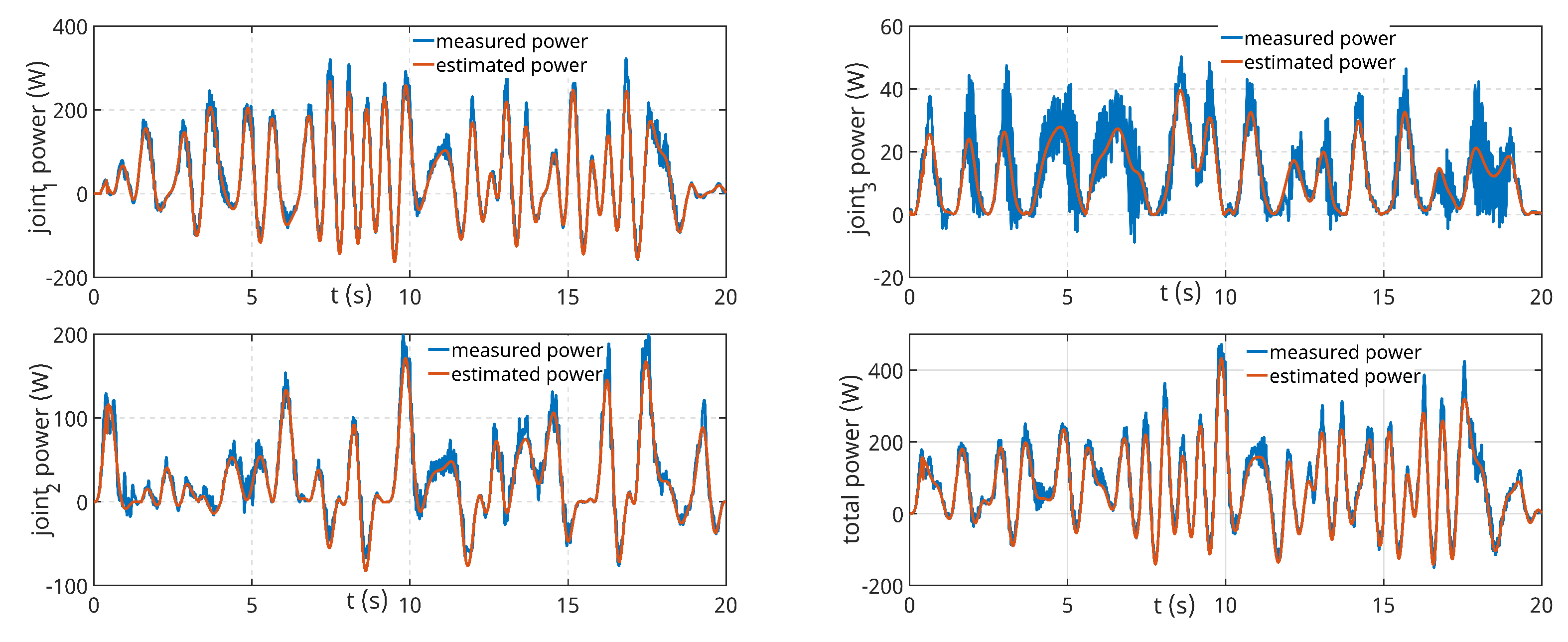
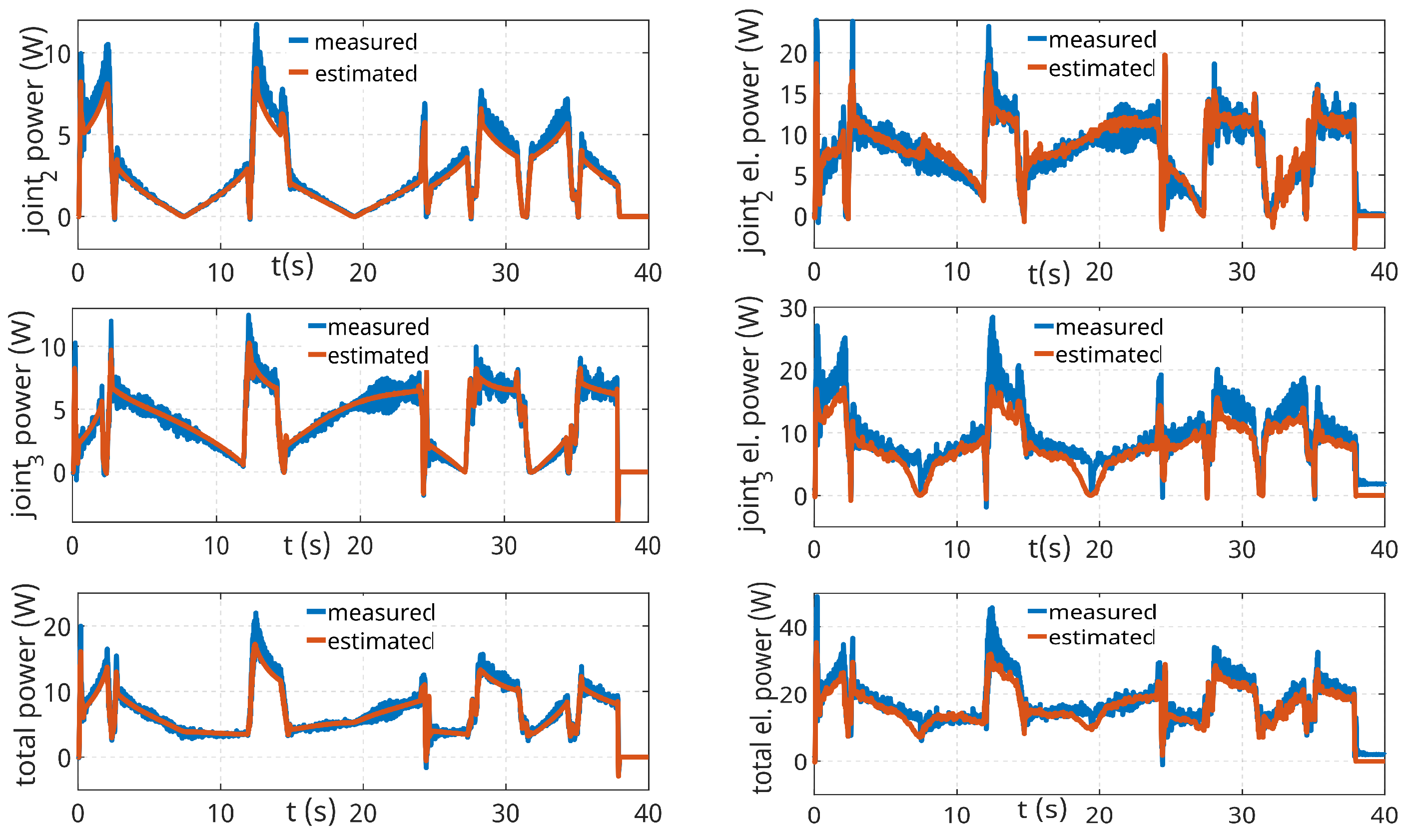
From the graphs shown in Figure 15 comparing the estimated and measured instantaneous mechanical power of individual joints as the robot moves along the validation trajectory, it can be concluded that the individual estimated power closely follows the behaviour of the measured power. The graph located at the bottom right of Figure 15 documents the overall mechanical power, which is important for possible comparison with simulation results from the Robot Studio environment and for assessing the overall accuracy of the model. Also, in this graph, it can be seen that the estimated power matches well the trend of the measured power.
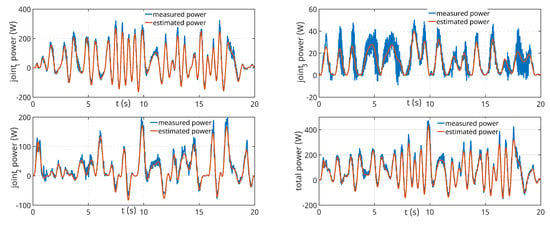
Figure 15.
Mechanical powers of individual robot axes and total power.
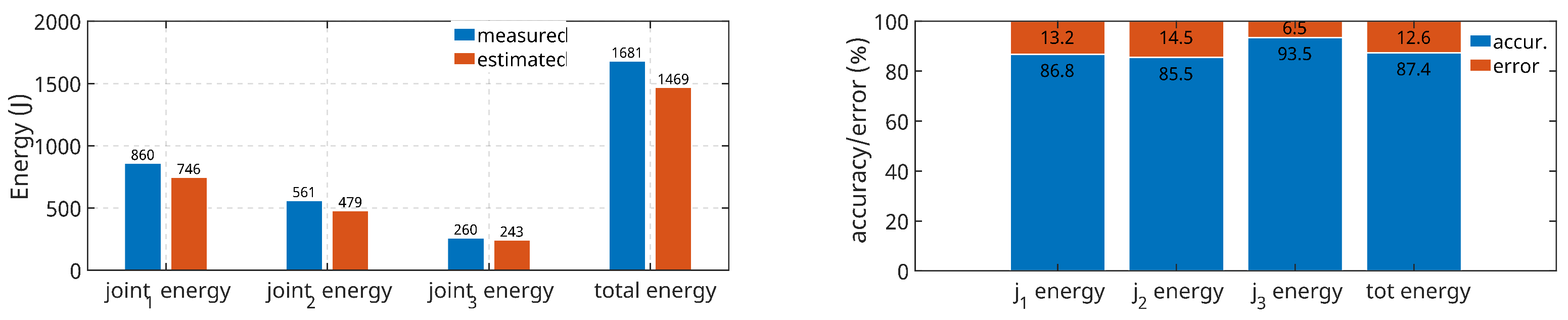
Next, a comparison is made based on the energies when the robot moves along an identical validation trajectory. The comparison is shown in Figure 16. The estimation accuracy for the first and second joint is found to be similar around 86.8 and 85.5%, respectively. For the third joint, the estimation accuracy reaches 93.5%. The overall estimation accuracy is 83.7%. The quality of the estimation or the magnitude of the difference between the energy calculated from the collected data and the energy calculated from the estimated torques can be affected by a number of factors. The main reasons contributing to the inaccuracy may be the use of a simplified friction model and a simple identification model in the form of ordinary least squares estimation (IDIM-OLS). Nevertheless, it can be concluded that very good results are obtained for the purpose of robot energy consumption prediction.
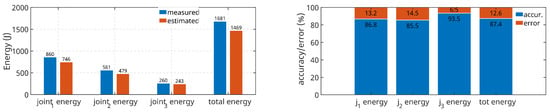
Figure 16.
Evaluation of the robot power consumption model through energy.
Both comparisons show that the energy consumption/mechanical power of the first joint is much higher than that of the third joint. At the same time, the energy consumption/mechanical power has a decreasing trend from the first joint to the last. This assumption is taken into account when planning the robot’s movement. The Printing Mantis robot is primarily designed to work on a horizontal surface, with the last horizontal links of the robot’s kinematic chain (the second and third links) being the ones that move the most. The first link of the robot is primarily used to change the configuration, rotates the other links and has minimal change in its speed. This approach minimizes the kinetic energy fluctuations of the entire robot mechanism when working on a horizontal surface [20]. With this assumption, we can expect a better overall energy estimation accuracy than 83.7%, which occurs when moving along the validation trajectory under the dominant action of all three axes. However, in reality, the motion of the printing robot involves as much as possible the third link of the robot, which also has the highest estimation accuracy.
7.2. Results from Comparing the Power Consumption of Different Printing Robots
Figure 17 shows graphs comparing the instantaneous mechanical power of different printing robots when moving along a uniform printing trajectory. From the left graph, it can be seen that the ABB IRB 4600 industrial robot achieves significantly higher instantaneous power compared to the other robots. For this reason, the right graph is added, which presents identical results, but the instantaneous power of the ABB robot is shown in a quarter scale for clarity. From these graphs, it can be concluded that the Printing Mantis robot achieves the lowest mechanical power even when all its cells are in motion under a scenario that represents an energy disadvantage (see Section 5.2.3). Higher mechanical power is required to move the gantry robot than the Printing Mantis robot.
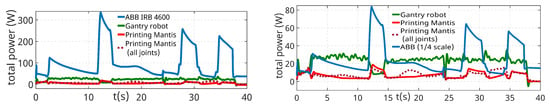
Figure 17.
Comparison of the instantaneous mechanical powers of individual printing robots.
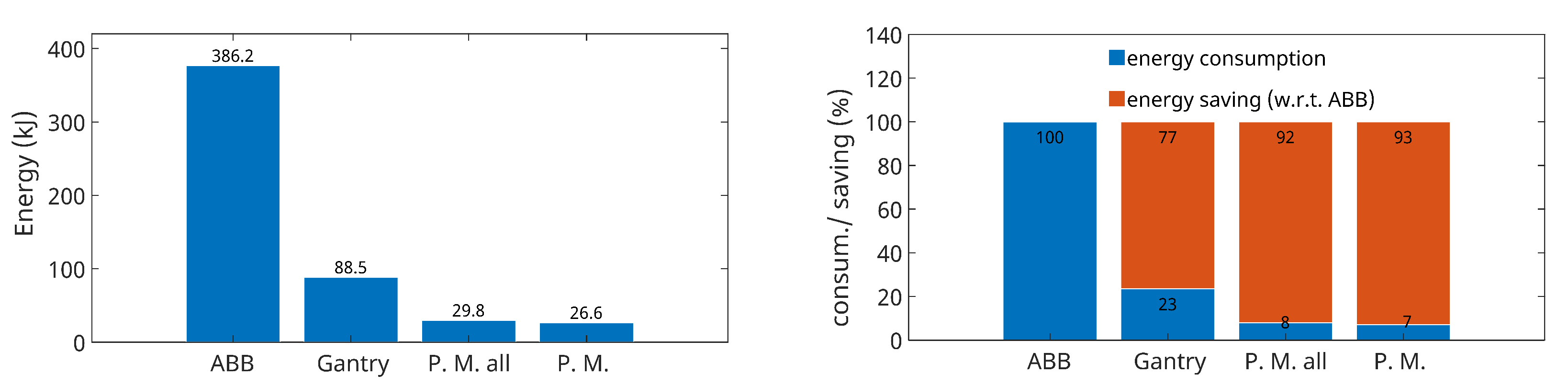
Figure 18 presents a comparison based on the energy consumption of moving the robots along a trajectory that represents a one-meter-high printed wall (see the printed wall Figure 12). In the left graph, the amount of energy required to move each robot can be seen. In the right graph, a relative comparison of the energy consumption against the ABB robot is made. From these graphs, it can be seen that if a gantry robot is used to print the reference wall, approximately 77% less mechanical energy will be required than if an industrial articulated robot is used. When using the unique Printing Mantis robot, even 92 or 93% less energy will be required (depending on the configuration used). The significantly greater amount of energy in an articulated robot may be due to the need to compensate for the gravitational forces of the individual robot links.
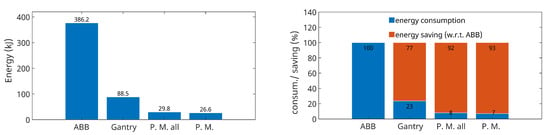
Figure 18.
Comparison of energy consumption of individual printing robots.
7.3. Results from a New Methodology for Determining Reduced Efficiency Maps
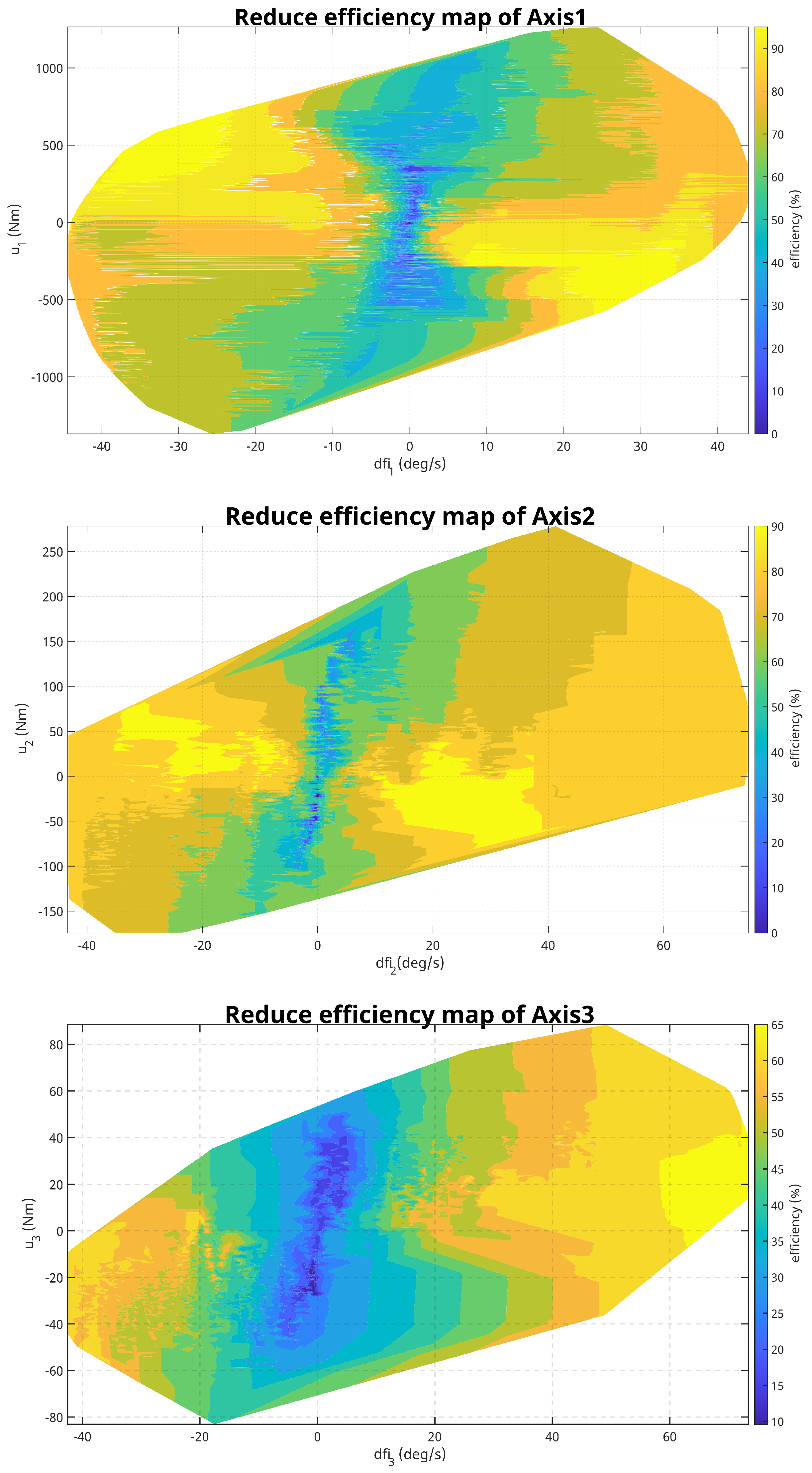
Reduced efficiency maps of each axis of the Printing Mantis robot can be found in Appendix A in Figure A1. Compared to the “classical” efficiency maps, the maps are evaluated for all four quadrants, i.e., also for negative speeds and negative torques. Due to the interaction of the individual robot joints, the individual robot actuators can move in both motor and generator modes. From the above efficiency maps, it can be seen that the efficiency of the individual robot drives depends significantly on the speed, the “load” torque, and the mode which it is in.
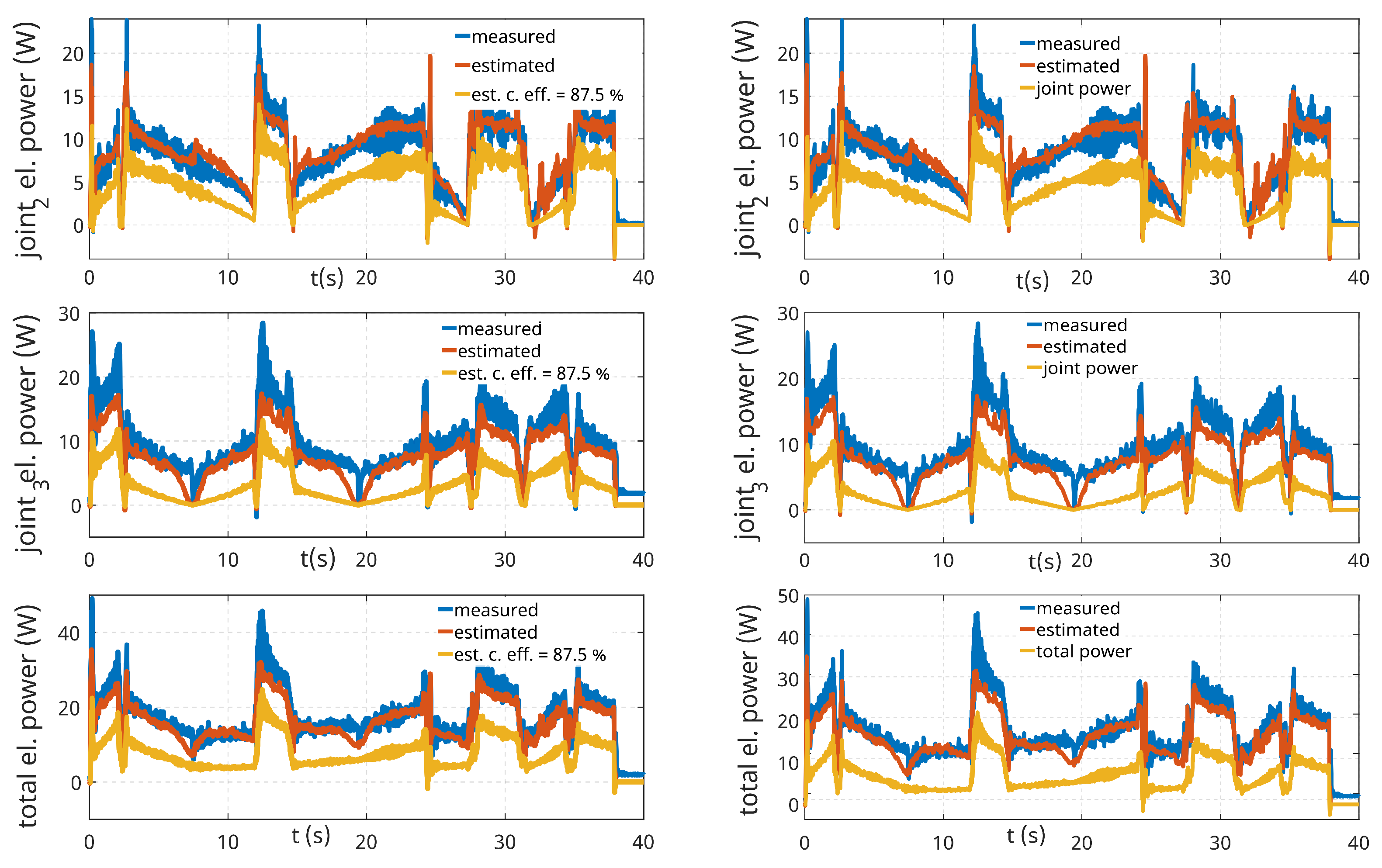
In the graphs shown in Figure 19, a comparison of the estimated and measured instantaneous power of the individual joints and the overall power when the robot moves along the print path can be seen on the left. From the estimated powers and the reconstructed powers based on the procedure see (Section 6.2), the estimated instantaneous electrical powers are then determined. From the plots, it can be seen that the individual estimated powers follow the behaviour of the measured powers well, which is to be expected based on the results of the previous Section 7.1. In the case of the estimated electrical power, the evaluation shows a slight degradation of the results, but still, the prediction of the electrical power is at an acceptable level.
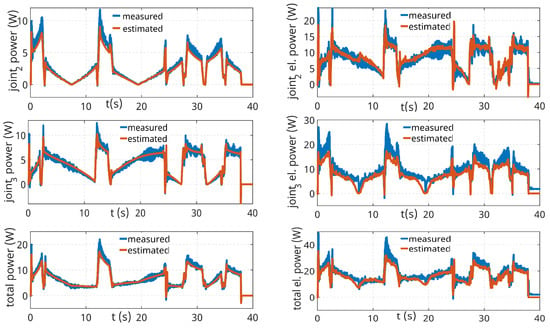
Figure 19.
Electrical instantaneous power of individual axes and total electrical power.
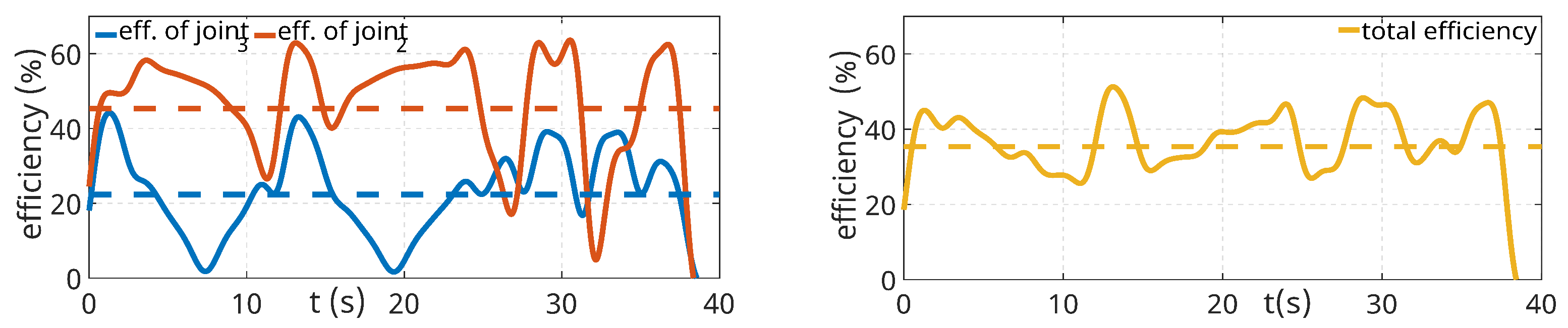
What is more important, however, is the fact that the electrical power inputs are significantly higher (in some places up to 2×) than the mechanical power outputs. Moreover, it can be seen from the graphs that the ratio between electrical and mechanical outputs is not constant. Figure 20 shows the instantaneous efficiency of each robot joint as the robot moves along the print path and the total efficiency. The dashed line indicates the average efficiency values. The graphs show that the efficiency of individual axes significantly changes during motion. Segments where efficiency is minimal correspond to cases where there is a change in the direction of velocity, resulting in a momentary axis stoppage, which manifests as minimal efficiency. Another potential factor contributing to minimal efficiency is the varied distribution of load during robot motion, whereby certain segments of the trajectory may impose minimal load on some drives.
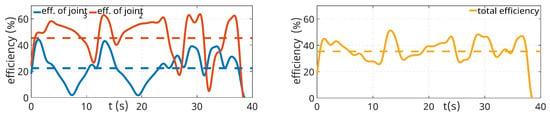
Figure 20.
Instantaneous vs. mean efficiency comparison.
That the efficiency of drives varies with load, speed, temperature, etc., is a well-known fact but one that is ignored in many publications. According to the information in the research described in Section 2, it appears that many publications consider constant efficiency for the robot power model [14,15,36] or do not consider efficiency [13]. The paper [14] does not give a specific figure for the considered efficiency, it just gives the efficiency of permanent synchronous motors in the range of 83–92%. In the paper [36], an efficiency (conversion) of 100% is considered. This is essentially the case where the electrical powers would match the mechanical powers.
Figure 21 shows a comparison of the actual measured electrical power consumption of the individual drives of the printing robot with the estimated power consumption under different efficiency considerations. The plots on the left demonstrate the comparison when considering a constant average efficiency of 87.5% according to [14]. The plots on the right demonstrate the comparison in the case of neglecting efficiency, where the estimated power inputs correspond to the articulated powers.
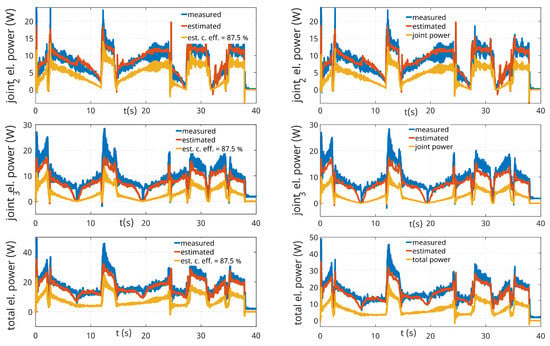
Figure 21.
Effect of different efficiency considerations on instantaneous robot power.
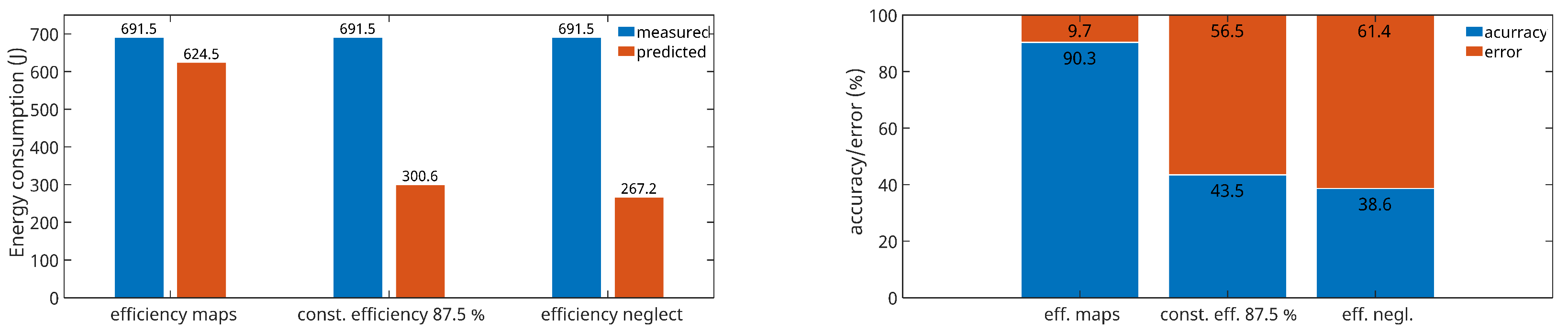
In Figure 22, the left graph shows a comparison of the energy consumption, quantifying the specific power consumption required to move the robot along the printing path. From the graphs, it can be seen that the total measured energy for the robot movement corresponds to 691.5 J. It can also be seen that in the case where constant efficiency is considered or efficiency is not taken into account, the predicted energy consumption is more than half of the measured one. This represents a very significant bias. The degree of bias in the prediction of the total power consumption of the printing robot with respect to considering/not considering efficiency is shown in the right graph in Figure 22. When neglecting efficiency, the accuracy of the energy consumption prediction is only 38.6%. When considering a constant efficiency of 87.5%, an accuracy of 43.5% is achieved. When reconstructing the efficiency from the proposed reduced efficiency maps, an accuracy of up to 90.3% is achieved.
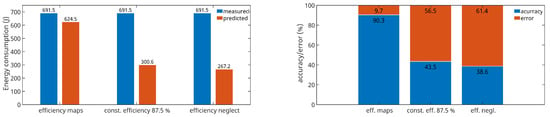
Figure 22.
Evaluating the impact of efficiency considerations on robot power consumption.
The accuracy of the electrical power prediction is even better than the accuracy of the mechanical power prediction presented in Section 7.1. This may seem somewhat surprising since the electrical power is calculated from the mechanical power. When performing the quantification of the accuracy of the total energy estimation as in Section 7.1, but using the printing trajectory instead of the validation trajectory, the accuracy of the mechanical energy estimation comes out to be 96.8%. The accuracy reported in Section 7.1 was evaluated for the dynamically demanding validation trajectory, and therefore, better results can be expected for the print trajectory, which has significantly less demanding dynamics. At the same time, a possible reason for the validity of the assumption made in Section 7.1 is the improvement in estimation accuracy when the third link, which has the highest estimation accuracy, dominates the motion.
8. Conclusions
In this paper, a detailed analysis of the energy consumption of robots used for 3DCP technology is performed. We present here a methodology to create an energy consumption model for a unique printing robot, Printing Mantis, which has been developed and optimized specifically for this technology. This methodology includes an innovative approach to determining reduced efficiency maps, which allows the inclusion of practically difficult-to-measure drive-efficiency parameters in the model. This is used to achieve the creation of a comprehensive energy consumption model of the printing robot that reflects its operating characteristics in a realistic environment. For the purpose of measuring the energy-related variables required to implement this methodology, the open control system of the printing robot was advantageously used together with the developed software tools. This choice does not result in a loss of versatility, as equivalent results can be handled using external hardware such as power analysers, as demonstrated in the relevant publications mentioned in the research section of this paper. Based on the methodology shown in Figure 14, the consumption model’s generation methodologies can be applied to arbitrary printing robots.
At the same time, all experimental results from this methodology were presented. During the identification experiment, the inertial parameters of the robot were obtained and used to model the mechanical energy consumption of the robot. The quality of the model was evaluated while the robot was moving along the validation trajectory, where the accuracy of the robot mechanical energy consumption model was evaluated to be 83.7%.
The parametric identification experiment also led to a new methodology for creating reduced-efficiency maps that allow reconstructing the efficiency for any desired print trajectory, thus contributing to the creation of a comprehensive model of the power consumption of the printing robot. The main advantages of this methodology lie in the significant reduction in the time required to perform the experiment, where the data are obtained during a classical identification experiment. In addition, there is no need for a dedicated measuring station with external measuring equipment and isolated measurements of individual actuators leading up to the disassembly of the robot. For these reasons, compared to traditional methods and experiments for obtaining efficiency data, this methodology appears to be a favourable alternative, especially in the context of robotics. As a potential drawback, the limited range of torques and velocities obtained using this method is limited by the choice of excitation trajectory. Therefore, the range over which the subsequent power prediction will be made must be carefully considered when designing the identification experiment.
In an experiment aimed at predicting the power consumption when the robot moves along a uniform printing trajectory, a prediction accuracy of up to 90.3% was achieved. This accuracy was obtained by using a comprehensive power consumption model using the aforementioned reduced-efficiency maps. Equally, different efficiency consideration cases (constant efficiency/neglect efficiency) were discussed in relation to the degradation rate of the electricity consumption prediction. It was emphasized that for 3DCP technology, it is particularly necessary to consider efficiency as a complex parameter depending on a number of parameters. The results showed that considering a constant efficiency for the determination of the electrical power input can lead to a power-prediction error of more than 50% and, if not considered, even to an error of more than 60%.
Additional experiments were conducted with the aim of analyzing how the kinematic structure of printing robots influences their energy consumption. Based on available information from literature research, it was found that a comparison of the energy efficiency of robots used in 3D concrete printing has not been conducted thus far. The article presents a methodology allowing the acquisition and comparison of truly measured energy data from two real workplaces with printing robots. This methodology is combined with energy simulation data obtained from a virtual workplace in the ABB RobotStudio environment. This approach enables a comparison of energy consumption for 3DCP among industrially articulated robots, with the ABB IRB4600 robot selected as a representative example. Real robots, including a printing gantry robot and the unique Printing Mantis robot, are also included. Based on the conducted experiments, a significant influence of the kinematic structure of the printing robot on its energy consumption in the context of 3DCP technology can be clearly stated. During 3DCP technology, where printing predominantly occurs in the horizontal plane, articulated robots commonly used in this field exhibit significantly higher energy consumption. The increased energy consumption is most likely caused by the necessity to compensate for the gravitational forces acting on their joints. However, specific numerical values should be interpreted with caution, as simulation results from the virtual workplace will always be influenced by the quality of the simulation model. Nevertheless, it can be assumed that the actual energy consumption of a real industrial robot will indeed be even higher.
The 3DCP technology is quite specific in its requirements in terms of the possible optimization of energy consumption. Similar to welding processes, motion profiles cannot be adjusted to save energy because printing is typically performed at a constant speed. Moreover, these speeds are quite slow and, based on actual measurements, it appears that the average efficiency of the drives during printing is around 30–50%. Part of this loss is of course due to mechanical losses such as friction, etc., which are always present. However, we assume that the fact that the motors of the printing robot do not operate at their optimum operating point at such low speeds has a considerable influence on this efficiency.
Based on our research, the following practical recommendations can be made. For 3DCP technology, it is advisable to use robots that are optimized for this technology, with the optimization of the kinematic structure of the printing robot being one of the most important and crucial measures to minimize energy consumption. Furthermore, it has proven important to pay attention to the efficiency of the actuators of the robots in this specific application. Thus, the goal of our further research is to carefully analyse the efficiency of the printing robot’s actuators and to address the design of optimal low-level control in order to significantly improve the overall efficiency environment.
Author Contributions
Conceptualisation, D.K. and T.M.; methodology, D.K.; software, T.M. and D.K.; validation and formal analysis, D.K.; investigation, D.K. and T.M.; resources, D.K., T.M. and J.Č.; visualisation, D.K. and T.M.; writing—original draft preparation, D.K. and T.M.; supervision, J.Č. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper was supported by the Student Grant Competition
(SGS) with reg. number SGS-2023-3404 at the Technical University of Liberec for the year 2023 and supported by the European Structural and Investment Funds of the Operational Programme Research, Development and Education, within the project “3D Print in civil engineering and architecture—3D STAR” reg. number CZ.02.1.01/0.0/0.0/16_025/0007424.
Data Availability Statement
All data presented in this study are included in the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3DCP | 3D Construction Printing |
| B&R | Bernecker and Rainer Industrial Automation company |
| ABB | Industrial automation company |
| IDIM | Inverse dynamic identification model |
| IRB | Industrial robot |
| ETH Zurich | Federal Institute of Technology Zurich |
| RBAM | Robot-based additive manufacturing |
| CNC | Computer Numerical Control |
| G-code | Programming language for CNC |
| DBM | Dynamic Behavior Modelling |
| CAD | Computer-aided design |
| PMSM | Permanent magnet synchronous motor |
| HMI | Human Machine Interface |
| EC | Energy consumption |
| RIP | Robot identification problem |
| IDIM-OLS | Inverse dynamic identification model with ordinary least squares estimation |
| IDIM-WOLS | Inverse dynamic identification model with weighted ordinary least squares |
| SCARA | Selective Compliance Articulated Robot Arm |
| DH | Denavit–Hartenberg |
| DOF | Degrees of freedom |
| IR’s | Industrial robots |
| BIRDY | Benchmark for Identification of Robot Dynamics |
| LS | Least Squares |
| PLC | Programmable logic controller |
| MTP | Motor terminal power |
| APC | Automation PC |
| MAD | Median absolute deviation |
Appendix A
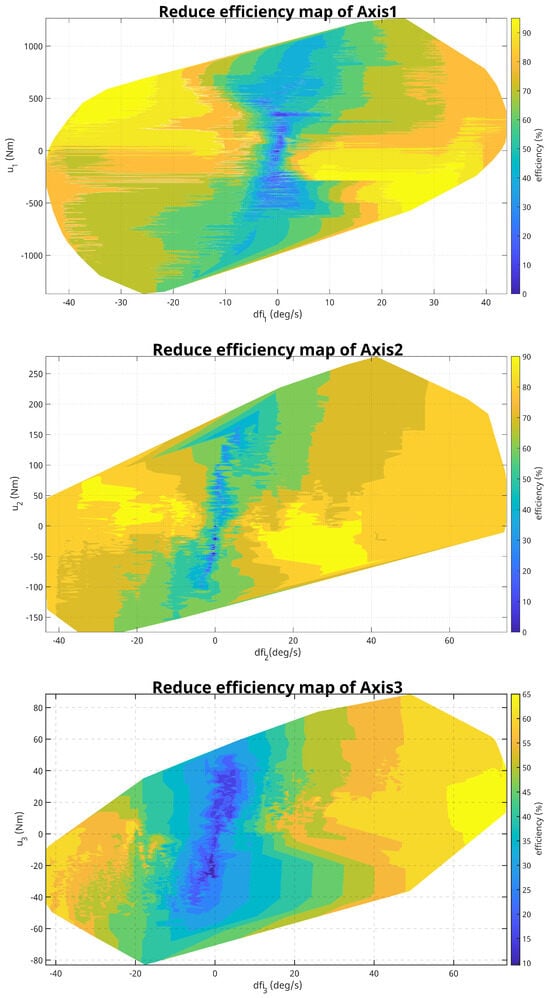
Figure A1.
Efficiency maps.
Figure A1.
Efficiency maps.
References
- Weng, Y.; Li, M.; Ruan, S.; Wong, T.N.; Tan, M.J.; Ow Yeong, K.L.; Qian, S. Comparative economic, environmental and productivity assessment of a concrete bathroom unit fabricated through 3D printing and a precast approach. J. Clean. Prod. 2020, 261, 121245. [Google Scholar] [CrossRef]
- Mohammad, M.; Masad, E.; Al-Ghamdi, S.G. 3D Concrete Printing Sustainability: A Comparative Life Cycle Assessment of Four Construction Method Scenarios. Buildings 2020, 10, 245. [Google Scholar] [CrossRef]
- Puzatova, A.; Shakor, P.; Laghi, V.; Dmitrieva, M. Large-Scale 3D Printing for Construction Application by Means of Robotic Arm and Gantry 3D Printer: A Review. Buildings 2022, 12, 2023. [Google Scholar] [CrossRef]
- Gislason, S.; Bruhn, S.; Breseghello, L.; Sen, B.; Liu, G.; Naboni, R. Lightweight 3D Printed Concrete Beams Show an Environmental Promise: A Cradle-to-Grave Comparative Life Cycle Assessment. Clean Technol. Environ. Policy 2022, 24, 2639–2654. [Google Scholar] [CrossRef]
- Anton, A.; Reiter, L.; Wangler, T.; Frangez, V.; Flatt, R.J.; Dillenburger, B. A 3D concrete printing prefabrication platform for bespoke columns. Autom. Constr. 2021, 122, 103467. [Google Scholar] [CrossRef]
- RobotStudio® 3D Printing PowerPac. Available online: https://new.abb.com/products/robotics/software-and-digital/application-software/3d-printing-powerpac (accessed on 9 February 2024).
- Lettori, J.; Raffaeli, R.; Bilancia, P.; Peruzzini, M.; Pellicciari, M. A review of geometry representation and processing methods for cartesian and multiaxial robot-based additive manufacturing. Int. J. Adv. Manuf. Technol. 2022, 123, 3767–3794. [Google Scholar] [CrossRef]
- Stupans, A.; Maksimkins, P.; Senfelds, A.; Ribickis, L. Industrial robot energy consumption analysis for gravity-induced opposing force minimization. In Proceedings of the 2022 IEEE 7th International Energy Conference (ENERGYCON), Riga, Latvia, 9–12 May 2022. [Google Scholar] [CrossRef]
- Gadaleta, M.; Berselli, G.; Pellicciari, M.; Grassia, F. Extensive experimental investigation for the optimization of the energy consumption of a high payload industrial robot with open research dataset. Robot. Comput.-Integr. Manuf. 2021, 68, 102046. [Google Scholar] [CrossRef]
- Guerra-Zubiaga, D.A.; Luong, K.Y. Energy consumption parameter analysis of industrial robots using design of experiment methodology. Int. J. Sustain. Eng. 2020, 14, 996–1005. [Google Scholar] [CrossRef]
- Paryanto; Brossog, M.; Kohl, J.; Merhof, J.; Spreng, S.; Franke, J. Energy Consumption and Dynamic Behavior Analysis of a Six-axis Industrial Robot in an Assembly System. Procedia CIRP 2014, 23, 131–136. [Google Scholar] [CrossRef]
- Othman, A.; Belda, K.; Burget, P. Physical modelling of energy consumption of industrial articulated robots. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2015. [Google Scholar] [CrossRef]
- Paes, K.; Dewulf, W.; Elst, K.V.; Kellens, K.; Slaets, P. Energy Efficient Trajectories for an Industrial ABB Robot. Procedia CIRP 2014, 15, 105–110. [Google Scholar] [CrossRef]
- Liu, A.; Liu, H.; Yao, B.; Xu, W.; Yang, M. Energy consumption modelling of industrial robot based on simulated power data and parameter identification. Adv. Mech. Eng. 2018, 10, 168781401877385. [Google Scholar] [CrossRef]
- Yan, K.; Xu, W.; Yao, B.; Zhou, Z.; Pham, D.T. Digital Twin-Based Energy modelling of Industrial Robots. In Methods and Applications for Modelling and Simulation of Complex Systems; Springer: Singapore, 2018; pp. 333–348. [Google Scholar] [CrossRef]
- Zhou, J.; Yi, H.; Cao, H.; Jiang, P.; Zhang, C.; Ge, W. Structural decomposition-based energy consumption modelling of robot laser processing systems and energy-efficient analysis. Robot. Comput.-Integr. Manuf. 2022, 76, 102327. [Google Scholar] [CrossRef]
- Paryanto; Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the energy consumption of industrial robots in manufacturing systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar] [CrossRef]
- Agustí-Juan, I.; Müller, F.; Hack, N.; Wangler, T.; Habert, G. Potential benefits of digital fabrication for complex structures: Environmental assessment of a robotically fabricated concrete wall. J. Clean. Prod. 2017, 154, 330–340. [Google Scholar] [CrossRef]
- Brousek, J.; Petr, T.; Beran, L.; Myslivec, T.; Kajzr, D.; Vozenilek, R.; Diblik, M.; Ristolainen, L. Robotic Arm Design, Development and Control for Printing Cement Mixtures. MM Sci. J. 2022, 2022, 5550–5558. [Google Scholar] [CrossRef]
- Zada, V.; Belda, K. Structure Design and Solution of Kinematics of Robot Manipulator for 3D Concrete Printing. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3723–3734. [Google Scholar] [CrossRef]
- Kajzr, D.; Myslivec, T.; Cernohorsky, J. An Open PLC-Based Robot Control System for 3D Concrete Printing. Robotics 2023, 12, 96. [Google Scholar] [CrossRef]
- Vojir, M.; Myslivec, T.; Petr, T.; Brousek, J.; Beran, L.; Diblik, M.; Keller, P.; Kajzr, D.; Vozenilek, R. A new way to design software for industrial automation—3d printer cement mixtures. MM Sci. J. 2021, 2021, 4223–4229. [Google Scholar] [CrossRef]
- Saidur, R. A review on electrical motors energy use and energy savings. Renew. Sustain. Energy Rev. 2010, 14, 877–898. [Google Scholar] [CrossRef]
- Swevers, J.; Ganseman, C.; Tukel, D.; de Schutter, J.; Brussel, H.V. Optimal robot excitation and identification. IEEE Trans. Robot. Autom. 1997, 13, 730–740. [Google Scholar] [CrossRef]
- Gautier, M. Numerical calculation of the base inertial parameters of robots. J. Robot. Syst. 1991, 8, 485–506. [Google Scholar] [CrossRef]
- Gautier, M. Dynamic identification of robots with power model. In Proceedings of the Proceedings of International Conference on Robotics and Automation, ROBOT-97, Albuquerque, NM, USA, 25 April 1997. [Google Scholar] [CrossRef]
- Janot, A.; Vandanjon, P.O.; Gautier, M. A Generic Instrumental Variable Approach for Industrial Robot Identification. IEEE Trans. Control. Syst. Technol. 2014, 22, 132–145. [Google Scholar] [CrossRef]
- Canudas de Wit, C.; Olsson, H.; Astrom, K.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control. 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Gautier, M.; Khalil, W. Direct calculation of minimum set of inertial parameters of serial robots. IEEE Trans. Robot. Autom. 1990, 6, 368–373. [Google Scholar] [CrossRef]
- Leboutet, Q.; Roux, J.; Janot, A.; Guadarrama-Olvera, J.R.; Cheng, G. Inertial Parameter Identification in Robotics: A Survey. Appl. Sci. 2021, 11, 4303. [Google Scholar] [CrossRef]
- Swevers, J.; Verdonck, W.; Schutter, J.D. Dynamic Model Identification for Industrial Robots. IEEE Control Syst. 2007, 27, 58–71. [Google Scholar] [CrossRef]
- Barnett, E.; Gosselin, C. Large-scale 3D printing with a cable-suspended robot. Addit. Manuf. 2015, 7, 27–44. [Google Scholar] [CrossRef]
- Myslivec, T.; Kajzr, D. Energy Consumption Comparison Experiment. Available online: https://youtu.be/ZYcKMpvWowc (accessed on 25 March 2023).
- Stockman, K.; Dereyne, S.; Vanhooydonck, D.; Symens, W.; Lemmens, J.; Deprez, W. Iso efficiency contour measurement results for variable speed drives. In Proceedings of the The XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Soong, W.L.; Pellegrino, G.; Armando, E. Efficiency maps of electrical machines. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Xiao, T.; Gu, Y.; Zhang, C.; Yang, G. A Feasible Method for Evaluating Energy Consumption of Industrial Robots. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).