Design and Analysis of VARONE a Novel Passive Upper-Limb Exercising Device
Abstract
1. Introduction
- Utilization of variable stiffness joints enabling the recording of kinetic (force) capabilities, facilitating the quantification of more precise and qualitative physical information;
- Utilizing the above-mentioned variable stiffness joints to provide adjustable resistance in each degree of freedom of the wrist motion. This allows for providing treatment exercises adjustable to patients with varying levels of injury;
- Provide a wrist device that can be combined with the wrist of other devices (such as, for example, NURSE) to enable a wider range of motion assessments and treatments.
- See the end of the document for further details on references.
2. The Attached Problem
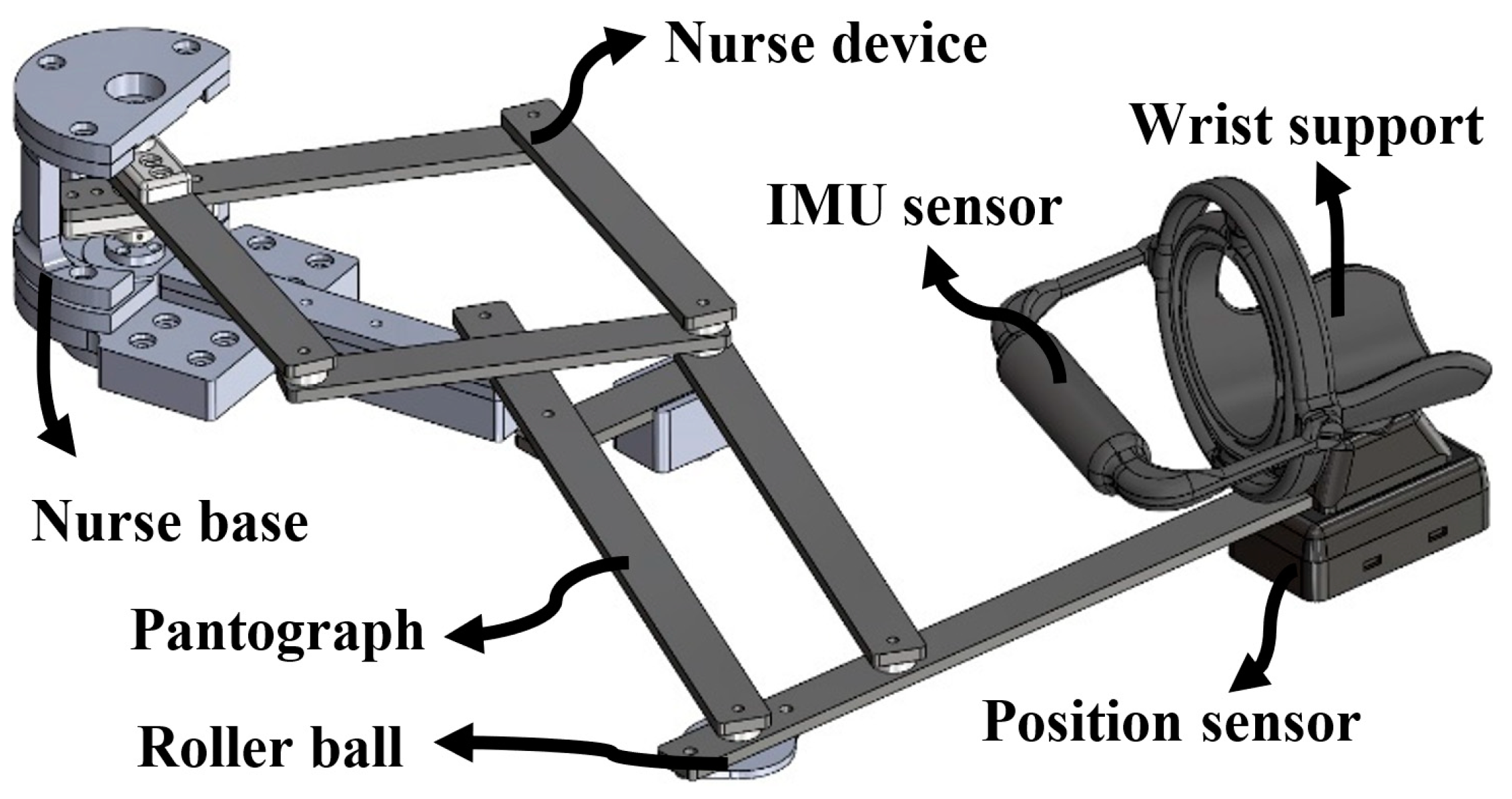
2.1. The NURSE Device
2.2. The Proposed Design Procedure for VARONE
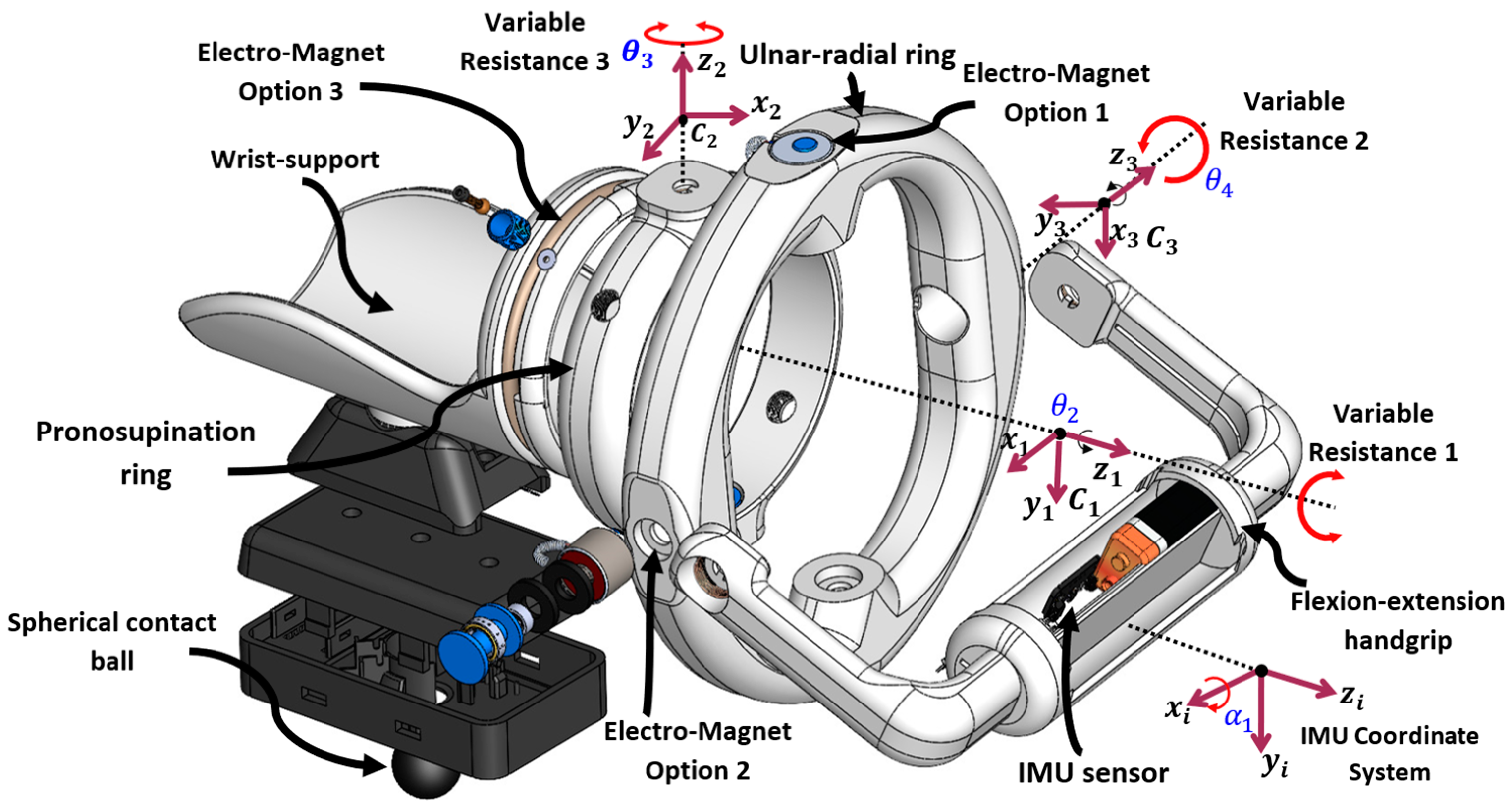
2.3. The Proposed Design Solution
3. Kinematic and F.E.M. (Finite Element Method) Analysis
3.1. The Proposed Design Procedure for VARONE
3.2. Inverse Kinematic Analysis
3.3. F.E.M. Analysis
4. Dynamic Analysis
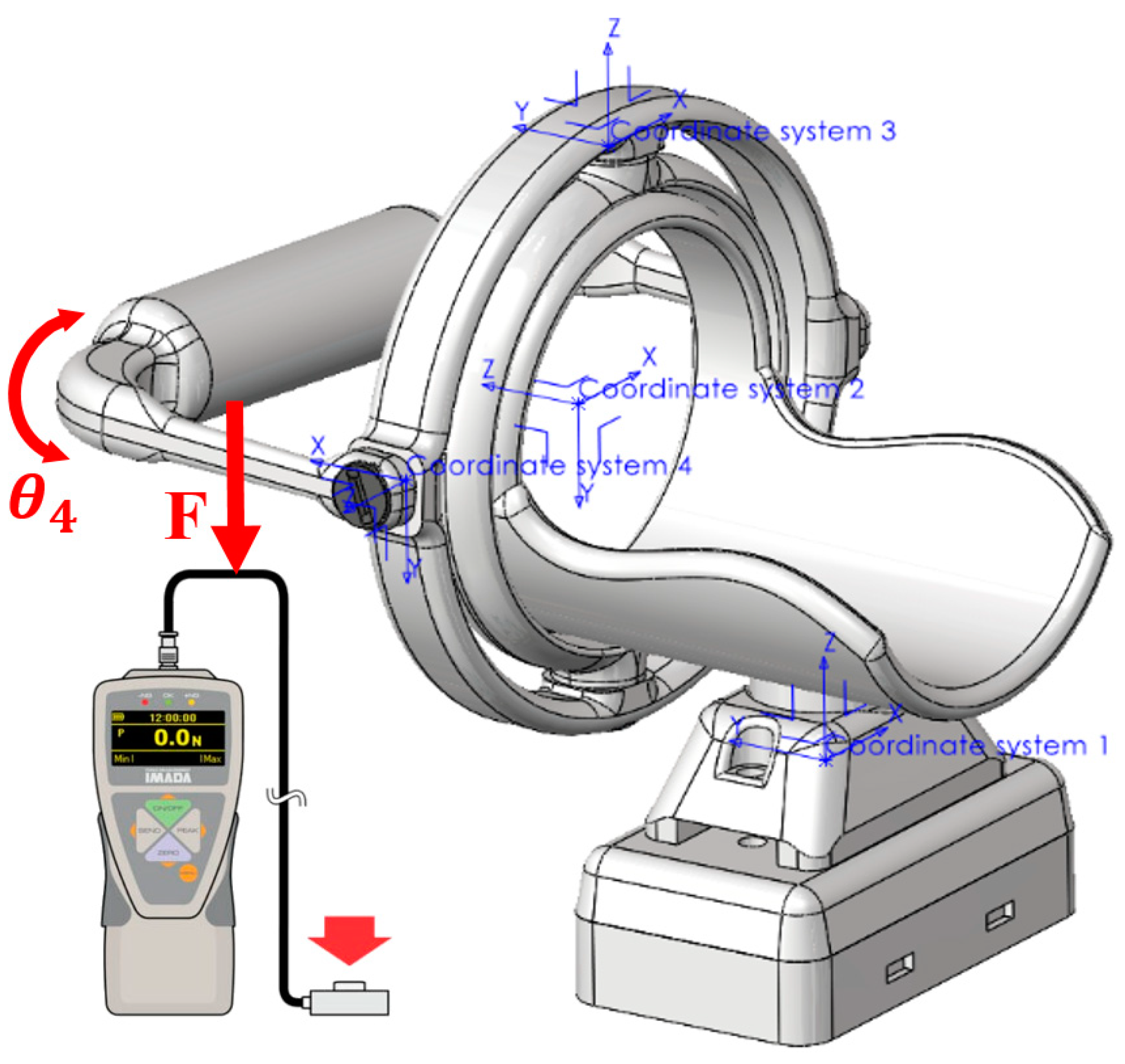
5. A Setup for Experimental Validation
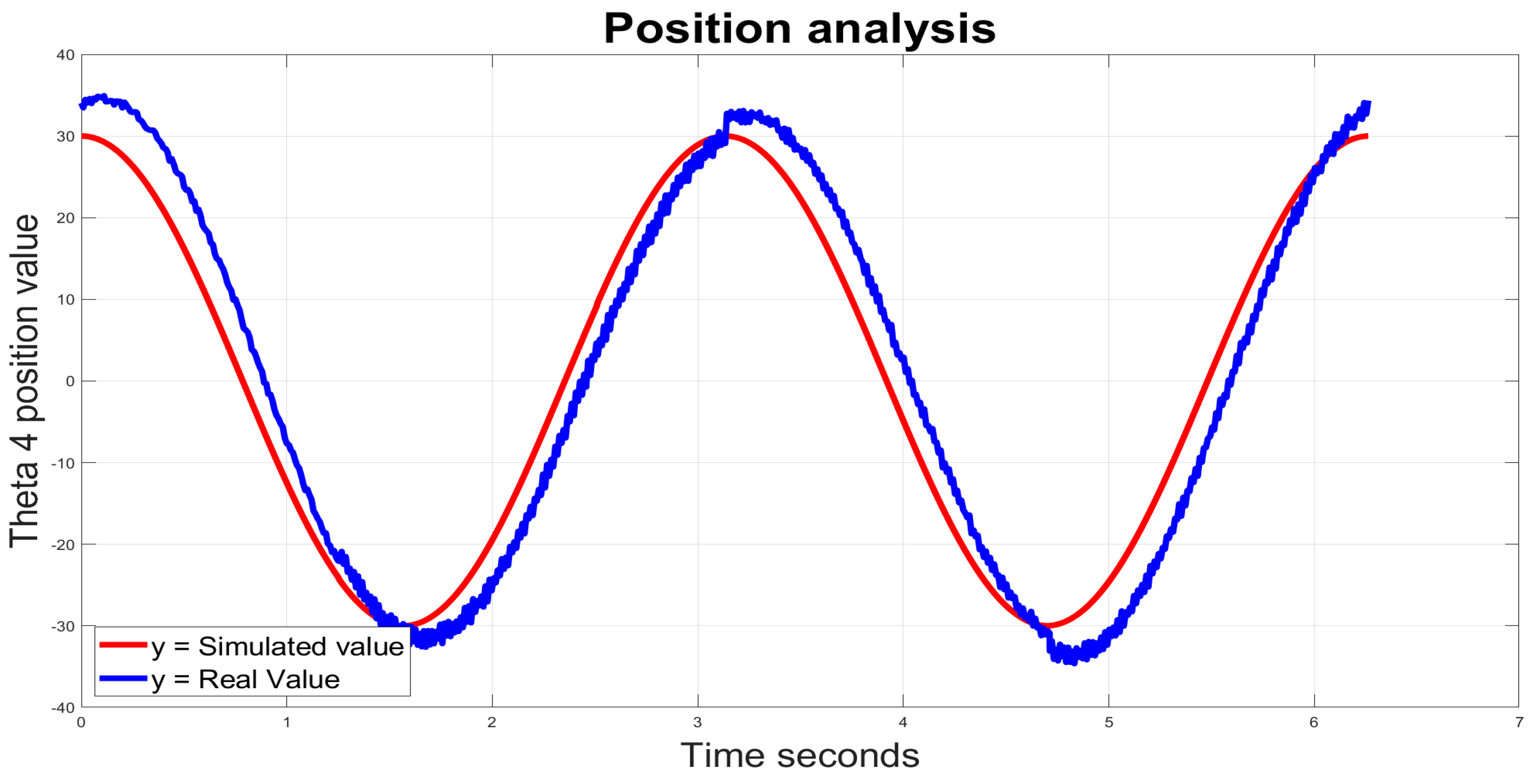
Validation Tests and Results
- Module MPU-9250;
- Module CC2640R2F;
- Lithium battery;
- Microprocessor ARM ABX00032;
- Imada ZTA-LM-110.
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Stroke Organization (WSO). Global Stroke Fact Sheet 2022. Int. J. Stroke 2022, 17, 478. [Google Scholar] [CrossRef] [PubMed]
- Waller, E.; Bowens, A.; Washmuth, N. Prevalence of and prevention for work-related upper limb disorders among physical therapists: A systematic review. BMC Musculoskelet. Disord. 2022, 23, 453. [Google Scholar] [CrossRef] [PubMed]
- Noé, E.; Gómez, A.; Bernabeu, M.; Quemada, I.; Rodríguez, R.; Pérez, T.; López, C.; Laxe, S.; Colomer, C.; Ríos, M.; et al. Guía: Principios básicos de la neurorrehabilitación del paciente con daño cerebral adquirido. Recomendaciones de la Sociedad Española de Neurorrehabilitación. Neurología 2023, n. 244612681. [Google Scholar] [CrossRef]
- Pike, S.; Lannin, N.A.; Wales, K.; Cusick, A. A systematic review of the psychometric properties of the Action Research Arm Test in neurorehabilitation. Aust. Occup. Ther. J. 2018, 65, 449–471. [Google Scholar] [CrossRef] [PubMed]
- Brunnstrom, S. Motor testing procedures in hemiplegia: Based on sequential recovery stages. Phys. Ther. 1966, 46, 357–375. [Google Scholar] [CrossRef]
- Fugl-Meyer, A.R.; Jääskö, L.; Leyman, I.; Olsson, S.; Steglind, S. The post-stroke hemiplegic patient. 1. a method for evaluation of physical performance. Scand. J. Rehabil. Med. 1975, 7, 13–31. [Google Scholar] [CrossRef]
- Bohannon, R.; Smith, M. Upper extremity strength deficits in hemiplegic stroke patients: Relationship between admission and discharge assessment and time since onset. Arch. Phys. Med. Rehabil. 1987, 68, 155–157. [Google Scholar] [PubMed]
- Wang, C.; Peng, L.; Hou, Z.-G.; Li, J.; Zhang, T.; Zhao, J. Quantitative Assessment of Upper-Limb Motor Function for Post-Stroke Rehabilitation Based on Motor Synergy Analysis and Multi-Modality Fusion. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 943–952. [Google Scholar] [CrossRef]
- Olesh, E.V.; Yakovenko, S.; Gritsenko, V. Automated Assessment of Upper Extremity Movement Impairment due to Stroke. PLoS ONE 2014, 9, e104487. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, D.; Liu, Y.; Lueth, T.C. FEM-Based Mechanics Modeling of Bio-Inspired Compliant Mechanisms for Medical Applications. IEEE Trans. Med. Robot. Bionics 2020, 2, 364–373. [Google Scholar] [CrossRef]
- Tschiersky, M.; Hekman, E.E.G.; Brouwer, D.M.; Herder, J.L. Gravity Balancing Flexure Springs for an Assistive Elbow Orthosis. IEEE Trans. Med. Robot. Bionics 2019, 1, 177–188. [Google Scholar] [CrossRef]
- Fan, H.; Wei, G.; Ren, L. Prosthetic and robotic wrists comparing with the intelligently evolved human wrist: A review. Robotica 2022, 40, 4169–4191. [Google Scholar] [CrossRef]
- Carbone, G.; Gherman, B.; Ulinici, I.; Vaida, C.; Pisla, D. Design issues for an inherently safe robotic rehabilitation device. Mech. Mach. Sci. 2018, 49, 1025–1032. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Jung, Y.; Lee, D.; Bae, J. A Passive Upper Limb Exoskeleton with Tilted and Offset Shoulder Joints for Assisting Overhead Tasks. IEEE/ASME Trans. Mechatron. 2022, 27, 4963–4973. [Google Scholar] [CrossRef]
- Demers, M.; Rowe, J.; Prochazka, A. Passive Devices for Upper Limb Training. In Neurorehabilitation Technology; Reinkensmeyer, D.J., Marchal-Crespo, L., Dietz, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Chen, J.; Li, X. Determining human upper limb postures with a developed inverse kinematic method. Robotica 2022, 40, 4120–4142. [Google Scholar] [CrossRef]
- Ferreira, F.; De Paula Rúbio, G.; Dutra, R.; Van Petten, A.; Vimieiro, C. Development of portable robotic orthosis and biomechanical validation in people with limited upper limb function after stroke. Robotica 2022, 40, 4238–4256. [Google Scholar] [CrossRef]
- Iranzo, S.; Piedrabuena, A.; Iordanov, D.; Martinez-Iranzo, U.; Belda-Lois, J.M. Ergonomics assessment of passive upper limb exoskeletons in an automotive assembly plant. Appl. Ergon. 2020, 87, 103120. [Google Scholar] [CrossRef]
- Kikuchi, T.; Sato, C.; Yamabe, K.; Abe, I.; Ohno, T.; Kugimiya, S.; Inoue, A. Upper limb training/assessment program using passive force controllable rehabilitation system. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 505–510. [Google Scholar] [CrossRef]
- Maura, R.M.; Rueda Parra, S.; Stevens, R.E.; Weeks, D.L.; Wolbrecht, E.T.; Perry, J.C. Literature review of stroke assessment for upper-extremity physical function via EEG, EMG, kinematic, and kinetic measurements and their reliability. J. NeuroEngineering Rehabil. 2023, 20, 21. [Google Scholar] [CrossRef] [PubMed]
- Bos, R.A.; Haarman, C.J.; Stortelder, T.; Nizamis, K.; Herder, J.L.; Stienen, A.H.; Plettenburg, D.H. A structured overview of trends and technologies used in dynamic hand orthoses. J. Neuroeng. Rehabil. 2016, 13, 62. [Google Scholar] [CrossRef]
- Miao, S.; Shen, C.; Feng, X.; Zhu, Q.; Shorfuzzaman, M.; Lv, Z. Upper limb rehabilitation system for stroke survivors based on multi-modal sensors and machine learning. IEEE Access 2021, 9, 30283–30291. [Google Scholar] [CrossRef]
- Chaparro-Rico, B.D.M.; Cafolla, D.; Ceccarelli, M.; Castillo-Castaneda, E. NURSE-2 DoF Device for Arm Motion Guidance: Kinematic, Dynamic, and FEM analysis. Appl. Sci. 2020, 10, 2139. [Google Scholar] [CrossRef]
- Sharma, S.; Dijkstra, T.; Prasad, R.V. Open Gimbal: A 3 Degrees of Freedom Open Source Sensing and Testing Platform for Nano- and Micro-UAVs. IEEE Sens. Lett. 2023, 7, 2502704. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Yusuf, E.; Nelissen, R.G.; Ioan-Facsinay, A.; Stojanovic-Susulic, V.; DeGroot, J.; van Osch, G.; Middeldorp, S.; Huizinga, T.W.J.; Kloppenburg, M. Association between weight or body mass index and hand osteoarthritis: A systematic review. Ann. Rheum. Dis. 2010, 69, 761–765. [Google Scholar] [CrossRef] [PubMed]
- Satisfaction Interview. Available online: https://forms.gle/i6JMMCriyZth3iZw9 (accessed on 7 February 2024).














| Joint | Movement | Rotation Ranges (Degrees) |
|---|---|---|
| Glenohumeral | Flexion/extension | 330°–0°–90° |
| Radiohumeral | Flexion/extension | 320°–0°–90° |
| Proximal/distal | Pronosupination | 270°–0°–60° |
| Radiocarpal | Flexion/extension | 320°–0°–75° |
| Radial/ulnar | 310°–0°–20° |
| Joint | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | 0 | |||
| 3 | ||||
| 4 | 0 | 0 |
| Properties | Value | Units |
|---|---|---|
| Heat Deflection Temperature (HDT) | 126 | °F |
| Density | 1.24 | g/cm3 |
| Tensible strength | 50 | MPa |
| Flexural strength | 80 | MPa |
| Impact strength | 96.1 | J/m |
| Shrink rate | 0.37–0.41% | in/in |
| Heat deflection temperature (HDT) | 126 | °F |
| Density | 1.24 | g/cm3 |
| Mesh Type | Solid Mesh |
|---|---|
| Mesher used | Curvature-based mesh |
| Jacobian points | 3 |
| Maximum element size | 68.34 mm |
| Minimum element size | 4.54 mm |
| Total nodes | 254,567 |
| Total elements | 257,980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amador, L.D.F.; Castillo Castañeda, E.; Laribi, M.A.; Carbone, G. Design and Analysis of VARONE a Novel Passive Upper-Limb Exercising Device. Robotics 2024, 13, 29. https://doi.org/10.3390/robotics13020029
Amador LDF, Castillo Castañeda E, Laribi MA, Carbone G. Design and Analysis of VARONE a Novel Passive Upper-Limb Exercising Device. Robotics. 2024; 13(2):29. https://doi.org/10.3390/robotics13020029
Chicago/Turabian StyleAmador, Luis Daniel Filomeno, Eduardo Castillo Castañeda, Med Amine Laribi, and Giuseppe Carbone. 2024. "Design and Analysis of VARONE a Novel Passive Upper-Limb Exercising Device" Robotics 13, no. 2: 29. https://doi.org/10.3390/robotics13020029
APA StyleAmador, L. D. F., Castillo Castañeda, E., Laribi, M. A., & Carbone, G. (2024). Design and Analysis of VARONE a Novel Passive Upper-Limb Exercising Device. Robotics, 13(2), 29. https://doi.org/10.3390/robotics13020029









