Development of a Pneumatically Actuated Quadruped Robot Using Soft–Rigid Hybrid Rotary Joints
Abstract
1. Introduction
2. Development of the Pneumatically Actuated Quadruped Robot
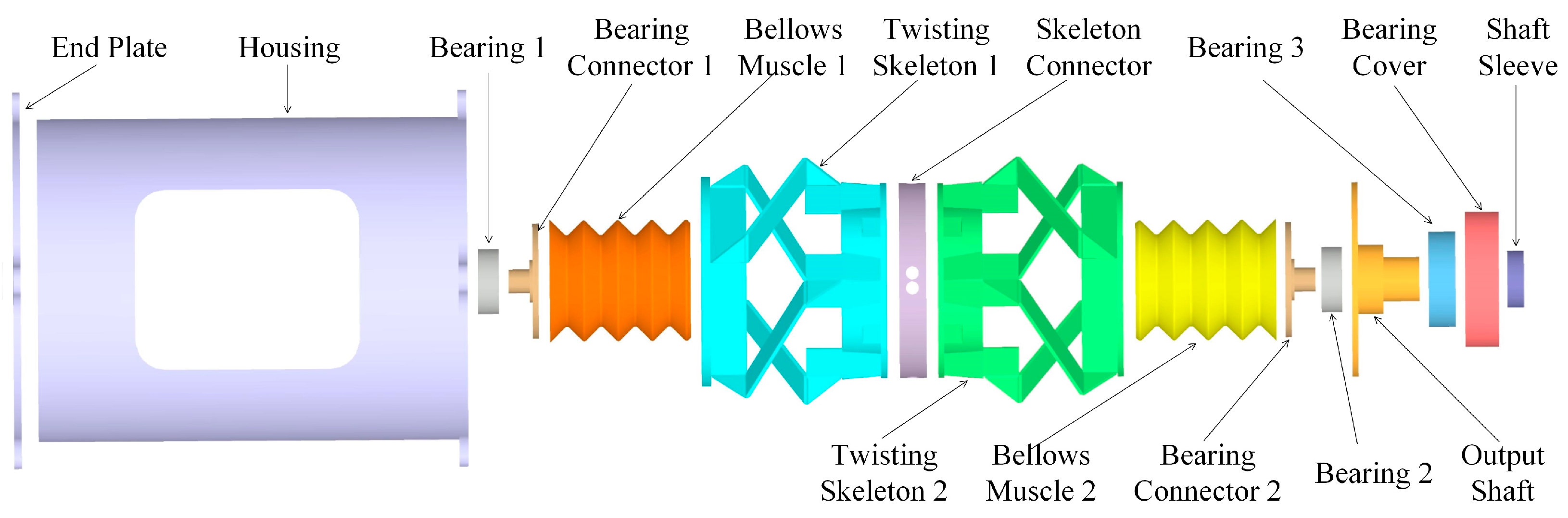
2.1. Design of the Soft–Rigid Hybrid Rotary Joint
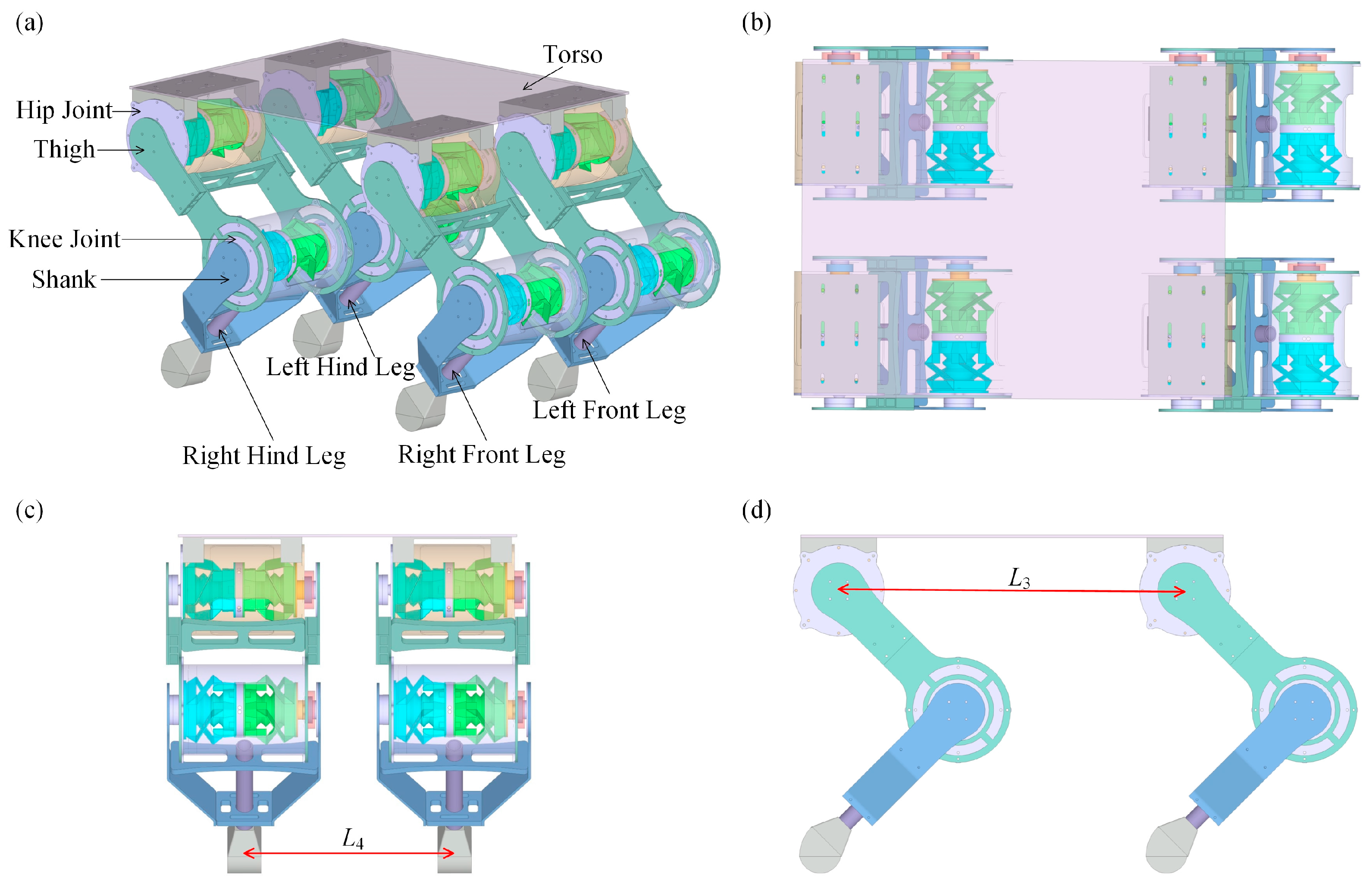
2.2. Integration of the Quadruped Robot
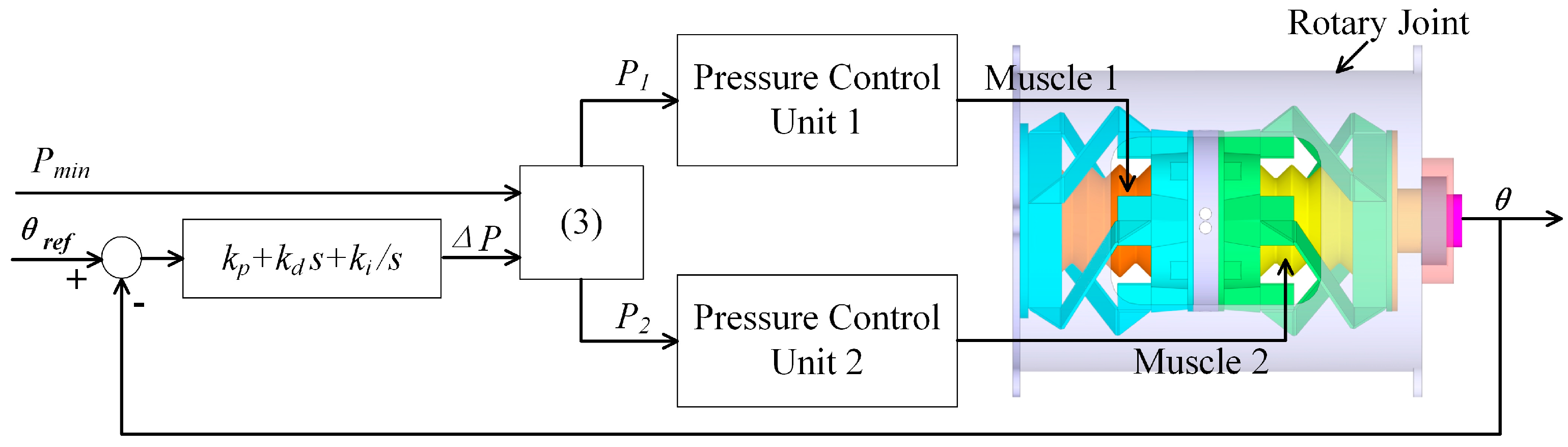
2.3. Controller for the Soft–Rigid Hybrid Rotary Joint
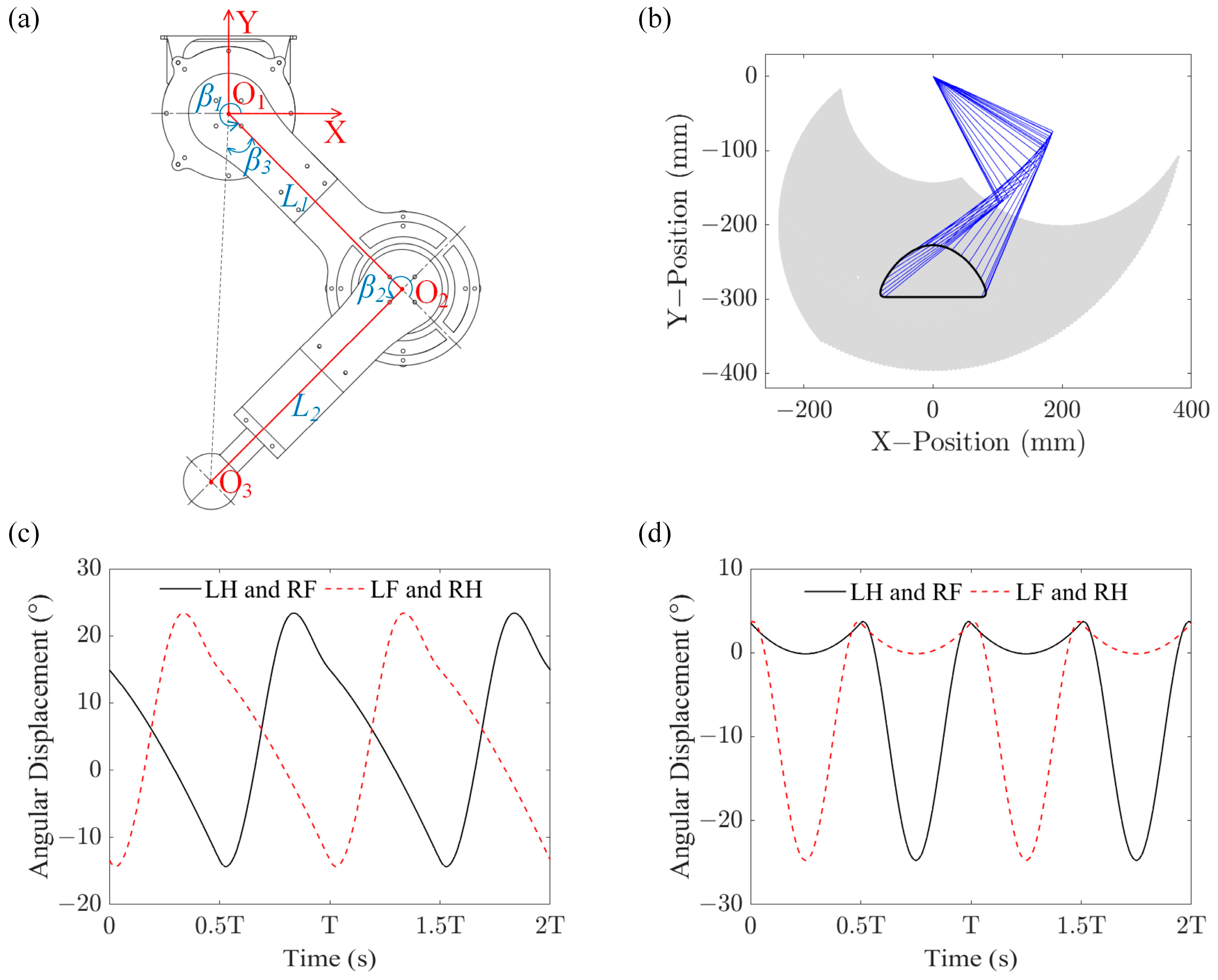
2.4. Gait Analysis
2.5. Foot Trajectory
3. Experimental Evaluation of the Rotary Joint and Integrated Quadruped Robot
3.1. Torque Evaluation of the Soft–Rigid Hybrid Rotary Joint
3.2. System Integration
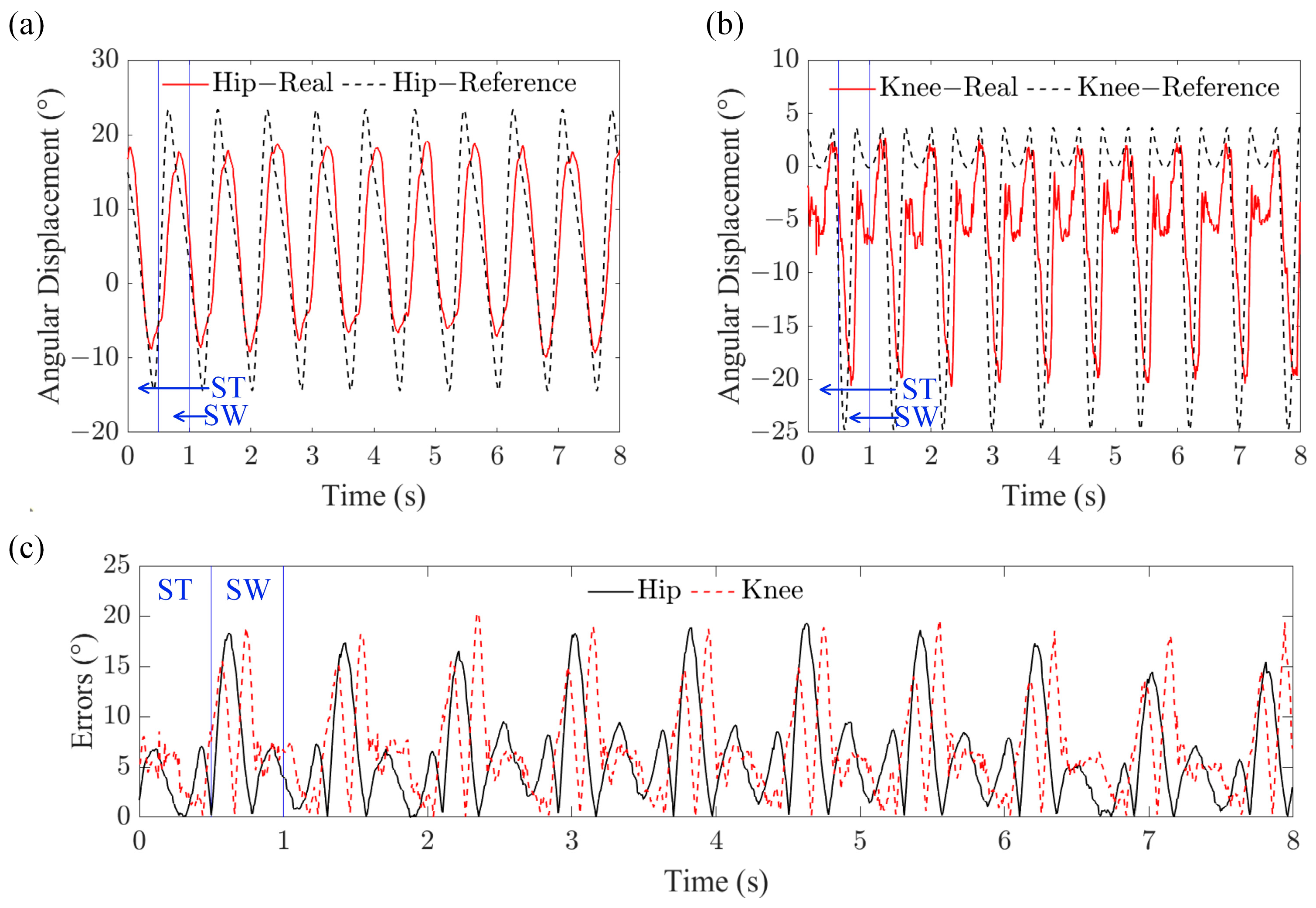
3.3. Trotting Gait Test of the Quadruped Robot
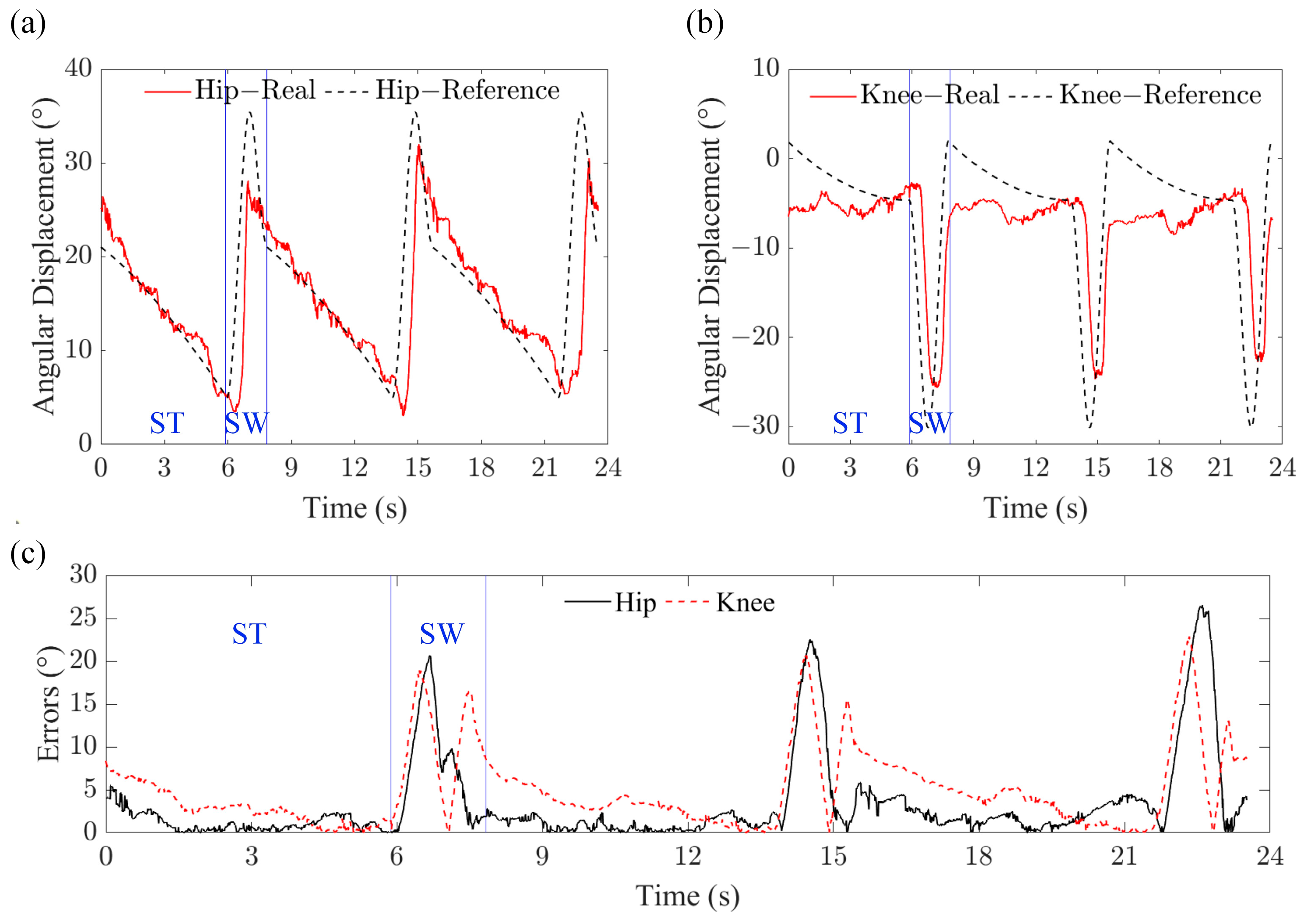
3.4. Walking Gait Test of the Quadruped Robot
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taheri, H.; Mozayani, N. A study on quadruped mobile robots. Mech. Mach. Theory 2023, 190, 105448. [Google Scholar] [CrossRef]
- Guzman, R.; Navarro, R.; Ferre, J.; Moreno, M. Rescuer: Development of a modular chemical, biological, radiological, and nuclear robot for intervention, sampling, and situation awareness. J. Field Robot. 2016, 33, 931–945. [Google Scholar] [CrossRef]
- Kawatsuma, S.; Fukushima, M.; Okada, T. Emergency response by robots to Fukushima-Daiichi accident: Summary and lessons learned. Ind. Robot Int. 2012, 39, 428–435. [Google Scholar] [CrossRef]
- Tibrea, S.; Nance, T.; Kriikku, E. Robotics in hazardous environments-real deployments by the savannah river national lab. J. S. C. Acad. Sci. 2011, 9, 5. [Google Scholar]
- Ducros, C.; Hauser, G.; Mahjoubi, N.; Girones, P.; Boisset, L.; Sorin, A.; Jonquet, E.; Falciola, J.M.; Benhamou, A. RICA: A tracked robot for sampling and radiological characterization in the nuclear field. J. Field Robot. 2017, 34, 583–599. [Google Scholar] [CrossRef]
- Bogue, R. Robots in the offshore oil and gas industries: A review of recent developments. Ind. Robot Int. J. Robot. Res. Appl. 2020, 47, 1–6. [Google Scholar] [CrossRef]
- Biswal, P.; Mohanty, P.K. Development of quadruped walking robots: A review. Ain Shams Eng. J. 2021, 12, 2017–2031. [Google Scholar] [CrossRef]
- Byrd, J.S.; Devries, K.R. A six-legged telerobot for nuclear applications development. Int. J. Robot. Res. 1990, 9, 43–52. [Google Scholar] [CrossRef]
- Jang, Y.; Seol, W.; Lee, K.; Kim, K.S.; Kim, S. Development of quadruped robot for inspection of underground pipelines in nuclear power plants. Electron. Lett. 2022, 58, 234–236. [Google Scholar] [CrossRef]
- Hutter, M.; Gehring, C.; Jud, D.; Lauber, A.; Bellicoso, C.D.; Tsounis, V.; Hwangbo, J.; Bodie, K.; Fankhauser, P.; Bloesch, M. Anymal—A highly mobile and dynamic quadrupedal robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016. [Google Scholar]
- Ramezani, M.; Brandao, M.; Casseau, B.; Havoutis, I.; Fallon, M. Legged robots for autonomous inspection and monitoring of offshore assets. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2020. [Google Scholar]
- Zimroz, R.; Hutter, M.; Mistry, M.; Stefaniak, P.; Walas, K.; Wodecki, J. Why should inspection robots be used in deep underground mines? In Proceedings of the 27th International Symposium on Mine Planning and Equipment Selection-MPES 2018, Las Condes, Chile, 18–23 November 2019. [Google Scholar]
- Baines, R.; Kramer-Bottiglio, R. Turtle-like robot adapts its shape and behaviour to move in different environments. Nature 2022, 610, 283–289. [Google Scholar] [CrossRef]
- Tolleymichael, T.; Shepherdrobert, F.; Gallowaykevin, C.; Woodrobert, J.; Whitesidesgeorge, M. A resilient, untethered soft robot. Soft Robot. 2014, 1, 213–223. [Google Scholar]
- Drotman, D.; Jadhav, S.; Sharp, D.; Chan, C.; Tolley, M.T. Electronics-free pneumatic circuits for controlling soft-legged robots. Sci. Robot. 2021, 6, eaay2627. [Google Scholar] [CrossRef]
- Matia, Y.; Kaiser, G.H.; Shepherd, R.F.; Gat, A.D.; Lazarus, N.; Petersen, K.H. Harnessing nonuniform pressure distributions in soft robotic actuators. Adv. Intell. Syst. 2023, 5, 2200330. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [PubMed]
- Drotman, D.; Jadhav, S.; Karimi, M.; De Zonia, P.; Tolley, M.T. 3D printed soft actuators for a legged robot capable of navigating unstructured terrain. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Marina Bay Sands, Singapore, 29 May–3 June 2017. [Google Scholar]
- Zou, J.; Lin, Y.; Ji, C.; Yang, H. A reconfigurable omnidirectional soft robot based on caterpillar locomotion. Soft Robot. 2018, 5, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Drotman, D.; Ishida, M.; Jadhav, S.; Tolley, M.T. Application-driven design of soft, 3-D printed, pneumatic actuators with bellows. IEEE/ASME Trans. Mechatron. 2018, 24, 78–87. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, X.; Xu, B.; Zhao, J. A new spiral-type inflatable pure torsional soft actuator. Soft Robot. 2018, 5, 527–540. [Google Scholar] [CrossRef] [PubMed]
- Nemiroski, A.; Shevchenko, Y.Y.; Stokes, A.A.; Unal, B.; Ainla, A.; Albert, S.; Compton, G.; Macdonald, E.; Schwab, Y.; Zellhofer, C. Arthrobots. Soft Robot. 2017, 4, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Wang, Y.; Liu, X.-J.; Zhao, H. Development of modular multi-degree-of-freedom hybrid joints and robotic flexible legs via fluidic elastomer actuators. Smart Mater. Struct. 2022, 31, 035034. [Google Scholar] [CrossRef]
- Sato, R.; Kazama, E.; Ming, A.; Shimojo, M.; Meng, F.; Liu, H.; Fan, X.; Chen, X.; Yu, Z.; Huang, Q. Design and control of robot legs with bi-articular muscle-tendon complex. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macao, China, 5–8 December 2017. [Google Scholar]
- Yamada, Y.; Nishikawa, S.; Shida, K.; Niiyama, R.; Kuniyoshi, Y. Neural-body coupling for emergent locomotion: A musculoskeletal quadruped robot with spinobulbar model. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Verrelst, B.; Ham, R.V.; Vanderborght, B.; Daerden, F.; Lefeber, D.; Vermeulen, J. The pneumatic biped “Lucy” actuated with pleated pneumatic artificial muscles. Auton. Robot. 2005, 18, 201–213. [Google Scholar] [CrossRef]
- Gorissen, B.; Milana, E.; Baeyens, A.; Broeders, E.; Christiaens, J.; Collin, K.; Reynaerts, D.; De Volder, M. Hardware sequencing of inflatable nonlinear actuators for autonomous soft robots. Adv. Mater. 2019, 31, 1804598. [Google Scholar] [CrossRef] [PubMed]
- Tsujita, K.; Kobayashi, T.; Masuda, T. Feasibility study on stability of gait patterns with changeable body stiffness using pneumatic actuators in a quadruped robot. Adv. Robot. 2009, 23, 503–520. [Google Scholar] [CrossRef]
- Tsujita, K.; Kobayashi, T.; Inoura, T.; Masuda, T. Gait transition by tuning muscle tones using pneumatic actuators in quadruped locomotion. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008. [Google Scholar]
- Fukuoka, Y.; Habu, Y.; Inoue, K.; Ogura, S.; Mori, Y. Autonomous speed adaptation by a muscle-driven hind leg robot modeled on a cat without intervention from brain. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211044936. [Google Scholar] [CrossRef]
- Fukuoka, Y.; Komatsu, R.; Machii, K.; Yokota, M.; Tobe, M.; Ibrahim, A.N.; Fukui, T.; Habu, Y. Pace Running of a Quadruped Robot Driven by Pneumatic Muscle Actuators: An Experimental Study. Appl. Sci. 2022, 12, 4146. [Google Scholar] [CrossRef]
- Wait, K.W.; Goldfarb, M. A pneumatically actuated quadrupedal walking robot. IEEE/ASME Trans. Mechatron. 2013, 19, 339–347. [Google Scholar] [CrossRef]
- Althoefer, K. Antagonistic actuation and stiffness control in soft inflatable robots. Nat. Rev. Mater. 2018, 3, 76–77. [Google Scholar] [CrossRef]
- Yi, J.; Chen, X.; Song, C.; Zhou, J.; Liu, Y.; Liu, S.; Wang, Z. Customizable three-dimensional-printed origami soft robotic joint with effective behavior shaping for safe interactions. IEEE Trans. Robot. 2018, 35, 114–123. [Google Scholar] [CrossRef]
- Tondu, B.; Ippolito, S.; Guiochet, J.; Daidie, A. A seven-degrees-of-freedom robot-arm driven by pneumatic artificial muscles for humanoid robots. Int. J. Robot. Res. 2005, 24, 257–274. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, K. A Novel Torsional Actuator Augmenting Twisting Skeleton and Artificial Muscle for Robots in Extreme Environments. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xian, China, 30 May–5 June 2021. [Google Scholar]
- Rong, X.; Li, Y.; Ruan, J.; Li, B. Design and simulation for a hydraulic actuated quadruped robot. J. Mech. Sci. Technol. 2012, 26, 1171–1177. [Google Scholar] [CrossRef]
- Yang, K.; Li, Y.; Zhou, L.; Rong, X. Energy efficient foot trajectory of trot motion for hydraulic quadruped robot. Energies 2019, 12, 2514. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, X.; Han, J. Active model-based control for pneumatic artificial muscle. IEEE Trans. Ind. Electron. 2016, 64, 1686–1695. [Google Scholar] [CrossRef]
- Duong, M.-D.; Pham, Q.-T.; Vu, T.-C.; Bui, N.-T.; Dao, Q.-T. Adaptive fuzzy sliding mode control of an actuator powered by two opposing pneumatic artificial muscles. Sci. Rep. 2023, 13, 8242. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Sun, N.; Yang, T.; Fang, Y. Reinforcement learning-based prescribed performance motion control of pneumatic muscle actuated robotic arms with measurement noises. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 1801–1812. [Google Scholar] [CrossRef]
- Hutter, M.; Remy, C.D.; Hoepflinger, M.A.; Siegwart, R. Scarleth: Design and control of a planar running robot. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Ruppert, F.; Badri-Spröwitz, A. Learning plastic matching of robot dynamics in closed-loop central pattern generators. Nat. Mach. Intell. 2022, 4, 652–660. [Google Scholar] [CrossRef]
- Carbone, G. Stiffness analysis and experimental validation of robotic systems. Front. Mech. Eng. 2011, 6, 182–196. [Google Scholar] [CrossRef]
- Vanderborght, B.; Van Ham, R.; Lefeber, D.; Sugar, T.G.; Hollander, K.W. Comparison of mechanical design and energy consumption of adaptable, passive-compliant actuators. Int. J. Robot. Res. 2009, 28, 90–103. [Google Scholar] [CrossRef]
- Vuong, N.-D.; Li, R.; Chew, C.-M.; Jafari, A.; Polden, J. A novel variable stiffness mechanism with linear spring characteristic for machining operations. Robotica 2017, 35, 1627–1637. [Google Scholar] [CrossRef]
- Mitsantisuk, C.; Ohishi, K.; Katsura, S. Variable mechanical stiffness control based on human stiffness estimation. In Proceedings of the 2011 IEEE International Conference on Mechatronics, Istanbul, Turkey, 13–15 April 2011. [Google Scholar]
- Zhang, L.; Li, Z.; Yang, C. Adaptive neural network based variable stiffness control of uncertain robotic systems using disturbance observer. IEEE Trans. Ind. Electron. 2016, 64, 2236–2245. [Google Scholar] [CrossRef]
- Petit, F.; Albu-Schäffer, A. Cartesian impedance control for a variable stiffness robot arm. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Jiang, Z.; Liu, C.; Zhang, K. A Variable Stiffness Continuum Parallel Manipulator With 3D Printed Pneumatic Artificial Muscles. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, St. Louis, MI, USA, 14–17 August 2022. [Google Scholar]
- Hyun, D.J.; Seok, S.; Lee, J.; Kim, S. High speed trot-running: Implementation of a hierarchical controller using proprioceptive impedance control on the MIT Cheetah. Int. J. Robot. Res. 2014, 33, 1417–1445. [Google Scholar] [CrossRef]
- Wensing, P.M.; Wang, A.; Seok, S.; Otten, D.; Lang, J.; Kim, S. Proprioceptive actuator design in the mit cheetah: Impact mitigation and high-bandwidth physical interaction for dynamic legged robots. IEEE Trans. Robot. 2017, 33, 509–522. [Google Scholar] [CrossRef]







| Length of the thigh L1 | 200 mm |
| Length of the shank L2 | 220 mm |
| Motion range of the hip joint | [240°, 360°] |
| Motion range of the knee joint | [210°, 330°] |
| Maximum torque of the hip joint | 5.83 Nm |
| Maximum torque of the knee joint | 5.83 Nm |
| Distance between front and rear legs L3 | 410 mm |
| Distance between left and right legs L4 | 250 mm |
| Weight of the robot leg | 1080 g |
| Weight of the quadruped robot | 5000 g |
| Gait | (LH, LF, RF, RH) | |
|---|---|---|
| Crawling | 0.8 | (0, 0.75, 0.25, 0.5) |
| Walking | 0.75 | (0, 0.75, 0.25, 0.5) |
| Trotting | 0.5 | (0, 0.5, 0, 0.5) |
| Pacing | 0.5 | (0, 0, 0.5, 0.5) |
| Bounding | 0.4 | (0, 0.5, 0.5, 0) |
| Robot | Type | Speed (BL/s) | Advantages | Limitations |
|---|---|---|---|---|
| Proposed robot | Soft–rigid hybrid | 0.36 | High locomotion speed, compact structure, and simplified modeling. | Difficulty in controller development for torque and stiffness control. |
| Untethered robot [14] | Soft | 0.0077 | Adaptability to adverse environments, including water and fire. | Slow locomotion speed; difficulty in kinematic modeling. |
| Hexapod robot [16] | Soft | 0.05 | 2D workspace of the feet. | Movement in one direction; difficulty in kinematic modeling. |
| Multigait robot [17] | Soft | 0.053 | Simple design and control to generate mobility. | Difficulties in predictive modeling and motion control. |
| Modular robot [19] | Soft | 0.033 | Capable of translational motion and rotation. | Low motion accuracy. |
| Hexapod robot [22] | Soft–rigid hybrid | Around 0.26 | Simplicity, lightweight design, and scalability. | Lack of sufficient traction; difficulty in controlling elastomeric balloons. |
| Walking robot [27] | Soft–rigid hybrid | 0.05 | No need for complex valves or bulky tethers. | Preprogrammed by hardware; difficult to move on rough surfaces. |
| Quadruped robot [31] | Soft–rigid hybrid | Around 1.2 | Adaption to speed variation; stable pace running. | Complicated structure. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Wang, Y.; Zhang, K. Development of a Pneumatically Actuated Quadruped Robot Using Soft–Rigid Hybrid Rotary Joints. Robotics 2024, 13, 24. https://doi.org/10.3390/robotics13020024
Jiang Z, Wang Y, Zhang K. Development of a Pneumatically Actuated Quadruped Robot Using Soft–Rigid Hybrid Rotary Joints. Robotics. 2024; 13(2):24. https://doi.org/10.3390/robotics13020024
Chicago/Turabian StyleJiang, Zhujin, Yan Wang, and Ketao Zhang. 2024. "Development of a Pneumatically Actuated Quadruped Robot Using Soft–Rigid Hybrid Rotary Joints" Robotics 13, no. 2: 24. https://doi.org/10.3390/robotics13020024
APA StyleJiang, Z., Wang, Y., & Zhang, K. (2024). Development of a Pneumatically Actuated Quadruped Robot Using Soft–Rigid Hybrid Rotary Joints. Robotics, 13(2), 24. https://doi.org/10.3390/robotics13020024







