Kinematic Reliability of Manipulators Based on an Interval Approach †
Abstract
1. Introduction
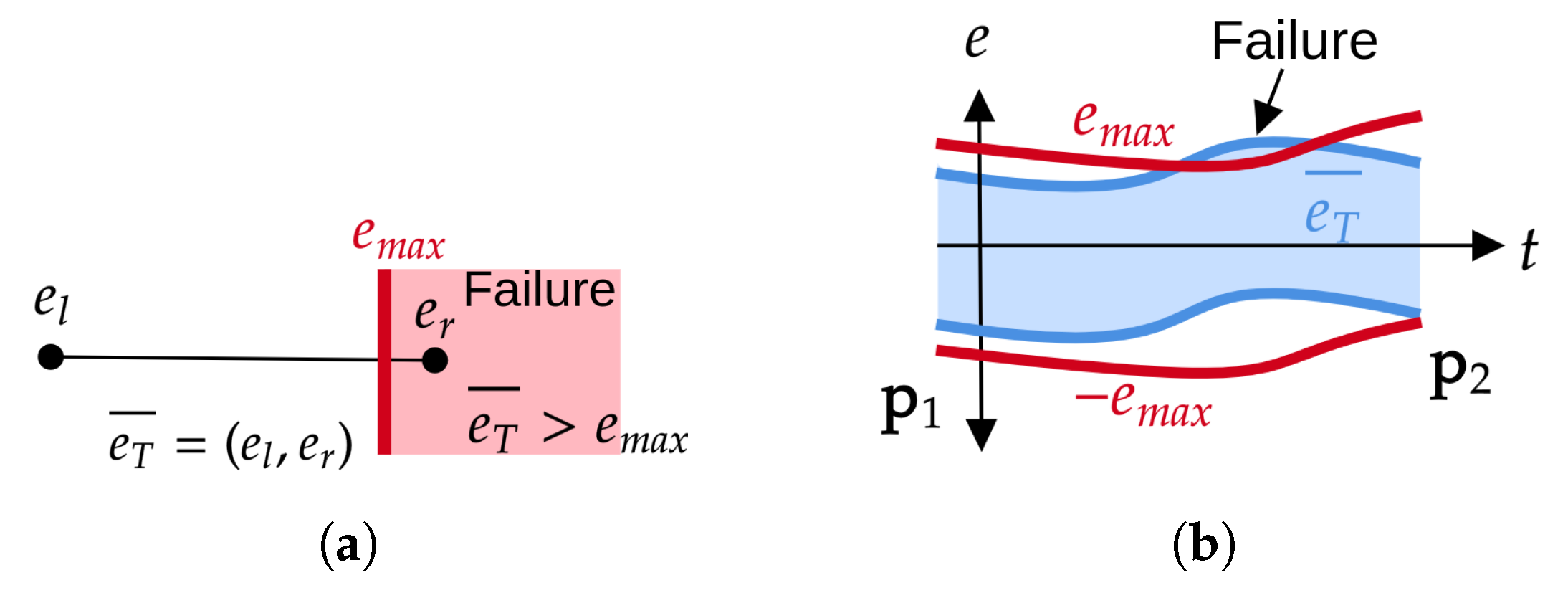
2. Interval Analysis and Reliability
3. Case Studies
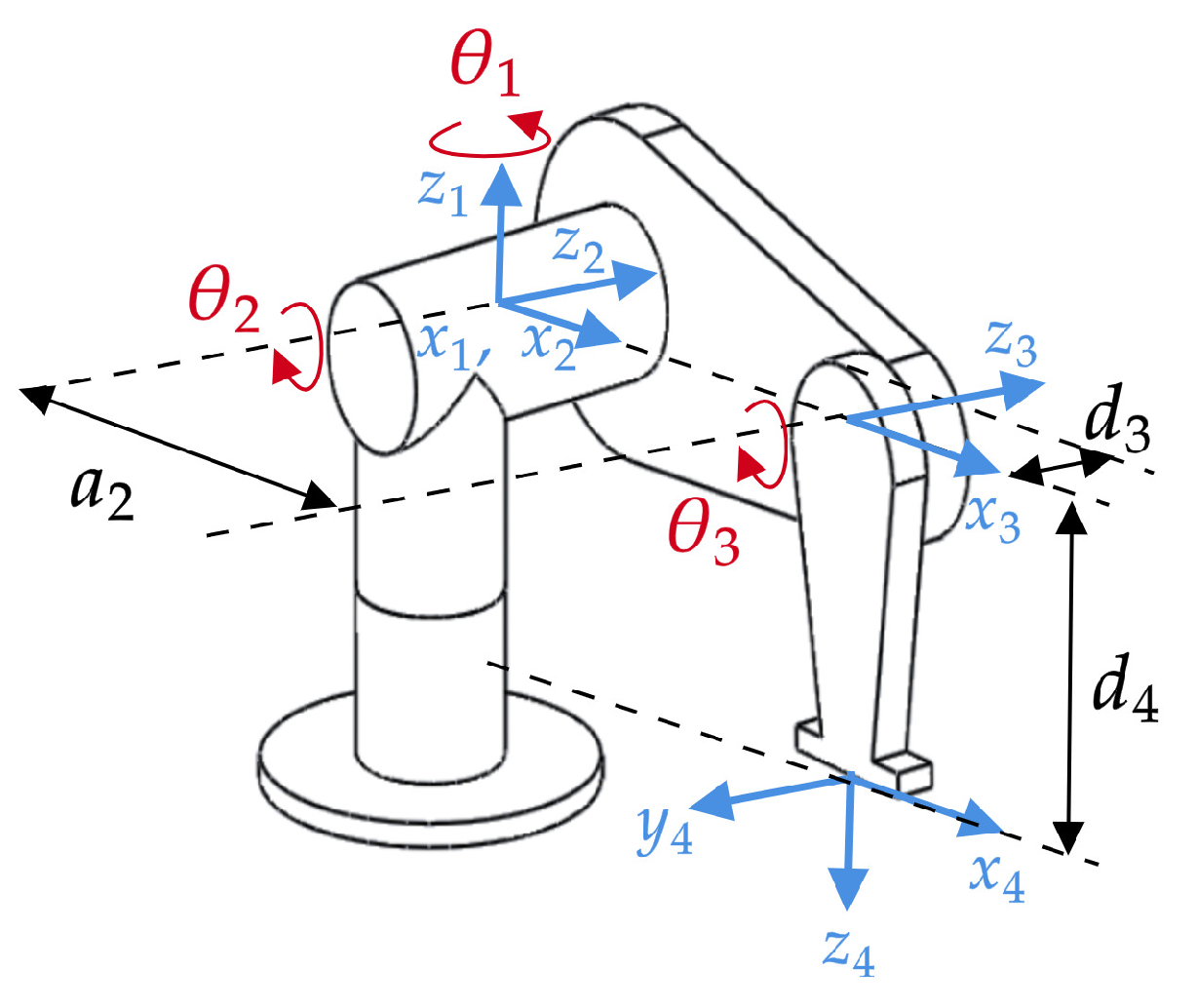
3.1. 3R Serial Manipulator Subjected to Clearances
3.1.1. Application of the Interval Approach
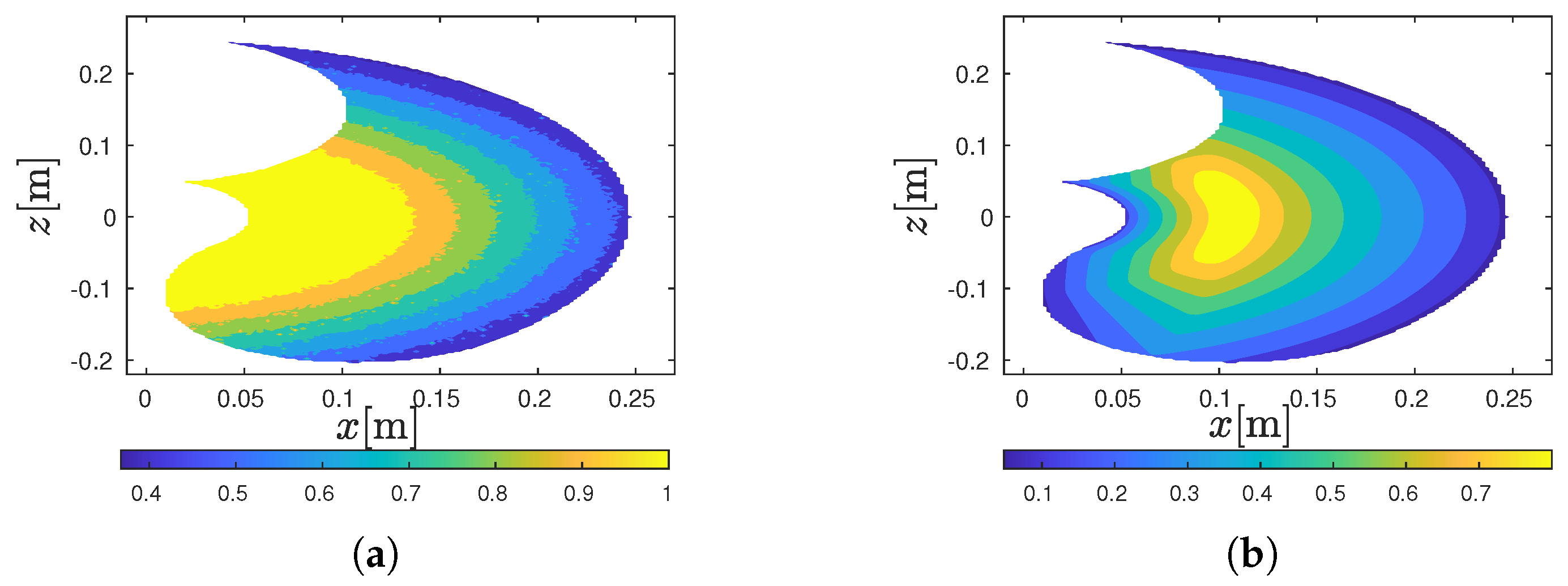
3.1.2. Results
3.2. Delta Parallel Manipulator
3.2.1. Application of the Interval Approach
3.2.2. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Lara-Molina, F.A.; Dumur, D. Global performance criterion of robotic manipulator with clearances based on reliability. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 624. [Google Scholar] [CrossRef]
- Zhan, Z.; Zhang, X.; Jian, Z.; Zhang, H. Error modelling and motion reliability analysis of a planar parallel manipulator with multiple uncertainties. Mech. Mach. Theory 2018, 124, 55–72. [Google Scholar] [CrossRef]
- Cui, G.; Zhang, H.; Zhang, D.; Xu, F. Analysis of the kinematic accuracy reliability of a 3-DOF parallel robot manipulator. Int. J. Adv. Robot. Syst. 2015, 12, 15. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, S.; Wu, J.; Wang, F.; Han, X. Kinematic trajectory accuracy reliability analysis for industrial robots considering intercorrelations among multi-point positioning errors. Reliab. Eng. Syst. Saf. 2023, 229, 108808. [Google Scholar] [CrossRef]
- Pandey, M.D.; Zhang, F. System reliability analysis of the robotic manipulator with random joint clearances. Mech. Mach. Theory 2012, 58, 137–152. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X. Kinematic reliability analysis of robotic manipulator. J. Mech. Des. 2020, 142, 44502. [Google Scholar] [CrossRef]
- Zhang, J.; Du, X. Time-dependent reliability analysis for function generation mechanisms with random joint clearances. Mech. Mach. Theory 2015, 92, 184–199. [Google Scholar] [CrossRef]
- Kim, J.; Song, W.J.; Kang, B.S. Stochastic approach to kinematic reliability of open-loop mechanism with dimensional tolerance. Appl. Math. Model. 2010, 34, 1225–1237. [Google Scholar] [CrossRef]
- Lara-Molina, F.A.; Dumur, D. A fuzzy approach for the kinematic reliability assessment of robotic manipulators. Robotica 2021, 39, 2095–2109. [Google Scholar] [CrossRef]
- Faes, M.; Moens, D. Recent trends in the modeling and quantification of non-probabilistic uncertainty. Arch. Comput. Methods Eng. 2020, 27, 633–671. [Google Scholar] [CrossRef]
- Kang, R.; Zhang, Q.; Zeng, Z.; Zio, E.; Li, X. Measuring reliability under epistemic uncertainty: Review on non-probabilistic reliability metrics. Chin. J. Aeronaut. 2016, 29, 571–579. [Google Scholar] [CrossRef]
- Nikolaidis, E.; Ghiocel, D.M.; Singhal, S. Engineering Design Reliability Handbook; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Chang, Q.; Zhou, C.; Wei, P.; Zhang, Y.; Yue, Z. A new non-probabilistic time-dependent reliability model for mechanisms with interval uncertainties. Reliab. Eng. Syst. Saf. 2021, 215, 107771. [Google Scholar] [CrossRef]
- Yang, C.; Lu, W.; Xia, Y. Positioning accuracy analysis of industrial robots based on non-probabilistic time-dependent reliability. IEEE Trans. Reliab. 2023, 73, 608–621. [Google Scholar] [CrossRef]
- Tang, Z.; Peng, J.; Sun, J.; Meng, X. Non-probabilistic reliability analysis of robot accuracy under uncertain joint clearance. Machines 2022, 10, 917. [Google Scholar] [CrossRef]
- Pritschow, G.; Eppler, C.; Garber, T. Influence of the dynamic stiffness on the accuracy of PKM. In Proceedings of the Chemnitz Parallel Kinematic Seminar, Chemnitz, Germany, 23–25 April 2002; pp. 313–333. [Google Scholar]
- Rao, S.; Bhatti, P. Probabilistic approach to manipulator kinematics and dynamics. Reliab. Eng. Syst. Saf. 2001, 72, 47–58. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Evolutionary algorithms and their applications to engineering problems. Neural Comput. Appl. 2020, 32, 12363–12379. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V. Comparison of three gorithms: GA, PSO, and DE. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [Google Scholar]
- Xiang, W.; Yan, S. Dynamic analysis of space robot manipulator considering clearance joint and parameter uncertainty: Modeling, analysis and quantification. Acta Astronaut. 2020, 169, 158–169. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, D.; Li, Z. Accuracy analysis of parallel manipulators with joint clearance. J. Mech. Des. 2009, 131, 11013. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Erkaya, S.; Uzmay, I. Experimental investigation of joint clearance effects on the dynamics of a slider-crank mechanism. Multibody Syst. Dyn. 2010, 24, 81–102. [Google Scholar] [CrossRef]
- Williams, R.L.; Albus, J.S.; Bostelman, R.V. 3D Cable-Based Cartesian Metrology System. J. Robot. Syst. 2004, 21, 237–257. [Google Scholar] [CrossRef]
- Williams, R.L., II. The Delta Parallel Robot: Kinematics Solutions. 2016. Available online: https://people.ohio.edu/williams/html/PDF/DeltaKin.pdf (accessed on 4 September 2024).
- Rackwitz, R. Practical Probabilistic Approach to Design. In Bulletin No. 112; Comite European du Beton: Paris, France, 1976. [Google Scholar]









| j | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | ||
| 3 | 0 | |||
| 4 | 0 | 0 |
| max | ||||||||
| (a) | (0, 0.0012) | 0.0011 | 1.0000 | 1.0000 | 5997 | |||
| (b) | (0, 0.0020) | 0.0017 | 0.7600 | 0.9999 | 5998 | |||
| (c) | (0, 0.0021) | 0.0019 | 0.7058 | 0.9990 | 5998 | |||
| (d) | (0, 0.0022) | 0.0020 | 0.6809 | 0.9973 | 5998 | |||
| (e) | (0, 0.0021) | 0.0019 | 0.7129 | 0.9990 | 4440 | |||
| (f) | (0, 0.0014) | 0.0013 | 1.0000 | 1.0000 | 5998 | |||
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Value [m] | 0.567 | 0.076 | 0.524 | 1.244 | 0.164 | 0.327 | 0.022 | 0.044 |
| (a) | 0.8652 | 1.0000 | 1.0000 | 2215 | 100,000 | 117 |
| (b) | 0.5939 | 0.9987 | 0.9989 | 2407 | 100,000 | 156 |
| (c) | 0.5928 | 0.9985 | 0.9989 | 2401 | 100,000 | 156 |
| (d) | 0.7986 | 0.9999 | 0.9999 | 2409 | 100,000 | 91 |
| (e) | 0.7793 | 1.0000 | 1.0000 | 2412 | 100,000 | 260 |
| (f) | 0.7807 | 1.0000 | 1.0000 | 2031 | 100,000 | 260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara-Molina, F.A.; Gonçalves, R.S. Kinematic Reliability of Manipulators Based on an Interval Approach. Robotics 2024, 13, 155. https://doi.org/10.3390/robotics13110155
Lara-Molina FA, Gonçalves RS. Kinematic Reliability of Manipulators Based on an Interval Approach. Robotics. 2024; 13(11):155. https://doi.org/10.3390/robotics13110155
Chicago/Turabian StyleLara-Molina, Fabian Andres, and Rogério Sales Gonçalves. 2024. "Kinematic Reliability of Manipulators Based on an Interval Approach" Robotics 13, no. 11: 155. https://doi.org/10.3390/robotics13110155
APA StyleLara-Molina, F. A., & Gonçalves, R. S. (2024). Kinematic Reliability of Manipulators Based on an Interval Approach. Robotics, 13(11), 155. https://doi.org/10.3390/robotics13110155







