Abstract
This study aims to provide a comprehensive critical review of the existing body of evidence pertaining to gait rehabilitation. It also seeks to introduce a systematic approach for the development of innovative design solutions in this domain. The field of gait rehabilitation has witnessed a surge in the development of novel robotic devices. This trend has emerged in response to limitations observed in most commercial solutions, particularly regarding their high costs. Consequently, there is a growing need to explore more cost-effective alternatives and create opportunities for greater accessibility. Within the realm of cost-effective options, linkage-based gait trainers have emerged as viable alternatives, prompting a thorough examination of this category, which is carried out in this work. Notably, there is a wide heterogeneity in research approaches and presentation methods. This divergence has prompted discourse regarding the standardization of key elements relevant to the proposals of new linkage-based devices. As a result, this study proposes a comprehensive and standardized design process and offers a brief illustration of the application of this design process through the presentation of a potential new design.
1. Introduction
Gait is a very important part of our day-to-day activities since it contributes greatly to our independence and quality of life [1]. A considerable number of different health conditions can negatively impact gait, namely stroke, spinal cord injury, traumatic brain injury, Parkinson’s disease, cerebral palsy, and many more [2]. At the same time, with scientific advances providing better health outcomes, life expectancy is becoming higher, and the elderly portion of the population is increasing globally [3]. Hence, chronic diseases must be added to the list of conditions that require some level of rehabilitation, including gait rehabilitation. Recent studies show that the global need for rehabilitation has already increased by 63% from 1990 to 2019 [4], and therefore a growing share of the population will need interventions that improve their abilities, including gait ability, demonstrating the importance of gait rehabilitation for health systems worldwide.
Locomotor training is an important rehabilitation component for recovering gait function after a neurologic injury or disease. Its main objective is to retrain the patient’s nervous system, seeking to restore motor skills associated with standing, posture, walking, and mobility. Based on neurorehabilitation principles, it aims to drive neural plasticity, using a task-specific approach [5]. Significant research efforts have been made lately to find meaningful and effective rehabilitation strategies to both allow better treatment outcomes and reach a larger portion of the population burdened with mobility impairments. However, despite many technological solutions and advancements, only one in eight people undergoing gait rehabilitation following a stroke can achieve independence in walking [6], and the quality of life achieved at the end of rehabilitation was found to not be long-lasting [7]. This ephemeral aspect of improvements from gait rehabilitation is supported by a review of studies evaluating electromechanical gait training coupled with physiotherapy. They found that improvements in independence in walking were not long-lasting but had low evidence quality and therefore required additional investigation [6]. This same review found that walking velocity also increased right after the end of the intervention phase but not at the follow-up phase (mean follow-up period ranging from 18 weeks to 22.3 weeks), but the same uncertainty of the conclusion from independence in walking applies.
Furthermore, costs are also an important aspect of gait rehabilitation strategies, in conjunction with a rising burden on therapists caused by an ever-increasing segment of the population demanding these health services. Without special equipment and structure, gait therapy can be particularly burdensome on therapists, requiring, in some cases, up to four professionals to perform a rehabilitation task routine [8]. Studies have also been conducted to assess the cost-effectiveness of some robotic devices compared to conventional gait therapy. In [9], a comparison between conventional training and overground robotic training was performed using a cohort study of spinal cord injury (SCI) patients from four different sites. Its results have shown more cost-effectiveness for each approach under different conditions: if the patient had an incomplete spinal cord injury, conventional training was most cost-effective. On the other hand, if the patient had a complete spinal cord injury, the most cost-effective approach would be overground robotic training. Concerns regarding a more widespread adoption of new therapies and robotic devices were also raised, emphasizing the need for cost-competitive solutions to really provide a positive impact across health systems [10].
There are different conceptualizations for a device architecture intended for gait training and gait rehabilitation. Motorized exoskeletons (wearable or stationary) and motorized end-effector types of devices are among the most adopted and tested in clinical trials. Since they need to employ expensive equipment and embedded technology, their asking price can be quite high, creating an obstacle to mass adoption. Linkage-based devices could be an option to reduce degrees of freedom (DoFs), reducing complexity and consequently reducing total cost to provide more affordable alternatives—in some cases, even without motorization. However, to get the best results from a proposed gait therapy, either by using highly technological devices or by using simpler and more cost-effective alternatives, doing so in accordance with motor learning principles is of paramount importance. Some of these principles are weight support on lower limbs to the maximum level possible, improving sensory inputs, improving kinematics for all motor tasks, improving rehabilitation strategies, and curtailing compensatory movements [5]. Other important principles listed in the literature are an early therapy start, guidance, intensity, similarity between the exercised task and the task to be learned, practice variability, motivation, and part-practice or whole-practice exercises [11].
Many reviews related to gait rehabilitation and gait devices’ technology have been performed over the years, as reported, for example, in [12,13,14]. They attempt to address important questions and assess the effectiveness of these devices as interventions in rehabilitation tasks [6]. However, the absence of some technical details and experimental data (for example, kinematic accuracy or the control strategy used during randomized controlled trials) makes it difficult to identify specific unique features on some gait trainers. As a result, the abovementioned trials proposed the grouping of different devices under the same category, such as, for example, grouping all exoskeleton devices in a single category even if they might have different control strategies. This issue is mentioned in [15], where a review of control strategies is performed but a lack of standardization in experimental protocols is found, which ultimately leads to a low level of confidence in the effectiveness of different control techniques in the clinical outcomes of gait rehabilitation.
Another characteristic of the existing review papers is that they were mostly focused on complex robotic devices, giving their main attention to the control aspects [13,15] or to the required motors/sensors [16,17], or with a focus on specific hardware features, as in the case of cable-driven devices [12]. The aim of this paper is to complement the current literature with a specific focus on linkage-based devices, evaluate the present research on this topic, and discuss and propose a specific design process that can provide a standardization of the mechanism design process for linkage-based gait trainers (references include experimental and clinical data, which provide the starting requirements for the proposed design procedure). Hence, the present review seeks to contextualize and present current gait trainers, provide a research overview of linkage-based devices intended for gait rehabilitation, and critically appraise current research, pointing out new opportunities for advancement and new research directions. It is divided as follows: Section 2 presents an overview of devices, and Section 3 presents the methodology for searching existing literature for linkage-based devices. Section 4 starts by introducing the requirements of a linkage-based gait trainer and displays the search results divided by topology and configuration. Section 5 discusses the current research and some opportunities related to common design elements and comparability issues. Section 6 presents a possible design following a proposed methodology and introduces some recommendations for future research. Section 7 concludes this review.
2. Current Gait Training Devices
Even with many design proposals aiming to facilitate and improve gait rehabilitation, only a portion arrives to patients and produces rehabilitation outcomes to be later analyzed, as in [6]. The devices employed are primarily complex robotic devices, using as their prime mover either an exoskeleton or an end-effector architecture with multiple degrees of freedom, embedded electronics, and computerized systems that provide different control strategies to be used in therapy. Often, they count on an active (motorized) body weight support system [18,19], configuring a whole rehabilitation system. These devices can be divided into four categories [6]: exoskeleton, end-effector, mobile-powered, and ankle joint assist devices. In addition to those categories, we included cable-driven devices, which have not been through the same extensive testing as the previous four categories but are worthy of note since they can provide important advantages, like not requiring perfect joint alignment and offering adaptability to different users and more versatility depending on the number of cables [12].
2.1. Exoskeleton
The Lokomat (Figure 1 reprinted with permission from ref. [20]. Copyright 2023 Elsevier) is one of the most well-known and extensively tested robotic gait trainers. It is a driven gait orthosis using a body weight support system (BWSS) that uses a treadmill as a gait surface and that can be integrated into serious games and biofeedback [20]. It possesses a drive system to move an exoskeleton structure attached to the user’s lower limbs bilaterally and optionally includes a pelvis module. This module enables gait training that is not constrained in the sagittal plane only, thus permitting balance training and a more realistic gait [21]. The exoskeleton’s movements are performed at the hip and knee joints, while the ankle joint is passively supported in the swing phase by foot lifters. The BWSS is a mechatronic system designed to provide unloading to the user and can respond dynamically during the gait cycle, seeking to maintain a consistent and accurate unloading force [22,23]. For control strategies during gait training, there are different techniques that can be used, such as challenge-based control, assistive strategies, or adaptive control [20,24]. It is equipped to use serious games [25] and biofeedback [26,27].

Figure 1.
The Lokomat, showing its orthosis and the body weight support with a user. Reprinted with permission from ref. [20]. Copyright 2023 Elsevier
2.2. End-Effector
The Gait Trainer II (GT II) [28] is an example of an end-effector type of device (Figure 2). It is based on the concept of performing a gait-like movement by guiding the patient’s feet, which are positioned on footplates. It does not restrain the user’s lower limbs but instead guides the patient’s feet through a planar trajectory, like what a therapist would do. This movement is achieved through a crank and rocker gear system that follows the ratio of 60 percent stance to 40 percent swing phases, following the natural gait proportion [29,30,31]. Attached to this system are two cranks controlling the vertical and horizontal positions of the center of mass (CoM). It also possesses a body weight support system (harness) and can be adjusted to different patients by using different gear sizes.
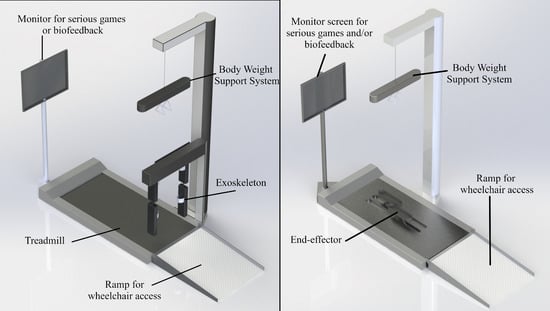
Figure 2.
A CAD representation for stationary gait trainers. At the (left), an exoskeleton-based gait trainer (similar to Lokomat) and to the (right) an end-effector-based gait trainer (similar to GT II).
2.3. Mobile Powered
Ekso is a mobile, powered orthosis composed of a fitted metal brace, a solid torso, rechargeable batteries, motors, and a computer. It is intended to be used with a walking aid (cane, crutch, or walker). The motorized joints are the hip and knee ones, while the ankle joint is a passive one [32]. It is intended to be used in rehabilitation institutions under therapist supervision and has the capabilities of sitting, standing, walking, and turning. The patient can initiate gait through a weight shift between legs, or the therapist can initiate it by using a handheld controller. Additionally, in the event of a power failure, it behaves like a passive leg brace, letting the hip joints free but locking the knee joints as a safety feature [33].
2.4. Ankle Joint Assist
The Anklebot (Figure 3) is a device intended, as the name says, to assist the ankle joint in preventing foot drop, which is a common complication in patients following stroke, multiple sclerosis, and spinal cord injury [34]. The ankle joint is responsible for important gait tasks like shock absorption, equilibrium, and serving as a controlling joint of the foot, which is the direct interface to the ground. The Anklebot aids in two of the ankle’s degrees of freedom: plantar/dorsiflexion and inversion/eversion. Brushless DC motors are responsible for actuation, and sensors (encoders) have the task of giving position information and feedback to the controller that yield some control modes, namely impedance control, proportional gain control, and derivative gain control. In addition to that, the Anklebot can be used as a clinical measurement tool [35,36].

Figure 3.
A person using the MIT-Anklebot on a split treadmill.
2.5. Cable-Driven
Cable-driven types of devices have some different architectures and therefore can be subclassified accordingly: serial exoskeleton, serial end-effector, parallel exoskeleton, and parallel end-effector [12]. They can bring the same benefits as robotic rehabilitation devices, with the additional advantage of being lightweight, simpler, and possible to use at home.
ROPES [37] is the acronym for RObotic Physical Exercise and System, describing a system for lower limb rehabilitation that treats hip, knee, and ankle joints. It is a serial-exoskeleton type of cable-driven device composed of a controller, seven motors, cables, linear springs, torsional springs, cuffs, a leg frame, and a fixed frame. It provides position-based impedance and trajectory control [38]. Movements can be performed in the sagittal plane and the frontal plane.
A broader view of the discussed gait devices can be seen in Table 1. Several of these devices were reviewed in systematic literature reviews like [6], with more focus on the possible benefits provided and evidence quality and less on evaluating their design and technical details. They were predominantly evaluated in randomized controlled trials (except for cable-driven devices, which do not appear in such trials at this point) with two arms (a control group and an experimental group). Their primary outcomes involved clinical gait measures like walking ability (FACs, functional ambulation categories), walking velocity, step length, and other clinical gait and rehabilitation measures.

Table 1.
Electromechanical gait devices.
The literature clearly reports that actual gait trainers still do not have proper characteristics for a wide market implementation, especially due to high complexity and costs. Linkage-based gait trainers can provide improvements in terms of cost reduction and simplicity of use. Therefore, there is high interest in designing novel linkage-based gait trainers. However, the design of linkage-based gait trainers is quite complex, requiring a very careful and systematic mechanism design procedure to consider a wide range of design variables, topologies, requirements, and constraints. The aim of this work is to review current designs and provide a systematic and standardized approach to generate new designs of linkage-based gait trainers according to specific needs.
3. Search Methodology
The literature on the addressed topic is very wide. Therefore, we decided to adopt a systematic search methodology, as described in the present section (Figure 4).
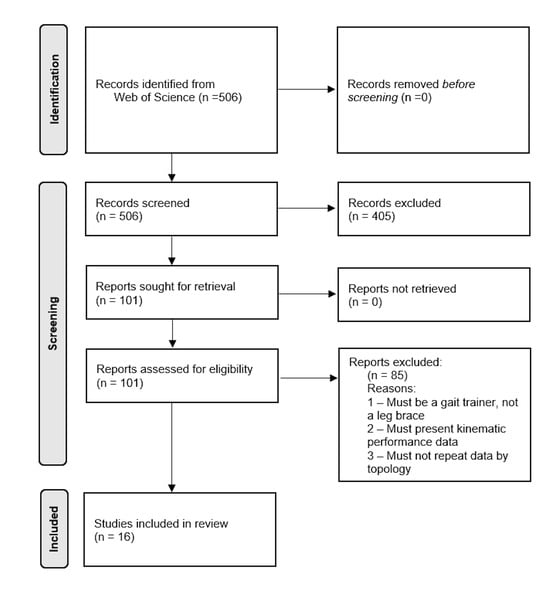
Figure 4.
A PRISMA-style [54] flowchart for the proposed literature review process.
For this review, papers were selected from the Web of Science with the following keywords (topics): gait, rehabilitation, linkage, gait trainer, four bar, five bar, six bar, seven bar, eight bar, and spatial linkage. Initial searches showed 506 papers, which were then refined by excluding papers unrelated to gait rehabilitation and/or gait trainers, resulting in a total of 101 papers. Then, papers were analyzed on a case-by-case basis for inclusion or exclusion in this review, with a stopping criterion after all topologies were represented.
The inclusion criteria are that the devices reported must have a function as a gait trainer, help guide the legs for performing a gait task (not a leg brace), and provide kinematic data. A device would also be excluded if it did not add information to the topology being represented in this review, besides those already selected. Current gait rehabilitation devices presented in the previous section have a higher degree of complexity, involving motorization and control systems, and tend to have higher costs, creating some difficulties towards broader adoption.
Many research efforts are being spent on making more affordable rehabilitation options that are at least as effective as the ones already presented briefly here. Amongst those devices, linkage-based devices (passive [55,56,57] or motorized) are noteworthy since they present the potential of guiding a kinematically similar movement to healthy gait and have received a lot of attention lately, with a diverse set of different propositions for gait training machines.
4. Linkage-Based Devices
There are many different choices to make when proposing a gait trainer. To keep motorization to a minimum or even allow manual actuation, the common option is to choose a closed-chain architecture with one degree of freedom. Other desirable characteristics for a gait trainer (valid not only for linkage-based devices but for any gait trainer) are listed below:
- Simplicity and low volume;
- Kinematic accuracy compared to human natural gait;
- Maximization of sensory inputs;
- Adaptability to different subjects.
A gait trainer, be it a fixed rehabilitation platform device or a mobile overground rehabilitation device, must consider space and weight constraints, which translate into topology simplicity and a low volume requirement (the smaller the number of links, the less space and device weight are required). Furthermore, to fulfill the objective of relearning gait and trying to take advantage of brain plasticity to achieve recovery [58], it is considered important to reproduce the gait pattern close to the natural gait pattern. Accordingly, for gait trainers, it is necessary to have some level of kinematic accuracy, even though a minimum level of accuracy is not yet known in terms of rehabilitation outcomes. Maximizing sensory inputs (such as ground contact forces) is important to motor learning [59] and can even be a predictor for recovery [60]. Also, the engineering solution must be flexible enough so that patients with different anthropometrical lengths and sizes can use it, and it must cost the least possible. The current literature on gait trainers provides a wide array of linkage-based devices, from the simplest four-bar closed chain to more complex devices such as an eight-bar or even spatial mechanisms. When using an end-effector approach, the focus is on guiding the ankle trajectory to reach kinematic similarity to a chosen baseline. Optimization methods and other synthesis techniques were used to reach the final dimensions and to decide which links should be adjustable so the desired flexibility criteria could be met. Another common characteristic is that the desired trajectory is usually made relative to the hip, meaning that the devices must move together with the hip joint, or the movement would be kinematically flawed and probably uncomfortable. The following subsections provide more details on these topologies.
4.1. Planar Four-Bar Linkages
A four-bar linkage (Figure 5) is a ubiquitous linkage used in many different applications. As the name says, there are four bars or links, each one united by a joint, often with the ground link omitted.
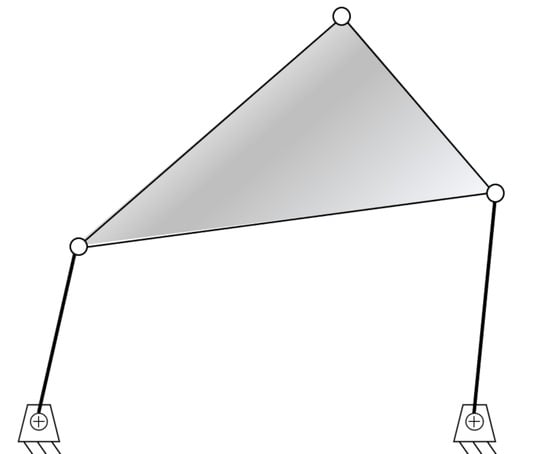
Figure 5.
A planar four-bar linkage.
Even within gait rehabilitation applications, the four-bar can be used in different forms to achieve different goals. In [61], the four-bar linkage was used as the main moving part of a device called RANK (Robotic ANKle), intended to prevent foot drop and aid walking. A comparison between gait trainers in [62] used a four-bar linkage to compare to six-bar and eight-bar linkages, using gait databases to build its kinematic baseline and performing evaluations regarding accuracy (root mean square error, RMSE) for both trajectory (path and timing) and path errors. The dimensional synthesis utilizes optimization to find the best mechanism variables for each topology (four-, six-, or eight-bar). The Linkage Design Gait Trainer (LGT) is a linkage-based gait trainer with a single degree of freedom (DoF). The four-bar linkage is coupled to a walking frame and guides the ankle joint as an end-effector type of device [63]. In [64], the linkage was synthesized using 50 points of a prescribed ankle trajectory. Another interesting proposal is made in [65], synthesizing a four-bar linkage without a baseline through topology optimization. A summary is presented at Table 2 below:

Table 2.
Four-bar linkages for gait rehabilitation.
4.2. Planar Five-Bar Linkages and Six Bar-Linkages
A five-bar linkage is proposed in [67] to guide a patient’s leg as a gait trainer. It consists of a combination of a 2R open chain with a 3R open chain and a pair of non-circular gears that connect the movement of the two cranks. For its synthesis, it used kinematic mapping for the rigid body guidance synthesis, using four predefined poses, achieving a posture error (angle difference) of 2.13° and a maximum error of 3.32 mm with a prototype. The motion baseline used was derived from kinematic data obtained from marker position measurements made at the knee joint and calf using a high-speed camera.
An exoskeleton leg is proposed in [68], using the five-bar linkage to guide the user’s leg and generate the ankle’s trajectory. Two of its links must move parallel to the user’s legs, and it is intended to guide the movements of the knee and hip joints only, using an elliptical cam as a crank. Kinematic analysis and simulations demonstrate the feasibility, followed by comparisons with experimental data acquired via wearable goniometers.
The UCI Gait Mechanism [69] is a mechanism design composed of two main linkages. The main linkage is a six-bar linkage to guide a patient’s leg as an end-effector (through the ankle joint). The other linkage is a cam-driven parallelogram linkage linked to the six-bar linkage for controlling foot orientation. The six-bar linkage is a Stephenson III six-bar (Figure 6)synthesized by a proposal of a combination between homotopy solutions (using Bertini homotopy solver) for path synthesis and gradient-based optimization, using various techniques (Mathematica’s built-in algorithms for optimization: “Newton”, “Gradient”, “InteriorPoint”, “QuasiNewton”, “ConjugateGradient”, and “ConjugateGradient” with “FletcherReeves” [70]. The foot orientation mechanism design is detailed in [71].
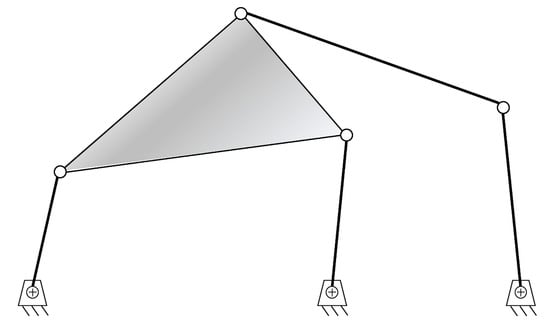
Figure 6.
A planar Stephenson III six-bar linkage.
Another proposal for a six-bar linkage came in [72], following an optimization procedure for dimensional synthesis. In this dimensional synthesis, a cooperative dual particle swarm optimization procedure was employed, using 60 precision points. The results show an average distance between the coupler point and the baseline trajectory of 3.5 mm. Not just path-oriented but time-dependent point-path trajectory is considered, and the results show no need for variable crank speed (constant crank speed will suffice to match gait requirements).
A machine learning-driven approach is presented in [73] for a six-bar linkage gait trainer design. Its approach is a subject-specific rehabilitation approach with subject-specific gait trajectories. A gait predictor model proposed by the authors produces subject-specific trajectories, which then serve as the basis for the linkage synthesis problem. A gait dataset [74] was employed to verify the accuracy of the gait predictor model, resulting in above 95% test accuracy. A neural-network framework called conditional–variational auto-encoders performs the linkage synthesis. The authors, however, warn that this approach, although capable of providing a selection of linkage candidates, cannot guarantee accuracy and requires further investigation.
Another example of linkage synthesis using artificial intelligence techniques is displayed in [75]. However, unlike all other design proposals already presented, this approach focuses on more than one joint for its linkage synthesis process (ankle and knee). The generated six-bar Stephenson III mechanism achieves the two joints’ trajectories by minimizing the MSE loss (inferior to 10−3 error), using a dataset [76] as a baseline for comparisons. Table 3 compiles the five-bar and six-bar topologies:

Table 3.
Five-bar linkages and six-bar linkages for gait rehabilitation.
4.3. Planar Higher-Order Linkages and Spatial Linkages
A seven-bar linkage concept was presented in [77], using a cam-linkage approach. The dimensional synthesis was realized by obeying a path and prescribed timing for comparison to a normative gait database from the Hong Kong Polytechnic University [78]. After an inverse kinematics analysis, an optimization procedure was realized in two conditions: with the hip joint assumed to be fixed in the vertical direction and with the hip movable. By means of a genetic algorithm implementation for the abovementioned optimization problem, dimensional parameters were found for both cases, and the results allowed for a constant crank rotation. Average residuals are 11.5 mm for the fixed case and 9.0 mm for the movable case.
The Mech-Walker [79] is an eight-bar linkage end-effector based on a Jansen eight-bar mechanism (Figure 7). Its synthesis is performed using the ankle path, considering position and time (prescribed timing). A global optimization algorithm (MultiStart) is utilized for minimizing the contour error (the orthogonal smallest distance separating the created trajectory and baseline trajectory). It also proposes a body weight support that supports the mechanism for the legs and generates the vertical motion of the center of mass (CoM).
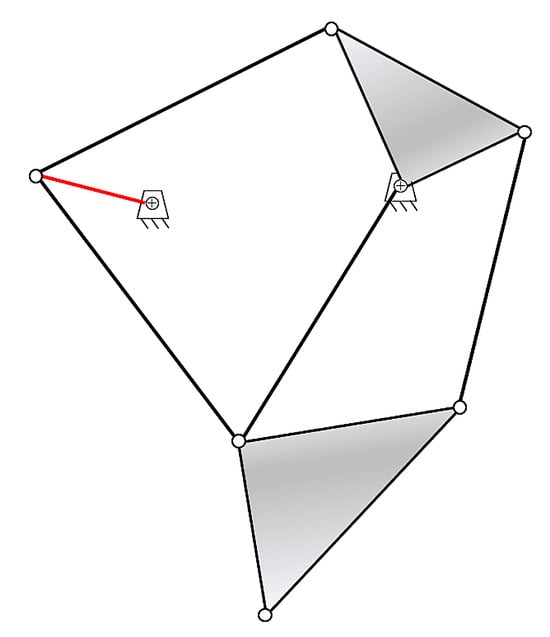
Figure 7.
A Jansen eight-bar linkage (crank link in red).
Another gait trainer proposition comes from [80], where an eight-bar Jansen linkage was designed to follow a natural trajectory during gait for the ankle. The device was created using a gait dataset [66] as a baseline that represents the gait kinematics of healthy individuals walking on a treadmill. A wooden proof-of-concept was made to test and validate design simulations under constant angular velocity.
The AutoLEE-II [81] is a bio-inspired exoskeleton that attempts to avoid the need for crutches, canes, or walkers, which are needed when using other gait devices. To achieve that, it needs to be able to maintain balance and protect its user against the risk of falls and the injuries that would follow. It is bio-inspired because the spatial mechanisms it employs seek to mimic the actual human joints, with all of them active, although with a different quantity of degrees of freedom. According to the biomechanical model it is following, the human hip has three degrees of freedom (abduction/adduction, flexion/extension, and endo/exo-rotation), the knee has one degree of freedom (flexion/extension), and the ankle has three (inversion/eversion, dorsi/plantar flexion, and endo/exo-rotation). For the hip, it utilizes a modified version of the parallelogram-based remote center-of-motion mechanism (RCM), following requirements of large range of motion, stiffness, and axis alignment. The knee joint is a parallelogram-based remote transmission mechanism. The ankle joint is modeled as a two-degree-of-freedom exoskeleton adopting a decoupled universal joint parallel linkage URR-USR/U. The kinematic model has seven links, and simulations demonstrate the feasibility of its self-balancing feature. In summary, the AutoLEE-II is a 12 DoF exoskeleton with a self-balancing feature using spatial mechanisms to mimic human joints. Table 4 groups all the higher-order and spatial mechanisms:

Table 4.
Planar higher-order mechanisms and spatial linkages for gait rehabilitation.
4.4. Critical Analysis and Discussion
This review provided a closer look at the research state of linkage-based devices designed for gait training. Even though these devices follow a similar general design path, there is considerable heterogeneity in design methods and accuracy measures. This heterogeneity brings interesting and diverse options; however, it is also important for future research to bring some minimal data regarding a design proposal to allow for some comparisons to be made.
In some cases, user-specific kinematic data are used as a baseline; in others, standardized datasets are employed. There is no standard form of evaluation of kinematic accuracy, and the design process is not always explicit. Measurements and data acquisition also vary greatly from a single high-speed video camera to a professional array of video cameras according to the best practices for measuring and analyzing clinical gait.
There can be some degree of variation between gait measurements obtained from a normative gait database and the experiments conducted by the design team of a new gait trainer. Therefore, it is important to be able to explain what the contributing factors for these variations are, i.e., if they are inherent to the design, if they come from the measurement systems used, or even if they can be regarded as normal variation as no individual will have the exact same gait as any other [84]. Measurement systems can also have an impact on cost, and to overcome this precision–cost challenge, different studies are seeking to obtain and validate open-source measurement systems with less expensive hardware. A study performed in [85] that compared open-source pose estimation against industry-standard optical motion capture using markers illustrated the promise of these new methods. They were able to achieve high levels of accuracy, and there is an expectation of continuous improvement as they progress in training these algorithms, which is an essential part of improving a machine learning algorithm’s performance.
The baseline of comparison is critical for a gait trainer’s design evaluation. Before evaluating the kinematic accuracy of a device, it is necessary to have a healthy gait baseline, which encompasses not only different individuals and different anthropometric measures but also different gait speeds. There are different gait databases available that can be used as a basis for comparison, and considering gait speeds is also important since there may be some variation in gait kinematics depending on gait speed, as shown in [86].
Kinematic accuracy is an important element in the linkage design of a gait trainer. The establishment of kinematic accuracy passes through the already mentioned measurement system (for experimental validation) and an appropriate choice of gait baseline. But with those available, it is necessary to quantify this accuracy by means of one or more indicators. Path synthesis linkage research has used several different accuracy indicators. Examples are the root mean square error (RMS) and peak errors in [62], absolute error, normalized-shape descriptor vector error (NSDV), and turning distance (TD) in [87], or mean squared error (MSE) in [75]. Alternatively, clinical gait analysis has different established indices of kinematic variability. Some examples are the coefficient of multiple correlation (CMC), mean absolute variability (MAV), root mean square deviation (RMSD), and linear fit method (LFM) [88]. As can be observed, path synthesis and clinical gait research do not exactly match when it comes to their kinematic accuracy indices. Although each indicator might have its own advantages and disadvantages, it can be argued that the whole research environment would benefit from a common base of indicators, allowing all personnel involved (designers, clinicians, and therapists) to be familiar with the accuracy measurements and permitting comparisons to be drawn based on these indicators.
Comparisons between different designs can prove important when comparing different outcomes from controlled trials and having to single out which feature is responsible for superior results. For instance, if a less kinematically accurate gait trainer achieves superior results when compared to another more accurate trainer, excluding other sources of bias, it might very well be possible that both have already achieved some minimal threshold of kinematic accuracy for rehabilitation, and the superior results are probably due to other characteristics. This is why a common basis of comparison can prove important for future research. In addition to that, some details regarding the topology choice are highly recommended to be shared, as they can be very useful for other researchers, not only to learn but also to avoid spending research efforts on topologies that were already deemed not promising and therefore outdated for the current goal of gait training.
5. Key Points towards the Design of New Linkage-Based Devices
A recommendation for future research can be made based on the points made in the previous section, especially regarding comparability. It is advisable that future research on gait trainers provide or specify the source for a gait baseline, preferably using gait databases or normative data. The gait databases and normative data can also have heterogeneity amongst themselves, but at least they provide details regarding measurement, population, and other conditions that might affect kinematic results. The topology choice criteria are commonly omitted, and disclosing this part, even briefly, helps future researchers make their own choices. In addition to details regarding topology choice, details about the design process and linkage synthesis can be relevant, especially for those also researching the efficacy and performance of such methods and presenting an optimized result. The measurement system used for evaluating a gait trainer is also important since it can provide a practical source of performance comparison. Different measurement systems have different measurement accuracies and must be clearly stated in the research to allow future readers to draw conclusions, replicate results, and compare. The choice of an indicator or a set of indicators to demonstrate kinematic accuracy compared to the chosen gait baseline is another relevant facet of gait research. Different indicators have their own advantages and disadvantages, and a common one would benefit the whole research community, be it the root mean squared error (RMSE) or any other indicator for the evaluation of goodness of fit.
Since the presented linkage-based devices are designed using rigid links and joints, they will repeat the gait patterns throughout the therapy session. This presents a disadvantage that was once present on robotic devices and was later dealt with by changing the control strategy, permitting compatibility with Bernstein’s principle of “repetition without repetition” [89]. It is advisable that future linkage-based gait trainers incorporate this feature in their designs so they can be truly comparable with their robotic counterparts. Many linkage-based gait trainers seek kinematic accuracy in the sagittal plane and start off the training by replicating what is to be considered a healthy pattern. The link adjustments, when they exist, are there to accommodate different anthropometric sizes and provide flexibility for the gait trainer to be used by a larger population. However, it can constitute additional flexibility and even a new approach if the patient can work towards a healthy gait gradually instead of going immediately to the final gait pattern. A linkage-based gait trainer that possesses this flexibility of adjusting the linkages to enable intermediary gait patterns towards the final one (the one contained in the baseline) might constitute an option for future research in this area, in line with motor adaptation concepts [90,91]. So, in summary, future research is recommended to present the following:
- References to serve as gait baselines, preferably from a database or normative data;
- Topology selection criteria and the kinematic synthesis process;
- Measurement systems and accuracy characteristics used to obtain experimental data;
- Kinematic accuracy indicator(s) aligned with the literature and clinical gait analysis;
- Compatibility with the Bernstein principle “repetition without repetition”;
- Possibility of gradual training towards a final kinematic trajectory;
- Target population based on anthropometrical lengths and sizes, grouped.
6. A Possible New Design of a Linkage-Based Gait Trainer
Gait trainers have a diverse degree of configuration and complexity, being generally composed of several elements, including a body weight support system (BWSS) and a gait guidance system (Figure 8). Gait guidance systems can employ an exoskeleton, end-effector, cable-driven, or linkage-based leg guidance system. These robotic devices control and guide the leg trajectories by employing different drive and control systems, can be fixed or mobile, and facilitate walking on a treadmill or overground. They can also include biofeedback and make use of serious games to improve therapy outcomes.
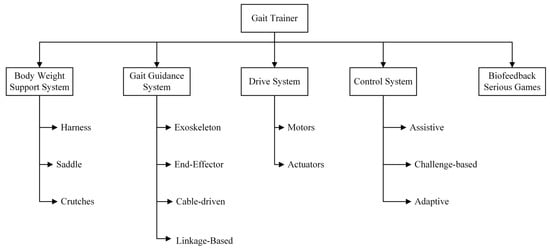
Figure 8.
A simplified representation of a gait trainer and its main components. They can also be fixed or mobile, and they train gait using a treadmill or directly overground.
A linkage-based gait trainer could come in several new configurations, depending on the choice of BWSS, drive system (motors and actuators), control system, and/or the inclusion of biofeedback systems and integration with serious games. Therefore, all of these systems must be considered for the complete design of a linkage-based gait trainer. However, the scope of this work is limited to the design of the linkage mechanism for a linkage-based gait trainer. After completion of the mechanism synthesis, further design steps should follow for the design and selection of, among other things, off-the-shelf and customized components, motors, sensors, and control.
With previous recommendations taken into consideration, a more general approach for the linkage design process could be as shown in Figure 9.
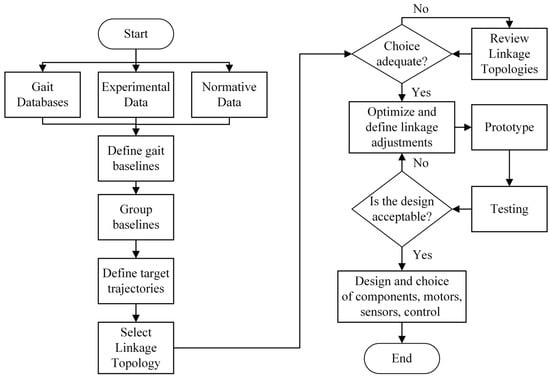
Figure 9.
The linkage design process applied to gait trainers.
This design process can serve as a guiding tool for new designs by assisting the designer in considering critical aspects of linkage-based design and facilitating communication and evaluation for future researchers and health practitioners. Next, taking into consideration the design recommendations and following the general approach described, a possible new linkage-based design is presented in more detail in the following subsections.
6.1. Gait Baselines
The choice is to extract trajectories of interest from a database [86] in order to form gait baselines. This dataset contains overground and treadmill gait kinematic and kinetic data from 42 healthy volunteers (24 young adults and 18 older adults). It used a 3D motion capture system, using 12 cameras, 5 force platforms, and a dual-belt split treadmill. A marker-set protocol was employed to define anatomical locations of interest [92], and the users performed the gait trials barefooted.
Using the gait database as the source of physiological gait data, some selections can be made based on anthropometric dimensions. The individuals from the public dataset have a height of 171.1 ± 10.5 cm with a mass of 68.4 ± 12.2 kg (young adults’ group) and a height of 161.8 ± 9.5 cm with a mass of 66.9 ± 10.1 kg (older adults’ group) [86]. Having different heights and consequently different leg lengths will result in different joint trajectories, which need to be accounted for in the design.
Another source of baselines for gait trajectories comes from the proposal of gradual training. Gait impairments create a distance between the considered physiological gait and the current pathological gait. A new proposal for a linkage-based gait trainer is that it should add flexibility not only to different anthropometrics but also to different stages of therapy and allow gradual gait training to be executed. Gradual training can bring similar benefits as sudden training but with a slower rate of decay [93].
After having a set of different target trajectories that the device must be able to reproduce, the next step would be to group them into similar ones and optimize their quantity. The similarity criteria applied could be waveform similarity [94] or different approaches for evaluating curve similarity.
After the grouping of target trajectories, a choice must be made regarding the number of different trajectories since it is not practical to have a completely individualized linkage-based gait trainer. There is neither the option of “one size fits all” nor the opposite, individual/specific gait training, but instead something in between these two extremes. However, it is important to maintain as a principle the avoidance of occasions where an individual could be trained in abnormal gait parameters, that is, a large mismatch between gait parameters trained and individual targets.
6.2. Linkage Topology Choice, Synthesis, and Optimization
Linkage topology choice (four-bar, six-bar, or eight-bar) must take into consideration specific project criteria such as space requirements, kinematic precision, availability of motor control, and other project-specific requirements. For this proposal, a six-bar was considered the best choice for being able to attain the kinematic precision of two joints (ankle and knee) with constant crank rotation [62,75].
With a topology chosen, the synthesis process can begin. As an example, six-bar synthesis can be performed by constraining a RR chain, as in [95]. The best fit to the target gait trajectories could be found by applying different approaches, such as gradient-based optimization, global optimization [71], and even machine learning approaches [75].
Using Figure 10 as an example, there are two loops in the six-bar linkage, loop 1 () and loop 2 (). Using the complex plane for formulating the kinematic equations, the vector loops are as follows:
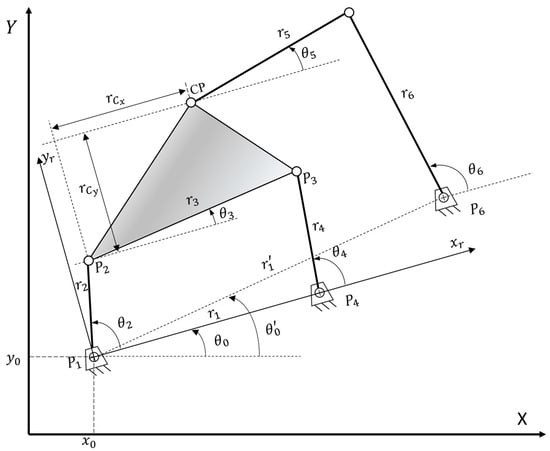
Figure 10.
A Stephenson III six-bar linkage and its design parameters.
Now, making use of Euler’s transform, , and making and , we can obtain the following:
Introducing the notation for the exponentials as was performed in [96], these equations become as follows:
This set of equations allows for the introduction of another set, using their complex conjugates:
These four equations characterize an initial configuration for the exemplified six-bar linkage. For a complete synthesis, it requires a system of equations that can be very large, depending on the number of task positions utilized. Details of this procedure are shown in [70,97], where the synthesis was performed using eleven task positions.
It is possible to improve upon the synthesis process by means of optimization techniques, using the synthesis solutions as initial guesses [70]. An example of an optimization procedure was performed in [98] for a four-bar linkage and for a six-bar linkage, using their proprietary algorithm, called MUMSA (Malaga University Mechanism Synthesis Algorithm).
The general optimization problem can be defined as shown below [99]:
where is the objective function to be optimized; represents the constraint functions; and is the linkage design vector, which is defined by its set of design variables and the search domain is defined by the interval .
The authors [98] define the optimization problem in two parts. The first part is as follows:
where is the number of precision points is the coordinated pair of desired precision points, and is the coordinated pair of generated precision points.
This first part optimizes the six-bar linkage so that the coupler, , goes into the predefined precision points. The second part goes as follows:
where is the required number of objective points for dwell period is the objective output angles, and is the generated output angles.
This second part is related to a requirement involving the input angle and output angle . Hence, the function to be minimized is as follows:
where is a set of design variables; are the penalty factors; and are the constraint functions.
The optimization problem employs three constraint functions regarding the specific case described in [98]. The constraint function is related to the Grashof condition, is related to the crank angle sequence, and is for avoiding the violation of the transmission angle (acute angle between coupler link and output link) condition. This is a procedure that must be followed for all different trajectories that the linkage will reproduce, mentioned in Section 6.1, defining all link adjustments required for the device. Additionally, a new design could contain a variable crank feature to allow kinematic variability for the walking task (Figure 11). This variability would consist of avoiding the kinematic repetition of successive steps by varying the crank length after each full rotation. To achieve this, cams can be used to vary the linkage’s crank length, r2, as in [100].
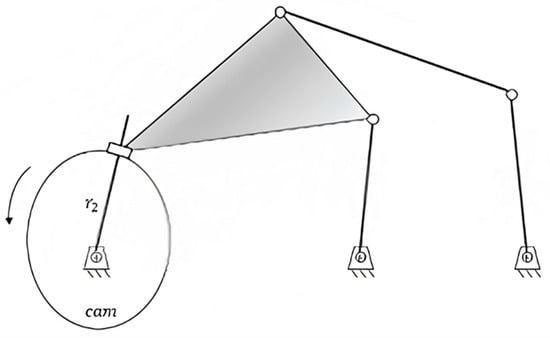
Figure 11.
A Stephenson III six-bar linkage using a cam for varying its crank length, r2.
This kinematic variability is introduced as a way of avoiding consecutive step repetition, which would happen with a rigid, fixed linkage configuration. By adjusting crank rotation and cam rotation appropriately, it is possible to keep a fixed step that varies its length after each cycle (each cycle corresponding to one crank full rotation) in a limited way depending on cam geometry.
6.3. Prototype and Testing
Proof-of-concept prototyping at a reduced size could be performed to demonstrate effectiveness in achieving design objectives and for evaluation. Real-size prototyping for trials would follow if those were successful.
The ideal measurement set should be the same as the dataset chosen—in this case, a motion capture system described in the reference dataset [86]. The similarity between trained gait trajectory and baseline is one of the aspects of interest; hence, it is crucial to perform appropriate measurements since measurement precision can vary significantly across different measurement equipment and methods [85].
6.4. Final Remarks
A new design for a gait trainer can be introduced by following the design methodology discussed before and making some choices, like the source for a gait baseline. It includes some important elements: a gait baseline, topology choice, the synthesis and optimization of a linkage-based proposal, a measurement methodology, and accuracy indices for kinematics. It can be related to a single joint or more, but the process remains the same, with slight changes in synthesis and optimization procedures (which could be multi-objective, for example, if the objective is to work with more than one joint like the knee and ankle). Link adjustments required to be able to execute different trajectories (required for different anthropometrics or in gradual training) are defined during the synthesis and optimization processes. Kinematic variability can be introduced by connecting a properly dimensioned cam (or association of cams) to the crank after the synthesis process, synchronized to the crank rotation, so it can vary its dimension after each full rotation.
7. Conclusions
This paper represents a comprehensive endeavor encompassing several key components. Firstly, it conducts a critical review of the current landscape in gait rehabilitation, emphasizing the limited effectiveness and high costs associated with existing robotic devices. This critical examination serves as a foundational premise for the subsequent research directions. Secondly, this paper proposes a systematic design approach to assist in the design process of such complex robotic devices for gait training. In light of the shortcomings identified in the existing robotic devices, this systematic approach aims to address the key design issues and facilitate the creation of innovative and cost-effective design solutions. It seeks to streamline the design process, enhance the effectiveness of rehabilitation devices, and mitigate the economic constraints that have hindered progress in the field. Finally, as a tangible demonstration of the proposed systematic design approach, this paper presents an exemplificative case study. This case study serves as a practical embodiment of the principles and methodologies outlined in the systematic approach. Through this example, key research elements are showcased, offering insights into their importance for the evaluation of research outcomes and the determination of critical success factors. In essence, this paper not only critically assesses the current state of gait rehabilitation devices but also pioneers a systematic design procedure intended to address the identified limitations. It culminates in a tangible case study that illustrates the application of this new design approach. By integrating these elements, this paper contributes to advancing the field of gait rehabilitation, fostering innovation, and promoting cost-effective solutions for the benefit of both researchers and healthcare practitioners.
Author Contributions
Conceptualization, T.S.d.P. and G.C.; methodology, T.S.d.P.; validation, T.S.d.P., G.C. and R.S.G.; formal analysis, G.C. and R.S.G.; investigation, T.S.d.P.; writing—original draft preparation, T.S.d.P.; writing—review and editing, T.S.d.P., R.S.G. and G.C.; visualization, T.S.d.P.; supervision, R.S.G. and G.C.; funding acquisition, R.S.G. and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001, by a fellowship from the National Counsel of Technological and Scientific Development (CNPq), number: 200689/2022-3; and by Next Generation EU, National Recovery and Resilience Plan, Investment PE8—Project Age-It: “Ageing Well in an Ageing Society” DM 1557, 11.10.2022 and PNRR MUR project PE0000013-FAIR.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Espuela, F.L.; Cuenca, J.P.; Díaz, C.L.; Sánchez, J.P.; Gamez-Leyva, G.; Naranjo, I.C. Sex differences in long-term quality of life after stroke: Influence of mood and functional status. Neurología 2020, 35, 470–478. [Google Scholar] [CrossRef]
- Grimmer, M.; Riener, R.; Walsh, C.J.; Seyfarth, A. Mobility related physical and functional losses due to aging and disease—A motivation for lower limb exoskeletons. J. Neuroeng. Rehabil. 2019, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- United Nations, Department of Economic Affairs, and Social DIvision. World Population Ageing, 2019: Highlights, UN. 2019. Available online: https://digitallibrary.un.org/record/3846855 (accessed on 20 April 2023).
- Cieza, A.; Causey, K.; Kamenov, K.; Hanson, S.W.; Chatterji, S.; Vos, T. Global estimates of the need for rehabilitation based on the Global Burden of Disease study 2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 2006–2017. [Google Scholar] [CrossRef] [PubMed]
- Harkema, S.J.; Behrman, A.L.; Barbeau, H. Evidence for Locomotor Training. In Locomotor Training; Oxford University Press: New York, NY, USA, 2011; pp. 21–39. [Google Scholar] [CrossRef]
- Mehrholz, J.; Thomas, S.; Kugler, J.; Pohl, M.; Elsner, B. Electromechanical-assisted training for walking after stroke. Cochrane Database Syst. Rev. 2020, 2020, CD006185. [Google Scholar] [CrossRef]
- Schindel, D.; Schneider, A.; Grittner, U.; Jöbges, M.; Schenk, L. Quality of life after stroke rehabilitation discharge: A 12-month longitudinal study. Disabil. Rehabil. 2021, 43, 2332–2341. [Google Scholar] [CrossRef]
- Morrison, S.A.; Backus, D. Locomotor Training: Is Translating Evidence into Practice Financially Feasible? J. Neurol. Phys. Ther. 2007, 31, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Pinto, D.; Heinemann, A.W.; Chang, S.-H.; Charlifue, S.; Field-Fote, E.C.; Furbish, C.L.; Jayaraman, A.; Tefertiller, C.; Taylor, H.B.; French, D.D. Cost-effectiveness analysis of overground robotic training versus conventional locomotor training in people with spinal cord injury. J. Neuroeng. Rehabil. 2023, 20, 10. [Google Scholar] [CrossRef]
- Calabrò, R.S.; Müller-Eising, C.; Diliberti, M.L.; Manuli, A.; Parrinello, F.; Rao, G.; Barone, V.; Civello, T. Who Will Pay for Robotic Rehabilitation? The Growing Need for a Cost-effectiveness Analysis. Innov. Clin. Neurosci. 2020, 17, 14–16. Available online: http://www.ncbi.nlm.nih.gov/pubmed/33898096 (accessed on 12 May 2023).
- Spiess, M.R.; Steenbrink, F.; Esquenazi, A. Getting the Best Out of Advanced Rehabilitation Technology for the Lower Limbs: Minding Motor Learning Principles. PM&R 2018, 10, S165–S173. [Google Scholar] [CrossRef]
- Xiong, H.; Diao, X. A review of cable-driven rehabilitation devices. Disabil. Rehabil. Assist. Technol. 2020, 15, 885–897. [Google Scholar] [CrossRef]
- Chaparro-Cárdenas, S.L.; Lozano-Guzmán, A.A.; Ramirez-Bautista, J.A.; Hernández-Zavala, A. A review in gait rehabilitation devices and applied control techniques. Disabil. Rehabil. Assist. Technol. 2018, 13, 819–834. [Google Scholar] [CrossRef] [PubMed]
- Mikolajczyk, T.; Ciobanu, I.; Badea, D.I.; Iliescu, A.; Pizzamiglio, S.; Schauer, T.; Seel, T.; Seiciu, P.L.; Turner, D.L.; Berteanu, M. Advanced technology for gait rehabilitation: An overview. Adv. Mech. Eng. 2018, 10, 168781401878362. [Google Scholar] [CrossRef]
- de Miguel-Fernández, J.; Lobo-Prat, J.; Prinsen, E.; Font-Llagunes, J.M.; Marchal-Crespo, L. Control strategies used in lower limb exoskeletons for gait rehabilitation after brain injury: A systematic review and analysis of clinical effectiveness. J. Neuroeng. Rehabil. 2023, 20, 23. [Google Scholar] [CrossRef] [PubMed]
- Slucock, T. A Systematic Review of Low-Cost Actuator Implementations for Lower-Limb Exoskeletons: A Technical and Financial Perspective. J. Intell. Robot. Syst. 2022, 106, 3. [Google Scholar] [CrossRef] [PubMed]
- Pinheiro, C.; Figueiredo, J.; Cerqueira, J.; Santos, C.P. Santos. Robotic Biofeedback for Post-Stroke Gait Rehabilitation: A Scoping Review. Sensors 2022, 22, 7197. [Google Scholar] [CrossRef]
- Gonçalves, R.S.; Rodrigues, L.A.O. Development of a Novel Parallel Structure for Gait Rehabilitation; IGI Global: Hershey, PA, USA, 2020; pp. 42–81. [Google Scholar] [CrossRef]
- Rodrigues, L.A.O.; Gonçalves, R.S. Development of a novel body weight support system for gait rehabilitation. Robotica 2023, 41, 1275–1294. [Google Scholar] [CrossRef]
- de Paiva, T.S.; Gonçalves, R.S.; Carbone, G.; Ceccarelli, M. Gait devices for stroke rehabilitation: State-of-the-art, challenges, and open issues. In Medical and Healthcare Robotics; Elsevier: Amsterdam, The Netherlands, 2023; pp. 87–122. [Google Scholar] [CrossRef]
- Calabrò, R.S.; Cacciola, A.; Bertè, F.; Manuli, A.; Leo, A.; Bramanti, A.; Naro, A.; Milardi, D.; Bramanti, P. Robotic gait rehabilitation and substitution devices in neurological disorders: Where are we now? Neurol. Sci. 2016, 37, 503–514. [Google Scholar] [CrossRef]
- Frey, M.; Colombo, G.; Vaglio, M.; Bucher, R.; Jorg, M.; Riener, R. A Novel Mechatronic Body Weight Support System. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 311–321. [Google Scholar] [CrossRef]
- Di Tommaso, F.; Tamburella, F.; Lorusso, M.; Gastaldi, L.; Molinari, M.; Tagliamonte, N.L. Biomechanics of Exoskeleton-Assisted Treadmill Walking. In Proceedings of the 2023 International Conference on Rehabilitation Robotics (ICORR), Singapore, 24–28 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Marchal-Crespo, L.; Reinkensmeyer, D.J. Review of control strategies for robotic movement training after neurologic injury. J. Neuroeng. Rehabil. 2009, 6, 20. [Google Scholar] [CrossRef]
- Michaud, B.; Cherni, Y.; Begon, M.; Girardin-Vignola, G.; Roussel, P. A serious game for gait rehabilitation with the Lokomat. In Proceedings of the 2017 International Conference on Virtual Rehabilitation (ICVR), Montreal, QC, Canada, 19–22 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Lunenburger, L.; Colombo, G.; Riener, R.; Dietz, V. Biofeedback in gait training with the robotic orthosis Lokomat. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 4888–4891. [Google Scholar] [CrossRef]
- Technical Data Sheet-Hocoma. Available online: https://www.hocoma.com/solutions/lokomat/techincal-data-sheet/ (accessed on 18 May 2023).
- Schmidt, H.; Werner, C.; Bernhardt, R.; Hesse, S.; Krüger, J. Gait rehabilitation machines based on programmable footplates. J. Neuroeng. Rehabil. 2007, 4, 2. [Google Scholar] [CrossRef]
- Hesse, S.; Uhlenbrock, D.; Werner, C.; Bardeleben, A. A mechanized gait trainer for restoring gait in nonambulatory subjects. Arch. Phys. Med. Rehabil. 2000, 81, 1158–1161. [Google Scholar] [CrossRef] [PubMed]
- Marchal-Crespo, L.; Riener, R. Robot-assisted gait training. In Rehabilitation Robotics; Elsevier: Amsterdam, The Netherlands, 2018; pp. 227–240. [Google Scholar] [CrossRef]
- Reha-Stim Medtec Inc. Gait Trainer GT II—Developed for Clinical Use by Practitioners. 2021. Available online: https://www.reha-stim.com (accessed on 20 June 2023).
- Sirlantzis, K.; Larsen, L.B.; Kanumuru, L.K.; Oprea, P. Robotics. In Handbook of Electronic Assistive Technology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 311–345. [Google Scholar] [CrossRef]
- FDA. 510(k) Premarket Notification K143690 for EksoTM. 2016. Available online: https://www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfpmn/pmn.cfm?ID=K143690 (accessed on 14 May 2023).
- Burns, F.; Calder, A.; Devan, H. Experiences of individuals with multiple sclerosis and stroke using transcutaneous foot drop electrical stimulators: A systematic review and meta-synthesis of qualitative studies. Disabil. Rehabil. 2023, 45, 1923–1932. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Krebs, H.I.; Iqbal, K.; Macko, N.R.; Macko, R.F.; Forrester, L.W. Robot-Aided Neurorehabilitation: A Novel Robot for Ankle Rehabilitation. IEEE Trans. Robot. 2009, 25, 569–582. [Google Scholar] [CrossRef]
- Roy, A.; Krebs, H.I.; Iqbal, K.; Macko, N.R.; Macko, R.F.; Forrester, L.W. Facilitating push-off propulsion: A biomechanical model of ankle robotics assistance for plantarflexion gait training in stroke. In Proceedings of the 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Sao Paulo, Brazil, 12–15 August 2014; IEEE: Piscataway, NJ, USA; pp. 656–663. [Google Scholar] [CrossRef]
- AAlamdari, A.; Krovi, V. Robotic Physical Exercise and System (ROPES): A Cable-Driven Robotic Rehabilitation System for Lower-Extremity Motor Therapy. In Proceedings of the Volume 5A: 39th Mechanisms and Robotics Conference, Boston, MA, USA, 2–5 August 2015; American Society of Mechanical Engineers: Boston, MA, USA, 2015. [Google Scholar] [CrossRef]
- Alamdari, A.; Krovi, V. Cable-Driven Articulated Rehabilitation System for Gait Training; University at Buffalo: Buffalo, NY, USA, 2016. [Google Scholar]
- Erbil, D.; Tugba, G.; Murat, T.H.; Melike, A.; Merve, A.; Mehmetali, Ç.C.; Akay, Ö.; Nigar, D. Effects of robot-assisted gait training in chronic stroke patients treated by botulinum toxin-a: A pivotal study. Physiother. Res. Int. 2018, 23, e1718. [Google Scholar] [CrossRef] [PubMed]
- Ertop, T.E.; Yuksel, T.; Konukseven, E.I. Realization of human gait in virtual fluid environment on a robotic gait trainer for therapeutic purposes. Rob. Auton. Syst. 2018, 105, 59–68. [Google Scholar] [CrossRef]
- Swank, C.; Wang-Price, S.; Gao, F.; Almutairi, S. Walking with a Robotic Exoskeleton Does Not Mimic Natural Gait: A Within-Subjects Study. JMIR Rehabil. Assist. Technol. 2019, 6, e11023. [Google Scholar] [CrossRef] [PubMed]
- Sankai, Y. HAL: Hybrid Assistive Limb Based on Cybernics. In Robotics Research. Springer Tracts in Advanced Robotics; Kaneko, M., Nakamura, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 66, pp. 25–34. [Google Scholar] [CrossRef]
- US Food and Drug Administration. 510(k) Summary of HAL for Medical Use (Lower Limb Type). 2020; pp. 1–18. Available online: https://www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfpmn/pmn.cfm?ID=K201559 (accessed on 17 February 2023).
- Hesse, S.; Uhlenbrock, D. A mechanized gait trainer for restoration of gait. J. Rehabil. Res. Dev. 2000, 37, 701–708. [Google Scholar]
- Reha Stim Medtec, A.G. DataSheet Gait Trainer GTII; Reha Stim Medtec AG: Schlieren, Switzerland; pp. 1–2.
- Hadj-Abdelkader, M.A.; Bourhis, G.; Cherki, B. Haptic feedback control of a smart wheelchair. Appl. Bionics Biomech. 2012, 9, 181–192. [Google Scholar] [CrossRef]
- Reha Technology, A.G. G-EOL–Robotic-Assisted Gait Therapy–Reha Technology. Available online: https://www.rehatechnology.com/en/g-eol/ (accessed on 17 February 2023).
- Ko, B.-W.; Song, W.-K. Kinematic Comparison of Gait Rehabilitation with Exoskeleton and End-Effector Devices. In Biosystems and Biorobotics; Springer International Publishing: Cham, Switzerland, 2017; Volume 16, pp. 213–217. [Google Scholar] [CrossRef]
- Hidayah, R.; Bishop, L.; Jin, X.; Chamarthy, S.; Stein, J.; Agrawal, S.K. Agrawal. Gait Adaptation Using a Cable-Driven Active Leg Exoskeleton (C-ALEX) With Post-Stroke Participants. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1984–1993. [Google Scholar] [CrossRef]
- Jin, X.; Cui, X.; Agrawal, S.K. Design of a cable-driven active leg exoskeleton (C-ALEX) and gait training experiments with human subjects. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 5578–5583. [Google Scholar] [CrossRef]
- Jin, X.; Cai, Y.; Prado, A.; Agrawal, S.K. Effects of exoskeleton weight and inertia on human walking. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1772–1777. [Google Scholar] [CrossRef]
- Alamdari, A.; Krovi, V. Design and Analysis of a Cable-Driven Articulated Rehabilitation System for Gait Training. J. Mech. Robot. 2016, 8, 5. [Google Scholar] [CrossRef]
- Wu, M.; Hornby, T.G.; Landry, J.M.; Roth, H.; Schmit, B.D. A cable-driven locomotor training system for restoration of gait in human SCI. Gait Posture 2011, 33, 256–260. [Google Scholar] [CrossRef] [PubMed]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, R.S.; Soares, G.; Carvalho, J.C. Conceptual design of a rehabilitation device based on cam-follower and crank-rocker mechanisms hand actioned. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 277. [Google Scholar] [CrossRef]
- Gonçalves, R.S.; Rodrigues, L.A.O. Development of nonmotorized mechanisms for lower limb rehabilitation. Robotica 2022, 40, 102–119. [Google Scholar] [CrossRef]
- Gonçalves, R.S.; Rodrigues, L.A.O.; Humbert, R.; Carbone, G. A User-Friendly Nonmotorized Device for Ankle Rehabilitation. Robotics 2023, 12, 32. [Google Scholar] [CrossRef]
- Takeuchi, N.; Izumi, S.-I. Rehabilitation with Poststroke Motor Recovery: A Review with a Focus on Neural Plasticity. Stroke Res. Treat. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ingemanson, M.L.; Rowe, J.R.; Chan, V.; Wolbrecht, E.T.; Reinkensmeyer, D.J.; Cramer, S.C. Somatosensory system integrity explains differences in treatment response after stroke. Neurology 2019, 92, e1098–e1108. [Google Scholar] [CrossRef]
- Park, S.-W.; Wolf, S.L.; Blanton, S.; Winstein, C.; Nichols-Larsen, D.S. The EXCITE Trial: Predicting a Clinically Meaningful Motor Activity Log Outcome. Neurorehabilit. Neural Repair 2008, 22, 486–493. [Google Scholar] [CrossRef]
- Taborri, J.; Mileti, I.; Mariani, G.; Mattioli, L.; Liguori, L.; Salvatori, S.; Palermo, E.; Patanè, F.; Rossi, S. RANK-Robotic Ankle: Design and testing on irregular terrains. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 9752–9757. [Google Scholar] [CrossRef]
- Lee, J.; Li, L.; Shin, S.Y.; Deshpande, A.D.; Sulzer, J. Kinematic comparison of single degree-of-freedom robotic gait trainers. Mech. Mach. Theory 2021, 159, 104258. [Google Scholar] [CrossRef]
- Kora, K.; Stinear, J.; McDaid, A. Design, Analysis, and Optimization of an Acute Stroke Gait Rehabilitation Device. J. Med. Devices 2017, 11, 1. [Google Scholar] [CrossRef]
- Ji, Z.; Manna, Y. Synthesis of a Pattern Generation Mechanism for Gait Rehabilitation. J. Med. Devices 2008, 2, 3. [Google Scholar] [CrossRef]
- Yu, J.; Han, S.M.; Kim, Y.Y. Simultaneous Shape and Topology Optimization of Planar Linkage Mechanisms Based on the Spring-Connected Rigid Block Model. J. Mech. Des. 2020, 142, 1. [Google Scholar] [CrossRef]
- Yun, Y.; Kim, H.-C.; Shin, S.Y.; Lee, J.; Deshpande, A.D.; Kim, C. Statistical method for prediction of gait kinematics with Gaussian process regression. J. Biomech. 2014, 47, 186–192. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Yao, K.; Zong, Y.; Ye, J.; Chen, J. Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device. Machines 2022, 10, 1110. [Google Scholar] [CrossRef]
- Geonea, I.; Tarnita, D.; Carbone, G.; Ceccarelli, M. Design and Simulation of a Leg Exoskeleton Linkage for Human Motion Assistance. In New Trends in Medical and Service Robotics. Mechanisms and Machine Science; Carbone, G., Ceccarelli, M., Pisla, D., Eds.; Springer: Cham, Switzerland, 2019; Volume 65, pp. 93–100. [Google Scholar] [CrossRef]
- Tsuge, B.Y.; McCarthy, J.M. An Adjustable Single Degree-of-Freedom System to Guide Natural Walking Movement for Rehabilitation. J. Med. Devices 2016, 10, 4. [Google Scholar] [CrossRef]
- Tsuge, B.Y.; Plecnik, M.M.; McCarthy, J.M. Homotopy Directed Optimization to Design a Six-Bar Linkage for a Lower Limb with a Natural Ankle Trajectory. J. Mech. Robot. 2016, 8, 6. [Google Scholar] [CrossRef]
- Tsuge, B.Y. Kinematic Synthesis of Lower Limb Supporting Linkages; University of California, Irvine: Irvine, CA, USA, 2015. [Google Scholar]
- Li, M.; Yan, J.; Zhao, H.; Ma, G.; Li, Y. Mechanically Assisted Neurorehabilitation: A Novel Six-Bar Linkage Mechanism for Gait Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 985–992. [Google Scholar] [CrossRef]
- Loya, A.; Deshpande, S.; Purwar, A. Machine Learning-Driven Individualized Gait Rehabilitation: Classification, Prediction, and Mechanism Design. Eng. Sci. Med Diagn. Ther. 2020, 3, 2. [Google Scholar] [CrossRef]
- Serrao, M.; Chini, G.; Bergantino, M.; Sarnari, D.; Casali, C.; Conte, C.; Ranavolo, A.; Marcotulli, C.; Rinaldi, M.; Coppola, G.; et al. Dataset on gait patterns in degenerative neurological diseases. Data Brief 2018, 16, 806–816. [Google Scholar] [CrossRef]
- Kapsalyamov, A.; Hussain, S.; Brown, N.A.; Goecke, R.; Hayat, M.; Jamwal, P.K. Jamwal. Synthesis of a six-bar mechanism for generating knee and ankle motion trajectories using deep generative neural network. Eng. Appl. Artif. Intell. 2023, 117, 105500. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Shao, Y.; Xiang, Z.; Liu, H.; Li, L. Conceptual design and dimensional synthesis of cam-linkage mechanisms for gait rehabilitation. Mech. Mach. Theory 2016, 104, 31–42. [Google Scholar] [CrossRef]
- Onen, U.; Botsali, F.M.; Kalyoncu, M.; Tinkir, M.; Yilmaz, N.; Sahin, Y. Design and Actuator Selection of a Lower Extremity Exoskeleton. IEEE/ASME Trans. Mechatron. 2014, 19, 623–632. [Google Scholar] [CrossRef]
- Haghjoo, M.R.; Lee, H.; Afzal, M.R.; Eizad, A.; Yoon, J. Mech-Walker:A Novel Single-DOF Linkage Device With Movable Frame for Gait Rehabilitation. IEEE/ASME Trans. Mechatron. 2021, 26, 13–23. [Google Scholar] [CrossRef]
- Shin, S.Y.; Deshpande, A.D.; Sulzer, J. Design of a Single Degree-of-Freedom, Adaptable Electromechanical Gait Trainer for People with Neurological Injury. Mech. Robot. 2018, 10, 4. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Yang, J.; Cao, W.; Wu, X. Design and analysis of a novel 12-DOF self-balancing lower extremity exoskeleton for walking assistance. Mech. Mach. Theory 2022, 167, 104519. [Google Scholar] [CrossRef]
- Bovi, G.; Rabuffetti, M.; Mazzoleni, P.; Ferrarin, M. A multiple-task gait analysis approach: Kinematic, kinetic and EMG reference data for healthy young and adult subjects. Gait Posture 2011, 33, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Abbasnejad, G.; Yoon, J.; Lee, H. Optimum kinematic design of a planar cable-driven parallel robot with wrench-closure gait trajectory. Mech. Mach. Theory 2016, 99, 1–18. [Google Scholar] [CrossRef]
- King, S.L.; Barton, G.J.; Ranganath, L.R. Interpreting sources of variation in clinical gait analysis: A case study. Gait Posture 2017, 52, 1–4. [Google Scholar] [CrossRef]
- Washabaugh, E.P.; Shanmugam, T.A.; Ranganathan, R.; Krishnan, C. Comparing the accuracy of open-source pose estimation methods for measuring gait kinematics. Gait Posture 2022, 97, 188–195. [Google Scholar] [CrossRef]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. A public dataset of overground and treadmill walking kinematics and kinetics in healthy individuals. PeerJ 2018, 2018, e4640. [Google Scholar] [CrossRef]
- Torres-Moreno, J.; Cruz, N.; Álvarez, J.; Redondo, J.; Giménez-Fernandez, A. An open-source tool for path synthesis of four-bar mechanisms. Mech. Mach. Theory 2022, 169, 104604. [Google Scholar] [CrossRef]
- Di Marco, R.; Scalona, E.; Pacilli, A.; Cappa, P.; Mazzà, C.; Rossi, S. How to choose and interpret similarity indices to quantify the variability in gait joint kinematics. Int. Biomech. 2018, 5, 1–8. [Google Scholar] [CrossRef]
- van Hedel, H.J.A.; Schuler, T.A.; Lieber, J. Clinical Application of Rehabilitation Therapy Technologies to Children with CNS Damage. In Neurorehabilitation Technology; Reinkensmeyer, D.J., Marchal-Crespo, L., Dietz, V., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 289–318. [Google Scholar] [CrossRef]
- Krakauer, J.W.; Hadjiosif, A.M.; Xu, J.; Wong, A.L.; Haith, A.M. Motor Learning. Compr. Physiol. 2019, 9, 613–663. [Google Scholar] [CrossRef] [PubMed]
- Bastian, A.J. Understanding sensorimotor adaptation and learning for rehabilitation. Curr. Opin. Neurol. 2008, 21, 628–633. [Google Scholar] [CrossRef] [PubMed]
- Leardini, A.; Sawacha, Z.; Paolini, G.; Ingrosso, S.; Nativo, R.; Benedetti, M.G. A new anatomically based protocol for gait analysis in children. Gait Posture 2007, 26, 560–571. [Google Scholar] [CrossRef] [PubMed]
- Torres-Oviedo, G.; Bastian, A.J. Natural error patterns enable transfer of motor learning to novel contexts. J. Neurophysiol. 2012, 107, 346–356. [Google Scholar] [CrossRef]
- Iosa, M.; Cereatti, A.; Merlo, A.; Campanini, I.; Paolucci, S.; Cappozzo, A. Assessment of Waveform Similarity in Clinical Gait Data: The Linear Fit Method. Biomed. Res. Int. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Plecnik, M.M.; McCarthy, J.M. Design of Stephenson linkages that guide a point along a specified trajectory. Mech. Mach. Theory 2016, 96, 38–51. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Soh, G.S. Geometric Design of Linkages; Springer Science+Business Media, LLC.: New York, NY, USA, 2011; p. 448. [Google Scholar]
- Plecnik, M.M.; McCarthy, J.M. Kinematic synthesis of Stephenson III six-bar function generators. Mech. Mach. Theory 2016, 97, 112–126. [Google Scholar] [CrossRef]
- Cabrera, J.; Ortiz, A.; Nadal, F.; Castillo, J. An evolutionary algorithm for path synthesis of mechanisms. Mech. Mach. Theory 2011, 46, 127–141. [Google Scholar] [CrossRef]
- Ben Hamida, I.; Laribi, M.A.; Mlika, A.; Romdhane, L.; Zeghloul, S.; Carbone, G. Multi-Objective optimal design of a cable driven parallel robot for rehabilitation tasks. Mech. Mach. Theory 2021, 156, 104141. [Google Scholar] [CrossRef]
- Soong, R.-C.; Chang, S.-B. Synthesis of function-generation mechanisms using variable length driving links. Mech. Mach. Theory 2011, 46, 1696–1706. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).