Cooperative Passivity-Based Control of Nonlinear Mechanical Systems

Abstract

In this work, we propose two cooperative passivity-based control methods for networks of mechanical systems. By cooperatively synchronizing the end-effector coordinates of the individual agents, we achieve cooperation between systems of different types. The underlying passivity property of our control approaches ensures that cooperation is stable and robust. Neither of the two approaches rely on the modeling information of neighbors, locally, which simplifies the interconnection of applicable systems and makes the approaches modular in their use. Our first approach is a generalized cooperative Interconnection-and-Damping Assignment passivity-based control (IDA-PBC) scheme for networks of fully actuated and underactuated systems. Our approach leverages the definition of end-effector coordinates in existing single-agent IDA-PBC solutions for underactuated systems to satisfy the matching conditions, independently of the cooperative control input. Accordingly, our approach integrates a large set of existing single-agent solutions and facilitates cooperative control between these and fully actuated systems. Our second approach proposes agent outputs composed of their end-effector coordinates and velocities to guarantee cooperative stability for networks of fully actuated systems in the presence of communication delays. We validate both approaches in simulation and experiments.

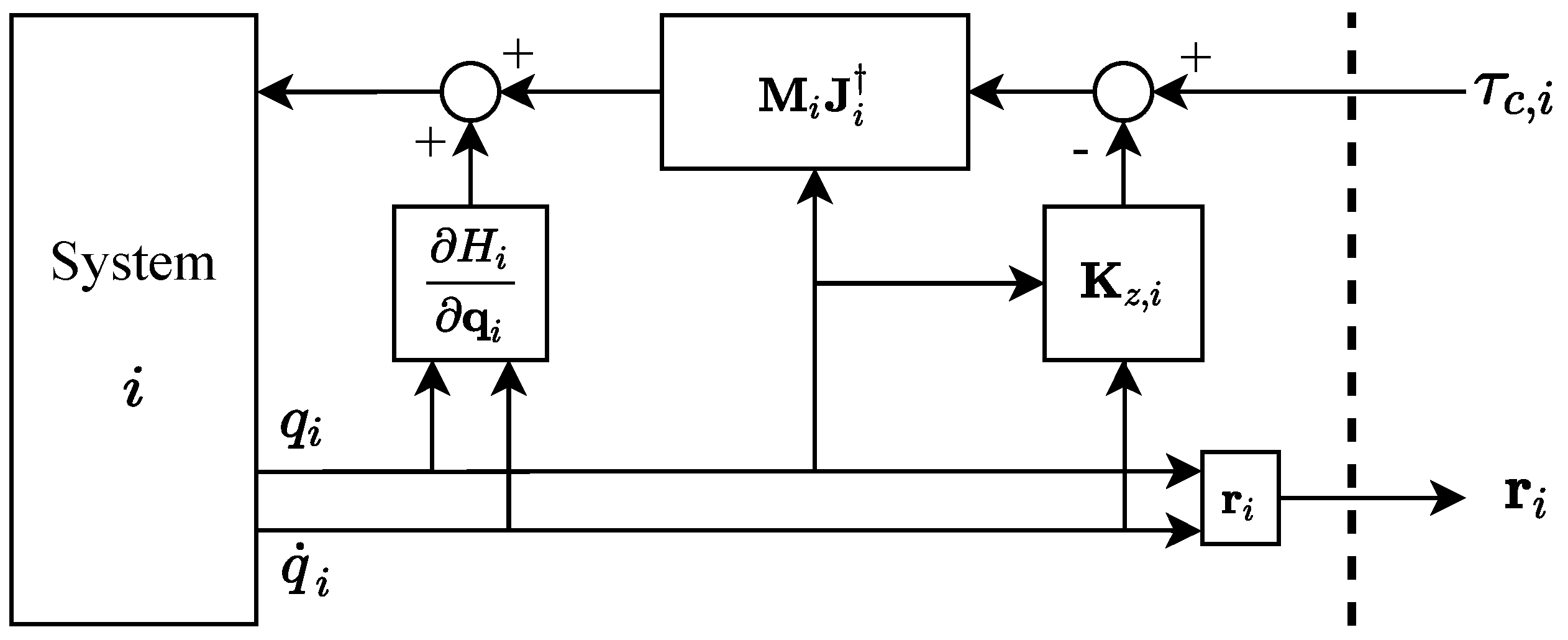
1. Introduction

The dynamics of mechanical systems are physically governed by their storage and dissipation of energy, and the power flow originating from the interaction with other systems. These systems are at rest when the energy in the system is minimal and the associated equilibrium tends to be stable and robust to perturbations. Passivity-based control (PBC) is a control methodology based on these principles, shaping the energy of a system via suitable control inputs to be minimal at the control objective. This generally results in robust stabilizing controllers, even when the system under study is nonlinear.

In this work, we propose two novel distributed control architectures for networks of mechanical systems that inherit the robust stability properties of PBC in a networked context. We use these properties to develop a framework in which system interconnections become robust and modular, i.e., independent of the individual system dynamics. Our approach is applicable to networks of systems, where each system has a different dynamical model. Such networks are referred to as heterogeneous. The aforementioned properties are useful in many engineering domains where interaction between varying system types is beneficial and can have applications in medical, logistic, or aerospace industries [1,2].

An important distinction between systems is their degree of actuation. The states of fully actuated systems can be influenced directly from the input. For these types of systems, distributed PBC controllers are well-established (see [3] for a summary). On the contrary, underactuated systems lack actuation in one or multiple directions of the state space. The resulting control problem for these systems is more complicated and a general approach is lacking. One of the most general frameworks for these types of systems is Interaction-and-Damping Assignment passivity-based control (IDA-PBC) [4], which controls the open-loop system to match, in closed-loop, a desired system with minimum energy at the control objective. Adding damping to the closed-loop system forces it towards the assigned equilibrium. Our first method is a cooperative extension of this method that applies to heterogeneous networks of systems with fully actuated or underactuated dynamics.

We formulate our cooperative objectives in generalized end-effector coordinates, which include Cartesian coordinates as a special case. Next to the case of synchronization, we provide control laws that stabilize the network of systems at a static configuration. With agents assigned as leader, the configuration is achieved at a user-specified reference position. We refer to this combination of control objectives as the Leader-Follower Formation Control (LFFC) problem.

In cooperative control, the communication network is critical for the performance and stability of the multi-agent system. Communication delays can be destabilizing and in a PBC context can cause the network to lose its passive behavior [5]. Our second method uses the scattering transformation (ST) [5] to transform the networked variables, making the network passive. We modify the outputs of the agents to include the generalized coordinates and their velocities. A local control law ensures passivity of the agents in the modified outputs as viewed from the network. We show that the cooperative control scheme converges to the cooperative objectives, even if the delays in the network vary over time or if communicated packets are lost.

Contribution: this work builds on our previous works [6,7]. We present the methods in the same framework and include simulations and experimental results. We present two distributed cooperative passivity-based controllers:

• A unified IDA-PBC scheme for cooperative stabilization of heterogeneous networks of fully actuated and underactuated agents that builds on existing single-agent IDA-PBC controllers. Our approach satisfies the matching conditions of each underactuated agent, independently of the cooperative input, by suitably defining the cooperative variables.
• A cooperative PBC scheme for fully actuated systems that is robust to time-varying delays and loss of communication packets, while the end-effector dynamics, by default, are transformed to behave as point-masses in the cooperative space, or follow desired dynamics as specified by the control designer.

Related Work

The design of stable controllers for a group of systems using passivity-based control is well-established. In particular, since feedback and parallel interconnections of passive systems are passive (and stable), complex nonlinear systems may be stabilized by ensuring passivity for individual systems and their controllers. In this context, it was shown in [8] that under a particular interaction topology (connected and undirected graph), control based on a well-designed potential function results in convergence to a desired set of equilibria for the group of agents, given that the individual agents are passive. For mechanical systems, control via passivity interacts with both the velocity and force of end-effectors. This makes it well-suited for control under interaction with the environment or other robots. Examples of its use are in bilateral teleoperation [5,9,10], where an operator controls the system remotely and in applications where the robot interacts directly with its environment [11]. Typically, passivity-based control design models the nonlinear plant dynamics using Euler-Lagrange (EL) or Hamiltonian dynamics [12], since these modeling techniques explicitly formulate the kinetic and potential energy of the system.

PBC methods for fully actuated systems are well-developed. LFFC methods for joint synchronization of a homogeneous network with fully actuated EL systems are proposed in [13,14]. These approaches achieve joint synchronization under different network topologies but are applicable only to a limited set of dynamical systems. The approach in [15] considers networks of underactuated flexible-joint manipulators. Their control law, relying on a suitable definition of the control error, synchronizes end-effector Cartesian coordinates when constant unknown communication delays are present. The work [16] considers similar systems with non-identical model parameters and variable communication delays in the network. Their approach is composed of a local gravity compensating term and a networked term with proportional and derivative action. Although these approaches are well-suited for the considered system types, they lack applicability in the general case. We propose a novel distributed LFFC method in generalized coordinates for networks of heterogeneous underactuated and/or fully actuated systems. We base our approach on IDA-PBC [4]. Our approach extends directly from a large set of single-agent solutions which include flexible link manipulators and the vast class of systems with one degree of underactuation [17]. In contrast to distributed IDA-PBC methods that tackle a specific set of systems, the proposed method applies to all systems in the aforementioned classes and does not require the control designer to solve nonlinear Partial Differential Equations (PDEs).

In addition, this architecture allows for the incorporation of other extensions to single-agent IDA-PBC where the matching conditions are unmodified, such as the work in [18], which introduces a suitable integral action to overcome matched and unmatched disturbances.

To additionally study the effect of communication delays, we consider the case of fully actuated system networks with varying communication delays and packet loss. In [19], a passivity-based controller for networks of heterogeneous fully actuated agents is developed in the EL framework, which is robust to time-varying time delays when velocities are sufficiently damped. Additionally, the method does not require velocity measurements. Similar model-free approaches were also presented [20,21]. Rather than formulating a condition on damping, another typical approach is to ensure that the communication channel is passive under delays, such that the closed-loop system including the communication network is passive and, therefore, stable. The most common approach for designing a passive communication channel is to transform the communicated variables to wave-variables, using the scattering transformation (ST) [5,10]. In contrast to the regular communicated variables, the power of wave-variables traveling through the network is well-defined. Hence their energy qualifies as a storage function, making the network passive. Although this approach is simple and effective, the ST modifies the dynamics of the communication channel which can lead to deteriorated performance. Therefore, alternative methods have been proposed that improve the transparency of the communication channel (i.e., its ability to mimic a direct communication link). Mainly, in [22], the Time Domain Passivity Approach (TDPA) consisting of a “passivity-observer” and “passivity-controller” are introduced into the network to monitor the energy and absorb energy, if necessary, such that passivity is guaranteed. Alternatively, the Passive Set Position Modulation (PSPM) approach [23] ensures passivity of the network with minimal performance loss for networks sending and receiving position data. Recently, an extension to the ST was presented in [24], which eliminates the dynamics of the transformed communication channel. Their solution approach adds a simple algebraic manipulation to the ST, preserving its properties while introducing an extra degree of freedom that overcomes the negative dynamic effects of the regular ST.

In this work, for simplicity, we apply the regular ST to achieve passive communication between agents, although the extension in [24] applies directly to the presented framework. In addition, we make use of Wave-Variable Modulation [25] in discrete-time to overcome time-varying delays and packet-loss. Our second method builds on two works. In the first [26], a PBC method incorporating the ST is applied to a multi-agent network of passive fully-actuated systems with communication delays. Their results show that synchronization of agent outputs emerge for a set of passive inter-agent control functions. The second method [27] shows that outputs r consisting of joint velocity and joint coordinates are passive and when applied in this framework result in synchronization of the joint coordinates in the presence of communication delays. Since for these outputs the notion of passivity is not related to physical energy, passivity in this setting is often referred to as r-passivity. In [28], this result is extended to the case of Cartesian coordinates, defining r by the Cartesian velocity and coordinates of the end-effector [28]. Our control approach is based on the same principles, but significantly simplifies the interconnection of heterogeneous systems. In particular, our framework allows the designer to explicitly characterize the local and cooperative damping, and the objectives of the multi-agent system. In addition, the cooperative dynamics can be set by a desired cooperative inertia matrix which, by virtue of the proposed controller, follow point-mass dynamics by default. Hence, the controlled network of heterogeneous systems behaves by default as a network of homogeneous systems, significantly reducing the design effort required for their interconnection.

Outline: the plant dynamics and control problems are formally introduced in Section 2. Fundamentals of passivity and IDA-PBC are reviewed in Section 3. Section 4 and Section 5 introduce the main contributions: cooperative IDA-PBC and r-PBC. The proposed methods are validated in simulations in Section 6 and in experiments in Section 7. A discussion is presented in Section 8 and conclusions are presented in Section 9.

Notation: we will denote vectors and matrices in bold. The left pseudo-inverse of matrix $\mathbf{A}$ is denoted by ${\mathbf{A}}^{†}={\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T$ such that ${\mathbf{A}}^{†}\mathbf{A}=\mathbf{I}$. Partial derivatives are assumed to be column vectors. We denote by ${\mathbf{I}}_n$ the identity matrix of dimension n and by ${\mathbf{0}}_{n\times m}$ the matrix with all zero entries of dimension $n\times m$. The quadratic form ${\left|\right|\mathbf{x}\left|\right|}_{\mathbf{Q}}^2$ is shorthand for ${\mathbf{x}}^T\mathbf{Q}\mathbf{x}$. The set $I_N$ refers to the set of indices $\{1,2,\cdots ,N\}$.

2. Problem Formulation

We consider simple mechanical systems in a Hamiltonian framework [12]. The kinetic energy of a simple mechanical system is determined by its inertia matrix $\mathbf{M}\left({\mathbf{q}}_i\right)={\mathbf{M}}^T\left({\mathbf{q}}_i\right)>{\mathbf{0}}_{n_i}$; we will often write system matrices without their explicit dependency on the joint-coordinates, i.e., ${\mathbf{M}}_i={\mathbf{M}}_i\left({\mathbf{q}}_i\right)$. Each agent i is modeled by

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{\mathbf{q}}}_i\\ {\dot{\mathbf{p}}}_i\end{array}\right]& =\left[\begin{array}{cc}{\mathbf{0}}_{n_i}& {\mathbf{I}}_{n_i}\\ -{\mathbf{I}}_{n_i}& -{\mathbf{R}}_i({\mathbf{q}}_i,{\mathbf{p}}_i)\end{array}\right]\left[\begin{array}{c}\frac{\partial H_i}{\partial {\mathbf{q}}_i}\\ \frac{\partial H_i}{\partial {\mathbf{p}}_i}\end{array}\right]+\left[\begin{array}{c}{\mathbf{0}}_{n_i\times m_i}\\ {\mathbf{F}}_i\left({\mathbf{q}}_i\right)\end{array}\right]{\mathbf{\tau }}_i,\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill {\mathbf{y}}_i& ={\mathbf{F}}_i^T{\mathbf{M}}_i^{-1}{\mathbf{p}}_i,\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill H_i& =\frac{1}{2}{\mathbf{p}}_i^T{\mathbf{M}}_i^{-1}{\mathbf{p}}_i+V_i.\hfill \end{array}$$

(1c)

The state is composed of the joint-coordinates ${\mathbf{q}}_i\in {\mathbb{R}}^{n_i}$ and momenta ${\mathbf{p}}_i\in {\mathbb{R}}^{n_i}$, which relate to the joint-velocities via ${\mathbf{p}}_i={\mathbf{M}}_i\left({\mathbf{q}}_i\right){\dot{\mathbf{q}}}_i$. The input ${\mathbf{\tau }}_i\in {\mathbb{R}}^{m_i}$ enters via the input matrix ${\mathbf{F}}_i\left({\mathbf{q}}_i\right)\in {\mathbb{R}}^{n_i\times m_i}$. The system is fully actuated if $m_i=n_i$ and $\mathrm{rank}\left({\mathbf{F}}_i\left({\mathbf{q}}_i\right)\right)=n_i$ and is underactuated if $m_i<n_i$. The natural damping ${\mathbf{R}}_i({\mathbf{q}}_i,{\mathbf{p}}_i)\in {\mathbb{R}}^{n_i\times n_i}$ is assumed to be zero throughout this work. The total system energy is given by the Hamiltonian $H_i({\mathbf{q}}_i,{\mathbf{p}}_i)\in \mathbb{R}$, which is composed of the kinetic energy and the potential energy $V_i\left({\mathbf{q}}_i\right)\in \mathbb{R}$.

The generalized end-effector coordinates, ${\mathbf{z}}_i\left({\mathbf{q}}_i\right)\in {\mathbb{R}}^l$, denote the controlled system variable, for example Cartesian end-effector coordinates for a robotic arm or the 2D position of a vehicle. The generalized end-effector velocities are computed from the end-effector Jacobian ${\mathbf{J}}_i\left({\mathbf{q}}_i\right)\in {\mathbb{R}}^{l\times n_i}$, defined by

$${\dot{\mathbf{z}}}_i={\mathbf{J}}_i\left({\mathbf{q}}_i\right){\dot{\mathbf{q}}}_i,{\mathbf{J}}_i\left({\mathbf{q}}_i\right)=\frac{\partial {}^T{\mathbf{z}}_i}{\partial {\mathbf{q}}_i}.$$

(2)

We are now ready to formally state our problem definitions.

Problem 1.

Consider a network of N heterogeneous mechanical agents modeled by (1a)–(1c), communicating over a delay-free, undirected and connected graph $\mathcal{G}(\Sigma ,\mathcal{E})$. The cooperative control objectives on each edge pair ${\mathcal{E}}_{ij},{\mathcal{E}}_{ji}$ are specified by the final inter-agent displacement vector ${\mathbf{z}}_{ij}^{*}=-{\mathbf{z}}_{ji}^{*}$. The problem is formally solved by satisfying the following objectives:

$$\begin{array}{cccc}& \underset{t\to \infty }{lim}\left|\right|{\dot{\mathbf{q}}}_i\left|\right|=0,\forall i\in {\mathcal{I}}_N\hfill & & \mathit{\left(}\mathit{Damping}\mathit{\right)}\hfill \end{array}$$

(3)

$$\begin{array}{cccc}& \underset{t\to \infty }{lim}\left|\right|{\mathbf{z}}_i-{\mathbf{z}}_i^{*}\left|\right|=0,\forall i\in {\mathcal{I}}_L\hfill & & \mathit{\left(}\mathit{Leaders}\mathit{\right)}\hfill \end{array}$$

(4)

$$\begin{array}{cccc}& \underset{t\to \infty }{lim}\left|\right|{\mathbf{z}}_i-{\mathbf{z}}_j+{\mathbf{z}}_{ij}^{*}\left|\right|=0,\forall {\mathcal{E}}_{ij}\hfill & & \mathit{\left(}\mathit{Formation}\mathit{\right)}\hfill \end{array}$$

(5)

where ${\mathcal{I}}_N=\{1,\cdots ,N\}$ and ${\mathcal{I}}_L$ represents indices of the leaders.

Problem 2.

Consider Problem 1, where the bidirectional edge pair ${\mathcal{E}}_{ij},{\mathcal{E}}_{ji}\in \mathcal{E}$ is subject to unknown time-varying delays $T_{ij}\left(t\right),T_{ji}\left(t\right)\ge 0$, satisfying ${\dot{T}}_{ij}\left(t\right)\le 1,{\dot{T}}_{ji}\left(t\right)\le 1$. We formulate condition (5) with delays as

$$\underset{t\to \infty }{lim}\left|\right|{\mathbf{z}}_i(t-T_{ij}\left(t\right))-{\mathbf{z}}_j\left(t\right)+{\mathbf{z}}_{ij}^{*}\left|\right|=0,\forall {\mathcal{E}}_{ij}.$$

(6)

3. Review of Passivity and Single-Agent IDA-PBC

The passivity property links a system’s externally supplied power, stored energy and dissipated energy. We formally define passivity as follows.

Definition 1

([26]). A system is said to be passive if there exists a $C^1$ storage function $V\left(\mathbf{x}\right)>0,\forall \mathbf{x}\in {\mathbb{R}}^n\setminus \left\{\mathbf{0}\right\}$, $V\left(\mathbf{0}\right)=0$, and a dissipation function $S\ge 0$ for which the passivity property

$$V\left(\mathbf{x}\left(t\right)\right)-V\left(\mathbf{x}\left(0\right)\right)={\int }_0^t\mathbf{y}{\left(s\right)}^T\mathbf{\tau }\left(s\right)ds-{\int }_0^{t}S\left(s\right)ds$$

(7)

holds. An equivalent expression, obtained by differentiation, is

$$\dot{V}+S={\mathbf{\tau }}^T\mathbf{y}.$$

(8)

When a passive system is not exchanging energy via its input–output port, that is if ${\mathbf{\tau }}^T\mathbf{y}=\mathbf{0}$, then we have $\dot{V}=-S\le 0$, which is one of the necessary conditions to construct Lyapunov functions. Hence, the passivity property is a stability property that extends to systems where energy is exchanged with an external system (e.g., a controller). The Hamiltonian dynamical Equations (1a)–(1c) can be shown to be passive.

The open-loop equilibrium ${\mathbf{q}}_{\mathrm{OL}}^{*}$ of the system generally does not coincide with the control objective ${\mathbf{q}}^{*}$. We therefore consider a control law $\mathbf{\tau }$, such that the closed-loop dynamics attain the desired passive dynamics (subscript d). Introducing a desired inertia matrix ${\mathbf{M}}_d\left(\mathbf{q}\right)={\mathbf{M}}_d{\left(\mathbf{q}\right)}^T>{\mathbf{0}}_n$, damping matrix ${\mathbf{K}}_v(\mathbf{q},\mathbf{p})>{\mathbf{0}}_m$ and ${\mathbf{J}}_2(\mathbf{q},\mathbf{p})=-{\mathbf{J}}_2{(\mathbf{q},\mathbf{p})}^T$ to introduce necessary gyroscopic forces, the desired dynamics are given by

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\dot{\mathbf{q}}\\ \dot{\mathbf{p}}\end{array}\right]& =\left[\begin{array}{cc}{\mathbf{0}}_n& {\mathbf{M}}^{-1}{\mathbf{M}}_d\\ -{\mathbf{M}}_d{\mathbf{M}}^{-1}& {\mathbf{J}}_2-\mathbf{F}{\mathbf{K}}_v{\mathbf{F}}^T\end{array}\right]\left[\begin{array}{c}\frac{\partial H_d}{\partial \mathbf{q}}\\ \frac{\partial H_d}{\partial \mathbf{p}}\end{array}\right]+\left[\begin{array}{c}{\mathbf{0}}_{n\times m}\\ \mathbf{F}\end{array}\right]\widehat{\mathbf{\tau }},\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill {\mathbf{y}}_d& ={\mathbf{F}}^T{\mathbf{M}}^{-1}\mathbf{p},\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill H_d& =\frac{1}{2}{\mathbf{p}}^T{\mathbf{M}}_d^{-1}\mathbf{p}+V_d\left(\mathbf{q}\right).\hfill \end{array}$$

(9c)

The desired potential function $V_d\left(\mathbf{q}\right)\ge 0$ is designed such that it attains a minimum at the control objective, i.e., ${\mathbf{q}}^{*}={\mathrm{argmin}}_{\mathbf{q}}{V}_d\left(\mathbf{q}\right)$ and is zero if and only if $\mathbf{q}={\mathbf{q}}^{*}$. Equations (1a)–(1c) and (9a)–(9c) directly yields a control law in the fully actuated case. For underactuated systems, we find a set of equations that can be decoupled using the full rank transformation

$$\left[\begin{array}{c}{\mathbf{F}}^T\\ {\mathbf{F}}^{\perp }\end{array}\right]\in {\mathbb{R}}^{n\times n},$$

where ${\mathbf{F}}^{\perp }$ is an annihilator of $\mathbf{F}$, such that ${\mathbf{F}}^{\perp }\mathbf{F}={\mathbf{0}}_{n-m\times m}$. This results in two sets of equations. The last $n-m$ rows denote necessary conditions for matching the plant with the desired dynamics and are referred to as the matching conditions. They are often split in a condition on kinetic energy terms

$${\mathbf{F}}^{\perp }\left(\frac{\partial }{\partial \mathbf{q}}\left({\mathbf{p}}^T{\mathbf{M}}^{-1}\mathbf{p}\right)-{\mathbf{M}}_d{\mathbf{M}}^{-1}\frac{\partial }{\partial \mathbf{q}}\left({\mathbf{p}}^T{\mathbf{M}}_d^{-1}\mathbf{p}\right)+2{\mathbf{J}}_2{\mathbf{M}}_d^{-1}\mathbf{p}\right)=\mathbf{0},$$

(10)

and in the potential energy terms

$${\mathbf{F}}^{\perp }\left(\frac{\partial V}{\partial \mathbf{q}}-{\mathbf{M}}_d{\mathbf{M}}^{-1}\frac{\partial V_d}{\partial \mathbf{q}}\right)=\mathbf{0}.$$

(11)

Whereas for fully actuated systems, the potential energy can be shaped directly; for underactuated systems, often the kinetic energy needs to be shaped along with the potential energy in order to achieve the control objective. Hence, the main problem in IDA-PBC design is to find a set of matrices ${\mathbf{M}}_d,{\mathbf{J}}_2$ and potential $V_d$ that satisfy the matching conditions (10) and (11). Although no general solutions to these equations exist, for sub classes of systems an explicit solution is available (e.g., for systems with one degree of underactuation such that $n-m=1$ [17]). Given a solution to the matching equations, the resulting IDA-PBC law is given by the first m rows

$$\begin{array}{cc}\hfill \mathbf{\tau }& ={\mathbf{F}}^{†}\left(\frac{\partial H}{\partial \mathbf{q}}-{\mathbf{M}}_d{\mathbf{M}}^{-1}\frac{\partial H_d}{\partial \mathbf{q}}+{\mathbf{J}}_2{\mathbf{M}}_d^{-1}\mathbf{p}\right)-{\mathbf{K}}_v{\mathbf{y}}_d.\hfill \end{array}$$

The proof of [17], Proposition 1, shows that $({\mathbf{q}}^{*},\mathbf{0})$ is stable if ${\mathbf{M}}_d$ is locally positive definite in a neighborhood around ${\mathbf{q}}^{*}$ and is asymptotically stable if, additionally, the equilibrium $({\mathbf{q}}^{*},\mathbf{0})$ is locally detectable from the output ${\mathbf{y}}_d$, which holds if ${\mathbf{y}}_d\to \mathbf{0}$ implies $\mathbf{q}\to {\mathbf{q}}^{*}$.

4. Cooperative IDA-PBC

In the following we solve Problem 1 for networks of fully actuated and underactuated systems.

4.1. Guaranteed Local Matching

The goal of our cooperative scheme is to satisfy the local matching conditions (10) and (11) for each agent, independent of the received cooperative input, and using existing single-agent solutions. We propose to use the coordinates $\mathbf{z}\left(\mathbf{q}\right)$ as the cooperative outputs and leverage the transformation from the coordinates $\mathbf{q}$ to $\mathbf{z}$ to satisfy the matching conditions, independently of the cooperative control input. This leaves the cooperative control input free for achieving the cooperative control objective. In particular, we pose the following necessary condition on the single-agent solution.

Assumption 1.

$${\mathbf{F}}^{\perp }{\mathbf{M}}_d{\mathbf{M}}^{-1}\frac{\partial \mathbf{z}}{\partial \mathbf{q}}={\mathbf{F}}^{\perp }{\mathbf{M}}_d{\mathbf{M}}^{-1}{\mathbf{J}}^T={\mathbf{0}}_{n-m\times l}.$$

Through this assumption, the input derived from the cooperative control input is exclusively in the actuated directions and ensures that the cooperative input cannot violate the matching conditions. The proposed cooperative control method relies on Assumption 1 to hold for the single-agent IDA-PBC solutions of each individual system. We note that the kernel of ${\mathbf{F}}^{\perp }{\mathbf{M}}_d{\mathbf{M}}^{-1}$ is of rank m such that there exists an m-dimensional subspace where the cooperative coordinates can be defined such that Assumption 1 holds. For the large class of systems with underactuation degree one, that is, where $n-m=1$, an explicit solution to the matching equations can be found in [17] where Assumption 1 is satisfied [29]. In particular, the cooperative coordinates $\mathbf{z}$ converge to the end-effector coordinates when the unactuated coordinate converges to zero. These solutions, therefore, allow us to control the end-effectors of these systems, cooperatively. Consider the following structure for the desired potential to accommodate local and cooperative control

$$V_d\left(\mathbf{q}\right)=V_s\left(\mathbf{q}\right)+V_c\left(\mathbf{z}\left(\mathbf{q}\right)\right),$$

(12)

with gradient

$$\frac{\partial V_d\left(\mathbf{q}\right)}{\partial \mathbf{q}}=\frac{\partial V_s\left(\mathbf{q}\right)}{\partial \mathbf{q}}+{\mathbf{J}}^T\frac{\partial V_c\left(\mathbf{z}\right)}{\partial \mathbf{z}}.$$

(13)

Substituting this desired potential function in the potential matching condition (11) and separating cooperative and local potentials results in the two conditions

$$\begin{array}{cc}\hfill {\mathbf{F}}^{\perp }\left(\frac{\partial V}{\partial \mathbf{q}}-{\mathbf{M}}_d{\mathbf{M}}^{-1}\frac{\partial V_s}{\partial \mathbf{q}}\right)& =\mathbf{0},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathbf{F}}^{\perp }{\mathbf{M}}_d{\mathbf{M}}^{-1}{\mathbf{J}}^T\frac{\partial V_c}{\partial \mathbf{z}}& =\mathbf{0}.\hfill \end{array}$$

(15)

Condition (14) is the single-agent matching condition (11) and is satisfied by construction. By virtue of the cooperative Jacobian $\mathbf{J}$ and Assumption 1, condition (15) holds for all cooperative inputs. The proposed decomposition has not modified the kinetic energy matching conditions (10), which are, therefore, satisfied by the single-agent solution. Hence, the proposed decomposition satisfies the matching conditions by design, independently of the cooperative input $\frac{\partial V_c}{\partial \mathbf{z}}$.

4.2. Multi-Agent IDA-PBC

In the following, we will formulate a multi-agent system from the set of single-agent systems and solve the IDA-PBC problem for the composed system. We formulate the uncontrolled dynamics as

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\dot{\overline{\mathbf{q}}}\\ \dot{\overline{\mathbf{p}}}\end{array}\right]& =\left[\begin{array}{cc}{\mathbf{0}}_{\overline{n}}& {\mathbf{I}}_{\overline{n}}\\ -{\mathbf{I}}_{\overline{n}}& {\mathbf{0}}_{\overline{n}}\end{array}\right]\left[\begin{array}{c}\frac{\partial \overline{H}}{\partial \overline{\mathbf{q}}}\\ \frac{\partial \overline{H}}{\partial \overline{\mathbf{p}}}\end{array}\right]+\left[\begin{array}{c}{\mathbf{0}}_{\overline{n}\times \overline{m}}\\ \overline{\mathbf{F}}\end{array}\right]\overline{\mathbf{\tau }},\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill \overline{\mathbf{y}}& ={\overline{\mathbf{F}}}^T{\overline{\mathbf{M}}}^{-1}\overline{\mathbf{p}},\hfill \end{array}$$

(16b)

$$\begin{array}{cc}\hfill \overline{H}& =\frac{1}{2}{\overline{\mathbf{p}}}^T{\overline{\mathbf{M}}}^{-1}\overline{\mathbf{p}}+\overline{V}\left(\overline{\mathbf{q}}\right),\hfill \end{array}$$

(16c)

in which the multi-agent variables are given by

$$\begin{array}{cc}\hfill & \overline{n}=\sum _{i=1}^N{n}_i,\overline{m}=\sum _{i=1}^N{m}_i,\overline{V}=\sum _{i=1}^N{V}_i,\hfill \\ \hfill & \overline{\mathbf{q}}=\left[\begin{array}{c}{\mathbf{q}}_1\\ ⋮\\ {\mathbf{q}}_N\end{array}\right],\overline{\mathbf{p}}=\left[\begin{array}{c}{\mathbf{p}}_1\\ ⋮\\ {\mathbf{p}}_N\end{array}\right],\overline{\mathbf{\tau }}=\left[\begin{array}{c}{\mathbf{\tau }}_1\\ ⋮\\ {\mathbf{\tau }}_N\end{array}\right],\overline{\mathbf{y}}=\left[\begin{array}{c}{\mathbf{y}}_1\\ ⋮\\ {\mathbf{y}}_N\end{array}\right],\hfill \\ \hfill & \overline{\mathbf{M}}=\left[\begin{array}{ccc}{\mathbf{M}}_1& & \\ & \ddots & \\ & & {\mathbf{M}}_N\end{array}\right],\overline{\mathbf{F}}=\left[\begin{array}{ccc}{\mathbf{F}}_1& & \\ & \ddots & \\ & & {\mathbf{F}}_N\end{array}\right].\hfill \end{array}$$

Similarly to the single-agent problem, we introduce the desired multi-agent dynamics

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\dot{\overline{\mathbf{q}}}\\ \dot{\overline{\mathbf{p}}}\end{array}\right]& =\left[\begin{array}{cc}{\mathbf{0}}_{\overline{n}}& {\overline{\mathbf{M}}}^{-1}{\overline{\mathbf{M}}}_d\\ -{\overline{\mathbf{M}}}_d{\overline{\mathbf{M}}}^{-1}& {\overline{\mathbf{J}}}_2-\overline{\mathbf{F}}{\overline{\mathbf{K}}}_v{\overline{\mathbf{F}}}^T\end{array}\right]\left[\begin{array}{c}\frac{\partial {\overline{H}}_d}{\partial \overline{\mathbf{q}}}\\ \frac{\partial {\overline{H}}_d}{\partial \overline{\mathbf{p}}}\end{array}\right]+\left[\begin{array}{c}{\mathbf{0}}_{\overline{n}\times \overline{m}}\\ \overline{\mathbf{F}}\end{array}\right]\widehat{\overline{\mathbf{\tau }}},\hfill \end{array}$$

(17a)

$$\begin{array}{cc}\hfill {\overline{\mathbf{y}}}_d& ={\overline{\mathbf{F}}}^T{\overline{\mathbf{M}}}_d^{-1}\overline{\mathbf{p}},\hfill \end{array}$$

(17b)

$$\begin{array}{cc}\hfill {\overline{H}}_d& =\frac{1}{2}{\overline{\mathbf{p}}}^T{\overline{\mathbf{M}}}_d^{-1}\overline{\mathbf{p}}+{\overline{V}}_d\left(\overline{\mathbf{q}}\right),\hfill \end{array}$$

(17c)

with ${\overline{\mathbf{M}}}_d$ a block-diagonal composition of single-agent solutions

$$\begin{array}{cc}\hfill & {\overline{\mathbf{M}}}_d=\left[\begin{array}{ccc}{\mathbf{M}}_{d,1}& & \\ & \ddots & \\ & & {\mathbf{M}}_{d,N},\end{array}\right]\hfill \end{array}$$

and similarly for ${\overline{\mathbf{K}}}_v,{\overline{\mathbf{J}}}_2$ (the case where ${\overline{\mathbf{M}}}_d$ and ${\overline{\mathbf{J}}}_2$ contain off-diagonal terms, which introduce interaction between systems; the interested reader is referred to [29], Section 7.2.2, for the treatment of such cases). We extend the decomposed potential (12) to the multi-agent case, by summing the local terms and coupling the cooperative terms, that is,

$${\overline{V}}_d={\overline{V}}_c({\mathbf{z}}_1,\cdots ,{\mathbf{z}}_N)+\sum _{i=1}^N{V}_{s,i}.$$

(18)

The cooperative desired potential function ${\overline{V}}_c$, which depends on all cooperative coordinates in the network, generates the cooperative inputs. Hence, the cooperative controller is a gradient descent approach over the cooperative potential energy function (i.e., forcing the end-effectors in the direction of the largest decrease in artificial energy). To solve Problem I we require that ${\overline{V}}_c=0$ if and only if (4) and (5) are satisfied, similar to the assignment of $V_s$ in the single-agent case. The following constructive proof solves the proposed multi-agent IDA-PBC problem.

Theorem 1.

Consider a network with N fully actuated and/or underactuated agents, where for each agent i, single-agent solutions for ${\mathbf{M}}_{d,i},{\mathbf{J}}_{2,i},V_{s,i}$ are known that satisfy (10) and (14), and the coordinates ${\mathbf{z}}_i$ are such that the Jacobian ${\mathbf{J}}_i$ satisfies Assumption 1. Then, the distributed control inputs

$${\mathbf{\tau }}_i={\mathbf{F}}_i^{†}\left(\frac{\partial H_i}{\partial {\mathbf{q}}_i}-{\mathbf{M}}_{d,i}{\mathbf{M}}_i^{-1}\frac{\partial {\overline{H}}_{d,i}}{\partial {\mathbf{q}}_i}+{\mathbf{J}}_{2,i}{\mathbf{M}}_{d,i}^{-1}{\mathbf{p}}_i\right)-{\mathbf{K}}_{v,i}{\mathbf{y}}_{d,i},$$

(19)

with

$${\overline{H}}_{d,i}=\frac{1}{2}{\mathbf{p}}_i^T{\mathbf{M}}_{d,i}^{-1}{\mathbf{p}}_i+V_{s,i}+{\overline{V}}_c$$

(20)

solve Problem 1.

Proof. 

We match the multi-agent plants (16a)–(16c) with the multi-agent desired dynamics (17a)–(17c). The resulting kinetic energy matching condition is decoupled into the single-agent kinetic matching condition (10) and is satisfied by the single-agent solutions. The potential energy matching conditions are

$${\mathbf{F}}_i^{\perp }\left(\frac{\partial V_i}{\partial {\mathbf{q}}_i}-{\mathbf{M}}_{d,i}{\mathbf{M}}_i^{-1}\frac{\partial {\overline{V}}_d}{\partial {\mathbf{q}}_i}\right)=\mathbf{0},\forall i\in {\mathcal{I}}_N.$$

(21)

Using the partitioning (18), these conditions are split into

$$\begin{array}{cc}\hfill {\mathbf{F}}_i^{\perp }\left(\frac{\partial V_i}{\partial {\mathbf{q}}_i}-{\mathbf{M}}_{d,i}{\mathbf{M}}_i^{-1}\frac{\partial V_{s,i}}{\partial {\mathbf{q}}_i}\right)& =\mathbf{0},\forall i\in {\mathcal{I}}_N,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\mathbf{F}}_i^{\perp }{\mathbf{M}}_{d,i}{\mathbf{M}}_i^{-1}{\mathbf{J}}_i^T\frac{\partial {\overline{V}}_c}{\partial {\mathbf{z}}_i}& =\mathbf{0},\forall i\in {\mathcal{I}}_N.\hfill \end{array}$$

(23)

Condition (22) is satisfied by the single-agent solution and (23) is satisfied by the choice of cooperative coordinates ${\mathbf{z}}_i$. Control law (19) is obtained from the matching equations. Invoking single-agent IDA-PBC stability proof [17], Proposition 1 ensures $\dot{\overline{\mathbf{q}}}\to \mathbf{0}$, ${\overline{V}}_d\to 0$, which implies $V_{s,i}\to 0,\forall i$ and ${\overline{V}}_c\to 0$. The latter, by construction, ensures that conditions (4) and (5) are satisfied. □

Notice that the cooperative input enters control law (19) via the gradient of ${\overline{V}}_c$ with respect to ${\mathbf{z}}_i$ and that we can compute its value by communicating these variables over the network. A possible choice for the cooperative potential function ${\overline{V}}_c$ is the squared sum of the cooperative control errors

$${\overline{V}}_c=\frac{1}{4}\sum _{i=1}^N\sum _{j=1}^N\left|\right|{\mathbf{z}}_i-{\mathbf{z}}_j+{\mathbf{z}}_{ij}^{*}{\left|\right|}_{{\mathcal{A}}_{ij}}^2+\frac{1}{2}\sum _{i=1}^N\left|\right|{\mathbf{z}}_i-{\mathbf{z}}_i^{*}{\left|\right|}_{{\mathcal{B}}_i}^2,$$

(24)

where the term ${\mathcal{A}}_{ij}$ denotes adjacency, i.e., ${\mathcal{A}}_{ij}>{\mathbf{0}}_{l\times l}$ if and only if node i and j are connected in the graph. The matrices ${\mathcal{B}}_i$ are leader matrices with non-zero weights if and only if the associated coordinate is tracking leader reference ${\mathbf{z}}_i^{*}$. This cooperative potential is positive semi-definite and its unique minimum satisfies (4) and (5).

4.3. Concluding Remarks

The proposed multi-agent IDA-PBC approach is applicable to fully actuated systems as well as a large class of existing underactuated systems, most notably those with underactuation degree one. We satisfy the matching conditions for all cooperative inputs and, therefore, the method is, to a degree, robust with regards to time delays in the communication network. However, our analysis on the composed multi-agent system assumes the absence of time delays and, hence, stability is not guaranteed when delays are present.

5. Cooperative r-Passivity-Based Control

In the following section we introduce, in the same context, an alternative PBC method for fully actuated systems that preserves the stability guarantee in the presence of time delays. We, therefore, solve Problem II for networks of heterogeneous fully actuated systems. Our approach is based on the cooperative PBC scheme proposed in [26] (see Figure 1), which we briefly summarize here.

5.1. Cooperative PBC with Communication Delays

Passive cooperation relies on passivity of the network. An approach for guaranteeing network passivity in the presence of delays is the scattering transformation (ST) [5]. The ST transforms the networked input $\mathbf{\tau }$ and output $\mathbf{r}$ of an agent into wave-variables, which are communicated over the network. The transformation, which acts on each side of the communication network, is given by

$$\begin{array}{cc}\hfill {\mathbf{s}}_{ij}^{+}=\frac{1}{\sqrt{2b}}(-{\mathbf{\tau }}_{jsi}+b{\mathbf{r}}_{js})& ;{\mathbf{s}}_{ij}^{-}=\frac{1}{\sqrt{2b}}(-{\mathbf{\tau }}_{jsi}-b{\mathbf{r}}_{js})\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\mathbf{s}}_{ji}^{+}=\frac{1}{\sqrt{2b}}({\mathbf{\tau }}_{isj}+b{\mathbf{r}}_{is})& ;{\mathbf{s}}_{ji}^{-}=\frac{1}{\sqrt{2b}}({\mathbf{\tau }}_{isj}-b{\mathbf{r}}_{is}),\hfill \end{array}$$

(26)

where $b>0$ tunes the virtual impedance of the network. The wave variables ${\mathbf{s}}_{ij}^{+},{\mathbf{s}}_{ij}^{-},{\mathbf{s}}_{ji}^{+}$ and ${\mathbf{s}}_{ji}^{-}$ are communicated over the network instead of the original inputs and outputs (see Figure 1). They transmit the information for cooperation over the network in packets of virtual energy. The transformation mimics physical communication lines, which obey an energy conservation law and are, therefore, passive. This passivity can be established by explicitly quantifying the energy stored in the network (see [5]). Since no energy is dissipated, the network is lossless in the presence of arbitrary constant delays. In [30], a delay-dependent gain is introduced into the network, which extends the passivity property to the case of time-varying delays under the assumption that ${\dot{T}}_{ij}\left(t\right)\le 1,\forall {\mathcal{E}}_{ij}$, i.e., the delay does not change faster than time itself. In discrete-time, time-varying delays and loss of packets both result in missing information on the receiving end [31]. In these cases, passivity can be preserved by passively reconstructing the wave references [31]. This strategy, in contrast to the continuous-time case, can handle delays that change faster than time itself.

The multi-agent PBC scheme of [26] consists of (i) a network with the ST (lossless), (ii) passive cooperative controls $\varphi (S_{jsi},U_{jsi})$ and (iii) passive agents ($S_i,U_i$). The following convergence property is obtained.

Theorem 2.

([26] Theorems 3.3 and 3.4). The control scheme depicted in Figure 1 with passive agents, passive controls and the ST (25) is asymptotically stable, and the system converges to the set where

$$S_{jsi}\to 0,\forall {\mathcal{E}}_{ij},S_i\to 0,\forall i\in {\mathcal{I}}_N,$$

(27)

where $S_{jsi}$ and $S_i$ denote the storage functions of the controls and agents, respectively.

The authors of [27] use the outputs

$${\mathbf{r}}_{q,i}={\dot{\mathbf{q}}}_i+\lambda {\mathbf{q}}_i,\lambda >0,$$

(28)

in the control scheme of Figure 1 to synchronize coordinates rather than velocities. In the following, we apply a modified version of these outputs and the scheme of Figure 1 to synchronize generalized end-effector coordinates.

5.2. r-Passivity for Coordinate Synchronization

Define the outputs as

$${\mathbf{r}}_i={\dot{\mathbf{z}}}_i+\lambda {\mathbf{z}}_i,\lambda >0,$$

(29)

where ${\mathbf{z}}_i\left({\mathbf{q}}_i\right)$ are generalized end-effector coordinates. The velocity component is necessary to show passivity, while the coordinate component ensures that the control objectives are observable from the output. The latter prevents drift when packets are lost in the network [27]. In the remainder, we use the term r-passive to refer to (sub)systems that are passive (notice that the passivity that we consider is virtual and it is not directly related to the physical energy of the system) with respect to the input–output pair $({\mathbf{\tau }}_i,{\mathbf{r}}_i)$. We propose to apply gradient descent on a cooperative potential as a cooperative control term, similarly to cooperative IDA-PBC. Specifically, we propose the potential

$${\overline{V}}_c^r=\frac{1}{4}\sum _{i=1}^N\sum _{j=1}^N\left|\right|{\mathbf{r}}_i-{\mathbf{r}}_{js}+\frac{\lambda }{2}{\mathbf{z}}_{ij}^{*}{\left|\right|}_{{\mathcal{A}}_{ij}}^2+\frac{1}{2}\sum _{i=1}^N\left|\right|{\mathbf{r}}_i-{\mathbf{r}}_i^{*}{\left|\right|}_{{\mathcal{B}}_i}^2.$$

(30)

Compared to the previous potential (24), the wave references replace the networked outputs. We will use the shorthand $-{\widehat{\mathbf{r}}}_{jsi}$ to denote the cooperative error term ${\mathbf{r}}_i-{\mathbf{r}}_{js}+\frac{\lambda }{2}{\mathbf{z}}_{ij}^{*}$, where the factor $\frac{\lambda }{2}$ compensates for the gain in the output and the ST. The cooperative control input of each agent is computed as the summed gradient over the networked outputs of its neighbors

$${\mathbf{\tau }}_{jsi}\left({\widehat{\mathbf{r}}}_{jsi}\right)=\frac{{\partial }^T{\overline{V}}_c^r\left({\widehat{\mathbf{r}}}_{jsi}\right)}{\partial {\widehat{\mathbf{r}}}_{jsi}},{\mathbf{\tau }}_i=\sum _{j\in {\mathcal{N}}_i}{\mathbf{\tau }}_{jsi},$$

(31)

where ${\mathcal{N}}_i$ denotes the set of neighbors of agent i. The cooperative controls (31) are odd, i.e., $-{\mathbf{\tau }}_{jsi}\left({\widehat{\mathbf{r}}}_{jsi}\right)={\mathbf{\tau }}_{jsi}(-{\widehat{\mathbf{r}}}_{jsi})$ and, hence,

$${\mathbf{\tau }}_{jsi}^T{\widehat{\mathbf{r}}}_{jsi}=S_{jsi}\ge 0,$$

which implies that these inter-agent couplings are r-passive.

5.3. Local Controller Design for r-Passivity

Although agents are passive in their regular input and output, they are generally not passive with respect to our modified output ${\mathbf{r}}_i$, which is necessary to invoke the results of [26] on the control scheme depicted in Figure 1. In the following, we show that for fully actuated systems, a control law exists that makes agents r-passive as viewed from the network. A novel controller design (see Figure 2), to which we refer as r-passivity-based control (r-PBC), is derived in the following theorem.

Theorem 3.

Agent i with dynamics (1a)–(1c), where $n_i=m_i$ and the r-PBC law

$${\mathbf{\tau }}_i=\frac{\partial H_i}{\partial {\mathbf{q}}_i}+{\mathbf{M}}_i{\mathbf{J}}_i^{†}\left({\mathbf{\tau }}_{c,i}-{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i\right),$$

(32)

where

$${\mathbf{K}}_{z,i}={\mathbf{J}}_i\left((\lambda +{\gamma }_i){\mathbf{I}}_{n_i}-{\mathbf{M}}_i^{-1}{\dot{\mathbf{M}}}_i\right)+{\dot{\mathbf{J}}}_i,$$

(33)

with ${\gamma }_i>0$ a tuning parameter, is r-passive with respect to the storage and dissipation functions

$$U_i=\frac{1}{2}{\mathbf{r}}_i^T{\mathbf{r}}_i+\frac{1}{2}{\gamma }_i\lambda {\mathbf{z}}_i^T{\mathbf{z}}_i,S_i={\gamma }_i{\dot{\mathbf{z}}}_i^T{\dot{\mathbf{z}}}_i.$$

(34)

Proof. 

The derivative of the storage function is

$$\begin{array}{cc}\hfill {\dot{U}}_i& ={\dot{\mathbf{r}}}_i^T{\mathbf{r}}_i+{\gamma }_i\lambda {\dot{\mathbf{z}}}_i^T{\mathbf{z}}_i\hfill \\ \hfill & ={({\dot{\mathbf{r}}}_i+{\gamma }_i{\dot{\mathbf{z}}}_i)}^T{\mathbf{r}}_i-{\gamma }_i{\dot{\mathbf{z}}}_i^T{\dot{\mathbf{z}}}_i.\hfill \end{array}$$

Substituting in the differential passivity property (8) yields

$${({\dot{\mathbf{r}}}_i+{\gamma }_i{\dot{\mathbf{z}}}_i)}^T{\mathbf{r}}_i={\mathbf{\tau }}_{c,i}^T{\mathbf{r}}_i.$$

Hence the l-dimensional dynamics that achieve r-passivity are

$${\mathbf{\tau }}_{c,i}={\dot{\mathbf{r}}}_i+{\gamma }_i{\dot{\mathbf{z}}}_i={\ddot{\mathbf{z}}}_i+(\lambda +{\gamma }_i){\dot{\mathbf{z}}}_i.$$

which may be expanded as

$$\begin{array}{cc}\hfill {\mathbf{\tau }}_{c,i}& =(\lambda +{\gamma }_i){\mathbf{J}}_i{\dot{\mathbf{q}}}_i+{\mathbf{J}}_i({\dot{{\mathbf{M}}_i}}^{-1}{\mathbf{p}}_i+{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i)+\dot{{\mathbf{J}}_i}{\dot{\mathbf{q}}}_i,\hfill \\ \hfill & ={\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i+{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i,\hfill \end{array}$$

Feeding back the velocity term ${\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i$ by defining ${\mathbf{\tau }}_{c,i}:={\widehat{\mathbf{\tau }}}_{c,i}+{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i$ reduces the passive dynamics to

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\tau }}}_{c,i}& +{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i={\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i+{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\tau }}}_{c,i}& ={\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i.\hfill \end{array}$$

(36)

To find the corresponding set of n-dimensional system dynamics, note that ${\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\mathbf{M}}_i{\mathbf{J}}_i^{†}={\mathbf{I}}_{l\times l}$; hence,

$${\mathbf{J}}_i{\mathbf{M}}_i^{-1}\left({\mathbf{M}}_i{\mathbf{J}}_i^{†}{\widehat{\mathbf{\tau }}}_{c,i}-{\dot{\mathbf{p}}}_i\right)={\widehat{\mathbf{\tau }}}_{c,i}-{\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i=\mathbf{0}.$$

(37)

To obtain passivity, we match these dynamics with the plant momenta equations, i.e.,

$${\dot{\mathbf{p}}}_i={\mathbf{M}}_i{\mathbf{J}}_i^{†}{\widehat{\mathbf{\tau }}}_{c,i}=-\frac{\partial H_i}{\partial {\mathbf{q}}_i}+{\mathbf{\tau }}_i.$$

(38)

The proposed control laws satisfy this equation. □

The cooperative convergence of the scheme with these r-passive agents, in the sense that $S_i\to 0$, $\dot{\mathbf{z}}\to \mathbf{0}$, is analyzed in Section 5.4. We remark that convergence of $S_i$ to zero merely implies ${\dot{\mathbf{z}}}_i\to \mathbf{0}$, i.e., only the cooperatively controlled velocities are damped. Therefore, we need to additionally damp the velocities in the null-space of the cooperative task in the case of redundant systems ($n_i>l$). In the following, we apply subtask optimization for this purpose as presented in [32].

Consider a potential function $V_{p,i}\left({\mathbf{q}}_i\right)\ge 0$ and the null-space definition ${\mathbf{J}}_i^{\perp }=({\mathbf{I}}_{n_i}-{\mathbf{J}}_i^{†}{\mathbf{J}}_i)$, which has the following properties:

$${\mathbf{J}}_i{\mathbf{J}}_i^{\perp }={\mathbf{0}}_{l\times n_i},{\mathbf{J}}_i^{\perp }{\mathbf{J}}_i^{†}={\mathbf{0}}_{n_i\times l},{\mathbf{J}}_i^{\perp }{\mathbf{J}}_i^{\perp }={\mathbf{J}}_i^{\perp }.$$

(39)

Then a subspace tracking error can be defined as [32]

$${\mathbf{e}}_{s,i}={\mathbf{J}}_i^{\perp }{\mathbf{w}}_i,{\mathbf{w}}_i={\dot{\mathbf{q}}}_i+\frac{\partial V_{p,i}}{\partial {\mathbf{q}}_i}.$$

(40)

The null-space definition serves to damp non-cooperative velocities without influencing the cooperative passivity properties, as we show in the following theorem.

Theorem 4.

Agent i with dynamics (1a)–(1c), where $n_i=m_i$ and the r-PBC law

$${\mathbf{\tau }}_i=\frac{\partial H_i}{\partial {\mathbf{q}}_i}+{\mathbf{M}}_i{\mathbf{J}}_i^{†}\left({\mathbf{\tau }}_{c,i}-{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i\right)-{\mathbf{M}}_i{\mathbf{J}}_i^{\perp }\left({\xi }_i\frac{\partial V_{p,i}}{\partial {\mathbf{q}}_i}+{\mathbf{K}}_{v,i}{\dot{\mathbf{q}}}_i+{\dot{\mathbf{J}}}_i^{\perp }{\mathbf{w}}_i\right),$$

(41)

with ${\mathbf{K}}_{z,i}$ defined by (33) and

$${\mathbf{K}}_{v,i}=\frac{{\partial }^T}{\partial {\mathbf{q}}_i}\left(\frac{\partial V_{p,i}}{\partial {\mathbf{q}}_i}\right)+{\xi }_i{\mathbf{I}}_{n_i}-{\mathbf{M}}_i^{-1}{\dot{\mathbf{M}}}_i,$$

(42)

with local constant gain ${\xi }_i>0$, is r-passive with respect to the storage and dissipation functions (34), while ${\mathbf{e}}_{s,i}\to \mathbf{0}$.

Proof. 

The proof of passivity follows the proof of Theorem 3. The last term of the proposed control law does not influence the cooperative dynamics since ${\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\mathbf{M}}_i{\mathbf{J}}_i^{\perp }={\mathbf{0}}_{l\times l}$. To show convergence of the non-cooperative coordinates, consider the Lyapunov candidate

$$U_i=\frac{1}{2}{\mathbf{e}}_{s,i}^T{\mathbf{e}}_{s,i}.$$

(43)

The derivative is

$$\begin{array}{cc}\hfill {\dot{U}}_i& ={\mathbf{w}}_i^T{\mathbf{J}}_i^{\perp }{\dot{\mathbf{w}}}_i+{\mathbf{w}}_i^T{\mathbf{J}}_i^{\perp }{\dot{\mathbf{J}}}^{\perp }{\mathbf{w}}_i.\hfill \\ \hfill & ={\mathbf{w}}_i^T{\mathbf{J}}_i^{\perp }\left({\ddot{\mathbf{q}}}_i+\dot{\frac{\partial V_{p,i}}{\partial {\mathbf{q}}_i}}\right)+{\mathbf{w}}_i^T{\mathbf{J}}_i^{\perp }{\dot{\mathbf{J}}}^{\perp }{\mathbf{w}}_i.\hfill \\ \hfill & ={\mathbf{w}}_i^T{\mathbf{J}}_i^{\perp }\left[{\dot{\mathbf{M}}}_i^{-1}{\mathbf{M}}_i{\dot{\mathbf{q}}}_i-{\mathbf{J}}_i^{\perp }\left({\xi }_i\frac{\partial V_{p,i}}{\partial {\mathbf{q}}_i}+{\mathbf{K}}_{v,i}{\dot{\mathbf{q}}}_i+{\dot{\mathbf{J}}}_i^{\perp }{\mathbf{w}}_i\right)+\dot{\frac{\partial V_{p,i}}{\partial {\mathbf{q}}_i}}\right]+{\mathbf{w}}_i^T{\mathbf{J}}_i^{\perp }{\dot{\mathbf{J}}}_i^{\perp }{\mathbf{w}}_i.\hfill \end{array}$$

where we substituted the dynamics described by the momenta ${\dot{\mathbf{p}}}_i$. Substituting the proposed ${\mathbf{K}}_{v,i}$ yields

$${\dot{U}}_i=-{\xi }_i{\mathbf{w}}_i{\mathbf{J}}_i^{\perp }{\mathbf{w}}_i=-{\xi }_i{\mathbf{e}}_{s,i}^T{\mathbf{e}}_{s,i}\le 0.$$

(44)

Hence, ${\mathbf{e}}_{s,i}\to \mathbf{0}$. □

A vanishing subspace tracking error, ${\mathbf{e}}_{s,i}\to \mathbf{0}$, results in tracking of the subtasks as long as its vector lies in the null-space of the cooperative task [32]. Since convergence to the minimum of $V_{p,i}$ implies that ${\mathbf{w}}_i={\dot{\mathbf{q}}}_i$, we find that the proposed local controller forces the non-cooperative velocities to zero.

5.4. Cooperative Synchronization

We now show that the multi-agent r-PBC scheme, locally controlled by r-PBC, solves Problem 2.

Theorem 5.

The control scheme depicted in Figure 1 with the ST (25) and (26), outputs (29), controls (30) and (31) and agents locally controlled by the r-PBC law (41) solves Problem 2.

Proof. 

Since the requirements for Theorem 2 are satisfied, we may invoke the following result

$$S_i\to 0,S_{jsi}\to 0.$$

This implies that, cooperatively, we have

$$S_{jsi}\to 0\iff {\widehat{\mathbf{r}}}_{jsi}\to \mathbf{0},{\mathbf{\tau }}_{jsi}\to \mathbf{0},\forall {\mathcal{E}}_{ij}\in \mathcal{E}.$$

(45)

Convergence of $S_i$ to zero for the dissipation functions in (34) implies ${\dot{\mathbf{z}}}_i\to \mathbf{0}$. Hence, convergence of the cooperative error ${\widehat{\mathbf{r}}}_{jsi}\to \mathbf{0}$ results in

$${\dot{\mathbf{z}}}_{js}=-\lambda ({\mathbf{z}}_{js}-{\mathbf{z}}_i-\frac{1}{2}{\mathbf{z}}_{ji}^{*}),\forall {\mathcal{E}}_{ij}\in \mathcal{E}.$$

Applying the coordinate transformation ${\widehat{\mathbf{z}}}_{jsi}={\mathbf{z}}_{js}-{\mathbf{z}}_i-\frac{1}{2}{\mathbf{z}}_{ji}^{*}$, we obtain

$${\dot{\widehat{\mathbf{z}}}}_{jsi}=-\lambda {\widehat{\mathbf{z}}}_{jsi}$$

(46)

which is a Hurwitz linear system that converges to ${\widehat{\mathbf{z}}}_{jsi}=\mathbf{0}$ exponentially. Reverting the transformation shows that

$$\underset{t\to \infty }{lim}{\mathbf{z}}_{js}-{\mathbf{z}}_i=\frac{1}{2}{\mathbf{z}}_{ji}^{*},\underset{t\to \infty }{lim}{\dot{\mathbf{z}}}_{js}=\mathbf{0},\forall {\mathcal{E}}_{ij}\in \mathcal{E}.$$

(47)

With this local limit established, we rewrite the scattering transformation to obtain cooperative convergence

$$\begin{array}{cc}\hfill {\mathbf{r}}_{js}& =\frac{1}{b}(-\sqrt{2b}{\mathbf{s}}_{ij}^{-}-{\mathbf{\tau }}_{jsi}),\hfill \\ \hfill {\mathbf{r}}_{is}& =\frac{1}{b}(\sqrt{2b}{\mathbf{s}}_{ji}^{+}-{\mathbf{\tau }}_{isj}),\forall ({\mathcal{E}}_{ij},{\mathcal{E}}_{ji})\in \mathcal{E}.\hfill \end{array}$$

Using (25) and (26) and the transport of signals through the network, this description results in

$$\underset{t\to \infty }{lim}{\mathbf{r}}_{js}=\underset{t\to \infty }{lim}\frac{1}{b}(-{\mathbf{\tau }}_{isj}(t-T_{ji})+b{\mathbf{r}}_{is}(t-T_{ji})-{\mathbf{\tau }}_{jsi})$$

and a similar description for ${\mathbf{r}}_{is}$ for all edge pairs. Since ${\mathbf{\tau }}_{jsi}\to \mathbf{0}$ and ${\mathbf{\tau }}_{isj}\to \mathbf{0}$, we obtain

$$\underset{t\to \infty }{lim}{\mathbf{r}}_{js}\left(t\right)=\underset{t\to \infty }{lim}{\mathbf{r}}_{is}(t-T_{ji}),\forall {\mathcal{E}}_{ij}\in \mathcal{E}.$$

(48)

Using (47) and (48) and the fact that ${\dot{\mathbf{z}}}_i\to \mathbf{0}$, we finally obtain

$$\underset{t\to \infty }{lim}{\mathbf{z}}_j(t-T_{ji})-{\mathbf{z}}_i={\mathbf{z}}_{ji}^{*},\forall {\mathcal{E}}_{ij}\in \mathcal{E}.$$

(49)

Which, together with a strongly connected network, implies synchronization of the agents.

□

Remark 1.

For the case of time-varying delays, we apply the modified ST, as presented in [30]. The convergence proof follows that of Theorem 5.

5.5. Cooperative Kinetic Energy Shaping

The proposed r-PBC laws shape agents for homogeneous cooperative behavior. Theoretically, this ensures that all systems have the same reaction to cooperative forces; however, if a system has unmodeled dynamics or friction, then its response may be damped, which can cause slow convergence or a steady-state offset. By including a desired inertia matrix ${\mathbf{M}}_{z,i}$ in the storage and dissipation functions (34), the designer gains control over the response of each system. The following theorem extends Theorem 3 with cooperative mass matrices. The results of Theorem 4 are unaffected by the cooperative dynamics and, therefore, also apply in this case.

Theorem 6.

Agent i with dynamics (1a)–(1c), where $n_i=m_i$ and the r-PBC law

$${\mathbf{\tau }}_i=\frac{\partial H_i}{\partial {\mathbf{q}}_i}+{\mathbf{M}}_i{\mathbf{J}}_i^{†}\left({\mathbf{M}}_{z,i}^{-1}{\mathbf{\tau }}_{c,i}-{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i-\frac{1}{2}{\mathbf{M}}_{z,i}{\dot{\mathbf{M}}}_{z,i}{\mathbf{r}}_i-{\gamma }_i({\mathbf{M}}_{z,i}^{-1}-{\mathbf{I}}_l){\dot{\mathbf{z}}}_i\right),$$

(50)

with ${\mathbf{K}}_{z,i}$ given by (33) and ${\mathbf{M}}_{z,i}>{\mathbf{0}}_l$, is r-passive with respect to the storage and dissipation functions

$$U_i=\frac{1}{2}{\mathbf{r}}_i^T{\mathbf{M}}_{z,i}{\mathbf{r}}_i+\frac{1}{2}{\gamma }_i\lambda {\mathbf{z}}_i^T{\mathbf{z}}_i,S_i={\gamma }_i{\dot{\mathbf{z}}}_i^T{\dot{\mathbf{z}}}_i.$$

(51)

Proof. 

The derivative of the storage function is

$${\dot{U}}_i={\dot{\mathbf{r}}}_i^T{\mathbf{M}}_{z,i}{\mathbf{r}}_i+\frac{1}{2}{\mathbf{r}}_i^T{\dot{\mathbf{M}}}_{z,i}{\mathbf{r}}_i+{\gamma }_i{\dot{\mathbf{z}}}_i^T({\mathbf{r}}_i-{\dot{\mathbf{z}}}_i).$$

Substituting in the differential passivity, Equation (8) gives the r-passive dynamics as

$${\mathbf{\tau }}_{c,i}={\mathbf{M}}_{z,i}{\dot{\mathbf{r}}}_i+\frac{1}{2}{\dot{\mathbf{M}}}_{z,i}{\mathbf{r}}_i+{\gamma }_i{\dot{\mathbf{z}}}_i.$$

Equivalently, by rearranging terms and inserting ${\mathbf{K}}_{z,i}$, we obtain

$${\mathbf{\tau }}_{c,i}={\mathbf{M}}_{z,i}{\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i+{\mathbf{M}}_{z,i}{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i+\frac{1}{2}{\dot{\mathbf{M}}}_{z,i}{\mathbf{r}}_i+{\gamma }_i({\mathbf{I}}_l-{\mathbf{M}}_{z,i}){\dot{\mathbf{z}}}_i.$$

Define the feedback law

$${\mathbf{\tau }}_{c,i}={\mathbf{M}}_{z,i}{\widehat{\mathbf{\tau }}}_{c,i}+{\mathbf{M}}_{z,i}{\mathbf{K}}_{z,i}{\dot{\mathbf{q}}}_i+\frac{1}{2}{\dot{\mathbf{M}}}_{z,i}{\mathbf{r}}_i+{\gamma }_i({\mathbf{I}}_l-{\mathbf{M}}_{z,i}){\dot{\mathbf{z}}}_i.$$

We obtain the dynamics ${\widehat{\mathbf{\tau }}}_{c,i}={\mathbf{J}}_i{\mathbf{M}}_i^{-1}{\dot{\mathbf{p}}}_i$, which match the dynamics of Theorem 3 (Equation (36)) and the rest of the proof follows analogously to the proof of Theorem 3. □

An application of Theorem 6 is the case where ${\mathbf{M}}_{z,i}={\eta }_i{\mathbf{I}}_l$. In this case, all cooperative inputs are multiplied by $\frac{1}{{\eta }_i}$ and the damping on the cooperative coordinates is scaled accordingly. The resulting cooperative behavior corresponds to a heavier or lighter cooperative system.

6. Simulation Results

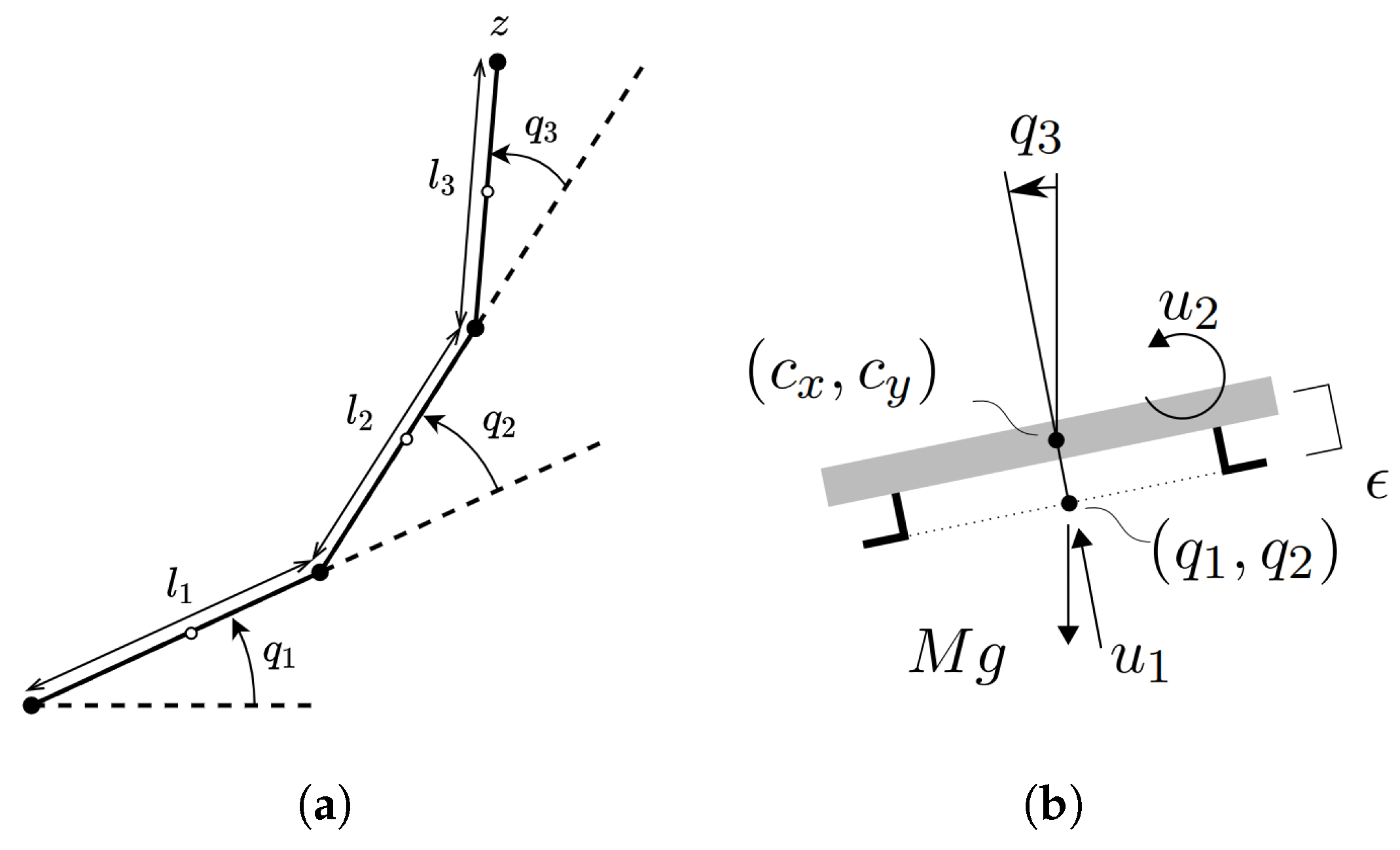
In the following section, we provide a qualitative comparison between IDA-PBC and r-PBC in simulation, with and without communication delays. We also provide results for the case of underactuated systems (IDA-PBC) and subtask optimization (r-PBC). To compare the two methods, we consider a scenario with two robotic manipulators, each with three joints as depicted in Figure 3a. The control objective is to reach consensus ${\mathbf{z}}_1={\mathbf{z}}_2$ in the 2-dimensional plane, without specifying a convergence point a priori. We define the inputs and joint-coordinates as the torque and angle of each joint, respectively. The end-effector dynamics of this system are nonlinear and the states have a redundant degree-of-freedom; hence, it is suitable to illustrate both approaches. For completeness, we first derive a model for the manipulator.

Denote by $x_k,y_k$ the center of gravity, by $m_k$ the mass, by $l_k$ the length and by $I_k$ the inertia each of link k, and let ${\gamma }_k=q_1+\cdots +q_k$. We can write the potential energy and end-effector position as

$$V\left(\mathbf{q}\right)=g\sum _k^3{y}_k{m}_k,\mathbf{z}\left(\mathbf{q}\right)=\left[\begin{array}{c}{x}_N+\frac{1}{2}{l}_{N}cos\left({\gamma }_N\right)\\ y_N+\frac{1}{2}{l}_{N}sin\left({\gamma }_N\right)\end{array}\right]\in {\mathbb{R}}^2.$$

If we define $\mathbf{w}={\left[\begin{array}{ccccccc}{x}_1& y_1& {\gamma }_1& \cdots & x_N& y_N& {\gamma }_N\end{array}\right]}^T$, then the kinetic energy may be expressed as

$$\begin{array}{cc}\hfill T(\mathbf{q},\dot{\mathbf{q}})& =\frac{1}{2}{\dot{\mathbf{w}}}^T\mathrm{diag}(m_1,m_1,I_1,\cdots ,m_N,m_N,I_N)\dot{\mathbf{w}}\hfill \\ \hfill & =\frac{1}{2}{\dot{\mathbf{w}}}^T{\mathbf{M}}_w\dot{\mathbf{w}}={\dot{\mathbf{q}}}^T\frac{{\partial }^T\mathbf{w}}{\partial \mathbf{q}}{\mathbf{M}}_w\frac{\partial \mathbf{w}}{\partial \mathbf{q}}\dot{\mathbf{q}}.\hfill \end{array}$$

An expression for the inertia matrix is then given by

$$\mathbf{M}\left(\mathbf{q}\right)=\frac{{\partial }^T\mathbf{w}}{\partial \mathbf{q}}{\mathbf{M}}_w\left(\mathbf{q}\right)\frac{{\partial }^T\mathbf{w}}{\partial \mathbf{q}}.$$

In the following simulations, let $l_k=0.5$ m, $m_k=2$ kg and $I_k$ = 0.05 kgm${}^2$ for each link. In all cases, we set the network gain ${\mathcal{A}}_{ij}=6{\mathbf{I}}_2$ and ${\mathcal{B}}_i={\mathbf{0}}_{2\times 2}$. In the case of IDA-PBC, we only compensate for gravity, i.e., ${\mathbf{M}}_d=\mathbf{M},V_s=0$. We inject damping on the joint coordinates using ${\mathbf{K}}_v=5{\mathbf{I}}_3$. Our r-PBC controller is parameterized by $\lambda =1$ and damped with ${\gamma }_i=3$. An advantage of the potential-based control terms used with both methods is that the 2-norm of the errors in the cooperative potentials (24) and (30) can be scaled to improve the convergence rate close to the consensus point. Denoting with d the cooperative error, we apply the following scaling

$$f\left(d\right)=\left\{\begin{array}{cc}{a}_1{d}^3+b_1{d}^2\hfill & 0\le d\le r\hfill \\ a_2{d}^3+b_2{d}^2+c_{2}d+e_2\hfill & r\le d\le 2R_w\hfill \\ 1\hfill & d\ge 2R_w\hfill \end{array}\right.,$$

originally presented in [33]. The inner radius r and outer radius $R_w$ are tuned to improve the rate of convergence. The resulting cooperative potential is

$${\overline{V}}_c=\frac{1}{4}\sum _{i=1}^N\sum _{j=1}^N{\mathcal{A}}_{ij}f\left(d_{ij}\right)+\frac{1}{2}\sum _{i=1}^N{\mathcal{B}}_{i}f\left(d_i\right),$$

where $d_{ij}$, $d_i$ denote the cooperative and leader tracking error, respectively.

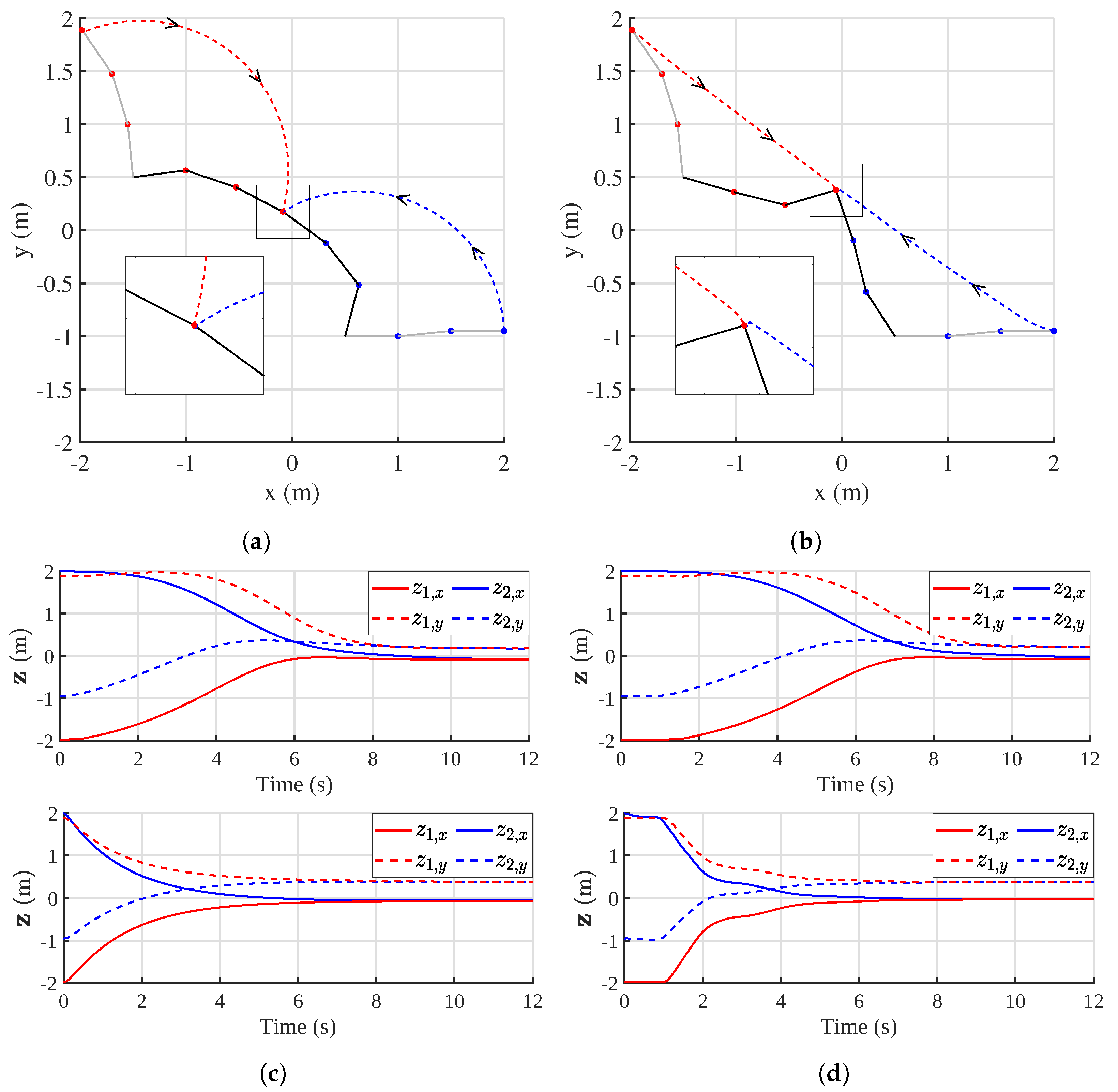
Figure 4a,b depict the cooperative trajectories in the absence of delay and Figure 4c shows the associated coordinates over time. Both methods converge cooperatively, but the transient response of cooperative IDA-PBC is slow compared to r-PBC and the end-effector travels a larger distance. We relate the performance gap to the input matrices. Where cooperative IDA-PBC is a transpose Jacobian method (as a result of the definition of the cooperative coordinates), r-PBC is a pseudo-inverse Jacobian method (for details see [34]). The latter directly maps a motion in cooperative coordinates to the required motion in joint angles, whereas transpose Jacobian methods are merely an approximation of this inverse mapping (a disadvantage of pseudo-inverse methods are kinematic singularities, also present in these examples, and a well-known solution is to apply subtask optimization to evade these configurations [32]). This is also visible at the end of the simulation where for IDA-PBC, the component of the cooperative force in the direction of the cooperative mapping is nearly zero, causing slow convergence near the consensus point.

We repeat the simulations with communication delays. The injected time varying delays follow a random walk process with 0.3 s $\le T\le 1.0$ s,$\dot{T}\le 0.5$ and are unique for the two edges, but consistent between simulations. The resulting coordinates over time are depicted in Figure 4d. The performance of IDA-PBC is further degraded near the consensus point, but the method remains stable, even though the delay is not incorporated in the design. For r-PBC, the transient behavior has changed. The cooperative energy is dissipated in distinct waves. This is clearly visible in the coordinates of the blue manipulator, which decays exponentially within a distinct set of time intervals (most visibly around 1 and 3 s). Nevertheless, the convergence rate is unaffected.

To illustrate cooperative IDA-PBC with underactuated and fully actuated systems, we replace one of the manipulators with an Unmanned Aerial Vehicle (UAV) moving in the x,y-plane (see Figure 3b). The system is actuated by a thrust force and a rotation in the plane around its center. Since thrust force is vertical with respect to the vehicle frame, it cannot move in all directions instantaneously and is underactuated. The cooperative end-effector is a point on the landing gear of the UAV at a distance $ϵ$ below its center of rotation. For completeness, we give the model and single-agent IDA-PBC solution; more details are given in [29], Chapter 11. The UAV joint configuration is defined by its $x,y$ position ($q_1,q_2$) and its orientation ($q_3$). Via the input transformation,

$$\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]=-\left[\begin{array}{c}ϵM{\dot{q_3}}^2\\ 0\end{array}\right]+\frac{g}{ϵ}\left[\begin{array}{c}ϵMcos{q}_3\\ Isin{q}_3\end{array}\right]+\frac{1}{ϵ}\left[\begin{array}{cc}-ϵMsin{q}_3& ϵMcos{q}_3\\ Icos{q}_3& Isin{q}_3\end{array}\right]\left[\begin{array}{c}{\tau }_1\\ {\tau }_2\end{array}\right],$$

with M and I being the scalar mass and inertia of the system, its Hamiltonian dynamics satisfy $\mathbf{M}={\mathbf{I}}_3$ and

$$V\left(\mathbf{q}\right)=\frac{g}{ϵ}cos{q}_3,\mathbf{F}\left(\mathbf{q}\right)=\left[\begin{array}{cc}1& 0\\ 0& 1\\ {ϵ}^{-1}cos{q}_3& {ϵ}^{-1}sin{q}_3\end{array}\right].$$

The transformed UAV dynamics have one degree of underactuation. The following IDA-PBC solution was derived in [17]:

$$\begin{array}{cc}\hfill & {\mathbf{M}}_d\left(q_3\right)=\left[\begin{array}{ccc}{k}_1ϵcos{q_3}^2+k_3& k_1ϵcos{q}_{3}sin{q}_3& k_{1}cos{q}_3\\ k_1ϵcos{q}_{3}sin{q}_3& -k_1ϵcos{q_3}^2+k_3& k_{1}sin{q}_3\\ k1cos{q}_3& k_{1}sin{q}_3& k_2\end{array}\right],V_s\left(q_3\right)=\frac{g}{k_1-ϵk_2}(1-cos{q}_3),\hfill \\ \hfill & \mathbf{J}=-\frac{k_1(k_1-ϵk_2)}{2}\left[\begin{array}{ccc}0& J_1& J_2\\ -J_1& 0& J_3\\ -J_2& -J_3& 0\end{array}\right],\hfill \\ \hfill & J_1={\mathbf{p}}^T{\mathbf{M}}_d^{-1}\left[\begin{array}{c}-2ϵcos{q}_3\\ 2ϵsin{q}_3\\ 1\end{array}\right],J_2={\mathbf{p}}^T{\mathbf{M}}_d^{-1}\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right],J_3={\mathbf{p}}^T{\mathbf{M}}_d^{-1}\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right].\hfill \end{array}$$

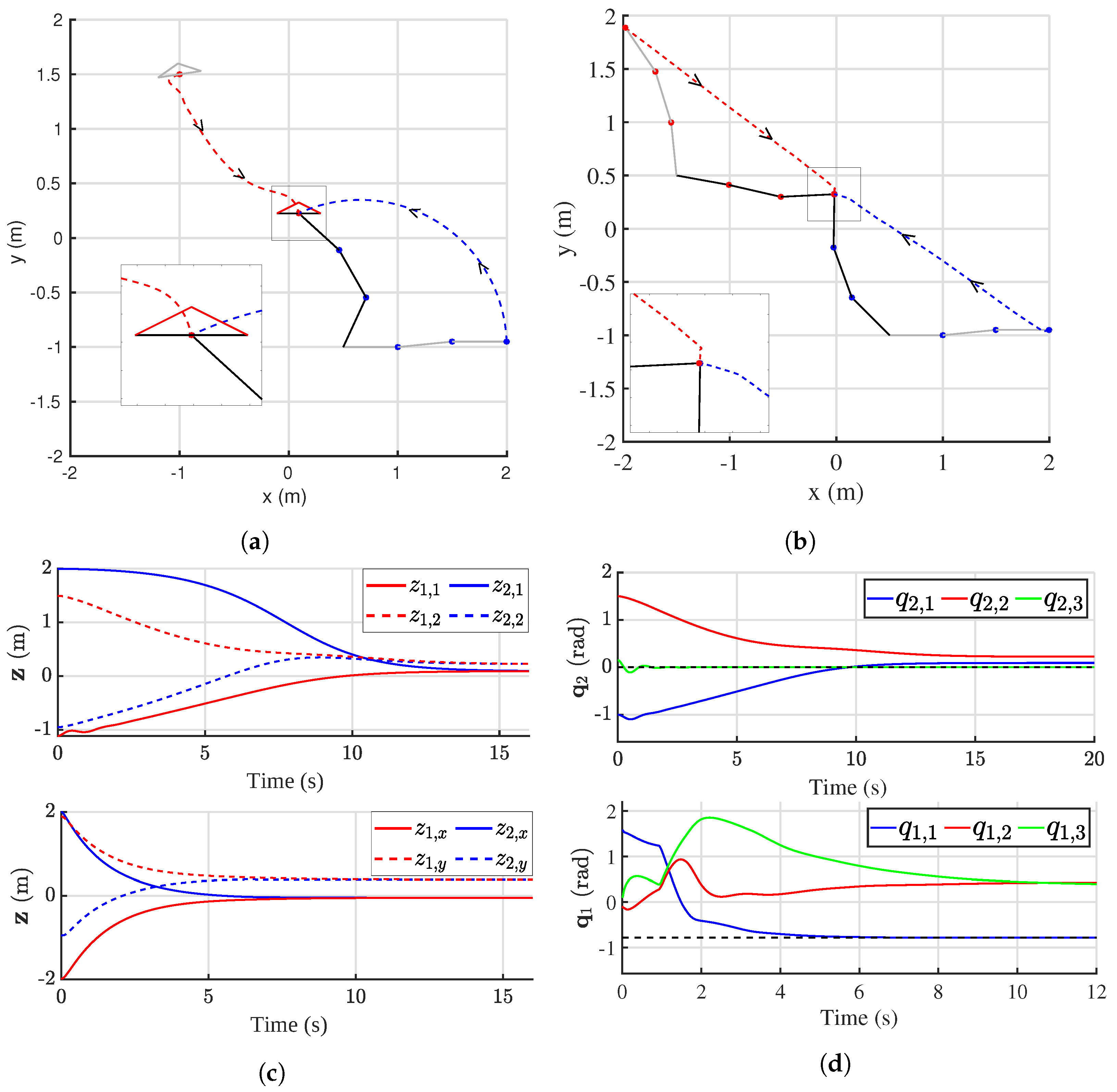
The resulting single-agent IDA-PBC law stabilizes the UAV in its upright position. We set the parameters of the solution as $k_1=2.0$, $k_2=6.67$ and $k_3=1.02$, which result in fast tracking in single-agent simulations. We tune the cooperative control gain as ${\mathcal{A}}_{ij}=\mathrm{diag}(0.5,1.0)$. The resulting trajectories and generalized end-effector coordinates are visualized in Figure 5a,c, respectively. The UAV stabilizes and descends to achieve consensus with the manipulator without overshooting the final consensus point. The joint-coordinates of the UAV are depicted in Figure 5d and show the stabilized orientation in the upright position.

Lastly, we validate subtask optimization of r-PBC. The simulation of two manipulators is repeated, specifying a local quadratic potential function $V_{s,1}=\frac{1}{2}{K}_{s,1}{e}_1^T{e}_1$, which penalizes the error $e_1=q_{1,1}-q_{1,1}^{*}$ with $K_{s,1}=30,q_{1,1}^{*}=-\frac{\pi }{4}$ and we set ${\xi }_i=1$. This explicitly controls the redundant degree of the first manipulator to a reference angle. Figure 5b,c depict the trajectories and generalized end-effector coordinates, respectively. Figure 5d plots the joint-coordinates over time. The first joint angle successfully tracks the reference angle. Additionally, the cooperative objective is achieved at a similar rate as for the case without local tracking. At the start of the simulation, the joints start moving directly in order to satisfy the local objective until around $T=1$ s, where the cooperative information is received and both the cooperative and local goals are achieved at the same time.

7. Experimental Results

The following section features an experimental evaluation of the proposed methods. The experimental setup consists of the Franka Emika Panda [35], a 7 Degree-Of-Freedom (DOF) robotic manipulator, and an Elisa3 differential drive robot [36]. The dynamics of these systems are vastly different in terms of inertia matrix, joint-coordinate description, potential energy function and degrees of freedom, and serve to illustrate the application scope of the proposed approaches.

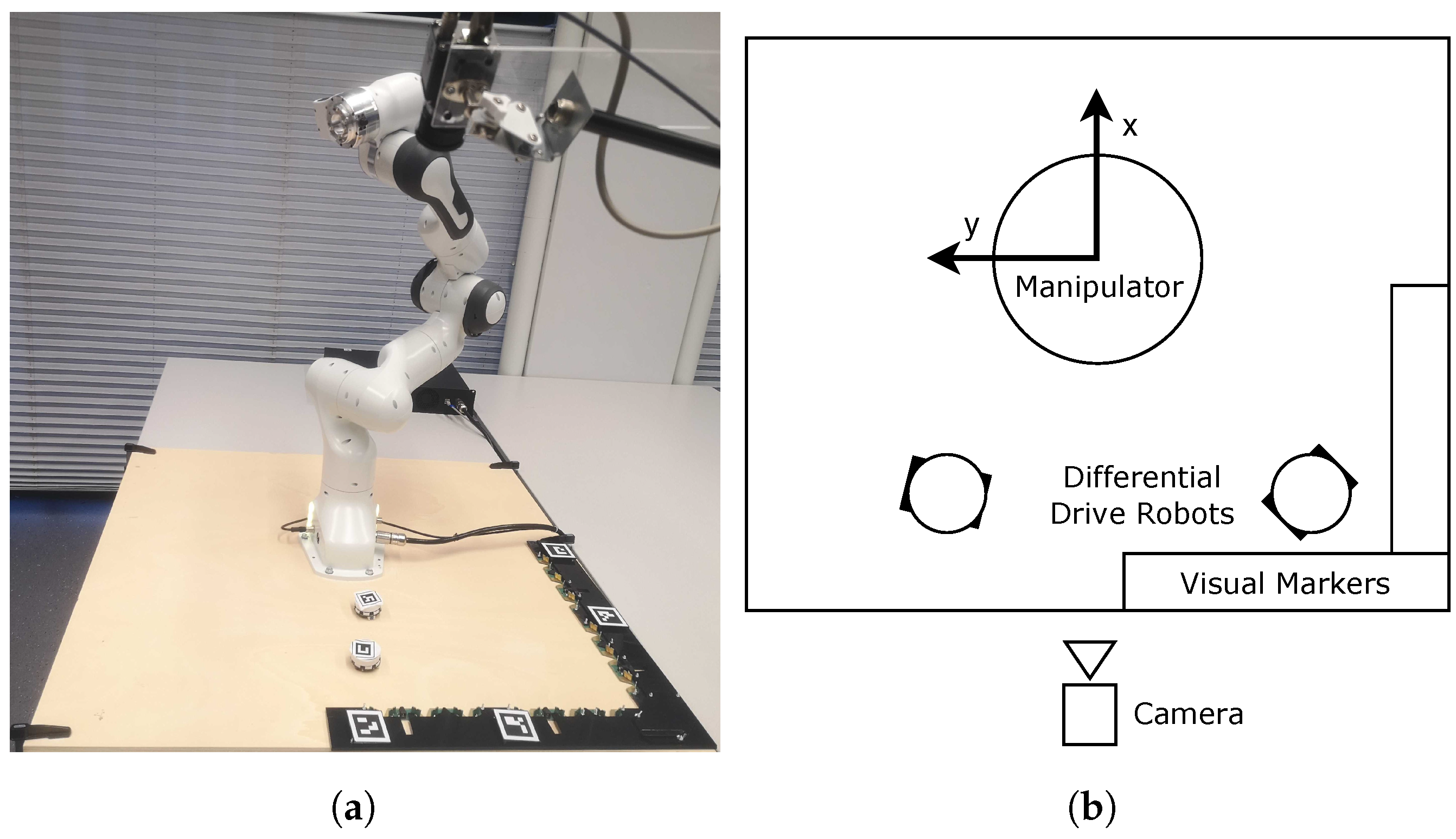
A photo and schematic of the experimental setup are provided in Figure 6a,b, respectively. Both systems are controlled from one PC. The robotic manipulator connects to the PC via an Ethernet connection, which is used to read joint-angles and to send the control commands at a rate of 1 kHz. Additionally, we obtain the inertia matrix and potential function through this data link, although in principle a basic model of the 3D, 7-link manipulator can be derived in the same way as the model derived in Section 6 for the 2D, 3-link manipulator. The differential drive robots are controlled via a wireless communication link at a rate of 100 Hz. Their position in the $x,y$-plane is detected via a camera system and a set of markers (See Figure 6a). We feedback linearize the dynamics of the robot around a point in front of the robot axis (see [37], Equation (5)). The resulting dynamics are that of a point mass in 2D, that is, $\mathbf{M}={\mathbf{I}}_2$, $\mathbf{J}=\mathbf{F}={\mathbf{I}}_2$. The cooperative coordinates are the $x,y$ coordinates as indicated in Figure 6b. Accordingly, the robotic manipulator has redundant degrees of freedom. We limit its motion by stabilizing the z coordinate at $0.4$. In practice, we observe unmodeled friction in the joints of the manipulator. To compensate, the cooperative mass of the system for r-PBC is scaled down to ${\mathbf{M}}_{z,\mathrm{panda}}=0.015{\mathbf{I}}_2$ and we set ${\mathbf{M}}_{z,\mathrm{elisa}}=0.05{\mathbf{I}}_2$.

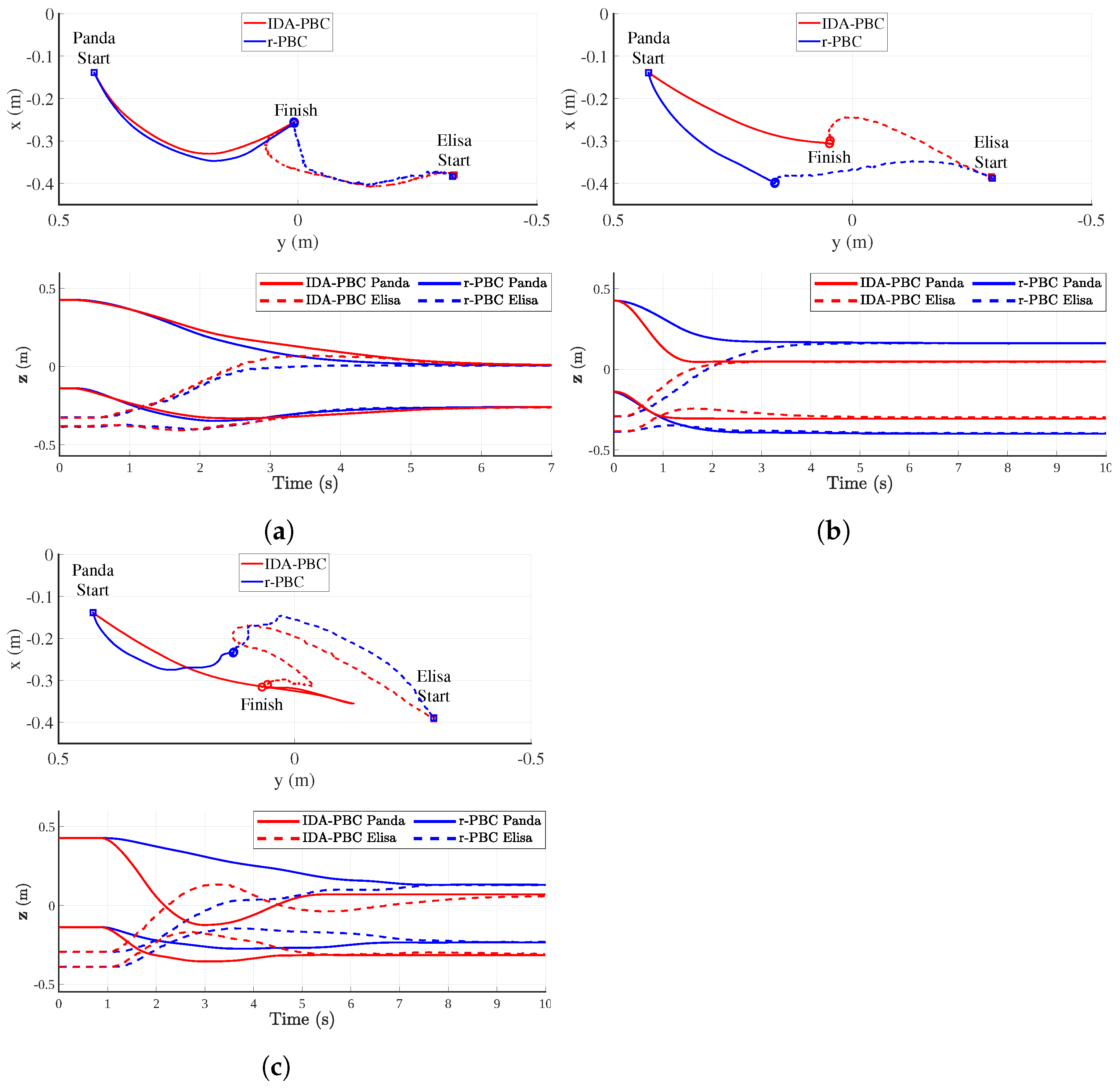
We validate the control methods in a consensus experiment. In the first experiment, the robotic manipulator is set as leader with reference $(-0.25,0.0)$. Trajectories and cooperative coordinates are depicted in Figure 7a. Both methods achieve consensus and converge to the leader reference. Due to the guidance of the leader, the trajectories of both approaches are similar. We repeat the experiment without the leader reference such that the objective is to reach consensus at an arbitrary point, as visualized in Figure 7b. Both methods converge faster than with a leader. With IDA-PBC, however, the driving robot is compensating for the slow convergence rate of the manipulator in the direction orthogonal to its end-effector orientation, similarly to the effect we remarked in Section 6. In contrast, using r-PBC, both systems have an approximately equal part in reaching consensus.

We repeat the leaderless experiment, injecting artificial communication delays generated from a random walk process. The delays are parameterized by 0.8 s $\le T\le$ 1.0 s, $\dot{T}\le 0.5$. Packet loss is generated by a Bernoulli drop model with $p=0.05$. To handle packet loss and time-varying delay, we passively reconstruct the wave variables on the receiving end of each edge using Wave-Variable Modulation (WVM) [25]. The reconstruction extracts maximum energy from the network while preserving passivity. Figure 7c depicts the resulting trajectories and cooperative coordinate evolution. Both methods show degraded performance compared to the case without delays. Although the r-PBC trajectories show oscillations in the cooperative plane, the consensus point is not passed by either system and cooperative consensus forms directly. The cooperative coordinates also reveal the wave-like convergence, similarly to the simulated case. We expect that the difference in consensus point with the undelayed case is due to the velocities that are included in the agent output r, used for control. In the undelayed case, the manipulator moves rapidly, causing the driving robot to anticipate its movement. In the delayed case, the driving robot receives this information later, at which point the manipulator may have already changed its course to meet the driving robot. The trajectories of IDA-PBC indicate a loss of cooperative dissipation in the presence of delays, which causes the systems to spiral towards the consensus point. This shows that delays can still destabilize this controller.

8. Discussion

The proposed cooperative IDA-PBC framework extends the application scope of cooperative PBC methods by including heterogeneous systems that satisfy Assumption 1 (e.g., [17]). This simplifies the interconnection between different system types, especially when a system is underactuated. r-PBC makes it simple to robustly connect fully actuated systems in practice, reducing interactive behavior by default to point-mass dynamics. In comparison to [28] this simplifies the interconnection of heterogeneous systems and makes it intuitive to tune cooperative interaction. Compared to other cooperative controllers, the wide applicability of the proposed passivity-based controllers and their computational efficiency (e.g., 1 kHz control rate) makes them well-suited for practical applications. Additionally, energy-based control leads to intuitive and stable behavior of all connected robots.

Several challenges remain to further improve the proposed methods. For IDA-PBC, there is no general single-agent solution for underactuated systems and it is unclear if Assumption 1 can be satisfied for any solution. Additionally, both schemes require a measurement of acceleration which may not always be available (e.g., for fully actuated systems, ref. [19] uses only velocity measurements). The r-PBC scheme theoretically relies on the assumption that the delay does not change faster than time itself. Although the assumption is mild, it may be possible to capture this case by further modifying the network. Future work could additionally explore including collision avoidance into these frameworks to further extend their applicability, for example, to combine passivity-based control with predictive control.

9. Conclusions

In this work, we presented two methods for distributed cooperative end-effector control of heterogeneous mechanical systems. The first method, cooperative IDA-PBC, incorporates fully actuated systems and underactuated systems for which a single-agent solution exists. The second method, based on r-passivity, stabilizes a network of fully actuated systems in the presence of time-varying delays. We demonstrated stability and convergence of both approaches in simulation and experiments with and without communication delays, using academic examples. Our cooperative IDA-PBC approach is theoretically limited to networks without delays, while r-PBC is limited to fully actuated systems. Further research may explore a merger of the two methods, by solving the matching conditions for an r-passive system description.