Abstract
This paper develops a three-degree-of-freedom sagittal-plane hybrid dynamical systems model of a Groucho-style bounding quadrupedal run. Simple within-stance controls using a modular architecture yield a closed-form expression for a family of hybrid limit cycles that represent bounding behavior over a range of user-selected fore-aft speeds as a function of the model’s kinematic and dynamical parameters. Controls acting on the hybrid transitions are structured so as to achieve a cascade composition of in-place bounding driving the fore-aft degree of freedom, thereby decoupling the linearized dynamics of an approximation to the stride map. Careful selection of the feedback channels used to implement these controls affords infinitesimal deadbeat stability, which is relatively robust against parameter mismatch. Experiments with a physical quadruped reasonably closely match the bounding behavior predicted by the hybrid limit cycle and its stable linearized approximation.
1. Introduction
Legged robots exhibit an increasingly successful steady state [1,2,3,4] and transitional [3,5,6,7] behaviors. Today’s most popular gait control methods for high-degree-of-freedom legged machines generally appeal to numerical optimization [8,9,10] and deep neural networks [11,12]. On the other hand, the project of composing more complicated, higher-degree-of-freedom behaviors from the analytically tractable, lower-degree-of-freedom constituents pioneered by Raibert nearly four decades ago [13] remains unfinished. Compositional operators with formal properties offer a historically established path to safe behavioral programming in robotics [14]. Even well short of such comprehensive goals, interim success in this endeavor promises both intuitive insight backed by formal rigor and stable gait controllers with functional dependence on task and environment parameters that specify the operating characteristics of useful legged machines. Such results are fundamentally hard owing to the non-integrability of legged machines’ high-dimensional nonlinear hybrid dynamics, and thus prior results of this nature are rare even for three-degree-of-freedom mechanisms [15,16,17,18]. The authors are not aware of any complete stability result for three- or higher-degree-of-freedom models of quadrupedal bounding (while a few contemporary three-degree-of-freedom stability results exist, e.g., [18], they are unable to describe a bounding gait).
This paper presents a parametrized family of controllers that stabilize a hybrid dynamical systems model of Groucho-style quadrupedal bounding arising from a simple three-degree-of-freedom sagittal-plane representation of a legged robot. The stability guarantees extensions over a specified range of variations in body mass, length, and moment of inertia that dictate the achievable range of commanded forward running speeds and thereby, in turn, the full set of controller parameters. These formal results arise from key approximations and a controller structure that exploits them to afford a decomposition of the full model into the cascade of a two-degree-of-freedom in-place bounding component forward coupled to drive a one-degree-of-freedom fore-aft component. In essence, this amounts to working closely with the double-integrator model as introduced in [19]. This model and the resulting controller are simple in the sense that they encode ground reaction force laws resulting in trivial continuous body dynamics, and they achieve the family of asymptotically stable limit cycles representing the desired steady-state gait using proportional control on the hybrid transitions. Nevertheless, the model is sufficiently faithful and the controller is sufficiently robust as to permit empirical implementation over many repeated trials (accumulating hundreds of body lengths) on a physical robot, Inu [20], displayed in Figure 1. Notably, we choose stance force commands to effect trivial continuous dynamics such that the state-space contraction provided by our imposed feedback laws occurs exclusively on the hybrid guards and resets. This choice affords an analytically tractable path to our formal stability proof and allows for a linearized version of deadbeat control that we believe is better conditioned to parametric and state uncertainty for use in an experimental setting than full deadbeat control.

Figure 1.
The controller presented in this work is empirically demonstrated on the Inu robot [20]. Empirical bounding corresponding to the analytically predicted limit cycles derived in Proposition 1, using the simplified dynamics of Section 2.3, is documented in Section 5.
1.1. Groucho Running
Groucho running [21]—also called called grounded running or flightless running—is a form of running in which the duration of ballistic flight either approaches or is equal to zero [22]. Such gaits are used by a wide range of animals for rapid legged locomotion (including birds, insects, arachnids, and mammals), over a varied number of size scales (from ants to elephants) and leg numbers (2, 4, 6, and 8) [23,24,25,26,27,28]. Theories for the utility of Groucho running include reducing viscera vertical oscillation, lowering peak leg forces, and increasing stability over uneven terrain—which can (but not always [29]) come at the cost of producing external mechanical work [30]. Beyond its intrinsic interest for biology, the focus of this paper on Groucho running is motivated by the limited peak leg force production of our experimental test platform Inu (as detailed in Section 5.1) that precludes any significant ballistic flight phase when running at full speed. More generally, the locomotion of force-limited legged machines is inherently important for engineers: any platform carrying a sufficiently heavy payload will be force-limited yet may nevertheless be able to achieve a rapid gait by running without an aerial phase.
1.2. Cascade Compositions
The use of simplified models for the control of legged running has a rich history of empirical [2,13,31] and analytical [32,33,34] success. We are particularly interested in modular approaches that can offer an analytically tractable path to formal results, as they decouple the stability problem into a composition of lower-dimensional subproblems. For example, “parallel composition”—approximation in terms of modules operating simultaneously in isolation—was pioneered empirically with great success by Raibert [13], and has been formally redeveloped in recent years for bipedal [15], quadrupedal [35], and more general [36] legged systems. While empirically very effective, this formal analysis of legged parallel composition uses the framework of hybrid dynamical averaging [37], requiring not only that the neglected “crosstalk” between modules be sufficiently small but that potentially deleterious components (that cannot be averaged away) be identified and compensated by feedback.
In this paper, we introduce a cascade composition (1) to control quadrupedal bounding, which—in contrast to parallel compositions—allows for arbitrarily large feedforward signals from one module to another cascaded module. From the analytical perspective, the cascade also achieves an eigenvalue separation property in the stride-map’s Jacobian that guarantees the local stability of coupled modules so long as they are stable in isolation, providing a separation of concerns to the designer. Cascade compositions have long been used to reduce the complexity of adding dimensionality to both continuous-time systems [38,39] and iterated maps [40]. However—to the best of our knowledge—their formal consideration for simplified models of dynamic quadrupedal locomotion has only been used to “extract” away fast actuator dynamics [41] or for similar situations with multiple timescales [42] that reduce to feedforward cascades in Fenichel normal form [43].
We say an iterated map is a cascade composition if it is of the form
where , , , . Such a system has the following block-triangular Jacobian:
in which the eigenvalues of consist of the eigenvalues of the smaller matrix and matrix . The task of showing that the spectral radius of has a modulus less than unity for a linearized stability analysis then reduces to establishing the same property individually for the smaller constituent matrices, and , which is generally a much easier task.
1.3. Controlling on Hybrid Transitions
The long-practiced tradition of achieving control through shaping a hybrid dynamical system’s guards and resets (the hybrid transitions) has been used since the earliest days of empirically successful dynamical robots when Raibert used the fact that a robot leg’s angle in flight could be freely set to affect touchdown conditions and thereby control forward running speed [13], inspiring many similarly conceived subsequent speed controllers [33,35,44]. This insight was generalized by Seyfarth [45], initiating a body of “swing-leg retraction” literature (e.g., [46,47]) that brought about two fundamental observations that bear on our work. First, minimally sensed stabilization is not only achievable by control on hybrid transitions [48,49], but can afford deadbeat performance as well with only a bit more sensing (here, deadbeat control refers to a strategy resulting in exact correction to perturbations in a finite—typically minimum—number of steps [50]). Specifically, as shown numerically [51] and analytically [52], proper feedforward servoing of sagittal leg angle in flight affords control over the apex height with no sensing required other than the detection of the apex and touchdown events, even when running over uneven terrain. Second, the implicit function theorem provides sufficient conditions for the existence of deadbeat control given a sufficiently expressive input vector using full state feedback [50]. Studies in humans [53] and birds [54,55,56] document some combination of feedforward and feedback hybrid transition control strategies during biological running, further motivating their study by roboticists.
Previous results on hybrid transition control (particularly the deadbeat literature) are limited in several ways. The majority of results are limited to simulation, and preliminary experimental work in this area [57] suggest performance is very sensitive to state estimation error or perhaps model parametric uncertainty, conceivably limiting the application of deadbeat results to robots in controlled environments such as motion capture feedback systems. For the purposes of this work, we do not consider control strategies to be deadbeat if they rely primarily on proportional-derivative continuous within-stance perturbation correction such as [58,59], since they do not formally satisfy our definition of exact correction. Differences between these approaches are discussed in Section 6.2, but real-world implementation obviously would benefit from a combination of these strategies. Even methods requiring no sensing aside from the detection of an apex suffer from the fact that the apex event is difficult to precisely detect in practice without motion capture data.
Aiming for greater robustness and avoiding the need to detect the apex event, we forgo deadbeat control for a linearized version of it and additionally use a combination of feedforward and feedback control—only using feedback on states that can be accurately measured onboard the robot. We also take inspiration from Blickhan’s studies indicating that humans vary both their leg angle and leg length in flight to affect touchdown conditions [60,61] and utilize our hybrid transition controller to vary both of these quantities. Moreover, we allow our hybrid transition controller to affect liftoff conditions. In these ways, we more fully leverage the affordance inherently provided by making and breaking contact in sagittal running.
1.4. Outline
Section 2 introduces a simplified hybrid dynamical systems model (3) representing a bounding quadruped, with a rigid-bar body and massless legs that exert ground reaction forces at the toes. Ground reaction force laws and hybrid transition behaviors are specified to produce the dynamics of a cascaded composition of two hybrid dynamical system modules. Simplifying assumptions (shown in Section 3 to be approximately valid) give these modules trivial dynamics. Section 3 formulates a stride map for a bounding gait, and factors it into a more easily analyzable half-stride map. A fixed point representing a hybrid periodic orbit is found in Proposition 1, and its properties are examined. Section 4 formulates control on the hybrid transitions to make the aforementioned periodic orbit an attracting limit cycle. Control weights are chosen in Proposition 2 so that the stride map representing the orbit is infinitesimally deadbeat. Section 5 details the empirical instantiation of the controlled model on the Inu robot. Experimental results indicate reasonably close correspondence with the theoretically predicted behavior of the simplified model. Section 6 provides a brief discussion about the ideas in the paper, and Section 7 provides concluding remarks. Proofs and lemmas are given in the appendices as well as a table of the symbols used in this work (given in Appendix A). Note that we rely heavily on forward references in this work to aid in matching initially stated assumptions to their consequences in the subsequent models (largely found in association with the corresponding figures) and analysis (focused mainly on their mathematical implications).
2. Model
This section introduces the simplified model shown in Figure 2 of a quadrupedal robot bounding in the sagittal plane. The model consists of a rigid bar representing a robot body with massless legs protruding from the hips that are able to generate ground reaction forces at the toes. This basic model has historically been used to describe sagittal quadrupeds since Raibert’s work in the 1980’s ([13], p. 139), typically using torques and radial forces generated at the hips (equivalent to ours through a change in coordinates). It has been used more recently with commanded Cartesian ground reaction forces to model both steady-state and transitional empirical behaviors [2,19]. In these studies, it is well established that this model is—for the purposes of achieving useful controllers—a sufficiently good approximation of the sagittal dynamics of physical bounding robots with a mass center roughly halfway between their hips and leg inertia sufficiently less than that of the body [2,13,35,62].
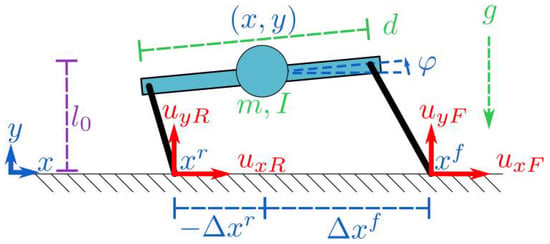
Figure 2.
The simplified massless-leg representation of a quadrupedal robot bounding in the sagittal plane. The model’s configuration is shown in blue and is given by the body’s location in with mass-center position and body pitch , as well as the horizontal location of the front and rear toes encoded either by their toe positions or splay distance from the mass center, . The physical parameters shown in green are the body’s mass m and moment of inertia I about its mass center, the body length d, and gravity’s acceleration g. Each leg in contact with the ground imparts a vertical () and horizontal () mass-specific ground reaction force law at each toe shown in red. Purple values relate to control parameters. The value is a nominal vertical leg length at the touchdown and liftoff events (used as a control parameter in (26)).
Section 2.1 gives a description of the model’s hybrid dynamical system for a non-aerial bound (because of the actuator limits described in Section 5.1) as depicted in Figure 3. Section 2.2 constrains the ground reaction force laws (20) and (21) and hybrid transitions (25) and (30) to enact a cascade composition. Section 2.3 introduces dynamical simplifications in the form of Approximations 1 and 2, and (34), that—together with the previous modeling choices—give the cascaded system the trivial dynamics depicted in Figure 4. These modeling and control choices yield simple closed-form expressions for the flow on the hybrid modes, (35) and (36), which in turn allow a closed-form expression for the targeted bounding limit cycles in Section 3 and a tractable stability analysis in Section 4.
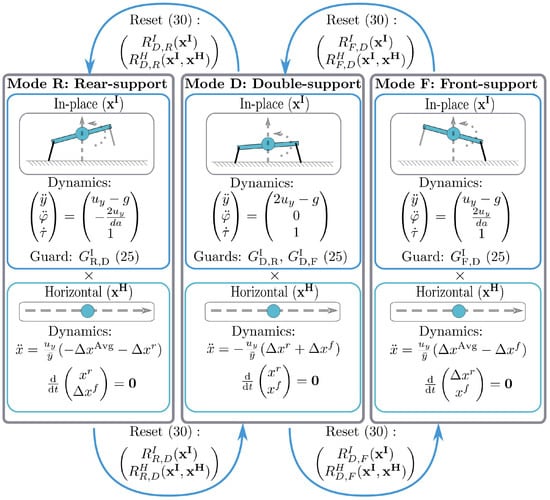
Figure 4.
Cascaded hybrid dynamics achieved through the choice of force laws and hybrid guards and resets as well as Approximation 1. The choice of force laws (20) and (21) decouple the continuous dynamics of the hybrid system (3) into the cross product of “in-place” and “horizontal” vector fields representing the behavior of the “in-place” vertical and pitching states as well as the “horizontal” fore-aft mass-center and toe position states . The isolated continuous dynamics—along with the hybrid guards being purely dependent on the in-place states (25) and the hybrid reset maps having a cascaded form (30)—endows a feedforward relationship between the in-place states and horizontal states in which a linearized stability analysis of a hybrid periodic orbit’s Poincaré map Jacobian has the separation-of-eigenvalues property indicated by (2), allowing for a more tractable analysis. A stable limit cycle is achieved by controlling the hybrid guards and the resets via (26), (31) and (32). In the vertical states, this is accomplished on the guards by vertically retracting the leg in stance to transition to flight and similarly by protracting the leg in flight to affect the onset of stance. In the horizontal states, this is accomplished on the resets by placing the toe position horizontally in flight in a similar fashion to Raibert’s neutral-point algorithm [13].
2.1. Hybrid Dynamical System Description
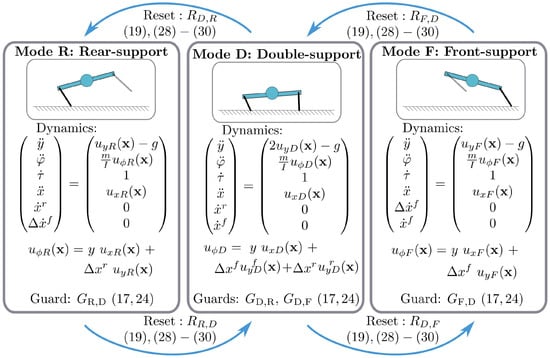
Following the convention of [63], we define the hybrid system representing the sagittal-plane massless-leg robot model depicted in Figure 2 and Figure 3 as the tuple
The set
represents the hybrid modes corresponding to front single-support , double-support , and rear single-support , respectively. No flight mode is given due to the actuator constraints of the Inu robot as explained in Section 5.1, but a similar analysis is possible by replacing the double-support phase with a flight phase—indeed, we will enforce Hamiltonian double-support dynamics (depicted in Figure 4) which, when compared to ballistic flight, are identical in the pitch degree of freedom () and topologically equivalent in the vertical degree of freedom (). By choosing Hamiltonian double-support dynamics, on which there can be no within-mode state convergence à la Liouville’s theorem ([64], p. 69), we give up the “full-actuation” of the hybrid mode both for the energetic benefits—still conjectural as outlined in Section 6.2—and to suggest the viability of our control scheme for use in the underactuated flight modes that would be accessible to a more highly powered robotic platform.
The allowed hybrid transitions are given by
The set of continuous domains is given by
where—to aid with the decoupling introduced in Section 2.2—we decompose each continuous domain into the product
for the “in-place” and “horizontal” respective state components that will form the basis for a cascaded composition (1), where
with state
where represents the “in-place” state components relating to vertical and pitching motions, and represents the “horizontal” state components relating to horizontal motions. We will drop the mode subscripts when appropriate.
The in-place state is given by
representing the configuration and velocity of the mass center’s height y and body pitch as depicted in Figure 2, as well as the integrated mode duration which is appended to the state so we can use mode duration as a state variable in the guard events, (26) and (58). Intuitively, these components represent the state of the robot when it is bounding in place.
The horizontal state in mode is given by
where—as depicted in Figure 2—x and , respectively, represent the mass center’s horizontal position and velocity; and , respectively, represent the front and rear foot position; and and , respectively, represent the relative distance of the front and rear toe to the mass center according to
The reason for switching between the and state representations is simply mathematical convenience as it allows us to represent the continuous evolution of the foot with a zero vector field in (14), where in stance a hip’s toe position does not move and in flight a hip’s toe position relative to its mass center can be controlled to not change.
The continuous dynamics of the system are shown in Figure 3. To represent them as first-order vector fields, we define the hybrid vector field as follows:
which restricts to the vector fields for each such that
where
In Section 2.3, and will be set to be constant throughout each of the stance modes. Until then, we use the more general functional form to illustrate in Section 2.2 that we can achieve a cascaded composition without requiring constant values. Note that is the sum of the double-support force components from each leg; how this force burden is distributed to the legs is an implementation detail. The experiments of Section 5 used an even distribution.
For simplicity, we approximate the height value as it appears in the pitching acceleration of (15) to be constant.
Approximation 1.
In the pitching acceleration components (15), we take the stance height terms y to be the constant .
Approximation 1 has the effect of replacing y with in the horizontal force law that will be introduced with (21). This assumption is approximately valid in the experiments of Section 5 as shown by the nearly constant height in the experimental data of that section. Note that the model is still three degrees of freedom since the robot’s vertical state (height and vertical velocity) remains variable in the translational compartments of the model (14). We have merely approximated the coupling of the mass-center height into the pitching dynamics (15) as constant. This, along with Approximation 2 and (34), will allow an explicit representation of a relevant hybrid periodic orbit derived in Section 3. Further implications of this assumption are discussed in Section 3.3.
The model’s physical parameters are the body length d, gravity’s acceleration g, the body mass m, and moment of inertia I. We also later introduce (22), a (24), and (26) as pseudo-physical parameters chosen by the user for the controller that are strongly influenced by the physical parameters.
The vertical and horizontal (mass-specific) force laws are, respectively,
which we later set in (21) and (34). The interval bounds on the codomain of are artificially imposed both to take into account actuator constraints (discussed in Section 5.1) and to specify the range of vertical forces over which the hybrid periodic orbit result described in Proposition 1 holds.
The collection of guards is
where for each . We assume that the robot’s hip is able to retract its legs in stance to force a flight event and similarly protract its legs in flight to influence the timing of a stance event, according to intersection with a guard set. The guards are considered part of the controller and are further specified in (25), (26), and in Section 4.1.
Finally, the hybrid reset map is given by
which restricts to
for each . The resets—considered part of the controller and specified in (30) and Section 4.2—move the horizontal state of the toes instantaneously in flight (taking advantage of the assumption of massless legs) and reset the mode timer component to zero. To avoid physically unrealistic situations, we require that the resets give all other states continuous motion across hybrid transitions as these states have associated mass.
2.2. Cascaded Composition
We impose a cascaded composition (Section 1.2) with the following choice of force laws and hybrid transitions. We first decouple the horizontal state from the in-place continuous dynamics by choice of horizontal and vertical force laws, giving the in-place acceleration components the form . To do so, we specify the vertical force law to be only a function of in-place state:
(which will be set to the constant in Section 2.3), and let the horizontal force law be given by the following (note that the smallest value of y is physically bounded by the kinematics to be far from zero so the quotient in (21) would never create a problem):
which makes the pitch dynamics act as if the only torque on the body were from a vertically applied associated with a leg splay of
We choose to set to equal , representing pitch dynamics that mimic the toes being directly below the hips—a choice that maximizes the platform’s achievable running speed as discussed in Section 3.5. In principle, any could be chosen, and so for generality we do not fix in our mathematical results. The resulting pitch dynamics from the force law (21) are
(which in Section 2.3 become the constants , , and with the choice ), where
is a dimensionless generalized Murphy number ([13], p. 193) induced by the leg splay and body parameters. When the leg splay distance goes to , then our definition agrees with Raibert’s presentation of the Murphy number, which he represented by the symbol j: “Murphy found that when the attitude of the body can be passively stabilized in a bounding gait. When , stabilization is not so easily obtained” ([13], p. 193). We use a generalized version of Murphy’s result because we feel that accounting for a toe not being directly under the hips when bounding in place is important, as the user may want to use an arbitrary leg splay. See Section 4.3 for a visual depiction of the Murphy number as it relates to this paper’s simplified model.
We next decouple the horizontal state from the in-place hybrid transitions. To do so, we first let only the in-place state components determine the guard intersections:
If instead we allowed the horizontal state to enter into the form of the guards, then the horizontal flow could influence the mode transitions via the time-to-guard-impact map and thereby affect the in-place state components, violating the feedforward dependence we are constructing.
Specifically, the model’s left and right hip height are given by the function . We define the mode guard by setting as the set of states in which a hip’s height is moving in the correct direction for a mode change and is equal to some value plus the value of a control function :
where the guard represents the rear leg’s touchdown event that initiates double support, represents the front leg’s liftoff event that initiates rear stance, represents the front leg’s touchdown event that initiates double support, and represents the rear leg’s liftoff event that initiates front stance.
In (26), the function is an involutory symmetry map intended to enforce a symmetric bound:
and the functions represent the control functions used to modify the touchdown or liftoff hip height from the nominal value of as a function of state so as to achieve the desired gait. The control functions are chosen in (58) of Section 4.1, but for now we require that they go to zero when the state lies on the desired gait and that their lie derivatives satisfy
so that the hip height at which touchdown occurs is never decreasing in time during flight and the hip height at which liftoff occurs is never increasing in time during stance—conditions that will be used in the proof of Proposition 1 to guarantee the existence of a specific hybrid periodic orbit. Here, and represent the in-place components of the vector field (14) in modes and , respectively. The value represents the leg length at touchdown and liftoff on the hybrid limit cycle and should be chosen to be sufficiently far from the workspace singularity as to have room to implement to stabilize the gait.
Approximation 2.
We use a small-angle approximation on the robot pitch for the purpose of checking guard intersections.
Thus, in the representation of the guards in (26), we take the hip heights to be
We expect this to be reasonably valid at lower levels of pitching such as those observed in the experiments of Section 5, but expect its validity will deteriorate if limiting behavior with high pitch is commanded.
Finally, we give the resets in the following cascaded form (1):
There is relatively little choice in how to reset the state components since they are largely physically determined; however, we are free to reset the mode timers as they are non-physical and to reset the horizontal toe positions in flight.
Specifically, we define the in-place resets as
for each , where simply zeros the timer component of the state. The horizontal resets represent the ability to stabilize the horizontal components of the model for a bounding gait, in the same manner as the guards for the in-place state components. In placing the foot horizontally ahead of or behind a nominal touchdown configuration according to some control function, it functions much like Raibert’s neutral-point controller [13]. This is defined as
where
is an involutory symmetry map intended to enforce a symmetric bound. The control functions (chosen in (63) of Section 4.2) modify the horizontal foot placement in flight prior to touchdown, and—like —we require that they go to zero when the state lies on the desired gait. The constant value (chosen in (51) of Section 3.3) represents a nominal touchdown leg splay magnitude.
Having removed all influence of the horizontal state from the in-place hybrid dynamics, we have endowed a feedforward structure in which the in-place state alone determines the in-place hybrid execution and which feeds forward into the horizontal dynamics, making any suitably chosen Poincaré map for the system have the cascaded architecture (1).
2.3. Dynamical Simplification
To further simplify the dynamics, we choose the (mass-specific) vertical force component generated at each foot to be the constant :
giving the in-place state components a mode-i flow of the form
Approximations 1 and 2 and (34) result in the simplified cascaded dynamics depicted in Figure 4. In particular, the choice of a constant vertical force gives rise to affine horizontal continuous dynamics with mass-center forward acceleration given by
and the corresponding mode-i horizontal-component flow of the form
where
3. Hybrid Periodic Orbit
The explicit flow representation (35), (36)—combined with guards (26) and resets (32)—yields expressions for the mode maps which are derived in Section 3.1 and composed in Section 3.2 to form a stride map for the model. We take advantage of symmetry to derive a simpler half-stride Poincaré map, and in Section 3.3 express a closed-form fixed point (Proposition 1) representing a hybrid periodic orbit. With the form of the hybrid periodic orbit in mind, Section 3.4 revisits the validity of Approximation 1, Section 3.5 discusses a forward-running speed limit associated with the kinematic limitations of a physical machine, and Section 3.6 discusses the actuator cost to enforce the cascaded decoupling of Section 2.2.
3.1. Choice of Poincaré Section
We now introduce a symmetry that expresses the dynamics of the mode and its transition into the mode as a mirror image of mode and its corresponding transition to . By restricting attention to only symmetric bounds, this observation affords a factorization of the resulting Poincaré map modeling a stride cycle as comprising a pair of successive half strides. These considerations in turn motivate our choice of a Poincaré section (with coordinates denoted by a ∼ superscript) as described below.
Each hybrid mode has an associated map taking a starting state to its value along the forward flow intersecting a guard. For convenience, we pre-compose this with the appropriate reset map, so that the hybrid mode-reset composition—which we refer to as the mode map and denote by —maps a starting state in mode i to the reset of where the forward flow intersects the guard . Specifically,
(recalling the forms of the resets (31), (32), the in-place flow (35), and the horizontal flow (36)) where we denote the separate components of as
and where
denotes the implicit time-to-impact map of the flow with the guard. Here represents the largest subset of over which is defined and over which the forward flow does not first intersect another guard. We show in the proof of Proposition 1 the existence of points , , , and ; hence, the sets are non-empty.
The involutory “bounding” symmetry map is defined as follows:
where is given by (27) and is given by (33). The map induces a flow conjugacy between and , as well on flows in . This, together with the guard symmetry (26) and reset symmetry (32), results in inducing a topological conjugacy between and , as well as between and .
The reduced domains are defined as equal to the domain without mode-timer or forward position x components, so as to be of use in defining a stride map whose Poincaré section has the property and does not contain an x component so as to permit stride map fixed points at speed. Specifically, let
(where we sometimes drop the mode subscripts when appropriate) and the reduced state as
Specifically, passage between and occurs according to the projection and lift maps:
3.2. Stride Map
We are interested in the asymptotic behavior of a bounding gait with a periodic hybrid mode sequence . To this end, the stride map is defined:
and is local to some fixed point in the interior of the domain, where is the largest subset of over which is defined. We show in the proof of Proposition 1 the existence of such a fixed point of , so is not empty.
To simplify the analysis, we use the fact that the stride map factors according to
where , such that
represents a “flipped” (by ) half stride of the stride map.
3.3. Stride Map Fixed Point
A stable fixed point of is a stable fixed point of , so we focus our attention on the asymptotic behavior of , which is simpler. We note that we are interested in a symmetric bound, so any fixed points of that we are discarding by virtue of not being fixed points of via the symmetry are not symmetric.
Proposition 1.
The fixed point is parametrized by the physical parameters of the system, the duration of the periodic orbit’s evolution in mode (equal to its duration in mode ), and the forward speed component of the fixed point. The term in (32) is given by
and the duration of the periodic orbit’s evolution in mode is equal to
Additionally, on the periodic orbit at the end of D before the reset is applied, the front and rear leg splays (to be used in used in (63)) are
Proof.
See [65] in Appendix D. □
The form of the fixed point does not give much insight into the nature of the resulting orbit and how parameter choices (particularly and ) affect it. As such, we give the minimum and maximum state variable values along the orbit associated with in Table 1 as well as numerical traces of the orbit in Figure 5. Recall that (16) and , where the interval constraint on guarantees a physically realistic double-support phase on the hybrid periodic orbit to capture the actuator constraints of Section 5.1. Additionally, the mass-center height varies by a value of
along the orbit.

Table 1.
Minimum and maximum state values along the hybrid periodic orbit associated with the fixed point of Proposition 1.
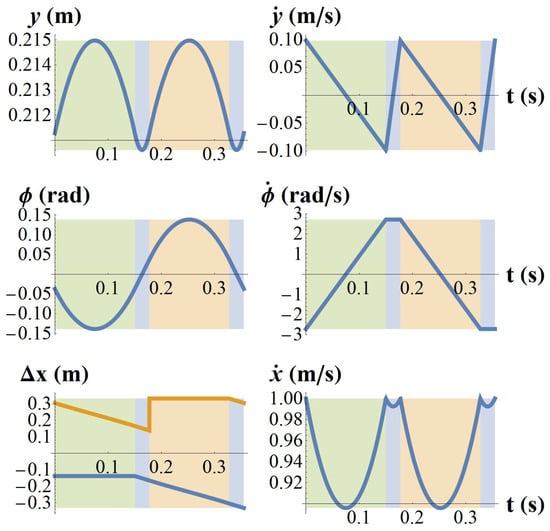
Figure 5.
Traces of the predicted hybrid periodic orbit over a full stride using the parameters of Table 2 at a commanded speed of 1 m/s are provided so as to give the reader an early intuition of what the periodic orbits will look like in the later experimental section. These state variable traces characterize a useful steady-state bounding gait with realistically small oscillations in body height and forward speed. The readers will notice that the traces of the hybrid dynamical system are smooth everywhere except for points corresponding with the guards and resets in the next mode. The background color indicates the mode (4). Green is , blue is , and yellow is . In the graph, the blue trace gives while the orange trace gives (12). Notice that deviations in body height y and forward speed are quite small, indicating a valid Approximation 1 as discussed in Section 3.4 and a small value of from Table 1.
The “user-specified” terms in the form of the hybrid periodic orbit (the terms not determined by the physical robot parameters) are , , and . The (mass-specific) applied vertical force at the toe can be thought of as analogous to a spring constant: increasing decreases vertical height and pitch oscillations (the reason that increasing the stance force decreases height y and pitch variations in the orbit is because the total stance time (54) is reduced by an increase in , giving the system configuration less time to change in stance—and while the variations in y and decrease with increasing , the total energy of the orbit increases), as well as total hip stance time (by decreasing the double-support time (52)), where the total hip’s stance time is equal to
The value of directly sets the single-support stance duration (equal to a hip’s flight duration) and can be thought of as the dominant determiner of a hip’s total stance time in cases with shorter double support . Our regime of operation involves a short double-support time ; however, the double-support time would be longer for very low vertical forces just barely supporting the weight of the robot—in this case, a change of variables of total support time might be more insightful. Larger values of increase vertical height and pitch oscillations. Smaller values of leave less time for the leg to reset its position in flight, and sufficiently small values will be prohibitive for the actuators. The value of sets the desired speed at mode transitions.
3.4. Constant Stance Height Approximation in Pitching Dynamics
With an explicit representation for the hybrid periodic orbit’s mass-center height variation (53) in hand, we revisit Approximation 1’s usage of a constant stance height in the pitching acceleration components of the dynamics (15). Approximation 1 will hold on the hybrid periodic orbit for height variation values of (53) that are small compared to the height of the robot.
For Inu, using the experimental parameters of m/ and s as indicated in Table 2, the height variation in the mass center along the desired limit cycle is equal to a deviation of 4 mm; thus, the height is only expected to change from its nominal value of meters during the periodic orbit, which begins to approach the noise floor on our sensors and is thus more than sufficient for a constant approximation assumption. This is illustrated in the experimental traces of Inu running in Section 5.2, where the mass-center height is approximately constant both in the experimental data and in the desired limit cycle.

Table 2.
Parameter values used in experiments. As explained near the end of Section 4.3, the nine control weights were used to place seven poles at the origin according to (A8), (A11) and (A4), fully determining both and while leaving constrained to a hypersurface. Having achieved infinitesimal deadbeat stability, we chose the remaining control parameters according to the constrained optimization procedure given in Appendix C to optimize various other performance metrics.
More generally, the validity of this approximation is strongly dependent on the duration of the hip’s stance but—for the following reasons—we expect it to hold for a large class of machines. In terms of the duration of the hip’s stance (equal to 205 ms on Inu with the parameters of Table 2), the mass center’s height deviation is equal to
which is maximized by when , resulting in a mass-center height deviation of . Stance durations of approximately 300 ms or less—where 300 ms is a relatively long stance duration for robots of Inu’s mass scale—result in mass-center height deviations of 1 cm or less—a small value compared to Inu’s nominal mass-center height of meters while running. In biology, the duration of stance has a strong scale dependence: it generally increases with body mass and animals up to the size of horses have been documented as having stance times of 300 ms or less [66]. In this study, ground contact time was found to be generally proportional to for animals with body mass M. If the same results were to hold for robots, even when using our antagonistic value of , we would expect that larger robots would satisfy Approximation 1 and that smaller robots (with much shorter stance times) would have an even smaller height deviation for their size. Of course, one could design a robot with an artificially long stance duration to break the validity of Approximation 1, but this would result in a severely speed-limited robot as discussed in Section 3.5. One would also need to reconsider the use of this approximation when using a much more energetic gait that has a significant flight phase, but this would assume a difference hybrid mode sequence than that considered in this work.
3.5. Speed Limit
The inherently limited workspace of a leg’s kinematic linkage induces a speed limit on running [67]. In our case, the leg linkage workspace must accommodate the maximum and minimum values of the leg splays and in Table 1 to physically instantiate the periodic orbit associated with the fixed point . This results in a horizontal leg sweep distance of , where recall is speed-dependent (51). The sweep distance has a complicated form in terms of the model parameters as involves the complicated expression (50); however, we can understand the dominant terms using a simple approximation.
The average forward speed in stance is approximated by , which is valid given a small value of the term in Table 1 relative to . This applies to Inu as indicated by the small speed deviations in both the hybrid periodic orbit in Figure 5 and the robot’s instantiation of those orbits as presented in Section 5.2. Then, the mass center’s (and thus the hip’s) horizontal sweep distance in stance is
A robot with a horizontal leg stroke distance that is kinematically limited to and with a stance time (limited from below by a value of achievable by the actuators) would physically be able to instantiate an orbit with a maximum running speed magnitude of
a value of m/s for Inu as explained in Section 5.1.
We now revisit our decision in Section 2.2 to set to equal so as to maximize the forward running speed. The horizontal interval that the legs sweep when operating on the periodic orbit is centered at a distance of from the mass center as calculated from Table 1. Assume that the leg linkage workspace permits an interval of horizontal reach centered at the hip. The horizontal leg sweep interval must be contained in the leg workspace interval for a physically realizable gait. The maximum speed that can be physically realized occurs when the horizontal leg sweep interval and leg workspace interval are identical, which requires that they be centered at the same point, which requires to equal .
3.6. Cost of Enforcing a Cascade
Proposition 1 allows us to revisit the cost of enforcing the cascade composition of Section 2.2 with the horizontal force law (21) along the hybrid periodic orbit. Very often in robotics, a disadvantage of canceling the natural system dynamics using control is that it requires significant actuation affordance. However—as we argue below—at lower speeds the horizontal forces needed to achieve this dynamic decoupling are quite small; they are only a fraction of the applied constant vertical force.
We quantify this by considering the maximum horizontal leg force magnitude encountered during a stride on the periodic orbit. This maximum value is obtained when the horizontal length from the toe to the mass center is furthest from (21). When operating on the hybrid periodic orbit, recall that the leg sweeps an interval of length centered at a distance from the mass center (Section 3.5), thus reaching out at a maximum distance of from the centered distance of and giving the horizontal force the following maximum stance magnitude:
The given maximum horizontal force is really a conservative upper bound, as it corresponds to the double-support mode and a sensible user would not program both the front and rear legs to generate opposing internal forces of this magnitude; rather, they could achieve the same total horizontal force on the body with much smaller horizontal toe forces to decrease internal forces. The user’s choice of front/rear force distribution in double support is elaborated on near the end of Section 2.1.
Putting this in terms of forward running speed using the approximation (55) gives
This force would be briefly equal to the applied specific vertical force in stance at an average stance speed of . Using a duration of hip stance of seconds and an average mass-center stance height of meters (Inu’s experimental parameters derived from Table 2) results in a speed of m/s, where the maximum horizontal and vertical forces are briefly equal. Inu is kinematically limited to a running speed of approximately m/s, so the platform cannot approach the high-cost-of-cascade-enforcement regime. On a quadruped that is not kinematically limited, higher speeds than require that the toes reach out sufficiently in front of or behind the hips to the point of causing the horizontal cascade-enforcement force to briefly eclipse the vertical at the beginning and end of stance. In these cases, we can consider the cascade enforcement to be “expensive” for the actuators. A shorter stance duration (54) would mitigate this cost; achieving this through reducing would increase the actuator cost of resetting the leg’s position in flight, and achieving this through increasing would also tax the actuators.
The approximate cost of enforcing the cascade is linear in speed (57), going to zero when bounding in place. Thus, at low speeds and small horizontal forces, we believe that the natural dynamics are themselves “almost” a feedforward cascade of the in-place module with the horizontal bead-on-a-wire dynamics, and that our choice of a horizontal force law represents only a slight “nudge” to the dynamics so as to complete this decoupling (Figure 4) and provide us with a tractable stability analysis.
4. Controller
Control of the system to achieve a symmetric bound occurs on the hybrid guards and resets. Recall from Section 2.2 that cascading the dynamics naturally places the in-place control gains in the guards and the horizontal control gains in the resets. A summary of our control strategy is as follows.
The in-place controllers perform feedback on the mode timers and hip heights, as time and kinematic configuration are the most accurately measured aspects of the state as discussed in Section 6.1. Instead of controlling the continuous value of the hip heights, we only control their value at the start of the mode. This has the practical benefit of providing hip height measurements for the controller even when the hip is in flight (having measured its value at liftoff), as well as the algebraic benefit of simplifying the stability calculations in Section 4.3 as the hip height values being controlled do not change over the course of a mode. The fact that six easily measurable quantities exist per half stride (two modes, each with one timer and two hip height measurements) results in six control gains. Four of the gains are used to place the four poles of the stride map corresponding to the four in-place components (recall that the presence of the timer coordinate in the dynamics gives four in-place Poincaré map components, not three), and the remaining two gains are used for optimization to meet other performance criteria.
The reset controllers perform feedback on the system’s forward speed and the two toe positions. This gives three gains (rather than six, as the controllers can only set the horizontal toe position in flight and not in stance) to place the three poles of the stride map corresponding to the three horizontal components. In principle, the horizontal controller could be chosen to take in additional inputs and thereby allow the user to optimize it for other performance criteria, for example the in-place mode timers and hip heights; however, we found that performance was reasonable without needing to introduce additional feedback paths.
Section 4.1 specifies the controller on the guards, which stabilizes the in-place state components. Section 4.2 specifies the controller on the resets, which stabilizes the horizontal state components. Section 4.3 presents the central stability result of the paper. Specifically, we present a choice of control weights that makes the Poincaré map Jacobian evaluated at the fixed point nilpotent (Proposition 2), making the closed-loop dynamics infinitesimally deadbeat.
4.1. Hybrid Guard Control
Recall that the hybrid guards intersections (25) and (26) require an appropriate hip height equal to some nominal value plus a (to-be-specified) state-dependent guard control function . We choose to use guard controllers that are functions of the mode timers and hip heights—giving six control gains as shown below in (58)—as mode time and kinematic configuration (hip height) are the most accurately measured aspects of the in-place state by our robot as discussed in Section 6.1. Specifically, we use guard control functions of the following form:
where the vectors represent control weights, , give the front and rear hip heights (29), and the functions give the mode’s initial hip heights (according to the hip heights that occurred when ) via
The values of in (58) are set as follows and represent “target” states for the controller to track; we choose them so that the control functions vanish by design along the hybrid orbit associated with a privileged fixed point of . Denote the lift (44) of the stride map fixed point in Proposition 1 from to by
and set in (58) to equal the in-place component of the state of the hybrid execution initialized at as it periodically enters mode i before entering mode j according to
Finally, let and in (58) agree with the durations of the hybrid trajectory in modes and , respectively.
Let and denote the i’th components of the control parameter vectors and , respectively. We impose the requirement that
so that the hip height necessary for touchdown is not decreasing in time and the hip height necessary for liftoff is not increasing in time, satisfying (28).
Intuitively, the guard control functions (58) act as proportional controllers and modify the nominal touchdown or liftoff hip heights according to a weighted sum of errors between scalar-valued functions of the state and constant “target” values. These scalar-valued functions consist of the hip height values at the start of the mode execution (calculated by back-flowing the state until the component coincides with 0 and examining the hip heights at that time instance, and physically implemented by measuring the state variables at the start of the mode) and the current mode duration according to . The “target” states were chosen to force the control functions to zero at the hybrid transitions along the privileged periodic orbit of Proposition 1 by setting them to equal the state along the orbit when the evolution initially enters mode i as it evolves to mode j. The control weights will be chosen in Section 4.3 and Appendix B to make the periodic hybrid trajectory associated with a stable hybrid limit cycle.
4.2. Hybrid Reset Control
Recall that the in-place components of the hybrid resets simply zero the mode timer variable , while the horizontal components of the reset place the foot horizontally in flight using a nominal value according to control functions (32). We choose reset control functions of the following form:
where
are control weight constants that will be chosen to stabilize the horizontal components of the gait in Section 4.3 and Appendix B. The values of are equal to the values in Proposition 1 so that the control functions vanish along the privileged fixed point of the stride map (on the periodic orbit’s intersection with , equals and equals ).
Intuitively, the reset control functions (63) act as proportional controllers—much like the guard control functions—to place the foot horizontally in flight so as to control the horizontal state components. Note that the reset takes place at the touchdown event, at which time the toe cannot move horizontally without undesirable slipping. Thus, in the physical implementation of , one should apply the control function continuously in flight (as in [52]) so that when touchdown does occur the toe is in the correct position to satisfy .
4.3. Controller Stability Analysis
In the half-stride map (47), the horizontal states have no influence on the in-place components of , giving the map the following cascade form:
and endowing a block-diagonal Jacobian (2) whose structure we will now take advantage of. The Jacobian of is given by
where
with in-place components
and horizontal components
The mode-map Jacobians have the form
where is given by (recalling the structure of the flow (35) and reset (31)):
and where (38), with resets (32) and (63), and horizontal flow (36). Note that all the factors of are lower block-triangular.
The half-stride map Jacobian has the form
indicating the eigenvalue separation property discussed in Section 1.2. Four of the eigenvalues are determined from , given by
where simplifies to . The remaining three eigenvalues are from , which has the form
where
and and are given in (37).
We can further simplify the Jacobian block . By multiplying the values of , (70) simplifies to
where
and—as specified in (72)—the points of evaluation for the terms all have in common that . The form of is given in Lemma A1.
We now have explicit expressions for all terms in the iterated map Jacobian (66) and can begin an analysis of the map’s local stability at . It remains to choose weights in the hybrid guards (26), (58) and weights (64) in the hybrid resets (32), (63) such that the spectral radius of (69) is less than unity.
Given the unwieldy form of the Jury stability criteria for fourth-order polynomials, we instead opt to obtain an infinitesimally deadbeat solution, by which we mean that all the eigenvalues of the Jacobian of the iterated map evaluated at the fixed point are equal to zero, a choice further discussed in Section 6.1.
Proposition 2.
Proof.
The component of in (69) is made nilpotent through the choice of gains and given in Lemma A2 (via the change in coordinates (A2)), assuming the invertibility of the matrix (A7) which we conjecture to be generically invertible (we numerically verified invertibility of (A7) when using the values from Table 2). The component of is made nilpotent through the choice of gains given in Lemma A3.
The eigenvalues of the block-triangular are given by the union of the eigenvalues of the diagonal blocks and . These diagonal blocks are nilpotent, and so is nilpotent. □
The procedure for choosing gains for infinitesimal deadbeat stability is algorithmic in the sense that the gain choices for and are explicitly given by Equation (A8) (via the change in coordinates (A2)) and (A11), respectively; and Equation (A4) constrains to a hypersurface (a hyperplane constraint in the coordinates of (A1)).
There still exists some freedom in choosing the control parameters as only a hypersurface constraint on the three-dimensional is required for infinitesimal deadbeat stability (nine control gains were used to place seven poles). We chose the remaining control parameters according to the procedure given in Appendix C. We found that selecting control parameters with parametric robustness and transients in mind was important; naively selecting values during the experiments resulted in poor performance. The numerical values chosen are shown in Table 2.
Slices of the numerically derived basin of attraction for the in-place components of the control scheme are depicted in Figure 6, using parameters given in Table 2 and enforcing the desired hybrid mode sequence. An enforced hybrid mode sequence is a conservative assumption compared to physical implementation on our robot where transient hybrid mode sequences are perfectly acceptable, and so we suspect that the actual basin of attraction without enforcing the hybrid mode sequence is larger.
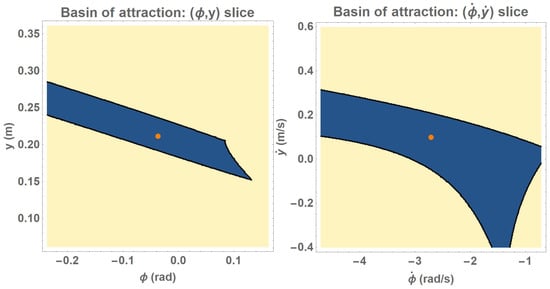
Figure 6.
Two slices of the numerically computed basin of attraction when the hybrid mode sequence is enforced, using parameters given in Table 2 (left—in the plane; right—in the plane). The blue region indicates the basin, and the center orange dot corresponds with the fixed point of the map . The enforcement of the hybrid mode sequence is a very conservative assumption for real-world implementation, as the ability to move through transient hybrid mode sequences is an inherent affordance of legs that provides robustness and motivates their use on machines.
The robustness of the in-place components of the control scheme to parametric uncertainty is indicated in Figure 7. While we can measure the majority of the physical parameters of the robot quite well, we have a difficult time accurately measuring the body’s moment of inertia, which is folded into the generalized Murphy number a, as well as the stance-specific vertical force . Here, we show the spectral radius of the Jacobian of when the “true” parameter values are varied from the parameter values used by the controller, evaluated at the fixed point that results from this parameter perturbation. The results of Figure 7 show that the controller will only destabilize when our error in estimating these two parameters is very large.
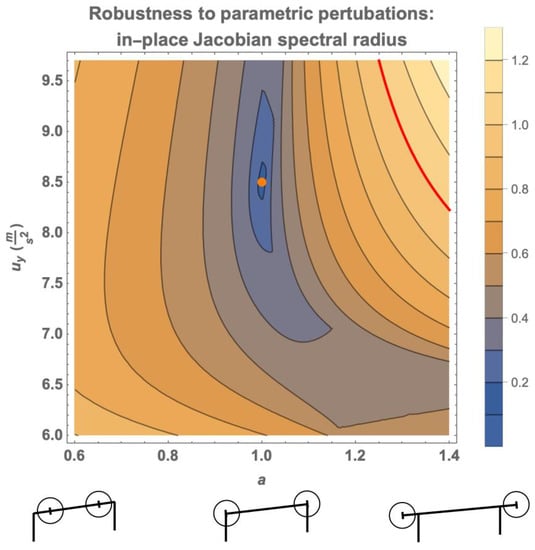
Figure 7.
Robustness of deadbeat solution to perturbations in the parameters and the unitless a, as indicated by the value of the spectral radius of the Jacobian of when the true parameter values are varied from the parameter values used by the controller in Table 2, evaluated at the fixed point that results from this parameter perturbation. To give the reader an intuition on the range of a displayed, below the graph are cartoon representations of the robot for a generalized Murphy value a of , , and , assuming all the robot mass is equally distributed at two point masses along the robot. The controller becomes unstable when the spectral radius exceeds unity, indicated by the red line. The parameters a and are the two parameters which are difficult to measure on the physical robot. The large distance from the unperturbed case (indicated by the orange dot) to the onset of destabilizing perturbations (indicated by the red line) suggests a large degree of robustness to uncertainty in these parameters.
The basin of attraction for the horizontal components of the controller is global, as the iterated dynamics are affine in . Of course, because is also a function of , convergence in is only guaranteed by our local stability analysis once approaches its limiting value. We can think of the dynamics of the combined system as containing an attracting invariant submanifold given by , on which the dynamics globally attract to .
We see from Figure 8 that the horizontal control scheme has a reasonable degree of robustness to parametric variation. Unlike the in-place control scheme, the horizontal does not have any free control parameters to optimize performance metrics other than for achieving infinitesimal deadbeat stability. Thus, this control scheme is hostage to whatever transients emerge as a result of the deadbeat control law Lemma A3, although we did not observe large transients in the experiments of Section 5. If we had, we could increase the number of state variables and control coefficients appearing in the input of the control functions (63)—for example, by introducing in-place state components—and then perform an optimization similar to the in-place control scheme to limit transients; however, this would come at the cost of added feedback paths along which noise and the negative effects of measurement uncertainty would grow.
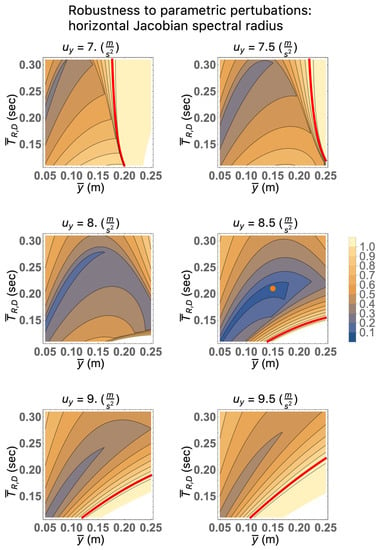
Figure 8.
Slices of the Jacobian spectral radius of evaluated at the appropriate fixed point with parametric perturbations in the parameters , , and —the only parameters entering into the Jacobian. This analysis uses numerical parameter values given in Table 2 as the unperturbed values. Here, the control is performed using the unperturbed parameters, showing the robustness of the control scheme to parametric uncertainty. The distance from the orange dot in the lower-left plot (representing the unperturbed parameter values) to the red line (indicating slices of the edge of stability) demonstrates that the controller can withstand sizable perturbations in parameter space before becoming unstable.
5. Empirical Demonstration of Controller
This section documents the implementation of the controller from Section 4 on the Inu robot. Section 5.1 describes the experimental setup and Section 5.2 gives the experimental results.
5.1. Setup
We demonstrate the controller of Section 4 implemented on the Inu robot [20], a direct-drive quadruped that has an articulated spine [68] (held rigid in these experiments). While the experiments of this paper do not utilize Inu’s flexible spine, we hope in future work to cascade another module that encapsulates an added degree of freedom representing a bendable back to the modeling composition and thus chose this robotic platform for continuity with future work.
The robot’s lack of gearing in the legs necessitates operating the actuators far from their operating point of maximum power (although the lack of gearing provides benefits such as proprioceptive ground contact detection [69,70]), which manifests itself in actuator saturation preventing the platform from achieving an aerial phase when running at faster speeds. We decided to forgo an aerial phase at slower speeds as well—hence the choice of hybrid modes (4)—to demonstrate consistent behavior across all feasible running speeds, and chose commanded vertically applied force and mode durations ( and in Table 2) according to what the actuators could achieve at higher speeds.
Inu’s parametric correspondence with the simplified model is given in Table 2. While most of the simplified model parameters are easily measurable to a high degree of accuracy, calculating the robot’s moment of inertia about its mass center (and hence its generalized Murphy number a) and the mass-specific vertically applied force is more difficult. Our lab does not have the equipment to accurately measure these two parameters; however, Figure 7 indicates a wide basin of stability to combined perturbations of these parameters and so we do not expect to see instability arise from our lack of good measurement capability.
The robot is kinematically limited to a horizontal leg stroke distance of 32 cm when using a nominal touchdown height of 22 cm. Since the hip’s stance time along the limit cycle (55) is equal to 205 ms, we know (as discussed in Section 3.5) that the forward running speed is theoretically limited to approximately m/s.
Inu executed a bounding run at several speeds to demonstrate the viability of the controller on physical hardware, using only its onboard MPU-6000 IMU (https://www.sparkfun.com/products/retired/11234, accessed on 24 July 2023) and motor encoders for sensing. A Vicon motion capture system (https://www.vicon.com/, accessed on 24 July 2023) was used to log experimental kinematic data of Inu’s mass-center and body-pitch trajectories and compare them with the predicted periodic orbits of the reduced-order model. The raw (unfiltered) trajectory data from motion capture are provided. In an effort to demonstrate the behavior of the in-place dynamics (65) in isolation, we first ran the robot without implementing the horizontal reset speed controller—instead using a simple PD loop to dampen out horizontal movement. In a second set of experiments, we used the full controller to test the behavior at speeds up to the theoretical limit. A simple feedforward yaw controller was implemented on the robot to steer during running: the user gives a joystick yaw input which the robot adds to the horizontal forces applied by the right toes and subtracts from the horizontal forces applied by the left toes. We found that adding a small amount of active damping in the controller implementation—specifically in the vertical and horizontal applied stance forces—was useful but not necessary to mitigate the effects of unmodeled friction [15]. Our controller’s implementation in C++ has been provided as Supplementary Material under the filenames VirtualPogostick.cpp and VirtualPogostick.h.
5.2. Results
The results of the experiments are summarized in Figure 9 and Figure 10. The in-place controller was run on Inu over the course of approximately 30 strides as shown in Figure 9, demonstrating a good empirical correspondence between the robot and the predicted orbit of the in-place controller. The full controller’s implementation in Figure 10 shows a reasonable agreement with the desired limit cycle at lower speeds, although the addition of the forward speed controller introduces more noise into the orbits as compared with the in-place controller. The predicted behavior was reliably repeatable over dozens of trials at many horizontal speed set points, , in the range allowed by (56). At higher speeds, we see the orbit of the pitch degree of freedom inconsistently sag during negative pitch values corresponding to when the front is in stance. This is due to the motors of the front body segment saturating when running at speed; the front is slightly inertially disadvantaged compared to the rear due to the battery weight being carried by the front. Inu can still run without falling when approaching the speed limit imposed by Inu’s kinematics; however, the legs are commanded to lift off prematurely when they near their kinematic singularity as shown in Figure 11, which results in inconsistent trajectories.
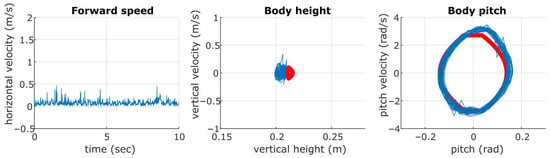
Figure 9.
The in-place component of the controller implemented on the Inu robot shows good correspondence between the actual (blue) and analytically predicted (red) behavior of the robot over approximately 30 strides (10 s) of motion capture data. Here, the horizontal toe position is maintained through the use of a simple PD controller with relatively high-magnitude derivative term to dampen out fore-aft oscillations.
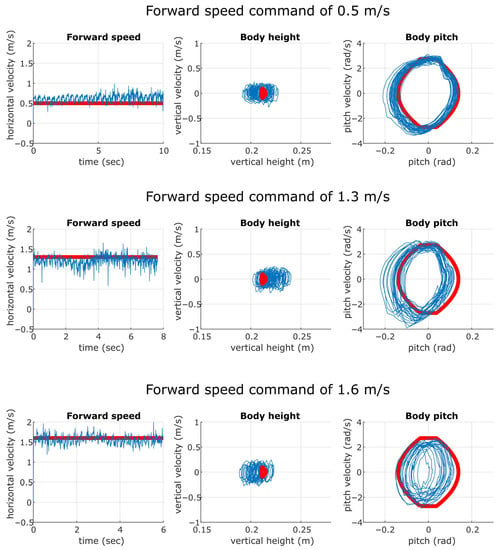
Figure 10.
Depicted are the actual (blue) and desired (red) orbits and trajectories under motion capture using the full controller of Section 4 on the Inu robot over various running speeds up to Inu’s kinematic speed limit. As further discussed Section 5.2, we see a reasonable agreement with the desired limit cycle at lower speeds (top). At higher speeds (middle), we see the orbit of the pitch degree of freedom inconsistently sag during negative pitch values corresponding to when the front is in stance, as the front is slightly heavier than the rear. Approaching the speed limit imposed by Inu’s kinematics (bottom), Inu’s legs are commanded to lift off prematurely when they near their kinematic singularity as shown in Figure 11, which results in inconsistent trajectories. The lower time durations of the faster experiments are the result of the robot running faster through the motion capture area.
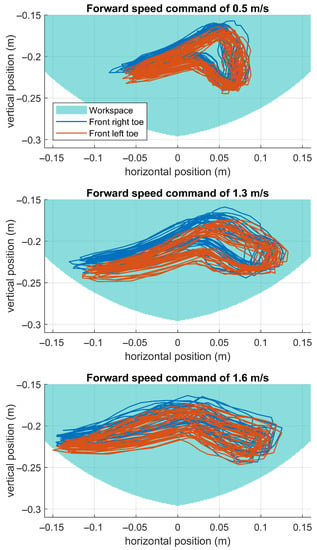
Figure 11.
Toe kinematic trajectories for the front legs in the local hip frame show that at running speeds of m/s, the leg linkage is close to singularity. This represents a constraint on maximum running speed, as the leg runs out of workspace to sweep the leg backwards in stance. Faster running could be achieved by either using longer legs to increase the workspace or by achieving shorter stance durations through increasing the applied vertical stance force. In future work, we will investigate the addition of a spine morphology to provide this added workspace without detracting from the hip’s torque generation affordance.
Inu is able to run up to its theoretical kinematic running speed of m/s, but Figure 11 demonstrates that Inu is at the limit of its available workspace at this speed. The robot was not able to exceed speeds higher than this, and commanding it to do so resulted in the legs hitting their kinematic singularity earlier in stance. This resulted in the robot stumbling, the onset of which lowered the running speed substantially. To run faster, either longer legs would be needed to increase the workspace (which would require greater motor torques via the increased lever arm) or a shorter stance duration would be required through increasing the applied vertical stance force. Both are precluded by Inu’s inherently torque-limited actuation. In future work, we will investigate the addition of a spine morphology to provide this added workspace without detracting from the hip’s torque generation affordance.
6. Discussion
6.1. Infinitesimally Deadbeat Nature of Our Result
Our stability result is not one that is deadbeat, but rather infinitesimally deadbeat as a result of achieving a nilpotent stride map Jacobian at the fixed point. As such, local convergence to the fixed point is not in a finite number of steps but rather super-exponential due to the vanishing of linear terms in the Taylor approximation of the k-th iteration of the stride map at the fixed point for some . We believe that finite step convergence often comes with the price of an increased control burden that—as suggested by the current general lack of deadbeat results “in the wild” without utilizing motion capture—is poorly conditioned to state/parameter uncertainty.
Specifically, a k-step deadbeat control law requires the cancellation of all nonlinear terms in the Taylor series of a system’s k-times composed Poincaré map local to the fixed point. Regarding state uncertainty, the canceling of the combined effect of these nonlinear terms can be worse-conditioned to errors in state measurement than only canceling the linear terms (sometimes much worse). We avoided the possibility of this ill conditioning by both choosing not to cancel the nonlinear terms and by designing feedback paths in our control law to only use states that we find we can accurately measure—time, kinematic configurations, and forward speed—thus eschewing the common method of detecting a hip’s apex event in flight as it is typically estimated from the hip’s vertical liftoff velocity, which we have difficulty measuring in stance due to its quickly changing nature. We are wary of using these feedback paths for deadbeat stability as the state measurement error inherent to operation in the physical world is still present in states that we can “accurately” measure, and an ill-conditioned canceling of dynamics can still magnify their adverse effects to result in a controller with poor empirical performance. Regarding parametric uncertainty, deadbeat control amounts to inverse dynamics and it is known that the cancellation of inertial terms can lead to poor parametric robustness. Rather, the empirical performance depicted in Figure 9 and Figure 10 demonstrates a reasonable degree of robustness to the state measurement error inherent to operation in the physical world and Figure 7 and Figure 8 indicate a reasonable degree of parametric robustness.
6.2. Controlling on the Hybrid Transitions
In controlling on the guards and resets, we are exploiting a natural affordance provided by the use of legs. The control affordance provided by hybrid transitions is important because it is in some sense independent of actuator power constraints: we achieve arbitrarily good pole placement with only modest control gains (Table 2). Instead, it is our specification of the (more or less highly energetic nature of the) desired hybrid periodic orbit (Proposition 1, Section 3.3) that depends strongly on actuator performance as shown in Section 3.6, but this is almost entirely independent of the stabilizing controller gains (Section 4). As we attempt to explain more precisely below, we believe that controlling the hybrid transitions frees scarce actuator power resources from the task of shaping the continuous dynamics into the proper “funnel” [71] required for stability, allowing their application to instead access dynamical regimes of higher energy operation. Settings rich in hybrid interactions are ripe for this style of control, and as such the intrinsic necessity of making and breaking contact that accompanies legged robots is an opportunity for exploiting the natural hybrid nature of the dynamics to achieve stability.
The costs inherent to our control formulation are twofold. First, the actuator cost is equal to the enforcement of the (piecewise) Hamiltonian dynamics through generating conservative potential field force laws at the toes. In the vertical, this is a constant force (20), in the horizontal the force is affine with respect to the leg horizontal toe position (21). Due to the simple and transparent nature of these force laws (constant and affine), a user can easily evaluate if they are prohibitively costly at any point in the workspace and—as long as the transients in state are not bad—should not expect that operation near the hybrid periodic orbit would be suddenly costly for the actuators. The fact that the Inu robot used in the experiments is inherently force-limited (Section 5.1), yet can tolerate using the force laws even as perturbations are corrected, suggests that the costs associated with it are not prohibitive.
Second, our hybrid transition control scheme consists of displacing the toe from some nominal location using proportional control. Practically, the toes can only tolerate so much displacement from the controllers (legs being limited in workspace, or perhaps needing to avoid a corner of the workspace with unfavorable actuator performance), which we relate to the tolerable state error as follows. If one puts interval constraints on the values that a control function , , , or (58), (63) may take, this is equivalent to being able to—on the hybrid transitions—tolerate perturbations from the periodic orbit that satisfy two halfspace constraints (whose hyperplanes are parallel and offset). For example, specifying that in (63) is equivalent to the requirement that
allowing the user to quantify the state errors tolerable by the leg mechanisms.
6.3. Cascade Compositions as Attracting Invariant Submanifolds
Stable fixed points of cascaded iterated maps necessarily have an attracting invariant submanifold. Let and be (respectively) n- and m-dimensional differentiable manifolds, and suppose the iterated map is a cascaded composition (1) with a stable fixed point . Then, is an invariant submanifold, and is attracting due to being attracting in . In our system, the attracting invariant submanifold is given by the horizontal dynamics along the in-place limit cycle. It is interesting to note that in the language of templates and anchors [72], traditionally the dynamics on the attracting invariant submanifold, called the template dynamics, drive the hybrid transitions, while in our case it is the dynamics that collapse to the attracting invariant submanifold—called the anchor dynamics—that do so.
7. Conclusions
This paper considered the problem of stabilizing a three-mechanical-degree-of-freedom simplified model of Groucho-style quadrupedal bounding in the sagittal plane. By using the continuous stance forces to effect trivial continuous dynamics and a cascade dynamical decoupling giving a useful eigenvalue separation condition in the stride map Jacobian, we analytically showed local stability by controlling the guards and resets to obtain an “infinitesimal” deadbeat result that we believe is better conditioned to parametric and state uncertainty than full deadbeat control for practical use in an experimental setting. The model, while simple, well approximates physical robot experiments implementing the running controller. Aside from the contribution of the running controller, we hope this paper motivates further progress in the analytical stability results of three-degree-of-freedom (and higher) legged locomotion models—a currently underdeveloped area of the literature that has the potential to greatly enhance the empirical performance of legged machines.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/robotics1010000/s1. Software implementation of controller: VirtualPogostick.cpp, VirtualPogostick.h
Author Contributions
Conceptualization, J.D. and D.E.K.; Methodology, J.D. and D.E.K.; Software, J.D.; Validation, J.D.; Formal Analysis, J.D. and D.E.K.; Investigation, J.D. and D.E.K.; Resources, D.E.K.; Data Curation, J.D.; Writing—Original Draft Preparation, J.D.; Writing—Review and Editing, J.D. and D.E.K.; Visualization, J.D.; Supervision, D.E.K.; Project Administration, J.D. and D.E.K.; Funding Acquisition, J.D. and D.E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-0822, by the Army Research Office under Grant No. W911NF-17-1-0229, and by a Vannevar Bush Fellowship held by the second author under ONR Grant No. N00014-16-1-2817 as sponsored by the Basic Research Office of the Assistant Secretary of Defense for Research and Engineering.
Data Availability Statement
The novel computer code developed for this article consists of our controller’s implementation in C++ as used in Section 5. This software has been provided as Supplementary Material under the filenames VirtualPogostick.cpp and VirtualPogostick.h.
Acknowledgments
The authors would like to thank Matthew Kvalheim for discussions and insights related to this paper’s mathematics.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Table of Symbols
Table A1 provides the reader with a description of the main symbols used in this manuscript.

Table A1.
Main symbols used in this work with reference to their equations of introduction.
Table A1.
Main symbols used in this work with reference to their equations of introduction.
| Symbol | Description |
|---|---|
| Hybrid system (3), (5), (6), (13), (17), (18) | |
| Hybrid modes (4) | |
| Mode domains (7), guards (25), resets (30), vector fields (14) | |
| Time, mass-center height, body pitch, mode timer (10), Figure 2 | |
| Mass-center and front/rear toe horizontal positions (11), Figure 2 | |
| Front, rear horizontal leg splay distance with regard to the mass-center (12) | |
| Mode i state (9), with in-place (10) and horizontal (11) components | |
| In-place state, configuration (10) | |
| Physical model parameters (Figure 2) | |
| Pseudo-physical simplifying parameters (22), (24), (26), Figure 2 | |
| In-place components of the guard set (25), (26) | |
| Front/rear hip heights (29) | |
| Guard “control” functions for touchdown, liftoff events (26), (58) | |
| In-place guard control weights (26) | |
| Front and rear initial hip height in mode i (59) | |
| “Bounding” symmetry map (41), (27), (33) | |
| Lie derivative (28) of scalar field V along vector field f at point x | |
| In-place (31), horizontal (32) reset function components | |
| Reset “control” functions (32), (63) | |
| Reset control weights (64) | |
| Nominal touchdown leg splay for front leg (32) | |
| Mass-center height Approximation 1 in pitching dynamics | |
| Vertical (16), (20), (34), horizontal (16), (21) mass-specific | |
| ground reaction force applied from each hip | |
| In-place (35), horizontal (36) mode-i flow | |
| simplified acceleration vector for mode i (35) | |
| Matrix components used in the description of (36) | |
| Mode i-to-j map (38), with in-place, horizontal components (39) | |
| Mode i time-to-impact map (40) with guard | |
| Reduced domain with horizontal, in-place components (42) | |
| State on with in-place and horizontal components (43) | |
| Projection and lift maps (44) | |
| In-place, horizontal projection, and lift maps (44) | |
| Stride (45) and “flipped” half-stride (47) maps | |
| Fixed point of (48) | |
| Leg splay components of (50) | |
| Total hip stance duration (54), leg-sweep distance (55) on the | |
| hybrid periodic orbit associated with | |
| Lift of (60) | |
| Mode i’s duration (52) and initial state (61) as it evolves into | |
| mode j under the hybrid execution from | |
| Simplified factors of ’s in-place component (73) |
Appendix B. Controller Stability Lemmas
This Appendix contains results related to the choice of control gains in Proposition 2, guaranteeing the infinitesimal deadbeat stability of the half-stride map (47) at the operating point (48). Lemma A1 gives the explicit form of the time-to-impact map Jacobians and . The control weight change in coordinates (A1) is given to assist in expressing the deadbeat gain expressions, which are presented in Lemmas A2 and A3 below.
Lemma A1.
Proof.
See [65] Appendix E. □
We introduce the following coordinate change to simplify the form of the time-to-guard-impact Jacobians above. Let
such that
This transformation is invertible via
where
Lemma A2.
The following choice of and make nilpotent assuming the conditions given in (A10) can be satisfied. Choose such that
which zeros one eigenvalue of and hence of . Denote the resulting Jordan decomposition of by
where the zero eigenvalue is placed in the upper-left element of and the explicit form of and is given in Equation (95) of [65] Appendix F. Let
and
Then choose
Proof.
See [65] Appendix F. □
Lemma A3.
The following choice of makes nilpotent. Let and
where and
Proof.
See [65] Appendix G. □
Appendix C. Control Gain Selection Procedure
The choice of control gains (A4), (A8), (A11) that grant the system infinitesimal deadbeat stability fully constrains and and constrains to a hypersurface. We chose where to place on this hypersurface as follows.
We chose to fix as a function of and via (A4), explicitly:
We then chose to set the value of to zero, severing a feedback path in (58) that corresponds to the hip’s usage of its own vertical height measurement in determining liftoff height. Setting to zero was observed in the experiment to improve performance. It is likely that this feedback path made the controller very sensitive to the sagging of the front body segment due to actuator saturation when running at faster speeds (depicted in Figure 10).
We chose using the following constrained optimization problem in an effort to reduce transients and control gain magnitudes, and to increase parametric robustness:
which are additionally subject to the constraints (A4), (A8), (A11) granting infinitesimal deadbeat stability, and where equals the coefficient vector for the characteristic polynomial of . The terms associated with are intended to keep the control inputs relatively small, the terms associated with are intended to reduce transients, and the terms associated with are intended to increase robustness to parametric uncertainty and measurement errors when applying control. We used , , and and numerically verified that the resulting control weights satisfied (A9). The numerical values chosen are shown in Table 2.
References
- Hyun, D.J.; Seok, S.; Lee, J.; Kim, S. High speed trot-running: Implementation of a hierarchical controller using proprioceptive impedance control on the MIT Cheetah. Int. J. Robot. Res. 2014, 33, 1417–1445. [Google Scholar] [CrossRef]
- Park, H.W.; Wensing, P.M.; Kim, S. High-speed bounding with the MIT Cheetah 2: Control design and experiments. Int. J. Robot. Res. 2017, 36, 167–192. [Google Scholar] [CrossRef]
- Boston Dynamics. Available online: http://www.bostondynamics.com (accessed on 24 July 2023).
- Ghost Robotics. Available online: https://www.ghostrobotics.io (accessed on 24 July 2023).
- Park, H.W.; Wensing, P.M.; Kim, S. Jumping over obstacles with MIT Cheetah 2. Robot. Auton. Syst. 2021, 136, 103703. [Google Scholar] [CrossRef]
- Topping, T.T.; Vasilopoulos, V.; De, A.; Koditschek, D.E. Composition of Templates for Transitional Pedipulation Behaviors. In Proceedings of the International Symposium on Robotics Research (ISRR), Geneva, Switzerland, 25–30 September 2022; pp. 626–641. [Google Scholar]
- Katz, B.; Di Carlo, J.; Kim, S. Mini cheetah: A platform for pushing the limits of dynamic quadruped control. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 6295–6301. [Google Scholar]
- Kuindersma, S.; Deits, R.; Fallon, M.; Valenzuela, A.; Dai, H.; Permenter, F.; Koolen, T.; Marion, P.; Tedrake, R. Optimization-based locomotion planning, estimation, and control design for the atlas humanoid robot. Auton. Robot. 2016, 40, 429–455. [Google Scholar] [CrossRef]
- Da, X.; Grizzle, J. Combining trajectory optimization, supervised machine learning, and model structure for mitigating the curse of dimensionality in the control of bipedal robots. Int. J. Robot. Res. 2019, 38, 1063–1097. [Google Scholar] [CrossRef]
- Di Carlo, J.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic locomotion in the MIT cheetah 3 through convex model-predictive control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, eaau5872. [Google Scholar] [CrossRef]
- Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning quadrupedal locomotion over challenging terrain. Sci. Robot. 2020, 5, eabc5986. [Google Scholar] [CrossRef]
- Raibert, M.H. Legged Robots That Balance; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Koditschek, D.E. What Is Robotics? Why Do We Need It and How Can We Get It? Annu. Rev. Control. Robot. Auton. Syst. 2021, 4, 1–33. [Google Scholar] [CrossRef]
- De, A.; Koditschek, D.E. Parallel composition of templates for tail-energized planar hopping. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4562–4569. [Google Scholar]
- Altendorfer, R.; Koditschek, D.; Holmes, P. Stability analysis of a clock-driven rigid-body SLIP model for RHex. Int. J. Robot. Res. 2004, 23, 1001–1012. [Google Scholar] [CrossRef]
- Chevallereau, C.; Westervelt, E.R.; Grizzle, J.W. Asymptotically stable running for a five-link, four-actuator, planar bipedal robot. Int. J. Robot. Res. 2005, 24, 431–464. [Google Scholar] [CrossRef]
- De, A.; Topping, T.T.; Caporale, J.D.; Koditschek, D.E. Mode-Reactive Template-Based Control in Planar Legged Robots. IEEE Access 2022, 10, 16010–16027. [Google Scholar] [CrossRef]
- Park, H.W.; Wensing, P.M.; Kim, S. Online Planning for Autonomous Running Jumps Over Obstacles in High-Speed Quadrupeds. In Proceedings of the Proceedings of the Robotics: Science and System (RSS), Rome, Italy, 13–17 July 2015. [Google Scholar] [CrossRef]
- Duperret, J.M.; Kramer, B.; Koditschek, D.E. Core Actuation Promotes Self-manipulability on a Direct-Drive Quadrupedal Robot. In Proceedings of the 2016 International Symposium on Experimental Robotics (ISER), Tokyo, Japan, 3–6 October 2016; pp. 147–159. [Google Scholar]
- McMahon, T.A.; Valiant, G.; Frederick, E.C. Groucho running. J. Appl. Physiol. 1987, 62, 2326–2337. [Google Scholar] [CrossRef]
- McMahon, T.A. The role of compliance in mammalian running gaits. J. Exp. Biol. 1985, 115, 263–282. [Google Scholar] [CrossRef]
- Schmitt, D.; Cartmill, M.; Griffin, T.M.; Hanna, J.B.; Lemelin, P. Adaptive value of ambling gaits in primates and other mammals. J. Exp. Biol. 2006, 209, 2042–2049. [Google Scholar] [CrossRef]
- Demes, B.; O’Neill, M.C. Ground reaction forces and center of mass mechanics of bipedal capuchin monkeys: Implications for the evolution of human bipedalism. Am. J. Phys. Anthropol. 2013, 150, 76–86. [Google Scholar] [CrossRef]
- Hutchinson, J.R.; Schwerda, D.; Famini, D.J.; Dale, R.H.; Fischer, M.S.; Kram, R. The locomotor kinematics of Asian and African elephants: Changes with speed and size. J. Exp. Biol. 2006, 209, 3812–3827. [Google Scholar] [CrossRef]
- Andrada, E.; Rode, C.; Blickhan, R. Grounded running in quails: Simulations indicate benefits of observed fixed aperture angle between legs before touch-down. J. Theor. Biol. 2013, 335, 97–107. [Google Scholar] [CrossRef]
- Reinhardt, L.; Blickhan, R. Level locomotion in wood ants: Evidence for grounded running. J. Exp. Biol. 2014, 217, 2358–2370. [Google Scholar] [CrossRef]
- Weihmann, T. Crawling at high speeds: Steady level locomotion in the spider Cupiennius salei—global kinematics and implications for centre of mass dynamics. PLoS ONE 2013, 8, e65788. [Google Scholar] [CrossRef]
- Rubenson, J.; Heliams, D.B.; Lloyd, D.G.; Fournier, P.A. Gait selection in the ostrich: Mechanical and metabolic characteristics of walking and running with and without an aerial phase. Proc. R. Soc. Lond. Ser. Biol. Sci. 2004, 271, 1091–1099. [Google Scholar] [CrossRef]
- Daley, M.A.; Usherwood, J.R. Two explanations for the compliant running paradox: Reduced work of bouncing viscera and increased stability in uneven terrain. Biol. Lett. 2010, 6, 418–421. [Google Scholar] [CrossRef] [PubMed]
- Altendorfer, R.; Moore, N.; Komsuoglu, H.; Buehler, M.; Brown, H.B., Jr.; Mcmordie, D.; Saranli, U.; Full, R.; Koditschek, D.E. RHex: A biologically inspired hexapod runner. Auton. Robot. 2001, 11, 207–213. [Google Scholar] [CrossRef]
- Westervelt, E.R.; Grizzle, J.W.; Koditschek, D.E. Hybrid zero dynamics of planar biped walkers. IEEE Trans. Autom. Control. 2003, 48, 42–56. [Google Scholar] [CrossRef]
- Poulakakis, I.; Grizzle, J.W. The spring loaded inverted pendulum as the hybrid zero dynamics of an asymmetric hopper. IEEE Trans. Autom. Control. 2009, 54, 1779–1793. [Google Scholar] [CrossRef]
- Sreenath, K.; Park, H.; Poulakakis, I.; Grizzle, J.W. A compliant hybrid zero dynamics controller for stable, efficient and fast bipedal walking on MABEL. Int. J. Robot. Res. 2011, 30, 1170–1193. [Google Scholar] [CrossRef]
- De, A.; Koditschek, D.E. Vertical hopper compositions for preflexive and feedback-stabilized quadrupedal bounding, pacing, pronking, and trotting. Int. J. Robot. Res. 2018, 37, 743–778. [Google Scholar] [CrossRef]
- De, A. Modular Hopping and Running via Parallel Composition. Ph.D. Thesis, The University of Pennsylvania, Philadelphia, PA, USA, 2017. [Google Scholar]
- De, A.; Burden, S.A.; Koditschek, D.E. A hybrid dynamical extension of averaging and its application to the analysis of legged gait stability. Int. J. Robot. Res. 2018, 37, 266–286. [Google Scholar] [CrossRef]
- Sontag, E.D. Further Facts about Input to State Stabilization. IEEE Trans. Autom. Control. 1990, 35, 473–476. [Google Scholar] [CrossRef]
- Vidyasagar, M. Decomposition Techniques for Large-Scale Systems with Nonadditive Interactions: Stability and Stabilizability. IEEE Trans. Autom. Control. 1980, 25, 773–779. [Google Scholar] [CrossRef]
- Laila, D.S.; Nešić, D. Changing supply rates for input-output to state stable discrete-time nonlinear systems with applications. Automatica 2003, 39, 821–835. [Google Scholar] [CrossRef]
- Boaventura, T.; Medrano-Cerda, G.A.; Semini, C.; Buchli, J.; Caldwell, D.G. Stability and performance of the compliance controller of the quadruped robot HyQ. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1458–1464. [Google Scholar]
- Jones, C.K. Geometric singular perturbation theory. In Dynamical Systems; Lecture Notes in Mathematics; Springer: Montecatini Terme, Italy, 1995; Volume 1609, pp. 44–118. [Google Scholar]
- Eldering, J.; Kvalheim, M.; Revzen, S. Global linearization and fiber bundle structure of invariant manifolds. Nonlinearity 2018, 31, 4202–4245. [Google Scholar] [CrossRef]
- Schmitt, J. A simple stabilizing control for sagittal plane locomotion. J. Comput. Nonlinear Dyn. 2006, 1, 348–357. [Google Scholar] [CrossRef]
- Seyfarth, A.; Geyer, H.; Herr, H. Swing-leg retraction: A simple control model for stable running. J. Exp. Biol. 2003, 206, 2547–2555. [Google Scholar] [CrossRef] [PubMed]
- Hobbelen, D.G.E.; Wisse, M. Swing-leg retraction for limit cycle walkers improves disturbance rejection. IEEE Trans. Robot. 2008, 24, 377–389. [Google Scholar] [CrossRef]
- Karssen, J.G.D.; Haberland, M.; Wisse, M.; Kim, S. The optimal swing-leg retraction rate for running. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4000–4006. [Google Scholar]
- Seyfarth, A.; Geyer, H.; Günther, M.; Blickhan, R. A movement criterion for running. J. Biomech. 2002, 35, 649–655. [Google Scholar] [CrossRef] [PubMed]
- Ghigliazza, R.M.; Altendorfer, R.; Holmes, P.; Koditschek, D. A simply stabilized running model. SIAM Rev. 2005, 47, 519–549. [Google Scholar] [CrossRef]
- Carver, S.G.; Cowan, N.J.; Guckenheimer, J.M. Lateral stability of the spring-mass hopper suggests a two-step control strategy for running. Chaos 2009, 19. [Google Scholar] [CrossRef]
- Wu, A.; Geyer, H. The 3-D spring-mass model reveals a time-based deadbeat control for highly robust running and steering in uncertain environments. IEEE Trans. Robot. 2013, 29, 1114–1124. [Google Scholar] [CrossRef]
- Council, G.; Yang, S.; Revzen, S. Deadbeat control with (almost) no sensing in a hybrid model of legged locomotion. In Proceedings of the International Conference on Advanced Mechatronic Systems, ICAMechS, Kumamoto, Japan, 10–12 August 2014; pp. 475–480. [Google Scholar]
- Blum, Y.; Lipfert, S.W.; Rummel, J.; Seyfarth, A. Swing leg control in human running. Bioinspir. Biomimetics 2010, 5, 026006. [Google Scholar] [CrossRef]
- Daley, M.A.; Biewener, A.A. Running over rough terrain reveals limb control for intrinsic stability. Proc. Natl. Acad. Sci. USA 2006, 103, 15681–15686. [Google Scholar] [CrossRef]
- Daley, M.A.; Usherwood, J.R.; Felix, G.; Biewener, A.A. Running over rough terrain: Guinea fowl maintain dynamic stability despite a large unexpected change in substrate height. J. Exp. Biol. 2006, 209, 171–187. [Google Scholar] [CrossRef]
- Birn-Jeffery, A.V.; Daley, M.A. Birds achieve high robustness in uneven terrain through active control of landing conditions. J. Exp. Biol. 2012, 215, 2117–2127. [Google Scholar] [CrossRef]
- Martin, W.C.; Wu, A.; Geyer, H. Experimental evaluation of deadbeat running on the ATRIAS biped. IEEE Robot. Autom. Lett. 2017, 2, 1085–1092. [Google Scholar] [CrossRef]
- Yim, J.K.; Fearing, R.S. Precision Jumping Limits from Flight-phase Control in Salto-1P. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 2229–2236. [Google Scholar]
- Yim, J.K.; Singh, B.R.P.; Wang, E.K.; Featherstone, R.; Fearing, R.S. Precision Robotic Leaping and Landing Using Stance-Phase Balance. IEEE Robot. Autom. Lett. 2020, 5, 3422–3429. [Google Scholar] [CrossRef]
- Grimmer, S.; Ernst, M.; Günther, M.; Blickhan, R. Running on uneven ground: Leg adjustment to vertical steps and self-stability. J. Exp. Biol. 2008, 211, 2989–3000. [Google Scholar] [CrossRef]
- Müller, R.; Blickhan, R. Running on uneven ground: Leg adjustments to altered ground level. Hum. Mov. Sci. 2010, 29, 578–589. [Google Scholar] [CrossRef]
- Poulakakis, I.; Smith, J.A.; Buehler, M. Modeling and Experiments of Untethered Quadrupedal Running with a Bounding Gait: The Scout II Robot. Int. J. Robot. Res. 2005, 24, 239–256. [Google Scholar] [CrossRef]
- Johnson, A.M.; Burden, S.A.; Koditschek, D.E. A hybrid systems model for simple manipulation and self-manipulation systems. Int. J. Robot. Res. 2016, 35, 1289–1327. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer Science & Business Media: New York, NY, USA, 2013; Volume 60. [Google Scholar]
- Duperret, J.; Koditschek, D.E. Extended Version of Stability of a Groucho-Style Bounding Run in the Sagittal Plane; Technical Report; University of Pennsylvania: Philadelphia, PA, USA, 2023. [Google Scholar]
- Farley, C.T.; Glasheen, J.; McMahon, T.A. Running springs: Speed and animal size. J. Exp. Biol. 1993, 185, 71–86. [Google Scholar] [CrossRef]
- Koechling, J.; Raibert, M. How fast can a legged robot run. In Proceedings of the American Society of Mechanical Engineers, Dynamic Systems and Control Division (Publication) DSC, Chicago, IL, USA, 27 November–2 December 1988; Volume 11, pp. 241–249. [Google Scholar]
- Duperret, J.M.; Koditschek, D.E. Empirical validation of a spined sagittal-plane quadrupedal model. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1058–1064. [Google Scholar]
- Seok, S.; Wang, A.; Chuah, M.Y.; Hyun, D.J.; Lee, J.; Otten, D.M.; Lang, J.H.; Kim, S. Design principles for energy-efficient legged locomotion and implementation on the MIT Cheetah robot. IEEE/ASME Trans. Mechatron. 2014, 20, 1117–1129. [Google Scholar] [CrossRef]
- Kenneally, G.; De, A.; Koditschek, D.E. Design Principles for a Family of Direct-Drive Legged Robots. IEEE Robot. Autom. Lett. 2016, 1, 900–907. [Google Scholar] [CrossRef]
- Conley, C. The gradient structure of a flow: I. Ergod. Theory Dyn. Syst. 1988, 8, 11–26. [Google Scholar]
- Full, R.J.; Koditschek, D.E. Templates and anchors: Neuromechanical hypotheses of legged locomotion on land. J. Exp. Biol. 1999, 202, 3325–3332. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).