Viewpoint Generation Using Feature-Based Constrained Spaces for Robot Vision Systems
Abstract
1. Introduction
1.1. Viewpoint Generation Problem Solved Using -Spaces
1.2. Related Work
1.2.1. Model-Based
1.2.2. Non-Model Based
1.2.3. Comparison and Need for Action
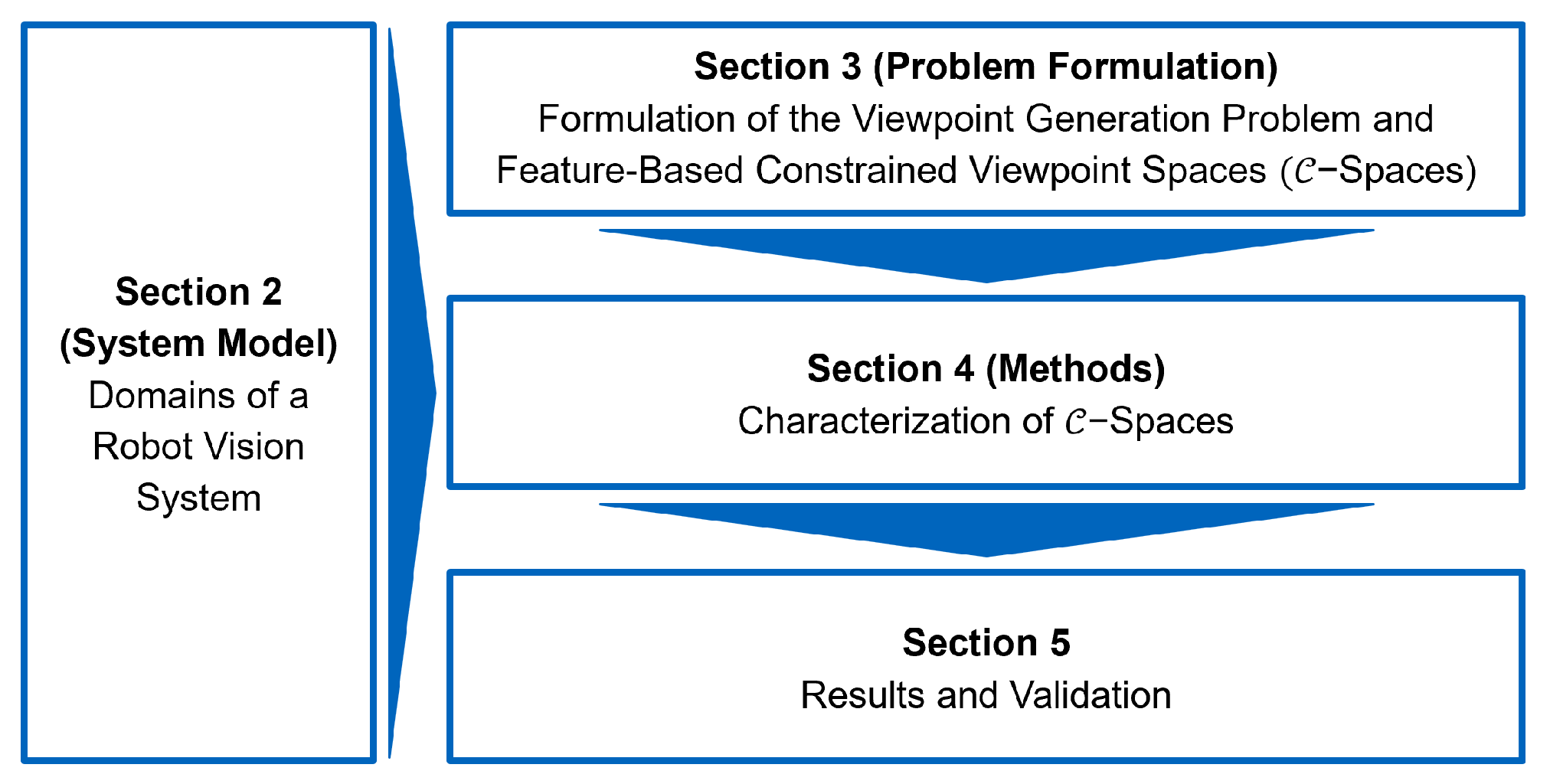
1.3. Outline
1.4. Contributions
- Mathematical, model-based, and modular framework to formulate the VGP based on s and generic domain models.
- Formulation of nine viewpoint constraints using linear algebra, trigonometry, geometric analysis, and Constructive Solid Geometry (CSG) Boolean operations, in particular:
- -
- Efficient and simple characterization of based on sensor frustum, feature position, and feature geometry.
- -
- Generic characterization of s to consider bi-static nature of range sensors extendable to multisensor systems.
- Exhaustive supporting material (surface models, manifolds of computed s, rendering results) to encourage benchmark and further development (see Supplementary Materials).
- Determinism, efficiency, and simplicity: s can be efficiently characterized using geometrical analysis, linear algebra, and CSG Boolean techniques.
- Generalization, transferability, and modularity: s can be seamlessly used and adapted for different vision tasks and RVSs, including different sensor imaging sensors (e.g., stereo, active light sensors) or even multiple range sensor systems.
- Robustness against model uncertainties: Known model uncertainties (e.g., kinematic model, sensor, or robot inaccuracies) can be explicitly modeled and integrated while characterizing s. If unknown model uncertainties affect a chosen viewpoint, alternative solutions guaranteeing constraint satisfiability can be found seamlessly within s.
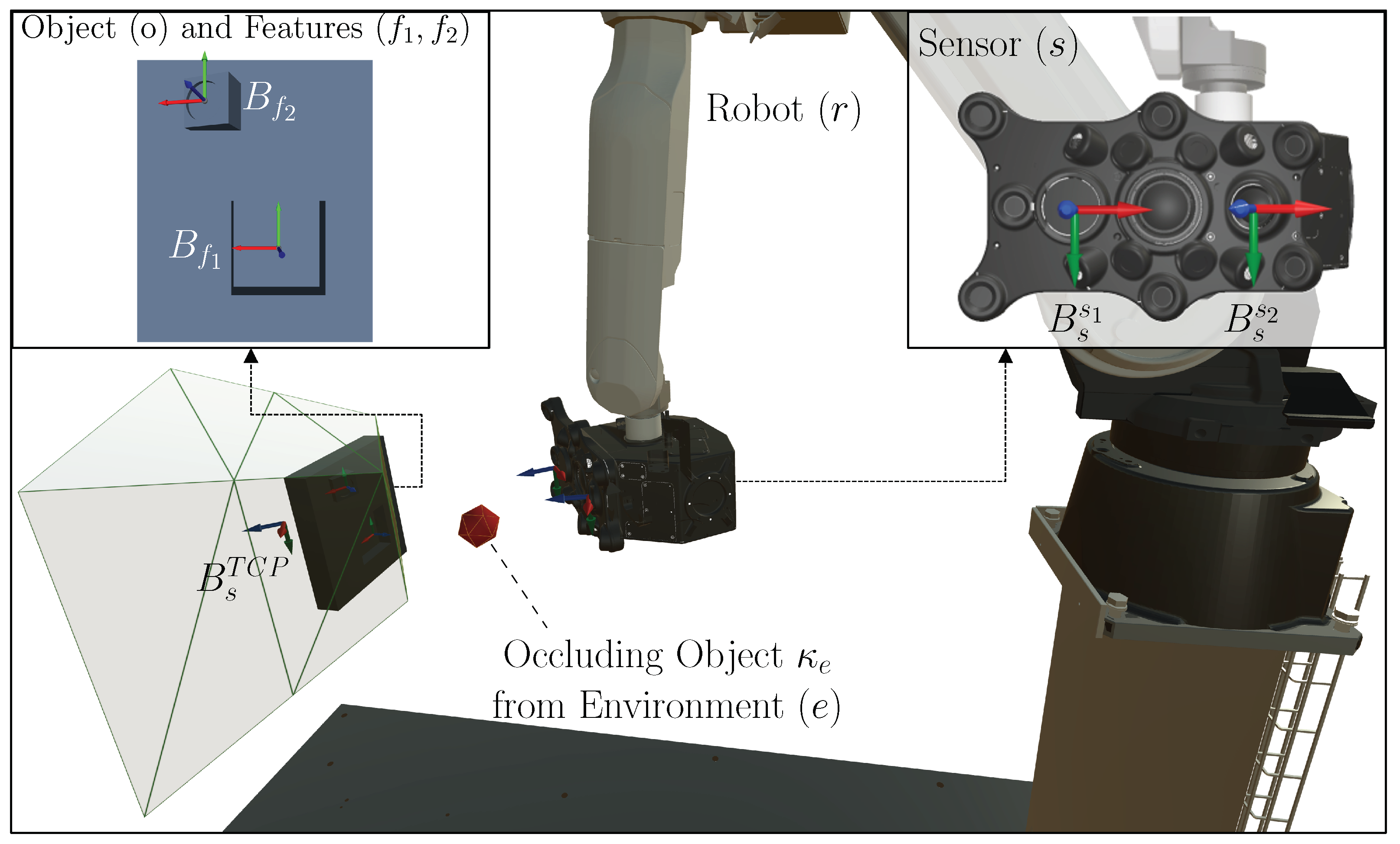
2. Domain Models of a Robot Vision System
2.1. General Notes
- General Requirements This paper follows a systematic and exhaustive formulation of the VGP, the domains of an RVS, and the viewpoint constraints to characterize s in a generic, simple, and scalable way. To achieve this, and similar to previous studies [11,33,36], throughout our framework the following general requirements (GR) are considered: generalization, computational efficiency, determinism, modularity and scalability, and limited a priori knowledge. The given order does not consider any prioritization of the requirements. A more detailed description of the requirements can be found in Table A1.
- Terminology Based on our literature research, we have found that a common terminology has not been established yet. The employed terms and concepts depend on the related applications and hardware. To better understand the relation of our terminology to the related work and in an attempt towards standardization, whenever possible, synonyms or related concepts are provided. Please note that in some cases, the generality of some terms is prioritized over their precision. This may lead to some terms not corresponding entirely to our definition; therefore, we urge the reader to study these differences before treating them as exact synonyms.
- Notation Our publication considers many variables to describe the RVS domains comprehensively. To ease the identification and readability of variables, parameters, vectors, frames, and transformations, we use the index notation given in Table A2. Moreover, all topological spaces are given in calligraphic fonts, e.g., , while vectors, matrices, and rigid transformations are bold. Table A3 provides an overview of the most frequently used symbols.
2.2. General Models
- Kinematic model Each domain comprises a Kinematics subsection to describe its kinematic relationships. In particular, all necessary rigid transformations (given in the right-handed system) are introduced to calculate the sensor pose. The pose of any element is given by its translation and a rotation component that can be given as a rotation matrix , Z-Y-X Euler angles or a quaternion . For readability and simplicity purposes, we use mostly the Euler angle representation throughout this paper. Considering the special orthogonal , the pose is given in the special Euclidean group [44]). in the feature’s coordinate system :
- Surface model A set of 3D surface models characterizes the volumetric occupancy of all rigid bodies in the environment. The surface models are not always explicitly mentioned within the domains. Nevertheless, we assume that the surface model of any rigid body is required if this collides with the robot or sensor or impedes the sensor’s sight to a feature.
2.3. Object
- Kinematics The origin coordinate system of o is located at frame . The transformation to the reference coordinate system is given in the world coordinate system by .
- Surface Model Since our approach does not focus on the object but rather on its features, the object may have an arbitrary topology.
2.4. Feature
- Kinematics We assume that the translation and orientation of the feature’s origin is given in the object’s coordinate system . In the case that the feature’s orientation is given by its minimal expression, i.e., just the feature’s surface normal vector . The full orientation is calculated by letting the feature’s normal to be the basis z-vector and considering the rest basis vectors and to be mutually orthonormal. The feature’s frame is given as follows:
- Geometry While a feature can be sufficiently described by its position and normal vector, a broader formulation is required within many applications. For example, dimensional metrology tasks deal with a more comprehensive catalog of geometries, e.g., edges, pockets, holes, slots, and spheres.
- Generalization and Simplification Moreover, we consider a discretized geometry model of a feature comprising a finite set of surface points corresponding to a feature with . Since our work primarily focuses on 2D features, it is assumed that all surface points lie on the same plane, which is orthogonal to the feature’s normal vector and co-linear to the z-axis of the feature’s frame .Towards providing a more generic feature model, the topology of all features is approximated using a square feature with a unique side length of and five surface points at the center and at the four corners of the square. Figure 4 visualizes this simplification to generalize diverse feature geometries.
2.5. Sensor
- Kinematics The sensor’s kinematic model considers the following relevant frames: , , and . Taking into account the established notation for end effectors within the robotics field, we consider that the frame lies at the sensor’s tool center point (TCP). We assume that the frame of the TCP is located at the geometric center of the frustum space and that the rigid transformation to a reference frame such as the sensor’s mounting point is known.Additionally, we consider that frame lies at the reference frame of the first imaging device that corresponds to the imaging parameters . We assume that the rigid transformation between the sensor lens and a known reference frame is also known. provides the transformation of the second imaging device at the frame . The second imaging device might be a second camera considering a stereo sensor or the light source origin in an active sensor system.
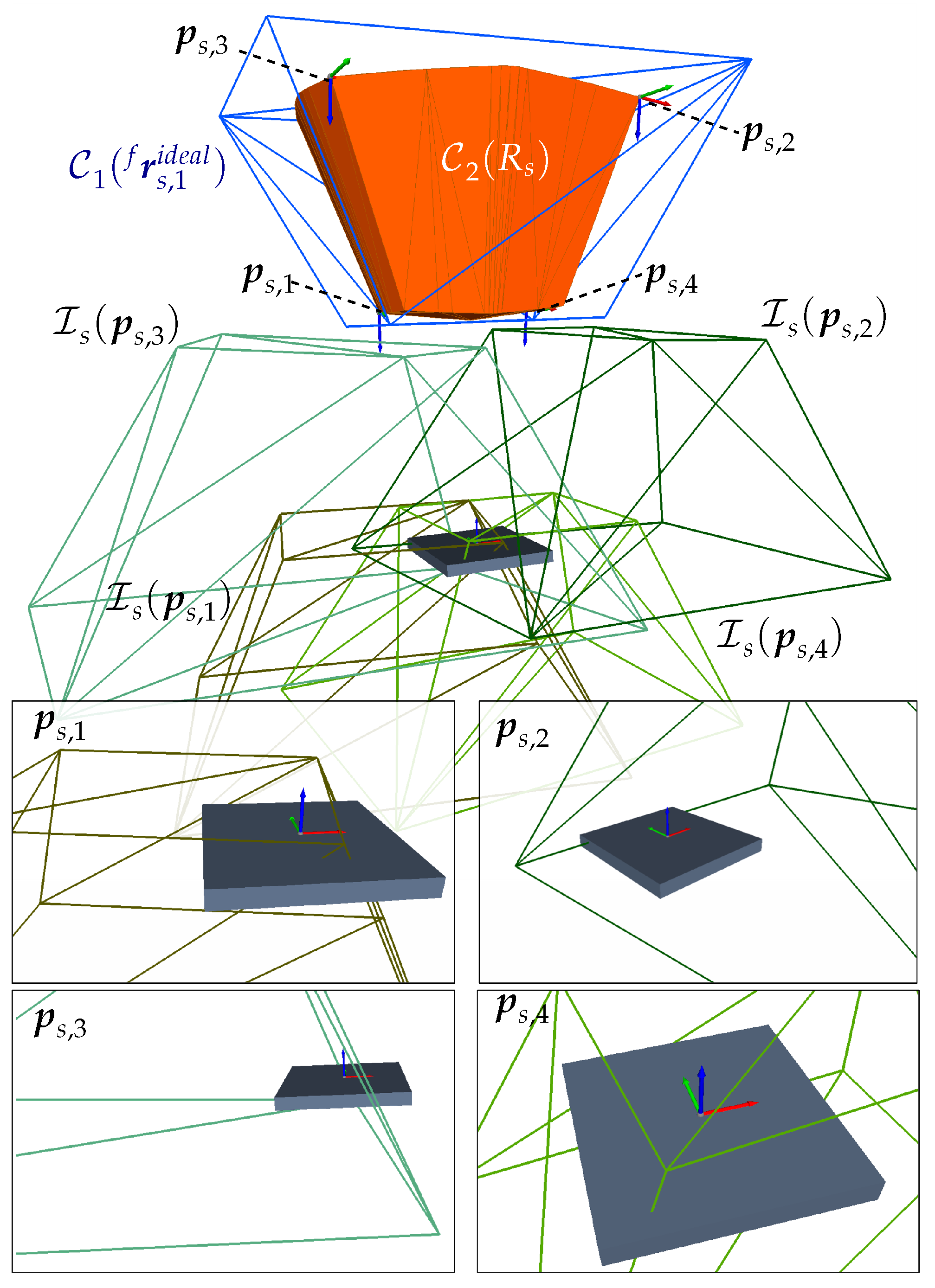
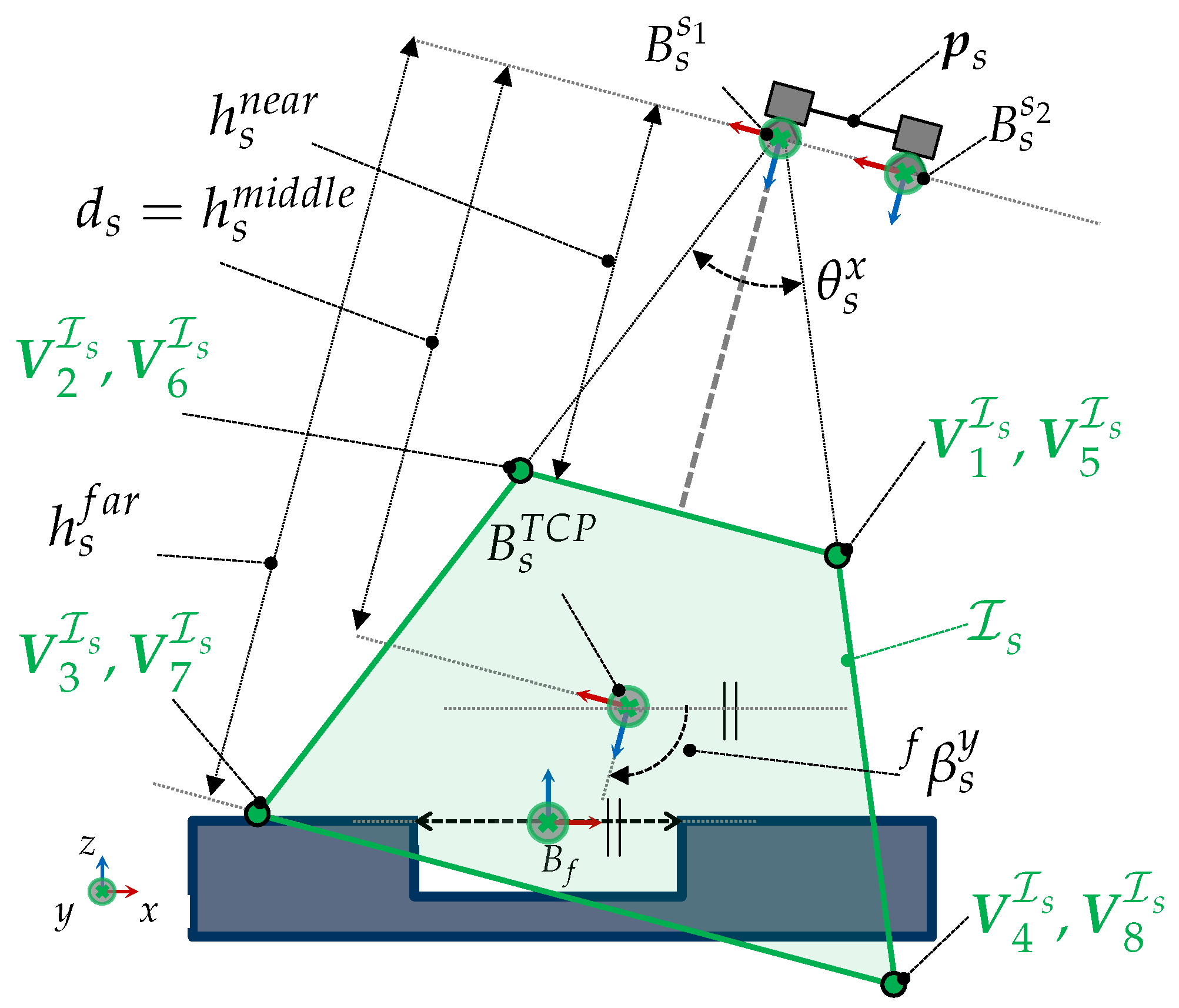
- Frustum space The frustum space (related terms: visibility frustum, measurement volume, field-of-view space, sensor workspace) is described by a set of different sensor imaging parameters , such as the depth of field and the horizontal and vertical field of view (FOV) angles and . Alternatively, some sensor manufacturers may also provide the dimensions and locations of the near , middle , and far viewing planes of the sensor. The sensor parameters allow only the topology of the to be described. To fully characterize the topological space in the special Euclidean, the sensor pose must be considered:The can be straightforwardly calculated based on the kinematic relationships of the sensor and the imaging parameters. The resulting 3D manifold is described by its vertices with and corresponding edges and faces. We assume that the origin of the frustum space is located at the TCP frame, i.e., . The resulting shape of the usually has the form of a square frustum. Figure 5 visualizes the frustum shape and the geometrical relationships of the .
- Range Image A range image (related terms: 3D measurement, 3D image, depth image, depth maps, point cloud) refers to the generated output of the sensor after triggering a measurement action. A range image is described as a collection of 3D points denoted by , where each point corresponds to a surface point of the measured object.
- Measurement accuracy The measurement accuracy depends on various sensor parameters and external factors and may vary within the frustum space [21]. If these influences are quantifiable an accuracy model can be considered within the computation of the . For example, ref. [34] proposed a method based on a Look-Up Table to specify quality disparities within a frustum.
- Sensor Orientation When choosing the sensor pose for measuring an object’s surface point or a feature, additional constraints must be fulfilled regarding its orientation. One fundamental requirement that must be satisfied to guarantee the acquisition of a surface point is the consideration of the incidence angle (related terms: inclination, acceptance, view, or tilt angle). This angle is expressed as the angle between the feature’s normal and the sensor’s optical axis (z-axis) and can be calculated as follows:The maximal incidence angle is normally provided by the sensor’s manufacturer. If the maximal angle is not given in the sensor specifications, some works have suggested empirical values for different systems. For example, ref. [46] propose a maximum angle of [47] suggests , while [48] propose a tilt angle of to . The incidence angle can also be expressed on the basis of the Euler angles (pan, tilt) around the x- and y-axes: .Furthermore, the rotation of the sensor around the optical axis is given by the Euler angle (related terms: swing, twist). Normally, this angle does not directly influence the acquisition quality of the range image and can be chosen arbitrarily. Nevertheless, depending on the lighting conditions or the position of the light source while considering active systems, this angle might be more relevant and influence the acquisition parameters of the sensor, e.g., the exposure time. Additionally, if the shape of the frustum is asymmetrical, the optimization of should be considered.
2.6. Robot
- Kinematics The robot base coordinate frame is placed at . We assume that the rigid transformations between the robot basis and the robot flange, , and between the robot flange and the sensor, , are known. We also assume that the Denavit-Hartenberg (DH) parameters are known and that the rigid transformation can be calculated using an inverse kinematic model. The sensor pose in the robot’s coordinate system is given byThe robot workspace is considered to be a subset in the special Euclidean, thus . This topological space comprises all reachable robot poses to position the sensor .
- Robot Absolute Position Accuracy It is assumed that the robot has a maximal absolute pose accuracy error of in its workspace and that the robot repeatability is much smaller than the absolute accuracy; hence, it is not further considered.
2.7. Environment
2.8. General Assumptions and Limitations
- Sensor compatibility with feature geometry: Our approach assumes that a feature and its entire geometry can be captured with a single range image.
- Range Image Quality: The sensor can acquire a range image of sufficient quality. Effects that may compromise the range image quality and have not been previously regarded are neglected include measurement repeatability, lighting conditions, reflection effects, and random sensor noise.
- Sensor Acquisition Parameters: Our work does not consider the optimization of acquisition sensor parameters such as exposure time, gain, and image resolution, among others.
- Robot Model: Since we assumed that a range image can just be statically acquired, a robot dynamics model is not contemplated. Hence, constraints regarding velocity, acceleration, jerk, or torque limits are not considered within the scope of our work.
3. Problem Formulation
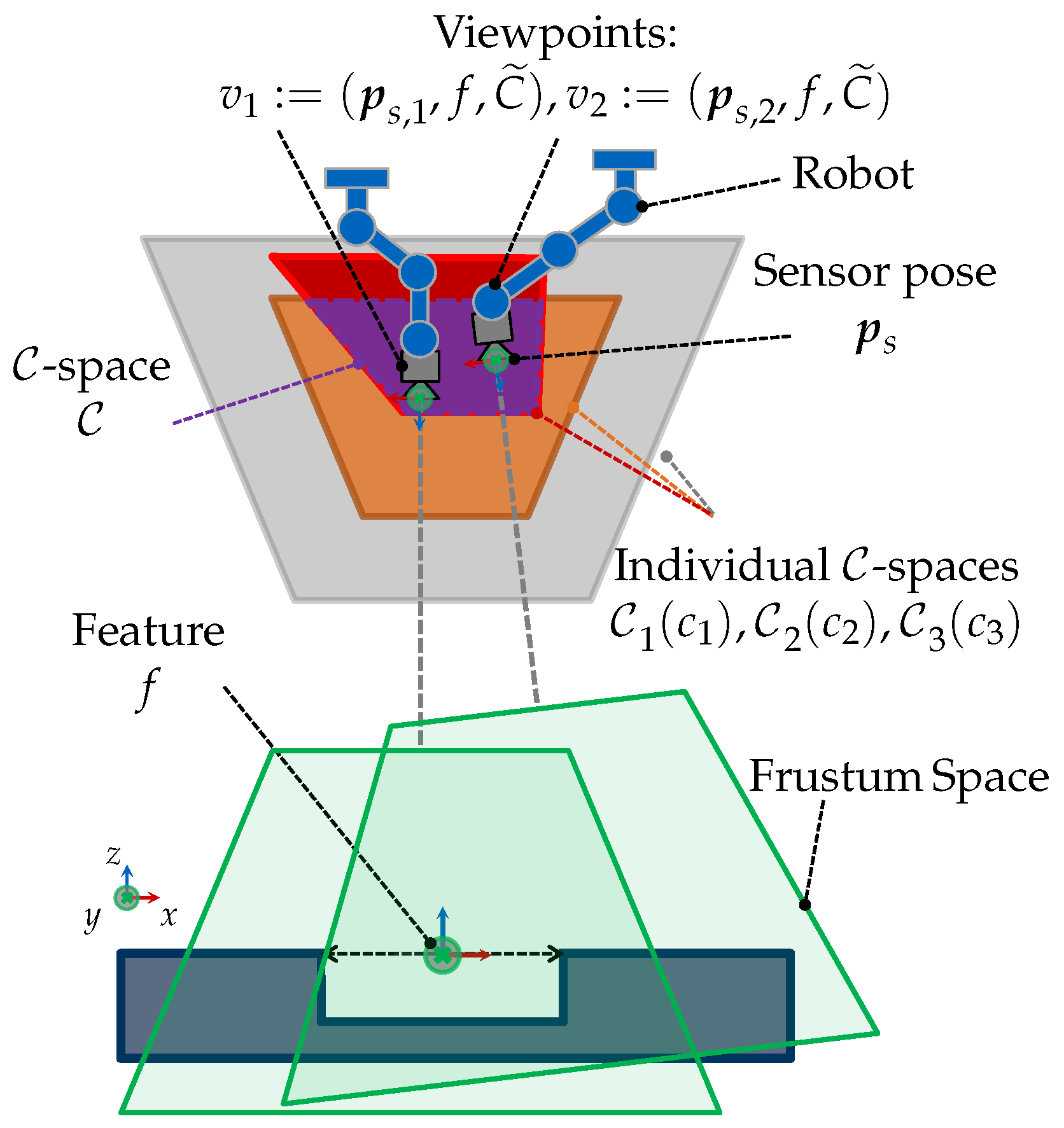
3.1. Viewpoint and -Space
3.2. Viewpoint Constraints
3.3. Modularization of the Viewpoint Planning Problem
3.4. The Viewpoint Generation Problem
3.5. VGP as a Geometrical Problem in the Context of Configuration Spaces
“Once the configuration space is clearly understood, many motion planning problems that appear different in terms of geometry and kinematics can be solved by the same planning algorithms. This level of abstraction is therefore very important.”[54]
3.6. VGP with Ideal -Spaces
3.7. VGP with -Spaces
3.7.1. Motivation
3.7.2. Formulation
- If an i constraint, , can be spatially modeled, there exists a topological space denoted as , which can be ideally formulated as a proper subset of the special Euclidean:In a broader definition, we consider that the topological space for each constraint is spanned by a subset of the Euclidean Space denoted as and a special orthogonal group subset given by . Hence, the topological space of a viewpoint constraint is given as follows:
- If there exists at least one sensor pose in the i , then this sensor pose fulfills the viewpoint constraint to acquire feature f; hence, a valid viewpoint exists .
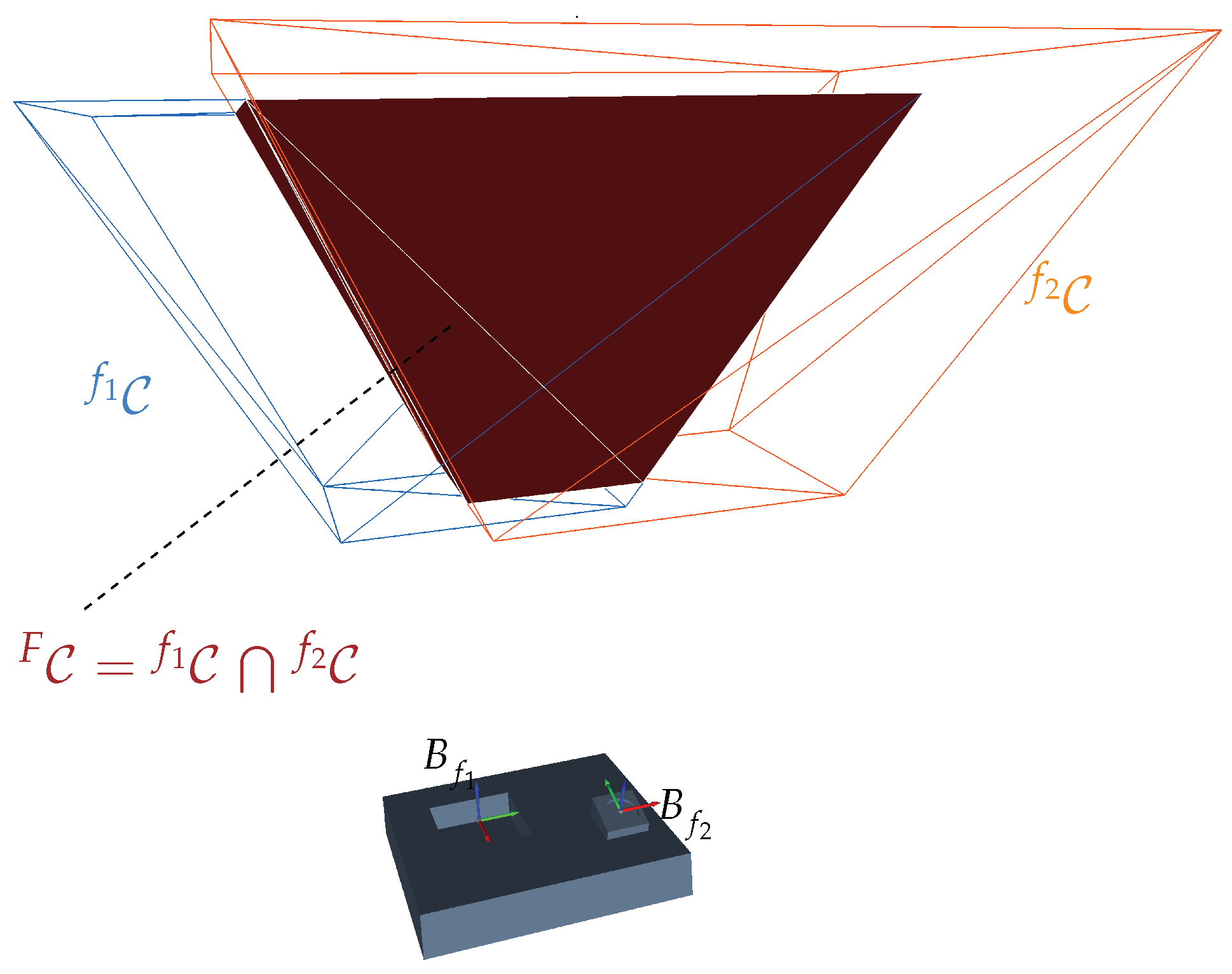
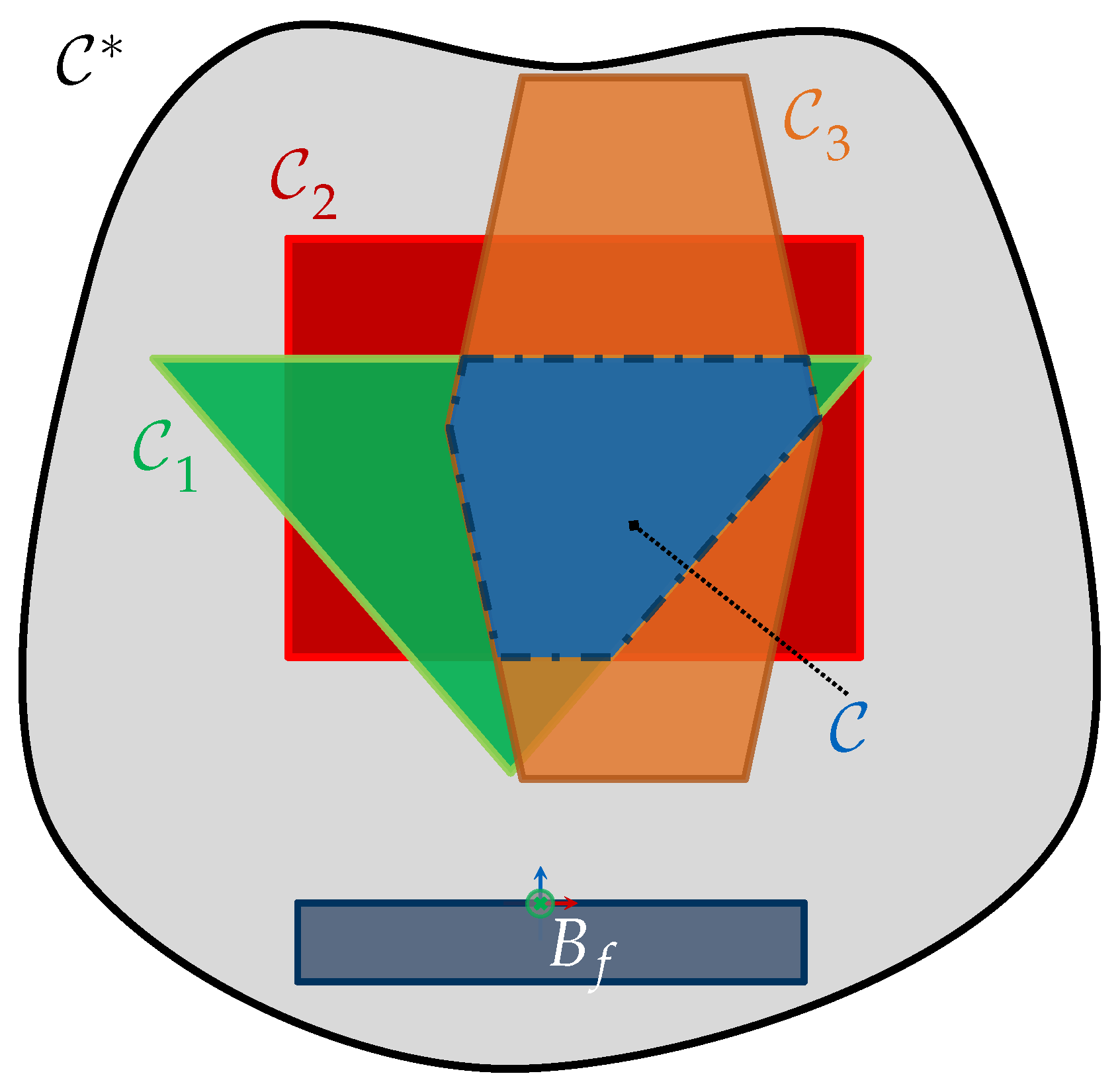
- If there exists a topological space, , for each constraint then the intersection of all individual constrained spaces constitutes the joint :
- If the joint constrained space is a non-empty set, i.e., , then there exists at least one sensor pose , and consequently a viewpoint that fulfills all viewpoint constraints.
4. Methods: Formulation, Characterization, and Verification of -Spaces
4.1. Frustum Space, Feature Position, and Fixed Sensor Orientation
4.1.1. Formulation
4.1.2. Characterization
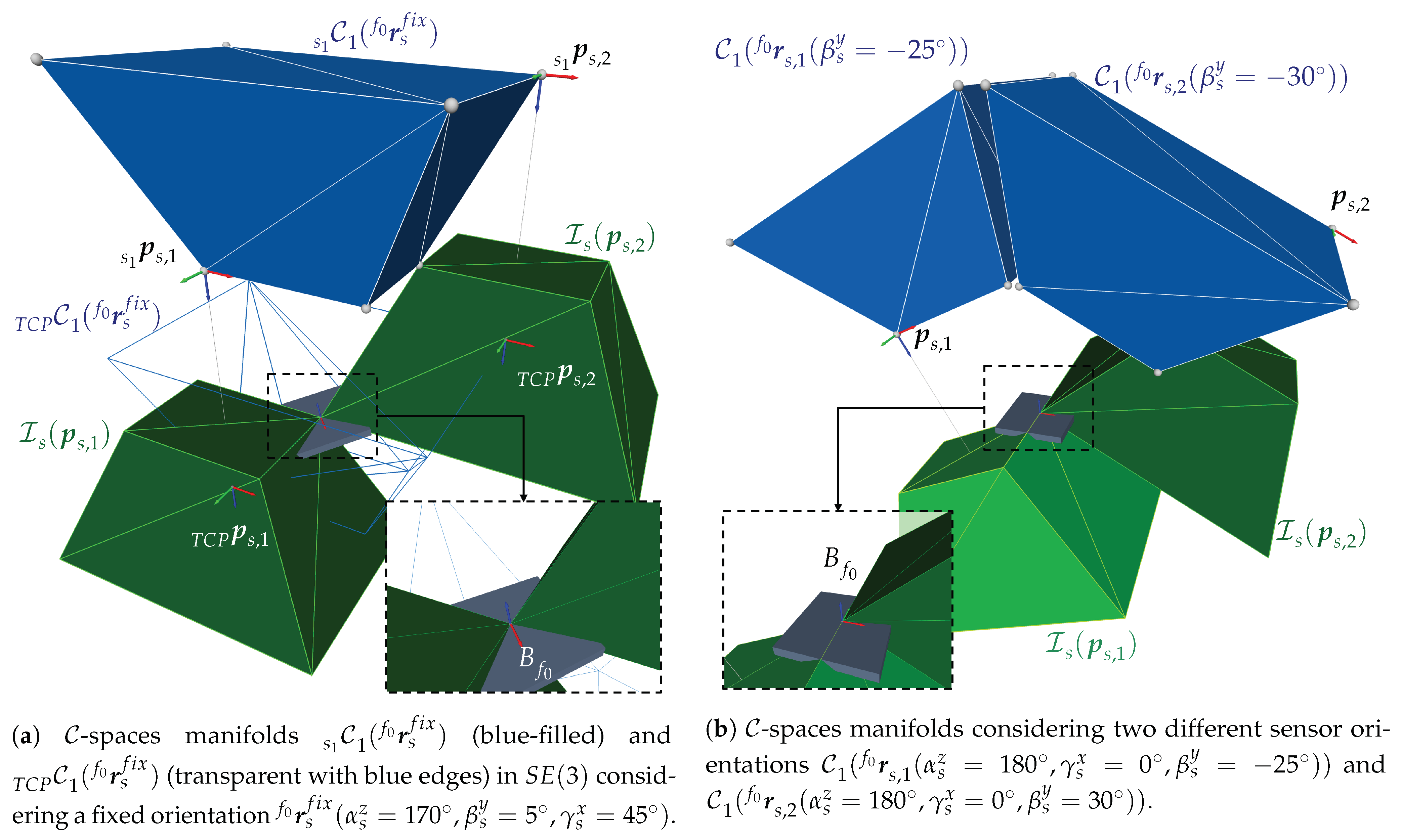
- Extreme Viewpoints Interpretation The simplest way to understand and visualize the topological space is to consider all possible extreme viewpoints to acquire a feature f. These viewpoints can be easily found by positioning the sensor so that each vertex (corner) of the , , lies at the feature’s origin , which corresponds to the position of the surface point . The position of such an extreme viewpoint corresponds to the k vertex of the manifold . Depending on the positioning frame of the sensor or , the space can be computed for the TCP() or the sensor lens (). The vertices can be straightforwardly computed following the steps given in Algorithm A1. The left Figure 7 illustrates the geometric relations for computing and a simplified representation of the resulting manifolds in for the sensor TCP and lens .
- Homeomorphism Formulation Note that the manifold illustrated in Figure 7a has the same topology as the . Thus, it can be assumed there exists a homeomorphism between both spaces such that . Letting the function h correspond to a point reflection over the geometric center of the frustum space, the vertices of the manifold can be straightforwardly estimated following the steps described in the Algorithm 1. The resulting manifold for the TCP frame is shown in Figure 7b.
| Algorithm 1 Homeomorphism Characterization of the Constrained Space |
|
- the frames of all vertices of the frustum space are known,
- the frustum space is a watertight manifold,
- and the space between connected vertices of the frustum space is linear; hence, adjacent vertices are connected only by straight edges.
4.1.3. Verification
4.1.4. Summary
4.2. Range of Orientations
4.2.1. Formulation
4.2.2. Characterization
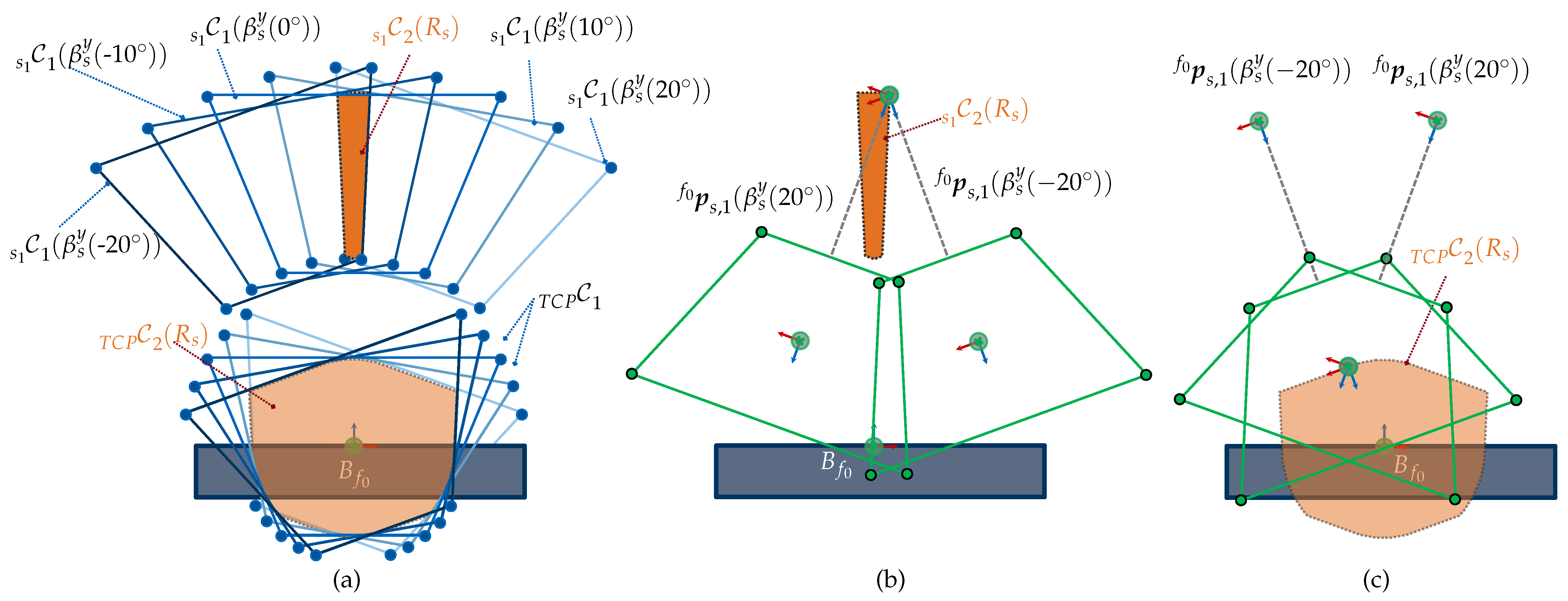
- Discretization without Interpolation Note that spans a topological space that is just valid for the sensor orientations in and that the sensor orientation cannot be arbitrary chosen within the range . This characteristic can be more easily understood by comparing the volume form, , of the s and , which would show that the is less restrictive:This characteristic can particularly be appreciated in the top of the manifold in Figure 9a. Thus, it should be kept in mind that the constrained space does not allow an explicit interpolation within the orientations of .
- Approximation of However, as can be observed from Figure 9, the topological space spanned while considering a step size of , , is almost identical to the space if we would relax the step size to , . Hence, it can be assumed for this case that the s are almost identical and the following condition will hold:
4.2.3. Verification
4.2.4. Summary
4.3. Feature Geometry
4.3.1. Formulation
4.3.2. Generic Characterization
4.3.3. Characterization of the -Space with Null Rotation
4.3.4. Rotation around One Axis
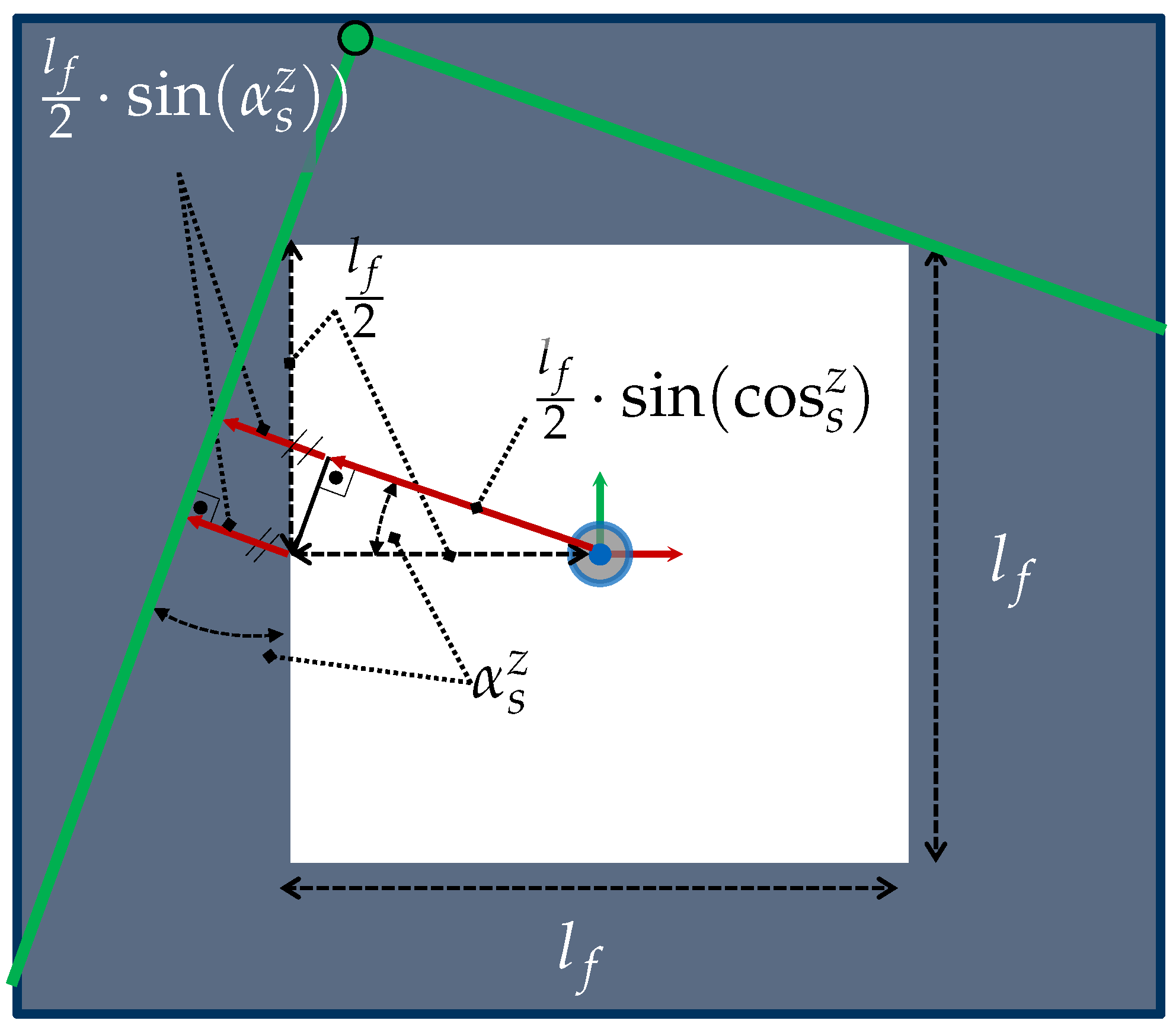
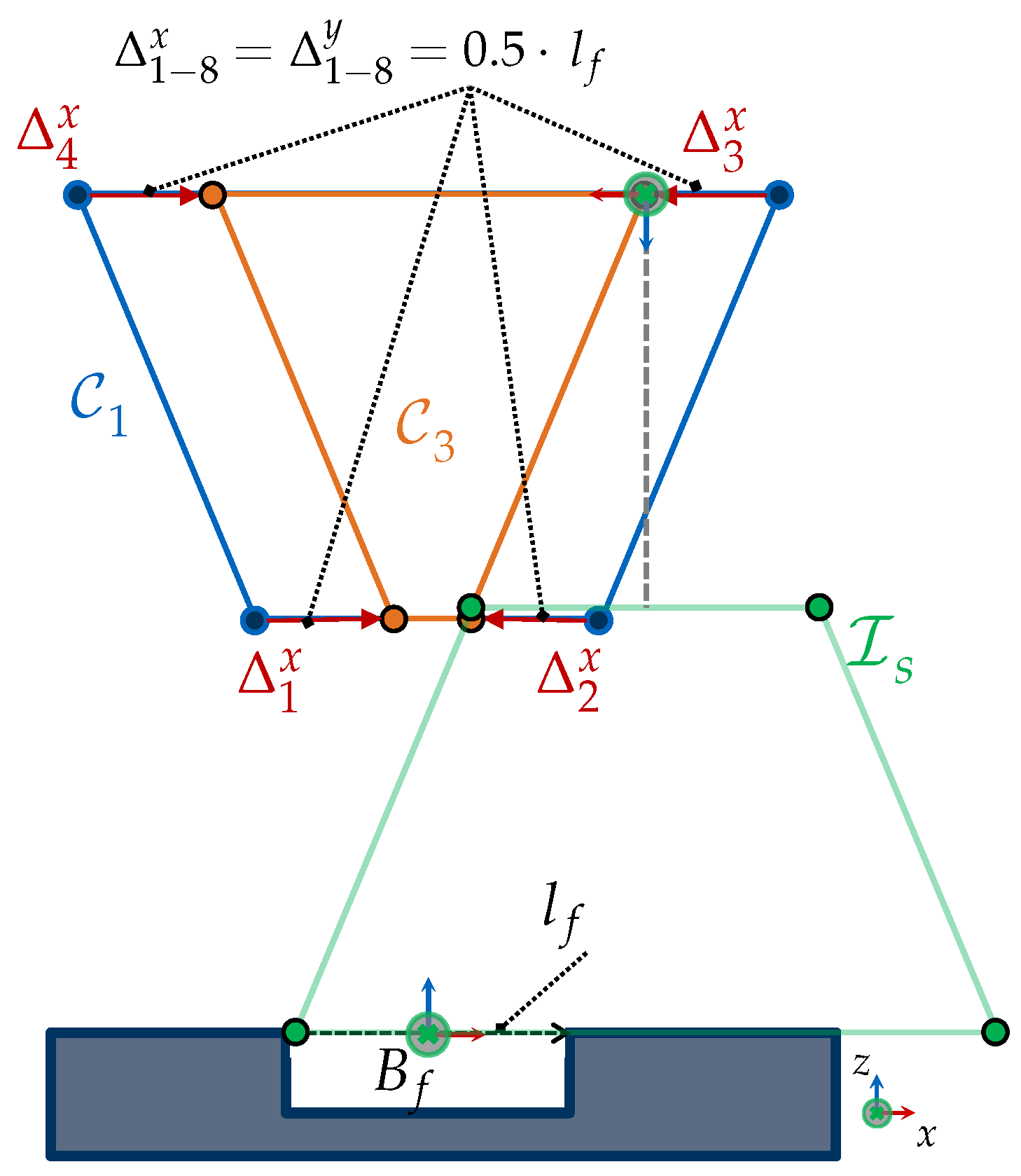
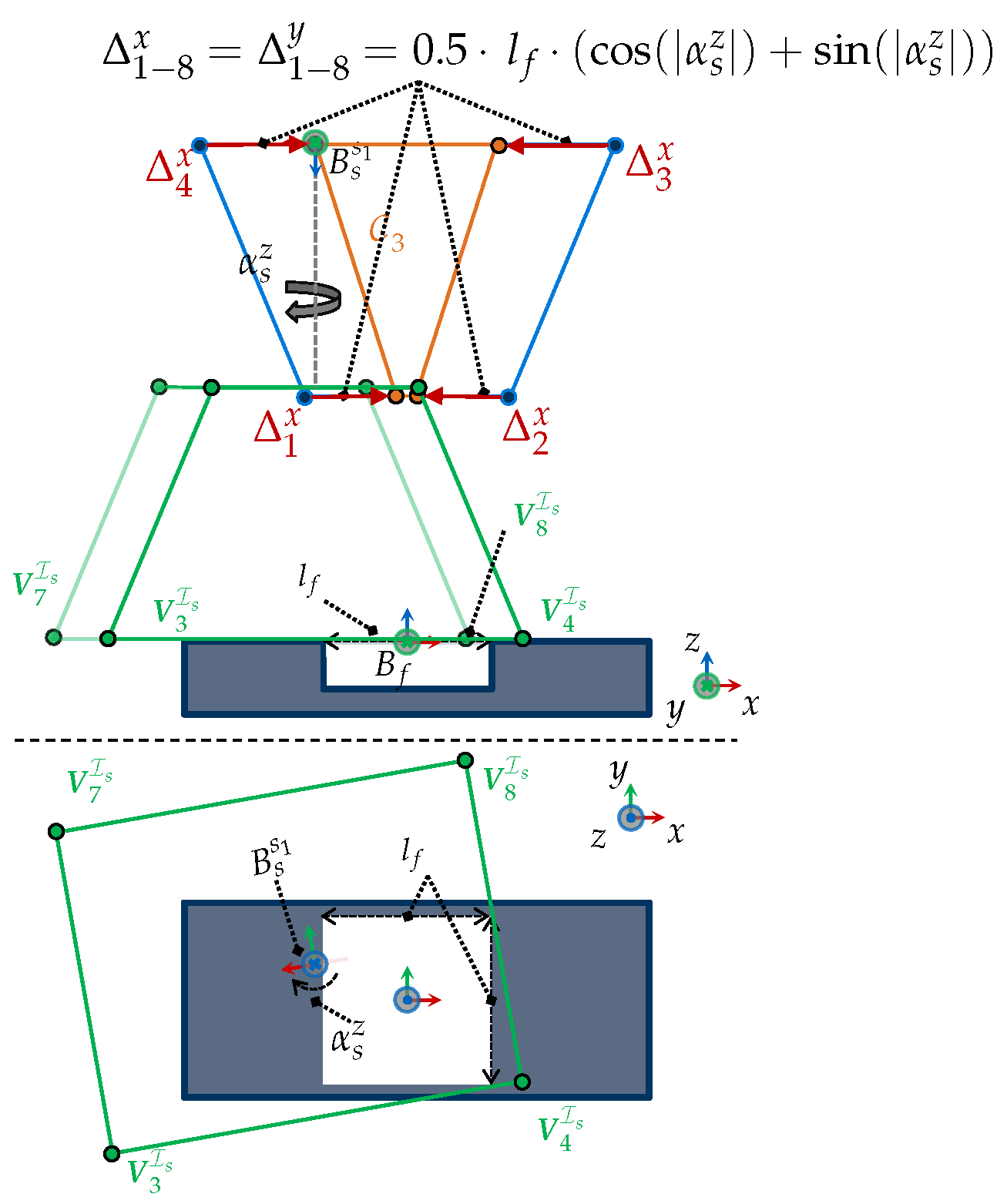
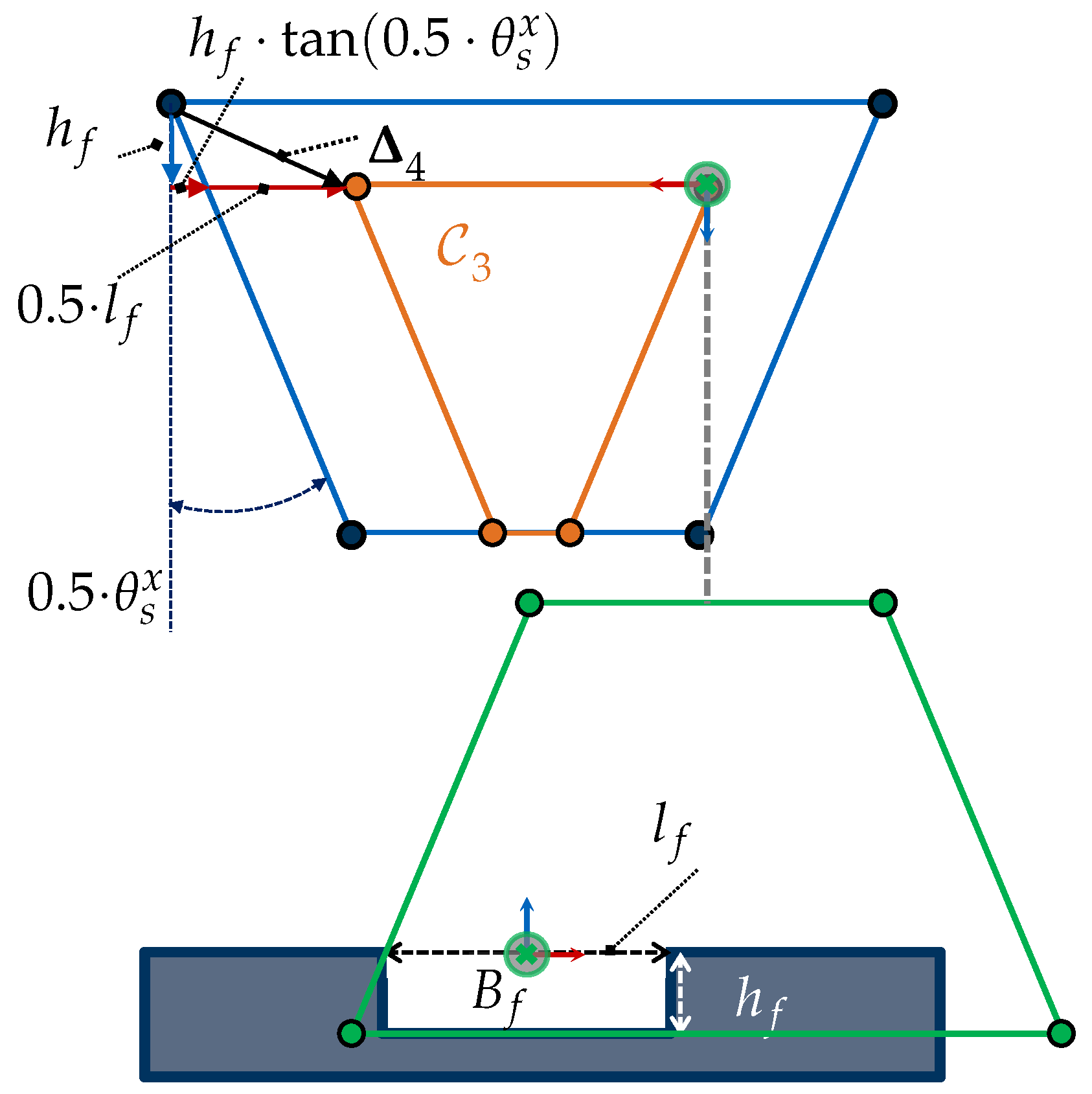
- Rotation around z-axis Assuming a sensor rotation around the optical axis, (see Figure 11), the is scaled just along the vertical and horizontal axes, using the following scaling factors:
- Rotation around x-axis or y-axis (): A rotation of the sensor around the x-axis, , or y-axis, , requires deriving individual trigonometric relationships for each vertex of . Besides the feature length, other parameters such as the FOV angles () and the direction of the rotation must be considered.The scaling factors for the eight vertices of the while considering a rotation around the x-axis or y-axis can be found in Table A5 regarding the following general auxiliary lengths for (left) and for (right):
4.3.5. Generalization to 3D Features
4.3.6. Verification
4.3.7. Summary
4.4. Constrained Spaces Using Scaling Vectors
4.4.1. Formulation
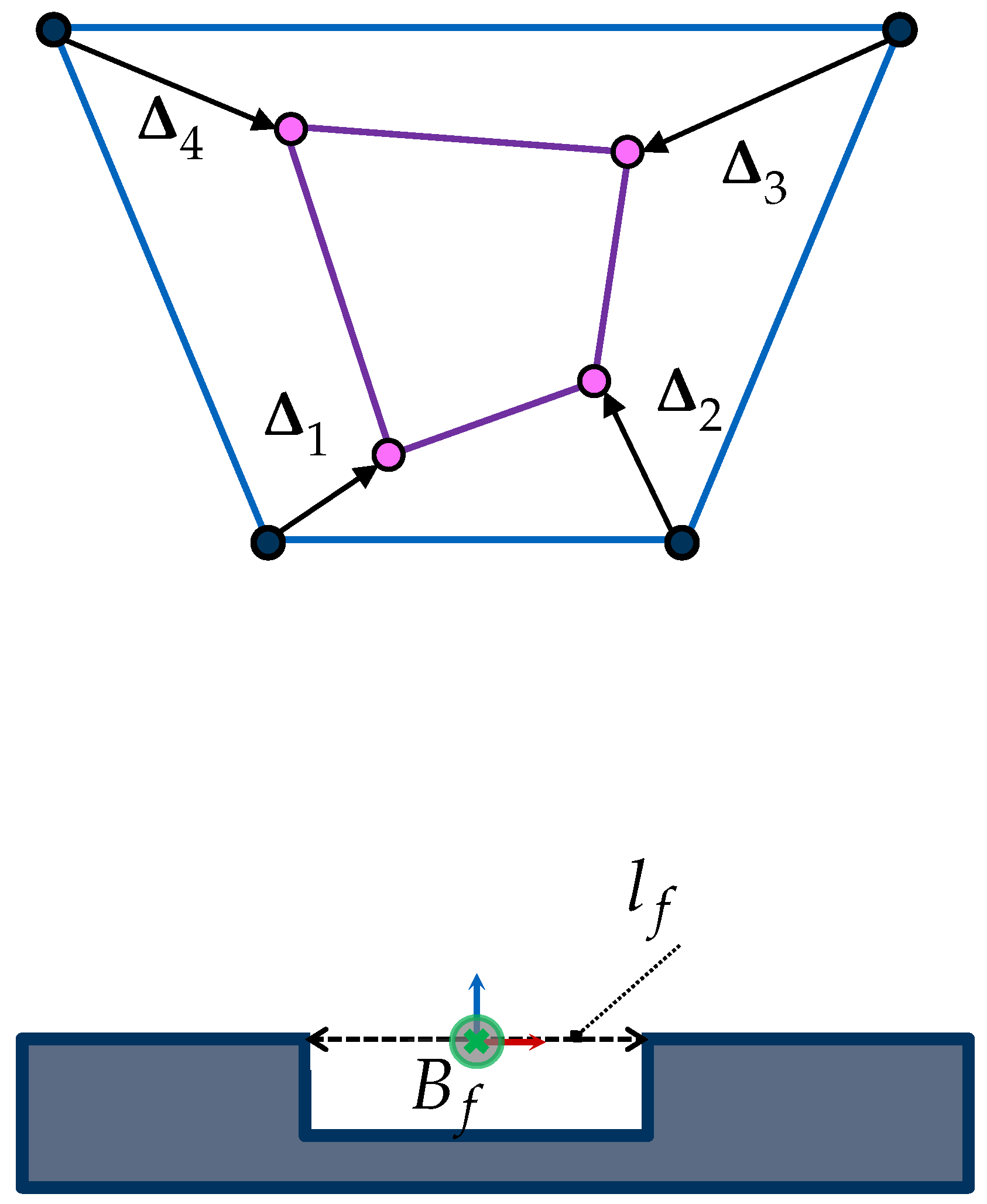
- Integrating Multiple Constraints The characterization of a jointed constrained space, which integrates several viewpoint constraints, can be computed using different approaches. On one hand, the constrained spaces can be first computed and intersected iteratively using CSG operations, as originally proposed in Equation (12). However, if the space spanned by such viewpoint constraints can be formulated according to Equation (27), the characterization of the constrained space can be more efficiently calculated by simply adding all scaling vectors:While the computational cost of CSG operations is at least proportional to the number of vertices between two surface models, note that the complexity of the sum of Equation (28) is just proportional to the number of viewpoint constraints.
- Compatible Constraints Within this subsection, we propose further possible viewpoint constraints that can be characterized according to the scaling formulation introduced by Equation (28).
- Kinematic errors: Considering the fourth viewpoint constraint and the assumptions addressed in Section 2.8, the maximal kinematic error is given by the sum of the alignment error , the modeling error of the sensor imaging parameters , and the absolute position accuracy of the robot :Assuming that the total kinematic error has the same magnitude in all directions, all vertices can be equally scaled. The vertices of the are computed using the scaling vector :
- Sensor Accuracy: If the accuracy of the sensor can be quantified within the sensor frustum, then similarly to the kinematic error, the manifold of the can be characterized using a scaling vector :
4.4.2. Summary
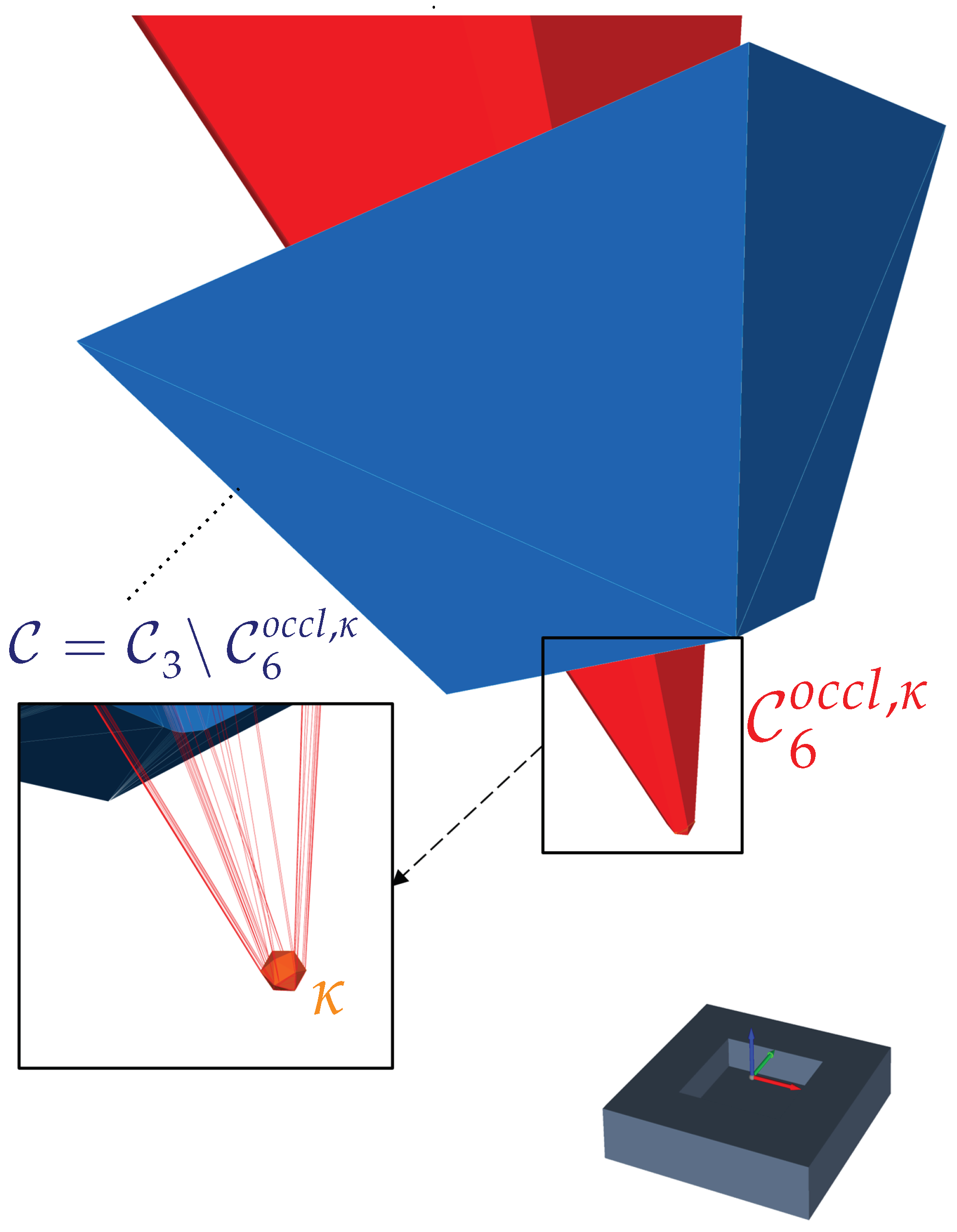
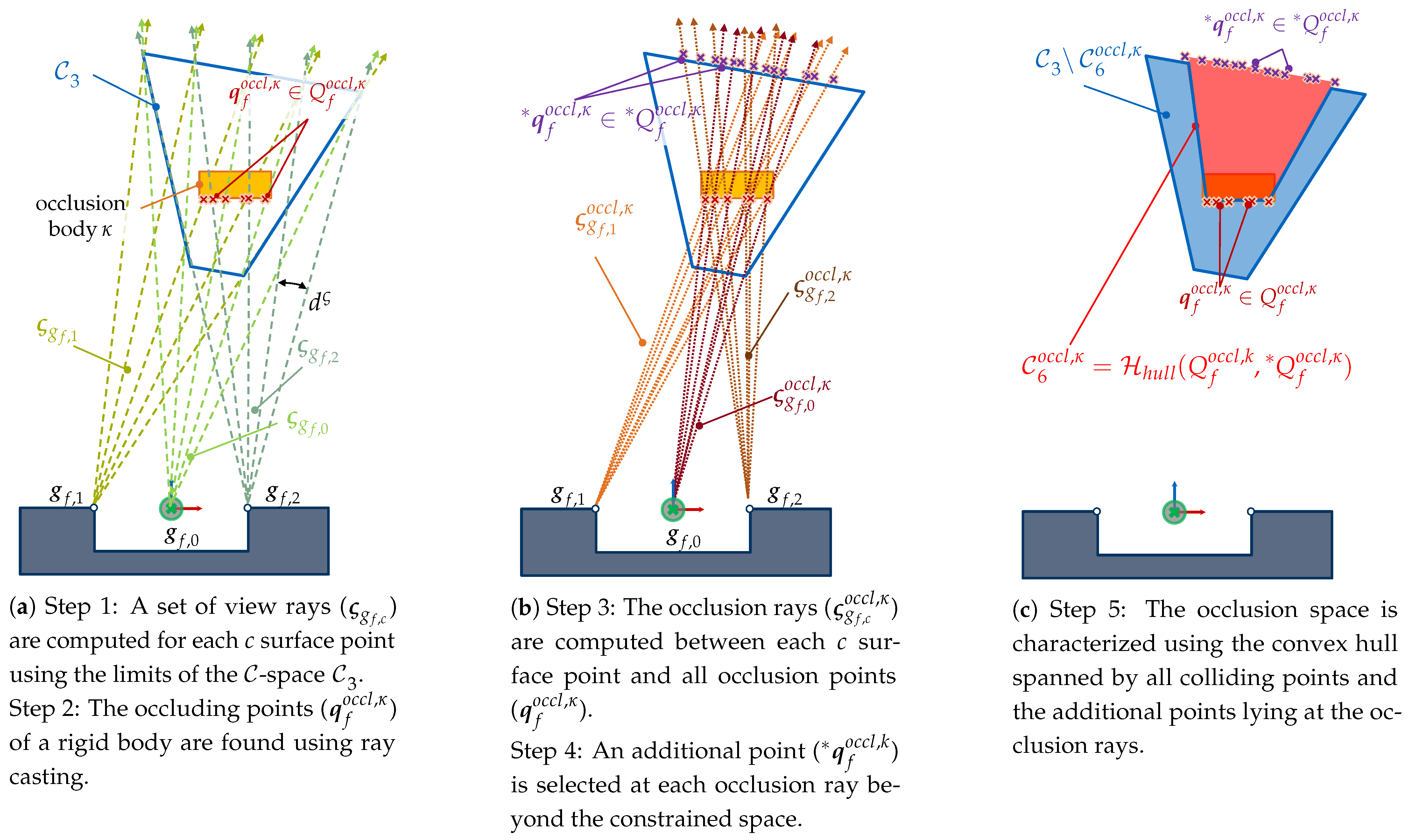
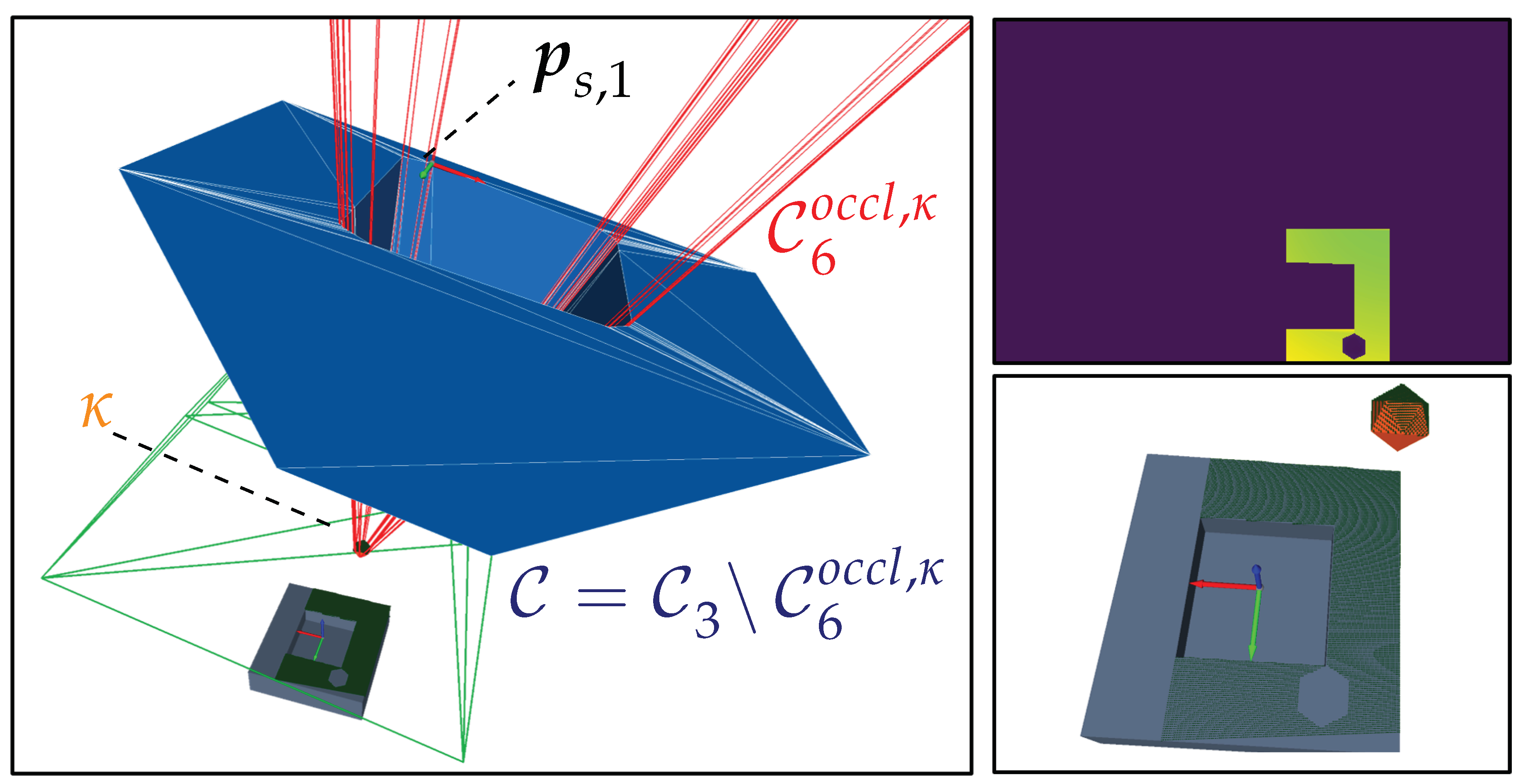
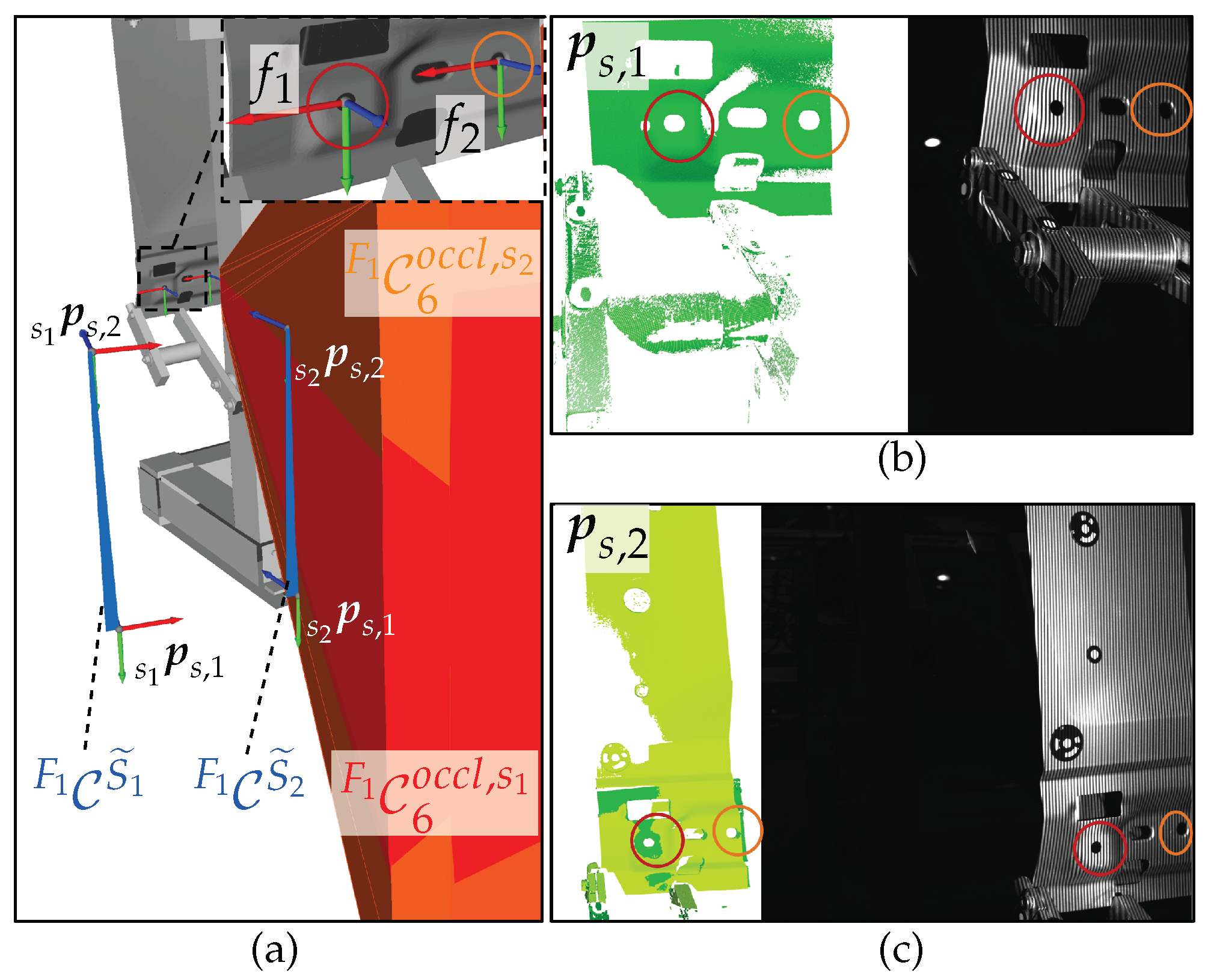
4.5. Occlusion Space
4.5.1. Formulation
4.5.2. Characterization
4.5.3. Verification
4.5.4. Summary
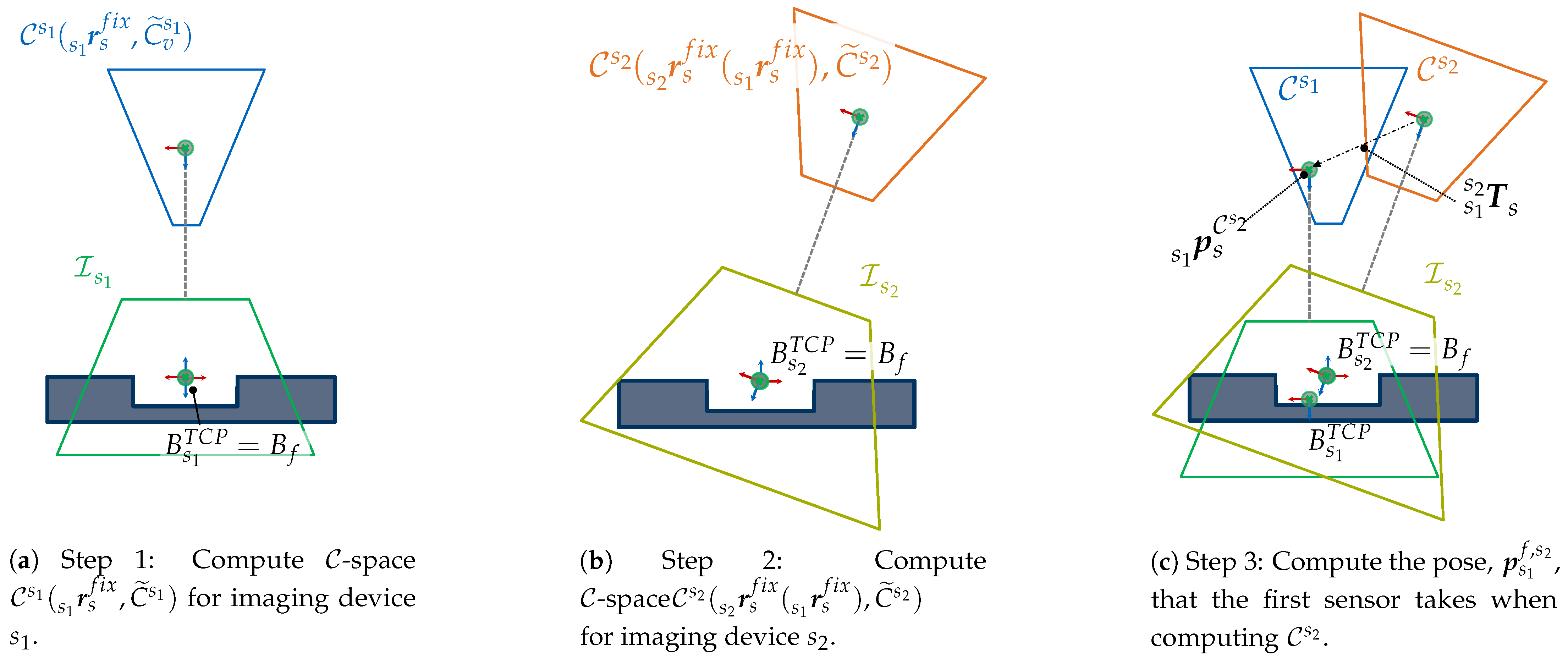
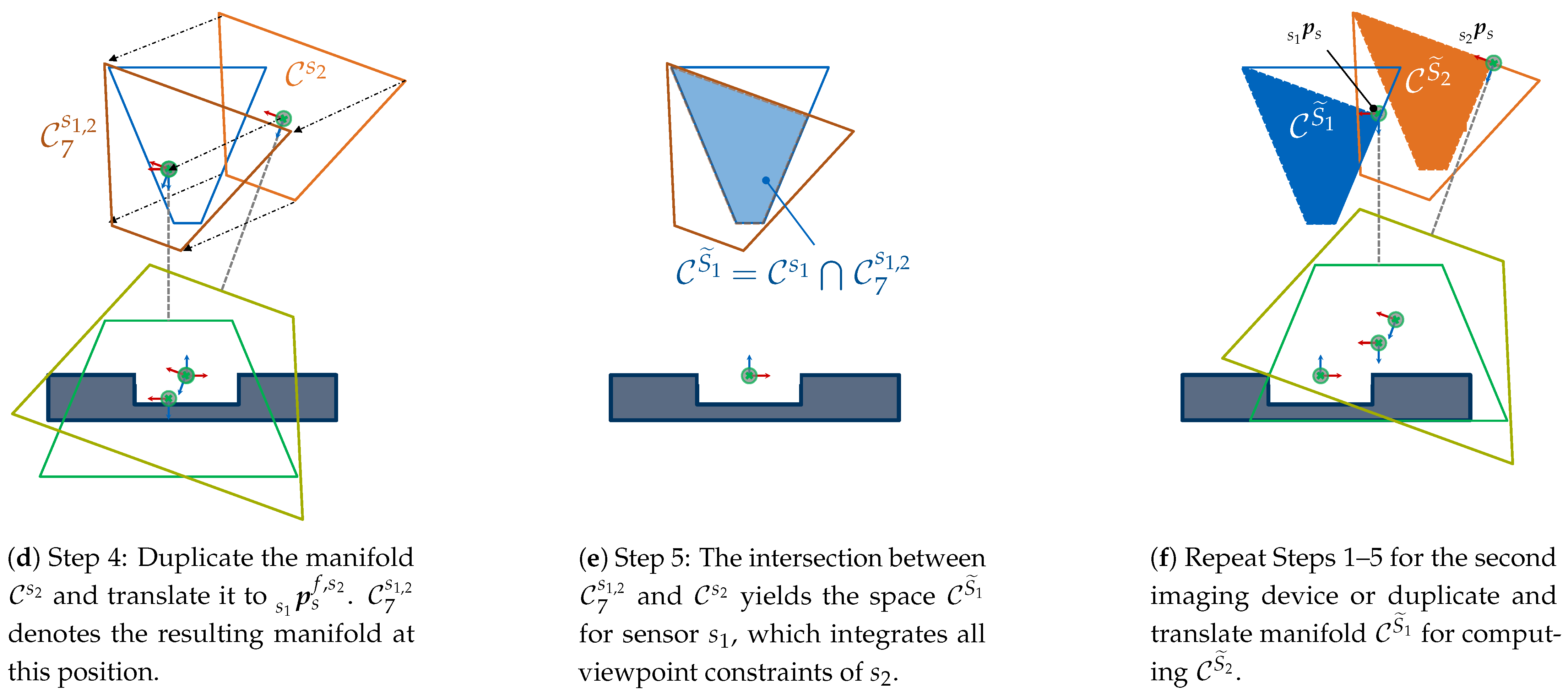
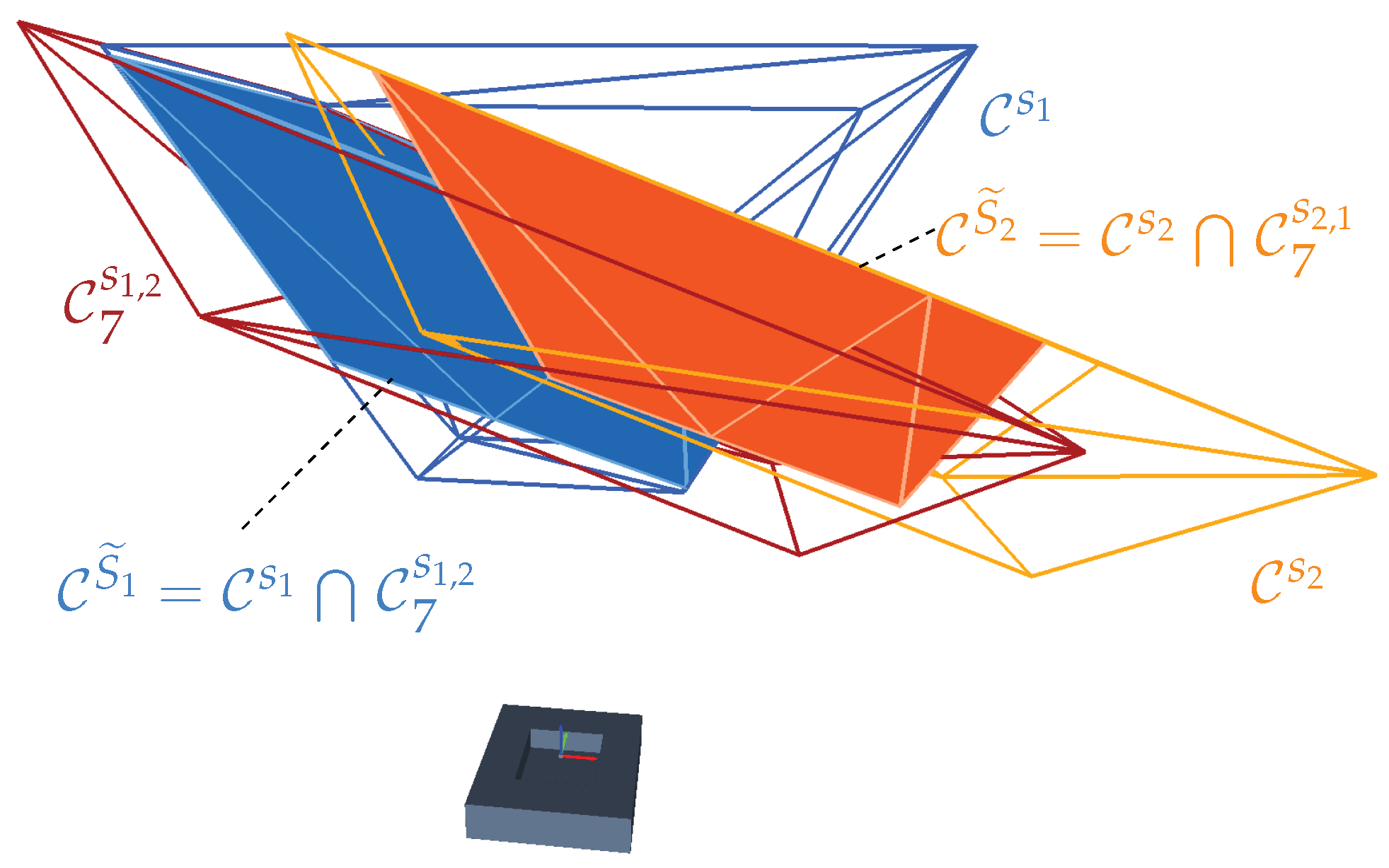
4.6. Multisensor
4.6.1. Formulation
4.6.2. Characterization
4.6.3. Verification
4.6.4. Summary
4.7. Robot Workspace
4.7.1. Formulation
4.7.2. Characterization and Verification
4.7.3. Summary
4.8. Multi-Feature Spaces
4.8.1. Characterization
4.8.2. Verification
4.8.3. Summary
4.9. Constraints Integration Strategy
5. Results
5.1. Technical Setup
5.1.1. Domain Models
- Sensors: We used two different range sensors for the individual verification of the s and the simulation-based and experimental analyses. The imaging parameters (cf. Section 2.5) and kinematic relations of both sensors are given in Table A6. The parameters of the lighting source of the ZEISS Comet PRO AE sensor are conservatively estimated values, which guarantee that the frustum of the sensor lies completely within the field of view of the fringe projector. A more comprehensive description of the hardware is provided in Section 5.
- Object, features, and occlusion bodies: For verification purposes, we designed an academic object comprising three features and two occlusion objects with the characteristics given in Table A7 in the Appendix A.
- Robot: We used a Fanuc M-20ia six-axis industrial robot and respective kinematic model to compute the final viewpoints to position the sensor.
5.1.2. Software
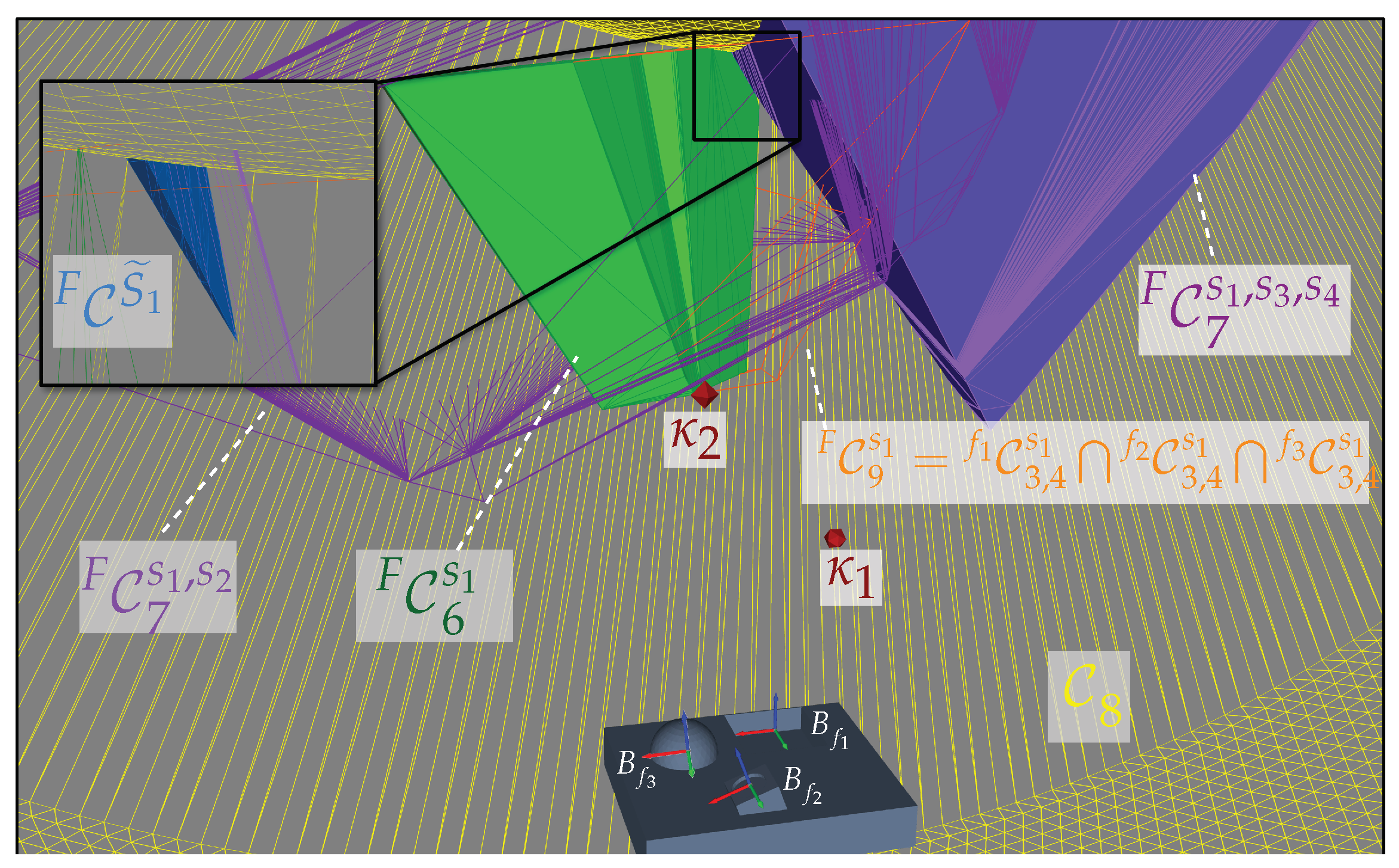
5.2. Academic Simulation-Based Analysis
5.2.1. Use Case Description
5.2.2. Results
5.2.3. Summary
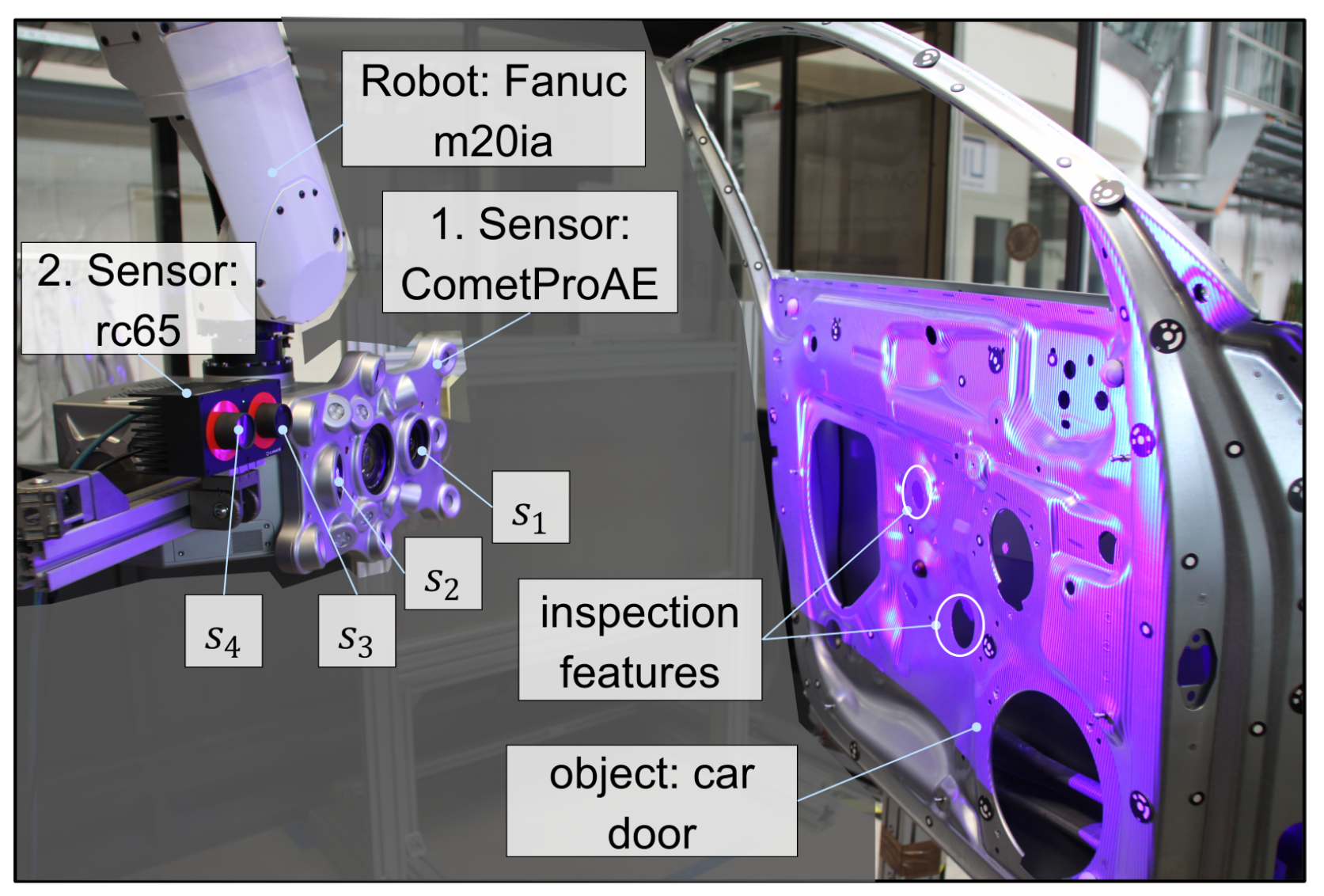
5.3. Real Experimental Analysis
5.3.1. System Description
5.3.2. Vision Task Definition
5.3.3. Results
5.3.4. Summary
6. Conclusions
6.1. Summary
6.2. Limitations and Chances
6.3. Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Feature-Based Constrained Space | |
| CSG | Constructive Solid Geometry |
| Frustum space | |
| RVS | Robot Vision System |
| VGP | Viewpoint Generation Problem |
| VPP | Viewpoint Planning Problem |
Appendix A. Tables
| General Requirement | Description |
|---|---|
| 1. Generalization | The models and approaches used should be abstracted and generalized at the best possible level so that they can be used for different components of an RVS and can be applied to solve a broad range of vision tasks. |
| 2. Computational Efficiency | The methods and techniques used should strive towards a low level of computational complexity. Whenever possible, analytical, and linear models should be preferred over complex techniques, such as stochastic and heuristic algorithms. Nevertheless, when considering offline scenarios, the trade-off between computing a good enough solution within an acceptable amount of time should be individually assessed. |
| 3. Determinism | Due to traceability and safety issues within industrial applications deterministic approaches should be prioritized. |
| 4. Modularity and Scalability | The approaches and models should consider in general a modular structure and promote their scalability. |
| 5. Limited a priori Knowledge | The parameters required to implement the models and approaches should be easily accessible for the end-users. Neither in-depth optics nor robotic knowledge should be required. |
| Notation | Index Description |
|---|---|
| |
| Notes | The indices r and b just apply for pose vectors, frames, and transformations. |
| Example | The index notation can be better understood consider following examples:
|
| Symbol | Description |
|---|---|
| General | |
| c | Viewpoint constraint |
| Set of viewpoint constraints | |
| f | Feature |
| F | Set of features |
| t imaging device of sensor s | |
| v | Viewpoint |
| Sensor pose in | |
| Spatial Dimensions | |
| B | Frame |
| Translation vector in | |
| Orientation matrix in | |
| Manifold vertex in | |
| Topological Spaces | |
| for a set of viewpoint constraints | |
| i of the viewpoint constraint | |
| Frustum space |
| Viewpoint Constraint | Description |
|---|---|
| 1. Frustum Space | The most restrictive and fundamental constraint is given by the imaging capabilities of the sensor. This constraint is fulfilled if at least the feature’s origin lies within the frustum space (cf. Section 2.5). |
| 2. Sensor Orientation | Due to specific sensor limitations, it is necessary to ensure that the maximal permitted incidence angle between the optical axis and the feature normal lies within an specified range; see Equation (5). |
| 3. Feature Geometry | This constraint can be considered an extension of the first viewpoint constraint and is fulfilled if all surface points of a feature can be acquired by a single viewpoint, hence lying within the image space. |
| 4. Kinematic Error | Within the context of real applications, model uncertainties affecting the nominal sensor pose compromise a viewpoint’s validity. Hence, any factor, e.g., kinematic alignment, robot’s pose accuracy, which affects the overall kinematic chain of the RVS must be considered (see Section 2.6). |
| 5. Sensor Accuracy | Acknowledging that the sensor accuracy may vary within the sensor image space (see Section 2.5), we consider that a valid viewpoint must ensure that a feature must be acquired within a sufficient quality. |
| 6. Feature Occlusion | A viewpoint can be considered valid if a free line of sight exists from the sensor to the feature. More specifically, it must be assured that no rigid bodies are blocking the view between the sensor and the feature. |
| 7. Bistatic Sensor and Multisensor | Recalling the bistatic nature of range sensors, we consider that all viewpoint constraints must be valid for all lenses or active sources. Furthermore, we also extend this constraint for considering a multisensor RVS comprising more than one range sensor. |
| 8. Robot Workspace | The workspace of the whole RVS is limited primarily by the robot’s workspace. Thus, we assume that a valid viewpoint exists if the sensor pose lies within the robot workspace. |
| 9. Multi-Feature | Considering a multi-feature scenario, where more than one feature can be acquired from the same sensor pose, we assume that all viewpoint constraints for each feature must be satisfied within the same viewpoint. |
| k Vertex of | Rotation around y-axis | Rotation around x-axis | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 | ||||||||
| Range Sensor | 1 | 2 | |
| Manufacturer | Carl Zeiss Optotechnik GmbH, Neubeuern, Germany | Roboception, Munich, Germany | |
| Model | COMET Pro AE | rc_visard 65 | |
| 3D Acquisition Method | Digital Fringe Projection | Stereo Vision | |
| Imaging Device | Monochrome Camera: | Blue Light LED-Fringe Projector: | Two monochrome cameras: |
| Field of view | , | , | , |
| Working distances and near, middle, and far planes relative to imaging devices lens. | |||
| Transformation between sensor lens and TCP | |||
| Transformation between imaging devices of each sensor , | |||
| Transformation between both sensors | , | ||
| Feature | , | |||||
| Topology | Point | Slot | Circle | Half-Sphere | Icosahedron | Octaeder |
| Generalized Topology | - | Square | Square | Cube | - | - |
| Dimensions in mm | , | , | edge length: | edge length: | ||
| Translation vector in object’s frame in mm | ||||||
| Rotation in Euler Angles in object’s frame in |
| Viewpoint Constraint | Description | Approach |
|---|---|---|
| 1 | Two sensors(, ) with two imaging devices each: . The imaging parameters of all devices are specified in Table A6. | Linear algebra and geometry |
| 2 | Relative orientation to the object’s frame: . | Linear algebra and geometry |
| 3 | A planar rectangular object with three different features (see Table A7). | Linear algebra, geometry, and trigonometry |
| 4–5 | The workspace of the second imaging device is restricted in the z-axis to the following working distance . | Linear algebra and geometry |
| 6 | Two objects with the form of an icosahedron () and a octahedron () occlude the visibility of the features. | Linear algebra, ray-casting, and CSG Boolean Operations |
| 7 | All constraints must be satisfied by all four imaging devices simultaneously. | Linear algebra and CSG Boolean Operations |
| 8 | Both sensors are attached to a six-axis industrial robot. The robot has a workspace of a half-sphere with a working distance of –. | CSG Boolean Operation |
| 9 | All features from the set G must be captured simultaneously. | CSG Boolean Operation |
Appendix B. Algorithms
| Algorithm A1 Extreme Viewpoint Characterization of the Constrained Space . |
|
| Algorithm A2 Characterization of the occlusion space . |
|
| Algorithm A3 Characterization of to integrate viewpoint constraints of a second imaging device . |
|
| Algorithm A4 Integration of for multiple features. |
|
| Algorithm A5 Strategy for the integration of viewpoint constraints. |
|
| Algorithm A6 Computation of View Rays for Occlusion Space. |
|
Appendix C. Figures


References
- Kragic, D.; Daniilidis, K. 3-D Vision for Navigation and Grasping. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 811–824. [Google Scholar] [CrossRef]
- Peuzin-Jubert, M.; Polette, A.; Nozais, D.; Mari, J.L.; Pernot, J.P. Survey on the View Planning Problem for Reverse Engineering and Automated Control Applications. Comput.-Aided Des. 2021, 141, 103094. [Google Scholar] [CrossRef]
- Gospodnetić, P.; Mosbach, D.; Rauhut, M.; Hagen, H. Viewpoint placement for inspection planning. Mach. Vis. Appl. 2022, 33, 2. [Google Scholar] [CrossRef]
- Chen, S.; Li, Y.; Kwok, N.M. Active vision in robotic systems: A survey of recent developments. Int. J. Robot. Res. 2011, 30, 1343–1377. [Google Scholar] [CrossRef]
- Tarabanis, K.A.; Allen, P.K.; Tsai, R.Y. A survey of sensor planning in computer vision. IEEE Trans. Robot. Autom. 1995, 11, 86–104. [Google Scholar] [CrossRef]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A Comprehensive Review of Coverage Path Planning in Robotics Using Classical and Heuristic Algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Tarabanis, K.A.; Tsai, R.Y.; Allen, P.K. The MVP sensor planning system for robotic vision tasks. IEEE Trans. Robot. Autom. 1995, 11, 72–85. [Google Scholar] [CrossRef]
- Scott, W.R.; Roth, G.; Rivest, J.F. View planning for automated three-dimensional object reconstruction and inspection. ACM Comput. Surv. (CSUR) 2003, 35, 64–96. [Google Scholar] [CrossRef]
- Mavrinac, A.; Chen, X. Modeling Coverage in Camera Networks: A Survey. Int. J. Comput. Vis. 2013, 101, 205–226. [Google Scholar] [CrossRef]
- Kritter, J.; Brévilliers, M.; Lepagnot, J.; Idoumghar, L. On the optimal placement of cameras for surveillance and the underlying set cover problem. Appl. Soft Comput. 2019, 74, 133–153. [Google Scholar] [CrossRef]
- Scott, W.R. Performance-Oriented View Planning for Automated Object Reconstruction. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2002. [Google Scholar]
- Cowan, C.K.; Kovesi, P.D. Automatic sensor placement from vision task requirements. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 407–416. [Google Scholar] [CrossRef]
- Cowan, C.K.; Bergman, A. Determining the camera and light source location for a visual task. In Proceedings of the 1989 International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; IEEE Computer Society Press: Washington, DC, USA, 1989; pp. 509–514. [Google Scholar] [CrossRef]
- Tarabanis, K.; Tsai, R.Y. Computing occlusion-free viewpoints. In Proceedings of the 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Champaign, IL, USA, 15–18 June 1992; IEEE Computer Society Press: Washington, DC, USA, 1992; pp. 802–807. [Google Scholar] [CrossRef]
- Tarabanis, K.; Tsai, R.Y.; Kaul, A. Computing occlusion-free viewpoints. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 279–292. [Google Scholar] [CrossRef]
- Abrams, S.; Allen, P.K.; Tarabanis, K. Computing Camera Viewpoints in an Active Robot Work Cell. Int. J. Robot. Res. 1999, 18, 267–285. [Google Scholar] [CrossRef]
- Reed, M. Solid Model Acquisition from Range Imagery. Ph.D. Thesis, Columbia University, New York, NY, USA, 1998. [Google Scholar]
- Reed, M.K.; Allen, P.K. Constraint-based sensor planning for scene modeling. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1460–1467. [Google Scholar] [CrossRef]
- Tarbox, G.H.; Gottschlich, S.N. IVIS: An integrated volumetric inspection system. Comput. Vis. Image Underst. 1994, 61, 430–444. [Google Scholar] [CrossRef]
- Tarbox, G.H.; Gottschlich, S.N. Planning for complete sensor coverage in inspection. Comput. Vis. Image Underst. 1995, 61, 84–111. [Google Scholar] [CrossRef]
- Scott, W.R. Model-based view planning. Mach. Vis. Appl. 2009, 20, 47–69. [Google Scholar] [CrossRef]
- Gronle, M.; Osten, W. View and sensor planning for multi-sensor surface inspection. Surf. Topogr. Metrol. Prop. 2016, 4, 024009. [Google Scholar] [CrossRef]
- Jing, W.; Polden, J.; Goh, C.F.; Rajaraman, M.; Lin, W.; Shimada, K. Sampling-based coverage motion planning for industrial inspection application with redundant robotic system. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5211–5218. [Google Scholar] [CrossRef]
- Mosbach, D.; Gospodnetić, P.; Rauhut, M.; Hamann, B.; Hagen, H. Feature-Driven Viewpoint Placement for Model-Based Surface Inspection. Mach. Vis. Appl. 2021, 32, 8. [Google Scholar] [CrossRef]
- Trucco, E.; Umasuthan, M.; Wallace, A.M.; Roberto, V. Model-based planning of optimal sensor placements for inspection. IEEE Trans. Robot. Autom. 1997, 13, 182–194. [Google Scholar] [CrossRef]
- Pito, R. A solution to the next best view problem for automated surface acquisition. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 1016–1030. [Google Scholar] [CrossRef]
- Stößel, D.; Hanheide, M.; Sagerer, G.; Krüger, L.; Ellenrieder, M. Feature and viewpoint selection for industrial car assembly. In Proceedings of the Joint Pattern Recognition Symposium, Tübingen, Germany, 30 August–1 September 2004; Springer: Berlin/Heidelberg, Germany; pp. 528–535. [Google Scholar] [CrossRef]
- Ellenrieder, M.M.; Krüger, L.; Stößel, D.; Hanheide, M. A versatile model-based visibility measure for geometric primitives. In Proceedings of the Scandinavian Conference on Image Analysis, Joensuu, Finland, 19–22 June 2005; pp. 669–678. [Google Scholar] [CrossRef]
- Raffaeli, R.; Mengoni, M.; Germani, M.; Mandorli, F. Off-line view planning for the inspection of mechanical parts. Int. J. Interact. Des. Manuf. (IJIDeM) 2013, 7, 1–12. [Google Scholar] [CrossRef]
- Koutecký, T.; Paloušek, D.; Brandejs, J. Sensor planning system for fringe projection scanning of sheet metal parts. Measurement 2016, 94, 60–70. [Google Scholar] [CrossRef]
- Lee, K.H.; Park, H.P. Automated inspection planning of free-form shape parts by laser scanning. Robot.-Comput.-Integr. Manuf. 2000, 16, 201–210. [Google Scholar] [CrossRef]
- Derigent, W.; Chapotot, E.; Ris, G.; Remy, S.; Bernard, A. 3D Digitizing Strategy Planning Approach Based on a CAD Model. J. Comput. Inf. Sci. Eng. 2006, 7, 10–19. [Google Scholar] [CrossRef]
- Tekouo Moutchiho, W.B. A New Programming Approach for Robot-Based Flexible Inspection Systems. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2012. [Google Scholar]
- Park, J.; Bhat, P.C.; Kak, A.C. A Look-up Table Based Approach for Solving the Camera Selection Problem in Large Camera Networks. In Workshop on Distributed Smart Cameras in conjunction with ACM SenSys; Association for Computing Machinery: New York, NY, USA, 2006; pp. 72–76. [Google Scholar]
- González-Banos, H. A randomized art-gallery algorithm for sensor placement. In Proceedings of the Seventeenth Annual Symposium on Computational Geometry-SCG ’01; Souvaine, D.L., Ed.; Association for Computing Machinery: New York, NY, USA, 2001; pp. 232–240. [Google Scholar] [CrossRef]
- Chen, S.Y.; Li, Y.F. Automatic sensor placement for model-based robot vision. IEEE Trans. Syst. Man Cybern. Part Cybern. Publ. IEEE Syst. Man Cybern. Soc. 2004, 34, 393–408. [Google Scholar] [CrossRef]
- Erdem, U.M.; Sclaroff, S. Automated camera layout to satisfy task-specific and floor plan-specific coverage requirements. Comput. Vis. Image Underst. 2006, 103, 156–169. [Google Scholar] [CrossRef]
- Mavrinac, A.; Chen, X.; Alarcon-Herrera, J.L. Semiautomatic Model-Based View Planning for Active Triangulation 3-D Inspection Systems. IEEE/ASME Trans. Mechatron. 2015, 20, 799–811. [Google Scholar] [CrossRef]
- Glorieux, E.; Franciosa, P.; Ceglarek, D. Coverage path planning with targetted viewpoint sampling for robotic free-form surface inspection. Robot.-Comput.-Integr. Manuf. 2020, 61, 101843. [Google Scholar] [CrossRef]
- Chen, S.Y.; Li, Y.F. Vision sensor planning for 3-D model acquisition. IEEE Trans. Syst. Man Cybern. Part Cybern. Publ. IEEE Syst. Man Cybern. Soc. 2005, 35, 894–904. [Google Scholar] [CrossRef] [PubMed]
- Vasquez-Gomez, J.I.; Sucar, L.E.; Murrieta-Cid, R.; Lopez-Damian, E. Volumetric Next-best-view Planning for 3D Object Reconstruction with Positioning Error. Int. J. Adv. Robot. Syst. 2014, 11, 159. [Google Scholar] [CrossRef]
- Kriegel, S.; Rink, C.; Bodenmüller, T.; Suppa, M. Efficient next-best-scan planning for autonomous 3D surface reconstruction of unknown objects. J.-Real-Time Image Process. 2015, 10, 611–631. [Google Scholar] [CrossRef]
- Lauri, M.; Pajarinen, J.; Peters, J.; Frintrop, S. Multi-Sensor Next-Best-View Planning as Matroid-Constrained Submodular Maximization. IEEE Robot. Autom. Lett. 2020, 5, 5323–5330. [Google Scholar] [CrossRef]
- Waldron, K.J.; Schmiedeler, J. Kinematics. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 11–36. [Google Scholar] [CrossRef]
- Beyerer, J.; Puente León, F.; Frese, C. Machine Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Biagio, M.S.; Beltrán-González, C.; Giunta, S.; Del Bue, A.; Murino, V. Automatic inspection of aeronautic components. Mach. Vis. Appl. 2020, 28, 591–605. [Google Scholar] [CrossRef]
- Bertagnolli, F. Robotergestützte Automatische Digitalisierung von Werkstückgeometrien Mittels Optischer Streifenprojektion; Messtechnikund Sensorik, Shaker: Aachen, Germany, 2006. [Google Scholar]
- Raffaeli, R.; Mengoni, M.; Germani, M. Context Dependent Automatic View Planning: The Inspection of Mechanical Components. Comput. Aided Des. Appl. 2013, 10, 111–127. [Google Scholar] [CrossRef]
- Beasley, J.; Chu, P. A genetic algorithm for the set covering problem. Eur. J. Oper. Res. 1996, 94, 392–404. [Google Scholar] [CrossRef]
- Mittal, A.; Davis, L.S. A General Method for Sensor Planning in Multi-Sensor Systems: Extension to Random Occlusion. Int. J. Comput. Vis. 2007, 76, 31–52. [Google Scholar] [CrossRef]
- Kaba, M.D.; Uzunbas, M.G.; Lim, S.N. A Reinforcement Learning Approach to the View Planning Problem. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5094–5102. [Google Scholar] [CrossRef]
- Lozano-Pérez, T. Spatial Planning: A Configuration Space Approach. In Autonomous Robot Vehicles; Cox, I.J., Wilfong, G.T., Eds.; Springer: New York, NY, USA, 1990; pp. 259–271. [Google Scholar] [CrossRef]
- Latombe, J.C. Robot Motion Planning; The Springer International Series in Engineering and Computer Science, Robotics; Springer: Boston, MA, USA, 1991; Volume 124. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Ghallab, M.; Nau, D.S.; Traverso, P. Automated Planning; Morgan Kaufmann and Oxford; Elsevier Science: San Francisco, CA, USA, 2004. [Google Scholar]
- Frühwirth, T.; Abdennadher, S. Essentials of Constraint Programming; Cognitive Technologies; Springer: Berlin, Germany; London, UK, 2011. [Google Scholar]
- Trimesh. Trimesh Github Repository. Available online: https://github.com/mikedh/trimesh (accessed on 16 July 2023).
- Roth, S.D. Ray casting for modeling solids. Comput. Graph. Image Process. 1982, 18, 109–144. [Google Scholar] [CrossRef]
- Glassner, A.S. An Introduction to Ray Tracing; Academic: London, UK, 1989. [Google Scholar]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Cagliari, Italy, 26–28 June 2006; Eurographics Association: Goslar, Germany, 2006; pp. 61–70. [Google Scholar]
- Bauer, P.; Heckler, L.; Worack, M.; Magaña, A.; Reinhart, G. Registration strategy of point clouds based on region-specific projections and virtual structures for robot-based inspection systems. Measurement 2021, 185, 109963. [Google Scholar] [CrossRef]
- Quigley, M.; Gerkey, B.; Conley, K.; Faust, J.; Foote, T.; Leibs, J.; Berger, E.; Wheeler, R.; Ng, A. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software; IEEE: Piscataway, NJ, USA, 2009; Volume 3, p. 5. [Google Scholar]
- Magaña, A.; Bauer, P.; Reinhart, G. Concept of a learning knowledge-based system for programming industrial robots. Procedia CIRP 2019, 79, 626–631. [Google Scholar] [CrossRef]
- Magaña, A.; Gebel, S.; Bauer, P.; Reinhart, G. Knowledge-Based Service-Oriented System for the Automated Programming of Robot-Based Inspection Systems. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1511–1518. [Google Scholar] [CrossRef]
- Zhou, Q.; Grinspun, E.; Zorin, D.; Jacobson, A. Mesh arrangements for solid geometry. ACM Trans. Graph. 2016, 35, 1–15. [Google Scholar] [CrossRef]
- Wald, I.; Woop, S.; Benthin, C.; Johnson, G.S.; Ernst, M. Embree. ACM Trans. Graph. 2014, 33, 1–8. [Google Scholar] [CrossRef]
- Unity Technologies. Unity. Available online: https://unity.com (accessed on 16 July 2023).
- Bischoff, M. ROS #. Available online: https://github.com/MartinBischoff/ros-sharp (accessed on 16 July 2023).
- Magaña, A.; Wu, H.; Bauer, P.; Reinhart, G. PoseNetwork: Pipeline for the Automated Generation of Synthetic Training Data and CNN for Object Detection, Segmentation, and Orientation Estimation. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 587–594. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magaña, A.; Dirr, J.; Bauer, P.; Reinhart, G. Viewpoint Generation Using Feature-Based Constrained Spaces for Robot Vision Systems. Robotics 2023, 12, 108. https://doi.org/10.3390/robotics12040108
Magaña A, Dirr J, Bauer P, Reinhart G. Viewpoint Generation Using Feature-Based Constrained Spaces for Robot Vision Systems. Robotics. 2023; 12(4):108. https://doi.org/10.3390/robotics12040108
Chicago/Turabian StyleMagaña, Alejandro, Jonas Dirr, Philipp Bauer, and Gunther Reinhart. 2023. "Viewpoint Generation Using Feature-Based Constrained Spaces for Robot Vision Systems" Robotics 12, no. 4: 108. https://doi.org/10.3390/robotics12040108
APA StyleMagaña, A., Dirr, J., Bauer, P., & Reinhart, G. (2023). Viewpoint Generation Using Feature-Based Constrained Spaces for Robot Vision Systems. Robotics, 12(4), 108. https://doi.org/10.3390/robotics12040108






