Abstract
In this paper, we suggest an implementation of non-commutative logic and apply its operators for decision-making in a group of autonomous agents. The suggested operators extend the uninorm and absorbing norm aggregators and use an additional asymmetry parameter that defines the “level of non-commutativity”. The value of this parameter is specified using the perception bias of humans measured in the experiments. The suggested operators and decision-making method are illustrated by the simulated behavior of mobile robots in the group, which verified the possibility of processing systematic sensing errors, as well as of distinguishing and mimicking the biased decisions.
1. Introduction
Based on “An Investigation of the Laws of Thought” by Bool [1], data analysis and decision-making are considered using the methods of formal logic and probability theory involving rational principles of judgement and reasoning. Logic formalizes the rules for deriving truthiness from the statements, and the probability theory provides rigorous methods for addressing uncertainty in the knowledge about the statements and events.
The combination of the concepts of uncertainty and truthiness gave a rise to the development of multivalued logic; the first version of such logic—the three-valued logic—was suggested by Łukasiewicz [2]. Later, Łukasiewicz and Tarski [3] extended this logic to the -valued logic.
A further development of the multivalued logic resulted in probabilistic logic [4] and fuzzy logic [5]. After formulation of the uninorm [6] and absorbing norm [7], fuzzy logic forms a basis for the development of non-Bayesian decision-making and of non-probabilistic methods of addressing uncertainty [8].
In parallel to the development of multivalued logics, Lambek [9] initiated the studies of non-commutative logics. At the beginning, these logics were developed for the representation of the syntactical and grammatical structures of natural languages [10,11], and then were adopted for modeling preference relations in the decision-making processes. Theoretical studies in these directions resulted in the invention of multivalued non-commutative operators [12] and multivalued non-commutative logics algebras [13] that allow for a direct consideration of the situations where truthiness depends on the order of the statements. In the context of decision-making by humans and by artificial agents, the multivalued non-commutative logic is considered as a possible tool for modeling the “irrational decisions” [14,15] and of the decisions with preferences; for the problems and the state-of-the-art in the field of decision-making with preferences, see, e.g., [16,17].
The attempts to use the multivalued non-commutative logics in decision-making gave rise to two main problems: how to implement the non-commutative logical operators, and how to define the correct “level of non-commutativity” of these operators.
In this paper, we suggest the implementation of non-commutative logical operators based on the extension of the uninorm and absorbing norm [18]. In addition to the neutral and absorbing elements, these norms are equipped with the asymmetry parameter which controls the “level of non-commutativity”.
To define the value of this parameter, we utilize the phenomenon of “the bias of the crowd” [19,20,21] in its basic form of the perceptional bias originated by Galton [22]. We consider the perception of weight, length and time and specify the asymmetry of the uninorm and absorbing norm by the difference between the perceived and real weights, lengths and times.
The activity of the obtained non-commutative logical operators is illustrated by their application for decision-making in the group of mobile robots. The simulations of the robots’ activity verified the possibility of using the suggested method for processing systematic sensing errors and modelling the decisions with “irrational” judgements.
The rest of this paper is organized as follows. In Section 2, starting from the previously defined algebra of multivalued logic, we define the non-commutative version of such algebra and indicate the meaning of the used parameters. In Section 3, we describe the conducted experiments, in which we found the perception bias used for the specification of the parameters of the non-commutative logic. In Section 4, we formally define the parameters of the logic using perception bias. In Section 5, we implement the obtained non-commutative logic for the control of mobile robots and simulate the group activity. In Section 6, we introduce the obtained results into a wider context of decision-making and discuss the further research. Section 7 briefly outlines the obtained results and concludes the discourse.
2. Non-Commutative Algebra of Multi-Valued Logic
In this section, we define the non-commutative algebra of multi-valued logic. Since it is based on the previously developed commutative algebra, we start with this algebra and then consider its non-commutative extension.
2.1. Algebra with Multi-Valued Logical Operators
Let be the uninorm [6] with the parameter called neutral or identity element such that is the -norm (or multivalued operator) and is the -conorm (or multivalued operator). In addition, let be the absorbing norm [7] with the parameter called absorbing element; this norm is a multivalued version of the operator.
Usually, it is assumed that the uninorm and absorbing norm are commutative and associative and that the uninorm is transitive. The elements and play the role of unit and zero for their operators such that and , .
The uninorm and the absorbing norm considered as operators on the interval form an algebra [18,23]
in which the uninorm acts as a summation with the zero and the absorbing norm acts as a multiplication with the unit .
If the norms and are commutative, then there exist the functions and called generator functions [24] such that for any
For the boundary values , it is assumed that the norms and act as appropriate Boolean operators with respect to the values of the elements and .
For completeness, in the algebra the inverse operations, subtraction and division are defined as
with the obvious condition .
If and for any , then the algebra is distributive with
for any .
Let us assume that for any the generator functions with the parameter are equivalent and are defined as follows:
Respectively, the inverse functions are
The graphs of these functions are shown in Figure 1.
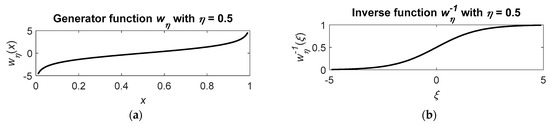
Figure 1.
Generator function (a) and its inverse function (b) with .
The uninorm and the absorbing norm are commutative; the graphs of these norms are shown in Figure 2.
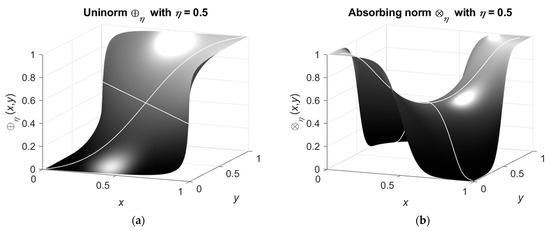
Figure 2.
Uninorm (a) and absorbing norm (b) with .
Algebra extends Boolean algebra with conjunction and disjunction operators, and its multivalued version with -norm and -conorm , and defines the multivalued logic with logical operators and . The uninorm is associated with the multivalued and operators, and the absorbing norm is associated with the multivalued operator. In addition, it acts as an arithmetic system on the interval , where the uninorm is associated with the arithmetical weighted summation “” and the absorbing norm is associated with the arithmetical multiplication “”, both for real numbers from the interval .
2.2. Non-Commutative Extension of the Algebra
The suggested definition of non-commutative version of the algebra is based on the definition of uninorm and absorbing norm using generator functions and given by Equations (2) and (3). Formally, we define the non-commutative uninorm and absorbing norm as follows:
with the same as above assumption about the boundary values. Similarly,
with .
In general, the operators and are non-commutative. The commutativity holds if, respectively, and . If and , then these operators are equivalent to the norms and .
The algebra
with the operators and is the non-commutative version of the algebra . For arbitrary parameters, this algebra is also non-distributive.
To illustrate the non-commutativity of the operators and , let us assume that generator functions and their inverses are defined by Equations (7) and (8) and that
In addition, let us assume that the and are defined as follows:
This means that, if , then and (cf. definitions of subjective false and subjective truth [25]). The graphs of the non-commutative uninorm and absorbing norm with these parameters are shown in Figure 3.
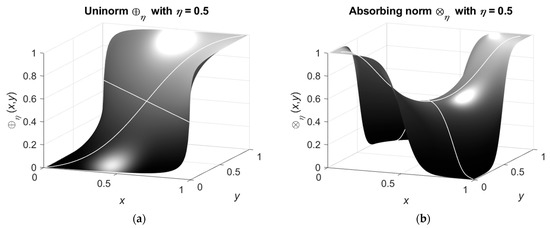
Figure 3.
Non-commutative uninorm (a) and absorbing norm (b) with , and .
The norms and preserve their general form (cf. the graphs of the commutative norms in Figure 2) but demonstrate clear dependence of the results on the order of the arguments. For example,
while
Similarly,
while
In this example, parameters , and are defined by Equations (15) and (16) such that ; then, the preference in the operations is given to the first operand in such a sense that the result is as great as the first operand is greater than the second operand. If the relation between the parameters is , then the preference is opposite, and the result is as great as the second operand is greater than the first operand. This observation is summarized in Table 1.

Table 1.
Dependence of the operations’ results on the relation between the parameters.
In addition, for reasons of symmetry, the substitution of the parameters and results in the equivalences
In summary, in the algebra the uninorm and absorbing norm are non-commutative and their results depend on the order of the operands
These norms provide the logical operations that can be used in the algorithms of decision-making with preferences [1,9] and for implementation of non-commutative logics [13]. Below, we illustrate such implementation by the decision-making in the group of mobile robots.
3. Perception Bias in Group
The definition of the exact values of the parameters , , and , , requires additional analysis of the considered situation and of the meaning of the parameters and arguments. Here, we assume that the decision-making is conducted by artificial agents that can perceive certain measured data and mimic the perceptional bias observed in the groups of humans.
The studies of perception bias in groups and of the bias of the crowd in general were originated by Galton in 1907. In his paper “Vox populi” [22], Galton presented the results of the survey about the estimated weight of the fat ox. It was found that the distribution of individual estimations is not normal and that the mean value of the estimated weights differs from the real weight of the ox. Nowadays, this paper is considered to belong to the origin of studies in the field of “the wisdom of the crowd” [26].
Following the Galton approach, we conducted three surveys that considered the estimations of weights, lengths and times, which are the basic physical values used in classical mechanics. However, in contrast to Galton, we used the values in the usual for ordinary people ranges—grams and kilograms for weights, centimeters and decimeters for lengths and seconds for times. The obtained estimations were used for definition of the values of the parameters , , and , , .
The surveys were organized as follows (with the approvement of the Ariel University Ethics Commission AU-ENG-EK-20230205, 5 February 2023). For the measurements, we used the following objects:
- The estimations of the weights were verified using the equivalently looking boxes with the weights kg, kg and kg;
- The estimations of the lengths were verified using the ropes (made from the same material) with the lengths cm, cm and cm;
- The estimations of times were verified using sounds of Hz of the durations s, s and s.
In all the cases, the non-round values were chosen in order to avoid the natural tendency of the humans to round the estimations.
The participants of the surveys were students at Ariel University and adults with academic degrees. The number of participants in the surveys ranged from to persons, the average age being (the youngest participant was years old and the oldest was years old). The results of the surveys are summarized in Table 2.

Table 2.
Results of the surveys: real and estimated values of the weights, lengths and times.
For all the considered weights, the means kg, kg and kg of the estimated values are smaller than the real weights kg, kg and kg of the objects. As found by the -test, the distributions of the weights’ estimations are not normal and the differences between the real weights and the means of the estimations are significant with a significance level .
The same tendency holds for the greater lengths: the means cm and cm of the estimated values are smaller than the real lengths cm and cm of the ropes. However, for the short rope, the mean estimated length cm is greater than its real length cm. For the short rope, the -test with shows that the distribution of the length estimations is normal and that the difference between the real length and the mean of the estimations is not significant, while for the longer ropes the distributions of the length’s estimations are not normal.
For the sounds’ durations, the tendency is opposite. For all considered durations, the means s, s and s of the estimated values are greater than the real durations s, s and s. However, the -test with shows that the distributions of the times’ estimations are normal and that the difference between the real length and the mean of the estimations is not significant. The histograms of the estimated values are shown in Figure 4.
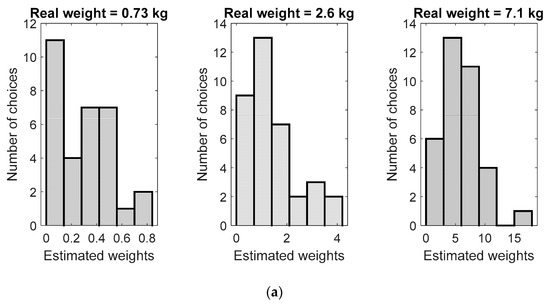
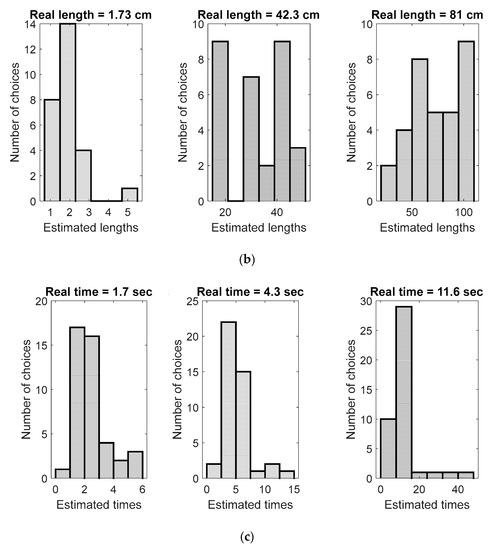
Figure 4.
Histograms of the estimated values: (a) the weights, (b) the lengths and (c) the times.
Thus, for all weights and for the longer ropes, the observed results coincide with Galton’s observation according to which the estimations are not normal, but for the short rope and for all the durations, the distributions of the observed results are normal. In addition, it is worth noting that, in contrast to Galton’s statement, the medians in the observed data also strongly differ from the real values and cannot be considered as better estimators than the means.
4. Definition of the Aggregators’ Parameters in Algebra
Parameters , , and , , of the uninorm and absorbing norm define the asymmetry of the logical operations: and (and the preference between them) in the uninorm and in the absorbing norm. The values of these parameters can be defined in several ways. Here, we suggest one possible definition of the parameters based on the considered above perception bias. Such definition coincides with the further application of the algebra for decision-making in mobile robots, where we assume that the decision-making depends on the perceived and stored objective data with no involvement of informal valuations and judgements. Additionally, the values and can be considered as systematic errors in perceiving information, and the values , and , —as the bounds of these errors. Then, the next use of these parameters is an attempt to make correct or at least rational decisions in the presence of such errors. In the considered scenarios, we use the perception bias observed in humans and implement it in the simulations of mobile robots’ activity.
As above, for both norms of equal parameters defined by Equations (14)–(16), i.e., we assume that , and . The value of the parameter based on the differences between real values of the weights, lengths and times and the means of the estimated values is defined as follows.
From Table 2, it follows that the differences between the real values and means of the estimations are in different ranges. Therefore, to unify these ranges we normalize the differences such that their values are in the range . The normalized difference between real values and the means of the estimations is
It is clear that and if , then . Here, we also assume that the considered values are not negative, so .
The values of the normalized difference are linearly transformed to the values of the parameter as follows:
In the decision-making processes, we apply the norms and with the parameter defined for the appropriate measurement—of the weights, the lengths and the times. It is worth noting again that the uninorm combines the multivalued and operators and the parameters , , define the preference between these operators and their asymmetry. The absorbing norm is a multivalued operator and the parameters , , define its asymmetry. Then, the use of these norms allows for making decisions and conducting judgements which are not necessarily commutative and therefore not necessarily distributive. In the considered simulations, we used these norms for making decisions about the distances between the robots, which then transformed into the attraction/repulsion forces.
The examples of the uninorm and absorbing norm for the estimations of the weight kg and of the time s are shown in Figure 5.
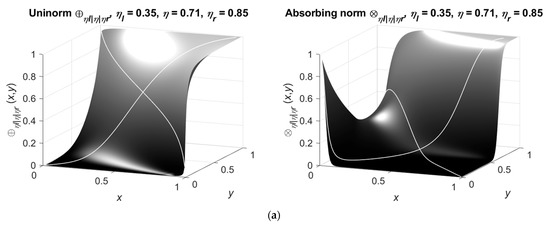
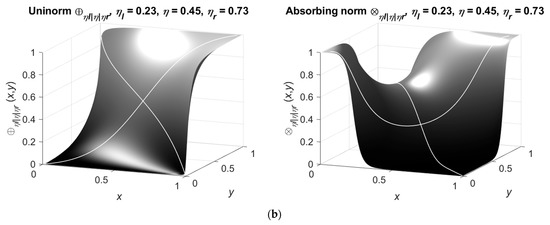
Figure 5.
Non-commutative uninorm and absorbing norm for the estimations (a) of the weight 0.73 kg and (b) of the time 1.70 s.
The values of the parameter change the curvature of the surface produced by the aggregations’ results that represents the biased influence of the perceived data to the decisions.
It is worth noting again that the suggested method based on the simple Formulas (21) and (22) is not a unique or preferred one and can be substituted by the other. For example, in the control of mobile robots [27], we used the extended algebra with commutative norms and action on the interval . In this case, the processing of the negative parameters and arguments was conducted on the level of generator function and its inverse without use of the Formula (22) or similar.
5. Control of Mobile Robots in and Group Activity
Let us consider the application of the suggested operators of the non-commutative algebra for the control of mobile robots acting in group. In the simulations, we use the previously defined construction of the robots [27], but for the robots’ control we apply the presented above non-commutative operators. As above, we consider the norms and with the parameters defined by Equations (15) and (16).
Let us assume that each robot includes two active elements—the head and the tail —and denote by and the states of these elements at time , respectively, for all The attraction/repulsion force between the robots is formed by four attraction/repulsion forces between the robots’ heads and tails
where is an attraction/repulsion coefficient,
is a distance between the robots’ heads and tails located in the points with the coordinates and at time , and
is a control with the attraction/repulsion value
The scheme of the robots and attraction and repulsion is shown in Figure 6.
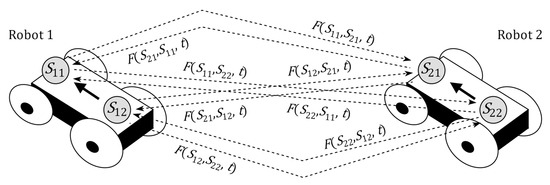
Figure 6.
Scheme of the robots and attraction/repulsion forces. The headings of the robots are specified by bold arrows.
It is worth noting that the function that defined the control value in Equation (25) is an inverse of the transformation used in Equation (22). It transforms the attraction/repulsion values to the control values .
The states and , , of the active elements are updated according to the rule of the subjective Markov process [25] as follows [27] ():
To illustrate the activity of the group of the robots, we simulated the motion of the group of robots in the gridded square domain of the size . The simulations were conducted using MATLAB®; the scripts were written using conventional tools without the use of specific toolboxes. In the uninorm and absorbing norm, we used a generator function and its inverse defined by Equations (7) and (8).
The distances between the robots are Euclidean, and the attraction/repulsion forces act between the neighboring robots up to the distance . The value of the attraction/repulsion coefficient is the tenth part of the domain diagonal that is .
For example, let us assume that at time the robots are in the same states , and and , and the distances between the active elements and are , . In addition, let the parameters of the uninorm and absorbing norm be equal, and the central elements be defined by the bias of the weight that is . Then, by Equations (15) and (16), and .
Using these parameters and the inverse generator function defined by Equation (8), we can calculate the attraction/repulsion forces between the active elements and , , of the robots. By Equation (26), we obtain the repulsion force between the heads and of the robots and the repulsion force between the tails and of the robots. In addition, the head of the first robot attracts the tail of the second robot with the force , and the tail of the second robot repulses the head of the first robot with the force .
As a result, the robots which at time were located in parallel such that the distances between their heads and between their tails are , (see Figure 7), change their direction. The distance between the heads of the robots increases with respect to the force value and the distance between the tails of the robots increases with respect to the force value . An additional change in direction is influenced by the attraction between the head and the tail as well as the repulsion between the tail and the head.
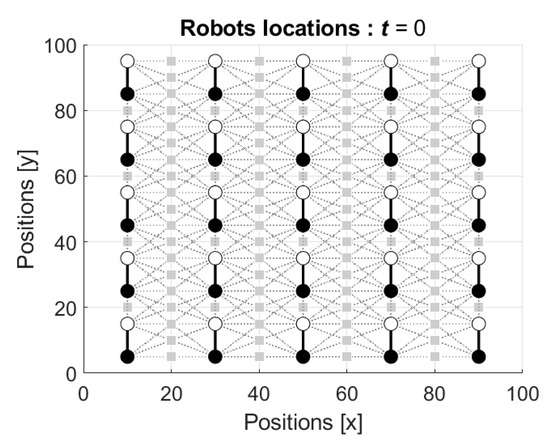
Figure 7.
Starting positions of the robots at time t = 0. While circles denote the “heads” of the robots and black circles denote the “tails” of the robots. The bodies of the robots are denoted by solid lines connecting heads and tails. The dotted lines denote connections between the robots.
In the simulations, the robots started from the ordered configuration shown in Figure 7. The states and , of the head and tail of each robot are specified by random with respect to the uniform distribution on the interval .
Figure 8 shows the activity of the group of the robots with the operators’ parameters corresponding to the human perception errors in estimating weight kg (see Figure 5a).
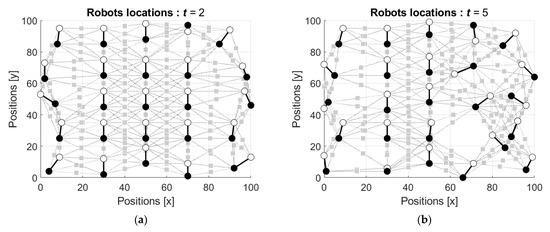
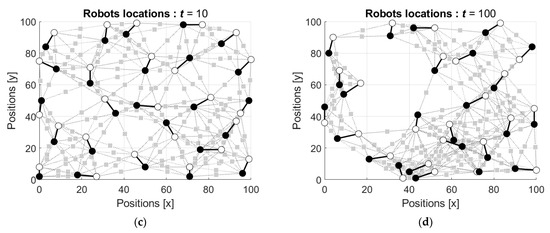
Figure 8.
Evolution of the initial configuration of the robots’ group with the operators’ parameters corresponding to the weight kg: (a) locations after two movements of each robot, ; (b) locations after five movements of each robot, ; (c) locations after ten movements of each robot, ; and (d) locations after the hundredth movement of each robot, .
The robots start from their positions in the nodes of the grid and with time repulse from one another. As a result, they leave the central part of the domain toward the borders. The simulated dynamics is shown in the movie in the Supplementary S1.
In contrast, if the robots use the operators with the parameters corresponding to the human perception errors in estimating time s (see Figure 5b), they attract each other. The activity of the group of such robots is shown in Figure 9.
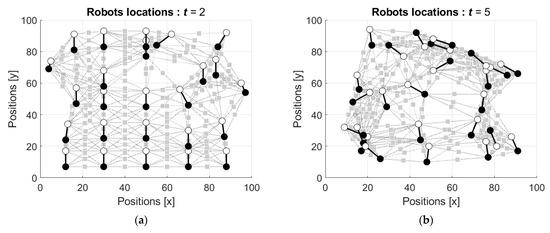
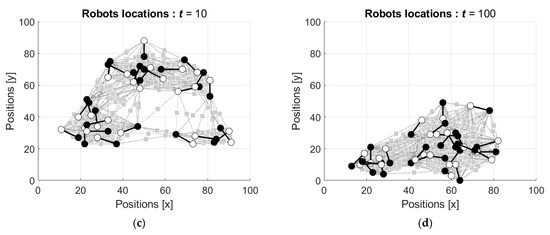
Figure 9.
Evolution of the initial configuration of the robots’ group with the operators’ parameters corresponding to the time s: (a) locations after two movements of each robot, ; (b) locations after five movements of each robot, ; (c) locations after ten movements of each robot, ; and (d) locations after the hundredth movement of each robot, .
As above, the robots start from their positions in the nodes of the grid, but in contrast to the previous case, they attract one another, and the group concentrates and moves as a swarm. The simulated dynamics is shown in the movie in the Supplementary S2.
For comparison, Figure 10 shows the activity of the robots with commutative operators with the parameters representing the absence of perception bias.
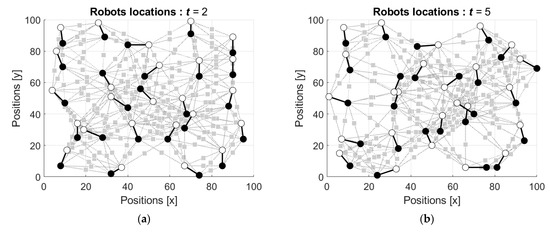
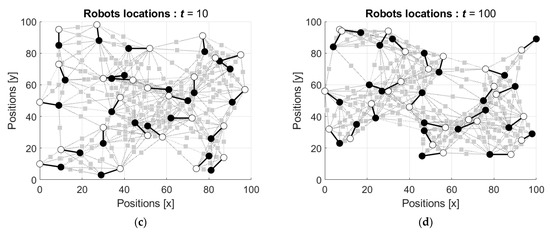
Figure 10.
Evolution of the initial configuration of the robots’ group with commutative operators with the parameters : (a) locations after two movements of each robot, ; (b) locations after five movements of each robot, ; (c) locations after ten movements of each robot, ; and (d) locations after the hundredth movement of each robot, .
In the case of commutative operators, the group does not demonstrate a certain motion tendency. However, for certain initial states and , the robots can form cliques with the average distance between them as . The simulated dynamics is shown in the movie in the Supplementary S3.
The simulations demonstrate that the behavior of the group of the robots depends on the parameters of the non-commutative uninorm and absorbing norm . For negative perception bias, while the average estimation is lower than the real value, the robots repulse each other, and the group disperses (see Figure 8). In contrast, for positive perception bias, while the average estimation is higher than the real value, the robots attract each other, and the group concentrates and moves as a unit (see Figure 9).
6. Discussion
This paper continued our previous works [18,27,28] on multivalued logic algebra based on parameterized uninorm and absorbing norm and suggested the non-commutative version of such algebra.
This work contains two main goals. The first is to construct a simple and computable implementation of non-commutative multivalued logic algebra, which can be used for decision-making under uncertainty. Additionally, the second is to form a basis for further analysis of irrational decisions and modelling the paradoxes of rationality [29].
We demonstrated the use of the suggested algebra to control mobile robots acting in a group, where the level of non-commutativity was defined by human perceptional bias. The conducted simulations verified the possibility of formal processing of systematic errors in sensing, and of distinguishing and mimicking the biased decisions.
Further work will concentrate on the modelling and analysis of irrational decisions. It appears to be true that, in many cases, the irrationality in the decisions is apparent and can be explained either by certain statistical errors [30] or by the non-commutativity and asymmetry of logical operations. In addition, it will be meaningful to consider the relation between the suggested logics’ algebra and the recently presented non-commutative fuzzy logic system [31]; knowledge about such relation will provide a wide framework for theoretical and practical studies on the control of autonomous agents.
The results of this work will allow for the use of non-commutative logic both for processing the sensed data and for forming rational decisions in irrational conditions.
7. Conclusions
We suggested the implementation of non-commutative multivalued logic algebra. The “level of non-commutativity” in this algebra is controlled by the external asymmetry parameter.
We defined the value of the asymmetry parameter on the base of the perception bias of humans, which was found in observations of expected values of basic physical measures—weight, length and time.
In the experiments, we considered the usual values of weights, lengths and times. It was observed that, for all weights from kg to kg and for the lengths cm and cm, the estimations’ distributions are not normal, and that the estimations’ means are lower than the real values of the considered measures. In contrast, for the length of cm and for all times from s to s, the estimations’ distributions are normal, and the estimations’ means are higher than the real values of the measures.
The operators of the suggested non-commutative multivalued logic algebra were used for the control of mobile robots acting in a group.
In the simulations, it was observed that, for negative perception bias (the estimations’ mean is lower than the real value), the group disperses, and for positive perception bias (estimations’ mean is higher that the real value), the group concentrates and moves as a unit.
As a result, we obtained the implementation of non-commutative multivalued logic algebra, the tendency and the values of the perception bias for basic physical measures as well as the method of control of mobile robots in the group based on the implemented algebra and taking into account the differences in the perception of different types of measures.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/robotics12030076/s1, Videos S1, S2 and S3.
Author Contributions
Conceptualization, E.K. and A.R.; methodology, E.K. and A.N.; software, E.K.; validation, A.N. and D.R.; formal analysis, E.K. and A.R.; investigation, E.K. and A.R.; resources, D.R.; data curation, A.N.; writing—original draft preparation, E.K. and D.R.; writing—review and editing, A.N. and A.R.; supervision, A.R.; project administration, E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon request and can be received from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bool, G. An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities; Walton and Maberly: London, UK, 1854. [Google Scholar]
- Łukasiewicz, J. On three-valued logic. Ruch Filoz. 1920, 5, 169–171. [Google Scholar]
- Łukasiewicz, J.; Tarski, A. Untersuchungen über den Aussagenkalkül. Comptes Rendus Des Séances De La Société Des Sci. Et Des Lett. De Vars. Cl. III 1930, 23, 30–50. [Google Scholar]
- Nilsson, N.J. Probabilistic logic. Artif. Intell. 1986, 28, 71–87. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Yager, R.; Rybalov, A. Uninorm aggregation operators. Fuzzy Sets Syst. 1996, 80, 111–120. [Google Scholar] [CrossRef]
- Batyrshin, I.; Kaynak, O.; Rudas, I. Fuzzy modeling based on generalized conjunction operations. IEEE Trans. Fuzzy Syst. 2002, 10, 678–683. [Google Scholar] [CrossRef]
- Aliev, R.A.; Huseynov, O.H. Decision Theory with Imperfect Information; World Scientific: Singapore, 2014. [Google Scholar]
- Lambek, J. The mathematics of sentence structure. Am. Math. Mon. 1958, 65, 154–170. [Google Scholar] [CrossRef]
- Schmerling, S. Asymmetric conjunction and rules of conversation. In Syntax and Semantics; Cole, P., Morgan, J., Eds.; Speech Acts; Academic Press: New York, NY, USA, 1975; Volume 3, pp. 211–231. [Google Scholar]
- Na, Y.; Huck, G. On extracting from asymmetrical structures. In The Joy of Grammar: A Festschrift in Honor of James; McCawley, D., Brentari, D., Larson, G., MacLeod, L., Eds.; John Benjamins: Amsterdam, The Netherlands, 1992; pp. 119–136. [Google Scholar]
- Yager, R.; Rybalov, A. Non-commutative self-identity aggregation. Fuzzy Sets Syst. 1997, 85, 73–82. [Google Scholar] [CrossRef]
- Ciungu, L. Non-Commutative Multi-Valued Logic Algebras; Springer: Cham, Switzerland; Heidelberg, Germany, 2014. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Ruggeri, K.; Alí, S.; Berge, M.L.; Bertoldo, G.; Bjørndal, L.D.; Cortijos-Bernabeu, A.; Davison, C.; Demić, E.; Esteban-Serna, C.; Friedemann, M.; et al. Replicating patterns of prospect theory for decision under risk. Nat. Hum. Behav. 2020, 4, 622–633. [Google Scholar] [CrossRef] [PubMed]
- Fodor, J.; De Baets, B.; Perny, P. (Eds.) Preferences and Decisions under Incomplete Knowledge; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Greco, S.; Pereira, R.; Squillante, M.; Yager, R.; Kacprzyk, J. (Eds.) Preferences and Decisions. Models and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kagan, E.; Rybalov, A.; Siegelmann, H.; Yager, R. Probability-generated aggregators. Int. J. Intell. Syst. 2013, 28, 709–727. [Google Scholar] [CrossRef]
- Payne, B.K.; Vuletich, H.A.; Lundberg, K.B. The bias of crowds: How implicit bias bridges personal and systemic prejudice. Psychol. Inq. 2017, 28, 233–248. [Google Scholar] [CrossRef]
- Connor, P.; Evers, E.R.K. The bias of individuals (in crowds): Why implicit bias is probably a noisily measured individual-level construct. Perspect. Psychol. Sci. 2020, 15, 1329–1345. [Google Scholar] [CrossRef] [PubMed]
- Payne, B.K.; Vuletich, H.A.; Lundberg, K.B. Critique of the bias-of-crowds model simply restates the model: Reply to Connor and Evers (2020). Perspect. Psychol. Sci. 2022, 17, 606–610. [Google Scholar] [CrossRef] [PubMed]
- Galton, F. Vox populi. Nature 1907, 75, 450–451. [Google Scholar] [CrossRef]
- Fodor, J.; Rudas, I.; Bede, B. Uninorms and absorbing norms with applications to image processing. In Proceedings of the Information Conference SISY: 4th Serbian-Hungarian Joint Symposium on Intelligent Systems, Subotica, Serbia, 29–30 September 2006; pp. 59–72. [Google Scholar]
- Fodor, J.; Yager, R.; Rybalov, A. Structure of uninorms. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1997, 5, 411–427. [Google Scholar] [CrossRef]
- Kagan, E.; Rybalov, A.; Yager, R. Subjective Markov process with fuzzy aggregations. In Proceedings of the 12th International Conference Agents and Artificial Intelligence ICAART 2020, Valetta, Malta, 22–24 February 2020; Volume 2, pp. 386–394. [Google Scholar]
- Landemore, H. Collective Wisdom—Old and New. Collective Wisdom: Principles and Mechanisms; Landemore, H., Elster, J., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 1–10. [Google Scholar]
- Kagan, E.; Rybalov, A. Subjective trusts for the control of mobile robots under uncertainty. Entropy 2022, 4, 790. [Google Scholar] [CrossRef] [PubMed]
- Kagan, E.; Rybalov, A. Subjective trusts and prospects: Some practical remarks on decision making with imperfect information. Oper. Res. Forum 2022, 3, 19. [Google Scholar] [CrossRef]
- Sorensen, R. Paradoxes of rationality. In The Oxford Handbook of Rationality; Mele, A.R., Rawling, P., Eds.; Oxford University Press: Oxford, UK, 2004; pp. 257–275. [Google Scholar]
- Szekely, G.J. Paradoxes of Probability Theory and Mathematical Statistics; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Teodorescu, M.; Teodorescu, H.N. Noncommutative logic systems with applications in management and engineering. Int. J. Comput. Commun. Control. 2021, 16, 1–19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).