Abstract
The paper presents the design and experimental study of a synthesis method based on reference signal generation systems. The method can be used for all actuators of redundant manipulators. The aforementioned systems aim to save the dynamic control accuracy of the working tools of serial manipulators when they move along arbitrary spatial trajectories, taking into account restrictions in all degrees of freedom and special cases of their link positions. The maintenance of the control accuracy could be ensured by eliminating the reach of all degrees of freedom of manipulators to their limits and to indicated special positions, characterized by an ambiguity when solving the inverse kinematic problems of various serial manipulators. This is in addition to preventing the reach of their working tools to the boundaries of the working area due to the use of a redundant degree of freedom when approaching the indicated undesirable positions. The experimental studies performed in this paper confirm the efficiency of the proposed method and allow accurate characteristics to be obtained.
1. Introduction
Currently, the use of serial manipulators for performing various technological operations in automatic mode is often significantly complicated by the fact that even when their working tools move inside their working areas, some degrees of freedom (DoF) can reach constraints. If this happens, a controller immediately stops the serial manipulator (SM) with an appropriate error message. In addition, the SM can reach a special (singular) position that is characterized by an ambiguity in the solution of the inverse kinematics problem (IKP). As a result, when the working tool (WT) continues to move along spatial trajectories, unexpected reversals can occur in the corresponding SM DoF. This may significantly change the WT velocity, and cause collisions with processed objects, tool breakage and other emergencies. In addition, when working with large objects, a part of the WT trajectory may be outside the SM working area. This will require additional reinstallation and the fixation of these objects.
If the trajectories of the SM WT are generated offline, that is, not during its movement, then for the elimination of the described negative situations, it is necessary to carry out numerous and laborious tests and manually make adjustments to the pre-planned trajectories. This is also necessary when unforeseen deformations [1,2] occur in the workpieces during their fixing. Most applications for the motion control problem of the 7-DoF manipulator are based on a priori known trajectories.
To expand the SM working area, it is possible to provide it with an additional linear DoF in a horizontal plane [3]. In this case, it is necessary to obtain a new IKP solution for a specific SM [4]. A similar problem was solved for a manipulator installed on an underwater vehicle [5], but only for its operation in a front semi-sphere working area. As a result, using the well-known IKP solution for the SM with the PUMA kinematic scheme and providing a linear displacement for the underwater vehicle near an object of work, it was possible to quickly calculate the generalized coordinates of the SM in specified ranges and significantly expand its working area.
However, for an industrial SM, the requirements for the range of variation in its generalized coordinates (including the redundant one) are significantly expanded and are not limited to only one semi-sphere. In addition, for this SM, the various variants of rotation of its DoF are possible, in which a tip of the WT will be in the same position. These variants are called configurations [6]. All of the above require the new IKP solution.
In particular, analytical approaches were used in [7,8,9,10], and a combination of an analytical approach with fuzzy logic was used in [11] for solving the IKP for the 7-DoF manipulator. The use of these solutions makes it possible to prevent the reach of all DoF to their limits, but the possibility of reverses appearing in certain DoF is not prevented. In addition, the scope of these methods is limited to manipulators with only one kinematic scheme.
In [12,13,14,15,16,17,18,19], methods for the iterative numerical solution of the IKP for redundant manipulators are presented, and their implementation is considered using the example of the 7-DoF SM. The application of the methods described in [12,13] makes it possible to unambiguously determine the current configurations of the SM, at the same time preventing their entry into singular positions and the WT, on the border of the working area. In addition, the application of the method described in [14], by introducing additional indicator functions, and of that described in [16,17], makes it possible to prevent the entry of all generalized coordinates of the SM into their limits. The methods described in [16,18] allow obstacles located in the SM working area to be avoided. A common disadvantage of these methods is the need for laborious calculations at each step of the pseudoinverse Jacobi matrices.
In [20], the hybrid numerical–analytical method is presented. This method allows the amount of computing to be reduced, obstacles to be avoided and singular SM positions to be entered, but this method can only be applied for a single kinematic scheme.
The method presented in [21] makes it possible to obtain a solution to the IKP by using a neural network with a fuzzy logic system. This method makes it possible to additionally prevent the possibility of all DoF limits being reached and of collisions of the WT with obstacles in the working area of the SM. A disadvantage of this method is the high labor intensity of the process of adjusting the SM control system.
In [22], a method is presented for the unambiguous solution of the IKP using the example of the 6-DoF SM, with the possibility of its extension for the redundant SM using neural networks. The study of [23] presents the modification of this method. This modified method additionally uses genetic algorithms to improve the accuracy of the obtained solutions. A common disadvantage of these methods is the need for the simultaneous parallel operation of three neural networks with the subsequent selection of the best result and optimization by means of genetic techniques. The methods described in [24,25] provide a method by which to solve the IKP without the use of neural networks and using evolutionary algorithms only. All of the above are computationally consuming technics.
Thus, this review of known methods has shown that effective IKP solutions for typical redundant SMs, taking into account the limits of their DoF and the elimination of possible reverses, have not yet been obtained.
This paper presents a method that can be used to automatically generating reference signals for all actuators of a typical manipulator of the PUMA type. This manipulator has additional excessive DoF for the linear displacement of its base in the horizontal plane. This method, by moving the SM base horizontally near the object of work, makes it possible to prevent the SM from entering the special positions of its kinematic scheme; these are characterized by the ambiguity of the IKP solution, the WT’s exit to the boundaries of its working area, as well as some of its DoF restrictions. This is especially important when a sharp decrease in the dynamic accuracy of the contour control of the WT is eliminated in certain sections of the working trajectories, when emergency situations occur, when the breakage of the WT and equipment is completely eliminated, and the working area of the SM is expanded. In addition, the proposed control method allows the most acceptable initial configuration of the SM to be correctly selected (out of many possible options), taking into account its kinematic scheme, the parameters of the links and the required initial position of the WT.
Note that the paper constitutes an extension of the conference papers [3,5,26], both theoretically and experimentally. Namely, papers [3,5] consider the application of the presented approach for controlling the SM installed on the body of an autonomous underwater vehicle moving near the object of work by means of only one DoF provided by the propulsion complex of the vehicle. In this case, the well-known IKP solution was used, which allows the SM to work only in the front semi-sphere of the apparatus. In [26], only the implementation of the system is described very briefly and only the simulation results are presented. In the presented work, firstly, a new IKP solution is obtained, taking into account all possible configurations of the SM and the extended ranges of the changes in the generalized coordinates. Secondly the results of the experimental studies of the synthesized system are presented.
The abbreviations and main notations used in the article are described in Table 1.

Table 1.
List of abbreviations and notations.
2. Task Definition
The purpose of this work is to create a new method based on the automatic movement of the WT of redundant SMs along arbitrary spatial trajectories without reducing the dynamic control accuracy and to provide experimental studies of it. This will be ensured by eliminating the reach of all DoF to their limits, eliminating the reach of the SM to singular positions, and that of the WT to the boundaries of the working area by using the redundant DoF of the SM when approaching these undesirable positions. This task is solved for the SM using the PUMA kinematic scheme, when the trajectories of their WT are unknown in advance. The same approach can be used for serial manipulators with other kinematic schemes.
3. Features of Solution of the Inverse Kinematic Problem for Manipulators with PUMA Kinematic Scheme
To solve this task, the article describes a method that implements the redundant DoF in order to move the SM near the object of work. This movement will change the WT position in the coordinate system (CS) associated with the SM base. To do this, it is necessary to solve the IKP and take into account all possible configurations (see Section 3), describe special positions and involve indicators (see Section 4). Then, one needs to synthesize the system based on the proposed method and test its performance by means of simulation (see Section 5). The results of the experimental studies are presented in Section 6.
The specified task is solved for the SM using the PUMA kinematic scheme, which is installed on a movable horizontal base (see Figure 1). In this figure, the following notation is used: Oxyz is the absolute coordinate system (CS); O′x′y′z′ is the CS associated with the movable SM base, located at point O′; qi is the generalized coordinate of the i-th DoF of the SM ; ei is the unit vector coinciding with the joint axes of the i-th DoF of the SM ; a′ = [a′x a′y a′z]T and b′ = [b′x b′y b′z]T are unit vectors located in the end effector plane that determine its orientation in the CS O′x′y′z′; R′ = [R′x R′y R′z]T and r′ = [r′x r′y r′z]T are position vectors of the characteristic point of the axis of the fifth joint and the tool center point (TCP) of the SM in the CS O′x′y′z′; R′ and r′ are points coinciding with ends of the vectors R′ and r′; W′(W′x; W′y; W′z) are coordinates of the characteristic point of axis of the third joint in the CS O′x′y′z′; Lj is the length of the j-th link of the SM ; L4 is distance between the points R′ and r′; and q7 is the displacement value of the CS O′x′y′z′ along the axis Ox.
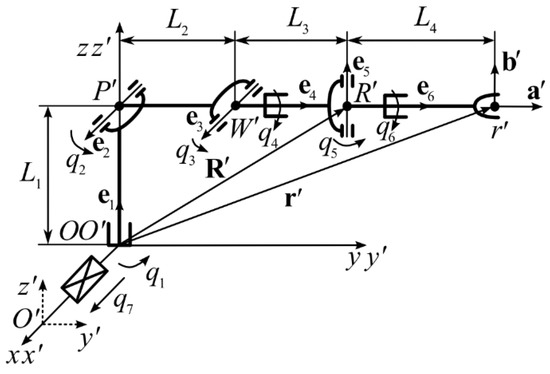
Figure 1.
6-DoF SM with PUMA kinematic scheme installed on a movable base.
The CS Oxyz and O′x′y′z′ either coincide (if q7 = 0) or their axes remain parallel. In this case, the axis Oz is always pointing vertically upward, and the axis Oy makes the right-handed CS with Ox and Oz.
The limits of generalized coordinates qi are as follows:
where qi min and qi max are the minimum and maximum values of the SM coordinate qi. The limits are equal qi min = −π and qi max = π for the SM in Figure 1.
qi min ≤ qi ≤ qi max,
The coordinates qi start from the SM position shown in Figure 1. For rotary DoF, a clockwise movement is considered negative, and a counterclockwise movement is considered positive. A rotation direction is determined relative to the corresponding vectors ei, if an observer looks from the arrow of the vector to its base.
For the SM (see Figure 1) it is convenient to divide the IKP solution into two parts [5], separately for transportable q1, q2, q3 and orienting q4, q5, q6 DoF.
The expressions used to determine q1–q3 can be obtained using geometry, shown in Figure 2a,b, taking into account the coordinates of the point R′ in the CS O′x′y′z′. The coordinates of this point are determined by the coordinates of the point r′, the value L4 and the spatial orientation of the vector a′ (see Figure 1). Figure 2a,b show that the same location of the point R′ in the CS O′x′y′z′ can be provided by different values of the generalized coordinates q1 (q1,1 or q1,2), q2 (q2,1 or q2,2) and q3 (q3,1 or q3,2). This ambiguous solution of the IKP should be taken into account when forming the corresponding generalized coordinates of the SM.
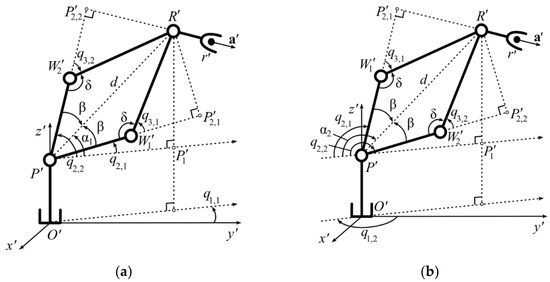
Figure 2.
Ambiguous setting of portable DoF of the SM at (a) k1 = 0; (b) k1 = ±1.
Figure 2a shows that the point R′ will have the same position in the CS O′x′y′z′ at two possible values of q1 (q1,1 or q1,2), differing by the angle π; this is due to a change in q2 and q3. As a result, without using additional logical conditions, one can write
where R′x = r′x − a′xL4, R′y = R′y − a′yL4 [5], and k1 is a coefficient that determines the choice of one of two possible SM configurations (k1 is equal to 0 or 1 if atan2(R′x, R′y) ≥ 0, otherwise −1). The choice is as follows: q1,1 for k1 = 0 and q1,2 for k1 = ±1. Moreover, the turn through the angle π should be carried out in the direction for which q1 does not go beyond the range [−π; π]. Therefore, the sign of q1,2 must be opposite to the sign of q1,1 calculated above.
q1 = −atan2(R′x, R′y) + πk1,
When determining q2 and q3, all possible SM configurations are considered, taking into account the different position of the characteristic point W′ of the axis of the third joint (see points W′1 and W′2 in Figure 2a,b, which correspond to different pairs of angles q2,1, q3,1 and q2,2, q3,2).
The value q3 can be defined as follows:
where si = sinqi, ci = cosqi.
q3 = atan2(s3, c3),
To determine c3, it is possible to use any of the equal triangles (all their sides are equal) P′W′1R′ or P′W′2R′ (for q1 = q1,1 in Figure 2a), where P′(0; 0; L1) are coordinates of the characteristic point of axis of the second joint in the CS O′x′y′z′. Using the cosine theorem for these triangles, when (cosδ = cos(π − q3,1) = cos(π + q3,2) = −c3), where δ is angle between the second and third SM links adjacent to the opposite angles q3,1 and q3,2 (q3,1 = −q3,2) for its different (see Figure 2a) configurations, and the side length P′R′ is equal to , and R′z = r′z − a′zL4 [5], c3 can be written as follows:
The expression used to determine s3 is as follows:
where k2 = ±1 is a parameter that determines the sign of s3 for the corresponding (of two) SM configurations (see Figure 2a). By substituting (4) and (5) into (3), it is possible to uniquely determine the possible values q3,1 (for k2 = −1) and q3,2 (for k2 = 1).
The possible values of the q2 (see q2,1 and q2,2 in Figure 2a,b) can be determined as follows:
where α is the angle between the horizontal plane passing through the point P′ and the straight line P′R′, which is equal to α1 for k1 = 0 or α2 for k1 = ±1; β is the angle between the second link and the straight line P′R′ (its sign coincides with sign of q3); and P′1(R′x; R′y; L1) are the projection coordinates of the point R′ on the horizontal plane passing through the point P′, in the CS O′x′y′z′.
q2 = α − β,
From the triangle P′P′1R′, for q1 = q1,1 (see Figure 2a), tgα1 = P′1R′/P′P′1 = (R′z − L1)/. From this expression, α1 can be written as follows:
and for q1 = q1,2 (see Figure 2b), the angle α is equal to
The angle β can be determined from the equal triangles P′P′2,1R′ or P′P′2,2R′ (see Figure 2a), where P′2,1 and P′2,2 are intersection points of perpendiculars omitted from point R′ to lines P′W′1 and P′W′2. For the triangle P′P′2,1R′, the equality of tgβ = P′2,1R′/(P′W′1 + W′1P′2,1) = (L3sinq3,1)/(L2 + L3cosq3,1) is true. Since q3,1 = −q3,2, then the angle β is equal to
β = atan2(L3s3, L2 + L3c3).
Considering the values and signs of α1 (or α2) (7)–(8) and β (9), the generalized coordinate q2 (6) can be uniquely determined.
To calculate the other generalized coordinates q4–q6, taking into account the extended range of their changes, the expressions previously obtained in [5] are used as initial ones:
where s23 = sin(q2 + q3) and c23 = cos(q2 + q3).
q4 = arccos((−a′xc1 − a′ys1)/s5),
q5 = arccos(−a′xs1c23 + a′yc1c23 + a′zs23),
q6 = arccos(b′x(s1s23c4 + c1s4) + b′y(−c1s23c4 + s1s4) + b′z(c23c4)),
The expressions (10)–(12) are valid for the unambiguous solution of the IKP for the considered SM, only when q4–q6 change in the ranges [0; π]. Therefore, it is necessary to modify these expressions to consider the ranges [−π; π].
When determining the coordinate q5 (11), which depends only on q1–q3, it is necessary to take into account two different SM configurations, at which q5 takes values with opposite signs and the required orientation of the vector a′ (see Figure 1) is provided by different angles q4. In view of the above, (11) should be rewritten as
where k3 is parameter equal to ±1 and determines the current configuration of the SM associated with different signs of q5.
q5 = k3arccos(−a′xs1c23 + a′yc1c23 + a′zs23),
Taking into account (10), only the modulus of q4 can be determined. Therefore, to determine the sign of q4, one should obtain the logical conditions that take into account the permanent coincidence of the vectors e6 and a′. To obtain these conditions, it is necessary to take into account that when q4 changes the directions of rotation, and q1–q3 (2)–(9) and q5 (13) are fixed, a different projection behavior (decrease or increase) of e6 onto the O′z′ axis is observed.
In Figure 3a,b, two variants of the position of the SM joints are shown. An analysis of these configurations makes it possible to determine the sign of q4. To simplify the explanations, it is assumed in these figures that q1 = 0. Therefore, the first three SM links are located in the O′y′z′ plane, and the angles q2 and q3 are different, but such that both figures are symmetric about the O′x′z′ plane. In these figures, the vectors e4 and e6 do not coincide, since the angles q5 ≠ 0. Therefore, when q4 changes and q5 = const, the point R′ moves along the circle p.
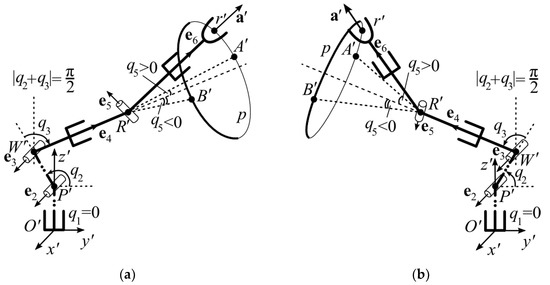
Figure 3.
Definition of q4 sign at (a) |q2 + q3| < π/2; (b) |q2 + q3| > π/2.
If the vector e5 lies in the plane O′y′z′, then it is assumed that q4 = 0, and then the vector e6 is located in the plane in which the vector e4 also lies, which is perpendicular to the vector e5. In this case, depending on the sign of q5 ≠ 0, vectors e6 in both figures will take positions R′A′ or R′B′, and their projections on the axis O′z′ will be equal to s23c5. In this case, the positions R′A′ will correspond to q5 > 0, and the positions R′B′—q5 < 0. The position of the last SM link (see Figure 3a) can correspond to two different pairs of angles q4 and q5 (in typical ranges [−π; π]), for example, π/4 and π/6, and -3π/4 and −π/6, respectively. In addition, in Figure 3b, there are two different pairs of these angles: −π/4 and π/6, and 3π/4 and −π/6.
Figure 3a,b show that for vectors a′ and e6, the condition a′z > s23c5 is true. Figure 3a shows that if |q2 + q3| < π/2 and q5 > 0, then when the TCP moves from position R′A′ to position R′ along the circle p q4 > 0, and if q5 < 0, then q4 < 0. If |q2 + q3| > π/2 and q5 > 0 (see Figure 3b), then q4 < 0, and if q5 < 0, then q4 > 0.
It is easy to show that if a′z < s23c5 (these SM configurations are not shown in Figure 3a,b), then in the above situations, the sign of q4 should be reversed. As a result, taking into account (10), in general form, the angle q4 can be written as follows:
where sign(x) = 1, if x ≥ 0, otherwise −1; k4 = a′z − s23c5, k5 = π/2 − |q2 + q3|.
q4 = sign(k3k4k5)arccos((−a′xc1 − a′ys1)/s5),
To satisfy the condition q5 ≠ 0 in (14), the synthesized SM control system prevents the complete zeroing of q5. The sign of q6 (12) is determined by the mutual position of vectors γ = [γx γy γz]T = e5 × b′ and a′. If these vectors coincide, then the angle q6 ≥ 0, else q6 < 0. If the vectors γ and a′ coincide, their scalar product satisfies the inequality k6 = γxa′x + γya′y + γza′z ≥ 0, otherwise it is negative, where γx = b′z(s1s4 − c1s23c4) − b′y(c23c4), γy = −b′z(c1s4 + s1s23c4) + b′x(c23c4), and γz = b′y(c1s4 + s1s23c4) − b′x(s1s4 − c1s23c4).
As a result, taking into account the sign, (12) can be rewritten as follows:
q6 = sign(k6)arccos(b′x(s1s23c4 + c1s4) + b′y(−c1s23c4 + s1s4) + b′z(c23c4)).
After obtaining the expressions that can be used to calculate all generalized coordinates q1–q6 (see (2)–(9) and (13)–(15)), taking into account all possible SM configurations, one of them must be chosen; for this, when the SM passes from its initial position to the final, the SM DoF is as far as possible from its limits and the SM, namely from its singular positions (their details will be discussed below). This configuration is uniquely specified by the vector K = [k1 k2 k3]T.
4. Description of Indicators Detecting the Approach of the Manipulator to Its Constraints and Singular Positions
As noted earlier, when solving the IKP of the indicated SM, it is necessary to consider its four singular positions (see Figure 4). In these positions, an ambiguous IKP solution arises and, therefore, unpredictable reversals appear in advance in some DoF.
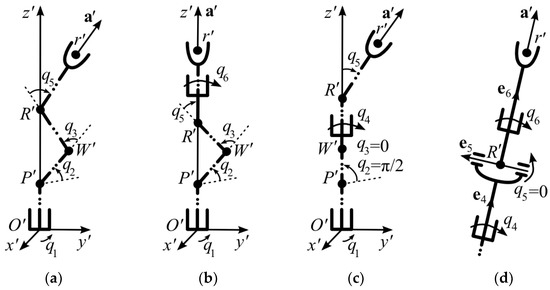
Figure 4.
Singular positions of the SM: (a) first (ambiguity of the q1, q4–q6); (b) second (ambiguity of the q1 and q6); (c) third (ambiguity of the q1 and q4); (d) forth (ambiguity of the q4 and q6).
At present, to avoid singular positions, universal numerical methods are widely used to solve the IKP. They involve performing iterative calculations, often (but not necessarily) associated with the calculation of pseudo-inverse Jacobi matrices [13,16,27]. Some papers, including [28,29], are devoted to the numerical solution of the IKP without computing the pseudoinverse Jacobi matrices. In these papers, a heuristic method is presented that is characterized by a high rate of convergence, which makes it possible to perform IKP solutions in just a few iterations, but the presence of redundant DoF significantly increases its computational complexity. Therefore, singular positions for the considered SM will be described below, and then a way to avoid them without the use of powerful computing devices will be proposed.
In the first singular position (see Figure 4a), the projection of R′ onto the horizontal plane O′x′y′ coincides with the origin of coordinates O′. In this position, many different values of the angle q1 are possible, which will correspond to different q4–q6. In the second singular position (see Figure 4b), the origin of coordinates O′, as well as points R′ and the TCP r′, lie on the same vertical line, and it is possible that there are many pairs q1 and q6. In the third singular position (see Figure 4c), the origin of coordinates O′, points W′ and R′ lie on the same vertical line, and the coordinates q1 and q4 are not uniquely determined. In the fourth singular position (see Figure 4d), the last links of the SM lie on one straight line, q5 = 0 and the coordinates q4 and q6 are undefined.
The appearance of the described singular positions and SM entrances to the constraints can be prevented by using an additional (redundant) linear DoF q7 (see Figure 1). A system for forming the reference signal for controlling this redundant DoF is presented in [5]. For its implementation, several special indicator functions are introduced. Their current values should indicate the approach of the SM to its special (critical) positions.
The value of the first indicator J1 tends to be 1 when any of the generalized coordinates qi approach their limits ±π, and it equals 0 when all DoF are in their average positions. As a result, the following expression can be used as the first indicator:
The value of the second indicator J2 tends to be 1 when the SM approaches the first three singular positions, at which point R′ is located on the O′z′ axis associated with the base of the SM. The expression for calculating this is as follows:
The third indicator J3 indicates the approach of the SM to its fourth singular position, at which q5 = 0. Its value can be calculated as follows:
J3 = 1 − |q5|/π.
The value of the fourth indicator J4 is equal to 1 if the WT approaches the border of the working area, where q3 = 0. Its value can be calculated as follows:
J4 = 1 − |q3|/π.
During the operation of the system, changes in these indicators (16)–(19) are monitored. If any of them show that the SM is approaching an undesirable position, then this system ensures the elimination of the above SM positions due to the redundant movement of the base along the q7 coordinate.
5. Results of Simulation
The simulation study of the developed system for generating reference signals was carried out in MATLAB Simulink for the SM (see Figure 5); this is part of the production chain, such as those described in [30,31]. A new detail appears in the working area of this robot at fixed (discrete) times. The equations of the SM motion were solved by means of fourth-order Runge–Kutta methods (ode45). Figure 5 shows a generalized simulation scheme that provides the generation of all main reference signals q1–q7. In this figure, the following notations are used: PD is a program device generating the current reference values of the TCP coordinates; is the position of redundant DoF measured by a sensor; G is a generator of a constant signal Δq7 > 0; IKP are blocks for solving the SM IKP, which form vectors of generalized coordinates q = [q1 q2 … q6]T and q+, respectively, for two different positions of the SM base, q7 and q7 + Δq7; C are controllers that calculate the current values of all four indicators (16)–(19) and select the largest J and J+ from them, respectively, for two different positions of the SM base, q7 and q7 + Δq7; 1 is a relay element that determines the magnitude and sign of constant speed ; 2 is a relay providing a connection from the output of the relay element 1 to the input of the electric drive controlling the coordinate q7; and 3 is an adder that generates the J-Jth signal (its input from the block G has a gain Jth/Δq7).
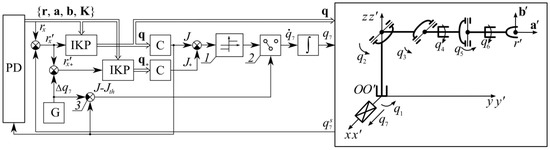
Figure 5.
Generalized simulation scheme.
The presented system works as follows.
In PD, taking into account the information from the vision system, a reference trajectory of the WT movement is generated. At the same time, at the output of this block, the reference values of the elements of vectors r, a and b in CS Oxyz are formed, as well as the vector K, which uniquely determines the current configuration of the SM. Taking into account these vectors and the continuously measured displacement of the SM along the redendant coordinate q7, the elements of the vector q are calculated in the IKP block, which are processed by the SM actuators, ensuring the movement of the WT along the trajectory.
When the SM approaches the specified undesirable positions, the redundant DoF q7 is activated. To control it in this system, the IKP (see second block IKP in Figure 5) is additionally solved for the SM position, shifted along the Ox axis at a distance of + Δq7. Then, for both positions ( and + Δq7) in the blocks C, the values J and J+ of the largest of the indicators (16)–(19) are calculated. Then, at the output of relay block 1, the direction in which the SM base must be shifted is determined in order to reduce the J and therefore avoid unwanted positions. In block 2, there is a switch that connects (or disconnects) the q7 actuator, taking into account the sign of the difference J − Jth.
The generalized coordinates of the SM vary in the ranges [−π; π] (1). The lengths of the SM links are L1 = L2 = L3 = 0.5 m and L4 = 0.15 m, their masses are m1 = 25 kg and m2 = m3 = 15 kg, and their cargo weight is mg = 5 kg. The inertia moments Jsi and Jni of the i-th SM links that are relative to their longitudinal axes and axes passing through the mass centers, and are perpendicular to their longitudinal axes, are Js1 = 0.1 kgm2, Js2 = 0.007 kgm2, Js3 = 0.005 kgm2, Jn2 = 0.55 kgm2 and Jn3 = 0.31 kgm2. DC motors of independent excitation or permanent magnets are used as the SM actuators. They have a well-known and verified mathematical model (see, for example [32]) that uses the following parameters: Kyi = 1, ipi = 100 ; Ri = 0.5 Ohm, Li = 0.01 H, KMi = 0.04 Nm/A, Kωi = 0.04 Vs/rad, JEi = 10−3 kgm2 ( and 7); and Ri = 1.4 Ohm, Li = 0.02 H, KMi = 0.06 Nm/A, Kωi = 0.06 Vs/rad, JEi = 0.3∙10−3 kgm2 . The nominal inertia moment Jnom i = 10−4 kgm2 of the shaft of the i-th ( and 7) actuator and the rotating parts of the gearbox is used in the self-tuning regulators [32] to compensate for the force–moment interactions between the SM DoF. Typical PID controllers are used in closed-loop actuators. The movement speed of the WT along a reference trajectory is set equal to 0.5 m/s, but in practice it can be variable and be adjusted according to the [33].
Figure 6, Figure 7 and Figure 8 show the MATLAB simulation results of the operation of the 6-DoF SM installed on the movable base (see Figure 5). The SM TCP moved along a complex spatial trajectory (see Figure 6), formed by using parametric splines of the third order [34]. This trajectory began at starting point 1 and then successively passed points 2–7. For this developed system, the elements of the matrix K were automatically defined as K = [0–11]T. The trajectory shape and WT orientation were chosen such that at q7 = 0, when the CS Oxyz and O′x′y′z′ coincided, the SM successively entered the undesirable positions described above.
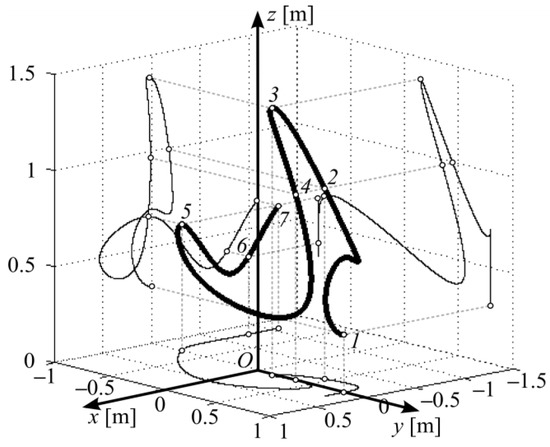
Figure 6.
Reference movement trajectory of the TCP.
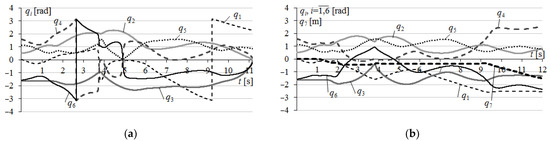
Figure 7.
Behavior of reference values q1–q6 at (a) q7 = 0; (b) q7 ≠ 0.
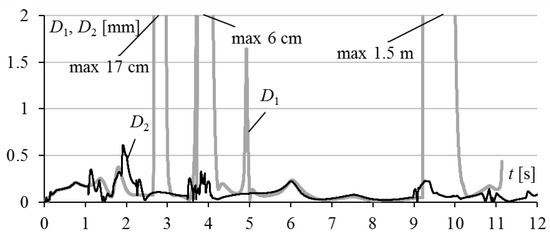
Figure 8.
Deviations in the TCP from the reference trajectory: D1 (q7 = 0) and D2 (q7 = var).
The behavior of the reference values of the generalized coordinates q1–q6 when the WT moves along the reference trajectory is shown in Figure 7a. During this movement, the SM enters two different singular positions; the three DoF reached their limits three times, and once at the end of movement the WT reached the border of the SM working area.
When the TCP passed point 2, the sign of k4 in (14) was changed. This led to the reference values of the generalized coordinates q4 and q6, which were reached in the limits (see the time moment 2.6 s in Figure 7a), sharply changing their values. When passing point 3, the SM approached the first singular position (see Figure 4a), at which point R′ was located strictly vertically above point O′ and the values q1, q4, q6 changed sharply (see 3.7 s in Figure 7a). When passing point 4, the SM entered the fourth singular position (see Figure 4d), at which q5 = 0 (see 4.9 s in Figure 7a) and reverses occurred in its fourth and sixth DoF. When passing point 5, the first DoF reached its limit (see 9.2 s in Figure 7a), and then sharply changed its value from −π to π. At point 6, the WT reached the border of the working area when q3 = 0 (see 11.2 s in Figure 7a), and the SM emergency stopped without reaching the required point 7.
Obviously, the emerging step changes in the reference values q1–q6 (see Figure 7a) could not be processed instantly by the SM actuator. As a result, the deviation D1 of the TCP from the reference trajectory near the special sections increased to unacceptable values—from min 1.7 mm to max 1.5 m (see Figure 8).
To prevent these negative situations, the proposed system was used, which ensures the movement of the SM base along the coordinate q7 while its configuration approaches the problem areas. The reference values q1–q6 generated by the system, taking into account the real value q7, which also changes in time during the process of moving along the trajectory, are shown in Figure 7b. This figure shows that the abrupt changes in the reference values in all the generalized coordinates of the SM are completely prevented, and that the deviation D2 in the SM TCP from the reference trajectory did not exceed 0.65 mm (see Figure 8) in all its sections and that the motion of the SM was fully completed (strictly at the end of the trajectory) at point 7 (see Figure 6).
6. Experimental Research of the Method Based on a Control Signal Generating System for Redundant Serial Manipulators
To test the operability and effectiveness of the above-described method of generating reference signals for all DoF of kinematically redundant SMs, in addition to simulation, an analysis of the operation of the created system was carried out in real operating modes. To do this, full-scale experiments were carried out with the 6-DoF SM, in the working area of which the workpiece was moved using a conveyor. This displacement is similar to the displacement of the SM base by the additional linear DoF q7. The general view of the robotic setup is shown in Figure 9.

Figure 9.
General view of the experimental setup. The following notations are used: 1 is the SM Mitsubishi RV-2FB-D; 2 is the Arduino Nano controller; 3 is the Cytron MD30B power amplifier; 4 is the gear motor Nidec 404.603; and 5 is the incremental rotary encoder E38S6-C-(600)B5-26G2.
This setup contains the SM 1 Mitsubishi RV-2FB-D (see Figure 9 and Figure 10), controlled by the CR750 controller (SM controller), the FESTO conveyor, which is controlled by the Arduino Nano controller 2, built on the basis of ATmega328, the Cytron MD30B power amplifier 3, the CHUX S-1500-36 power supply and the Nidec 404.603 4, the output shaft of which is connected via a gearbox to the belt drive of the shaft of sensor S 5 (incremental rotary encoder) E38S6-C-(600)B5-26G2. The generation of reference control signals for the SM 1 and the conveyor is carried out using a program written in C++, running on a personal computer (PC) and processing signals from the sensors of the SM 1 and the conveyor. The main characteristics of this setup are presented in Table 2 (the parameters and will be described later).
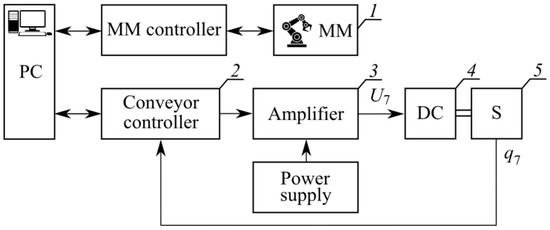
Figure 10.
Functional diagram of the robotic setup. The notations are the same as in Figure 9.

Table 2.
Main characteristics of the robotic setup.
The minimum and maximum values of the generalized coordinates qi indicated in Table 2 are determined by the mechanical constraints of the SM RV-2FB-D, which do not exceed the range [−π; π] specified in (1). This allows the use of Expressions (2)–(9) and (13)–(15), some of which, as will be shown below, must be modified. The purpose of the experiment was to use the described system (see Figure 5) to ensure the uninterrupted and accurate movement of the SM WT along the spatial trajectory and the contour of the part moved by the conveyor inside the working area of the SM. The reference signals for all DoF of the SM were generated automatically directly during the operation of the robotic setup.
6.1. Description of the Kinematic Scheme of the RV-2FB-D
In the kinematic scheme of the SM RV-2FB-D shown in Figure 11a, unlike the one used earlier (see Figure 1), the third link of the manipulator consists of two orthogonal segments connected at a point . The lengths of these segments are equal to = and = , and the distance between the points W′ and R′ is equal to
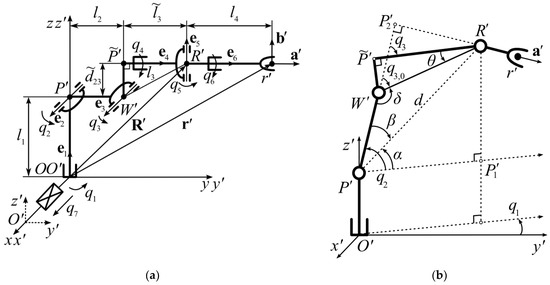
Figure 11.
Kinematic scheme of the SM RV-2FB-D: (a) kinematic scheme; (b) additional geometry.
All generalized qi coordinates of this SM are counted from the initial position pointed out in Figure 11a.
Since the construction of the third link of the MP does not affect the projection of the point R′ onto the horizontal plane O′x′y′, then using additional geometry (see Figure 11b) similar to Figure 2, Expression (2) can be used to calculate the value of q1. Figure 11b shows that q3 for the SM RV-2FB-D is equal to the angle between the segments and . Therefore, since q3 ≤ 0 (see Table 2), then
where , and q3,0 is the angle coinciding with q3 (3) in Figure 2. Moreover, since q3 ≤ 0, the sine of this angle calculated according to (5) is also negative or zero, hence k2 = −1.
q3 = q3,0 − θ,
The expressions for calculating the values of q2 (6)–(9) and the orienting DoF qi (13)–(15) remain unchanged, since the new value q3 (21) is included in them as a variable, which allows one to automatically take into account the change in the construction of the SM when solving the IKP.
6.2. Description of Indicators
The difference in the construction of the third link of the SM (see Figure 11a) leads to the need to correct expressions (16)–(19), which indicate the approach of the SM to its special positions, the approach of the DoF to their restrictions, and the WT to the boundary of the working area. It should be noted that the RV-2FB-D has three singular positions. In the first (see Figure 12a), the projection of the point R′ on the plane O′x′y′ coincides with the origin, leading to ambiguity in the definition of q1. In the second singular position (see Figure 12b), the origin, as well as the points R′ and R′, lie on the O′z′ axis. This ambiguously defines the pairs of angles q1 and q6. In the third singular position (see Figure 4d), at q5 = 0, the coordinates q4 and q6 are not defined.
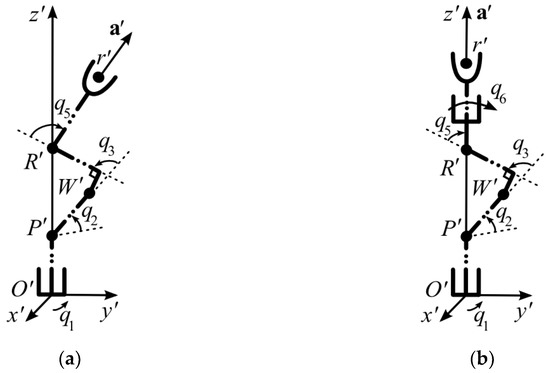
Figure 12.
Singular positions of the SM RV-2FB-D: (a) first; (b) second.
When calculating the value J1, which makes it possible to estimate the approach of the DoF to their limitations, it should be taken into account that qimin и qimax () for the SM RV-2FB-D (see Table 2) are different, and the range of variation in the coordinate q7 is limited. Therefore, instead of (16), it is necessary to use a more general expression:
where qci = (qimin + qimax)/2, , and is the width of the change range of qi*.
The values of J2 and J3 that reveal the approach of the SM to its singular positions (see Figure 4d and Figure 12) are calculated using (17) and (18), considering that the value L3 included in (17) for RV 2FB-D is equal to the distance between the points W′ and R′ (see Figure 11a) and is calculated according to (20).
The value of J4 tends to be 1 when the set r′, a′ and b′ approaches the boundary of the SM workspace, and the distance P′R′ becomes maximum, that is, the segments P′W′ and W′R′ are located on the same straight line (see Figure 13), and q3 = −θ (a minus sign indicates a rotation of the coordinates q3 clockwise). Considering that for the most efficient operation of the SM RV-2FB-D, it is advisable that its initial configuration is chosen such that the inequality q3 < −θ is fulfilled. As a result, one can write
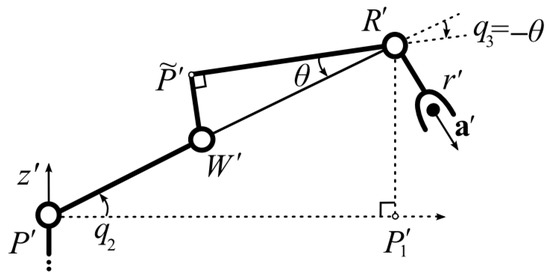
Figure 13.
Workspace boundary condition for the RV-2FB-D WT.
6.3. Results of Experimental Studies
During the experiment, the spatial motion of the RV-2FB-D WT along a trajectory composed of 39 parametric splines was studied. This movement began at the starting point 1 (see Figure 14), passed through intermediate points 2 and 3 to point 4, which are located at the initial processing place of the part, and continued along its contour (see Figure 15) through points 5, 6, 7 to point 8, where the part returns to the starting position 1. The reference signals for all DoF were generated using the system (see Figure 5). In the process of moving along this trajectory at q7 = 0, the SM consistently entered some of the undesirable positions. The elements of the matrix K, as described in Section 3, were automatically selected equal to K = [0 −1 1]T. The WT was moved using a constant velocity v*, equal to 25 mm/s.
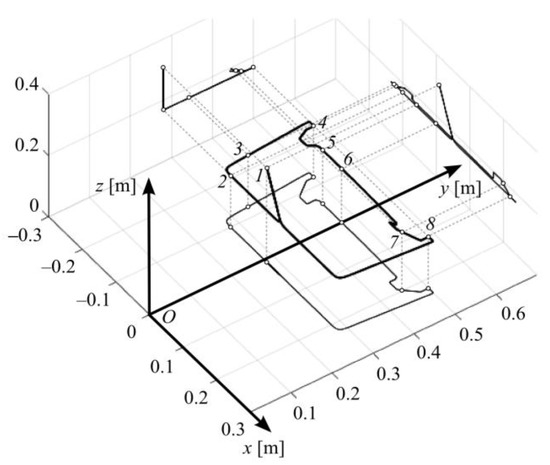
Figure 14.
Trajectory of the WT movement.

Figure 15.
Trajectory of the WT movement along the contour of the part.
The laws of change of the real values of qi measured by the SM sensors when the WT moves along the trajectory (see Figure 14) with a stationary conveyor (q7 = 0) are shown in Figure 16. During this movement, there were two restrictions reached: there was one entry into the singular position, and at the end of the movement, the WT reached the border of the working area.
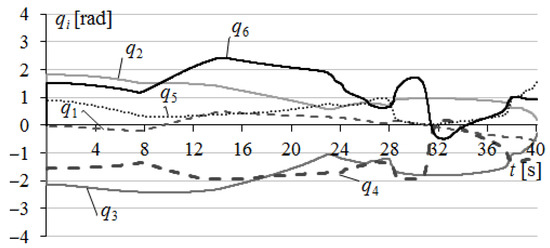
Figure 16.
Laws of change of real values of qi at q7 = 0.
When the WT moved between points 2 and 3 (see Figure 14), the fourth DoF of the MR reached the restriction (see q4 in the interval 12–16 s in Figure 16). This led to a sharp increase in the deviation D1 of the WT from the trajectory (see Figure 17) of up to 5.5 mm. Since this error appeared at the site of the approach of the WT to the workpiece, it did not lead to an emergency, but in the conditions of real operation, when moving the WT near to any objects, an emergency situation may occur. When moving between points 5 and 6, when the WT was already moving along the contour of the part, the fourth DoF again reached the restriction (see q4 in the interval 28–30 s in Figure 16) with an increase in the dynamic error D1 to 3.8 mm (see Figure 17). In addition, at the end of this interval, at point 6, the SM reached the fourth special position (see Figure 4d), in which q5 = 0 and reversals appear in the fourth and sixth DoF. At point 7, the WT reached the boundary of the working area when q3 = -θ (see 40 s in Figure 16), and the movement of the SM stopped before reaching the end of the contour of the part at point 8.
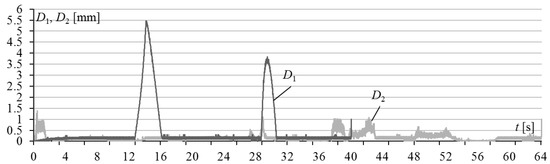
Figure 17.
Laws of variation in WT deviations from the trajectory D1 (at q7 = 0) and D2 (at q7 = var).
The system (see Figure 5) enables the prevention of the SM from entering these undesirable positions, in which there is a sharp drop in the control accuracy, or an emergency stop of the SM. When this system is running, the parameters are taken into account: = 12.5 mm/s, Jith = 0.8 and J4th = 0.7, and limits q7min = −0.3 m and q7max = 0.4 m. To control the DC motor of the conveyor, a typical PI controller is used, described by the equation U7 = kp7ε7 + kI7∫ε7dt, where U7 (see Figure 10) and ε7, respectively, are the input voltage and the control error of the conveyor electric drive; kp7 = 10000, kI7 = 300.
Figure 18 shows the laws of changing the real values of qi and q7 when using the conveyor to bypass the unwanted configurations of the SM. The first movement of the part by the conveyor along the coordinate q7 occurred immediately after the beginning of the movement of the WT along the trajectory, when q4 approached the restriction (see J1 (22)). The next movement along the coordinate q7 was performed in the interval 9–13 s, when the SM approached the third special position. This movement was completed when the part approached the end of the conveyor belt. At time moment 35–43 s, the WT approached the boundary of the working area and the condition q3 ≤ (1 − J4th)(q3min + θ) − θ, derived from (23), was fulfilled. The fourth movement along the coordinate q7, performed in the interval 49–58 s, is also associated with the approach of the SM to its third special position.

Figure 18.
Laws of change of real values of qi at q7 = var.
Thus, when moving the part by the conveyor, the exact and continuous movement of the WT was ensured in all sections of the trajectory, and all movement was completed exactly at the end of the trajectory at point 1 (see Figure 14). At the same time, deviations from the trajectory D2 (see Figure 17), although slightly increased in certain sections of the trajectory when the conveyor was moving, did not exceed 1.1 mm when the WT moved along the contour of the part. Videos of the aforementioned two experimental cases are available in accordance with the following links: https://youtu.be/WnVtIGuUlXQ (q7 = 0) and https://youtu.be/pNXDGmt2Sbc (q7 = var) (accessed date: 1 May 2023).
7. Conclusions
This paper presents the design and experimental research of a method that can be used for the automatic generation of reference signals for all actuators of a typical 6-DoF manipulator using a series kinematic scheme, which has an additional redundant DoF for the linear displacement of its base in the horizontal plane. The novelty of the proposed method comprises the fact that, by tracking the values of the special indicator functions and the simply synthesized system that does not require any significant computing power to implement, and by moving the base horizontally near a processed object and taking into account the various SM configurations, it is possible to prevent the SM from entering singular positions that are characterized by the ambiguity of the IKP solution, the reach of the WT to the boundaries of its working area, as well as the reach of some of its DoF to their limits. As a result, this is especially important when a sharp decrease in the dynamic accuracy of the WT contour control in certain sections of the working trajectories is eliminated, the occurrence of emergency situations and the breakdown of the WT and equipment is prevented, and the SM working area is expanded. The proposed method is especially effective in cases in which the planning of the trajectories of the SM WT is carried out and continues automatically after the start of the manipulation operations using vision systems. That is, the movement trajectories are unknown in advance (when the SM operates under conditions of uncertainty in the environment) and are formed taking into account the continuously changing working environment. Experimental studies of the proposed method were carried out and these confirmed its operability and effectiveness, and also confirmed the possibility of reducing the WT deviation from its trajectory from 5.5 mm to 1 mm, with the possibility of processing objects in a larger working area.
At the same time, we note that the application of the described method is limited by the following factors:
- (1)
- the necessary presence of at least one redundant DoF, which can be used to avoid the undesirable positions of the SM;
- (2)
- a sufficient speed of movement along this redundant DoF, so that, directly during the WT movement along the trajectory, due to redundancy, there is a physical opportunity to prevent the SM from approaching the indicated positions;
- (3)
- the type of spatial trajectory, which should not go beyond the boundaries of the SM working area, which is extended due to redundancy.
We also note the disadvantage arising from the use of the redundant DoF; this causes a certain decrease in the dynamic accuracy of the WT movement in the process of displacing the SM base near the object of work due to the presence of delays in the processing signals from the position sensor of this DoF. This can make it difficult to use it to perform certain technological operations, with increased requirements for accuracy.
Future directions for the development and improvement of the presented method are the control of the SM installed on mobile bases (for example, autonomous underwater vehicles) or its operation as part of robotic complexes with special positioning devices that provide movement along more than one redundant DoF.
Author Contributions
Conceptualization, V.F. and A.G.; methodology, I.G.; software, I.G.; validation, A.G. and I.G.; formal analysis, V.F.; investigation, A.G. and I.G.; resources, V.F.; data curation, I.G.; writing—original draft preparation, A.G. and I.G.; writing—review and editing, V.F.; visualization, I.G.; supervision, V.F.; project administration, A.G.; funding acquisition, V.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Russian Science Foundation (grant 22-19-00392).
Data Availability Statement
There is no data set associated with the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Filaretov, V.; Yukhimets, D.; Zuev, A.; Gubankov, A.; Mursalimov, E. An new approach for automatization of cutting of flexible items by using multilink manipulators with vision system. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014. [Google Scholar] [CrossRef]
- Filaretov, V.; Yukhimets, D.; Zuev, A.; Gubankov, A.; Mursalimov, E. Method of combination of three-dimensional models of details with their CAD-models at the presence of deformations. In Proceedings of the 12th IEEE International Conference on Automation Science and Engineering, Fort Worth, TX, USA, 21–25 August 2016. [Google Scholar] [CrossRef]
- Gubankov, A.; Gornostaev, I. Development of method of forming signals for the actuators of manipulators with redundant degrees of mobility. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing, St. Petersburg, Russia, 16–19 May 2017. [Google Scholar] [CrossRef]
- Yahya, S.; Moghavvemi, M.; Mohamed, H.A.F. Redundant manipulators kinematics inversion. Sci. Res. Essay 2011, 6, 5462–5470. [Google Scholar] [CrossRef]
- Filaretov, V.; Gubankov, A.; Gornostaev, I.; Konoplin, A. Synthesis method of reference control signals for manipulators installed on autonomous underwater vehicles. In Proceedings of the International Russian Automation Conference, Sochi, Russia, 8–14 September 2019. [Google Scholar] [CrossRef]
- Craig, J. Introduction to robotics: Mechanics and Control; Pearson Education International: New Jersey, NJ, USA, 2005. [Google Scholar]
- Gong, M.; Li, X.; Zhang, L. Analytical inverse kinematics and self-motion application for 7-DOF redundant manipulator. IEEE Access 2019, 7, 18662–18674. [Google Scholar] [CrossRef]
- Guo, J.; Xu, Y.; Huang, C.; Zhu, X.; Shao, C. An analytical solution to inverse kinematics of seven degree-of-freedom redundant manipulator. In Proceedings of the IEEE 9th Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 11–13 December 2020. [Google Scholar] [CrossRef]
- Kreft, W. Inverse kinematics determination and trajectory tracking algorithm development of a robot with 7 Joints. In Proceedings of the 16th International Conference on Control, Automation, Robotics and Vision, Shenzhen, China, 13–15 December 2020. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, H.; Jiang, C.; Du, H.; Gan, Y.; Chu, Z. Research on kinematics solution of 7-axis redundant robot based on self-motion. In Proceedings of the Chinese Automation Congress, Shanghai, China, 6–8 November 2020. [Google Scholar] [CrossRef]
- Crenganis, M.; Breaz, R.; Racz, G.; Bologa, O. The inverse kinematics solutions of a 7 DOF robotic arm using fuzzy logic. In Proceedings of the 7th Conference on Industrial Electronics and Applications, Singapore, 18–20 July 2012. [Google Scholar] [CrossRef]
- Seraji, H. Configuration control of redundant manipulators: Theory and implementation. Trans. Robot. Autom. 1989, 5, 472–490. [Google Scholar] [CrossRef]
- Lu, S.; Gu, Y.; Zhao, J.; Jiang, L. An iterative calculation method for solve the inverse kinematics of a 7-DOF robot with link offset. Lect. Notes Comp. Sci. 2017, 29, 729–739. [Google Scholar] [CrossRef]
- Wan, J.; Wu, H.T.; Ma, R.; Zhang, L. A study on avoiding joint limits for inverse kinematics of redundant manipulators using improved clamping weighted least-norm method. J. Mech. Sci. Technol. 2018, 32, 1367–1378. [Google Scholar] [CrossRef]
- Wang, X.; Cao, J.; Liu, X.; Chen, L.; Hu, H. An enhanced step-size Gaussian damped least squares method based on machine learning for inverse kinematics of redundant robots. IEEE Access 2020, 8, 68057–68067. [Google Scholar] [CrossRef]
- Kim, J.; Jie, W.; Kim, H.; Lee, M.C. Modified configuration control with potential field for inverse kinematic solution of redundant manipulator. IEEE/ASME Trans. Mechatron. 2021, 26, 1782–1790. [Google Scholar] [CrossRef]
- Marić, F.; Giamou, M.; Khoubyarian, S.; Petrović, I.; Kelly, J. Inverse kinematics for serial kinematic chains via sum of squares optimization. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May 2020–31 August 2020. [Google Scholar] [CrossRef]
- Liu, J.; Tong, Y.; Ju, Z.; Liu, Y. Novel method of obstacle avoidance planning for redundant sliding manipulators. IEEE Access 2020, 8, 78608–78621. [Google Scholar] [CrossRef]
- Redjimi, H.; Tar, J.K. Flexible solution of the inverse kinematic task for cooperating robots of different structures. In Proceedings of the IEEE 15th International Conference of System of Systems Engineering, Budapest, Hungary, 2–4 June 2020. [Google Scholar] [CrossRef]
- Jin, M.; Liu, Q.; Wang, B.; Liu, H. An efficient and accurate inverse kinematics for 7-DOF redundant manipulators based on a hybrid of analytical and numerical method. IEEE Access 2020, 8, 16316–16330. [Google Scholar] [CrossRef]
- Toshani, H.; Farrokhi, M. Real-time inverse kinematics of redundant manipulators using neural networks and quadratic programming: A Lyapunov-based approach. Robot. Auton. Syst. 2014, 62, 766–781. [Google Scholar] [CrossRef]
- Koker, R. A neuro-simulated annealing approach to the inverse kinematics solution of redundant robotic manipulators. Engin. Comp. 2013, 29, 507–515. [Google Scholar] [CrossRef]
- Koker, R. A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization. Inf. Sci. 2012, 222, 528–543. [Google Scholar] [CrossRef]
- Li, C.; Dong, H.; Li, X.; Zhang, W.; Liu, X.; Yao, L.; Sun, H. Inverse kinematics study for intelligent agriculture robot development via differential evolution algorithm. In Proceedings of the International Conference on Computer, Control and Robotics, Shanghai, China, 8–10 January 2021. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, W.; Qin, M.; Xie, B. Interval search genetic algorithm based on trajectory to solve inverse kinematics of redundant manipulators and its application. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020. [Google Scholar] [CrossRef]
- Filaretov, V.; Gubankov, A.; Gornostaev, I. Method of Formation of Reference Control Signals for Redundant Manipulators. J. Phys. Conf. Ser. 2021, 2096, 012110. [Google Scholar] [CrossRef]
- Hung, D.M.; Linh, D.T.; Ba, D.X. An Intelligent control method for redundant robotic manipulators with output constraints. In Proceedings of the International Conference on System Science and Engineering, Ho Chi Minh City, Vietnam, 26–28 August 2021; pp. 116–121. [Google Scholar] [CrossRef]
- Aristidou, A.; Lasenby, J. FABRIK: A fast, iterative solver for the inverse kinematics problem. Graph. Model. 2011, 73, 243–260. [Google Scholar] [CrossRef]
- Iakovlev, R.; Denisov, A.; Prakapovich, R. Iterative method for solving the inverse kinematics problem of multi-link robotic systems with rotational joints. In Proceedings of the 14th International Conference on Electromechanics and Robotics “Zavalishin’s Readings”, Kursk, Russia, 17–20 April 2019; pp. 237–251. [Google Scholar] [CrossRef]
- Ojstersek, R.; Acko, B.; Buchmeister, B. Simulation study of a flexible manufacturing system regarding sustainability. Int. J. Simul. Model. 2020, 19, 65–76. [Google Scholar] [CrossRef]
- Kliment, M.; Trebuna, P.; Pekarcikova, M.; Straka, M.; Trojan, J.; Duda, R. Production efficiency evaluation and products’ quality improvement using simulation. Int. J. Simul. Model. 2020, 19, 470–481. [Google Scholar] [CrossRef]
- Zuev, A.V.; Filaretov, V.F. Features of designing combined force/position manipulator control system. J. Comp. Syst. Sci. Int. 2009, 48, 146–154. [Google Scholar] [CrossRef]
- Filaretov, V.F.; Gubankov, A.S.; Gornostaev, I.V. The method of formation the reference speed of movement of the working tool of multilink manipulator. Mekhatronika Avtom. Upr. 2020, 21, 696–705. [Google Scholar] [CrossRef]
- Filaretov, V.F.; Gubankov, A.S.; Gornostaev, I.V. The Formation of motion laws for mechatronics objects along the paths with the desired speed. In Proceedings of the International Conference on Computer, Control, Informatics and Its Applications, Tangerang, Indonesia, 3–5 October 2016. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).