Estimation of Knee Assistive Moment in a Gait Cycle Using Knee Angle and Knee Angular Velocity through Machine Learning and Artificial Stiffness Control Strategy (MLASCS)
Abstract
1. Introduction
2. Knee Joint Data Collection of Walking Gait Cycle
2.1. Data Collection
2.2. Data Analyzing
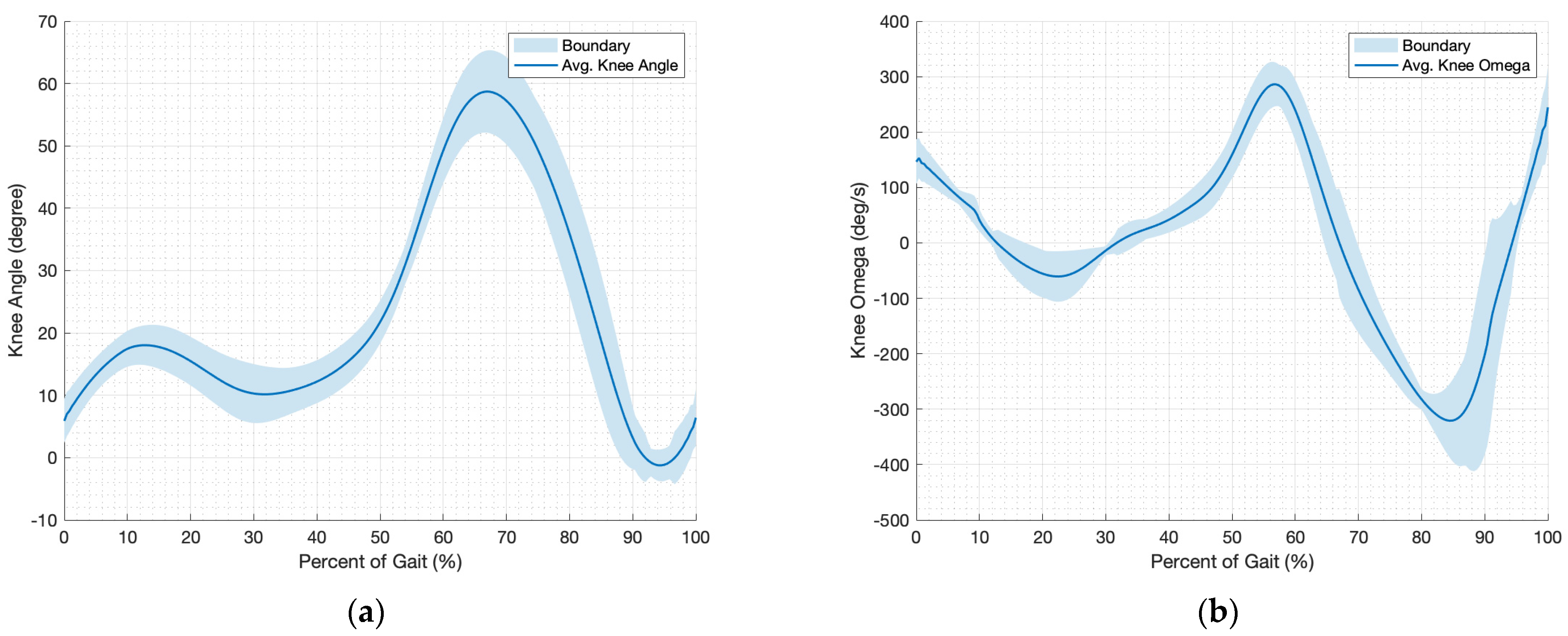
2.2.1. Kinematics of Knee
2.2.2. Kinetics of Knee
3. Machine Learning and Artificial Stiffness Control Strategy (MLASCS)
3.1. Classification and Training for Machine Learning Model
3.1.1. Classification
3.1.2. Training
3.1.3. Improving
3.2. Artificial Stiffness Control
3.2.1. Instantaneous Artificial Stiffness (IAS)
3.2.2. Artificial Stiffness Control Equations
4. Simulation and Validation
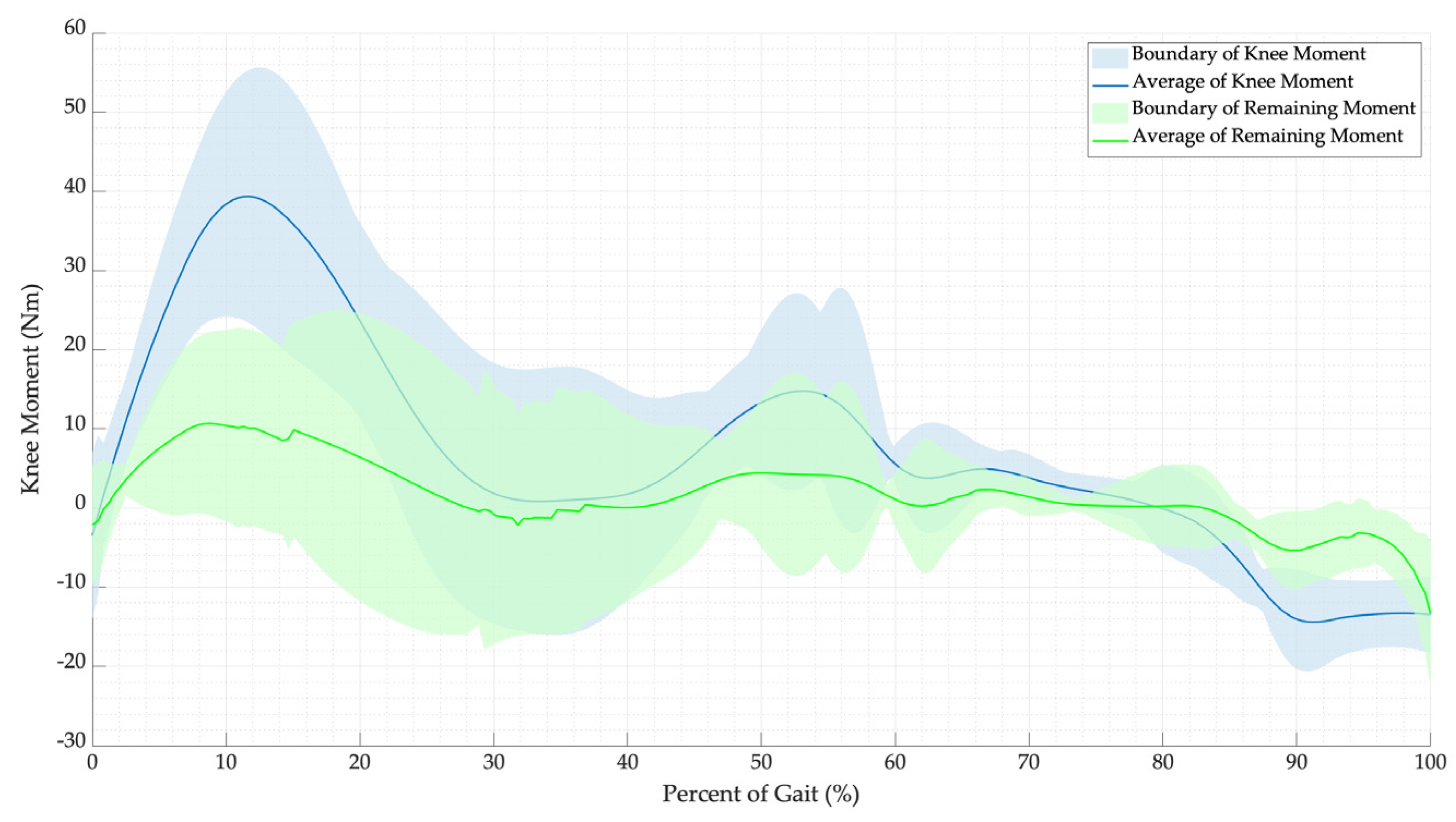
4.1. Supporting Moment Simulation
4.2. Effort over a Gait Cycle
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- O’Connor, J.J.; Shercliff, T.L.; Biden, E.; Goodfellow, J.W. The Geometry of the Knee in the Sagittal Plane. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1989, 203, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Forner-Cordero, A.; Pons, J.L.; Turowska, E.A.; Schiele, A. Kinematics and dynamics of wearable robots. In Wearable Robots: Biomechatronic Exoskeletons; Wiley: Hoboken, NJ, USA, 2008; pp. 47–85. [Google Scholar]
- Maeda, D.; Tominaga, K.; Oku, T.; Pham, H.T.T.; Saeki, S.; Uemura, M.; Hirai, H.; Miyazaki, F. Muscle synergy analysis of human adaptation to a variable-stiffness exoskeleton: Human walk with a knee exoskeleton with pneumatic artificial muscles. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012. [Google Scholar]
- Zhu, J.; Wang, Y.; Jiang, J.; Sun, B.; Cao, H. Unidirectional variable stiffness hydraulic actuator for load-carrying knee exoskeleton. Int. J. Adv. Robot. Syst. 2017, 14, 1729881416686955. [Google Scholar] [CrossRef]
- Anam, K.; Al-Jumaily, A.A. Active exoskeleton control systems: State of the art. Procedia Eng. 2012, 41, 988–994. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Li, H.; Jiao, Y. Assistive devices of human knee joint: A review. Robot. Auton. Syst. 2020, 125, 103394. [Google Scholar] [CrossRef]
- Ergin, M.A.; Patoglu, V. A self-adjusting knee exoskeleton for robot-assisted treatment of knee injuries. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4917–4922. [Google Scholar]
- Khamar, M.; Edrisi, M. Designing a backstepping sliding mode controller for an assistant human knee exoskeleton based on nonlinear disturbance observer. Mechatronics 2018, 54, 121–132. [Google Scholar] [CrossRef]
- Mazumder, O.; Kundu, A.S.; Chattaraj, R.; Lenka, P.K.; Gupta, K.; Bhaumik, S. Development of series elastic actuator based myoelectric knee exoskeleton for trajectory generation and load augmentation. In Proceedings of the Conference on Advances in Robotics ACM 2015, Goa, India, 2–4 July 2015; pp. 1–6. [Google Scholar]
- Dos Santos, W.M.; Caurin, G.A.; Siqueira, A.A. Design and control of an active knee orthosis driven by a rotary series elastic actuator. Control. Eng. Pract. 2017, 58, 307–318. [Google Scholar] [CrossRef]
- Han, Y.; Zhu, S.; Zhou, Z.; Shi, Y.; Hao, D. Research on a multimodal actuator-oriented power-assisted knee exoskeleton. Robotica 2017, 35, 1906–1922. [Google Scholar] [CrossRef]
- Han, Y.; Qi, B.; Yu, J. Development and experimental study of elastic actuator for a power-assisted knee exoskeleton. Robot 2014, 36, 668–675. [Google Scholar]
- Han, Y.; Wu, Z.; Xu, Y.; Wen, X.; Zhu, S.; Hao, D. The Knee Exoskeleton Mechanical Leg Based on Multi-modal Elastic Actuator. Jiqiren/Robot. 2017, 39, 498–504. [Google Scholar] [CrossRef]
- Yali, H.; Dabin, H.; Yu, S.; Songqing, Z.; Zhou, Z. The energy amplification characteristic research of a multimodal actuator. Int. J. Adv. Robot. Syst. 2016, 13, 93. [Google Scholar] [CrossRef]
- Félix, P.; Figueiredo, J.; Santos, C.P.; Moreno, J.C. Powered knee orthosis for human gait rehabilitation: First advances. In Proceedings of the 2017 IEEE 5th Portuguese Meeting on Bioengineering (ENBENG), Coimbra, Portugal, 16–18 February 2017. [Google Scholar]
- Figueiredo, J.; Félix, P.; Santos, C.P.; Moreno, J.C. Towards human-knee orthosis interaction based on adaptive impedance control through stiffness adjustment. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, London, UK, 17–20 July 2017. [Google Scholar]
- Nikitczuk, J.; Das, A.; Vyas, H.; Weinberg, B.; Mavroidis, C. Adaptive torque control of electro-rheological fluid brakes used in active knee rehabilitation devices. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Weinberg, B.; Nikitczuk, J.; Patel, S.; Patritti, B.; Mavroidis, C.; Bonato, P.; Canavan, P. Design, control and human testing of an active knee rehabilitation orthotic device. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007. [Google Scholar]
- Jiang, J.; Zhang, Z.; Wang, Z.; Qian, J. Study on real-time control of exoskeleton knee using electromyographic signal. In Proceedings of the Life System Modeling and Intelligent Computing: International Conference on Life System Modeling and Simulation, LSMS 2010, and International Conference on Intelligent Computing for Sustainable Energy and Environment, ICSEE 2010, Wuxi, China, 17–20 September 2010; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Shan, H.; Jiang, C.; Mao, Y.; Wang, X. Design and control of a wearable active knee orthosis for walking assistance. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC), Auckland, New Zealand, 22–24 April 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- el Zahraa Wehbi, F.; Huo, W.; Amirat, Y.; El Rafei, M.; Khalil, M.; Mohammed, S. Active impedance control of a knee-joint orthosis during swing phase. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Huang, T.-H.; Huang, H.P.; Cheng, C.-A.; Kuan, J.-Y.; Lee, P.-T.; Huang, S.-Y. Design of a new hybrid control and knee orthosis for human walking and rehabilitation. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Liu, L.; Lüken, M.; Leonhardt, S.; Misgeld, B.J.E. EMG-driven model-based knee torque estimation on a variable impedance actuator orthosis. In Proceedings of the 2017 IEEE International Conference on Cyborg and Bionic Systems (CBS), Beijing, China, 17–19 October 2017. [Google Scholar]
- Rogers, E.; Polygerinos, P.; Allen, S.; Panizzolo, F.A.; Walsh, C.J.; Holland, D.P. A quasi-passive knee exoskeleton to assist during descent. In Wearable Robotics: Challenges and Trends, Proceedings of the 2nd International Symposium on Wearable Robotics, WeRob2016, Segovia, Spain, 18–21 October 2016; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Shamaei, K.; Cenciarini, M.; Adams, A.A.; Gregorczyk, K.N.; Schiffman, J.M.; Dollar, A.M. Design and evaluation of a quasi-passive knee exoskeleton for investigation of motor adaptation in lower extremity joints. IEEE Trans. Biomed. Eng. 2014, 61, 1809–1821. [Google Scholar] [CrossRef] [PubMed]
- Shamaei, K.; Napolitano, P.C.; Dollar, A.M. A quasi-passive compliant stance control Knee-Ankle-Foot Orthosis. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Seattle, WA, USA, 24–26 June 2013. [Google Scholar]
- Yuan, B.; Li, B.; Chen, Y.; Tan, B.; Jiang, M.; Tang, S.; Wei, Y.; Wang, Z.; Ma, B.; Huang, J. Designing of a passive knee-assisting exoskeleton for weight-bearing. Proccedings of the 10th International Conference, Intelligent Robotics and Applications, ICIRA 2017, Wuhan, China, 16–18 August 2017; Part II 10. Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Saleem, A.; Khan, M.R.; Ahmmad, S.M. A novel knee exoskeleton for overweight person. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Sabah, Malaysia, 31 May–3 June 2015. [Google Scholar]
- Wu, S.-L.; Kazerooni, H. Design of a passive exoskeleton knee to assist toe clearance. In Proceedings of the Dynamic Systems and Control Conference 2017, Tysons, VA, USA, 11–13 October 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Chandrapal, M.; Chen, X.; Wang, W. Intelligent Assistive Knee Exoskeleton. In Mechatronics; Wiley: Hoboken, NJ, USA, 2013; pp. 195–237. [Google Scholar]
- Chaichaowarat, R.; Granados, D.F.P.; Kinugawa, J.; Kosuge, K. Passive knee exoskeleton using torsion spring for cycling assistance. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Chaichaowarat, R.; Kinugawa, J.; Kosuge, K. Unpowered Knee Exoskeleton Reduces Quadriceps Activity during Cycling. Engineering 2018, 4, 471–478. [Google Scholar] [CrossRef]
- Ranaweera, R.; Gopura, R.; Jayawardena, T.; Mann, G.K. Development of A Passively Powered Knee Exoskeleton for Squat Lifting. J. Robot. Netw. Artif. Life 2018, 5, 45–51. [Google Scholar] [CrossRef]
- Moyer, R.; Birmingham, T.; Dombroski, C.; Walsh, R.; Giffin, J.R. Combined versus individual effects of a valgus knee brace and lateral wedge foot orthotic during stair use in patients with knee osteoarthritis. Gait Posture 2017, 54, 160–166. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-H.; Shim, M.; Ahn, D.H.; Son, B.J.; Kim, S.-Y.; Kim, D.Y.; Baek, Y.S.; Cho, B.-K. Design of a knee exoskeleton using foot pressure and knee torque sensors. Int. J. Adv. Robot. Syst. 2015, 12, 112. [Google Scholar] [CrossRef]
- Celebi, B.; Yalcin, M.; Patoglu, V. AssistOn-Knee: A self-aligning knee exoskeleton. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Wang, J.; Li, X.; Huang, T.H.; Yu, S.; Li, Y.; Chen, T.; Carriero, A.; Oh-Park, M.; Su, H. Comfort-Centered Design of a Lightweight and Backdrivable Knee Exoskeleton. IEEE Robot. Autom. Lett. 2018, 3, 4265–4272. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, C.; Wang, Z.; Ma, Y.; Wang, C.; Wu, X. Design and control for a compliant knee exoskeleton. In Proceedings of the 2017 IEEE International Conference on Information and Automation, ICIA 2017, Macao, China, 18–20 July 2017. [Google Scholar]
- Shepherd, M.K.; Rouse, E.J. Design and Validation of a Torque-Controllable Knee Exoskeleton for Sit-to-Stand Assistance. IEEE/ASME Trans. Mechatron. 2017, 22, 1695–1704. [Google Scholar] [CrossRef]
- Karavas, N.; Ajoudani, A.; Tsagarakis, N.; Saglia, J.; Bicchi, A.; Caldwell, D. Tele-impedance based assistive control for a compliant knee exoskeleton. Robot. Auton. Syst. 2015, 73, 78–90. [Google Scholar] [CrossRef]
- Karavas, N.C.; Tsagarakis, N.G.; Caldwell, D.G. Design, modeling and control of a series elastic actuator for an assistive knee exoskeleton. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012. [Google Scholar]
- Karavas, N.C.; Tsagarakis, N.G.; Saglia, J.; Galdwell, D.G. A novel actuator with reconfigurable stiffness for a knee exoskeleton: Design and modeling. In Advances in Reconfigurable Mechanisms and Robots I; Springer: Berlin/Heidelberg, Germany, 2012; pp. 411–421. [Google Scholar]
- Lerner, Z.F.; Damiano, D.L.; Bulea, T.C. A lower-extremity exoskeleton improves knee extension in children with crouch gait from cerebral palsy. Sci. Transl. Med. 2017, 9, eaam9145. [Google Scholar] [CrossRef]
- Lerner, Z.F.; Damiano, D.L.; Park, H.S.; Gravunder, A.J.; Bulea, T.C. A Robotic Exoskeleton for Treatment of Crouch Gait in Children with Cerebral Palsy: Design and Initial Application. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 650–659. [Google Scholar] [CrossRef]
- Rifaï, H.; Mohammed, S.; Hassani, W.; Amirat, Y. Nested saturation based control of an actuated knee joint orthosis. Mechatronics 2013, 23, 1141–1149. [Google Scholar] [CrossRef]
- Rifai, H.; Mohammed, S.; Djouani, K.; Amirat, Y. Toward Lower Limbs Functional Rehabilitation Through a Knee-Joint Exoskeleton. IEEE Trans. Control. Syst. Technol. 2017, 25, 712–719. [Google Scholar] [CrossRef]
- Beyl, P.; Knaepen, K.; Duerinck, S.; Van Damme, M.; Vanderborght, B.; Meeusen, R.; Lefeber, D. Safe and compliant guidance by a powered knee exoskeleton for robot-assisted rehabilitation of gait. Adv. Robot. 2011, 25, 513–535. [Google Scholar] [CrossRef]
- Knaepen, K.; Beyl, P.; Duerinck, S.; Hagman, F.; Lefeber, D.; Meeusen, R. Human-robot interaction: Kinematics and muscle activity inside a powered compliant knee exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1128–1137. [Google Scholar] [CrossRef]
- Tung, W.; Kazerooni, H.; Hyun, D.J.; McKinley, S. On the design and control of exoskeleton knee. In Proceedings of the Dynamic Systems and Control Conference, Palo Alto, CA, USA, 21–23 October 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Elliott, G.A. Design and evaluation of a quasi-passive robotic knee brace: On the effects of parallel elasticity on human running. Appl. Adv. Technol. Transp. Eng. 2012, 75, 341–345. [Google Scholar]
- Elliott, G.; Marecki, A.; Herr, H. Design of a clutch-spring knee exoskeleton for running. J. Med. Devices Trans. ASME 2014, 8, 031002. [Google Scholar] [CrossRef]
- Elliott, G.; Sawicki, G.S.; Marecki, A.; Herr, H. The biomechanics and energetics of human running using an elastic knee exoskeleton. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Seattle, WA, USA, 24–26 June 2013. [Google Scholar]
- Pagani, C.H.F.; Potthast, W.; Brüggemann, G.-P. The effect of valgus bracing on the knee adduction moment during gait and running in male subjects with varus alignment. Clin. Biomech. 2010, 25, 70–76. [Google Scholar] [CrossRef]
- Pagani, C.H.F.; Willwacher, S.; Kleis, B.; Brüggemann, G.-P. Influence of a valgus knee brace on muscle activation and co-contraction in patients with medial knee osteoarthritis. J. Electromyogr. Kinesiol. 2013, 23, 490–500. [Google Scholar] [CrossRef]
- Dollar, A.M.; Herr, H. Design of a quasi-passive knee exoskeleton to assist running. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar]
- Tucker, M.R.; Moser, A.; Lambercy, O.; Sulzer, J.; Gassert, R. Design of a wearable perturbator for human knee impedance estimation during gait. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Karavas, N.; Ajoudani, A.; Tsagarakis, N.; Saglia, J.; Bicchi, A.; Caldwell, D. Tele-impedance based stiffness and motion augmentation for a knee exoskeleton device. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Saccares, L.; Brygo, A.; Sarakoglou, I.; Tsagarakis, N.G. A novel human effort estimation method for knee assistive exoskeletons. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, London, UK, 17–20 July 2017. [Google Scholar]
- Saccares, L.; Sarakoglou, I.; Tsagarakis, N.G. iT-Knee: An exoskeleton with ideal torque transmission interface for ergonomic power augmentation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016. [Google Scholar]
- Zhou, Z.; Liao, Y.; Wang, C.; Wang, Q. Preliminary evaluation of gait assistance during treadmill walking with a light-weight bionic knee exoskeleton. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016. [Google Scholar]
- Kamali, K.; Akbari, A.A.; Akbarzadeh, A. Implementation of a trajectory predictor and an exponential sliding mode controller on a knee exoskeleton robot. Modares Mech. Eng. 2016, 16, 79–90. [Google Scholar]
- Kardan, I.; Akbarzadeh, A. Robust output feedback assistive control of a compliantly actuated knee exoskeleton. Robot. Auton. Syst. 2017, 98, 15–29. [Google Scholar] [CrossRef]
- Kardan, I.; Akbarzadeh, A. Assistive control of a compliantly actuated single axis stage. In Proceedings of the 4th RSI International Conference on Robotics and Mechatronics, ICRoM 2016, Tehran, Iran, 26–28 October 2016. [Google Scholar]
- Witte, K.A.; Fatschel, A.M.; Collins, S.H. Design of a lightweight, tethered, torque-controlled knee exoskeleton. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, London, UK, 17–20 July 2017. [Google Scholar]
- Sridar, S.; Nguyen, P.H.; Zhu, M.; Lam, Q.P.; Polygerinos, P. Development of a soft-inflatable exosuit for knee rehabilitation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Liao, Y.; Zhou, Z.; Wang, Q. BioKEX: A bionic knee exoskeleton with proxy-based sliding mode control. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (Icit), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Li, B.; Yuan, B.; Tang, S.; Mao, Y.; Zhang, D.; Huang, C.; Tan, B. Biomechanical design analysis and experiments evaluation of a passive knee-assisting exoskeleton for weight-climbing. Ind. Robot. Int. J. 2018, 45, 436–445. [Google Scholar] [CrossRef]
- Jun, S.; Zhou, X.; Ramsey, D.K.; Krovi, V.N. Compliant knee exoskeleton design: Parallel coupled compliant plate (PCCP) mechanism and pennate elastic band (PEB) spring. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Chen, B.; Zi, B.; Wang, Z.; Qin, L.; Liao, W.-H. Knee exoskeletons for gait rehabilitation and human performance augmentation: A state-of-the-art. Mech. Mach. Theory 2019, 134, 499–511. [Google Scholar] [CrossRef]
- Malcolm, P.; Galle, S.; Derave, W.; De Clercq, D. Bi-articular knee-ankle-foot exoskeleton produces higher metabolic cost reduction than weight-matched mono-articular exoskeleton. Front. Neurosci. 2018, 12, 69. [Google Scholar] [CrossRef] [PubMed]
- Kong, K.; Bae, J.; Tomizuka, M. A compact rotary series elastic actuator for human assistive systems. IEEE/ASME Trans. Mechatron. 2011, 17, 288–297. [Google Scholar] [CrossRef]
- Pratt, J.E.; Krupp, B.T.; Morse, C.J.; Collins, S.H. The RoboKnee: An exoskeleton for enhancing strength and endurance during walking. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Ma, H.; Lai, W.-Y.; Liao, W.-H.; Fong, D.T.-P.; Chan, K.-M. Design and control of a powered knee orthosis for gait assistance. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Ma, H.; Chen, B.; Qin, L.; Liao, W.-H. Design and testing of a regenerative magnetorheological actuator for assistive knee braces. Smart Mater. Struct. 2017, 26, 035013. [Google Scholar] [CrossRef]
- Masouros, S.D.; Bull, A.M.J.; Amis, A.A. (i) Biomechanics of the knee joint. Orthop. Trauma 2010, 24, 84–91. [Google Scholar] [CrossRef]
- Dixit, S.; Difiori, J.P.; Burton, M.; Mines, B. Management of patellofemoral pain syndrome. Am. Fam. Physician 2007, 75, 194–202. [Google Scholar] [PubMed]
- Bertomeu, J.M.B.; Lois, J.M.B.; Guillem, R.B.; Del Pozo, Á.P.; Lacuesta, J.; Mollà, C.G.; Luna, P.V.; Pastor, J.P. Development of a hinge compatible with the kinematics of the knee joint. Prosthet. Orthot. Int. 2007, 31, 371–383. [Google Scholar] [CrossRef]
- Rose, J.; Gamble, J.G. Human Walking; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2006. [Google Scholar]
- Grimmer, M.; Schmidt, K.; Duarte, J.E.; Neuner, L.; Koginov, G.; Riener, R. Stance and swing detection based on the angular velocity of lower limb segments during walking. Front. Neurorobotics 2019, 13, 57. [Google Scholar] [CrossRef] [PubMed]
- Javanfar, A.; Bamdad, M. A developed multibody knee model for unloading knee with cartilage penetration depth control. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 1528–1540. [Google Scholar] [CrossRef]
- Mokri, C.; Bamdad, M.; Abolghasemi, V. Muscle force estimation from lower limb EMG signals using novel optimised machine learning techniques. Med. Biol. Eng. Comput. 2022, 60, 683–699. [Google Scholar] [CrossRef] [PubMed]
- Rattanasak, A.; Uthansakul, P.; Uthansakul, M.; Jumphoo, T.; Phapatanaburi, K.; Sindhupakorn, B.; Rooppakhun, S. Real-Time Gait Phase Detection Using Wearable Sensors for Transtibial Prosthesis Based on a kNN Algorithm. Sensors 2022, 22, 4242. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Chen, C.; Hu, J.; Sayeed, Z.; Qi, J.; Darwiche, H.F.; Little, B.E.; Lou, S.; Darwish, M.; Foote, C. Computer Vision and Machine Learning-Based Gait Pattern Recognition for Flat Fall Prediction. Sensors 2022, 22, 7960. [Google Scholar] [CrossRef] [PubMed]
- Robertson, D.; Caldwell, G.; Hamill, J.; Kamen, G.; Whittlesey, S. Research Methods in Biomechanics, 2nd ed.; Human Kinetics: Boston, MA, USA, 2013. [Google Scholar]
- Quarteroni, A.; Saleri, F.; Gervasio, P. Scientific Computing with MATLAB and Octave; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3. [Google Scholar]
- Fornberg, B. Generation of finite difference formulas on arbitrarily spaced grids. Math. Comput. 1988, 51, 699–706. [Google Scholar] [CrossRef]











| Setting | Detail |
|---|---|
| Preset | Fine KNN |
| Number of neighbors | 3 |
| Distance metric | Chebyshev |
| Distance weight | Equal |
| Standardize data | True |
| Trials | Data | Flexion Effort (FE) | Extension Effort (EE) | Total Effort (TE) | Reduction |
|---|---|---|---|---|---|
| Trial 1 | Effort without assist | 33.0% | 67.0% | 100% | 62.9% |
| Remaining effort | 25.2% | 11.9% | 37.1% | ||
| Trial 2 | Effort without assist | 30.9% | 69.1% | 100% | 63.4% |
| Remaining effort | 24.4% | 12.2% | 36.6% | ||
| Trial 3 | Effort without assist | 34.2% | 65.8% | 100% | 57.2% |
| Remaining effort | 21.8% | 21.0% | 42.8% | ||
| Trial 4 | Effort without assist | 35.1% | 64.9% | 100% | 59.4% |
| Remaining effort | 31.7% | 8.9% | 40.6% | ||
| Trial 5 | Effort without assist | 17.1% | 82.9% | 100% | 62.6% |
| Remaining effort | 11.0% | 26.4% | 37.4% | ||
| Trial 6 | Effort without assist | 16.8% | 83.2% | 100% | 36% |
| Remaining effort | 9.6% | 54.4% | 64.0% | ||
| Trial 7 | Effort without assist | 12.8% | 87.2% | 100% | 60% |
| Remaining effort | 15.3% | 24.7% | 40.0% | ||
| Trial 8 | Effort without assist | 14.1% | 85.9% | 100% | 45.8% |
| Remaining effort | 3.6% | 50.6% | 54.2% | ||
| Trial 9 | Effort without assist | 11.3% | 88.7% | 100% | 61.3% |
| Remaining effort | 1.8% | 36.9% | 38.7% | ||
| Average | Effort without assist | 17.7% | 82.3% | 100% | 28.3% |
| Remaining effort | 11.3% | 60.3% | 71.7% |
| Category | Variable Name | Axis | Variable Symbol | Unit |
|---|---|---|---|---|
| Force | Ground reaction force | x | GRFx | N |
| z | GRFz | N | ||
| Ankle reaction force | x | Fx, ankle | N | |
| z | Fz, ankle | N | ||
| Foot weight | −z | Wfoot | N | |
| Weight of the lower leg | −z | Wleg | N | |
| Moment | Ankle moment | y | Mankle | Nm |
| Knee moment | −y | Mknee | Nm | |
| Knee moment per body mass | −y | MPBknee | Nm/kg | |
| Average knee moment per body mass | −y | AMPBknee | Nm/kg | |
| Extension moment | - | EM | Nm | |
| Flexion moment | - | FM | Nm | |
| Point | Instantaneous center of rotation of the ankle | - | ICRankle | - |
| Instantaneous center of rotation of the knee | - | ICRknee | - | |
| Distance | Perpendicular distance between the ICRankle and the direction of the GRF | x | Rx, GRF | m |
| z | Rz, GRF | m | ||
| Perpendicular distance between the ICRankle and the direction of the Wfoot | x | Rcm, ankle | m | |
| Perpendicular distance between the ICRknee and the direction of the Wleg | x | Rcm, knee | m | |
| Perpendicular distance between the ICRknee and the direction of the ankle reaction force | x | Rx, leg | m | |
| z | Rz, leg | m | ||
| Mass | Body mass | - | mbody | kg |
| Foot mass | - | mfoot | kg | |
| Acceleration | Foot acceleration | x | ax, foot | m/s2 |
| z | az, foot | m/s2 | ||
| Foot angular acceleration | y | rad/s2 | ||
| Knee angular acceleration | y | rad/s2 | ||
| Moment of inertia | Moment of inertia around ICRankle | - | Iankle | kg-m2 |
| Moment of inertia around ICRknee | - | Iknee | kg-m2 | |
| Stiffness | Instantaneous artificial stiffness | - | IAS | Nm/deg |
| Instantaneous artificial stiffness per body mass | - | IASPB | Nm/kg-deg | |
| Instantaneous artificial stiffness per body mass equation in the initial place state | - | IASPBIP | Nm/kg-deg | |
| Instantaneous artificial stiffness per body mass equation in the final place state | - | IASPBFP | Nm/kg-deg | |
| Instantaneous artificial stiffness per body mass equation in the initial lift state | - | IASPBIL | Nm/kg-deg | |
| Instantaneous artificial stiffness per body mass equation in the final lift state | - | IASPBFL | Nm/kg-deg | |
| Effort over a gait cycle | Total effort over a gait cycle | - | TE | Nm-deg |
| Extension effort over a gait cycle | - | EE | Nm-deg | |
| Flexion effort over a gait cycle | - | FE | Nm-deg | |
| Others | Percent of gait | - | PoG | - |
| Centered finite difference | - | CFD | - | |
| Percentage of support | - | n | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pornpipatsakul, K.; Ajavakom, N. Estimation of Knee Assistive Moment in a Gait Cycle Using Knee Angle and Knee Angular Velocity through Machine Learning and Artificial Stiffness Control Strategy (MLASCS). Robotics 2023, 12, 44. https://doi.org/10.3390/robotics12020044
Pornpipatsakul K, Ajavakom N. Estimation of Knee Assistive Moment in a Gait Cycle Using Knee Angle and Knee Angular Velocity through Machine Learning and Artificial Stiffness Control Strategy (MLASCS). Robotics. 2023; 12(2):44. https://doi.org/10.3390/robotics12020044
Chicago/Turabian StylePornpipatsakul, Khemwutta, and Nopdanai Ajavakom. 2023. "Estimation of Knee Assistive Moment in a Gait Cycle Using Knee Angle and Knee Angular Velocity through Machine Learning and Artificial Stiffness Control Strategy (MLASCS)" Robotics 12, no. 2: 44. https://doi.org/10.3390/robotics12020044
APA StylePornpipatsakul, K., & Ajavakom, N. (2023). Estimation of Knee Assistive Moment in a Gait Cycle Using Knee Angle and Knee Angular Velocity through Machine Learning and Artificial Stiffness Control Strategy (MLASCS). Robotics, 12(2), 44. https://doi.org/10.3390/robotics12020044






