Inverse Kinematics of a Class of 6R Collaborative Robots with Non-Spherical Wrist
Abstract
1. Introduction
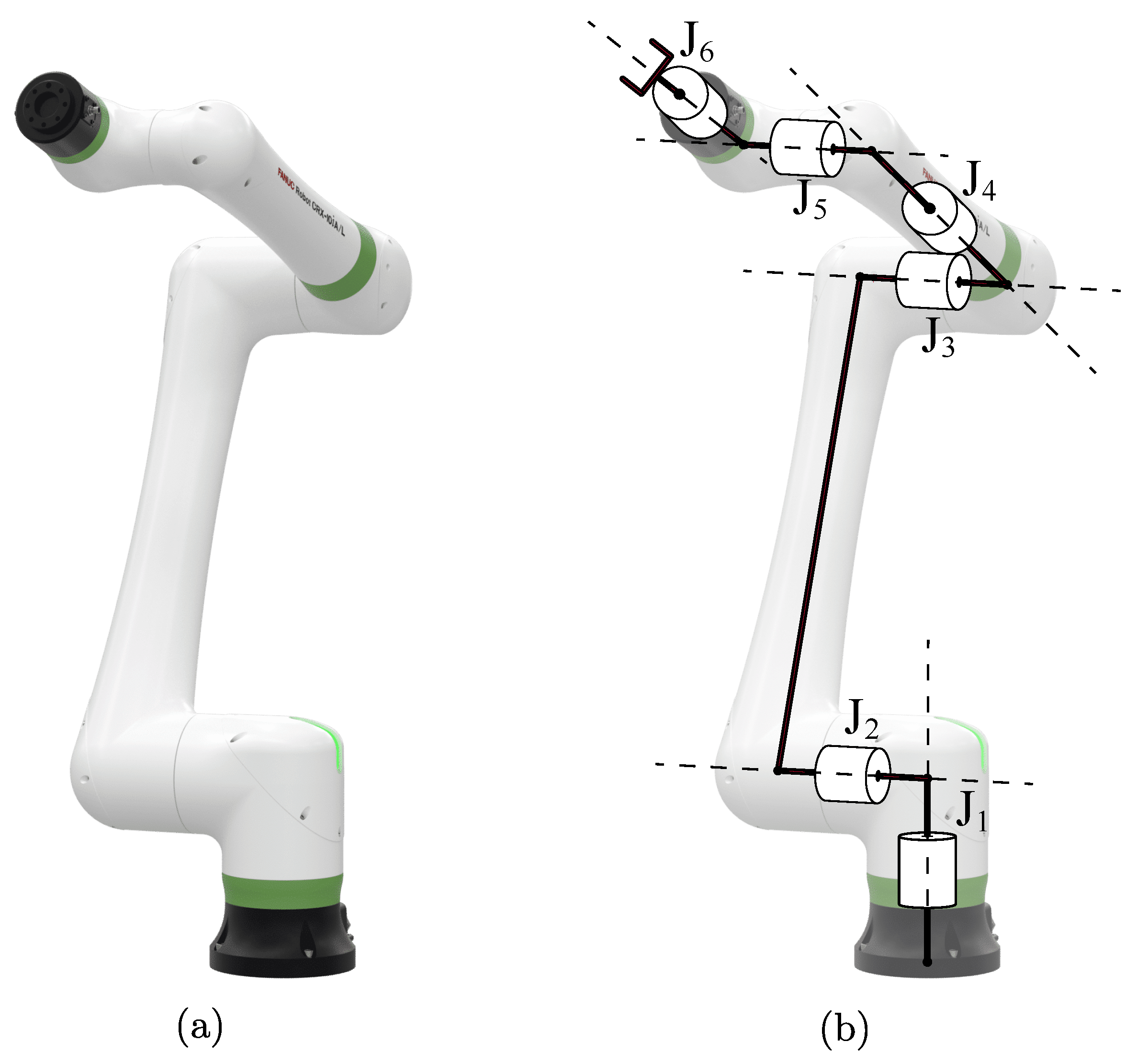
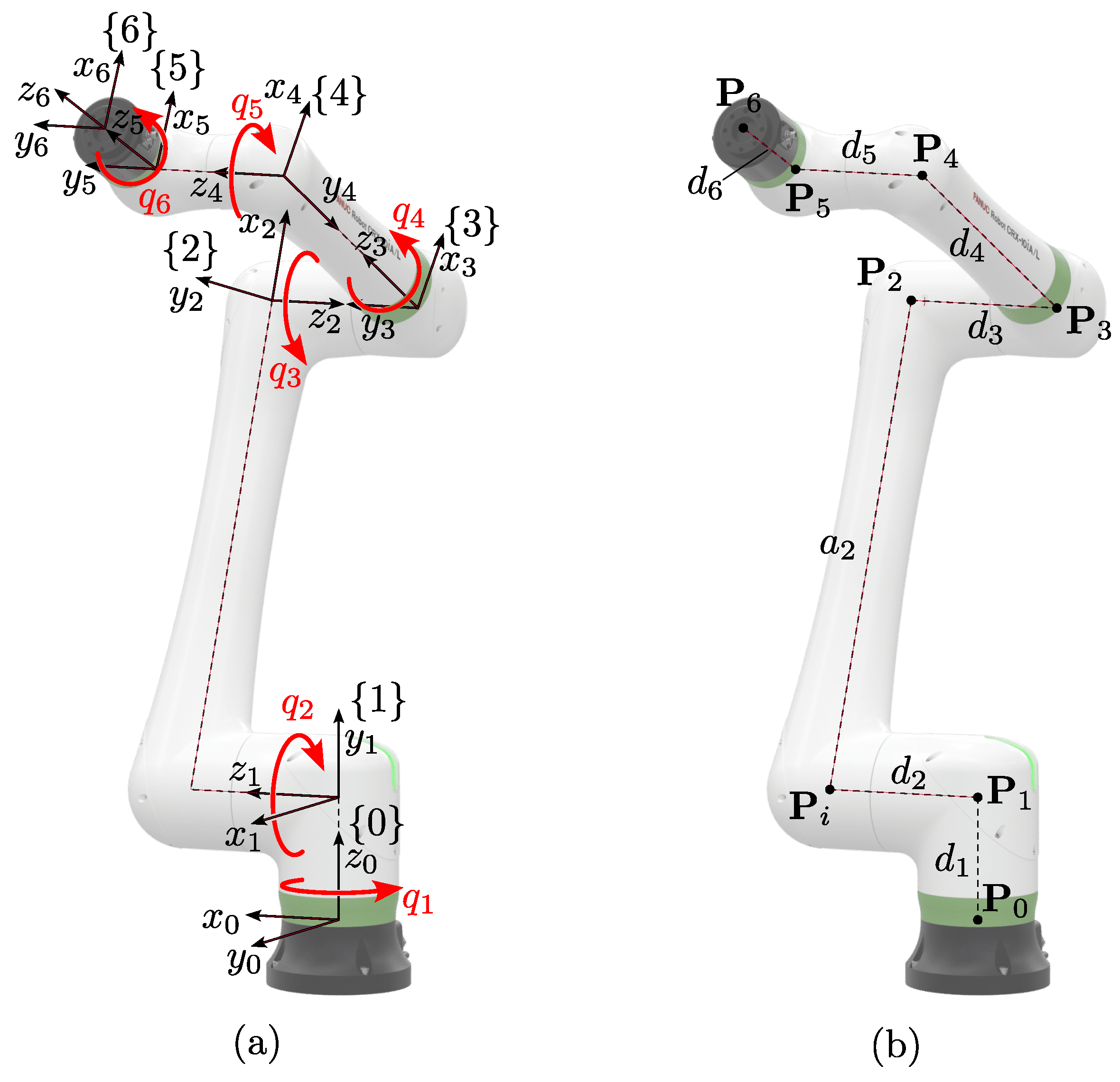
2. Robot Description
3. Inverse Kinematics Problem
3.1. System of Equations
3.2. System Solution
4. Implementation and Verification
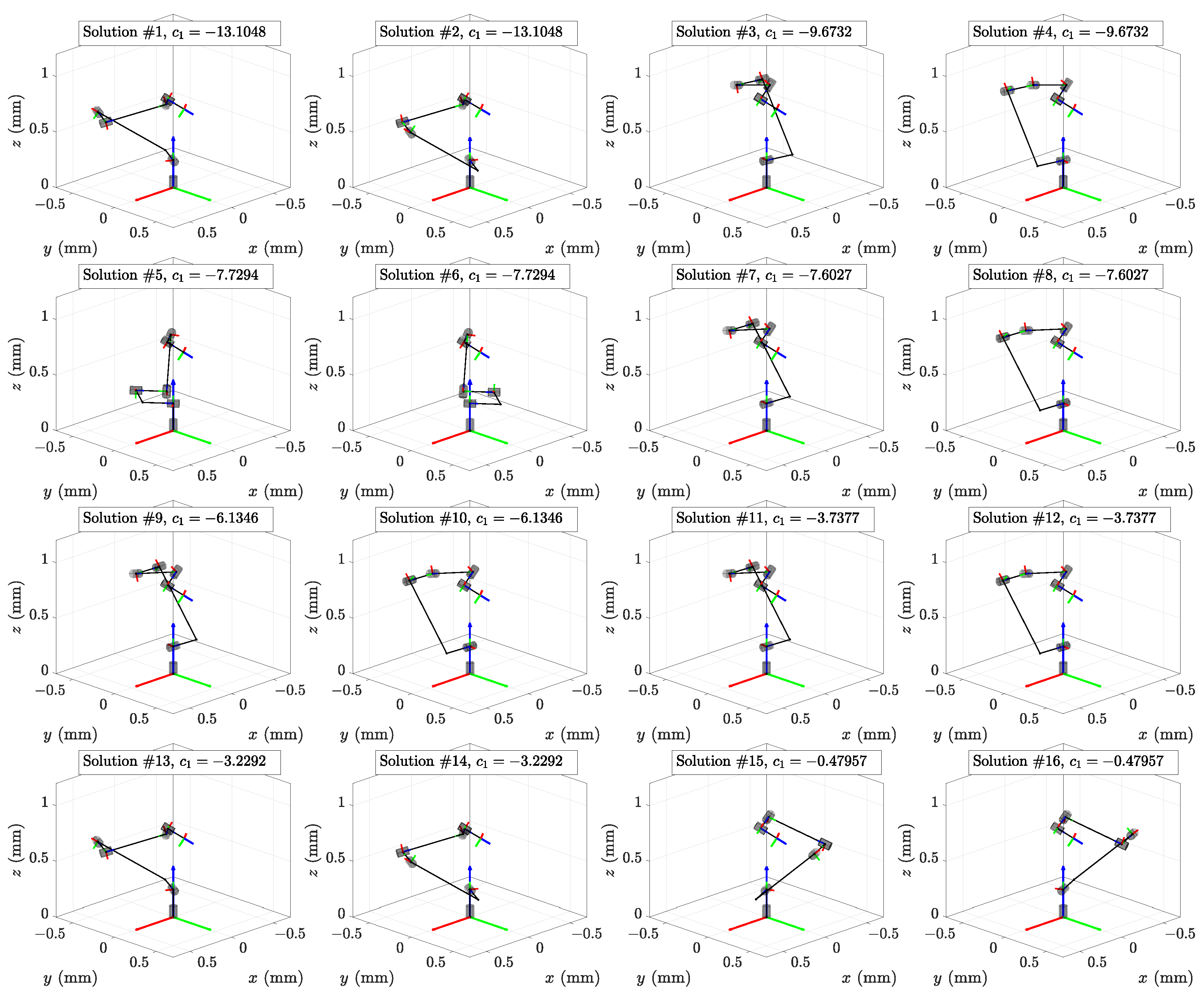
Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Coefficients of Polynomials Φh
Appendix B. Coefficients of Polynomials Xh
Appendix C. Coefficients of Polynomials Ωh
Appendix D. Univariate Polynomial
Appendix E. Joint Variables
References
- Matheson, E.; Minto, R.; Zampieri, E.G.; Faccio, M.; Rosati, G. Human–robot collaboration in manufacturing applications: A review. Robotics 2019, 8, 100. [Google Scholar] [CrossRef]
- Chiriatti, G.; Carbonari, L.; Costa, D.; Palmieri, G. Implementation of a Robot Assisted Framework for Rehabilitation Practices. In Proceedings of the Advances in Italian Mechanism Science: Proceedings of the 4th International Conference of IFToMM Italy, Naples, Italy, 7–9 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 541–548. [Google Scholar]
- Kyrarini, M.; Lygerakis, F.; Rajavenkatanarayanan, A.; Sevastopoulos, C.; Nambiappan, H.R.; Chaitanya, K.K.; Babu, A.R.; Mathew, J.; Makedon, F. A survey of robots in healthcare. Technologies 2021, 9, 8. [Google Scholar] [CrossRef]
- Holland, J.; Kingston, L.; McCarthy, C.; Armstrong, E.; O’Dwyer, P.; Merz, F.; McConnell, M. Service robots in the healthcare sector. Robotics 2021, 10, 47. [Google Scholar] [CrossRef]
- Galin, R.; Meshcheryakov, R. Automation and robotics in the context of Industry 4.0: The shift to collaborative robots. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Prague, Czech Republic, 18–22 June 2018; IOP Publishing: Bristol, UK, 2019; Volume 537, p. 032073. [Google Scholar]
- Maddikunta, P.K.R.; Pham, Q.V.; Prabadevi, B.; Deepa, N.; Dev, K.; Gadekallu, T.R.; Ruby, R.; Liyanage, M. Industry 5.0: A survey on enabling technologies and potential applications. J. Ind. Inf. Integr. 2021, 26, 100257. [Google Scholar] [CrossRef]
- Chiriatti, G.; Palmieri, G.; Scoccia, C.; Palpacelli, M.C.; Callegari, M. Adaptive Obstacle Avoidance for a Class of Collaborative Robots. Machines 2021, 9, 113. [Google Scholar] [CrossRef]
- Trinh, C.; Zlatanov, D.; Zoppi, M.; Molfino, R. A geometrical approach to the inverse kinematics of 6r serial robots with offset wrists. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 57144, p. V05CT08A016. [Google Scholar]
- Zohour, H.M.; Belzile, B.; St-Onge, D. Kinova Gen3-Lite manipulator inverse kinematics: Optimal polynomial solution. arXiv 2021, arXiv:2102.01217. [Google Scholar]
- Villalobos, J.; Sanchez, I.Y.; Martell, F. Singularity Analysis and Complete Methods to Compute the Inverse Kinematics for a 6-DOF UR/TM-Type Robot. Robotics 2022, 11, 137. [Google Scholar] [CrossRef]
- Raghavan, M.; Roth, B. A general solution for the inverse kinematics of all series chains. In Proceedings of the 8th CISM-IFTOMM Symposium on Robots and Manipulators, Krakow, Poland, July 1990. [Google Scholar]
- Raghavan, M.; Roth, B. Inverse Kinematics of the General 6R Manipulator and Related Linkages. J. Mech. Des. 1993, 115, 502–508. [Google Scholar] [CrossRef]
- Wang, Y.; Hang, L.b.; Yang, T.l. Inverse kinematics analysis of general 6r serial robot mechanism based on Gröbner base. Front. Mech. Eng. 2006, 1, 115–124. [Google Scholar] [CrossRef]
- Fu, Z.; Yang, W.; Yang, Z. Solution of inverse kinematics for 6R robot manipulators with offset wrist based on geometric algebra. J. Mech. Robot. 2013, 5, 031010. [Google Scholar] [CrossRef] [PubMed]
- Ghazvini, M. Reducing the inverse kinematics of manipulators to the solution of a generalized eigenproblem. Comput. Kinemat. 1993, 28, 15–26. [Google Scholar]
- Xiao, F.; Li, G.; Jiang, D.; Xie, Y.; Yun, J.; Liu, Y.; Huang, L.; Fang, Z. An effective and unified method to derive the inverse kinematics formulas of general six-DOF manipulator with simple geometry. Mech. Mach. Theory 2021, 159, 104265. [Google Scholar] [CrossRef]
- Li, G.; Xiao, F.; Zhang, X.; Tao, B.; Jiang, G. An inverse kinematics method for robots after geometric parameters compensation. Mech. Mach. Theory 2022, 174, 104903. [Google Scholar] [CrossRef]
- Sugihara, T. Solvability-unconcerned inverse kinematics by the Levenberg–Marquardt method. IEEE Trans. Robot. 2011, 27, 984–991. [Google Scholar] [CrossRef]
- Cho, G.R.; Lee, M.J.; Kim, M.G.; Li, J.H. Inverse kinematics for autonomous underwater manipulations using weighted damped least squares. In Proceedings of the 2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Republic of Korea, 28 June–1 July 2017; IEEE: New York, NY, USA, 2017; pp. 765–770. [Google Scholar]
- Zhao, J.; Xu, T.; Fang, Q.; Xie, Y.; Zhu, Y. A synthetic inverse kinematic algorithm for 7-DOF redundant manipulator. In Proceedings of the 2018 IEEE International Conference on Real-time Computing and Robotics (RCAR), Kandima, Maldives, 1–5 August 2018; IEEE: New York, NY, USA, 2018; pp. 112–117. [Google Scholar]
- Callegari, M.; Carbonari, L.; Costa, D.; Palmieri, G.; Palpacelli, M.C.; Papetti, A.; Scoccia, C. Tools and Methods for Human Robot Collaboration: Case Studies at i-LABS. Machines 2022, 10, 997. [Google Scholar] [CrossRef]
- Simas, H.; Di Gregorio, R. Collision Avoidance for Redundant 7-DOF Robots Using a Critically Damped Dynamic Approach. Robotics 2022, 11, 93. [Google Scholar] [CrossRef]
- Malik, A.; Lischuk, Y.; Henderson, T.; Prazenica, R. A Deep Reinforcement-Learning Approach for Inverse Kinematics Solution of a High Degree of Freedom Robotic Manipulator. Robotics 2022, 11, 44. [Google Scholar] [CrossRef]
- Pieper, D.; Roth, B. The Kinematics of Manipulators Under Computer Control. In Proceedings of the 2nd International Congress on Theory of Machines and Mechanisms, Zakopane, Poland, 23–27 September 1969; Volume 2, pp. 159–169. [Google Scholar]
| i | (rad) | (mm) | (mm) | (rad) | Motion Range (rad) |
|---|---|---|---|---|---|
| 1 | 0 | 250.3 | |||
| 2 | 710.0 | 260.4 | |||
| 3 | 0 | 260.4 | |||
| 4 | 0 | 540.0 | |||
| 5 | 0 | 150.0 | |||
| 6 | 0 | 0 | 160.0 |
| −13.105 | −0.262 | −22.831 | −3.5 | 46.7 | 766.9 |
| −9.673 | 1.672 | −4.490 | 10.5 | 49.4 | 938.7 |
| −7.730 | −18.981 | 8.395 | 176.8 | 147.5 | 949.1 |
| −7.603 | 0.844 | −3.933 | 2.6 | 37.9 | 926.8 |
| −6.135 | 0.372 | −3.417 | −1.2 | 26.1 | 917.3 |
| −3.738 | −0.223 | −2.270 | 2.7 | −8.0 | 901.1 |
| −3.230 | −0.296 | −4.901 | −5.4 | 15.5 | 781.5 |
| −0.667 + 0.50i | – | – | – | – | – |
| −0.667 − 0.50i | – | – | – | – | – |
| −0.480 | 1.417 | −0.041 | −7.3 | 16.0 | 900.0 |
| −0.233 + 0.01i | – | – | – | – | – |
| −0.233 − 0.01i | – | – | – | – | – |
| −0.088 + 0.04i | – | – | – | – | – |
| −0.088 − 0.04i | – | – | – | – | – |
| −0.041 + 0.02i | – | – | – | – | – |
| −0.041 − 0.02i | – | – | – | – | – |
| # | |||||||
|---|---|---|---|---|---|---|---|
| 1 | −13.105 | −30.30 | 33.99 | 136.01 | 143.27 | −48.79 | 77.61 |
| 2 | 149.69 | 146.00 | 43.98 | −36.72 | −48.79 | 77.61 | |
| 3 | −9.673 | −101.99 | 48.99 | 155.99 | −138.00 | −59.99 | −9.99 |
| 4 | 78.00 | 131.00 | 24.00 | 42.00 | −60.00 | −10.00 | |
| 5 | −7.730 | 39.90 | 28.21 | 161.19 | −75.16 | 116.22 | −90.34 |
| 6 | −140.09 | 151.78 | 18.80 | 104.83 | 116.22 | −90.34 | |
| 7 | −7.603 | −93.98 | 47.62 | 154.56 | −144.11 | −55.12 | −2.97 |
| 8 | 86.01 | 132.37 | 25.43 | 35.88 | −55.12 | −2.97 | |
| 9 | −6.135 | −93.98 | 47.62 | 154.56 | −144.11 | −55.12 | −2.97 |
| 10 | 86.01 | 132.37 | 25.43 | 35.88 | −55.12 | −2.97 | |
| 11 | −3.738 | −93.98 | 47.62 | 154.56 | −144.11 | −55.12 | −2.97 |
| 12 | 86.01 | 132.37 | 25.43 | 35.88 | −55.12 | −2.97 | |
| 13 | −3.230 | −29.41 | 33.90 | 135.67 | 142.25 | −49.24 | 78.79 |
| 14 | 150.58 | 146.09 | 44.32 | −37.74 | −49.24 | 78.79 | |
| 15 | −0.480 | 114.69 | 42.07 | 151.46 | −23.88 | 170.53 | 10.81 |
| 16 | −65.30 | 137.92 | 28.53 | 156.11 | 170.53 | 10.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbonari, L.; Palpacelli, M.-C.; Callegari, M. Inverse Kinematics of a Class of 6R Collaborative Robots with Non-Spherical Wrist. Robotics 2023, 12, 36. https://doi.org/10.3390/robotics12020036
Carbonari L, Palpacelli M-C, Callegari M. Inverse Kinematics of a Class of 6R Collaborative Robots with Non-Spherical Wrist. Robotics. 2023; 12(2):36. https://doi.org/10.3390/robotics12020036
Chicago/Turabian StyleCarbonari, Luca, Matteo-Claudio Palpacelli, and Massimo Callegari. 2023. "Inverse Kinematics of a Class of 6R Collaborative Robots with Non-Spherical Wrist" Robotics 12, no. 2: 36. https://doi.org/10.3390/robotics12020036
APA StyleCarbonari, L., Palpacelli, M.-C., & Callegari, M. (2023). Inverse Kinematics of a Class of 6R Collaborative Robots with Non-Spherical Wrist. Robotics, 12(2), 36. https://doi.org/10.3390/robotics12020036







