Abstract
How good is a robot? Three challenges arise from this question: first, defining performance from the robot’s observable behavior; second, quantifying performance with an index that is obtainable through direct measurement or computation, and representative of the measured quantity; third, ensuring that this procedure is repeatable and general, to enable performance comparison, benchmarking, and an increase of safety and efficiency standards. However, the landscape of performance metrics for industrial manipulators is fragmented, and limited effort is being made toward a unified framework. This survey aimed at collecting, classifying, and analyzing the key works on the topic, with a focus on mechanical performance metrics for industrial robots. Two diverging trends are outlined, with commercial standards adopting a limited set of metrics and academic research encouraging the development of new performance indices. The shortcomings of both approaches are highlighted, providing a perspective on how future research could proceed.
1. Introduction
Which robot should I buy? When acquiring industrial robots, we compare their specifications, such as accuracy, speed, weight, workspace size, installation size, or price, to select the one that is most suitable to our needs.
How large should my robot be? When designing a robot, we select its shape, topology, and dimensions to optimize its behavior for the desired task(s).
Which path should my robot follow? When moving a robot, we choose the fastest or most convenient path.
These questions have different answers, but they all require an evaluation or measurement of robot performance. In the first case, we can select an optimal solution by directly comparing the numerical specifications of the robots. In the other cases, we model the influence of design parameters (e.g., topology, shape, or dimensions) or operational parameters (e.g., motion variables or exerted force) on the outcome to identify the values that achieve the desired result in the best way possible. To do so, we need numbers that quantify how good a robot is at doing something.
Sometimes, the conventional specifications of a robot (i.e., what we find on a commercial datasheet) are enough to know if a robot meets our task requirements. However, specific scenarios might require task-oriented performance indices to examine different facets of a robot’s behavior and quantify the influence of a set of parameters on the outcome. Once this relationship is established, the optimal value of those parameters can be computed by maximizing or minimizing the chosen index, through a specific algorithm (e.g., goal attainment, Newton–Raphson, minimax, and genetic algorithms).
While a variety of metrics and optimization procedures have been proposed to measure and improve robot performance, different methods have often been developed independently from each other, with a fragmented research effort rather than aiming at a unified framework. As summarized in Table 1, only a few surveys on the topic can be found in the literature, and most of them refer to specific kinds of robots, applications, or metrics, rather than discussing robot performance in general terms.
Historically, works on general robot performance can be found from the 1980s [1,2,3], when the field appeared less scattered than nowadays. This can be attributed to the smaller variety of robotic systems on the market, mostly limited to industrial robotic arms [4]. The late 1990s and the early 2000s saw an increasing interest in performance metrics for manipulators, as documented by a rising number of related works [5,6] (see Appendix A for detailed numerical data). Works from those years often focused on parallel robots [7,8,9,10,11], and their comparison to serial architectures [9]. The widespread availability of mobile robots caused a surge in research papers on optimal path planning in the 2000s [12,13,14,15,16,17,18,19]. These works often focused on the optimization algorithm, and performance metrics were discussed as objective functions.
Despite a rising number of relevant publications (see Appendix A), the most recent general surveys on manipulator metrics can be found in the early 2010s [20,21], when new research trends divided the field even further. Human–robot interaction (HRI) faced the challenge of finding a quantitative, objective index for subjective characteristics, such as trust and comfort [20,21,22,23,24,25]. The solution was to shift from mechanical engineering to social sciences, merging methodologies from both disciplines. Multi-robot systems (e.g., swarms) also required tailored performance metrics to quantify robustness, flexibility, aggregation, and pattern formation [26,27,28,29,30].

Table 1.
Previous surveys on metrics for robot performance.
Table 1.
Previous surveys on metrics for robot performance.
| Reference(s) | Performance Metrics | Type(s) of Robot | Year(s) |
|---|---|---|---|
| [1] | Mechanics | Manipulators | 1984 |
| [4] | Mechanics, Logistics, Economics | Manipulators | 1991 |
| [5,6] | Mechanics | Manipulators | 2000–2006 |
| [7,8,9,10,11] | Mechanics | Manipulators (parallel) | 2005–2007 |
| [20,21] | Mechanics | Manipulators | 2012–2015 |
| [12,13] | Mechanics | Mobile robots (legged) | 2012 |
| [14,15,16,17,18] | Mechanics | Mobile robots (path planning) | 2007–2018 |
| [19] | Mechanics | Mobile robots (UAV) | 2020 |
| [20,23,24,25] | Mechanics, Logistics, Social | Human-robot interaction | 2006–2017 |
| [26,27] | Mechanics | Multiple robots | 2006 |
| [28,29,30] | Mechanics | Multiple robots (swarm) | 2007–2016 |
| [31] | Mechanics, Logistics | Manipulators | 2017 |
While all these applications call for distinct approaches, mechanical performance metrics are still at their core. Different methods have often been developed in parallel to obtain similar results, since efforts at standardizing performance, even within smaller subfields, has been scattered at best. This might suggest a lack of interest in the topic, but the rich literature published in recent years proves otherwise, hinting at researchers using and developing new metrics while working in isolated bubbles, due to a lack of a central driving force. Therefore, comparing robot performance is possible for similar robot designs and similar tasks, as in the example in Figure 1, but becomes difficult (or impossible) when different designs or operations are considered.
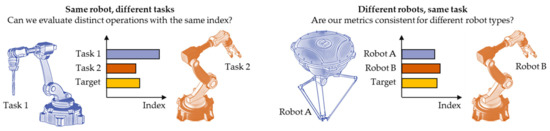
Figure 1.
The need for unified performance metrics is here explained with two examples. In the first one, we need to evaluate the performance of a robot during two different operations; without a standard set of metrics across different applications, it is difficult to estimate which task the robot is more suited to. In the second example, two different robots are both able to perform similar operations. Selecting the best robot, however, could be challenging if the formulation of the chosen performance index, or the experimental procedure to evaluate it, changes according to robot architecture, geometry, or motion parameters.
For this reason, this survey aimed at comparing and classifying existing metrics to provide an up-to-date and organized overview of performance evaluation for industrial manipulators. Previous general surveys, such as [20,21], report a comprehensive collection of metrics, but discussion is limited to technical features of isolated indicators. Conversely, an in-depth critical perspective on the whole field is here reported. Different approaches and metrics are described to highlight their advantages and disadvantages, with a focus on kinematic, static, and dynamic performance indices. The main optimization procedures are discussed in relation to different kinds of metrics. Finally, current research trends and open challenges in the field are analyzed to identify future research directions.
Overall, this review provides a comprehensive foundation to robot performance evaluation, explaining the main methodologies and techniques in this well-established, but fragmented, field and outlining the gap between commercial and research applications. As such, this article can interest both an industrial and academic audience, introducing the topic to engineers who are just approaching the field while providing an organized discussion with a critical perspective for experienced researchers.
2. Methodology
The term performance is interchangeably used to indicate both the act of executing a task or function and how well that task or function is done. When referring to robotic systems, performance metrics thus assess the capabilities of a robot through indicators that are usually, but not always, numerical (for example, robot topology can be classified through letters or categories, and capabilities can be represented by logical values).
Not unlike other kinds of measurement, performance metrics aim at facilitating the description, analysis, and comparison of robots by systematically assigning values to their properties. As such, these metrics must be meaningful and consistent throughout the field. Therefore, a general performance index would be favored over a specific one to compare a wider range of systems. However, generic metrics are often unable to capture every facet of interest and, thus, characterize specific functions of robot behavior. This need for a compromise between consistency and meaningfulness led to the development of different categories of performance metrics, for which a classification is here proposed, according to the index’s (in)dependency on pose, task, scale/unit, and physics (see Table 2).

Table 2.
A summary of the proposed classification (excluding physics).
2.1. Pose Dependency: Global and Local Metrics
Performance metrics can be classified according to their dependency on robot pose or configuration. A global index is independent from the robot’s motion variables, while a local index is a function of the robot’s current configuration and could result in a different value for each point of the workspace.
- Global metrics. Global metrics can either refer to pose-invariant features or represent an extension of local metrics. The latter is often obtained by taking the minimum, maximum, or average value of a local index throughout the workspace. A global index describes performance with a single number for an immediate comparison with other robots. However, global metrics are blind to gradients of behavior. A local index with a value of 0 in half of the workspace and 1 in the remaining half would result in a global index of 0.5 when taking the average value, while another robot with a local index of 0.5 throughout the entire workspace would be represented by the same global index but show stark differences in local behavior. This issue is often solved at a global level by taking the worst value of a local index as the global one, “flattening” performance to its worst in the workspace.
- Local metrics. Local metrics can describe how robot performance varies point by point, at the cost of higher complexity and the lack of a single value to characterize the system. While this approach prevents fast comparison to other robots, local metrics can be used to detect kinematic singularities and to enable further optimization on given tasks (e.g., path planning on a trajectory that optimizes a local index).
2.2. Task Dependency: Intrinsic and Extrinsic Metrics
An intrinsic index is a function of the robot’s parameters only (e.g., Jacobian matrix, link dimension) and is task-invariant, whereas an extrinsic index measures robot performance in relation to a specific task and is, thus, dependent on task parameters (e.g., trajectory, time limitations).
- Intrinsic metrics. A good performance on intrinsic metrics characterizes the capability of a robot to perform generally well and is, thus, suggested for robots designed or acquired for generic or flexible usage. Intrinsic indices are, thus, preferred in open-ended applications, such as commercial systems.
- Extrinsic metrics. When a set of tasks is clearly defined as the robot use case, extrinsic metrics might be more relevant, as they measure how good the robot is within stricter task-oriented requirements. In general, extrinsic indices are favored for specific operations that require performance close to the technological limits of the system (e.g., custom robots for specific tasks).
2.3. Physics: Kinematic, Static, and Dynamic Metrics
Performance metrics can be classified according to the kind of physical behavior that they aim to evaluate. Since this manuscript focuses on mechanical performance, the two main branches of physics involved are kinematics and dynamics. However, specific applications might require different metrics related, for example, to thermal or electromagnetic performance, or to any other relevant physics subfield. While these metrics are not discussed here, they should be considered when evaluating a system that cannot be fully characterized by classical mechanics.
- Kinematic metrics. Kinematic metrics characterize the behavior of a robotic system in relation to its motion and are a function of its architecture, topology, and geometry. Most of the data commonly found on commercial robot datasheets are kinematic metrics, including accuracy, repeatability, speed, and workspace. For robot analysis, Jacobian-based kinematic indices have arguably been the most successful to evaluate performance both at local and global levels.
- Static and dynamic metrics. Dynamic metrics quantify performance in terms of loads acting on the system and are significantly affected by the robot’s inertial characteristics. Commercial dynamic metrics are related to the robot’s payload and power consumption, whereas more complex indices are used for path planning. When the inertial effects on the system can be safely neglected, static metrics can be used, instead of dynamic ones, to simplify problem formulation and system evaluation.
- Other metrics. While most mechanical indicators are related to kinematics, statics, and dynamics, other kinds of metrics are sometimes used. For example, qualitative indicators and rate of success are common in human–robot interaction. These metrics tend to be field dependent and, as such, difficult to transfer to other robots.
2.4. Index Anatomy
In the previous paragraphs, performance metrics were introduced in a qualitative way. However, as our aim was to quantify the behavior of a robot and “translate” it into easily readable values, the form and derivation of an index are extremely important, as the same performance can be described in multiple different ways, whether we measure it in its absolute value or in a dimensionless, relative scale.
- Absolute metrics. An absolute index expresses the performance of a robot as acquired, evaluated, or computed in a measurement system. This implies that the index is measured against a scale and, thus, characterized by its own unit of measure, which could be, for example, meters, meters per second, kilograms, Newtons, or any other unit. The main advantage of an absolute index is immediacy, as any trained engineer, technician, or person in the trade can evaluate the index thanks to its familiarity with the unit. For example, if we are told that a robot has a payload of 4 kg, we instinctively know that it can be used to lift a shoe, might struggle with a heavy backpack, and will definitely fail with a car. However, an absolute number in a vacuum is useless: in the previous example, we are unconsciously evaluating the requirements (less than 1 kg for a shoe, between 1 and 10 kg for the backpack, around 1000 kg for the car) and comparing them to our limit. When requirements are not known, unfamiliar, or difficult to instinctively understand, the advantages of absolute metrics wane. Furthermore, if we are comparing systems that perform the same task in different ways, we might measure their performance with indices in different units or scales, which are not comparable in absolute values.
- Relative metrics. While less immediate to quantitively grasp than absolute metrics, relative indices enable better and faster comparison, independent from scale and unit. A relative index is usually obtained from an absolute index by dividing it by a reference value, which might be, for example, a requirement, a standard, or a previous measure. As such, relative metrics are dimensionless and only convey our distance from the reference. As such, a key challenge of relative metrics is selecting a meaningful reference. Even though the numerical value of a relative index is arbitrary, scales from 0 to 1, −1 to 1, or percentiles are usually preferred. Relative metrics might be seen as less meaningful than absolute ones: for example, lifting a load that is 60% of our payload does not tell us anything about how much that load is without additional information. However, they allow the establishment, at a glance, of not only whether our robot would succeed in a specific task, but also of our margin of success (or failure).
3. Standard Metrics
We usually start evaluating commercial robots from the technical specifications on their datasheet. Even though these metrics are mostly used to set performance boundaries, rather than to analyze the robot’s behavior in detail, they are the conventional performance indicators in robotics. A non-comprehensive list of common metrics among industrial robots is reported in Table 3. Most of these indicators, which usually appear on commercial robot datasheets, are global and intrinsic, as they aim at outlining the robot’s characteristics with immediacy, to enable comparison with competitors. Conversely, extrinsic and local metrics are suggested by the US National Institute of Standards and Technology (NIST) as key performance indicators to capture empirical evidence of performance in a desired operation [31].

Table 3.
Examples of metrics from robot specifications and standards [31].
While the datasheets of robots for specific applications, or with peculiar architectures, could include unusual indicators, the metrics in Table 3 are quite standardized across a wide range of robots, manufacturers, and markets. Furthermore, they are commonly used in research papers to characterize and optimize robot designs. However, their generality makes them suited to a coarse design selection, rather than a fine tuning of robot performance. As such, more refined kinematic, static, and dynamic metrics represent a better solution for complex optimization problems or demanding tasks.
4. Kinematic Performance
Kinematic indices only depend on a robot’s geometrical and motion parameters, considering neither forces and torques acting on the system nor its mass and inertial properties. Kinematic metrics, thus, include motion limits, such as motion range, collision avoidance, maximum speed, and maximum acceleration, as well as precision indicators, such as accuracy, repeatability, and resolution [7,32]. Common kinematic metrics are summarized in Table 4; while a more comprehensive listing can be found in previous surveys [20,21]. Herein, the most successful ones were selected with the aim of encouraging the use of widespread and general metrics, rather than new (but often similar or equivalent) ones that are relevant to a more limited number of works or systems.

Table 4.
Common performance metrics.
4.1. Precision
The performance of a robot in tasks where positioning is critical (e.g., machining tasks [40], pick and place [41]) is usually defined through precision metrics. Three common indicators are used in this regard: accuracy, repeatability, and resolution [32], illustrated in Figure 2. Several Jacobian-based indicators, detailed below, can also act as local indicators of robot precision.
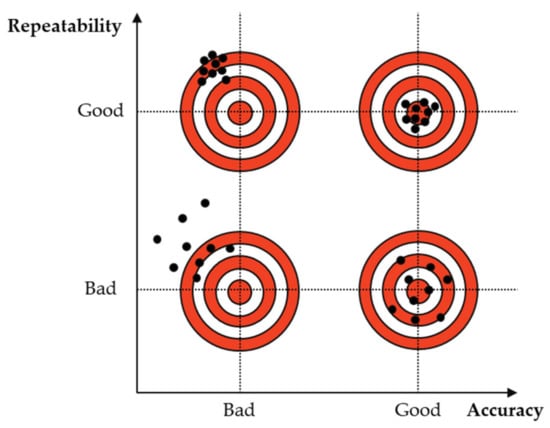
Figure 2.
A graphical representation of accuracy and repeatability in a task that requires hitting the center of a target: a low accuracy results in points being far from the center, whereas a low repeatability increases the area in which points are scattered.
- Accuracy. Robot accuracy represents how capable a robot is at achieving a desired pose. It is usually expressed as the displacement between the desired pose and the pose reached by the robot when the desired one is provided as input. Since the robot realizes a pose by calculating the corresponding actuation through its kinematics, accuracy is a function of its modeling parameters, including (but not limited to) the following: link lengths, joint type and position, other geometrical parameters, environment, tool, and fixture models. As such, accuracy can be increased by precise measurement, calibration, and tuning of these values [42,43,44,45,46].
- Repeatability. Complementary to accuracy, repeatability is the ability of a robot to return to the same pose multiple times. It is usually computed by commanding the robot to reach a set of poses in a recursive way and estimating the maximum radius among the spheres that enclose the set of locations reached for each configuration [32]. This metric is not related to accuracy. The spheres may not include the desired points at some (or all) of those locations, as we aim at measuring the robot’s reliability and consistency, rather than its margin of success. Whereas accuracy can be usually improved through calibration or error compensation, repeatability is a function of parameters that are intrinsic to the robot’s architecture and design, such as joint and motor backlash, friction, motion transmission, and assembly tolerances.
- Resolution. Resolution represents the smallest incremental motion that can be produced and measured by the manipulator. It mostly depends on the resolution of the robot’s sensors (e.g., motor encoders) and of its actuation technology (e.g., step size of a stepper motor) [32].
4.2. Workspace
The workspace of a robot represents a region of space that can be reached by its tool, or end-effector. This region can be obtained through different definitions with different results [7]. Common definitions for optimization include the reachable workspace (reachable points with at least one orientation [47,48]), translation workspace (reachable points with a given orientation [49,50,51]), orientation workspace (reachable orientations in a given point [52,53]), and the dexterous workspace (reachable points with all orientations [54,55,56,57]). When evaluating a robot in term of its workspace, we usually tend to use intrinsic metrics, computing workspace volume by considering the robot’s geometrical constraints, i.e., joint limits, actuation range, self-collision, singular configurations. However, extrinsic workspace metrics can be adopted when analyzing tasks where the workspace is characterized by obstacles or other environmental conditions that reduce the robot’s range of motion.
- Workspace volume. Most commercial datasheets provide workspace data both directly, by reporting the shape of the robot’s workspace, and indirectly, through joint limits. A single index is challenging to define, with the volume of workspace , evaluated either numerically, analytically, or geometrically (Figure 3, [58]) and expressed as arguably being the only popular one [7,21]. However, nonlinear kinematics and the lack of closed-form solutions for most architectures makes evaluating workspace volume complex and time-consuming, especially in recursive optimization algorithms where the computation is repeated a large number of times. Furthermore, workspace volume does not always represent the robot’s actual performance. Since shape is not considered, this value might include regions of space that are irrelevant for most tasks. To address this issue, an operational workspace, defined as the largest cylinder, sphere, parallelepiped, or prism inscribed in the reachable workspace, is sometimes used instead of the robot’s own workspace. Since workspace volume is an absolute index, relative formulations have been proposed to evaluate its size with respect to the size of the robot [59].
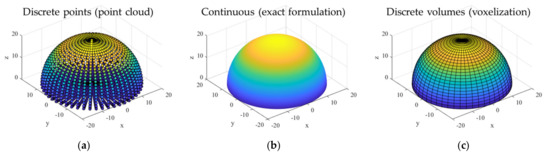 Figure 3. Three representations of the same workspace: a discrete point-based formulation (a), the exact workspace volume from an analytical or algebraic formulation (b), and a division in discrete volumes (c). The discrete point cloud can be easily computed through forward and inverse kinematics by discretizing actuator motion or target operational space, respectively; however, workspace volume can only be approximated from this formulation (unless the robot under examination is discretely actuated, e.g., [65]). Algebraic and analytical formulations are more complex but result into exact values. A volume discretization represents a compromise between the previous two methods.
Figure 3. Three representations of the same workspace: a discrete point-based formulation (a), the exact workspace volume from an analytical or algebraic formulation (b), and a division in discrete volumes (c). The discrete point cloud can be easily computed through forward and inverse kinematics by discretizing actuator motion or target operational space, respectively; however, workspace volume can only be approximated from this formulation (unless the robot under examination is discretely actuated, e.g., [65]). Algebraic and analytical formulations are more complex but result into exact values. A volume discretization represents a compromise between the previous two methods.
- Workspace index. Task-oriented workspace metrics can be obtained by including obstacles and specific environmental conditions in workspace volume computations, as mentioned earlier. However, a more significative index can be obtained by comparing the robot’s workspace to the desired operational volume. To avoid complicated modeling, this can be achieved by discretizing the workspace in voxels (the equivalent of a 3D pixel, i.e., a small cubic volume around a node of a 3D grid; other shapes or definitions of discrete volumes can be used) and comparing the number of objective voxels in the workspace to the total number of objective voxels as
This workspace index ranges from zero to one and represents the reachable percentage of the objective workspace [33]. Many recent works adopted similar workspace index definitions by comparing the workspace volume to a reference value [60,61,62,63,64].
4.3. Jacobian
A large family of kinematic performance metrics is defined through the Jacobian matrix of the robot, which represents the relationship between joint/actuator velocity and the resulting end-effector velocity [8,66] as:
where defines the position and orientation of the end-effector, is the current position of each actuator (up to the degrees of freedom of the robot), and and are their respective time derivatives. As such, the Jacobian links actuator performance, which is usually easily measurable, to the behavior of the end-effector, enabling a quick evaluation from accessible and reliable data and establishing a linear relationship between the manipulator motion and its corresponding actuation. As illustrated in Figure 4, this “amplification factor” from motor to end-effector is represented by mapping a bounded error at the actuators , described by the hypersphere , into an ellipsoid in the generalized Cartesian space as:
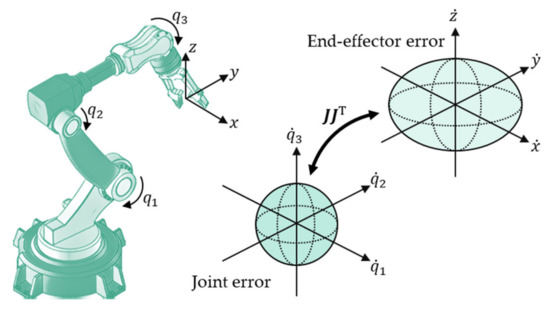
Figure 4.
Representation of the manipulability ellipsoid from actuation to cartesian space.
The shape and volume of this ellipsoid were proposed to characterize the manipulator dexterity [34]. However, this formulation suffers from its dependency on scale, dimensions, and frame, which can lead to physical inconsistencies [67,68]. Nevertheless, several metrics based on this concept have been proposed.
- Manipulability index. The manipulability index , proposed by Yoshikawa in 1983 [34], is computed as:
- Condition number. Given the above-mentioned limitations of manipulability measures, in 1991 Gosselin and Angeles proposed using the condition number of the Jacobian matrix as a measure of the accuracy of both the Cartesian velocity of the robot, as a function of joint rates, and the static load on the end-effector, as a function on load cells on the joint axes [35]. The condition number , defined as:
Represents the error amplification factor intrinsic to the robot’s structure. This formulation avoids the limitations of previous manipulability measures and, different to Yoshikawa’s manipulability index, conveniently ranges from one to ∞. As such, its reciprocal represents an “ideal” relative index with a value of zero in singular configurations and one corresponding to the best performance. The condition number has been fairly successful in recent works, with many examples in different fields and applications (e.g., [69,70,71]).
All these metrics characterize robot performance in a single pose, since the numerical values of the Jacobian matrix vary in different points of the workspace. Therefore, they can be used to identify an optimal operation path which only moves through a trajectory characterized by the highest possible values of these local indices. However, if we aim at characterizing the overall robot performance, this concept can be expanded to obtain a global index by evaluating an average throughout the workspace [72,73,74,75,76].
- Global conditioning index. The global conditioning index [35] is defined for a volume W as:
Other local metrics can be similarly expanded to formulate analog global indicators, evaluating the average of the index in the objective workspace volume.
Overall, Jacobian-based metrics are extensively used for both serial and parallel architectures in mechanism synthesis and design [69], workspace optimization [77,78], path planning [79], and control [80], as they capture robot performance both at a local and global level and can be easily adapted to evaluate a wide variety of situations. However, their limitations should not be overlooked. Since the Jacobian matrix is a non-homogeneous matrix, that includes both rotation and translation and is dependent on the choice of physical unit, numerical results from Jacobian-based calculations should always be critically evaluated to ensure they represent the robot’s real behavior.
4.4. Remarks
While kinematic performance is critical for all kinds of robots, it is worth noting that all the metrics introduced in this section were first developed to study manipulators. This can be partially attributed to robotic arms being the first robotic system to reach technological maturity; however, another key factor is that many manipulation and machining tasks are characterized by strict requirements on precision and speed that need to be satisfied before considering the dynamic aspects. Other systems, such as mobile robots, depend more on dynamic features, such as energy consumption, inertial effects, and dynamic balance [12]. Kinematic metrics are less relevant for those robots, as static or dynamic performance indicators are needed for a significant evaluation.
5. Static and Dynamic Performance
Static metrics evaluate the performance of a robot under the effect of a load and are common for relatively slow operations (with limited accelerations). Dynamic metrics generalize static formulations by considering inertial effects. The most common static and dynamic performance indicators are linked to force transmission, stiffness, and power consumption. These metrics are widely used and are critical for robots in dynamic environments, such as underwater and aerial robots, or those requiring dynamic balance for functioning, such as bipeds.
5.1. Statics
- Global transmission index. The concept of transmission performance has been used to evaluate robots since its introduction in the 1990s [81,82] and has been quite popular for the evaluation of parallel mechanisms [36,83,84,85]. The transmission index aims at measuring the quality and efficiency of a robot at transforming inputs into outputs. The following formulation:
Computes the Global Transmission Index as the cosine of its pressure angle , defined as the angle between the transmission wrench screw (characterizing the input load on the system) and the corresponding output twist screw (i.e., motion). Even though a more general formulation was published [36], the reported example in (7) is here preferred as being easier to understand. While wrench transmission is at the core of this index, most formulations of transmission metrics, including its general one [36], only depend on the kinematics of the system. As such, this measure could also be classified as a kinematic index.
- Stiffness matrix. Stiffness plays a key role in the operation and control of any robotic system, and it is often evaluated from the robot’s stiffness matrix, which describes the relationship from the static wrench and corresponding deflection [86]. When linear elasticity in the actuators is considered, two kinds of stiffness matrix are usually studied: a Cartesian stiffness matrix , which evaluates the deflection at the end-effector caused by wrench as:
These two stiffness matrices are linked by a Jacobian dependent relationship: since and , Equation (10) can be rewritten as , yielding:
This result is often used to characterize the end-effector’s elastic response to a load and can also be expanded to include passive joints [37]. A numerical index can be extracted from the stiffness matrix (e.g., determinant). With this formulation, stiffness evaluation is local and characterized by the disadvantages of Jacobian-based metrics. Different formulations (e.g., energy-based [87,88,89] or deflection-based [90]) can overcome this disadvantage at the cost of limited generality. Nevertheless, stiffness optimization is critical in tasks that require high precision, such as machining [91,92,93,94,95].
5.2. Dynamics
Whereas kinematic and static metrics characterize (quasi-)static configurations, dynamic metrics are needed to describe how motion affects robot performance (e.g., with inertial effects, Coriolis and centrifugal forces, and gravity). Therefore, dynamic metrics often depend on the task under examination and are used for path planning or control, rather than design or robot selection.
- Dynamic manipulability index. The manipulability index, while originally related to kinematics only, has been expanded for a dynamic formulation by including the inertia matrix of the system [38], as:
This index is intrinsic, and, as such, it can be used to evaluate the dynamic performance of the robot without defining an arbitrary task beforehand. However, as an expansion of the kinematic manipulability, it still suffers from the same limitations and posture dependency. Other kinematic concepts have been similarly adapted to include dynamics (e.g., conditioning index [96], inertial ellipsoid [97], and manipulability ellipsoid [98]), but their usage has been scattered because of more successful and/or efficient approaches to path planning (e.g., energy, potential field [99]).
- Energy consumption. A widely used indicator of dynamic performance is energy consumption. Given the large variety of robots that have been characterized with energy consumption indicators, including multi-robot systems [100], legged robots [101], wheeled robots [39], industrial robots [102,103], and drones [104], many formulation have been proposed, all directly modeling energy or power consumption. Further energy- and power-based indicators, such as the power manipulability index [105] and the energy performance index [106], achieve more general, relative, or intrinsic measures. Nevertheless, the immediacy of energy (or power) consumption (easy to read and use practically, for example, for dimensioning a battery or finding the most energy-efficient path [107,108]) makes it successful, despite its disadvantages (scale dependency, task dependency, and variety of formulations).
6. Optimization
Performance metrics are mostly used either for directly comparing robots or as a tool for design or motion optimization. Regarding the latter, any of the numerical indicators presented in the previous section can be used as an objective function of an optimization problem, which can be stated in its general form as:
where is a vector containing the design and control parameters of the entire system, and is the vector of the performance indicators to optimize. The system is limited by inequality constrains and equality constraints . The variables and are the number of parameters and of metrics to optimize, respectively, so that [109,110].
When a single index () is sufficient to characterize robot performance, the problem statement is reduced to a simple minimization problem and can quickly converge to a solution. However, when this is not the case, multi-objective optimization () is required, introducing additional challenges, such as selecting a representative set of metrics and identifying a single solution out of a set of optimal ones. These two challenges are strictly intertwined: multi-objective optimization leads to contradictory results when a feasible solution that minimizes simultaneously all the objective functions does not exist. Thus, it is necessary to find the optimal solutions to the problem (known as the Pareto front) as those solutions which cannot be improved in any of the objectives without degrading at least another one [109].
- Metrics selection. When selecting multiple metrics, robot behavior should be captured as widely as possible. Optimizing two Jacobian-based indices at the same time, for example, is likely to result in similar parameter sets which are both close to optimization, because of formulation similarities. A superficial reading might find this advantageous, as it removes the hassle of selecting the right solution, but an equivalent result is likely achieved by a single-objective optimization in a more efficient way. For this reason, the objective functions should be metrics with independent formulations and represent distinct facets of robot behavior. Whenever multiple distinct metrics yield similar results, a critical analysis is, thus, necessary to identify and remove redundant indicators.
- Finding a solution. Once the objective functions have been selected and the Pareto front computed, a single solution must be chosen out of all the feasible ones. While an arbitrary solution could be used, several procedures have been formulated to guide the user in making an informed decision [66,111,112,113]. More recently, machine learning has been replacing traditional optimization procedures, by providing an accurate and time-efficient solution for optimization problems that allow data-based approaches [114,115,116]. Data-driven approaches, such as learning, are evidently advantageous, not only for solution selection but also computation. However, their results should not be taken for granted: these techniques act as a black box between input (problem formulation) and output (optimal parameter set), and the reliability of their results should be carefully evaluated.
7. Discussion
7.1. Open Challenges
This manuscript provides a collection of popular robot performance metrics, highlighting the main methodologies and techniques for the evaluation of manipulators. However, three key challenges are faced when developing, or using, performance indicators:
- Index relevance. A successful index requires fine tuning between general description and describing a facet of the robot’s performance in detail. An index that is too generic might become meaningless, but a very specific index hinders comparison or loses immediacy. This challenge is exacerbated by the diverging needs of developers and users of robot performance metrics: industry and academia. Commercial and industrial applications favor intrinsic and/or global metrics, which cover a large variety of applications and robots and, thus, appeal to a wider audience. Researchers generally prefer extrinsic and/or local metrics, since generic metrics might neglect specific aspects required for a particular development.
- Fragmented research field. The indicators reported in this article, while being representative of the entire field, are only a small portion of it. Given the wide variety of robots and applications, no individual index or optimization method is expected to work for every scenario, but current usage of performance indices is extremely fragmented, and no standard exists, even within specific subfields and applications. Multiple causes are behind this issue, such as the following: specific tasks might benefit from a tailored performance index; the computation of an existing index might be difficult for a specific scenario, and a variant preferred; an index for a specific case might not be representative of performance in a more general scenario; or new designs (e.g., soft and continuum robots, and drones) might display features and behaviors that cannot be described by existing metrics.
- Limited research scope. Apart from these technical challenges, the lack of research focus on the topic represents an additional obstacle to the standardization and further development of the whole field. Research on performance indices is often a small part within large projects focusing on design or control. Thus, these metrics are perceived as a means to an objective end rather than the objective itself, hindering efforts toward a unified framework. This issue became clear when examining the relevant scientific literature: most works on the topics, including many of the general surveys referenced in this article, only mentioned metrics as a necessary part of optimization procedures, without discussing their formulation, relevance, and generality.
7.2. Future Outlook
Previous surveys on the topic ([20,21]) suggest defining new metrics to remove the dependency on scale, dimension, frame, and order of currently used ones. However, that position is not shared herein. First, these dependencies are generally seen as drawbacks. but can be convenient in some cases, providing immediacy and a clearer understanding of the physical meaning behind their numerical value. Moreover, relative metrics aim at being general but still depend on the reference value used to normalize them, which might be an arbitrary value, the minimum, mean, or maximum measured value, or a characteristic of the robot (e.g., size). Thus, while reckoning the value of advocating for dimensionless indices within a predetermined range, it would be detrimental for them to totally replace familiar metrics, such as speed, joint range, and payload.
In the author’s opinion, the following points are critical for the development of the field in the next decade:
- Standardization. With the field becoming wider and more scattered, researchers and engineers should start addressing performance metrics with a more structured, systematic approach and focus. Roboticists should be encouraged to adopt a unified set of performance metrics, rather than look for new indices, as the literature on the topic is getting increasingly difficult to navigate with the proliferation of similar, but distinct, metrics based on the same principles.
- Benchmarking. The definition of standard metrics should not be limited to their mathematical formulation but also address the need for a set of procedures to measure robot performance and for a database of relative benchmarks. Such a framework would enable a straightforward evaluation, comparison, and optimization of robotic systems, promoting best practices for an overall increase in safety, quality, and reliability in the entire field.
- Communication with stakeholders and policy makers. Existing national standards (e.g., [31]) are outpaced by the rapidly developing technologies. This two-speed issue between policy and research is exacerbated by the limited communication between scientists, stakeholders, and policy makers. Encouraging discussion between these three groups is fundamental in creating, and defining, a framework of general interest.
- Evaluating innovative designs. Many novel robot designs and architectures elude conventional definitions and models on which many performance metrics are defined. For example, continuum and soft manipulators cannot be described with rigid-body models, and their behavior radically differs from traditional robotic arms. Before evaluating these robots with conventional metrics, or trying to define new indicators, we must ask ourselves how their performance differs and which facet of it we are interested in capturing. For example, soft and compliant design cannot compete in precision or stiffness with rigid mechanisms, but easily succeeds in unstructured tasks where rigid manipulators fail. Once these robots reach technological maturity, new metrics will be needed to measure their new capabilities.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Search Methodology
The generation of the bibliography for this paper started with a keyword search on three databases: SCOPUS, Web of Science, and IEEE Xplore. In each database, articles containing at least a keyword from a first set {robot; manipulator; robotics} and a keyword from a second set {performance; optimization; metrics; index; indicator} were selected. Results were further refined by subject area {Engineering; Computer Science} in SCOPUS, by subject {Robotics; Automation Control Systems; Engineering, Mechanical} within the Science Citation Index Expanded (SCI-E) in Web of Science; and by subject {Manipulators; Kinematics; Optimization} in IEEE Xplore, with the results shown in Table A1 and Figure A1.
After removing duplicate studies, the resulting bibliography was sorted by number of references, and year of publication, and filtered to identify literature surveys. One step of backward and forward citation tracking (i.e., checking articles cited by, or that cited, a paper under study, performed through the above-mentioned databases and Google Scholar) was performed on seminal papers (top 50 most cited, weighted by the number of citations by years since publication not to penalize recent publications) to find references that might have been missed during the database search. Finally, a last set of publications was added from the author’s knowledge.
The reference list for this manuscript was refined from this bibliographical search to highlight the papers that introduced or described key indices, surveys on the topic, and selected publications chosen by number of citations and relevance to this review, with a priority on recently published works.

Table A1.
Results of database searches.
Table A1.
Results of database searches.
| Database | SCOPUS | Web of Science | IEEE Xplore |
|---|---|---|---|
| Total articles 1 | 150582 | 22479 | 32621 |
| Total journal | 95456 | 12404 | 5443 |
| Total conference | 13892 | 10298 | 27178 |
| Refined articles 1 | 6462 | 9644 | 7032 |
| Refined journal | 3231 | 9102 | 1247 |
| Refined conference | 2918 | 403 | 5785 |
1 Including indexed journal articles, conference papers, book chapters, and books.
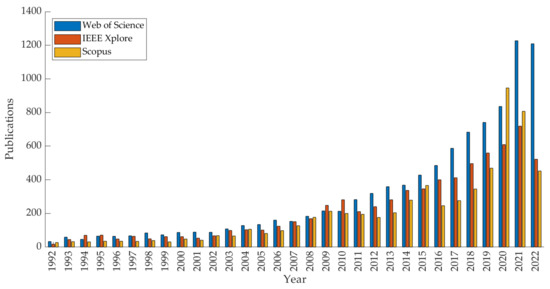
Figure A1.
Results of refined literature search. The number of papers by year shows how interest in the topic has grown over time, but this growth is not mirrored by an increasing number of surveys on the topic (see Table 1).
References
- Lau, K.; Hocken, R.J. A survey of current robot metrology methods. CIRP Ann. 1984, 33, 485–488. [Google Scholar] [CrossRef]
- Klein, C.A.; Blaho, B.E. Dexterity measures for the design and control of kinematically redundant manipulators. Int. J. Robot. Res. 1987, 6, 72–83. [Google Scholar] [CrossRef]
- Park, J.H.; Asada, H. Concurrent design optimization of mechanical structure and control for high speed robots. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; pp. 2673–2679. [Google Scholar]
- Boubekri, N.; Sahoui, M.; Lakrib, C. Development of an expert system for industrial robot selection. Comput. Ind. Eng. 1991, 20, 119–127. [Google Scholar] [CrossRef]
- Tanev, T.; Stoyanov, B. On the performance indexes for robot manipulators. Probl. Eng. Cybern. Robot. 2000, 49, 64–71. [Google Scholar]
- Kucuk, S.; Bingul, Z. Comparative study of performance indices for fundamental robot manipulators. Robot. Auton. Syst. 2006, 54, 567–573. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 128. [Google Scholar]
- Merlet, J.P. Jacobian, manipulability, condition number, and accuracy of parallel robots. J. Mech. Des. 2006, 128, 199–206. [Google Scholar] [CrossRef]
- Briot, S.; Bonev, I.A. Are parallel robots more accurate than serial robots? Trans. Can. Soc. Mech. Eng. 2007, 31, 445–455. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, N.; Wang, F. New indices for optimal design of redundantly actuated parallel manipulators. J. Mech. Robot. 2017, 9, 011007. [Google Scholar] [CrossRef]
- Olds, K.C. Global indices for kinematic and force transmission performance in parallel robots. IEEE Trans. Robot. 2015, 31, 494–500. [Google Scholar] [CrossRef]
- Silva, M.F.; Machado, J.T. A literature review on the optimization of legged robots. J. Vib. Control 2012, 18, 1753–1767. [Google Scholar] [CrossRef]
- Torres-Pardo, A.; Pinto-Fernández, D.; Garabini, M.; Angelini, F.; Rodriguez-Cianca, D.; Massardi, S.; Tornero-López, J.; Moreno, J.C.; Torricelli, D. Legged locomotion over irregular terrains: State of the art of human and robot performance. Bioinspiration Biomim. 2022, 17, 061002. [Google Scholar] [CrossRef]
- Castillo, O.; Trujillo, L.; Melin, P. Multiple objective genetic algorithms for path-planning optimization in autonomous mobile robots. Soft Comput. 2007, 11, 269–279. [Google Scholar] [CrossRef]
- Raja, P.; Pugazhenthi, S. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320. [Google Scholar] [CrossRef]
- Zafar, M.N.; Mohanta, J.C. Methodology for path planning and optimization of mobile robots: A review. Procedia Comput. Sci. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Patle, B.K.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Moreno, H.A.; Saltaren, R.; Carrera, I.; Puglisi, L.; Aracil, R. Índices de desempeño de robots manipuladores: Una revisión del estado del arte. Rev. Iberoam. Automática Inf. Ind. 2012, 9, 111–122. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Manipulator performance measures-a comprehensive literature survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef]
- Steinfeld, A.; Fong, T.; Kaber, D.; Lewis, M.; Scholtz, J.; Schultz, A.; Goodrich, M. Common metrics for human-robot interaction. In Proceedings of the 1st ACM SIGCHI/SIGART Conference on Human-Robot Interaction, Salt Lake City, UT, USA, 2–3 March 2006; pp. 33–40. [Google Scholar]
- Abou Saleh, J.; Karray, F. Towards generalized performance metrics for human-robot interaction. In Proceedings of the 2010 International Conference on Autonomous and Intelligent Systems, AIS 2010, Povoa de Varzim, Portugal, 21–23 June 2010; pp. 1–6. [Google Scholar]
- Pinto-Fernandez, D.; Torricelli, D.; Sanchez-Villamanan, M.D.C.; Aller, F.; Mombaur, K.; Conti, R.; Vitiello, N.; Moreno, J.C.; Pons, J.L. Performance evaluation of lower limb exoskeletons: A systematic review. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1573–1583. [Google Scholar] [CrossRef] [PubMed]
- Robinette, P.; Howard, A.M.; Wagner, A.R. Effect of robot performance on human–robot trust in time-critical situations. IEEE Trans. Hum.-Mach. Syst. 2017, 47, 425–436. [Google Scholar] [CrossRef]
- Balakirsky, S.; Scrapper, C.; Carpin, S.; Lewis, M. USARSim: Providing a framework for multi-robot performance evaluation. In Proceedings of the Performance Metrics for Intelligent Systems (PerMIS) Workshop, Gaithersburg, MD, USA, 21–23 August 2006; pp. 98–102. [Google Scholar]
- Mourikis, A.I.; Roumeliotis, S.I. Performance analysis of multirobot cooperative localization. IEEE Trans. Robot. 2006, 22, 666–681. [Google Scholar] [CrossRef]
- Prorok, A.; Hsieh, M.A.; Kumar, V. Formalizing the impact of diversity on performance in a heterogeneous swarm of robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5364–5371. [Google Scholar]
- Soysal, O.; Bahçeci, E.; Şahin, E. Aggregation in swarm robotic systems: Evolution and probabilistic control. Turk. J. Electr. Eng. Comput. Sci. 2007, 15, 199–225. [Google Scholar]
- Bayındır, L. A review of swarm robotics tasks. Neurocomputing 2016, 172, 292–321. [Google Scholar] [CrossRef]
- Zimmerman, T.A. Metrics and Key Performance Indicators for Robotic Cybersecurity Performance Analysis; US Department of Commerce, National Institute of Standards and Technology: Washington, DC, USA, 2017. [Google Scholar]
- Siciliano, B.; Khatib, O.; Kröger, T. (Eds.) Springer Handbook of Robotics; Springer: Berlin, Germany, 2008; Volume 200. [Google Scholar]
- Puglisi, L.J.; Saltaren, R.J.; Moreno, H.A.; Cárdenas, P.F.; Garcia, C.; Aracil, R. Dimensional synthesis of a spherical parallel manipulator based on the evaluation of global performance indexes. Robot. Auton. Syst. 2012, 60, 1037–1045. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of robotic mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. A global performance index for the kinematic optimization of robotic manipulators. J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]
- Chen, C.; Angeles, J. Generalized transmission index and transmission quality for spatial linkages. Mech. Mach. Theory 2007, 42, 1225–1237. [Google Scholar] [CrossRef]
- Pashkevich, A.; Klimchik, A.; Chablat, D. Enhanced stiffness modeling of manipulators with passive joints. Mech. Mach. Theory 2011, 46, 662–679. [Google Scholar] [CrossRef]
- Yoshikawa, T. Dynamic manipulability of robot manipulators. Trans. Soc. Instrum. Control Eng. 1985, 21, 970–975. [Google Scholar] [CrossRef]
- Liu, S.; Sun, D. Minimizing energy consumption of wheeled mobile robots via optimal motion planning. IEEE ASME Trans. Mechatron. 2013, 19, 401–411. [Google Scholar] [CrossRef]
- Russo, M.; Raimondi, L.; Dong, X.; Axinte, D.; Kell, J. Task-oriented optimal dimensional synthesis of robotic manipulators with limited mobility. Robot. Comput.-Integr. Manuf. 2021, 69, 102096. [Google Scholar] [CrossRef]
- Wu, G.; Bai, S.; Hjørnet, P. Architecture optimization of a parallel Schönflies-motion robot for pick-and-place applications in a predefined workspace. Mech. Mach. Theory 2016, 106, 148–165. [Google Scholar] [CrossRef]
- Elatta, A.Y.; Gen, L.P.; Zhi, F.L.; Daoyuan, Y.; Fei, L. An overview of robot calibration. Inf. Technol. J. 2004, 3, 74–78. [Google Scholar] [CrossRef]
- Russo, M.; Dong, X. A calibration procedure for reconfigurable Gough-Stewart manipulators. Mech. Mach. Theory 2020, 152, 103920. [Google Scholar] [CrossRef]
- Rozlivek, J.; Rustler, L.; Stepanova, K.; Hoffmann, M. Multisensorial robot calibration framework and toolbox. In Proceedings of the 2020 IEEE-RAS 20th International Conference on Humanoid Robots (Humanoids), Munich, Germany, 19–21 July 2021; pp. 459–466. [Google Scholar]
- Rodríguez-León, J.F.; Chaparro-Rico, B.D.; Russo, M.; Cafolla, D. An Autotuning Cable-Driven Device for Home Rehabilitation. J. Healthc. Eng. 2021, 2021, 6680762. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.N.; Le, P.N.; Kang, H.J. A performance comparison of the full pose-and partial pose-based robot calibration for various types of robot manipulators. Adv. Mech. Eng. 2021, 13, 16878140211047754. [Google Scholar] [CrossRef]
- Aboulissane, B.; El Bakkali, L.; El Bahaoui, J. Workspace analysis and optimization of the parallel robots based on computer-aided design approach. Facta Univ. Ser. Mech. Eng. 2020, 18, 079–089. [Google Scholar] [CrossRef]
- Zhang, X.; Wenxun, D.; Dai, L.; Chen, J.; Zhao, X. 2PPaRR-2PPaRU: Design, analysis, and optimization of a new 3T1R parallel manipulator with rotational pitch motion. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6053–6063. [Google Scholar] [CrossRef]
- Aboulissane, B.; El Haiek, D.; El Bakkali, L.; El Bahaoui, J. On the workspace optimization of parallel robots based on CAD approach. Procedia Manuf. 2019, 32, 1085–1092. [Google Scholar] [CrossRef]
- Antonov, A.; Glazunov, V. Position, velocity, and workspace analysis of a novel 6-DOF parallel manipulator with “piercing” rods. Mech. Mach. Theory 2021, 161, 104300. [Google Scholar] [CrossRef]
- Wang, J.; Lau, H.Y. Dexterity Analysis Based on Jacobian and Performance Optimization for Multi-Segment Continuum Robots. J. Mech. Robot. 2021, 13, 061012. [Google Scholar] [CrossRef]
- Qiang, H.; Wang, L.; Ding, J.; Zhang, L. Multiobjective optimization of 6-DOF parallel manipulator for desired total orientation workspace. Math. Probl. Eng. 2019, 2019, 5353825. [Google Scholar] [CrossRef]
- Deng, Z.; Hou, X.; Wang, S. Workspace Optimization of a 6-RSS Stewart-Gough Robotic Platform to Assist Ultrasound Diagnosis. In Proceedings of the 2021 IEEE 1st International Conference on Digital Twins and Parallel Intelligence (DTPI), Beijing, China, 15 July–15 August 2021; pp. 230–233. [Google Scholar]
- Kucuk, S. Dexterous workspace optimization for a new hybrid parallel robot manipulator. J. Mech. Robot. 2018, 10, 064503. [Google Scholar] [CrossRef]
- Yen, P.L.; Wang, C.H.; Lin, H.T.; Hung, S.S. Optimization design for a compact redundant hybrid parallel kinematic machine. Robot. Comput.-Integr. Manuf. 2019, 58, 172–180. [Google Scholar] [CrossRef]
- Zhi, X.; Bai, W.; Yeatman, E.M. Kinematic Parameter Optimization of a Miniaturized Surgical Instrument Based on Dexterous Workspace Determination. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 112–118. [Google Scholar]
- Huang, Y.; Li, Z.; Xing, K.; Gong, H. A manipulator size optimization method based on dexterous workspace volume. Cobot 2022, 1, 3. [Google Scholar] [CrossRef]
- Russo, M.; Ceccarelli, M. A geometrical formulation for the workspace of parallel manipulators. Robotica 2021, 40, 2581–2591. [Google Scholar] [CrossRef]
- Lee, T.W.; Yang, D.C.H. On the evaluation of manipulator workspace. J. Mech. Transm. Autom. Des. 1983, 105, 70–77. [Google Scholar] [CrossRef]
- Nabavi, S.N.; Shariatee, M.; Enferadi, J.; Akbarzadeh, A. Parametric design and multi-objective optimization of a general 6-PUS parallel manipulator. Mech. Mach. Theory 2020, 152, 103913. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, H.; Pan, X.; Hu, M. Configuration analysis and optimization of collaborative robots. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1319–1324. [Google Scholar]
- Zhang, D.; Liu, J.; Gao, A.; Yang, G.Z. An ergonomic shared workspace analysis framework for the optimal placement of a compact master control console. IEEE Robot. Autom. Lett. 2020, 5, 2995–3002. [Google Scholar] [CrossRef]
- Ganesh, S.S.; Rao, A.K. Design Optimization of a 3-DOF Star Triangle Manipulator for Machining Applications. Mater. Today Proc. 2020, 22, 1845–1852. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, J.; Gao, Q.; Cui, G.; Shi, K.; Yao, Y.A. Multi-objective optimization of a redundantly actuated parallel robot mechanism for special machining. Mech. Sci. 2022, 13, 123–136. [Google Scholar] [CrossRef]
- Russo, M.; Barrientos-Diez, J.; Axinte, D. A kinematic coupling mechanism with binary electromagnetic actuators for high-precision positioning. IEEE ASME Trans. Mechatron. 2021, 27, 892–903. [Google Scholar] [CrossRef]
- Kim, J.O.; Khosla, K. Dexterity measures for design and control of manipulators. In Proceedings of the IROS’91: IEEE/RSJ International Workshop on Intelligent Robots and Systems’ 91, Osaka, Japan, 3–5 November 1991; pp. 758–763. [Google Scholar]
- Doty, K.L.; Melchiorri, C.; Schwartz, E.M.; Bonivento, C. Robot manipulability. IEEE Trans. Robot. Autom. 1995, 11, 462–468. [Google Scholar] [CrossRef]
- Vahrenkamp, N.; Asfour, T.; Metta, G.; Sandini, G.; Dillmann, R. Manipulability analysis. In Proceedings of the 2012 12th IEEE—Ras International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 568–573. [Google Scholar]
- Russo, M.; Herrero, S.; Altuzarra, O.; Ceccarelli, M. Kinematic analysis and multi-objective optimization of a 3-UPR parallel mechanism for a robotic leg. Mech. Mach. Theory 2018, 120, 192–202. [Google Scholar] [CrossRef]
- Eryılmaz, C.; Omurlu, V.E. Sqp optimization of 6dof 3x3 upu parallel robotic system for singularity free and maximized reachable workspace. J. Robot. 2019, 2019, 3928705. [Google Scholar] [CrossRef]
- Khoshnoodi, H.; Rahmani Hanzaki, A.; Talebi, H.A. Kinematics, singularity study and optimization of an innovative spherical parallel manipulator with large workspace. J. Intell. Robot. Syst. 2018, 92, 309–321. [Google Scholar] [CrossRef]
- Simas, H.; Di Gregorio, R. Adaptive Extended Jacobian Can Improve the Global Conditioning Index of Redundant Robots. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec City, Canada, 26–29 August 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51814, p. V05BT07A015. [Google Scholar]
- Enferadi, J.; Nikrooz, R. The performance indices optimization of a symmetrical fully spherical parallel mechanism for dimensional synthesis. J. Intell. Robot. Syst. 2018, 90, 305–321. [Google Scholar] [CrossRef]
- Simas, H.; Di Gregorio, R. Smooth transition for collision avoidance of redundant robots: An on-line polynomial approach. Robot. Comput.-Integr. Manuf. 2021, 72, 102087. [Google Scholar] [CrossRef]
- Miao, Y.; Zhijiang, D.; Lining, S.; Wei, D. Optimal design, modeling and control of a long stroke 3-PRR compliant parallel manipulator with variable thickness flexure pivots. Robot. Comput.-Integr. Manuf. 2019, 60, 23–33. [Google Scholar] [CrossRef]
- Balaji, K.; Khan, B.S.H. Kinematic analysis and performance evaluation of novel PRS parallel mechanism. IOP Conf. Ser. Mater. Sci. Eng. 2018, 310, 012007. [Google Scholar] [CrossRef]
- Khalilpour, S.A.; Loloei, A.Z.; Taghirad, H.D.; Masouleh, M.T. Feasible kinematic sensitivity in cable robots based on interval analysis. In Cable-Driven Parallel Robots; Springer: Berlin/Heidelberg, Germany, 2013; pp. 233–249. [Google Scholar]
- Hosseini, M.A.; Daniali, H.R.M.; Taghirad, H.D. Dexterous workspace optimization of a tricept parallel manipulator. Adv. Robot. 2011, 25, 1697–1712. [Google Scholar] [CrossRef]
- Fang, H.C.; Ong, S.K.; Nee, A.Y.C. Robot path planning optimization for welding complex joints. Int. J. Adv. Manuf. Technol. 2017, 90, 3829–3839. [Google Scholar] [CrossRef]
- Guenard, N.; Hamel, T.; Mahony, R. A practical visual servo control for an unmanned aerial vehicle. IEEE Trans. Robot. 2008, 24, 331–340. [Google Scholar] [CrossRef]
- Tsai, M.J.; Lee, H.W. Generalized evaluation for the transmission performance of mechanisms. Mech. Mach. Theory 1994, 29, 607–618. [Google Scholar] [CrossRef]
- Takeda, Y.; Funabashi, H. Motion transmissibility of in-parallel actuated manipulators. JSME Int. J. Ser. C Dyn. Control Robot. Des. Manuf. 1995, 38, 749–755. [Google Scholar] [CrossRef][Green Version]
- Russo, M.; Ceccarelli, M.; Takeda, Y. Force transmission and constraint analysis of a 3-SPR parallel manipulator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4399–4409. [Google Scholar] [CrossRef]
- Che, L.; Chen, G.; Jiang, H.; Du, L.; Wen, S. Dimensional synthesis for a Rec4 parallel mechanism with maximum transmission workspace. Mech. Mach. Theory 2020, 153, 104008. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, G.; Jin, K.; Liu, S.; Gardoni, P.; Li, Z. Force/motion transmissibility analysis and parameters optimization of hybrid mechanisms with prescribed workspace. Eng. Anal. Bound. Elem. 2022, 139, 264–277. [Google Scholar] [CrossRef]
- Kövecses, J.; Angeles, J. The stiffness matrix in elastically articulated rigid-body systems. Multibody Syst. Dyn. 2007, 18, 169–184. [Google Scholar] [CrossRef]
- Caccavale, F.; Siciliano, B.; Villani, L. Robot impedance control with nondiagonal stiffness. IEEE Trans. Autom. Control 1999, 44, 1943–1946. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Yue, Y.; Wen, K.; Zhou, Y. Optimization of comprehensive stiffness performance index for industrial robot in milling process. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 544–549. [Google Scholar]
- Wolf, S.; Eiberger, O.; Hirzinger, G. The DLR FSJ: Energy based design of a variable stiffness joint. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5082–5089. [Google Scholar]
- Russo, M.; Sriratanasak, N.; Ba, W.; Dong, X.; Mohammad, A.; Axinte, D. Cooperative continuum robots: Enhancing individual continuum arms by reconfiguring into a parallel manipulator. IEEE Robot. Autom. Lett. 2021, 7, 1558–1565. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Li, J.R.; Xie, H.L.; Wang, Q.H.; Zhou, X.F. Region-based toolpath generation for robotic milling of freeform surfaces with stiffness optimization. Robot. Comput.-Integr. Manuf. 2020, 64, 101953. [Google Scholar] [CrossRef]
- Cvitanic, T.; Nguyen, V.; Melkote, S.N. Pose optimization in robotic machining using static and dynamic stiffness models. Robot. Comput.-Integr. Manuf. 2020, 66, 101992. [Google Scholar] [CrossRef]
- Celikag, H.; Sims, N.D.; Ozturk, E. Cartesian stiffness optimization for serial arm robots. Procedia CIRP 2018, 77, 566–569. [Google Scholar] [CrossRef]
- Xiong, G.; Ding, Y.; Zhu, L. Stiffness-based pose optimization of an industrial robot for five-axis milling. Robot. Comput.-Integr. Manuf. 2019, 55, 19–28. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Ma, O.; Angeles, J. Optimum design of manipulators under dynamic isotropy conditions. In Proceedings of the [1993] Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; pp. 470–475. [Google Scholar]
- Asada, H. Dynamic analysis and design of robot manipulators using inertia ellipsoids. In Proceedings of the 1984 IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 13–15 March 1984; Volume 1, pp. 94–102. [Google Scholar]
- Nabavi, S.N.; Akbarzadeh, A.; Enferadi, J.; Kardan, I. A homogeneous payload specific performance index for robot manipulators based on the kinetic energy. Mech. Mach. Theory 2018, 130, 330–345. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Autonomous Robot Vehicles; Springer: New York, NY, USA, 1986; pp. 396–404. [Google Scholar]
- Vergnano, A.; Thorstensson, C.; Lennartson, B.; Falkman, P.; Pellicciari, M.; Leali, F.; Biller, S. Modeling and optimization of energy consumption in cooperative multi-robot systems. IEEE Trans. Autom. Sci. Eng. 2012, 9, 423–428. [Google Scholar] [CrossRef]
- Roy, S.S.; Pratihar, D.K. Effects of turning gait parameters on energy consumption and stability of a six-legged walking robot. Robot. Auton. Syst. 2012, 60, 72–82. [Google Scholar] [CrossRef]
- Nilakantan, J.M.; Huang, G.Q.; Ponnambalam, S.G. An investigation on minimizing cycle time and total energy consumption in robotic assembly line systems. J. Clean. Prod. 2015, 90, 311–325. [Google Scholar] [CrossRef]
- Gadaleta, M.; Pellicciari, M.; Berselli, G. Optimization of the energy consumption of industrial robots for automatic code generation. Robot. Comput.-Integr. Manuf. 2019, 57, 452–464. [Google Scholar] [CrossRef]
- Modares, J.; Ghanei, F.; Mastronarde, N.; Dantu, K. Ub-anc planner: Energy efficient coverage path planning with multiple drones. In Proceedings of the 2017 IEEE international conference on robotics and automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6182–6189. [Google Scholar]
- Mansouri, I.; Ouali, M. The power manipulability–A new homogeneous performance index of robot manipulators. Robot. Comput.-Integr. Manuf. 2011, 27, 434–449. [Google Scholar] [CrossRef]
- Kaliński, K.J.; Mazur, M. Optimal control of 2-wheeled mobile robot at energy performance index. Mech. Syst. Signal Process. 2016, 70, 373–386. [Google Scholar] [CrossRef]
- Dos Santos, R.R.; Steffen, V.; Saramago, S.D.F.P. Optimal task placement of a serial robot manipulator for manipulability and mechanical power optimization. Intell. Inf. Manag. 2010, 2, 2779. [Google Scholar] [CrossRef]
- Vidussi, F.; Boscariol, P.; Scalera, L.; Gasparetto, A. Local and trajectory-based indexes for task-related energetic performance optimization of robotic manipulators. J. Mech. Robot. 2021, 13, 021018. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective optimization. In Search Methodologies; Springer: Boston, MA, USA, 2014; pp. 403–449. [Google Scholar]
- Zio, E.; Bazzo, R. A clustering procedure for reducing the number of representative solutions in the Pareto Front of multiobjective optimization problems. Eur. J. Oper. Res. 2011, 210, 624–634. [Google Scholar] [CrossRef]
- De la Fuente, D.; Vega-Rodríguez, M.A.; Pérez, C.J. Automatic selection of a single solution from the Pareto front to identify key players in social networks. Knowl.-Based Syst. 2018, 160, 228–236. [Google Scholar] [CrossRef]
- Sanchez-Gomez, J.M.; Vega-Rodríguez, M.A.; Pérez, C.J. Comparison of automatic methods for reducing the Pareto front to a single solution applied to multi-document text summarization. Knowl.-Based Syst. 2019, 174, 123–136. [Google Scholar] [CrossRef]
- Degrave, J.; Hermans, M.; Dambre, J. A differentiable physics engine for deep learning in robotics. Front. Neurorobotics 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kim, S.-H.; Kim, T.; Kang, B.B.; Lee, M.; Park, W.; Ku, S.; Kim, D.; Kwon, J.; Lee, H.; et al. Review of machine learning methods in soft robotics. PLoS ONE 2021, 16, e0246102. [Google Scholar] [CrossRef] [PubMed]
- Berkenkamp, F.; Krause, A.; Schoellig, A.P. Bayesian optimization with safety constraints: Safe and automatic parameter tuning in robotics. Mach. Learn. 2021, 1–35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).