Optimal Design of Energy Sources for a Photovoltaic/Fuel Cell Extended-Range Agricultural Mobile Robot
Abstract
1. Introduction
2. Materials and Methods
2.1. Project Background
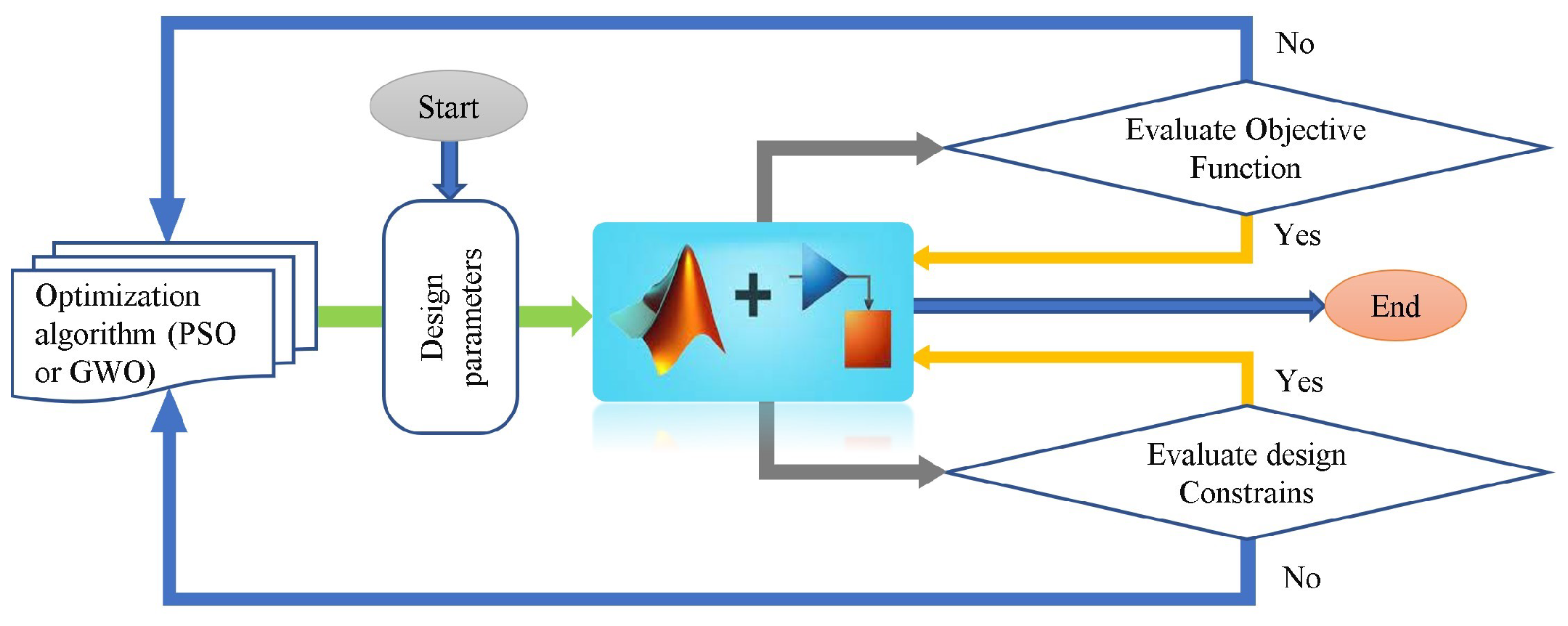
2.2. Proposed Design Process for the PV/FCAMR Architecture
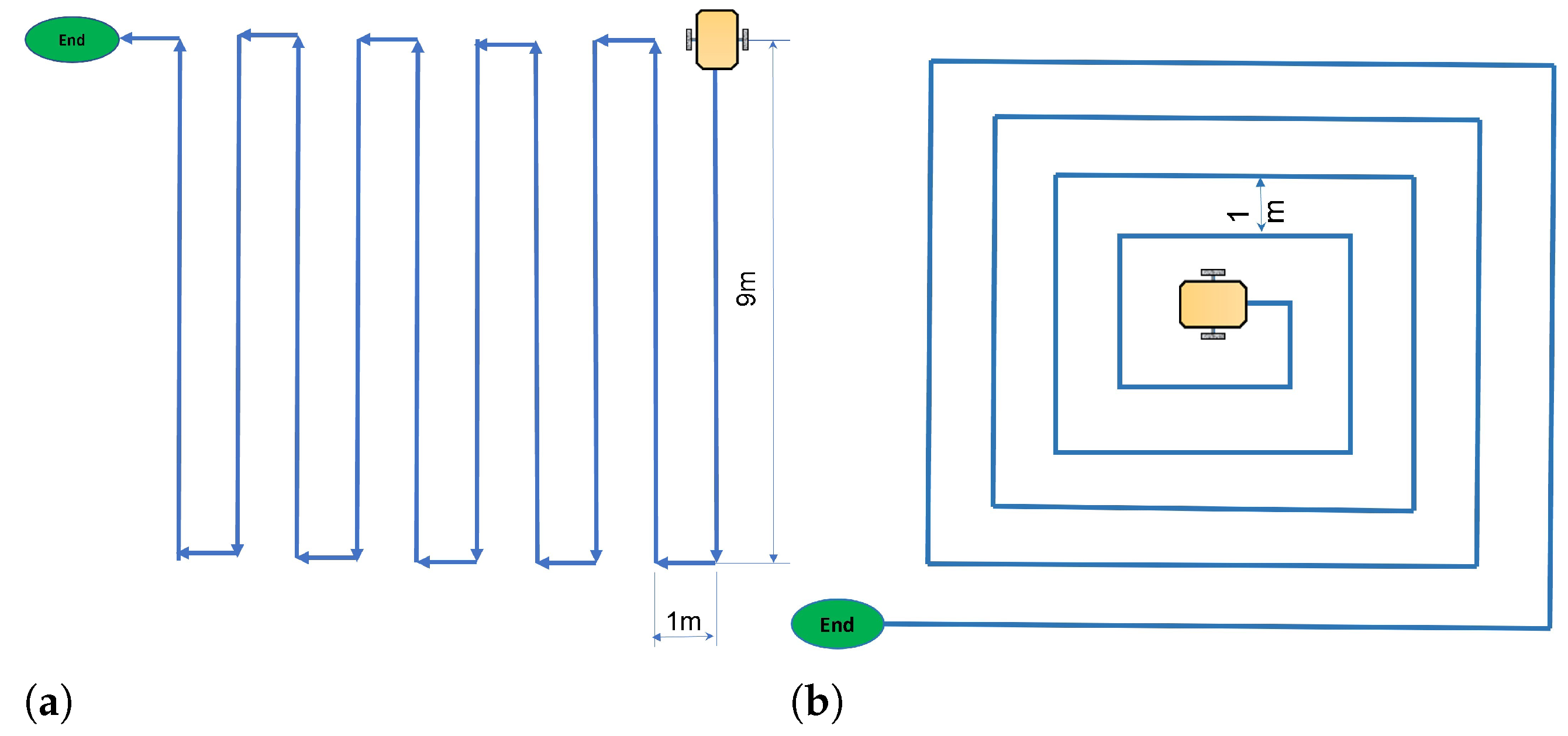
2.3. Working Cycle Design and Extraction
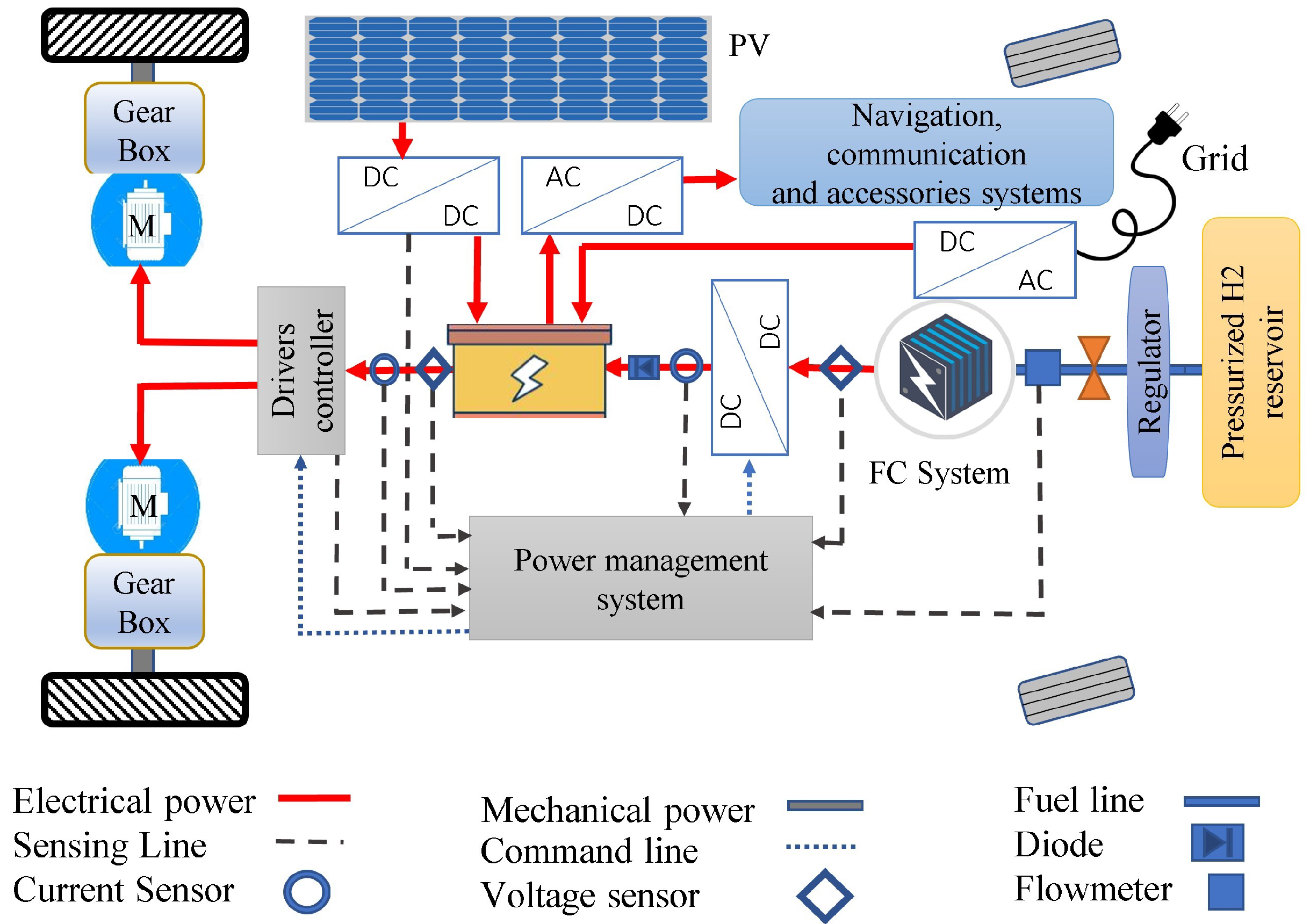
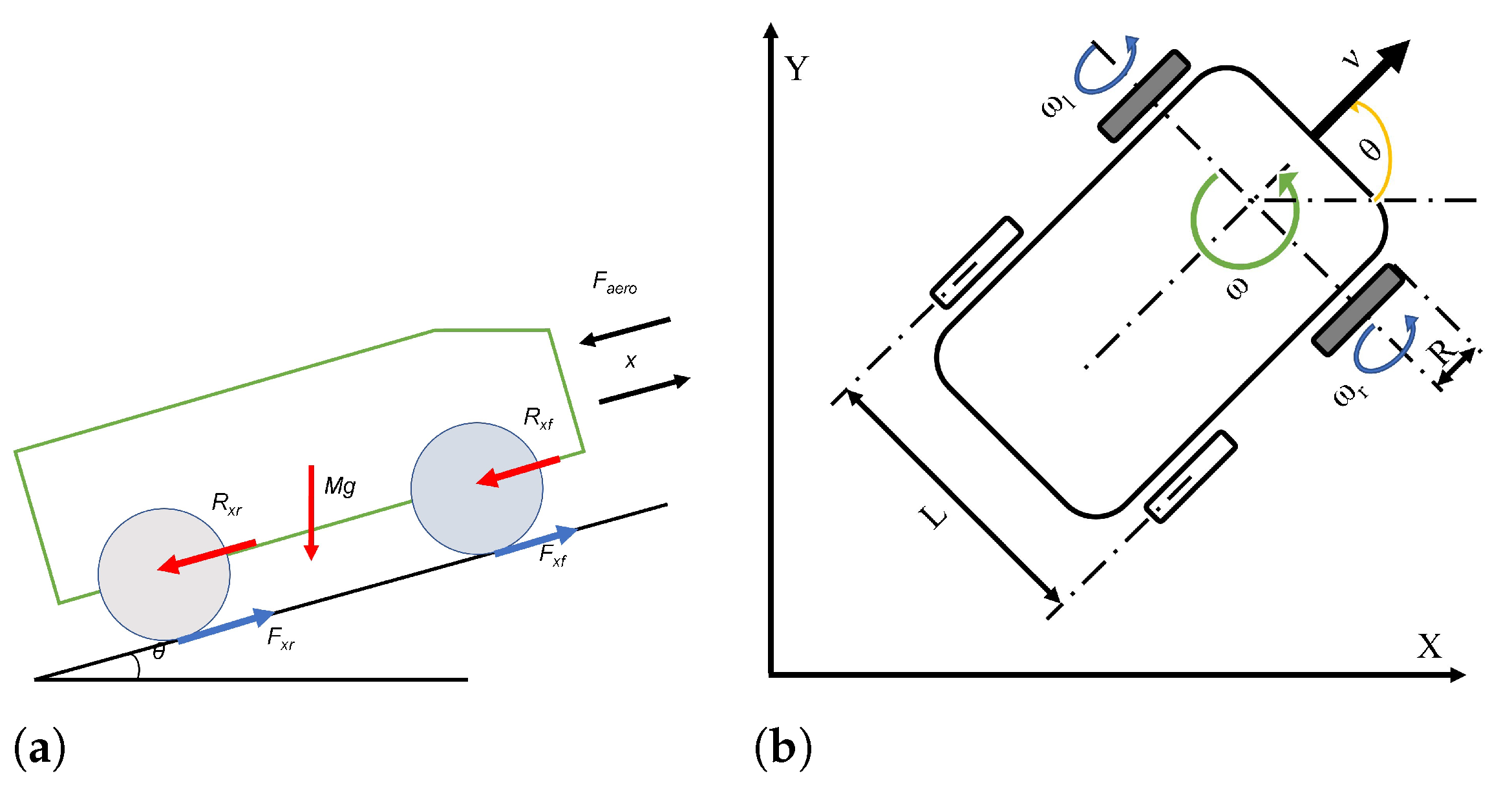
2.4. The FCAMR Powertrain Modeling
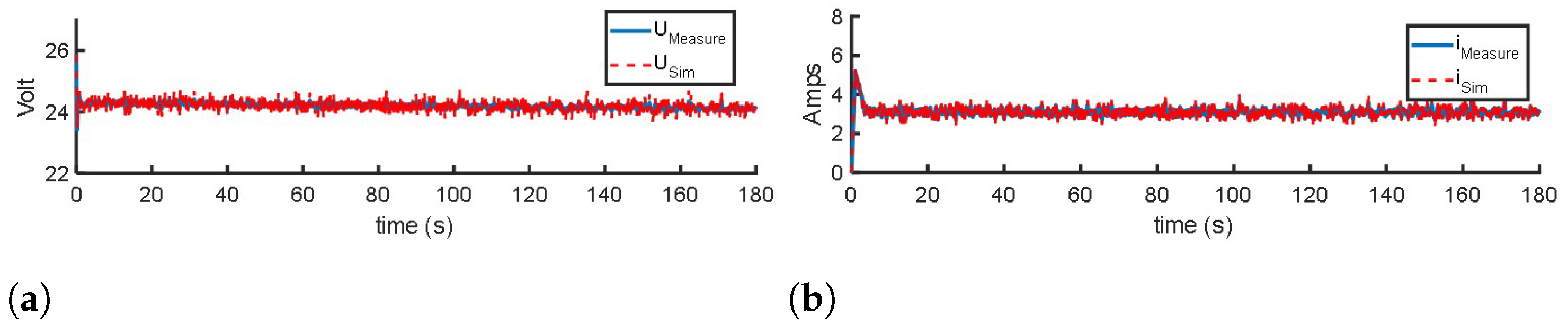
2.4.1. Powertrain Model Evaluation
2.4.2. Energy Requirements of Traction System
2.4.3. Initial Parameters of Energy Storage Subsystem
2.4.4. Fuel Cell as a Range Extender
2.4.5. Photovoltaic System as an Energy Assistance
3. Component Sizing and Design Optimization
3.1. Particle Swarm Optimization (PSO)
3.2. Grey Wolf Optimization (GWO)
- Observe, race, and approach prey;
- Chasing, turning and provoking the prey until it stops;
- Attack on prey.
3.3. Model-in-the-Loop Optimization Process and Problem Definition
- Maximum speed: 2 m/s;
- Maximum acceleration: 1 m/s;
- Gradeability ≥15% (1 m/s).
3.4. Energy Management Strategy
4. Results and Discussion
4.1. Working Cycle Evaluation
4.2. Optimization Performance Evaluation and Working Cycle Effect on Components Size of the FCAMR
4.3. Working Cycle and Optimization Effects on the FCAMR Energy Cost
4.4. Power Split between Power Sources on Different Working Cycles
5. Conclusions
- The FC system and battery pack size increased on working cycles with more rotational motion and stop-and-go situations. Therefore, the vehicle was less efficient, and the powertrain obtained higher cost in this working cycle. The drivetrain fuel consumption with a rule-based component sizing method is reduced by up to 12.21% compared to a PSO optimization-based method. The total cost of the PSO optimized powertrain was 8.79% lower than the one obtained by theoretical sizing method.
- Adding the PV system to the energy system increases the initial cost of the PV/FCAMR but slightly decreases the FC and battery pack size parameters. In addition, a PV system can extend the vehicle range by up to 5% and reduce fuel consumption costs by 7% compared to energy storage systems without PV.
- The proposed powertrain arrangement extends the autonomy of the basic pure electric system by 350% as opposed to the sole battery-powered system. This autonomy could allow the vehicle run for more than 10 h a day under the typical cycle with a hydrogen tank filled with 0.15 kg H2. The system studied in this research is a primary test bed for future works of the hybrid FCAMR in various applications such as seeding, spraying, and plant phenotyping. This technique could be used as a prototypical design strategy for other hybrid AMRs according to the customer’s needs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Despoudi, S.; Sivarajah, U.; Dora, M. Definition of Agricultural Supply Chains and Sustainability Issues. In From Linear to Circular Food Supply Chains: Achieving Sustainable Change; Springer International Publishing: Cham, Switzerlands, 2021; Chapter 1; pp. 3–14. [Google Scholar] [CrossRef]
- Rahman, M.M.; Khan, I.; Field, D.L.; Techato, K.; Alameh, K. Powering agriculture: Present status, future potential, and challenges of renewable energy applications. Renew. Energy 2022, 188, 731–749. [Google Scholar] [CrossRef]
- Ghobadpour, A.; Monsalve, G.; Cardenas, A.; Mousazadeh, H. Off-Road Electric Vehicles and Autonomous Robots in Agricultural Sector: Trends, Challenges, and Opportunities. Vehicles 2022, 4, 843–864. [Google Scholar] [CrossRef]
- Ghalazman, E.A.; Das, G.P.; Gould, I.; Zarafshan, P.; Rajendran, S.V.; Heselden, J.; Badiee, A.; Wright, I.; Pearson, S. Chapter 10—Applications of robotic and solar energy in precision agriculture and smart farming. In Solar Energy Advancements in Agriculture and Food Production Systems; Gorjian, S., Campana, P.E., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 351–390. [Google Scholar] [CrossRef]
- Kim, K.; Deb, A.; Cappelleri, D.J. P-AgBot: In-Row & Under-Canopy Agricultural Robot for Monitoring and Physical Sampling. IEEE Robot. Autom. Lett. 2022, 7, 7942–7949. [Google Scholar]
- Gai, J.; Xiang, L.; Tang, L. Using a depth camera for crop row detection and mapping for under-canopy navigation of agricultural robotic vehicle. Comput. Electron. Agric. 2021, 188, 106301. [Google Scholar] [CrossRef]
- Vibhute, A.S.; Tate Deshmukh, K.R.; Hindule, R.S.; Sonawane, S.M. Pest Management System Using Agriculture Robot. In Proceedings of the Techno-Societal 2020; Pawar, P.M., Balasubramaniam, R., Ronge, B.P., Salunkhe, S.B., Vibhute, A.S., Melinamath, B., Eds.; Springer International Publishing: Cham, Switzerlands, 2021; pp. 829–837. [Google Scholar]
- Huang, C.H.; Chen, P.J.; Lin, Y.J.; Chen, B.W.; Zheng, J.X. A robot-based intelligent management design for agricultural cyber-physical systems. Comput. Electron. Agric. 2021, 181, 105967. [Google Scholar] [CrossRef]
- Gao, X.; Li, J.; Fan, L.; Zhou, Q.; Yin, K.; Wang, J.; Song, C.; Huang, L.; Wang, Z. Review of wheeled mobile robots’ navigation problems and application prospects in agriculture. IEEE Access 2018, 6, 49248–49268. [Google Scholar] [CrossRef]
- Raj, R.; Aravind, A.; Akshay, V.; Chandy, M.; Sharun, N. A seed planting robot with two control variables. In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; pp. 1025–1028. [Google Scholar]
- Sun, S.; Li, C.; Paterson, A.H. In-field high-throughput phenotyping of cotton plant height using LiDAR. Remote Sens. 2017, 9, 377. [Google Scholar] [CrossRef]
- Jorgensen, R.; Sorensen, C.; Maagaard, J.; Havn, I.; Jensen, K.; Sogaard, H.; Sorensen, L. Hortibot: A system design of a robotic tool carrier for high-tech plant nursing. Agric. Eng. Int. CIGR Ejournal 2007, 9. [Google Scholar]
- Ristorto, G.; Gallo, R.; Gasparetto, A.; Scalera, L.; Vidoni, R.; Mazzetto, F. A mobile laboratory for orchard health status monitoring in precision farming. Chem. Eng. Trans. 2017, 58, 661–666. [Google Scholar]
- Green, O.; Schmidt, T.; Pietrzkowski, R.P.; Jensen, K.; Larsen, M.; Jørgensen, R.N. Commercial autonomous agricultural platform: Kongskilde Robotti. In Proceedings of the Second International Conference on Robotics, Associated High-Technologies and Equipment for Agriculture and Forestry: New Trends in Mobile Robotics, Perception and Actuation for Agriculture and Forestry, RHEA, Madrid, Spain, 21–23 May 2014; pp. 351–356. [Google Scholar]
- Qiu, Q.; Fan, Z.; Meng, Z.; Zhang, Q.; Cong, Y.; Li, B.; Wang, N.; Zhao, C. Extended Ackerman Steering Principle for the coordinated movement control of a four wheel drive agricultural mobile robot. Comput. Electron. Agric. 2018, 152, 40–50. [Google Scholar] [CrossRef]
- Aguiar, A.S.; dos Santos, F.N.; Cunha, J.B.; Sobreira, H.; Sousa, A.J. Localization and mapping for robots in agriculture and forestry: A survey. Robotics 2020, 9, 97. [Google Scholar] [CrossRef]
- Iqbal, J.; Xu, R.; Sun, S.; Li, C. Simulation of an autonomous mobile robot for LiDAR-based in-field phenotyping and navigation. Robotics 2020, 9, 46. [Google Scholar] [CrossRef]
- Oliveira, L.F.; Moreira, A.P.; Silva, M.F. Advances in agriculture robotics: A state-of-the-art review and challenges ahead. Robotics 2021, 10, 52. [Google Scholar] [CrossRef]
- Xu, R.; Li, C. A review of high-throughput field phenotyping systems: Focusing on ground robots. Plant Phenomics 2022, 2022. [Google Scholar] [CrossRef]
- Kumar, S.; Saket, R.; Dheer, D.K.; Holm-Nielsen, J.B.; Sanjeevikumar, P. Reliability enhancement of electrical power system including impacts of renewable energy sources: A comprehensive review. IET Gener. Transm. Distrib. 2020, 14, 1799–1815. [Google Scholar] [CrossRef]
- Chambers, M.; Birney, C.; Young, B.; Ingwersen, W. Proof of Concept for a US Air Emissions Physical Flows Account. In Proceedings of the 37th Iariw General Conference, Paper 662. Lexington, MA, USA, 22–26 August 2022. [Google Scholar]
- Li, M.; Bai, Y.; Zhang, C.; Song, Y.; Jiang, S.; Grouset, D.; Zhang, M. Review on the research of hydrogen storage system fast refueling in fuel cell vehicle. Int. J. Hydrogen Energy 2019, 44, 10677–10693. [Google Scholar] [CrossRef]
- Ghobadpour, A.; Amamou, A.; Kelouwani, S.; Zioui, N.; Zeghmi, L. Impact of powertrain components size and degradation level on the energy management of a hybrid industrial self-guided vehicle. Energies 2020, 13, 5041. [Google Scholar] [CrossRef]
- Rossi, C.; Pontara, D.; Falcomer, C.; Bertoldi, M.; Mandrioli, R. A hybrid–electric driveline for agricultural tractors based on an e-CVT power-split transmission. Energies 2021, 14, 6912. [Google Scholar] [CrossRef]
- Ghobadpour, A.; Boulon, L.; Mousazadeh, H.; Malvajerdi, A.S.; Rafiee, S. State of the art of autonomous agricultural off-road vehicles driven by renewable energy systems. Energy Procedia 2019, 162, 4–13. [Google Scholar] [CrossRef]
- Reddy, N.V.; Reddy, A.; Pranavadithya, S.; Kumar, J.J. A critical review on agricultural robots. Int. J. Mech. Eng. Technol. 2016, 7, 183–188. [Google Scholar]
- Vaideeswaran, V.; Bhuvanesh, S.; Devasena, M. Battery Management Systems for Electric Vehicles using Lithium Ion Batteries. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019; Volume 1, pp. 1–9. [Google Scholar]
- Castelli Dezza, F.; Musolino, V.; Piegari, L.; Rizzo, R. Hybrid battery–supercapacitor system for full electric forklifts. IET Electr. Syst. Transp. 2019, 9, 16–23. [Google Scholar] [CrossRef]
- Cardenas, A.; Guzman, C.; Martinez, W. EV Overnight Charging Strategy in Residential Sector: Case of Winter Season in Quebec. Vehicles 2021, 3, 557–577. [Google Scholar] [CrossRef]
- Noura, N.; Boulon, L.; Jemeï, S. A review of battery state of health estimation methods: Hybrid electric vehicle challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Albarbar, A.; Alrweq, M. Proton Exchange Membrane Fuel Cells: Design, Modelling and Performance Assessment Techniques; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fathabadi, H. Combining a proton exchange membrane fuel cell (PEMFC) stack with a Li-ion battery to supply the power needs of a hybrid electric vehicle. Renew. Energy 2019, 130, 714–724. [Google Scholar] [CrossRef]
- Monsalve, G.; Ltaief-Belhaji, N.; Amoriya, V.; Cardenas, A. Kinematic Navigation Control of Differential Drive Agricultural Robot. In Proceedings of the CISTEM 2022—4th International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 26–28 October 2022. [Google Scholar]
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K.M. Modern Electric, Hybrid electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Turkmen, A.C.; Solmaz, S.; Celik, C. Analysis of fuel cell vehicles with advisor software. Renew. Sustain. Energy Rev. 2017, 70, 1066–1071. [Google Scholar] [CrossRef]
- Taghavipour, A.; Vajedi, M.; Azad, N.L.; McPhee, J. A comparative analysis of route-based energy management systems for PHEVs. Asian J. Control. 2016, 18, 29–39. [Google Scholar] [CrossRef]
- Andriaminahy, F.; Amamou, A.; Kelouwani, S.; Zioui, N.; Ghobadpour, A.; Agbossou, K. Comparative study of vehicle aerodynamic and rolling resistance coefficients estimation methods. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–5. [Google Scholar]
- Iclodean, C.; Varga, B.; Burnete, N.; Cimerdean, D.; Jurchiş, B. Comparison of different battery types for electric vehicles. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 252, p. 012058. [Google Scholar]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Monsalve, G.; Cardenas, A.; Martinez, W. SoC Estimation Techniques for Efficient Agricultural Robots. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–7. [Google Scholar]
- Hissel, D.; Turpin, C.; Astier, S.; Boulon, L.; Péra, M.C.; Jemei, S. A Review on Existing Modeling Methodologies for PEM Fuel Cell Systems. In Proceedings of the Fundamentals and Development of Fuel Cells, FDFC’08, Nantes, France, 23–27 April 2008; pp. 1–6. [Google Scholar]
- Horizon. Horizon-Pem-Fuel-Cell-h-300-Manual. Available online: https://www.fuelcellstore.com/manuals/horizon-pem-fuel-cell-h-300-manual.pdf (accessed on 24 November 2022).
- NREL. PVWatts Calculator. Available online: https://pvwatts.nrel.gov/pvwatts.phpl (accessed on 25 August 2022).
- Marcinkoski, J.; Vijayagopal, R.; Kast, J.; Duran, A. Driving an industry: Medium and heavy duty fuel cell electric truck component sizing. World Electr. Veh. J. 2016, 8, 78–89. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; Li, B.; Ji, J.; Zhao, K.; Hu, C. A review of power management strategies and component sizing methods for hybrid vehicles. Renew. Sustain. Energy Rev. 2018, 96, 132–144. [Google Scholar] [CrossRef]
- Mozaffari, A.; Vajedi, M.; Chehresaz, M.; Azad, N.L. Multi-objective component sizing of a power-split plug-in hybrid electric vehicle powertrain using Pareto-based natural optimization machines. Eng. Optim. 2016, 48, 361–379. [Google Scholar] [CrossRef]
- Wei, C.; Hofman, T.; Ilhan Caarls, E.; van Iperen, R. A review of the integrated design and control of electrified vehicles. Energies 2020, 13, 5454. [Google Scholar] [CrossRef]
- Jain, M.; Desai, C.; Kharma, N.; Williamson, S.S. Optimal powertrain component sizing of a fuel cell plug-in hybrid electric vehicle using multi-objective genetic algorithm. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 3741–3746. [Google Scholar]
- Sarma, U.; Ganguly, S. Determination of the component sizing for the PEM fuel cell-battery hybrid energy system for locomotive application using particle swarm optimization. J. Energy Storage 2018, 19, 247–259. [Google Scholar] [CrossRef]
- Tu, J.; Bai, Z.; Wu, X. Sizing of a Plug-In Hybrid Electric Vehicle with the Hybrid Energy Storage System. World Electr. Veh. J. 2022, 13, 110. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Aljarah, I.; Mafarja, M.; Heidari, A.A.; Faris, H. Grey wolf optimizer: Theory, literature review, and application in computational fluid dynamics problems. In Nature-Inspired Optimizers; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2020; pp. 87–105. [Google Scholar]
- Miller, E.L.; Thompson, S.T.; Randolph, K.; Hulvey, Z.; Rustagi, N.; Satyapal, S. US Department of Energy hydrogen and fuel cell technologies perspectives. MRS Bull. 2020, 45, 57–64. [Google Scholar] [CrossRef]
- Stephens, T.; Birky, A.; Gohlke, D. Vehicle Technologies and Fuel Cell Technologies Office Research and Development Programs: Prospective Benefits Assessment Report for Fiscal Year 2018r; Report; Argonne National Lab.(ANL): Argonne, IL, USA, 2017. [Google Scholar]








| Element | Description |
|---|---|
| LIDAR Sensor | YDLIDAR X2 |
| GPS | BN-220 |
| IMU | MPU-6050 |
| Wheel Encoders | US Digital E3-500-375-NE-E-D-3 |
| Main Microprocessor | ARM Cortex-A72 processor |
| Main Microcontroller | Atmega 328p |
| Current Sensor | LEM CAS 25-NP |
| Motor Controller | AF160 |
| Motors | Ampflow E30-150-12-G16 |
| Specification | Symbol | Value |
|---|---|---|
| Vehicle total mass | m | 90 kg |
| Frontal area | A | 0.7 m |
| Aerodynamic drag coefficient | 0.45 | |
| Air density | 1.225 kg/m | |
| Wheel Radius (R) | R | 0.096 m |
| Wheelbase | L | 0.75 m |
| Rolling resistance coefficient | 0.1 | |
| Gearbox ratio | 16 | |
| Gravity acceleration | g | 9.81 m/s |
| Design | Initial | Lower | Upper |
|---|---|---|---|
| Variable | Value | Bound | Bound |
| FC power rating (W) | 300 | 40 | 1000 |
| Battery capacity (Ah) | 24 | 3 | 40 |
| Minimum SOC allowed (%) | 30 | 20 | 40 |
| Maximum SOC allowed (%) | 90 | 80 | 100 |
| Rectangular | Circular | Standard | |
|---|---|---|---|
| Parameters | Movement | Movement | Deviation |
| Pattern | Pattern | ||
| Travel distance (m) | 100 | 100 | 0 |
| Time (s) | 180 | 230 | 50 |
| Average linear velocity (m/s) | 0.56 | 0.43 | 0.13 |
| Maximum linear velocity (m/s) | 1.29 | 1.2 | 0.09 |
| Average power requirement (W) | 135.86 | 138.61 | 2.75 |
| Maximum power requirement (W) | 460.95 | 371.03 | 61.92 |
| Number of rotational movements (N) | 18 | 19 | 1 |
| Total energy requirement (kJh) | 6.79 | 8.86 | 2.06 |
| Working Cycle Movement Pattern | Fuel Consumption | ||
|---|---|---|---|
| Before Optimization | After Optimization | ||
| GWO | PSO | ||
| Rectangular | +55 | +51 | +50 |
| Circular | +62 | +58 | +56 |
| Mixed | +59 | +54 | +53 |
| Variable | Unit | Value | |
|---|---|---|---|
| GWO | PSO | ||
| FC nominal power | W | 239 | 229 |
| Battery Max Power | W | 615 | 630 |
| Battery Capacity | Wh | 562 | 571 |
| Hydrogen tank capacity | kg@ 300bar | 0.15 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghobadpour, A.; Cardenas, A.; Monsalve, G.; Mousazadeh, H. Optimal Design of Energy Sources for a Photovoltaic/Fuel Cell Extended-Range Agricultural Mobile Robot. Robotics 2023, 12, 13. https://doi.org/10.3390/robotics12010013
Ghobadpour A, Cardenas A, Monsalve G, Mousazadeh H. Optimal Design of Energy Sources for a Photovoltaic/Fuel Cell Extended-Range Agricultural Mobile Robot. Robotics. 2023; 12(1):13. https://doi.org/10.3390/robotics12010013
Chicago/Turabian StyleGhobadpour, Amin, Alben Cardenas, German Monsalve, and Hossein Mousazadeh. 2023. "Optimal Design of Energy Sources for a Photovoltaic/Fuel Cell Extended-Range Agricultural Mobile Robot" Robotics 12, no. 1: 13. https://doi.org/10.3390/robotics12010013
APA StyleGhobadpour, A., Cardenas, A., Monsalve, G., & Mousazadeh, H. (2023). Optimal Design of Energy Sources for a Photovoltaic/Fuel Cell Extended-Range Agricultural Mobile Robot. Robotics, 12(1), 13. https://doi.org/10.3390/robotics12010013






