1. Introduction
Accuracy is becoming a key factor in large-scale processes and relevant European projects such as LaVA or DynaMITE (EMPIR European Metrology Programme for Innovation and Research) face these issues from different perspectives in response to critical sectors such as Aerospace, Naval, or Wind Power [
1,
2,
3]. In these industries, tracking end-effectors of several industrial robots (arm robots or wire robots), or the position of automated guided vehicles (AGV), are becoming critical in the progression of tasks such as the assembly of large structures, inspections, or manufacturing [
4,
5,
6]. For example, an aeronautic requirement is to drill holes to ±0.25 mm [
7]. Moreover, apart from accuracy, the latency of these systems is a relevant issue in terms of production times [
8].
Laser Tracker (LT) is the most common tool for tool center point (TCP) pose estimation due to its reliability and ease of use. For this reason, it is used to run many robot calibrations [
9]. The main advantage of tracking the end-effector is that this method allows us to study the behavior of the industrial robot using different loads or during warm-up. Both are relevant issues that the robot testing standard ISO 92831 highlights for modification during the characterization of the robot [
10,
11]. However, this technology needs an extra accessory (i.e., T-MAC of LEICA) to measure six Degrees of Freedom (DoF) and this is the most expensive LT unit. Furthermore, these accessories—which are usually placed on the robot tool—add weight, which implies higher levels of uncertainty due to robot deflection. In this sense, the photogrammetry technology becomes a real alternative to LT since it can measure the six DoF of objects, adding some retroreflective strikers to the track elements. Moreover, the economic cost is less than that of LT with the required accessory.
There are two strategies used to improve the accuracy of an industrial robot using a photogrammetry system [
9]: Tracking the end-effector (eye-to-hand configuration) or fixing the cameras on the robot and calculating the position using references (eye-in-hand configuration). Both strategies can be used for in-process tracking or only for the calibration of the industrial robot (Denavit–Hartenberg parameters) [
12]. While the eye-to-hand methodology is usually chosen for tracking during the process to close the control loop, the second strategy, eye-in-hand, reduces the difficulty of the calibration procedure, since the photogrammetry system can be clamped and removed from the robot. For example, a robot can commit a 1.8 mm error under drilling effort, and after modeling the arm robot using neural networks, this error can be reduced to 0.227 mm [
13]. Since the robot arm faces diverse situations, different loads, thermal distortions, speed, etc., the first strategy is recommended for challenging applications.
This research is focused on how to industrialize a multi-camera tracking system (eye-to-hand). The work is organized as follows: Firstly, the relevance of the uncertainty of extrinsic parameters is studied using three different measurement systems—Coordinate Measuring Machine (CMM), Laser Tracker (LT), and a Portable Photogrammetry (PP) system. In this case, CMM is considered the ground truth due to the low level of measurement uncertainty (see the
Section 3 for more information). The other two systems are the candidates to be used in large-scale volumes to measure the reference targets. It is important to choose one of these two systems because CMM does not allow the measurement of objects out of its reach.
After comparing LT and PP, validation was carried out in an industrial scenario following the guideline VDI2634 part 1 [
14]. In this case, LT was the ground truth used to track the end-effector of a robotic arm as it is simultaneously tracked by a multi-camera (MC) system.
To end the research, a simple industrial application was carried out. The temperature of the joints was recorded while tracking the end-effector during a warm-up cycle. The aim was to determine the temperature-induced deviation.
Before explaining the development, the state of the art of this topic is presented.
2. State of the Art
Photogrammetry is becoming an alternative for meeting the requirements of industrial robots while minimizing the amount of investment. Currently, it is necessary to attach targets to the object and to a reference to solve the relative positions between both. One current trend is to skip the target and use natural targets such as drill holes or shapes of the object to solve the problem [
15]. For example, the detection of these features allows dynamic quadruped robots to be guided through a long industrial scenario without artificial targets [
16]. However, to achieve the measurement uncertainty requirement, retroreflective targets must be detected to track the object.
However, not only the targets are part of a successful application of photogrammetry. Several critical points must be studied including intrinsic parameters, extrinsic parameters, static and dynamic reference, and the layout of targets on the objects. Additionally, 2D detection is a key factor that has been extensively studied [
17,
18].
The intrinsic camera parameters correct the lens distortion and the camera sensor. Several models propose how to correct the lens distortion and how to carry out the calibration [
19].
The extrinsic parameters, or the camera pose, are the relative position and orientation of the camera with respect to a reference. In a photogrammetry system, coded targets usually help to calculate this position. In the case of a MC system, a previous measurement is required to determine the dimensions of the reference object and the tracked object [
9]. These parameters can be solved both in a pre-process task (static reference) and in real-time, that is, during the measurements (dynamic reference) [
20]. Static reference is recommended when the cameras are in static positions regarding the references, and it is likely that a significant number of the reference points may be hidden by the object. Instead, the dynamic reference takes relevance when the reference is moving with respect to the camera, or if cameras can be moved due to flexible clamping or thermal drift.
Another factor to consider is the distribution of the targets on the object. Incorrect distribution can result in a high-uncertainty solution. It is well known that a 3D object helps reduce the uncertainty of the measurement [
3]. In some cases, it is not possible to create a 3D structure, so the camera layout increases its weight on the error budgeting. The same concept can be applied to the design of the reference; a 3D scenario covering all camera sensors improves the calculation of the extrinsic parameters. Sometimes, it is difficult to correctly position the camera regarding the work volume. To resolve this issue Hänel et al. have developed a robust method to achieve a reliable camera location [
21].
The main aim is to measure the reference to calculate the extrinsic camera parameters in large-scale scenarios. This is also known as an Enhanced Reference System. As in the LT network, the distribution of reference points to link the sensors (cameras or LT) is relevant in order to obtain a reliable result [
22,
23]. Additionally, the high uncertainty of the measurement may cause incorrect camera pairing. However, in photogrammetry, it is possible to use another source to measure the reference network. For example, both CMM and LT can measure these points in addition to photogrammetry itself. Kang et al. [
24] studied a different approach using a turntable to move the artefact.
In this paper, the relevance of the uncertainty of the reference network will be studied according to the steps mentioned in the introduction. The novelty of this research is the study of which technology, LT or PP, is adequate to measure the reference point of a MC. PP is regularly used to measure the reference points [
25]; however, this paper will determine whether LT can improve the accuracy of MC systems.
Once this technology is mature, a multi-camera system will enable human–robot collaboration, allowing both to be placed in the same space. MC can prevent a collision. This technology will also provide a channel of communication via gestures. This communication between robots and humans is highly challenging [
26].
In the next section, the material will be explained.
3. Material
For this research, the layout is composed of four industrial cameras (Teledyne DALSA Genie Nano 4020, Teledyne DALSA, Waterloo, SC, Canada, 12.4 MP, focal lens 16 mm). The intrinsic camera parameters were calibrated following the strategy of [
27] where a CMM was used to carry out the task.
As mentioned previously, two scenarios are identified: A CMM in the laboratory, and a robotic cell in an industrial environment. In the first scenario (see
Figure 1), a CMM ZEISS © ACCURA (Zeiss, Oberkochen, Germany) with a length measurement error E0 in μm of 1.2 + L/350 (L in mm). A KUKA IIWA robot (KUKA, Augsburg, Germany) was used to move the tracking object inside the CMM workspace (see
Figure 1). In the second scenario, the robot was a Stäubli TX200 (Stäubli, Pfäffikon, Switzerland) that covers a larger volume of work. It is important to emphasize that the robot’s accuracy did not contribute to the uncertainty chain; the robot only moves the tracked object. In both scenarios, the LEICA AT 402 LT (HEXAGON, Stockholm, Sweden) was used. The main specifications of this LT are accuracy/typical values ±7.5 μm + 3 μm/m and ±15 μm + 6 μm/m of maximum permissible error (MPE).
Fifteen target nests were distributed along the granite of the CMM (1.5 m × 1 m) with different heights (up to 100 mm). These target nests allowed us to include a sphere to measure CMM (see
Figure 2), a Spherically Mounted Retroreflector (SMR) (HEXAGON, Stockholm, Sweden) to measure LT, and a hemisphere with one reflective target to measure PP.
Moreover, the coded targets have a binary codification around a circle which allows us to calculate a first approximation from the placement of the cameras. Using this approximation, the reference points are identified and used to calculate the final position of the cameras.
Two different trackable objects have been used; both have been adapted to the end-effector of the robot (see
Figure 3). In both cases, coded targets cover the end-effector using a 3D-printed structure to generate semispherical shapes. In this research, we placed the maximum number of targets, and this number will be optimized to reduce the quantity in the future.
Moreover, six nests have been clamped into the end-effector to present the possibility of measuring the same point using different measuring systems. The CMM measures the point by probing a 1.5′/38.1 mm diameter sphere, the LT by measuring the position of a same-sized spherically mounted reflector (SMR), and photogrammetry by mounting a special target on a hemisphere.
As only the non-coded targets have been measured by the CMM and LT, two steps are necessary to calculate the position of each camera. In the first, the coded targets provide a codification to the non-coded targets (see
Figure 4a), identifying and matching them to the LT and CMM measurements. The position and orientation of the cameras are then calculated by reducing the root mean square (RMS) of the reprojection of these points.
After solving the position of the camera with respect to the reference targets, a similar process is carried out to solve the position of the object with respect to the reference targets (see
Figure 4b). However, in this case, the information from all the cameras is considered. This improves the quality, reducing the uncertainty of the solution.
During the measurement of the tracked object, six non-coded targets were placed in the nest where the CMM (laboratory scenario) and LT (industrial scenario) measure the position of the object. In this way, MC can calculate the same position as CMM and LT. To determine the orientation, at least three points are required. For this kind of test, only the relative distance is required because the orientation of the tracked object is unmodified, and MC solves the same position measured by CMM and LT.
CMM Zeiss ACCURA is the ground truth, as the uncertainty of the process of measuring with this system relates to microns (1.2 + 900/350 = 3.8 μm), and is 10 times less than the expected error. The uncertainty sources are the machine, sphere (sphericity of 3 μm), and nests (up to 12 μm), so the sum of squares is 12.9 μm; the main contributor is the nest.
Moreover, the LT LEICA 402 and VSET (a PP system) have been used to measure the reference. VSET is a portable photogrammetry system developed by IDEKO [
28,
29].
Regarding the two scenarios, the four cameras were placed in a square shape using a photographic tripod in the laboratory test and metallic columns in the industrial case. In the CMM, the camera layout is around 2.5 m × 2.4 m and the height with respect to the reference plane is approximately 0.75 m. The movement allowed inside of CMM with the Iiwa robot was 455 mm × 376 mm × 454 mm. Meanwhile, the camera layout is smaller in the industrial scenario due to the surrounding fence (which is 2 m × 2.1 m), but the height with respect to the reference was twice as high to cover more volume, at around 1.5 m. In the industrial scenario, the work volume was 900 mm × 300 mm × 200 mm.
4. Methodology
This section analyses the methodology used to measure the extrinsic reference to calculate the poses of the cameras. This is a key point when industrializing a multi-camera system due to the limitations of accuracy. To carry out this analysis, a CMM was chosen as the ground truth and it was compared to two large-scale technologies: LT and PP. The CMM performance is two orders of magnitude better (1 µm) than the two studied systems (100 µm). The reference targets were measured three times per instrument and the best fit was run to match all the measurements. The repeatability of instruments was analyzed and the accuracy was compared to the CMM measurements.
Once the reference was measured, a test to check the performance of the MC was executed. This test consists of placing the tracked object in several positions and solving them. The only point modified during the test was the reference values of the three systems used to study their influence. To ensure that the single change was the reference measurement source, the same photos were processed by changing only this input. The main assumption is that the robot does not move among the different measurements, regardless of position. It was tested by repeating the same measurement 5 times in one position at the tested locations, and the repeatability was 0.003 mm (standard deviation k = 1). It is higher than a fixed element due to the contact of CMM against the robot.
The methodology used to compare the technologies was followed by the German standard VDI/VDE 2634 part 1, which is used to calculate the Length Measurement Error (LME) of a point-to-point measurement system. This guideline suggests manufacturing 7 bars, with each bar made of at least 5 test lengths, taking one of the sides as the origin of the deviations. The authors adapted this guideline and instead of manufacturing the bars, virtual bars were used, implementing the suggestion of the rate distance of the testing volume (see
Figure 5). A robot was used to help with the placement of the target spatial position, with the distance checked by the CMM in each position. The VDI-VDE2634 part 1 standard recommends this distribution to allow us to estimate the error in the volume with minimal effort. For each virtual bar tested, the robot moves the tracked object to the origin and then moves to the other positions (the blue dots in
Figure 5). The deviation is the difference between the CMM and MC measurements using one side of the bar as the origin. As mentioned, it is important to highlight that the robot did not participate in the uncertainty chain because the CMM measures the position.
CMM played two roles:
- (a)
It measured the target to calculate the extrinsic value.
- (b)
It measured the position of the VDI/VDE 2634 part 1.
Once the method used to measure the extrinsic references has been validated, an industrial scenario is tested. In this test, only photogrammetry was used to measure the targets to calculate the pose of the camera, and the same LT of the previous test was used as the ground truth. Regarding the laboratory test, the volume is greater due to the features of the robot (Stäubli TX200). This robot was placed on a table while the position of the reference markers was determined.
Once the relevance of this development was obtained, a thermal study was carried out. Specifically, the end-effector was tracked. The nominal robot distance can be modified due to the temperature, either by warming up the robot itself or via ambient change. This test allows us to estimate and confirm a correlation between position and temperature.
5. Results and Discussion
This section is divided into three subsections: A laboratory scenario, an industrial scenario, and experimental use. The temporal sequence was in the same order and the lessons from the laboratory scenario were applied to the industrial scenario.
5.1. Results and Discussion: Laboratory Scenario
Firstly, the 15 reference targets were measured three times according to the three measurement systems. Three values were presented: Time, repeatability, and accuracy with respect to CMM. The time is the duration of performing the measurement, the repeatability is the average of the standard deviation of all the targets, and the accuracy is the average of the magnitude error with respect to the CMM average positions. The results are shown in
Table 1, and as expected, the repeatability of CMM is the best. The repeatability obtained by CMM gives an indication of the reliability of the nest. Similarly, the repeatability of LT and photogrammetry has lower results, in that order. Thus, the portable photogrammetry is four times less precise than the LT, which provides theoretical values similar to the datasheet.
Table 1 shows the performance of each system, but not the influence on the final uncertainty. For this reason, the VDI/VDE 2634 part 1 was run three times and the photos were processed with the information of each reference target. These targets provide different extrinsic parameters and, accordingly, different results.
As
Figure 6 illustrates, the deviation of the MC with respect to CMM, when the reference points are measured by CMM, is between −0.031 mm and 0.026 mm.
Table 2 shows the results of using the different references. The best results are obtained using CMM, but with the same maximum LME as LT. In turn, when using PP, the results obtained show the difference, but the values (LME Maximum 0.049 mm) are acceptable because the aim is less than ±0.2 mm.
The main conclusion is that measurement uncertainty when using the PP and LT to measure the target reference is reflected in the measurement uncertainty of the MC, however, both technologies fulfill the aeronautic requirement of ±0.2 mm. Following this conclusion, for the industrial scenario, PP was the only system used to measure these points.
5.2. Results and Discussion: Industrial Scenario
A robotic cell was selected to test this technology in the most realistic environment. The main limitation is the space needed to place the camera on the enclosure walls, which are smaller than those in the laboratory (see
Figure 7a). Moreover, to obtain a relevant volume to track the end-effector of the robot, the camera heights were higher than in the CMM test.
Table 3 shows the main figures of this scenario.
As previously mentioned, the reference measuring system (ground truth) is a LT Leica AT402. It was placed in the entrance door out of the robotic cell due to a limitation of this LT reference to measure at a distance closer than 1 m (see
Figure 7b).
Figure 7c shows the measurement of the reference targets using PP.
Once the reference targets were measured, the end-effector of the robot was moved to the VDI/VDE 2634 part 1 positions inside the cube describe in
Figure 5. This guideline suggests measuring at least seven bars and five test lengths on each bar.
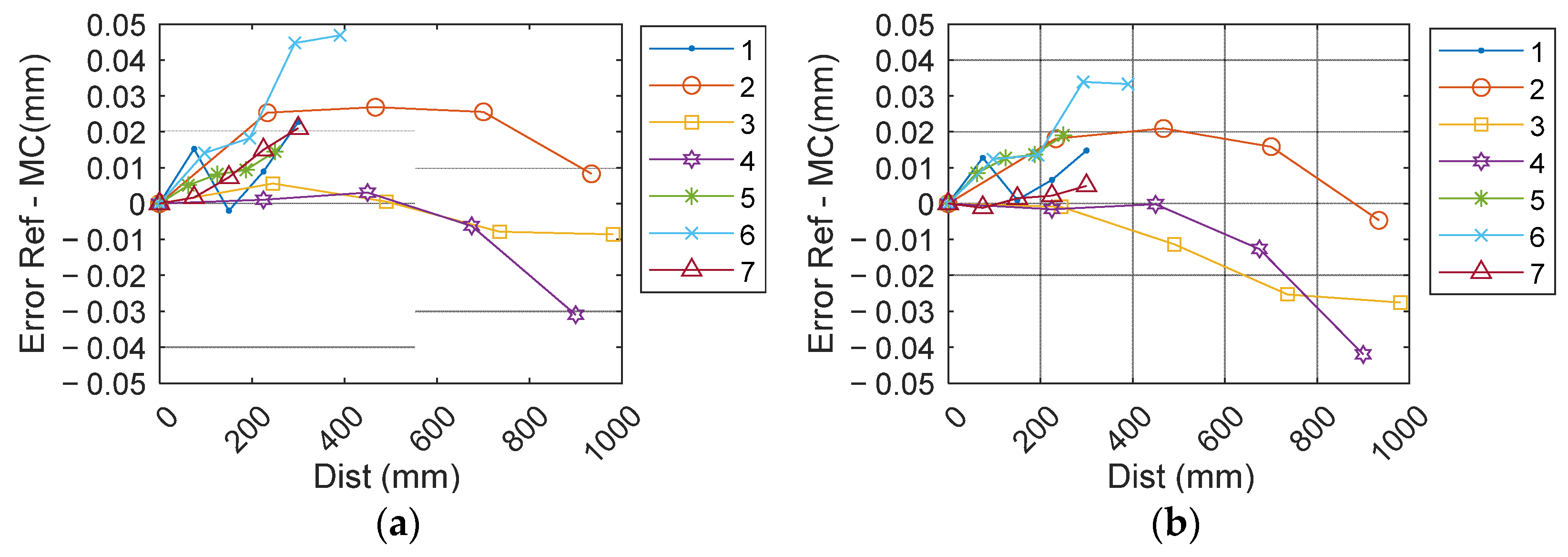
The trend in the deviation differs from the laboratory scenario. The authors consider that the differences in the tracked objects and the different layout of the reference may contribute to the modification of these trends. It was not possible to use the same object or to replicate the extrinsic reference. If the reference point had been measured by LT, the deviation could have been improved slightly.
The shape of the trends is noteworthy. In both cases, they are quite similar albeit with a different orientation (see
Figure 8). For example, the number 1 bar (colored in blue) has a higher deviation in case one. In contrast, the bar in the second case shows a similar trend but is reduced. This tilt with respect to the origin is also clear in bar numbers 2 (red), 3 (yellow), and 4 (purple). All have less value in the second test than the first, transferring to a negative position. The authors consider that the measurement uncertainty of the reference targets is this tilt effect. In both cases, the maximum–minimum error is around 0.075 mm. If it is necessary to reduce this, several factors can be modified. For example, the layout of the reference targets can be improved by creating a 3D structure with the targets, or a high number of cameras to provide a strong ray net.
5.3. Results and Discussion: Example of Use
To illustrate the advantages of the reliability and accuracy of the proposed solution, an example of use was run. For 3 days, the position of the end-effector during a warm-up cycle was recorded. At the same time, a thermal camera (FLIR SC5500) recorded the temperature of the robot, taking measurements of the joints as the most relevant data.
Figure 9 shows the early results.
Despite the information being insufficient to model the thermal behavior of this robot arm, the results demonstrate that MC allows us to study whether the warm-up cycle is modified. A slow warm-up will provide the option to study the transitory effects in X, and more warm-up movement of Y and Z will show more gradient in these axes. In conclusion, MC will allow us to study the thermal behavior of the robot.
6. Conclusions
This research explains how to measure the reference targets of a multi-camera system at large-scale volumes. Initially, a comparison was run in a laboratory scenario to check the performance of CMM, LT, and PP when measuring the reference targets. CMM was considered as ground truth, and the other two technologies as possible candidates to measure in large-scale volumes. Following the recommendation of the VDI VDE2634 part 1, the tracked object was moved to 35 positions in a volume where the MC could track the end-effector. The conclusion was that LT and PP allowed similar results to be obtained, and the positional uncertainty achieved the requirements for the robotic industry to branch into the aeronautic sector.
The second step was to replicate the test under industrial conditions. Following the conclusion of the laboratory test, LT took the role of ground truth and PP measured the reference targets. The MC was installed in a robotic cell. The positions of the camera were adapted to the narrow space due to the enclosure walls (see
Table 4) and the volume of work was increased thanks to the robot’s size. The value of LME raised due to the new conditions, less space, and greater volume.
Once the LME was measured, a first approach was run to determine the behavior of the robot during a warm-up cycle. Some parameters were modified to obtain reliable data to model the robot. For example, the X-axis (in the robot base) warms quite fast to record the transitory, while Y and Z axes have little effect during the warm-up cycle.
The following step was to carry out a test following the ISO 92831 to compare how much the multi-camera can improve the position uncertainty of the robot. Moreover, the warm-up cycle must be studied to model the robot’s behavior when it starts working from a cooled state.
To industrialize this solution, the targets on the end-effector must maintain their relative position to respect the robot end-effector. The same applies to the parts with respect to the reference points. If this assumption is broken, the accuracy of the system is compromised. So, during the design, the end-effector must be considered. Furthermore, the main limitation of designing a MC system is the number of cameras needed to maintain the cost-benefit ratio. Sometimes, there are external elements that block the vision of the end effort, and at this point, MC does not provide information. Therefore, an in-depth virtual study must be conducted to predict the influence of points of view on the accuracy.
Author Contributions
Conceptualization, P.P. and I.L.; methodology, P.P. and I.L.; software, I.L. and I.H.; validation, P.P. and I.L.; formal analysis, P.P. and I.L.; investigation P.P. and I.L.; writing—original draft preparation, P.P. and I.L.; writing—review and editing, P.P., I.L., I.H. and A.B.; supervision, A.B.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This project (Fibremach FTI 971442) has received funding from the European Union’s Horizon 2020 research and innovation programme (H2020-EU.3.–H2020-EU.2.1.). This project (DATA—Data Analytics, Tool efficiency and Automation for end-to-end aircraft life-cycle transformation N Expediente: IDI-20211064) has received funding from the Spanish CDTI PROGRAMA DUAL.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are thankful to our colleagues Alberto Mendikute, David Ruiz, and Jon Lopez de Zubiria who provided expertise that greatly assisted the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cvitanic, T.; Melkote, S.; Balakirsky, S. Improved State Estimation of a Robot End-Effector Using Laser Tracker and Inertial Sensor Fusion. CIRP J. Manuf. Sci. Technol. 2022, 38, 51–61. [Google Scholar] [CrossRef]
- Pfeifer, T.; Montavon, B.; Peterek, M.; Hughes, B. Artifact-Free Coordinate Registration of Heterogeneous Large-Scale Metrology Systems. CIRP Ann. 2019, 68, 503–506. [Google Scholar] [CrossRef]
- Robson, S.; MacDonald, L.; Kyle, S.; Boehm, J.; Shortis, M. Optimised Multi-Camera Systems for Dimensional Control in Factory Environments. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 1707–1718. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Q.; Yang, Z.; Jiang, Y.; Xu, J. A State-of-the-Art Review on Robotic Milling of Complex Parts with High Efficiency and Precision. Robot. Comput.-Integr. Manuf. 2023, 79, 102436. [Google Scholar] [CrossRef]
- Jian, S.; Yang, X.; Yuan, X.; Lou, Y.; Jiang, Y.; Chen, G.; Liang, G. On-Line Precision Calibration of Mobile Manipulators Based on the Multi-Level Measurement Strategy. IEEE Access 2021, 9, 17161–17173. [Google Scholar] [CrossRef]
- Trabasso, L.G.; Mosqueira, G.L. Light Automation for Aircraft Fuselage Assembly. Aeronaut. J. 2020, 124, 216–236. [Google Scholar] [CrossRef]
- Devlieg, R. High-Accuracy Robotic Drilling/Milling of 737 Inboard Flaps. SAE Int. J. Aerosp. 2011, 4, 1373–1379. [Google Scholar] [CrossRef]
- Kyle, S.; Robson, S.; Macdonald, L.; Shortis, M.; Boehm, J. Multi-Camera Systems for Dimensional Control in Factories; European Portable Metrology Conference-EPMC15: Manchester, UK, 2015. [Google Scholar]
- Balanji, H.M.; Turgut, A.E.; Tunc, L.T. A Novel Vision-Based Calibration Framework for Industrial Robotic Manipulators. Robot. Comput.-Integr. Manuf. 2022, 73, 102248. [Google Scholar] [CrossRef]
- Uhlmann, E.; Polte, J.; Mohnke, C. Constructive Compensation of the Thermal Behaviour for Industrial Robots. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1140, 012007. [Google Scholar] [CrossRef]
- Borrmann, C.; Wollnack, J. Enhanced Calibration of Robot Tool Centre Point Using Analytical Algorithm. Int. J. Mater. Sci. Eng. 2015, 3, 12–18. [Google Scholar] [CrossRef]
- Du, G.; Zhang, P. Online Robot Calibration Based on Vision Measurement. Robot. Comput.-Integr. Manuf. 2013, 29, 484–492. [Google Scholar] [CrossRef]
- Li, B.; Tian, W.; Zhang, C.; Hua, F.; Cui, G.; Li, Y. Positioning Error Compensation of an Industrial Robot Using Neural Networks and Experimental Study. Chin. J. Aeronaut. 2022, 35, 346–360. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. VDI/VDE. Optical 3D Measuring Systems, Imaging Systems with Point-by-Point Probing. In VDI/VDE 2634, Part 1; VDI/VDE: Düsseldorf, Germany, 2002. [Google Scholar]
- Schmitt, R.H.; Wolfschläger, D.; Masliankova, E.; Montavon, B. Metrologically Interpretable Feature Extraction for Industrial Machine Vision Using Generative Deep Learning. CIRP Ann. 2022, 71, 433–436. [Google Scholar] [CrossRef]
- Mattamala, M.; Ramezani, M.; Camurri, M.; Fallon, M. Learning Camera Performance Models for Active Multi-Camera Visual Teach and Repeat. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14346–14352. [Google Scholar]
- Hattori, S.; Akimoto, K.; Fraser, C.; Imoto, H. Automated Procedures with Coded Targets in Industrial Vision Metrology. Photogramm. Eng. Remote Sens. 2002, 68, 441–446. [Google Scholar]
- Zou, J.; Meng, L. Design of a New Coded Target With Large Coding Capacity for Close—Range Photogrammetry and Research on Recognition Algorithm. IEEE Access 2020, 8, 220285–220292. [Google Scholar] [CrossRef]
- El Ghazouali, S.; Vissiere, A.; Lafon, L.-F.; Mohamed Lamjed, B.; Nouira, H. Optimised Calibration of Machine Vision System for Close Range Photogrammetry Based on Machine Learning. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 7406–7418. [Google Scholar] [CrossRef]
- Chavdarova, T.; Baque, P.; Bouquet, S.; Maksai, A.; Jose, C.; Bagautdinov, T.; Lettry, L.; Fua, P.; Van Gool, L.; Fleuret, F. WILDTRACK: A Multi-Camera HD Dataset for Dense Unscripted Pedestrian Detection. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5030–5039. [Google Scholar]
- Hänel, M.L.; Schönlieb, C.-B. Efficient Global Optimization of Non-Differentiable, Symmetric Objectives for Multi Camera Placement. IEEE Sens. J. 2021, 22, 5278–5287. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, W.; Zhang, Y.; Xing, H.; Li, J.; Liu, S.; Zhang, L. An Accurate Calibration Method of Large-Scale Reference System. IEEE Trans. Instrum. Meas. 2020, 69, 6957–6967. [Google Scholar] [CrossRef]
- Icasio-Hernández, O.; Bellelli, D.A.; Brum Vieira, L.H.; Cano, D.; Muralikrishnan, B. Validation of the Network Method for Evaluating Uncertainty and Improvement of Geometry Error Parameters of a Laser Tracker. Precis. Eng. 2021, 72, 664–679. [Google Scholar] [CrossRef]
- Kang, H.; Seo, Y.; Park, Y. Geometric Calibration of a Camera and a Turntable System Using Two Views. Appl. Opt. 2019, 58, 7443. [Google Scholar] [CrossRef]
- Fu, B.; Han, F.; Wang, Y.; Jiao, Y.; Ding, X.; Tan, Q.; Chen, L.; Wang, M.; Xiong, R. High-Precision Multicamera-Assisted Camera-IMU Calibration: Theory and Method. IEEE Trans. Instrum. Meas. 2021, 70, 1004117. [Google Scholar] [CrossRef]
- Inkulu, A.K.; Bahubalendruni, M.V.A.R.; Dara, A.; SankaranarayanaSamy, K. Challenges and Opportunities in Human Robot Collaboration Context of Industry 4.0—A State of the Art Review. Ind. Robot. Int. J. Robot. Res. Appl. 2021, 49, 226–239. [Google Scholar] [CrossRef]
- Mendikute, A.; Leizea, I.; Yagüe-Fabra, J.A.; Zatarain, M. Self-Calibration Technique for on-Machine Spindle-Mounted Vision Systems. Measurement 2018, 113, 71–81. [Google Scholar] [CrossRef]
- Mendikute, A.; Zatarain, M. Automated Raw Part Alignment by a Novel Machine Vision Approach. Procedia Eng. 2013, 63, 812–820. [Google Scholar] [CrossRef]
- Puerto, P.; Heißelmann, D.; Müller, S.; Mendikute, A. Methodology to Evaluate the Performance of Portable Photogrammetry for Large-Volume Metrology. Metrology 2022, 2, 320–334. [Google Scholar] [CrossRef]
Figure 1.
This picture shows three of the four cameras of the multi-camera. This was set up in the laboratory during the measurement of the extrinsic targets using portable photogrammetry.
Figure 1.
This picture shows three of the four cameras of the multi-camera. This was set up in the laboratory during the measurement of the extrinsic targets using portable photogrammetry.
Figure 2.
Nest for transferring measurements between CMM, PP, and LT. (a) Nest. (b) Sphere measurement process used to obtain the extrinsic reference by CMM. (c) Spheri-cally mounted retroreflector (SMR) used to measure LT. (d) A retroreflective target in the hemisphere.
Figure 2.
Nest for transferring measurements between CMM, PP, and LT. (a) Nest. (b) Sphere measurement process used to obtain the extrinsic reference by CMM. (c) Spheri-cally mounted retroreflector (SMR) used to measure LT. (d) A retroreflective target in the hemisphere.
Figure 3.
Tracked object: (a) Used in the CMM scenario with a KUKA Iiwa robot and (b) used in the industrial scenario with a Stäubli TX200 robot.
Figure 3.
Tracked object: (a) Used in the CMM scenario with a KUKA Iiwa robot and (b) used in the industrial scenario with a Stäubli TX200 robot.
Figure 4.
Multi-camera solving process: (a) Coded and non-coded targets. (b) In red, the roto-translation from MC to Tracked object. The green arrow shows the roto-translation from reference targets to MC, and the aim of this process is in blue; the roto-translation from reference targets to tracked object.
Figure 4.
Multi-camera solving process: (a) Coded and non-coded targets. (b) In red, the roto-translation from MC to Tracked object. The green arrow shows the roto-translation from reference targets to MC, and the aim of this process is in blue; the roto-translation from reference targets to tracked object.
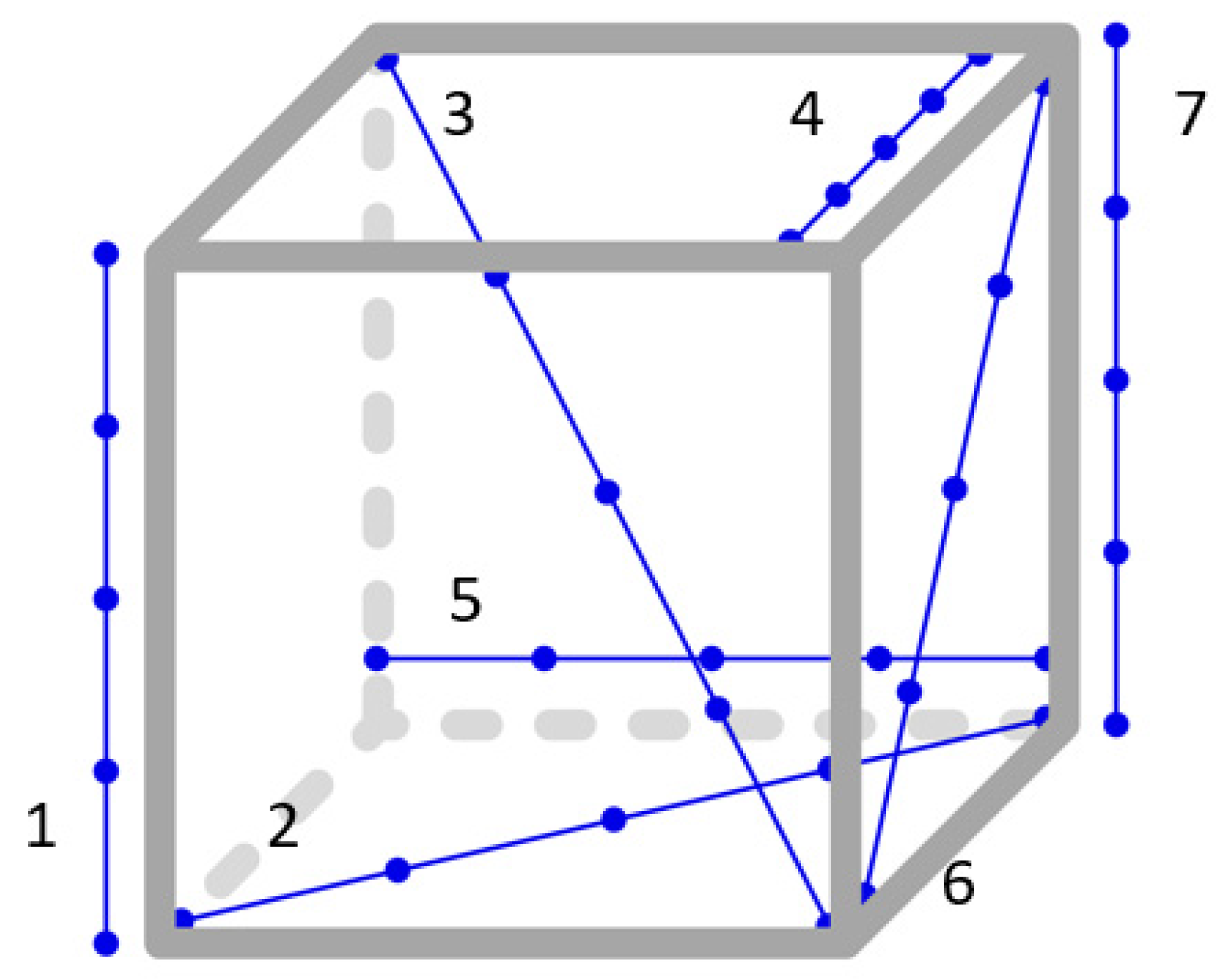
Figure 5.
Layout of the 7 bars in cubic volume (image adapted from VDI/VDE 2634 part 1).The blue line are the bars and the dots are the points where is measured.
Figure 5.
Layout of the 7 bars in cubic volume (image adapted from VDI/VDE 2634 part 1).The blue line are the bars and the dots are the points where is measured.
Figure 6.
Difference between the value measured by CMM and by MC. Numbers 1 to 7 are the bar with respect to
Figure 5.
Figure 6.
Difference between the value measured by CMM and by MC. Numbers 1 to 7 are the bar with respect to
Figure 5.
Figure 7.
Pictures of the industrial test scenario: (a) general view, layout of the cameras, (b) LT Leica AT402 is measuring the SMR, and (c) portable photogrammetry system measuring the reference target.
Figure 7.
Pictures of the industrial test scenario: (a) general view, layout of the cameras, (b) LT Leica AT402 is measuring the SMR, and (c) portable photogrammetry system measuring the reference target.
Figure 8.
Results used to measure the deviation of the MC with respect to LT following VDI-VDe 2634 part 1. (a) first measurement (LME 0.047 mm), and (b) second measurement (LME 0.041 mm).
Figure 8.
Results used to measure the deviation of the MC with respect to LT following VDI-VDe 2634 part 1. (a) first measurement (LME 0.047 mm), and (b) second measurement (LME 0.041 mm).
Figure 9.
Results of a warm-up cycle of three days. (a) Position recorded by the MC (X, Y horizontal and Z Vertical), (b) an example image of Stäubli RX 600 using the thermal camera, and (c) comparison, at the same time (h), of the temperature of the part between joints 3 and 4 (red line) and position X, horizontal direction, in the blue line.
Figure 9.
Results of a warm-up cycle of three days. (a) Position recorded by the MC (X, Y horizontal and Z Vertical), (b) an example image of Stäubli RX 600 using the thermal camera, and (c) comparison, at the same time (h), of the temperature of the part between joints 3 and 4 (red line) and position X, horizontal direction, in the blue line.
Table 1.
Repeatability and accuracy of the CMM, LT, and PP measuring the reference targets.
Table 1.
Repeatability and accuracy of the CMM, LT, and PP measuring the reference targets.
| k = 1 XYZ (mm) | CMM | LT | PP |
|---|
| Time (min) | 15 | 12 | 16 |
| Repeatability | 0.0004 | 0.007 | 0.031 |
| Accuracy with respect to CMM | - | 0.010 | 0.043 |
Table 2.
Results of VDI/VDE 2634 part 1 using different extrinsic reference.
Table 2.
Results of VDI/VDE 2634 part 1 using different extrinsic reference.
| (µm) | Extrinsic Reference Measurement |
|---|
| CMM | LT | PP |
|---|
| LME Maximum | 31 | 31 | 49 |
| LME Average | 1 | 3 | 9 |
| LME standard deviation k = 1 | 10 | 11 | 16 |
Table 3.
Dimensions of industrial scenario: Position of the cameras and volume work. * All cameras are at the same height, 1500 mm from the table.
Table 3.
Dimensions of industrial scenario: Position of the cameras and volume work. * All cameras are at the same height, 1500 mm from the table.
| (mm) | Camera Position | Volume Work |
|---|
| Industrial scenario | X | 2000 | 900 |
| Y | 2100 | 300 |
| Z | 1500 * | 200 |
Table 4.
Summary of the results from the two scenarios.
Table 4.
Summary of the results from the two scenarios.
| (mm) | Camera Position | Volume Work of the Robot | Average LME |
|---|
| Laboratory using industrial tool (photogrammetry) | X 2500 | X 455 | 0.031 mm |
| Y 2400 | Y 376 |
| Z 750 * | Z 454 |
| Industrial | X 2000 | X 900 | 0.045 mm |
| Y 2100 | Y 300 |
| Z 1500 * | Z 200 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).